スポンサードリンク
スポンサードリンク
1. 信号処理で使う複素数の計算
(1) 複素数の大きさ(絶対値)・偏角・オイラーの公式
オイラーの公式は、次の2つのバージョンを覚えておきましょう。\[\begin{align*}
e^{i \theta} & = \cos \theta + i \sin \theta \\
e^{- i \theta} & = \cos \theta - i \sin \theta
\end{align*}\]
※ \( - i \theta \) バージョンも覚えておくと、計算がラクになります！
(2) 複素数の組み合わせによる演算
特に計算例でも挙げている (実数)÷(複素数) 型の公式は、知っているのと知っていないのでは計算時間に大きく差が出るので、是非使いこなせるようになりましょう！
スポンサードリンク
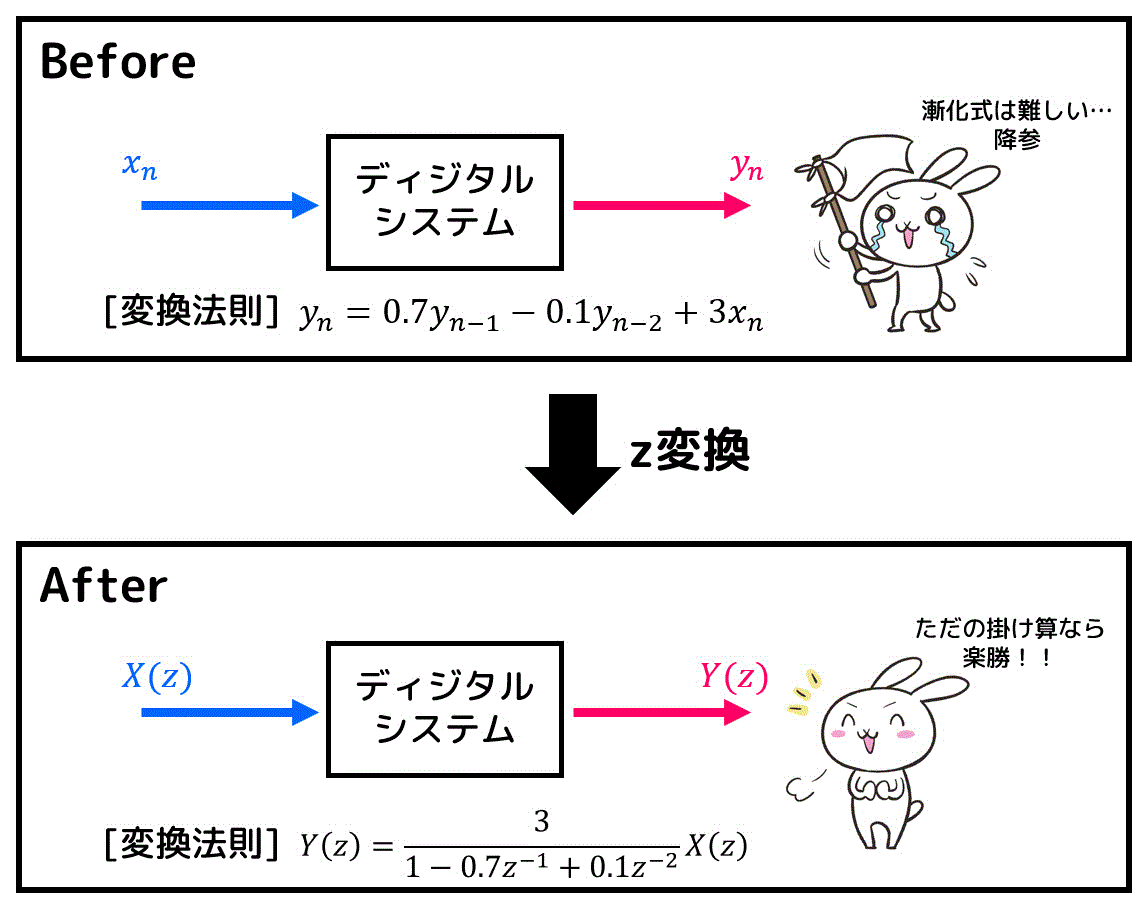
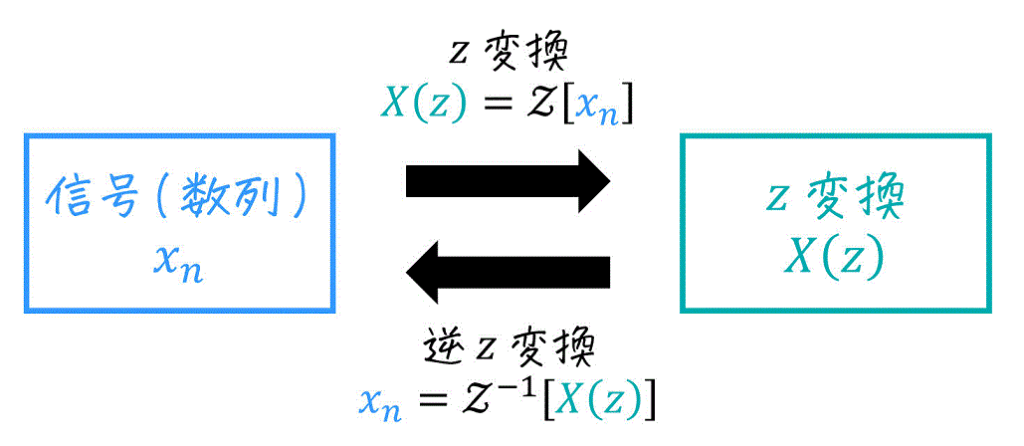
2. z変換・逆z変換関連
※ 数列（ディジタル信号）\( x_n \) のことを \( x(n) \) や \( x[n] \) と表現することもあります。どの表現を使っているかはお使いの参考書や受講している講義を確認してください。
(1) 定義式
(i) z変換
期末試験では、定義式から \( z \) 変換を計算することはありませんが、\( z \) 変換の定義式を確認しましょう。
\[
\mathcal{Z} [ x_n ] = X (z) = \sum^{\infty}_{n = 0} x_n z^{-n}
\]
[変数の意味]
\( x_n \) … 数列（ディジタル信号）
\( X(z) \) … \( x_n \) の \( z \) 変換
(ii) 逆z変換
元の数列 \( x_n \) とそのz変換 \( X(z) \) は1対1対応しているので、\( z \) 変換された式を逆にたどることで逆z変換ができます。
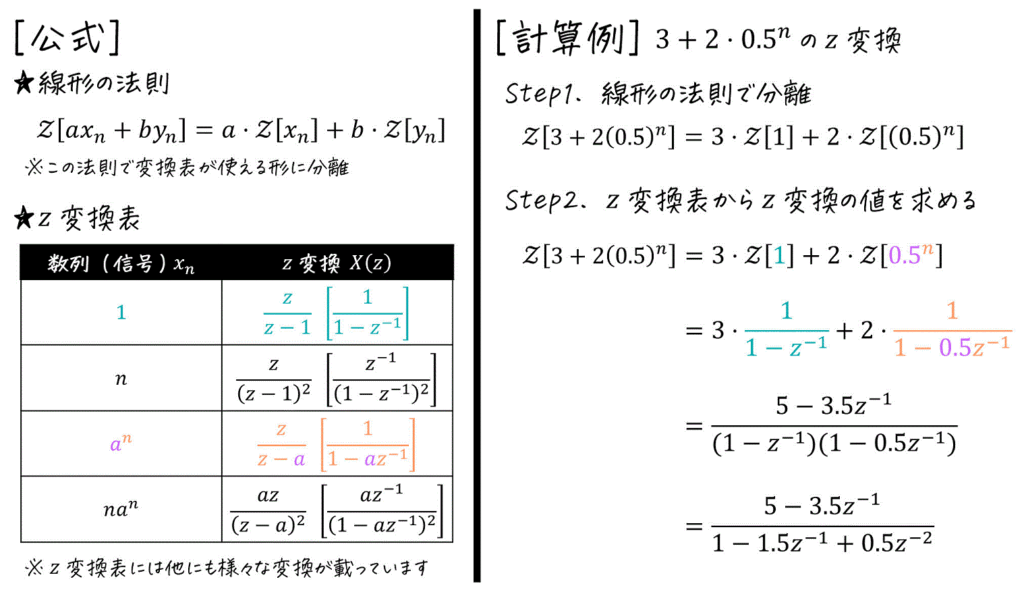
(2) z変換表を用いたz変換の計算
実際に試験で \( z \) 変換を計算する際には、数列とその \( z \) 変換が記載された \( z \) 変換表を読み取りながら計算をします。
（z変換表はこちらからダウンロード可能です！）
線形の法則もよく出てくるのでこちらも頭にいれておきましょう[1]とはいっても、積分の分解公式\[\int f(x) + g (x) \ dx = \int f(x) \ dx + \int g(x) \ … Continue reading。
(3) z変換表を用いた逆z変換の計算
逆z変換も、z変換のときと同様に「z変換表」を使って計算します。
（z変換表はこちらからダウンロード可能です！）
こちらも、線形の法則を使うので頭に入れておきましょう。
\( z \) 変換、逆 \( z \) 変換の練習をもっとしたい人は、こちらの記事で可能です！
(4) 逆z変換と部分分数分解
逆z変換をする際には、ほぼ100%部分分数分解を使います。
★Step1. 分母を因数分解する\[
\frac{5}{1 - 0.24 z^{-1} - 0.2 z^{-2} } = \frac{5}{(1-0.6 z^{-1})(1 + 0.4 z^{-1})}
\]
★Step2. 分解の形をつくる\[
\frac{5}{(\textcolor{magenta}{1-0.6 z^{-1}})(\textcolor{deepskyblue}{1 + 0.4 z^{-1}}) } = \frac{a}{\textcolor{magenta}{1 - 0.6 z^{-1}}} + \frac{b}{\textcolor{deepskyblue}{1 + 0.4z^{-1}}}
\]
★Step5. あとは代入するだけ！\[
\frac{5}{(1-0.6 z^{-1})(1 + 0.4 z^{-1})} = \frac{3}{ 1 - 0.6 z^{-1} } + \frac{2}{ 1 + 0.4 z^{-1} }
\]
※ 教科書には留数定理を使うなど難しいことを書いていますが、そんな知識は一切不要です。
信号処理の単位を取るための必須計算なので、覚えておきましょう。
(5) z変換のシフト公式
[因果系システム[2]後ろで改めて説明しますが、\( x_{-1} \), \( x_{-2} \), … のように信号（数列）のマイナス項目 \( x_{-k} \) … Continue readingの場合]（試験に出るのは99%こっち！）
\[
\begin{align*}
\mathcal{Z}[x_{n-1}] & = z^{-1} X(z) \\
\mathcal{Z}[x_{n-2}] & = z^{-2} X(z) \\
\mathcal{Z}[x_{n-3}] & = z^{-3} X(z) \\
\mathcal{Z}[x_{n-k}] & = z^{-k} X(z)
\end{align*}
\]
[因果系システムではない場合]（覚えなくていいです）
\[
\begin{align*}
\mathcal{Z}[x_{n-1}] & = z^{-1} X(z) + x_{-1} \\
\mathcal{Z}[x_{n-2}] & = z^{-2} X(z) + x_{-1} z^{-1} + x_{-2} \\
\mathcal{Z}[x_{n-3}] & = z^{-3} X(z) + x_{-1} z^{-2} + x_{-2} z^{-1} + x_{-3} \\
\mathcal{Z}[x_{n-k}] & = z^{-k} X(z) + x_{-1} z^{-(k-1)} + x_{-2} z^{-(k-2)} + \cdots + x_{-k}
\end{align*}
\]
※ 因果系システムの信号は、\( x_{-k} \)（マイナス項目）がすべて0なので、シフト公式を単純化できる。
(6) 初期値定理と最終値定理
\( X(z) \) の逆 \( z \) 変換を計算することなく \( x_0 \) と \( x_{\infty} \) を計算できるので、結構使える公式です。
※ 例に出した \( X(z) \) を逆z変換すると \( x_n = 3 + 2 \cdot 0.5^n \) となります[3]実際に \( n = 0 \) を代入すると、\( x_0 = 3 + 2 \cdot 0.5^0 = 5 \)、\( n \to \infty \) とすると、\( x_n = 3 \) … Continue reading。
ここまでの \( z \) 変換の内容をさらに確認したい人は、こちらの記事をご確認ください！
スポンサードリンク
3. ディジタルシステム関連
※ ディジタルシステムは、\( x_{-1} \), \( x_{-2} \), … のような「信号のマイナス項目」がすべて0のシステムである因果的システムであるとします。なお、期末試験の場合、基本的に出題されるディジタルシステムは因果的システムなのであまり気にしなくてOKです。
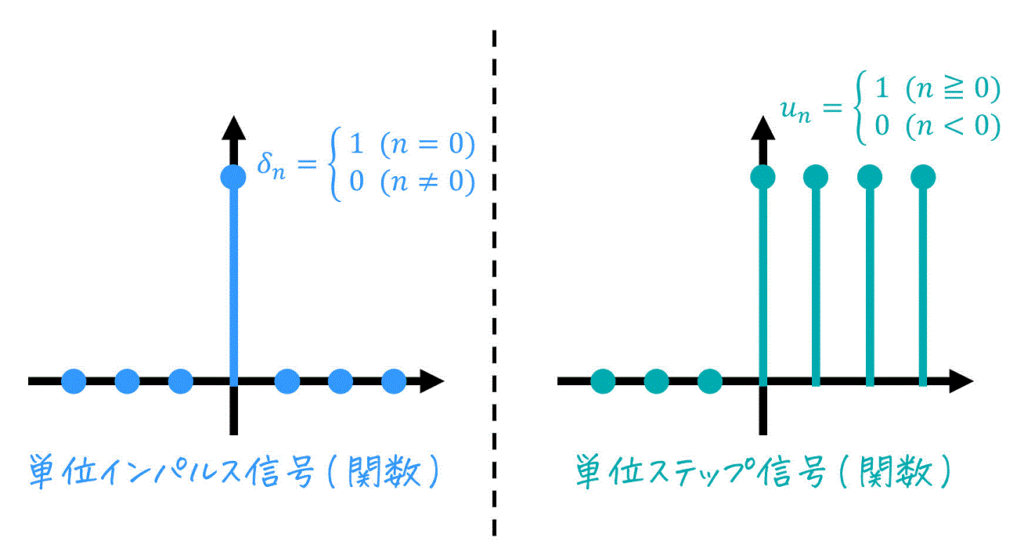
(1) 単位インパルス信号と単位ステップ信号
(2) 伝達関数
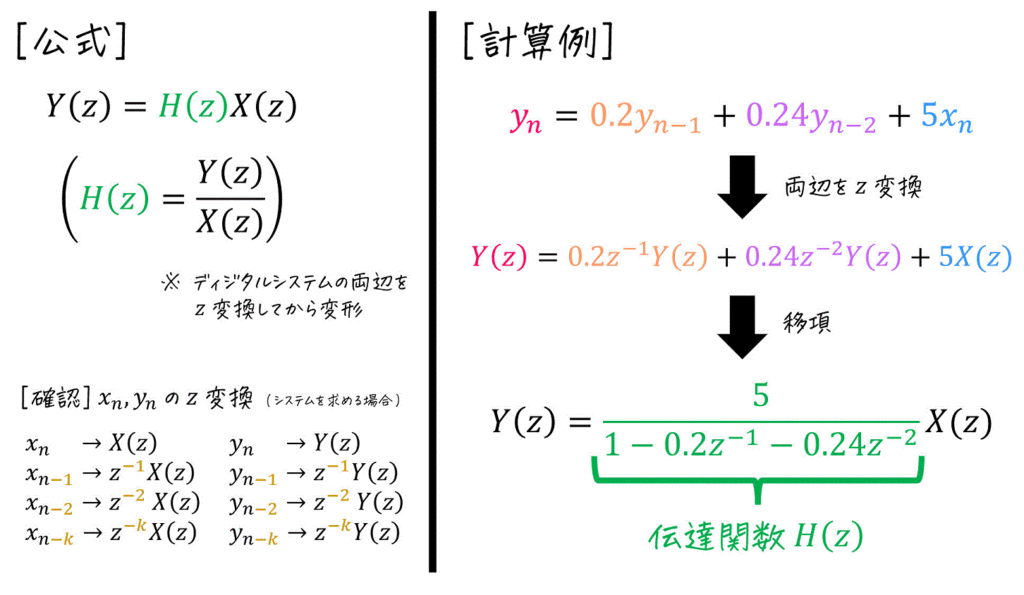
(3) インパルス応答
※ \( n < 0 \) のときのインパルス応答の値は0です。なお、\( n \geqq 0 \) と記述する代わりにインパルス応答を使って\[
h_n = \left( 3 \cdot 0.6^n + 2 \cdot (-0.4)^n \right) u_n
\]のように表してもOKです。
(4) ステップ応答
2種類求め方がありますが、特にこだわりの無い限り「(i) インパルス応答から計算」を推奨します。（(ii)の伝達関数から求めると部分分数分解に時間がかかるので…）
(i) インパルス応答から計算 [推奨]
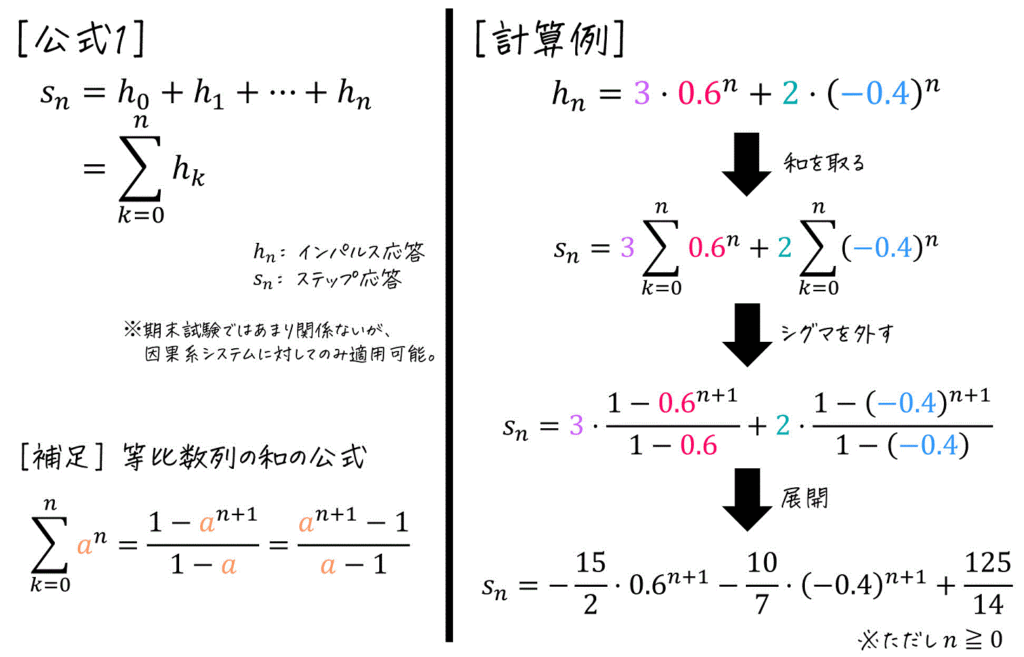
※ インパルス応答から計算をしているため、インパルス応答を間違えてしまうと、ステップ応答も自動的に間違えてしまいます。なのでインパルス応答は慎重に計算しましょう。
※ \( n < 0 \) のときのステップ応答の値は0です。なお、\( n \geqq 0 \) と記述する代わりにステップ応答を使って\[
s_n = \left( - \frac{15}{2} \cdot 0.6^{n+1} - \frac{10}{7} (-0.4)^{n+1} + \frac{125}{14} \right) u_n
\]のように表してもOKです。
(ii) 伝達関数から計算
※ \( n < 0 \) のときのステップ応答の値は0です。なお、\( n \geqq 0 \) と記述する代わりにステップ応答を使って\[
s_n = \left( - \frac{9}{2} \cdot 0.6^{n} + \frac{4}{7} (-0.4)^{n} + \frac{125}{14} \right) u_n
\]のように表してもOKです。
(5) 任意の入力に対する出力の計算
インパルス応答 \( h_n \) を求めることで、入力信号 \( x_n \) をたたみこみ演算を用いて求めることができます。
※ \( n < 0 \) のときの \( y_n \) の値は0です。なお、\( n \geqq 0 \) と記述する代わりにステップ応答を使って\[
y_n = \left( - 9 \cdot 0.6^n + 19 \cdot (-0.4)^n \right) u_n
\]のように表してもOKです。
ディジタルシステムの基礎「項目(1)〜(5)」についてさらに復習したい方は、下の記事をご覧ください。
(6) 零点と極
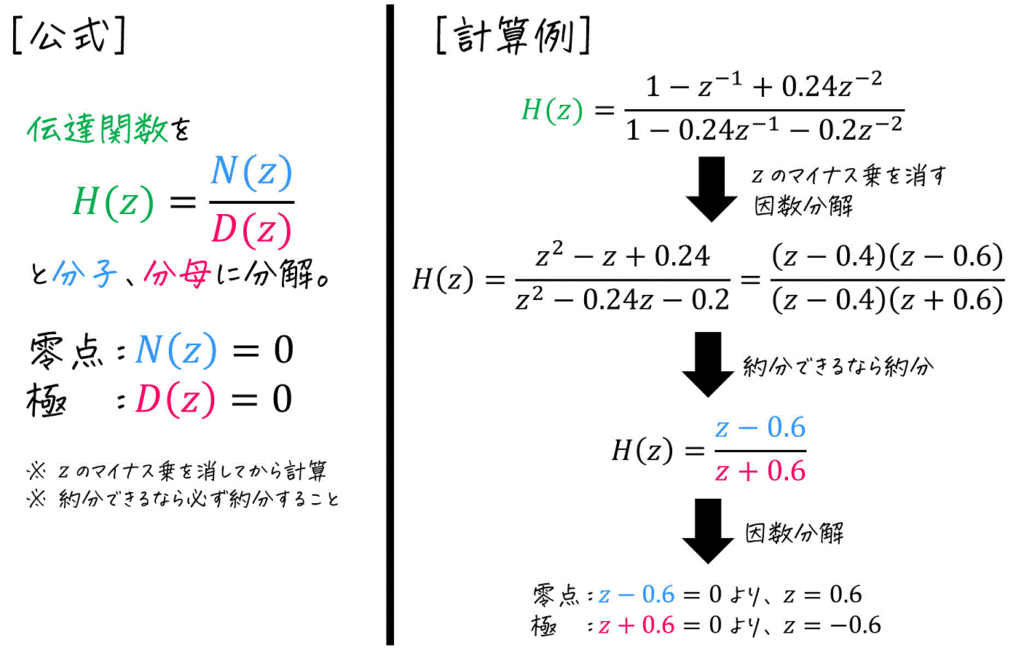
※ 最初に \( z \) のマイナス乗を消すのは、\( z = 0 \) となる極や零点を見逃さないため
(7) システムの安定性
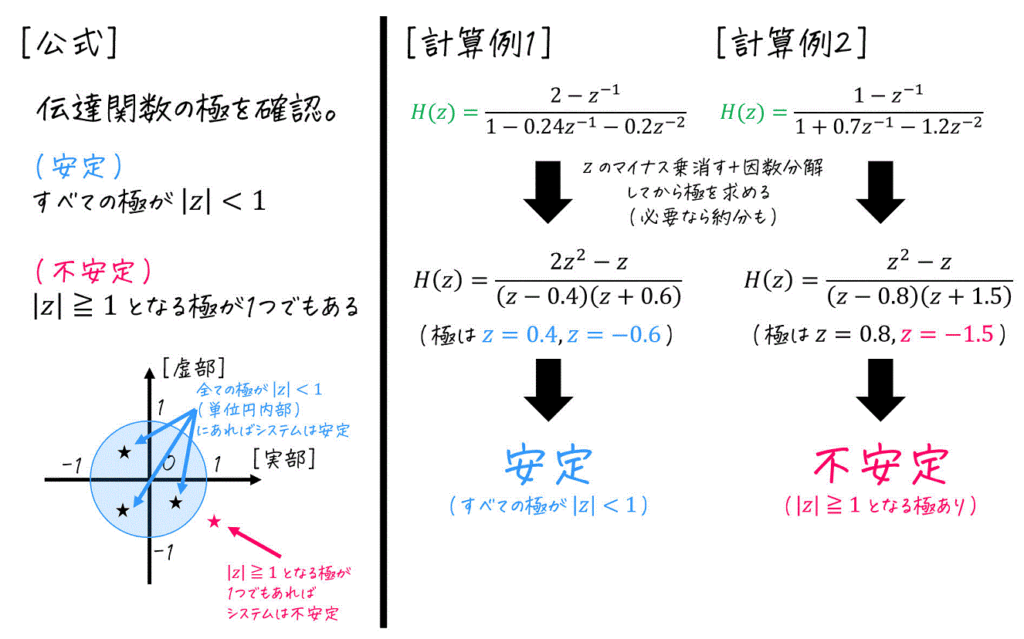
「(6)零点と極」、「(7)システムの安定性」についてさらに復習したい方は、下の記事をご覧ください。
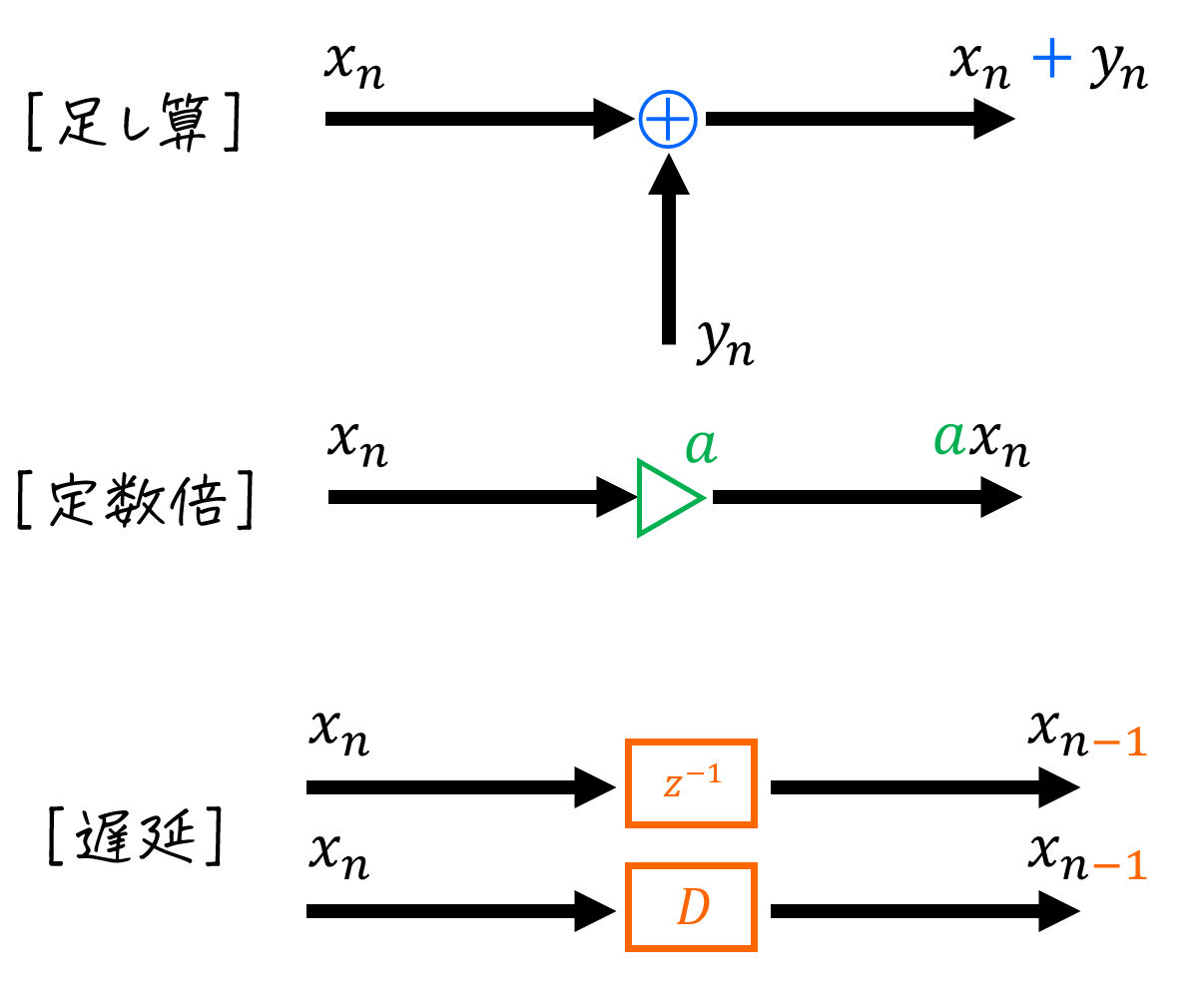
(8)ブロック図についてさらに復習したい方は、下の記事をご覧ください。
(8) ブロック図の読み書き
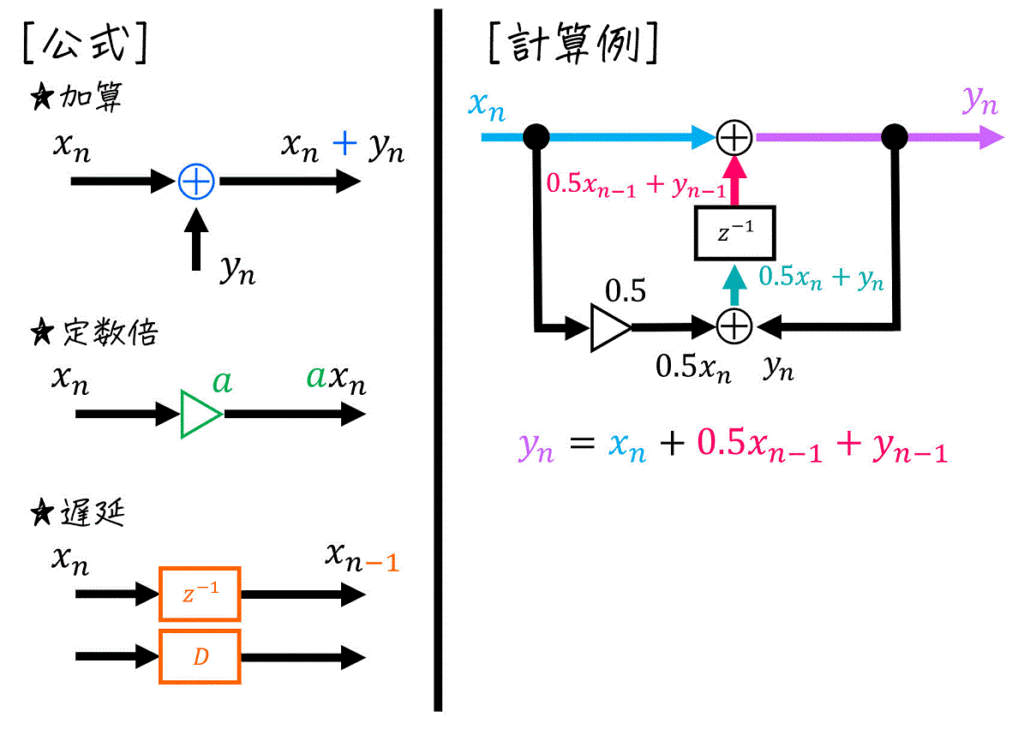
「(8)ブロック図」についてさらに復習したい方は、下の記事をご覧ください。
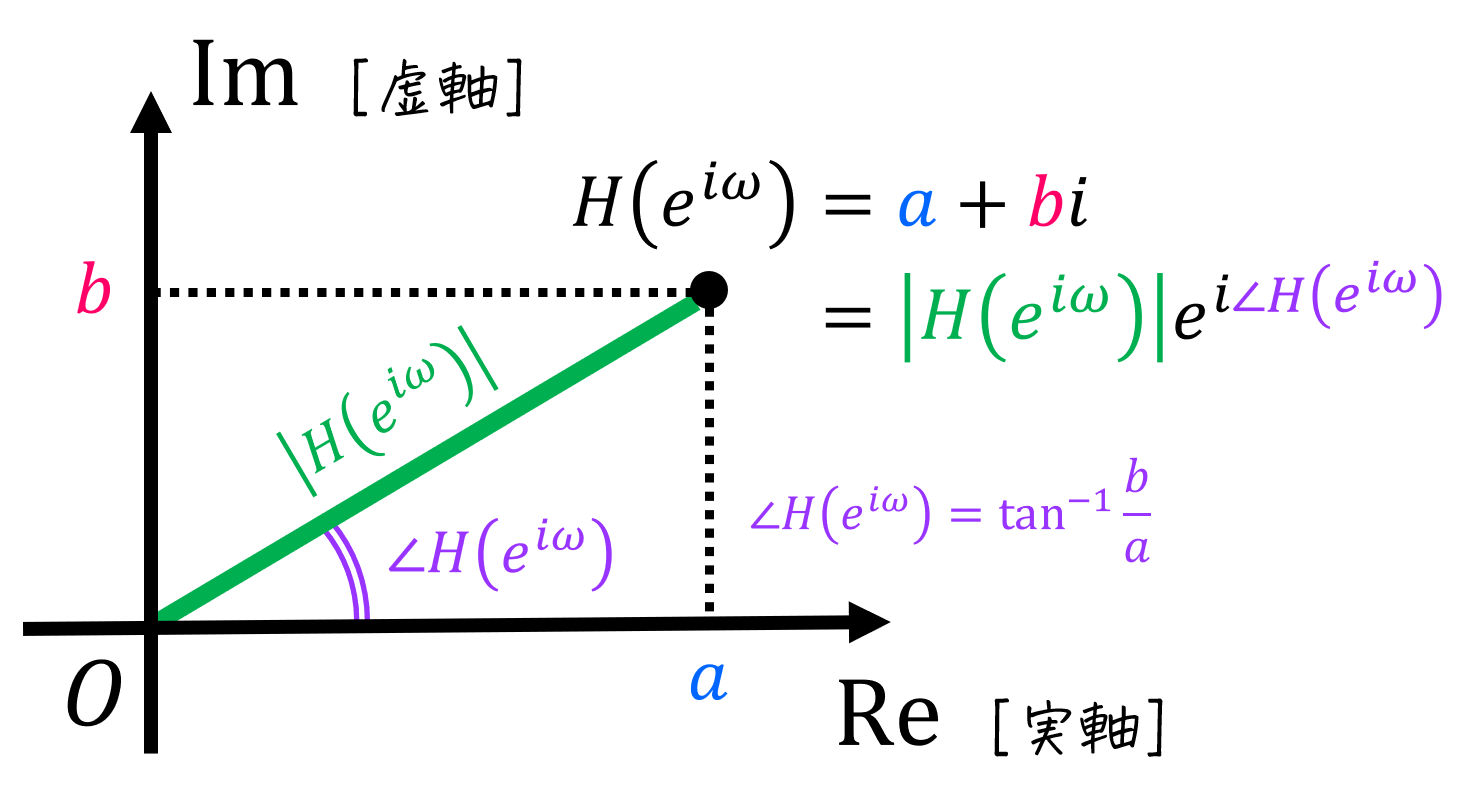
(9) 周波数応答の計算
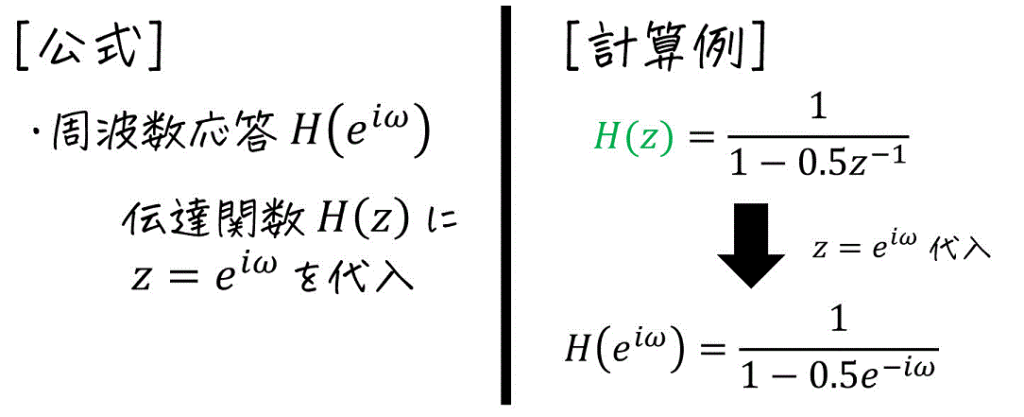
(10) 振幅特性・位相特性の計算
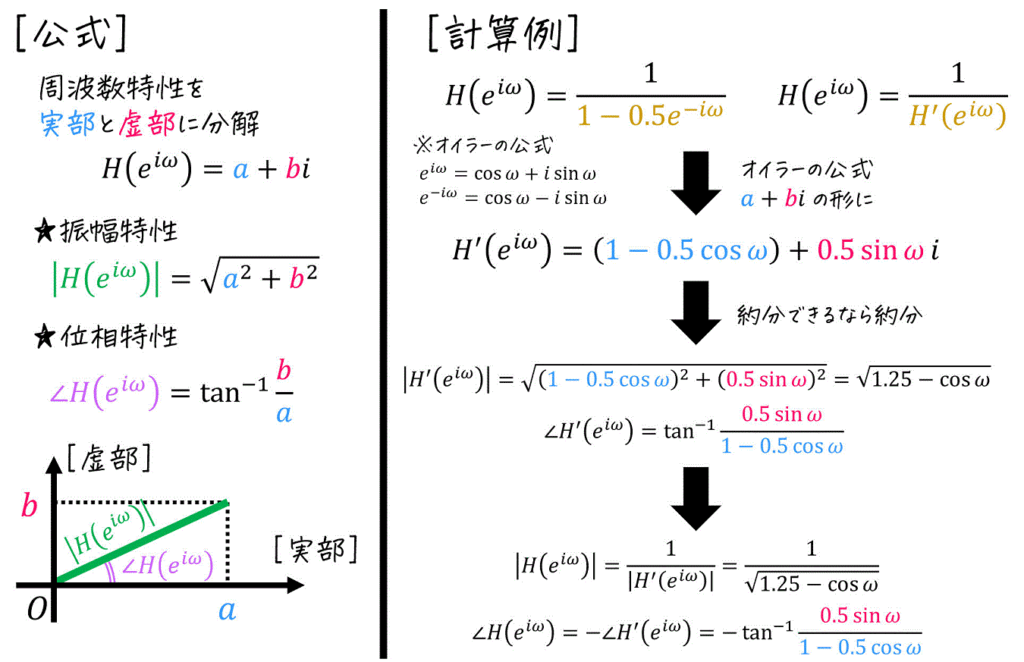
「(9)周波数特性」、および「(10)振幅特性・位相特性」についてさらに復習したい方は、下の記事をご覧ください。
(11) FIRフィルタ・IIRフィルタ
FIRフィルタ：出力 \( y_n \) を過去の出力 \( \textcolor{magenta}{y_{n-1}} \), \( \textcolor{magenta}{y_{n-2}} \), … を使わずに表現できるようなフィルタ。(FIR → Finite Impulse Response)
[例]\[y_n = \frac{1}{2} x_n + \frac{1}{4} x_{n-1} + \frac{1}{7} x_{n-2}
\] [特徴]
- インパルス応答 \( h_n \) が有限
- 必ず安定なシステムとなる
- コンピュータ上での計算時間がかかる
IIRフィルタ：出力 \( y_n \) が過去の出力 \( \textcolor{magenta}{y_{n-1}} \), \( \textcolor{magenta}{y_{n-2}} \), … を用いて表現されるフィルタ。(IIR → Infinite Impulse Response)
[例]\[y_n = \frac{1}{5} \textcolor{magenta}{y_{n-1}} + \frac{1}{2} \textcolor{magenta}{y_{n-2}} + x_{n}
\] [特徴]
- インパルス応答 \( h_n \) が無限
（収束はするが有限の \( n \) では \( h_n = 0 \) にはならない） - 不安定なシステムになることもある
- コンピュータ上での計算時間が少なめ
4. フーリエ関連
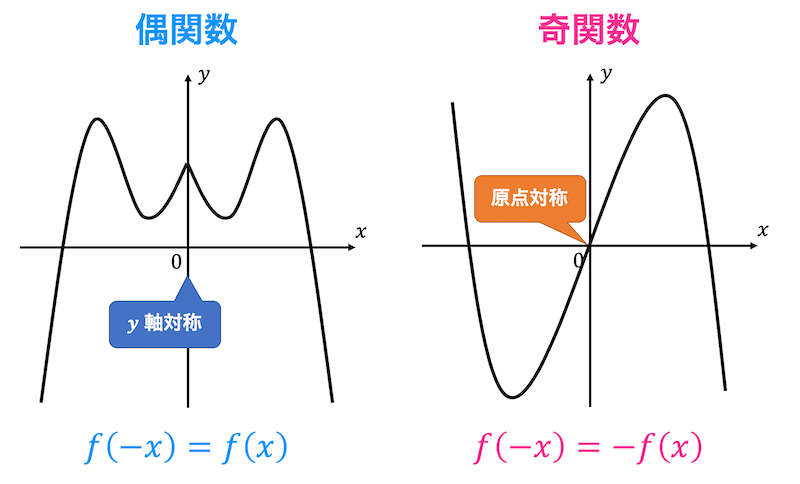
[基礎知識] 偶関数と奇関数
フーリエ関連の計算では、偶関数か奇関数であることを利用して行う計算が多くあるので、偶関数と奇関数について少し復習をしましょう。
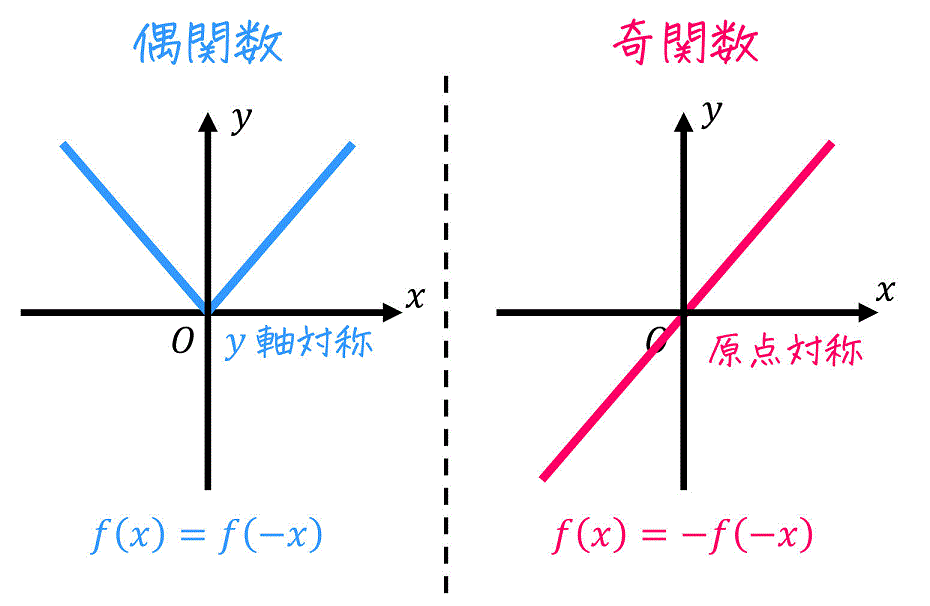
偶関数の例: \( x^2 \), \( x^4 \), …, \( x^{2n} \), \( \cos x \)
奇関数の例: \( x \), \( x^3 \), …, \( x^{2n+1} \), \( \sin x \), \( \tan x \)
(偶関数) × (偶関数) ＝ (偶関数)
(偶関数) × (奇関数) ＝ (偶関数)
(奇関数) × (奇関数) ＝ (偶関数)
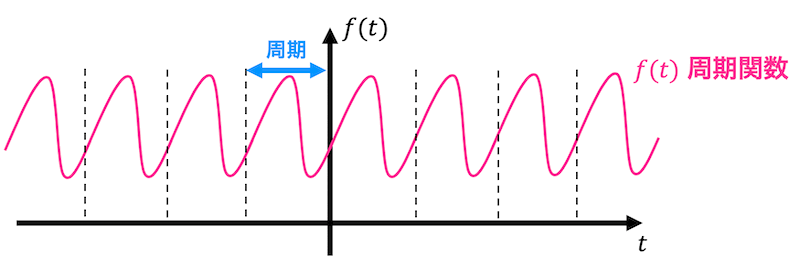
(1) フーリエ級数展開
f(t) = \frac{a_0}{2} + \sum^{\infty}_{k = 1} (a_k \cos k \omega t + b_k \sin k \omega t )
\] [\( a_k \), \( b_k \) の計算]
\[\begin{align*}
a_k & = \frac{2}{T} \int^{T}_{0} f(t) \cos k \omega t \ dt \ \ (k = 0, 1, 2, \cdots ) \\
b_k & = \frac{2}{T} \int^{T}_{0} f(t) \sin k \omega t \ dt \ \ (k = 0, 1, 2, \cdots )
\end{align*}\]
[\( \omega \) の計算]\[
\omega = \frac{ 2 \pi }{T}
\]
※1 [公式] の部分で、\( f(t) = \) の \( = \) を \( \sim \) と表記することもあり。
※2 積分範囲は1周期であればどこでもOK。例えば、\( - T/2 \leqq t \leqq T/2 \) としてもOK。
※3 \( f(t) \) が偶関数のときは \( b_k = 0 \)、\( f(t) \) が奇関数のときは \( a_k = 0 \) となる。
「フーリエ級数展開」について復習したい人、および計算例を確認したい人は下の記事をご覧ください。
（計算記述量が多いため、総まとめ内には計算例を用意していません。）
(2) 複素フーリエ級数展開
f(t) = \sum^{\infty}_{k = - \infty} c_k e^{i k \omega t}
\] [\( c_k \), \( \omega \) の計算]\[
c_k = \frac{1}{T} \int^{T}_{0} f(t) e^{-i k \omega t} \ dt, \ \ \ \omega = \frac{ 2 \pi }{T}
\]
「複素フーリエ級数展開」について復習したい人、および計算例を確認したい人は下の記事をご覧ください。
（計算記述量が多いため、総まとめ内には計算例を用意していません。）
(3) フーリエ変換 [重要！]
\( f(t) \) が偶関数もしくは奇関数のときは、フーリエ変換 \( F ( \omega ) \) を次の方法で計算することもできる。
(1) \( f(t) \) が偶関数のとき（フーリエ余弦変換）\[
F( \omega ) = 2 \int^{\infty}_{0} f(t) \cos \omega t \ dt
\]
(2) \( f(t) \) が奇関数のとき（フーリエ正弦変換）\[
F( \omega ) = -2i \int^{\infty}_{0} f(t) \sin \omega t \ dt
\]
「フーリエ変換」についてさらに復習したい人は下の記事をご覧ください。
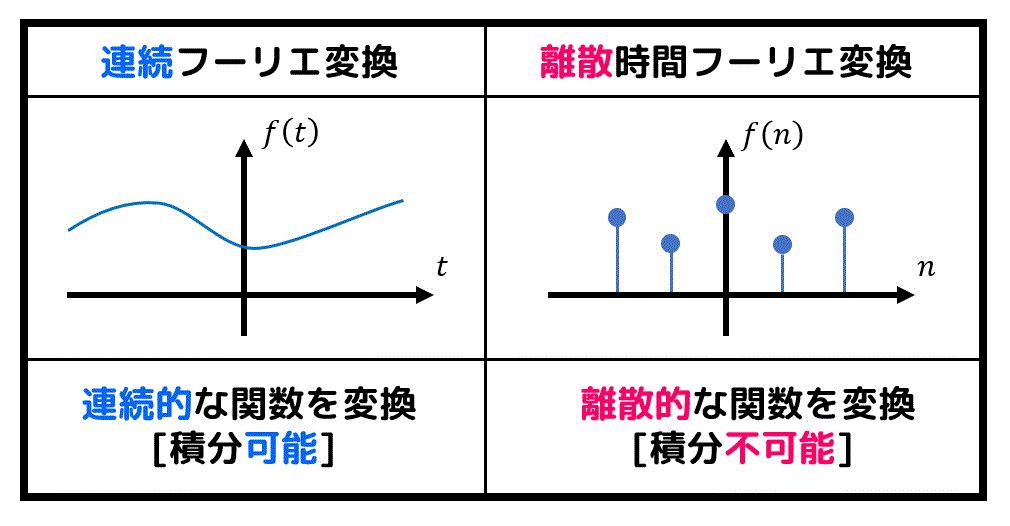
(4) 離散時間フーリエ変換
他のフーリエ変換に比べて、テストへの出題頻度はそこまで高くないので、時間がない人は他のフーリエ系の復習をしましょう。
F( e^{i \omega t} ) = \sum^{\infty}_{n = - \infty} f(n) e^{- i \omega n}
\] [離散時間フーリエ逆変換]\[
\begin{align*}
f(n) & = \frac{1}{2 \pi} \int^{\pi}_{- \pi} F ( e^{i \omega} ) e^{i \omega n} \ d \omega
\\ & = \frac{1}{2 \pi} \int^{2 \pi}_{0} F ( e^{i \omega} ) e^{i \omega n} \ d \omega
\end{align*}
\]\( \omega \) の周期は1周期分であれば \( 0 \leqq \omega \leqq 2 \pi \) や \( - \pi \leqq \omega \leqq \pi \) に限らずどこでもOK。
「離散時間フーリエ変換」について復習したい人、および計算例を確認したい人は下の記事をご覧ください。
（試験の出題頻度が高くないため、総まとめ内には計算例を用意していません。）
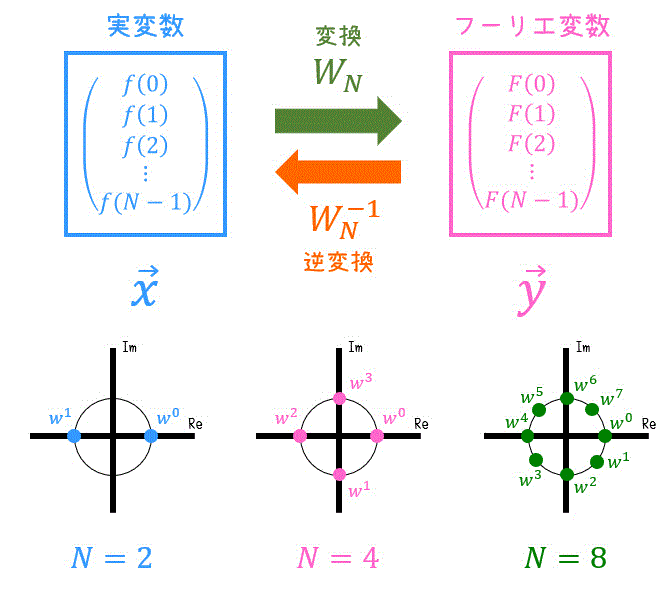
(5) 離散フーリエ変換 [重要]
※ \( N \) 点離散フーリエ変換の公式です
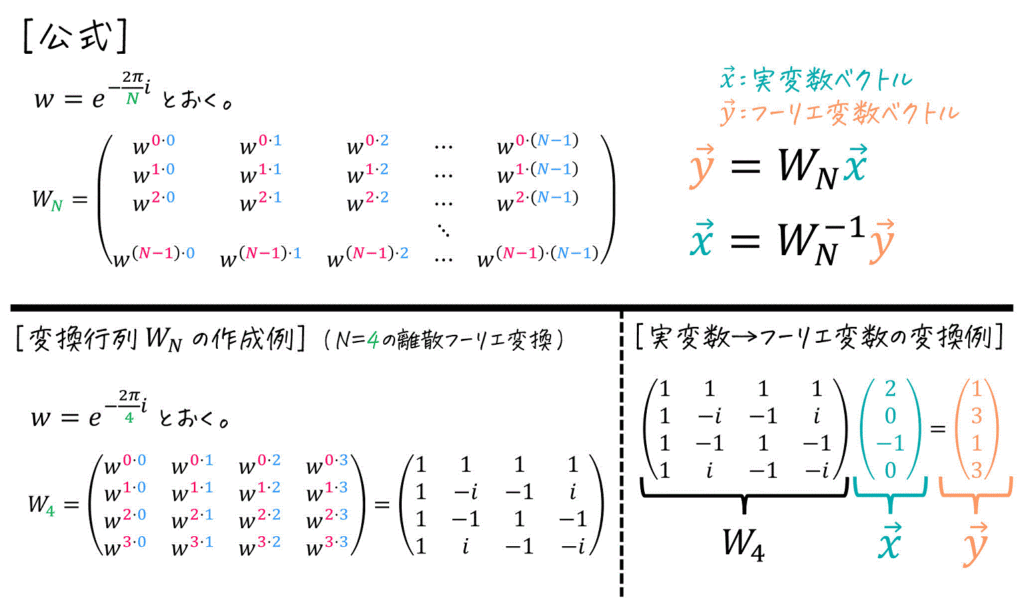
回転因子 \( w \)、変換行列 \( W_N \) の作り方、実際の変換 \( \vec{y} = W_N \vec{x} \) ともに重要な概念なので確実に頭に入れておきましょう。
「離散フーリエ変換」についてさらに復習したい人は下の記事をご覧ください。
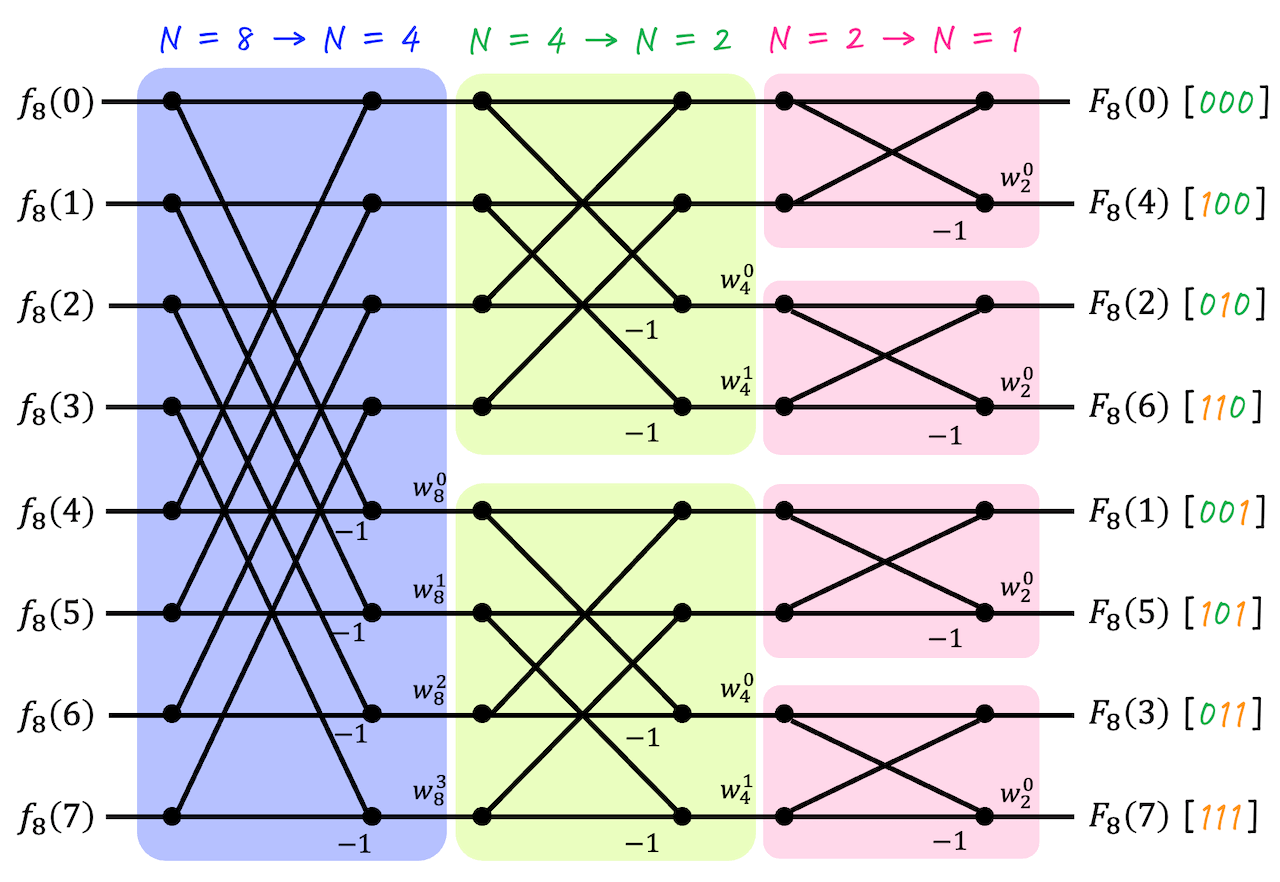
(6) 高速フーリエ変換
\( N \) が2のべき乗（2, 4, 8, … のように \( 2^a \) の \( a \) 部分が自然数となる値）となるときは、フーリエ変換を効率よく解くことができます。
「高速フーリエ変換」について復習したい人は下の記事をご覧ください。
注釈
| ↑1 | とはいっても、積分の分解公式\[ \int f(x) + g (x) \ dx = \int f(x) \ dx + \int g(x) \ dx \]に似ているので、数3を経験した理系にとっては簡単な公式だと思います。 |
|---|---|
| ↑2 | 後ろで改めて説明しますが、\( x_{-1} \), \( x_{-2} \), … のように信号（数列）のマイナス項目 \( x_{-k} \) の値がすべて0になるようなシステムのことを指します。 |
| ↑3 | 実際に \( n = 0 \) を代入すると、\( x_0 = 3 + 2 \cdot 0.5^0 = 5 \)、\( n \to \infty \) とすると、\( x_n = 3 \) になることから、たしかに初期値定理・最終値定理が有効であることがわかりますね。 |
関連広告・スポンサードリンク
![うさぎでもわかる計算機システム Part02 2の補数表現 [基本情報対応]](https://www.momoyama-usagi.com/wp-content/uploads/2021/05/20190615204157-1-150x150.gif)
