スポンサードリンク
こんにちは、ももやまです。
今回は平面グラフ・平面的グラフについてまとめていきたいと思います。
前回の記事はこちら!(第17羽)
マッチングについてです! 「2人組をうまく組めるのか」などを離散数学(グラフ理論)の力で解いていく方法などの解説しているので興味がある人はぜひご覧ください!
目次
スポンサードリンク
1.平面グラフ・平面的グラフとは
(1) 平面グラフ
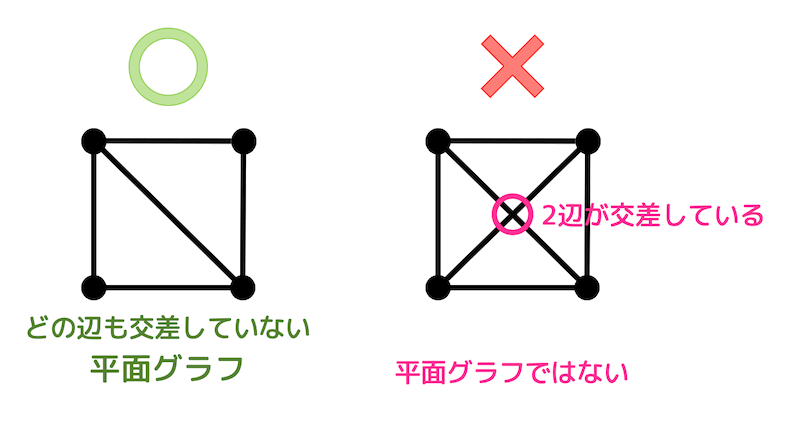
どの2辺も交差していないグラフのことを平面グラフと呼びます。
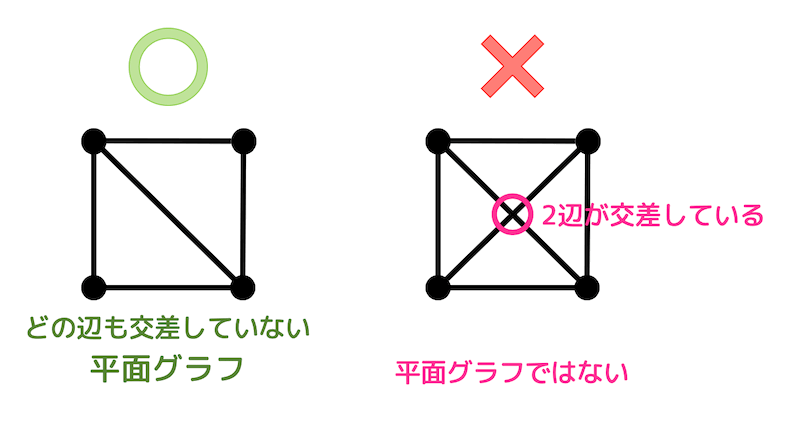
左側のグラフはどの辺も交差せずに書かれていますよね。なので平面グラフです。
しかし、右側のグラフは赤い○の部分で2辺が交差していますよね。なので平面グラフではありません。
(2) 平面的グラフ
平面グラフでもないグラフであっても、交差しないように辺を書き直すことによってどの2辺も交差しないように書けるグラフのことを平面的グラフと呼びます。
(グラフ理論の用語を使って説明すると、平面グラフと同型なグラフが平面的グラフとなります。)
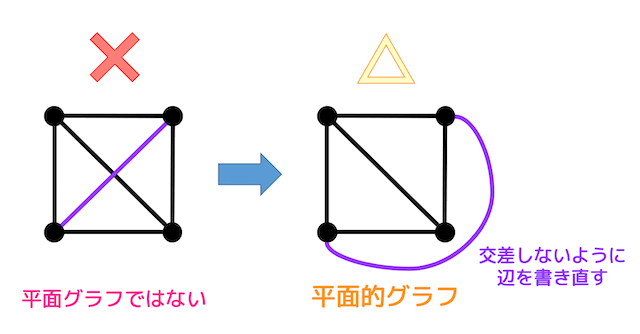
先程説明したとおり、左側のグラフは平面グラフではありませんね。
しかし、右側のように紫の辺を書き直すことによって2辺が交差しないように描くことができますね。なので平面的グラフとなります*1。
(3) 平面グラフと地図
国・県・市などを頂点、隣り合っている国や県(領域)同士を辺で結ぶことにより、地図を下のように平面グラフで表現することができます!
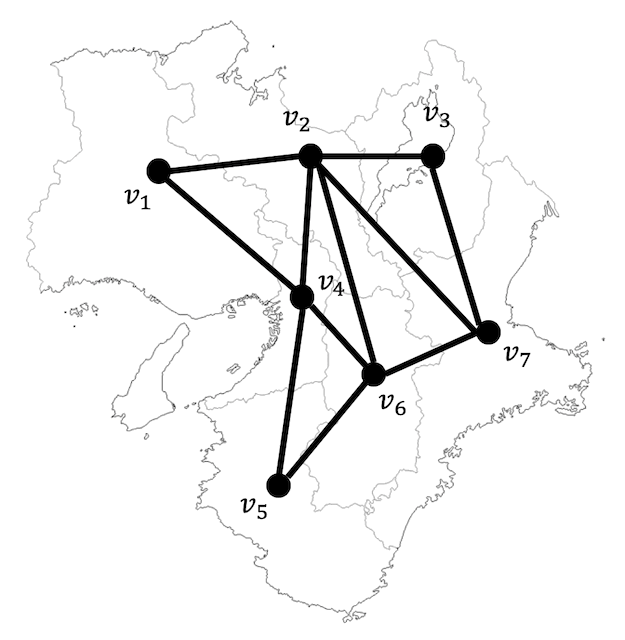
地図を平面グラフで表現することにより、隣り合う領域を異なるが同じ色にならないように彩色するような問題を離散数学・グラフ理論的に考えることができます!
彩色についてはこちらの記事にまとめたのでもし興味があればご覧ください!
スポンサードリンク
2.平面グラフにおける面(領域)の数え方
平面グラフは、平面を辺によっていくつかの面(領域)に分けることができます。
では、面の数を数える方法を例題を通じて説明していきましょう!
例題1
つぎの(1), (2)の平面グラフの面の数を数えなさい。
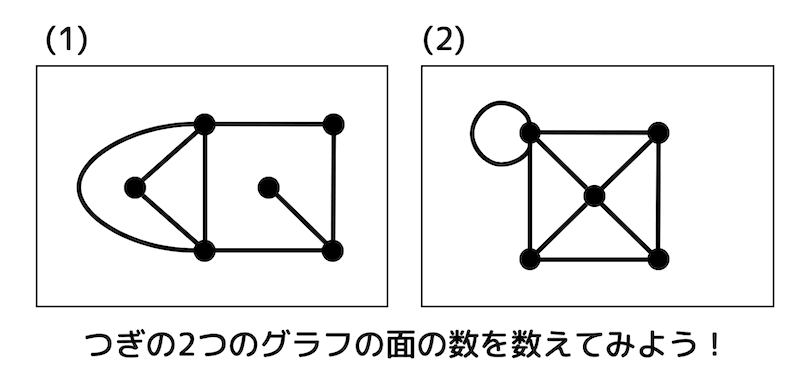
解説1
(1)
辺で囲まれている面1〜面3は数え間違えないでしょう。
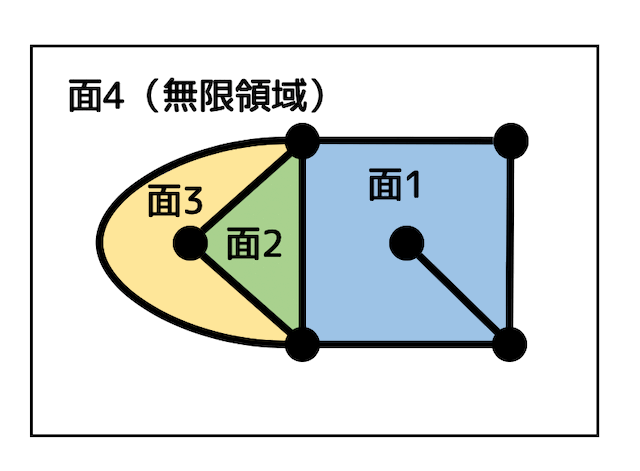
しかし平面グラフの領域を数える際には、辺で囲まれた領域に加え、外側の無限に続く領域も1つの領域(面)として数えます。
なので、面の数は、辺で囲まれている3つの面と外側の1つの面の合計4つとなります。
(2)
(1)と同じように数えていきましょう。
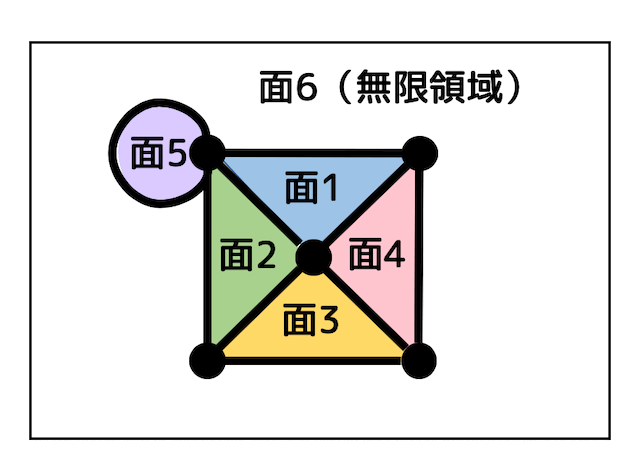
よって面の数はは辺で囲まれている5つの面と外側の1つの面の合計6つとなります。
(ループがあっても普通に数えていけばOKです!)
スポンサードリンク
3.オイラーの公式
(1) オイラーの公式とは
連結な平面グラフであれば、頂点数 \( p \)、辺の数 \( q \)、面の数 \( r \) に対して次のような公式が成立します。
連結な平面グラフの頂点の数を \( p \)、辺の数を \( q \)、面の数を \( r \) とすると、\[
p - q + r = 2
\]が成立する。(ただし \( p \geqq 1 \) )
オイラーの公式が本当に成立するのかを確かめるため2つほどグラフを用意してみました。
例題2
例題1と同じ(1), (2)の平面グラフがオイラーの公式の条件を満たしていることを確認しなさい。
解説2
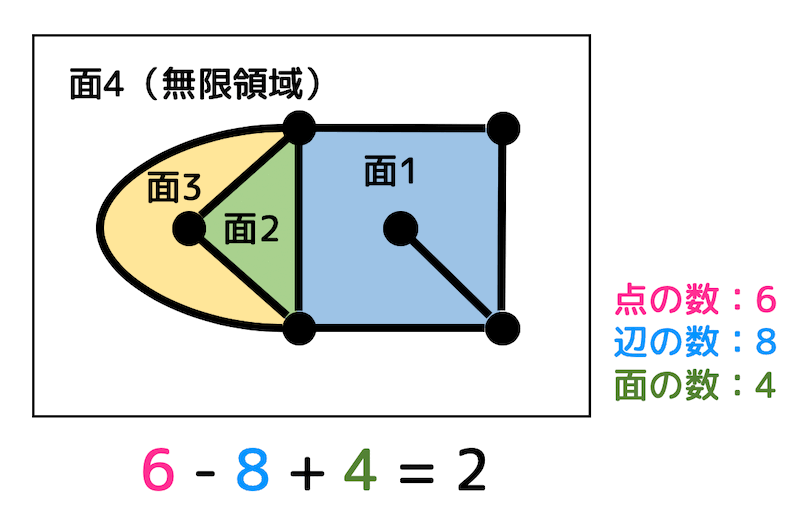
(1)
点の数が6、辺の数が8、面の数が4となり、\[
p - q + r = 6 - 8 + 4 = 2
\]となり、確かにオイラーの公式を満たす。
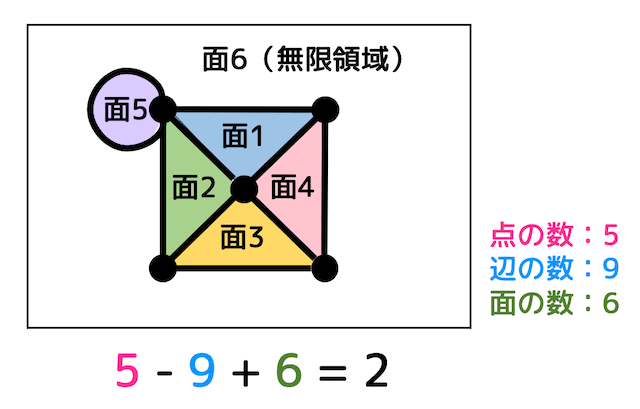
(2)
点の数が5、辺の数が9、面の数が6となり、\[
p - q + r = 5 - 9 + 6 = 2
\]となり、確かにオイラーの公式を満たす。
(2) 点の数、辺の数のみを用いた平面的グラフの判定法
(i) 通常の単純で連結なグラフの場合
同型なグラフであったとしても面の数は辺の配置によって変わってくるので面の数を平面的グラフかどうかの判定材料に使うのはめんどくさいですよね。
実は面の数を使わなくても、頂点数と辺数のみであるグラフが平面的グラフでないかどうかある程度判定することができるのです。
(同型なグラフであれば頂点数と辺数は必ず同じですからね!)
まずは判定式をみてみましょう。
連結な単純平面グラフの頂点の数を \( p \)、辺の数を \( q \) とすると、\[
q \leqq 3p - 6
\]が成立する。(ただし \( p \geqq 3 \) )
なぜ \( q \leqq 3p - 6 \) が成立するのかを説明していきます。
まず、連結な平面グラフにはオイラーの公式\[
p - q + r = 2
\]が成立しますね。(\( p \) は頂点数、\( q \) は辺数、\( r \) は面数、領域数)
ここで、\( L \) を領域を構成する辺の数の総和とします。
1つの領域を作るために、少なくとも3つの辺が必要ですよね。
グラフの領域数は全部で \( r \) なので、グラフにあるすべての領域を表現するためには少なくとも \( 3r \) 個の辺が必要ですね。なので \( L \geqq 3r \) となります。
また、1つの辺は2つの領域を区切る境界となっていますよね。なので、\( L = 2q \) が成立します。
2つの式を連立させると、\[
3r \leqq 2q
\]が成立しますね。
ここで、オイラーの公式 \( r = 2 - p + q \) に代入すると、\[
3(2-p+q) = 3r \leqq 2q \\
q \leqq 3p - 6
\]となり、たしかに \( q \leqq 3p - 6 \) が導出できますね。
連結で単純な平面的グラフの頂点の数を \( p \)、辺の数を \( q \) とすると、\[
q \leqq 3p - 6
\]が成立する。(ただし \( p \geqq 3 \) )
この条件を使うことで、単純で連結なグラフが平面グラフでないかどうかを判定することができます。
\( q \leqq 3p - 6 \) を満たさないグラフは確実に平面グラフでないと言えますが、\( q \leqq 3p - 6 \) を満たすからといって確実に平面グラフであるとは限らないので注意してください。
また、\( q \leqq 3p - 6 \) を用いることで次のような定理も導くことができます。
連結で単純な平面的グラフであれば、次数5以下の点が必ず1つ以上存在する。
証明
頂点数 \( p \)、辺数 \( q \) の連結で単純な平面グラフの次数がすべて6以上と仮定する。
すると、次数の合計は少なくとも \( 6p \) 以上でなければならない。
ここで次数の総和はグラフの辺の数の2倍であるので(握手定理*2)、辺 \( q \) の数は少なくとも \( 3p \) 個以上なくてはならない。つまり、\( q \geqq 3p \) である*3。… (1)
また、連結で単純なグラフなので頂点数と辺数の関係として \( q \leqq 3p - 6 \) が必ず成立する。… (2)
(1), (2) より頂点数 \( p \) および辺数 \( q \) に対し、\[
3p \leqq q \leqq 3p - 6
\]が成立する。
しかし、上の式を満たす \( p,q \) は存在しないため仮定に矛盾する。
よって、少なくとも1つは次数5以下の点が存在することが示された。
(ii) 3辺で構成される領域がないグラフの場合
3辺で構成される領域がない(グラフに三角形の面がない)グラフにはより厳しい条件式を適用することができます。
3辺で構成される領域がないたため、領域はすべて4つ以上の辺で構成されていますね。
なのでグラフにあるすべての領域を表現するためには少なくとも \( 4r \) 個の辺が必要となり、 \( L \geqq 4r \) が成立しますね。
1つの辺は2つの領域を区切る境界なので \( L = 2q \) が成立しますね(ここは同じ)。
連立させると、\[
4r \leqq 2q
\]が成立するのでオイラーの公式 \( r = 2 - p + q \) より\[
4(2-p+q) = 4r \leqq 2q \]\[
q \leqq 2p - 4
\]となり、\( q \leqq 2p - 4 \) というより厳しい条件式が導出できます。
3辺で構成される領域がない(三角形の面がない)連結で単純な平面的グラフの頂点の数を \( p \)、辺の数を \( q \) とすると、\[
q \leqq 2p - 4
\]が成立する。(ただし \( p \geqq 3 \) )
上の公式が使える有名なグラフとして、2部グラフがあげられます。
2部グラフであれば、長さが奇数の閉路は1つもありませんよね*4。なので3辺で構成される領域は存在せず、\( q \leqq 2p - 4 \) を適用することができます。
では、実際に上の公式を使って平面的グラフでないことを示す練習をしてみましょう。
例題3
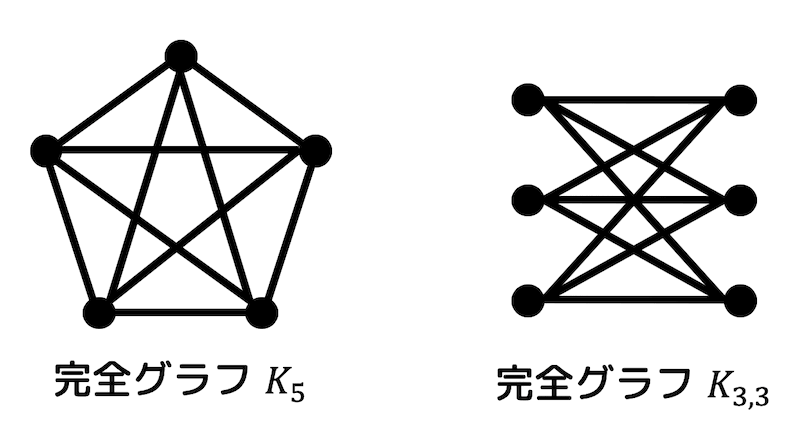
完全グラフ \( K_5 \), \( K_{3,3} \) が平面的グラフではないことを示しなさい。
解説3
完全グラフ \( K_5 \)
\( K_5 \) の頂点数は5、辺数は10である。
ここで \( K_5 \) が平面グラフと仮定する。頂点数 \( p \)、辺数 \( q \) に対し、\[
q \leqq 3p - 6
\]が成立する。
しかし、頂点数 \( p = 5 \)、辺数 \( q = 10 \) を代入すると、\[
10 \leqq 15 - 6 = 9
\]となり、仮定に矛盾する。
よって、完全グラフ \( K_5 \) は平面グラフではない。
完全グラフ \( K_{3,3} \)
\( K_{3,3} \) の頂点数は6、辺数は9である。
ここで \( K_{3,3} \) が平面グラフと仮定する。\( K_{3,3} \) は2部グラフなので頂点数 \( p \)、辺数 \( q \) に対し、\[
q \leqq 2p - 4
\]が成立する。
しかし、頂点数 \( p = 6 \)、辺数 \( q = 9 \) を代入すると、\[
9 \leqq 12 - 4 = 8
\]となり、仮定に矛盾する。
よって、完全グラフ \( K_{3,3} \) は平面グラフではない。
(\( q \leqq 3p - 6 \) だけでは平面グラフでないことを示せないので \( K_{3,3} \) が2部グラフ、つまり三角形の面がないことを使う必要があります。)
4.クラトフスキーの定理
先程 \( K_5 \) と \( K_{3,3} \) が平面グラフでないことを先程示しましたね。
クラトフスキーの定理は、\( K_{5} \) と \( K_{3,3} \) にちなんだ定理となっています。
ある単純グラフ \( G \) が平面的グラフであるための必要十分条件は、完全グラフ \( K_5 \) または \( K_{3,3} \) の一部分を含んでいないことである。
※ただし \( K_5 \) または \( K_{3,3} \) の辺上に頂点が追加されたような形が含まれていても平面グラフではない。
クラトフスキーの定理を使うことで先程説明した \( q \leqq 3p - 6 \) (もしくは \( q \leqq 2p -4 \) )が成立しないようなグラフに対しても平面グラフでないことを示すことができます。
では実際にクラトフスキーの定理の使い方を例題を用いて説明していきましょう。
例題4
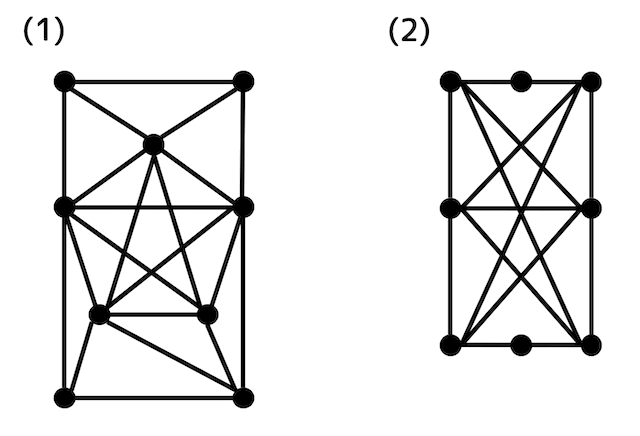
クラトフスキーの定理を用いてつぎの(1), (2)のグラフが平面グラフではないことを示しなさい。
解説4
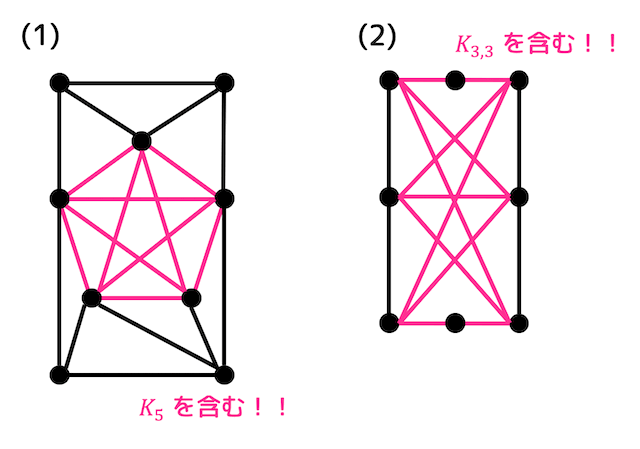
(1)は赤色の辺の部分が \( K_5 \) となっているため平面グラフではありません。
(2)は赤色の辺の部分が \( K_{3,3} \) となっているため平面グラフではありません。
((2)のように \( K_5 \) や \( K_{3,3} \) を構成する辺の途中に点があっても平面グラフでないことを示すことができます。)
5.練習問題
では1問だけですが、練習してみましょう。
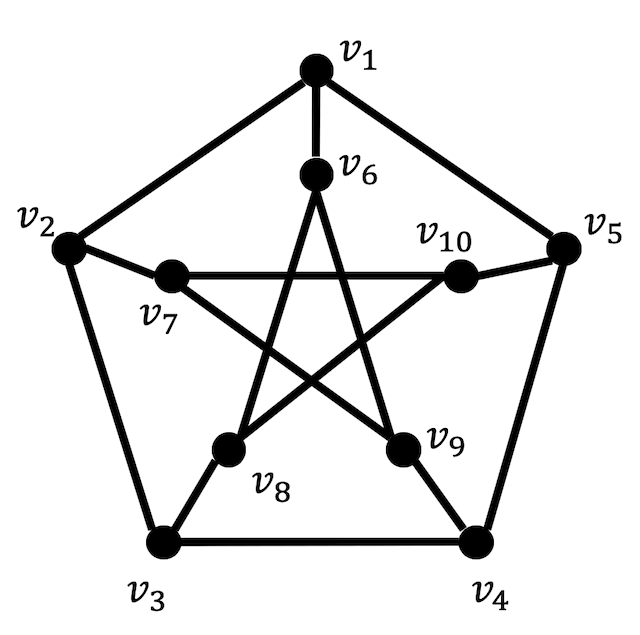
練習
次のグラフが平面的グラフか。理由とともに答えなさい。
(ピーターセングラフと呼ばれる比較的有名なグラフです。)
6.練習問題の答え
答え:平面的グラフではない。
理由
上のグラフは、右のように変形を行うことができる。
(左のグラフと右のグラフは同型)
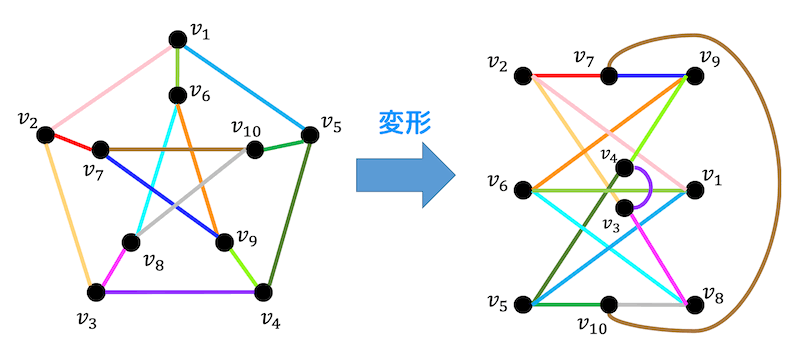
すると、赤色の辺の部分が完全グラフ \( K_{3,3} \) となるのでクラトフスキーの定理より、上のグラフは平面グラフではない。
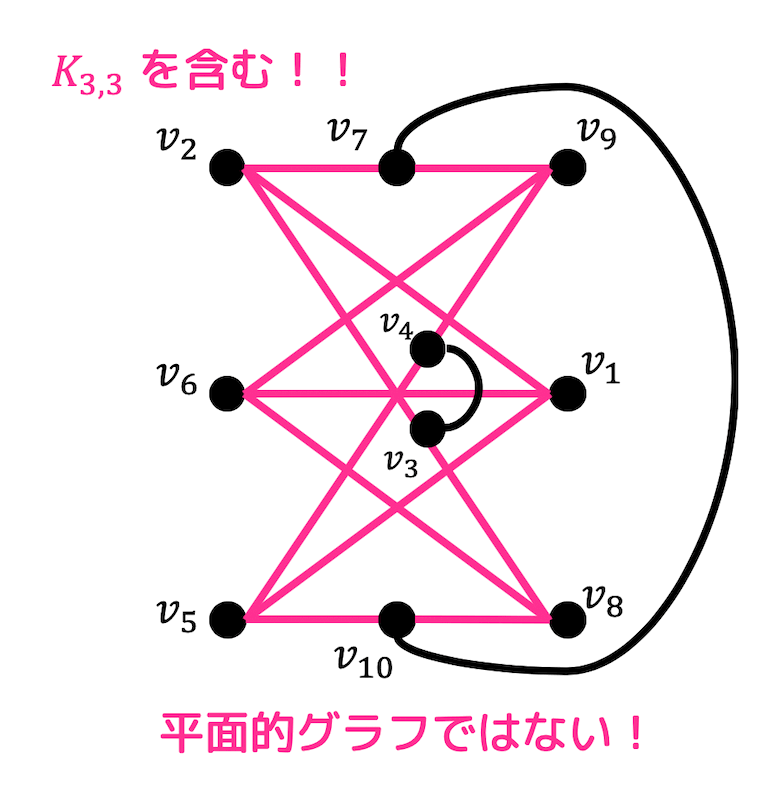
ちなみに頂点数 \( p \) と辺数 \( q \) から \( q \leqq 2p - 4 \) を用いて(三角形の面がないので)平面グラフでないかどうかを判定しようとすると、\( p = 10 \), \( q = 15 \) なので、\[
q = 15 \leqq 16 = 2p - 4
\]となり、\( q \leqq 2p - 4 \) が成立してしまうので平面的グラフでないことを示すことはできません。
7.さいごに
今回は平面グラフ・平面的グラフについてまとめました。
平面グラフ(平面的グラフ)の知識を使うことで、例えば電気回路を基盤に焼き付けることができるかどうか判定できたり、地図を何色かで色わけするとき(次回説明します)に役に立ちます。
次回はグラフの頂点や辺を色分けしていく彩色問題についてまとめいきたいと思います。
次回が離散数学(グラフ理論)の最終回となるので次回もぜひご覧ください!
次回記事はこちら!
(頂点や辺・平面グラフの彩色問題についてです!)
関連広告・スポンサードリンク