【MATLAB入門】超基本な9つのテクニック

2020年10月28日 2021年5月27日 27分19秒

ももうさ

スポンサードリンク

警告: 整合性のない脚注開始用の簡単コード:

この警告が見当違いであれば、管理画面の全般設定 > 脚注の開始・終了用の簡単コード > 簡単コードの整合性を検査にある構文検査の機能を無効にしてください。

整合性のない脚注開始用の簡単コード:

“i)の条件) を使うことで、条件を満たしている要素だけを抽出できる。意外と便利なので、これは覚えておこう。 a = [10 16 13 22 30 37 12 8]; a(a >= 20) % [22 30 37] a(mod(a,3) == 0) % [30 12] (iii) 何番目の要素が条件を満�…”

こんにちは、ももやまです。

今回はMATLABを初めて使う人が知っておいたらいいなと思う技を9つ紹介したいと思います。

これからMATLABを使う人も、ちょっとMATLABを触ったよという人もぜひご覧いただけたら幸いです。

スポンサードリンク

１．型の定義は不要

C言語やJavaなどの場合、下のように変数を使う際に int や double でどんな形にするかを定義してあげる必要があります。

int    a =  100; // a を整数型で定義、初期値100
double b = 33.4; // b を実数型で定義、初期値33.4

一方MATLABの場合変数を定義することなく、下のようにいきなり代入をすることができます。

PythonやRubyと同じスタイルだと思っていただけたらOKです。

a =  100; % "%"の右側はコメントとなります。Cだと //、Pythonだと # に相当します
b = 33.4; % セミコロン ; の有無については次の章で説明します。

ただし、1回も代入したことがない変数を使うとエラーが出るので気を付けましょう。

a = 100 / c; % cは何も代入されていないため、エラーが出る
% エラー内容: 関数または変数 'c' が認識されません。

スポンサードリンク

２．セミコロンを抜くと出力結果が表示される

MATLABでは、セミコロンを抜いた行に対して実行結果を出力させることができます。

例えば、下のプログラムの場合、3行目の c = a / b の計算結果を表示します。

a = 5;
b = 3;
c = a / b  % この行のセミコロン ; に対する実行結果が表示される

実行すると、下のように c の計算結果を表示します。

c =
        1.6667

スポンサードリンク

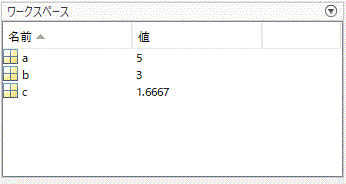
３．ワークスペースの活用

MATLABでは、それぞれの変数にどんな値が入っているかをワークスペースでかんたんに確認することができます。

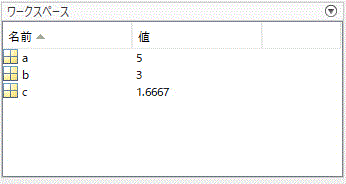
しかし、サイズが大きい配列・行列になると「3×4 double」のように値が表示されていないように見えます。

このように値が表示されない場合は、該当する変数の部分をクリックすると、別ウィンドウで変数の値が表示されるのでご安心ください。

４．コメントアウトなど

MATLABでも、他の言語と同じようにコメントを残す（コメントアウトする）ことができます。

残し方を確認しておきましょう。

(1) 直後〜行末までのコメントアウト

% 以降の部分はコメントアウトされ、プログラム上で無視されます。

C言語だと // に相当。

a = 5;
b = 3; 
a * b  % この部分がコメントアウトされる。次の行には引き継がれない。

(2) 複数行をまとめてコメントアウトする方法1

複数行をまとめてコメントしたいときはありますね。

ただ、1行ごとに % をつけていくと日が暮れてしまいます。

MATLABでは、複数行を選択した状態で以下のコマンドを押すことでコメントアウトを実施／解除することができます。

	実施	解除
Win	Ctrl + R	Ctrl + T
Mac	Command + /	Command + T

※WindowsとMacで微妙にコマンドが違うので注意！

(3) 複数行をまとめてコメントアウトする方法2

C言語では /* と */ で囲まれた部分は、次の行を超えてもコメントアウトされますね。

MATLABでも、%{ と %} で囲うことで、行を超えたコメントアウトをすることができます。

x = 100;
%{
a = 5;
b = 3; 
c = a * b
%}
y = 200;

上の場合だと、a, b, c が出てくる3行がコメントアウトされていることがわかりますね。

ただし、%{ と　%} を書く行には余計な文字を入れないようにしましょう。（余計な文字を入れるとうまくコメントアウトができません）

x = 100;
%{ aaa ← 余計な文字を書くのはNG
a = 5;
b = 3; 
c = a * b
%}
y = 200;

(4) セクション機能を使ってみよう

プログラムを大まかに区切る際にはMATLABのセクション機能を使うと便利です。

下のように、%% のあとにセクション名を入れることで実現できます。

%% 定義セクション
A = [1 2; 3 4];
B = [4 3; 2 1];
x = [1 0]';
 
%% 演算セクション
C = A * B;
y = B * x;
 
 
%% 出力セクション
y

セクション機能を使うことで、プログラムのどの部分でどのような操作をしているのかを明示することができます。（本当はセクションやらコメントを入れないでもわかるようなプログラムがいいんですけどね…。）

５．配列・行列（2次元配列）の基礎

(1) 配列の初期化

MATLABで配列を使う場合、下のように初期値となる要素を区切って入れて初期化するのもありです。

a = [1, 2, 3, 4, 5]; % a = [1 2 3 4 5]; のようにスペースをあけてもOK

配列のサイズ（要素数）が少なければ、上のような方法でも大丈夫です。しかし、サイズが100、1,000と増えたら宣言するだけでコードが長くなってしまいます。

そこで、サイズの大きい配列を宣言する際には全部の要素を0に初期化する zeros、全部の要素を1に初期化する ones が使われます。

a = zeros(1,100);  % サイズが 100の配列aを宣言 (どの要素も値は0)
b =  ones(1,1000); % サイズが1000の配列bを宣言 (どの要素も値は1)

実際に値を代入する際には、下のように配列の何番目に何を代入するかを書きます。括弧は角括弧 [] ではなく丸括弧 () なので要注意！

また、宣言のときは zeros(1,3) のように1を書く必要がありましたが、実際に代入する際には a(3) のように 1, を書く必要はありません。

a(5) = 100; % 5番目の要素に100を代入
b(3) =  40; % 3番目の要素に40を代入

ほかにも配列はMATLAB独特の表記法が多いので、プログラミングに慣れている人は下の3点に注意しましょう。

宣言時は zeros(1,3) のように 1, を忘れない
a[3] ではなく a(3)（丸括弧を使う）
配列のスタートは0ではなく1

あれ、zeros(100) じゃないの？

上の例を見て、なんで a = zeros(100); やら b = zeros(1000); じゃダメなのと思った人も多いかと思います。

しかし、なぜかMATLABの仕様では zeros(n) や ones(n) とすると、n×nの行列（2次元配列）ができてしまいます。

なので、配列を使うときは zeros(1,n) のように 1, を入れてあげるのを忘れないようにしましょう。

(2) 行列（2次元配列）の初期化

MATLABでは、行列（2次元配列）を用いた計算を行うことが多いと思います。

なので、行列の初期化も確認しておきましょう。

(i) 具体値を代入

MATLABで行列（2次元配列）を代入する際には、行ごとに ; で区切って入力します。

例えば、 $A = (\begin{array}{ccc} 1 & 3 & 5 \\ 2 & 4 & 6 \\ 3 & 6 & 10 \end{array})$ の行列を定義するのであれば、下のように定義します。

A = [1 3 5; 2 4 6; 3 6 10];
% 1行目-> 1, 3,  5; 
% 2行目-> 2, 4,  6;
% 3行目-> 3, 6, 10 (最後の行の ; は不要

(ii) zeros, onesを用いた初期化

しかし、大きい行列をいちいち定義するのはめんどくさいですね。

そこで、n行m列の行列を初期化する場合、

zeros(n,m) (初期値オール0)
ones(n,m) (初期値オール1)

のいずれかを使います。使用例は下のような感じです。

A = zeros(30,20);   % 30行20列の行列Aを宣言 (どの要素も値は0)
B =  ones(500,800); % 500行800列の行列Bを宣言 (どの要素も値は1)
% 行列は大文字が使わることが多いので大文字で宣言しました。小文字で宣言してもOKです。

(余談) MATLABにおけるベクトル（配列）と行列

要素数がnの配列を宣言する際に zeros(1,n) と書くのでしたね。

実は、MATLABでは配列を1行n列の行列（n次元の横ベクトル）*1として扱われています。

(3) 配列の一部分を取り出す

配列の一部分を取り出す方法について確認しておきましょう。

覚えておくと良いポイントは、下の2つです。

a(from:to) で、from 番目から to 番目の要素を抽出
a(:) ですべての要素を抽出（2次元以上のときは使います）

a = [32 11 47 39 8 3 90]; % 要素は7つ
 
b = a(3)     % a(3) → 3番目の要素(47)
% b = 47
 
c = a(1:4)   % a(1:4) → 1番目～4番目の要素
% c = [32 11 47 39]
 
d = a(3:end) % endで末尾の要素を指定可能
% d = [47 39 8 3 90]
 
e = a(:)     % a(:) : → すべての要素を指定
% e = a と同じ

(4) 行列の一部を取り出す

(3)の配列を取り出すとほぼ同じように行列（2次元以上の配列）から一部の要素を取り出すことができます。

P, Qにどんな要素が代入されるか少し考えてみましょう。

P = [3 2 1; -1 3 5; 8 -4 6]; % 3×3行列
 
Q = P(:,1)
R = P(1:2,:)

2次元の場合、P(抽出する行,抽出する列) で抽出を行えます。

Q =
 
     3
    -1
     8
 
-> P(:,1) なので、1列目のすべての行を抽出
 
 
R =
 
     3     2     1
    -1     3     5
 
-> P(1:2:,:) なので、1～2行目のすべての列を抽出

６．行列（ベクトル）の演算

MATLABでは行列計算・ベクトル計算もライブラリなしに行うことができます。

何個か例を見てみましょう。

(1) 足し算・引き算

(i) $A = (\begin{array}{ccc} 1 & 2 \\ 5 & 4 \end{array}), B = (\begin{array}{ccc} - 3 & 1 \\ 2 & - 1 \end{array})$ に対して、 $A + B$ の計算。

A = [ 1,2; 5, 4]; % 行列Aの定義
B = [-3,1; 2,-1]; % 行列Bの定義
A + B  % A+Bの結果の出力
A - B  % A-Bの結果の出力

[出力結果]

(2) 掛け算

$A = (\begin{array}{ccc} 1 & 2 \\ 5 & 4 \end{array}), B = (\begin{array}{ccc} - 3 & 1 \\ 2 & 0 \end{array})$ に対して、 $A B$ の計算。

A = [ 1,2; 5,4]; % 行列Aの定義
B = [-3,1; 2,0]; % 行列Bの定義
A * B  % ABの結果の出力

[出力結果]

(3) 逆行列の使用

$A = (\begin{array}{ccc} 1 & 2 \\ 5 & 4 \end{array}), B = (\begin{array}{ccc} - 3 & 1 \\ 2 & 0 \end{array})$ に対して、 $A B^{- 1}$ の計算。

A = [ 1,2; 5,4]; % 行列Aの定義
B = [-3,1; 2,0]; % 行列Bの定義
%% 下の3つのうち、どの表現を使ってもOK
A * inv(B) % Bの逆行列B^-1はinv(B)
A / B      % 割り算のように表現してもOK
A * B^-1   % inv(B)をB^-1と表記してもOK

[出力結果]

ans =
 
   -5.0000   -7.0000
  -13.0000  -17.0000
 
ans =
 
    -5    -7
   -13   -17
 
ans =
 
   -5.0000   -7.0000
  -13.0000  -17.0000

逆行列の他にも行列の階数、固有値（固有ベクトル）のように線形代数で出てくる基本的な内容は、すでに関数が用意されているため、あっという間に求めることができます。（気になる人は調べてみましょう）

(4) 行列・ベクトルの転置

$A = (\begin{array}{ccc} 1 & 2 & 3 \\ 3 & 2 & 1 \end{array}), \vec{b} = (\begin{array}{ccc} 1 2 - 1 \end{array})$ を転置させたもの $^{t} A$ , $^{t} \vec{b}$ の計算。

A = [1,2,3; 3,2,1];
b = [1; 2; -1];
 
A'  % 行列Aの転置
b'  % ベクトルbの転置

(5) 内積・ベクトルがなす角の計算

a = [1; 2; -1];
b = [4; 3; -5];
 
%% 内積の求め方は2通り
i_prod1 = dot(a,b)     % 内積の算出
i_prod2 = a' * b       % 1×nベクトルとn×1ベクトルの積は内積と同じ
 
theta = subspace(a,b)  % ベクトルのなす角度を計算 (弧度法)
rad2deg(theta)         % 度数法への変換

７．条件分岐

(1) if文

if文の書き方は、他の言語とほぼ同じなのでかんたんにチェックしておきましょう。

x   = rand; % 0以上1未満の値をランダムで設定
res = 30;
 
if x >= 0.7
    res = 100; % xが0.7以上の場合ここ
elseif x >= 0.3
    res = 50;  % xが0.7未満で、かつxが0.3以上ならここ
else
    res = 0;   % xが0.3未満ならここ
end
 
res % 結果出力

ちなみに同じようなプログラムは、Pythonでは下のような感じで書けます。

import random
 
x = random.random() # 0以上1未満のランダムな値を生成
res = 30
 
if x >= 0.7:
    res = 100
elif x >= 0.3:
    res = 50
else:
    res = 0
     
print(res)

(2) switch文

switch文はif文ほどは使いませんが、一応確認しておきましょう。

条件分岐が多数になる際には、if を使うより switch のほうがスッキリします。

x = randi(4); % 1以上4以下のランダムな整数を生成
 
switch x % xの値によって場合分け
    case 1 % xが1のとき
        disp('1が選ばれました')
    case 2 % xが2のとき
        disp('2が選ばれました')
    case 3 % xが3のとき
        disp('3が選ばれました')
    otherwise % どれにも該当しないとき
        disp('1,2,3以外が選ばれました')
end

８．各種ループ

(1) forループの基礎

forループの書き方も確認しておきましょう。

start  =  1; % 初期値
step   =  3; % ステップ数（1回のループごとに増える値）
finish = 10; % 終了条件（この値を「超えたら」ループ終了）
 
for i = start:step:finish
    i % i = 1, 4, 7, 10 が出力
end

上のMATLABプログラムは、下のC言語と同じ動きをします。

int start  =  1;
int step   =  3;
int finish = 10; 
 
int main() {
    for(int i = start; i <= finish; i += step) {
        printf("i = %d\n",i); % i = 1, 4, 7, 10 が出力
    }
}

[注意] Pythonとのfor文の違い

※ Pythonを使ったことがある人は必ずお読みください

Pythonでfor文を書く際には、下のように range(start,finish,step) を用いて記述します。

MATLABのfor文では、終了条件 finish を超えたら終了に対し、Pythonでは finish 以上になったら終了します。

例えば下のプログラムの場合、i = 1, 4, 7 の場合は出力されます。しかし、i = 10 で finish 以上の値となってしまうため、i = 10 では出力されません。

start  =  1 # 初期値
step   =  3 # ステップ数（1回のループごとに増える値）
finish = 10 # 終了条件（この値を「以上で」ループ終了）
 
for i in range(start,finish,step):
    print(i) # i = 1, 4, 7 が出力（10は出力されない！）

Pythonでfor文を使ったことがある人は、下の2点をごちゃごちゃにしないように注意しましょう。

MATLABは、終了条件を超えたらループ終了
Pythonは、終了条件以上でループ終了

(2) ステップ数の省略

ただし、ステップ数が1のときは「ステップ数」を省略することができます。Cで言うと、下のようにステップ数部分に i++ を書くような場合に相当します。

int main() {
    for(int i = 1; i <= 10; i++) {
        // 処理内容
    }
}

例えば上のC言語のような処理は、MATLABでは下のように表せます。

for i = 1:10
    % 処理内容 (i = 1,2,3,…,10とループする)
end

(3) whileを使ったループ

while を使った書き方も確認しておきましょう。

とはいっても、こちらは他の言語とあまり変わらないので、軽く触れるだけにしましょう。

[MATLAB]

i = 10;
while i > 0
   i = i - 3 % i -= 3 だとエラー出る
end

上のMATLABプログラムは、下の2つのプログラムと全く同じです。

[C言語]

#include <stdio.h>
int main(void){
    int i = 10;
    while(i > 0) {
        i -= 3;
        printf("i = %d\n",i);
    }
}

[Python]

i = 10
while i > 0:
    i -= 3
    print(i)

(4) breakとかcontinueの使い方

(i) break

ループを強制的に抜けるときには break を使います。

使い方の例としては、特定の条件を満たすまで while 1（無限ループ）を行い、条件を満たした段階で強制終了する際などに使えます。

下のプログラムは、階数が2以下の3行4列の行列を作成、出力するプログラムです。

A = zeros(3,4); % 初期化（3行4列）
while 1
    A = randi([-5 5],3,4); % 3行4列の行列を作成、各要素は-5以上5以下のランダムな整数
    if rank(A) <= 2 
       break; % Aの階数が2以下なら強制終了
    end
end
 
A % 行列Aを出力

行列が出てくるとMATLABっぽさが出てきますね。

(ii) continue

continue は今現在のループを終了させ、自動的に次のステップに移動させることができます。

例えば、下のプログラムを見てみましょう。

for i = 1:10
   if mod(i,2) == 0 % 他の言語でいう i % 2 == 0 と同じ
      continue; % ここを通ったら自動的に次のiへ
   end
   i % continue; を通らないときはここが実行される
end

上のプログラムを実行すると、i が 1, 3, 5, 7, 9のときのみ結果が表示され、それ以外のときは continue があるため実行されません。

９．覚えておくと便利！　配列の一括処理

MATLABでは、複数の配列に対して条件に

(1) 配列に要素を追加

a = [3 2 6]; % 追加元の配列
a = [a 1] % 1を末尾に追加 → a = [3 2 6 1]

(2) 配列の連接

a = [3 2];
b = [9 7]; % 連接する配列
a = [a b] % 配列を連接 → a = [3 2 9 7] 

(3) 配列の要素全部に対して一括に計算

a = [10 16 13 22 30 37 12 8];
a = a * 3 - 1; % 配列の全要素に対して、3倍-1を行う。
% a = [27 45 36 63 87 108 33 21];

(4) 配列の要素全部に対して条件判定

(i) 条件を満たす要素は1、満たしていない要素は0に

a = [10 16 13 22 30 37 12 8];
 
a >= 20  % 20以上かどうか
% [0 0 0 1 1 1 0 0]
 
mod(a,3) == 0 % 3で割り切れるかどうか
% [0 0 0 0 1 0 1 0]

(ii) 条件を満たしているものだけを抽出

配列名((i)の条件) を使うことで、条件を満たしている要素だけを抽出できる。

意外と便利なので、これは覚えておこう。

a = [10 16 13 22 30 37 12 8];
 
a(a >= 20) % [22 30 37]
a(mod(a,3) == 0) % [30 12]

(iii) 何番目の要素が条件を満たしているかを出力

find((i)の条件) とすることで、何番目の要素が条件を満たしているかを出力できる。

ただし先頭は1番目なので注意。

a = [10 16 13 22 30 37 12 8];
 
find(a >= 20) % 4,5,6番目が条件を満たしている → [4 5 6]
find(mod(a,3) == 0) % [5 7]

(5) 配列のソート

配列のソートも1文で書けるので便利。

a = [10 16 13 22 30 37 12 8];
 
sort(a)           % 昇順('ascend')は省略可
sort(a,'descend') % 降順

さいごに

今回はMATLAB初心者が知っておくといい9つの技を紹介しました。

MATLABでは、他にも

グラフの出力
画像処理

など様々なことをすることができます。

次回は、MATLABで超基本的な画像処理をやってみましょう。ではまた次回。

*1:実は zeros(n,1) とし、n行1列の行列と考えることもできます。配列として扱う場合、1行n列、n行1列どちらで考えてもOKです。

関連広告・スポンサードリンク

この記事を書いた人

ももうさ

数学と情報が得意な元工業大生（院卒）です。数学科目と情報科目をわかりやすく説明するブログを書いてます！

１．型の定義は不要

２．セミコロンを抜くと出力結果が表示される

３．ワークスペースの活用

４．コメントアウトなど

(1) 直後〜行末までのコメントアウト

(2) 複数行をまとめてコメントアウトする方法1

(3) 複数行をまとめてコメントアウトする方法2

(4) セクション機能を使ってみよう

５．配列・行列（2次元配列）の基礎

(1) 配列の初期化

あれ、zeros(100) じゃないの？

(2) 行列（2次元配列）の初期化

(i) 具体値を代入

(ii) zeros, onesを用いた初期化

(余談) MATLABにおけるベクトル（配列）と行列

(3) 配列の一部分を取り出す

(4) 行列の一部を取り出す

６．行列（ベクトル）の演算

(1) 足し算・引き算

(2) 掛け算

(3) 逆行列の使用

(4) 行列・ベクトルの転置

(5) 内積・ベクトルがなす角の計算

７．条件分岐

(1) if文

(2) switch文

８．各種ループ

(1) forループの基礎

[注意] Pythonとのfor文の違い

(2) ステップ数の省略

(3) whileを使ったループ

(4) breakとかcontinueの使い方

(i) break

(ii) continue

９．覚えておくと便利！ 配列の一括処理

(1) 配列に要素を追加

(2) 配列の連接

(3) 配列の要素全部に対して一括に計算

(4) 配列の要素全部に対して条件判定

(i) 条件を満たす要素は1、満たしていない要素は0に

(ii) 条件を満たしているものだけを抽出

(iii) 何番目の要素が条件を満たしているかを出力

(5) 配列のソート

さいごに

９．覚えておくと便利！　配列の一括処理