うさぎでもわかる離散数学（グラフ理論）　第8羽　グラフの基礎2　歩道・小道・道・回路・閉路とは

こんにちは、ももやまです。

今回も離散数学（グラフ理論）の基礎について説明したいと思います。

今回はグラフをたどり方に関する歩道、小道、道、回路、閉路についてです。

前回の離散数学（グラフ理論）の記事はこちら！

www.momoyama-usagi.com

「グラフってなんだっけ？」と思ったひとはこちらの記事で復習しましょう。

スポンサードリンク

１．歩道・小道・道

まずは歩道、小道、道についてです。

(1) 歩道

歩道とは、グラフをどのようにたどったかを点と辺の列で表したものを表します。

つまり、グラフのたどり方を書いたものが歩道になるのです！

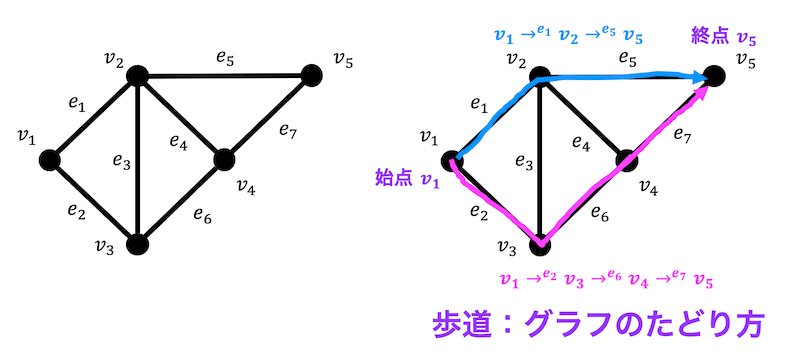
例えば左下のグラフの場合で考えてみましょう。

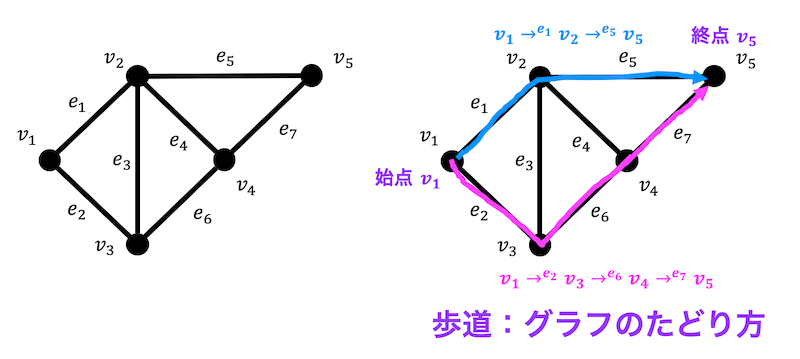
点 \( v_1 \) から点 \( v_5 \) のたどり方*1としては、\[
\color{blue}{v_1 \xrightarrow{e_1} v_2 \xrightarrow{e_5} v_5} \\
\color{orangered}{v_1 \xrightarrow{e_2} v_3 \xrightarrow{e_6} v_4\xrightarrow{e_7} v_5}
\]がありますね*2。

これらはすべて歩道となります。

また、たどったときに通った辺の数を歩道の長さと呼びます。

上の図の場合、\[
\color{blue}{v_1 \xrightarrow{e_1} v_2 \xrightarrow{e_5} v_5}
\]とたどると歩道の長さは2となり、\[
\color{orangered}{v_1 \xrightarrow{e_2} v_3 \xrightarrow{e_6} v_4\xrightarrow{e_7} v_5}
\]とたどると歩道の長さは3となります。

さらに、下のように同じ辺や点を2回以上たどっても歩道ということができます。

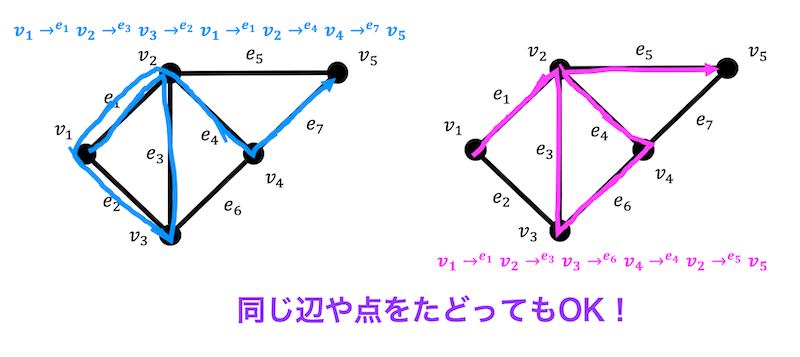
（歩道の長さは左が6、右が5です。）

左上の図の場合、辺 \( e_1 \) と点 \( v_1 \), \( v_2 \) を2回たどっていますね。
右上の図の場合、辺は2回以上たどっていませんが点 \( v_2 \) は2回たどっていますね。

(2) 小道

同じ辺が2つ以上含まれていないような歩道のことを小道と言います。

言い換えると、同じ辺を2回以上通らないようにたどったものが小道です。

たとえ同じ点を2回通っていたとしても同じ辺を2回以上通らなければOKというところに注意が必要です。

例として下の4つのたどり方をみてみましょう。

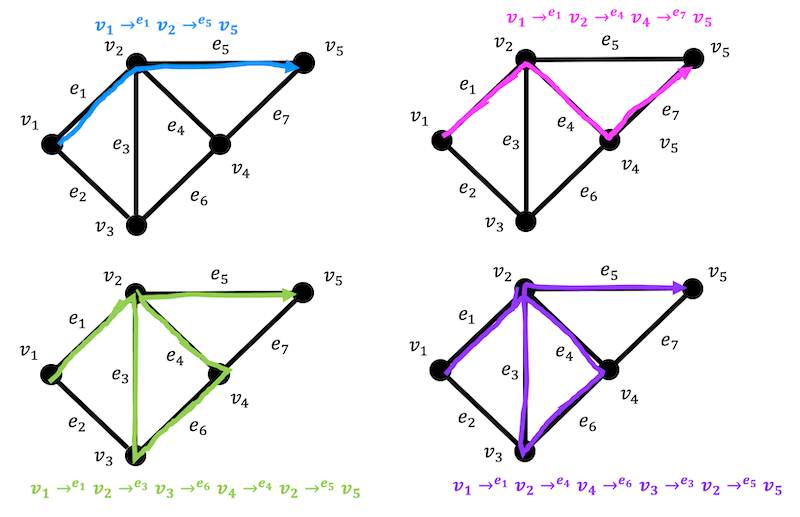
（下2つは同じ点 \( v_2 \) を2回通っていますが同じ辺は2回以上通っていないので小道です。）

(3) 道

同じ点が2回以上含まれていないような歩道のことを道と言います。

言い換えると、同じ点を2回以上通らないようにたどったものが道です。

また例をみてみましょう。（(2)の例と同じです。）

上の2つのグラフは同じ点を2回以上通っていませんね。なので道ですね！
（小道でもあり道でもある）

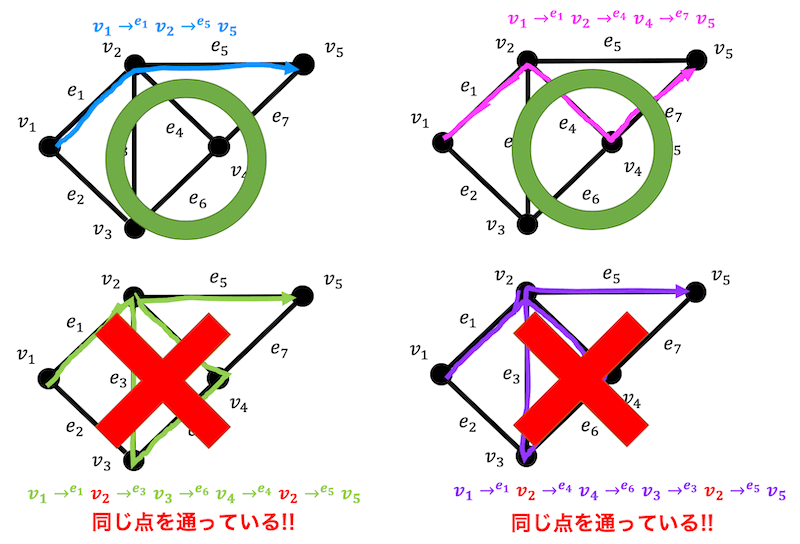
しかし下2つは同じ点 \( v_2 \) を2回通っていますね。なので道ではありません。
（小道ではあるけど道ではない）

ではここまでおさらいしておきましょう。

ところで、上の2つのたどり方は道でもあり、小道でもありましたね。

実はこれは偶然ではなく、道であるようなたどり方は必ず小道にもなるのです！

例えばこのグラフをみてみましょう。このグラフは同じ辺を2回たどっていますね。

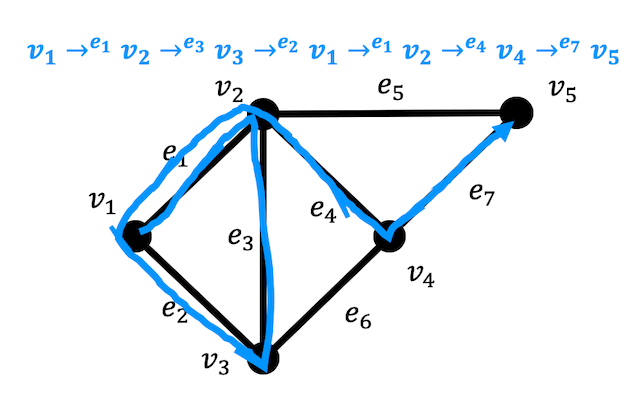
同じ辺を2回以上通るようにたどろうとしたとき、どこかの点も必ず2回以上たどる必要がありますね。

これを言い換えると、同じ点を2回以上通っていなければ（道の条件）必ず同じ辺も2回以上通っていない（小道の条件）ですよね。

なので道であるたどり方は小道でもある、といえますよね。

スポンサードリンク

２．回路・閉路

歩道はたどり方のはじめの点と終わりの点にとくに指定はありませんでしたね。

しかし、回路・閉路はともにたどりはじめの点とたどり終わりの点が同じである必要があります。

(1) 回路

回路はたどりはじめの点とたどり終わりの点が等しい小道を表します。

つまり、同じ辺を2回以上通らずにたどり始めの点に帰ってくるようなたどり方が回路となります。

回路の例を3つほどみてみましょう。

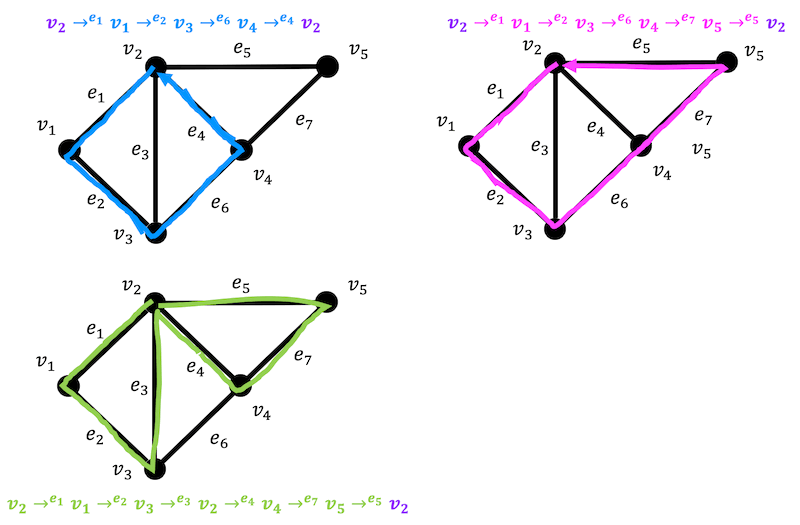
3つとも同じ辺は通らずにはじめの点に戻ってきてますね！

なので回路といえますね！

(2) 閉路

閉路はたどりはじめの点とたどり終わりの点が同じ道を表します*3。

つまり、同じ点を2回以上通らずにたどり始めの点に帰ってくるようなたどり方が閉路となります。

また例をみてみましょう。（(1)の例と同じです。）

上の2つのグラフは同じ点を2回以上通っていませんね。なので道ですね！
（閉路でもあり回路でもある）

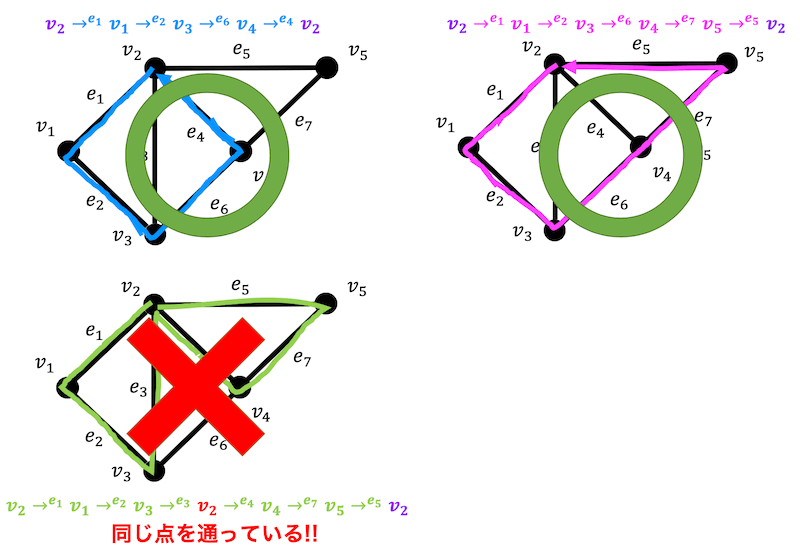
しかし下のグラフは同じ点 \( v_2 \) を2回通っていますね。なので閉路ではありません。
（回路であるが、閉路ではない。）

回路と閉路の違いは、たどる際に同じ辺を2回以上通らずにはじめの点に戻るのか、同じ点を2回以上通らずにはじめの点に戻るのかの違いだけです。

また、先ほど同じ点を2回以上通っていなければ必ず同じ辺も2回以上通っていない（道であれば必ず小道である）と言いましたね。

回路、閉路の場合も同じように閉路であれば必ず回路であるということができるのです！

スポンサードリンク

３．歩道・小道・道・回路・閉路の関係

今まで紹介した歩道、小道、道、回路、閉路の関係をベン図に表すと下のようになります。

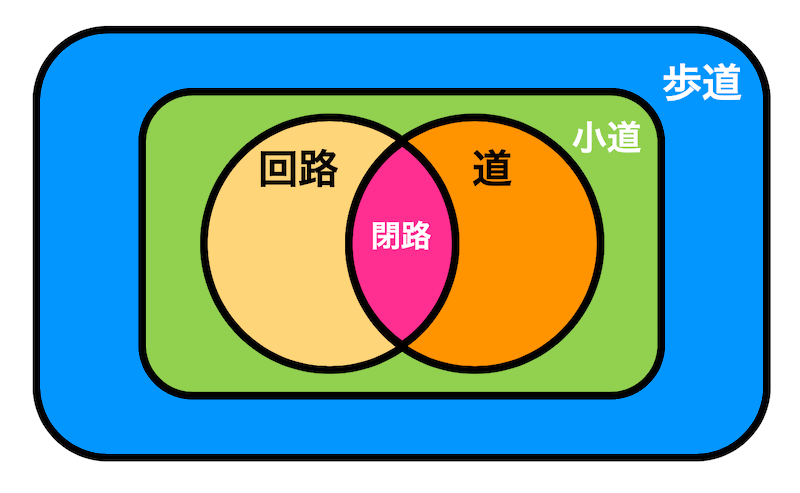
例えば回路は小道、歩道の一部であること、閉路とは、道、回路、小道、歩道の一部であることがわかります。

４．練習問題

では、2問練習をしましょう。

2問目は少し難しめの証明問題となっているので、余裕がある人はぜひチャレンジしましょう。

練習1

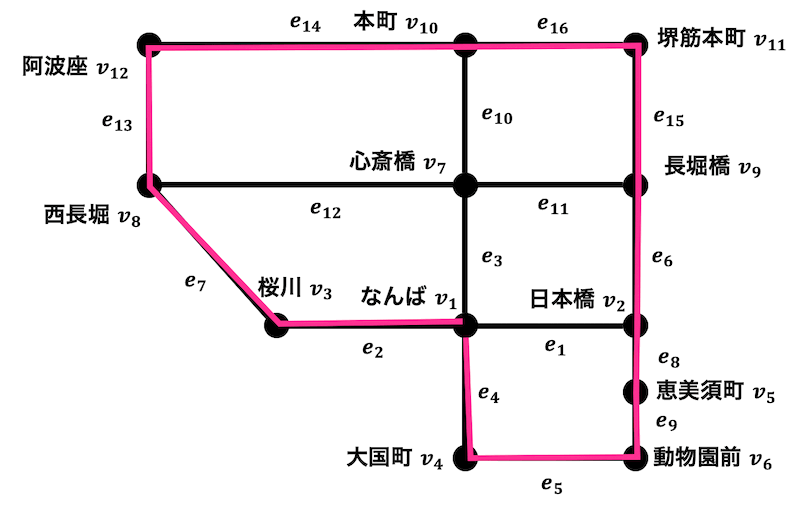
つぎのようなグラフ（路線図） \( G \) がある。

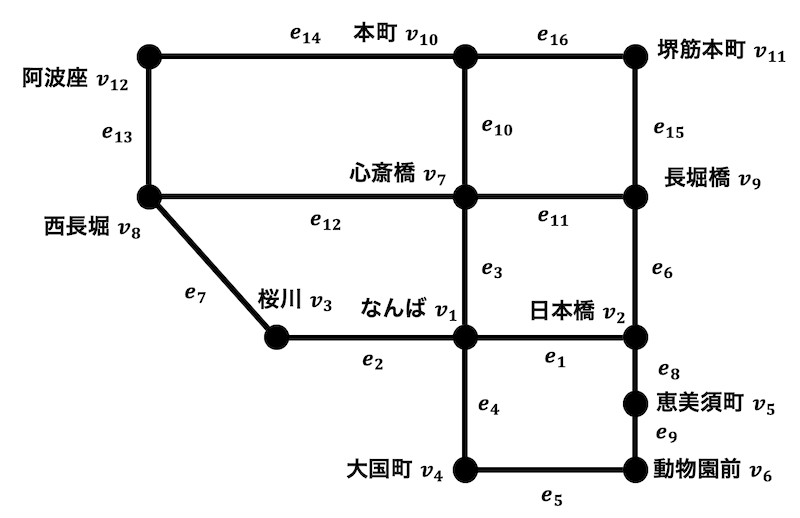
このグラフについて、つぎの問いに答えなさい。

※答える際には頂点の番号、もしくは駅名をたどった順番を羅列するだけで構わない。例えば、\( v_1 \) から \( v_8 \) の経路（歩道）をたどる際には、\[
v_1, v_7, v_8
\]もしくは「なんば、心斎橋、西長堀」と答えればよい。

(1) 始点がなんば \( v_1 \)、終点が堺筋本町 \( v_{11} \) かつ長さが8である道ではない小道を1つ求めなさい。

(2) 始点がなんば \( v_1 \)、終点が堺筋本町 \( v_{11} \) かつ長さが10である道を求めなさい。

(3) \( v_1 \) を始点とするできる限り長さが大きい回路を1つ求め、その回路の長さを答えなさい。

(4) \( v_1 \) を始点とするできる限り長さが大きい閉路を1つ求め、その閉路の長さを答えなさい。

（ ※ (3), (4)はできる限り長さが大きい（長い？）ものを求められるようにがんばりましょう。）

練習2

「2点間に道が存在する」という関係がある。

実はこの関係は点集合上において同値関係となる。これを示しなさい。

[ヒント]

同値関係ということは、関係が

• 反射性
• 対称性
• 推移性

の3つをすべて満たすことを示せばよい。

さらに示す際には点集合上のどの2点を選んでも必ずたどり方（歩道）が道になることを示すのがよい。

同値関係を忘れてしまった人はこちらの記事から復習しましょう。

www.momoyama-usagi.com

５．練習問題の答え

解答1

(1)

道ではない小道ということは、同じ頂点を2回通り、かつ同じ辺を2回以上たどらないようなたどり方をすればよい。

たどり方の例（例なので答えは他にもあります。）\[
v_1, v_4, v_6, v_5, v_2, v_1, v_7, v_{10}, v_{11}
\]

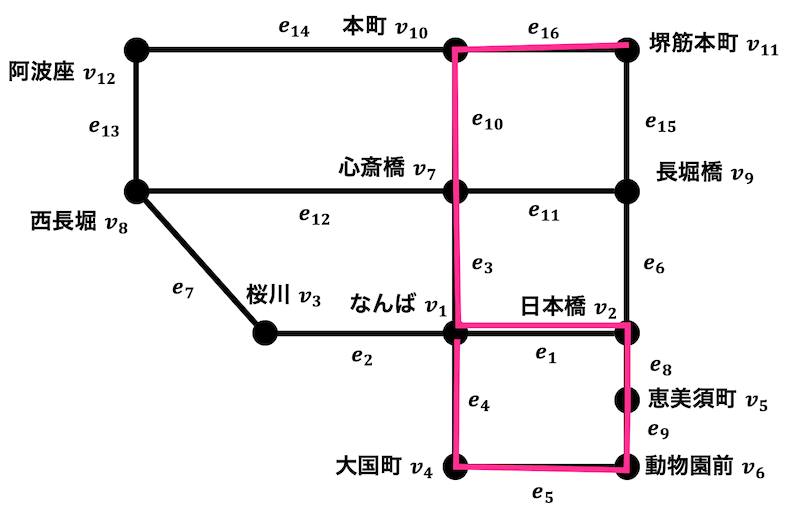
(2)

道なので同じ点を2回以上通らないようにたどらなければならない。

たどり方の例（例なので答えは他にもあります。）\[
v_1, v_4, v_6, v_5, v_2, v_9, v_7, v_8, v_{12}, v_{10}, v_{11}
\]

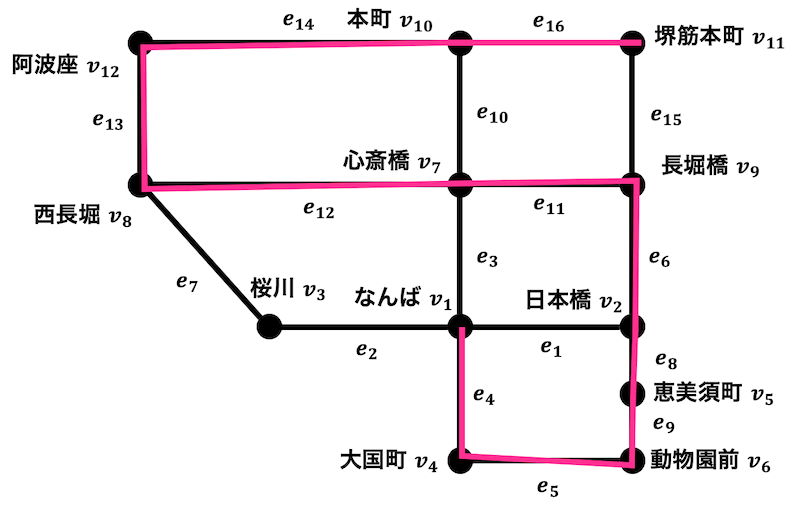
(3)

回路なので、同じ辺を2回以上たどらないようにはじめの点に戻ってくればよい。

例えば、\[
v_1, v_4, v_6, v_5, v_2, v_1, v_3, v_8, v_{12}, v_{10}, v_{11}, v_9, v_7, v_1
\]とたどることで長さ13の回路を得ることができる。

（長さ14以上の回路を見つけた人はDMやらコメントやらでお知らせください。辺の数が16本なので長さ17以上の回路は絶対に見つかりません。）

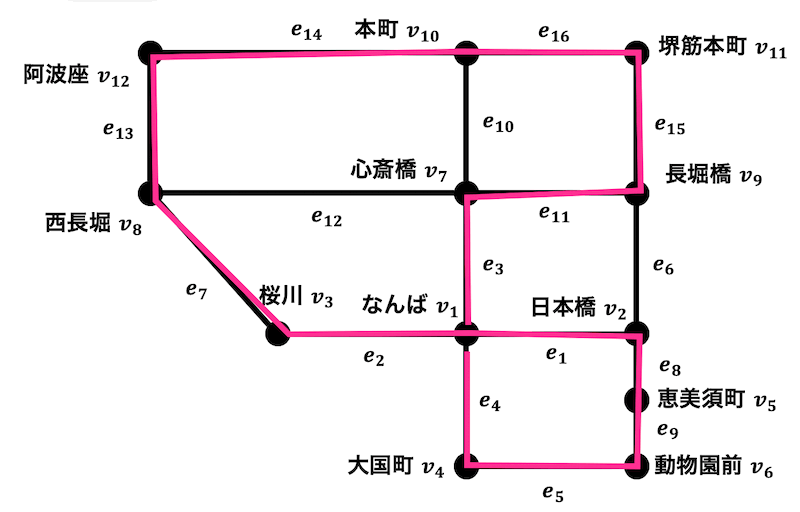
(4)

閉路なので、同じ点を2回以上たどらないようにはじめの点に戻ってくればよい。

例えば、\[
v_1, v_4, v_6, v_5, v_2, v_9, v_{11}, v_{10}, v_{12}, v_8, v_3, v_1
\]とたどることで長さ11の閉路を得ることができる。

（長さ12の閉路を見つけた人はコメントお願いします。ちなみに点の数が12個しかないので長さ13以上の閉路は絶対に見つかりません。）

解答2

同値関係ということで、反射性、対称性、推移性の3つをすべてしめせばよい。

(1) 反射性

任意の点 \( v \) から \( v \) への歩道が道であることを示せばよい。

始点と終点が同じ歩道は明らかに始点と終点以外は同じ点を通らない。よって任意の点 \( v \) から \( v \) への歩道は必ず道となり、(1)が示せた。

(2) 対称性

長さ \( n \) の始点が \( v_1 \)、終点が \( v_n \) のある歩道 \( v_1, v_2, \cdots, v_{n-1}, v_n \) が道であるならば、歩道 \( v_n, v_{n-1}, \cdots, v_2, v_1 \) も道になる。

言い換えると、道である歩道を逆にたどっていっても道であるのは明らかである。

よって対称性が示せた。

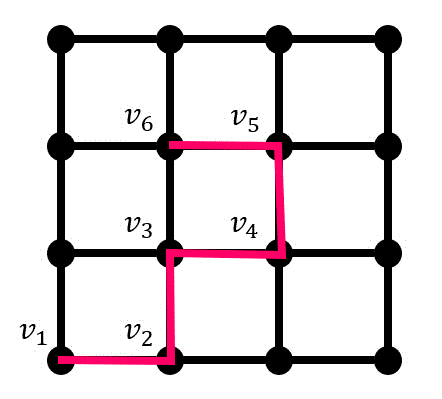
↓ 例えば下の図の歩道を \( v_1 \) から \( v_6 \) まで昇順にたどっていくのと、\( v_6 \) から \( v_1 \) まで降順にたどっていってもたどる点は同じですよね*4。

(3) 推移性

\( v_1 \) から \( v_n \) までたどるある道1 \( v_1, v_2, \cdots, v_n \) と道2 \( u_1, u_2, \cdots, u_n \) があるとする。

（ただし \( v_n = u_1 \) とする。）

(i) \( v_1, v_2, \cdots ,v_n \) と \( u_1, u_2, \cdots, u_n \) に重複する点がない場合

重複する点がない場合は道1と道2をそのままつなげ、\[
v_1, v_2, \cdots v_n, u_2, u_3, \cdots ,u_n
\]としても道となる。

↓イメージ
（確かに道1と道2をつなげても道になっていますよね）

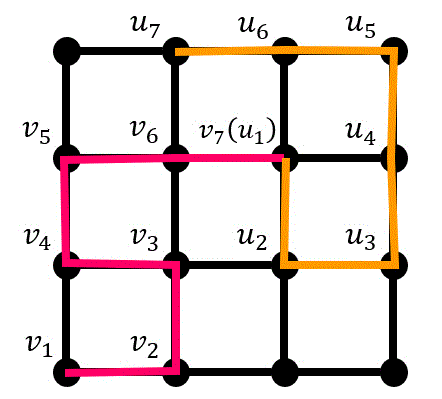
よって(i)の場合は推移性が成り立つ。

(ii) \( v_1, v_2, \cdots ,v_n \) と \( u_1, u_2, \cdots, u_n \) に重複する点がある場合

重複する点がない場合は道1と道2をそのままつなげると同じ点を2回以上通るため道とはならない。

そこで、道1と道2の重複する点のうち、道1で最初に現れる点を \( v_k \) とし、\( x = v_k = u_l \) とする。

少しわかりにくいのでわかりやすく例を2つみてみよう。

例えば、下の図で表されるような道があるとする。（道1が赤色、道2がオレンジ色です。）

この図の場合、\( v_3 \) と \( u_9 \) が同じ点のため、\( x = v_3 = u_9 \) とし、\[
v_1, v_2, x, u_{10}, u_{11}
\]とたどれば道になりますよね。

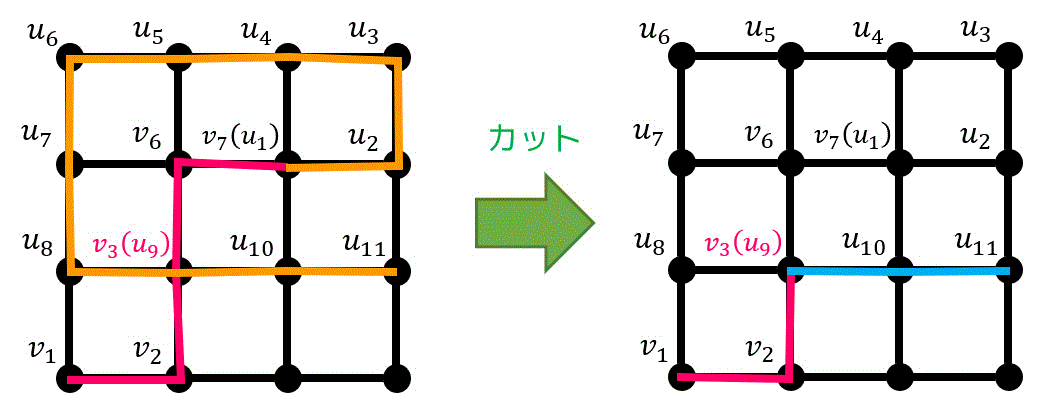
もう1つ例を見てみると、この図の場合、\( v_2 \) と \( u_4 \)、\( v_3 \) と \( u_5 \)、\( v_6 \) と \( u_6 \) の3か所で同じ点を2回通っているため、道1の中で最初に重複する点 \( v_2 \) を \( x = v_2 = u_4 \) とおき、経路を\[
v_1, x, u_5, u_6, u_7, u_8, u_9
\]とすれば同じ点を2回以上通らず道となる。

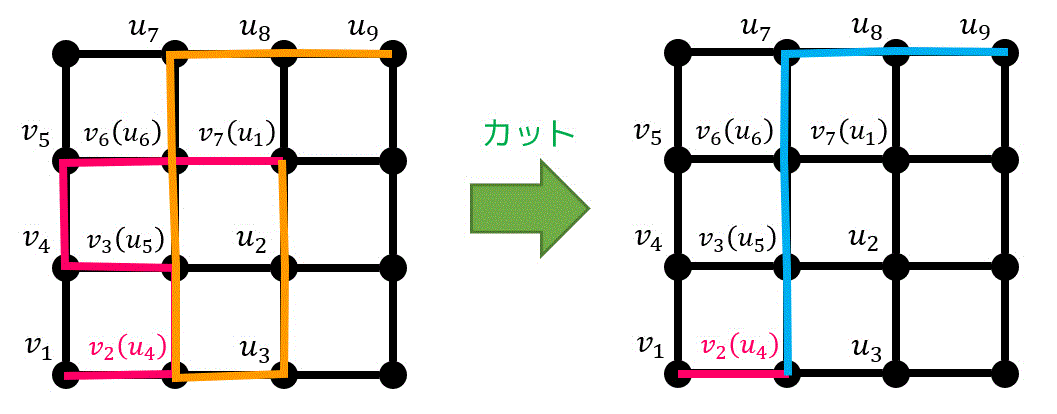
なので道1で最初に現れる点を \( v_k \) とし、\( x = v_k = u_l \) とおき、\[
v_1, v_2, \cdots v_{k-1}, x, u_{l+1}, \cdots u_n
\]とすれば同じ点を2回以上通らないので道となり、(ii)の場合も推移性が成り立つ。

(i), (ii), (iii) がすべて成り立つので同値関係が成り立つことが示され、題意は満たされた。

６．さいごに

今回はグラフの基礎として歩道、小道、道、回路、閉路の5つの用語についてわかりやすくまとめました。

教科書や参考書などには定義がややこしく書いていますが、簡単に言うとグラフのたどり方に制限があるだけなので慣れればパズルになって楽しいと思います。

次回もグラフ理論の用語をまとめていきたいと思います。

では、また次回。さらば。