スポンサードリンク
こんにちは、ももやまです。
工学部の数学で、「フーリエ級数展開」という言葉を聞いたことがある人は多いかと思います。しかし、「あれなにやってんだ!?」と思った人もいるかもしれません。
今回はそんな「フーリエ級数展開」について仕組み・計算方法についてわかりやすく説明していきたいと思います。
目次 [hide]
スポンサードリンク
1.フーリエ級数展開とは
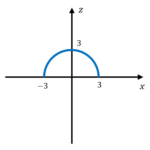
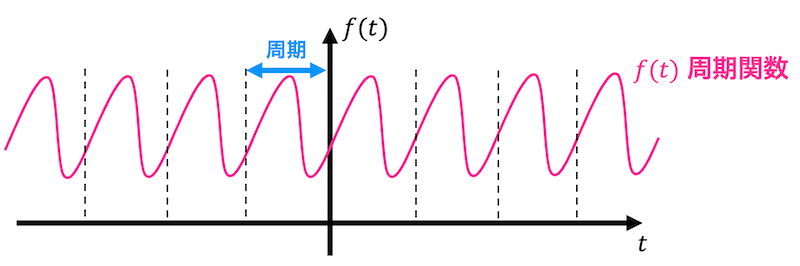
まずは下のグラフをみてみましょう。
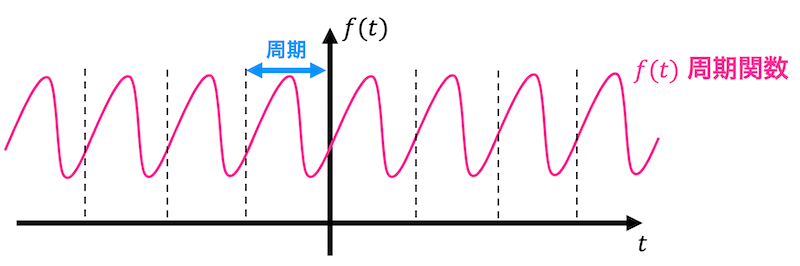
この関数のグラフはある一定の間隔で同じ形の曲線を繰り返していますね。このような関数のことを周期関数と呼びます。数式で書くと、すべての自然数
フーリエ級数展開は、周期関数を皆さんおなじみの偶関数
スポンサードリンク
2.フーリエ級数展開で用いる三角関数の積分
フーリエ級数展開の公式を説明する前にまずは下の公式を導出するために必要な三角関数の積分の復習をしましょう。
三角関数の加法定理・倍角の公式・積和の公式などを用いた積分を行います。加法定理・倍角・積和公式を忘れてしまった人は下の復習用記事を載せたのでそちらをご覧ください。
※今回は
まずは
つぎに、
また、
同じようにして、
最後に公式2の
この積分は0にならないので要注意です。
同様にして、
以上で確認は終了です。
では実際にフーリエ級数展開の公式を見てみましょう!
スポンサードリンク
3.周期が2πの場合のフーリエ級数展開の公式
では、早速フーリエ級数展開がどんな式なのかをみていきましょう。
こちらで、周期
(1) 計算公式
まずは周期関数
最初に公式をみてみましょう。
※積分範囲は
色をつけて公式を少しわかりやすくしてみました!

つまり、周期関数
少し難しい用語を使うと、周期関数
しかし、フーリエ係数
なぜこんな値になっているのかを下のほうで説明していきましょう。
(i) 初期値の導出
まずは初期値のフーリエ係数
すると、
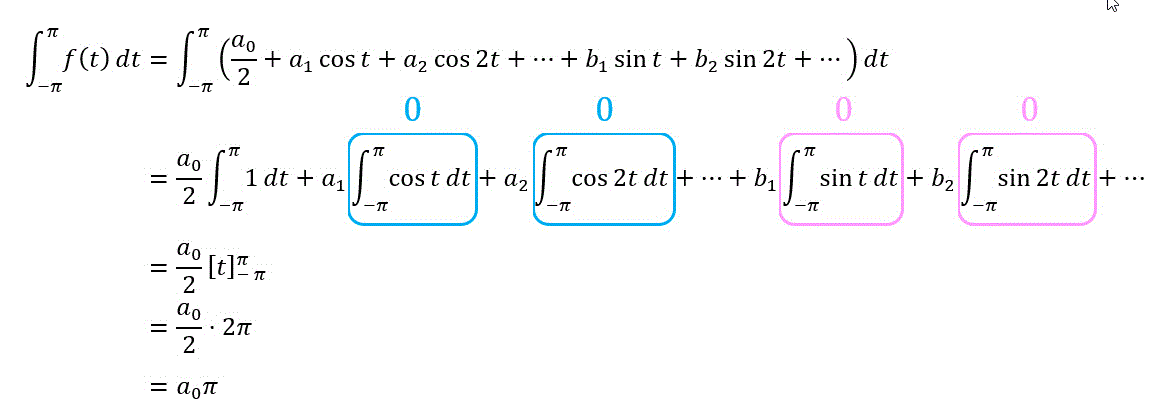
と計算できますね。
よって、
(ii) cos の項の導出
つぎに偶関数
すると、
さらに両辺を
すると、
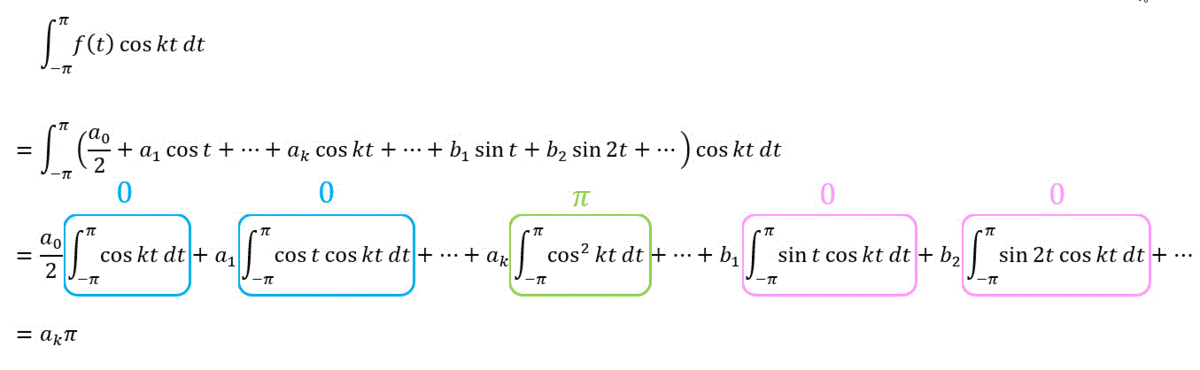
と計算できます。よって、
ここで初項
初項をあえて
(覚えるべき公式も減りますし!)
(iii) sin の項の導出
最後に奇関数
すると、
さらに両辺を
すると、
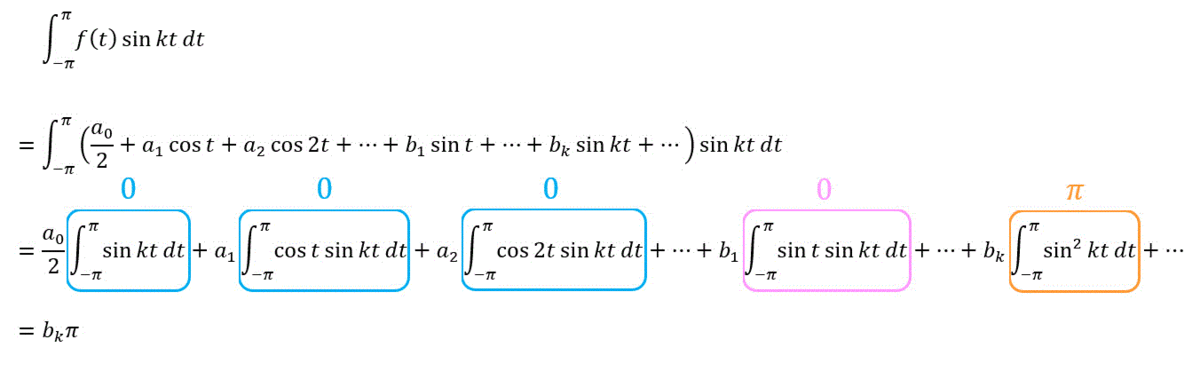
となりますね!
と計算できます。よって、
ところで
先ほどの公式に
なので、奇関数の初項
(2) f(t)が偶関数・奇関数の場合
周期関数
(i) f(t) が偶関数の場合
(ii) f(t) が奇関数の場合
周期
(フーリエ余弦級数、フーリエ・コサイン級数と呼ばれます。)
また、周期関数
(フーリエ正弦級数、フーリエ・サイン級数と呼ばれます。)
周期2πの偶関数・奇関数のときのフーリエ級数展開
4.周期Tの場合のフーリエ級数展開の公式
先ほどは周期が
ですが、実際の周期関数(波形とか)が
なので今度はあらゆる周期に対応したフーリエ級数展開の公式を考えてみましょう。
周期
ここで、物理をやったことがある人なら「見たことあるような式」だなと思ったかもしれません。実はこれ、角速度*7
すると、周期
まず周期
よって、積分式は、
あとは変数
※積分範囲は
こちらも色などをつけてみやすく表現したバージョンも用意しました。
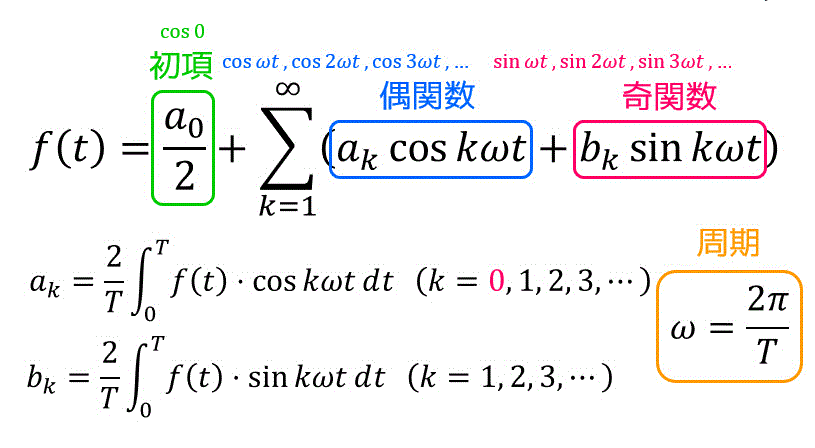
周期が
周期
(フーリエ余弦級数、フーリエ・コサイン級数と呼ばれます。)
また、周期関数
(フーリエ正弦級数、フーリエ・サイン級数と呼ばれます。)
周期Tの偶関数・奇関数のときのフーリエ級数展開
ではここで1問計算練習をしてみましょう!
例題
下の図ような周期関数
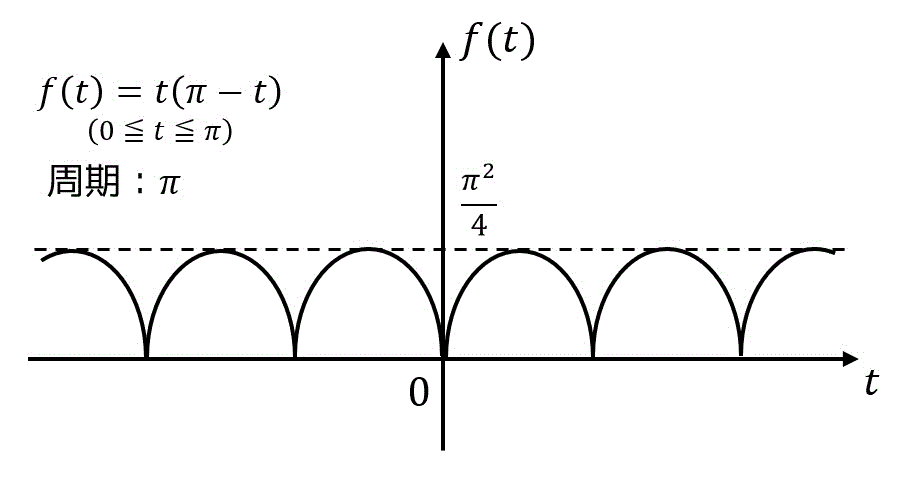
解説
また、周期が
さらにグラフより
(i)
(ii)
多項式と三角関数の積で表された関数を積分する際には部分積分を行うのですが、下の記事で説明している部分積分の連鎖公式を適用していくと比較的早く部分積分を行うことができます。
計算式は、
よって、
5.フーリエ級数展開を用いた無限級数の求め方
先ほど求めたフーリエ級数展開から様々な無限級数の和を導くことができます。
先ほど求めた周期が
よって、
(この無限級数はバーゼル問題と呼ばれています。)
さらに
よって、
ただし、このようにフーリエ級数展開から無限級数を求める際には、代入する
6.練習問題
では、3問ほど練習してみましょう!
練習1
下の図のような周期関数
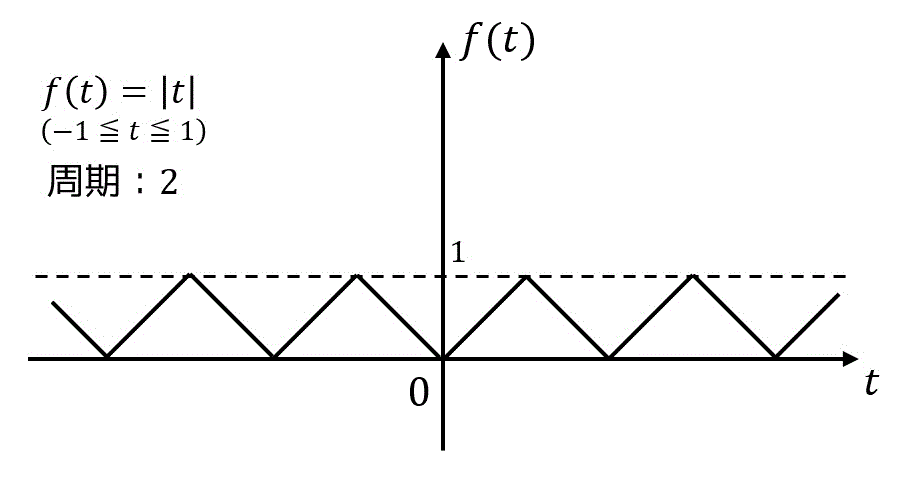
(1)
(2) (1)から
練習2
下の図のような周期関数
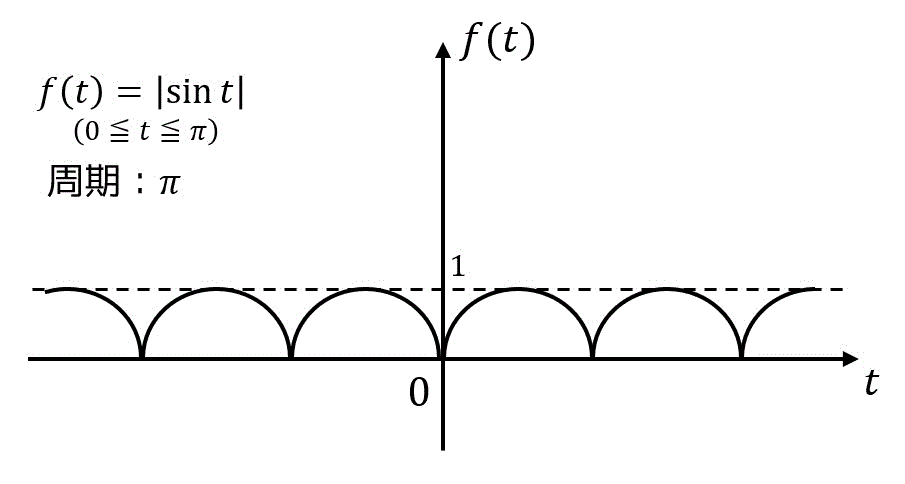
練習3
下の図のような周期関数
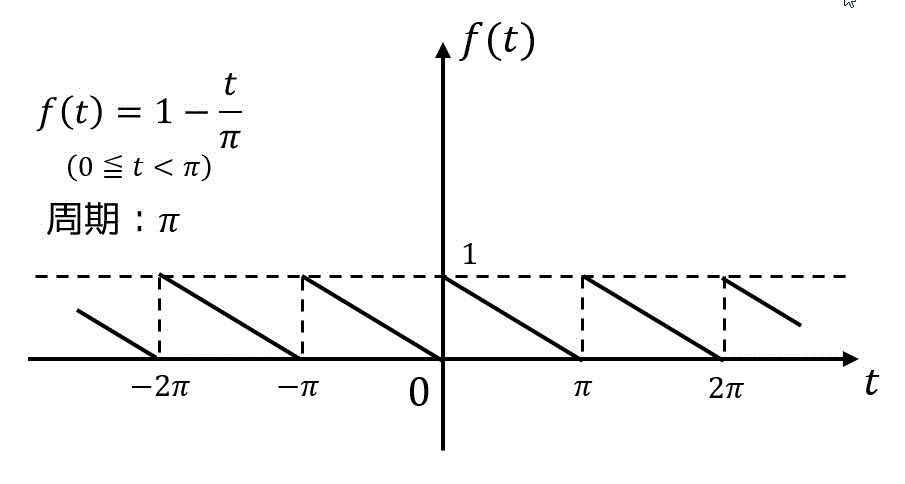
(1)
(2) (1)から
7.練習問題の答え
解答1
(1)
(i)
(ii)
よって、フーリエ級数展開は
(2)
ここで、
目標の形は、
解答2
(i)
(ii)
よって、フーリエ級数展開は
解答3
すると、グラフは
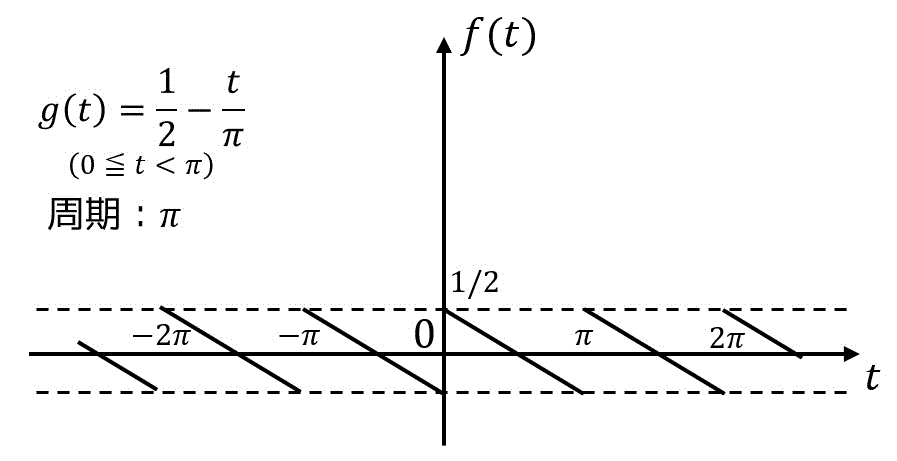
となる。グラフより、
さらに周期
よって、フーリエ級数展開は
(2)
目標の形は、
8.さいごに
今回はフーリエ級数展開の簡単なしくみ、および計算方法を例題などを踏まえながらまとめました。
この記事を読んでフーリエ級数展開の仕組みなどが少しでもわかっていただければ本当にありがたいです。
余裕があれば複素フーリエ級数展開、フーリエ変換についてもまとめてみようかと思います。
また、フーリエ級数展開の計算は結構めんどくさいものが多いのでしっかりと計算練習をしておきましょう。
*1:公式1
*2:途中で不連続な箇所があるような関数だと思ってください。例えば、練習3の
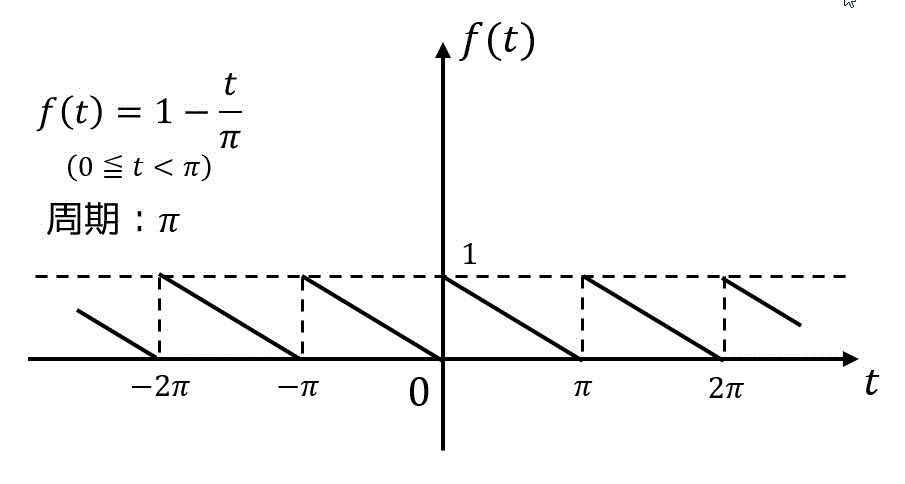
のような関数でもフーリエ級数展開できるよってことです。
*3:
(逆にいうと、関数
*4:例えば、
*5:
*6:心拍数の平均が60bpm〜80bpmなので0.75〜1秒に1周期となる。
*7:角速度とは単位時間あたりに進む角度を表します。今回の場合は角度というよりも波の変化の速さと考えるのがいいと思います。例えば角速度が2倍になれば波の変化の速さも2倍になり、周期は1/2となります。
*8:つまり、
*9:
関連広告・スポンサードリンク