スポンサードリンク
こんにちは、ももやまです!
今回は複素積分を使って不定積分をせずに実数範囲の積分を求める方法についてまとめました!
ちなみに留数定理を用いた実関数の定積分は院試とかで結構見かけるので院試受けるかもしれない人は長期記憶に入れときましょう!
前回の複素解析の記事はこちら!
ローラン展開や4つの特異点の分類などについてまとめているので、「あれれ」と思った人はこちらの記事で復習しましょう。
目次
スポンサードリンク
1.複素積分の便利さ
例えば、\[
\int^{\infty}_{- \infty} \frac{1}{1+x^2} \ dx
\]の積分をどう計算するかを考えてみましょう。
この場合だと、\[\begin{align*} &
\int^{R}_{- R} \frac{1}{1+x^2} \ dx
\\ = & 2 \int^{R}_{0} \frac{1}{1+x^2} \ dx
\\ = & 2 \left[ \tan^{-1} x \right]^{R}_0
\\ = & 2 \tan^{-1} R
\end{align*} \]と計算でき、\[
\lim_{R \to\infty} \tan^{-1} R = \frac{\pi}{2}
\]なので、\[\begin{align*} &
\int^{\infty}_{- \infty} \frac{1}{1+x^2} \ dx
\\ = & \lim_{R \to \infty} \int^{R}_{- R} \frac{1}{1+x^2} \ dx
\\ = & \ 2 \cdot \frac{\pi}{2}
\\ = & \ \pi
\end{align*} \]と求められますね。
では、\[
\int^{\infty}_{- \infty} \frac{1}{x^4+1} \ dx
\]だとどうでしょうか。
おそらく不定積分をしようとした瞬間あきらめたくなりますよね。実際不定積分をしてみると、\[\begin{align*} &
\int^{\infty}_{- \infty} \frac{1}{x^4+1} \ dx
\\ = & - \frac{ \sqrt{2} }{8} \log (x^2 - \sqrt{2}x + 1) + \frac{\sqrt{2} }{8} ( x^2 + \sqrt{2} x + 1) - \frac{ \sqrt{2} }{4} (1 - \sqrt{2} x ) + \frac{ \sqrt{2} }{4} (1 + \sqrt{2} x) + C
\end{align*}\]とかいうえげつないことになりますよね。
そこで今回は不定積分をせずに複素解析の力を使って定積分\[
\int^{\infty}_{- \infty} \frac{1}{x^4+1} \ dx
\]の値を出す話を考えてみましょう。
と言っても「複素解析なのになんで実関数の積分??」って思うかもしれません。
スポンサードリンク
2.実関数の積分に必要な複素解析の道具
では次に実関数を複素解析の力を使って解くために必要な知識を紹介していきたいと思います。
(1) 特異点・極
まずは特異点について少し説明しましょう。
例えば\[
f(z) = \frac{1}{z-z_0}
\]の \( z = z_0 \) のように、分母が0になるなどの理由で正則ではないような点のことを孤立特異点と呼びます。
さらに、\( g(z) \) が \( z = z_0 \) のときも正則であるとき、\[
f(z) = \frac{g(z)}{(z-z_0)^k}
\]の \( z = z_0 \) の点のことを、\( k \) 位の極と呼びます。
(とくに \( k = 1 \) の極のことを単純極と呼ぶこともあります。)
(2) 留数
(i) 留数とは
留数とは、留まる数、言い換えると積分しても0にならないような数を表しています。
複素積分の場合、積分範囲 \( C \) の内部で \( f(z) \) が正則である場合、コーシーの積分定理\[
\oint_c f(z) \ dz = 0
\]が成立しましたね。
しかし、積分範囲 \( C \) の内部が正則ではない場合、積分結果は0にはなりません。このように積分後に0とならずに留まってしまうような数のことを留数と呼びます。
(ii) 留数の求め方
ではどうやって留数を求めていくのかを説明していきましょう。
留数はローラン展開の -1 次の項\[
\frac{a_{-1}}{z-z_0}
\]として求めることができるのですが、いちいちローラン展開を考えるのはめんどくさいですよね。
なので、もっと簡単に導出する方法を考えましょう。
(a) 1位の極(単純極)のとき
まずは1位の極をもつ場合です。このときのローラン展開は\[
f(z) = \frac{a_{-1}}{z-z_0} + a_0 + a_1 (z - z_0 ) + a_2 (z-z_0)^2 + \cdots
\]と求めることができます。
このときの \( a_{-1} \) を求めればよいですね。なので無理やり \( (z - z_0) \) を掛けて分数を消しましょう。さらに \( a_0 \) 以降の余分な項を消してやるために極限 \( z \to z_0 \) を取りましょう。つまり、\[\begin{align*} &
\lim_{z \to z_0} (z - z_0) f(z) \\ = &
\lim_{z \to z_0} (z - z_0) \left( \frac{a_{-1}}{z-z_0} + a_0 + a_1 (z - z_0) \right)
\\ = & \lim_{z \to z_0} \left( a_{-1} + a_0 (z - z_0) + a_1 (z-z_0)^2 + \cdots \right)
\\ = & \ a_{-1}
\end{align*}\]と計算すればよいのです。
複素関数 \( f(z) \) が \( z = z_0 \) において1位の極をもつ場合、その留数は\[
\mathrm{Res} \ f(z_0) = \lim_{z \to z_0} (z - z_0) f(z) = a_{-1}
\]と求められる。
※ \( a_{-1} \) はローラン展開の-1次の項の係数を表す
(b) 2位以上の極(\( m \) 位の極をもつ)のとき
つぎに2位以上の極(\( m \) 位とする)をもつ場合です。このときのローラン展開は\[
f(z) = \frac{ a_{-m} }{ (z-z_0)^m } + \cdots + \frac{ a_{-1} }{ (z-z_0) } + a_0 + a_1 (z - z_0) \cdots
\]と求めることができます。
このときの \( a_{-1} \) を求めればよいですね。ですが1位と同じような解き方をすると極限が発散してしまいうまく求められません。
そこで、式全体に無理やり \( (z - z_0)^m \) を掛けてさらに \( m-1 \) 回微分をしてから極限を取りましょう。つまり、\[\begin{align*} &
\lim_{z \to z_0} \frac{ d^{m-1} }{ d z^{m-1} } (z - z_0)^m f(z) \\ = &
\lim_{z \to z_0} \frac{ d^{m-1} }{ d z^{m-1} } (z - z_0)^m \left( \frac{ a_{-m} }{ (z-z_0)^m } + \cdots + \frac{ a_{-1} }{ (z-z_0) } + a_0 + a_1 (z - z_0) \cdots \right)
\\ = & \lim_{z \to z_0} \frac{ d^{m-1} }{ d z^{m-1} } \left( a_{-m} + a_{-m+1} (z - z_0) + \cdots a_{-1} (z-z_0)^{m-1} + a_0 (z - z_0)^m + \cdots \right)
\\ = & \lim_{z \to z_0} \left( (m-1)! a_{-1} + m! a_0 (z- z_0) + \frac{1}{2} a_1 (z-z_0)^2 + \cdots \right)
\\ = & (m-1)! a_{-1}
\end{align*}\]と計算すればよいのです。
複素関数 \( f(z) \) が \( z = z_0 \) において2位以上の \( m \) 位の極をもつ場合、その留数は\[
\mathrm{Res} \ f(z_0) = \frac{1}{(m-1)!} \lim_{z \to z_0} \frac{d^{m-1}}{dz^{m-1}} (z - z_0)^m f(z) = a_{-1}
\]と求められる。
※ \( a_{-1} \) はローラン展開の-1次の項の係数を表す
例えば2位の極の場合、\( m = 2 \) を代入して\[\begin{align*}
\mathrm{Res} \ f(z_0) = \lim_{z \to z_0} \frac{d}{dz} (z - z_0)^2 f(z) = a_{-1}
\end{align*}\]となり、3位の極の場合、\( m = 3 \) を代入して\[\begin{align*}
\mathrm{Res} \ f(z_0) = \frac{1}{2} \lim_{z \to z_0} \frac{d^2}{dz^2} (z - z_0)^3 f(z) = a_{-1}
\end{align*}\]と求めることができます。
(3) 留数定理
留数とは積分後に0とならずに留まってしまうような数のことを指すことを先ほど説明しましたね。
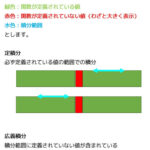
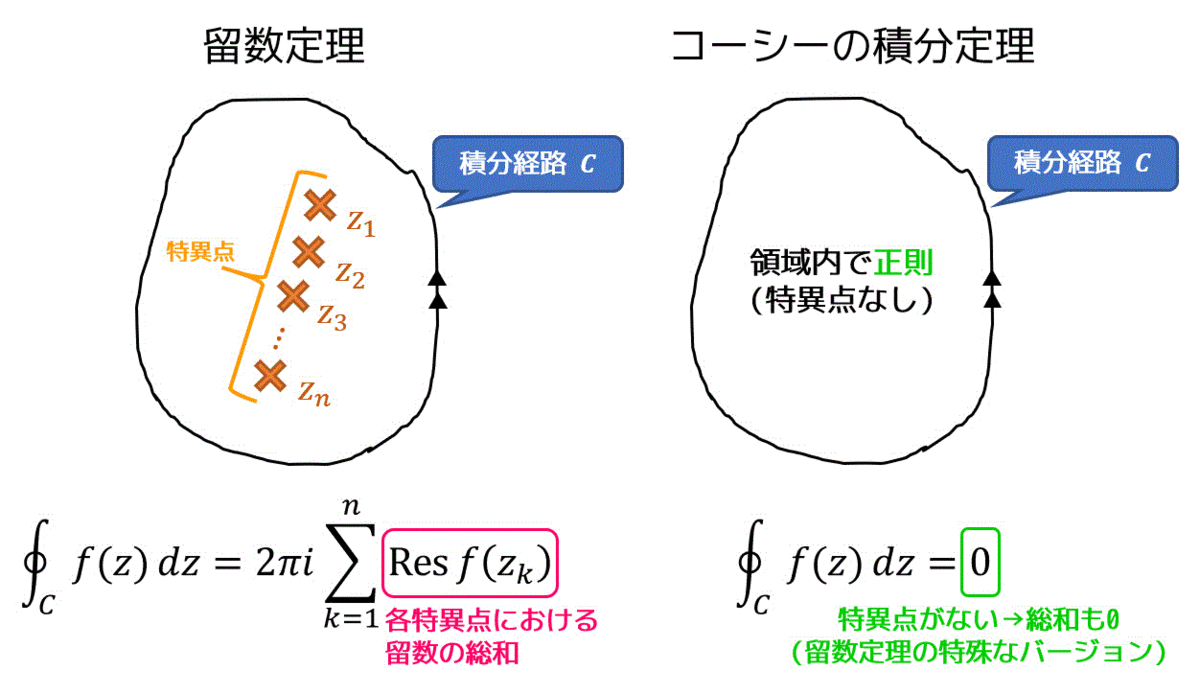
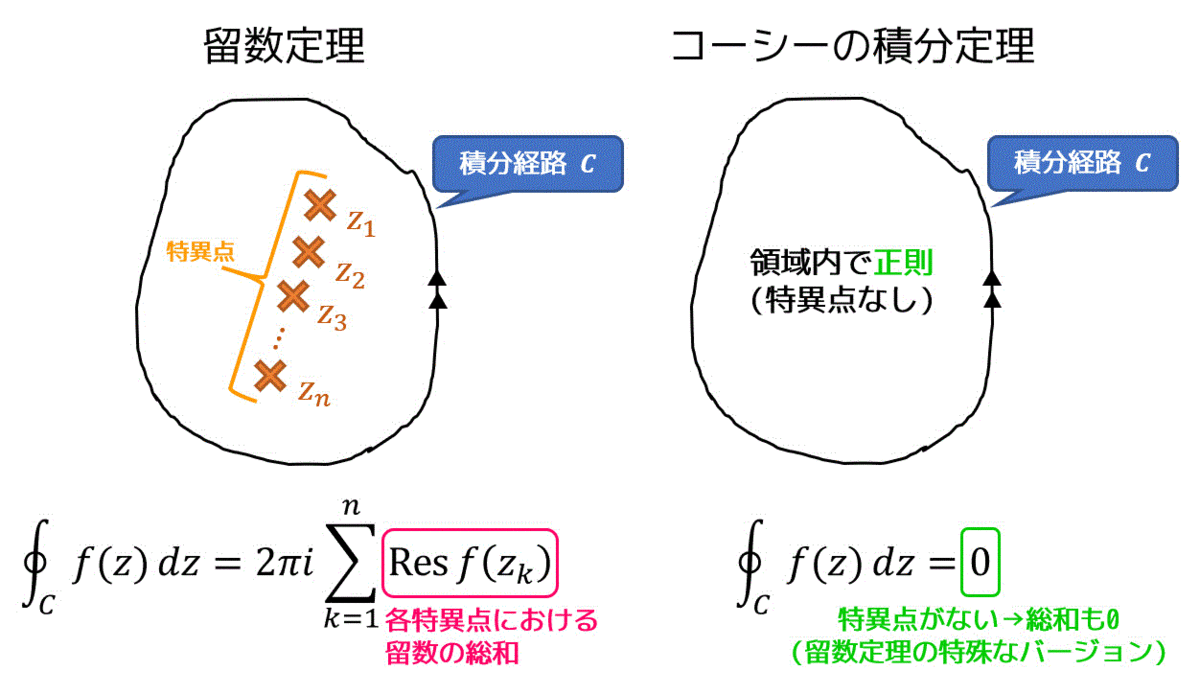
留数定理は、積分領域内にある0とならずに留まってしまう数(留数)をすべて足し込むことで積分結果を求めることができるよ! っていう定理です。数式で書くと、\[
\oint_c f(z) \ dz = 2 \pi i \sum^{n}_{k = 1} \mathrm{Res} \ f(z_k)
\]となります。
図で表すと下のようになります! コーシーの積分定理とも比較しています。
スポンサードリンク
3.
では実際に複素解析の力を使って\[
\int^{\infty}_{- \infty} \frac{1}{x^4+1} \ dx
\]を積分をしてみましょう。
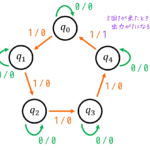
Step1:積分経路を決める
まずは複素積分を複素数平面上のどの経路で1周積分するのかを決める必要があります。
今回の場合は、経路に積分範囲が負の無限大から正の無限大なので、負の無限大から正の無限大を含むようにする必要があります。
なので、下のような半径 \( R \) の半円とし、向きは \( -R \) から \( R \) 方向としてください。
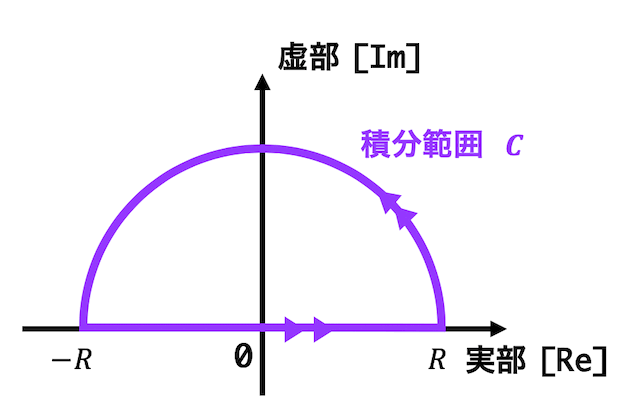
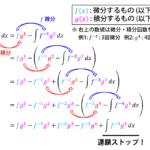
つぎに、この積分範囲を \( -R \) から \( R \) の直線部分 \( C_1 \) と半円部分 \( C_2 \) に分割します。
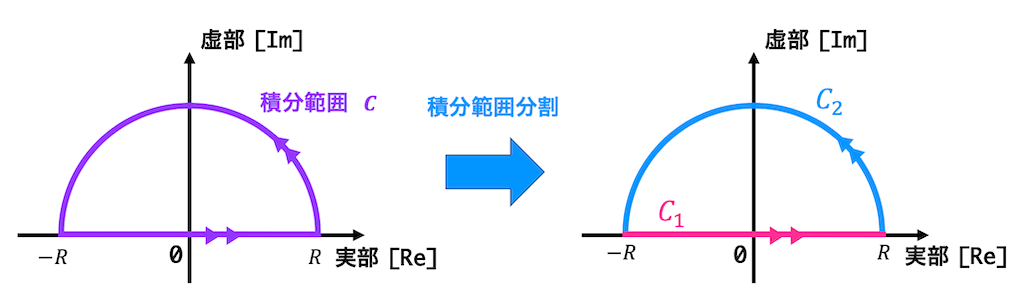
式で書くと、\[
\oint_C \frac{1}{1+z^4} \ dz = \color{orangered}{\oint_{C_1} \frac{1}{1+z^4} \ dz} + \color{royalblue}{\oint_{C_2} \frac{1}{z^4+1} \ dz}
\]となりますね。
ここで \( C_1 \) の積分は \( -R \) から \( R \) までの実軸の積分ですね。なので、\[
\color{orangered}{\oint_{C_1} \frac{1}{z^4+1} \ dz} = \int^{R}_{-R} \frac{1}{x^4 + 1} \ dx
\]ですね。
Step2:余分な部分が0であることを示す
ここで、\[
\color{royalblue}{\oint_{C_2} \frac{1}{z^4 + 1} \ dz}
\]は実積分を求めるにあたって邪魔ですよね。なのでこの部分が0であることを示しましょう。
\( C_2 \) 上の点を \( z = R e^{i \theta} \) とする。
すると \( dz = i R e^{i \theta} \ d \theta \) と表せる。よって、\[\begin{align*}
& \oint_{C_2} \left| \frac{1}{z^4+1} \ dz \right|
\\ = & \int^{\pi}_{0} \left| \frac{1}{R^4 e^{4 i \theta} + 1} \right| \cdot \left| i R e^{i \theta} d \theta \right|
\\ \leqq & \int^{\pi}_0 \frac{R}{R^4 - 1} \ d \theta
\\ = & \ \frac{R \pi}{R^4 - 1}
\end{align*}\]となる。*1ここで、\[
\lim_{R \to \infty} \frac{R \pi}{R^4 - 1} = 0
\]より、\[
\oint_{C_2} \frac{1}{z^4 + 1} \ dz = 0
\]であることが示せた。
よって、\[
\oint_C \frac{1}{z^4 + 1} \ dz = \int^{R}_{-R} \frac{1}{x^4 + 1} \ dx
\]が成り立つ。
Step3:積分範囲内にある特異点を求める
つぎに、\[
\oint_C \frac{1}{z^4 + 1} \ dz
\]を求めるために、まずは被積分関数\[
\frac{1}{z^4 + 1}
\]の特異点を求めます。\( z^4 + 1 = 0 \) を満たせばいいので、\[
z^4 = -1 = e^{(1+ 2n) i\pi}
\]を満たすような \( z \) が特異点となる。そのような特異点 \( z \) は、\[
z = e^{\frac{\pi}{4} i}, \ e^{\frac{3}{4} \pi i} , \ e^{\frac{5}{4} \pi i} , \ e^{\frac{7}{4} \pi i}
\]の4つである。
それぞれの特異点を図示すると下のようになる。
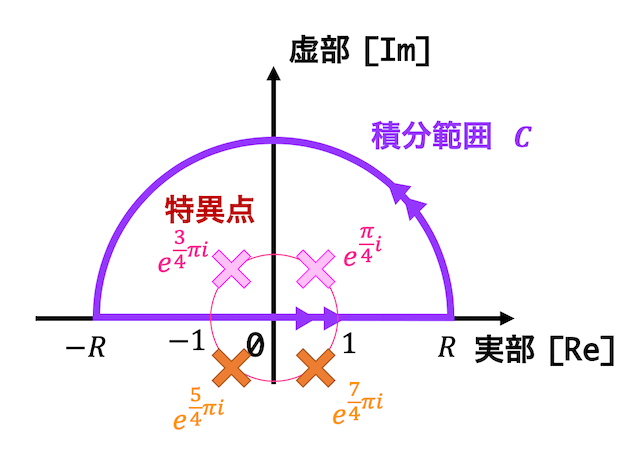
4つの特異点の中で積分範囲 \( C \) の中にあるような点は\[
z = e^{\frac{\pi}{4} i}, \ e^{\frac{3}{4} \pi i}
\]の2つである。ここで、\[
\alpha = e^{\frac{\pi}{4} i} , \ \beta = e^{\frac{3}{4} \pi i}
\]とおく。
Step4:それぞれの積分領域内の特異点における留数を求める
つぎにそれぞれの特異点における留数を求めます。\[\begin{align*}
\mathrm{Res} \ f(\alpha) & = \lim_{z \to \alpha} \frac{z - \alpha}{z^4 + 1}
\\ & = \lim_{z \to \alpha} \frac{1}{4 z^3}
\\ & = \frac{1}{4} e^{- \frac{3}{4} \pi i}
\\ & = \frac{1}{4} \left( \cos \left( - \frac{3}{4} \pi \right) + i \sin \left( - \frac{3}{4} \pi \right) \right)
\\ & = \frac{1}{4} \left( - \frac{ \sqrt{2} }{2} - \frac{ \sqrt{2} }{2} i \right)
\end{align*}\]\[\begin{align*}
\mathrm{Res} \ f(\beta) & = \lim_{z \to \beta} \frac{z - \beta}{z^4 + 1}
\\ & = \lim_{z \to \beta} \frac{1}{4 z^3}
\\ & = \frac{1}{4} e^{- \frac{9}{4} \pi i}
\\ & = \frac{1}{4} e^{- \frac{\pi}{4} i}
\\ & = \frac{1}{4} \left( \cos \left( - \frac{\pi}{4} \right) + i \sin \left( - \frac{\pi}{4} \right) \right)
\\ & = \frac{1}{4} \left( \frac{ \sqrt{2} }{2} - \frac{ \sqrt{2} }{2} i \right)
\end{align*}\]となる*2。
留数定理の計算のコツはロピタルの定理を使うことです。
ロピタルの定理ってなんだったっけと思った人は下の記事をご覧ください。
Step5:留数の合計に2πiを掛けたものが積分値
最後に留数を全部足し合わせ、\( 2 \pi i \) を掛けます。\[\begin{align*}
\oint_C \frac{1}{z^4 + 1} \ dz = & \int^{R}_{-R} \frac{1}{x^4 + 1} \ dx
\\ = & \ 2 \pi i \left( \frac{1}{4} \left( - \frac{ \sqrt{2} }{2} - \frac{ \sqrt{2} }{2} i \right) + \frac{1}{4} \left( \frac{ \sqrt{2} }{2} - \frac{ \sqrt{2} }{2} i \right) \right)
\\ = & \ 2 \pi i \cdot \left( - \frac{ \sqrt{2} }{4} i \right)
\\ = & \ \frac{ \sqrt{2} }{2} \pi
\end{align*}\]となるので、\[\begin{align*}
\int^{\infty}_{- \infty} \frac{1}{x^4+1} \ dx
& = \lim_{R \to \infty} \int^{R}_{-R} \frac{1}{x^4 + 1} \ dx
\\ & = \ \frac{ \sqrt{2} }{2} \pi
\end{align*}\]と求められます。
以上の5ステップで複素解析の力を使って不定積分を行わずに定積分を行うことができます。
4.置換積分と留数積分の併用
また、例えば、\[
\int^{\infty}_{- \infty} \frac{1}{x^4+a^4} \ dx
\]のように余計な \( a^4 \) が積分領域内にあったとしても、\[
x = ay , \ \ \ \ dx = a \ dy
\]と置換することで、\[\begin{align*}
\int^{\infty}_{- \infty} \frac{1}{x^4+a^4} \ dx & = \int^{\infty}_{- \infty} \frac{1}{(ya)^4+a^4} \cdot a \ dy
\\ & = \int^{\infty}_{- \infty} \frac{a}{a^4 y^4+a^4} \ dy
\\ & = \frac{1}{a^3} \int^{\infty}_{- \infty} \frac{1}{y^4+1} \ dy
\end{align*}\]と変形することで、\[
\int^{\infty}_{- \infty} \frac{1}{y^4+1} \ dy = \frac{ \sqrt{2} }{2} \pi
\]であることを用いて、\[\begin{align*} &
\int^{\infty}_{- \infty} \frac{1}{x^4+a^4} \ dx
\\ = & \ \frac{1}{a^3} \int^{\infty}_{- \infty} \frac{1}{y^4+1} \ dy
\\ = & \ \frac{ \sqrt{2} }{2a^3} \pi
\end{align*} \]と求めることもできます!
(置換積分をしてから複素解析をすると複素解析が若干簡単になるよ!)
5.練習問題
では、3問ほど練習しましょう!
練習1
定積分\[
\int^{\infty}_{- \infty} \frac{1}{x^6 + 1} \ dx
\]を求めなさい。
練習2
定積分\[
\int^{\infty}_{- \infty} \frac{1}{(x^2 + 1)^2} \ dx
\]を求めなさい。
練習3
定積分\[
\int^{\infty}_{- \infty} \frac{1}{(x^2 + a^2)(x^2 + b^2)} \ dx
\]を求めなさい。
6.練習問題の答え
解答1
Step1:積分範囲の図示
積分範囲を下のようにする。

さらに積分範囲を \( -R \) から \( R \) の直線部分 \( C_1 \) と半円部分 \( C_2 \) に分割する。

式で表すと、\[
\oint_C \frac{1}{z^6 + 1} \ dz = \color{orangered}{\oint_{C_1} \frac{1}{z^6 + 1} \ dz} + \color{royalblue}{\oint_{C_2} \frac{1}{z^6 + 1} \ dz}
\]となる。
ここで \( C_1 \) の積分は \( -R \) から \( R \) までの実軸の積分なので、\[
\color{orangered}{\oint_{C_1} \frac{1}{z^6 + 1} \ dz} = \int^{R}_{-R} \frac{1}{z^6 + 1} \ dx
\]となる。
Step2:余計な部分が0であることを示す。
つぎに、\[
\oint_{C_2} \frac{1}{z^4+1} \ dz = 0
\]を示す。
\( C_2 \) 上の点を \( z = R e^{i \theta} \) とする。
すると \( dz = i R e^{i \theta} \ d \theta \) となるので\[\begin{align*}
& \oint_{C_2} \left| \frac{1}{z^6+1} \ dz \right|
\\ = & \int^{\pi}_{0} \left| \frac{1}{R^6 e^{6 i \theta} + 1} \right| \cdot \left| i R e^{i \theta} d \theta \right|
\\ \leqq & \int^{\pi}_0 \frac{R}{R^6 - 1} \ d \theta
\\ = & \ \frac{R \pi}{R^6 - 1}
\end{align*}\]となる。
ここで、\[
\lim_{R \to \infty} \frac{R \pi}{R^6 - 1} = 0
\]より、\[
\oint_{C_2} \frac{1}{z^6 + 1} \ dz = 0
\]であることが示せた。
よって、\[
\oint_C \frac{1}{z^6 + 1} \ dz = \int^{R}_{-R} \frac{1}{x^6 + 1} \ dx
\]が成り立つ。
Step3:領域内の特異点を調べる
被積分関数\[
\frac{1}{z^6 + 1}
\]の特異点は、\( z^6 + 1 = 0 \) を満たせばいいので、\[
z^6 = -1 = e^{(1+ 2n) i\pi}
\]を満たすような \( z \) が特異点となる。そのような特異点 \( z \) は、\[
z = e^{\frac{\pi}{6} i}, \ e^{\frac{\pi}{2} i} , \ e^{\frac{5}{6} \pi i} , \ e^{\frac{7}{6} \pi i}, \ \ e^{\frac{3}{2} \pi i} , \ \ e^{\frac{11}{6} \pi i}
\]の6つである。
それぞれの特異点を図示すると下のようになる。
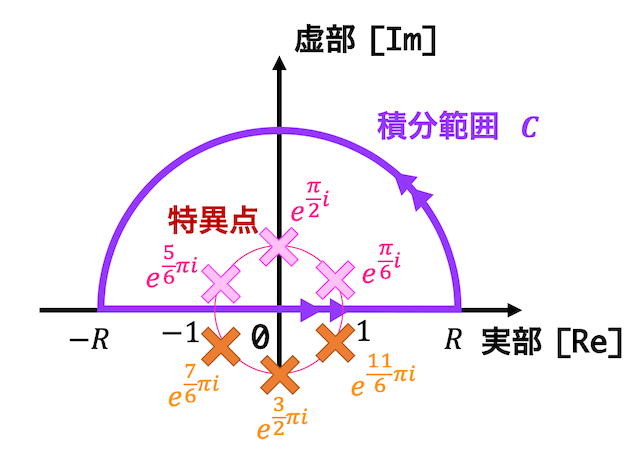
6つの特異点の中で積分範囲 \( C \) の中にあるような点は\[
z = e^{\frac{\pi}{6} i}, \ e^{\frac{\pi}{2} i} , \ e^{\frac{5}{6} \pi i}
\]の3つである。ここで、\[
\alpha = e^{\frac{\pi}{6} i} , \ \beta = e^{\frac{\pi}{2} i}, \ \gamma = e^{ \frac{5}{6} \pi i}
\]とおく。
Step4:それぞれの特異点における留数を算出
それぞれの特異点 \( \alpha \), \( \beta \), \( \gamma \) における留数は、\[\begin{align*}
\mathrm{Res} \ f(\alpha) & = \lim_{z \to \alpha} \frac{z - \alpha}{z^6 + 1}
\\ & = \lim_{z \to \alpha} \frac{1}{6 z^5}
\\ & = \frac{1}{6} e^{- \frac{5}{6} \pi i}
\\ & = \frac{1}{6} \left( \cos \left( - \frac{5}{6} \pi \right) + i \sin \left( - \frac{5}{6} \pi \right) \right)
\\ & = - \frac{ \sqrt{3} }{12} - \frac{1}{12} i
\end{align*}\]\[\begin{align*}
\mathrm{Res} \ f(\beta) & = \lim_{z \to \beta} \frac{z - \beta}{z^6 + 1}
\\ & = \lim_{z \to \beta} \frac{1}{6 z^5}
\\ & = \frac{1}{6} e^{- \frac{5}{2} \pi i}
\\ & = \frac{1}{6} e^{- \frac{\pi}{2} i}
\\ & = \frac{1}{6} \left( \cos \left( - \frac{\pi}{2} \right) + i \sin \left( - \frac{\pi}{2} \right) \right)
\\ & = - \frac{1}{6} i
\end{align*}\]\[\begin{align*}
\mathrm{Res} \ f(\gamma) & = \lim_{z \to \gamma} \frac{z - \gamma}{z^6 + 1}
\\ & = \lim_{z \to \gamma} \frac{1}{6 z^5}
\\ & = \frac{1}{6} e^{- \frac{25}{6} \pi i}
\\ & = \frac{1}{6} e^{- \frac{\pi}{6} i}
\\ & = \frac{1}{6} \left( \cos \left( - \frac{\pi}{6} \right) + i \sin \left( - \frac{\pi}{6} \right) \right)
\\ & = \frac{ \sqrt{3} }{12} - \frac{1}{12} i
\end{align*}\]となる。
Step5:留数を合計する
よって、\[\begin{align*}
\oint_C \frac{1}{z^6 + 1} \ dz = & \int^{R}_{-R} \frac{1}{x^6 + 1} \ dx
\\ = & \ 2 \pi i \left( - \frac{ \sqrt{3} }{12} - \frac{1}{12} i \right) + \left( - \frac{1}{6} i \right) + \left( \frac{ \sqrt{3} }{12} - \frac{1}{12} i \right)
\\ = & \ 2 \pi i \cdot \left( - \frac{ 1 }{3} i \right)
\\ = & \ \frac{ 2 }{3} \pi
\end{align*}\]となるので、\[\begin{align*}
\int^{\infty}_{- \infty} \frac{1}{x^6+1} \ dx
& = \lim_{R \to \infty} \int^{R}_{-R} \frac{1}{x^6 + 1} \ dx
\\ & = \frac{ 2 }{3} \pi
\end{align*}\]と求められる。
解答2
Step1:積分範囲の図示
積分範囲を下のようにする。

さらに積分範囲を \( -R \) から \( R \) の直線部分 \( C_1 \) と半円部分 \( C_2 \) に分割する。

式で表すと、\[
\oint_C \frac{1}{(z^2 + 1)^2} \ dz = \color{orangered}{\oint_{C_1} \frac{1}{(z^2 + 1)^2} \ dz} + \color{royalblue}{\oint_{C_2} \frac{1}{(z^2 + 1)^2} \ dz}
\]となる。
ここで \( C_1 \) の積分は \( -R \) から \( R \) までの実軸の積分なので、\[
\color{orangered}{\oint_{C_1} \frac{1}{(z^2 + 1)^2} \ dz} = \int^{R}_{-R} \frac{1}{(z^2 + 1)^2} \ dx
\]となる。
Step2:余計な部分が0であることを示す。
つぎに、\[
\oint_{C_2} \frac{1}{(z^2 + 1)^2} \ dz = 0
\]を示す。
\( C_2 \) 上の点を \( z = R e^{i \theta} \) とする。
すると \( dz = i R e^{i \theta} \ d \theta \) となるので\[\begin{align*}
& \oint_{C_2} \left| \frac{1}{(z^2 + 1)^2} \ dz \right|
\\ = & \int^{\pi}_{0} \left| \frac{1}{(R^2 e^{2 i \theta} + 1)^2} \right| \cdot \left| i R e^{i \theta} d \theta \right|
\\ \leqq & \int^{\pi}_0 \frac{R}{(R^2 - 1)^2 } \ d \theta
\\ = & \ \frac{R \pi}{(R^2 - 1)^2}
\end{align*}\]となる。
ここで、\[
\lim_{R \to \infty} \frac{R \pi}{(R^2 - 1)^2} = 0
\]より、\[
\oint_{C_2} \frac{1}{(z^2 + 1)^2} = 0
\]であることが示せた。
よって、\[
\oint_C \frac{1}{(z^2 + 1)^2} \ dz = \int^{R}_{-R} \frac{1}{(z^2 + 1)^2} \ dx
\]が成り立つ。
Step3:領域内の特異点を調べる
被積分関数\[
\frac{1}{(z^2 + 1)^2}
\]の特異点は、\( z^2 + 1 = 0 \) を満たせばいいので、\[
z^2 = -1 = e^{(1+ 2n) i\pi}
\]を満たすような \( z \) が2価の特異点となる。そのような特異点 \( z \) は、\[
z = e^{\frac{\pi}{2} i}, \ e^{\frac{3}{2} \pi i}
\]の2つである。
それぞれの特異点を図示すると下のようになる。
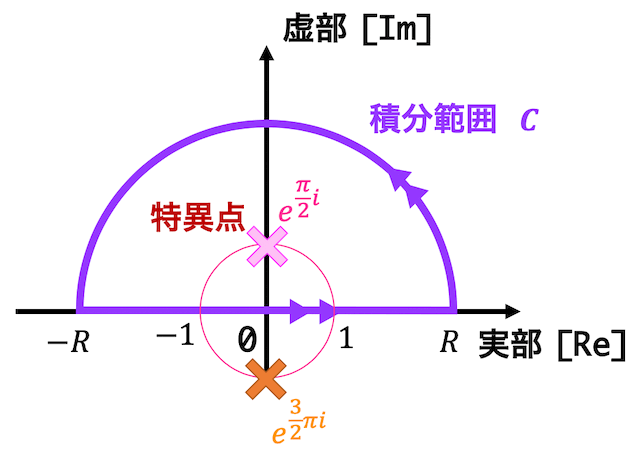
2つの特異点の中で積分範囲 \( C \) の中にあるような点は\[
z = e^{\frac{\pi}{2} i}
\]の1つである。ここで、\[
\alpha = e^{\frac{\pi}{2} i}
\]とおく。
Step4:それぞれの特異点における留数を算出
それぞれの特異点 \( \alpha \) における留数は、\[\begin{align*}
\mathrm{Res} \ f(\alpha) & = \lim_{z \to \alpha} \frac{d}{dz} \frac{(z - \alpha)^2}{(z^2 +1)^2}
\\ & =\lim_{z \to \alpha} \frac{d}{dz} \frac{(z - \alpha)^2}{(z - \alpha)^2 (z + \alpha)^2}
\\ & =\lim_{z \to \alpha} \frac{d}{dz} \frac{1}{(z + \alpha)^2}
\\ & =\lim_{z \to \alpha} - \frac{2}{(z + \alpha)^3}
\\ & = - \frac{2}{(2 \alpha)^3}
\\ & = - \frac{1}{4} e^{ - \frac{3}{2} i \pi }
\\ & = \frac{1}{4} \left( \cos \left( - \frac{3}{2} \pi \right) + i \sin \left( - \frac{3}{2} \pi \right) \right)
\\ & = - \frac{1}{4} i
\end{align*}\]となる。
Step5:留数を合計する
よって、\[\begin{align*}
\oint_C \frac{1}{(z^2 + 1)^2} \ dz = & \int^{R}_{-R} \frac{1}{(x^2 + 1)^2} \ dx
\\ = & \ 2 \pi i \left( - \frac{ 1}{4}i \right)
\\ = & \ \frac{\pi}{2}
\end{align*}\]となるので、\[\begin{align*}
\int^{\infty}_{- \infty} \frac{1}{(x^2+1)^2} \ dx
& = \lim_{R \to \infty} \int^{R}_{-R} \frac{1}{(x^2 + 1)^2} \ dx
\\ & = \ \frac{\pi}{2}
\end{align*}\]と求められる。
解答3
Step1:積分範囲の図示
積分範囲を下のようにする。

さらに積分範囲を \( -R \) から \( R \) の直線部分 \( C_1 \) と半円部分 \( C_2 \) に分割する。

式で表すと、\[
\oint_C \frac{1}{(z^2 + a^2)(z^2 + b^2)} \ dz = \color{orangered}{\oint_{C_1} \frac{1}{(z^2 + a^2)(z^2 + b^2)} \ dz} + \color{royalblue}{\oint_{C_2} \frac{1}{(z^2 + a^2)(z^2 + b^2)} \ dz}
\]となる。
ここで \( C_1 \) の積分は \( -R \) から \( R \) までの実軸の積分なので、\[
\color{orangered}{\oint_{C_1} \frac{1}{(z^2 + a^2)(z^2 + b^2)} \ dz} = \int^{R}_{-R} \frac{1}{(z^2 + a^2)(z^2 + b^2)} \ dx
\]となる。
Step2:余計な部分が0であることを示す。
つぎに、\[
\oint_{C_2} \frac{1}{(z^2 + a^2)(z^2 + b^2)} \ dz = 0
\]を示す。
\( C_2 \) 上の点を \( z = R e^{i \theta} \) とする。
すると \( dz = i R e^{i \theta} d \theta \) となるので\[\begin{align*}
& \oint_{C_2} \left| \frac{1}{(z^2 + a^2)(z^2 + b^2)} \ dz \right|
\\ = & \int^{\pi}_{0} \left| \frac{1}{ (R^2 e^{2 i \theta} + a^2)(R^2 e^{2 i \theta} + b^2) } \right| \cdot \left| i R e^{i \theta} d \theta \right|
\\ \leqq & \int^{\pi}_0 \frac{R}{(R^2 - a^2)(R^2 - b^2)} \ d \theta
\\ = & \ \frac{R \pi}{(R^2 - a^2)(R^2 - b^2)}
\end{align*}\]となる。
ここで、\[
\lim_{R \to \infty} \frac{R \pi}{(R^2 - a^2)(R^2 - b^2)} = 0
\]より、\[
\oint_{C_2} \frac{1}{(z^2 + a^2)(z^2 + b^2)} \ dz = 0
\]であることが示せた。
よって、\[
\oint_C \frac{1}{(z^2 + a^2)(z^2 + b^2)} \ dz = \int^{R}_{-R} \frac{1}{(x^2 + a^2)(x^2 + b^2)} \ dx
\]が成り立つ。
Step3:領域内の特異点を調べる
被積分関数\[
\frac{1}{(z^2 + a^2)(z^2 + b^2)}
\]の特異点は、\[(z^2 + a^2)(z^2 + b^2)= 0\] を満たせばいいので、\[
z = -a = a e^{(1+ 2n) i\pi}, \ \ \ z = -b = b e^{(1+ 2n) i\pi}
\]を満たすような \( z \) が特異点となる。そのような特異点 \( z \) は、\[
z = a e^{\frac{\pi}{2} i}, \ b e^{\frac{\pi}{2} i} , \ a e^{\frac{3}{2} \pi i} , \ b e^{\frac{3}{2} \pi i}
\]の4つである。
それぞれの特異点を図示すると下のようになる。
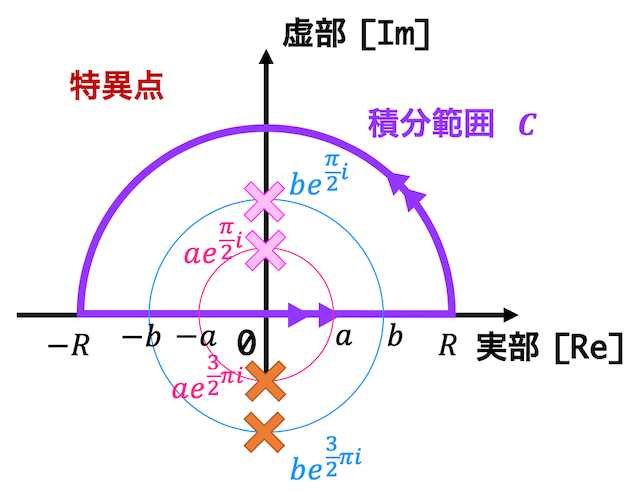
4つの特異点の中で積分範囲 \( C \) の中にあるような点は\[
z = a e^{\frac{\pi}{2} i}, \ b e^{\frac{\pi}{2} i}
\]の2つである。ここで、\[
\alpha = a e^{\frac{\pi}{2} i}, \ \beta = b e^{\frac{\pi}{2} i}
\]とおく。
Step4:それぞれの特異点における留数を算出
それぞれの特異点 \( \alpha \), \( \beta \) における留数は、\[\begin{align*}
\mathrm{Res} \ f(\alpha) & = \lim_{z \to \alpha} \frac{z - \alpha}{(z^2 + a^2)(z^2 + b^2)}
\\ & = \lim_{z \to \alpha} \frac{z - \alpha}{z^4 + (a^2+b^2)z^2 + a^2 b^2}
\\ & = \lim_{z \to \alpha} \frac{1}{4z^3 + 2 (a^2+b^2)z}
\\ & = \frac{1}{4a^3 e^{ \frac{3}{2} \pi } + 2 (a^2+b^2) a e^{ \frac{\pi}{2} i }}
\\ & = \frac{1}{ - 4 a^3i + 2 (a^3 + ab^2) i }
\\ & = -\frac{1}{ - 2 a^3i + 2 ab^2 i} \cdot i^2
\\ & = \frac{i}{ 2 a^3 - 2 ab^2}
\\ & = \frac{i}{ 2a(a^2-b^2)}
\end{align*}\]\[\begin{align*}
\mathrm{Res} \ f(\alpha) & = \lim_{z \to \beta} \frac{z - \beta}{(z^2 + a^2)(z^2 + b^2)}
\\ & = \lim_{z \to \beta} \frac{z - \beta}{z^4 + (a^2+b^2)z^2 + a^2 b^2}
\\ & = \lim_{z \to \beta} \frac{1}{4z^3 + 2 (a^2+b^2)z}
\\ & = \frac{1}{4b^3 e^{ \frac{3}{2} \pi } + 2 (a^2+b^2) b e^{ \frac{\pi}{2} i }}
\\ & = \frac{1}{ - 4 b^3i + 2 (b^3 + a^2 b) i }
\\ & = -\frac{1}{ - 2 b^3i + 2 a^2 b i} \cdot i^2
\\ & = \frac{i}{ 2 b^3 - 2 a^2 b}
\\ & = \frac{i}{ 2 b(b^2-a^2)}
\end{align*}\]となる。
Step5:留数を合計する
よって、\[\begin{align*}
\oint_C \frac{1}{(z^2 + a^2)(z^2 + b^2)} \ dz = & \int^{R}_{-R} \frac{1}{(x^2+a^2)(x^2+b^2)} \ dx
\\ = & \ 2 \pi i \left( \frac{i}{ 2a(a^2-b^2)} + \frac{i}{ 2b(b^2-a^2)} \right)
\\ = & \ 2 \pi i \left( \frac{(b-a)i}{2ab(a^2-b^2)} \right)
\\ = & \ \frac{\pi}{ab(a+b)}
\\ = & \ \frac{\pi}{a^2 b + ab^2}
\end{align*}\]となるので、\[\begin{align*}
\int^{\infty}_{- \infty} \frac{1}{(x^2+a^2)(x^2+b^2)} \ dx
& = \lim_{R \to \infty} \int^{R}_{-R} \frac{1}{(x^2+a^2)(x^2+b^2)} \ dx
\\ & = \ \frac{\pi}{a^2 b + ab^2}
\end{align*}\]と求められる。
部分分数分解をすると、\[\begin{align*} &
\int^{\infty}_{- \infty} \frac{1}{(x^2+a^2)(x^2+b^2)} \ dx
\\ = & \ \frac{1}{b^2-a^2} \int^{\infty}_{- \infty} \frac{1}{x^2+a^2} \ dx + \ \frac{1}{a^2-b^2} \int^{\infty}_{- \infty} \frac{1}{x^2+b^2} \ dx
\end{align*}\]と変形できる。
ここで、\[\begin{align*} &
\int^{\infty}_{- \infty} \frac{1}{x^2+a^2} \ dx
\\ = & \int^{\infty}_{- \infty} \frac{a}{a^2 s^2+a^2} \ ds
\\ = & \frac{1}{a} \int^{\infty}_{- \infty} \frac{1}{ s^2+1} \ ds
\end{align*}\]\[\begin{align*} &
\int^{\infty}_{- \infty} \frac{1}{x^2+b^2} \ dx
\\ = & \int^{\infty}_{- \infty} \frac{b}{b^2 s^2+b^2} \ dt
\\ = & \frac{1}{b} \int^{\infty}_{- \infty} \frac{1}{ t^2+1} \ dt
\end{align*}\]となるので、\[\begin{align*} &
\int^{\infty}_{- \infty} \frac{1}{(x^2+a^2)(x^2+b^2)} \ dx
\\ = & \ \frac{1}{a(b^2-a^2)} \int^{\infty}_{- \infty} \frac{1}{s^2+1} \ ds + \ \frac{1}{b(a^2-b^2)} \int^{\infty}_{- \infty} \frac{1}{t^2+1} \ dt
\end{align*}\]となる。
さらに、\[
\int^{\infty}_{- \infty} \frac{1}{x^2+1} \ dx = \pi
\]なので、\[\begin{align*} &
\int^{\infty}_{- \infty} \frac{1}{(x^2+a^2)(x^2+b^2)} \ dx
\\ = & \ \frac{1}{a(b^2-a^2)} \pi + \ \frac{1}{b(a^2-b^2)} \pi
\\ = & \ \frac{a-b}{ab(a^2-b^2)} \pi
\\ = & \ \frac{1}{ab(a+b)} \pi
\\ = & \ \frac{1}{a^2 b + ab^2} \pi
\end{align*}\]と求めることも可能。
7.さいごに
今回は留数定理を用いて実関数の定積分を求める方法についてまとめました。
不定積分をすることが難しいような積分であっても複素解析の力を借りることで不定積分をせずに積分結果を求めることができることがわかりましたね!
今回は積分範囲が半円だけでしたが、半円だと解けないような問題もあるので注意しましょう。また、留数定理にはロピタルの定理が有効なのでなるべく計算量を減らすためにもロピタルの定理は使えるようになっておきましょう!
*1:\[\begin{align*}
| e^{i \theta } | & = | \cos \theta + i \sin \theta |
\\ & = \sqrt{ \cos^2 \theta + \sin^2 \theta }
\\ & = \ 1
\end{align*}\]なので、\[
|iR e^{i \theta}| = |iR| |e^{i \theta}| = R
\]となる。また、\[
|R^4 + 1| \geqq |R^4| - |1| = R^4 - 1
\]なので、\[\begin{align*}
\frac{1}{| R^4 e^{4 i \theta} + 1 |} & = \frac{1}{|R^4 + 1|}
\\ & \leqq \frac{1}{R^4 - 1}
\end{align*}\]となる。
*2:1行目から2行目の計算\[
\lim_{z \to \alpha} \frac{z - \alpha}{z^4 + 1} = \lim_{z \to \alpha} \frac{1}{4 z^3}
\]でロピタルの定理を使うことでめんどくさい計算を省略しています。
関連広告・スポンサードリンク