スポンサードリンク
こんにちは、ももやまです。
前回は、Dフリップフロップを用いて順序回路を設計する方法について説明しました。
今回は、JKフリップフロップを用いて順序回路を設計する方法について学んでいきましょう!
目次
スポンサードリンク
[復習] JKフリップフロップとは
まずは、今回の順序回路の設計で使うJKフリップフロップについて軽く復習しましょう。
(1) JKフリップとは
JKフリップフロップは、2つの変数 \( J \), \( K \) を入力とすることで、次状態 \( Q_{n+1} \) を0, 1とするだけでなく、現状態 \( Q_n \) をそのまま保持したり、反転したりすることができる多機能なフリップフロップです。
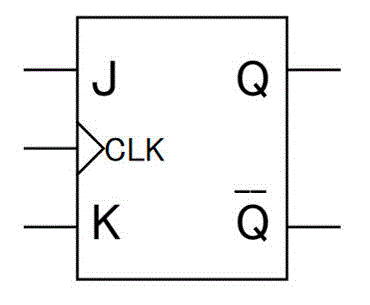
(\( \bar{Q} \) は、\( Q \) を反転した値を出力する)
JKフリップフロップの具体的な動きを、下の特性表[1]入力 \( J \), \( K \) および現状態 \( Q_n \) から次状態 \( Q_{n+1} \) がどのようになるかを表にしたもので確認しましょう。
JKフリップフロップの状態遷移表(特性表)
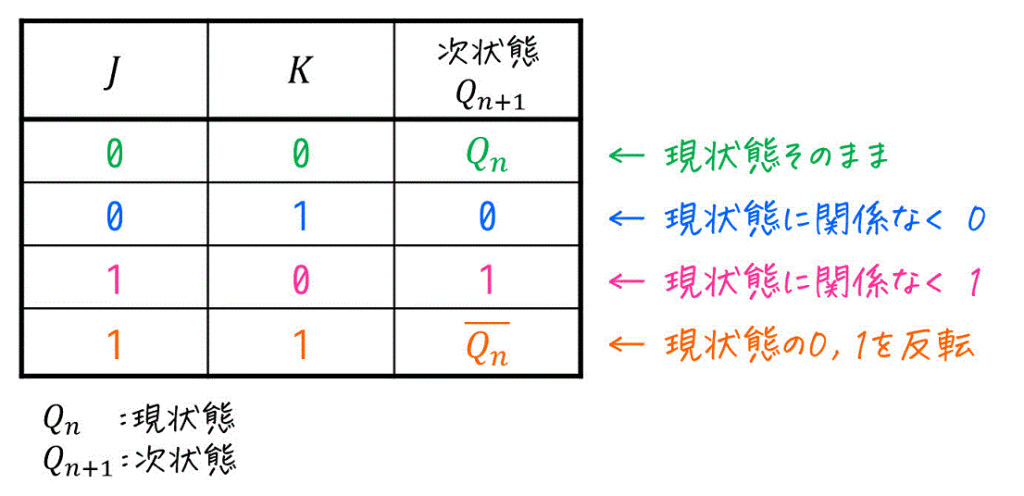
なお、特性表の書き方はテキストや講義によって結構変わってきます。例えば、下のように現状態 \( Q_n \) を0, 1で場合分けしてから書く書き方があります。
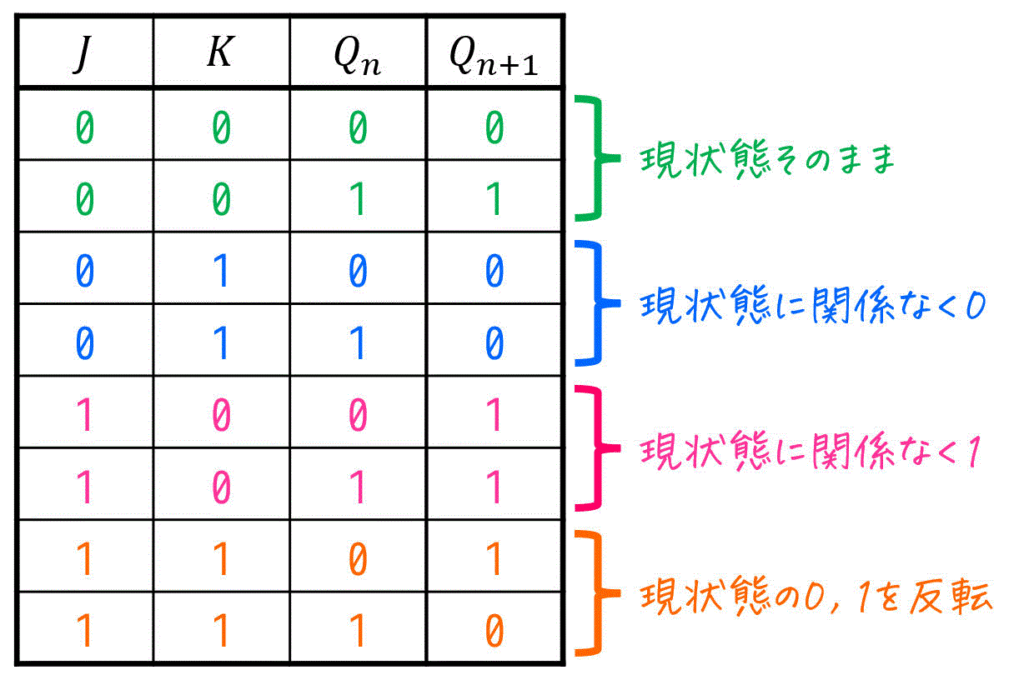
(2) JKフリップフロップの励起表
(1)では、「各入力 \( J \), \( K \) および現状態 \( Q_{n} \) から、次状態 \( Q_{n+1} \) がどうなるか」を表にすることで確認しましたね。この表は、特性表と呼ばれます。
一方、順序回路の設計をする際には「現状態 \( Q_n \) から次状態 \( Q_{n+1} \) に遷移させるためには、フリップフロップにどんな値を入力すればよいか」を考える必要があります。
そこで、特性表から「現状態 \( Q_n \) から次状態 \( Q_{n+1} \) に遷移させるためには、どんな値をフリップフロップに入力すべきか」を求め、結果を表で列挙することにしましょう。
(この表は励起表(れいきひょう)と呼ばれます。)
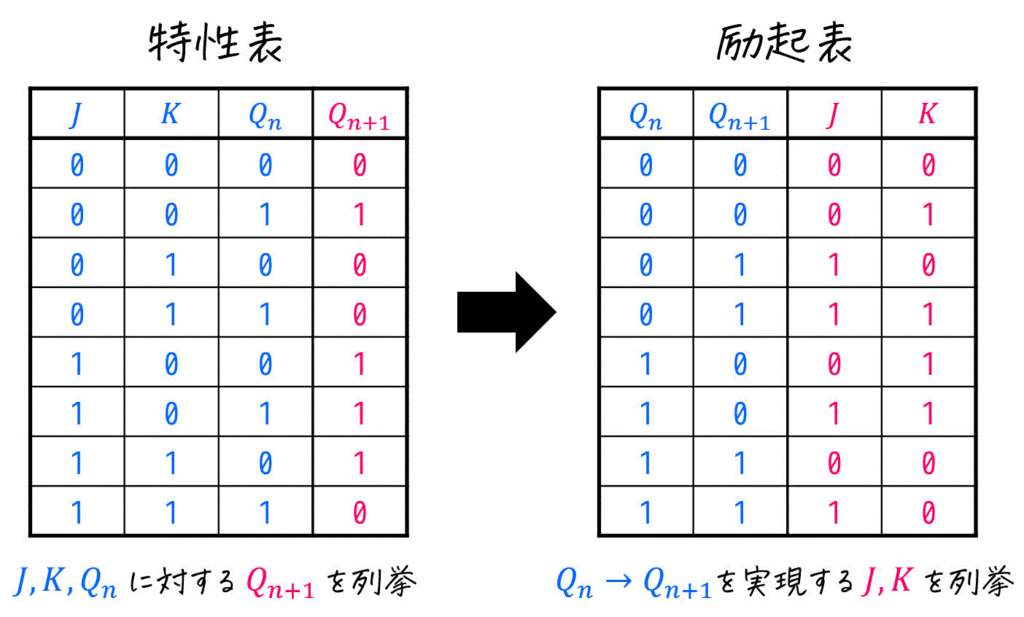
励起表の表記法も、特性表のときと同じように何通りかあります。そこで今回は、最も簡潔に書けて、なおかつ実際に順序回路の設計でも使いやすいに変形していきましょう。
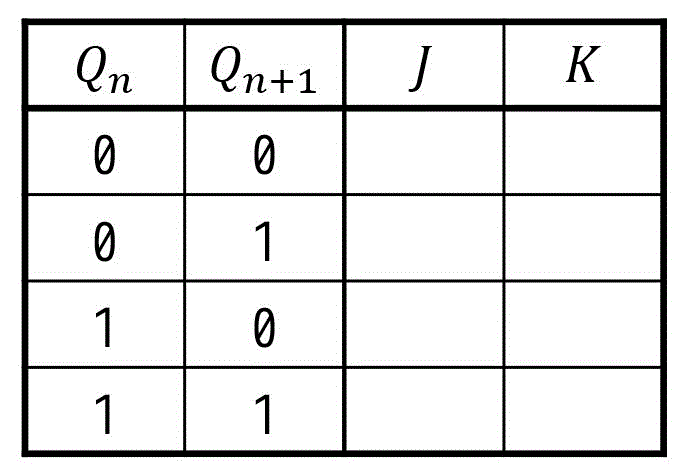
(シンプルにまとまった励起表と命名します)
まずは、先ほど変形した励起表の現状態 \( Q_n \) の値に注目しましょう。すると、
- \( Q_n = 0 \) のとき … \( K \) が0だろうが1だろうが \( J \) の値だけで \( Q_{n+1} \) の値が決まる
→ \( K \) の値はどうでもいい - \( Q_n = 1 \) のとき … \( J \) が0だろうが1だろうが \( K \) の値だけで \( Q_{n+1} \) の値が決まる
→ \( J \) の値はどうでもいい
ことがわかりますね。
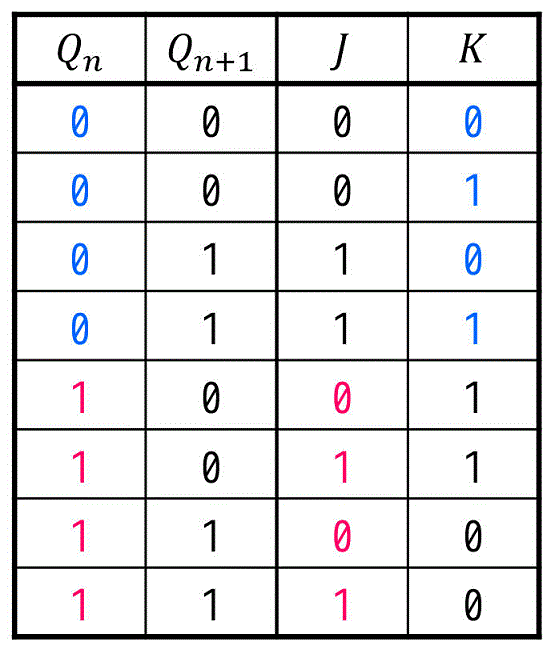
つまり、現状態 \( Q_n = 0 \) のときは \( K \) がDon't Careに、現状態 \( Q_n = 1 \) のときは \( J \) がDon't Careになることがわかりますね。
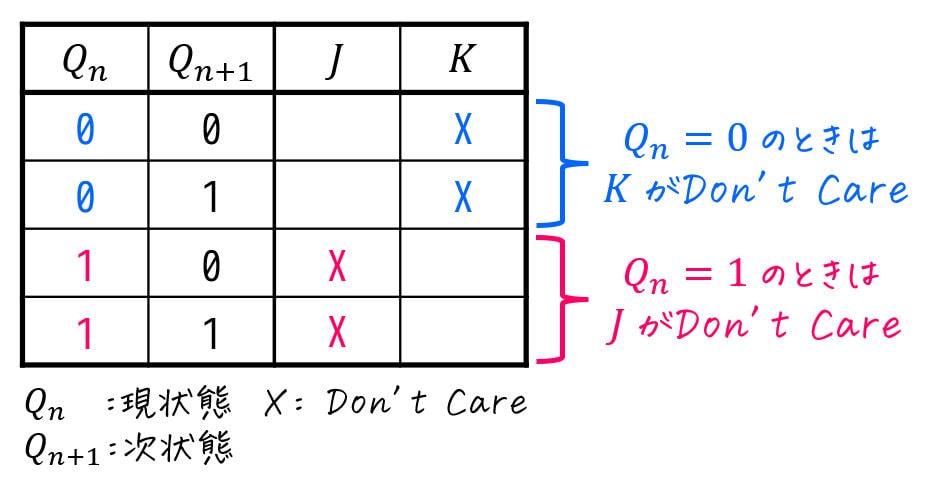
再び変形した(8行ある方の)励起表に戻りましょう。すると、
- 現状態 \( Q_n \) と次状態 \( Q_{n+1} \) が同じとき [ \( Q_n = Q_{n+1} \) ]
→ Don't Careではない方のFF入力は0 - 現状態 \( Q_n \) と次状態 \( Q_{n+1} \) が異なるとき [ \( Q_n \not = Q_{n+1} \) ]
→ Don't Careではない方のFF入力は1
こともわかりますね。
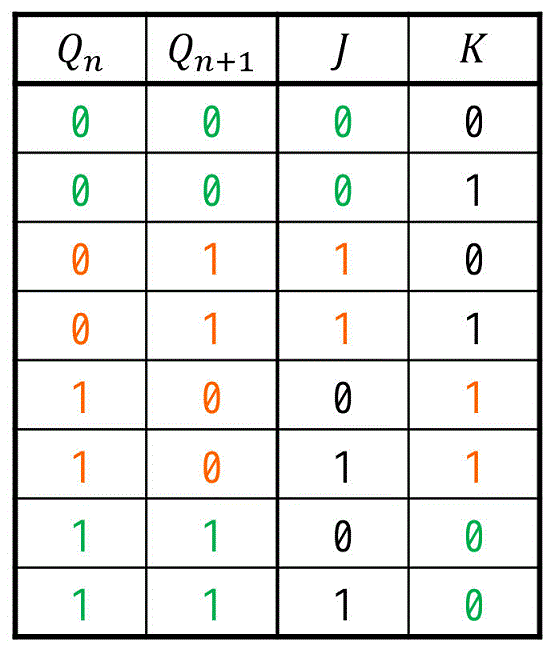
よって、シンプルにまとまった表の空欄を、下のように埋めることができます。
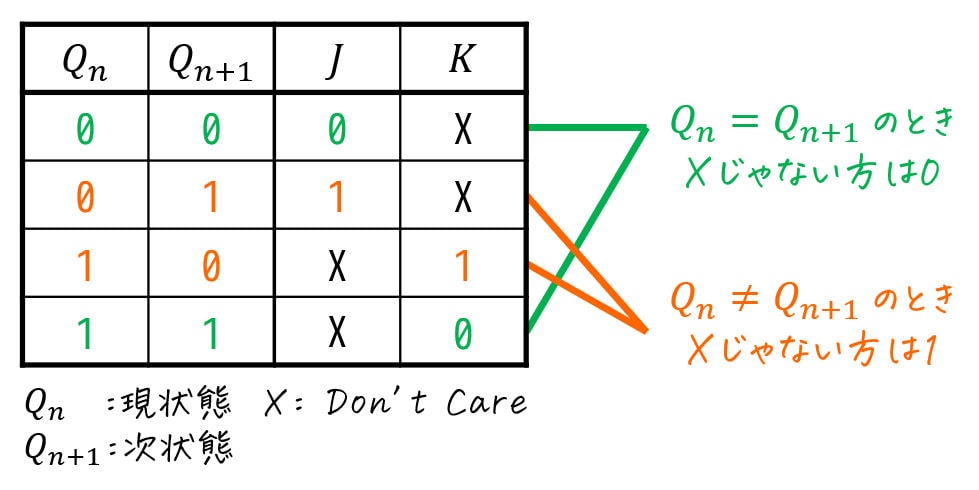
よって、JKフリップフロップの「シンプルにまとまった励起表」は下のようになります。
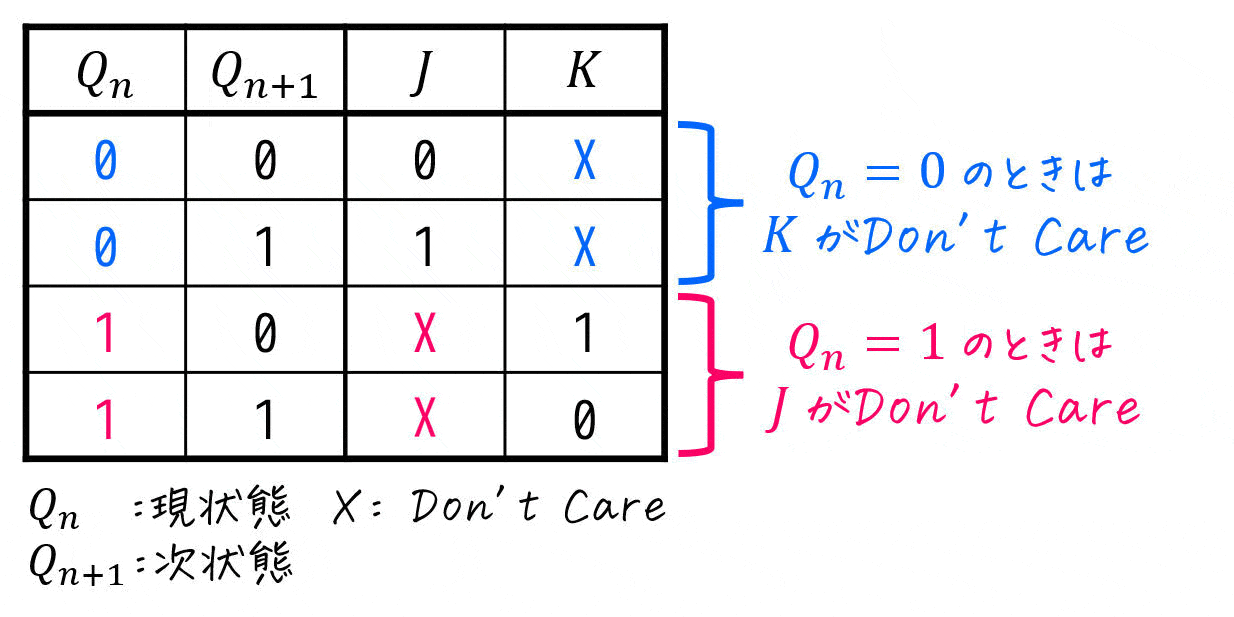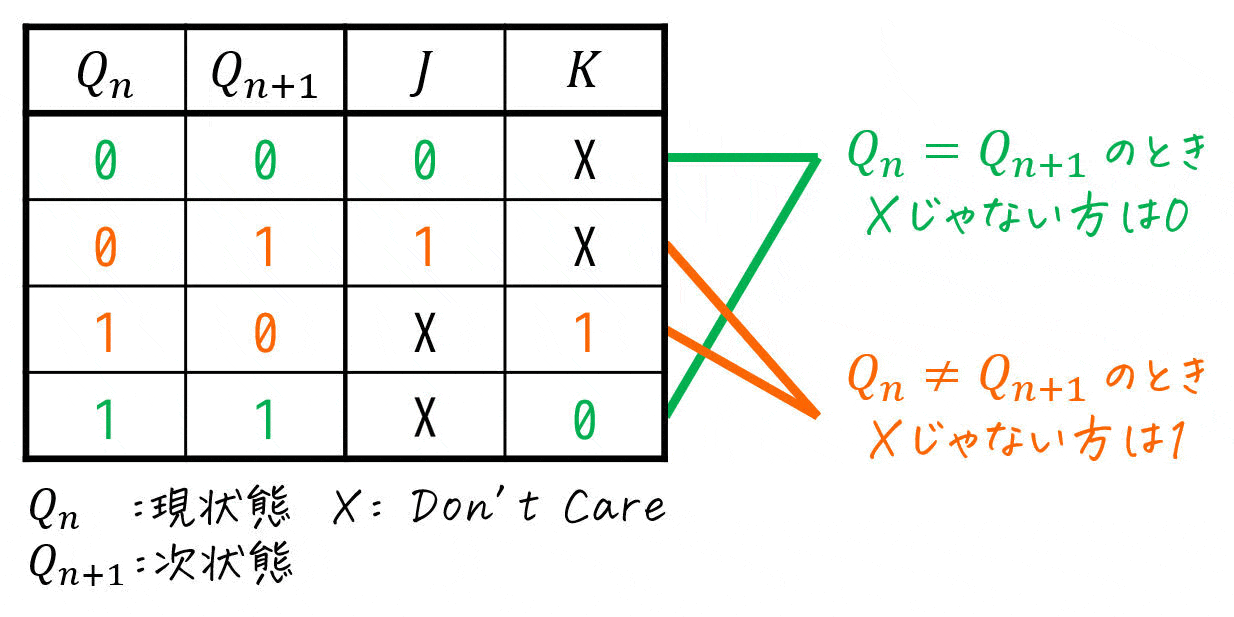
[おまけ] 何故JKフリップフロップが使われるのか
「Dフリップフロップで順序回路が書けるのに、なんでわざわざJKフリップフロップでの順序回路の書き方も習わなきゃいけないんだよ」と思った人もいるかと思います。
その疑問の答えですが、実は「JKフリップフロップで順序回路を作ると、Don't Careがうまく働くおかげでDフリップフロップのときよりも単純な(ゲートの数が少ない)順序回路が作れる。」という大きなメリットがあるからです。
※ どれくらい単純になるかは、実際に例題で体感してみてください!
(最後にDフリップフロップとの比較も載せています)
スポンサードリンク
[例題1] カウンタの設計
まずは、最も基本的な順序回路であるカウンタをJKフリップフロップを使って設計してみましょう。例題を用意したので、まずは例題の流れに沿ってみましょう。
※ 途中までDフリップフロップのときと全く同じ例題です。
1が入力された回数をカウントし、偶数回になったときに「1」、それ以外のときに「0」が出力される回路を考える。このとき、[1], [2]の問いに答えなさい。
[1] まずは状態遷移図・状態遷移表を設計する。(i) 入力変数、出力変数は最低何個必要か答えなさい。
(ii) 内部状態は最低何個必要か答えなさい。
(状態遷移図を書くために定義する必要がある状態は最低何個か?)
(iii) 状態遷移図を書きなさい。
(iv) 状態遷移表を書きなさい。
(i) 順序回路を作るために必要なフリップフロップは最低何個か答えなさい。
(ii) [1](ii)で定義した状態を各JKフリップフロップの状態に対応させ、励起表[2] … Continue readingに順序回路の出力値を追記した形の状態遷移表(励起出力表)を完成させなさい。だだし、Don’t Careの場合は X を書くこと。
(iii) 各フリップフロップの入力方程式(励起関数)、および出力の方程式(出力)関数を求めなさい。(カルノー図を用いて出来る限り簡単な形で表しなさい)
(iv) 回路図を書きなさい。
※ 励起表に順序回路の出力値を追記した形の状態遷移表(励起出力表)の例を下に示す。
(フリップフロップが2個、入力変数・出力変数が1個の場合)
[参考] 励起出力表の書き方
(FF2個・入力変数1個・出力変数1個)
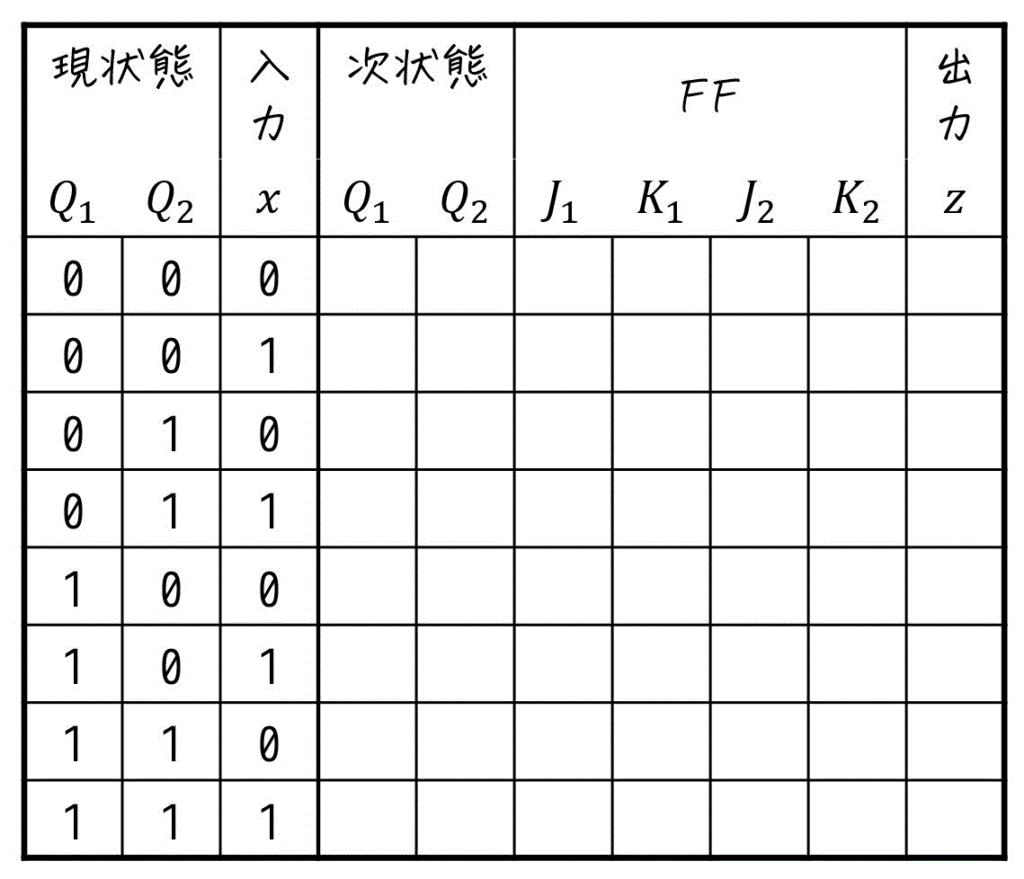
どんなフリップフロップを使おうが、設計の前には状態遷移図・状態遷移表の設計が必須です。なので、まずは状態遷移図・状態遷移表を作ってみましょう。
※ 状態遷移図や状態遷移表の書き方に自信がない人や、もう1度詳しく復習をしたい方は、下の記事にて復習ができます。
※ すでに状態遷移表・状態遷移図の書き方に自信がある人は、[1]の説明は流し読みでOKです。
[1] 状態遷移図・状態遷移表の設計
まずは与えられた問題の処理を実現するために状態遷移図・状態遷移表を設計していきましょう。
(i) 入力変数・出力変数を考える
最初、与えられた問題から必要な入力変数・出力変数を考え、さらに定義することを考えます。
今回の場合、与えられた問題文を詳しく書くと、「1つの入力変数の値が1であるかどうかをカウントし、1がカウントされた回数が偶数回になるごとに、1つの出力変数から1を出力する」となりますね。
よって、入力変数・出力変数はそれぞれ
- 入力変数 … 1つ(\( x \) と定義)
- 出力変数 … 1つ(\( z \) と定義)
となります。
(ii) 内部状態を考える
入力変数、出力変数を考えたら、つぎに内部状態を定義しましょう。
ここで、必要な内部状態を考える際には、与えられた問題文を満たす回路を作るためにどんな状態を記憶すればよいかを考えます。
今回の場合は、1の数をカウントして偶数か奇数かを判定するため、
- 1のカウント回数が偶数の状態
- 1のカウント回数が奇数の状態
の2つさえ記憶できてしまえばOKです[3]偶数に1を足すと必ず奇数に、奇数に1を足すと偶数になるため、具体的に1が何回入力されたかをカウントする必要はない。。
そのため、内部状態は最低2個必要です。
(iii) 状態遷移図を考える
内部状態を考え終わったら、いよいよ状態遷移図の設計に入ります。
状態遷移図は、
- 考えた状態に \( q_0 \) などの名前をつける
- 状態を並べる
- 状態遷移を書く(各入力ごとの状態遷移先[次状態]、および出力を書く)
の3ステップで書いてきましょう。
まずは、下のように[1](ii)で考えた状態に名前をつけます。
今回は、最後に商品が出てから
- 1のカウント回数が偶数の状態 → \( q_0 \)
- 1のカウント回数が奇数の状態 → \( q_1 \)
とつけることにします。
つぎに、名前をつけた各状態を並べます。

あとは、各状態ごとに各入力 \( x = 0 \), \( x = 1 \) における遷移先(次状態)を書いていけばOKです。
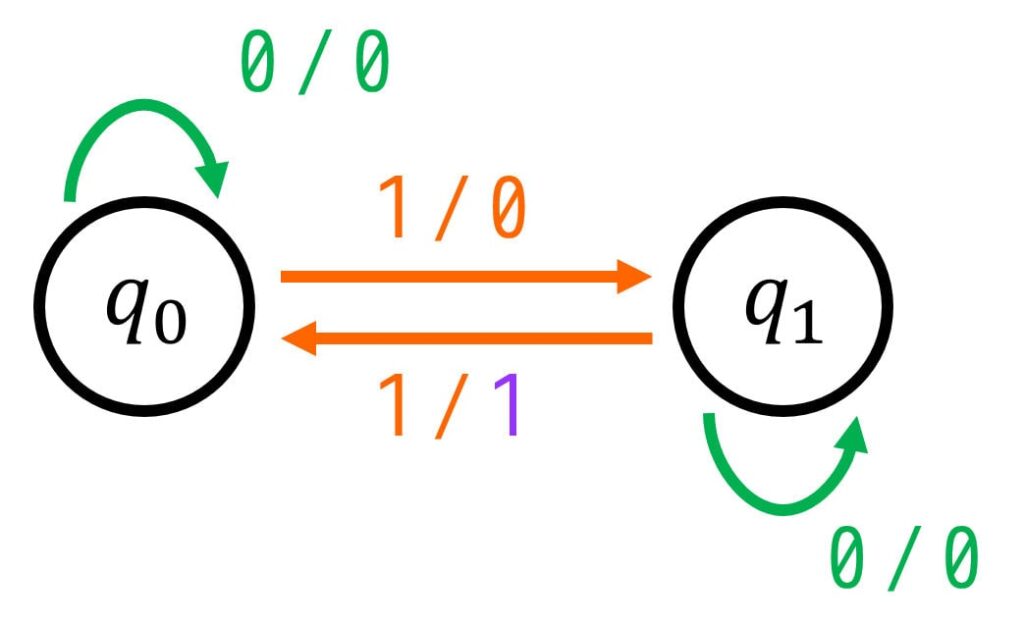
今回の場合は、
- 入力 \( x = 0 \) のときは、1の数のカウントは変化しない
→ 偶数個 \( q_0 \) のときは偶数個 \( q_0 \)、奇数個 \( q_1 \) のときは奇数個 \( q_1 \)
→ 1が入力されてないときは、「1の入力回数は増えない」ので、出力は \( z = 0 \) - 入力 \( x = 0 \) のときは、1の数のカウントが1増える
→ 偶数個 \( q_0 \) のときは奇数個 \( q_1 \)、奇数個 \( q_1 \) のときは偶数個 \( q_0 \)
→ 偶数個から奇数個になるときは、「1の入力回数が偶数回」とはならないため、出力は \( z = 0 \)
→ 奇数個から偶数個になるときに、「1の入力回数が偶数回」となるため、出力は \( z = 1 \)
を状態遷移図に落とし込んで矢印を追記していけばOKです。
[余談] 状態数の最小化
もし、「順序回路の状態数最小化」を習っている場合は、ここで「順序回路の状態数最小化」を適用することで、より簡単な状態遷移表、および順序回路を設計できる可能性があります。
(iv) 状態遷移表
状態遷移図を書き終わったら、つぎは状態遷移表を書いていきましょう。状態遷移図からたどれば、あっという間に書くことができます。
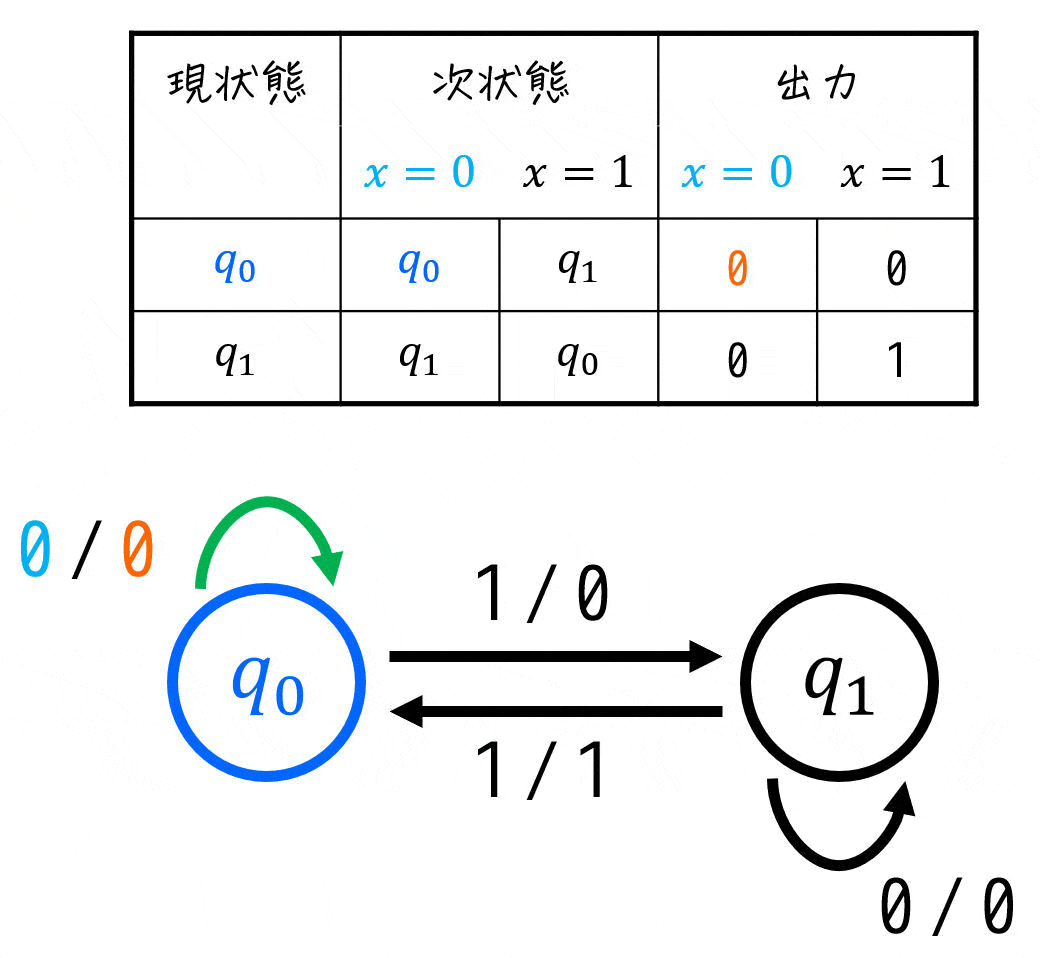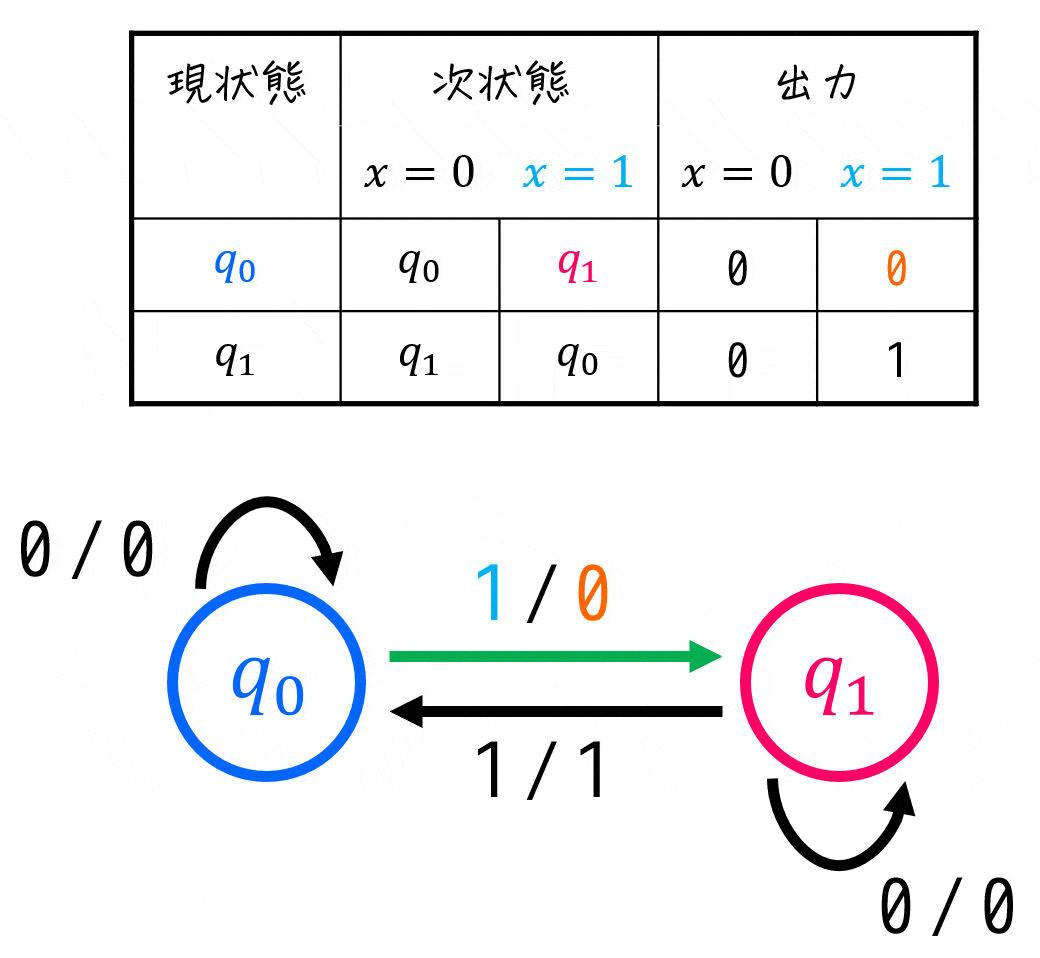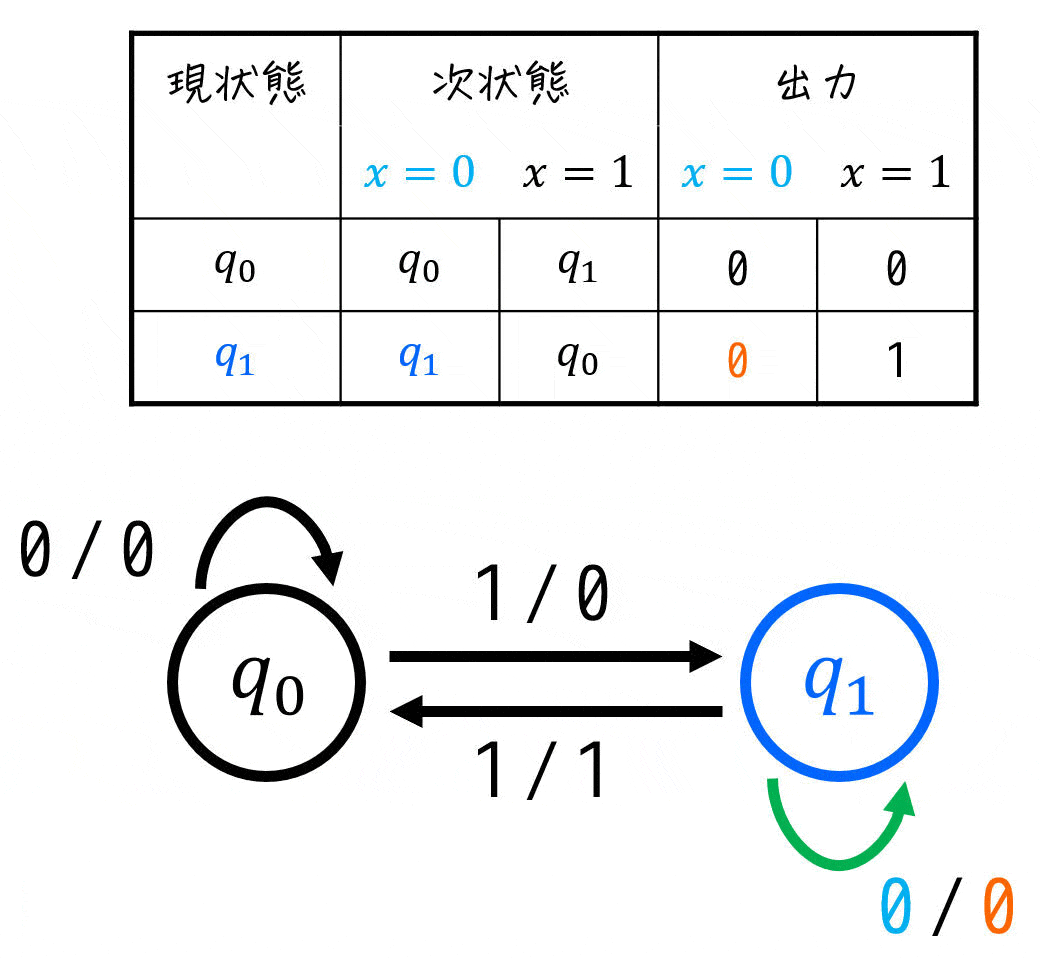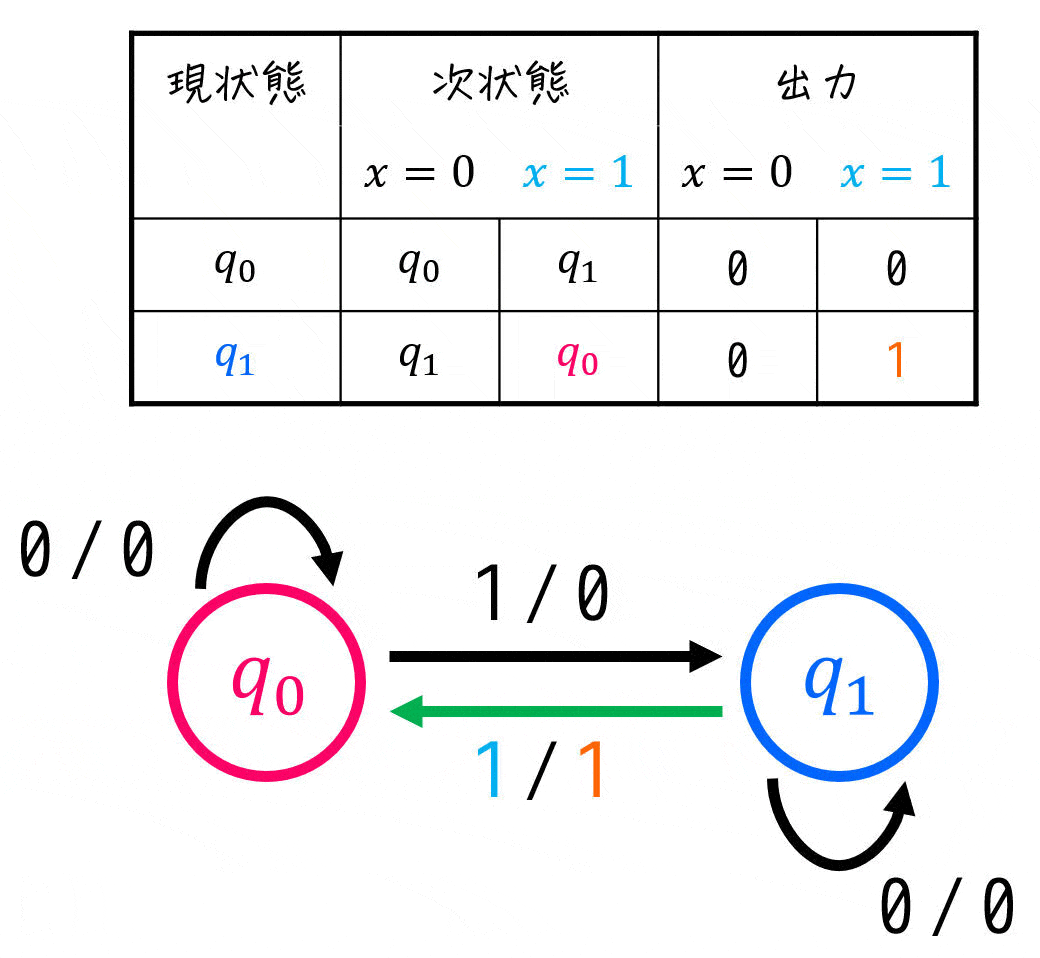
※ 自信があれば、状態遷移図を書かずにいきなり状態遷移表を書いてもOKです。
ここまで出来たら、状態遷移図・状態遷移表の設計の完了です。
ここから、さらに実際に順序回路を作成するための作業をしていきましょう。
[2-i] 必要なフリップフロップの数を考える(ここはD-FFと同じ)
順序回路を書く際に最初にすることは、状態遷移図の設計で定義した内部状態を記憶するために必要なフリップフロップの数を考えることです。
今回の場合は、\( q_0 \), \( q_1 \) の2状態を記憶すればOKなので、必要なフリップフロップは1個となります[4]1個のフリップフロップで2つの状態、2個のフリップフロップで4つの状態、3個のフリップフロップで8つの状態、…、\( n \) 個のフリップフロップで … Continue reading。
ここで、定義した内部状態の数 \( a \) と必要なフリップフロップの数 \( n \) について復習しましょう。
フリップフロップ(D-FF, T-FF, JK-FF, SR-FFの種類は問わない)の個数と、記憶できる状態の最大数の関係を表にしたものを下に記す。
| FFの個数 | 記憶できる状態数 |
|---|---|
| 1 | 2 |
| 2 | 4 |
| 3 | 8 |
| 4 | 16 |
| ︙ | ︙ |
| \( n \) | \( 2^n \) |
数学的に考えたい人は、ある \( a \) 個の状態を記憶するために必要なフリップフロップの数 \( n \) は、\[
\textcolor{red}{2^{n-1}} < a \leqq \textcolor{blue}{2^{n}}
\]を満たすような不等式を満たすような \( n \) を求める、と頭に入れておくのもあり。
\( 2^{n-1} \) … フリップフロップが1個不足してギリギリ回路が記憶できない場合
\( 2^{n} \) … フリップフロップがギリギリ足りている場合
※ ここからDフリップフロップとは異なる過程となります。
[2-ii] 励起表と出力値を合体させた表を書く(励起出力表)
必要なフリップフロップの数を考えたあとは、つぎに、「フリップフロップの現状態 \( Q \) ・各入力」から「フリップフロップの次状態 \( Q \)」 に遷移させるためには、JK-FFの入力値をどのようにすればよいかを考えていきます。
そこでJK-FFの入力値を考えるために、先ほど説明した「各フリップフロップの現状態・入力」に対して、「次状態と、次状態を満たすためのFFの入力(と順序回路の出力)」を下のように表にしたものを書きます。励起出力表と名付けることにしましょうか。
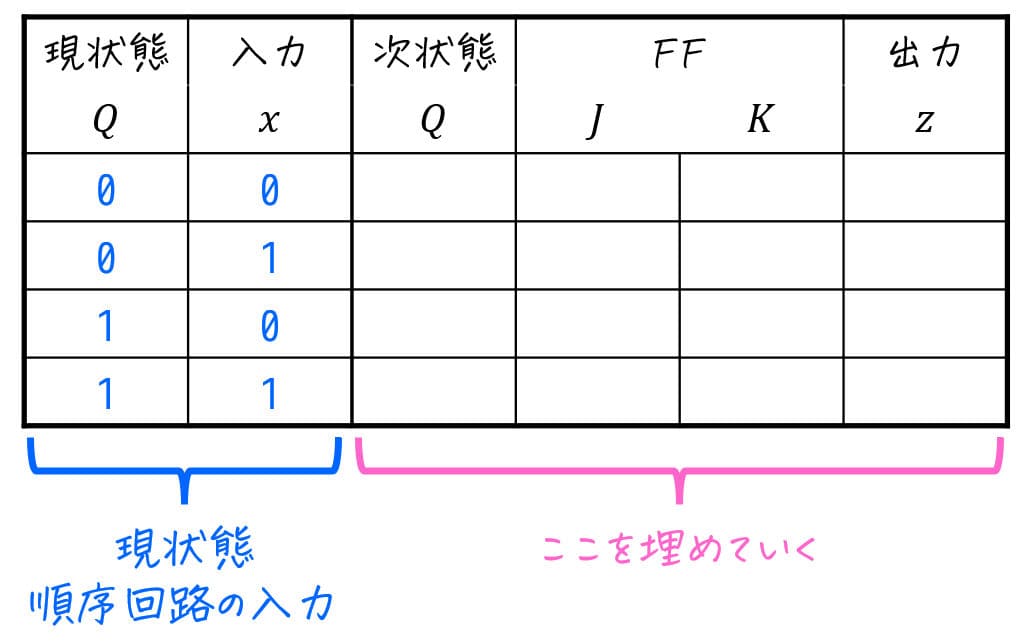
Step1. 定義した状態を、フリップフロップの状態の値に割り当てる
まずは、[1]で定義した状態を実際にフリップフロップの値状態に割り当てます。
今回の場合は、フリップフロップは1つなので、1つのフリップフロップを各状態に割り当てていきましょう。
- 状態 \( q_0 \) → \( Q = 0 \)
- 状態 \( q_1 \) → \( Q = 1 \)
※ フリップフロップの数が複数のときは、各状態を複数個のフリップフロップの組み合わせで割り当てます。(割り当ての例: 状態 \( q_0 \) → \( (Q_1,Q_2) = (0,0) \)。)
Step2. 状態遷移表から励起表の次状態・出力を埋める(ここまでD-FFと同じ流れ)
つぎに、「[1](4) 状態遷移表の設計」で作成した状態遷移表から励起出力表を作り上げていきます。
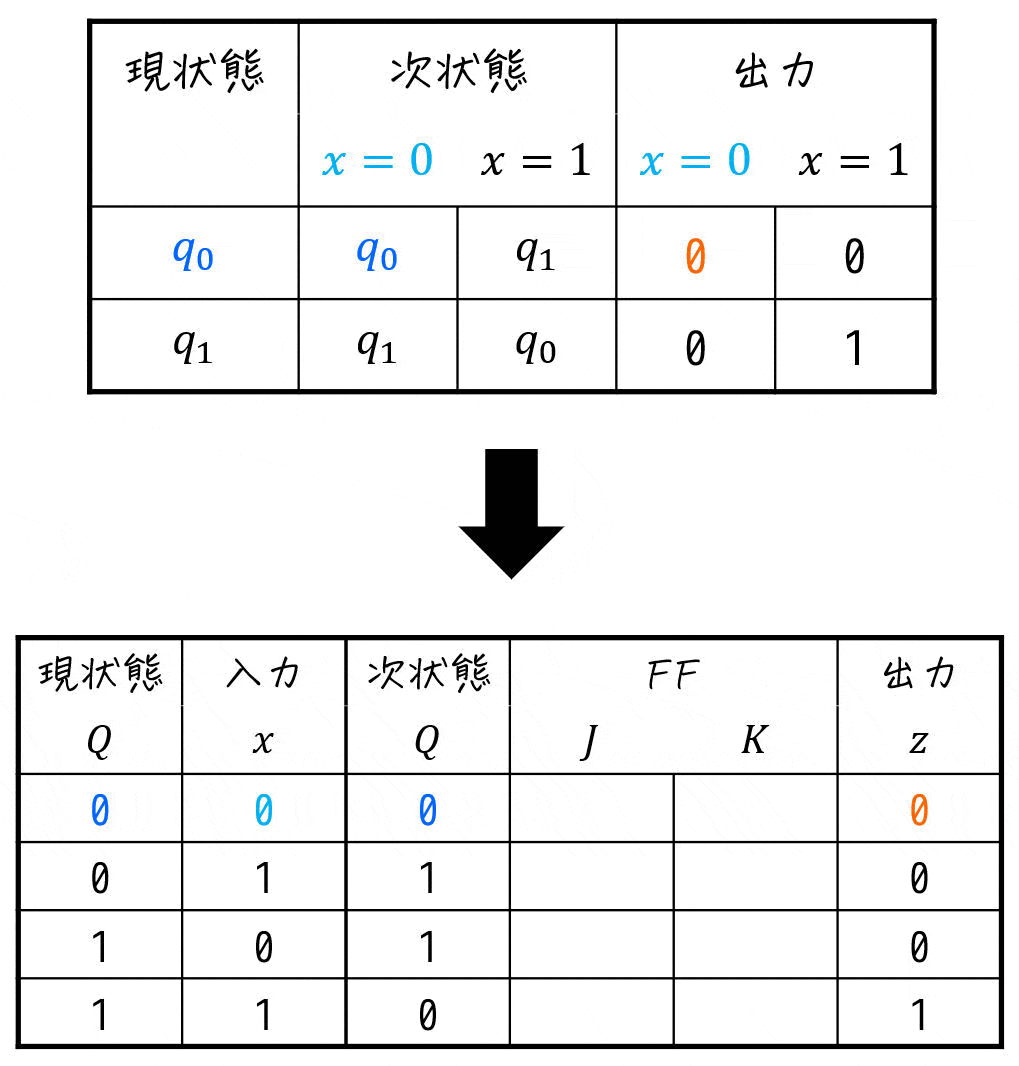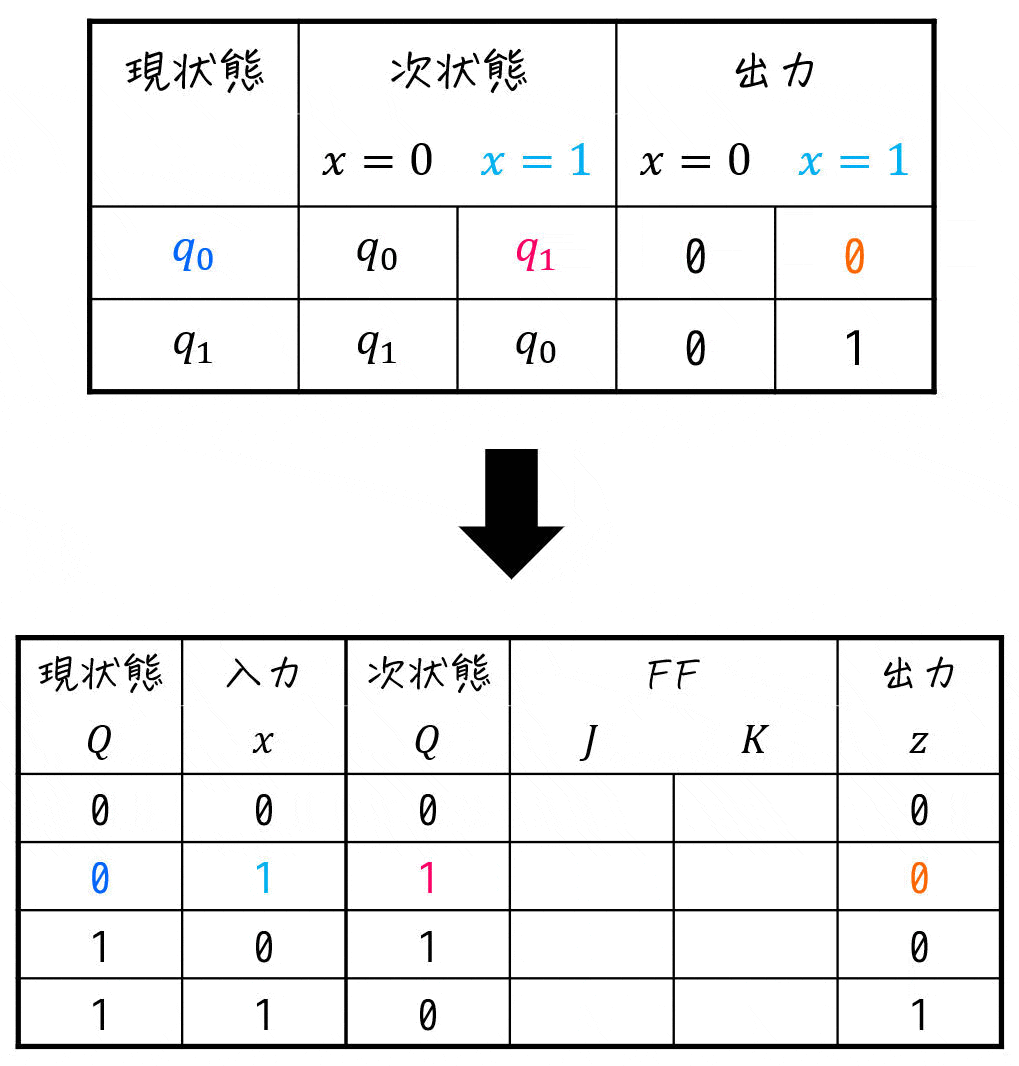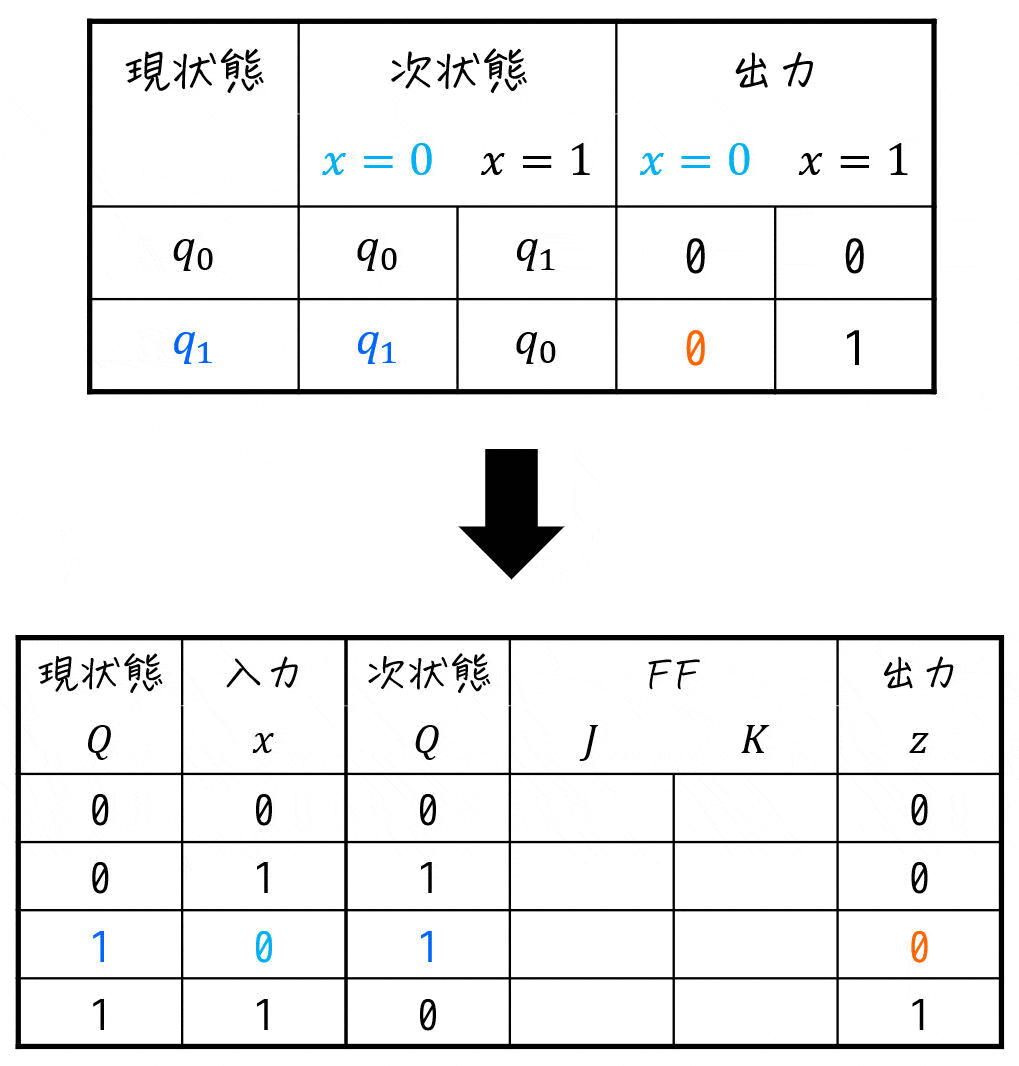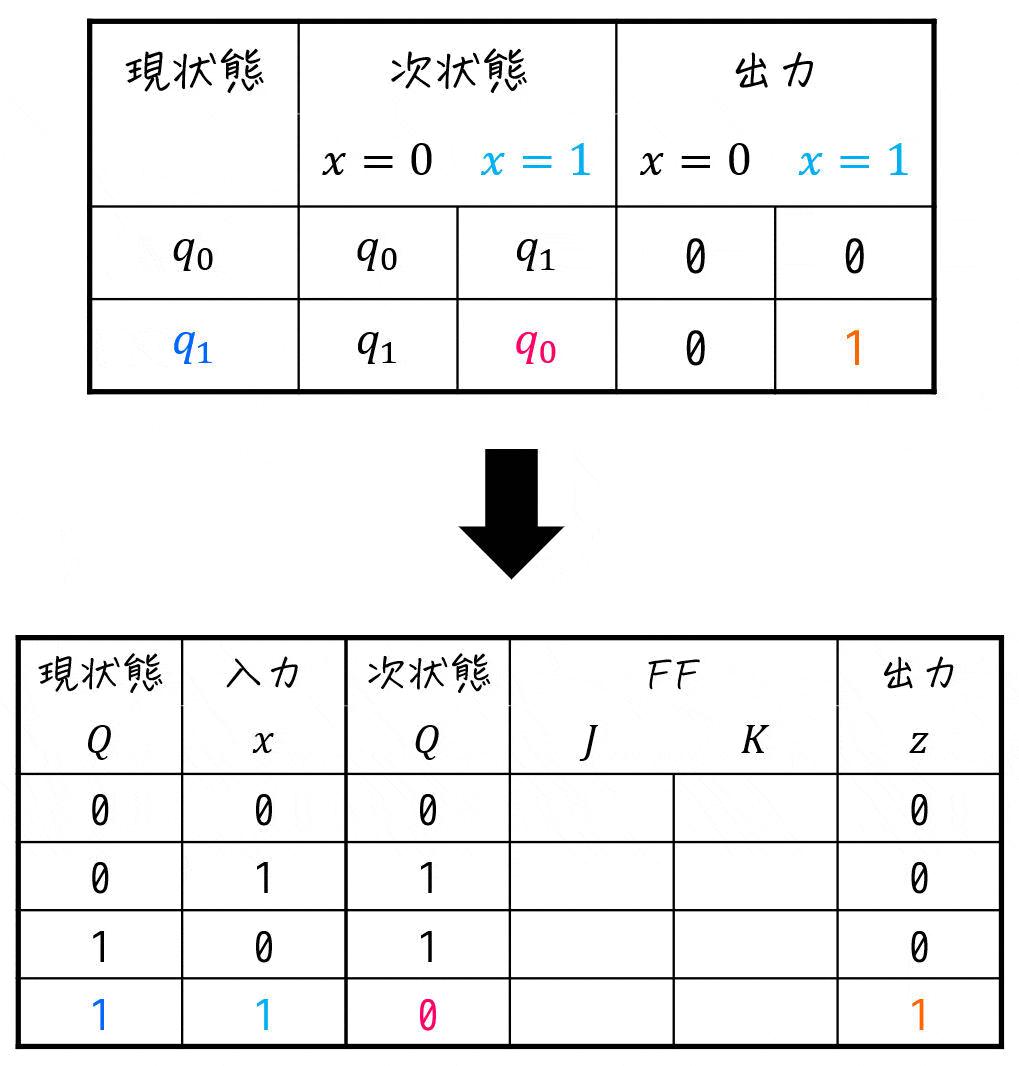
Step3. 次状態からFFの入力値を求める
あとは、励起出力表にある残りの空白であるJK-FFの入力値 \( J \), \( K \) を、現状態と次状態の値から次の2つのステップで求めます。
- 現状態 \( Q \) が0, 1かを確認し、\( J \), \( K \) のどちらがX (Don't Care)になるかを確認
- 現状態 \( Q \) と次状態 \( Q \) の変化を確認し、Xではない方の値を埋める
1) 現状態から、Don't Careが \( J \), \( K \) どちらであるかを確認
まずは現状態 \( Q \) に着目しましょう。ここで、
- 現状態 \( Q = 0 \) のとき … \( K \) が0だろうが1だろうが \( J \) の値だけで次状態 \( Q \) の値が決まる
→ \( K \) の値はどうでもいい - 現状態 \( Q = 1 \) のとき … \( J \) が0だろうが1だろうが \( K \) の値だけで次状態 \( Q \) の値が決まる
→ \( J \) の値はどうでもいい
でしたね。そのため、
- 現状態 \( Q = 0 \) のとき → \( K \) が X (Don't Care)
- 現状態 \( Q = 1 \) のとき … \( J \) が X (Don't Care)
をFFの空欄に埋めていきます。
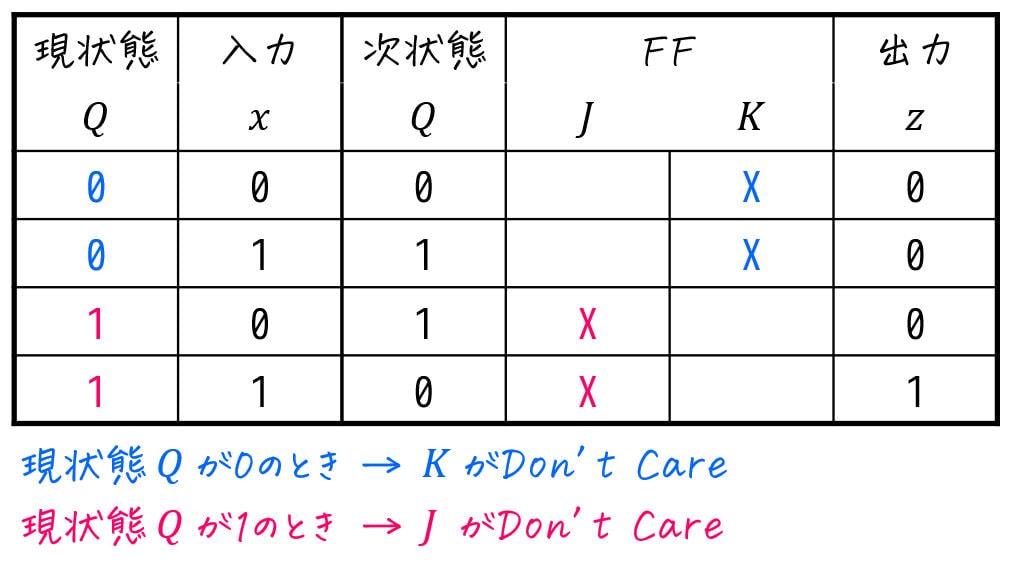
2) 現状態と次状態の変化を確認
次に、現状態 \( Q \) と次状態 \( Q \) の変化に着目します。ここで、
現状態 \( Q \) と次状態 \( Q \) が同じとき
→ Don't Careではない方のFF入力は0
現状態 \( Q \) と次状態 \( Q \) が異なるとき
→ Don't Careではない方のFF入力は1
でしたね。そのため、
現状態 \( Q \) = 次状態 \( Q \) → Don't Careではない方のFF入力に0
現状態 \( Q \) ≠ 次状態 \( Q \) → Don't Careではない方のFF入力に1
を埋まっていない空欄に入れていきます。
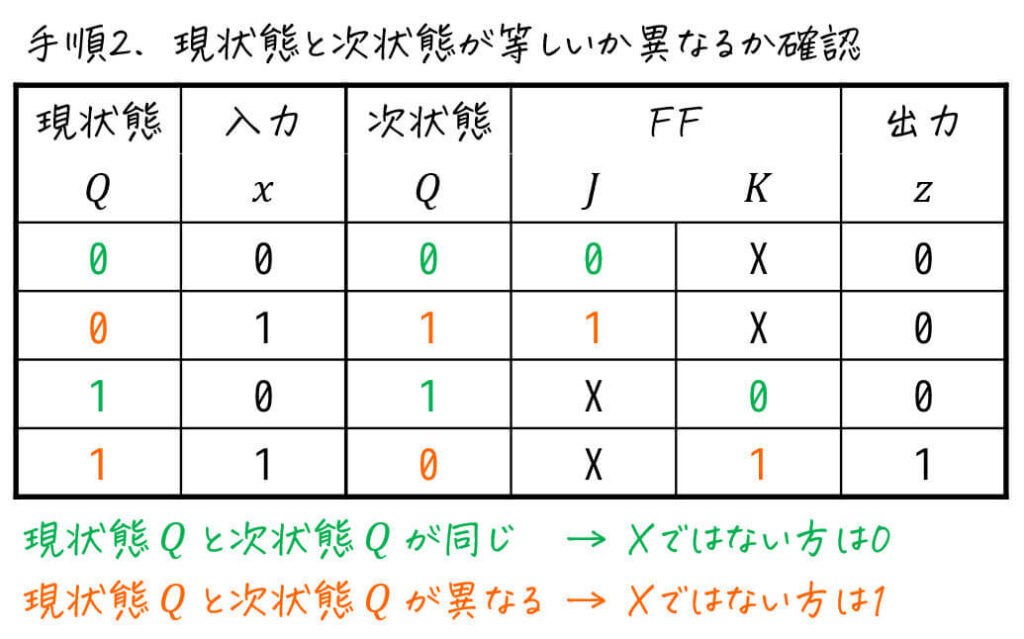
これで、励起出力表の完成です。
[2-iii] 励起関数(FFの入力方程式)・順序回路の出力方程式を作る
完成した励起出力表から、FFの入力方程式(励起関数)、および順序回路の出力方程式を考えていきましょう。
ここで、\( J \), \( K \) には X (Don't Care) が含まれているので、カルノー図を用いて簡略化することにしましょう[5]JK-FFの場合、\( J \), \( K \) ともにDon't … Continue reading。ただし \( z \) はカルノー図を書かなくても励起出力表から \( z = Q x \) とすぐにわかる[6]\( z \) については、X (Don't Care) が一切含まれていない上に、1がついている箇所が1箇所なため。ので、今回はカルノー図は省略します。
※ カルノー図の復習をしたい人は →→ こちら ←← から!
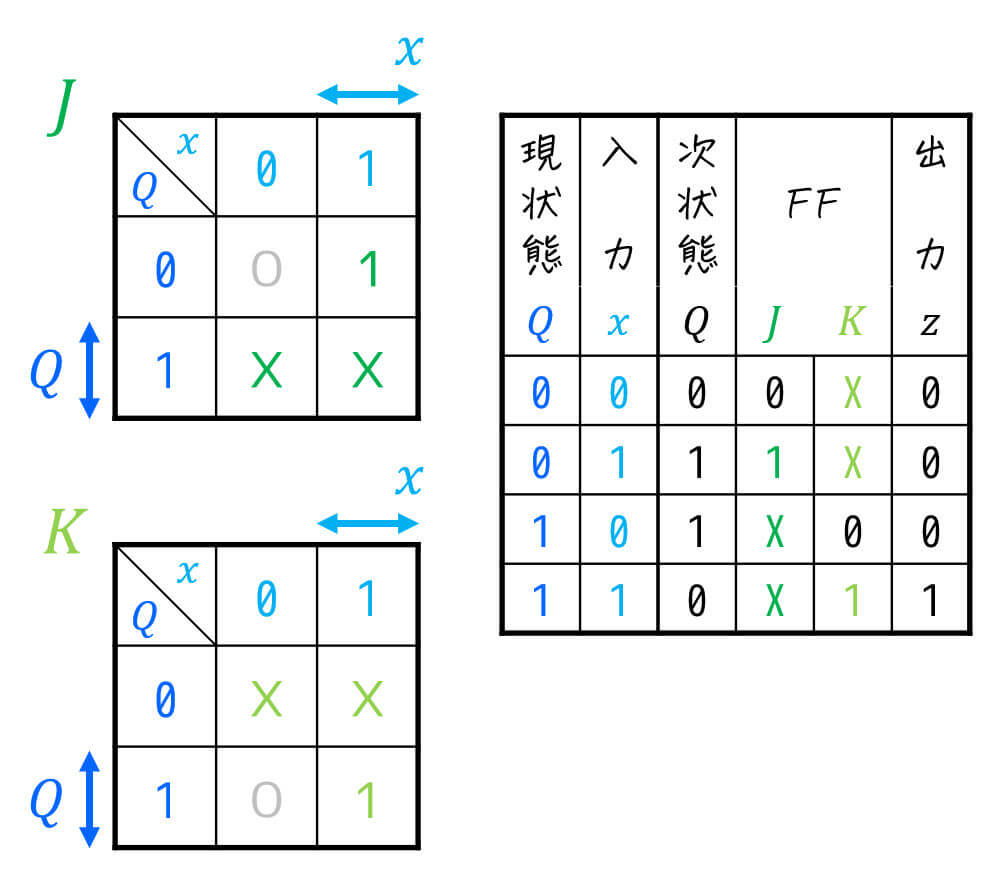
カルノー図を書き終わったら、\( J \), \( K \) を簡略化していきましょう。
[\( J \) へのカルノー図の適用過程]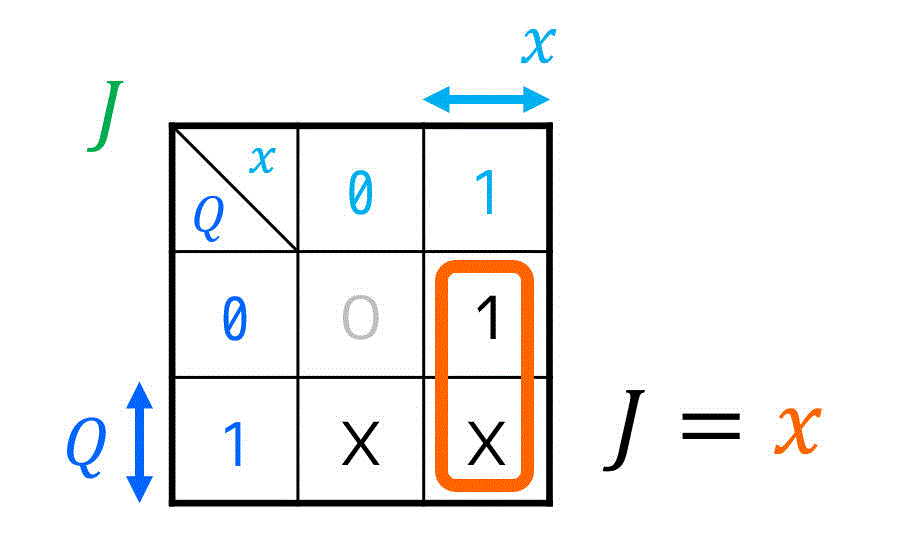
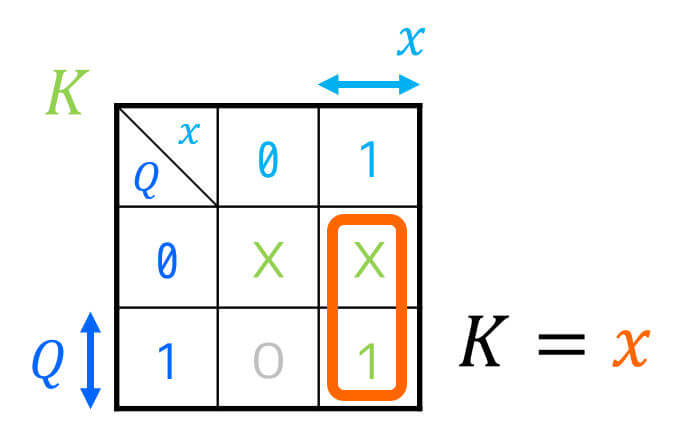
(不安な人は書いてもOK。ただし、基本的には不要)
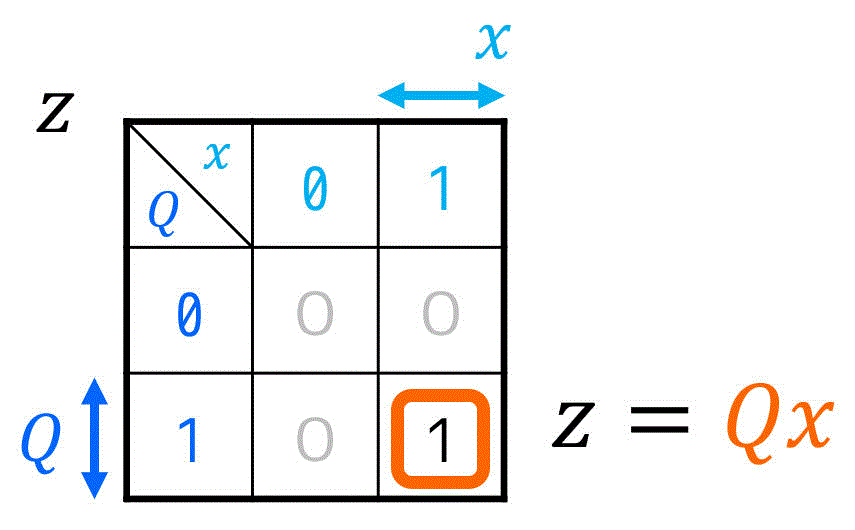
[2-iv] 順序回路を設計する
いよいよ順序回路を設計していきましょう!
[2-iii]で作った励起関数 \( J = x \), \( K = x \) と、出力方程式 \( z = Q \cdot x \) を使って、順序回路を作れば設計完了です!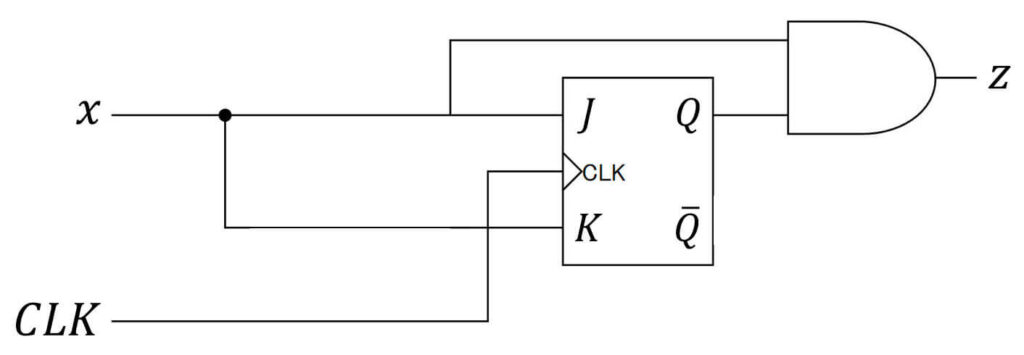
(最終的な答え)
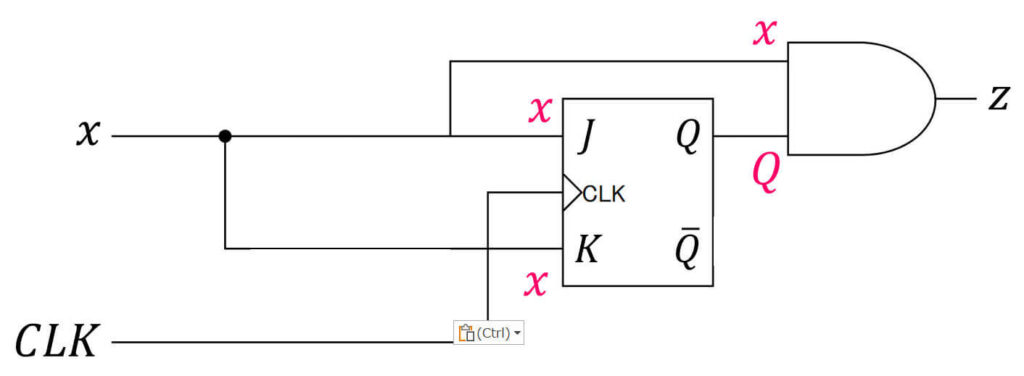
※ ここで、順序回路内に出てきた各ゲートの入力値を明記してわかりやすくしたバージョンも書いたので、参考にしてください。
スポンサードリンク
[例題2] 自動販売機の設計
今度は、もう少し複雑な順序回路である、自動販売機の回路をJKフリップフロップで表現してみましょう。
つぎの[仕様]を満たす200円のおもちゃを販売するガチャガチャ(自動販売機)の回路を設計したい。
[仕様]- 100円硬貨のみを受け付け、投入金額が200円になると商品が出てくる。
- 返却ボタンを搭載する。返却ボタンを押すと、投入された硬貨がすべて返却され、投入金額がリセットされる。
- 商品が出たかどうか、硬貨が返却されたかどうかをこの回路で判定すること。
- 1度に2枚以上の硬貨が投入されることは考えなくてよい。
- 硬貨の投入と、返却ボタンを押す動作が同時に生じることは考えなくてよい。
(i) 入力変数、出力変数は最低何個必要か答えなさい。
(ii) 内部状態は最低何個必要か答えなさい。
(状態遷移図を書くために定義する必要がある状態は最低何個か?)
(iii) 状態遷移図を書きなさい。
(iv) 状態遷移表を書きなさい。
(i) 順序回路を作るために必要なフリップフロップは最低何個か答えなさい。
(ii) [1](ii)で定義した状態を各JKフリップフロップの状態に対応させ、励起表に順序回路の出力値を追記した表を書きなさい。(Don’t Careの場合は X を書くこと)
(iii) 各フリップフロップの入力方程式(励起関数)、および出力の方程式(出力)関数を求めなさい。ただし、カルノー図を用いて最簡形にすること。
(iv) 回路図を書きなさい。
[1] 状態遷移図・状態遷移表の設計
どんなフリップフロップを使って順序回路を作る場合でも、まずは状態遷移図・状態遷移表を設計していきます。
(i) 入力変数・出力変数を考える
- 入力変数(2個)
- 100円硬貨が投入されたかを表す変数 \( x \)
(投入されていない → 0、投入された → 1) - 返却ボタンが押されたかを表す変数 \( y \)
(押されていない→ 0、押された → 1)
- 100円硬貨が投入されたかを表す変数 \( x \)
- 出力変数(2個)
- 商品が出たかを表す変数 \( z \)
(出なかった → 0、出た → 1) - 硬貨が返却されるかを表す変数 \( r \)
(返却される → 0、返却されない → 1)
- 商品が出たかを表す変数 \( z \)
※ 各変数に何を割り当てるかは自由なので、上の例の通りに割り当てなくてもOKです。
(例: 100円硬貨が投入された状態を0、投入されていない状態を1)
よって、答えは
- 入力変数: 2個
- 出力変数: 2個
となります。
(ii) 内部状態を考える
内部状態 = 記憶すべき状態、でしたね。
そのため、今回は最後に商品が出てから投入された合計金額を100円単位[7]100円硬貨以外の硬貨は入ってこないため、合計金額は必ず100円単位となる。で記憶すればOKですね。
(+商品が出る or 返却ボタンが押されると、投入金額の合計は0円にリセットされる)
そのため、
- 最後に商品が出てから合計0円投入された状態(硬貨が投入されていない状態)
- 最後に商品が出てから合計100円投入された状態
の2種類の状態さえ記憶すれば、回路が表せますね[8]合計200円投入すると商品が出てくるため、「最後に商品が出てから合計300円投入された状態」を記憶する必要はありません。。
よって、必要な内部状態は最低2個であることがわかります。
(iii) 状態遷移図の設計
(ii)で考えた状態に名前を付けましょう。
- 合計0円投入された状態 → \( q_0 \)
- 合計100円投入された状態 → \( q_1 \)
つぎに、(名前を付けた)状態を並べましょう。

あとは、各状態からの遷移先(次状態)と、そのときの入出力を矢印で表せばOKです。
今回の場合は、
- \( x = 0 \), \( y = 0 \) が入力された場合
- 硬貨も投入されておらず、返却ボタンも押されていないため、合計金額(状態)が変わらない。
→ 商品が出ず、硬貨の返却もないためので出力は \( z = 0 \), \( r = 0 \)。(現状態と次状態が同じ)
- 硬貨も投入されておらず、返却ボタンも押されていないため、合計金額(状態)が変わらない。
- \( x = 1 \), \( y = 0 \) が入力された場合(100円硬貨が投入された場合)
- \( q_0 \) : 合計金額が100円アップ
→ \( q_0 \) から \( q_1 \) に遷移 - \( q_1 \): 合計が200円になるので、商品が出てくる。投入金額も0円にリセットされる。
→ \( z = 1 \) を出力し、次状態は \( q_0 \) に遷移
- \( q_0 \) : 合計金額が100円アップ
- \( x = 0 \), \( y = 1 \) が入力された場合(返却ボタンが押された場合)
→ 硬貨が投入されないため、投入合計金額が200円になることは絶対にない。よって、商品は出てこないため、出力 \( z \) は \( z = 0 \) となる。状態遷移・返却については、場合分けが必要。- 投入金額が0円 \( q_0 \) のとき→ お金が投入されていないので、お金が返却されない(何も起こらない)。よって、\( r = 0 \) で、状態は \( q_0 \) のまま
- 投入金額が100円 \( q_1 \) のとき → お金が投入されているため、お金が返却され、投入金額が0円(状態 \( q_0 \))にリセットされる。よって、\( r = 1 \) で、状態は \( q_0 \) に遷移
を満たすように矢印を追加すればOKです。
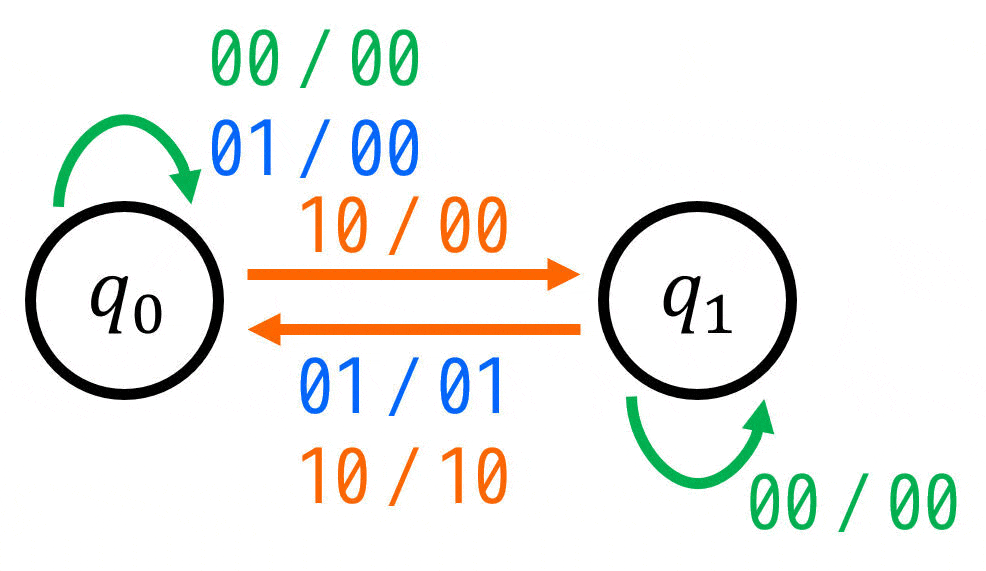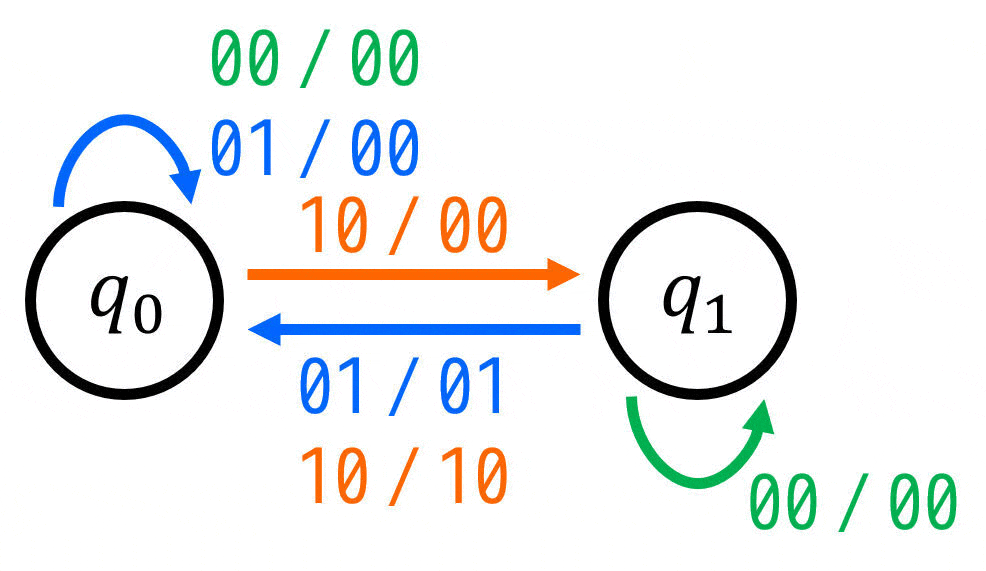
(入力 / 出力 = \( xy \) / \( zr \))
※ 入力・出力がともに複数あるので、変数をどの順番で書くかも明記しましょう。今回は「入力 / 出力 = \( xy \) / \( zr \)」で表すことにします。
(iv) 状態遷移表の設計
(iii)で書いた状態遷移図を元に、状態遷移表を書いていきましょう。
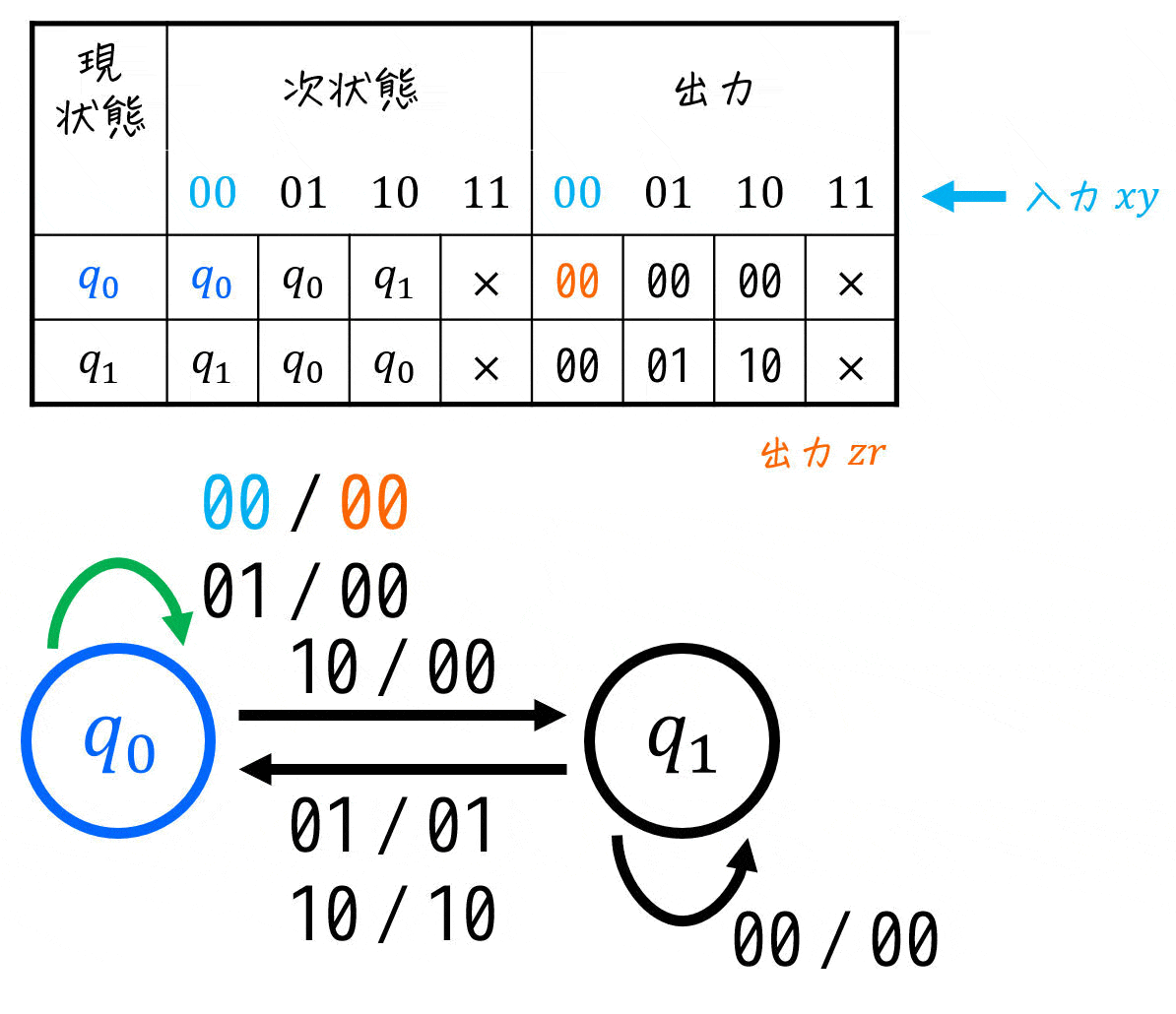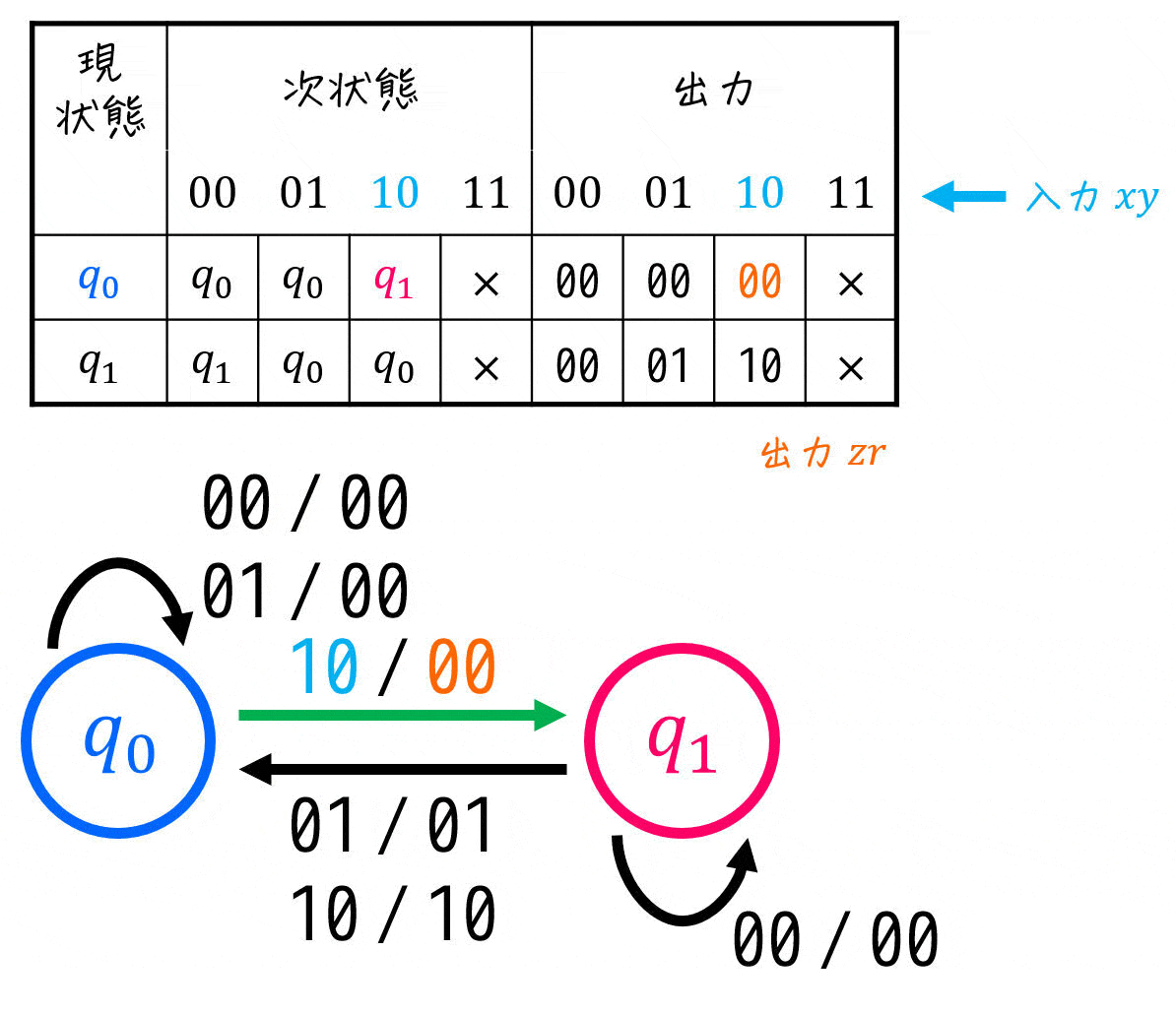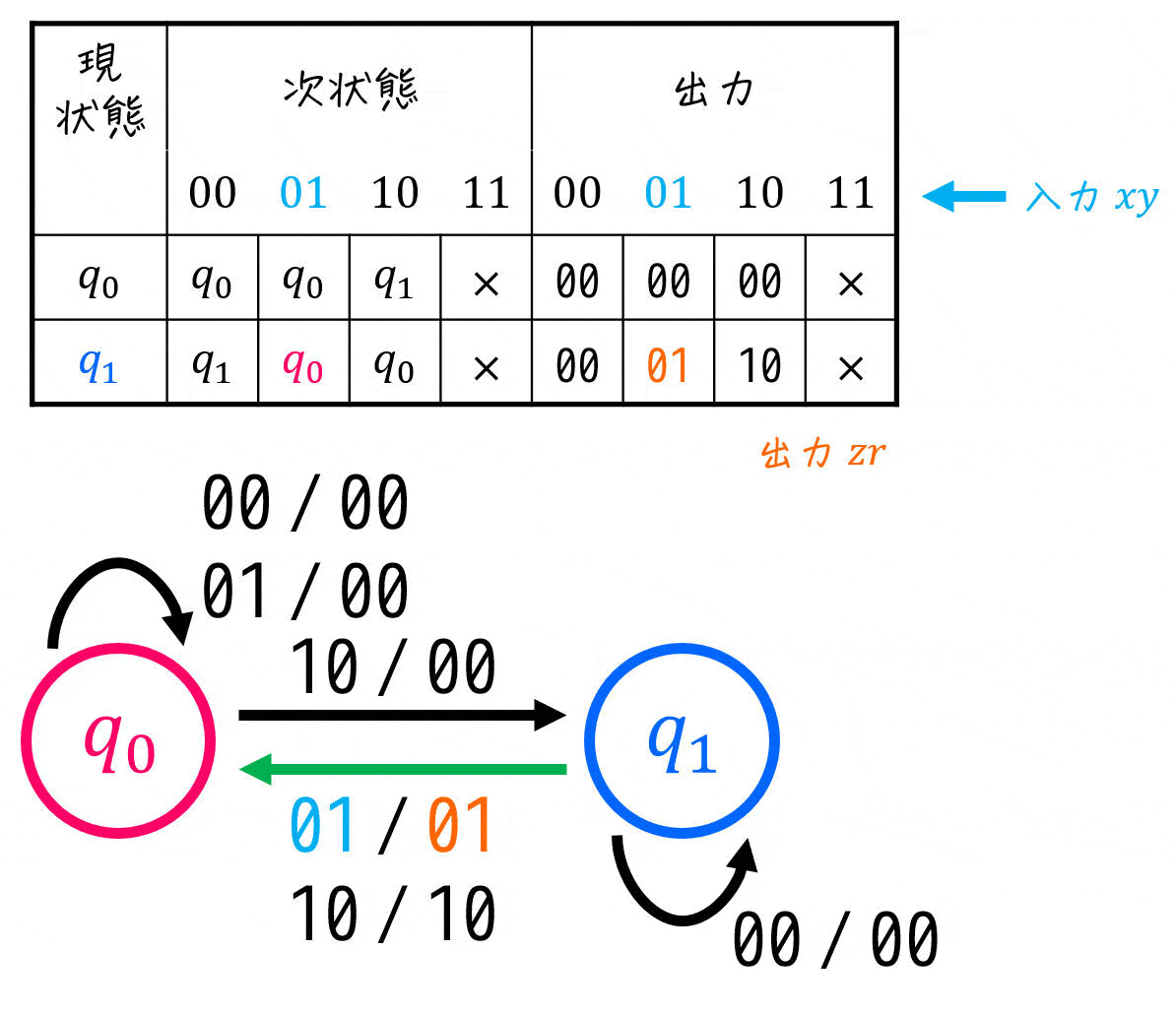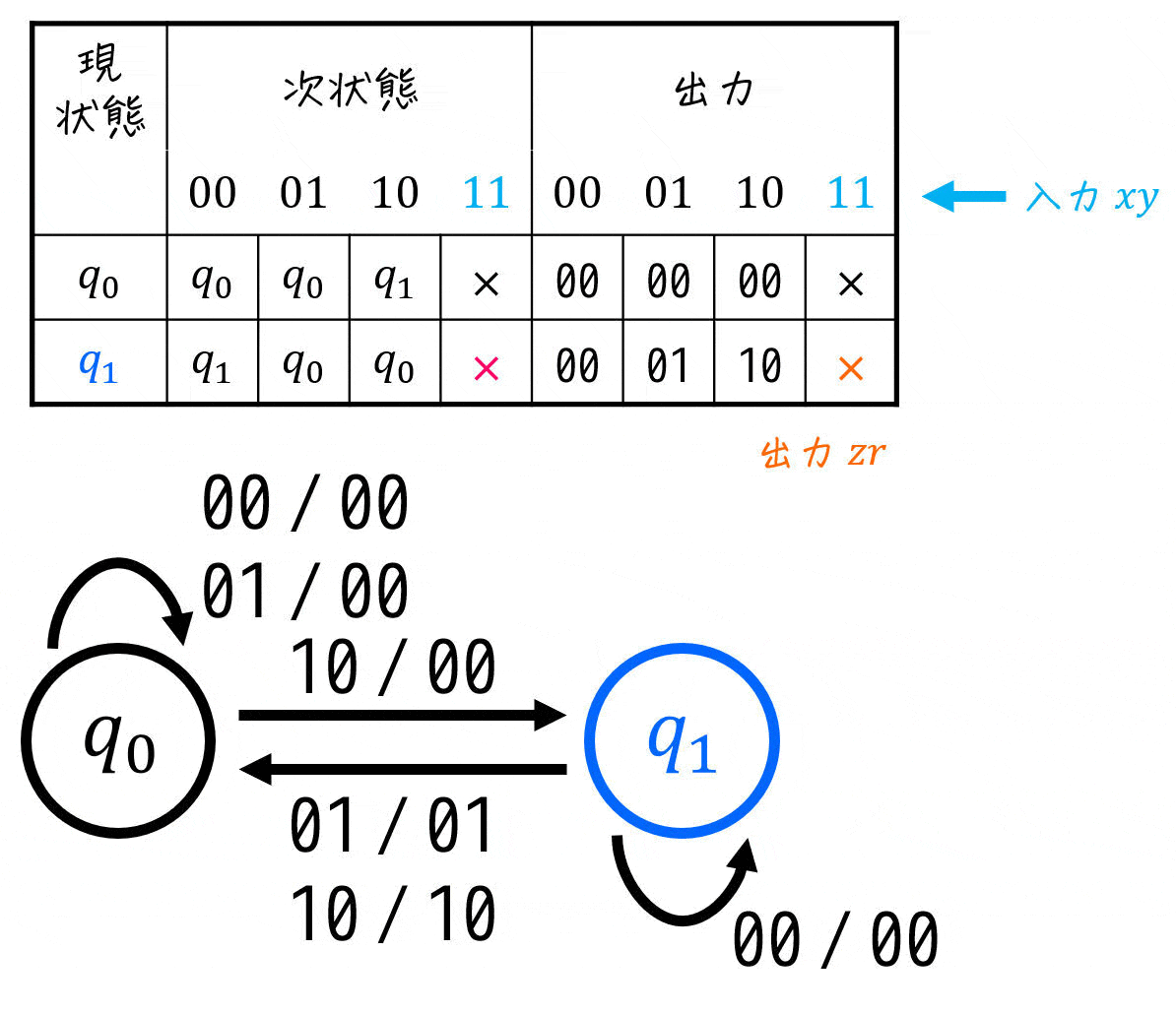
これで、状態遷移図・状態遷移表の設計の完了です。なので、ここからは実際に順序回路をしていきましょう。
[2-i] 必要なフリップフロップの数を考える
作成した状態が2つなので、1つのフリップフロップでこの2状態を記憶させることができますね。
よって、必要なフリップフロップの数は1つです。
[2-ii] 励起表と出力値を合体させた表(励起出力表)を書く
つぎに、
- 「JKフリップフロップの現状態 \( Q \) ・各入力 \( J \), \( K \)」からどの「JKフリップフロップの次状態 \( Q \)」 に遷移すればよいか
([1]で作った状態遷移表を見ながら) - 現状態 \( Q \) から次状態 \( Q \) に遷移させるためには、JKフリップフロップの入力 \( J \), \( K \) をどうすればよいか
の2つを下のように、励起表に出力値 \( z \), \( r \) を含んだ表を書くことで示します。
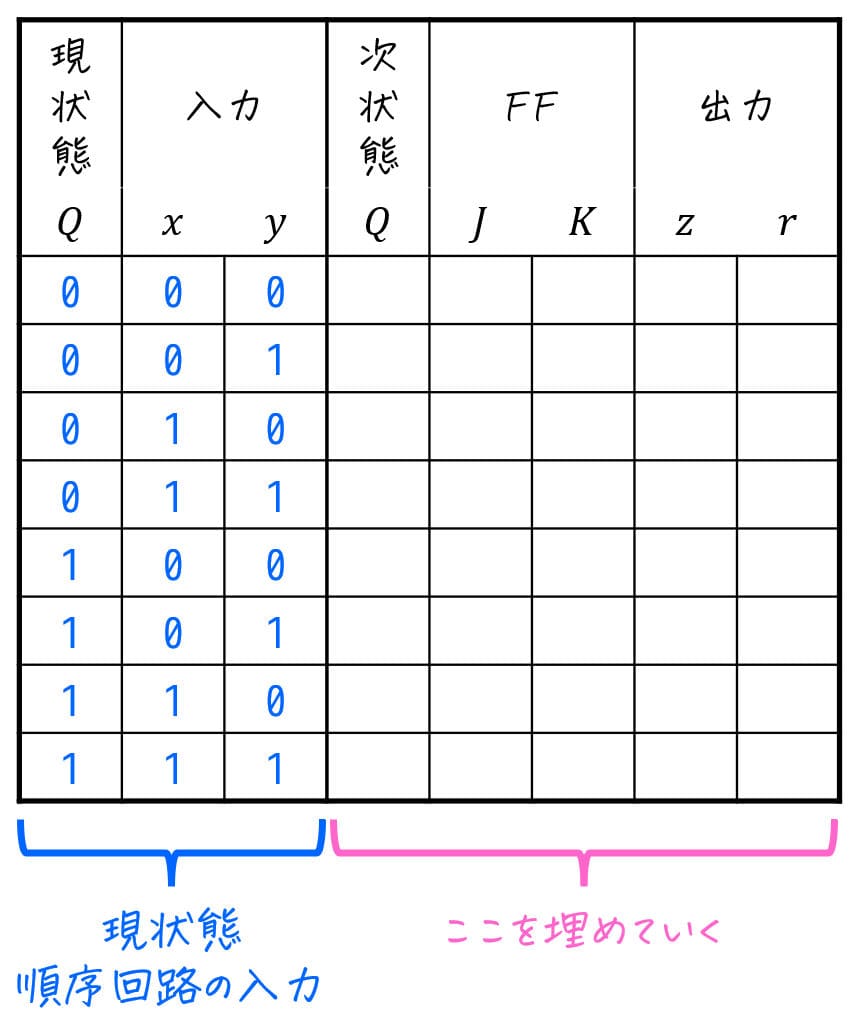
Step1. 定義した状態を、フリップフロップの状態の値に割り当てる
まずは、[1]で定義した状態を実際にフリップフロップの値状態に割り当てます。
今回、フリップフロップは1つなので、1つのフリップフロップを各状態に割り当てていきましょう。
- 状態 \( q_0 \) → \( Q = 0 \)
- 状態 \( q_1 \) → \( Q = 1 \)
※ 割り当て方は自由なので、\( q_0 \) → \( Q = 1 \)、\( q_1 \) → \( Q = 0 \) としてもOKです。
Step2. 状態遷移表から励起表の次状態・出力を埋める
つぎに、「[1](4) 状態遷移表の設計」で作成した状態遷移表から励起表を作り上げていきます。
ここで、入力が \( (x,y) = (1,1) \) のときは考えなくてよいので、このときは次状態、出力をともにDon't Care(つまりX)とします。
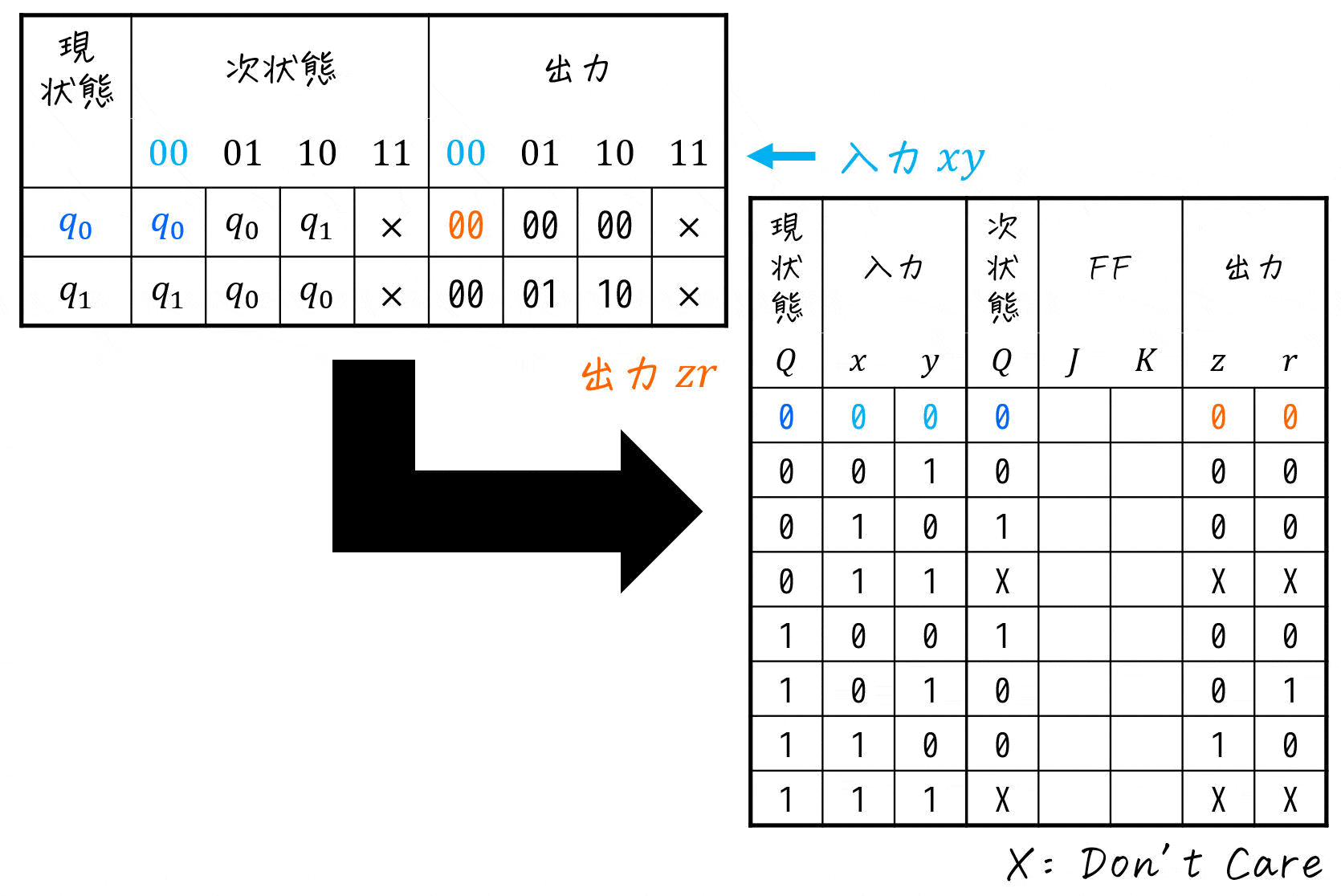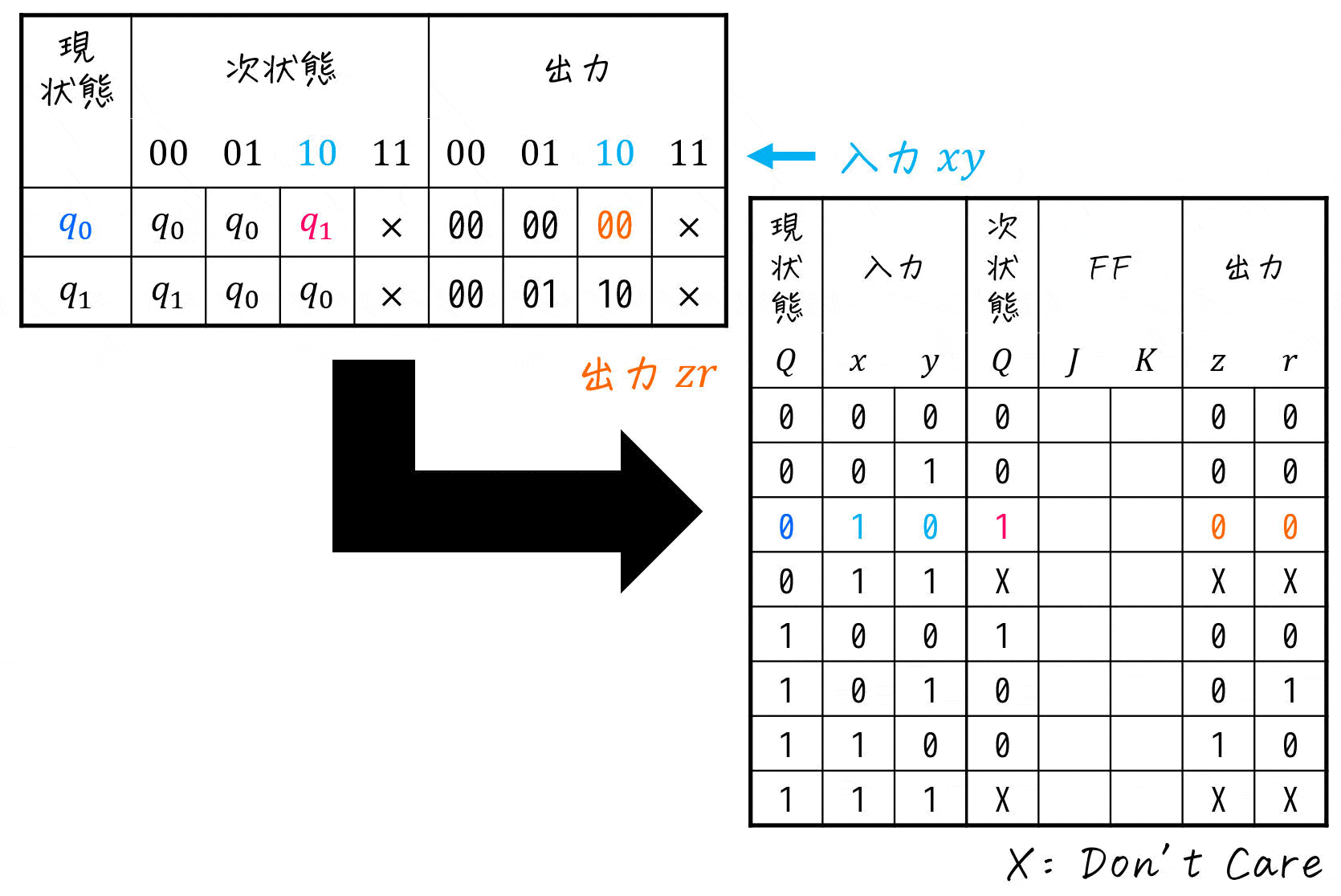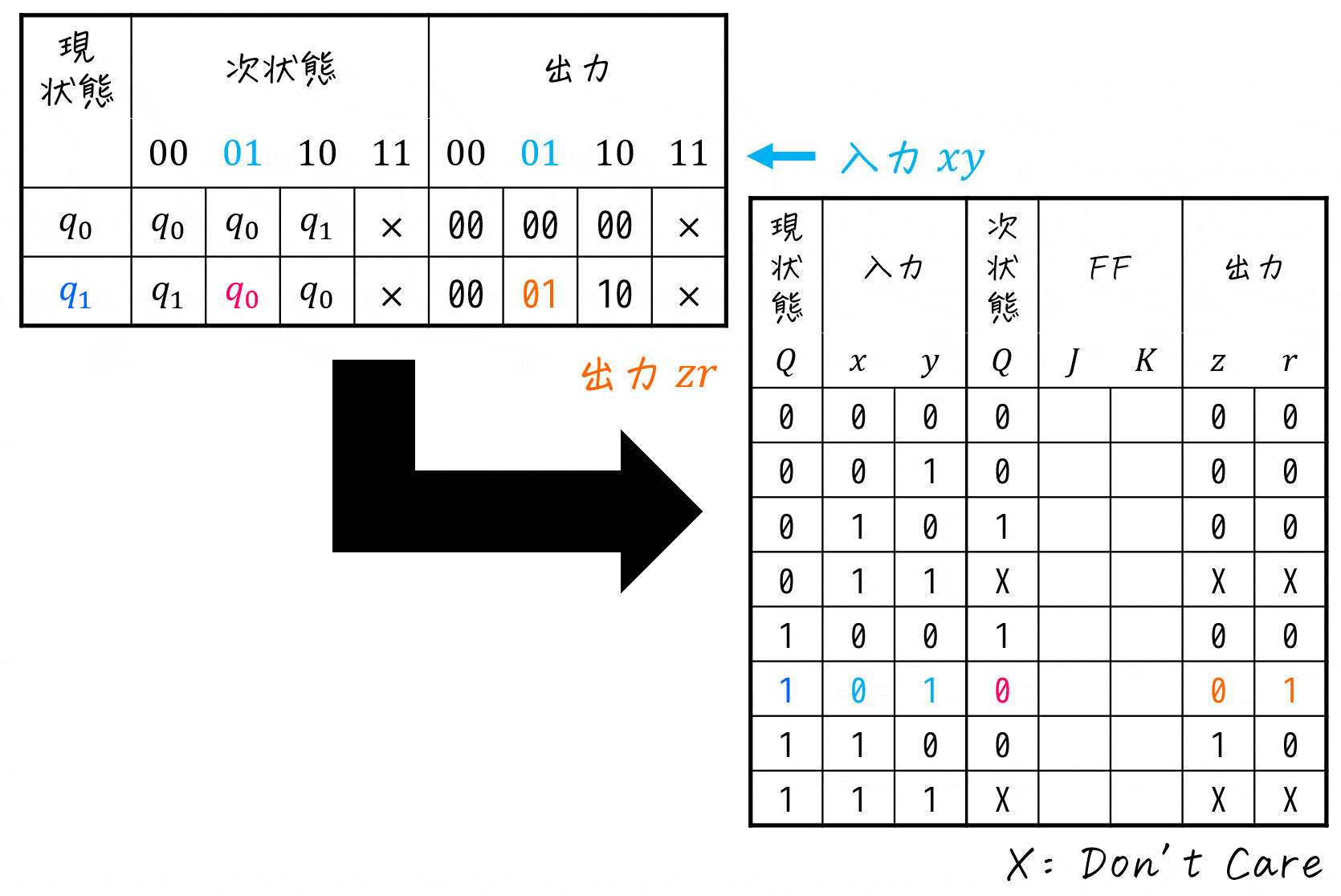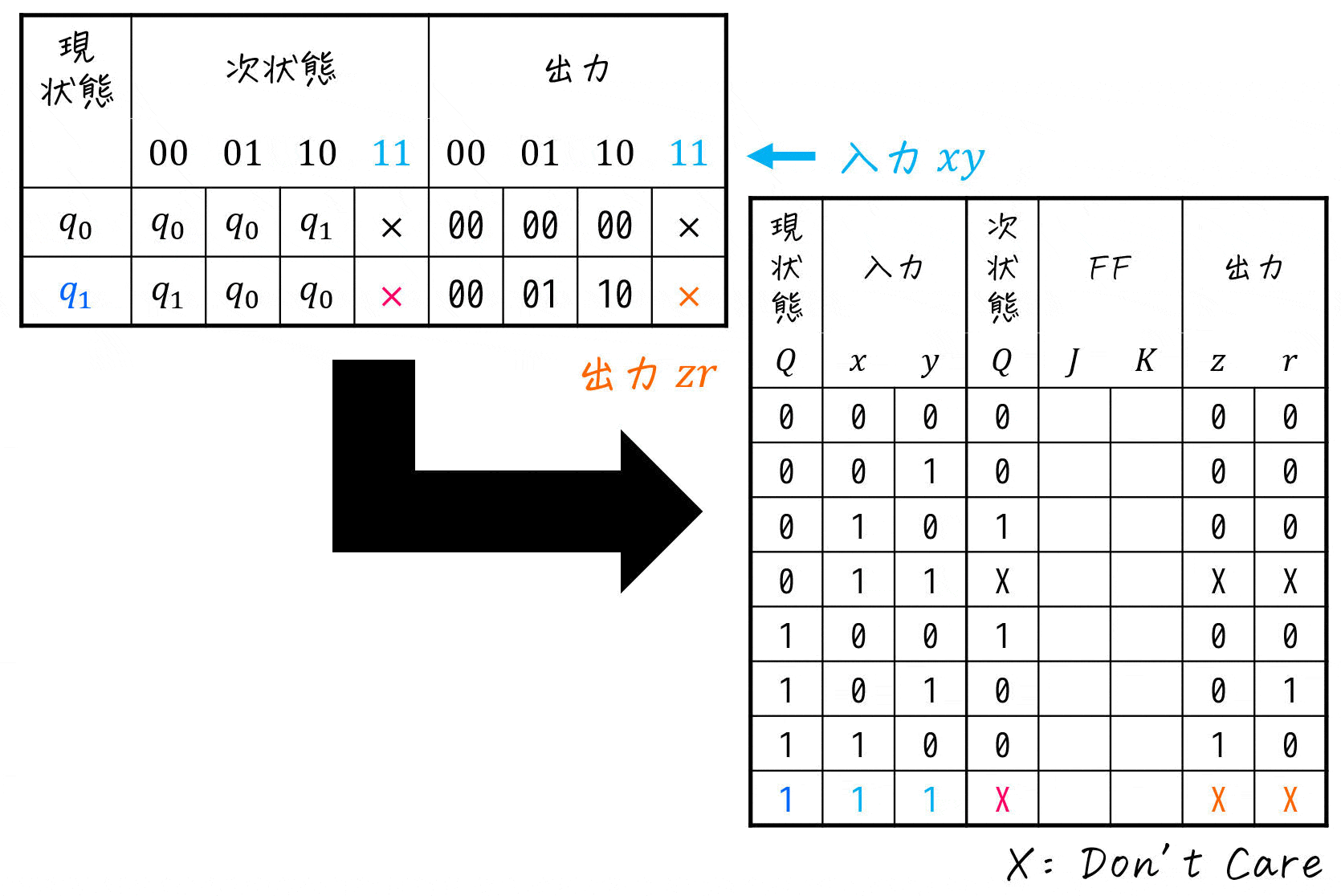
Step3. 次状態からFFの入力値を求める
最後に、次の1, 2の順で励起表の空欄部分である、FFの入力値を埋めていきます。
- 現状態 \( Q \) が0, 1かを確認し、\( J \), \( K \) のどちらがX (Don't Care)になるかを確認
- 現状態 \( Q \) と次状態 \( Q \) の変化を確認し、Xではない方の値を埋める
※ 硬貨の投入 \( x = 1 \) と、返却ボタンを押す動作 \( y = 1 \) が同時に生じることは考えなくてよいため、\( (x,y) = (1,1) \) のときは、FFの入力 \( J \), \( K \) および出力 \( z \), \( r \) はDon't Careとなります。
1) 現状態から、Don't Careが \( J \), \( K \) どちらであるかを確認
まずは、
- 現状態 \( Q = 0 \) のとき → \( K \) に X (Don't Care)
- 現状態 \( Q = 1 \) のとき … \( J \) に X (Don't Care)
をFFの空欄に埋めていきます。
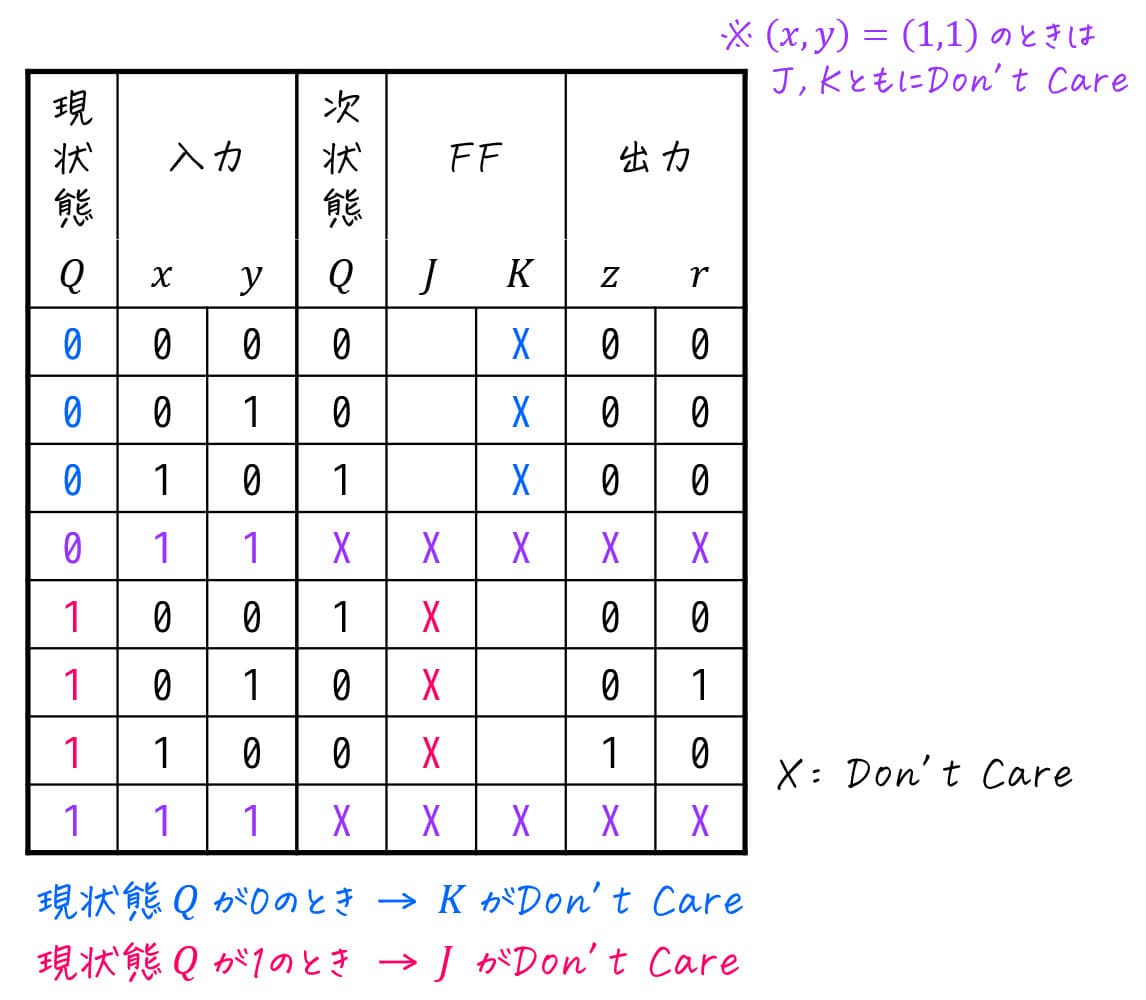
2) 現状態と次状態の変化を確認
つぎに、
現状態 \( Q \) = 次状態 \( Q \) → Don't Careではない方のFF入力に0
現状態 \( Q \) ≠ 次状態 \( Q \) → Don't Careではない方のFF入力に1
を空欄に入れていきます。

これで、励起出力表の完成です。
[2-iii] 励起関数(FFの入力方程式)・順序回路の出力方程式を作り、簡略化する
完成した励起表(と出力値)が含まれた励起出力表から、FFの入力方程式(励起関数)、および順序回路の出力方程式を考えていきましょう。
励起出力表(完成Ver)
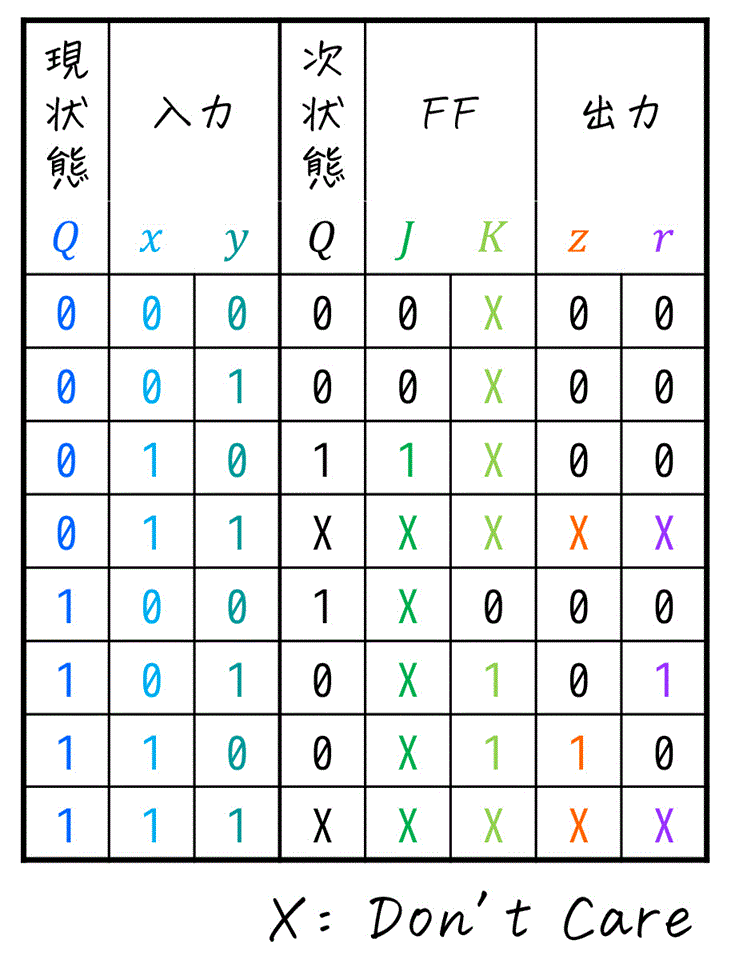
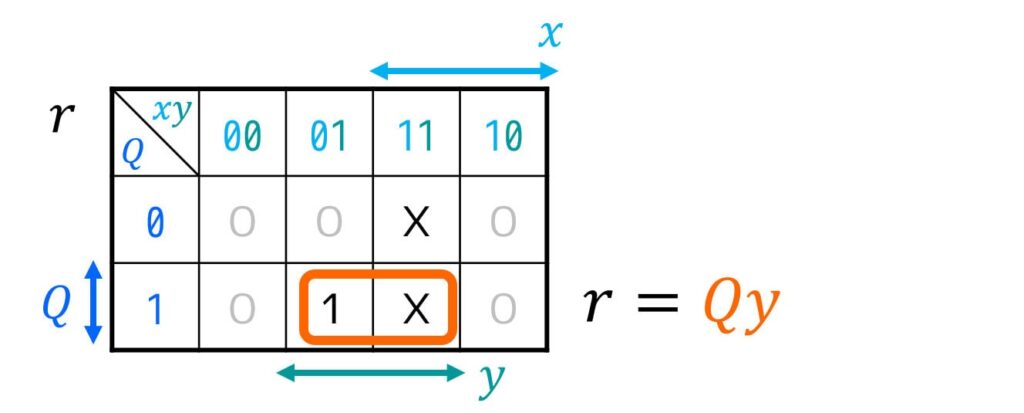
\( J \), \( K \), \( z \), \( r \) ともにDon't Careが含まれていて複雑なので、カルノー図を使って励起関数(FFの入力方程式)\( D \) と順序回路の出力方程式 \( z \), \( r \) を簡略化することを考えましょう。
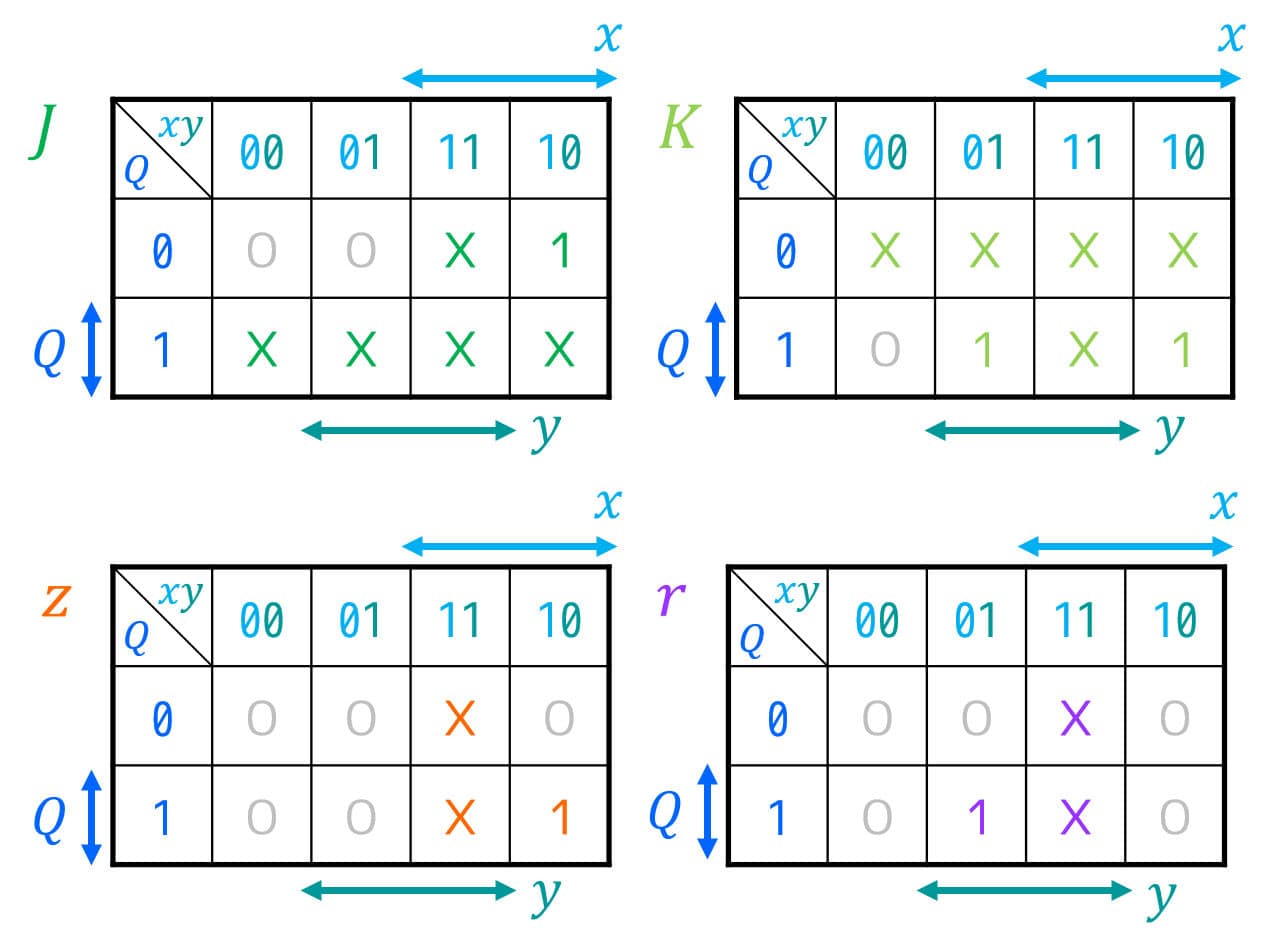
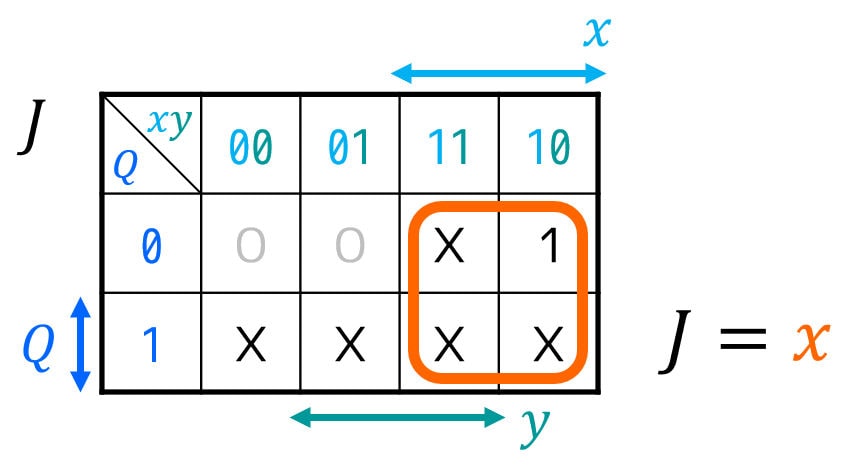
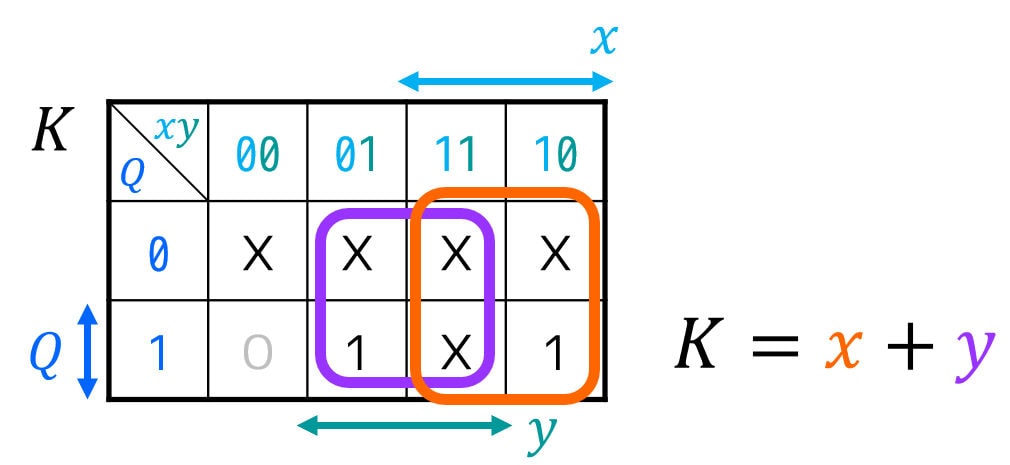
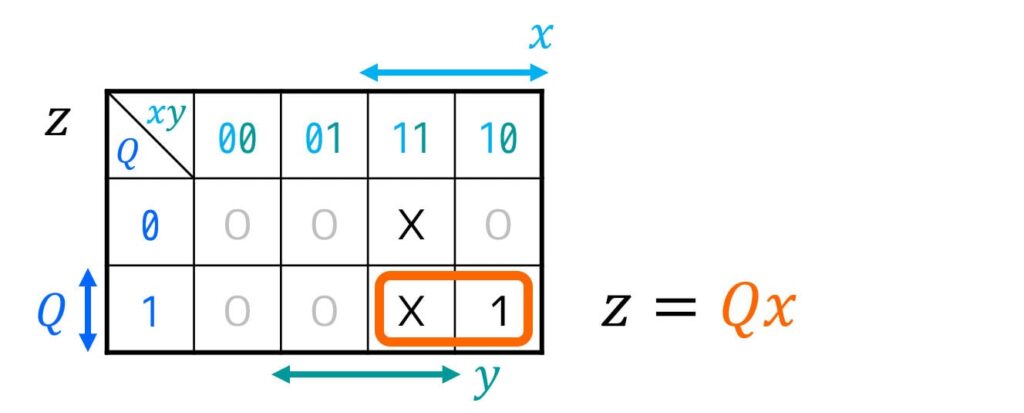
※ カルノー図を使う復習をしたい人は、このリンクの記事をご覧ください。
(例題などで使い方をわかりやすく解説しています!)
[2-iv] 励起関数(FFの入力方程式)・順序回路の出力方程式を作り、簡略化する
最後に、[2-iii]で作成した励起関数 \( J \), \( K \) 、出力方程式 \( z \), \( r \) の式\[\begin{align*}
J & = x \\
K & = x + y \\
z & = Q x \\
r & = Q y
\end{align*}\]を用いて、順序回路を作れば設計完了です!
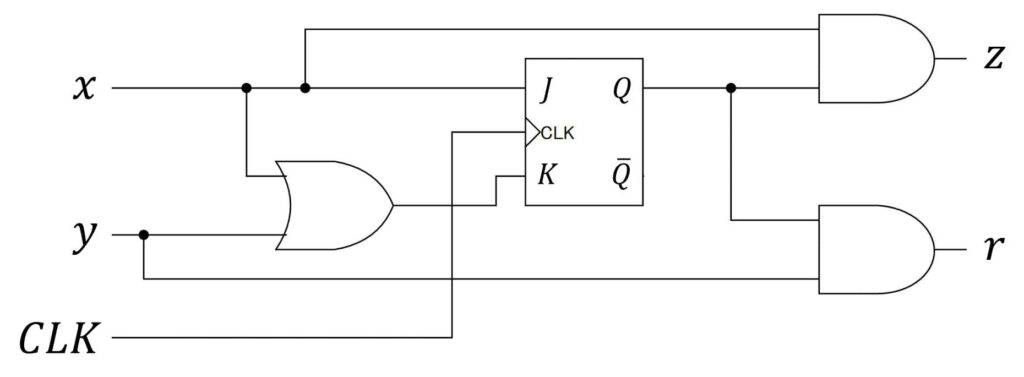
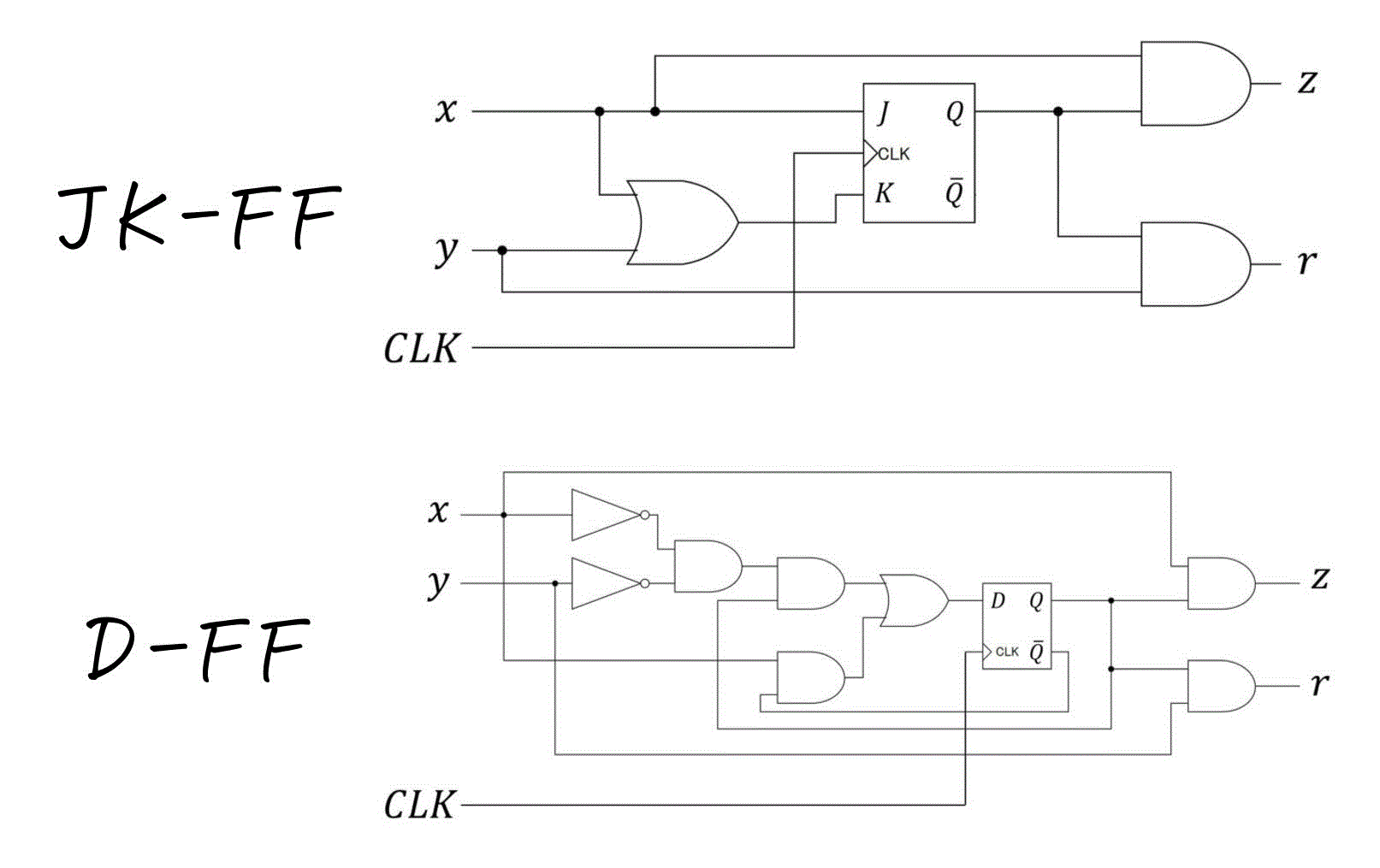
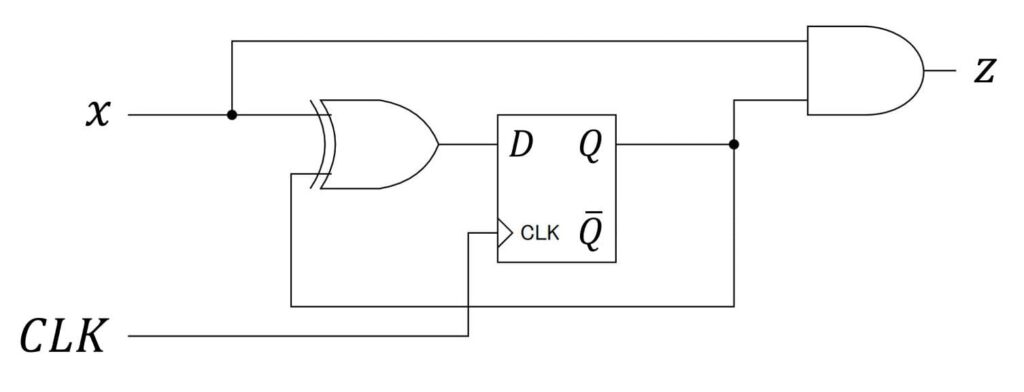
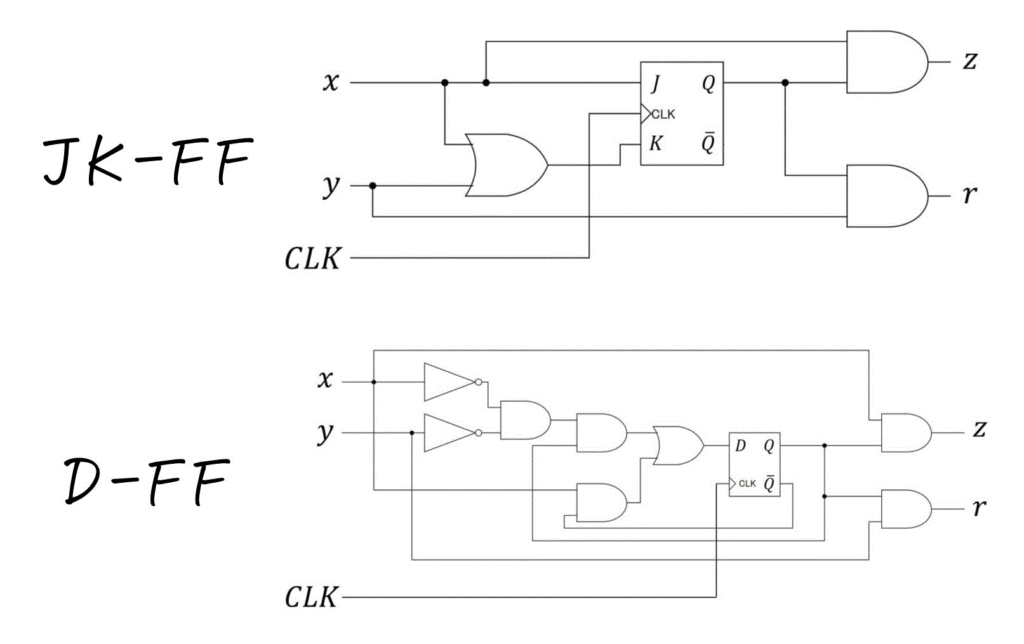
※ 少し回路が複雑なので、順序回路内に出てきたANDゲート、ORゲートの入力値を明記したバージョンも下に載せております。参考までにどうぞ。
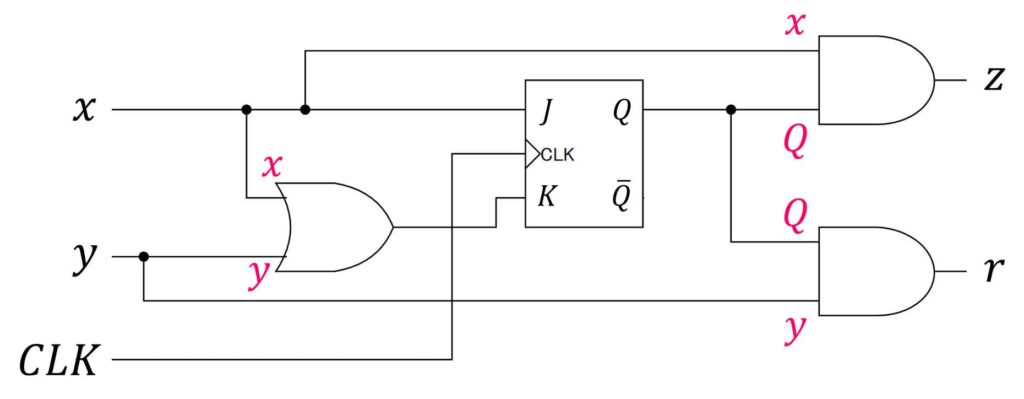
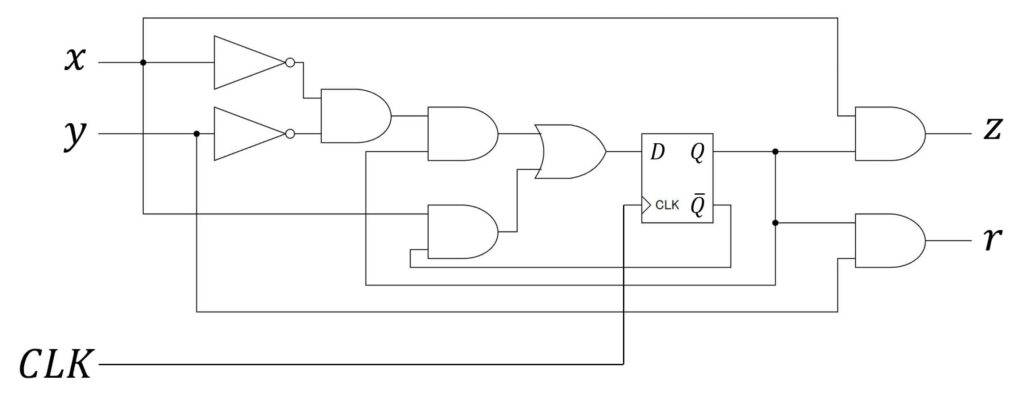
同じ仕様でも、JKフリップフロップを使うことで、(Dフリップフロップに比べて)ゲート(論理回路の部品)を減らせ、より単純な順序回路が設計できることがわかりますね。
[練習問題1] 4進アップカウンタの設計
実際に2問例題を解くことで、JKフリップフロップを用いた順序回路の設計の流れをなんとなく理解することはできましたか?
ここからは、例題よりも少し複雑な順序回路を設計する練習問題を解いてみましょう。
1が入力された回数をカウントし、4回入力されたときに「1」、それ以外のときに「0」が出力される回路を考える。このとき、[1], [2]の問いに答えなさい。
[1] まずは状態遷移図・状態遷移表を設計する。(i) 入力変数、出力変数は最低何個必要か答えなさい。
(ii) 内部状態は最低何個必要か答えなさい。
(状態遷移図を書くために定義する必要がある状態は最低何個か?)
(iii) 状態遷移図を書きなさい。
(iv) 状態遷移表を書きなさい。
(i) 順序回路を作るために必要なフリップフロップは最低何個か答えなさい。
(ii) [1](ii)で定義した状態を各JKフリップフロップの状態に対応させ、励起表に順序回路の出力値を追記した励起出力表を完成させなさい。(Don’t Careとなる部分には X を書くこと)
(iii) 各フリップフロップの入力方程式(励起関数)、および出力の方程式(出力)関数を最簡形で求めなさい。
(iv) 回路図を書きなさい。(CLKの配線は省略してよい)
[1] 状態遷移図・状態遷移表の設計
(i) 入力変数・出力変数を考える
- 入力変数(1個)
- 0, 1を入力する変数 \( x \)
- 出力変数(1個)
- 1が4回入力されたかを判定する変数 \( z \)
(4回入力されていない → 0、4回入力された → 1)
- 1が4回入力されたかを判定する変数 \( z \)
(ii) 内部状態を考える
内部状態 = 記憶すべき状態、を考えます。
今回は「1が4回入力されるごとに1を出力する」回路を作りたいので、最後に1が出力されてからの入力の数を記憶(=内部状態として定義)しましょう。
よって、最低でも
- 最後に1が出力されてから1が0回入力された状態
(1が入力されていない状態) - 最後に1が出力されてから1が1回入力された状態
- 最後に1が出力されてから1が2回入力された状態
- 最後に1が出力されてから1が3回入力された状態
の4個を定義する必要があります[9] … Continue reading。
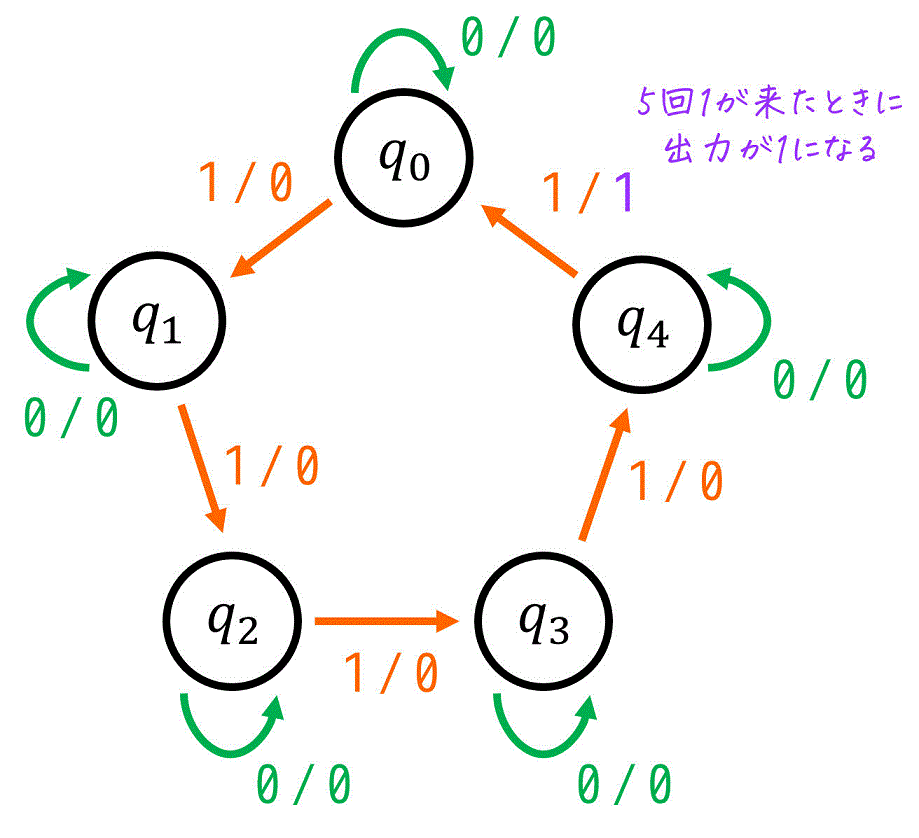
(iii) 状態遷移図の設計
まずは、(2)で考えた状態に下のような名前を付けましょう。
- 最後に1が出力されてから1が0回入力された状態: \( q_0 \)
- 最後に1が出力されてから1が1回入力された状態: \( q_1 \)
- 最後に1が出力されてから1が2回入力された状態: \( q_2 \)
- 最後に1が出力されてから1が3回入力された状態: \( q_3 \)
つぎに、(名前を付けた)状態を並べましょう。

あとは、各状態からの遷移先(次状態)と、そのときの入出力を矢印で表せばOKです。
今回の場合は、
- 0が入力された場合:1が入力された回数が変化しないため、状態が変わらず、出力は0
(現状態と次状態が同じ) - 1が入力された場合:
- \( q_0 \) ~ \( q_2 \): 1の数が1個増えた状態に遷移
- \( q_3 \): 1の数が5個になるので、1を出力し、1の回数を0回にリセット。
を満たすように矢印を追加すればOKです。
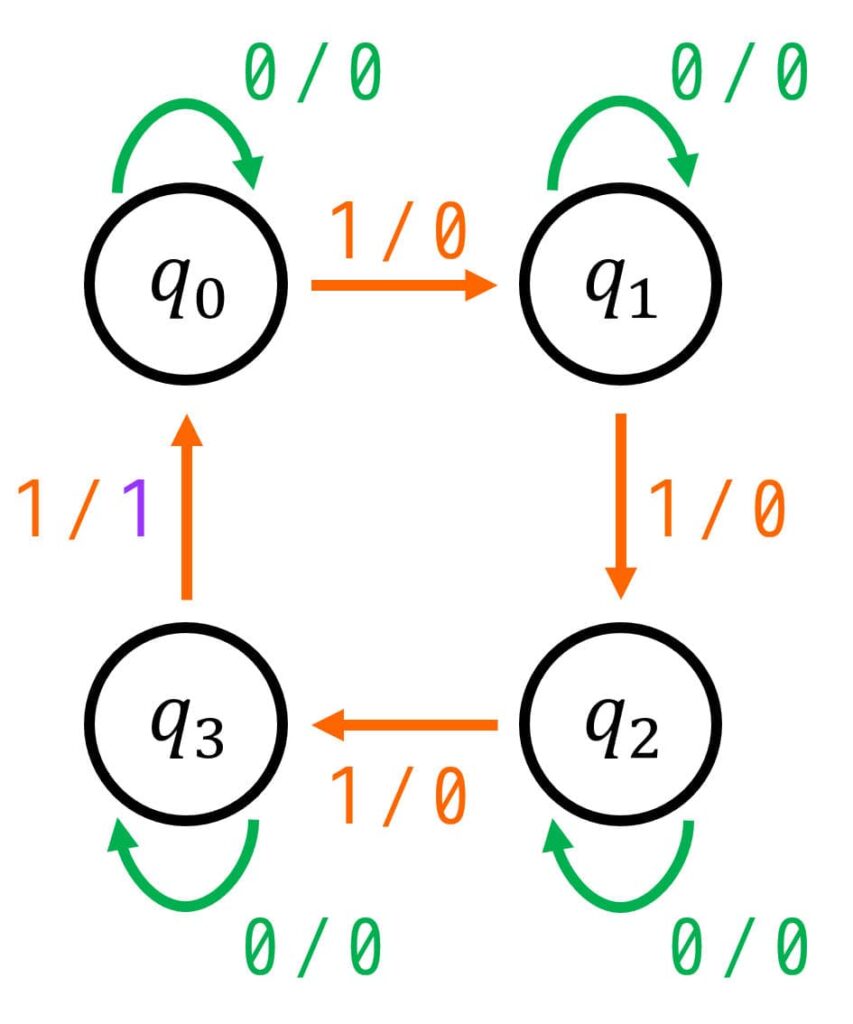
(iv) 状態遷移表の設計
(iii)で書いた状態遷移図を元に、状態遷移表を書いていきましょう。
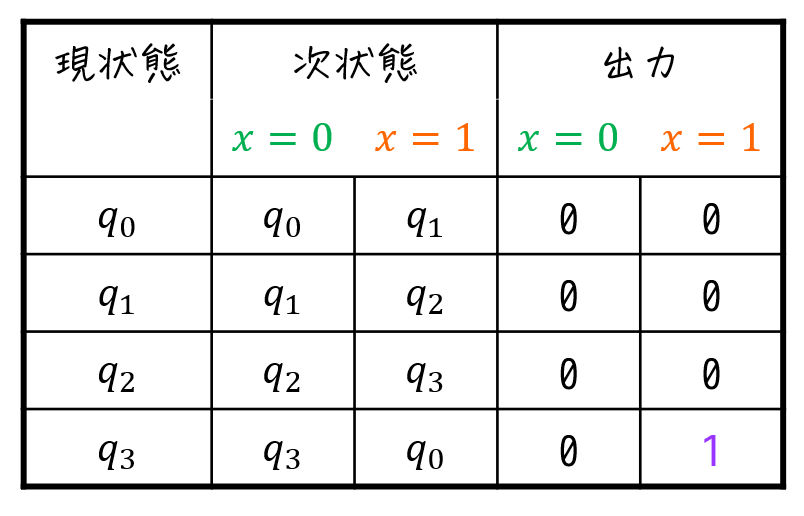
※ 自信がある人は、状態遷移図を書かずに状態遷移表を書くのもありです。
これで、状態遷移図・状態遷移表の設計の完了です。なので、実際に順序回路を作成するための作業をしていきましょう。
[2-i] 必要なフリップフロップの数を考える
今回は、作成した状態が4つですね。
4つの状態を記憶させるためには、最低でも2ビットの記憶領域が必要ですね。そのため、最低でも2つのフリップフロップが必要です。
※ 公式 \( 2^{\textcolor{red}{n}-1} < 4 \leqq 2^{\textcolor{red}{n}} \) を使って \( \textcolor{red}{n = 2} \) と判断してもOKです。
[2-ii] 励起表と出力値を合体させた表を書く
つぎに、
- 「Dフリップフロップの現状態 \( Q \) ・各入力」からどの「Dフリップフロップの次状態 \( Q \)」 に遷移すればよいか
([1]で作った状態遷移表を見ながら) - 現状態 \( Q \) から次状態 \( Q \) に遷移させるためには、Dフリップフロップの入力をどうすればよいか
の2つを下のように、励起表に出力値 \( z \)を含んだ状態遷移表で示します。
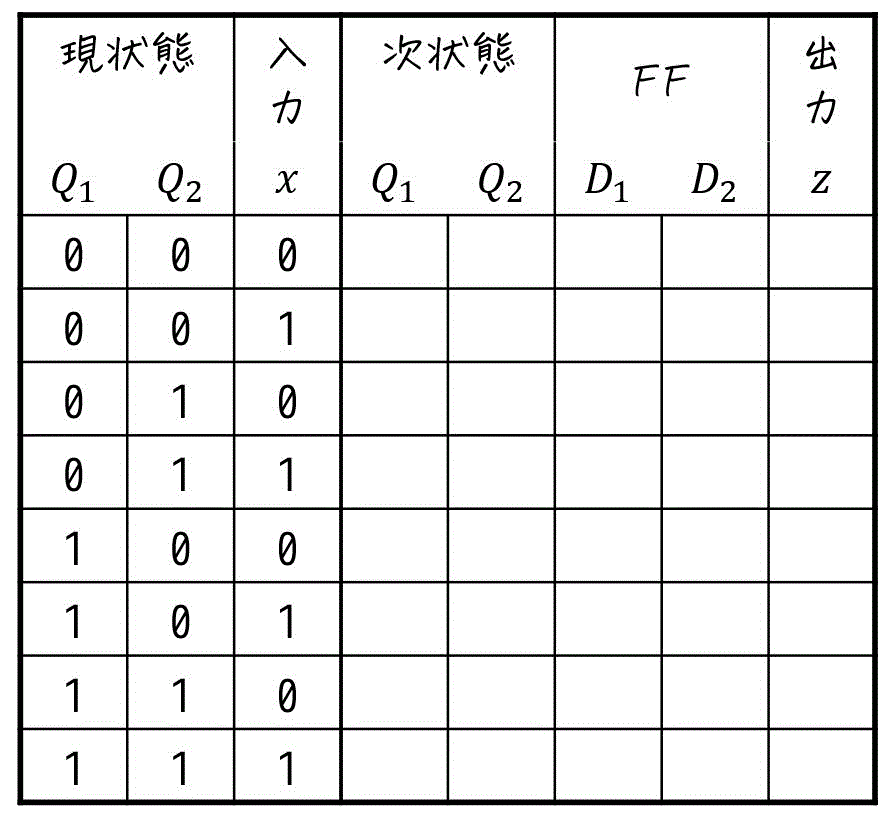
Step1. 定義した状態を、フリップフロップの状態の値に割り当てる
まずは、[1]で定義した状態を実際にフリップフロップの値状態に割り当てます。
今回、フリップフロップは2つなので、2つのフリップフロップの値 \( Q_1 \), \( Q_2 \) を組み合わせて各状態に割り当てていきましょう。
※ JKフリップフロップはDon't Careが多いので、状態をFFの値に割り当てるときに、あまり工夫をする必要はありません[10]\( q_2 \) を \( (Q_1,Q_2) = (1,1) \)、\( q_3 \) を \( (Q_1,Q_2) = (1,0) \) と工夫した場合、\[\begin{align*}J_1 & = Q_2 x \\ K_1 & = \bar{Q_2} x \\J_2 & = … Continue reading。
Step2. 状態遷移表から励起表の次状態・出力を埋める
つぎに、「[1](4) 状態遷移表の設計」で作成した状態遷移表から励起表を作り上げていきます。
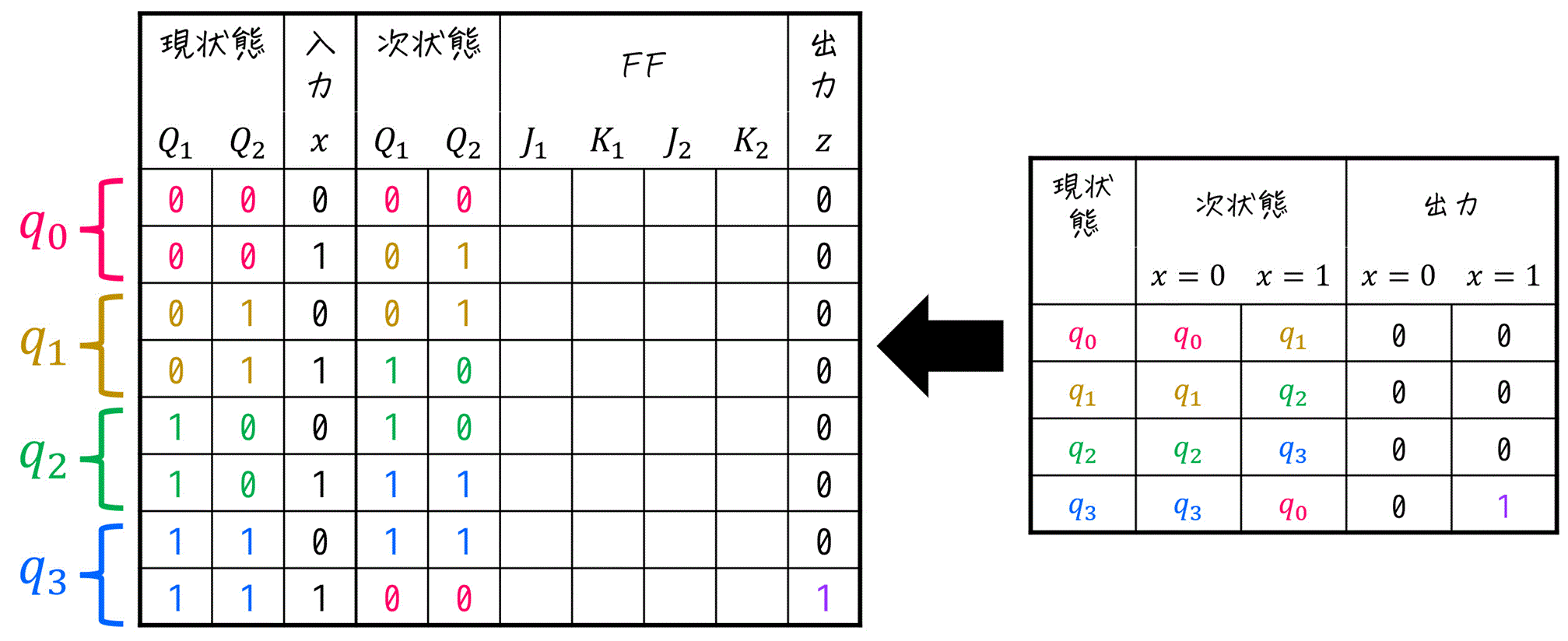
Step3. 次状態からFFの入力値を求める
あとは、次の1, 2の順で励起表の空欄部分である、FFの入力値を埋めればOKです。
- 現状態 \( Q \) が0, 1かを確認し、\( J \), \( K \) のどちらがX (Don't Care)になるかを確認
- 現状態 \( Q \) と次状態 \( Q \) の変化を確認し、Xではない方の値を埋める
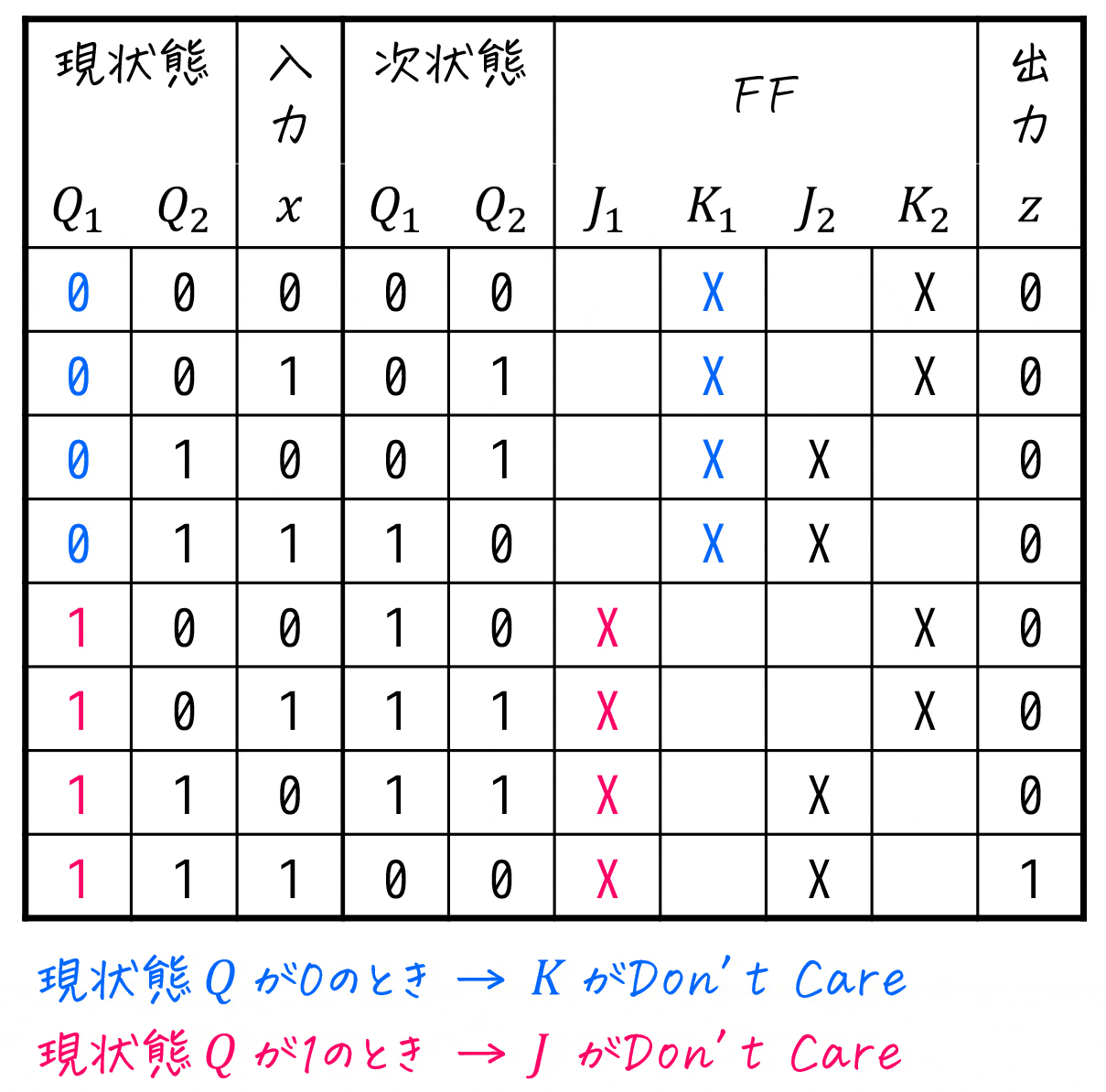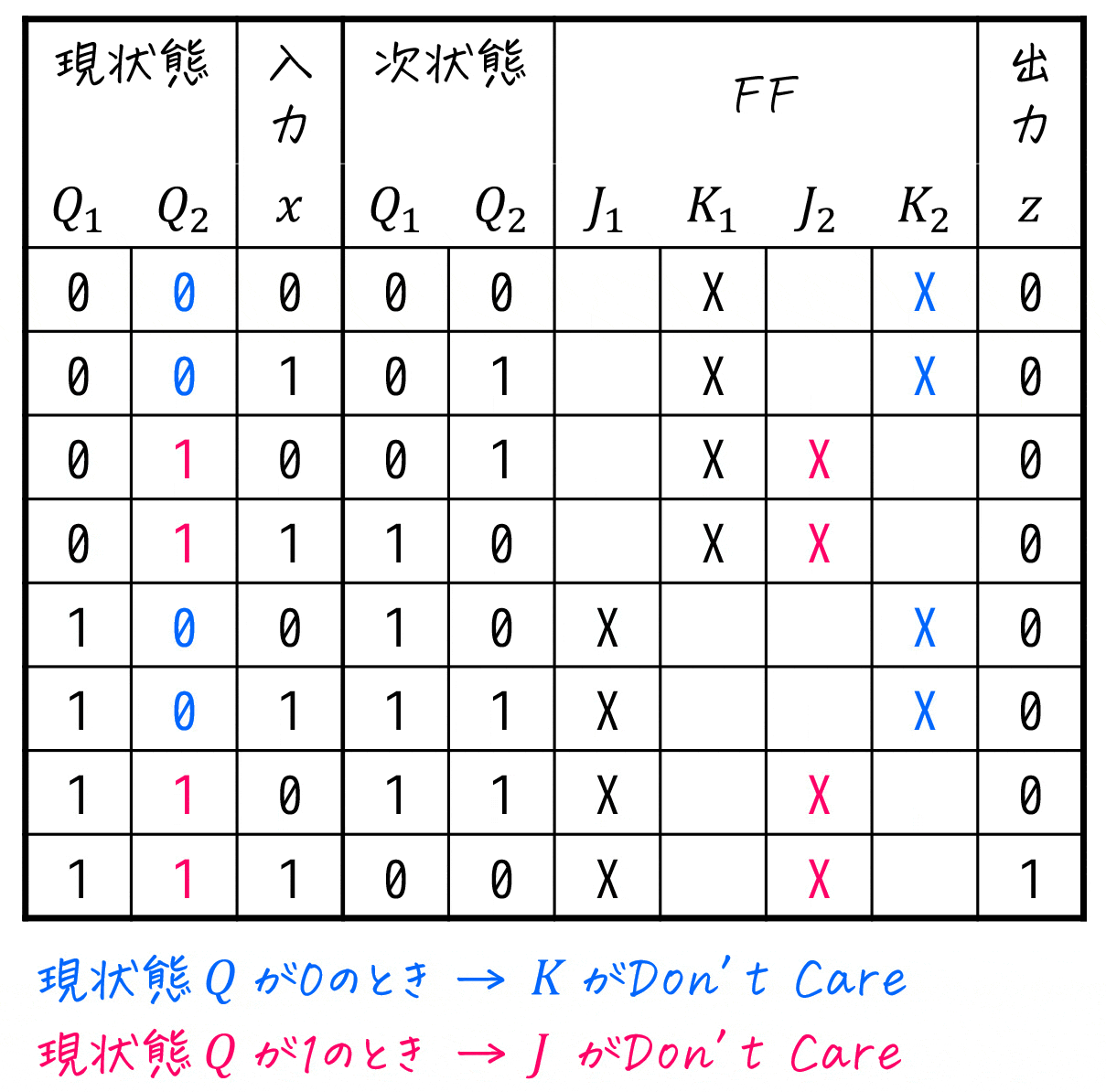
1) 現状態から、Don't Careが \( J \), \( K \) どちらであるかを確認
まずは、
- 現状態 \( Q_1 = 0 \) のとき → \( K_1 \) に X (Don't Care)
- 現状態 \( Q_2 = 0 \) のとき → \( K_2 \) に X (Don't Care)
- 現状態 \( Q_1 = 1 \) のとき … \( J_1 \) に X (Don't Care)
- 現状態 \( Q_2 = 1 \) のとき … \( J_2 \) に X (Don't Care)
をFFの空欄に埋めていきます。
2) 現状態と次状態の変化を確認
つぎに、状態 \( Q_1 \), \( Q_2 \) それぞれに対して、
現状態 = 次状態 → Don't Careではない方のFF入力に0
現状態 ≠ 次状態 → Don't Careではない方のFF入力に1
を空欄に入れていきます。
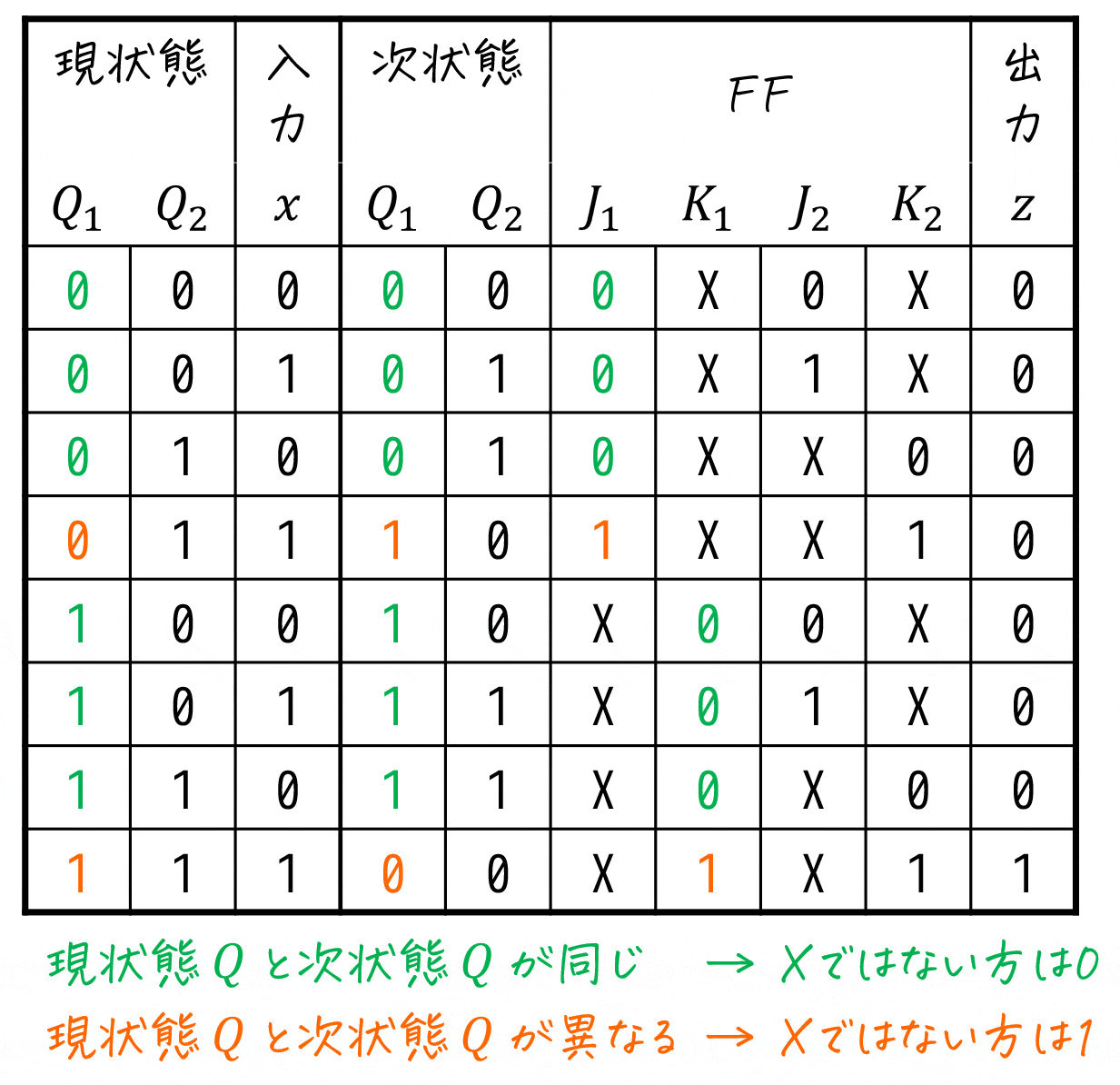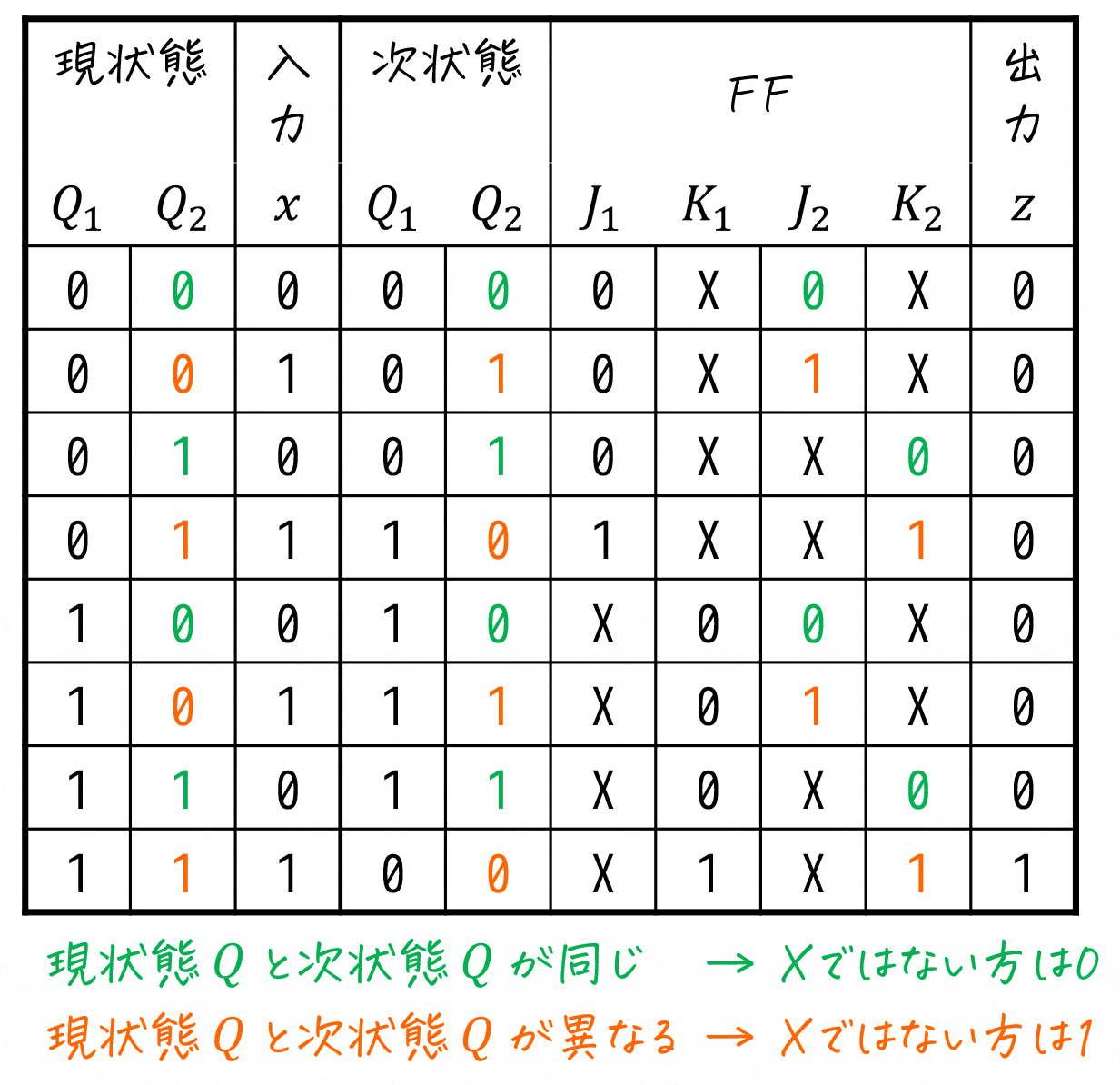
これで、励起出力表の完成です。
[2-iii] 励起関数(FFの入力方程式)・順序回路の出力方程式を作り、簡略化する
完成した励起表(と出力値)が含まれた表から、FFの入力方程式(励起関数)、および順序回路の出力方程式を考えていきましょう。
励起出力表(完成Ver)
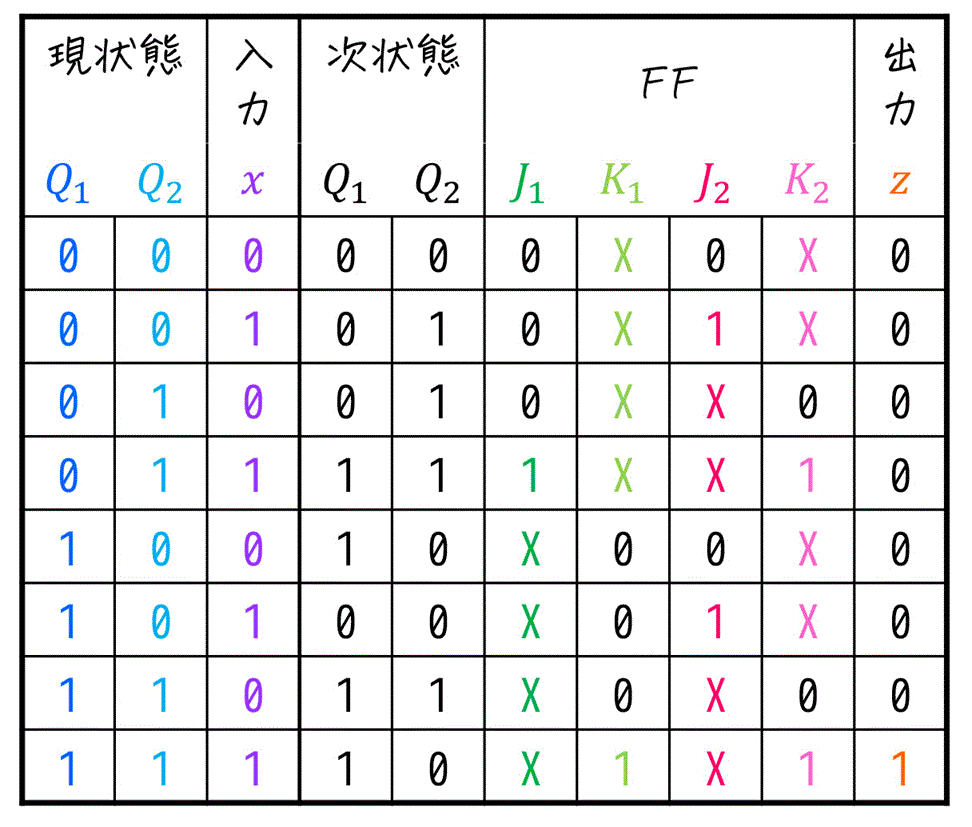
まず、出力 \( z \) は1がある箇所が1箇所なのと、Don't Careが存在しないので、カルノー図を書かなくても主加法標準形を求めるだけで、\( z = Q_1 \overline{Q_2} x \) と最簡形を求めることができます。
※ カルノー図を書くと下のようになります。
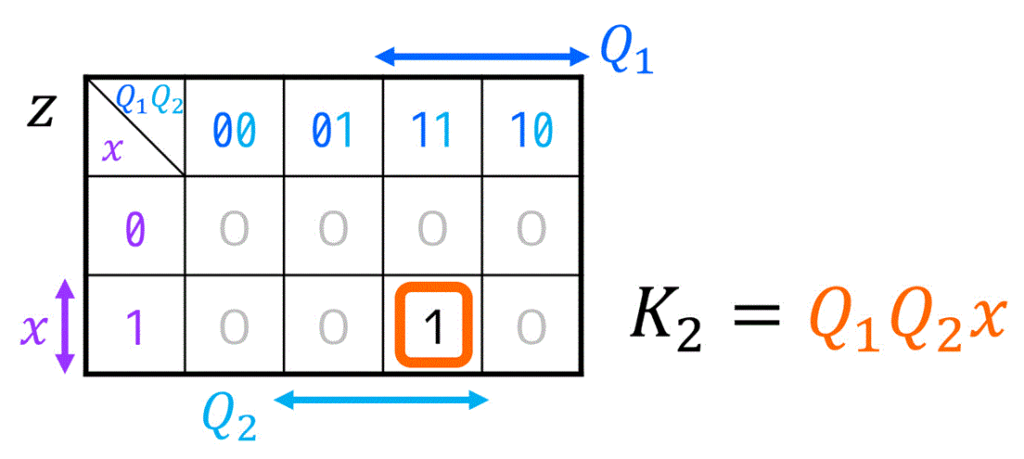
しかし、FFの入力 \( J \), \( K \)、および出力 \( z \), \( c \) にDon’t Careが多く含まれるため、下のようにカルノー図を書いて最簡形の励起関数を求めることをおすすめします。
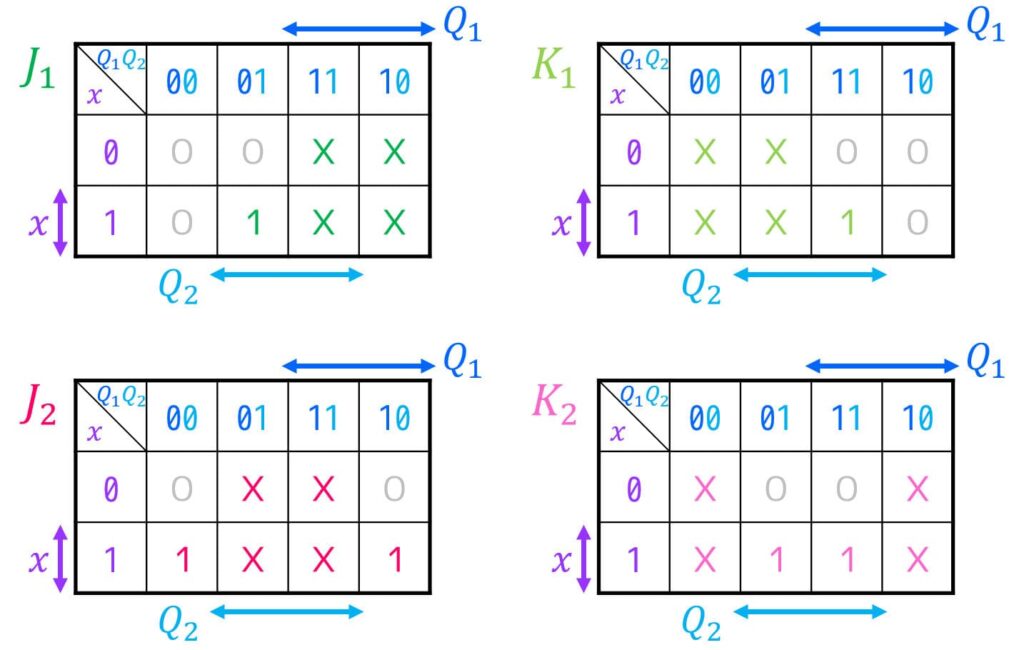
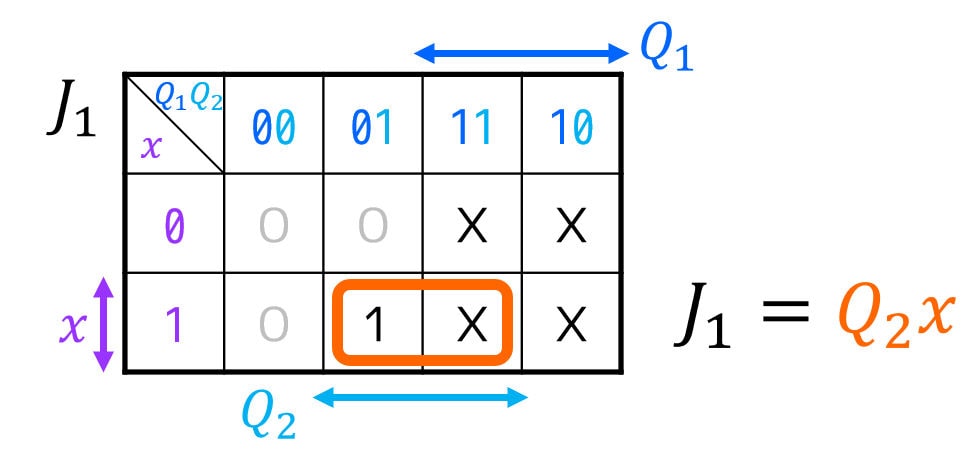
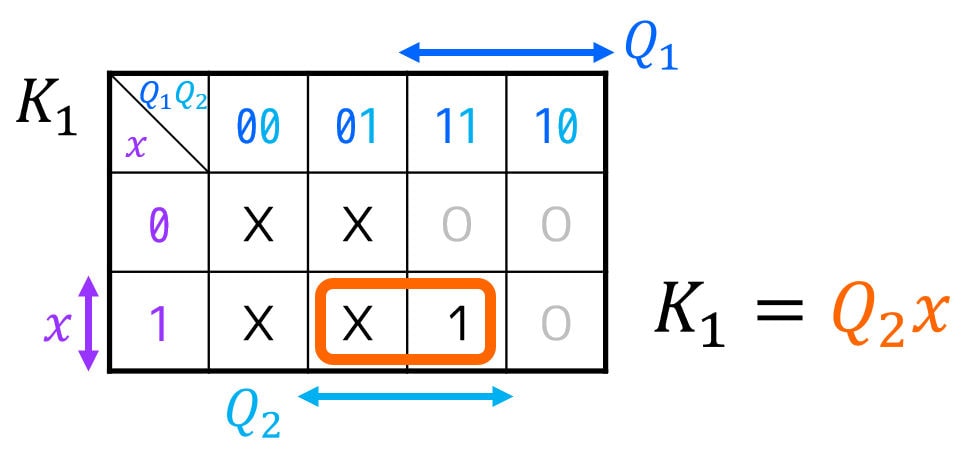
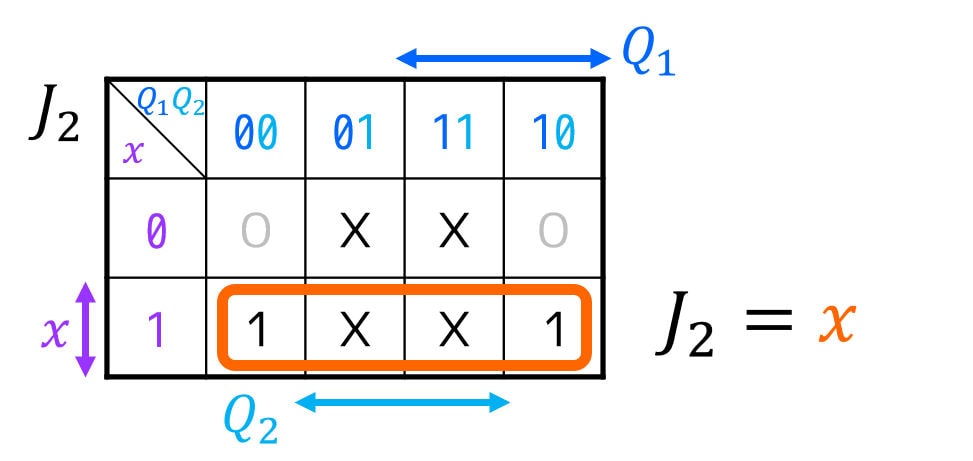
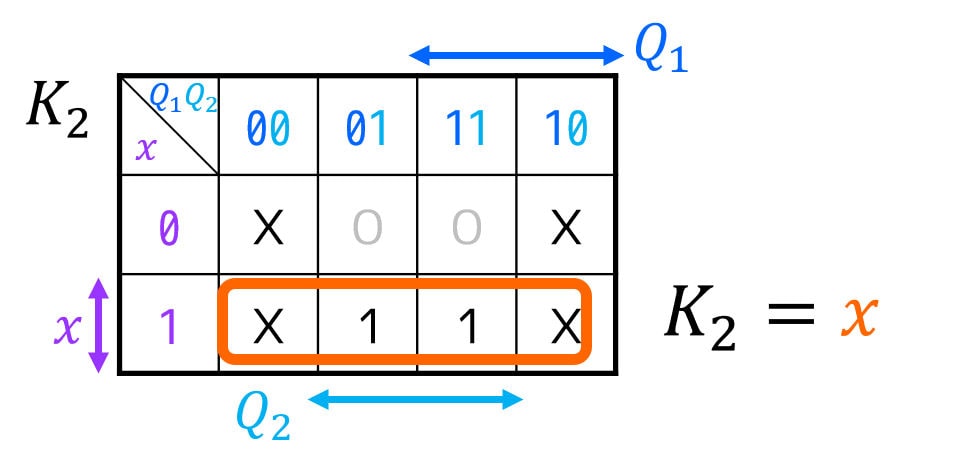
[2-iv] 励起関数(FFの入力方程式)・順序回路の出力方程式を作り、簡略化する
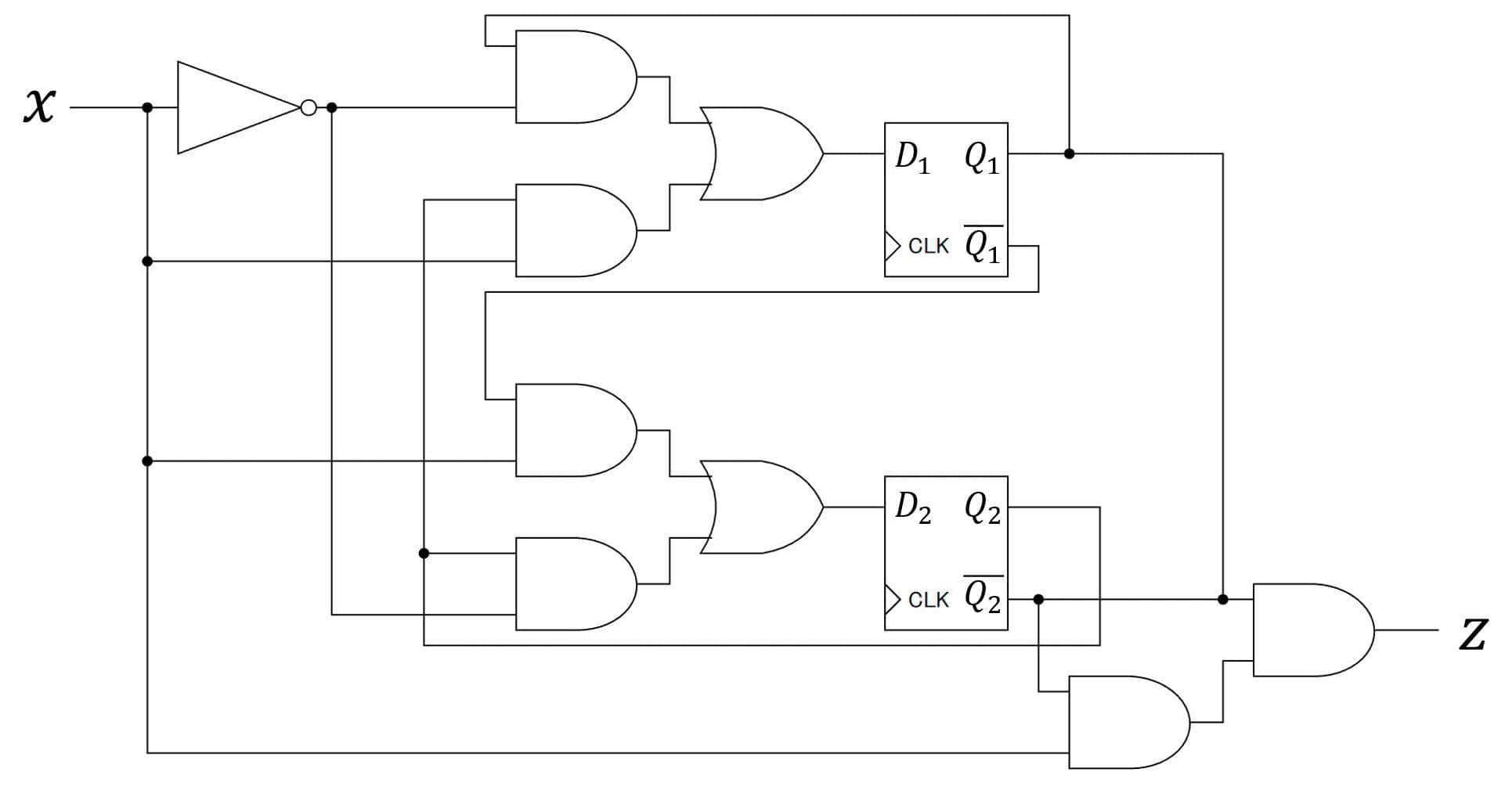
最後に、[2-iii]で作成した最簡形の励起関数 \( J \), \( K \)、および出力方程式 \( z \), \( c \) の式\[\begin{align*}
J_1 & = Q_2 x \\
K_1 & = Q_2 x \\
J_2 & = x \\
K_2 & = x \\
z & =
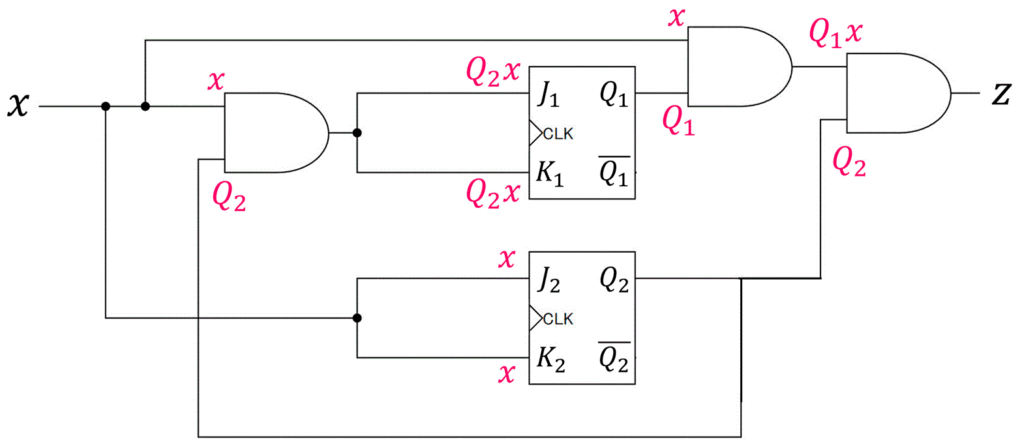
\end{align*}\]を用いて、順序回路を作れば設計完了です!
※ CLKの線は省略しています
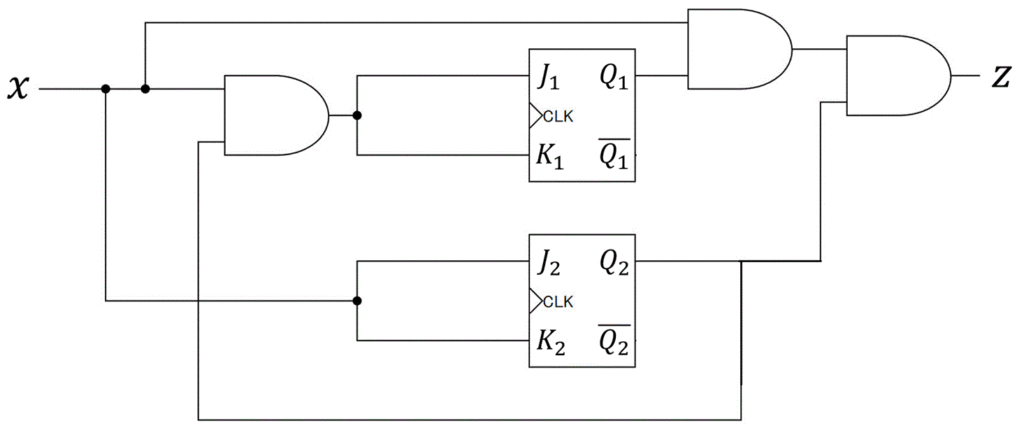
※ 少し回路が複雑なので、順序回路内に出てきたANDゲート、ORゲートの入力値を明記したバージョンも下に載せております。参考までにどうぞ。
練習問題2. 自動販売機の設計
最後に、例題2の自動販売機の[仕様]を少し変えた問題にチャレンジしてみましょう!
つぎの[仕様]を満たす200円のおもちゃを販売するガチャガチャ(自動販売機)の回路を設計したい。
[仕様]- 100円硬貨と500円硬貨を受け付け、投入金額が合計200円になると商品が出てくる。
- 投入金額が200円を超えた場合は、おつりが返って来る。
- 商品が出たかどうか、おつりが返ってきたかどうかをこの回路で判定すること。
- 1度に2枚以上の硬貨が投入されることは考えなくてよい。
次の(1)~(4)の問いに答えなさい。
[1], [2]の問いに答えなさい。 [1] まずは状態遷移図・状態遷移表を設計する。(i) 入力変数、出力変数は最低何個必要か答えなさい。
(ii) 内部状態は最低何個必要か答えなさい。
(状態遷移図を書くために定義する必要がある状態は最低何個か?)
(iii) 状態遷移図を書きなさい。
(iv) 状態遷移表を書きなさい。
(i) 順序回路を作るために必要なフリップフロップは最低何個か答えなさい。
(ii) [1](ii)で定義した状態を各JKフリップフロップの状態に対応させ、励起表に順序回路の出力値を追記した励起出力表を書きなさい。ただし、Don’t Careとなる部分には X を書くこと。
(iii) 各フリップフロップの入力方程式(励起関数)、および出力の方程式(出力)関数を求めなさい。ただし、カルノー図で最簡形にすること。
(iv) 回路図を書きなさい。(CLKの配線は省略してよい。)
[1] 状態遷移図・状態遷移表の設計
(i) 入力変数・出力変数を考える
- 入力変数(2個)
- 100円硬貨が投入されたかを表す変数 \( x \)
(投入されていない → 0、投入された → 1) - 500円硬貨が投入されたかを表す変数 \( y \)
(投入されていない → 0、投入された → 1)
- 100円硬貨が投入されたかを表す変数 \( x \)
- 出力変数(2個)
- 商品が出たかを表す変数 \( z \)
(出なかった → 0、出た → 1) - おつりが出たかを表す変数 \( c \)
(出なかった → 0、出た → 1)
- 商品が出たかを表す変数 \( z \)
※ 0と1の割り当て方法は、上の方法以外でもOKです。
(例: 100円硬貨が投入された状態を0、投入されていない状態を1とする)
よって、答えは
- 入力変数: 2個
- 出力変数: 2個
となります。
(ii) 内部状態を考える
内部状態 = 記憶すべき状態、でしたね(だいぶ定着しましたか?)。
今回は、最後に商品が出てから投入された合計金額を100円単位で記憶すればOKなので、
- 最後に商品が出てから合計0円投入された状態(硬貨が投入されていない状態)
- 最後に商品が出てから合計100円投入された状態
の2種類の状態を記憶すれば、回路が表せます。
(200円以上なら商品を出す+必要であればおつりを出すだけなので、200円以上の状態を記憶する必要はない)
よって、必要な内部状態は最低2個であることがわかります。
(iii) 状態遷移図を考える
まずは、(2)で考えた状態に
- 合計投入金額が0円: \( q_0 \)
- 合計投入金額が100円: \( q_1 \)
と名前を付けましょう。そして、これらの状態を並べます。

あとは、各状態からの遷移先(次状態)と、そのときの入出力を矢印で表せばOKです。
今回の場合は、
- \( x = 0 \), \( y = 0 \) が入力された場合(硬貨が投入されなかった場合)
- 投入が入力されていないため、合計金額(状態)が変わらない。
→ 商品もおつりも出ないので出力は \( z = 0 \), \( c = 0 \)。(現状態と次状態が同じ)
- 投入が入力されていないため、合計金額(状態)が変わらない。
- \( x = 1 \), \( y = 0 \) が入力された場合(100円硬貨が投入された場合)
- \( q_0 \) : 合計金額が100円に(\( q_0 \) から \( q_1 に遷移)
- \( q_1 \): 合計が200円になるので、商品が出てくる。投入金額が0円にリセットされる。
→ \( z = 1 \) を出力し、次状態は \( q_0 \) に遷移
- \( x = 0 \), \( y = 1 \) が入力された場合(500円硬貨が投入された場合)
- 500円硬貨が投入されるため、現在の合計金額(状態)に関わらず必ず合計金額300円を超えるし、おつりも発生する。
→ どんな場合でも出力は \( z = 1 \), \( c = 1 \) となり、合計金額は0円にリセットされる(次状態は \( q_0 \) となる)。
- 500円硬貨が投入されるため、現在の合計金額(状態)に関わらず必ず合計金額300円を超えるし、おつりも発生する。
を満たすように矢印を追加すればOKです。
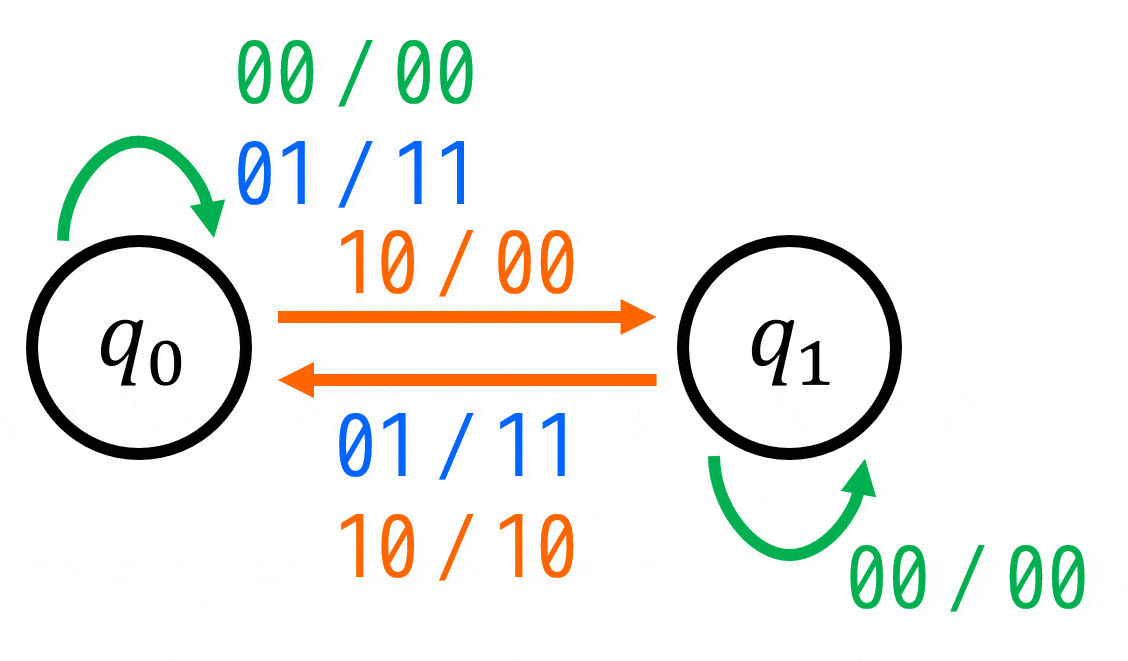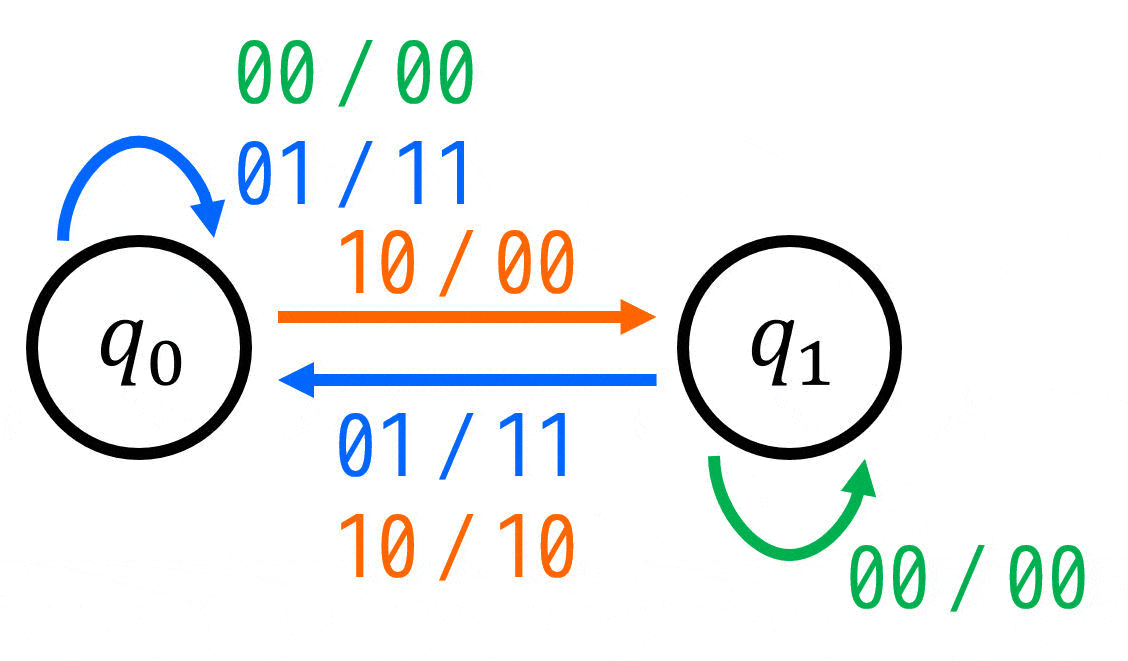
(iv) 状態遷移表を考える
(iii)で考えた状態遷移図を表にすればOKです。
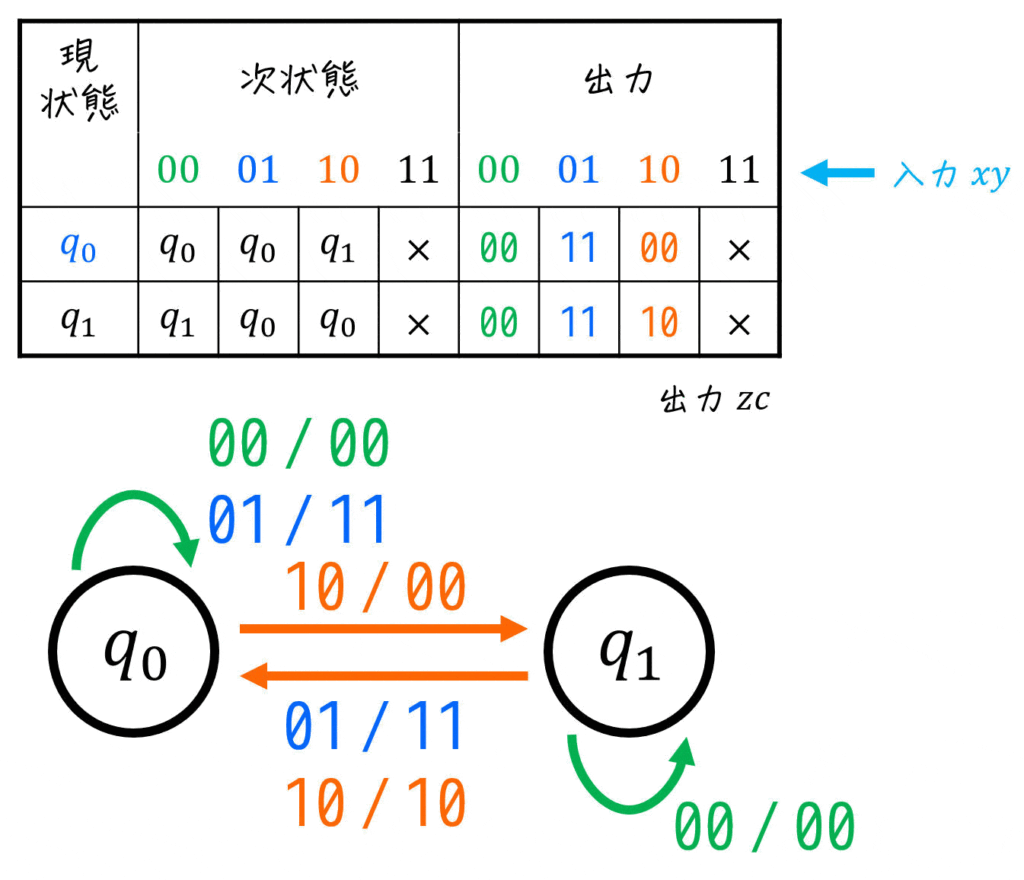
これで状態遷移図・状態遷移表ができましたので、ここからは順序回路の設計に入っていきましょう。
[2-i] 必要なフリップフロップの数を考える
今回は、作成した状態が2つですね。
状態数が2つであれば、1個のフリップフロップで記憶ができるので、必要なフリップフロップの数は最低1個です。
[2-ii] 励起表と出力値を合体させた表を書く
つぎに、
- 「JKフリップフロップの現状態 \( Q \) ・各入力」からどの「JKフリップフロップの次状態 \( Q \)」 に遷移すればよいか
([1]で作った状態遷移表を見ながら) - 現状態 \( Q \) から次状態 \( Q \) に遷移させるためには、JKフリップフロップの入力をどうすればよいか
の2つを下のように、励起表に出力値 \( z \), \( c \) を含んだ遷移出力表の空欄を埋めていくことで示します。

Step1. 定義した状態を、フリップフロップの状態の値に割り当てる
まずは、[1]で定義した状態を実際にフリップフロップ(1つ)の値状態に割り当てます。
- 状態 \( q_0 \) → \( Q = 0 \)
- 状態 \( q_1 \) → \( Q = 1 \)
※ 割り当て方は自由なので、\( q_0 \) → \( Q = 1 \)、\( q_1 \) → \( Q = 0 \) としてもOKです。
Step2. 状態遷移表から励起表の次状態・出力を埋める
つぎに、「[1](4) 状態遷移表の設計」で作成した状態遷移表から励起表を作り上げていきます。
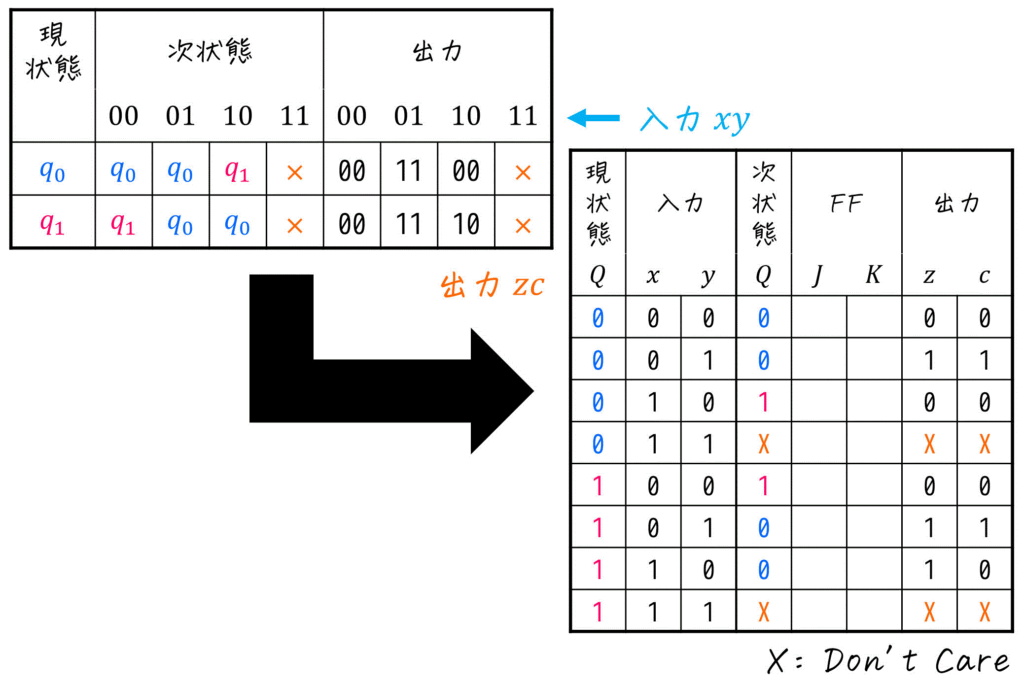
Step3. 次状態からFFの入力値を求める
最後に、次の1, 2の順で励起表の空欄部分である、FFの入力値を埋めていきます。
- 現状態 \( Q \) が0, 1かを確認し、\( J \), \( K \) のどちらがX (Don't Care)になるかを確認
- 現状態 \( Q \) と次状態 \( Q \) の変化を確認し、Xではない方の値を埋める
※ 100円硬貨の投入 \( x = 1 \) と、500円硬貨の投入 \( y = 1 \) が同時に生じることは考えなくてよいため、\( (x,y) = (1,1) \) のときは、FFの入力 \( J \), \( K \) および出力 \( z \), \( r \) はDon't Careとなります。
1) 現状態から、Don't Careが \( J \), \( K \) どちらであるかを確認
まずは、
- 現状態 \( Q = 0 \) のとき → \( K \) に X (Don't Care)
- 現状態 \( Q = 1 \) のとき … \( J \) に X (Don't Care)
をFFの空欄に埋めていきます。
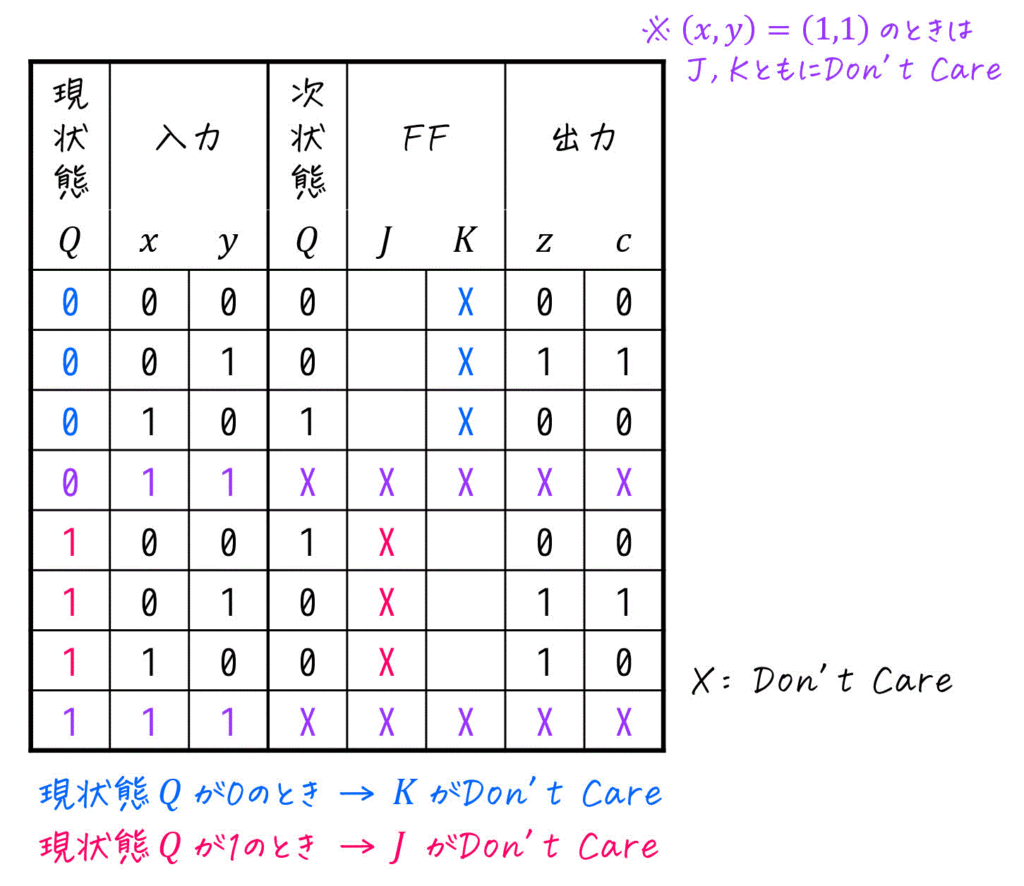
2) 現状態と次状態の変化を確認
つぎに、
現状態 \( Q \) = 次状態 \( Q \) → Don't Careではない方のFF入力に0
現状態 \( Q \) ≠ 次状態 \( Q \) → Don't Careではない方のFF入力に1
を空欄に入れていきます。

これで、励起出力表の完成です。
[2-iii] 励起関数(FFの入力方程式)・順序回路の出力方程式を作り、簡略化する
完成した励起表(と出力値)が含まれた表から、FFの入力方程式(励起関数)、および順序回路の出力方程式を考えていきましょう。
励起出力表(完成Ver)
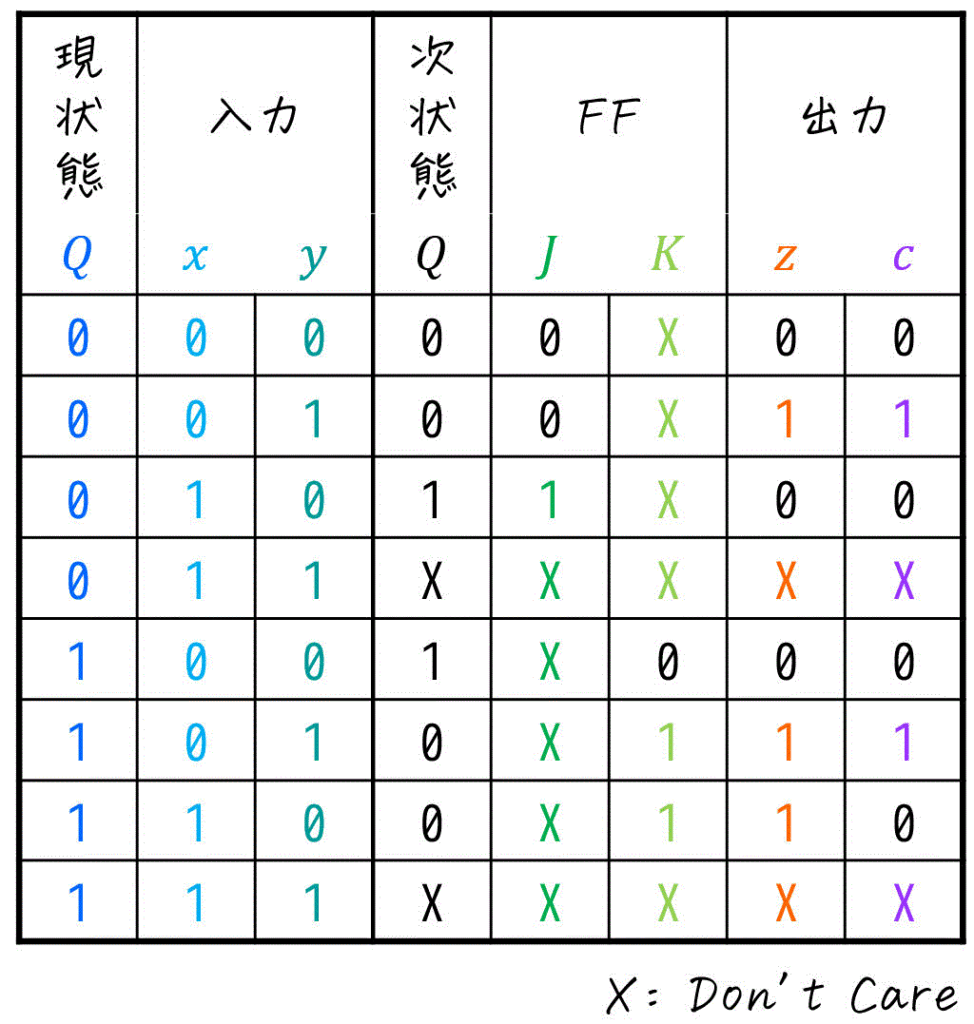
今回はFFの入力 \( J \), \( K \)、および出力 \( z \), \( c \) にDon’t Careが多く含まれるため、下のようにカルノー図を書いて最簡形の励起関数を求めることをおすすめします。
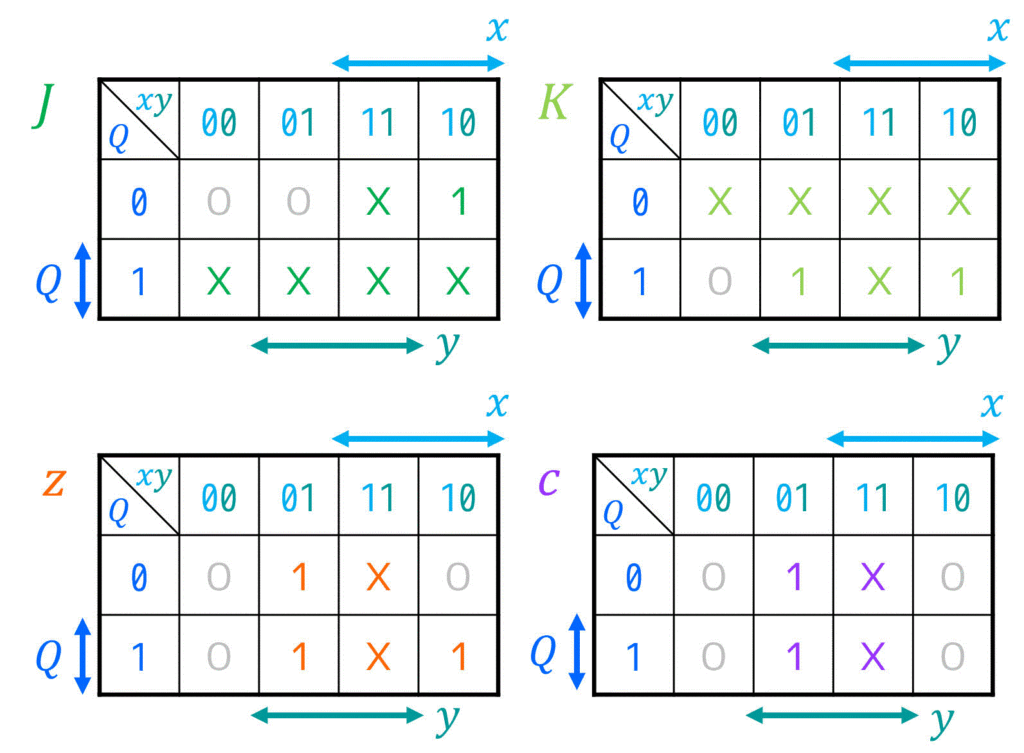


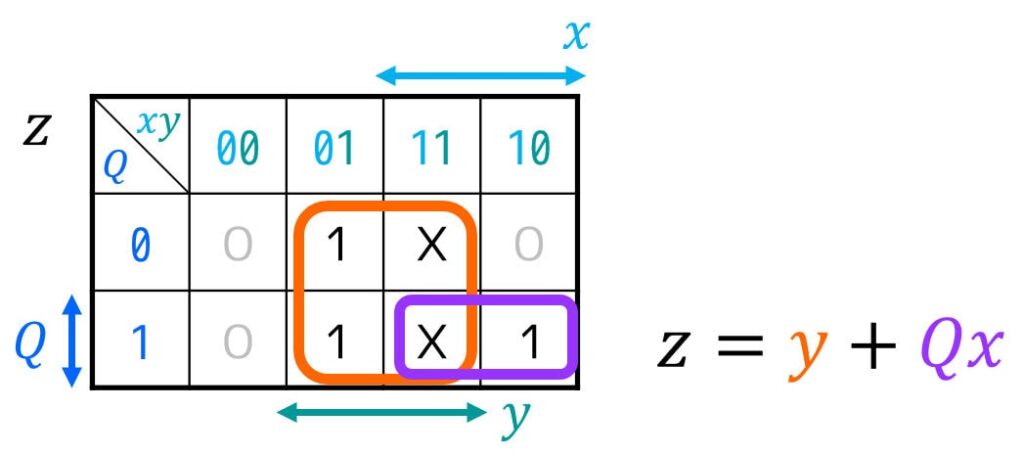
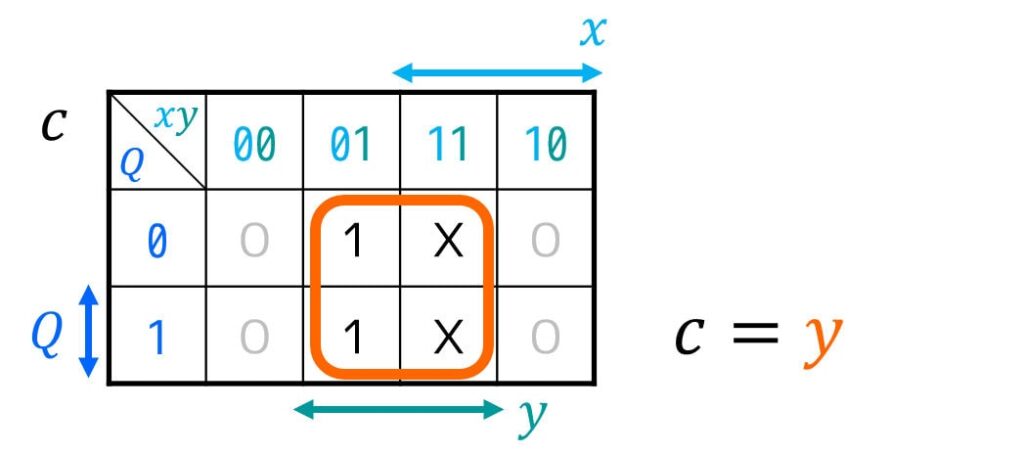
[2-iv] 励起関数(FFの入力方程式)・順序回路の出力方程式を作り、簡略化する
最後に、[2-iii]で作成した最簡形の励起関数 \( J \), \( K \)、および出力方程式 \( z \), \( c \) の式\[\begin{align*}
J & = x \\
K & = x + y \\
z & = y + Qx \\
c & = y
\end{align*}\]を用いて、順序回路を作れば設計完了です!
※ CLKの線は省略しています
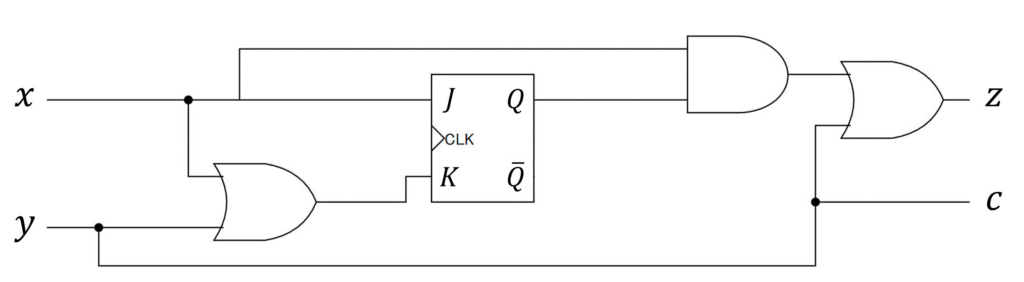
※ 少し回路が複雑なので、順序回路内に出てきたANDゲート、ORゲートの入力値を明記したバージョンも下に載せております。参考までにどうぞ。
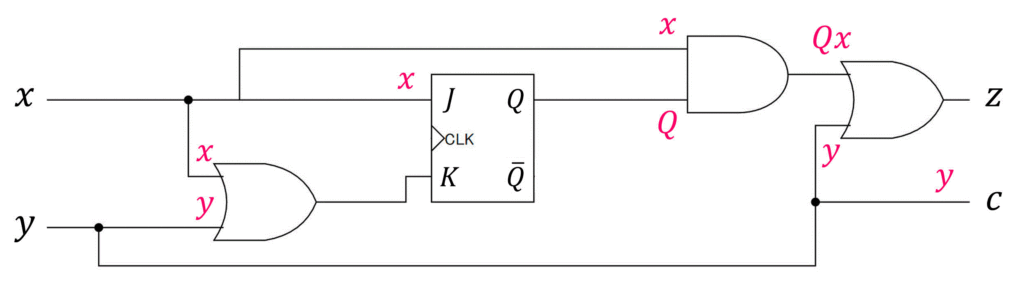
[まとめ] JKフリップフロップを用いた順序回路の設計手順
今回は、JKフリップフロップを用いて順序回路を設計する流れを例題や練習問題に沿って学習しました。
Dフリップフロップの順序回路の書き方をすでに学習していた人は、JKフリップフロップで書いた場合の順序回路の単純さに驚いた人もいるかもしれません。
では最後に、JKフリップフロップを用いた順序回路の設計手順を確認しましょう。
- 必要な入力変数・出力変数は何かを考える。
- 必要な内部状態(状態)を考え、\( q_0 \), \( q_1 \) などの名前を付ける。
- 状態遷移図・状態遷移表を書く
(必要があればここで状態の最小化を行う)
- 内部状態の数から、Dフリップフロップが何個必要かを考える。
(内部状態が \( a \) 個の状態のとき、必要なフリップフロップの数は \( 2^{n-1} < a \leqq 2^n \) を満たす \( n \) と等しい) - [1]で作った内部状態をDフリップフロップに割り当て、下の1-3の手順に従い、「励起表に出力値を加えた表」を作成する。
- 状態遷移表から励起表の次状態・出力を埋める
- 現状態を確認し、\( J \), \( K \) のどちらが X (Don't Care) かを確認する
- 現状態と次状態が等しいか異なるかを確認し、\( J \), \( K \) の X (Don't Care) ではない方の値を埋める
- 「励起表に出力値を加えた表」から、励起関数(FFの入力方程式)と順序回路の出力方程式を作り、カルノー図で簡略化する。
- 励起関数(FFの入力方程式)と順序回路の出力方程式から、順序回路を実際に設計する。
注釈
| ↑1 | 入力 \( J \), \( K \) および現状態 \( Q_n \) から次状態 \( Q_{n+1} \) がどのようになるかを表にしたもの |
|---|---|
| ↑2 | 「それぞれのフリップフロップの現状態の各入力」対する「フリップフロップの次状態、フリップフロップの入力値、順序回路の出力値」を示した表。 |
| ↑3 | 偶数に1を足すと必ず奇数に、奇数に1を足すと偶数になるため、具体的に1が何回入力されたかをカウントする必要はない。 |
| ↑4 | 1個のフリップフロップで2つの状態、2個のフリップフロップで4つの状態、3個のフリップフロップで8つの状態、…、\( n \) 個のフリップフロップで \( 2^n \) 状態を記憶できることを思い出しましょう。また、\( a \) 個の状態を記憶するために必要なフリップフロップの数は、\[ 2^{n-1} < a \leqq 2^n \]を満たす \( n \) と等しくなるので、この不等式を解くことで求めてもOKですね。 |
| ↑5 | JK-FFの場合、\( J \), \( K \) ともにDon't Careが必ず含まれるので、励起出力表を見ながらカルノー図を作成し、入力方程式を簡略化する方法を強くおすすめします。 |
| ↑6 | \( z \) については、X (Don't Care) が一切含まれていない上に、1がついている箇所が1箇所なため。 |
| ↑7 | 100円硬貨以外の硬貨は入ってこないため、合計金額は必ず100円単位となる。 |
| ↑8 | 合計200円投入すると商品が出てくるため、「最後に商品が出てから合計300円投入された状態」を記憶する必要はありません。 |
| ↑9 | 「最後に1が出力されてから1が3回入力された状態」を記憶している際に1を入力すると、1の入力が4回となり、出力が1になる。そのため、最後に1が出力されてから1が入力された回数は0に戻る。そのため、「最後に1が出力されてから1が4回入力された状態」を記憶する必要はない(このときは「1が0回入力された状態」を記憶すればOK) |
| ↑10 | \( q_2 \) を \( (Q_1,Q_2) = (1,1) \)、\( q_3 \) を \( (Q_1,Q_2) = (1,0) \) と工夫した場合、\[\begin{align*} J_1 & = Q_2 x \\ K_1 & = \bar{Q_2} x \\ J_2 & = \textcolor{red}{\overline{Q_1}} x \\ K_2 & = \textcolor{red}{Q_1} x \end{align*}\]となります。工夫せずに \( q_2 \) を \( (Q_1,Q_2) = (1,1) \)、\( q_3 \) を \( (Q_1,Q_2) = (1,0) \) とした場合\[\begin{align*} J_1 & = Q_2 x \\ K_1 & = Q_2 x \\ J_2 & = x \\ K_2 & = x \end{align*}\]よりもなぜか、工夫して割り当てた方が式が少し複雑な形となります。 |
関連広告・スポンサードリンク