スポンサードリンク
こんにちは、ももやまです。
前回は「順序回路の設計で出てくる状態遷移図の状態数を最小化する」方法について説明しました。
しかし、この方法は各状態における各入力ごとの状態遷移先と出力が決まっている場合にのみ使える最小化方法です。言い換えると、状態遷移先や出力が決まっていない(Don't Careが含まれている)状態遷移表は最小化することができません。
そこで今回は、「状態遷移先が出力が決まっていない、つまり遷移先や出力に Don't Careが含まれている」場合(不完全指定順序回路)でも最小化をする方法を勉強していきましょう。
スポンサードリンク
1. 不完全指定順序回路とは
状態遷移表の遷移先(次状態)や出力に Don't Careが含まれているような順序回路のことを不完全指定順序回路と呼びます。
不完全指定順序回路には2種類あり、
- そもそも遷移先が Don't Careになっている場合
- 遷移先は決まっているが、出力が Don't Careになっている場合
があります。
(1) そもそも遷移先がDon't Careになっている場合
ある現状態から、ある入力を与えたときの次状態が定義されていない状態です。
次状態とそのときの出力の両方が同時に Don't Careになるのが特徴です。
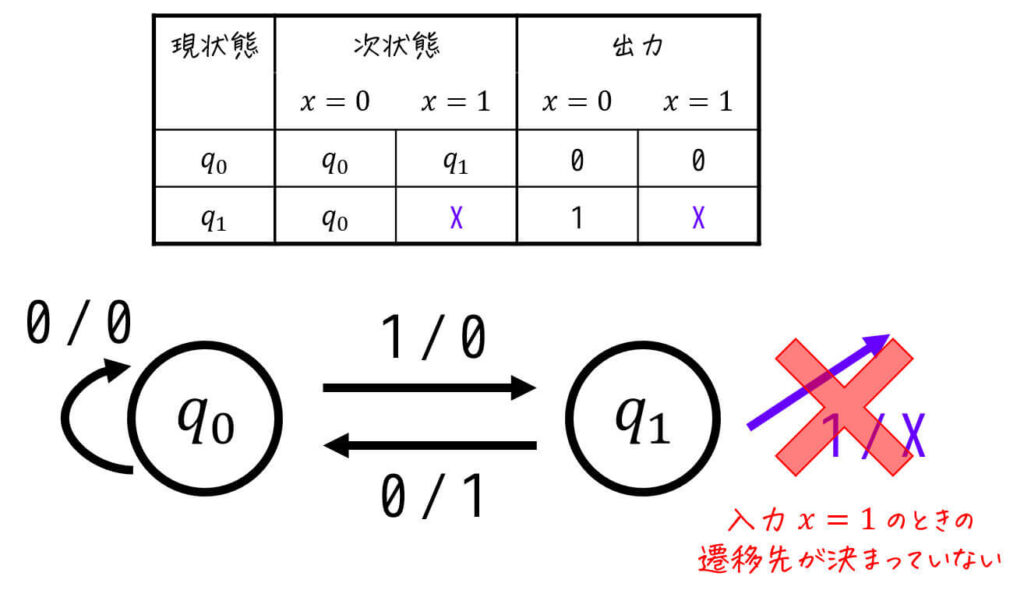
上の例の場合、\( q_1 \) に対して \( x = 1 \) を入力した際の次状態と出力が X (Don't Care) になっていますね。
(2) 遷移先は決まっているが、出力が Don't Careになっている場合
ある現状態から、ある入力を与えたときの次状態は定義されていますが、出力が定義されていない状態です。
出力部分だけが Don't Careになるのが特徴です。
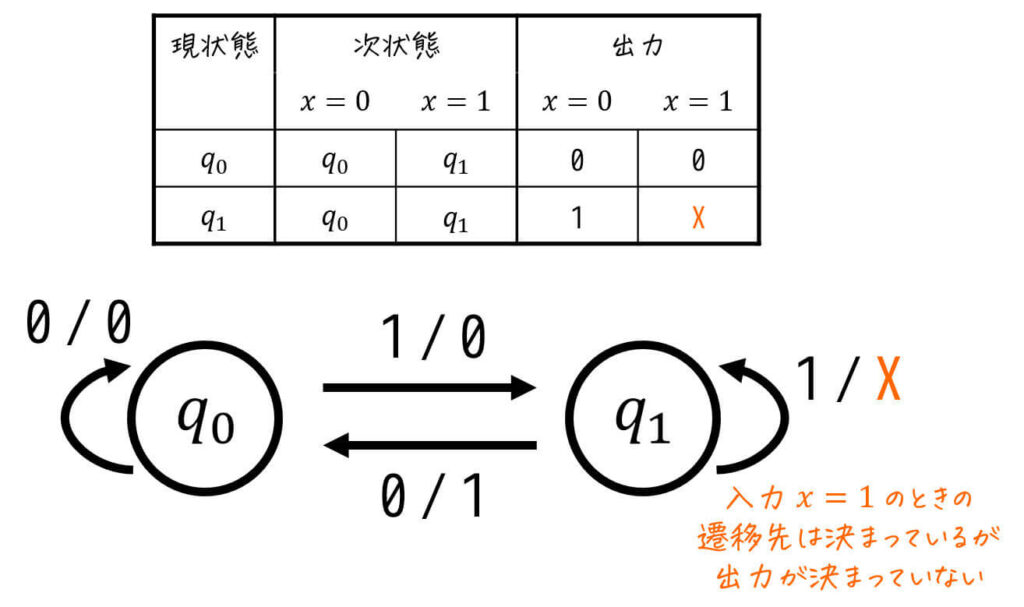
上の例の場合、\( q_1 \) に対して \( x = 1 \) を入力した際の次状態は \( q_0 \) と決まっていますが、出力が X (Don't Care) になっていますね。
スポンサードリンク
2. 例題で流れを確認しよう
それでは、実際に不完全指定順序回路の状態最小化の流れを、例題で確認しましょう。
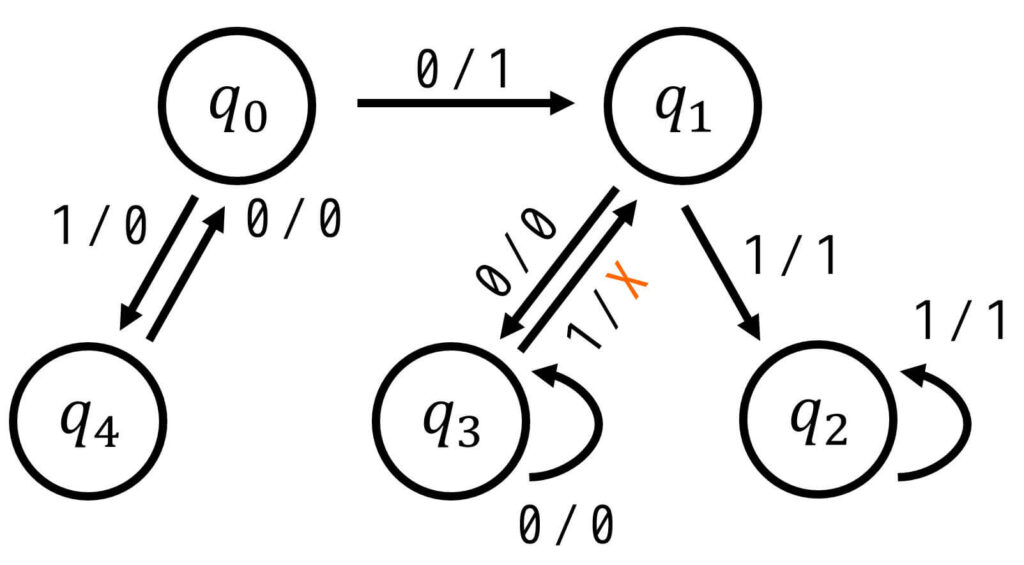
次の状態遷移図で表されるを不完全指定順序回路の状態数が最小になるように(最小化)し、状態遷移図の形で答えなさい。
※ X は Don't Careを表す
Step1. 状態遷移表を作成する
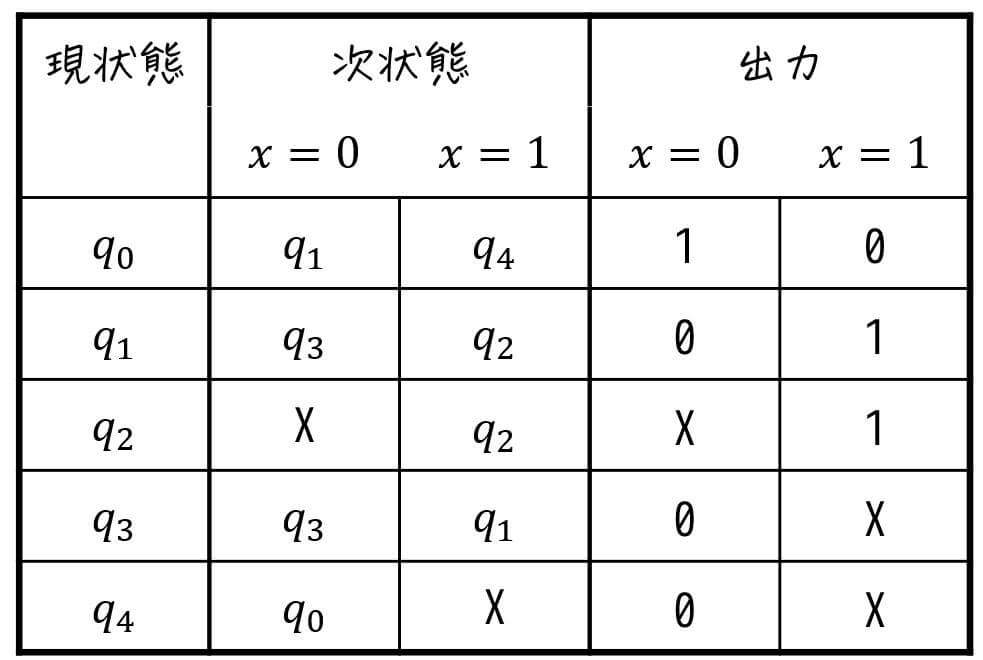
まずは、状態遷移図を状態遷移表に落としこみましょう。
ここで、ある入力に対しての遷移先(矢印)が書かれていない場合がDon't Careになる点に要注意です。今回の場合は、
- \( q_2 \) のときに \( x = 0 \) を入力したとき
- \( q_4 \) のときに \( x = 1 \) を入力したとき
が存在しないので、この2つが「次状態・出力」ともにDon't Careとなります。
Step2. 両立性が成り立つ (ひとまとめに出来る可能性がある) 状態のペアを探す
前回の(Don't Careが含まれない)順序回路では、等価となる状態(ひとまとめにできる状態)の組み合わせをグループ分けすることで求めていきましたね。
しかし、Don't Careが含まれる場合は「単にグループ分けするだけ」では等価となる状態を見つけることができません[1]イメージとしては、単独では Don't Careのおかげでひとまとめに出来ても、ひとまとめにしたペア同士を状態遷移表に適用する際に Don't … Continue reading。
そこで、Don't Careが含まれるような順序回路を最小化する際には、グループ化をする前に「ひとまとめにできる可能性がある状態のペア」を下の三角表に求めていきます。
ここで、「ひとまとめにできる可能性」のことを「両立性」と呼びましょう。
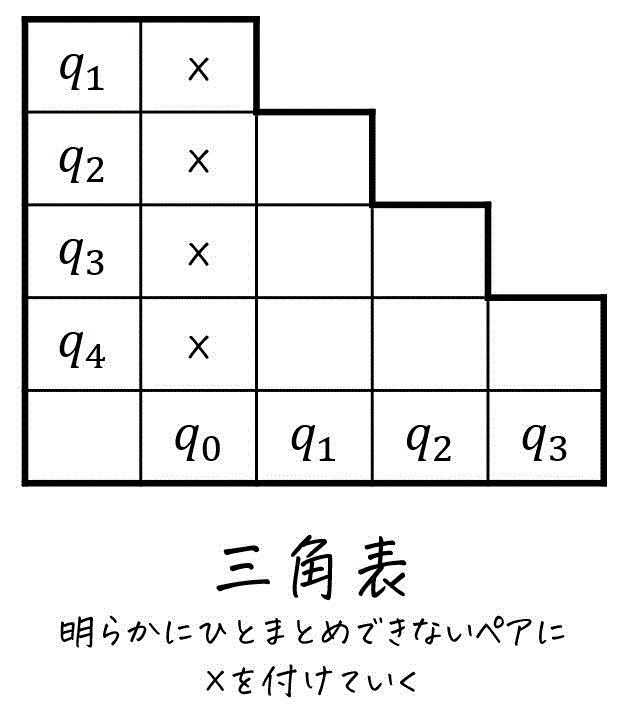
言い換えると、Step2では100%ひとまとめ出来ないペアを探していく作業をします。
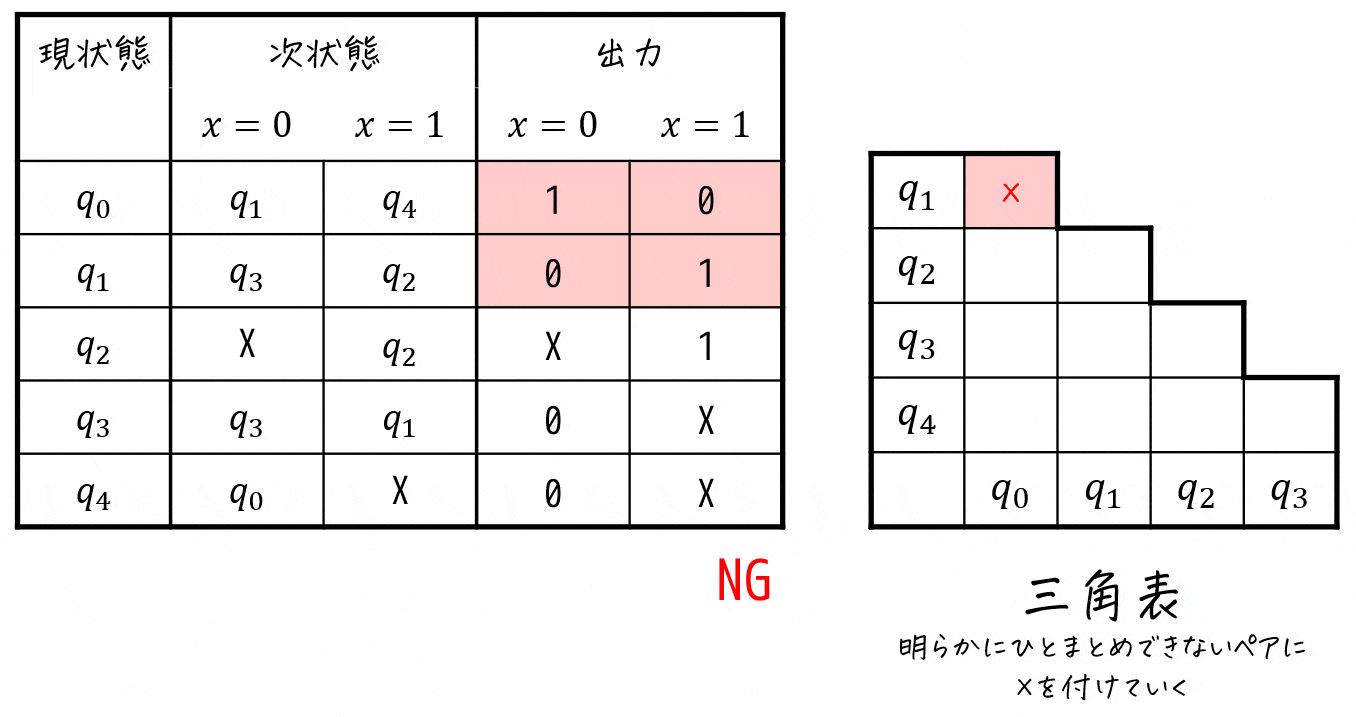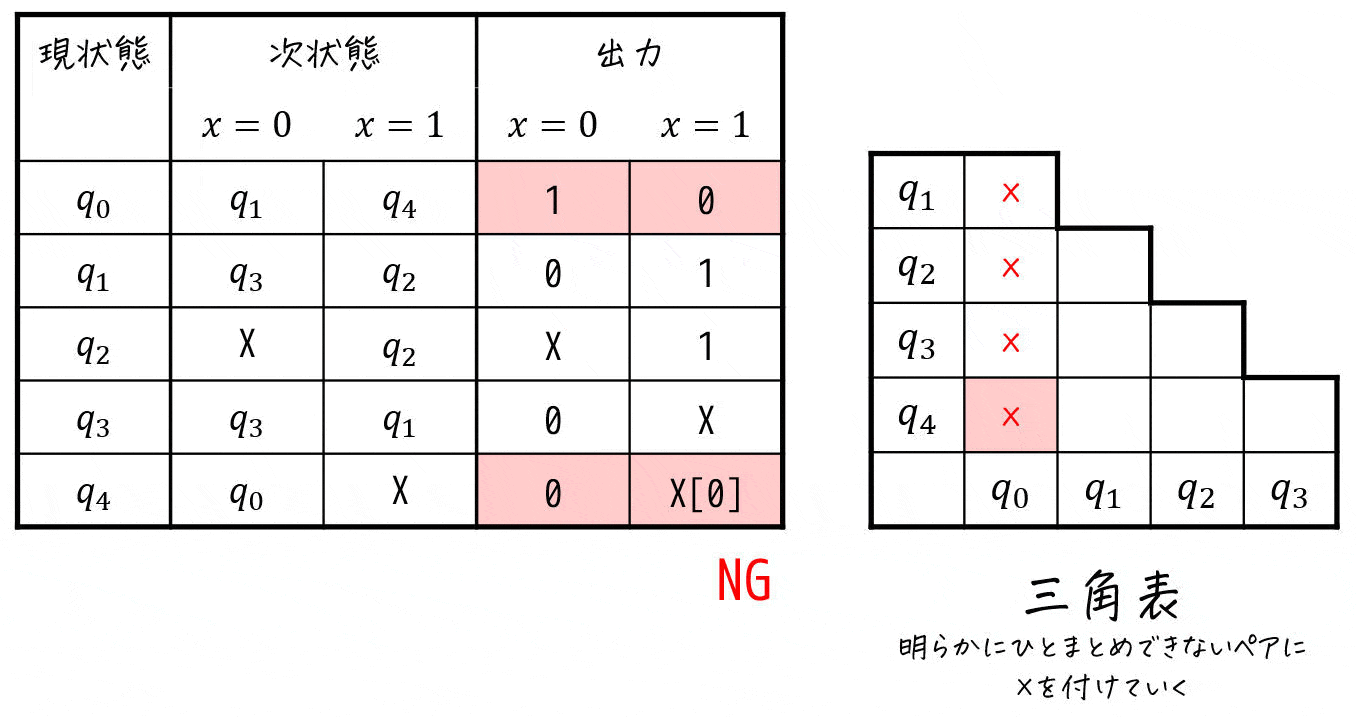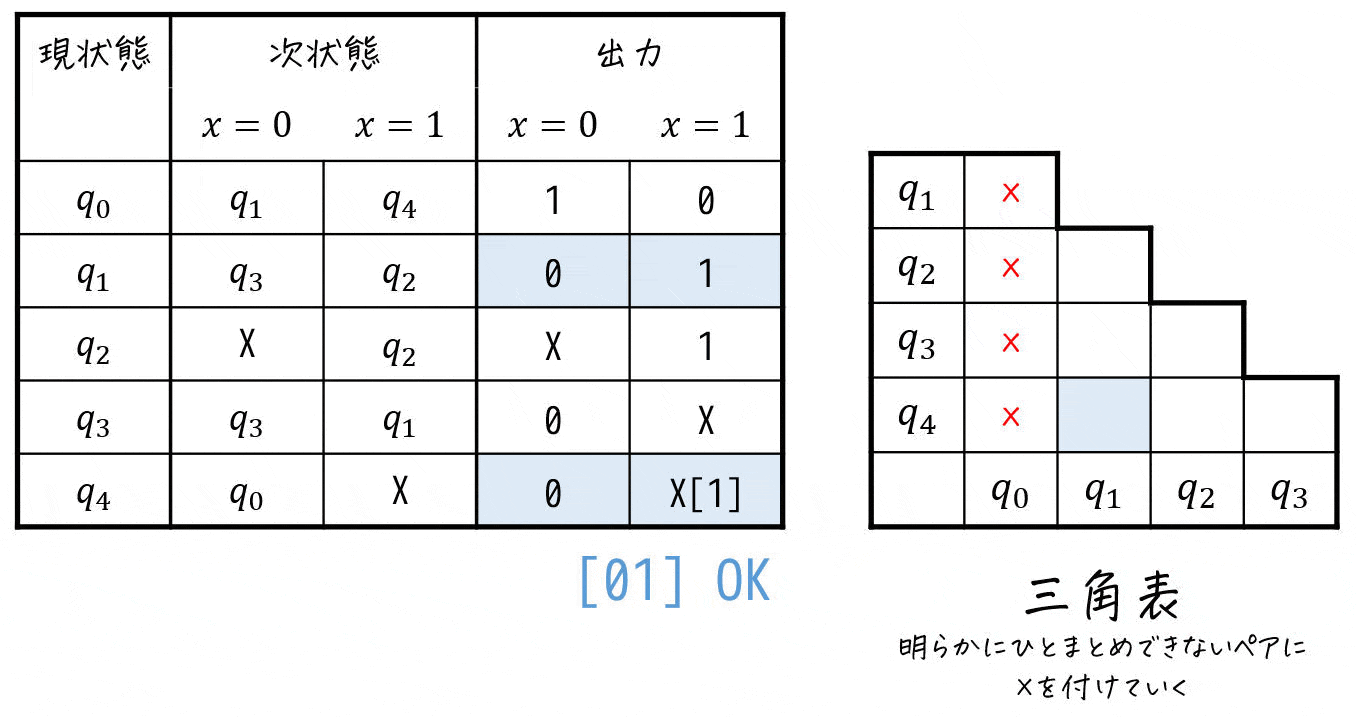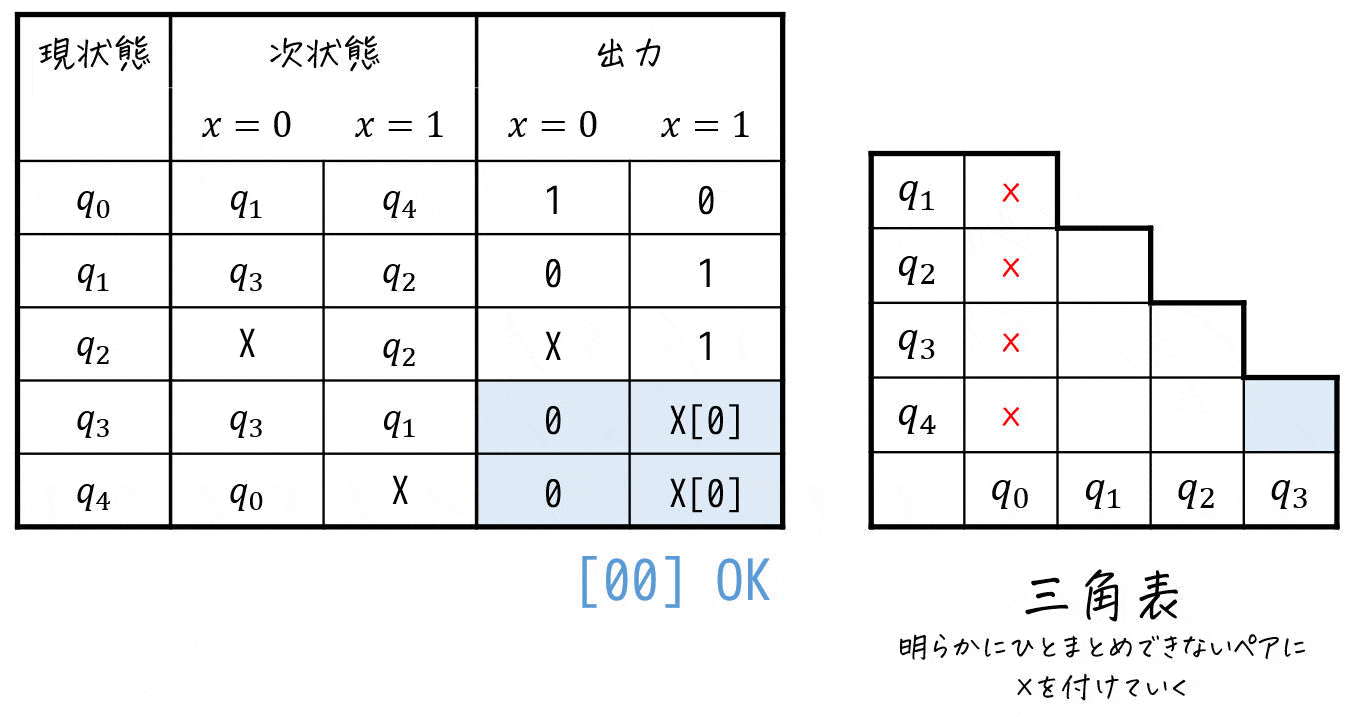
Step2-1. 出力を確認し、ひとまとめ出来ないペアを探す
まずは、下のように「出力が異なる状態」を探すことでひとまとめに出来ないペアを探していきます[2]出力が異なる状態は、100%ひとまとめにすることはできないため。。
ここで、Don't Careはワイルドカード (0, 1どちらでもOK)的な役割をすると考えてください。
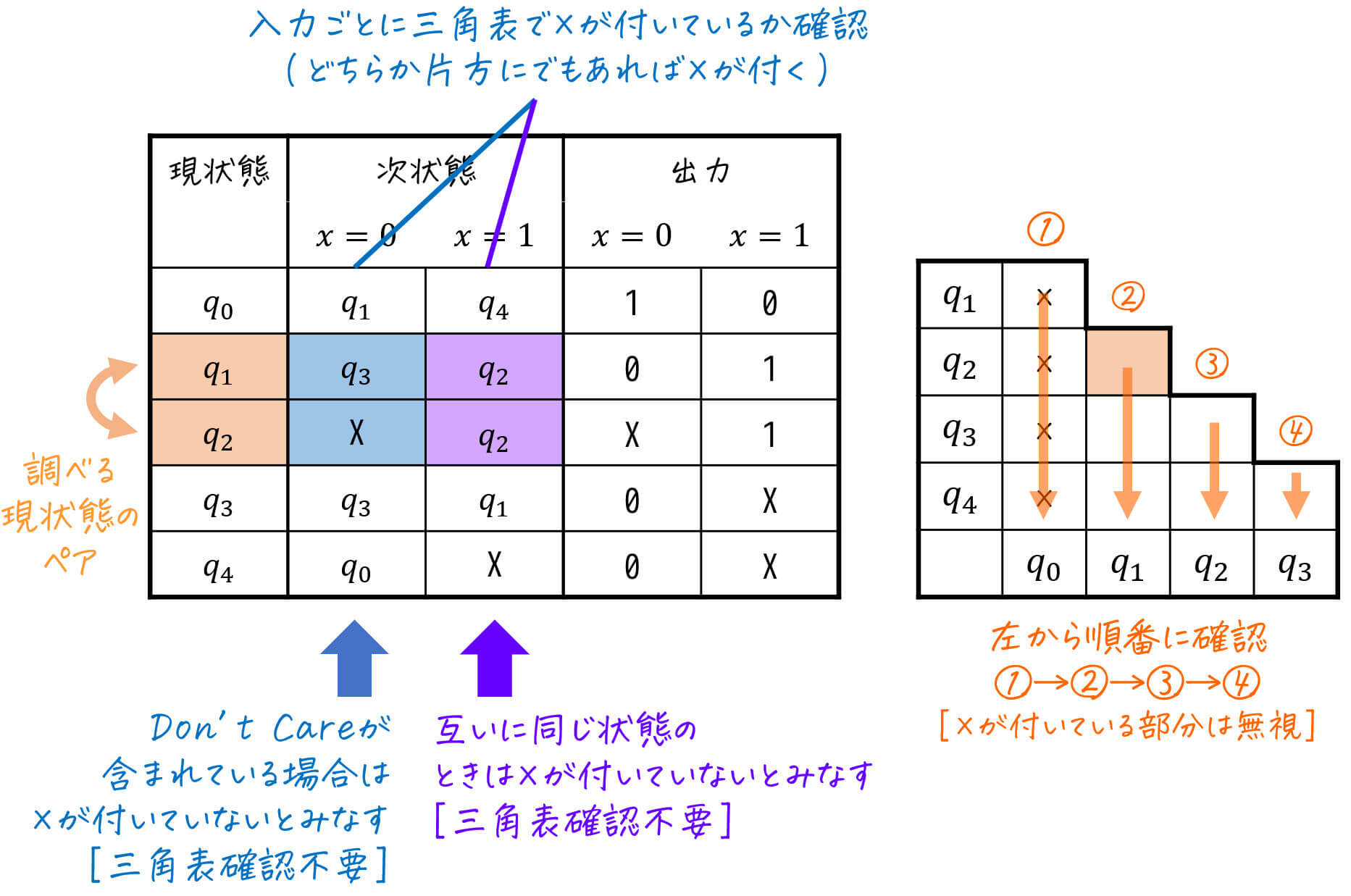
Step2-2. 三角表からひとまとめに出来ないペアを探す
つぎに、三角表の×が付いていない(ひとまとめができる可能性がある)ペアに対し、「同じ入力を与えたときにひとまとめにできない(三角表で×が付いている)ペアに遷移する」ペアに×を付けていきます。
基本的なルールとしては
- ×が付いていない各ペアに対し、次状態の各入力ごとのペアに着目
- 着目した次状態のどれか1つの入力のペアでも「三角表に×が付いていれば」、現状態のペアに×を付ける
- ×が付いた場合、スタート地点(振り出し)に戻る
- 三角表の右下に到達したら終了
となります。
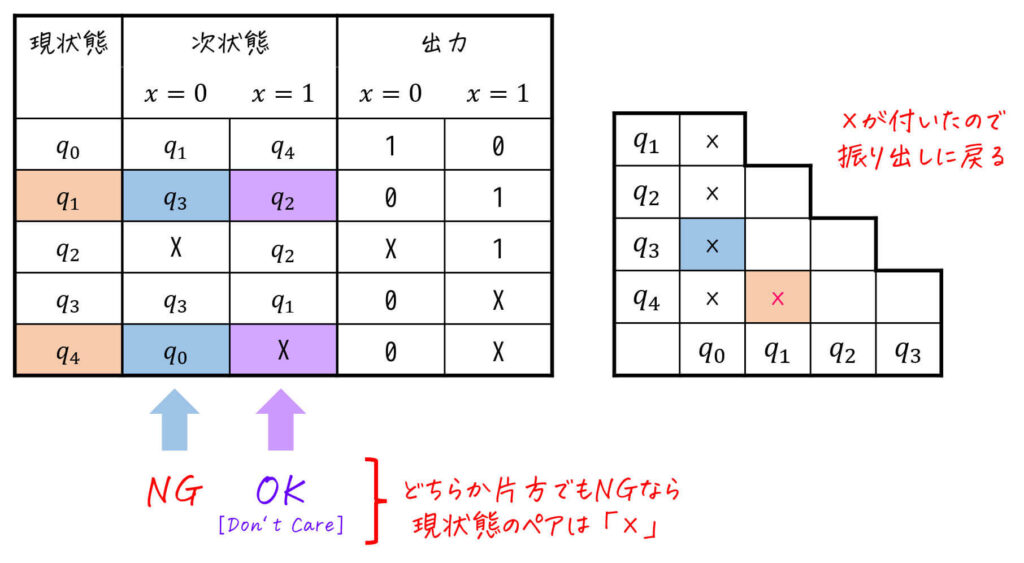
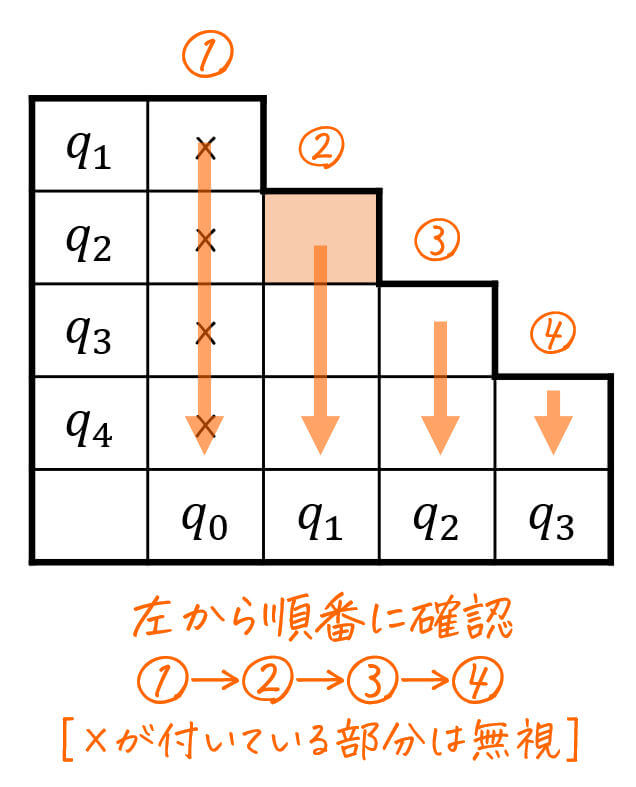
(全パターンが網羅できれば必ずしもこの順番でなくてもOK)
ただし、
- ペアのどちらか片方にでも X (Don't Care) が付いている場合
- ペアがともに同じ状態の場合
場合は、その入力のペアには「×」が付いていないとみなします。
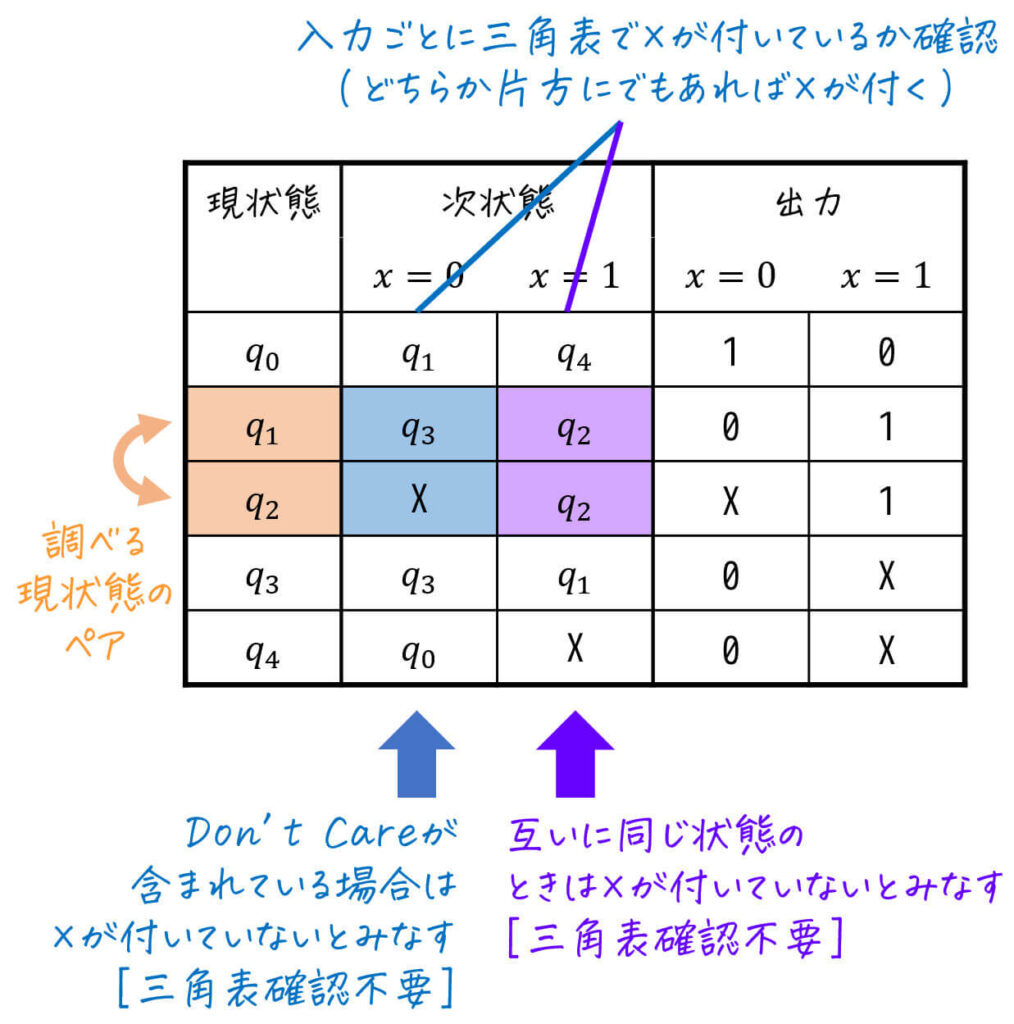
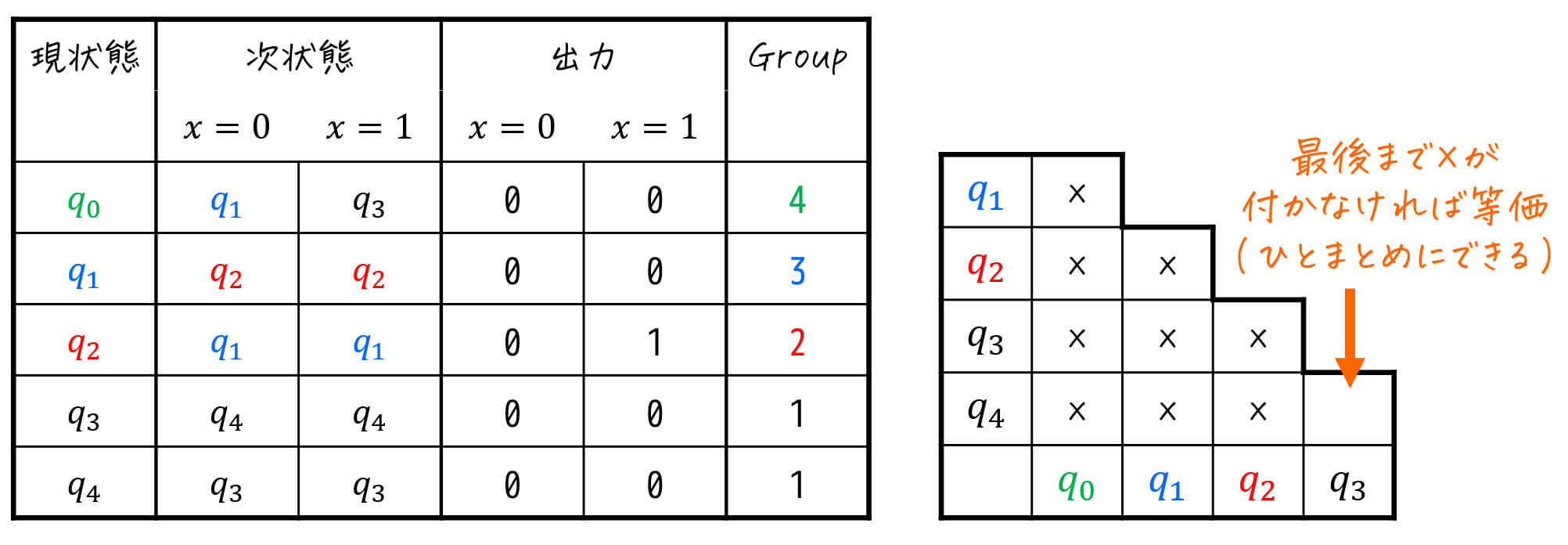
★ 今回の状態遷移表 & 三角表に適用すると…?
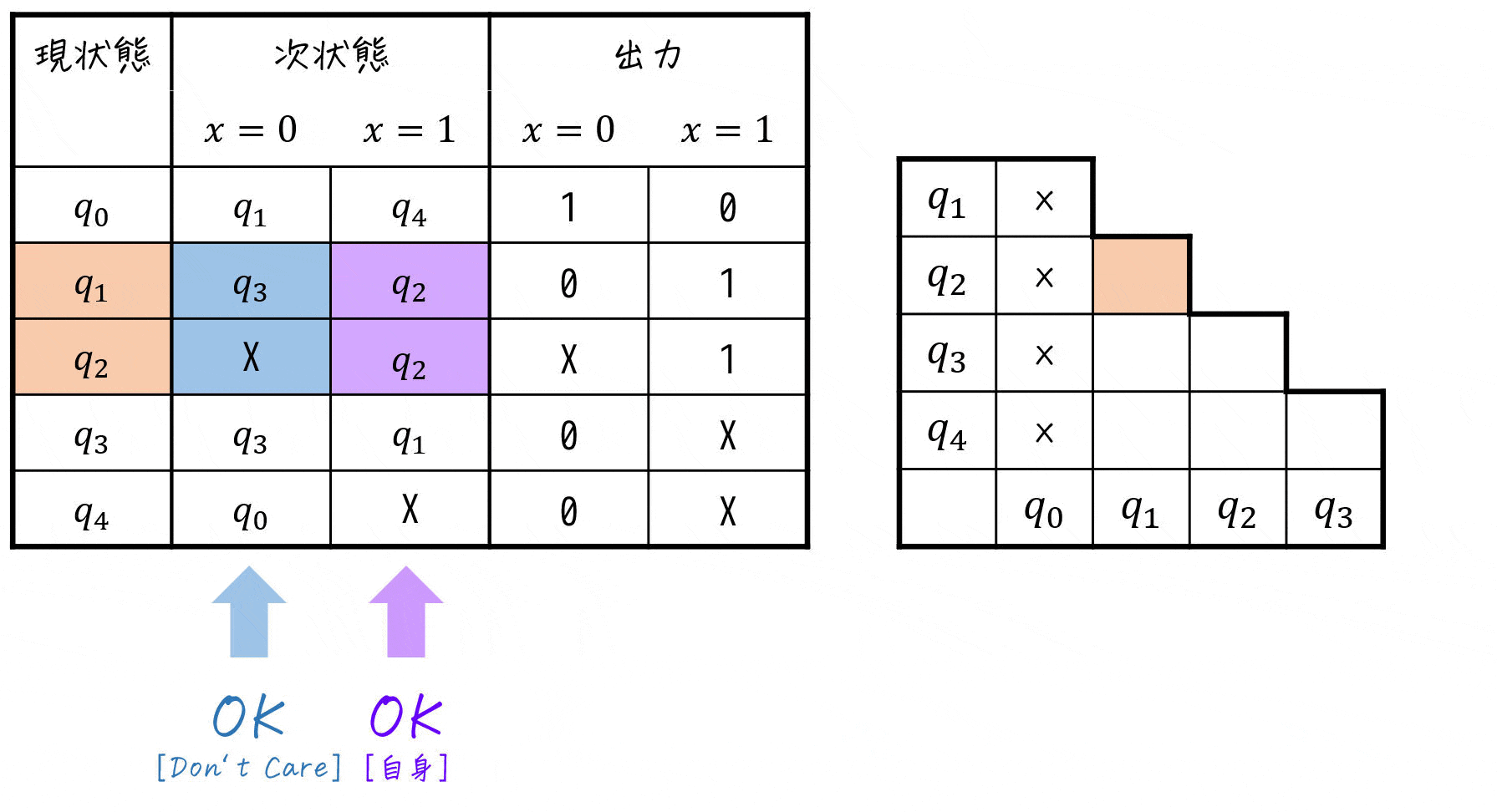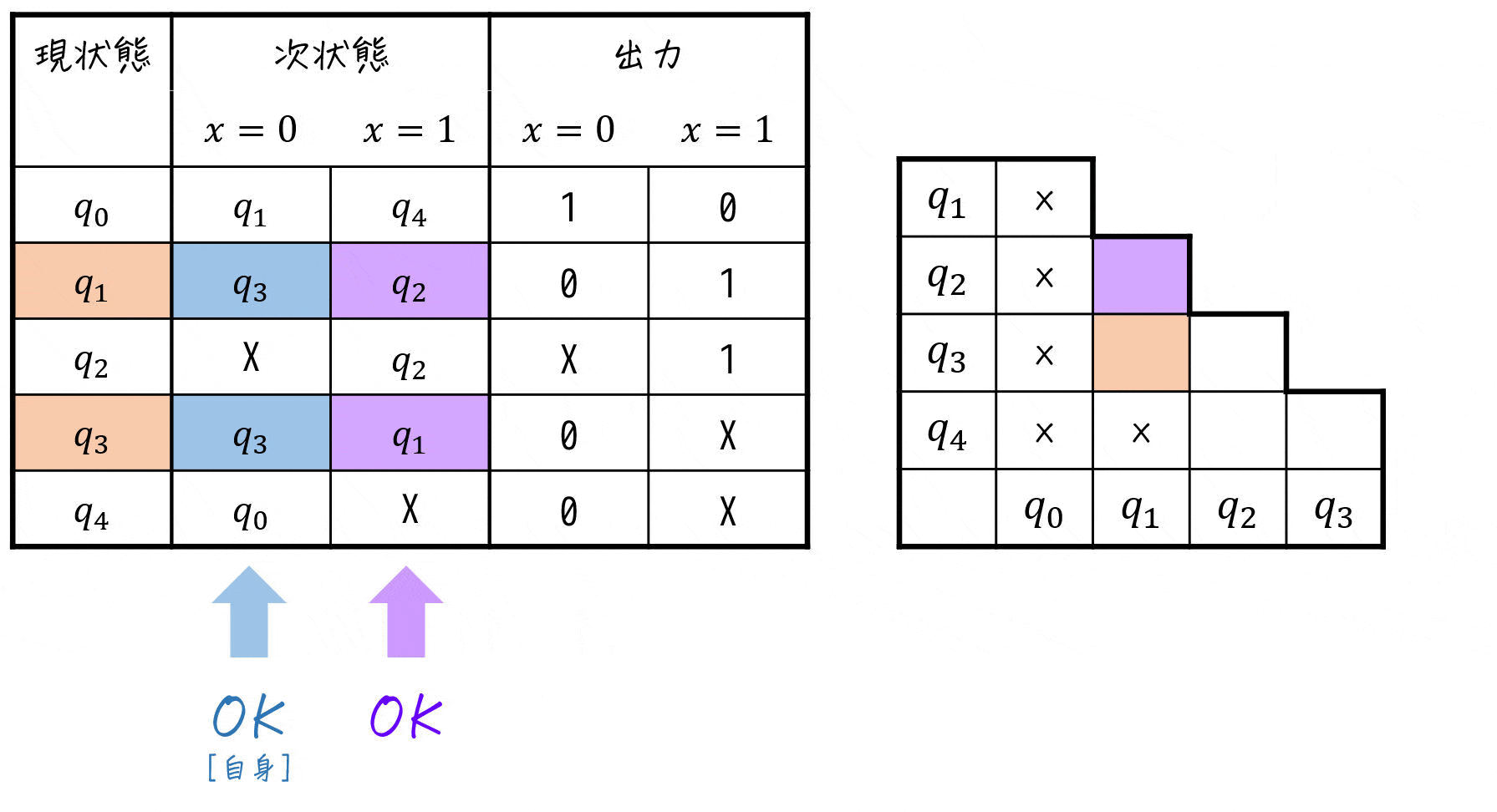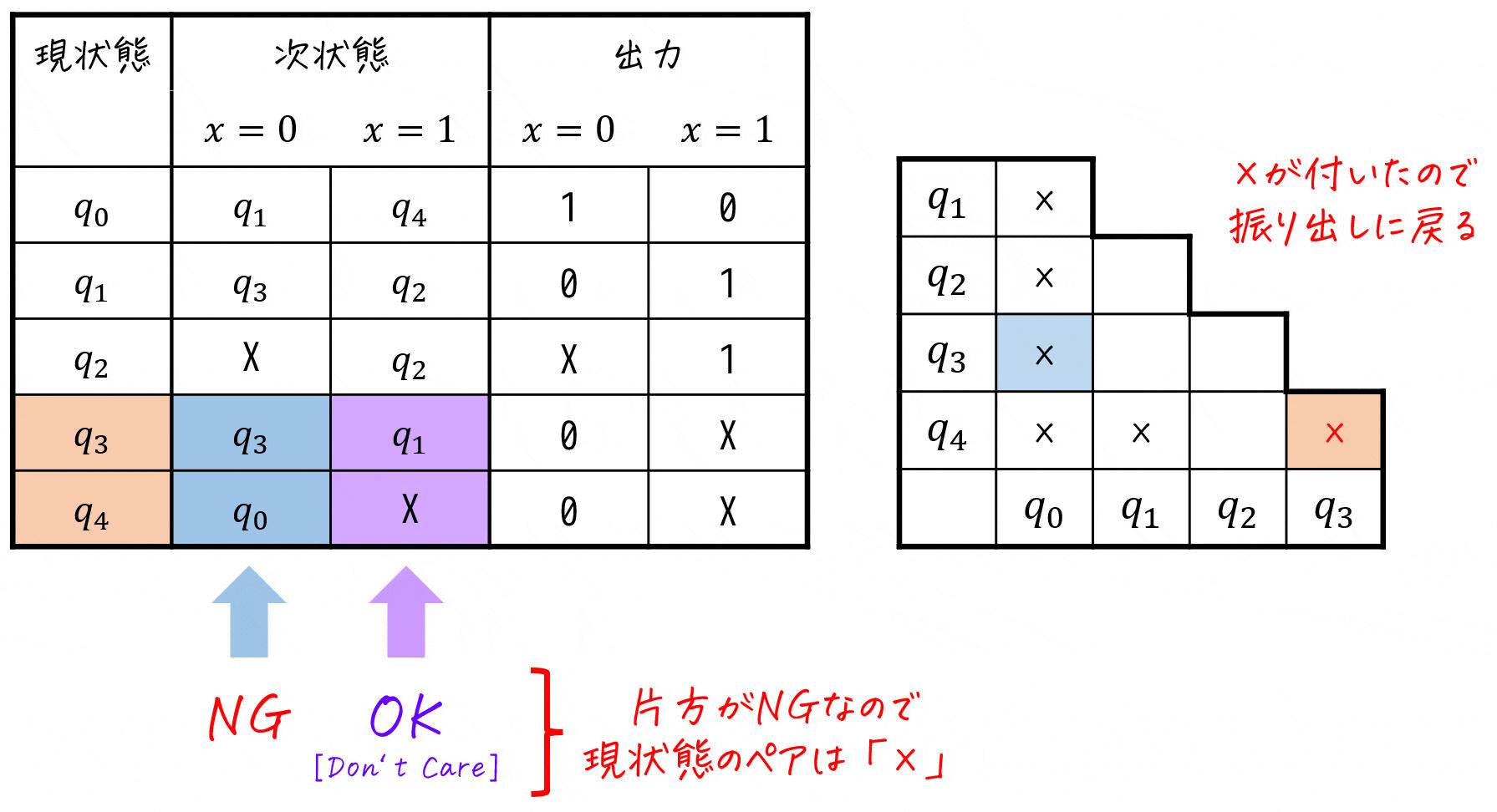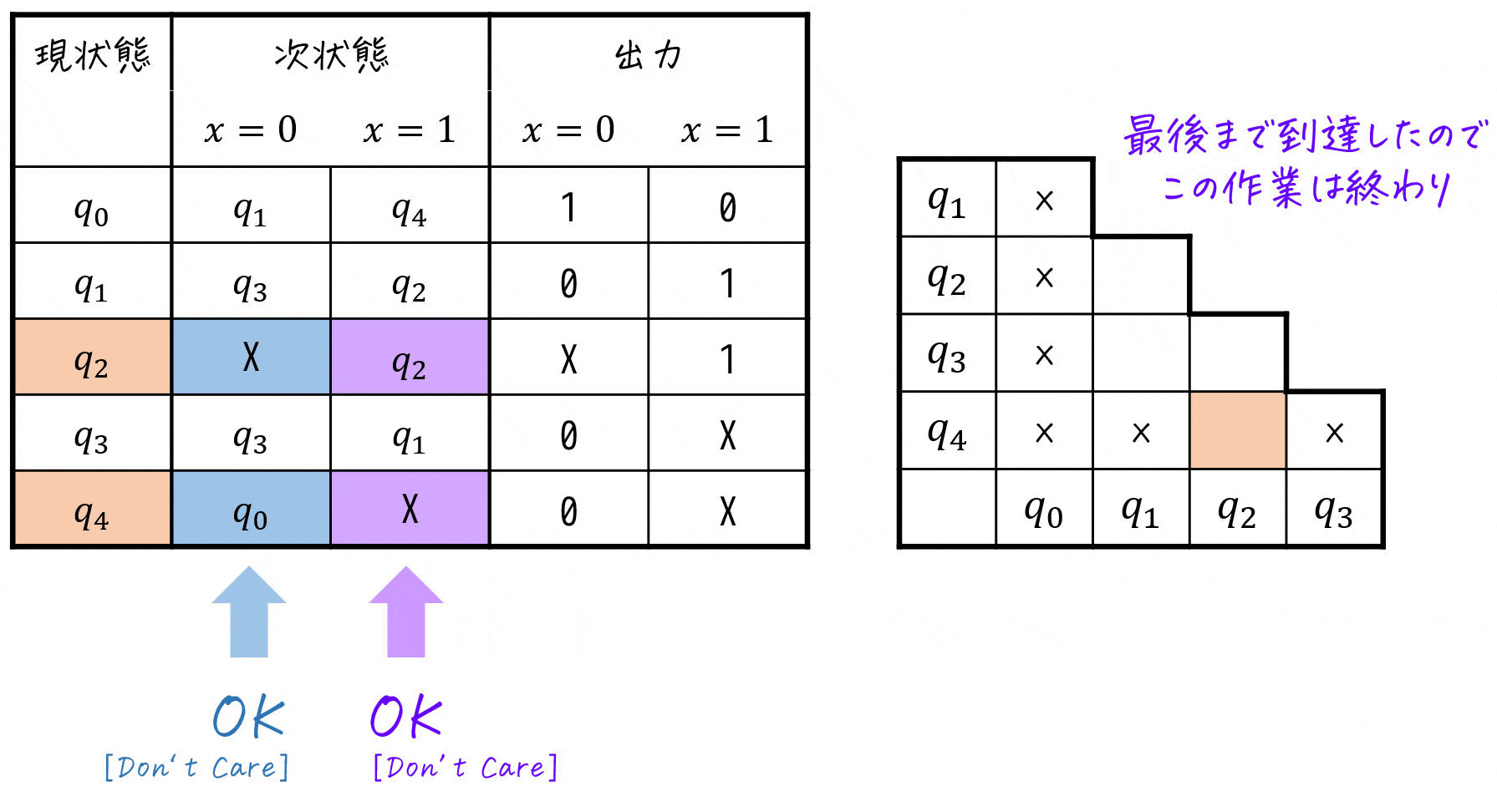
適用の結果、下のように三角表が求まりました。
この「×」が付いていない部分が両立性が成り立つ(ひとまとめに出来る可能性がある)ペアです。
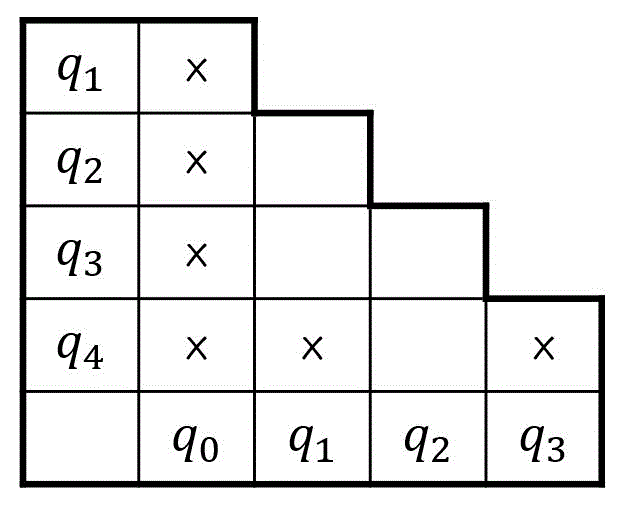
(×がないペアが両立性成立)
よって、状態群\[
\{ q_1, q_2 \}, \{ q_1, q_3 \}, \{ q_2 , q_3 \}, \{ q_2, q_4 \}
\]に両立性が成り立つ(ひとまとめに出来る可能性がある)ことがわかりました。
※ 両立性が成り立つ状態を \( \{ \ \ \ \} \) で表すことにします。例えば、\( a \), \( b \) に両立性が成り立つ場合は、\( \{ a,b \} \) と表記します。
Step3. 3状態以上の両立性が成立するか確認
つぎに「3状態以上に両立性が成立するか」を確認します。
ここで、3状態以上に両立性が成立するかの確認は次の通りです。
- 3状態の両立性 \( \{ a,b,c \} \) の確認
→ \( \{ a,b \} \), \( \{ b,c \} \), \( \{ a,c \} \) がすべて成立すること
(どの2状態を取ってきても両立性が成り立つこと) - 4状態の両立性 \( \{ a,b,c,d \} \) の確認
→ \( \{ a,b,c \} \), \( \{ a,b,d \} \), \( \{ a,c,d \} \), \( \{ b,c,d \} \) がすべて成立すること
(どの3状態を取ってきても両立性が成り立つこと) - 5状態の両立性 \( \{ a,b,c,d,e \} \) の確認
→ \( \{ a,b,c,d \} \), \( \{ a,b,c,e \} \), \( \{ a,b,d,e \} \), \( \{ a,c,d,e \} \), \( \{ b,c,d,e \} \) がすべて成立すること
→(どの4状態を取ってきても両立性が成り立つこと)
※ 一般化すると、\( n \) 状態の両立性を確認するためには、どの \( n - 1 \) 状態を取ったとしても両立性が成り立つことが条件となる。
両立性が成立するかどうかは、下のように樹形図を書いて表現していくとわかりやすいです。
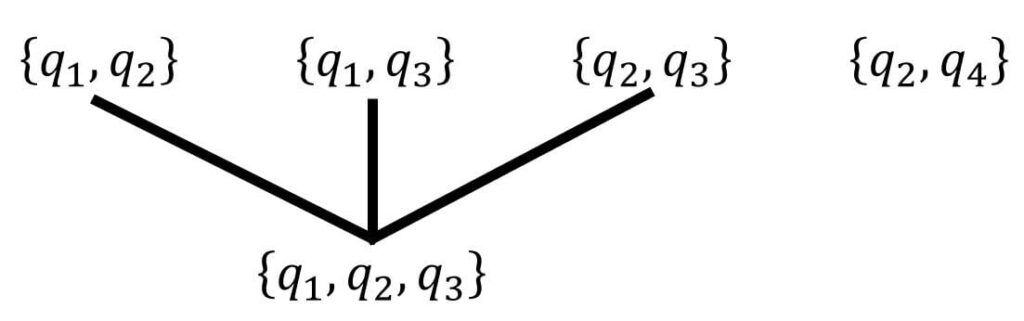
今回の場合、状態群 \( \{ q_1, q_2 \} \), \( \{ q_1, q_3 \} \), \( \{ q_2 , q_3 \} \) の両立性が成立することから、\( \{ q_1, q_2, q_3 \} \) の両立性が成り立つことが分かりますね。
Step4. 両立性から最小化できる状態群の組み合わせを決定する
つぎに、両立性が成り立つ状態(と単独の状態)から、なるべく少ない状態数で問題文の状態をすべて満足できるような組み合わせを考えます。
※ 組み合わせを考える際には、「両立性が成り立つ状態群(と単独の状態)」に含まれる「与えられた状態(今回の場合は \( q_0 \) ~ \( q_4 \))」を〇で表した表を書くことをおすすめします。
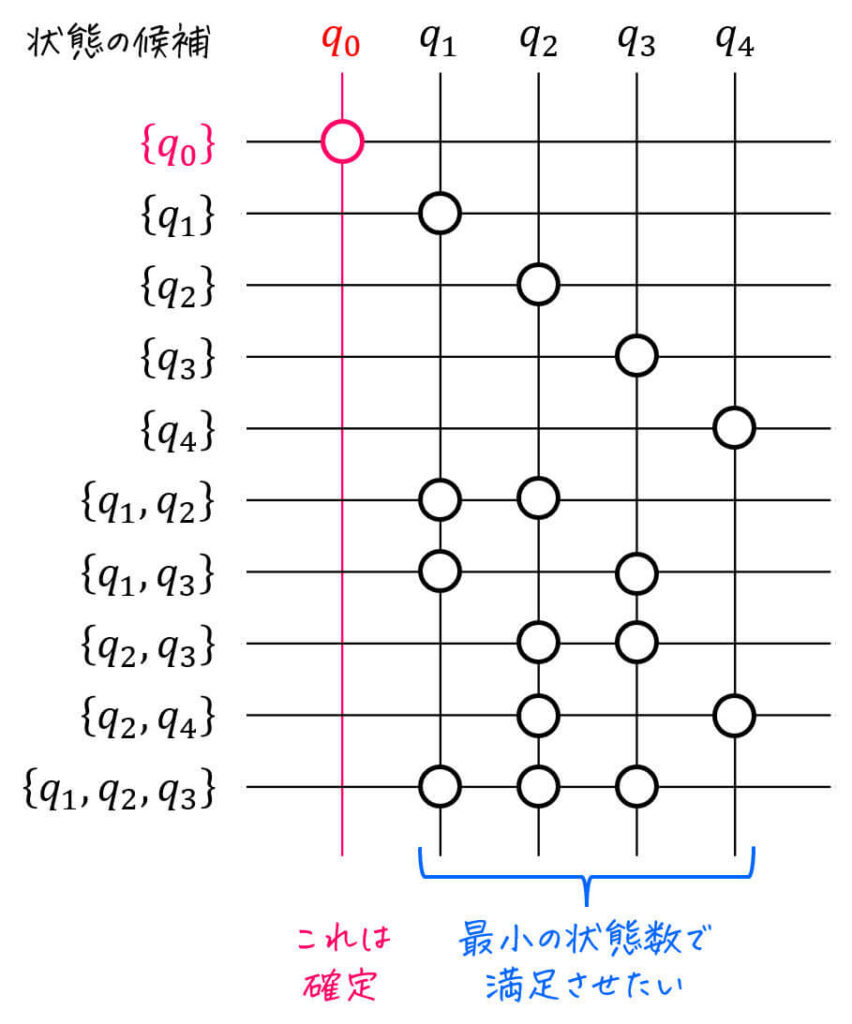
Step4-1. 単独でしか満足できない状態 (必須状態) を探す
実際に表を見ると、\( q_0 \) はどの状態に対しても両立性が成り立たないので、\( q_0 \) 単品は確定で必要ですね。なので、これをグループ1としましょう。
Step4-2. 最小のグループ数で全状態を満足させる
なので、残りの \( q_1 \), \( q_2 \), \( q_3 \), \( q_4 \) をなるべく少ない状態数(グループ数)で満足できるようなペアを考えてみましょう。
ここでは、
- 両立性が成立する状態群から1つ選択し、グループに加える
(なるべく多くの状態がある状態群から選ぶ) - 加えたときに追加で必要な状態を「同じ入力であれば同じグループに遷移する」点で考える
- 最小状態で出来そうなら完成
- 最小状態で出来なさそうなら、1に戻り、他の状態群を選択する
まずは、3状態がまとまった状態群 \( \{ q_1, q_2, q_3 \} \) をグループ2に加えてみましょう。
※ なるべく多くの状態がまとまったものから順にグループだと仮定していきます。
ここで、X (Don't Care) はワイルドカード、つまりどのグループとして扱ってもよい状態だと思ってください。
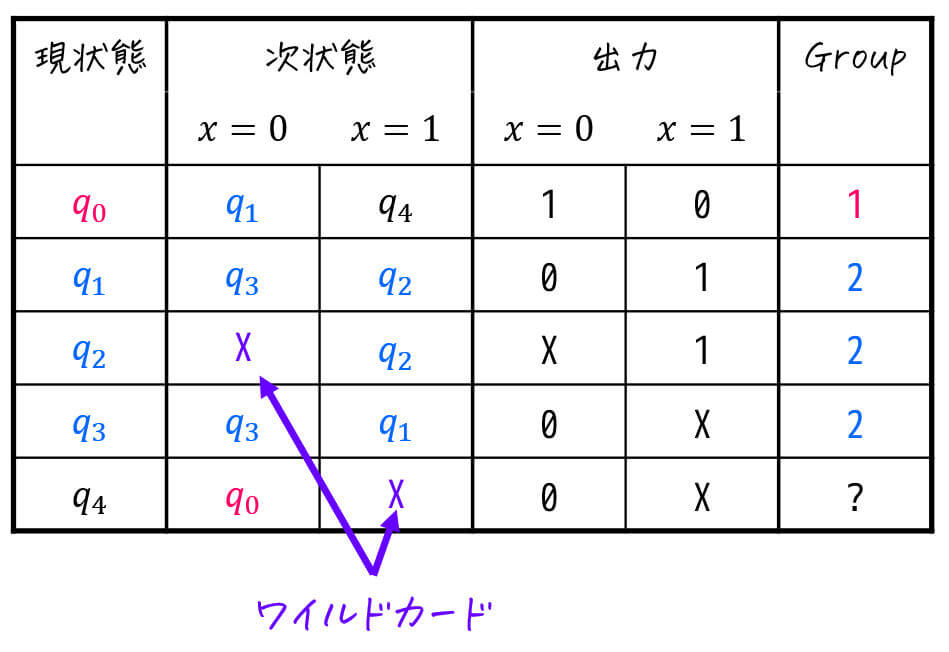
ここでGroup2の色のペアを確認すると、\( x = 0 \), \( x = 1 \) のとき共に同じGroup2に遷移していることがわかりますね。
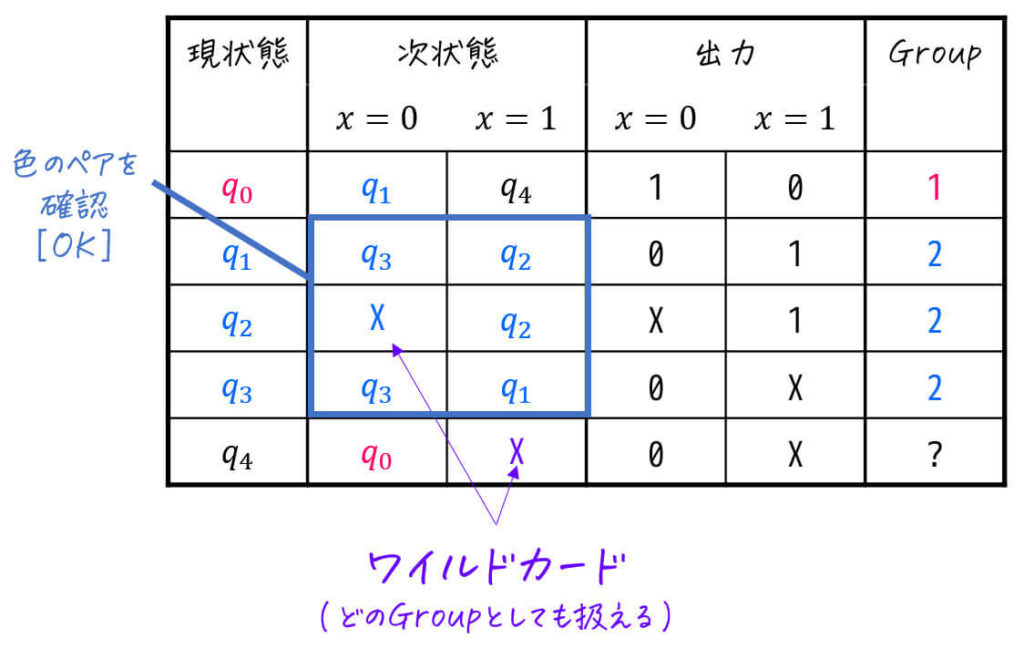
あとは、まだ追加していない \( q_4 \) をGroup3とすれば、どの状態も「同じ入力を与えたときに同じグループに遷移する」状態が作れますね。
(ここで、\( q_4 \) に \( x = 1 \) を入力したときの X (Don't Care) は、どのグループにしても状態数が変わらないのでそのままDon't Careとして扱います[3]もちろん具体的にGroup1, 2, 3を設定してもOKです。ただし、順序実際に回路を設計する際に少し複雑になりますが…。。)
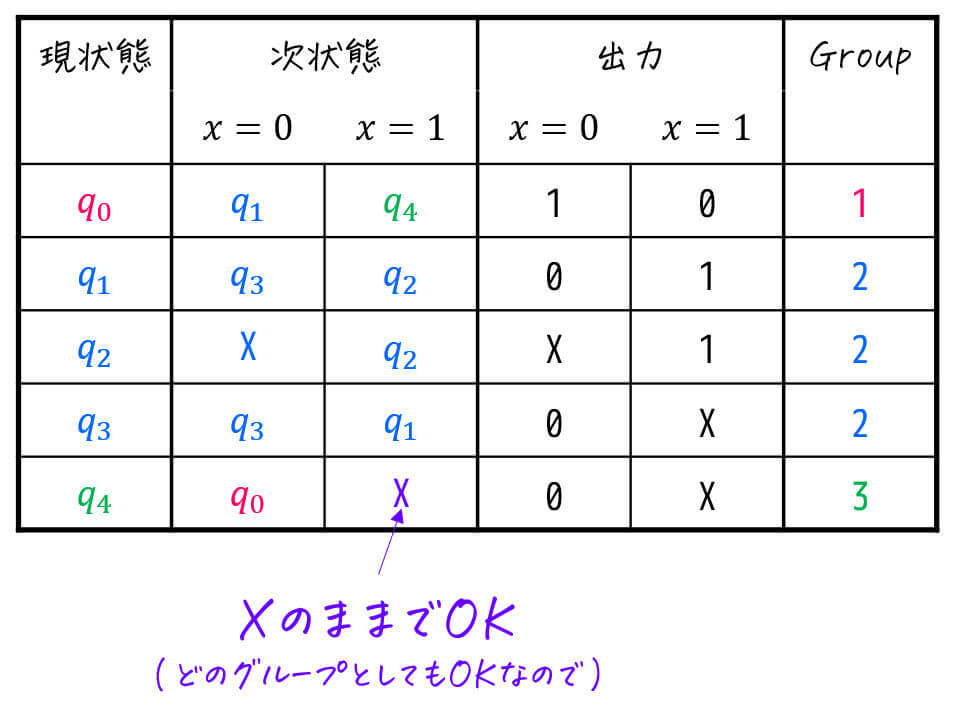
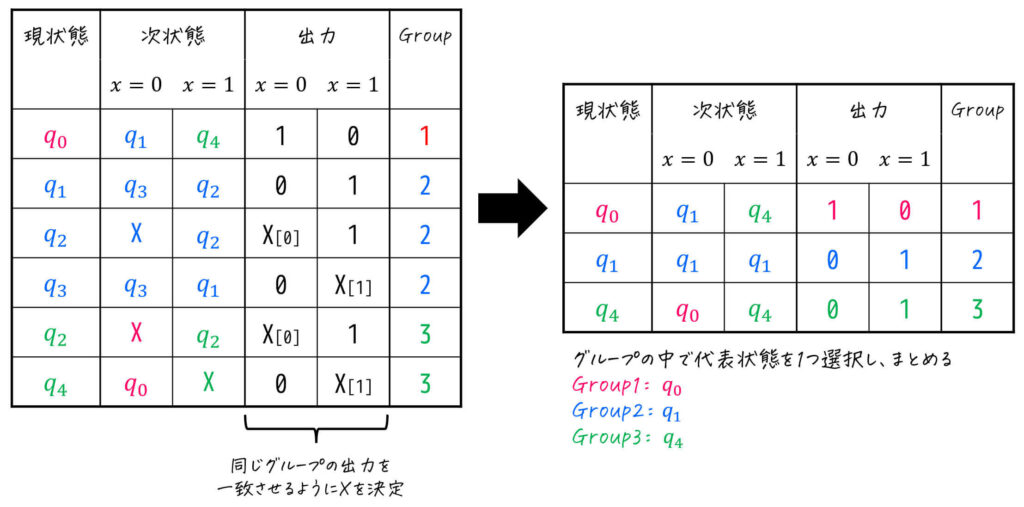
Step4-3. 各グループ内で代表状態を1つ選択し、まとめる
グループが確定したら、代表状態を1つ選択してまとめましょう。
ここで X (Don't Care) は、他のグループの出力に合うように設定してください[4]0, 1どちらを入れても成立する場合はXのままでOKです。。
今回は、下のようにまとめてみましょう[5]各グループごとに全く新しい名前(例:Group1を"1"、Group2を"2"、Group3を"3"とする)としてもOKです。。
- Group1の状態 → \( q_0 \) にまとめる
- Group2の状態 → \( q_1 \) にまとめる
- Group3の状態 → \( q_4 \) にまとめる
Step5. Step4で書いた状態遷移表を状態遷移図にする
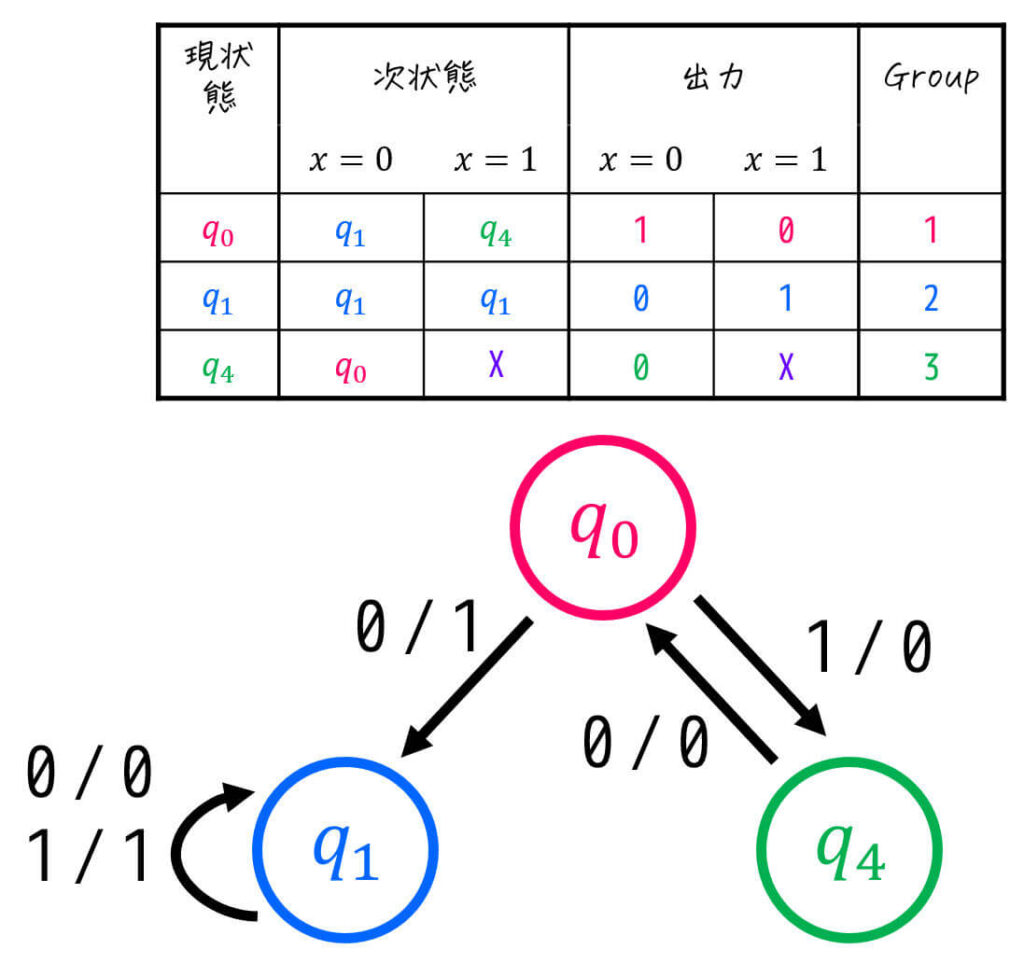
あとは、状態遷移表を状態遷移図に落とし込めば完成です!
(ここで Don't Careがある場合には表記に気を付けましょう。今回の例の場合、\( q_4 \) から \( x = 1 \) を入力としたときの遷移が存在しない点に注意が必要です。
スポンサードリンク
3. グループ分けの際の補足 [Step4-2]
例題のStep4-2で行った「状態郡を組み合わせたグループ分け」について、2点補足をしておきます。
[補足1] 状態が複数グループに属してもOK
与えられた状態をすべて満足するように状態群を選べていれば、状態が複数グループに属していてもOKです。
例えば、状態群から\[
\textcolor{red}{ \{ q_0 \} } , \textcolor{blue}{ \{ q_1, q_2, q_3 \} }, \textcolor{green}{ \{ q_2, q_4 \} }
\]と選択し、それぞれ
- \( q_0 \) → Group1
- \( q_1, q_2, q_3 \) → Group2
- \( q_2, q_4 \) → Group3
とした場合、\( q_2 \) がGroup2, 3両方に属しますが、全状態が1回以上出てきているのでOKです。
ただしこの場合、
- 2つ以上のグループに属する状態は、グループごとに現状態を記述する
- 次状態に出てくる状態が2つ以上のグループに属する場合、各状態ごとに都合のいい方を選択する
ことに注意してください。
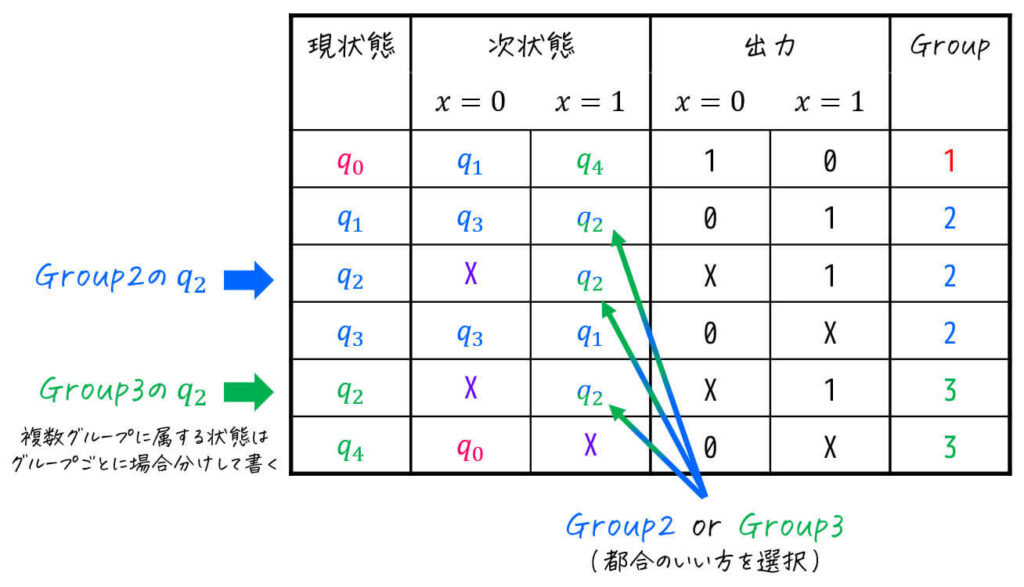
あとは、Group2, 3両方に属する \( q_2 \) に対して都合のいい方を選んでから、代表状態を選び、まとめればOKです。

[補足2] グループ分けが1発でうまくいかない場合
両立性はあくまでも「1つにまとめられる可能性」なので、選んだ状態群によっては、1発でグループ分けがうまくいかないことがあります。
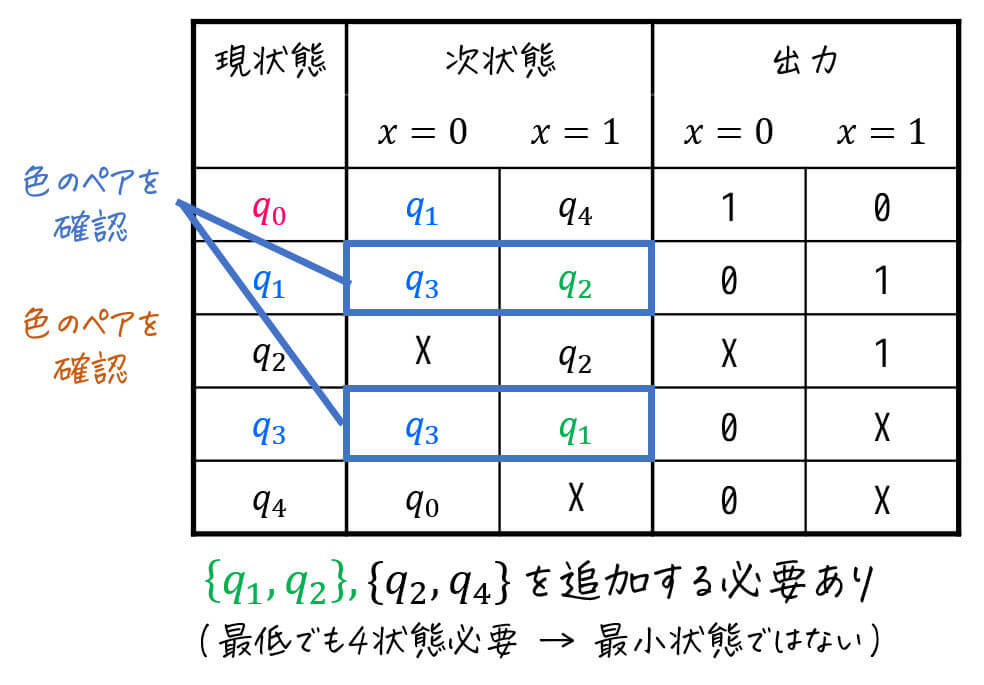
例えば今回の例題の場合、\( \{ q_0 \} \) に加えて、状態群から \( \{ q_1, q_3 \} \), \( \{ q_2, q_4 \} \) の合計3状態で最小化できそうかと思うかもしれません。
しかし、実際に\( \{ q_1, q_3 \} \) をグループに加えてみると、最低でも \( \{ q_1, q_2 \} \) および \( \{ q_2, q_4 \} \) を加える必要があることがわかります[6]\( q_1, q_3 \) の入力 \( x = 1 \) に着目すると、\( (q_1, q_2) \) が出てくるため、最低でもこのペアは同じ状態に属せるように状態 \( \{ q_1, q_2 \} \) … Continue reading。
そのため、\( \{ q_0 \} \), \( \{ q_1, q_3 \} \), \( \{ q_2, q_4 \} \) を使った最小化は出来ない(最低でもこれら3つの状態に加えて1つ別の状態が必要)なことがわかります。
4. 練習問題にチャレンジ
それでは、不完全指定順序回路の最小化の練習を、例題より少し複雑な問題でしてみましょう。
次の状態遷移表で表されるを不完全指定順序回路の状態数が最小になるように(最小化)し、状態遷移図の形で答えなさい。
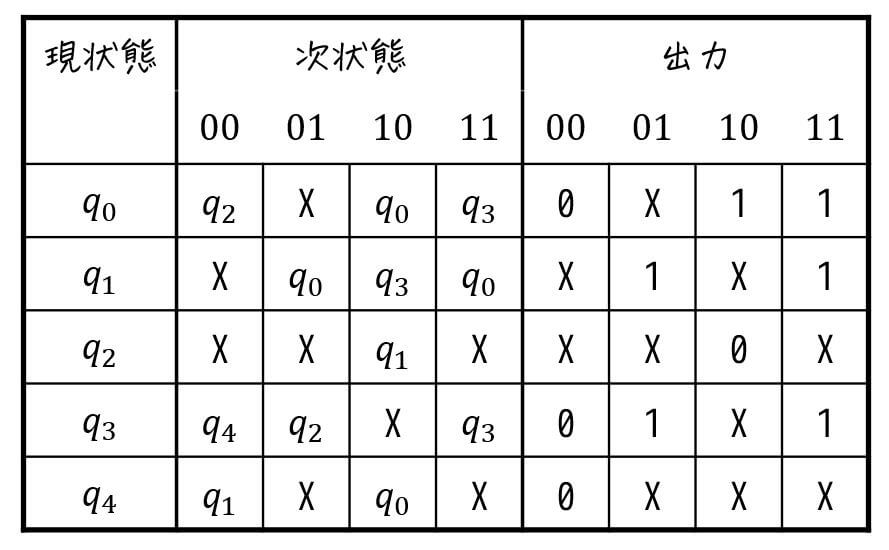
※1 X は Don't Careを表す
※2 表の 00, 01, 10, 11は2変数の入力を表す
[解説]
今回は、最初から状態遷移表が与えられているので、Step1は不要です。
Step2. 両立性が成り立つペアを探す
Step2-1. 出力の組み合わせから両立性が成り立たないペアを見つける
まずは、出力に着目しながら両立性が成り立たないペアを見つけて行きましょう。
※ X (Don't Care) はワイルドカードなので、0, 1どちらか片方を入れて成り立てばOKです。
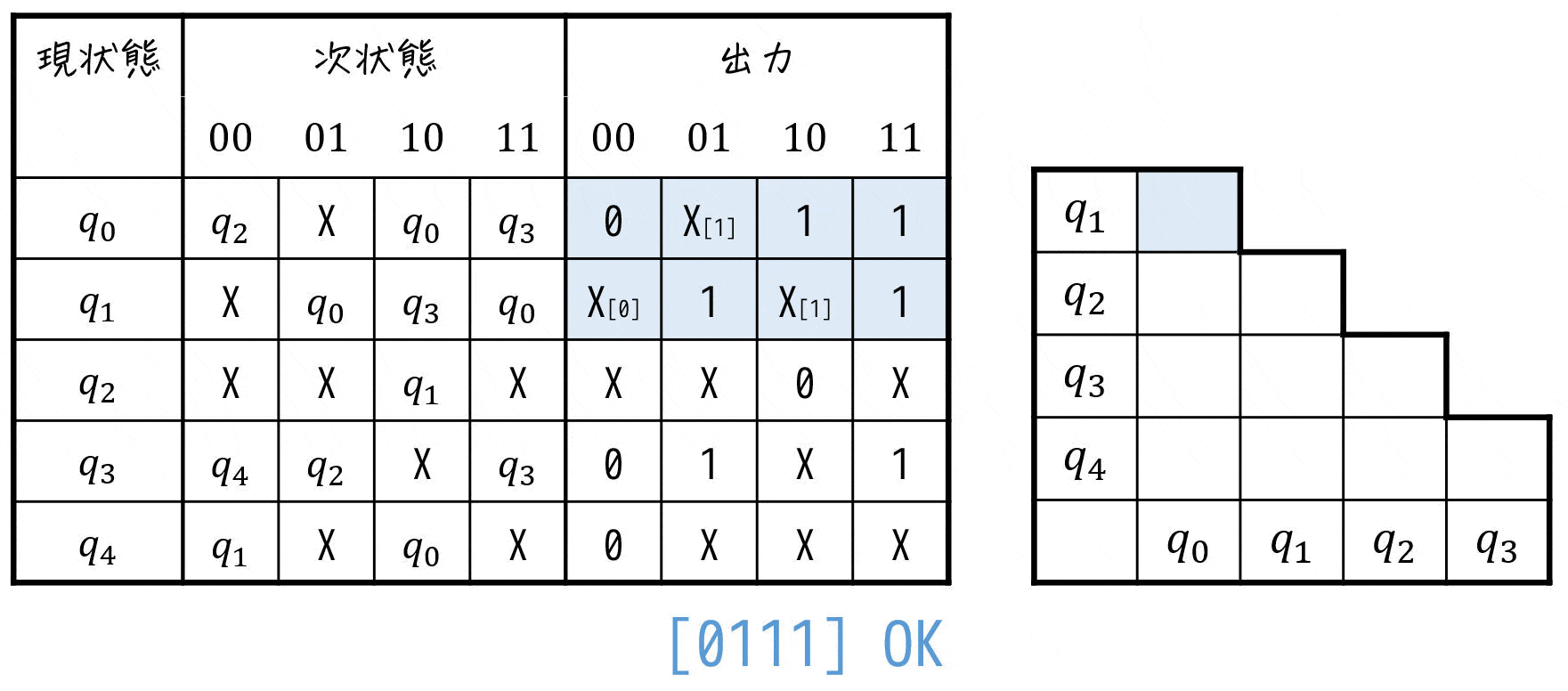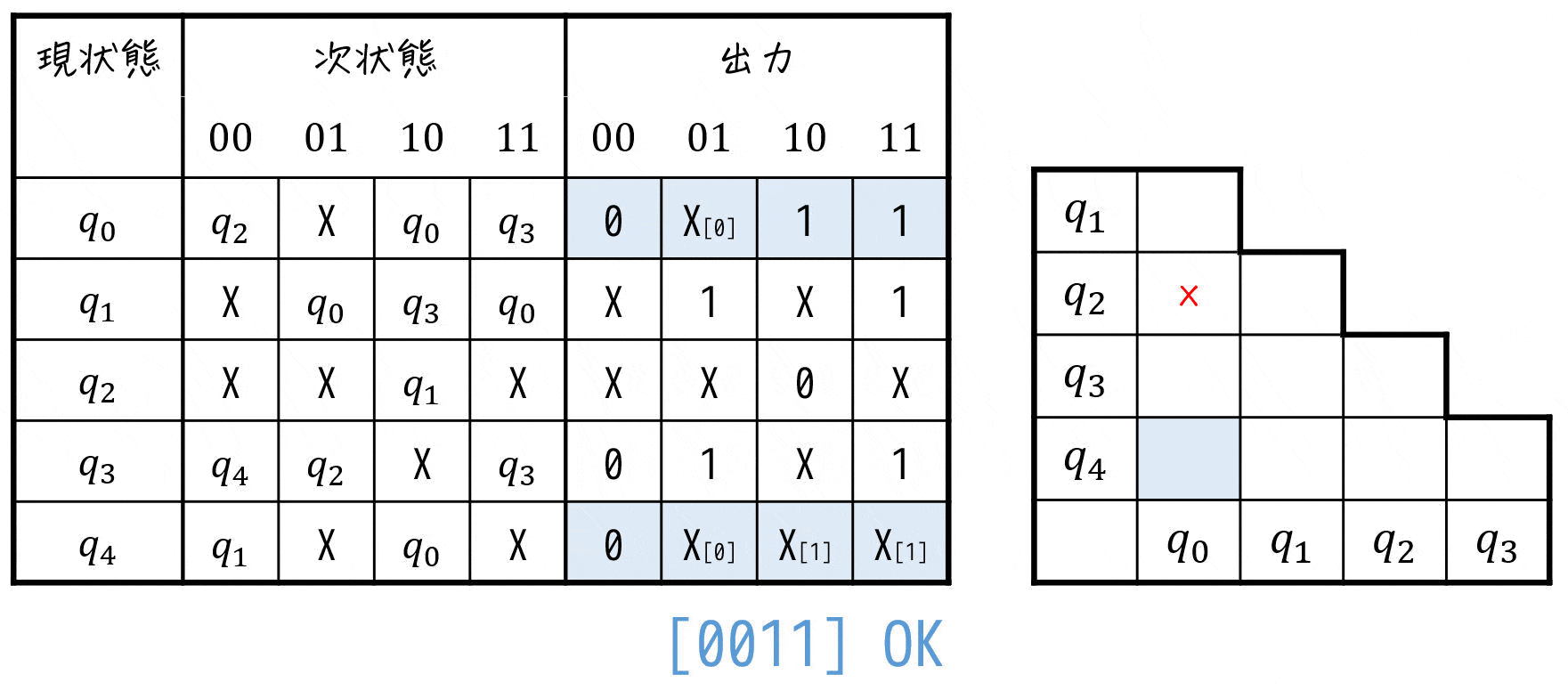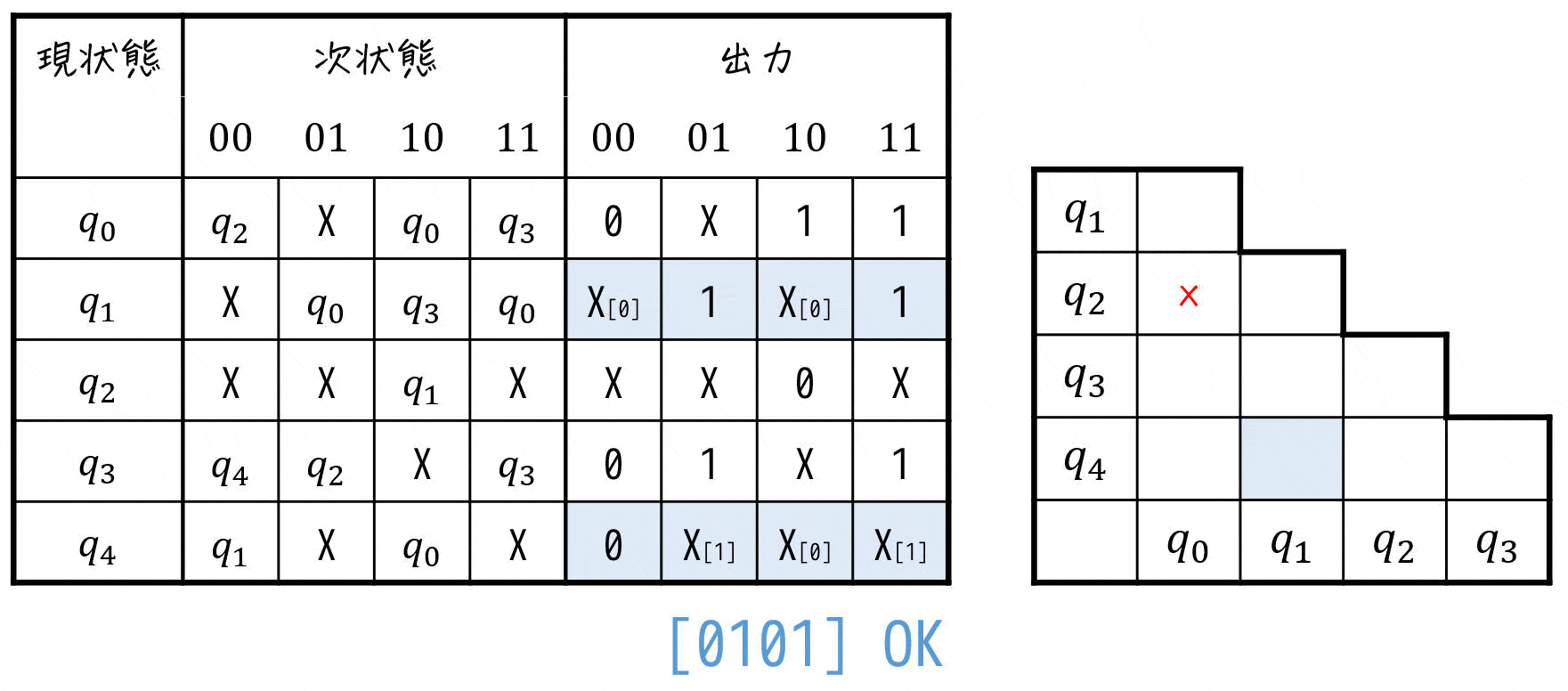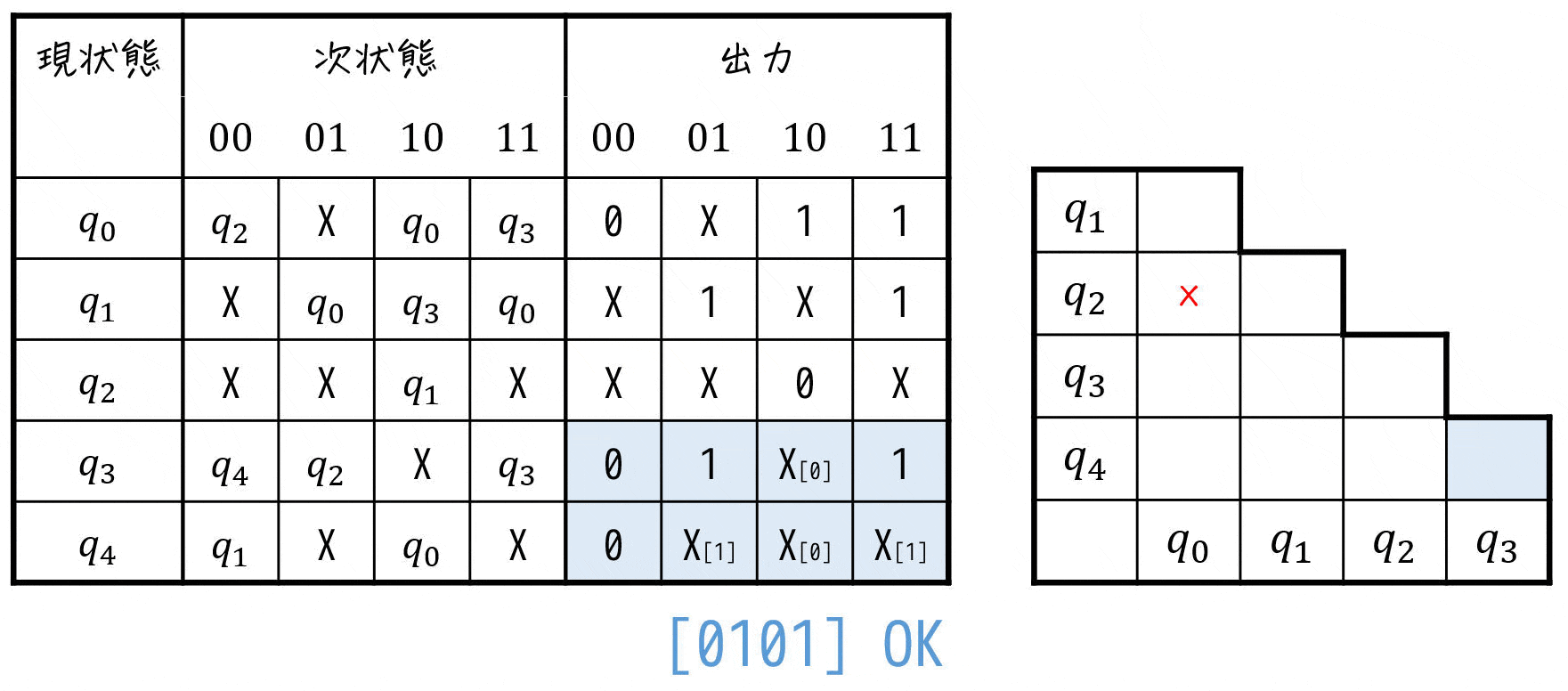
すると、三角表は下のようになります。
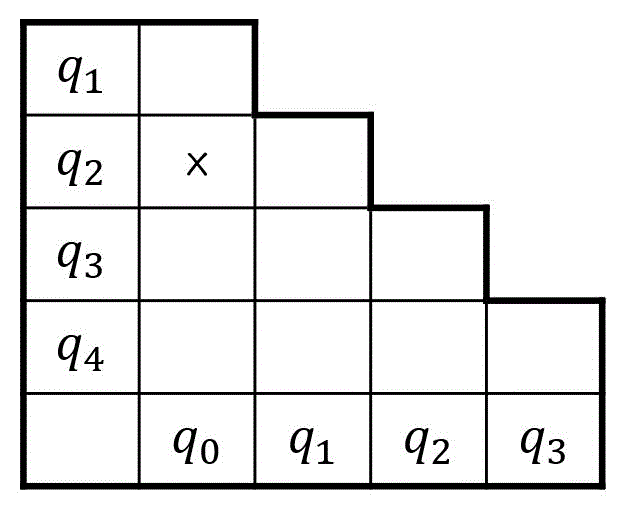
Step2-2. 三角表からひとまとめに出来ないペアを探す
つぎに、「次状態の入力と三角表」に着目しながら両立性が成り立たないペアを探しましょう。
具体的には、
- ×が付いていない各ペアに対し、次状態の各入力ごとのペアに着目
- 着目した次状態のどれか1つの入力のペアでも「三角表に×が付いていれば」、現状態のペアに×を付ける
- ×が付いた場合、スタート地点(振り出し)に戻る
を「三角表の右下」に到達するまで続けます。
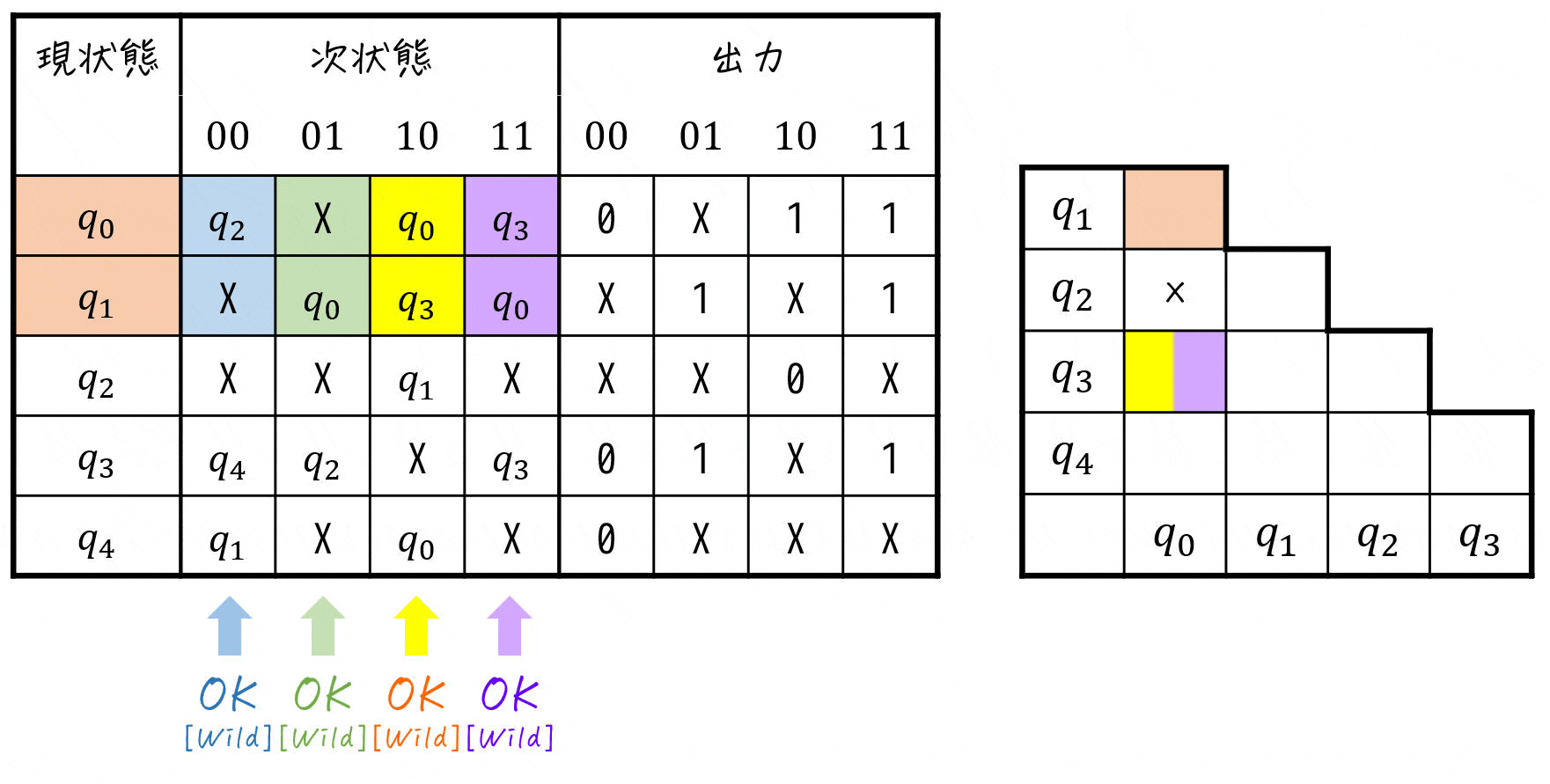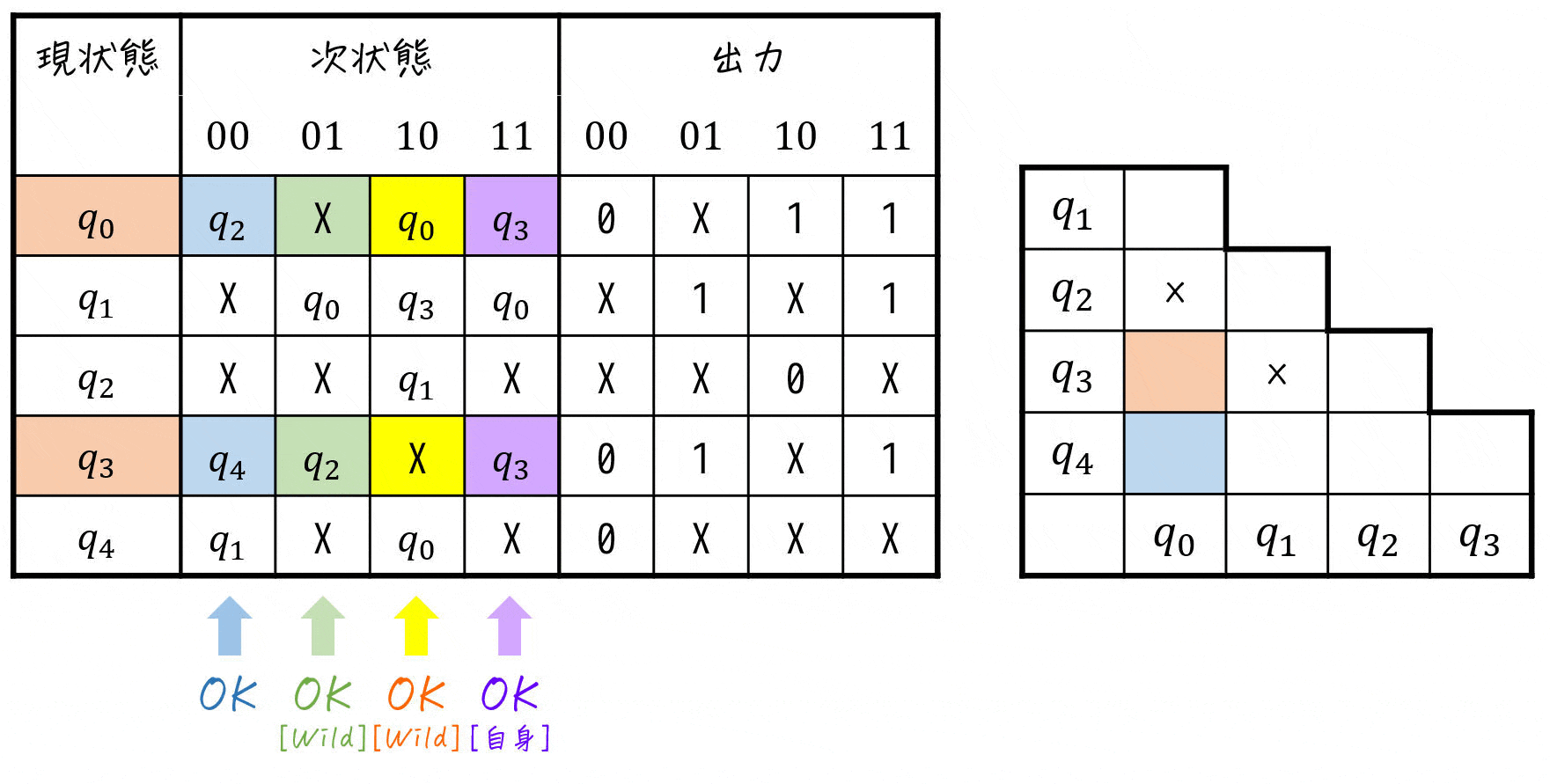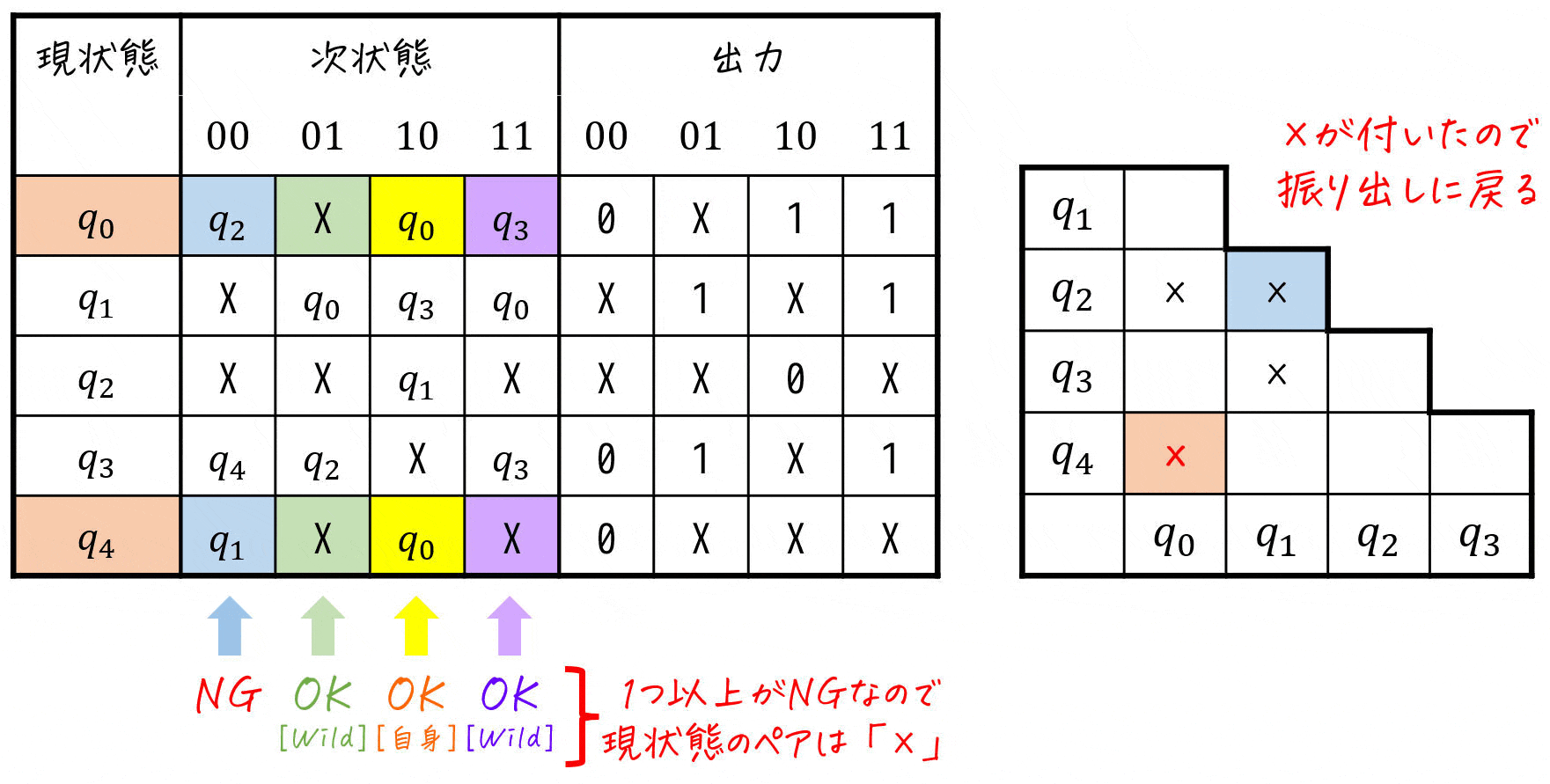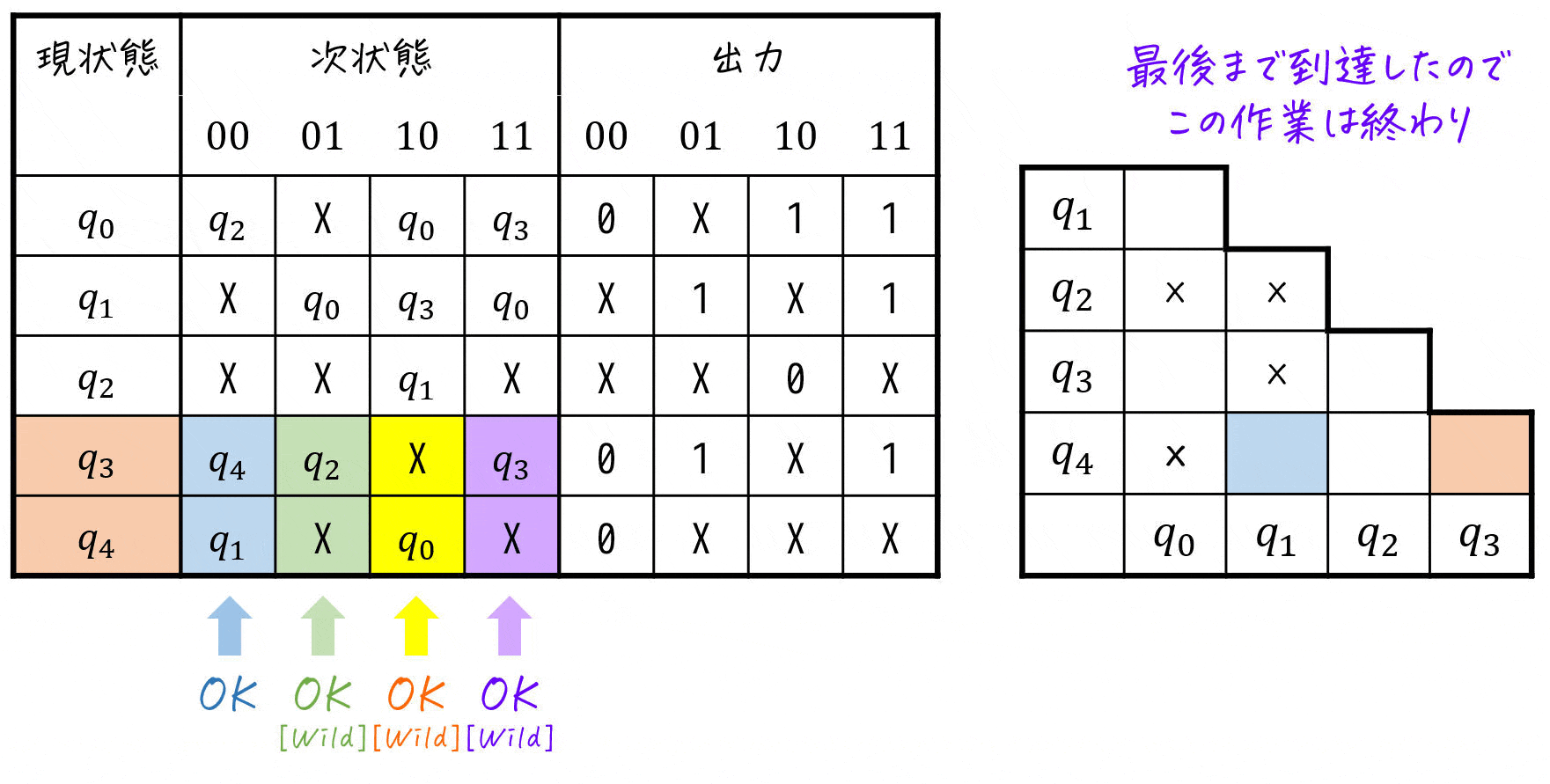
※ スペースの関係上、X (Don't Care) とペアになっている部分には [Don't Care] の代わりに [wild] と表記しています。
すると、三角表は下のようになります。
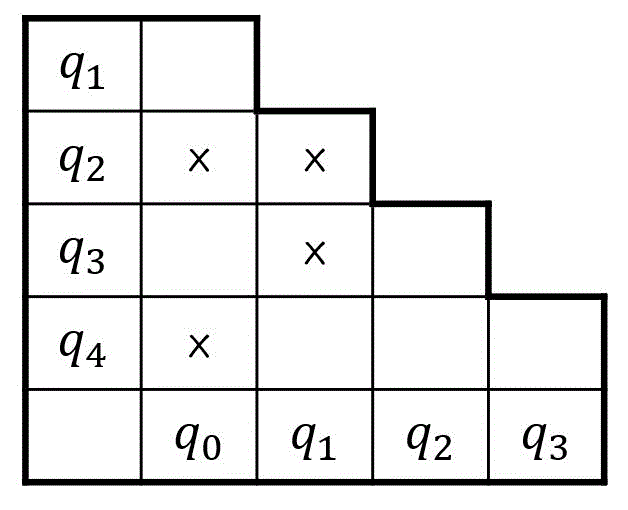
つまり、×がついていない\[
\{ q_0 , q_1 \}, \{ q_0, q_3 \}, \{ q_1, q_4 \}, \{ q_2, q_3 \}, \{ q_2, q_4 \}, \{ q_3, q_4 \}
\]の状態郡が両立性を持つペアとなります。
Step3. 3状態以上の両立性が成立するか確認
つぎに、3状態以上の状態群でも両立性が成立するかどうかを樹形図を書くなどで確認しましょう。
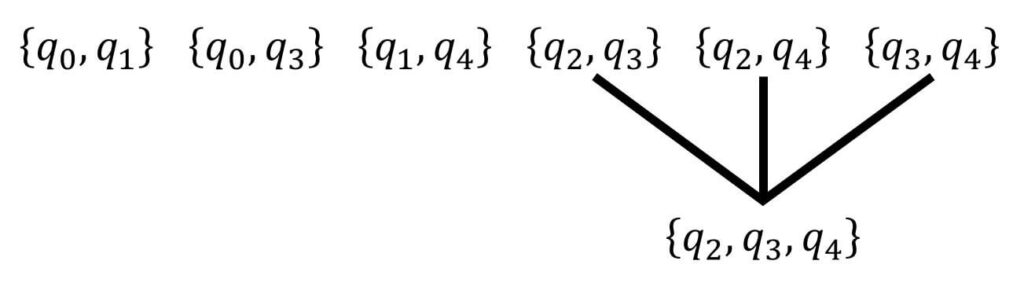
今回は \( \{ q_2, q_3 \} \), \( \{ q_2, q_4 \} \), \( \{ q_3, q_4 \} \) に両立性が成立するので、\( \{ q_2, q_3, q_4 \} \) の3状態ある状態群に対して両立性が成立します。
Step4. 両立性から最小化できる状態群の組み合わせを決定する
Step4-1. 単独でしか満足できない状態 (必須状態) を探す
表を書くことでもわかるのですが、今回は \( q_0 \) ~ \( q_4 \) 単独でしか満足できない状態はありません。
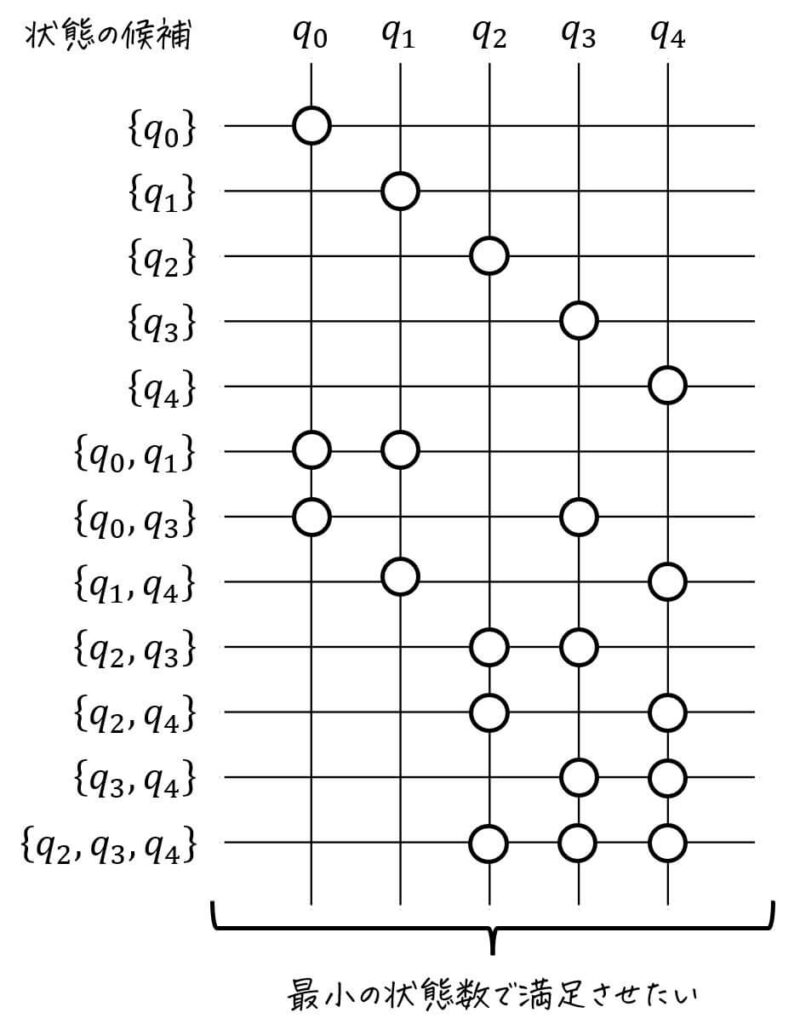
そのため、\( q_0 \) ~ \( q_4 \) を最小の状態数で満足させることを Step4-2 で考えます。
Step4-2. 最小のグループ数で全状態を満足させる
まず真っ先に
- 3状態ある状態群 \( \{ q_2, q_3, q_4 \} \) をGroup1とする
- 残りの \( \{ q_0, q_1 \} \) がGroup2になってくれればいいな
が思いつくと思います。(この組み合わせなら2状態で表現できますし。)
なので、\( \{ q_2, q_3, q_4 \} \) をGroup1とし、各入力00, 01, 10, 11ごとの遷移先を確認しましょう。
すると、
- 00が入力のとき:Group1の状態から「\( q_4 \), \( q_1 \) に遷移する」
→ \( \{ q_0, q_1 \} \) を別グループ (Group2) として追加が必要 - 10が入力のとき:Group1の状態から「\( q_0 \), \( q_1 \) に遷移する」
→ \( \{ q_1, q_4 \} \) を別グループ (Group3) として追加が必要
となるため、最低でも3グループが必要となることがわかりますね。
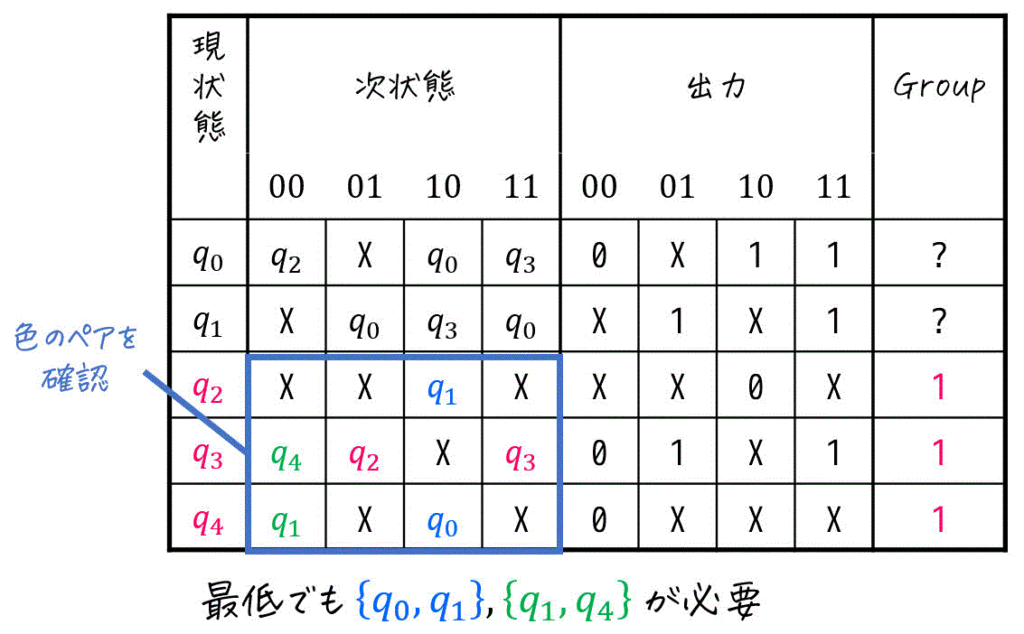
さらに、Group2 \( \{ q_0, q_1 \} \) から各入力00, 01, 10, 11ごとの遷移先を確認します。
すると、入力10, 11のときに \( q_0 \), \( q_3 \) に遷移するので、 \( \{ q_0, q_3 \} \) も別グループ (Group4) として追加する必要があります。
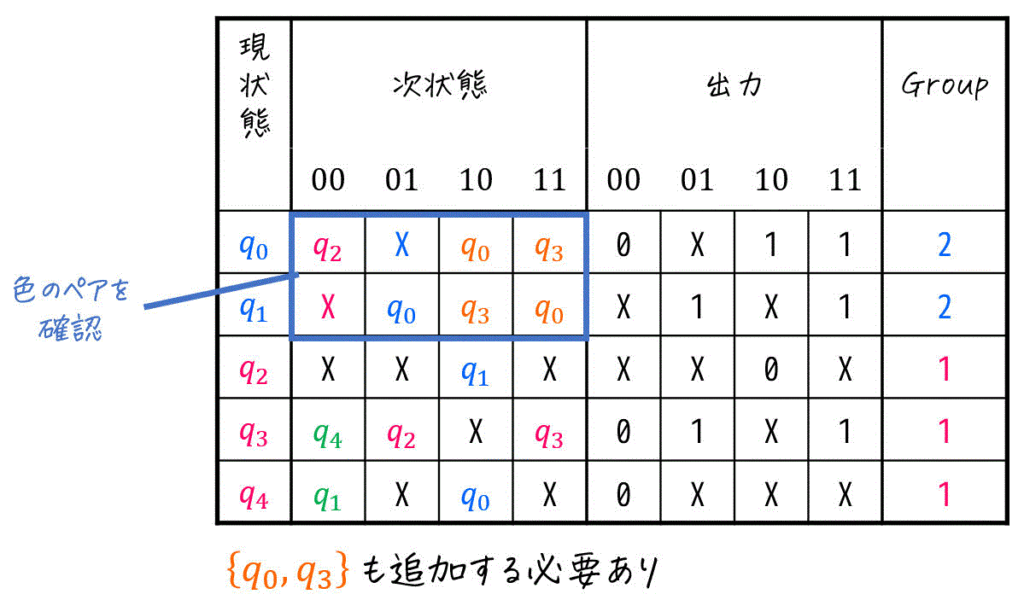
この時点で4グループ出てきてしまっているため、いったん \( \{ q_2, q_3, q_4 \} \) をグループに加えた場合は保留します。
代わりに、今度は \( \{ q_0, q_1 \} \) をGroup1としてみましょう。
すると、入力10, 11のときに \( q_0 \), \( q_3 \) に遷移するので、 \( \{ q_0, q_3 \} \) を同じ状態にするためにGroup2に加えましょう。
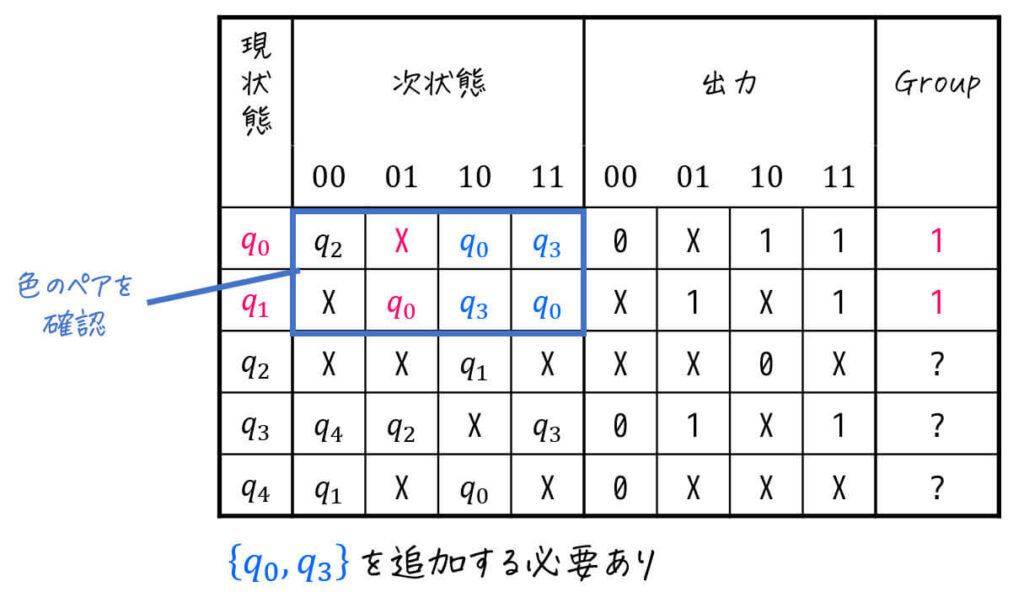
今度は、\( \{ q_0, q_3 \} \)[Group2] の次状態に着目しましょう。
すると、入力00のときに \( q_2 \), \( q_4 \) に遷移するので、\( \{ q_2, q_4 \} \) を同じ状態にするためにGroup3に加えます。
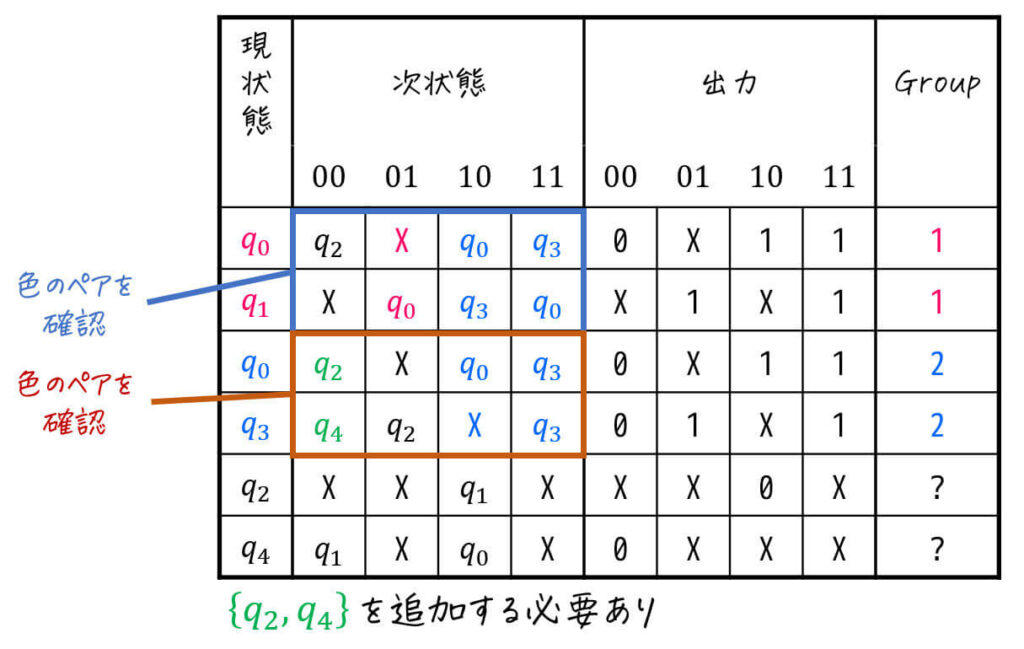
さらに \( \{ q_2, q_4 \} \) [Group3] の次状態に着目しましょう。
すると、00, 01, 10, 11どの入力をしたときも必ず Group1, Group2, Group3 の組み合わせ(もしくはDon't Careが片方にでもある)状態となっていますね。
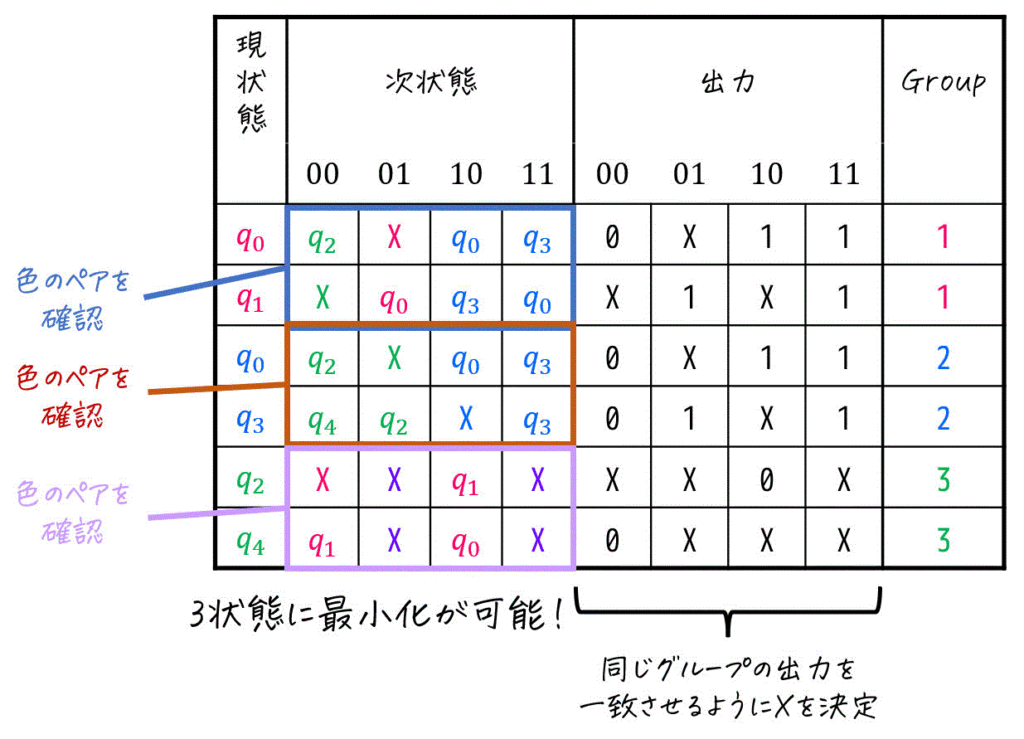
そのため、
- Group1: \( \{ q_0, q_1 \} \)
- Group2: \( \{ q_0, q_3 \} \)
- Group3: \( \{ q_2, q_4 \} \)
とした3状態に最小化が可能です。
Step4-3. 各グループ内で代表状態を1つ選択し、まとめる
あとは、下の表をグループごとにまとめればOKです。
(事前に同じグループの出力を一致させるために X に何を入れればよいかを小さく記入しています)
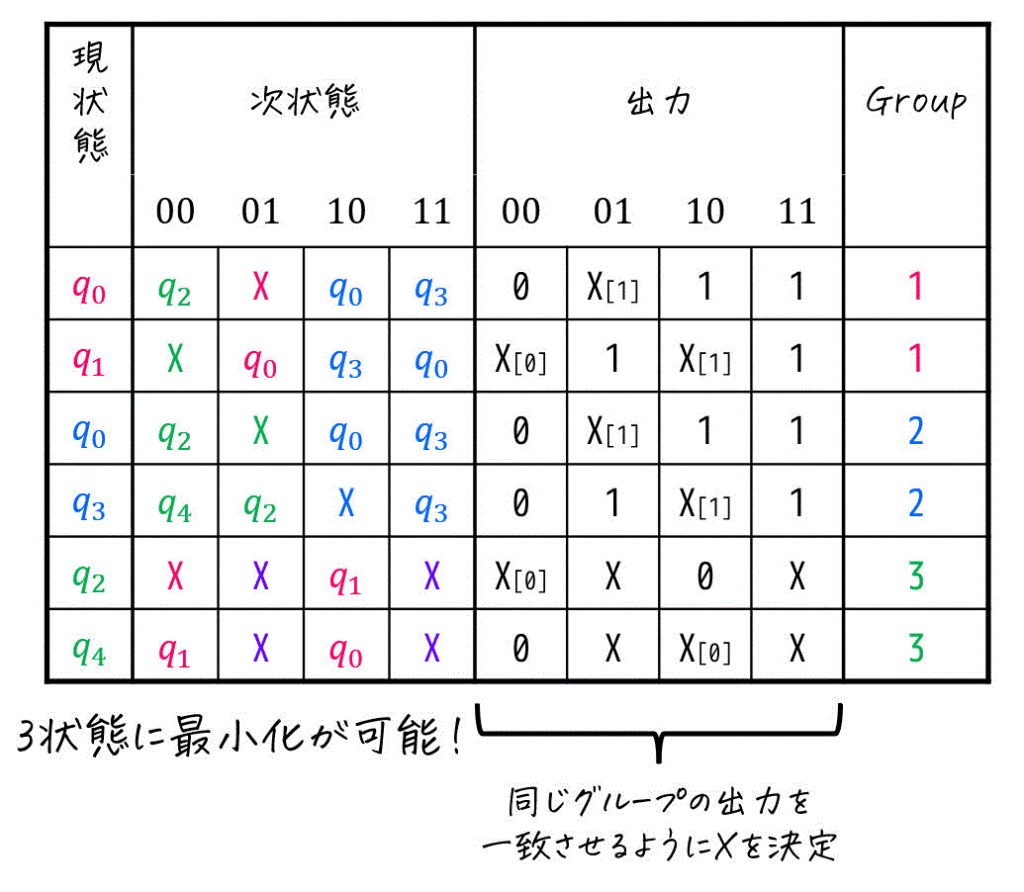
具体的には、
- Group1: \( \{ q_0, q_1 \} \) → 代表 \( q_0 \)
- Group2: \( \{ q_0, q_3 \} \) → 代表 \( q_3 \)
- Group3: \( \{ q_2, q_4 \} \) → 代表 \( q_4 \)
と代表を決め、出力部分の X (Don’t Care) の値を決定してから状態遷移表を作成すればOKです。
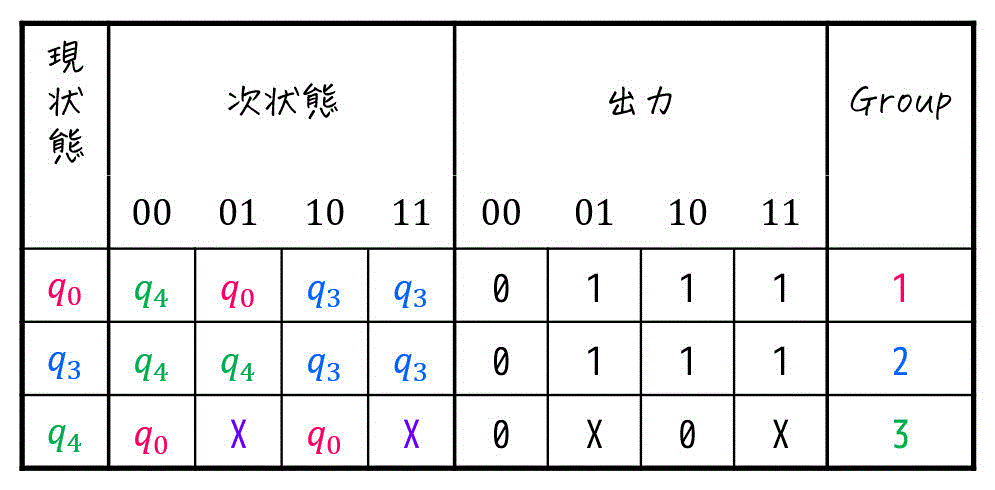
Step5. 状態遷移図に変換する
あとは、Step4-3で作った状態遷移表を状態遷移図に変換すればOKです。
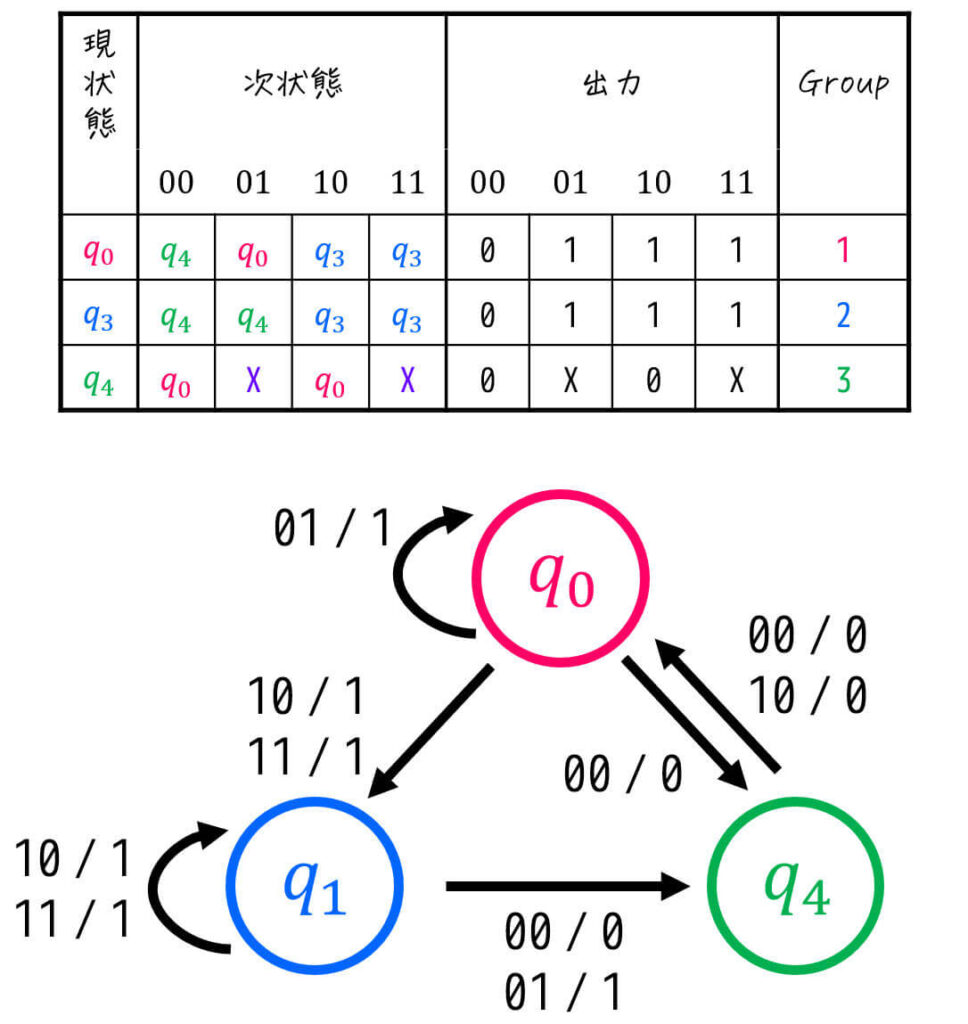
5. さいごに
今回は順序回路の状態遷移図に X [Don't Care] が含まれる不完全指定順序回路の状態最小化についてみていきました。
通常の順路回路の状態最小化より難易度が少し高く、理解が難しい部分ですがこの記事を見て理解の助けになれば幸いです。
これにて、順序回路に関する記事は全て終了です! 今まで見てくださり、ありがとうございましたm(__)m
(工業大学生ももやまのうさぎ塾では、「うさぎでもわかる」をモットーに様々な大学数学系・情報系の科目を解説しています。なので、もし他の理系科目でわからないなと思うことがあれば、「(分野名) (単元名) うさぎ」などと是非調べてみてください。きっと、理解の助けになる私の記事が出てくるかなと思います。)
6. 参考文献
近畿大学 - 順序回路の状態数の最小化
[アクセス日: 2022/07/31]
https://www.info.kindai.ac.jp/LC/lecture/LogicCircuits12note.pdf
注釈
| ↑1 | イメージとしては、単独では Don't Careのおかげでひとまとめに出来ても、ひとまとめにしたペア同士を状態遷移表に適用する際に Don't Careが干渉し、2種類のペアをひとまとめに出来ない可能性があるからです。 |
|---|---|
| ↑2 | 出力が異なる状態は、100%ひとまとめにすることはできないため。 |
| ↑3 | もちろん具体的にGroup1, 2, 3を設定してもOKです。ただし、順序実際に回路を設計する際に少し複雑になりますが…。 |
| ↑4 | 0, 1どちらを入れても成立する場合はXのままでOKです。 |
| ↑5 | 各グループごとに全く新しい名前(例:Group1を"1"、Group2を"2"、Group3を"3"とする)としてもOKです。 |
| ↑6 | \( q_1, q_3 \) の入力 \( x = 1 \) に着目すると、\( (q_1, q_2) \) が出てくるため、最低でもこのペアは同じ状態に属せるように状態 \( \{ q_1, q_2 \} \) を新しいグループとして追加する必要がある。また、\( \{q_2, q_4 \} \) がまだ満足していないため、\{ q_2, q_4 \} \) も新しいグループとして追加する必要がある。 |
関連広告・スポンサードリンク