![うさぎでもわかる画像処理 Part02 トーンカーブと画像処理 [Python・MATLABコード付き]](https://www.momoyama-usagi.com/wp-content/uploads/ip1-18.jpg)
スポンサードリンク
こんにちは、ももやまです。
皆さんは、スマートフォンで撮影した画像を「他の人にLINEで送る」、「SNSに投稿をする」際にに画像を加工したことってありませんか?
この画像の加工、実は画像処理の技術がたっぷり詰まっているんですよ…!
そこで今回は、
- 画像の加工の仕組みの中でも最も基本的な画像処理とは何か?
- 最も基本的な画像処理で出てくるトーンカーブとは何か?
- 実際の画像処理の例を見てみよう!
- カラー画像特有の画像処理テクニックを見てみよう!
の4つについて勉強していきましょう。
[注意] コンピュータ上でどのように画像が扱われているかを全く知らない人は、下の記事を読んで勉強することをおすすめします。
(※ 画素、画素値などの専門的な用語が何を表しているのか、およびカラー画像の扱い方を知っていれば読み飛ばしてOKです。))
目次
スポンサードリンク
1. 最も基本的な画像処理とは?
(1) グレースケール画像の場合
画像処理には様々な方法がありますが、上で説明した通り最も単純で基本的な方法は、下のように元の画像の画素値に対して、一定のルールに基づいて画素値を書き換えてあげる方法です。
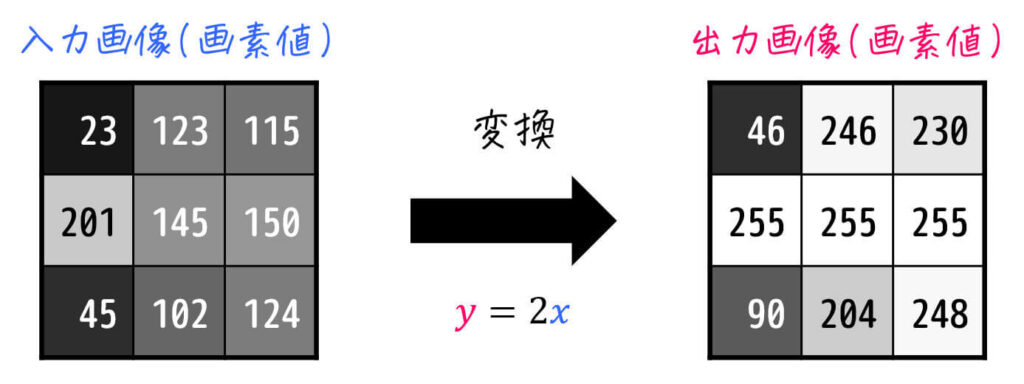
(例: 各画素値を2倍)
例えば、上の例で紹介したルール[1]入力画像の画素値 \( x \) を2倍したものを出力画像の画素値 \( y \) とする、つまり \( y = 2x \) の変換を行うルールを用いて実際に画像処理をすると、下のような出力画像を生成することができます。
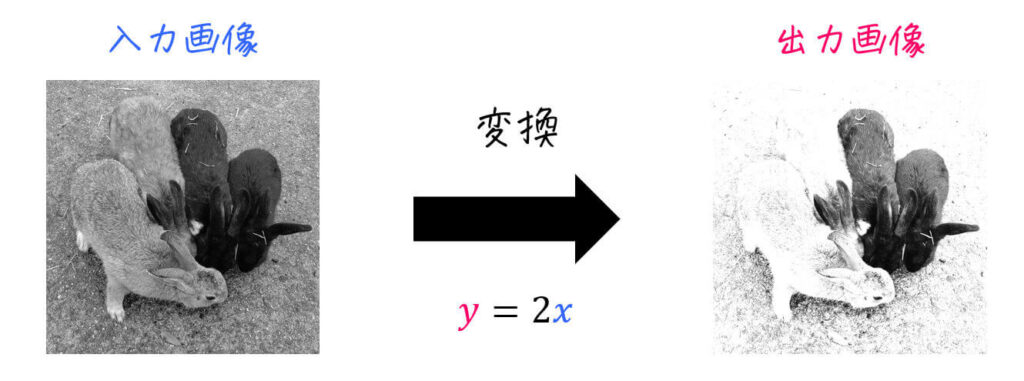
もちろん「単に画素値を2倍にする」のような単純な変換だけでなく、下のように複雑な式を使って画像処理をすることもできます。
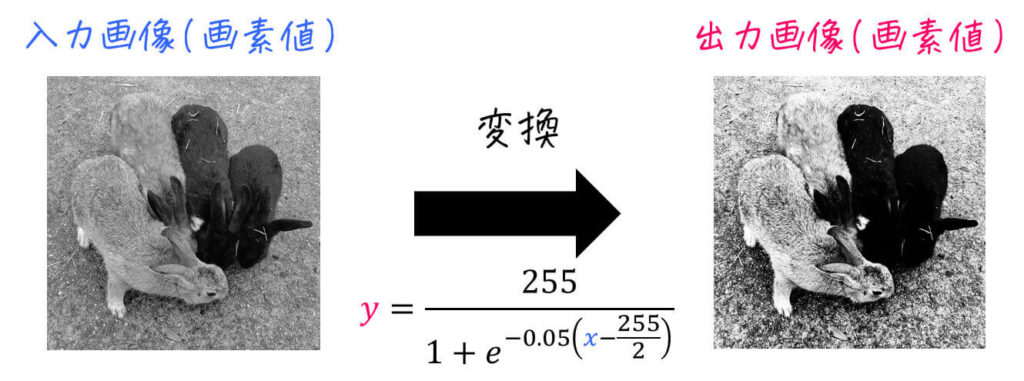
(コントラストをアップさせる変換)
(2) カラー画像の場合
カラー画像の場合も、基本的には「最も基本的な画像処理」の仕方は同じです。
しかし、グレースケール画像と異なる点として、カラー画像はコンピュータ上では「R(赤)成分の画像」、「G(緑)成分の画像」、「B(青)成分の画像」の3種類を組み合わせて表現されます。

言い換えると、グレースケール画像では1種類の画素値しかなかったのに対し、カラー画像の各画素には、
- R成分の画素値
- G成分の画素値
- B成分の画素値
の3種類の画素値が与えられております。
なので、カラー画像の画像処理は、R, G, B各成分の画素値を一定のルールに基づいて書きかえることで実現されます。
この3種類(R成分、G成分、B成分)の画素値の書き換えのルールとしては、大きく分けても
- R, G, B各成分を同じルールに基づいて書き換える
- R, G, B各成分の一部を書き換える
の2種類あるため、グレースケール画像に比べて画像処理の幅は広がります。
例1. R, G, B各成分を同じルールに基づいて書き換える場合
まずはR, G, B各成分を同じルールで変換すると、どのような画像が生まれるかを見てみましょう。
(下で示した変換ルール1に従って変換をします)
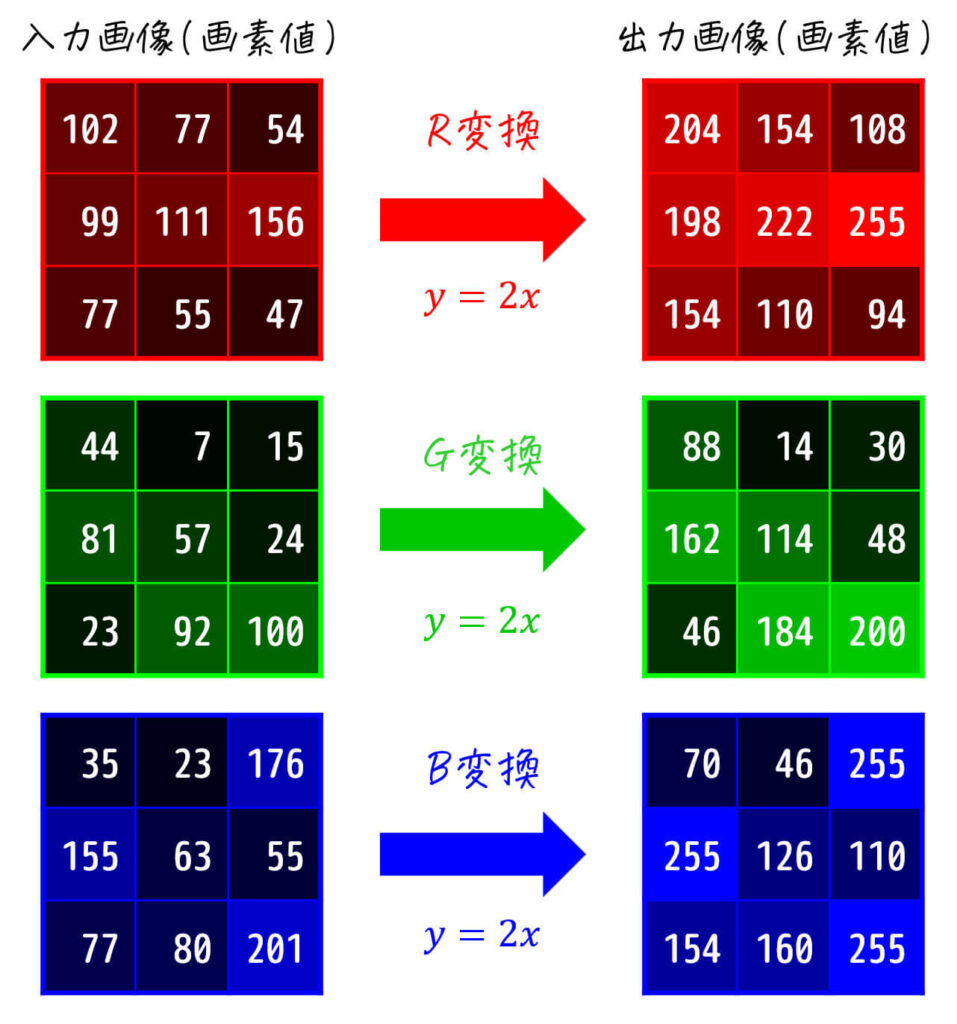
(R, G, B成分ともに画素値×2の変換)
実際に変換を行うと、明るさが変わった画像が出力されます。
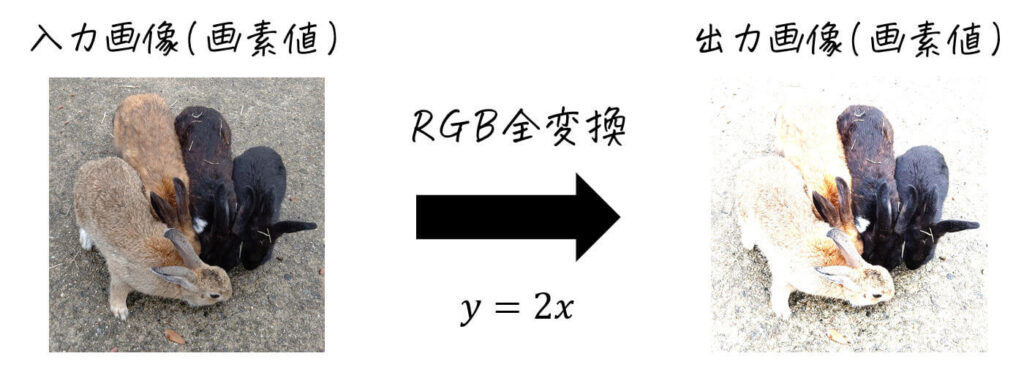
このように、R, G, B成分を同じルール変換することで、画像の明るさやコントラストを調整することができます。
例2. R, G, B各成分の一部をルールに従って書き換える場合
今度は、R, G, B各成分うち、一部を書き換えた場合はどうなるかを見てみましょう。
(下で示した変換ルール2に従って変換をします)
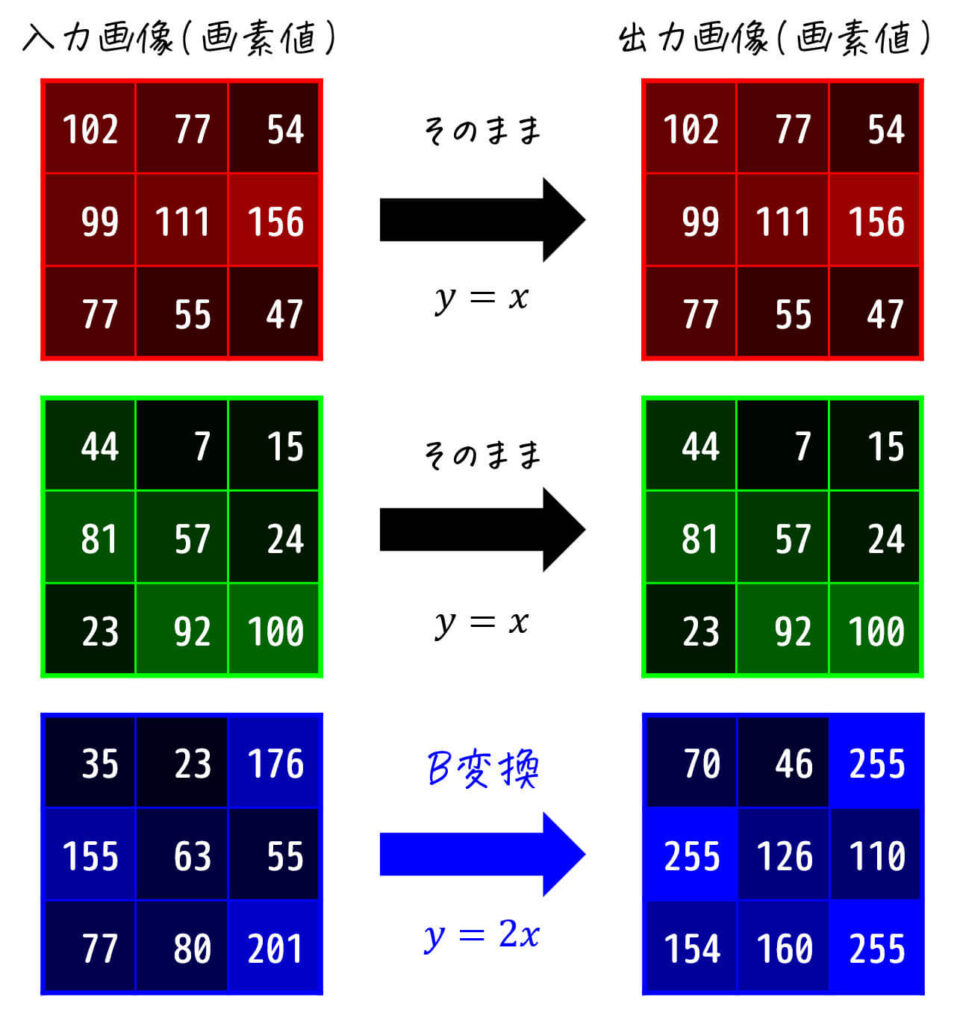
(B成分のみ画素値×2の変換、R, G成分はそのまま)
すると、下のように特定の色が強調された(弱めた)ような出力画像が出てきます。
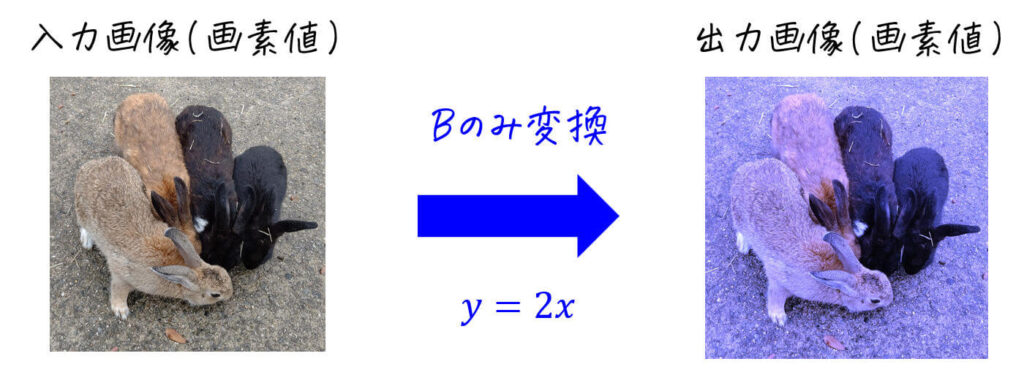
このように、R, G, B成分の一部を変換することで、画像内の色のバランスを調整することができます。
スポンサードリンク
2. トーンカーブ
(1) なぜトーンカーブを使うのか
画像処理で行う画素値の変換が「各画素値を2倍にする」のように単純なものであれば、数式だけでも画像処理の内容が直観的に理解できるかもしれません。
しかし、下のように複雑な数式になると、(数学が得意な一部分の人を除き)画像処理の内容は直観的には理解できませんよね。

そこで画像処理の世界では、どのような変換を行ったかを下のような入力画素値 \( x \) に対する出力画素値 \( y \) を表したグラフで表現します。このグラフのことをトーンカーブと呼びます。
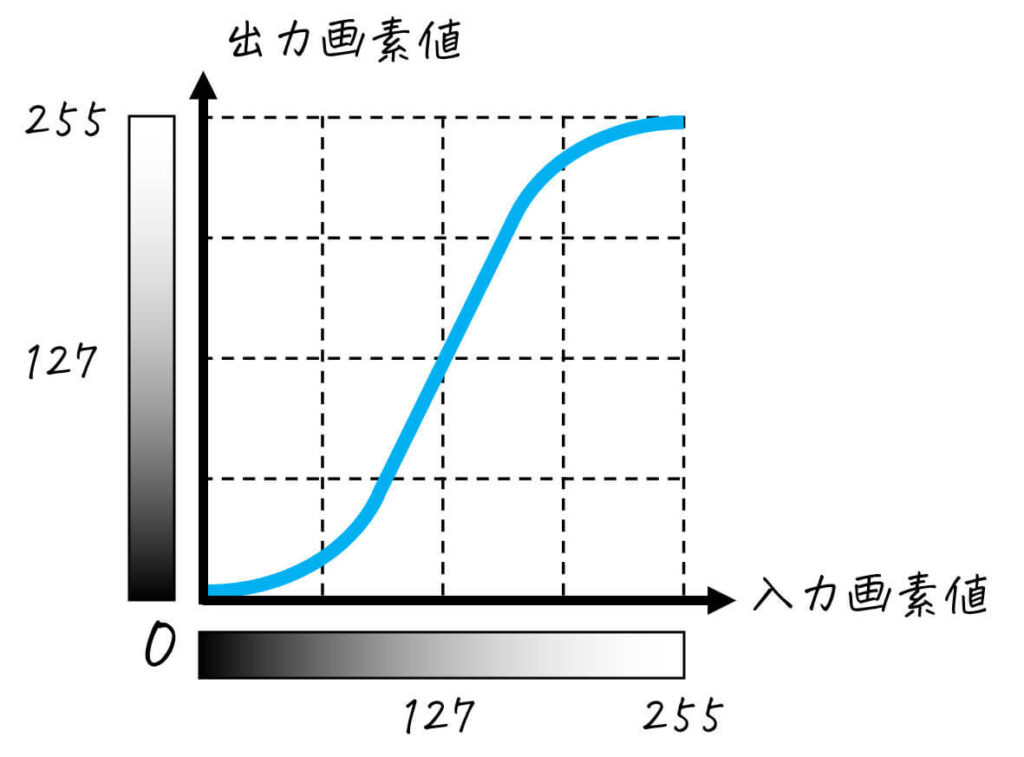
変換内容を数式ではなくグラフで示すことで、より画像処理の内容を直観的に確認することができますね!
(2) トーンカーブの読み方
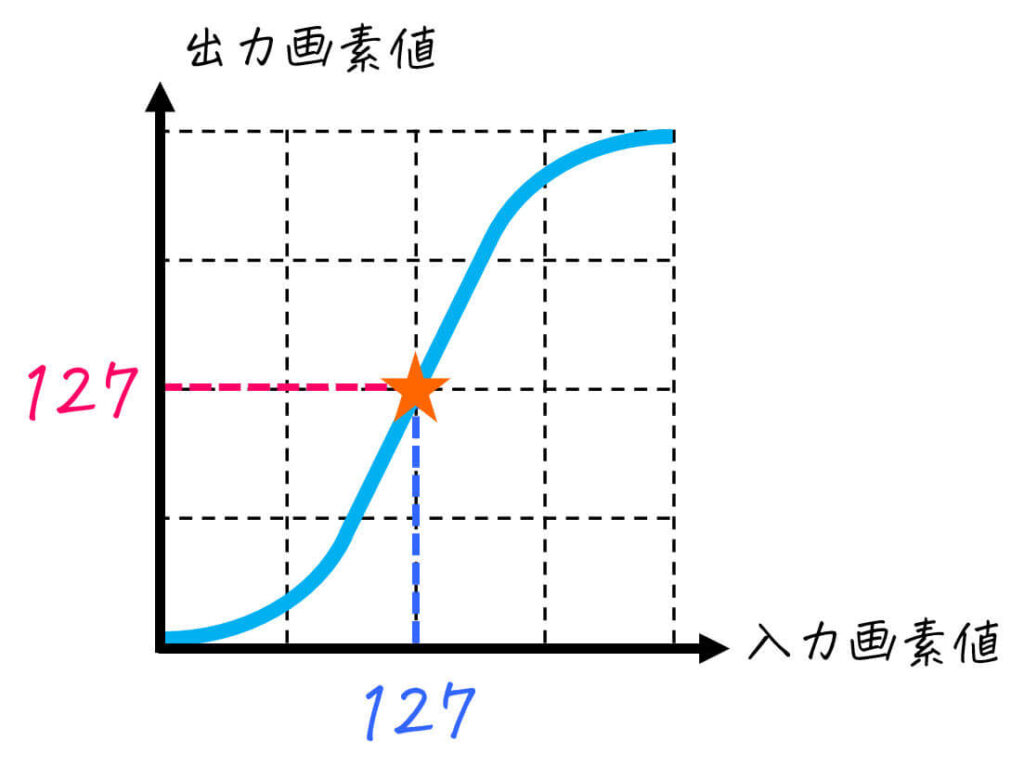
ここで、入力画素値 \( x \) が127のときを例にして、トーンカーブから出力画素値 \( y \) を読み取る方法を確認しましょう。
入力画素値 \( x \) [横軸の値] が127のときの出力画素値 \( y \) [縦軸の値] を見てみると、127近くにあることがわかりますね。
(3) カラー画像の場合のトーンカーブ
カラー画像の場合は、下のようにR成分、G成分、B成分それぞれのトーンカーブを示します。
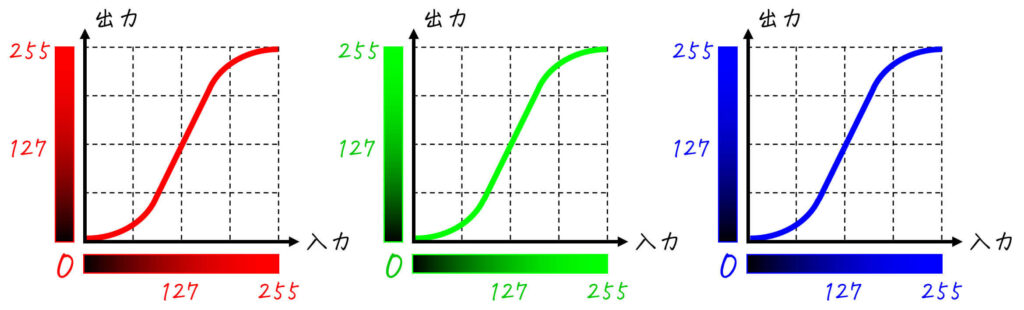
(R, G, B成分を全て同じルールで変換する場合)
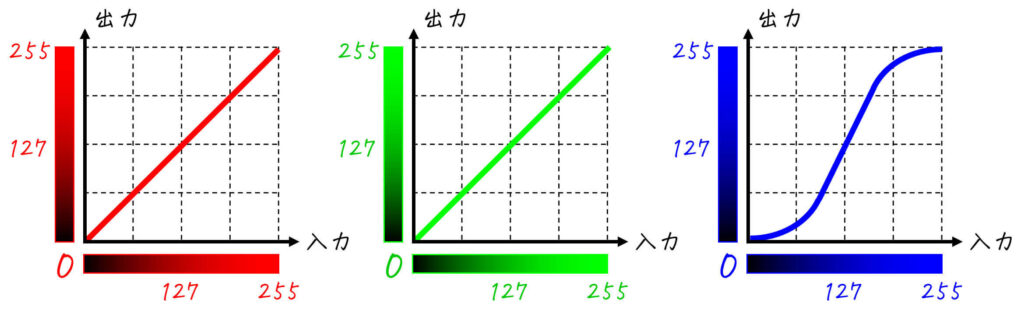
(R, G, B成分を異なるルールで変換する場合)
スポンサードリンク
3. 基本的な4種のトーンカーブ [Python, MATLABコード付き]
ここからは、画像処理の中でも最も基本的な4種類のトーンカーブについて
- グレースケール画像のとき
- カラー画像のとき(R, G, B成分全て同じトーンカーブを適用)
それぞれでみていきましょう。
さらに、変換をするための Python, MATLABコードも紹介します!
(Pythonを使用する場合、numpy, cv2 をインストールする必要があるので注意!)
(1) 折れ線型トーンカーブ
単純に画素値を \( k \) 倍する処理をすることで、画像全体の明るさを変更するトーンカーブです
数式で書くと、\[ y = kx \]となります。
(入力画素値: \( x \), 出力画素値: \( y \))
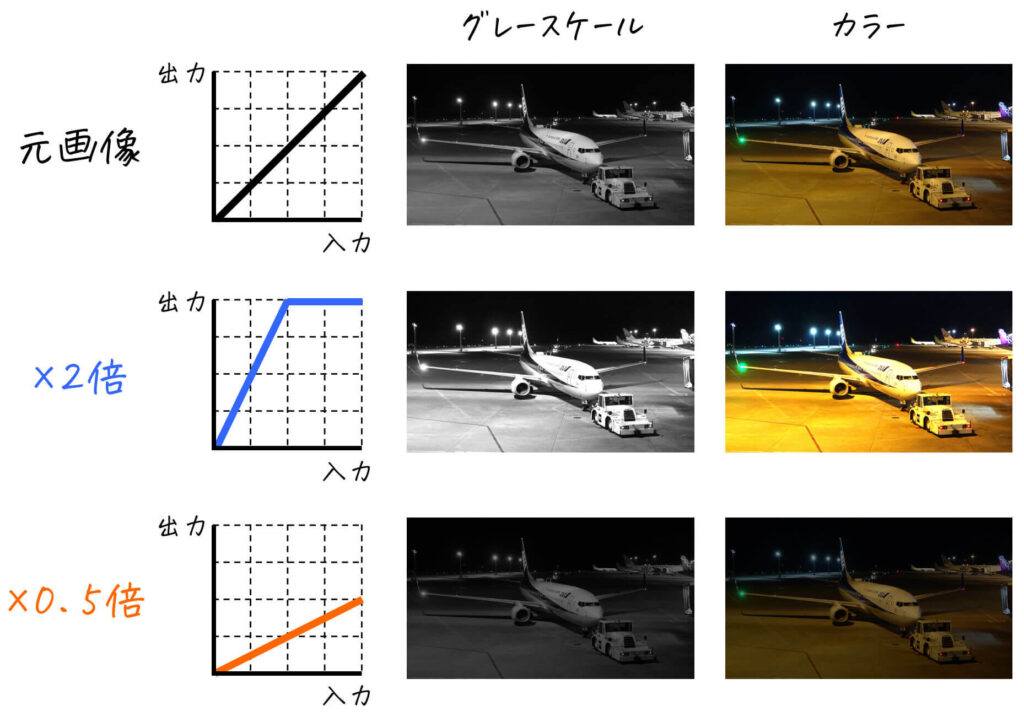
(1-a) 画素値をk倍 (k > 1)
\( k \) に1より大きい値を入れると、元の画像よりも明るくなります。
例) \( k = 2 \)、つまり画素値を2倍する変換 \( y = 2x \)
[グレースケール画像]
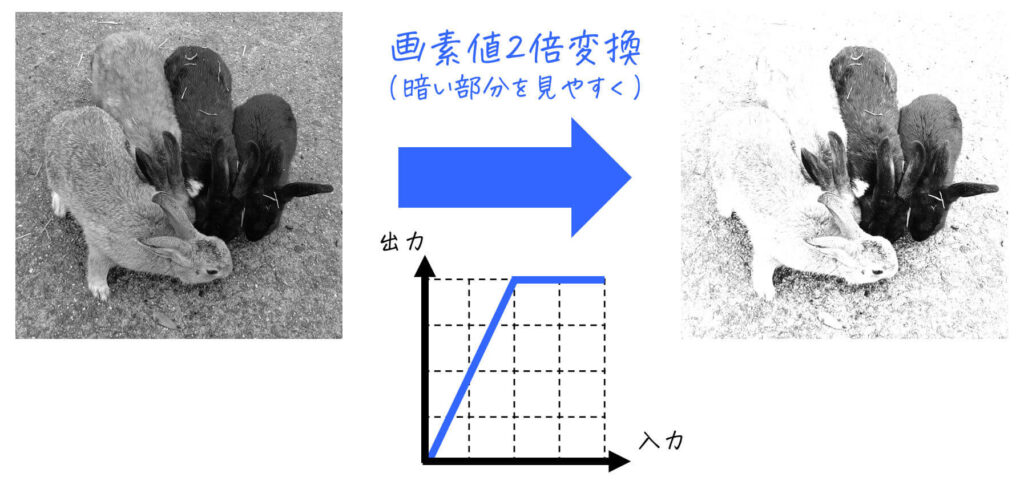
(画像の明るさ2倍)
[カラー画像]
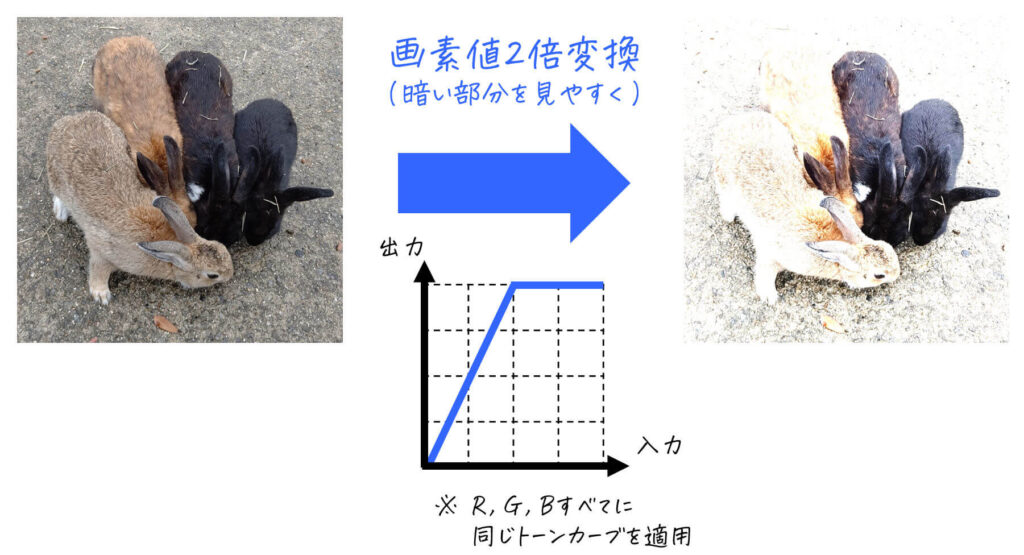
ただし、計算結果 \( kx \) が255を超える場合は出力画素値 \( y \) が255を超えず、255でとどまる点に要注意です[2]余談ですが、画素値255オーバーしていて画像が白くなる現象のことを、「白飛びする」とか「サチる」などと呼ぶことがあります。。
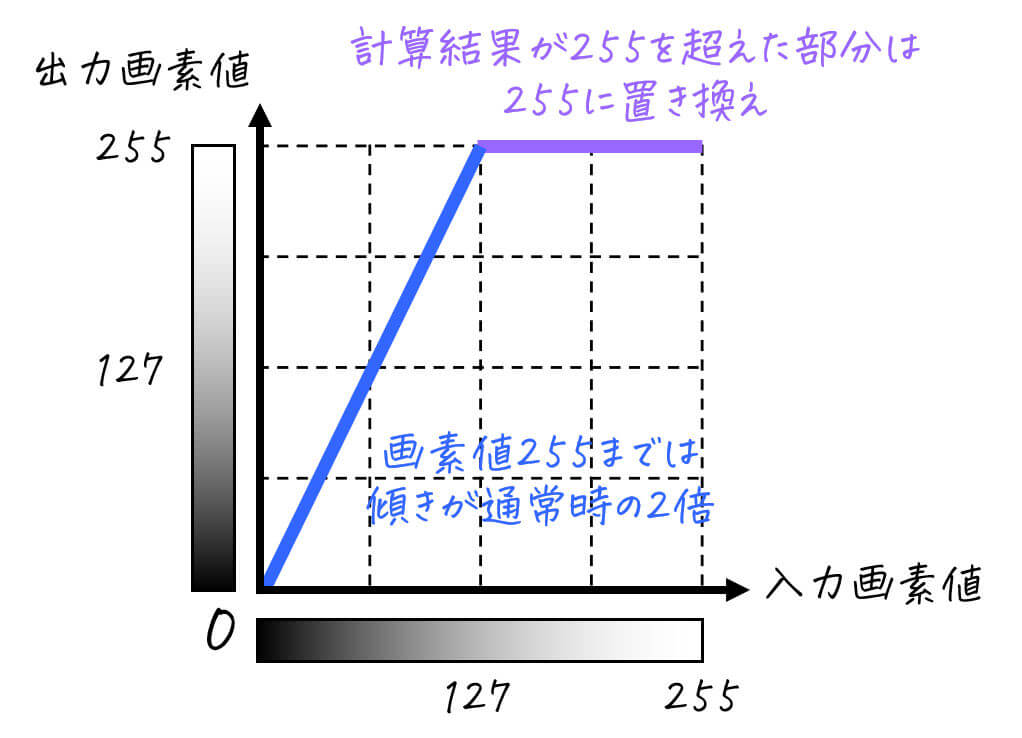
(1-b) 画素値をk倍 (k < 1)
\( k \) に1より小さい値を入れると、元の画像よりも暗くなります。
例) \( k = 1/2 \)、つまり画素値を1/2倍する変換 \( y = \frac{1}{2} x \)
[グレースケール画像]
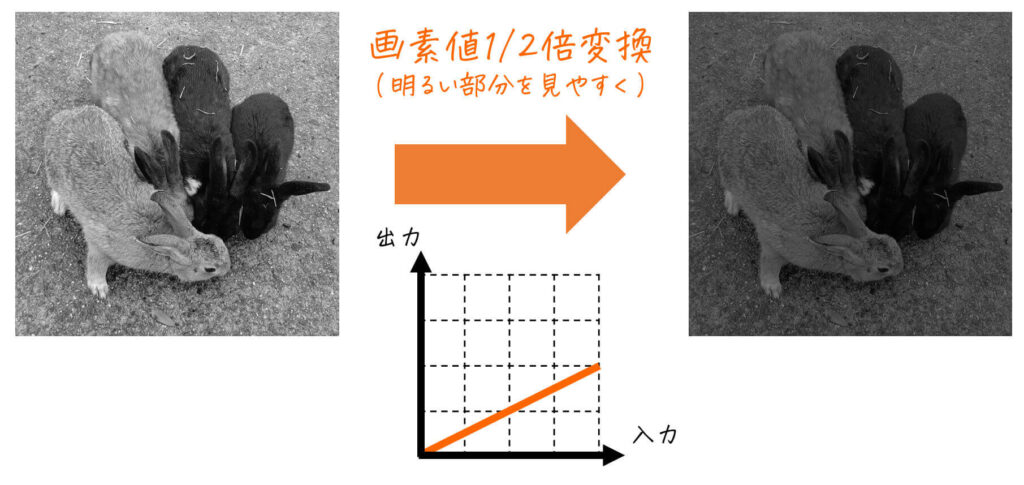
[カラー画像]
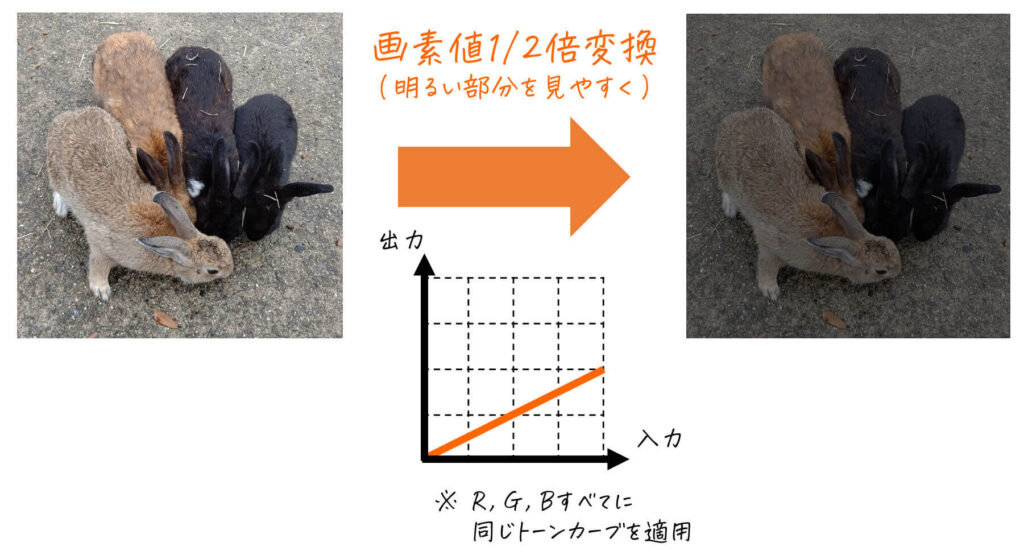
(1-c) ソースコード
入力画像 input_img、倍率 k を引数とすることで、折れ線型トーンカーブを適用した画像を返す関数を紹介します。
[Python]
import numpy as np
def polygonalTone(input_img,k):
return np.dot(k,input_img) # np.dot は画素値が255を超える画素を自動的に255に置き換えてくれる
[MATLAB]
function output_img = polygonalTone(input_img,k)
% MATLABではオーバーフローはそのまま255となるので、特別な対策は不要
output_img = k * input_img;
end
折れ線型トーンカーブまとめ
(2) 初期値付き折れ線型トーンカーブ
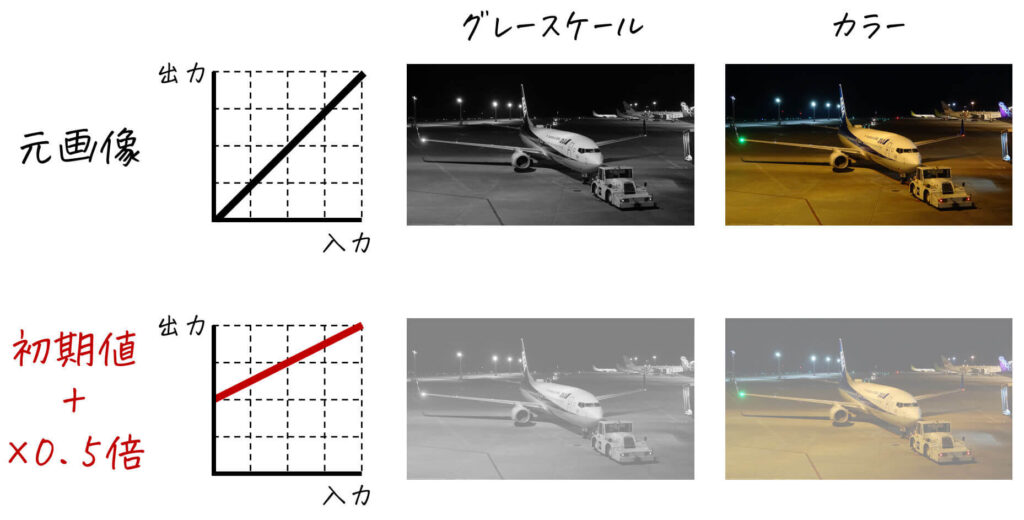
単純に入力画素値を \( k \) 倍する処理に加えて、一定値 \( a \) を出力画素値に加えます。
式で書くと、\[
y = kx + a
\]ですね。(入力画素値: \( x \), 出力画素値: \( y \))
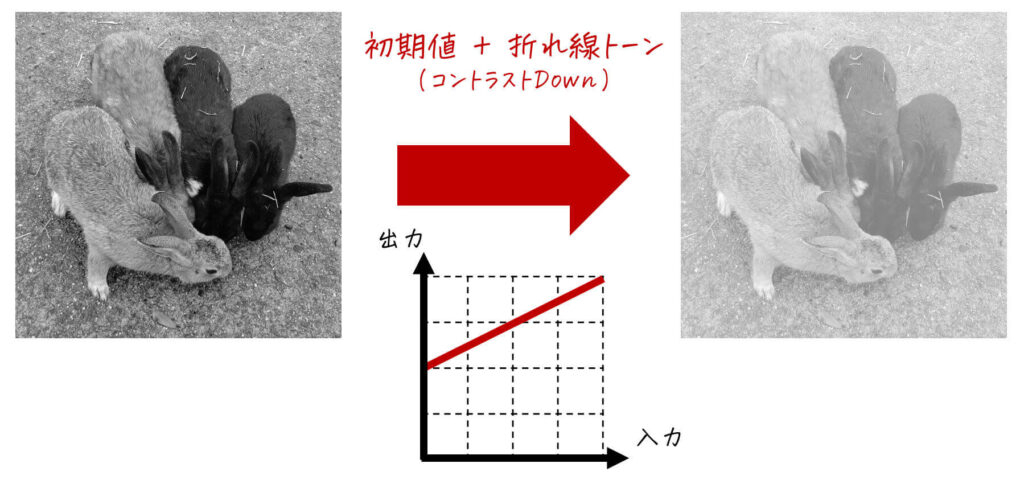
例) 初期値 \( a = 127 \)、\( k = 1/2 \) のとき → コントラストを下げた画像が出力される
[グレースケール画像]
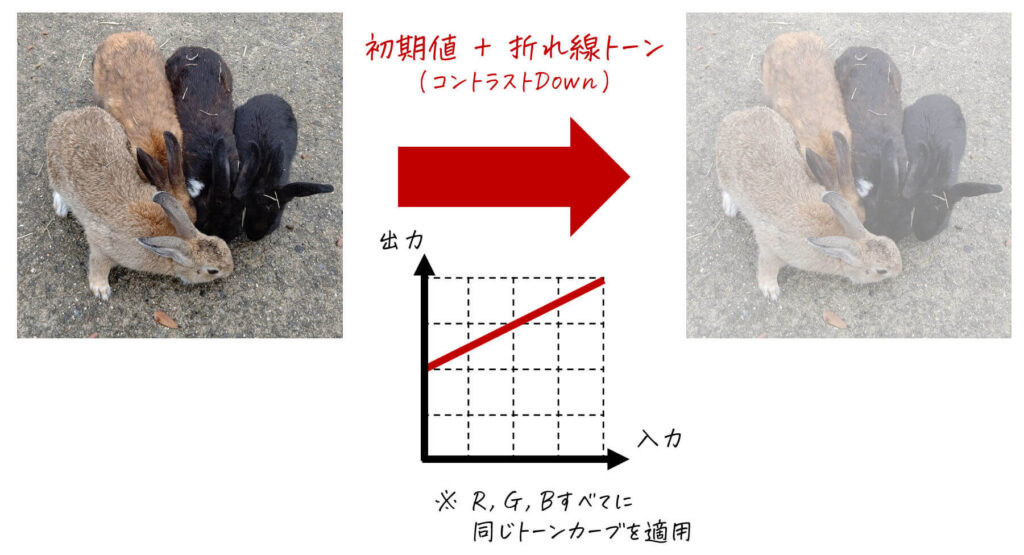
[カラー画像]
ソースコード
入力画像 input_img、倍率 k 、初期値 a を引数とすることで、初期値付き折れ線型トーンカーブを適用した画像を返す関数を紹介します。
[Python]
import numpy as np
def polygonalToneWithIni(input_img,k,a):
return a + np.dot(k,input_img) # np.dot は画素値が255を超える画素を自動的に255に置き換えてくれる
[MATLAB]
function output_img = polygonalToneWithIni(input_img,k,a)
output_img = a + k * input_img;
end
初期値付き折れ線型トーンカーブまとめ
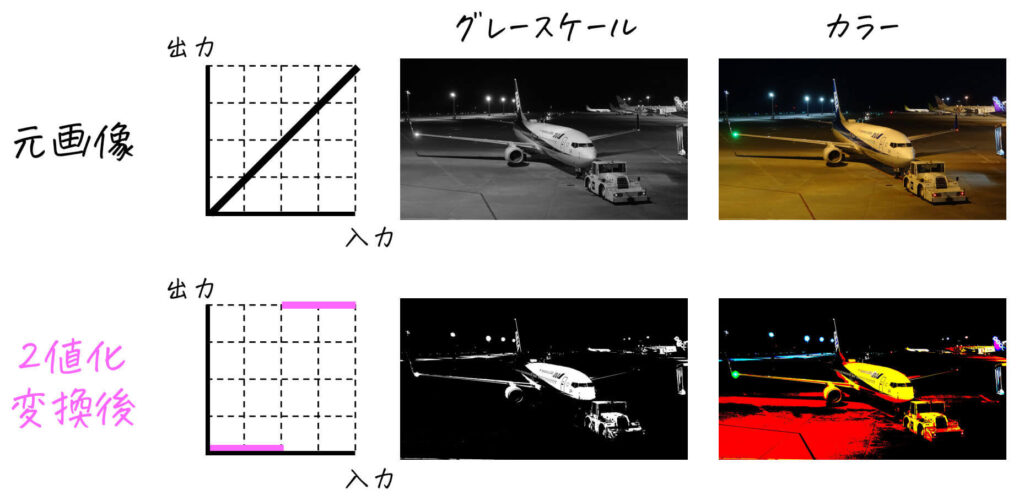
(3) 2値化
画像内の明るい部分(画素)を真っ白(画素値255) に、暗い部分(画素)を真っ黒(画素値0) に変換する処理です。言い換えると、画像内の各画素を「真っ白」or「真っ黒」の2色にする処理と言えます。
数式で書くと、\[
y = \left\{ \begin{array}{cc} 255 & ( x \geqq a ) \\ 0 & ( x < a ) \end{array} \right.
\]となります。(※ \( a \) はしきい値、入力画素値: \( x \)、出力画素値: \( y \))
例) 画素値128以上を白、128未満を黒とする場合 \( a = 128 \)
[グレースケール画像の場合]
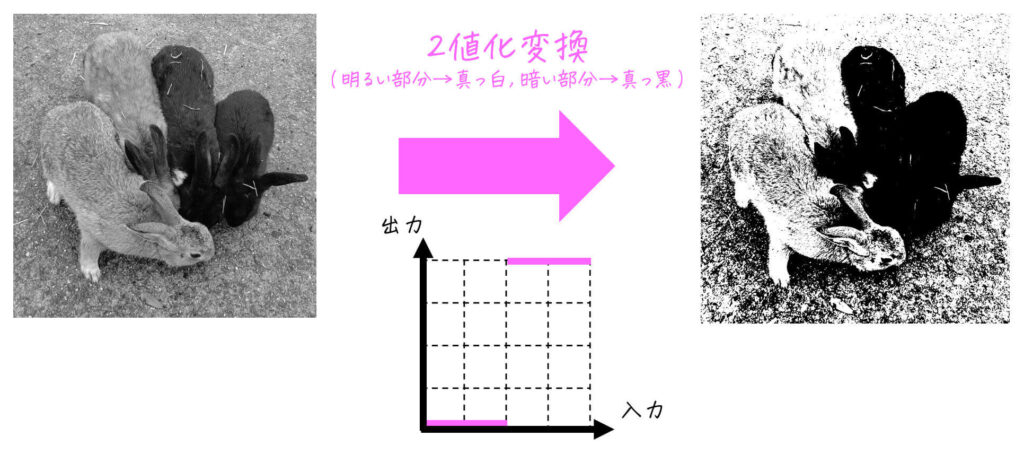
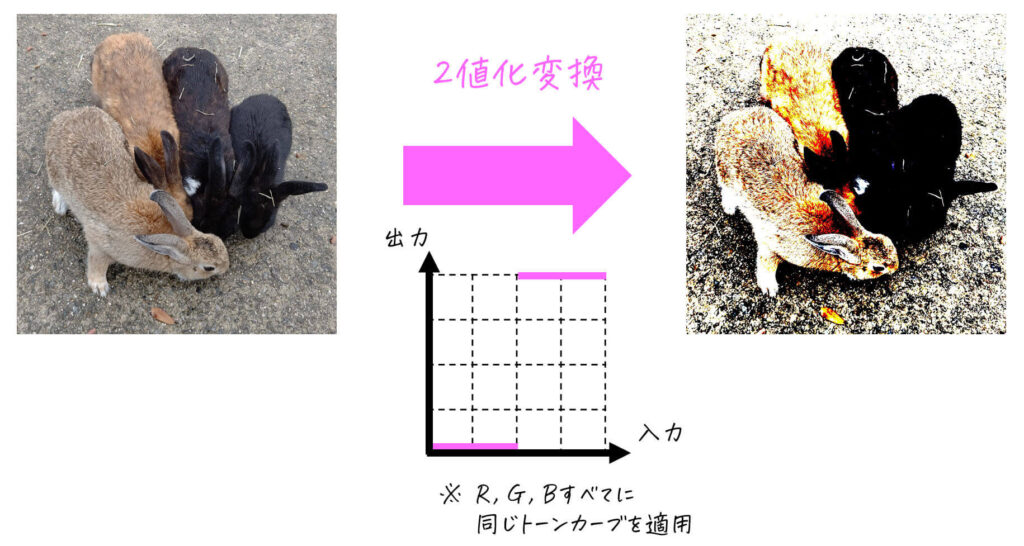
[カラー画像の場合]
R成分, G成分, B成分それぞれに2値化判定を行います[3]例えば、R成分の画素値が 200, G成分の画素値が150, B成分の画素値が100であれば、R, … Continue reading。
ソースコード
入力画像 input_img、しきい値 threshold を引数とすることで、2値化を適用した画像を返す関数のソースコードです。
[Python]
import numpy as np
def binTone(input_img,threshold):
# しきい値 threshold 以上を真っ白(画素値255)、しきい値未満を真っ黒(画素値0)とする
return np.where(input_img >= threshold, 255, 0)
[MATLAB]
function output_img = binTone(input_img,threshold)
output_img = (input_img >= 128) * 255;
end
2値化まとめ
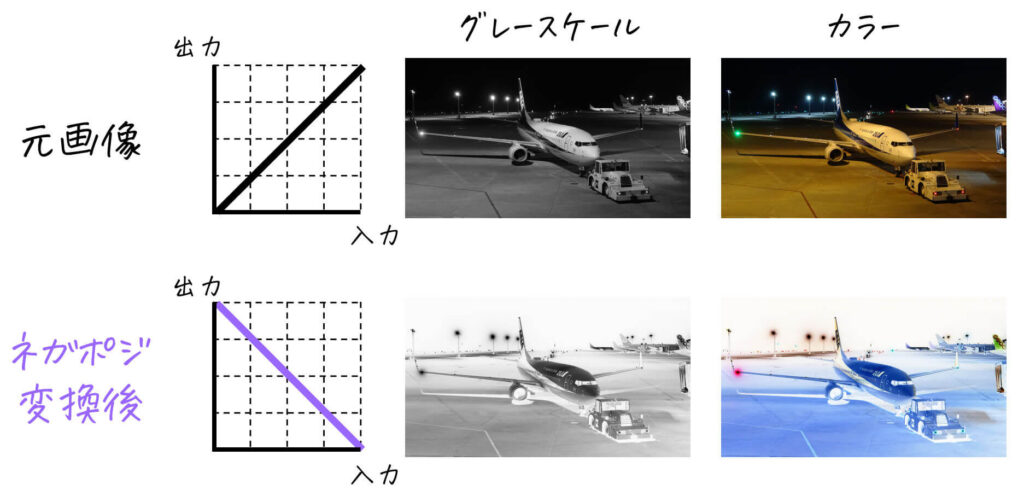
(4) ネガポジ変換
画像内の濃淡を入れ替える変換です。言い換えると、画像内の明るい画素を暗い画素に、暗い画素を明るい画素に変換する処理です。
数式で書くと、\[
y = 255 - x
\]です。(入力画素値: \( x \), 出力画素値: \( y \))
[グレースケール画像の場合]
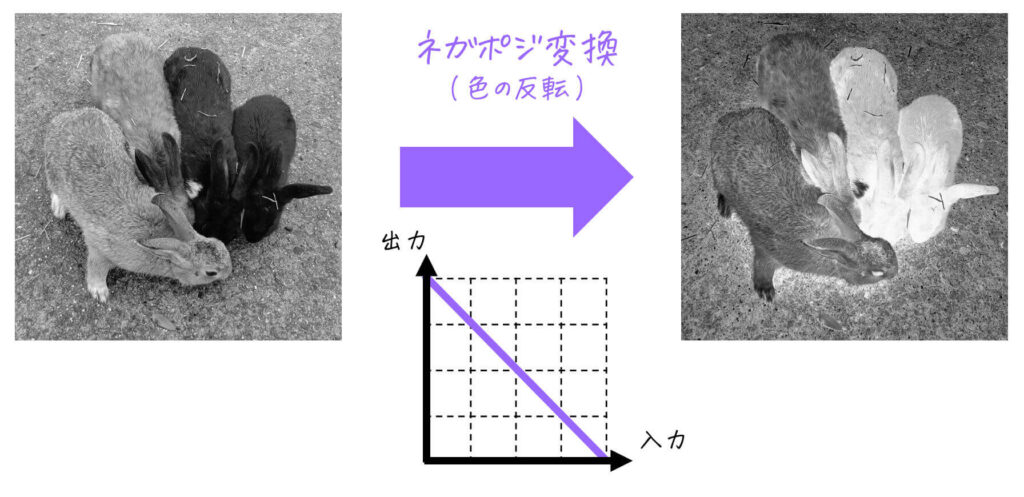
白うさぎは黒うさぎに、黒うさぎは白うさぎになりますね。
[カラー画像の場合]
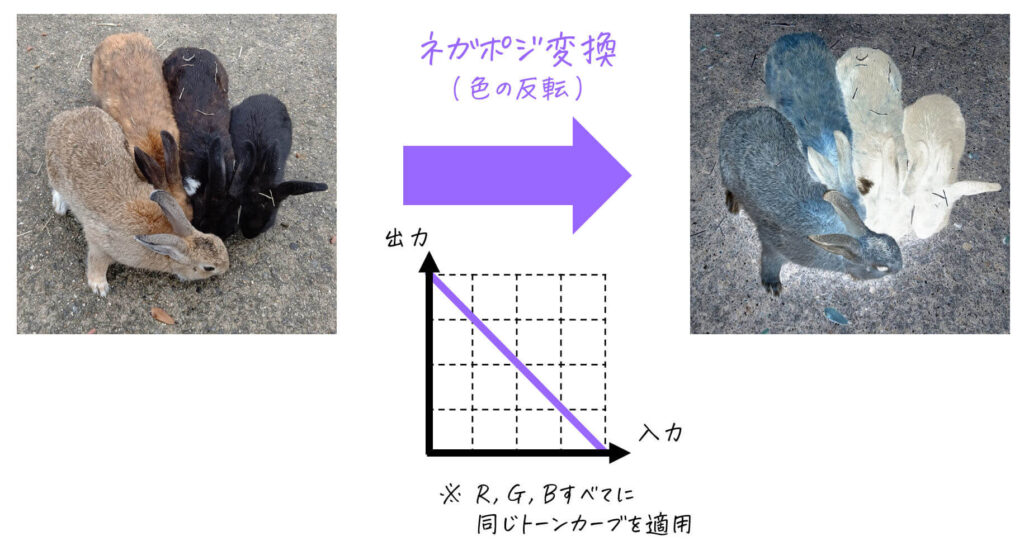
ソースコード
入力画像 input_img を引数とすることで、ネガポジ変換を適用した画像を返す関数のソースコードです。
[Python]
import numpy as np
def negaposiTone(input_img):
return 255 - input_img
[MATLAB]
function output_img = negaposiTone(input_img)
output_img = 255 - input_img;
end
ガンマ補正(変換)まとめ
4. 応用的なトーンカーブ [Python, MATLABコード付き]
先ほど(3章)よりも少し複雑なトーンカーブも見ていきましょう。
(1) ガンマ補正(変換)
(1-a) ガンマ変換とは
理論的には「画素値を \( n \) 倍にすると、ディスプレイ(などの出力装置)の明るさも \( n \) 倍に変化」します。(この状態のことをリニアと呼びます。)
しかし、実際の出力装置(ディスプレイなど)は必ずしも理論的な変化をするとは限りません。
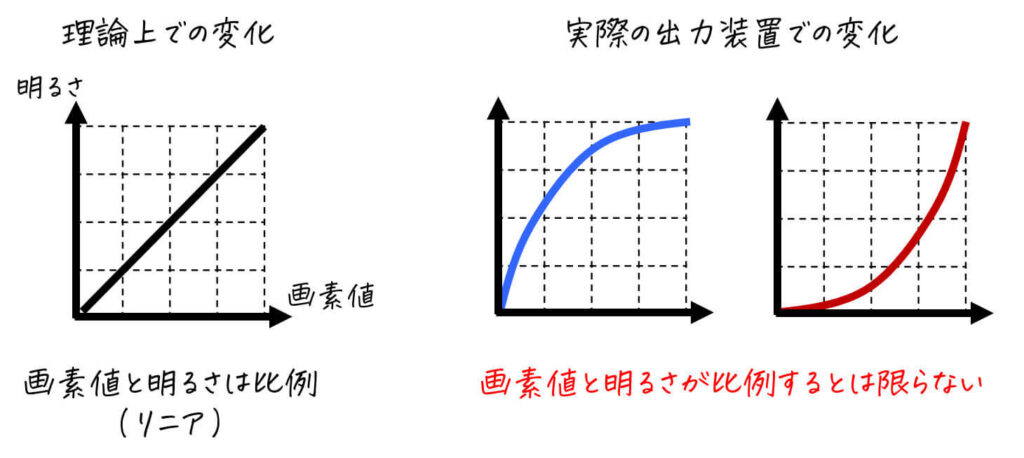
そこで、実際の出力装置をリニアに近づけるための処理を行います。この処理のことをガンマ補正と呼びます。
ガンマ補正では、入力画素値 \( x \)、出力画素値 \( y \) に対して\[
y = 255 \left( \frac{x}{255} \right)^{\gamma}
\]の処理を与えます[4]指数部分を \( \frac{1}{ \gamma } \) とし、\[y = 255 \left( \frac{x}{255} \right)^{ \frac{1}{\gamma} }\]と表記することも多いです。というのも、元画像 \( y \) … Continue reading
(※ \( \gamma \) は出力装置ごとに最も適した値を設定する)
(1-b) ガンマ変換と明るさの関係
実際にガンマ値 \( \gamma \) を変化させながらガンマ補正を行うと、どんな画像が生成できるかを見てみましょう。
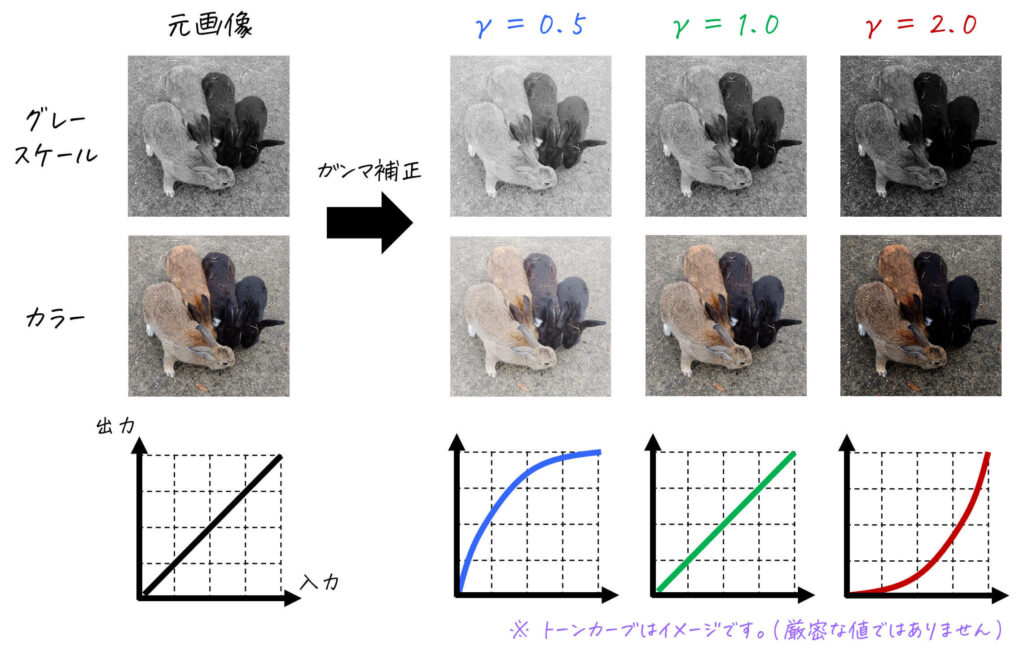
具体的には、
- ガンマ値 \( \gamma > 1 \) → 元の画像より暗くなる変換
- ガンマ値 \( \gamma = 1 \) → 元の画像と全く同じ変換(明るさ変化なし)
- ガンマ値 \( \gamma < 1 \) → 元の画像より明るくなる変換
となります[5]ガンマ補正を逆数\[y = 255 \left( \frac{x}{255} \right)^{ \frac{1}{\gamma} }\] で定義した場合は、 ガンマ値 \( \gamma > 1 \) → … Continue reading。
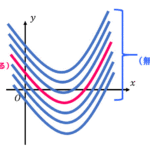
(1-c) 様々なガンマ値とトーンカーブ
ガンマ値を 0.25 ~ 4 まで変化させるとトーンカーブはどのように変化するかを、実際にグラフを描画することで確認してみましょう。
各グラフのガンマ値は下の通りです。
- 紫 → \( \gamma = 0.25 \)
- 青 → \( \gamma = 0.50 \)
- 緑 → \( \gamma = 1.00 \)
- 黄 → \( \gamma = 2.00 \)
- 赤 → \( \gamma = 4.00 \)
(1-d) ソースコード紹介
入力画像 input_img, およびガンマ値 gamma を引数とすることで、ガンマ変換を行う関数です。
※ 途中の計算で小数が出てくるため、いったん計算結果を小数で出してから整数型(uint8)に変換しています。
[Python]
import numpy as np
def gammaTone(input_img,gamma):
output_float = 255 * np.power(input_img / 255, gamma) # 計算結果をいったん実数型(float)で保持
return output_float.astype(np.uint8)
[MATLAB]
function output_img = gammaTone(input_img,gamma)
output_double = 255 * power(double(input_img) / 255,gamma); % 計算結果をいったん実数型(double)で保持
output_img = uint8(output_double);
end
ガンマ補正まとめ
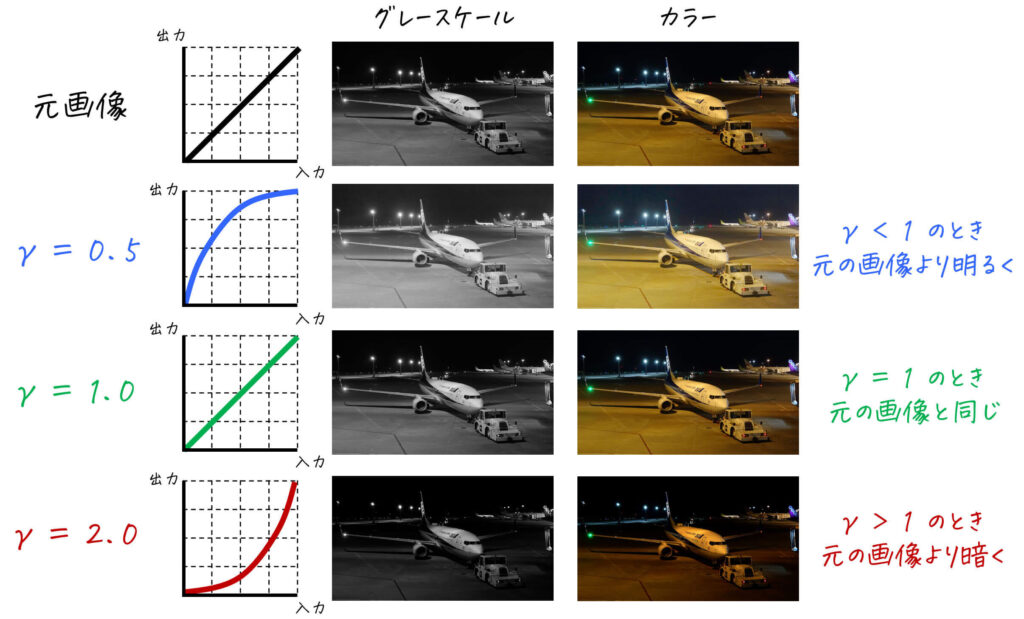
(2) S字トーンカーブ変換
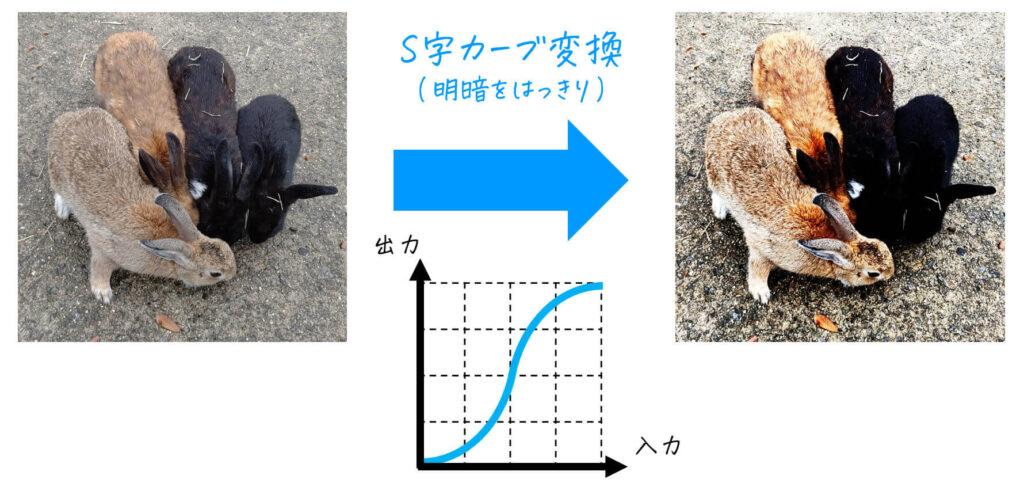
下のように、S字カーブを描くトーンカーブを用いて変換を行うと、コントラストが高くなった画像を出力することができます。
数式でS字カーブを描くためには\[
y = \frac{255}{2} \left\{ 1 - \cos \left( \frac{\pi}{255} x \right) \right\}
\]のように三角関数を使う方法や、ロジスティック方程式\[
y = \frac{255}{1 + ae^{ -b \left( x - \frac{255}{2} \right) } }
\]を使う方法があります[6] … Continue reading。(ただし \( a > 0 \), \( b > 0 \))
[グレースケール画像]
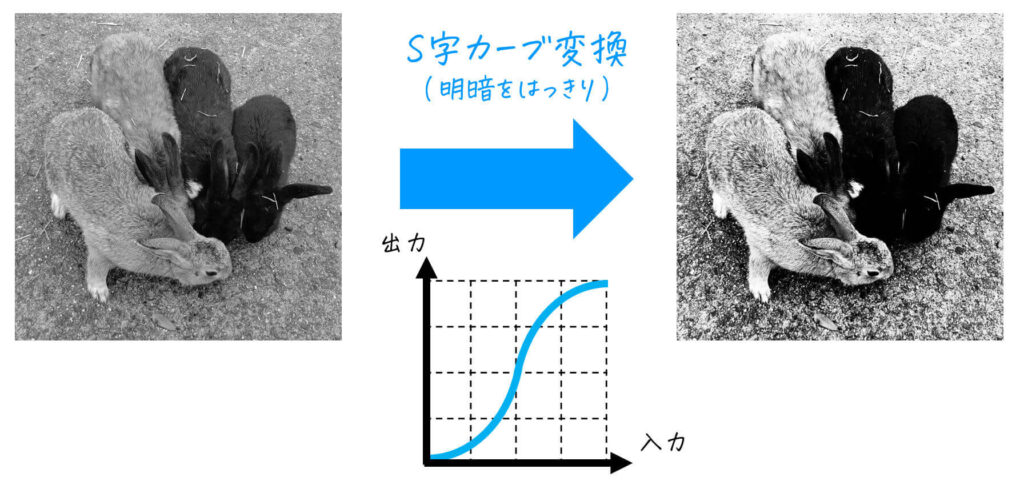
[カラー画像]
ソースコード
入力画像 input_img を引数とすることで、S字変換を適用した画像を返す関数のソースコードです。(ロジスティック方程式を利用しました)
※ 途中の計算で小数が出てくるため、いったん計算結果を小数で出してから整数型(uint8)に変換しています。
[Python]
import numpy as np
def sigmoidTone(input_img):
output_float = 255 / (1 + np.exp(-0.05 * (input_img - 127.5) ) ) # 計算結果をいったん実数型(float)で保持
return output_float.astype(np.uint8)
[MATLAB]
function output_img = sigmoidTone(input_img)
output_double = 255 ./ (1 * exp(-0.05 * (double(input_img) - 127.5))); % 計算結果をいったん実数型(double)で保持
output_img = uint8(output_double);
end
S字カーブ変換まとめ
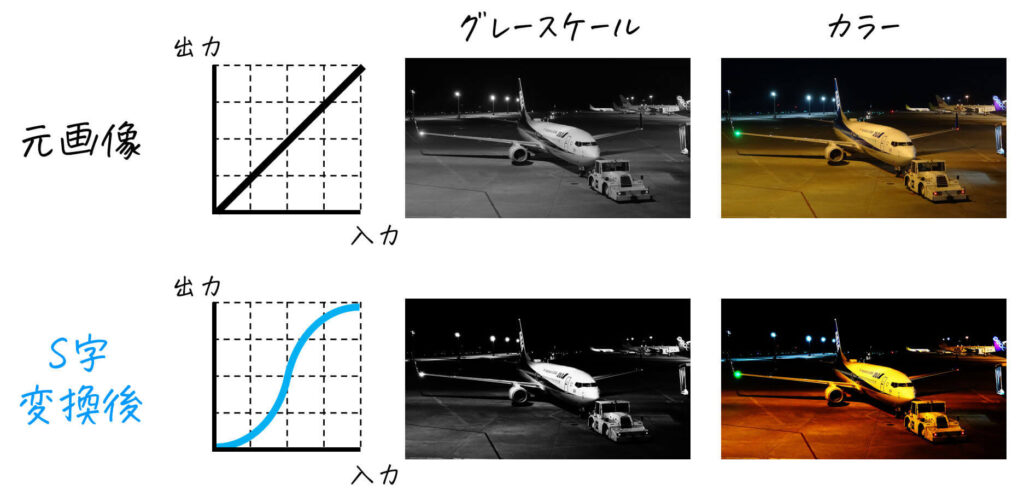
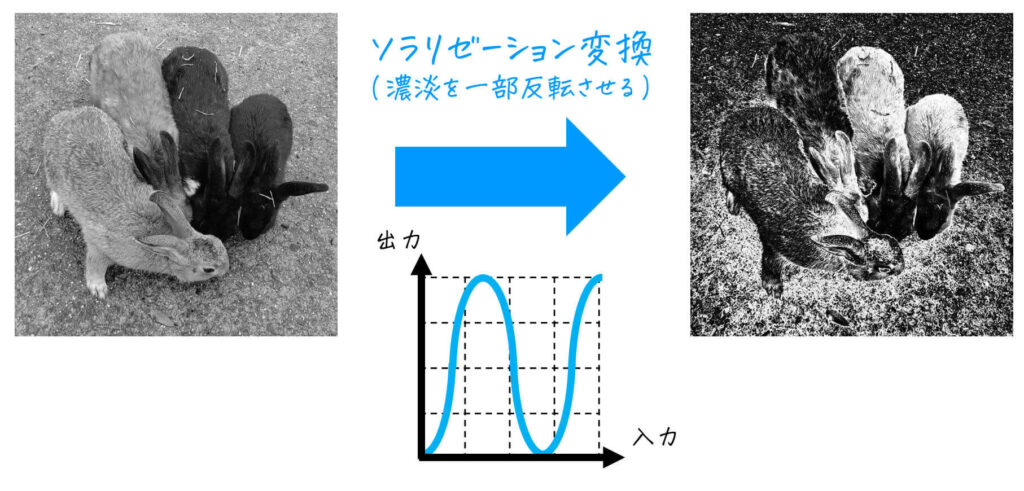
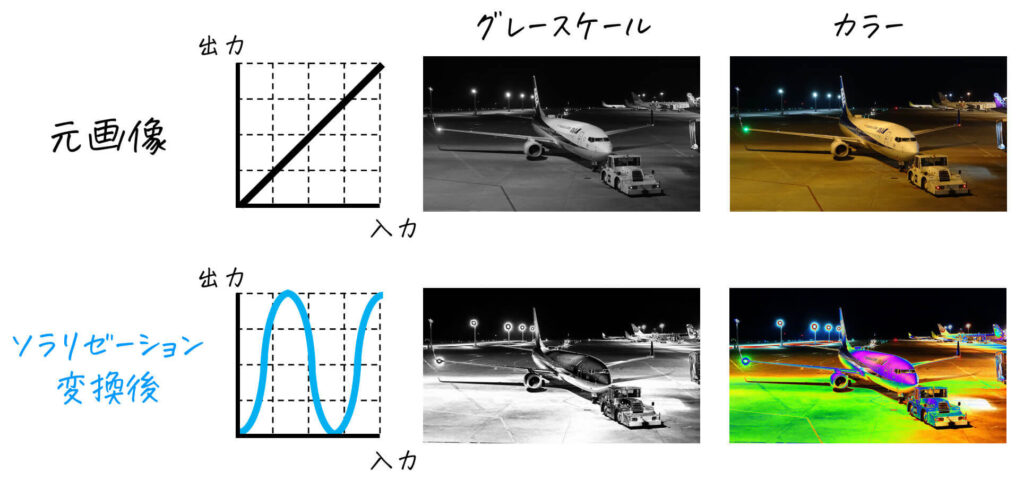
(3) ソラリゼーション変換
濃淡の一部分を反転することで、ネガとポジが混ざり合った効果を持つ画像を生み出します。
数式では\[
y = \frac{255}{2} \left\{ 1 - \cos \left( \frac{3 \pi}{255} x \right) \right\}
\]のように三角関数を使うことで表現可能です[7]導出方法ですが、まず \( - \cos x \) の \( 0 \leqq x \leqq 3 \pi \) のグラフに着目します。あとは、このグラフの周期を \( 2 \pi \) から 170 に変換するように … Continue reading。
[グレースケール画像]
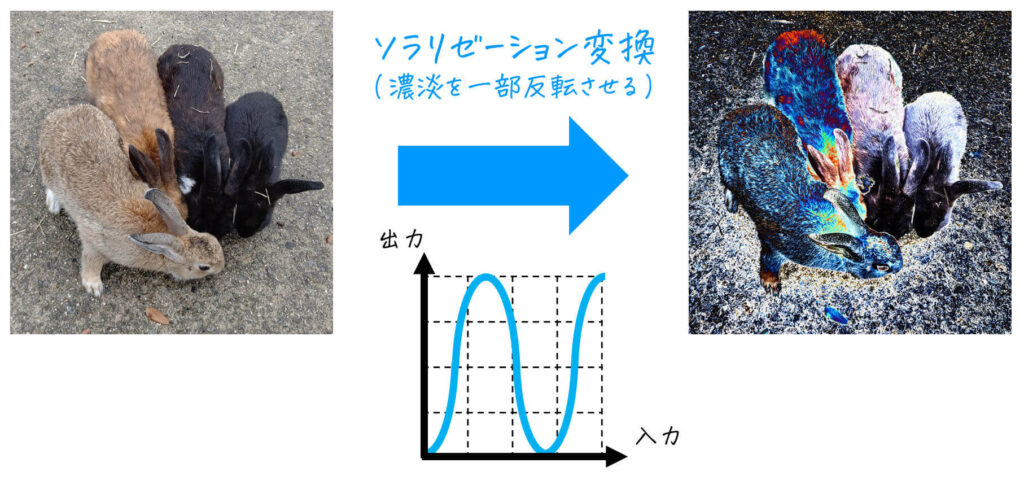
[カラー画像]
あら不思議。虹色のうさぎさんが出てきましたね。
ソースコード
入力画像 input_img を引数とすることで、ソラリゼーション変換を適用した画像を返す関数のソースコードです。
※ 途中の計算で小数が出てくるため、いったん計算結果を小数で出してから整数型(uint8)に変換しています。
[Python]
import numpy as np
import math
def solaTone(input_img):
output_float = 127.5 - 255 / 2 * np.cos(3 * math.pi / 255 * input_img)
return output_float.astype(np.uint8)
[MATLAB]
function output_img = solaTone(input_img)
output_double = 127.5 - 255 / 2 * cos(3 * pi / 255 * double(input_img)); % 計算結果をいったん実数型(double)で保持
output_img = uint8(output_double);
end
ソラリゼーション変換まとめ
5. カラー画像特有の画像処理 [Python, MATLABコード付き]
カラー画像では、全体のコントラストを変える画像処理の他にも、色を調整するという画像処理のテクニックがあります。
具体的には、R, G, Bのトーンカーブに対し、「カラー画像のR, G, Bのうちの一部にトーンカーブを適用し、色のバランスを変える」ということをします。
ただ文章で説明されるより、実際に例を見たほうが分かりやすいと思うので、実際に2パターンほど「カラー画像特有の画像処理テクニック」を見ていきましょう!
(1) 特定の色を強調する変換
特定の色を強調する場合は、強調したい色のトーンカーブに「折れ線型トーンカーブ \( k > 1 \)」を適用し、残りの成分には何もしません。
[適用するトーンカーブ]
例えば、赤色(R成分)を強める変換をしてみましょう。ここで、R成分に \( k = 1.2 \) の折れ線型トーンカーブを適用します。
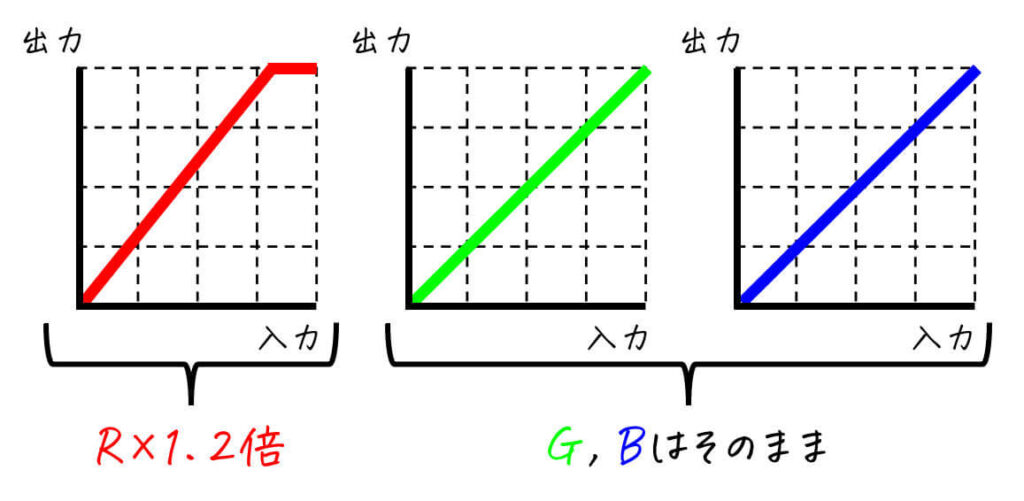
[変換結果]
赤色が強調された画像が得られましたね。

(2) 特定の色を弱める変換
今度は、特定の色を弱める変換を見てみましょう。
特定の色を弱める場合は、弱めたい色のトーンカーブに「折れ線型トーンカーブ \( k < 1 \)」を適用し、残りの成分には何もしません。
[適用するトーンカーブ]
例えば、青色(B成分)を弱める変換をしてみましょう。ここで、B成分に \( k = 0.8 \) の折れ線型トーンカーブを適用します。
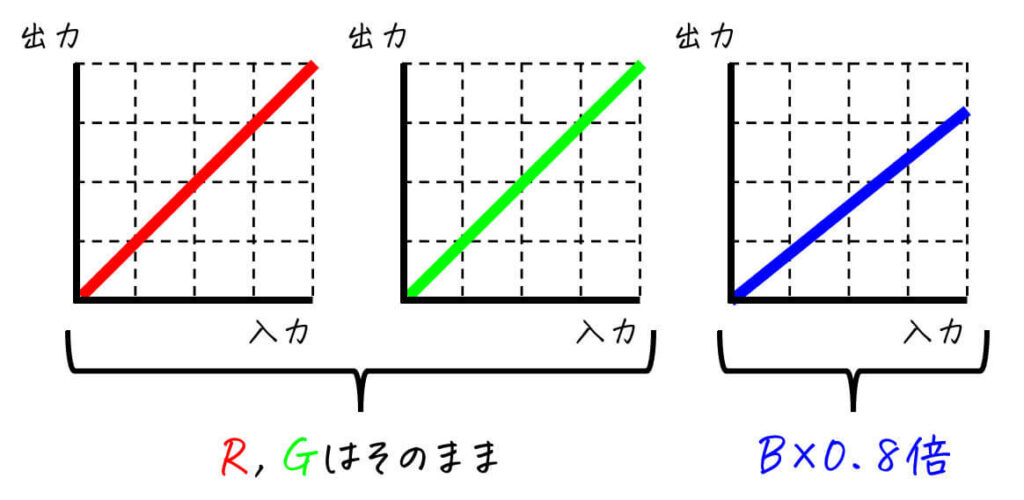
[変換結果]
青色が弱まった画像が得られましたね。言い換えると、赤色と緑色の度合いが高い画像が生成できましたね。

(3) ソースコード
入力画像 input_img, 成分の倍率 k 、色 color を引数とすることで、特定の色を強めたり弱めたりすることができる関数を紹介します。
※ 少し関数が複雑なので、使用例を付けております。
[Python]
import numpy as np
import cv2
# color -> (0,1,2,3) が (青,緑,赤,全色[明るさ調整]) に対応
def polygonalTone(input_img,k,color):
output_img = 1.0 * input_img # 1.0を掛けることでoutput_imgが255越えしても255でストップする
if color == 3:
output_img = np.dot(k,input_img)
else:
output_img[:,:,color] = np.dot(k,input_img[:,:,color])
return output_img
## 使用例
#画像読み込み
input_color = cv2.imread(INPUT_PATH)
# (1) 赤を強める [R x 1.2]
output_color = polygonalTone(input_color,1.2,2)
cv2.imwrite(OUTPUT_PATH,output_color)
# (2) 青を弱める [B x 0.8]
output_color = polygonalTone(input_color,0.8,0)
cv2.imwrite(OUTPUT_PATH + "color_sky2.jpg",output_color)
[MATLAB]
% color -> (1,2,3,4) が (赤,緑,青,全色[明るさ調整]) に対応
function output_img = polygonalToneColor(input_img,k,color)
output_img = input_img;
if color == 4
output_img = input_img * k;
else
output_img(:,:,color) = input_img(:,:,color) * k;
end
end
%% 使用例
% カラー画像読み込み
input_color = imread(INPUT_PATH);
%% 画像処理ここから
% (1) 赤を強める[R x 1.2]
output_color = polygonalToneColor(input_color,1.2,1);
imwrite(output_color,OUTPUT_PATH);
% (2) 青を弱める[B x 0.8]
output_color = polygonalToneColor(input_color,0.8,3);
imwrite(output_color,OUTPUT_PATH);
6. 実際にプログラムを動かして画像処理を体験しよう!
3~5章で各画像処理を行うための関数を説明してきましたが、やはり実際にプログラムを動かして画像処理を体験したいですよね。
そこで、こちらに「すぐに実行できる」ソースコードと実行方法を書いた説明を用意しました! 実際にプログラムを動かしてみたい方は是非ご覧ください!
7. 練習問題でおさらい!
それでは、ここまでの内容を練習問題で復習しましょう!
練習1. トーンカーブのおさらい [基本編]
つぎの(1)~(5)の変換が表すトーンカーブを、図1内の [トーンカーブの選択肢] から選び、①~⑥の番号で答えなさい。また、図2の「元画像」に対して(1)~(5)の変換を適用するとどのような画像が生成されるか。最も適切なものを図2内の [変換画像 (猫)] から選び、ア~カの記号で答えなさい。
(1) 画素値を2倍にする変換
(2) 画素値を1/2倍にする変換
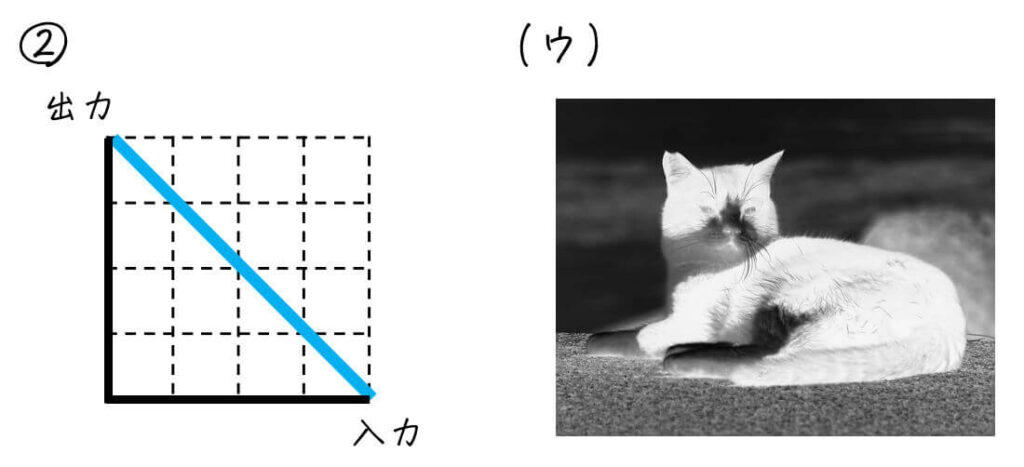
(3) ネガポジ変換
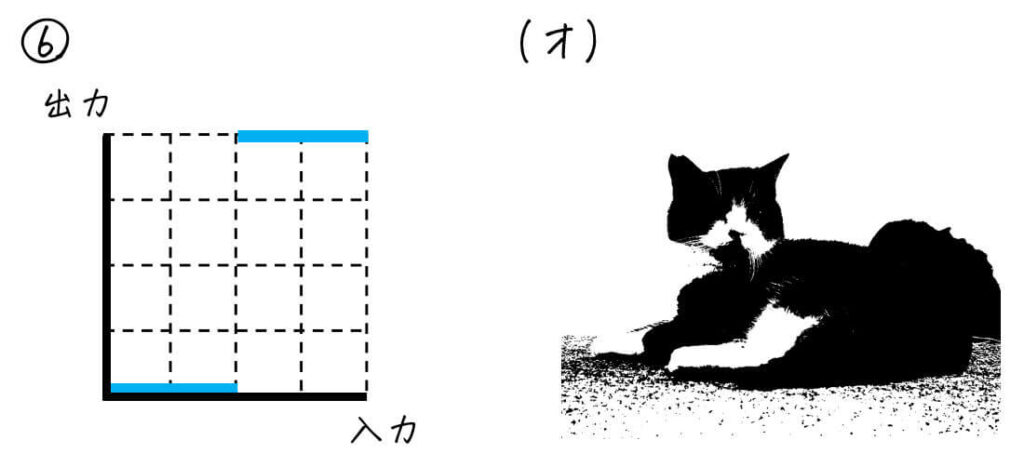
(4) 2値化変換
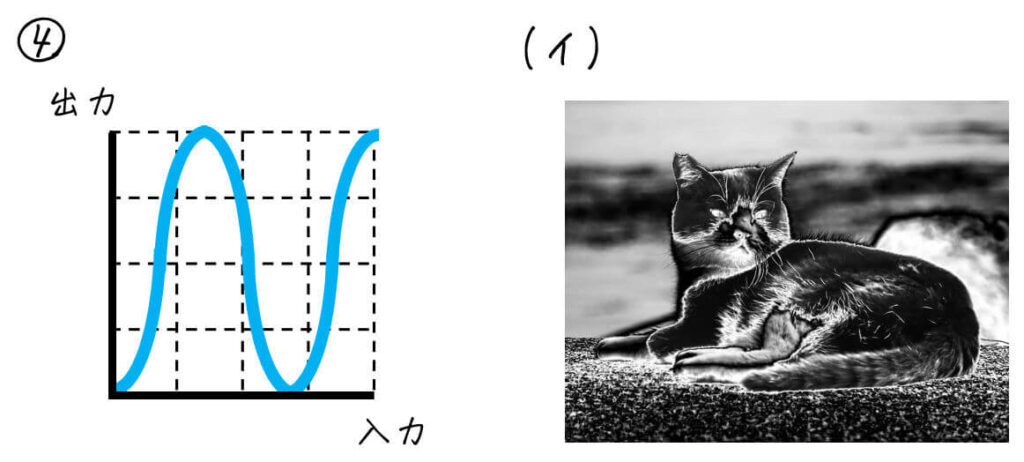
(5) ソラリゼーション
[トーンカーブの選択肢]
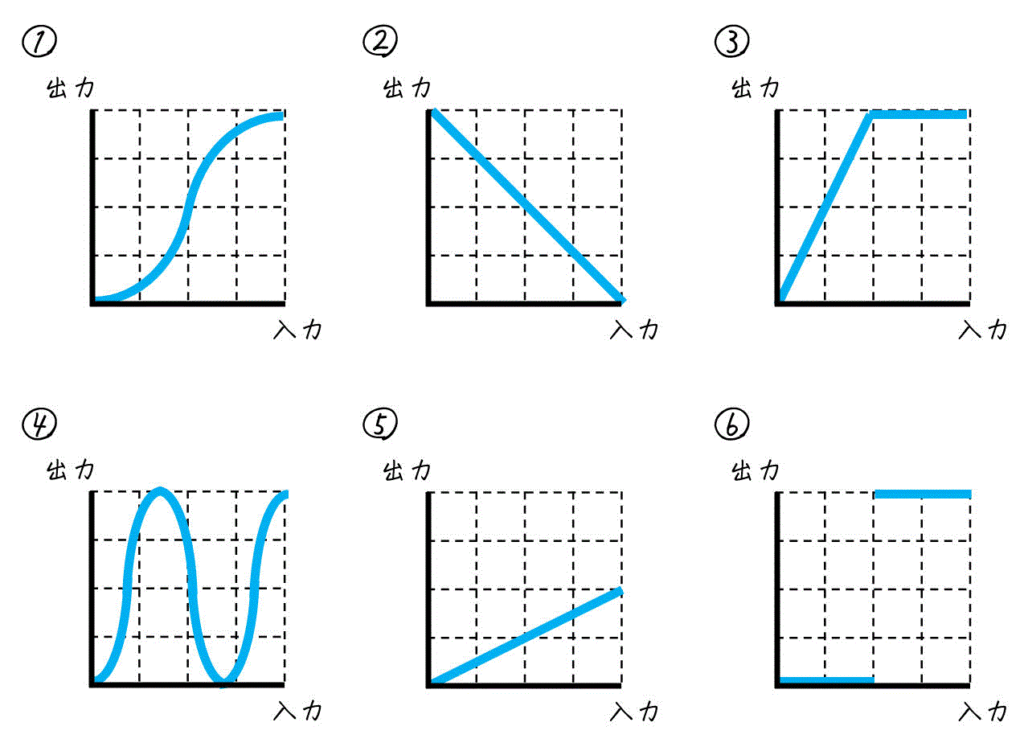
[画像の選択肢]

練習2. トーンカーブのおさらい [応用編]
つぎの①, ②, ③ が示す変換を ①→②→③ の順に適用した。
① 画素値を2倍にする変換
② 画素値を1/2倍にする変換
③ ネガポジ変換
このとき、「入力画素値」と「③適用後の出力画素値」の関係を表すトーンカーブを図3を参考にしながら答えなさい。
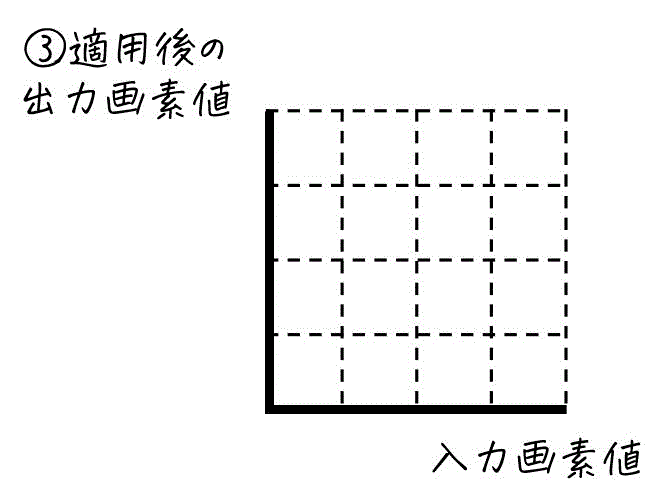
練習3. カラー画像とトーンカーブ
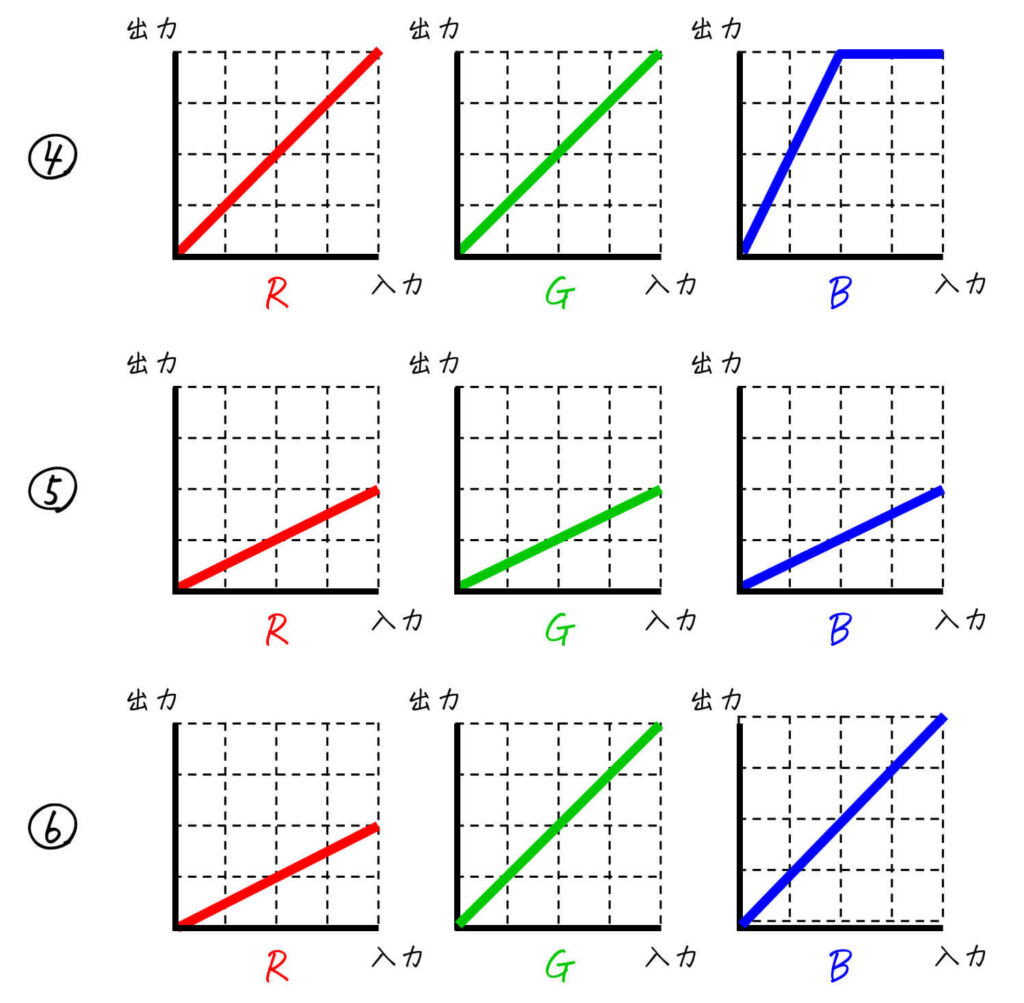
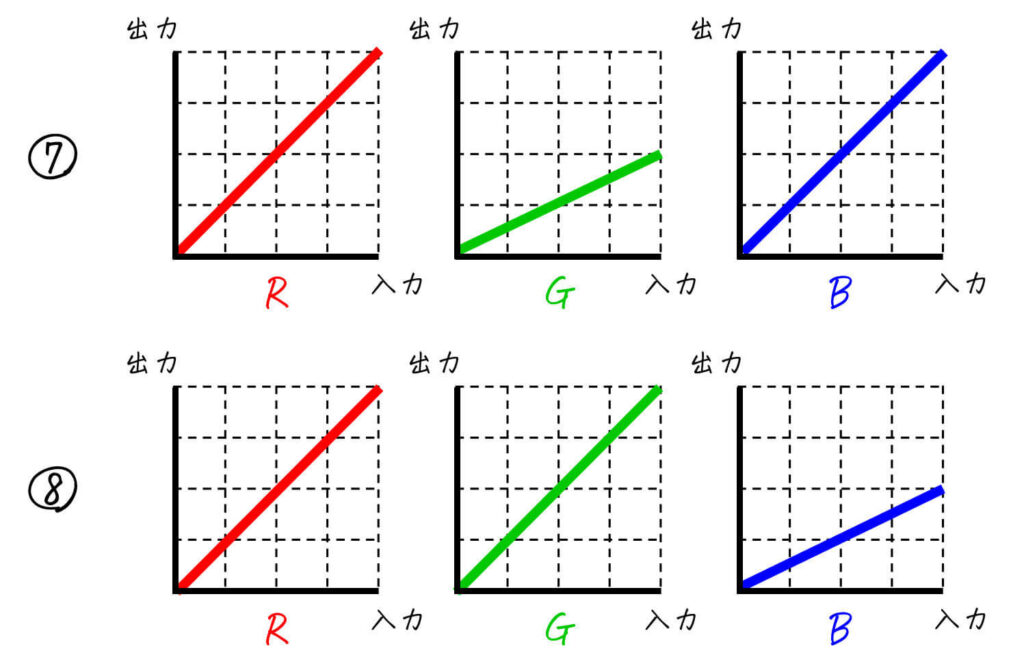
つぎのカラー画像に対して、(1)変換1, (2)変換2, (3)変換3 を適用し、新たなカラー画像を作成した。このとき、(1)~(3)の変換で用いたR, G, Bトーンカーブの組み合わせとして正しいものを [R, G, Bトーンカーブの組み合わせ] 内の①~⑧から1つ選び、番号で答えなさい。

[R, G, Bトーンカーブの組み合わせ]
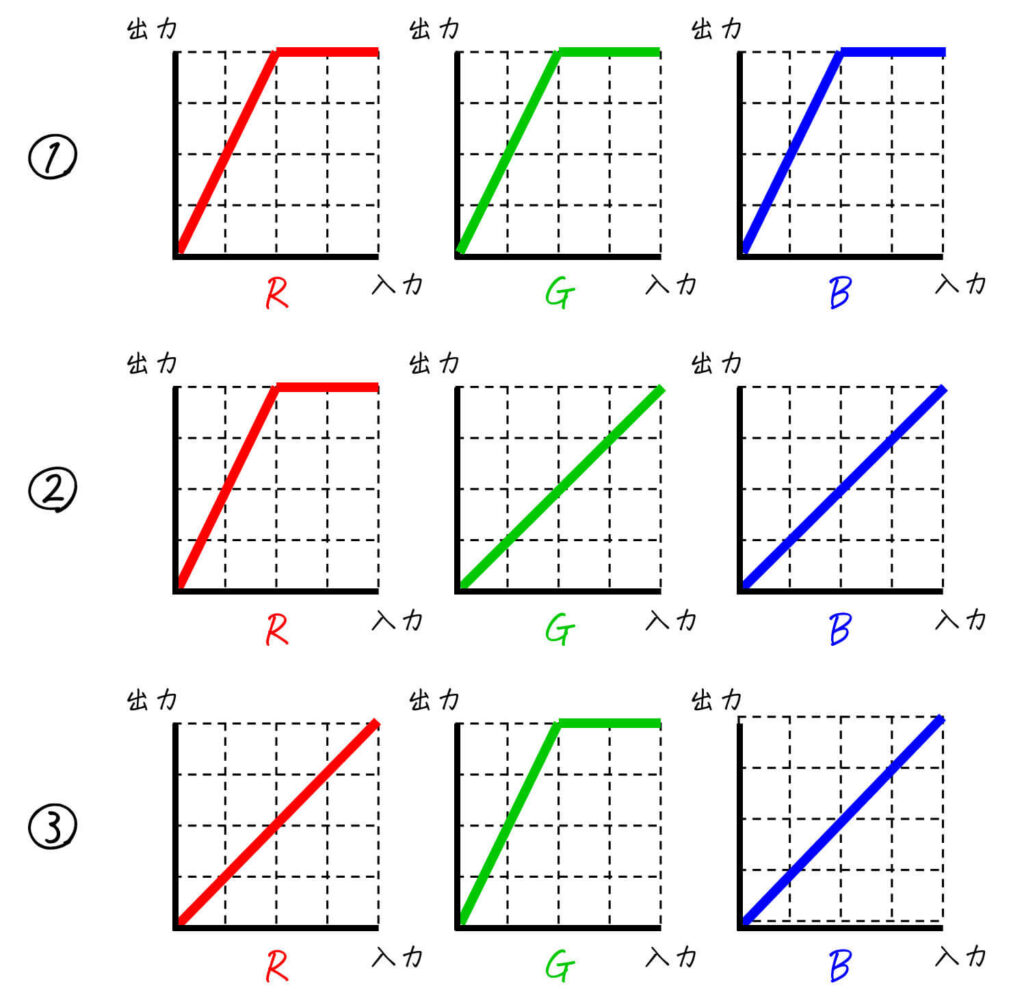
8. 練習問題の答え
解答1. トーンカーブのおさらい [基本編]
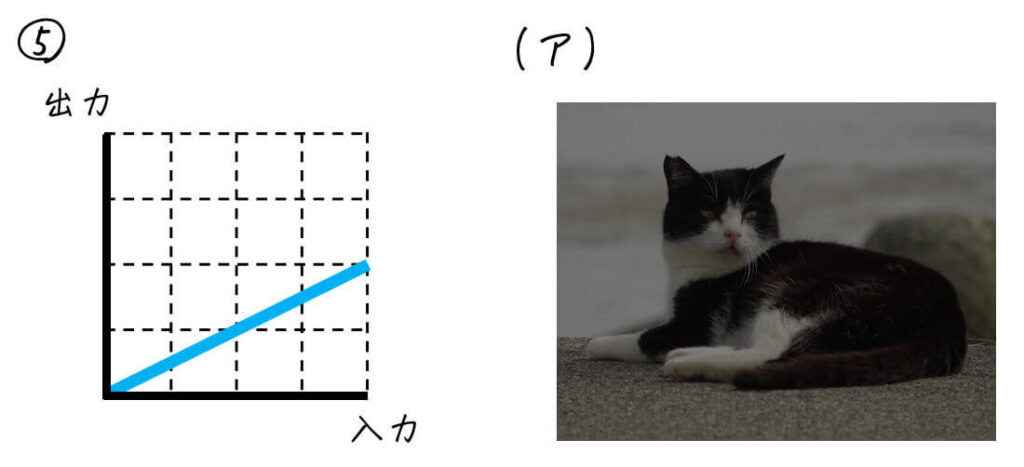
(1) 画素値を2倍にする変換
全体的に明るくなっている写真を選べばOK。
画素値を明るくすると、真っ白な画素(画素値255)が出てくるのも (エ) を選ぶ決め手かも。
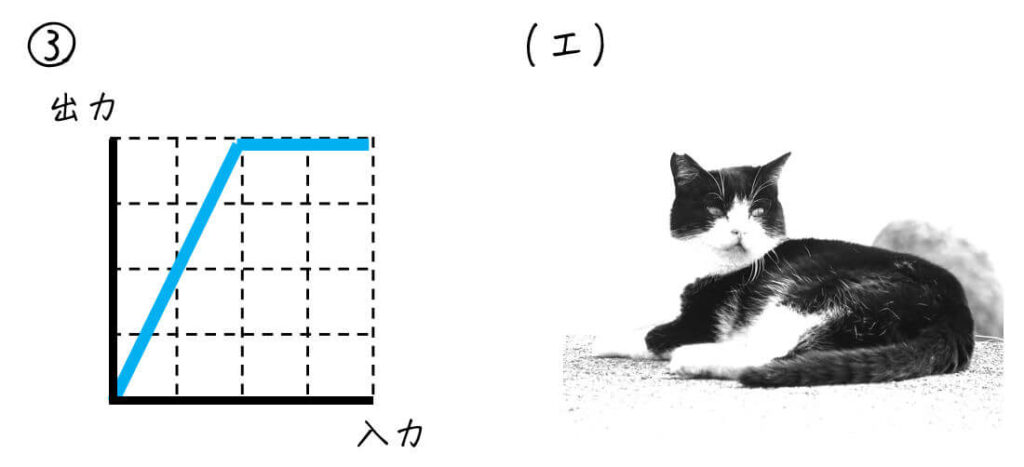
(2) 画素値を1/2倍にする変換
全体的に暗くなっている写真を選べばOK。
(3) ネガポジ変換
白黒が完全に入れ替わっている(黒猫が白猫になっている)画像は (ウ) 以外にない。
(4) 2値化変換
(オ) 以外の画像には、「真っ黒」or「真っ白」ではない部分があるので2値化変換ではない。
(5) ソラリゼーション
画像の一部分だけがネガポジ変換されているのがポイント
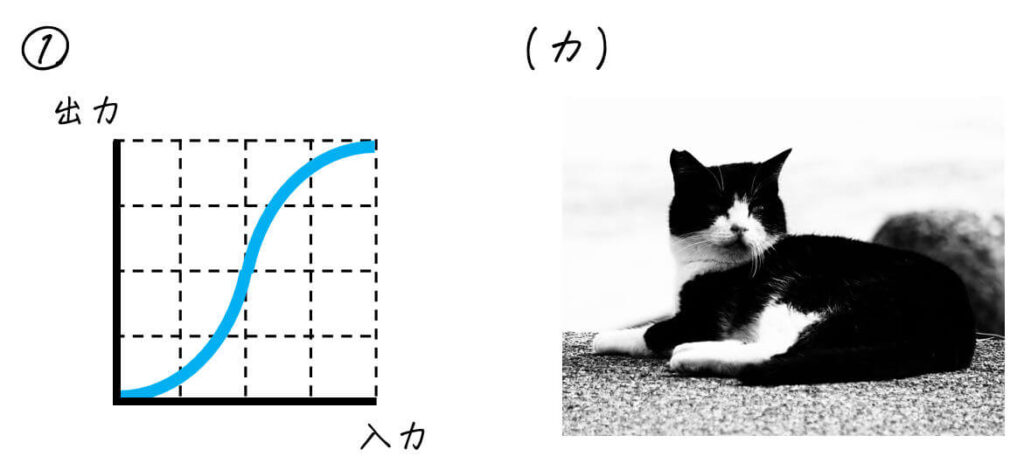
[おまけ] 残りものの画像は…?
(1)~(5)で選ばれなかった選択肢は、「S字カーブの変換」に対応しています。
変換の前後でコントラストが高くなっている(暗い部分と明るい部分がはっきりしている)のが特徴です。
解答2. トーンカーブのおさらい [応用編]
[解答]
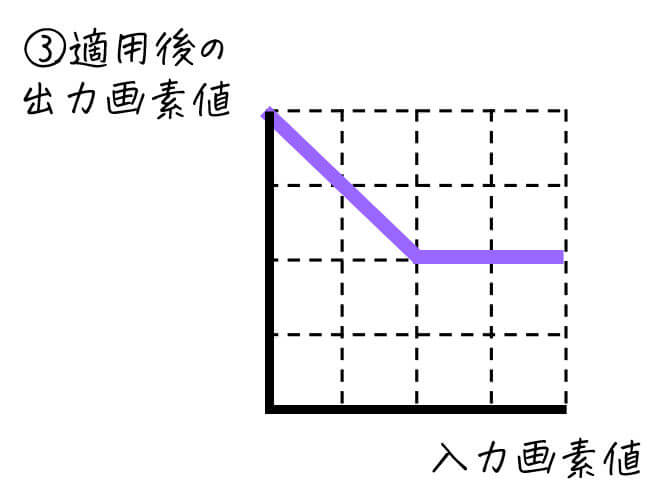
[変換過程]
元画像 → ①適用後
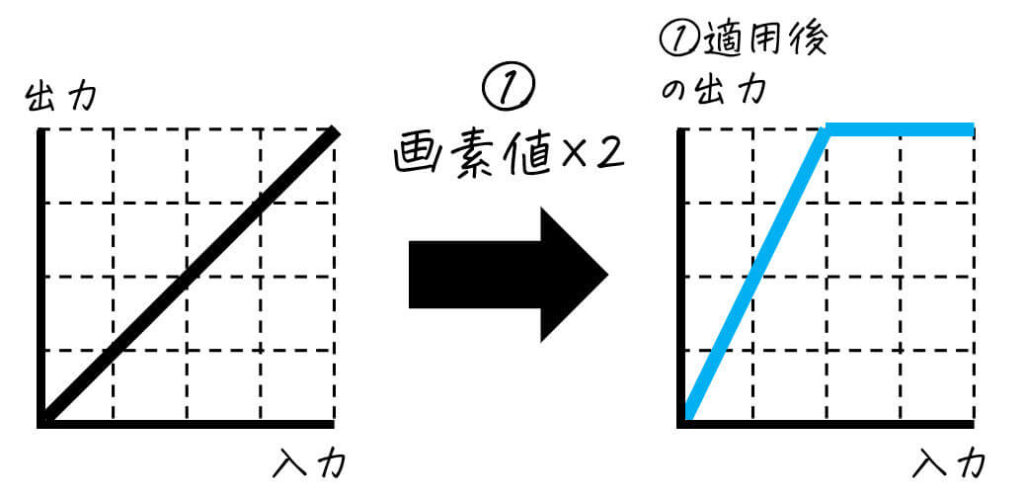
①適用後 → ②適用後
画素値を2倍にしてから1/2倍(0.5倍)に戻しても、画素値が255オーバーになった部分は元画像のようには戻らないのがポイント。
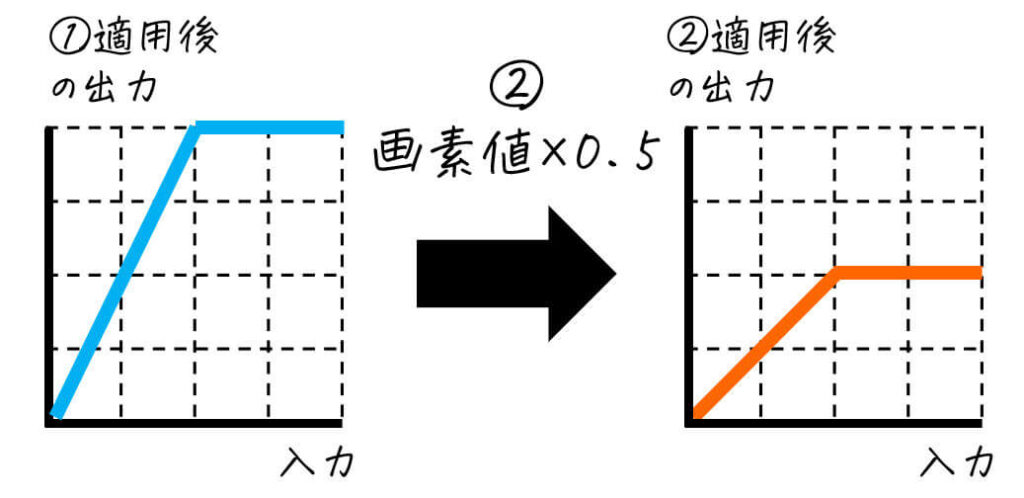
②適用後 → ③適用後(答え)
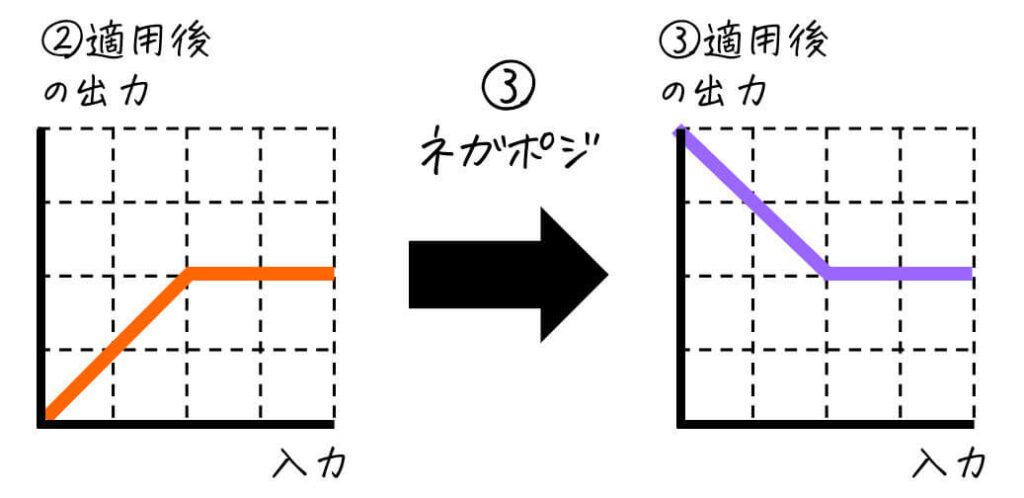
解答3. カラー画像とトーンカーブ
(1) 正解: ④
元画像に比べて、圧倒的に青色の成分が強くなっているのが決め手。
また、全体的に画像が明るくなったり暗くなったりしていないので、①や⑤のように全体の画素値を2倍(1/2倍)するトーンカーブではないのもポイント。

(2) 正解: ⑥
画像の赤部分がかなり消えていて、青と緑を中心とした画像になっているのが決め手。
また、(1)と同じく全体的に画像が明るくなったり暗くなったりしていないので、①や⑤のように全体の画素値を2倍(1/2倍)するトーンカーブではないのもポイント。

(3) 正解: ⑤
全体的に画像が暗くなっている点に着目。
また、(1)や(2)のように画像の色の度合いが変わっていないのもポイントの1つ。

9. さいごに
今回は、
- 画像処理の最も基本的な部分である「画素値を一定のルールに従っていじる」点の説明
- 画素値の変換で使う一定のルールを図でわかりやすく示した「トーンカーブ」について
- 代表的なトーンカーブの例
- カラー画像の画像処理の例
という点について説明し、最後に練習問題をおさらいしていきました。
次回は、まわりの画素にも着目した画像処理についてみていきましょう!
注釈
| ↑1 | 入力画像の画素値 \( x \) を2倍したものを出力画像の画素値 \( y \) とする、つまり \( y = 2x \) の変換を行うルール |
|---|---|
| ↑2 | 余談ですが、画素値255オーバーしていて画像が白くなる現象のことを、「白飛びする」とか「サチる」などと呼ぶことがあります。 |
| ↑3 | 例えば、R成分の画素値が 200, G成分の画素値が150, B成分の画素値が100であれば、R, G成分の画素値はしきい値の128以上なので、出力される画素値は255となる一方、B成分の画素値はしきい値の128未満なので、出力される画素値は0となります。(画素値はR: 255, G: 255, B: 0 となる) |
| ↑4 | 指数部分を \( \frac{1}{ \gamma } \) とし、\[ y = 255 \left( \frac{x}{255} \right)^{ \frac{1}{\gamma} } \]と表記することも多いです。というのも、元画像 \( y \) にガンマ値 \( \gamma \) がかかった状態\[ x =255 \left( \frac{y}{255} \right)^{ \gamma } \]を補正するためには、元のガンマ値の逆数 \( \frac{1}{ \gamma } \) でガンマ補正\[ y = 255 \left( \frac{x}{255} \right)^{ \frac{1}{\gamma} } \]をすればよいですね。なので、指数部分が \( \frac{1}{ \gamma } \) となっている上式を定義することで「ガンマ値 \( \gamma \) がかかった画像を補正する変換」と考えることができますね。 |
| ↑5 | ガンマ補正を逆数\[y = 255 \left( \frac{x}{255} \right)^{ \frac{1}{\gamma} }\] で定義した場合は、
と、明暗が反転するので注意が必要です。 |
| ↑6 | 微分方程式を習ったことがある人は、変数分離系について習うときに聞いたことがあるかもしれません。ロジスティック方程式についてより詳しく知りたい人はこちらの記事をご覧ください! |
| ↑7 | 導出方法ですが、まず \( - \cos x \) の \( 0 \leqq x \leqq 3 \pi \) のグラフに着目します。あとは、このグラフの周期を \( 2 \pi \) から 170 に変換するように \( x \) 部分を変化させ、さらに値域が \( -1 \leqq y \leqq 1 \) から \( 0 \leqq y \leqq 255 \) になるように変換させることでこのグラフを作成できます。\ |
関連広告・スポンサードリンク
![うさぎでもわかる画像処理 Part02 トーンカーブと画像処理 [Python・MATLABコード付き]](https://www.momoyama-usagi.com/wp-content/uploads/image_pro1-1.gif)