うさぎでもわかる複素解析　Part2　複素関数の微分可能性とコーシー・リーマンの関係式

こんにちは、ももやまです。

今回は複素関数の微分可能性、およびコーシー・リーマンの関係式についてまとめています。

 

 

前回の複素解析の記事（Part1）はこちら！

www.momoyama-usagi.com

複素数平面の復習なので複素数平面が理解できている方はスルーでOKです！

 

スポンサードリンク

１．複素関数の連続性・微分可能性

まずは、複素関数の連続性および微分可能性について実関数と比較しながらみていきましょう。

(1) 実関数の連属性・微分可能性

まずは実関数 \( f(x) \) における連続性と微分可能性について確認していきましょう。

 

実関数で連続性や微分可能性を確認する際には、正の方向（右側極限）と負の方向（左側極限）の2方向からそれぞれ極限を取り、2つの極限が一致するかを確かめることで連続性および微分可能性を確認することができます。

(2) 複素関数の連属性・微分可能性

では本題の複素関数における連続性、微分可能性についてみていきましょう。

 

実関数とほとんど同じように見えますよね。

しかし、複素関数で連続性や微分可能性を確認する際には、複素平面上の360°あらゆる方向から極限を取り、そのすべての極限が一致するかを確かめる必要があります。

そのため、実関数に比べて連続性や微分可能性を判定するのがめんどくさくなります。そこで使われるのが次の章で紹介するコーシー・リーマンの関係式です。

 

ちなみに複素関数 \( f(z) \) があらゆる複素平面上で微分可能なとき、 複素関数 \( f(z) \) は正則関数（正則である）といいます。

 

スポンサードリンク

２．コーシー・リーマンの関係式と微分可能性

複素関数がつぎに示すコーシーリーマンの関係式を満たすかを確認することで、上の極限を調べることなく複素関数が微分可能性かどうかを調べることができます。

 

このように、複素関数を実部と虚部に分け、それぞれを偏微分し、互いの偏微分の結果を比較することで複素関数が微分可能かを調べることができます。

（万が一偏微分が怪しいなって人はこちらで復習しましょう。）

 

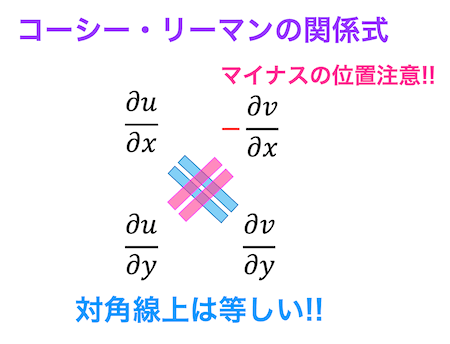
偏微分の結果をどのように比べてるのか上の式だと少しわかりにくいので下のように偏微分の結果を並べることを考えましょう。

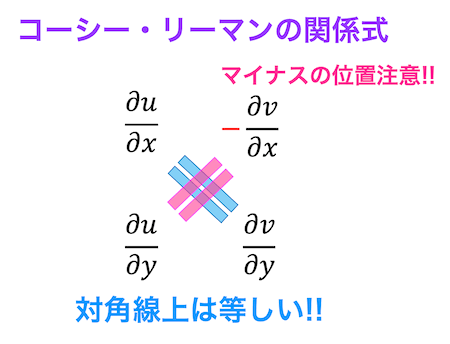
このとき、互いの対角線上の成分\[\frac{\partial u}{\partial x} = \frac{\partial v}{\partial y} , \ \ \ \frac{\partial u}{\partial y} = \color{red}{-} \frac{\partial v}{\partial x}  \]の値は等しいとき、コーシーリーマンの関係式が成立します。

 

またどっちにマイナスをつけるんだっけと解いている最中に迷うことがあるかもしれません。

でも簡単に覚える方法があります。2×2行列のサラスの公式*1を思い出してください。

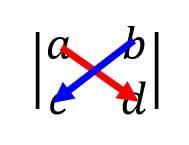
2次正方行列のサラスでは、赤色方向（左上→右下）の積から青色方向（左下→右上）の積の値を引きますね。サラスの公式の引く方向に対してマイナスが付くと考えるとコーシー・リーマンの公式でどっちにマイナスが来るかを覚えることができます。

 

では、簡単な例題を1問解いてみましょう。

例題

複素関数\[
f(z) = y - ix
\]が正則関数かどうかを判定しなさい。

解説

まずは複素関数 \( f(z) \) を実部 \( u(x,y) \) と虚部 \( v(x,y) \) に分離します。\[
u(x,y) = y , \ \ \ v(x,y) = -x
\]となりますね。

ここで、\[
\frac{\partial u}{\partial x} = 0 \ \ \ \ \ \frac{\partial v}{\partial x} = -1 \\
\frac{\partial u}{\partial y} = 1 \ \ \ \ \ \frac{\partial v}{\partial y} = 0 
\]となりますね。

よって、コーシー・リーマンの関係式\[
\frac{\partial u}{\partial x} = \frac{\partial v}{\partial y} , \ \ \ \  \frac{\partial u}{\partial y} = \color{red}{-} \frac{\partial v}{\partial x} 
\]を満たすので正則関数である。

 

スポンサードリンク

３．練習

では、3問ほど複素関数の微分可能性（正則かどうか）についての練習問題を解きましょう。

 

練習1

複素関数\[
f(z) = z^2
\]が正則関数かどうかを判定しなさい。

 

 

練習2

複素関数\[
f(z) = |z|^2
\]が正則関数かどうかを判定しなさい。

 

練習3

複素関数\[
f(z) = ax^2y - 2y^3 + (bxy^2 + cx^3) i
\]が正則関数となるような \( a \), \( b \), \( c \) の値を求めなさい。

 

 

練習4

正則な複素関数 \( f(z) \) の実部が \( x^2 - y^2 + 2x + 4y \) で表されるとき、複素関数 \( f(z) \) を求めなさい。

 

 

４．練習問題の答え

解答1

\[\begin{align*}
f(z) & = (x+yi)^2 \\ & = x^2 - y^2 + 2xyi
\end{align*} \]となる。

複素関数 \( f(z) \) を実部 \( u(x,y) \) と虚部 \( v(x,y) \) に分離すると、\[
u(x,y) = x^2 - y^2 , \ \ \ v(x,y) = 2xy
\]となる。

ここで、\[
\frac{\partial u}{\partial x} = 2x \ \ \ \ \ \frac{\partial v}{\partial x} = 2y \\
\frac{\partial u}{\partial y} = -2y \ \ \ \ \ \frac{\partial v}{\partial y} = 2x 
\]と計算できる。

よって、コーシー・リーマンの関係式\[
\frac{\partial u}{\partial x} = \frac{\partial v}{\partial y} , \ \ \ \  \frac{\partial u}{\partial y} = \color{red}{-} \frac{\partial v}{\partial x} 
\]を満たすので正則関数である。

解答2

\[
|z| = \sqrt{x^2 + y^2}
\]なので、\[
|z|^2 = x^2 + y^2
\]である*2。

複素関数 \( f(z) \) を実部 \( u(x,y) \) と虚部 \( v(x,y) \) に分離すると、\[
u(x,y) = x^2+y^2 , \ \ \ v(x,y) = 0
\]となる。

ここで、\[
\frac{\partial u}{\partial x} = 2x \ \ \ \ \ \frac{\partial v}{\partial x} = 0 \\
\frac{\partial u}{\partial y} = 2y \ \ \ \ \ \frac{\partial v}{\partial y} = 0 
\]と計算できる。

よって、\[
\frac{\partial u}{\partial x} \not = \frac{\partial v}{\partial y} , \ \ \ \  \frac{\partial u}{\partial y} \not = \color{red}{-} \frac{\partial v}{\partial x} 
\]となるのでコーシー・リーマンの関係式を満たさず、正則関数ではない。

（※コーシー・リーマンの関係式\[
\frac{\partial u}{\partial x} = \frac{\partial v}{\partial y} , \ \ \ \  \frac{\partial u}{\partial y} = - \frac{\partial v}{\partial x} 
\]のどちらか一方でもを満たさない場合、正則関数ではありません。）

（\( z^2 \) と \( |z|^2 \) では正則かどうかも変わっちゃうんです！）

解答3

複素関数 \( f(z) \) を実部 \( u(x,y) \) と虚部 \( v(x,y) \) に分離すると、\[
u(x,y) = ax^2 y - 2y^3 , \ \ \ v(x,y) = bxy^2 + cx^3
\]となる。

ここで、\[
\frac{\partial u}{\partial x} = 2a xy \ \ \ \ \ \frac{\partial v}{\partial x} = by^2 + 3c x^2 \\
\frac{\partial u}{\partial y} = ax^2 - 6y^2 \ \ \ \ \ \frac{\partial v}{\partial y} = 2b xy 
\]と計算できる。

複素関数が正則関数となるためには、コーシー・リーマンの関係式\[
\frac{\partial u}{\partial x} = \frac{\partial v}{\partial y} , \ \ \ \  \frac{\partial u}{\partial y} = - \frac{\partial v}{\partial x} 
\]を満たせばよい。

よって、\[
\left\{ \begin{array}{l} 2axy = 2bxy \\ ax^2 - 6y^2 = -3cx^2-by^2 \end{array}\right. 
\]の関係式が成立する。\( a \), \( b \), \( c \) の値は\[
\left\{ \begin{array}{l} a = b \\ a = -3c \\ b = 6 \end{array}\right. 
\]の連立方程式を解くことにより求められる。

よって \( a = 6 \), \( b = 6 \), \( c = -2 \) と求められる。

解答4

複素関数 \( f(z) \) の実部を \( u(x,y) \)、虚部を \( v(x,y) \) とする。すると、\[
u(x,y) = x^2 - y^2 + 2x + 4y
\]となるので、\[
\frac{\partial u}{\partial x} = 2x + 2 , \ \ \ \ \  \frac{\partial u}{\partial y} = -2y + 4
\]となる。

ここで、複素関数 \( f(z) \) は正則なのでコーシー・リーマンの関係式\[
\frac{\partial u}{\partial x} = \frac{\partial v}{\partial y} , \ \ \ \  \frac{\partial u}{\partial y} = - \frac{\partial v}{\partial x} 
\]が成立する。つまり、\[
\frac{\partial u}{\partial y} = - \frac{\partial v}{\partial x}  = 2y - 4 \\
\frac{\partial u}{\partial x} = \frac{\partial v}{\partial y} = 2x + 2
\]が成立する。

ここで \(  \frac{\partial v}{\partial x} \) を \( x \) で積分すると \( x \) だけの関数 \( k(x) \) を用いて\[\begin{align*}
\int \frac{\partial v}{\partial x} \ dx  & = \int 2y - 4 \ dx \\ & = 2xy - 4x + k(x) = v
\end{align*} \]と表せる。また、\(  \frac{\partial v}{\partial y} \) を \( y \) で積分すると \( y \) だけの関数 \( k(y) \) を用いて\[\begin{align*}
\int \frac{\partial v}{\partial y} \ dy  & = \int 2x + 2 \ dx \\ & = 2xy + 2y + k(y) = v
\end{align*} \]と表せる。

（積分する文字以外は定数と考えましょう！）

 

よって両者を比較することにより、虚部 \( v(x,y) \) は任意定数 \( C \) を用いて\[
v(x,y) = 2xy - 4x + 2y + C
\]と表せる。

 

よって、関数 \( f(z) \) は、\[\begin{align*}
f(z) & = u(x,y)  + i v(x,y)
\\ & = x^2 - y^2 + 2x + 4y + (2xy - 4x + 2y + C) i
\end{align*} \]となる。

 

５．さいごに

今回は、複素関数の微分可能性、およびコーシー・リーマンの関係式についてまとめました。

コーシー・リーマンの関係式のマイナスの位置を間違えないようにきちんとサラスの公式を思い出してマイナスの位置を覚えておきましょう。