スポンサードリンク
こんにちは、ももうさです。
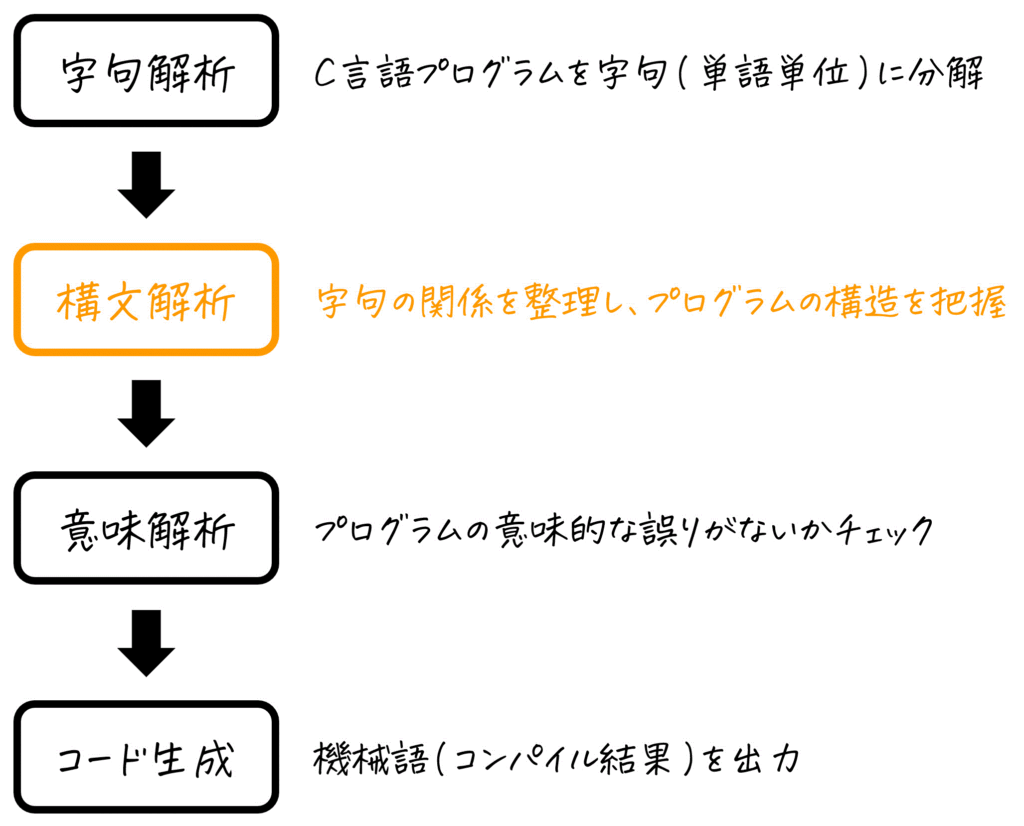
第2羽となる今回から、コンパイラの処理の中の第2フェーズである「構文解析」で出てくる様々な仕組みについて数記事にわけて見ていきましょう。
皆さんは、高校で英語を習う際に「英文の構造を把握してから」英文を理解したり、和訳したりした思い出があると思います[1]SV, SVC, SVO, SVOO, SVOCの5種類。。

コンパイラの世界でも同じように、「書かれたプログラムの構造を把握しながら」C言語などの高級言語をコンピュータ上で実行できる形(機械語)に翻訳するコンパイルが実行されるのですが、その際にコンピュータ上でプログラムの構造を
今回は、コンパイラで「書かれたプログラムの構造を(文法的に)把握する」する際に出てくる「解析木」や「構文木」について、例題や練習問題も踏まえながら学習していきましょう。
目次
スポンサードリンク
[復習] 文脈自由文法とは
まずは、コンピュータ上で文法を表現する方法の1つである文脈自由文法について復習しましょう。
文脈自由文法は、
- 非終端記号 \( N \)
- 終端記号 \( \Sigma \)
- 生成規則 \( P \)
- 出発記号 \( S \)
の4つの要素で構成されており、この4種類で「文字列が文法のルールを満たしているか否か」を判定します。
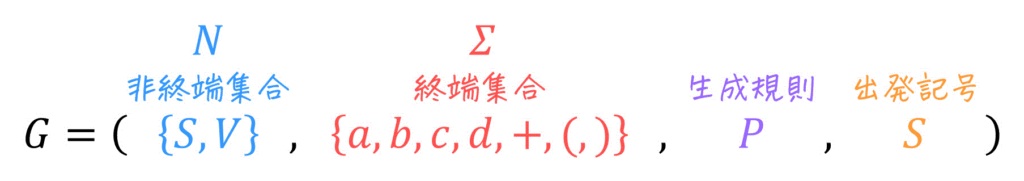
(\( G = (P,S) \) のように \( N \), \( \Sigma \) を省略することもあり)
ここからは、具体的にそれぞれ4種類の記号がどのような働きをしているかを見ていきましょう。
(1) 非終端記号
文法を表現する際に使う「仮の変数」です。数学でいう「nとおく。」のnみたいなものだと思ってください。
非終端記号は、(4)で説明する生成規則に書き換えることが可能です。\( S \), \( E \), \( T \) などのアルファベット大文字で書かれることが多いです。
[余談] アルファベット大文字以外にも、<式>, <変数>. <数字> など、<名前> の形で非終端記号が表されることもあります。(基本情報や応用情報がまさにこの形で非終端記号を使っています)
(2) 終端記号
実際に文字列内に出てくる(仮の変数ではない)文字や記号が終端記号です。(4) で説明する生成規則によって書き換えることが出来ないのが特徴です。
終端記号には、\( a \), \( b \) などの小文字や数字、英単語、単語、記号(括弧・演算記号など)などの日常的に使われる文字(文字列)が指定されることが多いです。
(3) 生成規則
文法のルールを表す文脈自由文法の心臓部分です。
実際に「ある文字列」が文法のルールを満たしているか否かは、(4)で出てくる出発記号 \( S \) を生成規則 \( P \) で書き換えていった際に出てくる終端記号「ある文字列」を表現できるかどうかで判定します。
[Point] 生成規則のまとめ書き
\( S \to AB \), \( S \to C \) のように、同じ文字列から生成される規則は、\[
S \to AB | C
\]のように | を用いてまとめて書くのが一般的なので覚えておきましょう!
(4) 出発記号
名前の通り、生成規則を最初に加える非終端記号を指します。
ここで、実際に文脈自由文法についての復習問題を解いてみましょう。
つぎの文脈自由文法\[
G = ( \{ S, A\} , \{ a \}, \{ S \to Aa , \ A \to a | Aaa \}, S )
\]の文法にあてはまる文字列は (ア)・(イ) のどちらか。
(ア) \( aaaa \)
(イ) \( aaaaa \)
[解答] (ア)
実際に、出発記号 \( S \) から連鎖的に文法規則を適用していき、(ア)と(イ)のどちらが文法規則を適用した際に現れるかを確認すればOKです。
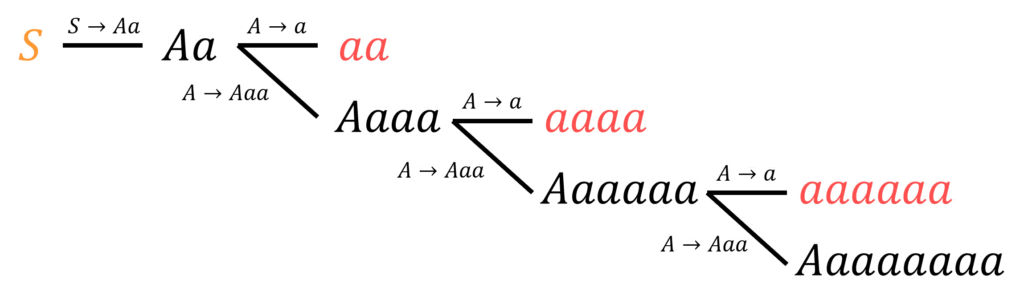
(出発記号 \( S \) に文法規則を適用していき、終端記号だけになるまで変換を続けていく)
すると、\( aaaa \) という文字列が出てきますね。よって答えは(ア)です。
文脈自由文法についてもう少し復習したいなという人は、下の記事をご覧ください!
[余談] 生成規則の書き方について
生成規則は、基本的に\[
P = \{ S \to Aa , \ A \to a \ | \ Aaa \}
\]のように「(生成元の非終端集合) → (生成される文字列)」の形で書くのが一般的ですが、\[
S \to Aa, \ \ A \to a \ | \ Aaa
\]のように文字列を列挙して書く方法や、
S ::= Aa
A ::= a
A ::= Aaa
のように \( \to \) を ::= と書く手法もあります[2]基本情報や応用情報で出てくる文脈自由文法がまさに (生成元)::=(生成先) のような書き方をしています。(BNF記法などとも呼ばれます。)。
文脈自由文法について復習できたところで、いよいよ「解析木」や「構文木」の書き方を見ていきましょう!
スポンサードリンク
1. 解析木の書き方
解析木は、出発記号 \( S \) からどのような文法規則を適用すると与えられた文字列になるのかを表した図です。
と言われても少しわかりにくいと思うので、実際に例題を見ながら「解析木」の書き方、および解析木がどんなものなのかを見ていきましょう。
次の文脈自由文法で表される文法 \( G \) がある。\[
G = \left( \ \{ S, V \} \ , \ \{ a,b,c,d \} \ , \ P \ , \ S \ \right)
\]\[\begin{align*}
P = \{ \ \ S & \to V \ | \ (S+S) \ | \ S * S \\
V & \to a \ | \ b \ | \ c \ | \ d \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \}
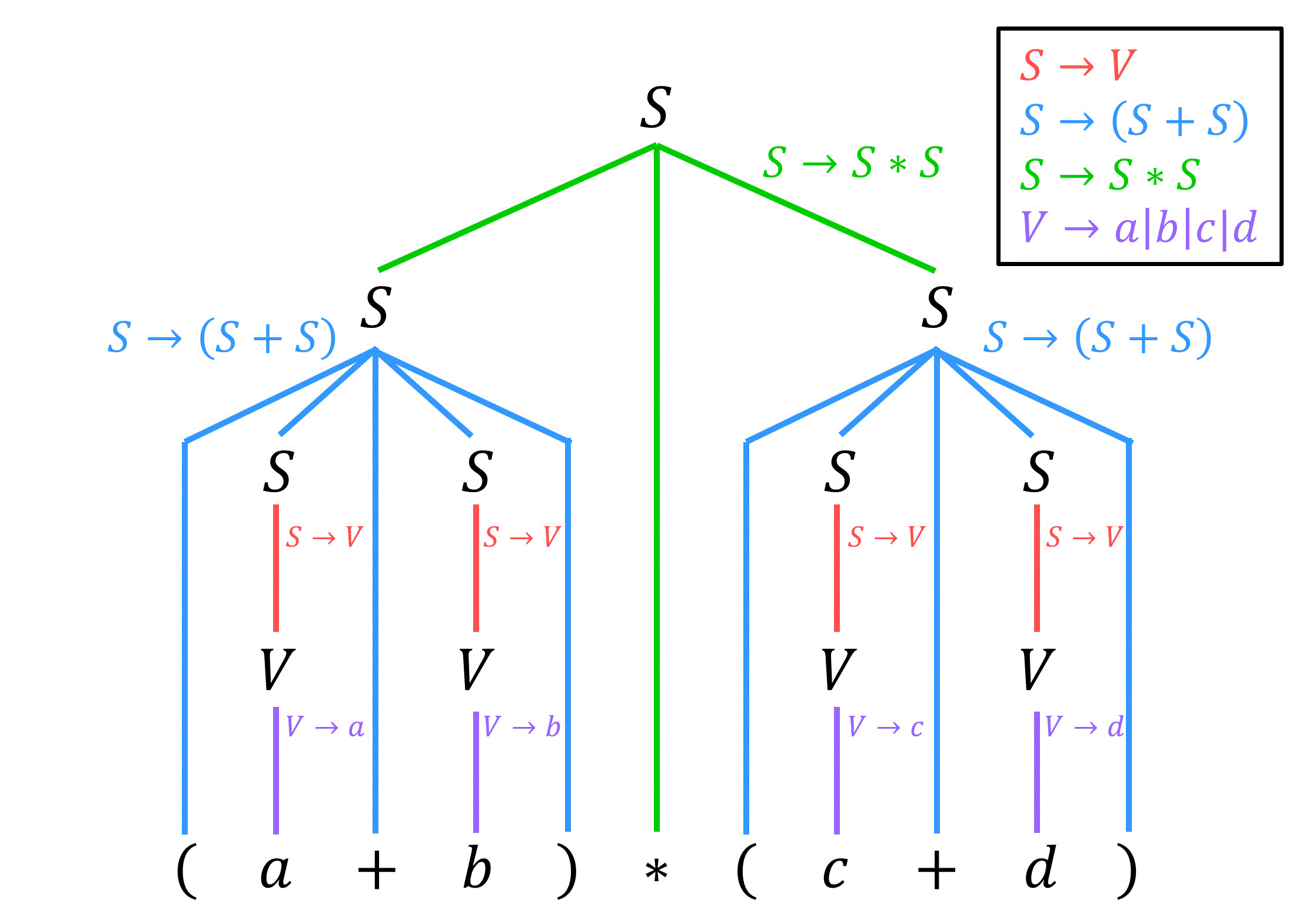
\end{align*}\]この文法 \( G \) に対し、以下の文字列 \( (a+b) * (c+d) \) の解析木を書きなさい。
[基本情報技術者平成23年秋期 午前問4] (改題)
[解説1]
解析木は、「与えられた文字列が出発記号 \( S \) からどのような生成規則 \( P \) が適用して出てきたか」を表します。
つまり、解析木を書く問題は与えられた文字列から生成規則を逆方向にたどっていき、出発記号 \( S \) に戻すパズルだと思っていただけたらOKです[3]生成規則を逆方向にたどるとは、例えば \( A \to B + C \) の生成規則に対して、\( B+ C \) を \( A \) に変換することを表します。。
ということで、早速例題の生成規則 \( P \) からなる文法 \( G \) に対する文字列 \( (a+b) * (c+d) \) の解析木を書いていきましょう。
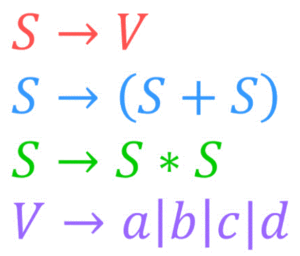
( \( V \) 以外 | を使わずに書いた場合)
Step1. 方針を建てる
やみくもに生成規則を逆にたどっていくのではなく、まず方針をたてましょう。
方針を建てる際には、生成規則内で1回しか出てこない非終端記号に着目できる場合は、その規則を使っていきます[4]この問題では、どの非終端記号 + , * , a, b, c, d も1回ずつを使っているので、。
[方針1] \( (S+S) \) の形を作り出す
まず、括弧と+が生成される規則は \( S \to (S+S) \) の1つにしか出てきません。なので、括弧 ( ) 部分は下のように \( (S+S) \) の形を作ってから \( S \to (S+S) \) を逆にたどるのかなという方針を立てます。
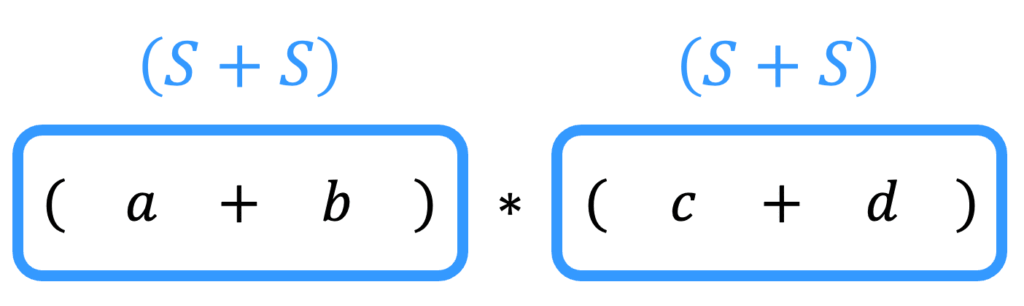
[方針1]
[方針2] \( S*S \) の形を作り出す
また、\( * \) が生成される規則は \( S \to S * S \) の1つにしかないので、\( * \) は、下のように \( S*S \) を作ってから \( S \to S*S \) を逆にたどるのかなと方針を立てます。
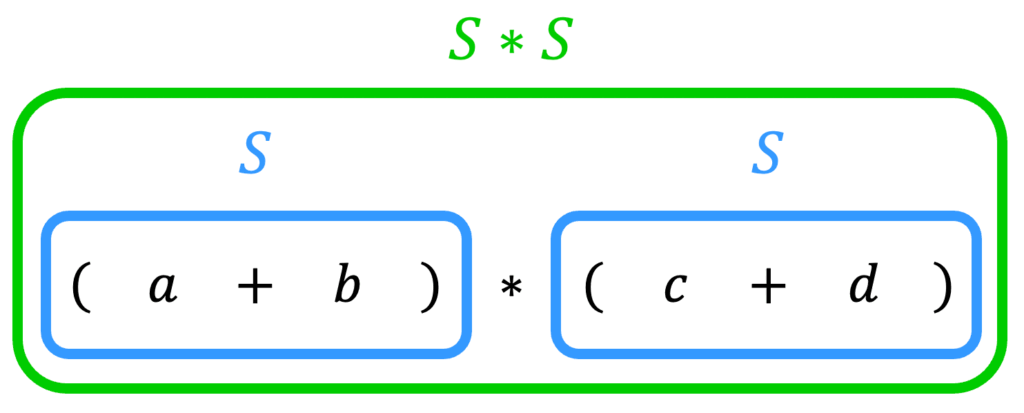
[木構造]
方針がたてれたところで、いよいよ解析木を作っていきましょう。
まず、\( V \to \ a \ | \ b \ | \ c \ | \ d \) を逆に適用することで、 \( a \), \( b \), \( c \), \( d \) を \( V \) に変換します。

つぎに、\( V \) が生成される規則は \( S \to V \) の1つだけですね。
なので、先程出てきた \( V \) に対して生成規則を逆にたどることで \( S \) にします。
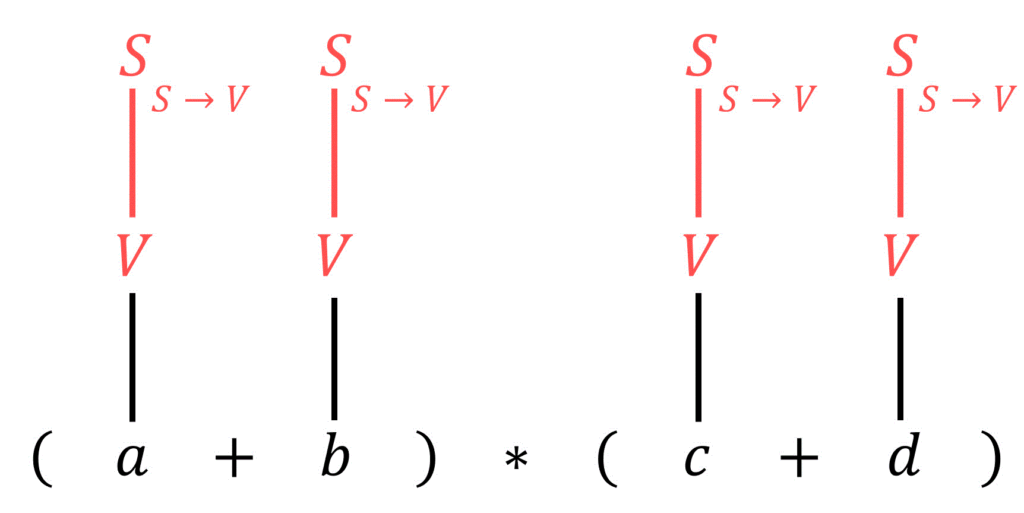
すると、文字列は \( (S+S) * (S+S) \) となります。
ここで、[方針1]で登場した \( (S+S) \) の形が2つ出てきましたね。なので、\( S \to (S+S) \) の規則を逆に適用して、\( (S+S) \) を \( S \) にします。
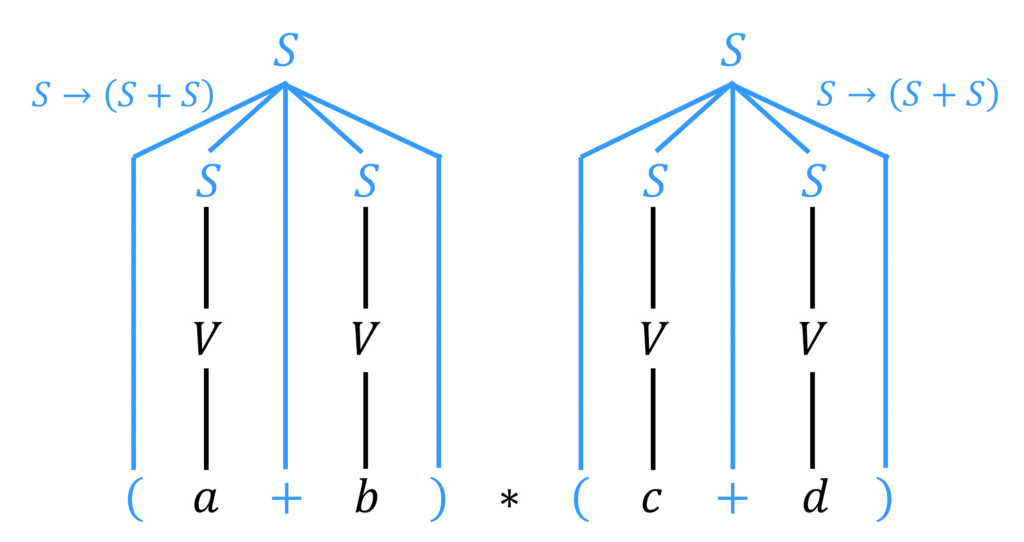
すると、文字列が \( S*S \) の形となり、[方針2]で登場した \( S*S \) の形となりました。
なので、最後に \( S \to S * S \) を逆に適用すれば、めでたく文字列を出発記号 \( S \) にすることができます!
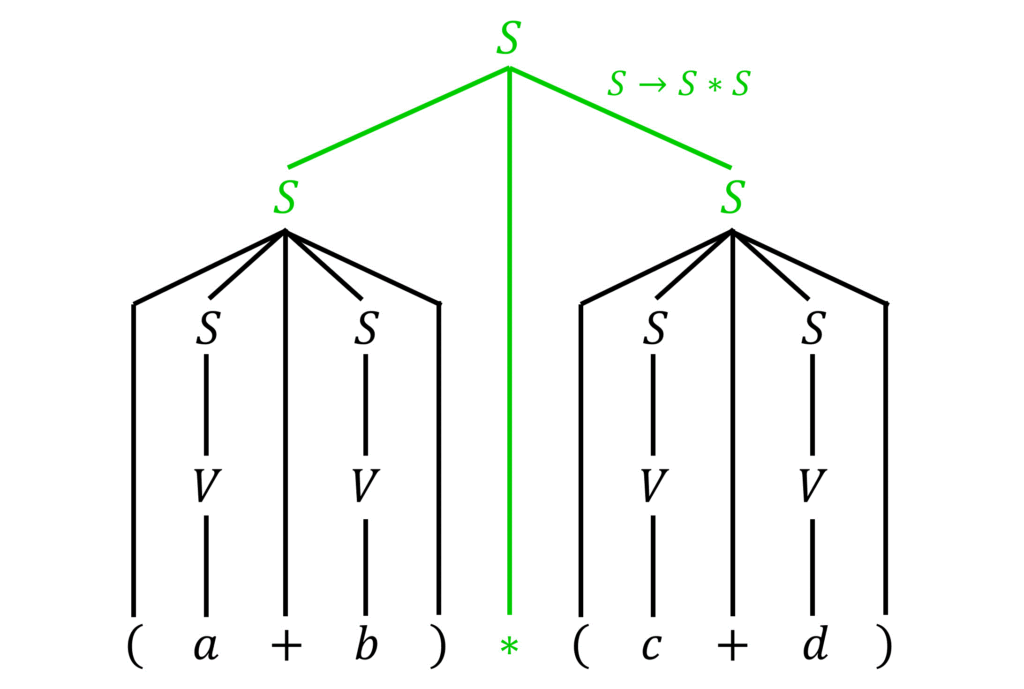
よって、解析木は下のようになります。
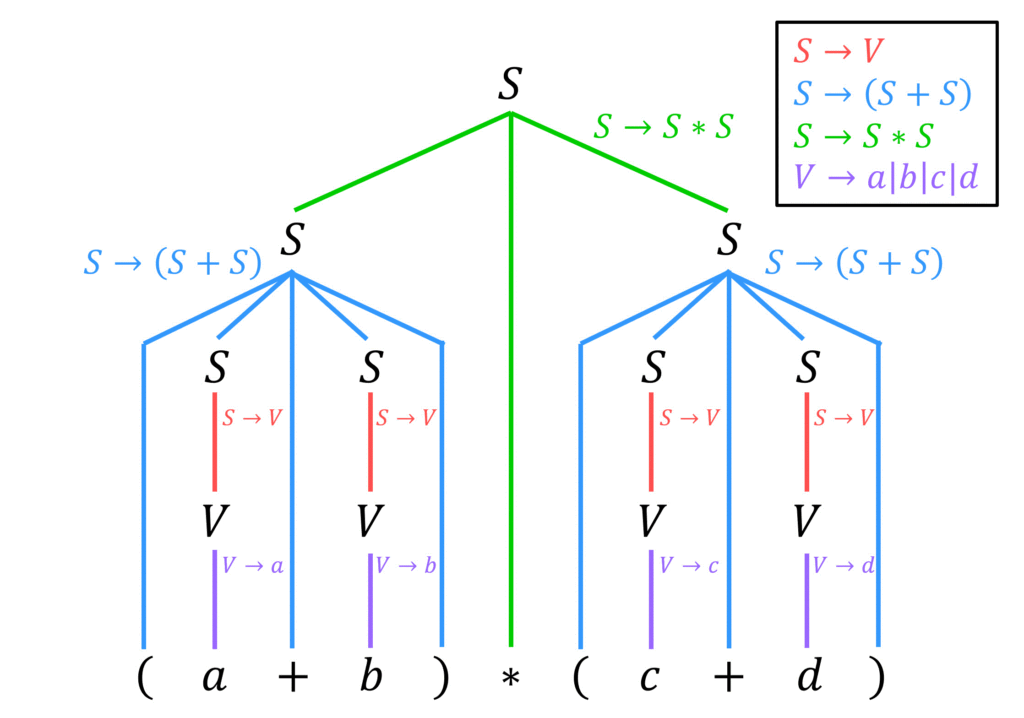
(例題1の答え)
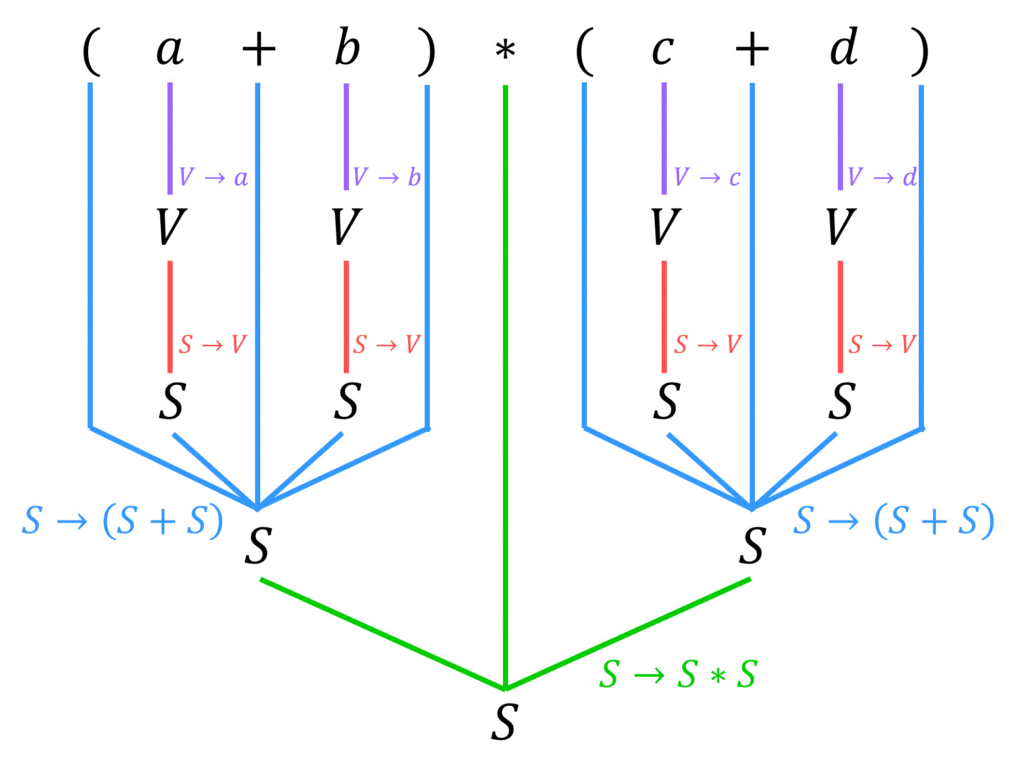
スポンサードリンク
2. 構文木の書き方
解析木から「非終端記号」や「括弧などの関係ない記号」を取り除いたものが構文木となります。
先程の例題1を使って、解析木から構文木を作ってみましょう!
例題1と同じ、次の文脈自由文法で表される文法 \( G \) がある。\[
G = \left( \ \{ S, V \} \ , \ \{ a,b,c,d \} \ , \ P \ , \ S \ \right)
\]\[\begin{align*}
P = \{ \ \ S & \to V \ | \ (S+S) \ | \ S * S \\
V & \to a \ | \ b \ | \ c \ | \ d \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \}
\end{align*}\]この文法 \( G \) に対し、以下の文字列 \( (a+b) * (c+d) \) の構文木を書きなさい。ただし、構文木を書く際には括弧を省くこと。
[解説2]
例題1で書いた解析木はこちらです。
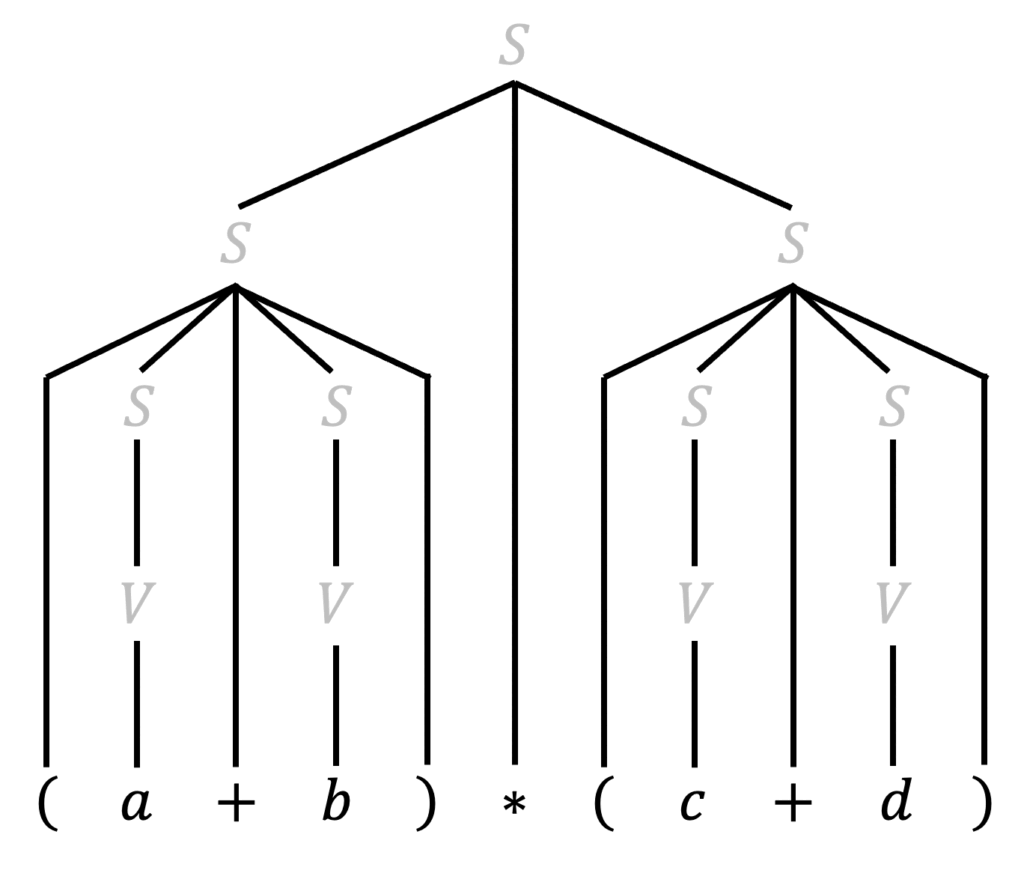
まず、この解析木から下のの2つの操作をします。
- 非終端記号の削除
- 余計な括弧 ( ) の除去
さらに、削除された(2つ以上の子をもつ)非終端記号の部分に対し、1つの子を削除された非終端記号の部分に移動させます[5]移動させる終端記号の選び方ですが、出発記号 \( S \) … Continue reading。
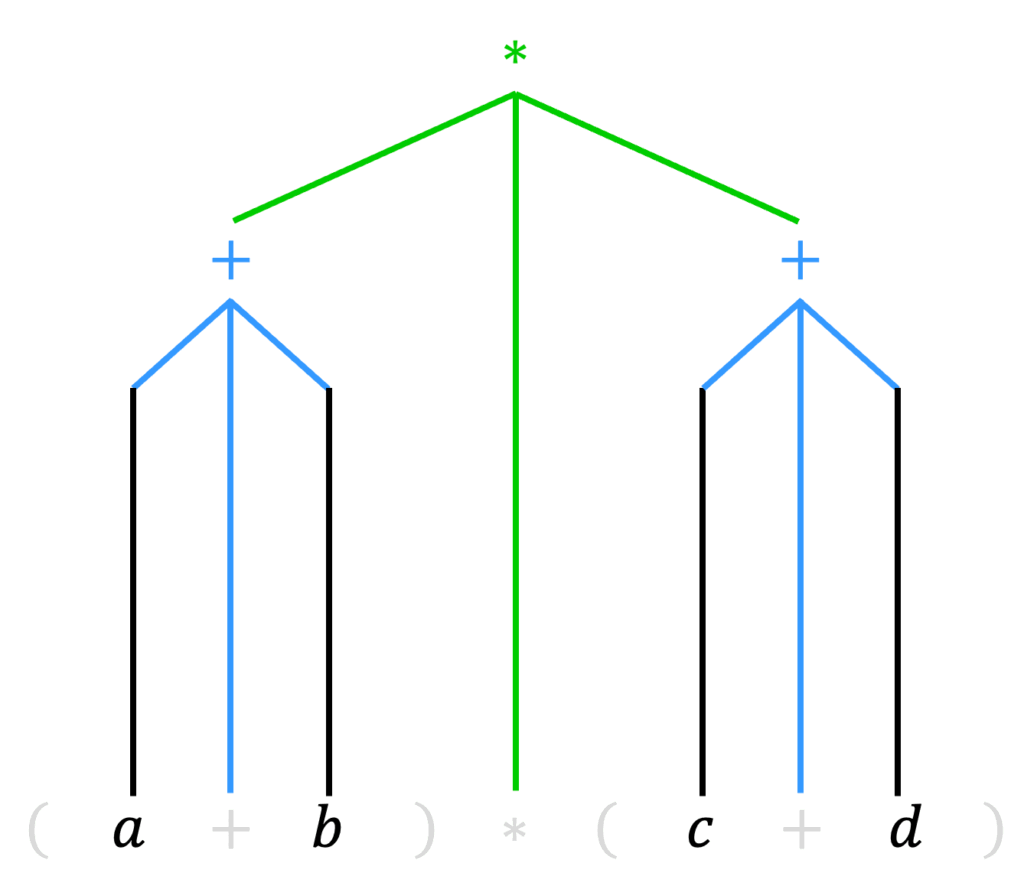
すると、下のような構文木が出来上がります。
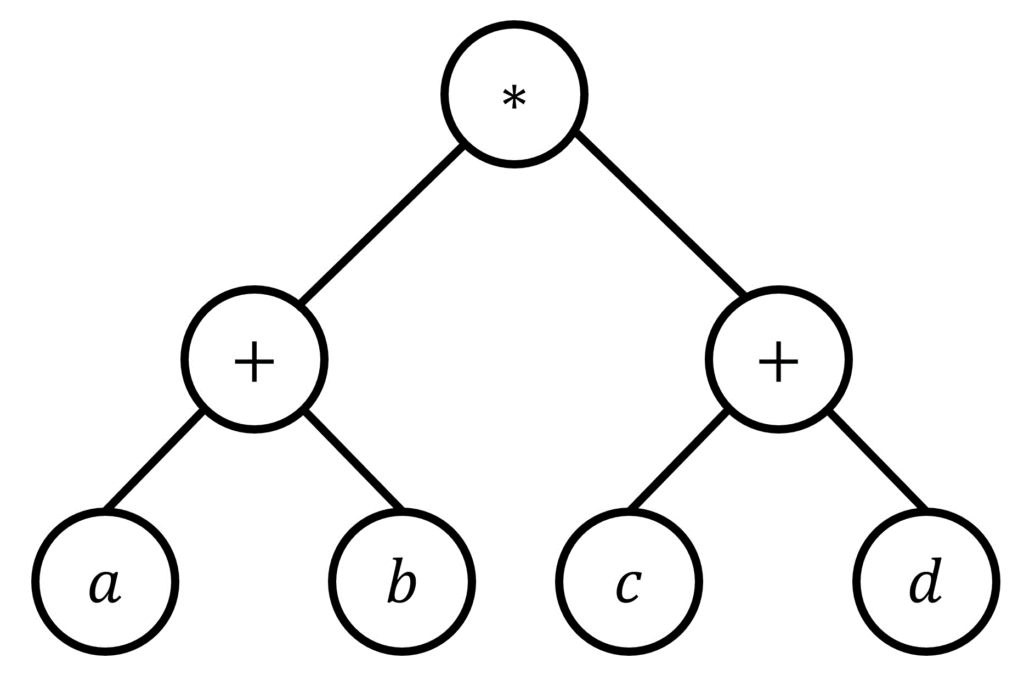
(例題2の答え)
3. 練習問題にチャレンジ!
実際に解析木(や構文木)が書けるかどうか、2種類の練習問題にてチャレンジしてみましょう!
練習1. 解析木・構文木を書いてみよう
次の文脈自由文法で表される文法 \( G \) がある。\[
G = \left( \ \{ S, E, T \} \ , \ \{ i, =, + , ( , ) \} \ , \ P \ , \ S \ \right)
\]\[\begin{align*}
P = \{ \ \ S & \to E \ | \ i =S \\ E & \to T \ | \ E + T \\ T & \to i \ | \ ( S )
\ \ \ \ \ \ \ \ \ \ \ \ \}
\end{align*}\]つぎの(1), (2)の問いに答えなさい。
(1) 文法 \( G \) に対し、文字列 \( i = (i+i) \) の解析木を書きなさい。
(2) 文法 \( G \) に対し、文字列 \( i = (i+i) \) の構文木を書きなさい。ただし、構文木を書く際には括弧を省くこと。
練習2. 解析木が書ける文字列はどっち?
次の文脈自由文法で表される文法 \( G \) がある。\[
G = \left( \ \{ S, E \} \ , \ \{ i, +, ( , ) \} \ , \ P \ , \ S \ \right)
\]\[\begin{align*}
P = \{ \ \ S & \to E \ | \ S + E \\ E & \to i \ | \ (S)
\ \ \ \ \ \ \ \ \ \ \ \ \}
\end{align*}\]つぎの(1), (2)の問いに答えなさい。
(1) 次の (ア), (イ) のうち、文法 \( G \) を満たす文字列はどちらか答えなさい。
(ア) \( ( ( i ) + i ) \)
(イ) \( i + ( + i ) \)
(2) (1)で答えた方の文字列に対して解析木を書きなさい。
4. 練習問題の答え
解答1.
(1) 解析木
最初に | でつながれている生成規則を1個ずつ省略せずに書き直してから、方針をたてましょう。
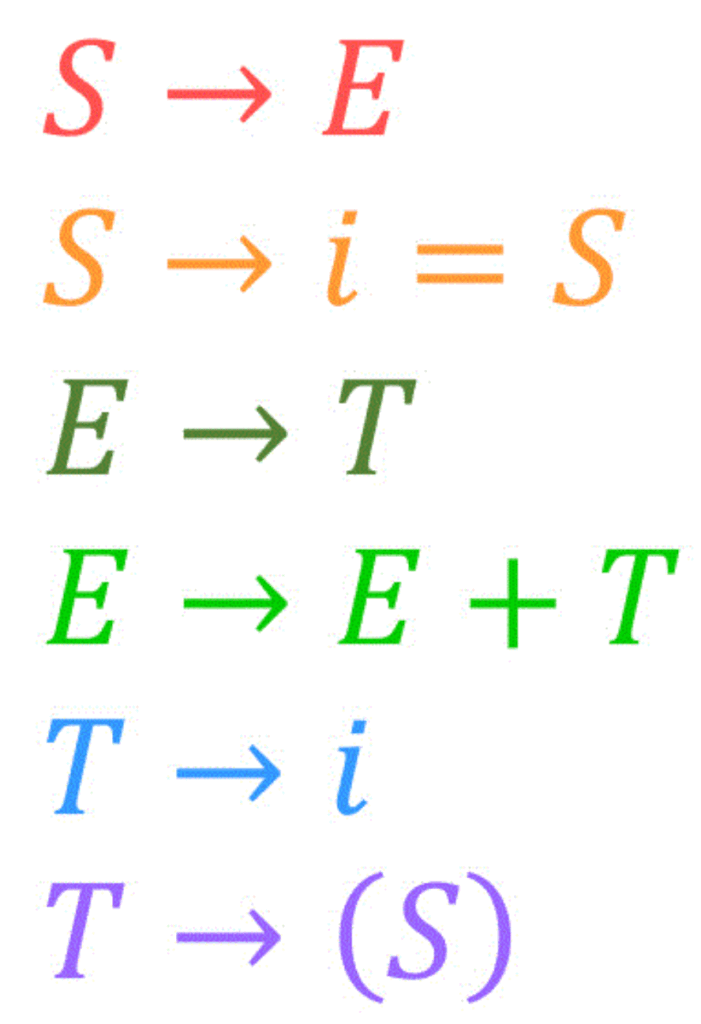
★ 方針 ★
[方針1]まず、\( + \) が生成できる規則は、\( E \to E + T \) 1つのみですね。
なので、文字列の \( i + i \) の部分を生成規則を逆にたどっていくことで \( E+T \) にすることを考えます。
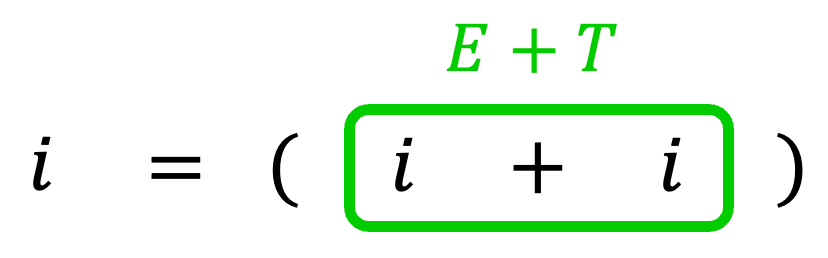
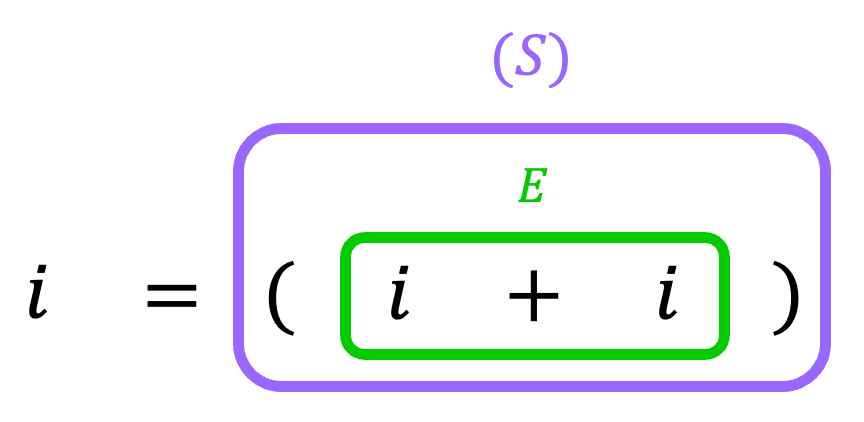
また、括弧が生成できる規則は、\( T \to (S) \) のみです。
そのため、文字列中に括弧が出てくる \( (i+i) \) 部分について、生成規則を逆にたどっていくことにより、\( (S) \) にすることを考えます。
さらに、\( = \) が生成できる規則は \( S \to i = S \) のみです。
なので、\( i = \textcolor{orange} {( i+ i)} \) 部分については、生成規則を逆にたどっていくことで \( i = \textcolo{orange}{ S } \) にすることを目指します[6]\( \textcolor{blue}{i =} (i+i)\) の \( \textcolor{blue}{ i = } \) の部分は終端記号なため、実質 \( \textcolor{orange}{ (i+i) } \) 部分を \( \textcolor{orange}{S} \) … Continue reading。
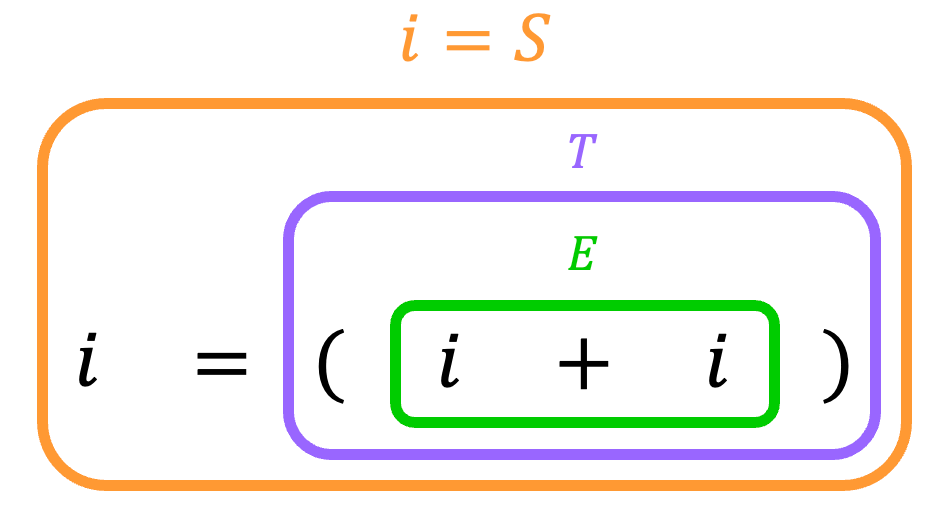
[解析木の作り方]
方針をたてられたので、生成規則を逆にたどっていく(以下:逆にたどっていくことを逆変換と表記します)ことにより、解析木を創りましょう。
まずは、[方針1] の通り、\( i + i \) から生成規則を逆変換していくことにより、\( E \) にします。
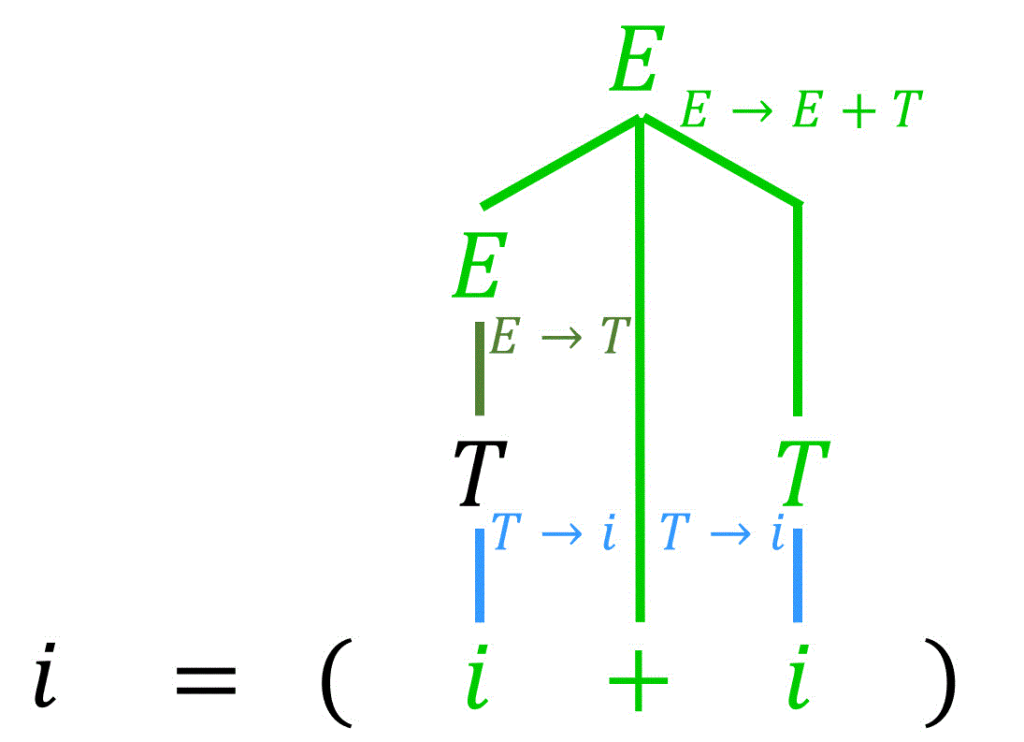
つぎに、[方針2] の通り、括弧部分を逆変換によりひとまとめにします。
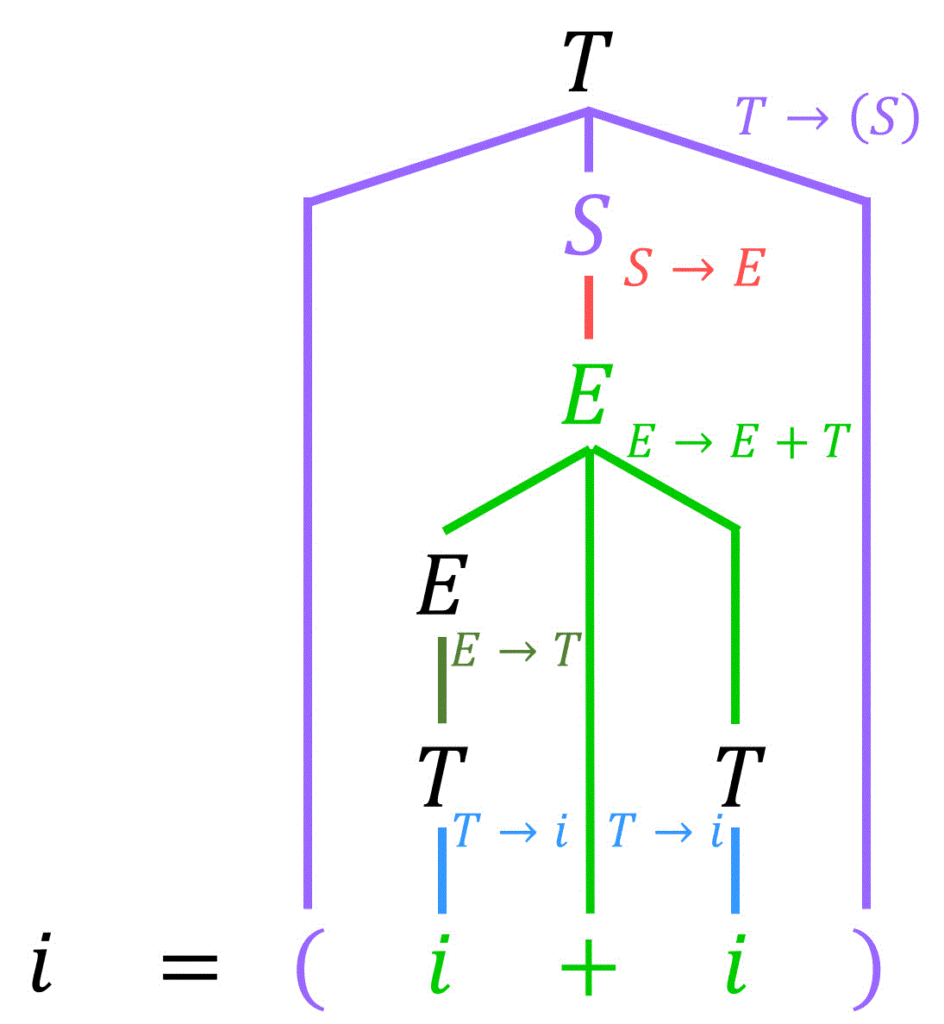
最後に、[方針3] の通り、\( = \) を逆変換によりまとめれば、出発記号 \( S \) だけになるため、解析木の完成です!
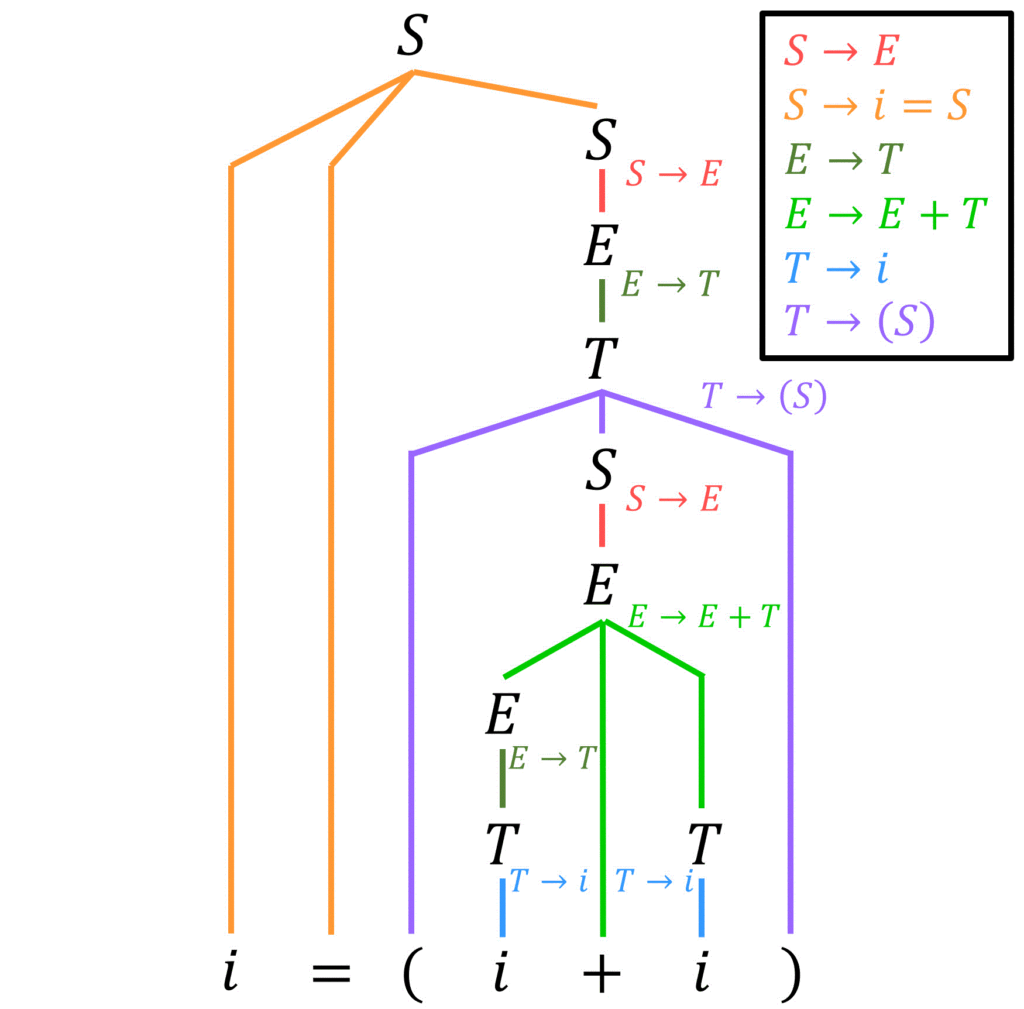
練習問題1(1)の答え
(2) 構文木
まず、(1)で求めた解析木から、
- 非終端記号の削除
- 括弧の除去
をします。
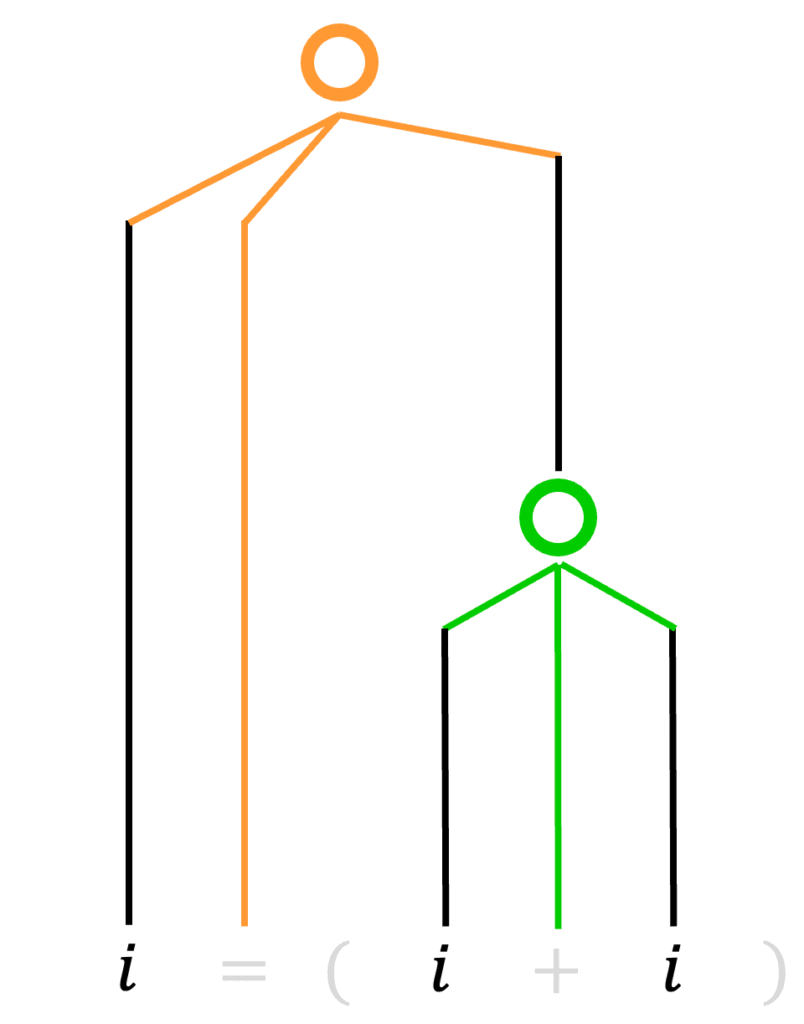
つぎに、削除された非終端記号のうち、○の部分(2つ以上の子をもつ部分)に対し、1つの子を削除された非終端記号の部分に移動させます。
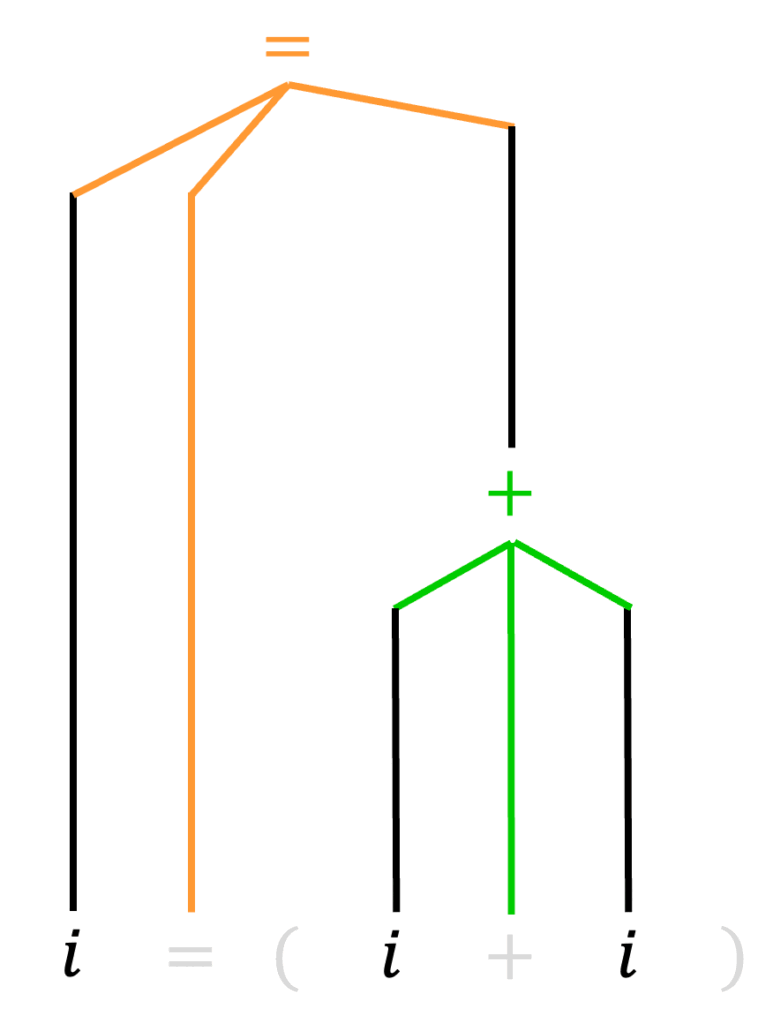
すると、下のような構文木が完成します。
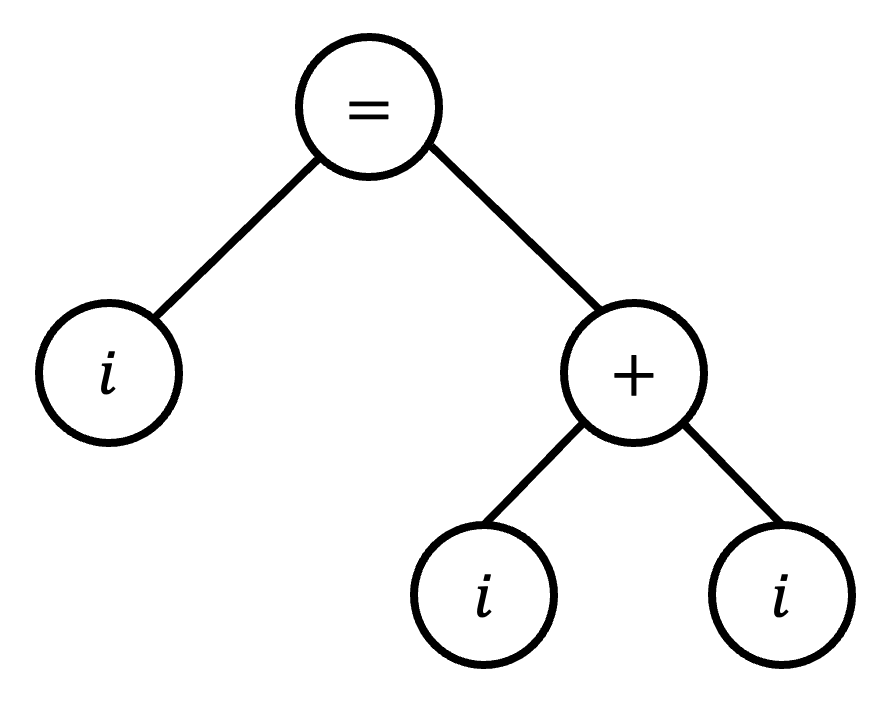
(練習問題1(2)の答え)
解答2.
(1) 文字列が文法を満たしているかの判定
文字列が文法 \( G \) を満たしているかを判定する際には、文字列の一部分を切り出してその部分が文法的に満たせそうかを確認する方法がおすすめです。
今回は、
(ア) \( ( ( i ) + i ) \)
(イ) \( i + ( + i ) \)
の2つの文字列のうち、どちらが文法を満たしているのかを判定するのでしたね。
なので、まずは文字列の一部分が文法を満たしているのかを確認していきましょう。
まず、(ア) の \( (i) \) と \( (i)+i \) に着目して構文木を書いてみましょう。
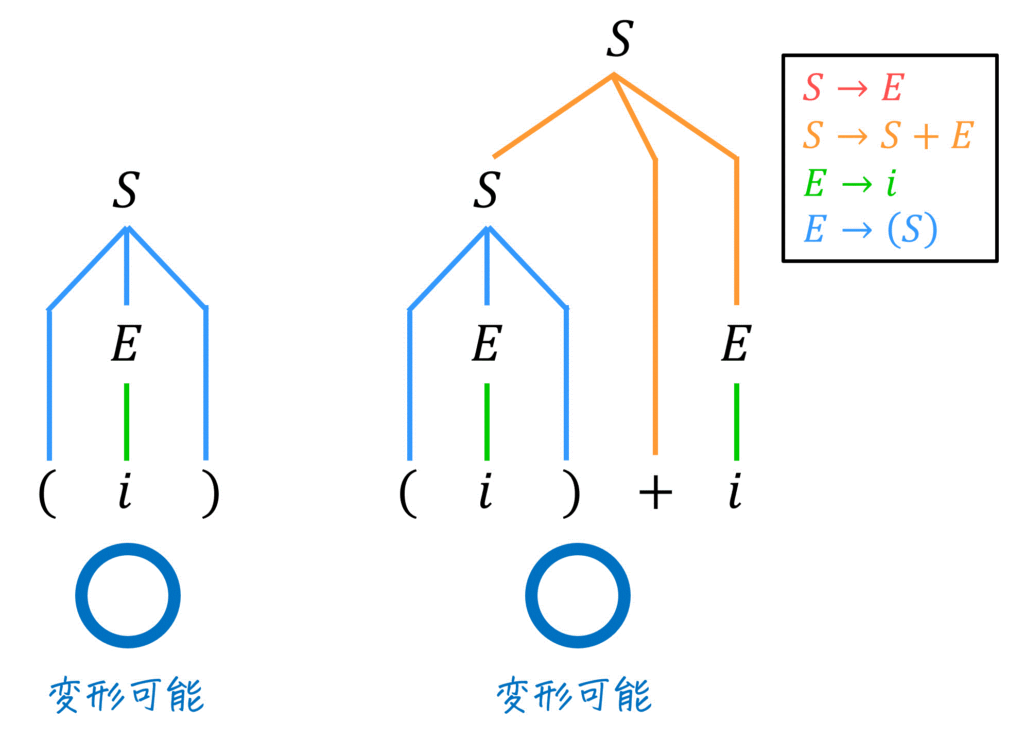
すると、どちらも \( S \) 1文字に書き換えることができました[7]一部分が \( S \) 1文字に書き換えられなからといって、与えられた文字列が文法を満たしていないとは限らない点に注意が必要です。。
さらに、\( \textcolor{red}{( i ) + i} \) が \( \textcolor{red}{S} \) に書き換えられることが分かったので、(ア) の文字列 \( ( \textcolor{red}{( i ) + i} ) \) は \( ( \textcolor{red}{S} ) \) に書き換えられそうですね。
ここで、\( (S) \) は、\( S \to E \to (S) \) で導出できるため、(ア)の文字列は文法 \( G \) を満たすことがわかります。
一方 (イ) の規則はどうでしょうか。
文字列 \( (+i) \) 部分を変形しながら見ていきましょう。
すると、\( (+E) \) までは逆変換することができます。しかし、\( + \) を逆変換できる式は \( S \to S + E \) の1種類しか存在しない上、生成規則的に \( S \) に空文字 \( \varepsilon \) は入らなさそうなため、どう頑張っても \( (+E) \) から文字列を逆変換することができません。
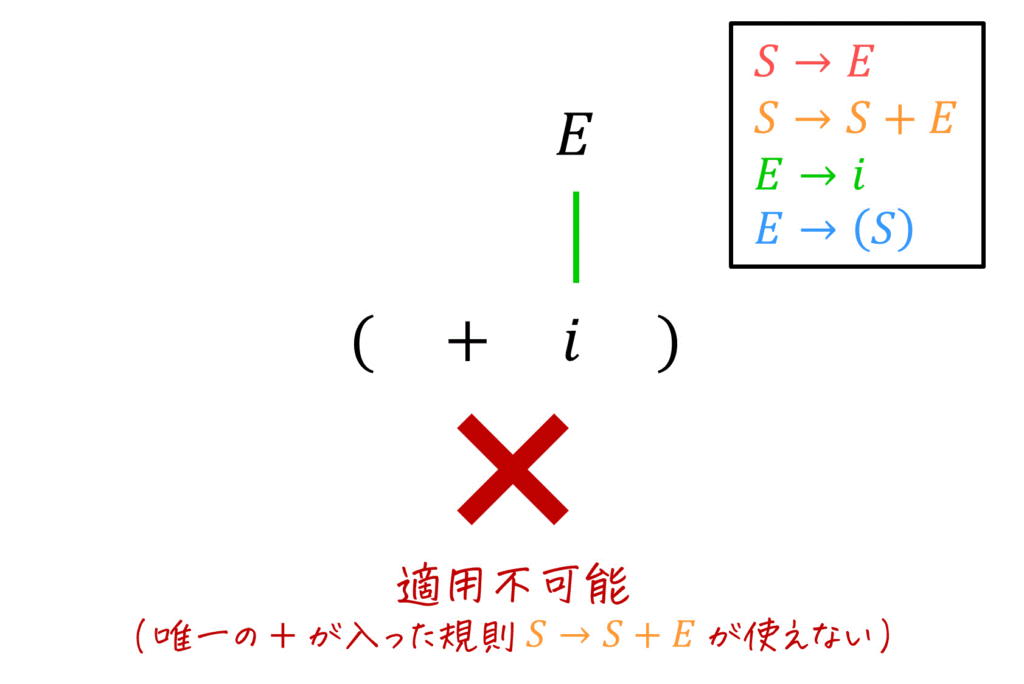
そのため、(イ) は文法 \( G \) を満たしませんね。
よって、文法 \( G \) を満たす文字列は (ア) となります。 ← (1) の答え
(2) 解析木
文法 \( G \) を満たす (ア) の文字列 \( ( ( i ) + i ) \) を書いていけばOKです。
ここで、(1)で書いた文字列の一部分 \( (i) \) と \( (i)+i \) の解析木を確認しましょう。
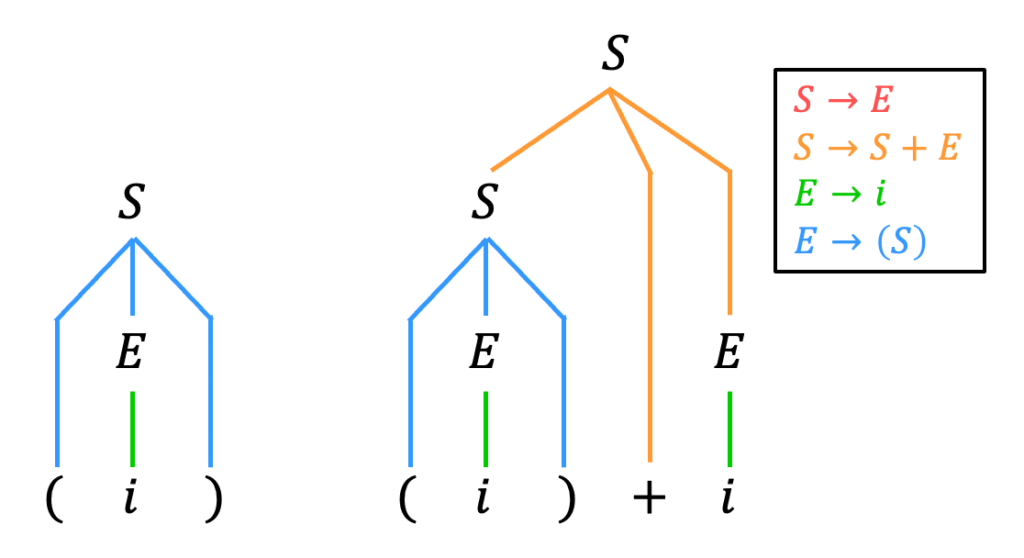
あとは、この解析木を参考にしながら (ア) の文字列全体 \( ( ( i ) + i ) \) の解析木を書けばOKです!
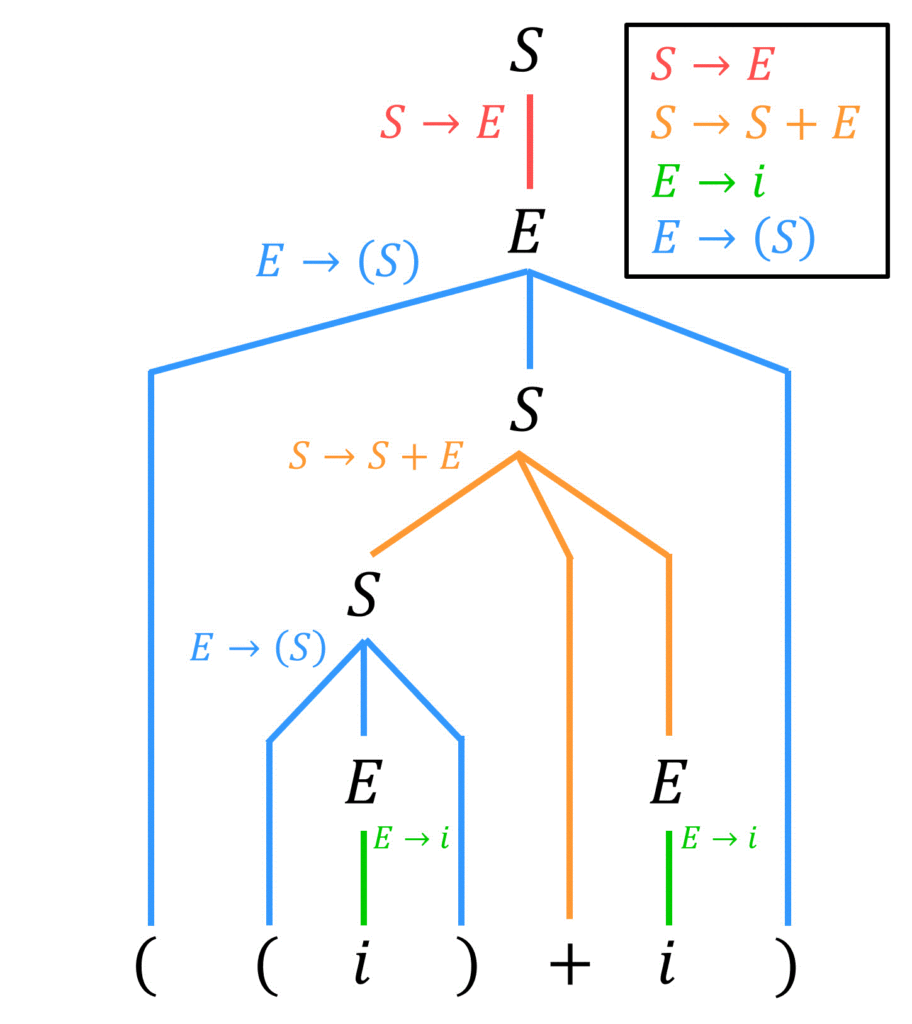
注釈
| ↑1 | SV, SVC, SVO, SVOO, SVOCの5種類。 |
|---|---|
| ↑2 | 基本情報や応用情報で出てくる文脈自由文法がまさに (生成元)::=(生成先) のような書き方をしています。(BNF記法などとも呼ばれます。) |
| ↑3 | 生成規則を逆方向にたどるとは、例えば \( A \to B + C \) の生成規則に対して、\( B+ C \) を \( A \) に変換することを表します。 |
| ↑4 | この問題では、どの非終端記号 + , * , a, b, c, d も1回ずつを使っているので、 |
| ↑5 | 移動させる終端記号の選び方ですが、出発記号 \( S \) から生成された際に、一番最初に生成された終端記号が親になると思っていただけたらOKです。基本的に数式の構文解析の場合、* や + などの演算子が親に来ることがほとんどです。(例 1, 2, + の中からであれば + が親になる) |
| ↑6 | \( \textcolor{blue}{i =} (i+i)\) の \( \textcolor{blue}{ i = } \) の部分は終端記号なため、実質 \( \textcolor{orange}{ (i+i) } \) 部分を \( \textcolor{orange}{S} \) にすることを目指せばOKです。 |
| ↑7 | 一部分が \( S \) 1文字に書き換えられなからといって、与えられた文字列が文法を満たしていないとは限らない点に注意が必要です。 |
関連広告・スポンサードリンク