スポンサードリンク
こんにちは、ももやまです。
コンパイラ(言語処理系)の勉強をしていると、
- LL(1)文法
- First集合
- Follow集合
- Director集合
などの不思議な用語が出てきますよね。しかも、これらの定義(特にFirst集合やFollow集合)の定義は少し難解です。
文法 \( G = ( V_N, V_T, P, S ) \)に関して、記号列 \( \alpha \in ( V_N \cup V_T )^* \)、非終端記号 \(A \in V_T \) について、\( \mathrm{First} \ ( \alpha ) \), および \( \mathrm{Follow} \) は次のように定義される。\[
コンパイラ補助資料 佐々木晃 より
\mathrm{First} \ ( \alpha ) = \left\{ a \mid a \in V_T , \alpha \overset{*}{\Rightarrow} a \cdots \right\}
\]\[
\mathrm{Follow} \ ( A ) = \left\{ a \mid a \in V_T , S \overset{*}{\Rightarrow} \cdots Aa \cdots \right\}
\]ただし \( \alpha \overset{*}{\Rightarrow} \varepsilon \) なら \( \varepsilon \in \mathrm{First} \ ( \alpha ) \) とする。
そこで今回は、
- LL(1)文法とはそもそも何か?
- First, Follow, Director集合を求めて何がうれしいのか
- First, Follow, Director集合の求め方
の3点を中心に、LL(1)文法とFirst・Follow・Director集合のお勉強をしていきましょう。
本記事では特に指示がない限り、文章中に出てくる小文字・大文字・ギリシャ文字は
- 小文字 \( a \), \( b \), \( c \), \( d \), … → 終端記号
- 大文字 \( S \), \( A \), \( B \), \( C \), … → 非終端記号
- \( \varepsilon \) → 空文字
を表します。
スポンサードリンク
1. LL(1)文法とは
ある文字列 \( \alpha \) が文法規則を満たすかどうかを一番単純に調べる方法は、下のように「出発記号 \( S \) から変換規則を総当たりで試していき、試した中に \( \alpha \) が含まれるか」を調べることです。
しかし、やみくもに総当たりで試す方法は、処理的にかなり無駄が発生してしまいます[1] … Continue reading。
そこで、構文解析をする際に1文字だけ先読みし、どの生成規則を使えばよいかを決めてから実際に変換していく方法が考えられました。
このように、1文字だけ先読みすれば、文字列を後戻りすることなく構文解析ができる(文法を満たすか確認できる)文法からなる文法のことをLL(1)文法と呼びます[2] … Continue reading。
LL(1)文法とは言えない文法(=1文字だけ先読みするだけでは文字列を後戻りせずに構文解析ができない)文法の例も見てみましょう。
例えば、非終端記号(かつ出発記号) \( S \)、終端記号 \( a \), \( b \)、生成規則\[
S \to aaS , \ \ S \to abS , \ \ S \to b
\]からなる文法規則があるとします。
この文法規則に \( \textcolor{red}{a} bab \) という文字列が当てはまるかどうかを1文字先読みで見ていきましょう。
しかし、1文字目 \( \textcolor{red}{a} \) が出てくる生成規則には、
- \( S \to \textcolor{red}{a} aS \)
- \( S \to \textcolor{red}{a} b S \)
の2つがあるため、1文字先読みしただけでは \( S \to aaS \), \( S \to abS \) どちらの生成規則を適用すればいいかわかりません。
この例から分かる通り、LL(1)文法かどうかは文法の生成規則のみで決まります。
ここで、LL(1)文法を満たす生成規則であるかを機械的に確認する手法として導入されたのがFirst・Follow・Director集合という概念なのです!
つぎの第2章からは、
- 実際にFirst, Follow, Director集合の求め方の解説
- なぜ機械的にLL(1)文法を満たすのかがわかるのか
の2点について解説していきます。
スポンサードリンク
2. First集合
(1) First 集合とはなにか
First集合 \( \mathrm{First} ( \alpha ) \) は、「ある文字列 \( \textcolor{magenta}{\alpha} \) に対して生成規則を適用して(複数回適用OK)全て終端記号にした際に、先頭(1文字目)に出てくる可能性がある文字を集めた集合」を表します。
数式で書くと、\[
\mathrm{First} ( \textcolor{magenta}{\alpha} ) = \left\{ \textcolor{orange}{a} \mid \textcolor{orange}{a} \in \textcolor{green}{V_T} , \textcolor{magenta}{\alpha} \textcolor{deepskyblue}{\overset{*}{\Rightarrow}} \textcolor{orange}{a} \cdots \right\}
\]となります。(色部分を日本語の説明に対応させています)
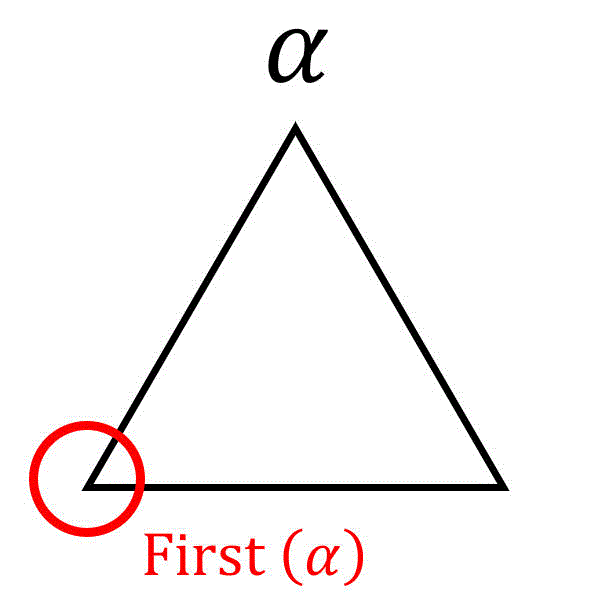
例えば、\( \mathrm{First} ( \alpha ) = \{ a, b, c\} \) の場合、\( \alpha \) に生成規則を適用していった際に出来る文字列の先頭(1文字目)が \( a \), \( b \), \( c \) のいずれかであることを表します。
(2) First 集合で頭にいれておくべき公式
※ 公式を丸暗記するのではなく、理屈を理解してから頭に入れましょう。
規則1[R1] First(a) … 終端記号1文字 \( a \) の場合
終端記号 \( a \) は、これ以上生成規則を適用することが出来ない文字を表すのでしたね。そのため、\( a \) はどう頑張っても他の文字に変換されることはありません。
よって、終端記号1文字 \( a \) のFirst集合の要素は終端記号 \( a \) だけとなります。\[
\mathrm{First} ( a ) = a
\]※ 空文字 \( \varepsilon \) のFirst集合は、\( \mathrm{First} ( \varepsilon ) = \{ \varepsilon \} \) となります。言い換えると、\( \mathrm{First} ( \alpha ) = \{ \varepsilon \} \) は、\( \alpha \) が空文字であることを表します。
※ 以後、この規則を用いた変換をする場合は \( \overset{ \mathrm{R1} }{=} \) と = の上にR1(規則1)を用いていることを示します。
規則2[R2] First(A) … 非終端記号1文字の場合
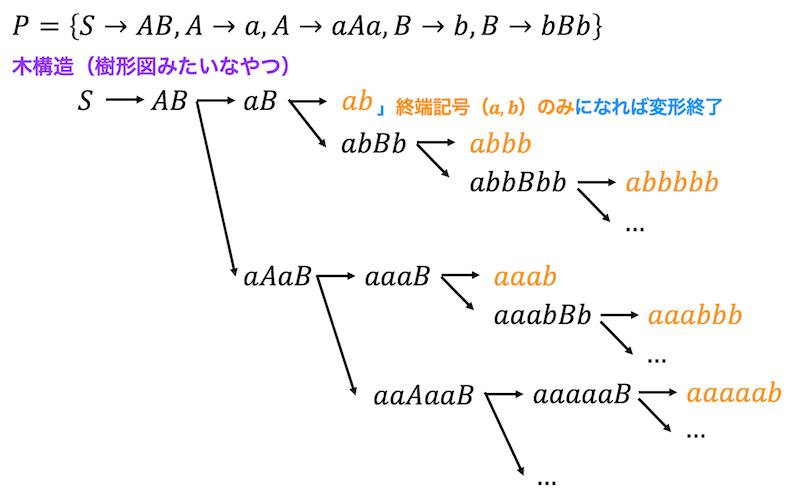
非終端記号 \( A \) のFirst集合 \( \mathrm{First} ( A ) \) を求める際、下のように樹形図を書いていって先頭1文字目に出てる文字を地味に探しても正しい答えは出てきますが、列挙ミスが発生する場合があります。
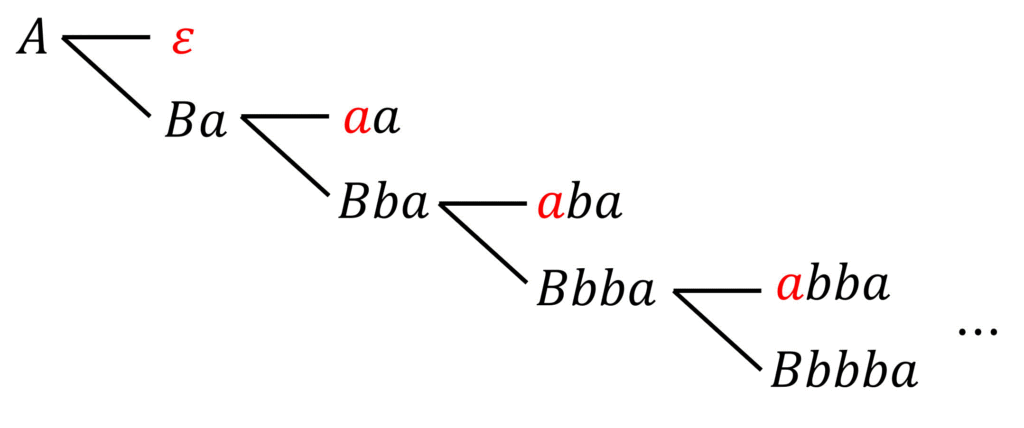
なのでもう少し機械的に \( \mathrm{First} ( A ) \) を求めてみましょう。
例えば、\( A \to BC \) という生成規則があったとします。これを言い換えると、「\( BC \) に対して生成規則を適用し、すべて終端記号に変換した際に出てくる文字列」は、必ず「\( A \) に対して生成規則を適用し、すべて終端記号に変換した際に出てくる文字列」 として出てきますね。
言い換えると、「\( BC \) に生成先を適用してすべて終端記号にした際に出てくる先頭文字 \( \mathrm{First} (BC) \) の集合」の要素に、「\( A \) に生成先を適用してすべて終端記号にした際に出てくる先頭文字 \( \mathrm{First} (A) \) の集合」が含まれますね。
つまり、 \( \mathrm{First} ( A ) \) を機械的に求める手順としては、\( A \) から生成規則 \( A \to \alpha \), \( A \to \beta \), … を探していき、その生成先の文字列 \( \alpha \), \( \beta \), … のFirst集合 \( \mathrm{First} ( \alpha ) \), \( \mathrm{First} ( \beta ) \) の要素をすべてFirst集合 \( \mathrm{First} (A) \) の要素とすればOKです。
1つ例を見てみましょう。\( A \) から始まる生成規則 \( A \to \textcolor{red}{\varepsilon} \), \( A \to \textcolor{blue}{aB} \), \( A \to \textcolor{green}{Cb} \) が3つあったとします。
この場合、\( \mathrm{First} (A) \) の要素は、\( \mathrm{First} ( \textcolor{red}{ \varepsilon } ) \), \( \mathrm{First} ( \textcolor{blue}{ aB } ) \), \( \mathrm{First} ( \textcolor{green}{ Cb } ) \) の和\[
\mathrm{First} ( A ) = \underbrace{ \mathrm{First} ( \textcolor{red}{\varepsilon} ) }_{ A \to \textcolor{red}{\varepsilon} } \cup \underbrace{ \mathrm{First} ( \textcolor{blue}{a B} ) }_{ A \to \textcolor{blue}{ aB } } \cup \underbrace{ \mathrm{First} ( \textcolor{green}{Cb} ) }_{ A \to \textcolor{green}{Cb} }
\]となります。
ここで1点注意が必要です非終端記号 \( A \) から空文字 \( \varepsilon \) が生成される可能性があるときには、\( \mathrm{First} ( A ) \) の要素に \( \varepsilon \) が加わる点に注意してください。
※ 以後、この規則を用いた変換をする場合は \( \overset{ \mathrm{R2} }{=} \) と = の上にR2(規則2)を用いていることを示します。
規則3[R3] First(αβ…) … 2文字以上の場合
First集合は、「文字列に生成規則を加えて全て終端記号にした際に、先頭に来る可能性がある終端記号」を表しているのでしたね。
そのため、(First集合を求めるだけであれば)最初の1文字さえわかってしまえば、(最初の1文字が空文字とはならない限り)残りの後ろは何が来ようが関係ありません。
よって、文字列 \( \alpha \beta \cdots \) のFirst集合 \( \mathrm{First} ( \alpha \beta \cdots ) \) は、\( \alpha \) に空文字が来ない限り(= \( \varepsilon \notin \mathrm{First} (\alpha ) \) の場合)は \( \mathrm{First} ( \alpha ) \) と等しくなります。
一方、\( \alpha \) に空文字が来る可能性があるとき(= \( \varepsilon \in \mathrm{First} (\alpha ) \) の場合)は、2文字目が先頭になる可能性があるため、1文字目に加えて2文字目 \( \beta \cdots \) の先頭文字 \( \mathrm{First} ( \beta \cdots ) \) も追加で調べます。つまり、\[
\mathrm{First} ( \alpha \beta \cdots ) = \left( \mathrm{First} ( \alpha ) - \{ \varepsilon \} \right) \cup \mathrm{First} ( \beta \cdots )
\]が成立します。
※ \( \varepsilon \) を引いた理由は、2文字目 \( \beta \) の先頭に空文字 \( \varepsilon \) が来ない場合、文字列 \( \alpha \beta \cdots \) に \( \beta \) の文字列が残り、文字列 \( \alpha \beta \cdots \) が空文字 \( \varepsilon \) になることはないからです。
まとめると、2文字以上の文字列 \( \alpha \beta \cdots \) のFirst集合 \( \mathrm{First} ( \alpha \beta \cdots ) \) は、\[
\mathrm{First} ( \alpha \beta \cdots ) = \left\{ \begin{array}{ccc} \mathrm{First} ( \alpha ) & \varepsilon \notin \mathrm{First} ( \alpha ) \\ \left( \mathrm{First} ( \alpha ) - \{ \varepsilon \} \right) \cup \mathrm{First} ( \beta \cdots ) & \varepsilon \in \mathrm{First} ( \alpha ) \end{array} \right.
\]で求めることができます。
※ 以後、この規則を用いた変換をする場合は \( \overset{ \mathrm{R3} }{=} \) と = の上にR3(規則3)を用いていることを示します。
注意: 左再帰 A → Aα が含まれる場合のFirst集合
\( \textcolor{red}{A} \to \textcolor{blue}{A} bc \) のように「生成先の文字列の先頭が生成元の文字列になっている」場合、First集合を求めていくと\[\begin{align*}
\mathrm{First} (A) & \overset{ \mathrm{R2} }{=} \mathrm{First} (Abc)
\\ & \overset{ \mathrm{R3} }{=} \mathrm{First} (A)
\end{align*}\]となり、求めたい集合 \( \mathrm{First} (A) \) が計算途中に出てくるというよくわからないことが起こります。
この形になった場合は、計算途中に出てくる \( \mathrm{First} (A) \) は無視してOKです。例えば、\[
\mathrm{First} (A) = \underbrace{ \mathrm{First} (A) }_{ \mathrm{無視} } \cup \mathrm{First} (b)
\]となった場合は、左辺にも右辺にも出てくる \( \mathrm{First} (A) \) を無視し、\[
\mathrm{First} (A) = \mathrm{First} (b)
\]として計算してください[3] \( A \to Ab \) のように左再帰文法となる規則を適用しても、先頭文字列は \( A \) のまま変わらないため、無視しても問題ない。。
また、\[
\textcolor{red}{A \to Bb, \ \ \ B \to Aa} , \ \ \ A \to c
\]のように、見た目に左再帰になる生成規則は含まれてはいないものの、変形していくと、\[
\textcolor{red}{A} \to Bb \to \textcolor{red}{A}ab
\]のように間接的に左再帰の形が出てくる場合、\[\begin{align*}
\mathrm{First} ( A ) & = \mathrm{First} (B) \cup \mathrm{First} (c) \\
\mathrm{First} (B) & = \mathrm{First} (A)
\end{align*}\]のように、一意には答えを決定できないような形が出てくることがあります。
しかし、左再帰になる規則の部分だけに着目してみると、\( \mathrm{First} (A) = \mathrm{First} (B) \), \( \mathrm{First} (B) = \mathrm{First} (A) \) 以外の式が出てこず、特に新しい要素が足される気配(例えば \( \mathrm{First} (c) \) はありません。
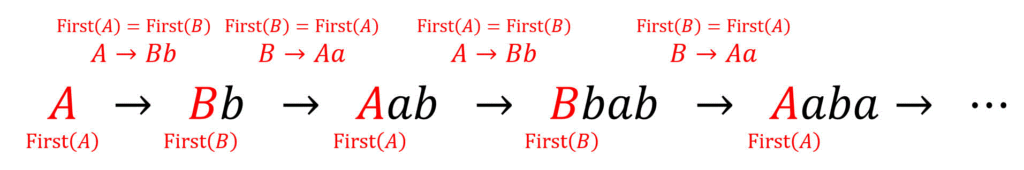
そのため、間接的な左再帰が出てきた際(=一意に答えが決定できないような形が出てきた場合)には、間接的な左再帰が出てくる式(例えば \( A \to B b \), \( B \to Aa \))をすべて無視し、残りの生成規則からFirst集合を求めてください。ただし、間接的な左再帰に寄与している非終端記号(今回の例だと \(A \), \( B \))同士のFirst集合は等しくなる点は忘れないでください。
今回の場合は、\( A \to Bb \), \( B \to Aa \), \( A \to c \) のうちの赤文字部分が間接的な左再帰なため、まずは間接的な左再帰とは関係ない生成規則 \( A \to c \) から\[\begin{align*}
\mathrm{First} (A) & \overset{ \mathrm{R1} }{=} \mathrm{First} (c)
\\ & = \{ c \}
\end{align*}\]と求めます。さらに、間接的な左再帰に寄与している \(A \), \( B \) のFirst集合は等しくなるため、\[
\mathrm{First} (B) = \mathrm{First} (A) = \{ c \}
\]と求めることができます[4]いったん\[\begin{align*}\mathrm{First} (A) & = \mathrm{First} (B) \cup \mathrm{First} (c)\\ & = \underbrace{ \mathrm{First} (A) }_{ \mathrm{無視} } \cup \mathrm{First} (c)\\ & = … Continue reading。
公式1[R1] 終端記号1文字 \( a \) のFirst集合の要素はそのまま \( a \) \[
\mathrm{First} ( a ) \overset{ \mathrm{R1} }{=} \{ a \}
\]
※1: 例題・練習問題で公式1を適用する場合は \( \overset{ \mathrm{R1} }{=} \) と表記
※2: \( \mathrm{First} ( \varepsilon ) = \{ \varepsilon \} \) である。
※3: \( \mathrm{First} ( \alpha ) = \{ \varepsilon \} \) は、\( \alpha \) が空文字であることを表す( \( \alpha = \varepsilon \) )
公式2[R2] 非終端記号1文字 \( A \) のFirst集合の要素は、\( A \) から生成される生成規則 \( A \to \textcolor{red}{\alpha} \), \( A \to \textcolor{blue}{\beta} \), \( A \to \textcolor{green}{\gamma} \), … の生成先(右辺)のFirst集合の和\[
\mathrm{First} ( A ) \overset{ \mathrm{R2} }{=} \underbrace{ \mathrm{First} ( \alpha ) }_{A \to \textcolor{red}{\alpha}} \cup \underbrace{ \mathrm{First} ( \beta ) }_{A \to \textcolor{blue}{\beta}} \cup \underbrace{ \mathrm{First} ( \gamma ) }_{A \to \textcolor{gamma}{\gamma}} \cup \cdots
\]
※1. 例題・練習問題で公式2を適用する場合は \( \overset{ \mathrm{R2} }{=} \) と表記
※2. \( \textcolor{magenta}{A} \to \textcolor{magenta}{A} \alpha \) のような左再帰が含まれる文法が出てきた場合は無視する(間接的な左再帰、例えば \( A \to B \alpha \), \( B \to A \beta \) など)が出てきた場合も無視するが、間接的な左再帰に寄与する非終端記号(例の場合だと \( A \), \( B \))同士のFirst集合は等しくなる。)。
公式3[R3] 2文字以上の文字列 \( \alpha \beta \) のFirst集合の要素は、1文字目 \( \alpha \) に空文字の可能性がなければ1文字目のFirst集合、1文字目 \( \alpha \) に空文字の可能性があれば1文字目 \( \alpha \) と2文字目 \( \beta \) のFirst集合\[
\mathrm{First} ( \alpha \beta \cdots ) \overset{ \mathrm{R3} }{=} \left\{ \begin{array}{ccc} \mathrm{First} ( \alpha ) & ( \textcolor{red}{ \varepsilon \notin \mathrm{First} ( \alpha ) } ) \\ \mathrm{First} ( \alpha ) \cup \mathrm{First} ( \beta \cdots ) & ( \textcolor{blue}{ \varepsilon \in \mathrm{First} ( \alpha ) } )\end{array} \right.
\]
※1: 例題・練習問題で公式3を適用する場合は \( \overset{ \mathrm{R3} }{=} \) と表記
※2: 1文字目も2文字目も空文字の可能性があれば、1文字目~3文字目のFirst集合の和を取ればOK[5]一般化すると、1文字目からn文字目までの文字すべてに空文字があれば、1文字目~n+1文字目の和を取ればOK。。
(3) 例題で確認!
ここからは、1題例題を実際に解いてみましょう。
次の文法 \( G \) がある。\[
G = \left( \ \{ S,A,B \} \ , \ \{ a,b,c,d \} \ , \ P \ , \ S \ \right)
\]\[\begin{align*}
P = \{ \ \ \ \ S & \to aA \\ A & \to bBa \ | \ \varepsilon \\ B & \to Sc \ | \ d \ \ \ \ \ \ \ \}
\end{align*}
\]この文法 \( G \) に対し、
(1) \( \mathrm{First} (S) \)
(2) \( \mathrm{First} (A) \)
(3) \( \mathrm{First} (B) \)
をそれぞれ求めなさい。
解説の前に、First集合を求める手順について確認しておきましょう。
ある非終端記号 \( A \) のFirst集合 \( \mathrm{First} (A) \) は次の手順で求める。
Step1. \( A \) が生成元となる規則\[\begin{align*}
A & \to \alpha \\ A & \to \beta \\ A & \to \gamma \\ & \ \ \vdots
\end{align*}\]をすべて探す。
Step2. Step1で探したすべての生成規則の生成先(右辺)\( \alpha \), \( \beta \), \( \gamma \) のFirst集合 \( \mathrm{First} ( \alpha ) \), \( \mathrm{First} ( \beta ) \), \( \mathrm{First} ( \gamma ) \) を求める。
Step3. Step2で求めたFirst集合の和を取る。\[
\mathrm{First} (A) = \underbrace{ \mathrm{First} (\alpha) }_{A \to \alpha} \cup \underbrace{ \mathrm{First} (\beta) }_{A \to \beta} \cup \underbrace{ \mathrm{First} (\gamma) }_{A \to \gamma} \cup \cdots
\]
First(S) の求め方
\( S \) が生成元になる規則は、\( S \to \textcolor{red}{ aA } \) ただ1つですね。
そのため、\[\begin{align*}
\mathrm{First} (S) & \overset{ \mathrm{R2} }{=} \underbrace{ \mathrm{First} ( \textcolor{red}{aA} ) }_{S \to \textcolor{red}{aA} }
\\ & \overset{ \mathrm{R3} }{=} \mathrm{First} (a)
\\ & \overset{ \mathrm{R1} }{=} \{ a \}
\end{align*}\]で計算できます。
First(A) の求め方
\( A \) が生成元になる規則は、\( A \to bBa \ | \ \varepsilon \)、つまり \( A \to \textcolor{red}{bBa} \) と \( A \to \textcolor{blue}{\varepsilon} \) の2つですね。
そのため、\[\begin{align*}
\mathrm{First} (A) & \overset{ \mathrm{R2} }{=} \underbrace{ \mathrm{First} ( \textcolor{red}{bBa} ) }_{A \to \textcolor{red}{bBa} } \cup \underbrace{ \mathrm{First} (\textcolor{blue}{\varepsilon}) }_{A \to \textcolor{blue}{\varepsilon}}
\end{align*}\]を求めればOKです。
ここで、それぞれのFirst集合は、\[\begin{align*}
\mathrm{First} (bBa) & \overset{ \mathrm{R3} }{=} \mathrm{First} (b)
\\ & \overset{ \mathrm{R1} }{=} \{ b \}
\end{align*}\]\[\begin{align*}
\mathrm{First} ( \varepsilon ) & \overset{ \mathrm{R1} }{=} \{ \varepsilon \}
\end{align*}\]となるため、求めたいFirst集合は\[\begin{align*}
\mathrm{First} (A) & \overset{ \mathrm{R2} }{=} \mathrm{First} (bBa) \cup \mathrm{First} (\varepsilon )
\\ & = \{ b \} \cup \{ \varepsilon \}
\\ & = \{ b, \varepsilon \}
\end{align*}\]と計算できます。
First(B) の求め方
\( B \) が生成元になる規則は、\( B \to Sc \ | \ d \)、つまり \( B \to \textcolor{red}{Sc} \) と \( B \to \textcolor{blue}{d} \) の2つですね。
そのため、\[\begin{align*}
\mathrm{First} (B) & \overset{ \mathrm{R2} }{=} \underbrace{ \mathrm{First} ( \textcolor{red}{Sc} ) }_{B \to \textcolor{red}{Sc}} \cup \underbrace{ \mathrm{First} ( \textcolor{blue}{d} ) }_{B \to \textcolor{blue}{d}}
\end{align*}\]を求めればOKです。
ここで、それぞれのFirst集合は、\[\begin{align*}
\mathrm{First} (Sc) & \overset{ \mathrm{R3} }{=} \mathrm{First} (S)
\\ & \overset{(1) }{=} \{ a \}
\end{align*}\]\[\begin{align*}
\mathrm{First} ( d ) & \overset{ \mathrm{R1} }{=} \{ d \}
\end{align*}\]となるため、求めたいFirst集合は\[\begin{align*}
\mathrm{First} (B) & \overset{ \mathrm{R2} }{=} \mathrm{First} (Sc) \cup \mathrm{First} ( d )
\\ & = \{ a \} \cup \{ d \}
\\ & = \{ a,d \}
\end{align*}\]と計算できます。
※ \( \overset{(1) }{=}\) は、(1)の答え \( \mathrm{First} \ (S) = \{ a \} \) を使っていることを表しています。
スポンサードリンク
3. Follow集合
(1) Follow 集合とはなにか
Follow集合 \( \mathrm{Follow} ( A ) \) は、「ある非終端記号1文字 \( \textcolor{magenta}{A} \) 以降の文字をの直後に来る可能性がある文字(終端記号)の候補を集めた集合」を表します。
数式で書くと、\[
\mathrm{Follow} ( \textcolor{magenta}{A} ) = \left\{ \textcolor{orange}{a} \mid \textcolor{orange}{a} \in \textcolor{green}{V_T} , \textcolor{magenta}{\alpha} \overset{*}{\Rightarrow} \cdots A \textcolor{orange}{a} \cdots \right\}
\]となります。(色部分を日本語の説明に対応させています)
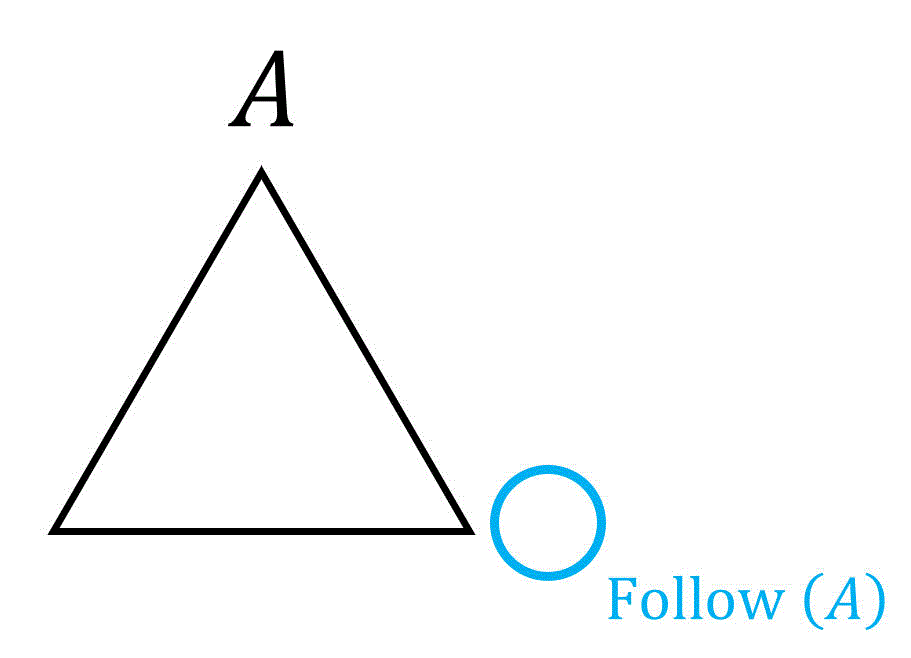
(水色の丸部分に来る終端記号の文字の候補を表す)
例えば、\( \mathrm{Follow} ( A ) = \{ a, b \} \) の場合、\( A \) の後ろの文字列をすべて終端記号にした際、\( A \) の直後に来る文字列が \( a \), \( b \) のいずれかであることを表します。
1点注意が必要なのは、Follow集合の要素に「空文字 \( \varepsilon \)」が出てくることは絶対にありません。
その代わりに、「\( A \) の直後に来る文字はありません(=\( A \) が文字列の終端になりますよ)」というのを表す記号 \( \$ \) がFollow集合の要素で使われます。
(2) Follow 集合で頭にいれておくべき3つの公式
各非終端記号に対してFollow集合を求めていくときには、公式1~公式3で出てきた要素すべての和を取ることで求めます。
そこで、この「(2) Follow集合で頭にいれておくべき3つの公式」では、公式1~公式3の式の紹介だけでなく、何故この式でFollow集合が求められるのかまで説明していきます。
公式1. 出発記号 S の直後は必ず文字列の終端 $
文脈自由文法では、下のようにどの文字列も出発記号 \( S \) から与えられた生成規則により変換されていき、導出されます。\[
S \xrightarrow{S \to AaB} AaB \xrightarrow{A \to aA} aAaB \xrightarrow{A \to a} aaaB \xrightarrow{B \to b} aaab
\]
そのため、出発記号の後ろは必ず文字列の終端となりますね。

そのため、最初に出発記号に対するFollow集合 \( \mathrm{Follow} (S) \) に対しては、文字列の終端を表す \( \$ \) を要素に追加します。\[
\mathrm{Follow} (S) + = \{ \$ \}
\]
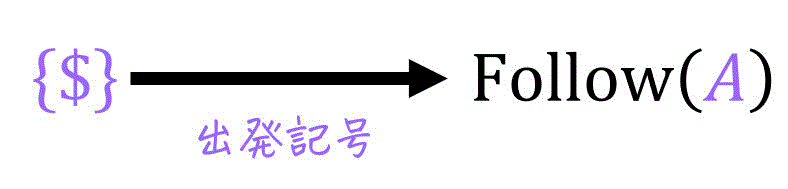
※1: 出発記号ではない非終端記号に対しては何もしなくてOKです。
※2: \( X += Y \) は、(集合 \( X \) に含まれない)集合 \( Y \) の要素を集合 \( X \) に加えることを表します。数式で書くと、\( X = X \cup Y \) です。
公式2. 直後の文字が空文字にならない場合
Follow集合は、「ある非終端記号の直後に来る(終端記号の)文字の候補」を表すため、Follow集合を求める際には、まずは生成規則の生成元ではなく、生成先側の文字列に着目します。
例えば、\( S \to a \textcolor{magenta}{A} \textcolor{blue}{c} B \) という規則があったとします。この規則を適用すると、\( \textcolor{magenta}{A} \) の直後には必ず \( \textcolor{blue}{c} B \) という文字が来ますよね。
このように、\( S \to a \textcolor{magenta}{A} \textcolor{blue}{c} B \) のような求めたい非終端記号 \( \textcolor{magenta}{A} \) が生成されている規則を見つけ、その直後に来る文字(今回は \( c \))を見つけ出す(+非終端記号であれば終端記号に変換する)ことでFollow集合を求められそうですね。
もう少し一般化して、\( \mathrm{Follow} (A) \) の求め方を公式化していきましょう。
まず、求めたい非終端記号 \( \textcolor{magenta}{A} \) が生成されている規則を探し出し、生成先の文字列を \( \textcolor{magenta}{A} \) より前にある文字列 \( \textcolor{gray}{\alpha} \) と \( \textcolor{magenta}{A} \) より後ろにある文字列 \( \textcolor{blue}{\beta} \) に分け、\( S \to \textcolor{gray}{\alpha} \textcolor{magenta}{A} \textcolor{blue}{\beta} \) の形にします。
例えば、\( S \to a \textcolor{magenta}{A} cB \) であれば、\[
S \to \textcolor{gray}{ \underbrace{a}_{\alpha}} \textcolor{magenta}{A} \textcolor{blue}{\underbrace{cB}_{\beta}}
\]より、\( \textcolor{gray}{\alpha = a} \), \( \textcolor{blue}{\beta = cB} \) となります。
※1 \( \textcolor{gray}{\alpha} \) はFollow集合の計算ではいらない子なので、求めなくてもOK。
※2 \( \alpha \), \( \beta \) に空文字が来てもOK。例えば、\( S \to \textcolor{gray}{a} \textcolor{magenta}{A} \) であれば、\( \textcolor{gray}{\alpha = a } \), \( \textcolor{blue}{\beta = \varepsilon} \) となる。
ここで、\( \mathrm{Follow} (A) \) というのは、\( A \) の直後に出てくる文字列でしたね。
また、先ほど生成規則を \( S \to \textcolor{gray}{\alpha} \textcolor{magenta}{A} \textcolor{blue}{\beta} \) と書き換えましたね。つまり、「 \( \textcolor{magenta}{A} \) の直後に出てくる文字列」というのは、「\( \textcolor{blue}{\beta} \) の先頭に来る文字列」と言い換えることができますね。さらにもう1段階言い換えると、「\( \textcolor{blue}{\beta} \) の先頭に来る文字列」は \( \mathrm{First} ( \textcolor{blue}{\beta} ) \) と書くことができますね。
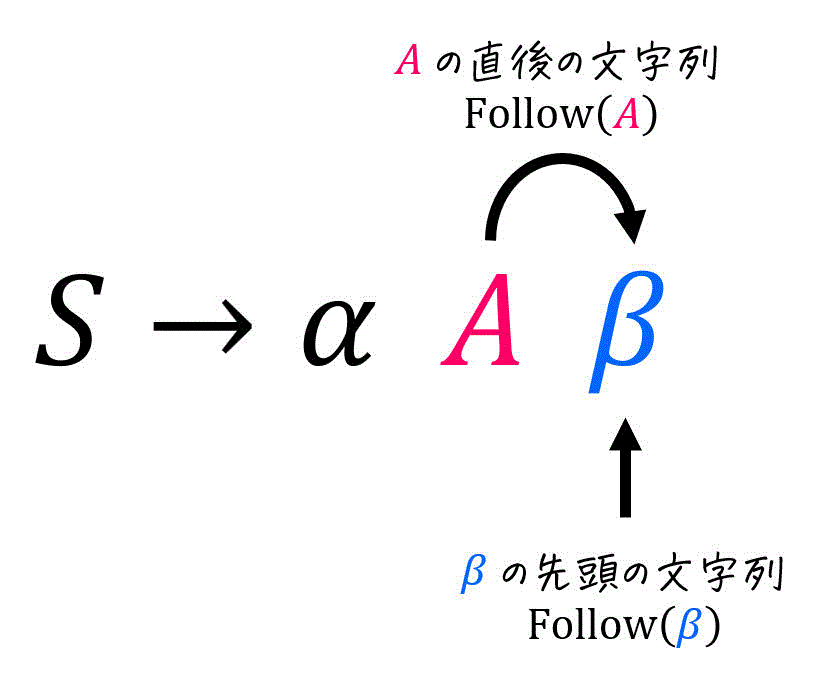
そのため、生成規則 \( S \to \alpha \textcolor{magenta}{A} \textcolor{blue}{\beta} \) に対して、Follow集合に\[
\mathrm{Follow} ( \textcolor{magenta}{A} ) + = \mathrm{First} ( \textcolor{blue}{\beta} )
\]と \( \mathrm{First} ( \textcolor{blue}{\beta} ) \) を追加します。
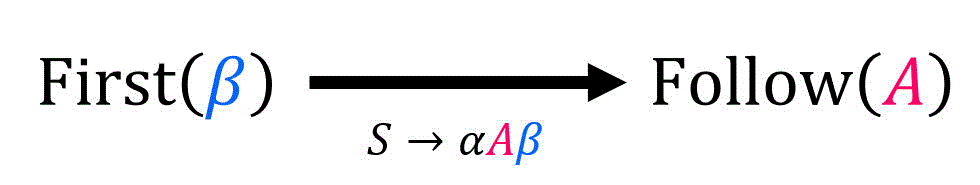
ただし、First集合の要素に \( \varepsilon \) が含まれる場合は、\( \varepsilon \) を無視してからFollow集合に追加してください。例えば、\( S \to \alpha A \beta \) に対して、\( \mathrm{First} ( \beta ) = \{ b, c, \varepsilon \} \) であれば、\[\begin{align*}
\mathrm{Follow} ( A) + & = \mathrm{First} ( \beta )
\\ & = \{ b,c \}
\end{align*}\]と、Follow集合に \( b \), \( c \) の要素を加えます。そのため、\( S \to \alpha A \) のように \( A \) の直後の文字列 \( \beta \) がそもそも存在しない場合は、この公式でFollow集合の追加は行われません[6]\( \beta \) がそもそも存在しない、つまり \( \beta = \varepsilon \) のときは、\( \mathrm{First} ( \beta ) = \mathrm{First} ( \varepsilon ) \overset{ \mathrm{R1} }{=} \{ … Continue reading。
さらに、\( \mathrm{First} ( \beta ) \) に \( \varepsilon \) が含まれる(= \( \beta \) が空文字になる可能性がある)場合や、\( S \to \alpha A \) のように、 そもそも \( A \) が生成先の文字列の末尾になる場合は公式2を確認します。
公式3. 直後の文字が空文字になる可能性がある場合
生成規則 \( S \to \alpha A \textcolor{blue}{\beta} \) において、
- \( \textcolor{blue}{\beta} \) 部分がそもそも存在しない
(つまり \( A \to \alpha A \) となるとき) - \( \textcolor{blue}{\beta} \) 部分が存在していた場合でも \( S \to \alpha \alpha A \textcolor{blue}{B} \), \( B \to \varepsilon \) のように \( \textcolor{blue}{\beta} \) に空文字が来る可能性がある場合
(つまり \( \varepsilon \in \mathrm{First} ( \beta ) \) となる場合)
は、生成先 \( \alpha A \textcolor{blue}{\beta} \) に着目するだけでは、\( A \) の直後に来る文字列(= \( \mathrm{Follow} (A) \))がわかりません。
ここで、\( S \) の直後の文字を \( \textcolor{blue}{X} \) としてから、\( S \textcolor{magenta}{X} \) に生成規則 \( \textcolor{purple}{S \to aA} \) を適用することを考えましょう。すると、\[ \textcolor{purple}{S} \textcolor{blue}{X} \to \textcolor{purple}{aA} \textcolor{blue}{X} \]となり、「\( A \) の直後の文字」が「\( S \) の直後の文字」と同じになっていることがわかりますね。
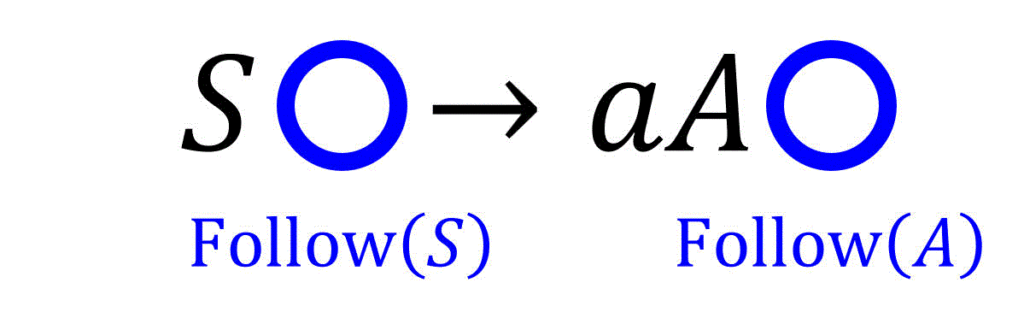
つまり、\( S \to \varepsilon \in \mathrm{First} ( \beta ) \) 、つまり \( \beta \) 部分が空文字になる(つまり \( \textcolor{blue}{S} \to a \textcolor{magenta}{A} \) となる)可能性がある場合は\[
\mathrm{Follow} ( \textcolor{magenta}{A} ) += \mathrm{Follow} ( \textcolor{blue}{S} )
\]と、生成元 \( \textcolor{blue}{S} \) の非終端記号の直後の文字、つまり \( \mathrm{Follow} (\textcolor{blue}{S}) \) を \( \mathrm{Follow} (\textcolor{blue}{A}) \) に追加します。
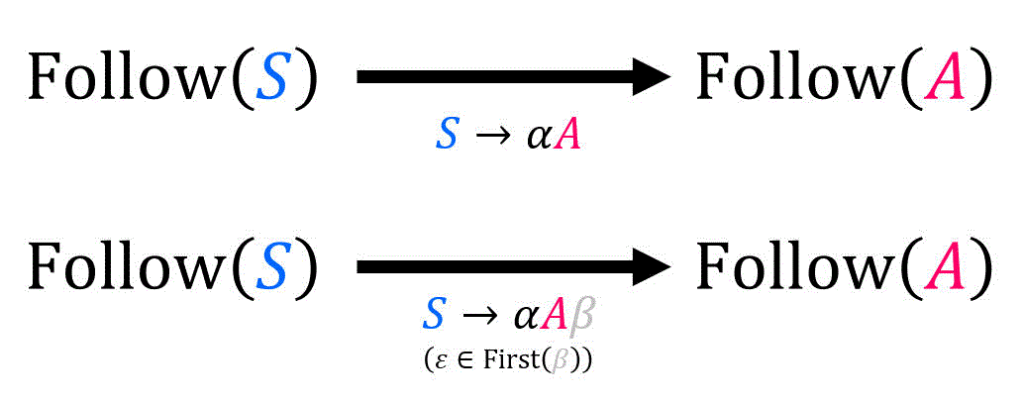
(本記事では分かりやすさ重視のため、2つに分けています)
注意: 右再帰 A → αAが含まれる場合
\( \textcolor{red}{A} \to ab \textcolor{blue}{A} \) のように「生成先の文字列の終端が生成元の文字列になっている」生成規則の場合、\[\begin{align*}
\mathrm{Follow} (A) + & = \mathrm{Follow} (A)
\\ & = \mathrm{Follow} (A) \cup \mathrm{Follow} (A)
\end{align*}\]となるため、\( \mathrm{Follow} (A) \) に要素が一切追加されません。
そのため、右再帰 \( A \to \alpha A \) となる文法に対しては、Follow集合を求める際には無視してください。
特に注意が必要なのが、\[
A \to aB , \ \ \ B \to bA
\]のように見た目は右再帰な規則は含まれていないものの、変形してみると\[
A \to aB \to abA
\]のように間接的に右再帰な規則が含まれる場合です。
この場合、生成規則 \( A \to aB \) に対しては\( \textcolor{blue}{A} \to a \textcolor{magenta}{B} \) より\[\begin{align*}
\mathrm{Follow} ( \textcolor{magenta}{B} ) + & = \mathrm{Follow} ( \textcolor{blue}{A} )
\\ & = \mathrm{Follow} (B) \cup \mathrm{Follow} (A)
\end{align*}\]が成立するため、\( \mathrm{Follow} (B) \) に対して、\( \mathrm{Follow} (A) \) の要素を追加されるような式が出てきます。
さらに、\( \mathrm{Follow} (A) \) を求めていきましょう。\( \textcolor{blue}{B} \to b \textcolor{magenta}{A} \) より\[\begin{align*}
\mathrm{Follow} ( \textcolor{magenta}{A} ) + & = \mathrm{Follow} ( \textcolor{blue}{B} )
\\ & = \mathrm{Follow} (A) \cup \mathrm{Follow} (B)
\end{align*}\] なり、\( \mathrm{Follow} (A) \) に対して \( \mathrm{Follow} (B) \) を追加するような式が出てきます。
すると、
- \( \mathrm{Follow} (A) \) を求めるためには追加される要素である \( \mathrm{Follow} (B) \) を求める必要がある
- \( \mathrm{Follow} (B) \) を求めるためには追加される要素である \( \mathrm{Follow} (A) \) を求める必要がある
という「無限ループ」が発生し、訳が分からないことが起こってしまいます。
ここで、式ではなく意味的に考えてみましょう。ある非終端記号 \( A \) Follow集合 \( \mathrm{Follow} (A) \) とは、「\( A \) の直後に来る非終端記号の候補を集めた集合」でしたね。
そこで、ある非終端記号 \( A \) を間接的な右再帰規則 \( A \to aB \), \( B \to bA \) だけで変換していくことで、Follow集合がどうなるかを見てみましょう。
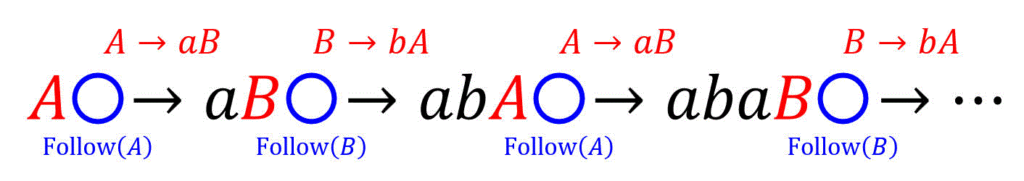
すると、\( A \to aB \) の変化から、\( A \) の直後の非終端記号(\( \mathrm{Follow} (A) \))と \( B \) の直後の非終端記号(\( \mathrm{Follow} (B) \) には変化がないことがわかりますね。また\( aB \to abA \) の変化から、\( B \) の直後の非終端記号(\( \mathrm{Follow} (B) \))と \( A \) の直後の非終端記号(\( \mathrm{Follow} (A) \) にも変化がないことがわかりますね。
よって、\( A \to aB \), \( B \to bA \) のような間接的な右再帰規則が含まれている場合、Follow集合に追加されるような要素は存在しないこと、および \( \mathrm{Follow} (A) \), \( \mathrm{Follow} (B) \) が等しくなることがわかりますね[7]\( \textcolor{blue}{A} \to a \textcolor{magenta}{B} \) より、\[\begin{align*}\mathrm{Follow} ( \textcolor{magenta}{B} ) + & = \mathrm{Follow} ( \textcolor{magenta}{A} )\\ & = … Continue reading。
そのため、Follow集合を求める際には、直接的な右再帰規則 \( A \to \alpha A \) だけでなく、間接的な右再帰規則 \( A \to aB \), \( B \to bA \) が含まれている場合(=一意に答えが決定できないような形が出てきた場合)でも、間接的な左再帰が出てくる式(例えば \( A \to aB \), \( B \to bA \) )をすべて無視し、残りの生成規則からFollow集合を求めてください。ただし、間接的な左再帰に寄与している非終端記号(今回の例だと \(A \), \( B \))同士のFirst集合は等しくなる点は忘れないでください。
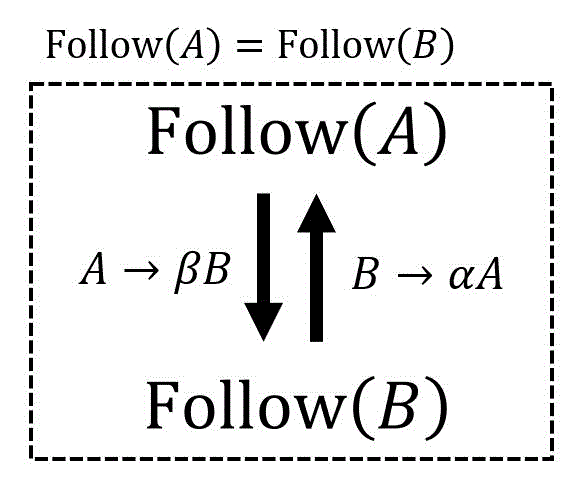
Follow集合は等しくなる(=一心同体)
Follow集合は[公式1]~[公式3]で出てきた要素の和で求められる。
※ ただし、\( X += Y \) は、\[
X = X \cup Y
\]を表す。(集合 \( Y \) の要素を集合 \( X \) に加える)
[公式1] 出発記号 \( S \) の場合は文字列の終端を表す \( \$ \) を追加する。\[\begin{align*}
\mathrm{Follow} (S) += \{ \$ \} \end{align*}\]

- \( A \) より前の文字列 \( \alpha \)
- \( A \) より後ろの文字列 \( \beta \)
に分けて \( S \to \textcolor{gray}{\alpha} \textcolor{magenta}{A} \textcolor{blue}{\beta} \) の形に分けたあと、公式1・公式2のどちらか(もしくは両方)を適用し、\( \mathrm{Follow} (\textcolor{magenta}{A}) \) に集合を追加する。
※ \( \textcolor{gray}{\alpha} \) と \( \beta \) は空文字でもOK。
例1: \( B \to \textcolor{magenta}{A} \textcolor{blue}{c} \) のとき: \( \textcolor{gray}{\alpha = \varepsilon} \), \( \textcolor{blue}{\beta = c} \)
例2: \( B \to \textcolor{gray}{d} \textcolor{magenta}{A} \) のとき: \( \textcolor{gray}{\alpha = d} \), \( \textcolor{blue}{\beta = \varepsilon} \)
例3: \( B \to\textcolor{magenta}{A} \) のとき: \( \textcolor{gray}{\alpha = \varepsilon} \), \( \textcolor{blue}{\beta = \varepsilon} \)
[公式2]
\( \textcolor{blue}{\beta} \) (空文字ではない)何かしらの文字列があれば、\( \mathrm{First} ( \beta) \) を除くすべての集合を \( \mathrm{Follow} (\textcolor{magenta}{A}) \) に加える。\[
\mathrm{Follow} (\textcolor{magenta}{A}) += \mathrm{First} ( \textcolor{blue}{\beta}) - \{ \varepsilon \}
\]※ \( \beta \) がそもそも空文字(つまり \( S \to \alpha A \))の場合はこの公式を適用しない。
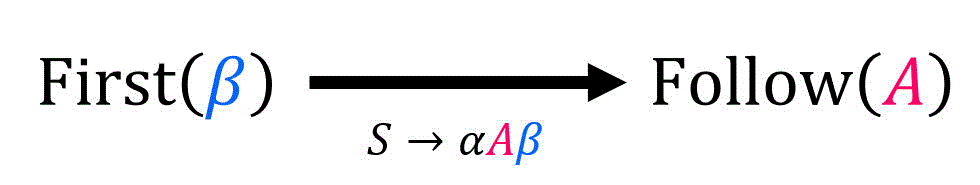
[公式3]
\( \beta \) がそもそも空文字(つまり \( \textcolor{blue}{S} \to \alpha \textcolor{magenta}{A} \))もしくは空文字ではないが \( \mathrm{First} ( \beta ) \) の要素に \( \varepsilon \) が含まれる場合は、集合 \( S \) のFollow集合 \( \mathrm{Follow} (\textcolor{blue}{S}) \) を \( \mathrm{Follow} (\textcolor{magenta}{A}) \) に加える。 \[
\mathrm{Follow} (\textcolor{magenta}{A}) += \mathrm{Follow} (\textcolor{blue}{S})
\]

※ \( \textcolor{red}{A} \to \alpha \textcolor{red}{A} \) のような→再帰が含まれる文法が出てきた場合は無視する(間接的な右再帰、例えば \( A \to \alpha B \), \( B \to \beta A \) など)が出てきた場合も無視するが、間接的な左再帰に寄与する非終端記号(例の場合だと \( A \), \( B \))同士のFollow集合は等しくなる。)。
(3) 例題で確認!
ここからは、例題1でも出てきた文法を使って、実際にFollow集合を求め方を見ていきましょう。
次の文法 \( G \) がある。\[
G = \left( \ \{ S, A, B \} \ , \ \{ a,b,c,d \} \ , \ P \ , \ S \ \right)
\]\[\begin{align*}
P = \{ \ \ \ \ S & \to aA \\ A & \to bBa \ | \ \varepsilon \\ B & \to Sc \ | \ d \ \ \ \ \ \ \ \}
\end{align*}
\]この文法 \( G \) に対し、
(1) \( \mathrm{Follow} (S) \)
(2) \( \mathrm{Follow} (A) \)
(3) \( \mathrm{Follow} (B) \)
をそれぞれ求めなさい。
※ 必要であれば例題1で求めた\[\begin{align*}
\mathrm{First} (S) & = \{ a \}
\\ \mathrm{First} (A) & = \{ b, \varepsilon \}
\\ \mathrm{First} (B) & = \{ a,d \}
\end{align*}\]を用いてもよい。
解説の前に、もう1度Follow集合を求める手順について確認しておきましょう。
ある非終端記号 \( A \) のFollow集合 \( \mathrm{Follow} (A) \) はつぎの「準備」の後、下に示す公式[R1]と公式[R2]で出てくる要素を全て追加することで求められる。
[公式1] 出発記号かどうかの確認
\( A \) が出発記号であるか確認し、出発記号であれば要素に \( \$ \) を加えた状態でスタート。それ以外の場合は要素なしでスタート。
- \( A \) が出発記号である: \( \mathrm{Follow} (A) += \{ \$ \} \)
- \( A \) が出発記号でない: なにもしない

[公式2], [公式3] では \( S \to \textcolor{gray}{ab} \textcolor{magenta}{A} \textcolor{blue}{Bc} \) のような生成先に \( \textcolor{blue}{S} \) が出てくる規則それぞれに対し、\( S \to \textcolor{gray}{\alpha} \textcolor{magenta}{A} \textcolor{blue}{\beta} \) のように \( \textcolor{magenta}{A} \) の前の文字列 \( \textcolor{gray}{\alpha} \) と \( \textcolor{magenta}{A} \) の後の文字列 \( \textcolor{blue}{\beta} \) に分けてから考える。
※ \( \textcolor{gray}{\alpha} \), \( \textcolor{blue}{\beta} \) は空文字OK。例えば、\( S \to A \) であれば、\( \textcolor{gray}{\alpha} \), \( \textcolor{blue}{\beta} \) ともに空文字 \( \varepsilon \) となる。
[公式2] \( \beta \not = \varepsilon \) であれば適用
生成規則 \( S \to \textcolor{gray}{\alpha} \textcolor{magenta}{A} \textcolor{blue}{\beta} \) に対し、\( \textcolor{blue}{\beta} \) が空文字ではない場合、\( \mathrm{First} ( \textcolor{blue}{\beta} ) \) の要素を加える。ただし \( \varepsilon \) は加えない。\[
\mathrm{Follow} ( \textcolor{magenta}{A} ) += \mathrm{First} ( \textcolor{blue}{\beta} ) - \{ \varepsilon \}
\]
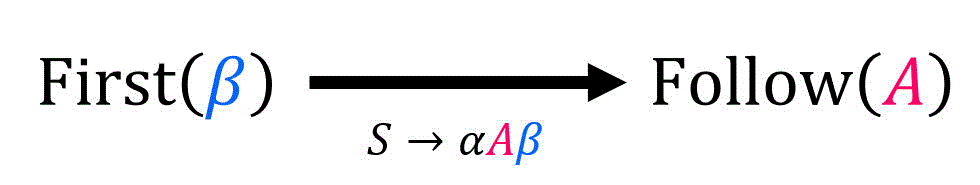
[公式3] \( \varepsilon \in \mathrm{First} ( \beta ) \) であれば適用
\( \textcolor{blue}{S} \to \alpha \textcolor{magenta}{A} \) のように \( \beta = \varepsilon \) となる場合や、\( \textcolor{blue}{S} \to \alpha \textcolor{magenta}{A} \beta \) の形だが \( \varepsilon \in \mathrm{First} ( \textcolor{blue}{\beta} ) \) となる場合は、\( \mathrm{Follow} ( \textcolor{blue}{S} ) \) の要素を加える。\[
\mathrm{Follow} ( \textcolor{magenta}{A} ) += \mathrm{Follow} ( \textcolor{blue}{S})
\]

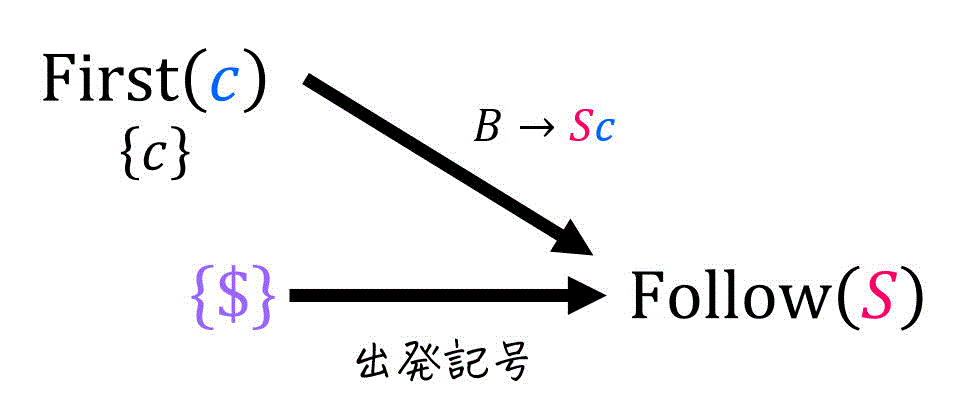
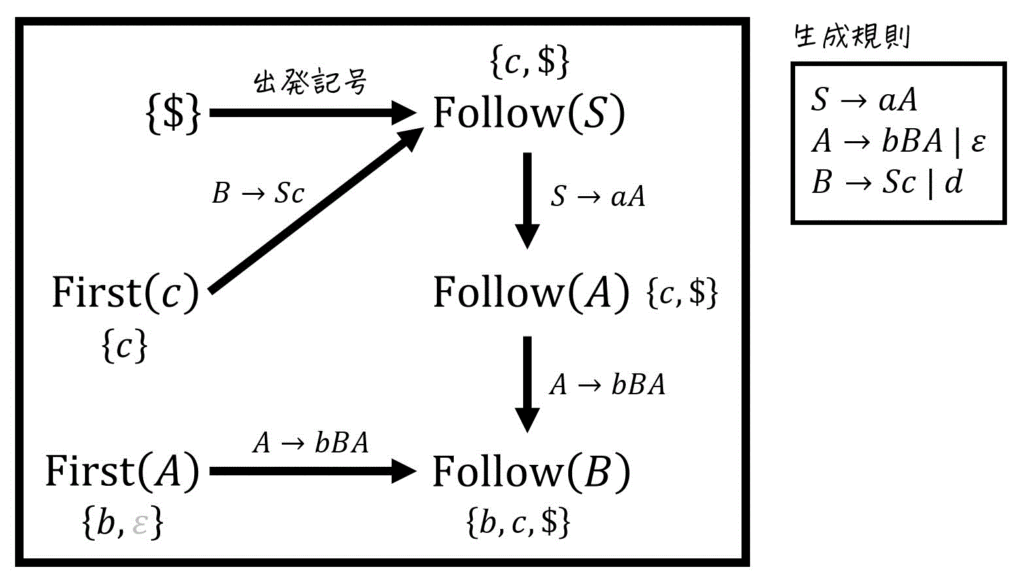
(1) Follow(S) の求め方
まず、\( S \) は出発記号なので、初期状態として要素 \( \$ \) を加えます。
つぎに、\( \textcolor{magenta}{S} \) が生成先に出てくる規則は、\( B \to \textcolor{magenta}{S} c \) 1つだけなので、この生成規則に着目しましょう。
着目した生成規則の生成先 \( \textcolor{magenta}{S} \textcolor{blue}{c} \) において、\( \textcolor{magenta}{S} \) より後の文字列は \( \textcolor{blue}{c} \) ですね。よって、\( \textcolor{blue}{\beta} = \textcolor{blue}{c} \) となります。
[公式2] \( \textcolor{blue}{ \beta = c } \not = \varepsilon \) なので〇
生成規則 \( B \to \textcolor{magenta}{S} \textcolor{blue}{ \underbrace{ c }_{ \beta } } \) より、\( \mathrm{Follow} ( \textcolor{magenta}{S} ) \) に追加される要素は、\[\begin{align*}
\mathrm{Follow} ( \textcolor{magenta}{S} ) + & = \mathrm{First} ( \textcolor{blue}{c} ) - \{ \varepsilon \}
\\ & \overset{ \mathrm{R1} }{=} \{ c \} - \{ \varepsilon \}
\\ & = \{ c \}
\end{align*}\]と求められます。よって、\( \mathrm{Follow} ( \textcolor{magenta}{S} ) \) に \( c \) が追加されます。
[公式3] \( \varepsilon \notin \mathrm{First} ( \textcolor{blue}{c} ) = \{ c \} \) なので×
よって、\[\begin{align*}
\mathrm{Follow} (S) & = \{ $ \} \cup \{ c \}
\\ & = \{ c, \$ \}
\end{align*}\]となります。
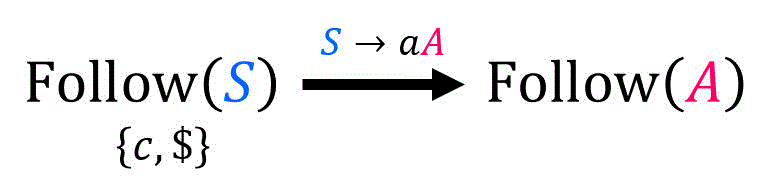
(2) Follow(A) の求め方
[公式1] \( A \) は出発記号ではないため×
つぎに、\( \textcolor{magenta}{A} \) が生成先に出てくる規則は、\( S \to aA \), \( A \to bBA \) の2つがありますが、\( \textcolor{deepskyblue}{A} \to bB \textcolor{deepskyblue}{A} \) は右再帰なので無視します。そのため、[公式2], [公式3] に当てはめる生成規則は \( S \to aA \) だけでOKです。
着目した規則の生成先 \( a \textcolor{magenta}{A} \) において、\( \textcolor{magenta}{A} \) より後の文字列はありません(=空文字です)ね。よって、 \( \textcolor{blue}{\beta} = \textcolor{blue}{\varepsilon} \) です。
[公式2] \( \textcolor{blue}{ \beta = \varepsilon } \) なので×
[公式3] \( \varepsilon \in \mathrm{First} ( \textcolor{blue}{ \varepsilon } ) = \{ \varepsilon \} \) なので〇
生成規則 \( \textcolor{blue}{S} \to a \textcolor{magenta}{A} \) より、\( \mathrm{Follow} ( \textcolor{magenta}{A} ) \) に追加される要素は、
\[\begin{align*}
\mathrm{Follow} ( \textcolor{magenta}{A} ) + & = \mathrm{Follow} ( \textcolor{blue}{S} )
\\ & \overset{ \mathrm{(1)} }{=} \{ c, \$ \}
\end{align*}\]と求められます。よって、\( \mathrm{Follow} ( \textcolor{magenta}{A} ) \) に \( c, \$ \) が追加されます。
したがって、\( \mathrm{Follow} (A) \) は\[\begin{align*}
\mathrm{Follow} (A) & = \{ c, \$ \}
\end{align*}\]と計算できます。
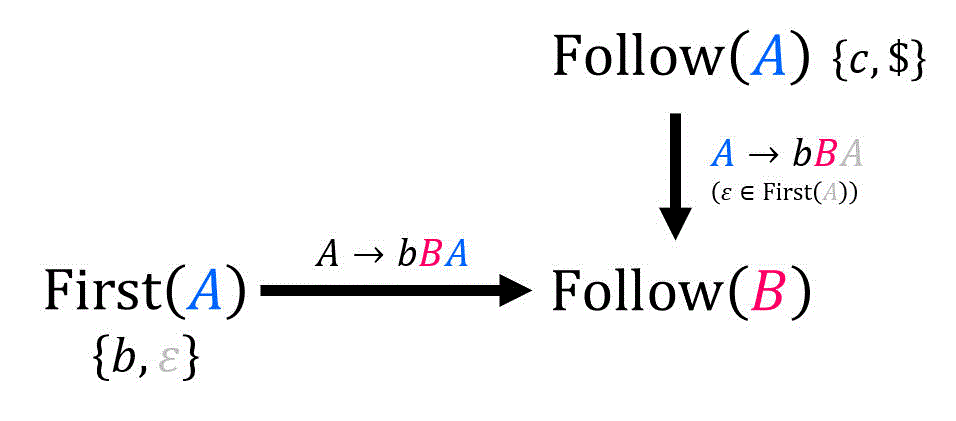
(3) Follow(B) の求め方
[公式1] \( B \) は出発記号ではないため×
ここで、\( \textcolor{magenta}{B} \) が生成先に出てくる規則は、\( A \to b \textcolor{magenta}{B} A \) の1つだけですね。なので [公式2], [公式3] に当てはめる生成規則は \( A \to b \textcolor{magenta}{B} A \) だけです。
着目した生成規則の生成先 \( b \textcolor{magenta}{B} A \) において、\( \textcolor{magenta}{B} \) より後の文字列は \( \textcolor{blue}{A} \) ですね。よって、\( \textcolor{blue}{\beta} = \textcolor{blue}{A} \) となります。
[公式2] \( \textcolor{blue}{ \beta = A } \not = \varepsilon \) なので〇
生成規則 \( A \to \textcolor{gray}{b} \textcolor{magenta}{B} \textcolor{blue}{ \underbrace{ A }_{ \beta } } \) より、\( \mathrm{Follow} ( \textcolor{magenta}{B} ) \) に追加される要素は、\[\begin{align*}
\mathrm{Follow} ( \textcolor{magenta}{B} ) + & = \mathrm{First} ( \textcolor{blue}{A} ) - \{ \varepsilon \}
\\ & = \{ b, \varepsilon \} - \{ \varepsilon \}
\\ & = \{ b \}
\end{align*}\]と求められます。よって、\( \mathrm{Follow} ( \textcolor{magenta}{B} ) \) に \( b \) が追加されます。
[公式3] \( \varepsilon \in \mathrm{First} ( \textcolor{blue}{ A } ) = \{ b, \varepsilon \} \) なので〇
生成規則 \( \textcolor{blue}{A} \to b \textcolor{magenta}{B} A \) より、\( \mathrm{Follow} ( \textcolor{magenta}{B} ) \) に追加される要素は、
\[\begin{align*}
\mathrm{Follow} ( \textcolor{magenta}{B} ) + & = \mathrm{Follow} ( \textcolor{blue}{A} )
\\ & \overset{ \mathrm{(2)} }{=} \{ c, \$ \}
\end{align*}\]と求められます。よって、\( \mathrm{Follow} ( \textcolor{magenta}{B} ) \) に \( c, \$ \) が追加されます。
したがって、\( \mathrm{Follow} (B) \) は\[\begin{align*}
\mathrm{Follow} (B) & = \{ b \} \cup \{ c, \$ \}
\\ & = \{ b, c, \$ \}
\end{align*}\]と計算できます。
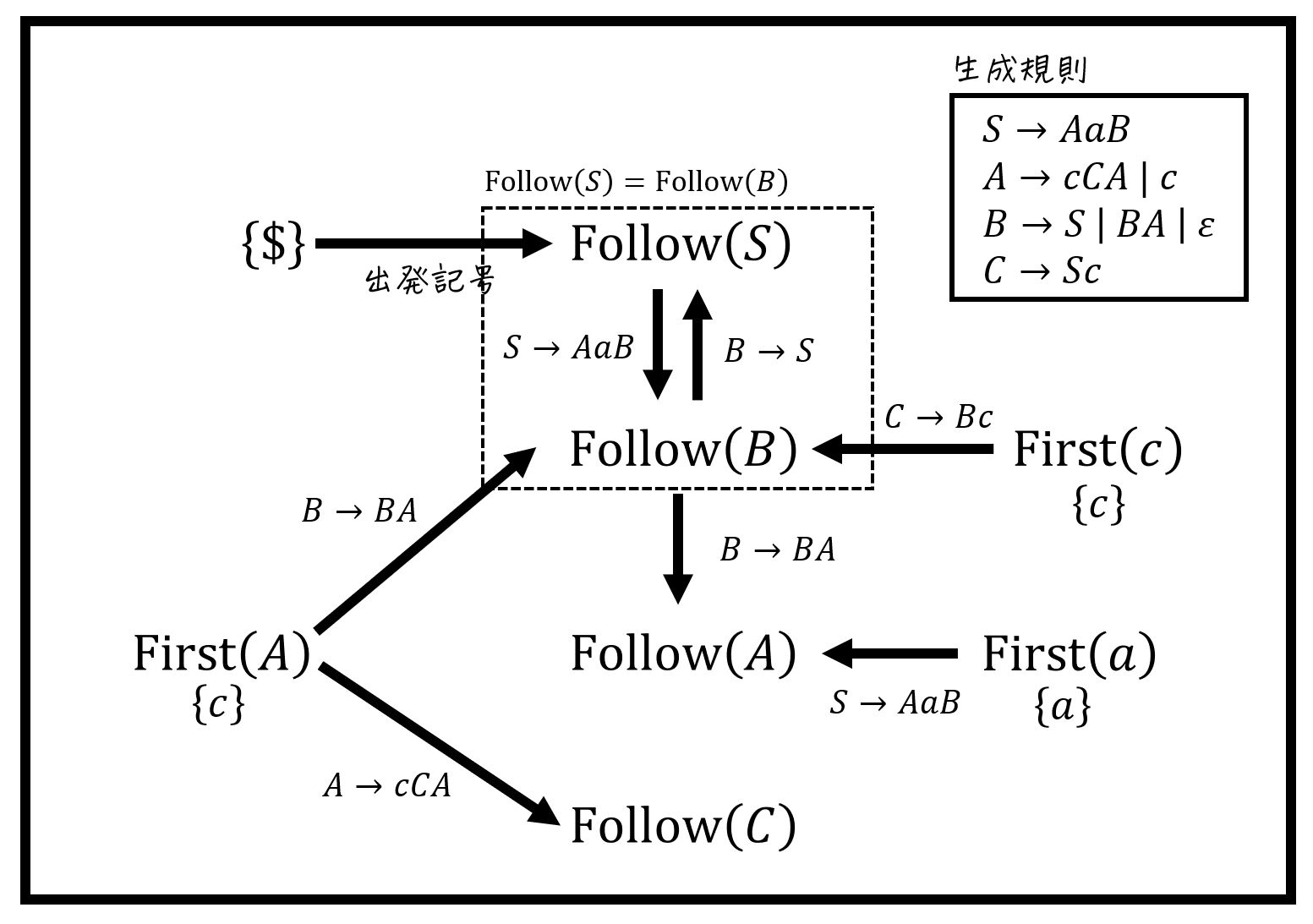
(4) Follow集合の計算ミスを防ぐコツ:図を書く
※ このアイデアは、国島 丈生様のこちらのサイトを参考にさせていただきました。
(FOLLOW()の計算を間違えにくくする工夫)
Follow集合は、First集合に比べて計算が複雑になるため、計算ミスがかなり出てきます[8]実際に私もよく計算ミスします。。
そこで、今回の記事では下の図ように「Follow集合にどの集合の要素が追加されているか」を図で表現しています[9]下の図の場合「\( \mathrm{Follow} (S) \) を求めるためには \( \mathrm{First} (c) \) と \( \{ \$ \} \) の要素を追加すればOK」ということを表しています。。
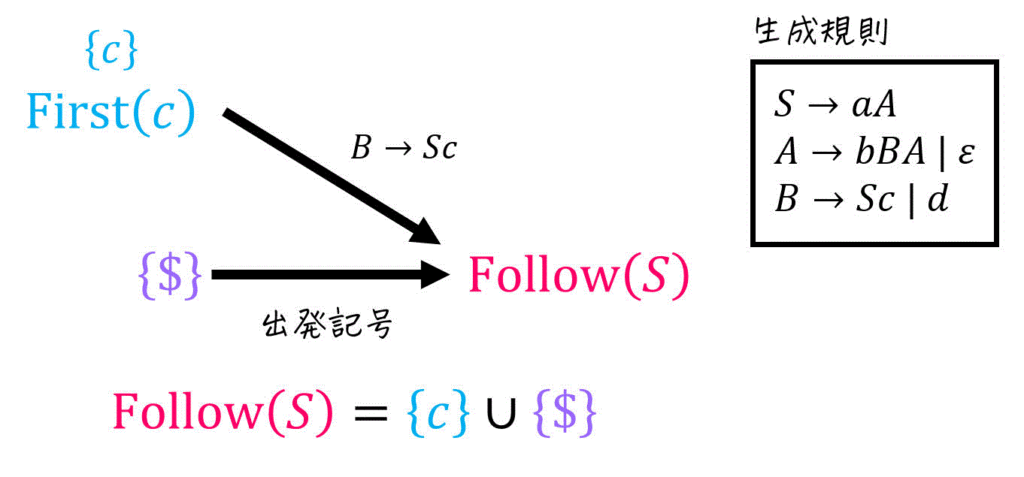
(例題2の(1)に相当)
さらに、各非終端記号ごとに書いたFollow集合の計算図示を下のように1つにまとめることで、Follow集合同士の関係(どのFollow集合の要素がどのFollow集合に加えられているのか)も明確にすることができます。
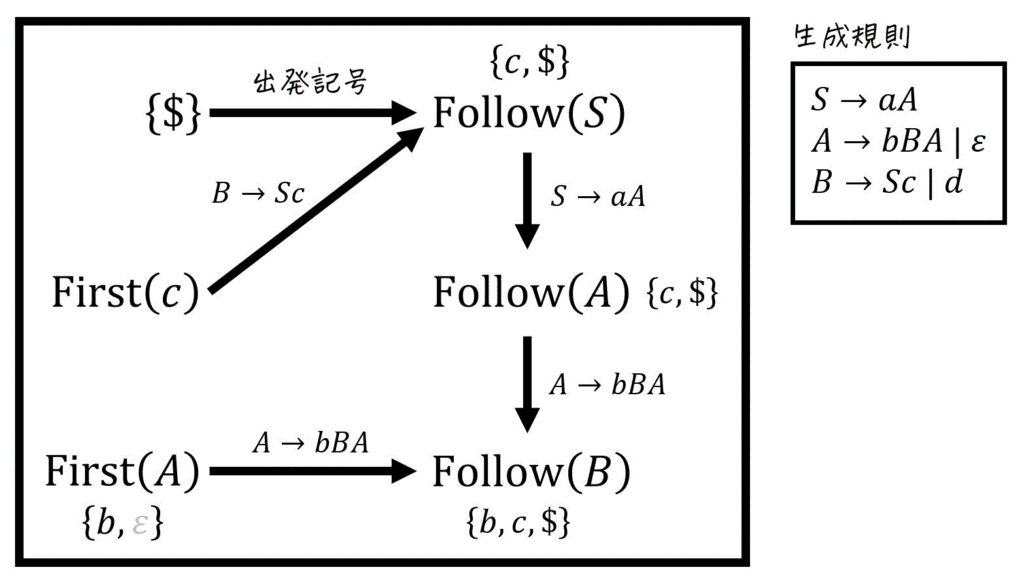
図を書くことで、「矢印に従って集合を追加していく」するだけで簡単にFollow集合を求めることができます!
※ 追加時に \( \varepsilon \) が出てくる場合は無視してください。
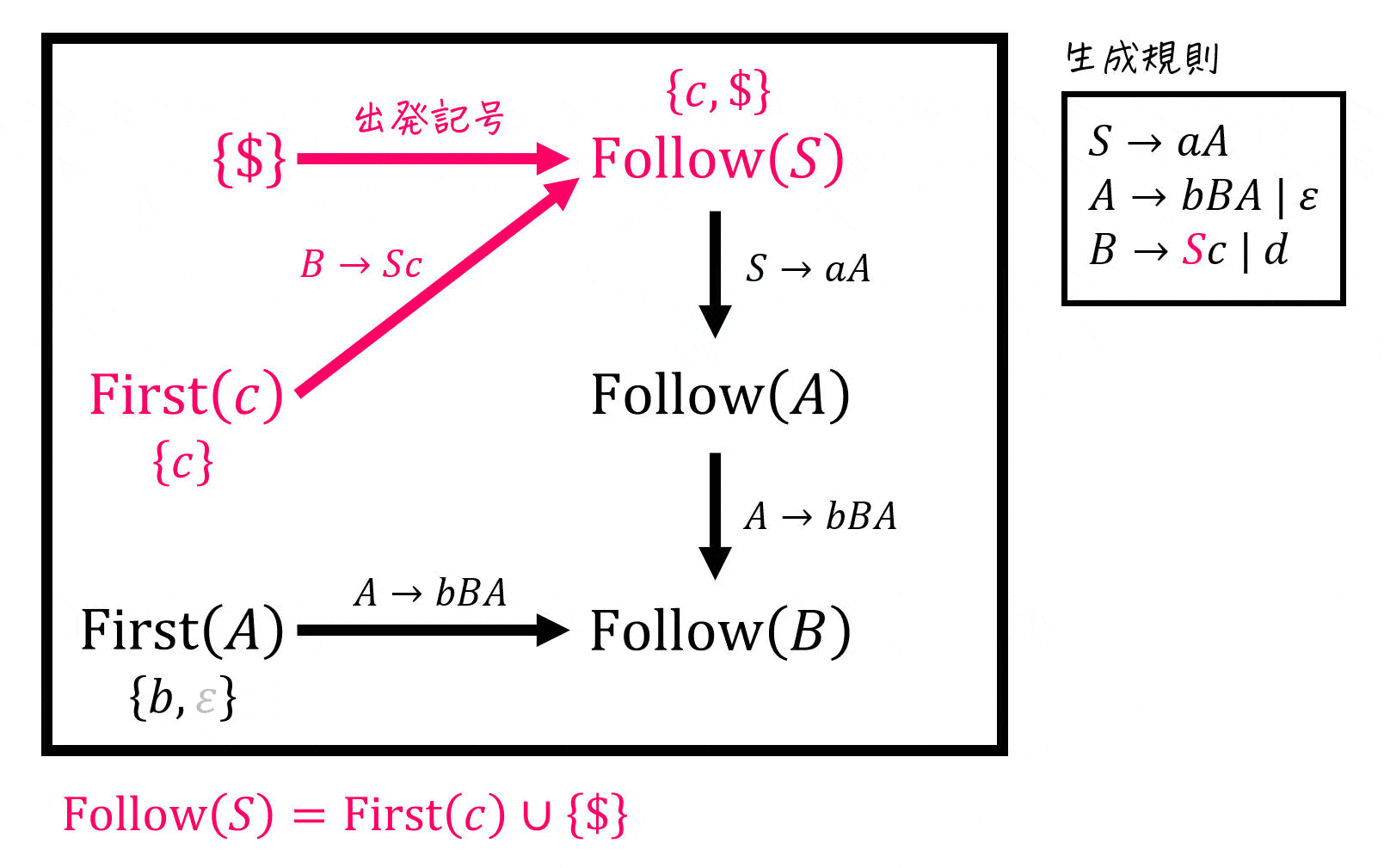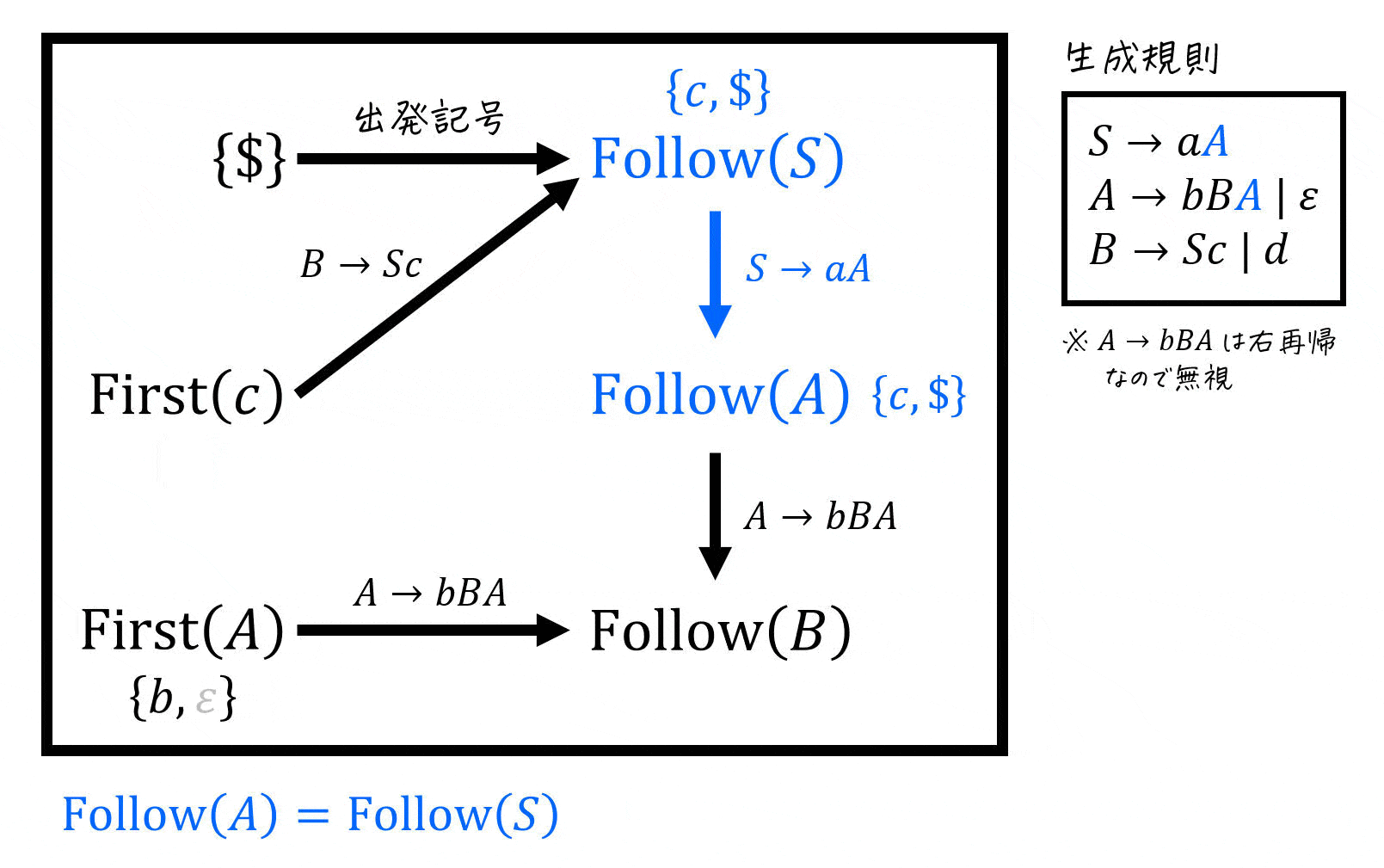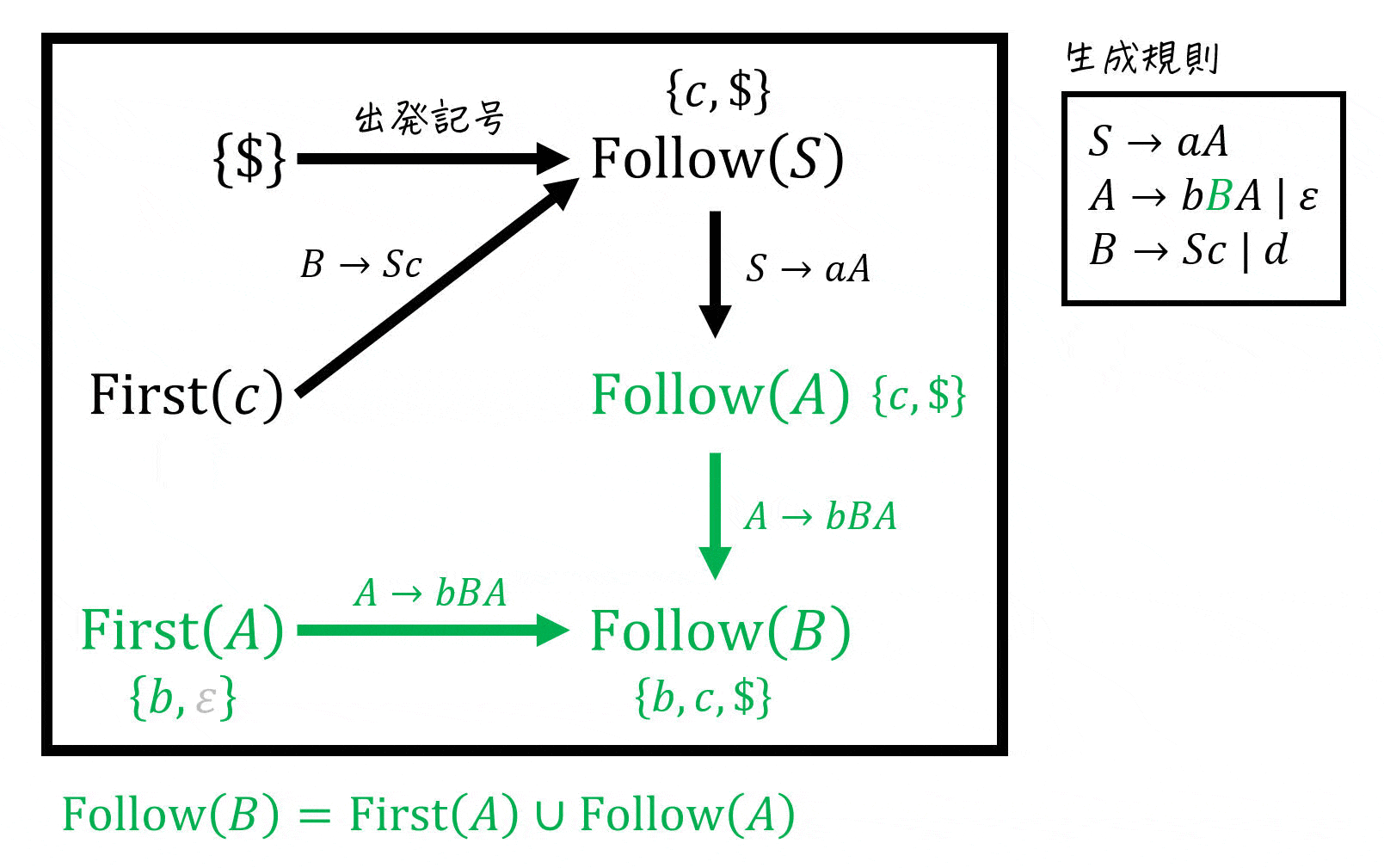
さらに図を書くもう1つメリットは検算が容易にできることです。
理由は、「ある集合 \( A \) の要素を集合 \( B \) に追加」した場合、集合の包含関係 \( A \subseteq B \) は必ず成立するからです[10]集合 \( B \) に集合 \( A \) の要素を追加したのに、集合 \( B \) の要素の中に集合 \( A \) … Continue reading。
例えば、下の図は \( \mathrm{First} (c) \) の要素を \( \mathrm{Follow} (S) \) に追加しているため、\( \mathrm{First} (c) \subseteq \mathrm{Follow} (S) \) が必ず成立します。
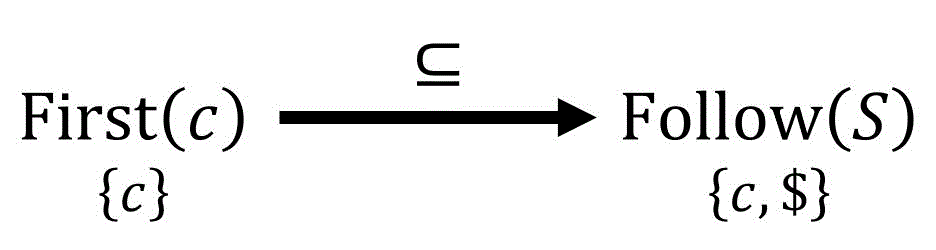
この包含関係を、書いた図の中に出てくる矢印それぞれ(下の図の場合は5か所)でチェックします[11]具体的には、\( \{ $ \} \subseteq \mathrm{Follow} (S) \), \( \mathrm{First} (c) \subseteq \mathrm{Follow} (S) \), \( \mathrm{Follow} (S) \subseteq \mathrm{Follow} (A) \), \( \mathrm{First} (A) … Continue reading。矢印すべての箇所で包含関係が成り立っていればOKです。
※ 1つでも成り立っていないものがあれば、計算ミスをしています。
4. Director集合とLL(1)文法の判定
(1) Director集合とは
ある文法がLL(1)文法、つまり「1文字の先読みをするだけで、与えられた文字列を構文解析できる文法」とはどのような文法なのかをもう少し詳しく見ていきましょう。
例えば、文字列 \( baba \) が生成規則\[\begin{align*}
S & \to aS \\
S & \to bA \\
S & \to bAb \\
A & \to a
\end{align*}\]の文法を満たすか「1文字の先読み」で判定することを考えましょう。
まず、1文字目を先読みすると \( b \) となりますね。出発記号 \( S \) から \( \textcolor{blue}{b} \) で始まる規則を探そうとしますが、\( S \to \textcolor{blue}{b} A \) と \( S \to \textcolor{blue}{b} Ab \) の2つが存在してしまっているため、どちらの文法規則を使っていいかわかりません。
このように、同じ非終端記号から生成される文字列を終端記号にした文字列の先頭が\[
S \to \textcolor{blue}{b}A , \ \ \ S \to \textcolor{blue}{b} A b
\]のように重複していると、「1文字の先読みだけでは、どの構文規則を適用すればよいかわからなくなるため、与えられた文字列を構文解析できない」ことがわかりますね。
言い換えると、LL(1)文法であるかを判定するためには、同一非終端記号から生成されるすべての生成規則に対し、生成される可能性がある「終端記号の文字列の先頭文字」がすべて異なっていればOKですね。
(2) Director集合の定義と計算公式
LL(1)文法であるかを機械的に判定するために登場したのがDirector集合です。
Director集合は、生成規則 \( \textcolor{magenta}{A} \to \textcolor{deepskyblue}{\alpha} \) に対し、「\( \textcolor{magenta}{A} \) から生成される文字列 \( \textcolor{deepskyblue}{\alpha} \) をすべて終端記号にしたときの先頭に来る文字の候補」を表しており、\[
\mathrm{Director} ( \textcolor{magenta}{A} , \textcolor{deepskyblue}{\alpha} )
\]と表記します。
[Director集合の計算公式1] αに空文字が来ない場合
ここで、生成規則 \( A \to \alpha \) の生成先 \( \textcolor{deepskyblue}{\alpha} \) をすべて終端記号にしたときの先頭に来る文字の候補というのは、\( \alpha \) に空文字が来ない限り \( \mathrm{First} ( \textcolor{deepskyblue}{\alpha} \) と書き換えることができます。
よって、\( \alpha \) に空文字が来ない場合(\( = \varepsilon \notin \mathrm{First} ( \alpha ) \))は、\[
\mathrm{Director} ( \textcolor{magenta}{A} , \textcolor{deepskyblue}{\alpha} ) = \mathrm{First} ( \textcolor{deepskyblue}{\alpha} )
\]でDirector集合を求めることが可能です。
[Director集合の計算公式2] αに空文字が来る可能性がある場合
しかし、\( A \to \varepsilon \) が代入される可能性がある(\( = \varepsilon \in \mathrm{First} ( \alpha ) \))場合、下のように \( A \to \varepsilon \) が適用されることで \( A \) のつぎの文字列 \( X \) が先頭に出てくる可能性があります。\[
A \textcolor{blue}{X} \xrightarrow{A \to \varepsilon} \textcolor{blue}{X}
\]そのため、\( \varepsilon \in \mathrm{First} ( \textcolor{deepskyblue}{\alpha} ) \) となる場合は \( \mathrm{First} ( \textcolor{deepskyblue}{\alpha} ) \) に加えて \( A \) の直後に来る終端記号の文字を表す \( \mathrm{Follow} ( \textcolor{magenta}{A} ) \) もDirector集合に加えます。
よって、\( \alpha \) に空文字が来る場合(\( = \varepsilon \in \mathrm{First} ( \alpha ) \))は、\[
\mathrm{Director} ( \textcolor{magenta}{A} , \textcolor{deepskyblue}{\alpha} ) = \mathrm{Follow} ( \textcolor{magenta}{A} )
\]でDirector集合を求めることが可能です。
ある生成規則 \( \textcolor{magenta}{A} \to \textcolor{deepskyblue}{ \alpha } \) に対し、\( \textcolor{magenta}{A} \) を変形した際に先頭に来る文字列の候補をDirector集合と呼び、\( \mathrm{Director} ( \textcolor{magenta}{A} , \textcolor{deepskyblue}{\alpha} ) \) で記す。
ここで、Director集合はつぎのように計算ができる。
[公式1] \( \alpha \) が空文字とならない場合( \( \varepsilon \notin \mathrm{First} ( \alpha ) \) )\[\mathrm{Director} ( \textcolor{magenta}{A} , \textcolor{deepskyblue}{\alpha} ) = \mathrm{First} ( \textcolor{deepskyblue}{\alpha} ) - \{ \varepsilon \}
\] [公式2] \( \alpha \) が空文字となりうる場合( \( \varepsilon \in \mathrm{First} ( \alpha ) \) )\[
\mathrm{Director} ( \textcolor{magenta}{A} , \textcolor{deepskyblue}{\alpha} ) = \mathrm{First} ( \textcolor{deepskyblue}{\alpha} ) \cup \mathrm{Follow} ( \textcolor{magenta}{A} ) - \{ \varepsilon \}
\]
※ 特に \( A \to \varepsilon \) の場合、\[
\mathrm{Director} ( \textcolor{magenta}{A} , \textcolor{deepskyblue}{\alpha} ) = \mathrm{Follow} ( \textcolor{magenta}{A} )
\]と計算できる。([公式2]の変形)
(3) Director集合を用いたLL(1)文法の判定
LL(1)文法であるかどうかは、同一非終端記号から生成されるすべての生成規則に対し、生成される可能性がある「非終端記号の文字列の先頭文字」がすべて異なっていればOKでしたね。
このLL(1)文法であるかの判定をDirector集合を用いて書くと下のようになります。
ある文法がLL(1)文法であることを確認するためには、2つ以上の生成元を持つすべての非終端記号に対し、同じ生成元 \( A \) のどの2つの規則 \( A \to \alpha_i \), \( A \to \alpha_j \) を選んでも\[
\mathrm{Director} ( A , \alpha_i) \cap \mathrm{Director} ( A , \alpha_j ) = \phi
\]が成立すればLL(1)文法である。(1つでも成り立たないものがあった時点でLL(1)文法ではない。)
生成規則\[\begin{align*}
A & \to \alpha_1 | \ \alpha_2 \\
B & \to \beta_1 \\
C & \to \gamma_1 | \ \gamma_2 \ | \ \gamma_3
\end{align*}\]からなる文法の場合、2つ以上の生成元を持つ非終端記号は \( A \)(2つ)と \( C \)(3つ)である。
(i) \( A \) で確認する内容\[
\mathrm{Director} ( A , \alpha_1 ) \cap \mathrm{Director} ( A , \alpha_2 ) = \phi
\]
(ii) \( C \) で確認する内容\[\begin{align*}
\mathrm{Director} ( C , \gamma_1 ) \cap \mathrm{Director} ( C , \gamma_2 ) & = \phi \\
\mathrm{Director} ( C , \gamma_1 ) \cap \mathrm{Director} ( C , \gamma_3 ) & = \phi \\
\mathrm{Director} ( C , \gamma_2 ) \cap \mathrm{Director} ( C , \gamma_3 ) & = \phi
\end{align*}\]※ 3つの生成規則の中から2つを選ぶ組み合わせは、(生成規則1, 生成規則2), (生成規則1, 生成規則3), (生成規則2, 生成規則3) の3通りあるので、3通りとも調べる必要あり。
この(i), (ii)で出てきた式(合計4つ)がすべて成立すればLL(1)文法であることが言えます。一方、どれか1つでも成立しなかった時点でLL(1)文法ではありません。
(4) 例題で確認してみよう
Director集合の算出、およびLL(1)文法の確認を例題で確認していきましょう。
次の文法 \( G \) がある。\[
G = \left( \ \{ S, A, B \} \ , \ \{ a,b,c,d \} \ , \ P \ , \ S \ \right)
\]\[\begin{align*}
P = \{ \ \ \ \ S & \to aA \\ A & \to bBa \ | \ \varepsilon \\ B & \to Sc \ | \ d \ \ \ \ \ \ \ \}
\end{align*}
\]この文法 \( G \) がLL(1)文法であることを確認しなさい。
※ 必要であれば例題1, 例題2で求めた\[\begin{align*}
\mathrm{First} (S) & = \{ a \}
\\ \mathrm{First} (A) & = \{ b, \varepsilon \}
\\ \mathrm{First} (B) & = \{ a,d \}
\\ \mathrm{Follow} (S) & = \{ c, \$ \}
\\ \mathrm{Follow} (A) & = \{ c, \$ \}
\\ \mathrm{Follow} (B) & = \{ b. c, \$ \}
\end{align*}\]を用いてもよい。
[解説]
LL(1)文法であるか判定するためには、2つ以上の生成規則を持つ各非終端記号に対して、Director集合を取り、その積を確認します。
(i) \( A \) が生成元の生成規則 \( A \to bBa \), \( A \to \varepsilon \) に対してDirector集合確認
\( \textcolor{magenta}{A} \to \textcolor{deepskyblue}{bBa} \) のDirector集合\[\begin{align*}
\mathrm{Director} ( \textcolor{magenta}{A} , \textcolor{deepskyblue}{bBa} ) & = \mathrm{First} ( \textcolor{deepskyblue}{bBa})
\\ & \overset{ \mathrm{R3} }{=} \mathrm{First} ( b )
\\ & \overset{ \mathrm{R1} }{=} \{ b \}
\end{align*}\]
\( \textcolor{magenta}{A} \to \textcolor{gray}{\varepsilon} \) のDirector集合\[\begin{align*}
\mathrm{Director} ( \textcolor{magenta}{A} , \textcolor{gray}{\varepsilon} ) & = \mathrm{Follow} ( \textcolor{magenta}{A} )
\\ & = \{ c, \$ \}
\end{align*}\]
\( A \) に関する各Director集合の積を取ると、\[\begin{align*}
\mathrm{Director} ( A, bBa ) \cap \mathrm{Director} ( A, \varepsilon ) & = \{ b \} \cap \{ c , \$ \}
\\ & = \phi
\end{align*}\]となるためOK。
(ii) \( B \) が生成元の生成規則 \( B \to Sc \), \( B \to d \) に対してDirector集合確認
\( \textcolor{magenta}{B} \to \textcolor{deepskyblue}{Sc} \) のDirector集合\[\begin{align*}
\mathrm{Director} ( \textcolor{magenta}{B} , \textcolor{deepskyblue}{Sc} ) & = \mathrm{First} ( \textcolor{deepskyblue}{Sc} )
\\ & \overset{ \mathrm{R3} }{=} \mathrm{First} (S)
\\ & = \{ a \}
\end{align*}\]
\( \textcolor{magenta}{B} \to \textcolor{deepskyblue}{d} \) のDirector集合\[\begin{align*}
\mathrm{Director} ( \textcolor{magenta}{B} , \textcolor{deepskyblue}{d} ) & = \mathrm{First} ( \textcolor{deepskyblue}{d} )
\\ & \overset{ \mathrm{R1} }{=} \{ d \}
\end{align*}\]
\( B \) に関する各Director集合の積を取ると、\[\begin{align*}
\mathrm{Director} ( B, Sc ) \cap \mathrm{Director} ( B, d ) & = \{ a \} \cap \{ d \}
\\ & = \phi
\end{align*}\]となるためOK。
(i), (ii)よりLL(1)文法であることが確認できた。
※ \( S \) に対しては、\( S \to a A \) の1つの生成規則しかないため、Director集合は求めなくてOK。
5. 練習問題
それでは、ここまでの学習内容を練習問題を通じておさらいしていきましょう。
今回は、2問の練習問題を用意しています。
練習1.
次の文法 \( G \) がある。\[
G = \left( \ \{ S, A, B \} \ , \ \{ a,b,c,d \} \ , \ P \ , \ S \ \right)
\]\[\begin{align*}
P = \{ \ \ \ S & \to aAa \\ A & \to bB \ | \ SB \\ B & \to cB \ | \ dAb \ | \ \varepsilon \ \ \}
\end{align*}
\]つぎの(1)~(3)の問いに答えなさい。
(1) \( \mathrm{First} (S) \), \( \mathrm{First} (A) \), \( \mathrm{First} (B) \) を求めなさい。
(2) \( \mathrm{Follow} (S) \), \( \mathrm{Follow} (A) \), \( \mathrm{Follow} (B) \) を求めなさい。
(3) この文法 \( G \) はLL(1)文法かどうかを理由を踏まえて答えなさい。
練習2.
次の文法 \( G \) がある。\[
G = \left( \ \{ S, A, B, C \} \ , \ \{ a,b,c,d \} \ , \ P \ , \ S \ \right)
\]\[\begin{align*}
P = \{ \ \ \ S & \to AaB \\ A & \to cCA \ | \ c \\ B & \to S \ | \ BA \ | \ \varepsilon \\ C & \to Bc \ \ \ \ \ \ \ \ \ \ \ \ \ \ \}
\end{align*}
\]つぎの(1)~(4)の問いに答えなさい。
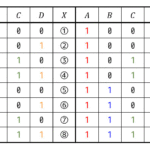
(1) \( \mathrm{First} (S) \), \( \mathrm{First} (A) \), \( \mathrm{First} (B) \), \( \mathrm{First} (C) \) を求めなさい。
(2) \( \mathrm{Follow} (S) \), \( \mathrm{Follow} (A) \), \( \mathrm{Follow} (B) \), \( \mathrm{Follow} (C) \) を求めなさい。
(3) この文法 \( G \) はLL(1)文法かどうかを理由を踏まえて答えなさい。
6. 練習問題の答え
解答1.
規則\[\begin{align*}
P = \{ \ \ \ S & \to aAa \\ A & \to bB \ | \ SB \\ B & \to cB \ | \ dAb \ | \ \varepsilon \ \ \}
\end{align*}
\]で表される文法に対してFirst集合、Follow集合、Director集合を求めてLL(1)文法を判定する。
(1) First集合の算出
[略解]\[\begin{align*}\mathrm{First} (S) & = \{ a \} \\
\mathrm{First} (A) & = \{ a,b \} \\
\mathrm{First} (B) & = \{ c,d, \varepsilon \}
\end{align*}\]
(i) \( \mathrm{First} (S) \) の計算
\( S \) が生成元の規則は \( S \to \textcolor{red}{aAa} \) の1つだけなので、\( S \to \textcolor{red}{aAa} \) だけに着目すればOK。
\[\begin{align*}
\mathrm{First} (S) & \overset{ \mathrm{R2} }{=} \underbrace { \mathrm{First} (\textcolor{red}{aAa}) }_{S \to \textcolor{red}{aAa}}
\\ & \overset{ \mathrm{R3} }{=} \mathrm{First} (a)
\\ & \overset{ \mathrm{R1} }{=} \{ a \}
\end{align*}\]
(ii) \( \mathrm{First} (A) \) の計算
\( A \) が生成元の規則は \( A \to bB \) と \( A \to SB \) の2つがある。
そのため、\( \mathrm{First} (A) \) を求める際には \( A \to \textcolor{red}{bB}\) と \( A \to \textcolor{blue}{SB} \) の2つの規則に着目すればOK。\[
\mathrm{First} (A) \overset{ \mathrm{R2} }{=} \underbrace{ \mathrm{First} (\textcolor{red}{bB}) }_{ A \to \textcolor{red}{bB} } \cup \underbrace{ \mathrm{First} (\textcolor{blue}{SB}) }_{ A \to \textcolor{blue}{SB} }
\]
ここでそれぞれの項のFirst集合は以下のように計算できる。
\[\begin{align*}
\mathrm{First} (bB) & \overset{ \mathrm{R3} }{=} \mathrm{First} (b)
\\ & \overset{ \mathrm{R1} }{=} \{ b \}
\end{align*}\]
\[\begin{align*}
\mathrm{First} (SB) & \overset{ \mathrm{R3} }{=} \mathrm{First} (S)
\\ & \overset{ \mathrm{(1)} }{=} \{ a \}
\end{align*}\]
よって、\[\begin{align*}
\mathrm{First} (A) & \overset{ \mathrm{R2} }{=} \underbrace{ \mathrm{First} (bB) }_{ A \to bB } \cup \underbrace{ \mathrm{First} (SB) }_{ A \to SB }
\\ & = \{ b \} \cup \{ a \}
\\ & = \{ a, b \}
\end{align*}\]となる。
(iii) \( \mathrm{First} (B) \) の計算
\( B \) が生成元の規則は \( B \to cB \), \( B \to dAb \), \( B \to \varepsilon \) の3つがある。
そのため、\( \mathrm{First} (B) \) を求める際には \( B \to \textcolor{red}{cB} \), \( B \to \textcolor{blue}{dAb} \), \( B \to \textcolor{green}{\varepsilon} \) の3つの規則に着目すればOK。\[
\mathrm{First} (B) \overset{ \mathrm{R2} }{=} \underbrace{ \mathrm{First} (\textcolor{red}{cB}) }_{ B \to \textcolor{red}{cB} } \cup \underbrace{ \mathrm{First} (\textcolor{blue}{dAb}) }_{B \to \textcolor{blue}{dAb}} \cup \underbrace{ \mathrm{First} (\textcolor{green}{\varepsilon}) }_{B \to \textcolor{green}{\varepsilon}}
\]
ここでそれぞれの項のFirst集合は以下のように計算できる。
\[\begin{align*}
\mathrm{First} (cB) & \overset{ \mathrm{R3} }{=} \mathrm{First} (c)
\\ & \overset{ \mathrm{R1} }{=} \{ c \}
\end{align*}\]
\[\begin{align*}
\mathrm{First} (dAb) & \overset{ \mathrm{R3} }{=} \mathrm{First} (d)
\\ & \overset{ \mathrm{(1)} }{=} \{ d \}
\end{align*}\]
\[\begin{align*}
\mathrm{First} (\varepsilon) \overset{ \mathrm{R1} }{=} \{ \varepsilon \}
\end{align*}\]
よって、\[\begin{align*}
\mathrm{First} (B) & \overset{ \mathrm{R2} }{=} \mathrm{First} (cB) \cup \mathrm{First} (dAb) \cup \mathrm{First} (\varepsilon)
\\ & = \{ c \} \cup \{ d \} \cup \{ \varepsilon \}
\\ & = \{ c,d, \varepsilon \}
\end{align*}\]となる。
(2) Follow集合の算出
[略解]\[\begin{align*}\mathrm{Follow} (S) & = \{ a,b,c,d, \$ \} \\
\mathrm{Follow} (A) & = \{ a,b \} \\
\mathrm{Follow} (B) & = \{ a,b \}
\end{align*}\]
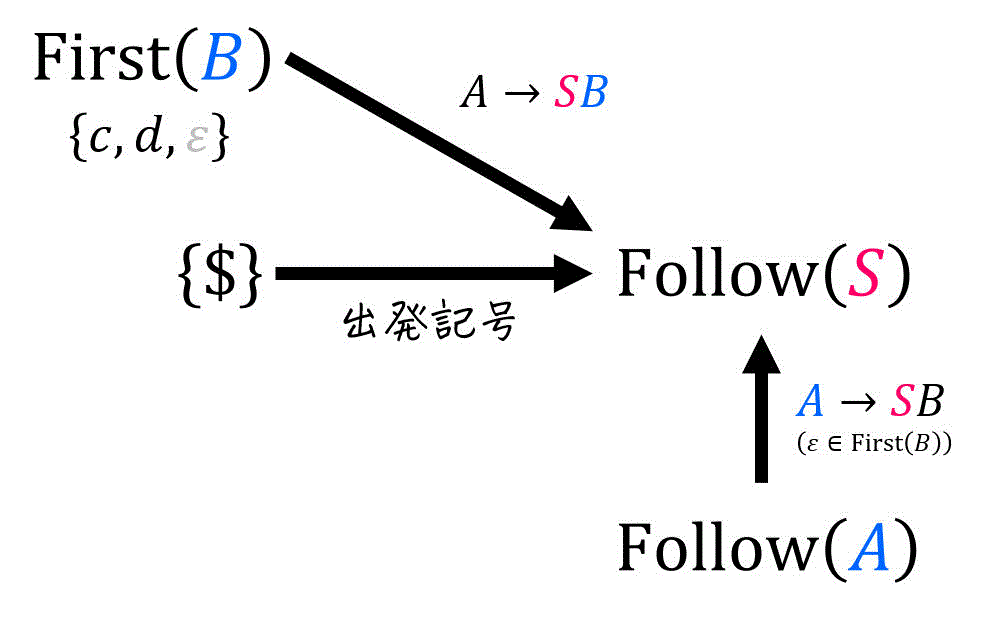
(i) \( \mathrm{Follow} (S) \) の算出式
[公式1] \( S \) は出発記号? → Yes。なので、\( \mathrm{Follow} (S) \) に \( \$ \) を追加。\[\mathrm{Follow} (S) += \{ \$ \}
\]
\( \textcolor{magenta}{S} \) が生成先に含まれる規則は、\( A \to \textcolor{magenta}{S} B \) のみなので、\( A \to \textcolor{magenta}{S} B \) にのみ着目すればOK。
ここで、\( A \to \textcolor{magenta}{ S } \textcolor{blue}{ \underbrace{B}_{ \beta } } \) より、\( \textcolor{blue}{\beta = B} \) とおく。
[公式2] \( \beta \not = \varepsilon \)? → \( \beta = B \not = \varepsilon \) なのでYes。なので、\( A \to \textcolor{magenta}{S} \textcolor{blue}{ B } \) に対し、以下の集合の要素を追加。\( A\[\begin{align*}
\mathrm{Follow} ( \textcolor{magenta}{S} ) + & = \mathrm{First} ( \textcolor{blue}{B} ) - \{ \varepsilon \}
\\ & = \{ c,d, \varepsilon \} - \{ \varepsilon \}
\\ & = \{ c,d \}
\end{align*}\]
なので、\( \textcolor{blue}{A} \to \textcolor{magenta}{S} B \) に対し、以下の集合の要素を追加。\[\begin{align*}
\mathrm{Follow} ( \textcolor{magenta}{S} ) + & = \mathrm{Follow} ( \textcolor{blue}{A} )
\end{align*}\]
よって、\( \mathrm{Follow} (S) \) に追加される要素は以下の図で示す通り。
(ii) \( \mathrm{Follow} (A) \) の算出式
[公式1] \( A \) は出発記号? → No。\( \textcolor{magenta}{A} \) が生成先に含まれる規則は、\( S \to a \textcolor{magenta}{A} a \), \( B \to d \textcolor{magenta}{A} b \) の2つなので、この2つの規則に着目すればOK。
[a] \( S \to a \textcolor{magenta}{A} a \) に着目したとき
\( S \to a \textcolor{magenta}{ A } \textcolor{blue}{ \underbrace{a}_{ \beta } } \) とおく。(つまり \( \textcolor{blue}{\beta = a} \))
[公式2] \( \beta \not = \varepsilon \)? → \( \textcolor{blue}{\beta = a} \not = \varepsilon \) なのでYes。なので、\( S \to a \textcolor{magenta}{A} \textcolor{blue}{ a } \) に対し、以下の集合の要素を追加。\[\begin{align*}
\mathrm{Follow} ( \textcolor{magenta}{A} ) + & = \mathrm{First} ( \textcolor{blue}{a} )
\\ & = \{ a \}
\end{align*}\]
[b] \( B \to d \textcolor{magenta}{A} b \) に着目したとき
[公式2] \( \beta \not = \varepsilon \)? → \( \textcolor{blue}{\beta = b} \not = \varepsilon \) なのでYes。なので、\( S \to d \textcolor{magenta}{A} \textcolor{blue}{ b } \) に対し、以下の集合の要素を追加。\[\begin{align*}
\mathrm{Follow} ( \textcolor{magenta}{A} ) + & = \mathrm{First} ( \textcolor{blue}{b} )
\\ & = \{ b \}
\end{align*}\]
よって、\( \mathrm{Follow} (A) \) に追加される要素は以下の図で示す通り。
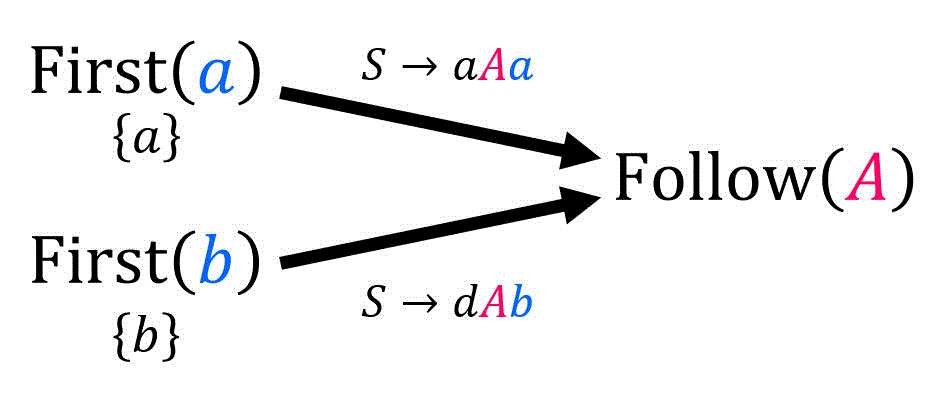
(iii) \( \mathrm{Follow} (B) \) の算出式
[公式1] \( B \) は出発記号? → No。\( \textcolor{magenta}{B} \) が生成先に含まれる規則は、\( A \to b \textcolor{magenta}{B} \), , \( A \to S \textcolor{magenta}{B} \) ,\( B \to c \textcolor{magenta}{B} \) の3つ。ただし、\( B \to c \textcolor{magenta}{B} \) は右再帰規則のため無視。なので、\( A \to b \textcolor{magenta}{B} \), \( A \to S \textcolor{magenta}{B} \) の2つの規則に着目すればOK。
[a] \( A \to b \textcolor{magenta}{B} \) に着目したとき
\( A \to b \textcolor{magenta}{ B } \) の \( \textcolor{magenta}{B} \) の後ろの文字が存在しない。そのため、\( \textcolor{blue}{\beta = \varepsilon} \) である。
[公式2] \( \beta \not = \varepsilon \)? → \( \textcolor{blue}{\beta = \varepsilon} \) なのでNo。 [公式3] \( \varepsilon \in \mathrm{First} ( \beta ) \)? → \( \mathrm{First} ( \textcolor{blue}{\beta} ) = \mathrm{First} ( \textcolor{blue}{ \varepsilon } ) = \{ \varepsilon \} \) なのでYes。なので、\( \textcolor{blue}{A} \to b \textcolor{magenta}{B} \) に対し、以下の集合の要素を追加。\[\begin{align*}
\mathrm{Follow} ( \textcolor{magenta}{B} ) + & = \mathrm{Follow} ( \textcolor{blue}{A} )
\end{align*}\]
[b] \( A \to S \textcolor{magenta}{B}\) に着目したとき
\( A \to S \textcolor{magenta}{ B } \) の \( \textcolor{magenta}{B} \) の後ろの文字が存在しない。そのため、\( \textcolor{blue}{\beta = \varepsilon} \) である。
[公式2] \( \beta \not = \varepsilon \)? → \( \textcolor{blue}{\beta = \varepsilon} \) なのでNo。 [公式3] \( \varepsilon \in \mathrm{First} ( \beta ) \)? → \( \mathrm{First} ( \textcolor{blue}{\beta} ) = \mathrm{First} ( \textcolor{blue}{ \varepsilon } ) = \{ \varepsilon \} \) なのでYes。なので、\( \textcolor{blue}{A} \to S \textcolor{magenta}{B} \) に対し、以下の集合の要素を追加。\[\begin{align*}
\mathrm{Follow} ( \textcolor{magenta}{B} ) + & = \mathrm{Follow} ( \textcolor{blue}{A} )
\end{align*}\]
※ 式から察している人もいるかもしれませんが、[a] の生成式と全く同じ結果が出てきます。
よって、\( \mathrm{Follow} (B) \) に追加される要素は以下の図で示す通り。
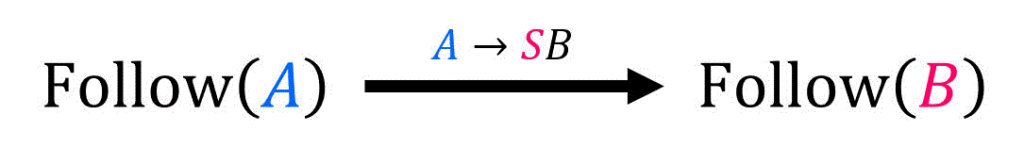
(代表として \( A \to SB \) を選択)
それぞれの計算結果をまとめてFollow集合を算出
先ほど出した \( \mathrm{Follow} (S) \), \( \mathrm{Follow} (A) \), \( \mathrm{Follow} (B) \) の計算過程を1つの図に表すと、下のようになる。
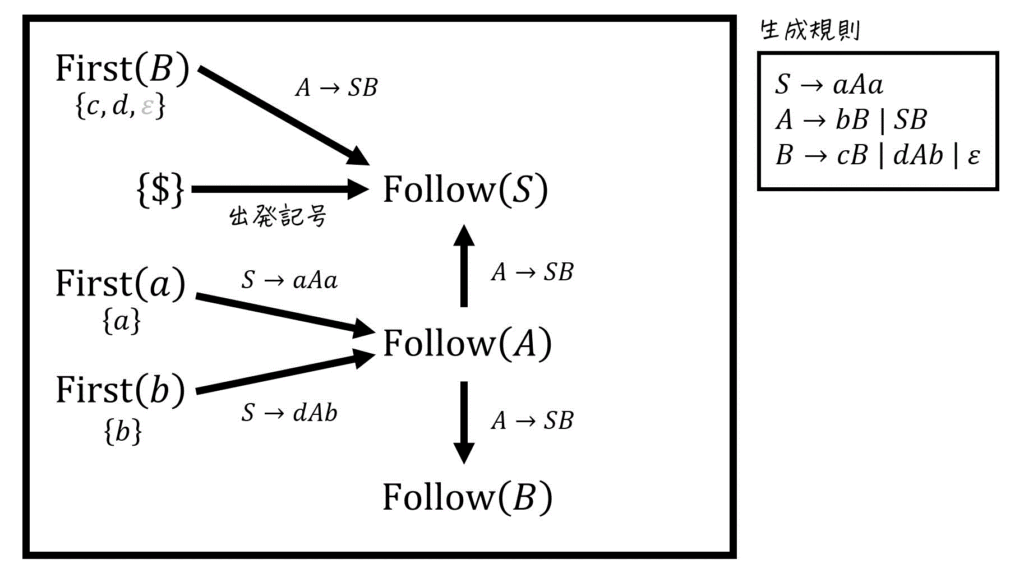
あとは、求められるFollow集合から順にFollow集合を求めていけばOK。
※ 今回の場合は、\( \mathrm{Follow} (A) \) を求めてから、\( \mathrm{Follow} (S) \) と \( \mathrm{Follow} (B) \) を求めていく流れになりますね(\( \mathrm{Follow} (S) \) と \( \mathrm{Follow} (B) \) はどっちから求めてもOK)。
(ii) \( \mathrm{Follow} (A) \) の計算結果
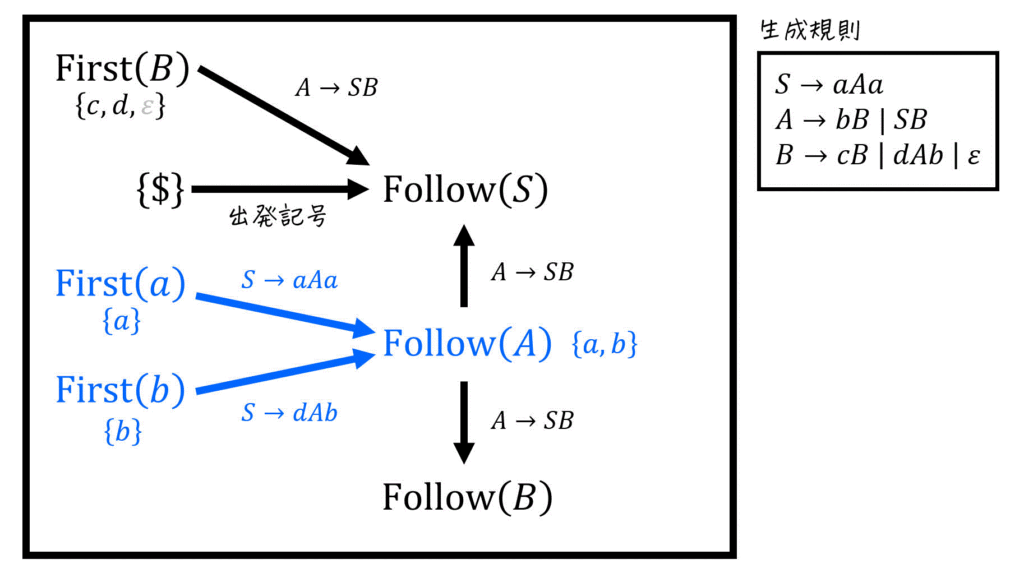
\mathrm{Follow} (A) & = \mathrm{First} (a) \cup \mathrm{First} (b) - \{ \varepsilon \}
\\ & = \{ a \} \cup \{ b \}
\\ & = \{ a, b \}
\end{align*}\]
(i) \( \mathrm{Follow} (S) \) の計算結果
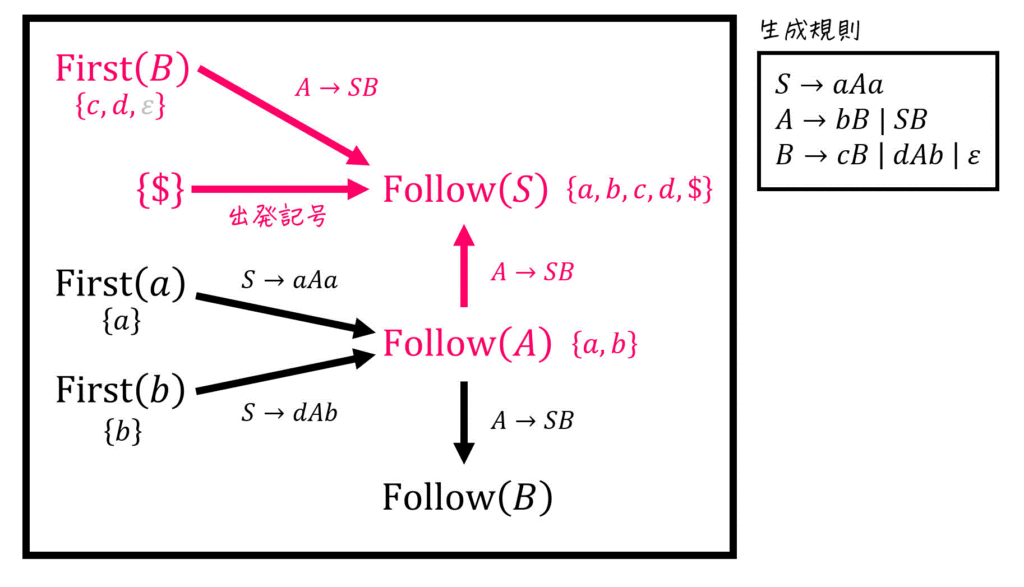
\mathrm{Follow} (S) & = \mathrm{First} (B) \cup \mathrm{Follow} (A) \cup \{ \$ \} - \{ \varepsilon \}
\\ & = \{ c, d, \varepsilon \} \cup \{ a,b \} \cup \{ \$ \} - \{ \varepsilon \}
\\ & = \{ a, b, c, d, \$ \}
\end{align*}\]※ \( \varepsilon \) を無視するのを忘れずに
(iii) \( \mathrm{Follow} (B) \) の計算結果
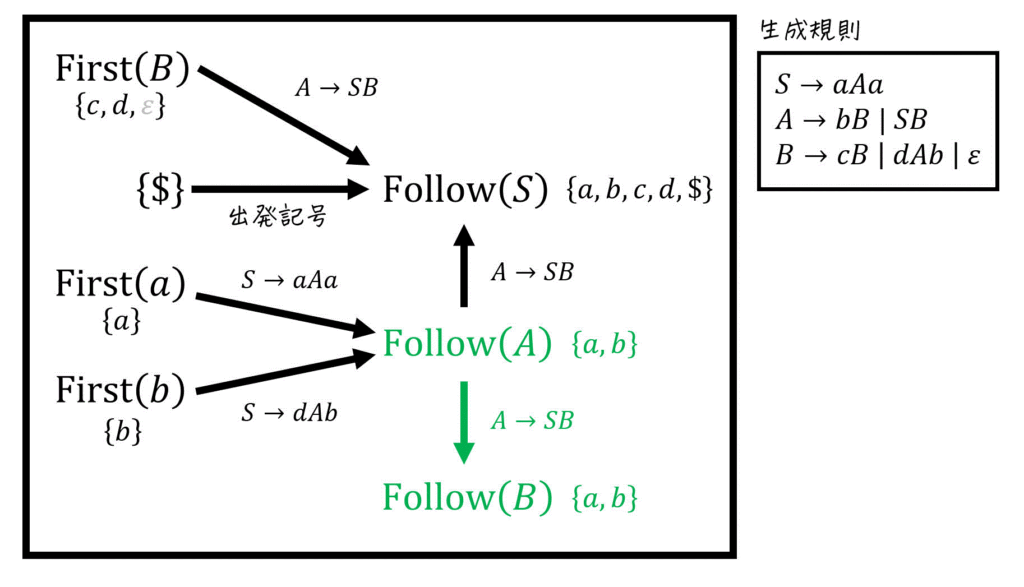
\mathrm{Follow} (B) & = \mathrm{Follow} (A)
\\ & = \{ a, b \}
\end{align*}\]※Follow集合の要素には \( \varepsilon \) が出てこないので、\( \varepsilon \) を引いていません。(引いてもOKです。)
(3) Director集合の算出とLL(1)文法の判定
各非終端記号に対して、生成元から2つ以上の生成規則を持つものは、
- \( A \) が生成元となる規則:\( A \to bB \), \( A \to SB \)
- \( B \) が生成元となる規則:\( B \to cB \), \( B \to dAb \), \( B \to \varepsilon \)
である。あとは、非終端記号ごとに「どの生成規則同士の積をとっても、Director集合が空集合になること」を確認すればOK。
1) \( A \) が生成元の生成規則 \( A \to bB \), \( A \to SB \) に対してDirector集合確認
\( \textcolor{magenta}{A} \to \textcolor{deepskyblue}{bB} \) のDirector集合\[\begin{align*}
\mathrm{Director} ( \textcolor{magenta}{A} , \textcolor{deepskyblue}{bB} ) & = \mathrm{First} ( \textcolor{deepskyblue}{bB} )
\\ & \overset{ \mathrm{R3} }{=} \mathrm{First} ( b )
\\ & \overset{ \mathrm{R1} }{=} \{ b \}
\end{align*}\]
\( \textcolor{magenta}{A} \to \textcolor{deepskyblue}{SB} \) のDirector集合\[\begin{align*}
\mathrm{Director} ( \textcolor{magenta}{A} , \textcolor{deepskyblue}{SB} ) & = \mathrm{First} ( \textcolor{deepskyblue}{SB} )
\\ & \overset{ \mathrm{R3} }{=} \mathrm{First} ( S )
\\ & = \{ a \}
\end{align*}\]
\( A \) に関する各Director集合同士の積を取ると、\[\begin{align*}
\mathrm{Director} ( A, bB ) \cap \mathrm{Director} ( A, SB ) & = \{ b \} \cap \{ a \}
\\ & = \phi
\end{align*}\]となるためOK。
2) \( B \) が生成元の生成規則 \( B \to cB \), \( B \to dAb \), \( B \to \varepsilon \)に対してDirector集合確認
\( \textcolor{magenta}{B} \to \textcolor{deepskyblue}{cB} \) のDirector集合\[\begin{align*}
\mathrm{Director} ( \textcolor{magenta}{B} , \textcolor{deepskyblue}{cB} ) & = \mathrm{First} ( \textcolor{deepskyblue}{cB} )
\\ & \overset{ \mathrm{R3} }{=} \mathrm{First} ( c )
\\ & \overset{ \mathrm{R1} }{=} \{ c \}
\end{align*}\]
\( \textcolor{magenta}{B} \to \textcolor{deepskyblue}{dAb} \) のDirector集合\[\begin{align*}
\mathrm{Director} ( \textcolor{magenta}{B} , \textcolor{deepskyblue}{dAb} ) & = \mathrm{First} ( \textcolor{deepskyblue}{dAb} )
\\ & \overset{ \mathrm{R3} }{=} \mathrm{First} ( d )
\\ & \overset{ \mathrm{R1} }{=} \{ d \}
\end{align*}\]
\( \textcolor{magenta}{B} \to \textcolor{gray}{\varepsilon} \) のDirector集合\[\begin{align*}
\mathrm{Director} ( \textcolor{magenta}{B} , \textcolor{gray}{\varepsilon} ) & = \mathrm{Follow} ( \textcolor{magenta}{B} )
\\ & = \{ a, b \}
\end{align*}\]
\( B \) に関する各Director集合同士の積を取ると、\[\begin{align*}
\mathrm{Director} ( B, cB ) \cap \mathrm{Director} ( B, dAb ) & = \{ c \} \cap \{ d \}
= \phi \\
\mathrm{Director} ( B, cB ) \cap \mathrm{Director} ( B, \varepsilon ) & = \{ c \} \cap \{ a,b \}
= \phi \\
\mathrm{Director} ( B, dAb ) \cap \mathrm{Director} ( B, \varepsilon ) & = \{ d \} \cap \{ a,b \}
= \phi
\end{align*}\]となるためOK。
1), 2) より、題意の文法はLL(1)文法である。
解答2.
規則\[\begin{align*}
P = \{ \ \ \ S & \to AaB \\ A & \to cCA \ | \ c \\ B & \to S \ | \ BA \ | \ \varepsilon \\ C & \to Bc \ \ \ \ \ \ \ \ \ \ \ \ \ \ \}
\end{align*}
\]で表される文法に対してFirst集合、Follow集合、Director集合を求めてLL(1)文法を判定する。
(1) First集合の算出
[略解]\[\begin{align*}\mathrm{First} (S) & = \{ c \} \\
\mathrm{First} (A) & = \{ c \} \\
\mathrm{First} (B) & = \{ c, \varepsilon \} \\
\mathrm{First} (C) & = \{ c \}
\end{align*}\]
(i) \( \mathrm{First} (S) \) の計算 (途中まで)
\( S \) が生成元の規則は \( S \to \textcolor{red}{AaB} \) の1つだけなので、\( S \to \textcolor{red}{AaB} \) だけに着目すればOK。
\[\begin{align*}
\mathrm{First} (S) & \overset{ \mathrm{R2} }{=} \underbrace{ \mathrm{First} ( \textcolor{red}{AaB} ) }_{S \to \textcolor{red}{AaB}}
\\ & \overset{ \mathrm{R3} }{=} \mathrm{First} (A)
\end{align*}\]※ まだ \( \mathrm{First} (A) \) が求まっていないため保留
(ii) \( \mathrm{First} (A) \) の計算(と \( \mathrm{First} (S) \) の計算再開)
\( A \) が生成元の規則は \( A \to cCA \) と \( A \to c \) の2つがある。
そのため、\( \mathrm{First} (A) \) を求める際には \( A \to \textcolor{red}{cCA} \) と \( A \to \textcolor{blue}{c} \) の2つの規則に着目すればOK。\[
\mathrm{First} (A) \overset{ \mathrm{R2} }{=} \underbrace{ \mathrm{First} (\textcolor{red}{cCA}) }_{A \to \textcolor{red}{cCA}} \cup \underbrace{ \mathrm{First} ( \textcolor{blue}{c}) }_{A \to \textcolor{blue}{c}}
\]
ここでそれぞれの項のFirst集合は以下のように計算できる。
\[\begin{align*}
\mathrm{First} (cCA) & \overset{ \mathrm{R3} }{=} \mathrm{First} (c)
\\ & \overset{ \mathrm{R1} }{=} \{ c \}
\end{align*}\]
\[\begin{align*}
\mathrm{First} (c) & \overset{ \mathrm{R1} }{=} \{ c \}
\end{align*}\]
よって、\[\begin{align*}
\mathrm{First} (A) & \overset{ \mathrm{R2} }{=} \mathrm{First} (cCA) \cup \mathrm{First} (c)
\\ & = \{ c \} \cup \{ c \}
\\ & = \{ c \}
\end{align*}\]となる。また、\( \mathrm{First} (S) \) も
\[\begin{align*}
\mathrm{First} (S) & \overset{ \mathrm{R2} }{=} \mathrm{First} (AaB)
\\ & \overset{ \mathrm{R3} }{=} \mathrm{First} (A)
\\ & = \{ c \}
\end{align*}\]と求められる。
(iii) \( \mathrm{First} (B) \) の計算
\( B \) が生成元の規則は \( B \to S \), \( B \to BA \), \( B \to \varepsilon \) の3つがある。
ただし、\( B \to B A \) は左再帰の文法なので無視する。そのため、\( \mathrm{First} (B) \) を求める際には \( B \to \textcolor{red}{cB} \), \( B \to \textcolor{blue}{dAb} \) の2つの規則に着目すればOK。\[
\mathrm{First} (B) \overset{ \mathrm{R2} }{=} \underbrace{ \mathrm{First} (\textcolor{red}{cB}) }_{B \to \textcolor{red}{ cB }} \cup \underbrace{ \mathrm{First} ( \textcolor{blue}{dAb} ) }_{B \to \textcolor{blue}{dAb} }
\]
ここで、\[\begin{align*}
\mathrm{First} (\varepsilon) \overset{ \mathrm{R1} }{=} \{ \varepsilon \}
\end{align*}\]なので、\( \mathrm{First} (B) \) は\[\begin{align*}
\mathrm{First} (B) & \overset{ \mathrm{R2} }{=} \mathrm{First} (S) \cup \mathrm{First} (\varepsilon)
\\ & = \{ c \} \cup \{ \varepsilon \}
\\ & = \{ c, \varepsilon \}
\end{align*}\]と計算できる。
(iv) \( \mathrm{First} (C) \) の計算
\( C \) が生成元の規則は \( C \to \textcolor{red}{Bc} \) だけなので、この規則のみに着目する。
よって、\[\begin{align*}
\mathrm{First} (C) & \overset{ \mathrm{R2} }{=} \underbrace{ \mathrm{First} ( \textcolor{red}{Bc} ) }_{C \to \textcolor{red}{Bc}}
\\ & \overset{ \mathrm{R3} }{=} \left( \mathrm{First} (B) - \{ \varepsilon \} \right) \cup \{ c \} \ \ \because \left( \varepsilon \in \mathrm{First} (B) \right)
\\ & = \{ c \} \cup \{ c \}
\\ & = \{ c \}
\end{align*}\]※ \( \mathrm{First} (B) \) に \( \varepsilon \) が含まれているため、公式が変化する点に注意!
(2) Follow集合の算出
[略解]\[\begin{align*}\mathrm{Follow} (S) & = \{ c , \$ \} \\
\mathrm{Follow} (A) & = \{ a, c, \$ \} \\
\mathrm{Follow} (B) & = \{ c, \$ \} \\
\mathrm{Follow} (C) & = \{ c \}
\end{align*}\]
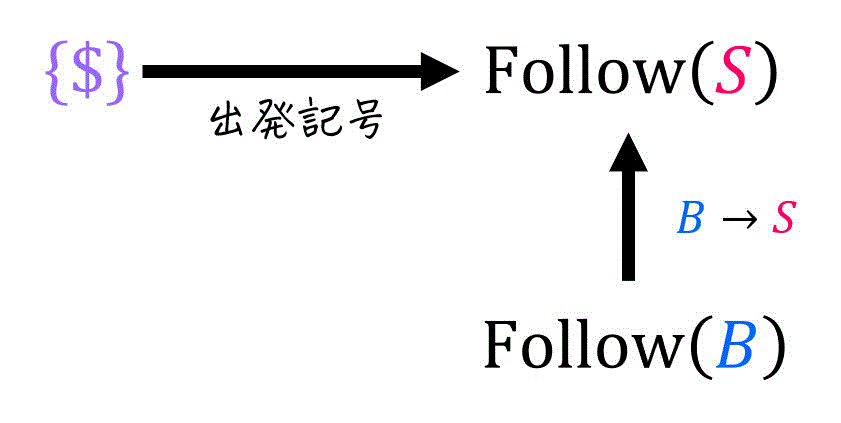
(i) \( \mathrm{Follow} (S) \) の算出式
[公式1] \( S \) は出発記号? → Yes。なので、\( \mathrm{Follow} (S) \) に \( \$ \) を追加。\[\mathrm{Follow} ( \textcolor{magenta}{S} ) += \{ \$ \}
\]
ここで、\( \textcolor{magenta}{S} \) が生成先に含まれる規則は、\( B \to \textcolor{magenta}{S} \) のみなので、\( B \to \textcolor{magenta}{S} \) にのみ着目すればOK。
\( B \to \textcolor{magenta}{ S } \) において、 \( \textcolor{magenta}{S} \) の後ろの文字が存在しない。そのため、\( \textcolor{blue}{\beta = \varepsilon} \) である。
[公式2] \( \beta \not = \varepsilon \)? → \( \textcolor{blue}{\beta = \varepsilon} \) なのでNo。 [公式3] \( \varepsilon \in \mathrm{First} ( \beta ) \)? → \( \mathrm{First} ( \textcolor{blue}{\beta} )= \mathrm{First} ( \textcolor{blue}{\varepsilon} ) = \{ \varepsilon \} \) なのでYes。なので、\( \textcolor{blue}{B} \to \textcolor{magenta}{S} \) に対し、以下の集合の要素を追加。\[\begin{align*}
\mathrm{Follow} ( \textcolor{magenta}{S} ) + & = \mathrm{Follow} ( \textcolor{blue}{B} )
\end{align*}\]
よって、\( \mathrm{Follow} (S) \) で追加する要素(計算過程)は以下の図の通りである。
(ii) \( \mathrm{Follow} (A) \) の算出式
[公式1] \( A \) は出発記号? →No。なにもしない。ここで、\( \textcolor{magenta}{A} \) が生成先に含まれる規則は、\( S \to \textcolor{magenta}{A} a B \), \( A \to cC \textcolor{magenta}{A} \), \( B \to B \textcolor{magenta}{A} \) の3つがあるが、\( A \to cC \textcolor{magenta}{A} \) は右再帰な規則なので無視。よって、\( S \to \textcolor{magenta}{A} a B \), \( B \to B \textcolor{magenta}{A} \) の2つに着目すればOK。
[ii-a] \( S \to a \textcolor{magenta}{A} a B \) に着目したとき
\( S \to a \textcolor{magenta}{ A } \textcolor{blue}{ \underbrace{aB}_{ \beta } } \) とおく。(つまり \( \textcolor{blue}{\beta = a} \))
[公式2] \( \beta \not = \varepsilon \)? → \( \textcolor{blue}{\beta = aB} \not = \varepsilon \) なのでYes。なので、\( S \to a \textcolor{magenta}{A} \textcolor{blue}{ aB } \) に対し、以下の集合の要素を追加。\[\begin{align*}
\mathrm{Follow} ( \textcolor{magenta}{A} ) + & = \mathrm{First} ( \textcolor{blue}{aB} )
\\ & \overset{ \mathrm{R3} }{=} \mathrm{First} ( \textcolor{blue}{a} )
\\ & \overset{ \mathrm{R1} }{=} \{ a \}
\\ & = \{ a \}
\end{align*}\]
[ii-b] \( B \to B \textcolor{magenta}{A} \) に着目したとき
この規則では、\( \textcolor{magenta}{S} \) の後ろの文字が存在しない。そのため、\( \textcolor{blue}{\beta = \varepsilon} \) である。
[公式2] \( \beta \not = \varepsilon \)? → \( \textcolor{blue}{\beta = \varepsilon} \) なのでNo。 [公式3] \( \varepsilon \in \mathrm{First} ( \beta ) \)? → \( \mathrm{First} ( \beta ) = \{ \varepsilon \} \) なのでYes。なので、\( \textcolor{blue}{B} \to B \textcolor{magenta}{A} \) に対し、以下の集合の要素を追加。\[\begin{align*}
\mathrm{Follow} (\textcolor{magenta}{A} ) + & = \mathrm{Follow} ( \textcolor{blue}{B} )
\end{align*}\]
よって、\( \mathrm{Follow} (A) \) に追加される要素は以下の図で示す通り。
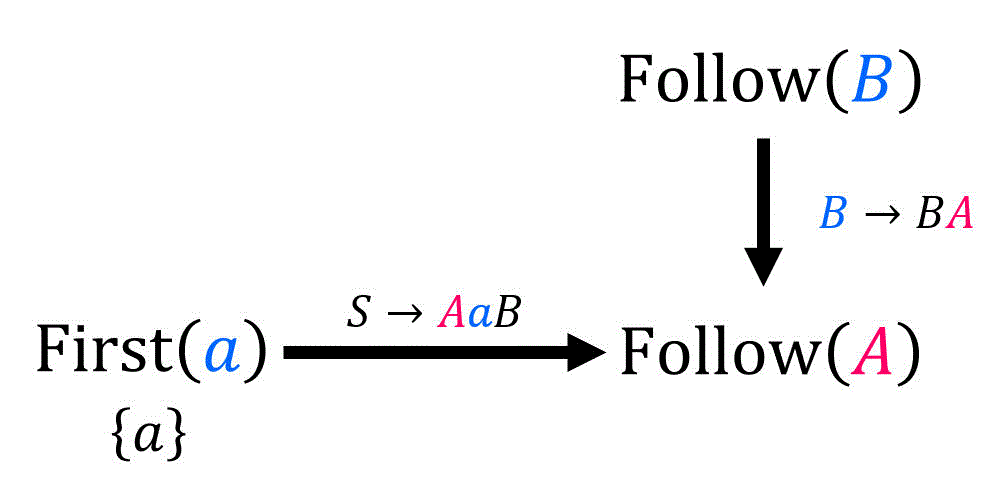
(iii) \( \mathrm{Follow} (B) \) の算出式
[公式1] \( B \) は出発記号? →No。なにもしない。ここで、\( \textcolor{magenta}{B} \) が生成先に含まれる規則は、\( S \to Aa \textcolor{magenta}{B} \), \( B \to \textcolor{magenta}{B} A \), \( C \to B \textcolor{magenta}{c} \) の3つがあるため、この3つの規則に着目すればOK。
[iii-a] \( S \to Aa \textcolor{magenta}{B} \) に着目したとき
この規則では、\( \textcolor{magenta}{B} \) の後ろの文字が存在しない。そのため、\( \textcolor{blue}{\beta = \varepsilon} \) である。
[公式2] \( \beta \not = \varepsilon \)? → \( \textcolor{blue}{\beta = \varepsilon} \) なのでNo。 [公式3] \( \varepsilon \in \mathrm{First} ( \beta ) \)? → \( \mathrm{First} ( \textcolor{blue}{\beta} )= \mathrm{First} ( \textcolor{blue}{\varepsilon} ) = \{ \varepsilon \} \) なのでYes。なので、\( \textcolor{blue}{S} \to A a\textcolor{magenta}{B} \) に対し、以下の集合の要素を追加。\[\begin{align*}
\mathrm{Follow} (\textcolor{magenta}{B} ) + & = \mathrm{Follow} ( \textcolor{blue}{S} )
\end{align*}\]
[iii-b] \( B \to \textcolor{magenta}{B} A \) に着目したとき
\(B \to \textcolor{magenta}{ B } \textcolor{blue}{ \underbrace{A}_{ \beta } } \) とおく。(つまり \( \textcolor{blue}{\beta = A} \))
[公式2] \( \beta \not = \varepsilon \)? → \( \textcolor{blue}{\beta = A} \not = \varepsilon \) なのでYes。なので、\( B \to a \textcolor{magenta}{B} \textcolor{blue}{ A } \) に対し、以下の集合の要素を追加。\[\begin{align*}
\mathrm{Follow} ( \textcolor{magenta}{B} ) + & = \mathrm{First} ( \textcolor{blue}{A} )
\\ & = \{ c \}
\end{align*}\]
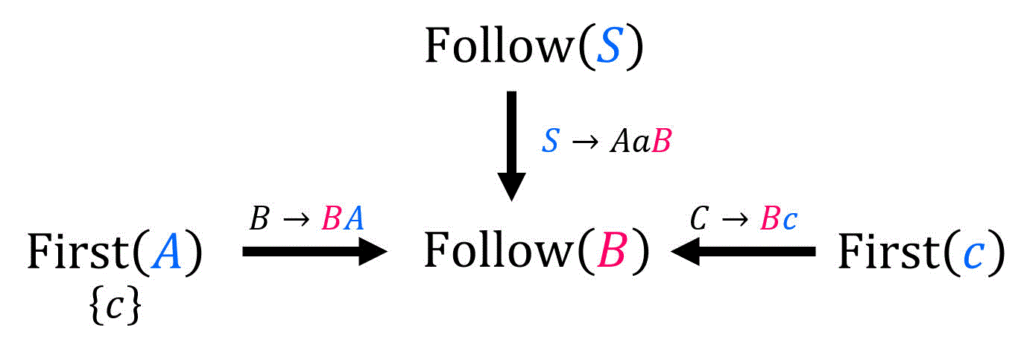
[iii-c] \( C \to \textcolor{magenta}{B} c \) に着目したとき
\(C \to \textcolor{magenta}{ B } \textcolor{blue}{ \underbrace{c}_{ \beta } } \) とおく。(つまり \( \textcolor{blue}{\beta = c} \))
[公式2] \( \beta \not = \varepsilon \)? → \( \textcolor{blue}{\beta = c} \not = \varepsilon \) なのでYes。なので、\( C \to a \textcolor{magenta}{B} \textcolor{blue}{ c } \) に対し、以下の集合の要素を追加。\[\begin{align*}
\mathrm{Follow} ( \textcolor{magenta}{B} ) + & = \mathrm{First} ( \textcolor{blue}{c} )
\\ & = \{ c \}
\end{align*}\]
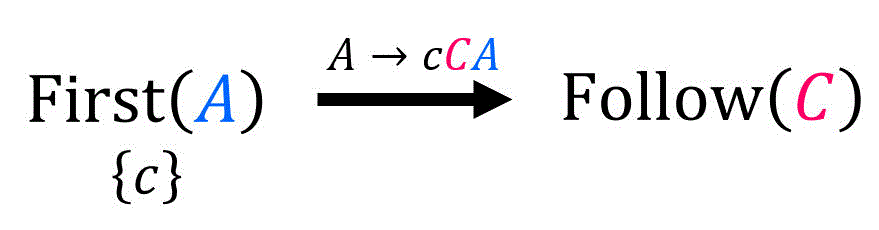
(iv) \( \mathrm{Follow} (C) \) の算出式
[公式1] \( C \) は出発記号? →No。なにもしない。ここで、\( \textcolor{magenta}{C} \) が生成先に含まれる規則は、\( A \to c \textcolor{magenta}{C} A \) のみ。なのでこの規則に着目すればOK。
この規則について、\(A \to c \textcolor{magenta}{ C } \textcolor{blue}{ \underbrace{A}_{ \beta } } \) とおく。(つまり \( \textcolor{blue}{\beta = A} \))
[公式2] \( \beta \not = \varepsilon \)? → \( \textcolor{blue}{\beta = A} \not = \varepsilon \) なのでYes。なので、\( C \to c \textcolor{magenta}{C} \textcolor{blue}{ A } \) に対し、以下の集合の要素を追加。\[\begin{align*}
\mathrm{Follow} ( \textcolor{magenta}{C} ) + & = \mathrm{First} ( \textcolor{blue}{A} )
\\ & = \{ c \}
\end{align*}\]
よって、\( \mathrm{Follow} (C) \) に追加される要素は以下の図で示す通り。
それぞれの計算結果をまとめてFollow集合を算出
先ほど出した \( \mathrm{Follow} (S) \), \( \mathrm{Follow} (A) \), \( \mathrm{Follow} (B) \), \( \mathrm{Follow} (C) \) の計算過程を1つの図に表すと、下のようになる。
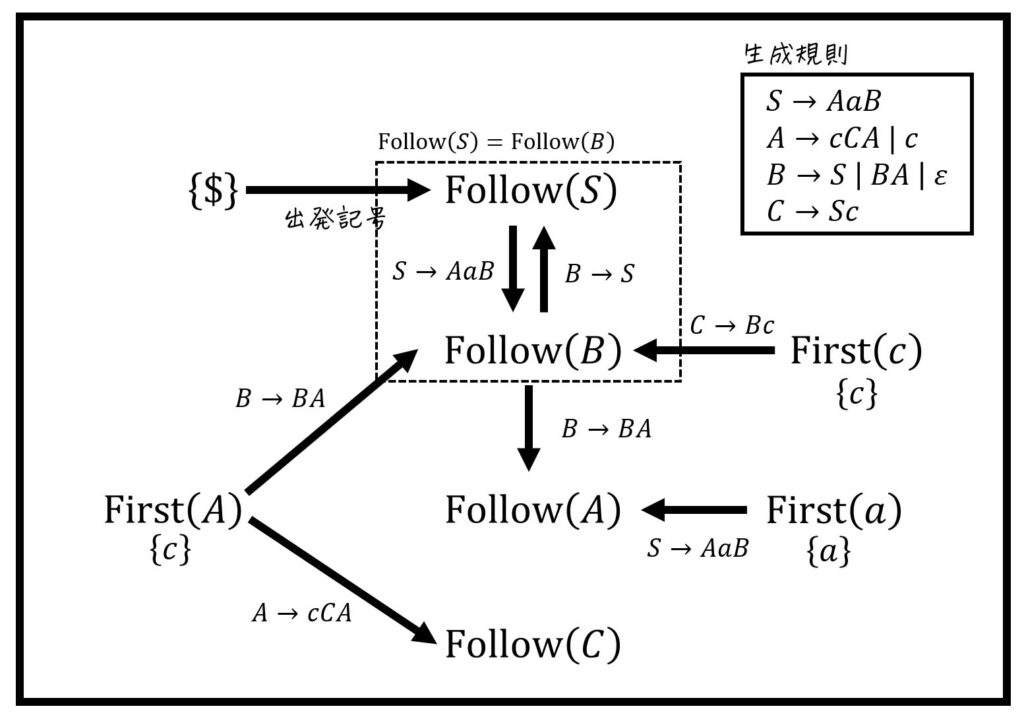
※ 点線部分は、間接的な右再帰により、2つのFollow集合が等しい(=一心同体)になっていることを表す。つまり \( \mathrm{Follow} (S) = \mathrm{Follow} (B) \)。
あとは、求められるFollow集合から順にFollow集合を求めていけばOK。
※ 今回の場合は、\( \mathrm{Follow} (A) \) 集合は点線部分のFollow集合が求まらないと計算できません。それ以外の集合は自由な順番で計算できます。
(iv) \( \mathrm{Follow} (C) \) の計算結果
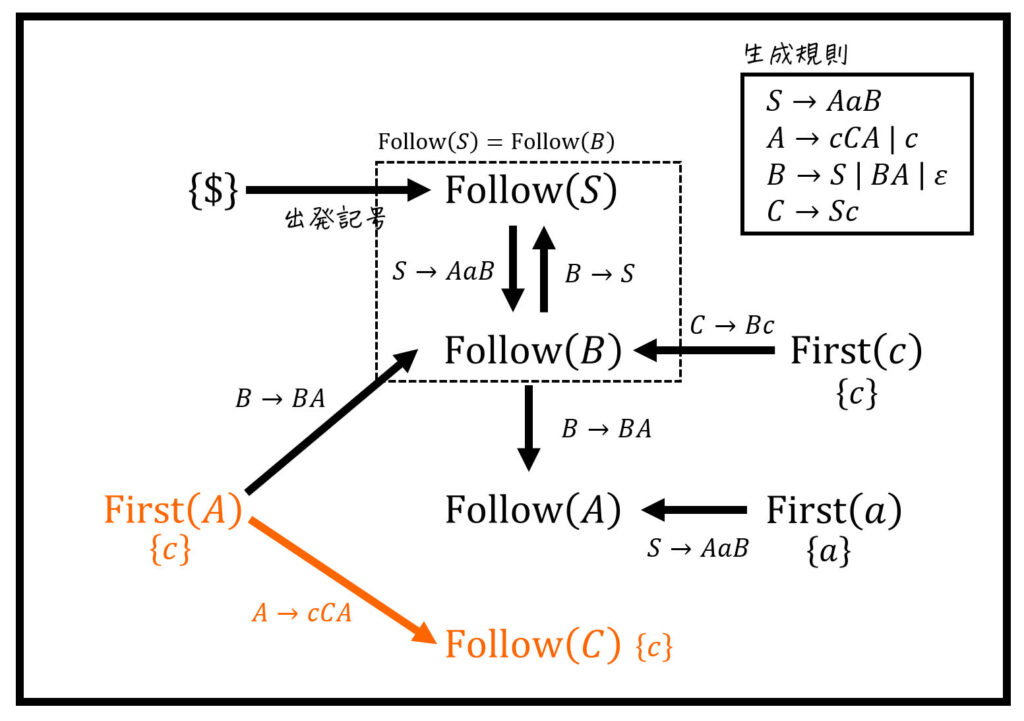
\mathrm{Follow} (C) & = \mathrm{First} (a)
\\ & = \{ c \}
\end{align*}\]
(i), (iii) \( \mathrm{Follow} (S) \), \( \mathrm{Follow} (B) \) の計算結果(2つのFollow集合は等しい)
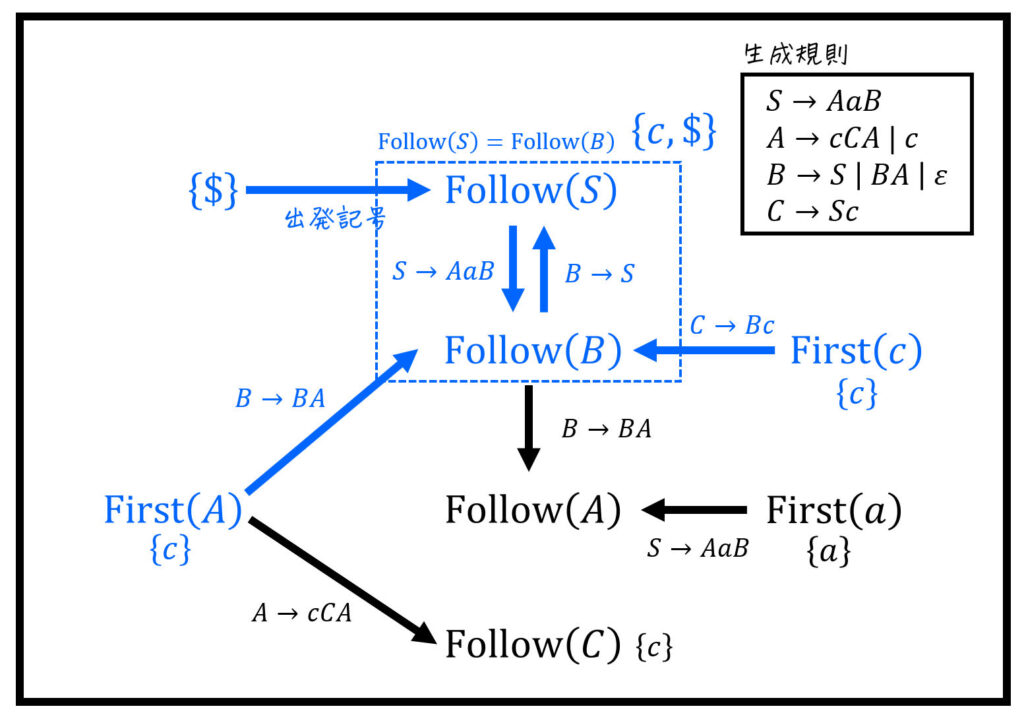
\mathrm{Follow} (S) & = \{ \$ \} \cup \mathrm{First} (A) \cup \mathrm{First} (c)
\\ & = \{ \$ \} \cup \{ c \} \cup \{ c \}
\\ & = \{ c , \$ \}
\end{align*}\]※ \( \mathrm{Follow} (B) \) 加えられている要素もいったん \( \mathrm{Follow} (S) \) に足している。
\[\begin{align*}
\mathrm{Follow} (B) & = \mathrm{Follow} (S)
\\ & = \{ c , \$ \}
\end{align*}\]
(ii) \( \mathrm{Follow} (A) \) の計算結果
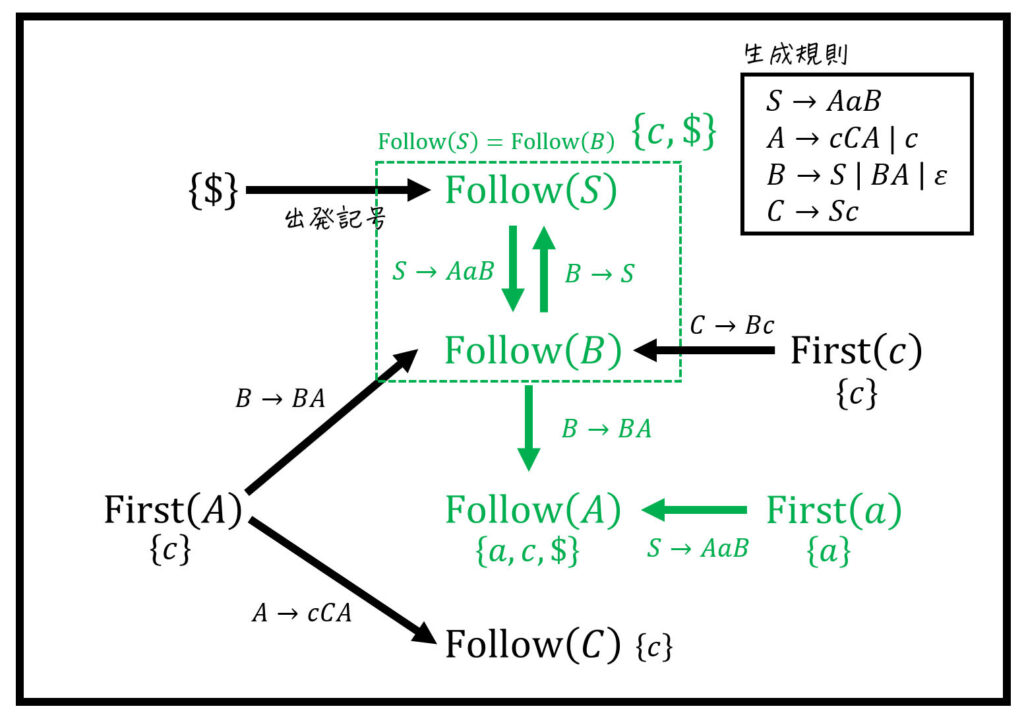
\mathrm{Follow} (A) & =\mathrm{Follow} (B) \cup \mathrm{First} (a)
\\ & = \{ c, \$ \} \cup \{ a \}
\\ & = \{ a, c , \$ \}
\end{align*}\]※ \( \mathrm{Follow} (B) \) を \( \mathrm{Follow} (S) \) としてもOK。
(3) Director集合の計算・LL(1)文法の判定
各非終端記号に対して、生成元から2つ以上の生成規則を持つものは、
- \( A \) が生成元となる規則:\( A \to cCA \), \( A \to c \)
- \( B \) が生成元となる規則:\( B \to S \), \( B \to BA \), \( B \to \varepsilon \)
である。あとは、非終端記号ごとに「どの生成規則同士の積をとっても、Director集合が空集合になること」を確認すればOK。
1) \( A \) が生成元の生成規則 \( A \to cCA \), \( A \to c \) に対してDirector集合確認
\( \textcolor{magenta}{A} \to \textcolor{deepskyblue}{cCA} \) のDirector集合\[\begin{align*}
\mathrm{Director} ( \textcolor{magenta}{A} , \textcolor{deepskyblue}{cCA} ) & = \mathrm{First} ( cCA )
\\ & \overset{ \mathrm{R3} }{=} \mathrm{First} ( c )
\\ & \overset{ \mathrm{R1} }{=} \{ c \}
\end{align*}\]
\( \textcolor{magenta}{A} \to \textcolor{deepskyblue}{c} \) のDirector集合\[\begin{align*}
\mathrm{Director} ( \textcolor{magenta}{A} , \textcolor{deepskyblue}{c} ) & = \mathrm{First} ( c )
\\ & \overset{ \mathrm{R1} }{=} \{ c \}
\end{align*}\]
\( A \) に関する各Director集合同士の積を取ると、\[\begin{align*}
\mathrm{Director} ( A, cCA ) \cap \mathrm{Director} ( A, c ) & = \{ c \} \cap \{ c \}
\\ & = \{ c \}
\end{align*}\]となるためNG。
よって、題意の文法はLL(1)文法ではない。
※ 1つでも \( \phi \) にならないものがあればその時点でLL(1)文法ではないことが確認できるため、他のDirector集合は求めなくてOKです。
7. さいごに
かなり長い記事となっていましたが、以上が
- LL(1)文法
- First集合
- Follow集合
- Director集合
に関する説明でした。
この記事を見て、少しでもLL(1)文法やFirst, Follow, Director集合の計算の方法について理解いただけたのであれば非常にうれしいです。
次回は、左再帰な文法についての「問題点」と「左再帰を解消する方法」について説明する予定です。
[練習問題の中に入れられなかったおまけ問題] 生成規則 \( A \to B \) に対するDirector集合 \( \mathrm{Director} (A,B) \) を求めなさい。ただし、\[\begin{align*}\mathrm{First} (A) & = \{ a \} \\
\mathrm{First} (B) & = \{ b, \varepsilon \} \\
\mathrm{Follow} (A) & = \{ c \} \\
\mathrm{Follow} (B) & = \{ d, \$ \}
\end{align*}\]とする。解答はこの注釈に書いています[12]\( \varepsilon \in \mathrm{First} (B) \) なので、\( B \) が空文字になる可能性を考慮するのがミソです。\[\begin{align*}\mathrm{Director} (A,B) & = \mathrm{First}(B) \cup … Continue reading。
注釈
| ↑1 | 10文字弱、かつ生成規則が4つであればやみくもにやってもそこまで時間はかかりませんが、実際のプログラムに対して構文解析をする場合、膨大な文字数かつ膨大な生成規則があるため、やみくもにやっていると日が暮れてしまいます。 |
|---|---|
| ↑2 | もう少し詳しく言うと、LL(1)文法はトップダウン構文解析(出発記号を起点として、どんどん生成規則を用いて分解していきながら解析する方法)において、1文字だけ先読みすることで文字列を後戻りすることなく構文解析ができる文法です。 |
| ↑3 | \( A \to Ab \) のように左再帰文法となる規則を適用しても、先頭文字列は \( A \) のまま変わらないため、無視しても問題ない。 |
| ↑4 | いったん\[\begin{align*} \mathrm{First} (A) & = \mathrm{First} (B) \cup \mathrm{First} (c) \\ & = \underbrace{ \mathrm{First} (A) }_{ \mathrm{無視} } \cup \mathrm{First} (c) \\ & = \mathrm{First} (c) \end{align*}\]のように、左辺に出てくるFirst集合(今回は \( \mathrm{First} (A) \) )が右辺にも出てくる形にしてから、左辺にも右辺にも出てきたFirst集合を無視して計算してもOKです。 |
| ↑5 | 一般化すると、1文字目からn文字目までの文字すべてに空文字があれば、1文字目~n+1文字目の和を取ればOK。 |
| ↑6 | \( \beta \) がそもそも存在しない、つまり \( \beta = \varepsilon \) のときは、\( \mathrm{First} ( \beta ) = \mathrm{First} ( \varepsilon ) \overset{ \mathrm{R1} }{=} \{ \varepsilon \} \) となるため、\( \varepsilon \) を無視すると追加できる集合がなくなる。 |
| ↑7 | \( \textcolor{blue}{A} \to a \textcolor{magenta}{B} \) より、\[\begin{align*} \mathrm{Follow} ( \textcolor{magenta}{B} ) + & = \mathrm{Follow} ( \textcolor{magenta}{A} ) \\ & = \mathrm{Follow} (B) \cup \mathrm{Follow} (A) \end{align*}\]の式が導出でき、\( \textcolor{blue}{B} \to b \textcolor{magenta}{A} \) より、\[\begin{align*} \mathrm{Follow} ( \textcolor{magenta}{A} ) + & = \mathrm{Follow} ( \textcolor{magenta}{B} ) \\ & = \mathrm{Follow} (A) \cup \mathrm{Follow} (B) \end{align*}\]となるため、数式的にも \( \mathrm{Follow} (A) = \mathrm{Follow} (B) \) が言える。\ |
| ↑8 | 実際に私もよく計算ミスします。 |
| ↑9 | 下の図の場合「\( \mathrm{Follow} (S) \) を求めるためには \( \mathrm{First} (c) \) と \( \{ \$ \} \) の要素を追加すればOK」ということを表しています。 |
| ↑10 | 集合 \( B \) に集合 \( A \) の要素を追加したのに、集合 \( B \) の要素の中に集合 \( A \) の一部の要素は実は入っていない、なんてことは起こりませんよね…? |
| ↑11 | 具体的には、\( \{ $ \} \subseteq \mathrm{Follow} (S) \), \( \mathrm{First} (c) \subseteq \mathrm{Follow} (S) \), \( \mathrm{Follow} (S) \subseteq \mathrm{Follow} (A) \), \( \mathrm{First} (A) \subseteq \mathrm{Follow} (B) \), \( \mathrm{Follow} (A) \subseteq \mathrm{Follow} (B) \) 5つが成立しているかすべて確かめればOKです。 |
| ↑12 | \( \varepsilon \in \mathrm{First} (B) \) なので、\( B \) が空文字になる可能性を考慮するのがミソです。\[\begin{align*} \mathrm{Director} (A,B) & = \mathrm{First}(B) \cup \mathrm{Follow} (A) - \{ \varepsilon \} \\ & = \{ a,b \} \end{align*}\] |
関連広告・スポンサードリンク