スポンサードリンク
記事修正履歴
9月23日:誤字・数式ミス修正、表現の微妙な修正をしました。指摘してくださった方、どうもありがとうございました!
こんにちは、ももやまです。
今までは決定性オートマトンを書いていくことを中心に説明していきました。
しかし今回は、いよいよみんなが(;´Д`) うぅっ。。となる証明、具体的にはある言語が正則でないことを示す方法についてまとめていきたいと思います。
なんとか理解していきましょう……。
前回の記事(第05羽)はこちら!
目次
スポンサードリンク
1.有限指数・右不変とは
マイヒル・ネロード(Myhill–Nerode)の定理で使われる有限指数、右不変についてまずは説明しておきましょう。
(1) 有限指数
\( \Sigma^* \) 上の*1同値な関係 \( R \) があるとします。\( \Sigma^* \) を \( R \) で割った商集合 \( \Sigma^* / R \) の要素が有限個であるとき、二項関係 \( R \) が有限指数を持つといいます。
(商集合について忘れてしまった人は下の記事で復習をしましょう。)
(2) 右不変
\( \Sigma^* \) 上の二項関係 \( R \) が\[
x \ R \ y \to 任意の \ z \in \Sigma^* \ に対し \ xz \ R \ yz
\]を満たすとき、右不変であると言います。
簡単に説明すると、二項関係が満たされている両者の文字列に右側から同じものを連接しても関係が成り立つのが右不変です。
スポンサードリンク
2.Myhill–Nerodeの定理
では、本題のMyhill-Nerode(マイヒル・ネロード)の定理に入ります。
マイヒルネ・ロード(My昼寝・ロード)じゃないですよw(まぁ証明聞くと眠くなりますよねw)
Myhill-Nerodeの定理を下に示しておきます。
以下のその1、その2、その3はすべて同値である。
その1:\( \Sigma \) 上の言語 \( L \) が正則である
その2:言語 \( L \) は有限指数かつ右不変な同値関係 \( R \) による同値類の和で表される
その3:\( \Sigma^* \) 上の2項関係 \( \underset{L}{\equiv} \) は有限指数(かつ右不変)な同値関係となる。ただし \( \underset{L}{\equiv} \) は\[
x \ \underset{L}{\equiv} \ y \Leftrightarrow 任意の \ z \in \Sigma^* \ に対し xz \in L \Leftrightarrow yz \in L
\]となる。
( ゚д゚)ポカーン ってなった人が多いと思います。
でも大丈夫です。こんな定理なんだなーって思っておいてください。
スポンサードリンク
3.Myhill–Nerodeの定理と正則でない証明
ここからが本題です。
ある言語 \( L \) が正則(正規言語)であることを示したければ、言語 \( L \) を受理する有限オートマトンを作成すればOKでしたね。
しかし、ある言語 \( L \) が正則ではないことを示すために有限オートマトンが書けないことを示すのは難しいですよね。
そこで使われるのがMyhill-Nerodeの定理です。Myhill-Nerodeの定理と背理法をうまい具合に組み合わせることで言語 \( L \) が正則でないことを示すことができちゃうのです。
試しに1問例題を出してみましょう。
例題1
\( \Sigma = \{ a, b\} \) とする。このとき、言語\[
L = \left\{ a^n b^n \ \middle| \ \ n \in \mathbb{N} \ \right\}
\]が正則でないことを示したい。
以下の証明を穴埋めすることで証明を完成させなさい。
ただし、( 1 )・( 3 ) は適切な二項関係 \( \underset{L}{\equiv} \) を用いた式を、( 2 ) は \( i,j \) を用いた関係式を書くこと。
\( \Sigma^* \) 上の二項関係 \( \underset{L}{\equiv} \) をつぎのように定義する。\[
x \ \underset{L}{\equiv} \ y\underset{def}{\Leftrightarrow} \forall z \in \Sigma^* \ \ \left( xz \in L \Leftrightarrow yz \in L \right)
\]
\( L \) が正則であると仮定すると、Myhill-Nerodeの定理より、\( \underset{L}{\equiv} \) は有限指数かつ右不変な同値関係となる。
(1) 有限指数であるから ( 1 ) となる自然数 \( i,j \) が存在する。
(ただし ( 2 )である。)
(2) 右不変であるから ( 3 ) が成立する。
( 4 ) \( \in L \) なので \( \underset{L}{\equiv} \) の定義より ( 5 ) \( \in L \) となる。
しかし、( 2 ) なので ( 5 ) \( \notin L \) となる。
これは仮定に矛盾する。よって \( L \) は正則でないことが示された。
解説1
解答
( 1 ) … \( a^i \underset{L}{\equiv} a^j \)
( 2 ) … \( i \not = j \)(一応 \( i \lt j \), \( i \gt j \) もOK)
( 3 ) … \( a^i b^i \underset{L}{\equiv} a^j b^i \)
( 4 ) … \( a^i b^i \)
( 5 ) … \( a^j b^i \)
証明解説

流れとしては
- Myhill-Nerodeを使うために \( \underset{L}{\equiv} \) を定義
- 仮定より有限指数が成立するので \( (文字)^i \underset{L}{\equiv} (文字)^j \) の関係*2を作る(よく使う関係式は \( i \not = j \), \( i \gt j \), \( i \lt j \) の3つ*3。)
- 仮定より右不変も成立するので2で作成した二項関係の両方に同じ文字列を連接することで二項関係の一方(左辺)を \( L \) に属する言語、もう一方(右辺)を \( L \) に属さない言語にし、矛盾させる
となります。
今回は\[
L = \left\{ a^n b^n \ \middle| \ \ n \in \mathbb{N} \ \right\}
\]が正則でないことを示したいので、2項関係の一方が \( \underset{L}{\equiv} \) に属し、もう一方が \( \underset{L}{\equiv} \) に属さないような例を1つ見つけてやります。
まず有限指数を使う部分では\[
a^i \underset{L}{\equiv} a^j
\]としましょう。左辺を \( L \) に属する言語、右辺を \( L \) に属さない言語にするためには、両辺に \( \color{blue}{b^i} \) を連接させればよいことがわかりますね。よって右不変より\[
a^i \color{blue}{b^i} \underset{L}{\equiv} a^j \color{blue}{b^i}
\]も成立しますね。
ここで、\( a^i b^i \in L \) は明らかですよね。なので左辺は \( L \) に属しています。また、\( i \not = j \) なので \( a^j b^i \notin L \) になりますね。
\( L \) が正則であることを仮定しているため、Myhill-Nerodeの定理も成り立つはずなのに \( a^i \color{blue}{b^i} \in L \), \( a^j \color{blue}{b^i} \notin L \) となるのは矛盾していますよね。
なので、仮定が誤りとなり、\( L \) は正則ではないことがわかります。
4.正則な言語と正則でない言語の差
では、正則な言語と正則でない言語にはどこに差があるのでしょうか。
基本的にどんなに長い文字列でも判定するために無限の状態数(記憶数の上限がない)を記憶する必要があるような言語は正則ではありません。例えば、\[
L = \left\{ a^n b^n \ \middle| \ \ n \geqq 0 \right\}
\]は(上限がない) \( a \) の数と \( b \) の数を記憶させる必要がありますね。なので正則ではありませんね。ですが、\[
L = \left\{ a^n b^n \ \middle| \ \ n \leqq 1000 \right\}
\]とすると、\( n = 1001 \) 以上の場合、絶対に受理されないので受理されるかどうかの判定は \( n = 1000 \) (有限)まですればよいので有限オートマトンで表すことができ、正則と言えます*4。
また、\[
L = \left\{ a^{2n} \ \middle| \ \ n\geqq 0 \right\}
\]も一見無限の記憶が必要に見えるのですが、どんな大きな数でも2で割ったあまりは0(偶数)か1(奇数)のどちらか(2状態)ですよね。この2状態のうちのどちらかを覚えておけばおいので有限の状態数で済みます。よって正則です。
実際に正則かどうかを判定するのは慣れが必要だと思うので下に用意した練習問題で少し練習してみましょう。
5.練習問題
では、練習してみましょう。
練習1
つぎの(1)〜(4)の言語 \( L \) が正則ではないことを証明しなさい。
ただし、\( n \) は整数とする。
(1)
※ \( |w|_a \), \( |w|_b \) はそれぞれ \( a \) の文字数、\( b \) の文字数を表します。\[
L = \left\{w \ \middle| \ \ w \in \Sigma^* , \ |w|_a > |w|_b \right\}
\]
(2)
\( w^R \) は語 \( w \) の反転を表します。\[
L = \left\{w \ \middle| \ \ w \in \Sigma^* , \ w = w^R \right\}
\]
(3)\[
L = \left\{wxw \ \middle| \ \ w \in \Sigma^+ , \ x \in \Sigma^* \right\}
\](9月23日修正:問題を差し替えました。)
(4)\[
L = \left\{x a^n b^n \ \middle| \ \ x \in \Sigma^* , n \geqq 1 \right\}
\]
練習2
次の \( L_1 \) 〜 \( L_5 \) の中から正則な言語を2つ選び、番号で答えなさい。
※指示がない限り \( m,n \) は0以上の整数とする。また、\( w^R \) は語(文字列) \( w \) の反転を、\( |w|_a \) は \( w \) に含まれる
\[
L_1 = \left\{a^m b^n b^m \ \middle| \ \ m,n \geqq 0 \ \right\} \\
L_2 = \left\{a^m b^n b^n \ \middle| \ \ m,n \geqq 0 \ \right\} \\
L_3 = \left\{ww^R \ \middle| \ \ w \in \Sigma^* ,\ \ |w| \leqq 1000 \ \right\} \\
L_4 = \left\{w \ \middle| \ \ w \in \Sigma^* ,\ \ -3 \leqq |w|_a - |w|_b \leqq 3 \ \right\} \\
L_5 = \left\{a^n w b^n \ \middle| \ \ w \in \Sigma^* ,\ \ |w| \leqq 1000 \right\}
\]
6.練習問題の答え
解答1
(1)

(2)

(3)
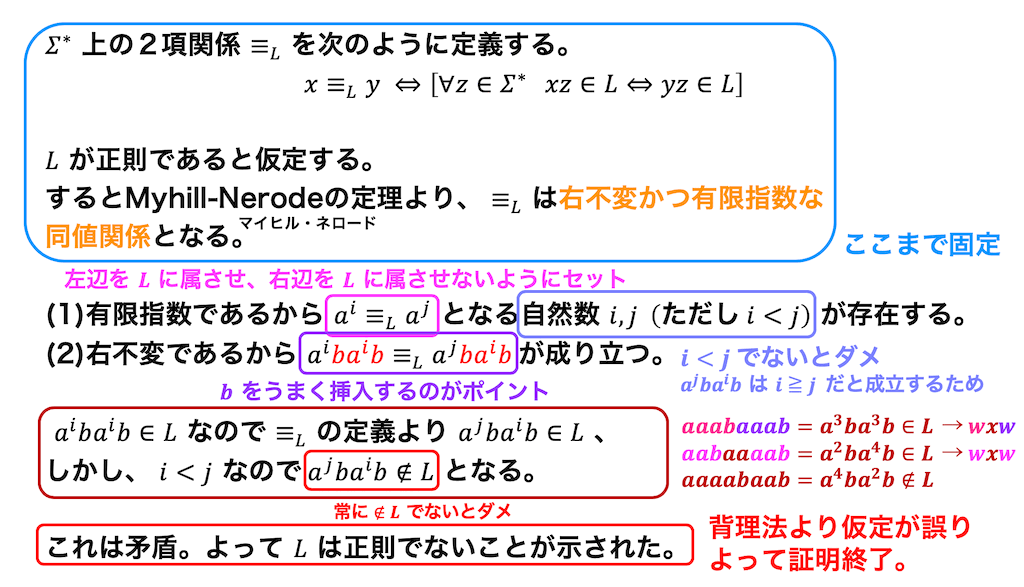
(4)

解答2
解答:\( L_2 \), \( L_3 \)
それぞれの解説
言語 \( L_1 \)
\( a^m b^n b^m \)(\( b \) の数が \( a \) の数以上なら正則)なので無限に続く文字列が受理するかどうか判定するために(上限数がない) \( a \) の数を記憶させる必要があるため、正則ではない。
(簡潔な証明)
有限指数より、\( a^i \underset{L_1}{\equiv} a^j \) となる \( i,j \) (ただし \( i \gt j \) )が存在、右不変より \( a^i b^i \underset{L}{\equiv} a^j b^i \) となる。
\( a^i b^i \in L_1 \) だが \( a^j b^i \notin L_1 \) より \( \underset{L_1}{\equiv} \) の定義と矛盾し、正則でない。
言語 \( L_2 \)
\( a^m b^n b^n \) ということは \( a^m b^{2n} \) と同等。
つまり、\( a^m \) のあとに \( b^{2n} \) を連接するような言語である。
\( a^m \) (\( a \) だけで構成されるような文字列を受理する言語)はもちろん正則、\( b^{2n} \) (\( b \) だけが偶数文字並ぶような文字列を受理する言語)も正則なので、当然連接したものも正則となる。
言語 \( L_3 \)
\( |w| \lt 1000 \) がポイント
\( w \) が1000文字以下と決められているので、\( w \) 1001文字以上の文字列の判定は不要(絶対受理しないため)
なので1000文字分(有限)の記憶で受理するかどうかの判定が可能なため、正則である。
言語 \( L_4 \)
\( -3 \leqq |w|_a - |w|_b \leqq 3 \) がポイント。
\( |w|_a \) の文字数、\( |w|_b \) の文字数をそれぞれ記憶し、判定しないと受理可能かどうかは調べられない。無限の記憶必要でなので正則ではない。
(簡潔な証明)
有限指数より、\( a^i \underset{L_4}{\equiv} a^j \) となる \( i,j \) (ただし \( i \gt j \) )が存在、右不変より \( a^i b^{i+3} \underset{L_4}{\equiv} a^j b^{i+3} \) となる。
\( a^i b^{i+3} \in L_4 \) だが \( a^j b^{i+3} \notin L_4 \) より正則でない。
言語 \( L_5 \)
\( |w| \leqq 1000 \) がポイント。
ただし、範囲が有限だからといって正則とすぐには判定しないように。
\( a^n w b^n \) ということは \( w \) が1000文字以下なら無条件に受理、しかし判定したい文字列が1000文字以上だからといって無条件に受理しないとは限らず、始点と終点の \( a \) の文字数と \( b \) の文字数が一致すれば受理する。そのため受理するかどうかを判定するために(上限数がない)始点と終点の \( a \) の文字、\( b \) の文字の数を記憶させる必要がある。よって正則ではない。
(9月23日追記:簡潔な証明 読者の方に書いていただきました、ありがとうございます!)
有限指数より、\( a^i \underset{L_5}{\equiv} a^j \) となる \( i,j \) (ただし \( i \lt j \) )が存在、右不変より \( a^i a^{1000} b^i \underset{L_5}{\equiv} a^j a^{1000} b^i \) となる。
\( a^i a^{1000} b^i \in L_5 \) だが \( a^j a^{1000} b^i\notin L_5 \) より \( \underset{L_5}{\equiv} \) の定義と矛盾し、正則でない。
6.さいごに
今回はオートマトンと言語理論において、正則ではない言語であること、つまり有限オートマトンが書けないことを証明するための道具に使えるMyhill-Nerodeの定理についてまとめました。
今後は正則な言語かどうかの判定を行い、正則の場合は決定性オートマトンの記述、正則ではない場合はMyhill-Nerodeの定理における証明をする必要があります。しかし、最初はなかなか難しいと思うので次の次の記事で練習問題を持ってこようと思います。
練習問題はこちら!↓
次回は文脈自由文法について軽く説明します。
Next 第07羽 文脈自由文法についてはこちら!
*1:任意の文字列上のと思ってください。
*2:実際には\( (文字)^i \underset{L}{\equiv} (文字)^j \) の形以外にも \( a^{i^2}\underset{L}{\equiv} a^{j^2} \) や \( a^i b^i \underset{L}{\equiv} a^j b^j \) などの形も使えるけど基本的には\( (文字)^i \underset{L}{\equiv} (文字)^j \) の形をつくると思ってください。
*3:実際には他にもあるけど基本的にはこの3つを使えばOK!
*4:\( n \geqq 1001 \) のときは強制的に非受理にすればOK。なので無限の記憶は不要。
関連広告・スポンサードリンク