スポンサードリンク
こんにちは、ももやまです。
前回は言語の補集合、和、積、差を求め、決定性オートマトンで表す方法についてまとめましたね。
今回は言語の連接および閉包演算の結果を決定性オートマトンで表す方法についてまとめていきたいと思います。
前回の記事「言語の演算(前編)」はこちら!↓↓↓
目次
スポンサードリンク
1.文字列(語)の連接とは
文字列の連接とは、2つの文字をくっつけて新たな1つの文字列を作ることをいいます。
例えば、"dashi" という文字列と "jiru" という文字列をくっつけると "dashijiru" になります。
文字列の連接には順番があるので注意しましょう。
例えば "dashi" と "jiru" を連接すると "dashijiru" になりますが、順番を入れ替えた "jiru" と "dashi" を連接すると "jirudashi" になります。
スポンサードリンク
2.連接演算 \( L_1 \cdot L_2 \)
(1) 連接を受理する言語とは
連接 \( L_1 \cdot L_2 \) を受理するような言語とは、言語 \( L_1 \) を受理する文字列と言語 \( L_2 \) を受理するような文字列をくっつけた言語を受理するような文字列を表します。例えば言語 \( L_1 \), \( L_2 \) を\[
L_1 = \{ a, aa, aaa \} \\
L_2 = \{b,bb,bbb \}
\]とすれば*1、\[
L_1 \cdot L_2 = \{ ab,abb,abbb,aab,aabb,aabbb,aaab,aaabb,aaabbb \}
\]のように \( L_1 \) を受理したあとに続けて \( L_2 \) も受理するようなものが受理されていることがわかります。
(2) 状態遷移図を用いた連接演算
では、2つの決定性オートマトンを使って実際に連接を受理するようなオートマトンを例題を1つ使って作成してみましょう。
例題1
次の状態遷移図で示される \( L_1 \), \( L_2 \) を連接した言語 \( L_1 \cdot L_2 \) を受理するような決定性オートマトンを書きなさい。
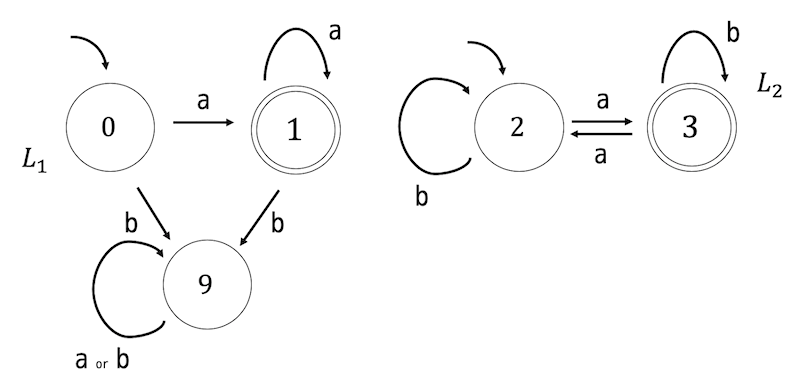
解説1
連接 \( L_1 \cdot L_2 \) は、\( L_1 \) を受理したあとに続けて \( L_2 \) も受理するようなものを表します。
これを表現するために、\( L_1 \) の受理状態に遷移するようなものを \( L_2 \) の初期状態にも遷移させる処理を行います。つまり、下のようにある状態から \( L_1 \) の受理状態に向けられている矢印を \( L_2 \) の初期状態にも向けます。
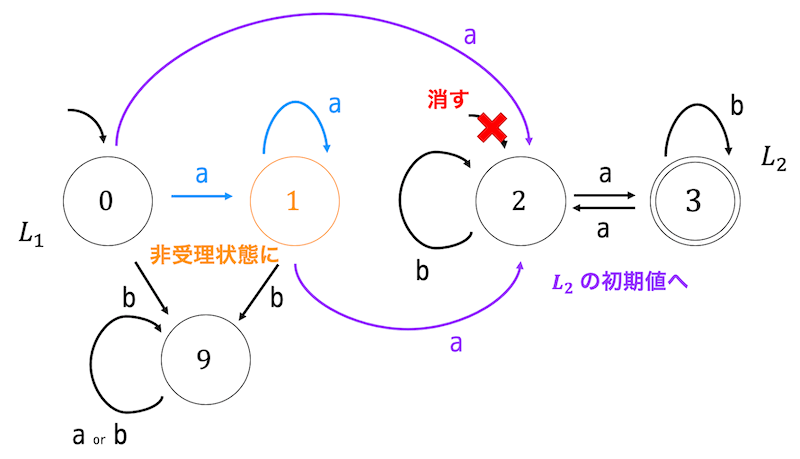
ここで注意することが2つあります。
まず、\( L_1 \) 単品だけで受理させないようにするために \( L_1 \) の受理状態はすべて非受理状態とします*2。
つぎに \( L_2 \) 単品だけで受理させないようにするために \( L_2 \) の初期状態を消します*3。
(ただしあとで説明する例外があるので注意!!)
すると、連接 \( L_1 \cdot L_2 \) を受理する非決定性オートマトンが完成します。なのであとはこれを決定性オートマトンに直す処理をするだけです。
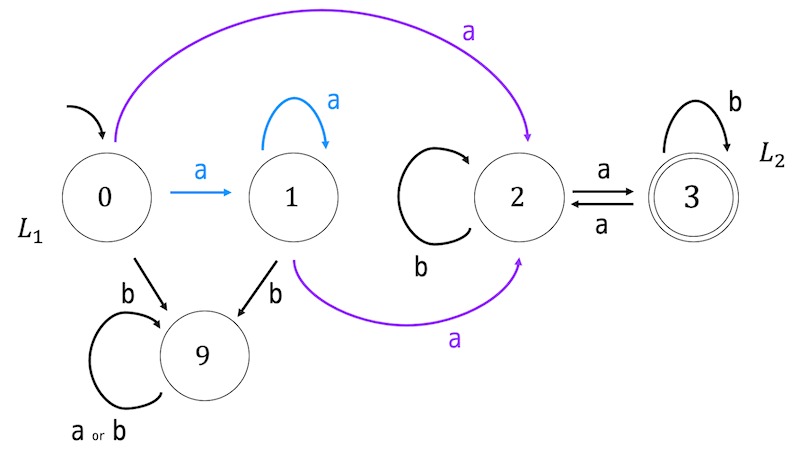
状態数が増えてくるとごちゃごちゃしてくるので状態ごとの各文字における遷移可能な状態を下のようにメモしておくと状態遷移表を書く助けになるかもしれません。
0 → a: 12 b: 9
1 → a: 12 b: 9
2 → a: 3 b: 2
3 → a: 2 b: 3
9 → a: 9 b: 9
地道にがんばると、7状態出てきます。状態遷移表と状態遷移図は下のようになります。
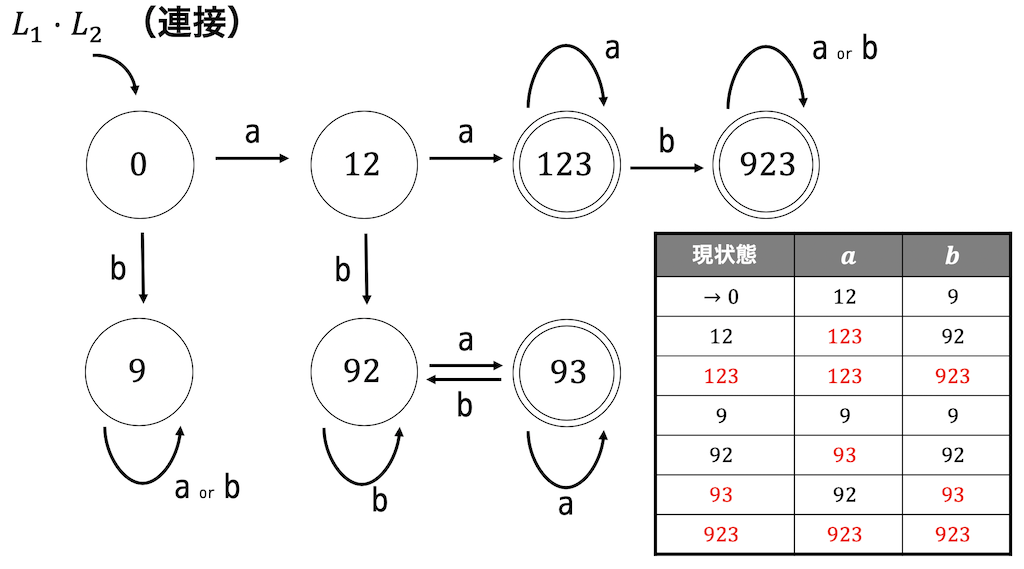
※状態が複数桁で表されているのは複数個の状態が含まれていることを表します。例えば123とあれば状態1、状態2、状態3がすべて含まれる状態を表します。
「あれぇ、7状態もあるのか (*´Д`)=3ハァ・・・」と思った人、安心してください。
この状態数をへらす技を次回説明する予定です。なので期待しておいてください!
(3) (注意!)連接元が空語を受理する場合の連接演算
ただし、連接元 \( L_1 \) が空の言語 \( \varepsilon \) を受理する場合は注意が必要です。
例題2
次の状態遷移図で示される \( L_1 \), \( L_2 \) を連接した言語 \( L_1 \cdot L_2 \) を受理するような決定性オートマトンを書きなさい。
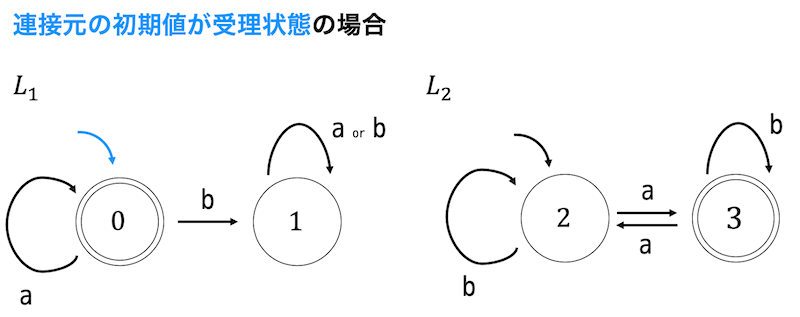
解説2
例題1と同じように \( L_1 \) の受理状態に遷移するようなものを \( L_2 \) の初期状態にも遷移させる処理を行うためにある状態から \( L_1 \) の受理状態に向けられている矢印を \( L_2 \) の初期状態にも向けます。
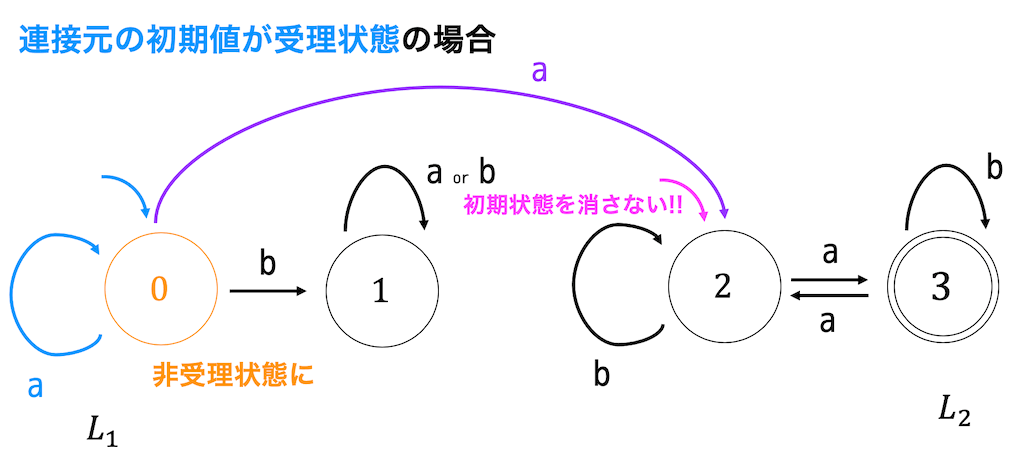
ここで、\( L_2 \) の初期状態を削除しないように気をつけてください!
\( L_1 \) が空語を受理するということは、\( L_2 \) 単品だけで受理するような言語がありますよね。なので、\( L_2 \) の初期状態が必要となるのです。
初期値の矢印も \( L_1 \) の受理状態に向けられているので \( L_2 \) の初期状態に向けるとおぼえておくといいと思います。
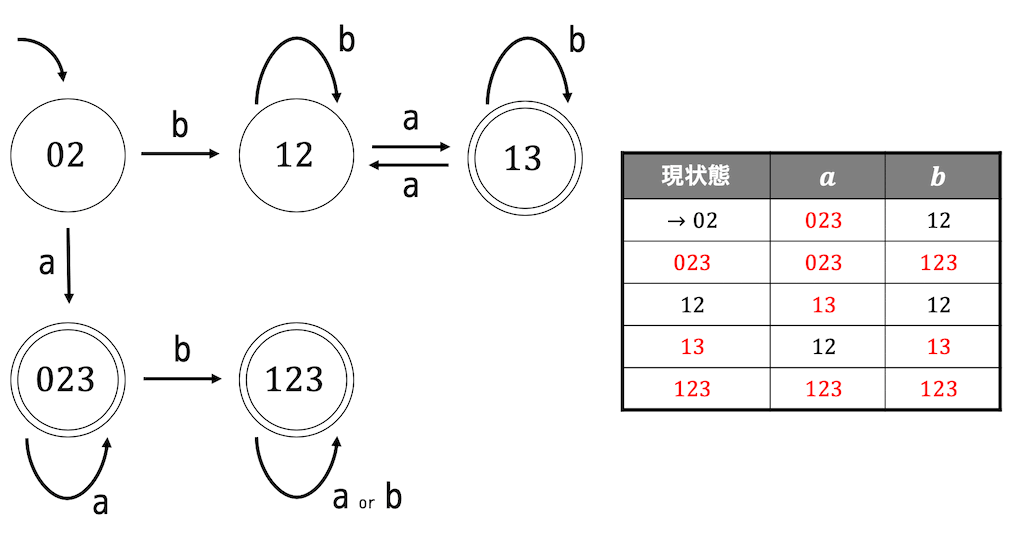
あとは状態遷移表を書いて非決定性なオートマトンを決定性に直すだけです。
各状態における文字ごとの遷移可能先
0 → a: 02 b: 1
1 → a: 1 b: 1
2 → a: 3 b: 2
3 → a: 2 b: 3
連接元を \( L_1 \)、連接先を \( L_2 \) とするとき、連接 \( L_1 \cdot L_2 \) を受理する決定性オートマトンの求め方は以下の通りである。
Step1:ある状態から \( L_1 \) の受理状態に向けられている矢印をすべて \( L_2 \) の初期状態にも向ける(もとの矢印は消さない)
Step2:\( L_1 \) の受理状態をすべて非受理受理状態にする
Step3:\( L_1 \) が空語 \( \varepsilon \) を受理するかを確認(初期値が受理状態であれば空語を受理する)、受理する場合は \( L_2 \) の初期状態をそのままに、受理しない場合は \( L_2 \) の初期状態を削除
Step4:連接 \( L_1 \cdot L_2 \) を受理する非決定性オートマトンが求まるのであとは決定性オートマトンに直す
以上の4ステップで求められる。
決定性オートマトン連接演算の求め方
スポンサードリンク
3.スター閉包(クリーネ閉包)
(1) スター閉包とは
言語 \( L \) に属するあらゆる文字列を集めた言語を \( L^* \) と表します。これをスター閉包(もしくはクリーネ閉包)と呼びます。
言い換えると、言語 \( L \) に属する文字列の一部を0回以上使って表現することができる言語がスター閉包となります*4。
例えば、\( L = \{a \} \) とすると、\[
L* = \{ \varepsilon, a, aa, aaa, aaaa, \cdots \}
\]となり、\( L = \{aa, bb \} \) とすると、\[
L* = \{ \varepsilon, aa,bb,aaaa,aabb,bbbb, \cdots \}
\]となります。
また、空文字 \( \varepsilon \) はどんな言語のスター閉包であろうが必ず受理します。
(2) 状態遷移図を用いたスター閉包の求め方
では、状態遷移図を用いたスター閉包の求め方を説明していきましょう。
例題3
次の状態遷移図で示される \( L \) のスター閉包(クリーネ閉包) \( L^* \) を受理するような決定性オートマトンを書きなさい。
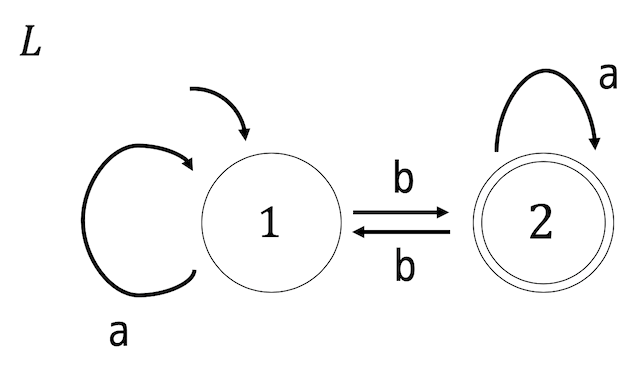
解説3
スター閉包は、言語 \( L \) に属する文字列の一部を0回以上使って表される言語のことでしたね。
これを表現するために、スター閉包は \( L \) の受理状態に遷移するようなものを自分自信の言語 \( L \) の初期状態にも遷移させる処理を行います。つまり、下の図ようにある状態から \( L \) の受理状態に向けられている矢印を自分自身の言語 \( L \) の初期状態にも向けます。
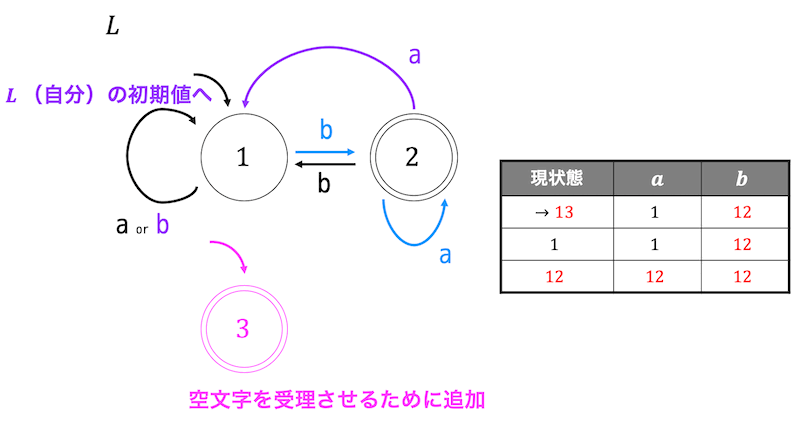
ここで1つ注意する点としては、スター閉包は言語 \( L \) に属する言語を1回も使わない場合も受理されるので必ず空文字も受理しますよね。なので、空文字を受理するオートマトンも追加します。
すると、スター閉包 \( L^* \) を受理する非決定性オートマトンが完成します。なのであとはこれを決定性オートマトンに直す処理をするだけです。
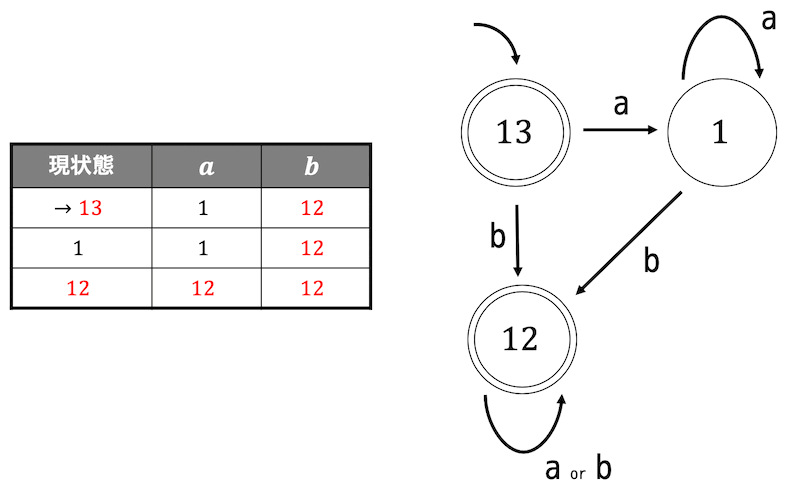
言語 \( L \) のスター閉包 \( L^* \) を求める方法は以下の通りである。
Step1:ある状態から \( L \) の受理状態に向けられている矢印をすべて自分自身 \( L \) の初期状態にも向ける(もとの矢印は消さない)
Step2:空語を受理するオートマトンを追加する
Step3:Step1、Step2で作成したオートマトンを1つの非決定性オートマトンとみて決定性オートマトンになおしていく。
以上の3ステップで求められる。
閉包演算の求め方
4.連接・スター閉包と正則言語
有限オートマトン(決定性非決定性限らず)を書くことをできるような言語を正則な言語と呼ぶことは前回説明しましたね。
連接、スター閉包と正則性を下に示しておきます。
ある言語 \( L_1 \), \( L_2 \) がともに正則なとき、言語の連接 \( L_1 \cdot L_2 \) は正則となる。
また、ある言語 \( L \) が正則であるとき、言語 \( L \) のスター閉包 \( L^* \) も正則となる。
言い換えると、2つの言語 \( L_1 \), \( L_2 \) の(決定性オートマトンにおける)状態遷移図がかければ必ず連接 \( L_1 \cdot L_2 \) を受理するような決定性オートマトンが書け、言語 \( L \) の状態遷移図がかければ必ずスター閉包 \( L^* \) の状態遷移図も書けることがわかりますね。
しかし、この逆( \( L_1 \cdot L_2 \) が正則ならば \( L_1 \), \( L_2 \) が正則)は成り立つでしょうか? 前回と同じように少し考えてみましょう。
(前回のように練習問題に入れたのでぜひ考えてください、最後のほうに答えを載せています。)
5.練習問題
では、2問練習してみましょう。(いつもより少し少ないです…)
練習1
\( \Sigma = \{a,b \} \) とする。つぎの非決定性オートマトン \( M_1 \) および決定性オートマトン \( M_2 \) で与えられる言語 \( L(M_1) \), \( L(M_2) \) がある。
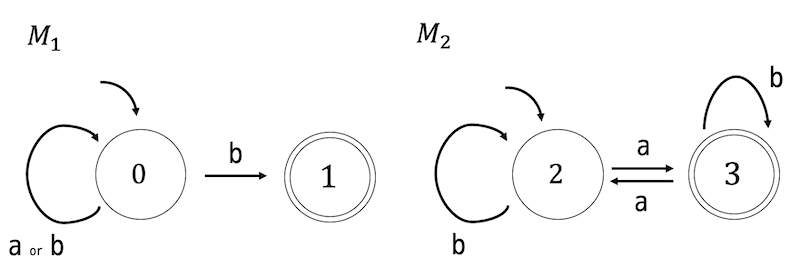
(1) \( M_1 \) を決定性オートマトンに直しなさい。(復習)
(2) 連接 \( L(M_1) \cdot L(M_2) \) を受理する決定性オートマトンを求めなさい。
練習2
つぎの(1)〜(5)の文章が正しければ○、誤っていれば×を答えなさい。簡単な理由も書くこと。
( \( L_1 \cdot L_2 \) は言語 \( L_1 \), \( L_2 \) の連接を表し、\( L^* \) は \( L \) のスター閉包を表す。
(1) ある言語 \( L_1 \), \( L_2 \) がともに正則ならばもちろん \( L_1 \cdot L_2 \) は必ず正則となる。
(2) ある言語 \( L_1 \cdot L_2 \) が正則ならばもちろん \( L_1 \), \( L_2 \) ともに必ず正則となる。
(3) ある言語 \( L_1 \) が正則で別のある言語 \( L_2 \) が正則でないならば \( L_1 \cdot L_2 \) は必ず正則とはならない。
(4) ある言語 \( L^* \) が正則ならばもちろん \( L \) も必ず正則である。
(5) ある言語 \( L^* \) が正則でないならばもちろん \( L \) も必ず正則でない。
6.練習問題の答え
解答1
連接の演算も決定性オートマトンに直してから行うことを強くおすすめします*5
(1)
復習。さすがに慣れてきますよね。
状態遷移表を書いて状態遷移図に直せばOK。
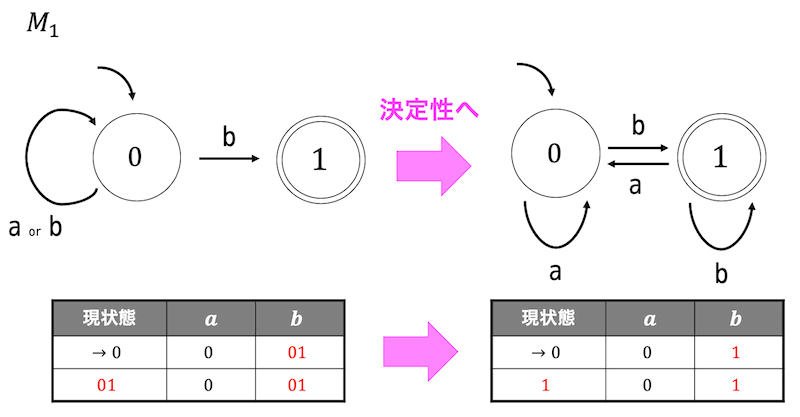
(2)
まずは、連接 \( L(M_1) \cdot L(M_2) \) を受理する非決定性オートマトンを作成します。
- \( L_1 \) の受理状態に向けられている矢印を \( L_2 \) の初期状態にも追加
- \( L_1 \) の受理状態を非受理状態に
- \( L_1 \) の初期状態が受理状態ではないので、\( L_2 \) の初期状態を削除
の3ステップを行うと、下のような状態遷移図が完成します。
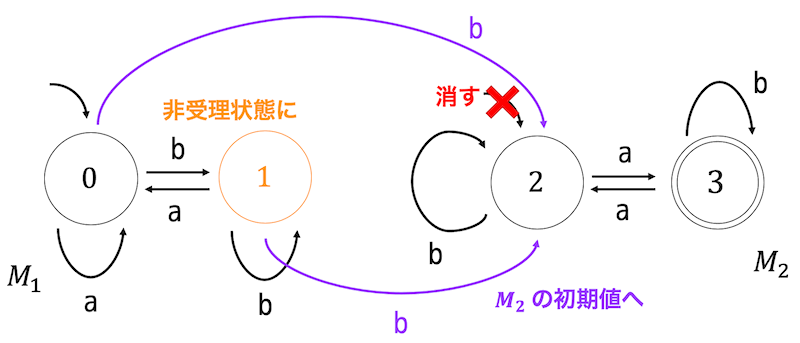
あとはこの非決定性オートマトンを決定性オートマトンに直せば完成です。
全部で6状態となります。
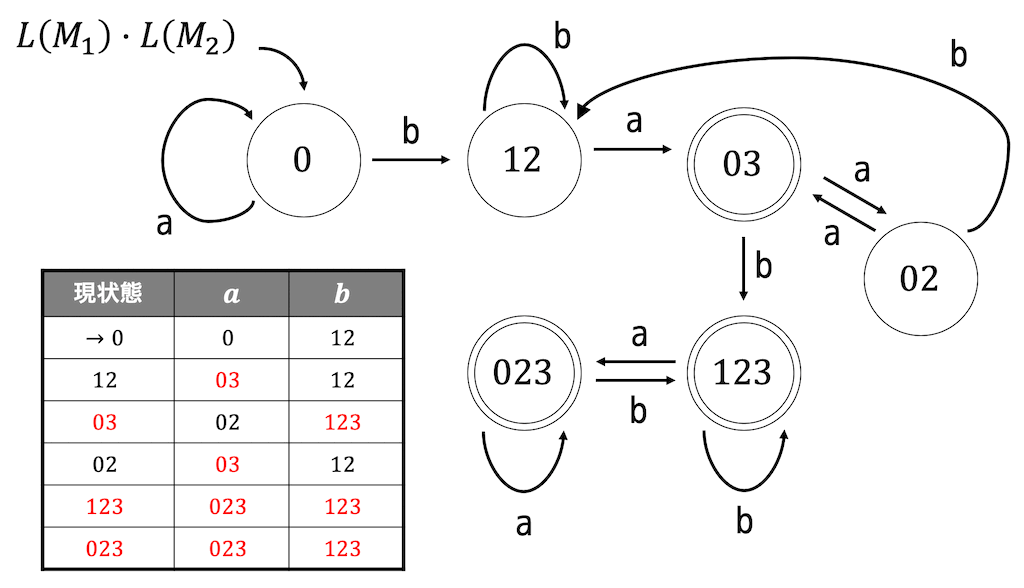
6状態もあるのか(´Д`)ハァ… と思ったそこのあなた
実は123と023はまとめて1つの状態とし、合計5状態にすることができます。
(まとめる方法は次回教えたいと思います!)
解答2
前回のように反例として \( \Sigma^* \) や \( \varepsilon \) を考えるのがおすすめ。ですが、和演算や積演算に比べて反例の設定が少しめんどくさいものが多いです。
連接では \( L_1 \cdot L_2 \) の \( L_1 \) が空語 \( \varepsilon \) を受理する場合、\( L_2 \) の言語はすべて \( L_1 \cdot L_2 \) でも受理されることを使います。
(もちろん逆に \( L_2 \) が空語を受理する場合は \( L_1 \) の言語は \( L_1 \cdot L_2 \) でも受理されます。)
正則でない言語を \( N \) とします。
(1)
解答:○
理由:定義そのものだから。
(2)
解答:×
理由:\( L_1 = N \cup \{ \varepsilon \} \), \( L_2 = \Sigma^* \) とすれば、\( L_1 \cdot L_2 = \Sigma^* \) となり、\( L_1 \cdot L_2 \) が正則なのに \( L_1 \) が正則ではなくなり、反例となる。
(\( L_1 \) を空語を受理する正則でない言語とするのがポイント。)
(3)
解答:×
理由:\( L_1 = \Sigma^* \)、\( L_2 = N \cup \{ \varepsilon \} \) とすれば \( L_1 \cdot L_2 = \Sigma^* \) となり、\( L_1 \) が正則、\( L_2 \) が正則でないのに \( L_1 \cdot L_2 \) が正則となり、反例となる。
(4)
解答:×
理由:\( L = N \cup \{ a,b \} \) とする*6。すると \( L^* \) は \( a \), \( b \) を1文字以上使った文字列、つまりすべての文字列を受理する \( \Sigma^* \) と一緒になる。なので反例となる。
( \( \Sigma = \{a,b\} \) と仮定して反例設定しています。本当は \( N \cup \Sigma \) などと記述するのがいいかもしれません。)
(5)
解答:○
理由:対偶を取ると「\( L \) が正則ならばもちろん \( L^* \) も正則である」となり、定義と一緒になる。定義はもちろん真なので対偶も真。
7.さいごに
今回は言語の連接、閉包させたものを決定性オートマトンで表す方法についてまとめました。
連接を求める際にはかなりめんどくさい非決定性オートマトンを決定性オートマトンに直す必要があるため、それぞれの状態がどこに遷移できるのかをメモ程度に書いておくことをおすすめします。
また、連接演算の結果出てきた決定性オートマトンはかなり状態数が多くて複雑でしたね。次回はこの状態数をなるべく少なくする方法についてまとめていこうと思います。
Next「第05羽」はこちら!↓
*1:集合に入っているのが受理するような文字列を表しています。今回の場合、\( L_1 \) は文字列 \( a \), \( aa \), \( aaa \) を受理するような言語、\( L_2 \) は文字列 \( b \), \( bb \), \( bbb \) を受理するような言語を表します。
*2:\( L_1 \) に受理状態が含まれていると、連接先 \( L_2 \) に関係なく受理してしまうような言語が発生してしまうため。
*3:\( L_2 \) に初期状態が含まれていると、連接元 \( L_1 \) に関係なく受理してしまう言語が発生してしまうため。ただし、のちに説明するが連接元 \( L_1 \) が空語 \( \varepsilon \) を受理する場合は初期状態を外さない例外が発生する。
*4:例えば、言語 \( L \) に属する文字列が \( a \), \( b \) だとすると、\( a \), \( b \) それぞれ0回以上使った言語がすべて受理されます。
*5:非決定性オートマトンのまま連接の演算をすると状態数が多くなり、めんどくさいことになる。
*6:\( L \) が1文字で表現できる文字列を受理できる場合、\( L^* \) は必ずどんな文字列であろうが受理するため。
関連広告・スポンサードリンク