スポンサードリンク
こんにちは、ももやまです。
今回は行列の対角化を用いて、行列のべき乗( \( n \) 乗)を求める方法についてまとめていきたいと思います。
対角化を行い行列の \( n \) 乗を求める方法は期末試験、編入学試験、院試、数検など様々な試験に頻出します。
前回までのうさぎでもわかる線形代数「第17羽 直交行列を用いた対角化」はこちら↓
対角化の知識を使うのでまだ読んでいない方はこちらも読みましょう!
スポンサードリンク
1.対角行列
普通に行列 \( A \) の \( n \) 乗を求めるのはかなりめんどくさいです。
しかし、対角行列であれば簡単に \( n \) 乗を求められますね。
D = \left(
\begin{array}{cccc}
t_1 & 0 & \ldots & 0 \\
0 & t_2 & \ldots & 0 \\
\vdots & \vdots & \ddots & \vdots \\
0 & 0 & \ldots & t_k
\end{array}
\right)
\]の \( n \) 乗は、それぞれの成分を \( n \) 乗したものとなる。
数式を用いて表すと、\[
D^n = \left(
\begin{array}{cccc}
t_1^n & 0 & \ldots & 0 \\
0 & t_2^n & \ldots & 0 \\
\vdots & \vdots & \ddots & \vdots \\
0 & 0 & \ldots & t_k^n
\end{array}
\right)
\]となる。
例えば、\[
D = \left( \begin{array}{ccc} 3 & 0 & 0 \\ 0 & 3 & 0 \\ 0 & 0 & 4 \end{array} \right)
\]のべき乗 \( D^n \) は、\[
D^n = \left( \begin{array}{ccc} 3^n & 0 & 0 \\ 0 & 3^n & 0 \\ 0 & 0 & 4^n \end{array} \right)
\]と求められます。簡単ですね。
ある行列 \( A \) を対角化すると、対角行列 \( D \) を用いて、\[
P^{-1} AP = D
\] と表せますね。この対角行列を \( n \) 乗することを考えましょう。

と変形することができます。つまり、\[
D^n = P^{-1} A^n P
\]が成立します。ここで、行列 \( A \) は、\[
P D^n P^{-1} = P P^{-1} A^n P P^{-1} = A^n \\
A^n = P D^n P^{-1}
\]と求めることができます。
P^{-1} AP = D
\]と対角化することにより、行列 \( A \) の \( n \) 乗は\[
A^n = P D^n P^{-1}
\]と求めることができる。
このように、行列を対角化することにより、\( n \) 乗を簡単に出すことができちゃいます!
スポンサードリンク
2.例題
まずは2次正方行列のべき乗 \( A^n \) を求めてみましょう。
基本的に
- 行列の固有値を出す
- 行列の固有ベクトルを出し、対角化
- 正則行列 \( P \) の逆行列を算出
- \( A^n = P D P^{-1} \) に入れて計算
の4ステップで計算ができます。
練習問題では3次正方行列にチャレンジしてもらいます。
例題1
行列 \( A \) \[
A = \left( \begin{array}{ccc} 2 & 4 \\ 1 & -1 \end{array} \right)
\]のべき乗 \( A^n \) を求めなさい。
解説1
Step1:固有値の算出
行列 \( A \) の固有値を \( t \) とすると、固有方程式は、\[\begin{align*}
|A-tE| = & \left| \begin{array}{ccc} 2-t & 4 \\ 1 & -1-t \end{array} \right|
\\ = & (t-2)(t+1) - 4
\\ = & t^2 - t - 6
\\ = & (t-3)(t+2) = 0
\end{align*} \]より固有値は3, -2となる。
Step2:固有ベクトルの算出、対角化
(1) 固有値が3のときの固有ベクトル\[ \begin{align*}
(A-3E) = &
\left( \begin{array}{ccc} -1 & 4 \\ 1 & -4 \end{array} \right) \\ \to \ &
\left( \begin{array}{ccc} 1 & -4 \\ 0 & 0 \end{array} \right)
\end{align*} \]となる。\[
x - 4y = 0
\]を解くと、任意定数 \( k \) を用いて\[
\left( \begin{array}{ccc} x \\ y \end{array} \right) = k \left( \begin{array}{ccc} 4 \\ 1 \end{array} \right)
\]と表せるので、固有ベクトル \( \vec{p_1} \) は、\[
\vec{p_1} = \left( \begin{array}{ccc} 4 \\ 1 \end{array} \right)
\]となる。
(2) 固有値が-2のときの固有ベクトル\[ \begin{align*}
(A-3E) = &
\left( \begin{array}{ccc} 4 & 4 \\ 1 & 1 \end{array} \right) \\ \to \ &
\left( \begin{array}{ccc} 1 & 1 \\ 0 & 0 \end{array} \right)
\end{align*} \]となる。\[
x + y = 0
\]を解くと、任意定数 \( k \) を用いて\[
\left( \begin{array}{ccc} x \\ y \end{array} \right) = k \left( \begin{array}{ccc} 1 \\ -1 \end{array} \right)
\]と表せるので、固有ベクトル \( \vec{p_1} \) は、\[
\vec{p_1} = \left( \begin{array}{ccc} 1 \\ -1 \end{array} \right)
\]となる。
よって、固有ベクトル \( \vec{p_1} \), \( \vec{p_2} \) を用いて、正則行列 \( P \) を\[
P = \left( \vec{p_1}, \vec{p_2} \right) = \left( \begin{array}{ccc} 4 & 1 \\ 1 & -1 \end{array} \right)
\]とすると、\[
P^{-1} AP = \left( \begin{array}{ccc} 3 & 0 \\ 0 & -2 \end{array} \right) = D
\]と対角化できる。
AP = PD = \left( \begin{array}{ccc} 12 & -2 \\ 3 & 2 \end{array} \right)
\]となればOK。
Step3:行列 \( P \) の逆行列の算出
逆行列 \( P^{-1} \) を求める。\[ \begin{align*}
P^{-1} & = \frac{1}{ |P| } \left( \begin{array}{ccc} 1 & 1 \\ 1 & -4 \end{array} \right)
\\ & = \frac{1}{ 5 } \left( \begin{array}{ccc} 1 & 1 \\ 1 & -4 \end{array} \right)
\end{align*} \]となる*1。
Step4:\( A^n \) の算出
行列 \( A \) のべき乗 \( A^n \) は\[
A^n = P D^n P^{-1}
\]と求められるので、\[ \begin{align*}
A^n & = \left( \begin{array}{ccc} 4 & 1 \\ 1 & -1 \end{array} \right) \left( \begin{array}{ccc} 3^n & 0 \\ 0 & (-2)^n \end{array} \right) \cdot \frac{1}{5} \left( \begin{array}{ccc} 1 & 1 \\ 1 & -4 \end{array} \right)
\\ & = \frac{1}{5} \left( \begin{array}{ccc} 4 \cdot 3^n & (-2)^n \\ 3^n & - (-2)^n \end{array} \right) \left( \begin{array}{ccc} 1 & 1 \\ 1 & -4 \end{array} \right)
\\ & = \frac{1}{5} \left( \begin{array}{ccc} 4 \cdot 3^n + (-2)^n & 4 \cdot 3^n - 4 (-2)^n \\ 3^n - (-2)^n & 3^n + 4(-2)^n \end{array} \right)
\end{align*} \]と計算できる。
スポンサードリンク
3.実対称行列のn乗の場合
行列 \( A \) が実対象行列だった場合、直交行列で対角化を行い、 \( A^n \) を出す方法もあります。
直交行列についての対角化があれって思った人やまだよくわかっていない人はこちらの記事で復習しましょう!
直交行列 \( P \) にすることで、逆行列 \( P^{-1} \) が \( {}^t\!P \)(転置)に等しくなるので逆行列を求める手間が軽減されます。
(その代わりルートとか出てくるので計算がややこしくなるかもしれませんが……)
例題2
行列\[
A = \left( \begin{array}{ccc} 2 & 1 \\ 1 & 2 \end{array} \right)
\]を直交行列 \( P \) を用いて対角化し、行列 \( A \) のべき乗 \( A^n \) を求めなさい。
解説2
Step1:固有値の算出
固有値を \( t \) とすると、固有方程式は、\[\begin{align*}
|A-tE| = & \left| \begin{array}{ccc} 2-t & 1 \\ 1 & 2-t \end{array} \right|
\\ = & (t-2)^2 - 1
\\ = & t^2 -4t + 3
\\ = & (t-1)(t-3) = 0
\end{align*} \]より固有値は1, 3となる。
Step2:固有ベクトルの算出、対角化
(1) 固有値が1のときの固有ベクトル\[ \begin{align*}
(A-1E) = &
\left( \begin{array}{ccc} 1 & 1 \\ 1 & 1 \end{array} \right) \\ \to \ &
\left( \begin{array}{ccc} 1 & 1 \\ 0 & 0 \end{array} \right)
\end{align*} \]となる。\[
x + y = 0
\]を解くと、任意定数 \( k \) を用いて\[
\left( \begin{array}{ccc} x \\ y \end{array} \right) = k \left( \begin{array}{ccc} 1 \\ -1 \end{array} \right)
\]と表せる。
固有ベクトル \( \vec{p_1} \) は大きさを1に正規化した、\[
\vec{p_1} = \frac{1}{\sqrt{2}}\left( \begin{array}{ccc} 1 \\ -1 \end{array} \right)
\]となる。
(2) 固有値が3のときの固有ベクトル\[ \begin{align*}
(A-3E) = &
\left( \begin{array}{ccc} -1 & 1 \\ 1 & -1 \end{array} \right) \\ \to \ &
\left( \begin{array}{ccc} 1 & -1 \\ 0 & 0 \end{array} \right)
\end{align*} \]となる。\[
x - y = 0
\]を解くと、任意定数 \( k \) を用いて\[
\left( \begin{array}{ccc} x \\ y \end{array} \right) = k \left( \begin{array}{ccc} 1 \\ 1 \end{array} \right)
\]と表せる。
固有ベクトル \( \vec{p_2} \) は大きさを1に正規化した、\[
\vec{p_2} = \frac{1}{\sqrt{2}} \left( \begin{array}{ccc} 1 \\ 1 \end{array} \right)
\]となる。
よって、\( \vec{p_1} \), \( \vec{p_2} \) は正規直交基底となるので、直交行列\[
P = \left( \vec{p_1}, \vec{p_2} \right) = \frac{1}{\sqrt{2}} \left( \begin{array}{ccc} 1 & 1 \\ -1 & 1 \end{array} \right)
\]を用いて、\[
P^{-1} AP = \left( \begin{array}{ccc} 1 & 0 \\ 0 & 3 \end{array} \right)
\]と対角化できます。
[検算ポイント2:\( AP = PD \) を確認] \[
AP = PD = \frac{1}{\sqrt{2}} \left( \begin{array}{ccc} 1 & 3 \\ -1 & 3 \end{array} \right)
\]となればOK。
Step3:逆行列の算出(楽)
ここで、行列 \( P \) は直交行列なので、逆行列は\[
P^{-1} = {}^t\!P = \frac{1}{\sqrt{2}} \left( \begin{array}{ccc} 1 & -1 \\ 1 & 1 \end{array} \right)
\]となる。
Step4:べき乗 \( A^n \) の計算
行列 \( A \) のべき乗 \( A^n \) は\[
A^n = P D^n P^{-1}
\]と求められるので、\[ \begin{align*}
A^n & = \frac{1}{\sqrt{2}} \left( \begin{array}{ccc} 1 & 1 \\ -1 & 1 \end{array} \right) \left( \begin{array}{ccc} 1^n & 0 \\ 0 & 3^n \end{array} \right) \cdot \frac{1}{\sqrt{2}} \left( \begin{array}{ccc} 1 & -1 \\ 1 & 1 \end{array} \right)
\\ & = \frac{1}{2} \left( \begin{array}{ccc} 1 & 3^n \\ -1 & 3^n \end{array} \right) \left( \begin{array}{ccc} 1 & -1 \\ 1 & 1 \end{array} \right)
\\ & = \frac{1}{2} \left( \begin{array}{ccc} 1 + 3^n & 4 \cdot -1 + 3^n \\ -1 + 3^n & 1 + 3^n \end{array} \right)
\end{align*} \]と計算できる。
4.行列の極限
行列のべき乗 \( n \) の \( n \) を無限に飛ばすことで、行列 \( A \) を掛け続けるとどこに収束するかを求めることができます。
例題3
行列 \( A \) \[
A = \left( \begin{array}{ccc} \frac{4}{7} & \frac{3}{7} \\ \frac{2}{7} & \frac{5}{7} \end{array} \right) = \frac{1}{7} \left( \begin{array}{ccc} 4 & 3 \\ 2 & 5 \end{array} \right)
\]について、行列 \( A \) のべき乗 \( A^n \) を求め、\[
\lim_{n \to \infty} A^n
\]を求めなさい。
解説3
Step1:固有値の算出
固有値を \( t \) とすると、固有方程式は、\[\begin{align*}
|A-tE| = & \left| \begin{array}{ccc} \frac{4}{7} - t & \frac{3}{7} \\ \frac{2}{7} & \frac{5}{7} - t \end{array} \right|
\\ = & \frac{1}{7} \left| \begin{array}{ccc} 4 - 7t & 3 \\ 2 & 5 - 7t \end{array} \right|
\\ = & (7t-4)(7t-5) - 6
\\ = & 49t^2 - 9t + 14
\\ = & (7t-2)(7t-7) = 0
\end{align*} \]より固有値は \( 2/7, 1 \) となる。
(\( 7t = s \) とかおくと大きい数字でなくていいかも…?)
Step2:固有ベクトルの算出、対角化
(1) 固有値が 2/7 のときの固有ベクトル\[ \begin{align*}
\frac{1}{7} (A-2E) = &
\frac{1}{7} \left( \begin{array}{ccc} 2 & 3 \\ 2 & 3 \end{array} \right) \\ \to \ &
\left( \begin{array}{ccc} 2 & 3 \\ 0 & 0 \end{array} \right)
\end{align*} \]となる。\[
2x + 3y = 0
\]を解くと、任意定数 \( k \) を用いて\[
\left( \begin{array}{ccc} x \\ y \end{array} \right) = k \left( \begin{array}{ccc} 3 \\ -2 \end{array} \right)
\]と表せるので、固有ベクトル \( \vec{p_1} \) は、\[
\vec{p_1} = \left( \begin{array}{ccc} 3 \\ -2 \end{array} \right)
\]となる。
(2) 固有値が1のときの固有ベクトル\[ \begin{align*}
\frac{1}{7} (A-7E) = &
\frac{1}{7} \left( \begin{array}{ccc} -3 & 3 \\ 2 & -2 \end{array} \right) \\ \to \ &
\left( \begin{array}{ccc} 1 & -1 \\ 0 & 0 \end{array} \right)
\end{align*} \]となる。\[
x - y = 0
\]を解くと、任意定数 \( k \) を用いて\[
\left( \begin{array}{ccc} x \\ y \end{array} \right) = k \left( \begin{array}{ccc} 1 \\ 1 \end{array} \right)
\]と表せるので、固有ベクトル \( \vec{p_2} \) は、\[
\vec{p_2} = \left( \begin{array}{ccc} 1 \\ 1 \end{array} \right)
\]となる。
よって、固有ベクトル \( \vec{p_1} \), \( \vec{p_2} \) を用いて、正則行列 \( P \) を\[
P = \left( \vec{p_1}, \vec{p_2} \right) = \left( \begin{array}{ccc} 3 & 1 \\ -2 & 1 \end{array} \right)
\]とすると、\[
P^{-1} AP = \left( \begin{array}{ccc} \frac{2}{7} & 0 \\ 0 & 1 \end{array} \right) = D
\]と対角化できる。
AP = PD = \frac{1}{7} \left( \begin{array}{ccc} 6 & 7 \\ -4 & 7 \end{array} \right)
\]となればOK。
Step3:逆行列の算出
つぎに、逆行列 \( P^{-1} \) を求める。\[ \begin{align*}
P^{-1} & = \frac{1}{ |P| } \left( \begin{array}{ccc} 3 & 1 \\ -2 & 1 \end{array} \right)
\\ & = \frac{1}{ 5 } \left( \begin{array}{ccc} 1 & -1 \\ 2 & 3 \end{array} \right)
\end{align*} \]となる。
Step4:べき乗 \( A^n \) の算出
行列 \( A \) のべき乗 \( A^n \) は\[
A^n = P D^n P^{-1}
\]と求められるので、\[ \begin{align*}
A^n & = \left( \begin{array}{ccc} 3 & 1 \\ -2 & 1 \end{array} \right) \left( \begin{array}{ccc} \left( \frac{2}{7} \right)^n & 0 \\ 0 & 1^n \end{array} \right) \cdot \frac{1}{5} \left( \begin{array}{ccc} 1 & -1 \\ 2 & 3 \end{array} \right)
\\ & = \frac{1}{5} \left( \begin{array}{ccc} 3 \cdot \left( \frac{2}{7} \right)^n & 1 \\ -2 \cdot \left( \frac{2}{7} \right)^n & 1 \end{array} \right) \left( \begin{array}{ccc} 1 & -1 \\ 2 & 3 \end{array} \right)
\\ & = \frac{1}{5} \left( \begin{array}{ccc} 3 \cdot \left( \frac{2}{7} \right)^n + 2 & -3 \cdot \left( \frac{2}{7} \right)^n + 3 \\ -2 \cdot \left( \frac{2}{7} \right)^n + 2 & 2 \cdot \left( \frac{2}{7} \right)^n + 3 \end{array} \right)
\end{align*} \]と計算できる。
Step5:\( n \to \infty \) へ
ここで、\( n \to \infty \) のとき、\[
\left( \frac{2}{7} \right)^n = 0
\]なので*2、\[ \begin{align*}
\lim_{n \to \infty} A^n & = \frac{1}{5} \left( \begin{array}{ccc} 3 \cdot \left( \frac{2}{7} \right)^n + 2 & -3 \cdot \left( \frac{2}{7} \right)^n + 3 \\ -2 \cdot \left( \frac{2}{7} \right)^n + 2 & 2 \cdot \left( \frac{2}{7} \right)^n + 3 \end{array} \right) \\ & = \frac{1}{5} \left( \begin{array}{ccc} 2 & 3 \\ 2 & 3 \end{array} \right)
\end{align*}
\]となる。
つまり、行列 \( A \) を掛けていけばいくほど、\[
\frac{1}{5} \left( \begin{array}{ccc} 2 & 3 \\ 2 & 3 \end{array} \right)
\]に収束することを表しています。
[別解]
\( n \to \infty \) を \( D^n \) に適用させると計算が楽になる。\[
\left( \frac{2}{7} \right)^n = 0
\]なので、\[ \begin{align*}
\lim_{n \to \infty} A^n & = \lim_{n \to \infty} P D^n P^{-1}
\\ & = \left( \begin{array}{ccc} 3 & 1 \\ -2 & 1 \end{array} \right) \left( \begin{array}{ccc} 0 & 0 \\ 0 & 1 \end{array} \right) \cdot \frac{1}{5} \left( \begin{array}{ccc} 1 & -1 \\ 2 & 3 \end{array} \right)
\\ & = \frac{1}{5} \left( \begin{array}{ccc} 0 & 1 \\ 0 & 1 \end{array} \right) \left( \begin{array}{ccc} 1 & -1 \\ 2 & 3 \end{array} \right)
\\ & = \frac{1}{5} \left( \begin{array}{ccc} 2 & 3 \\ 2 & 3 \end{array} \right)
\end{align*}
\]と計算するのもOK。
5.練習問題
では、2問練習しましょう。
練習1
行列 \( A \) \[
A = \left( \begin{array}{ccc} 1 & -1 & -2 \\ 2 & 4 & 2 \\ 1 & 1 & 4 \end{array} \right)
\]のべき乗 \( A^n \) を求めなさい。
練習2
行列 \( A \) \[
A = \left( \begin{array}{ccc} \frac{1}{9} & \frac{4}{9} & \frac{4}{9} \\ \frac{1}{9} & \frac{4}{9} & \frac{4}{9} \\ \frac{4}{9} & \frac{4}{9} & \frac{1}{9} \end{array} \right) = \frac{1}{9} \left( \begin{array}{ccc} 1 & 4 & 4 \\ 4 & 1 & 4 \\ 4 & 4 & 1 \end{array} \right)
\]について、行列 \( A \) のべき乗 \( A^n \) を求め、\[
\lim_{n \to \infty} A^n
\]を求めなさい。
(ヒント:実対象行列なので直交行列を用いた対角化が使える)
6.練習問題の答え
解答1
Step1:固有値の算出
固有値を \( t \) とすると、固有方程式は、\[\begin{align*}
|A-tE| = & \left| \begin{array}{ccc} 1-t & -1 & -2 \\ 2 & 4-t & 2 \\ 1 & 1 & 4-t \end{array} \right|
\\ = & \left| \begin{array}{ccc} 3-t & 3-t & 0 \\ 2 & 4-t & 2 \\ 1 & 1 & 4-t \end{array} \right|
\\ = & (3-t) \left| \begin{array}{ccc} 1 & 1 & 0 \\ 2 & 4-t & 2 \\ 1 & 1 & 4-t \end{array} \right|
\\ = & (3-t) \left| \begin{array}{ccc} 1 & 1 & 0 \\ 0 & 2-t & 2 \\ 0 & 0 & 4-t \end{array} \right|
\\ = & (3-t)(2-t)(4-t) = 0
\end{align*} \]より固有値は2,3,4となる。
(上三角行列の行列式は対角成分の積)
Step2:固有ベクトルの算出、対角化
それぞれの固有値に対する固有ベクトル \( \vec{p_1} \), \( \vec{p_2} \), \( \vec{p_3} \) を求める。
(1) 固有値が2のときの固有ベクトル\[ \begin{align*}
(A-2E) = &
\left( \begin{array}{ccc} -1 & -1 & -2 \\ 2 & 2 & 2 \\ 1 & 1 & 2 \end{array} \right) \\ \to \ &
\left( \begin{array}{ccc} 1 & 1 & 2 \\ 0 & 0 & -2 \\ 0 & 0 & 0 \end{array} \right) \\ \to \ &
\left( \begin{array}{ccc} 1 & 1 0 \\ 0 & 0 & 1 \\ 0 & 0 & 0 \end{array} \right)
\end{align*} \]となる。\[
\left\{ \begin{array}{l} x + y = 0 \\ z = 0 \end{array}\right.
\]を解くと、任意定数 \( k \) を用いて\[
\left( \begin{array}{ccc} x \\ y \\ z \end{array} \right) = k \left( \begin{array}{ccc} 1 \\ -1 \\ 0 \end{array} \right)
\]と表せるので、固有ベクトル \( \vec{p_1} \) は、\[
\vec{p_1} = \left( \begin{array}{ccc} 1 \\ -1 \\ 0 \end{array} \right)
\]となる。
(2) 固有値が3のときの固有ベクトル\[ \begin{align*}
(A-3E) = &
\left( \begin{array}{ccc} -2 & -1 & -2 \\ 2 & 1 & 2 \\ 1 & 1 & 1 \end{array} \right) \\ \to \ &
\left( \begin{array}{ccc} 1 & 1 & 1 \\ 0 & -1 & 0 \\ 0 & 0 & 0 \end{array} \right) \\ \to \ &
\left( \begin{array}{ccc} 1 & 0 & 1 \\ 0 & 1 & 0 \\ 0 & 0 & 0 \end{array} \right)
\end{align*} \]となる。\[
\left\{ \begin{array}{l} x + z = 0 \\ y = 0 \end{array}\right.
\]を解くと、任意定数 \( k \) を用いて\[
\left( \begin{array}{ccc} x \\ y \\ z \end{array} \right) = k \left( \begin{array}{ccc} 1 \\ 0 \\ -1 \end{array} \right)
\]と表せるので、固有ベクトル \( \vec{p_2} \) は、\[
\vec{p_2} = \left( \begin{array}{ccc} 1 \\ 0 \\ -1 \end{array} \right)
\]となる。
(3) 固有値が4のときの固有ベクトル\[ \begin{align*}
(A-4E) = &
\left( \begin{array}{ccc} -3 & -1 & -2 \\ 2 & 0 & 2 \\ 1 & 1 & 0 \end{array} \right) \\ \to \ &
\left( \begin{array}{ccc} 0 & 2 & -2 \\ 0 & -2 & 2 \\ 1 & 1 & 0 \end{array} \right) \\ \to \ &
\left( \begin{array}{ccc} 1 & 1 & 0 \\ 0 & 1 & -1 \\ 0 & 0 & 0 \end{array} \right)
\end{align*} \]となる。\[
\left\{ \begin{array}{l} x + y = 0 \\ y - z = 0 \end{array}\right.
\]を解くと、任意定数 \( k \) を用いて\[
\left( \begin{array}{ccc} x \\ y \\ z \end{array} \right) = k \left( \begin{array}{ccc} -1 \\ 1 \\ 1 \end{array} \right)
\]と表せるので、固有ベクトル \( \vec{p_3} \) は、\[
\vec{p_3} = \left( \begin{array}{ccc} -1 \\ 1 \\ 1 \end{array} \right)
\]となる。
よって、固有ベクトル \( \vec{p_1} \), \( \vec{p_2} \), \( \vec{p_3} \) を用いて、正則行列 \( P \) を\[
P = \left( \vec{p_1}, \vec{p_2}, \vec{p_3} \right) = \left( \begin{array}{ccc} 1 & 1 & -1 \\ -1 & 0 & 1 \\ 0 & -1 & 1 \end{array} \right)
\]とすると、\[
P^{-1} AP = \left( \begin{array}{ccc} 2 & 0 & 0 \\ 0 & 3 & 0 \\ 0 & 0 & 4 \end{array} \right) = D
\]と対角化できる。
AP = PD = \left( \begin{array}{ccc} 2 & 3 & -4 \\ -2 & 0 & 4 \\ 0 & -3 & 4 \end{array} \right)
\]となればOK。
Step3:逆行列の算出
つぎに、逆行列 \( P^{-1} \) を求める。
3次正方行列なので掃き出し法で解く。\[ \begin{align*} &
\left( \begin{array}{ccc|ccc} 1 & 1 & -1 & 1 & 0 & 0 \\ -1 & 0 & 1 & 0 & 1 & 0 \\ 0 & -1 & 1 & 0 & 0 & 1 \end{array} \right) \\ \to \ &
\left( \begin{array}{ccc|ccc} 1 & 1 & -1 & 1 & 0 & 0 \\ 0 & 1 & 0 & 1 & 1 & 0 \\ 0 & -1 & 1 & 0 & 0 & 1 \end{array} \right) \\ \to \ &
\left( \begin{array}{ccc|ccc} 1 & 0 & -1 & 0 & -1 & 0 \\ 0 & 1 & 0 & 1 & 1 & 0 \\ 0 & 0 & 1 & 1 & 1 & 1 \end{array} \right) \\ \to \ &
\left( \begin{array}{ccc|ccc} 1 & 0 & 0 & 1 & 0 & 1 \\ 0 & 1 & 0 & 1 & 1 & 0 \\ 0 & 0 & 1 & 1 & 1 & 1 \end{array} \right)
\end{align*} \] となるので、\[
P^{-1} = \left( \begin{array}{ccc} 1 & 0 & 1 \\ 1 & 1 & 0 \\ 1 & 1 & 1 \end{array} \right)
\]となる。
Step4:べき乗 \( A^n \) の算出
行列 \( A \) のべき乗 \( A^n \) は\[
A^n = P D^n P^{-1}
\]と求められるので、\[ \begin{align*}
A^n & = \left( \begin{array}{ccc} 1 & 1 & -1 \\ -1 & 0 & 1 \\ 0 & -1 & 1 \end{array} \right) \left( \begin{array}{ccc} 2^n & 0 & 0 \\ 0 & 3^n & 0 \\ 0 & 0 & 4^n \end{array} \right) \left( \begin{array}{ccc} 1 & 0 & 1 \\ 1 & 1 & 0 \\ 1 & 1 & 1 \end{array} \right)
\\ & =
\left( \begin{array}{ccc} 2^n & 3^n & -4^n \\ -2^n & 0 & 4^n \\ 0 & -3^n & 4^n \end{array} \right) \left( \begin{array}{ccc} 1 & 0 & 1 \\ 1 & 1 & 0 \\ 1 & 1 & 1 \end{array} \right)
\\ & = \left( \begin{array}{ccc} 2^n + 3^n - 4^n & 3^n - 4^n & 2^n - 4^n \\ -2^n + 4^n & 4^n & -2^n + 4^n \\ -3^n + 4^n & -3^n + 4^n & 4^n \end{array} \right)
\end{align*} \]と計算できる。
解答2
Step1:固有値の算出
固有値を \( t \) とすると、固有方程式は、\[\begin{align*}
|A-tE| = & \left| \begin{array}{ccc} \frac{1}{9} - t & \frac{4}{9} & \frac{4}{9} \\ \frac{4}{9} & \frac{1}{9} -t & \frac{4}{9} \\ \frac{4}{9} & \frac{4}{9} & \frac{1}{9} - t \end{array} \right|
\\ = & \frac{1}{9} \left| \begin{array}{ccc} 1 - 9t & 4 & 4 \\ 4 & 1-9t & 4 \\ 4 & 4 & 1-9t \end{array} \right|
\\ = & \frac{1}{9} \left| \begin{array}{ccc} 9 - 9t & 9-9t & 9-9t \\ 4 & 1-9t & 4 \\ 4 & 4 & 1-9t \end{array} \right|
\\ = & (1-t) \left| \begin{array}{ccc} 1 & 1 & 1 \\ 4 & 1-9t & 4 \\ 4 & 4 & 1-9t \end{array} \right|
\\ = & (1-t) \left| \begin{array}{ccc} 1 & 1 & 1 \\ 0 & -3-9t & 0 \\ 0 & 0 & -3-9t \end{array} \right|
\\ = & (1-t)(3+9t)(3+9t)
\\ = & 9(1-t)(1+3t)(1+3t) = 0
\end{align*} \]より固有値は \( -1/3 \)(2重解), 1 となる。
[検算ポイント1:固有値の和は対角成分の和になっていることを確認(1/3になればOK)]
Step2:固有ベクトルの算出、対角化
直交行列を用いて対角化を行うため、\( \vec{p_1} \), \( \vec{p_2} \), \( \vec{p_3} \) は正規直交基底をなすような固有ベクトルとする。
(1) 固有ベクトルが-1/3のとき
\[ \begin{align*}
(A-1E) = &
\frac{1}{9} \left( \begin{array}{ccc} 4 & 4 & 4 \\ 4 & 4 & 4 \\ 4 & 4 & 4 \end{array} \right) \\ \to \ &
\left( \begin{array}{ccc} 1 & 1 & 1 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \end{array} \right)
\end{align*} \]となる。\[
x + y + z = 0
\]を解くと任意定数 \( s \), \( t \) を用いて\[
\left( \begin{array}{ccc} x \\ y \\ z \end{array} \right) = s \left( \begin{array}{ccc} 1 \\ -1 \\ 0 \end{array} \right) + t \left( \begin{array}{ccc} 1 \\ 0 \\ -1 \end{array} \right)
\]となる。
ここで、ベクトル\[
\vec{a_1} = \left( \begin{array}{ccc} 1 \\ -1 \\ 0 \end{array} \right) \ \ \
\vec{a_2} = \left( \begin{array}{ccc} 1 \\ 0 \\ -1 \end{array} \right)
\]は固有ベクトルだが、互いに直交していない。
なので、グラムシュミットを用いることで \( \vec{a_1} \), \( \vec{a_2} \) を正規直交化する。
\( \vec{a_1} \), \( \vec{a_2} \) を正規直交化したベクトルを \( \vec{p_1} \), \( \vec{p_2} \) とする(固有ベクトル)。\[
\vec{p_1} = \frac{1}{ |\vec{a_1}| } \vec{a_1} = \frac{1}{ \sqrt{2} } \left( \begin{array}{ccc} 1 \\ -1 \\ 0 \end{array} \right)
\]となる。
\[
\vec{a_2} \cdot \vec{u_1} = \frac{1}{ \sqrt{2} } = \frac{1}{ \sqrt{2} }
\]なので、\[\begin{align*}
\vec{b_2} & = \vec{a_2} - \left( \vec{a_2} \cdot \vec{u_1} \right) \vec{u_1}
\\ & = \left( \begin{array}{ccc} 1 \\ 0 \\ -1 \end{array} \right) - \frac{1}{ \sqrt{2} }\cdot \frac{1}{ \sqrt{2} } \left( \begin{array}{ccc} 1 \\ -1 \\ 0 \end{array} \right)
\\ & = \frac{1}{2} \left( \begin{array}{ccc} 2 \\ 0 \\ -2 \end{array} \right) - \frac{1}{2} \left( \begin{array}{ccc} 1 \\ -1 \\ 0 \end{array} \right)
\\ & = \frac{1}{2} \left( \begin{array}{ccc} 1 \\ 1 \\ -2 \end{array} \right)
\end{align*} \]となる。
よって、\[ \vec{p_2} = \frac{1}{ | \vec{b_2} | } \vec{b_2} = \frac{1}{ \sqrt{6} } \left( \begin{array}{ccc} 1 \\ 1 \\ -2 \end{array} \right) \]となる。
よって、正規直交化された固有ベクトルは、\[
\vec{p_1} = \frac{1}{ \sqrt{2} } \left( \begin{array}{ccc} 1 \\ -1 \\ 0 \end{array} \right) \ \ \ \vec{p_2} = \frac{1}{ \sqrt{6} } \left( \begin{array}{ccc} 1 \\ 1 \\ -2 \end{array} \right)
\]となる。
(2) 固有ベクトルが1のとき
重解ではないのでただ正規化するだけでOK。
\[ \begin{align*}
\frac{1}{9} (A-9E) = &
\left( \begin{array}{ccc} -8 & 4 & 4 \\ 4 & -8 & 4 \\ 4 & 4 & -8 \end{array} \right) \\ \to \ &
\left( \begin{array}{ccc} 0 & 12 & -12 \\ 0 & -12 & 12 \\ 4 & 4 & -8 \end{array} \right) \\ \to \ &
\left( \begin{array}{ccc} 1 & 1 & -2 \\ 0 & 1 & -1 \\ 0 & 0 & 0 \end{array} \right) \\ \to \ &
\left( \begin{array}{ccc} 1 & 0 & -1 \\ 0 & 1 & -1 \\ 0 & 0 & 0 \end{array} \right)
\end{align*} \]となる。\[
\left\{ \begin{array}{l} x - z = 0 \\ y - z = 0 \end{array}\right.
\]を解くと任意定数 \( k \) を用いて\[
\left( \begin{array}{ccc} x \\ y \\ z \end{array} \right) = k \left( \begin{array}{ccc} 1 \\ 1 \\ 1 \end{array} \right)
\]となる。
大きさを1に正規化した固有ベクトル \( \vec{p_3} \) は、\[
\vec{p_3} = \frac{1}{\sqrt{3}} \left( \begin{array}{ccc} 1 \\ 1 \\ 1 \end{array} \right)
\]となる。
よって、\( \vec{p_1} \), \( \vec{p_2} \), \( \vec{p_3} \) は正規直交基底となるので、直交行列\[
P = \left( \vec{p_1}, \vec{p_2}, \vec{p_3} \right) = \frac{1}{\sqrt{6}} \left( \begin{array}{ccc} \sqrt{3} & 1 & \sqrt{2} \\ - \sqrt{3} & 1 & \sqrt{2} \\ 0 & -2 & \sqrt{2} \end{array} \right)
\]を用いて、\[
P^{-1} AP = \left( \begin{array}{ccc} -\frac{1}{3} & 0 & 0 \\ 0 & -\frac{1}{3} & 0 \\ 0 & 0 & 1 \end{array} \right)
\]できる。
[検算ポイント2:\( AP = PD \) の確認]\[
AP = PD = \frac{1}{ 9 \sqrt{6} } \left( \begin{array}{ccc} -3 \sqrt{3} & -3 & 9 \sqrt{2} \\ 3 \sqrt{3} & -3 & 9 \sqrt{2} \\ 0 & 6 & 9 \sqrt{2} \end{array} \right)
\]
Step3:\( A^n \) の算出
ここで、行列 \( P \) は直交行列なので、逆行列は\[
P^{-1} = {}^t\!P = \frac{1}{\sqrt{6}} \left( \begin{array}{ccc} \sqrt{3} & - \sqrt{3} & 0 \\ 1 & 1 & -2 \\ \sqrt{2} & \sqrt{2} & \sqrt{2} \end{array} \right)
\]となる。
行列 \( A \) のべき乗 \( A^n \) は\[
A^n = P D^n P^{-1}
\]と求められるので、
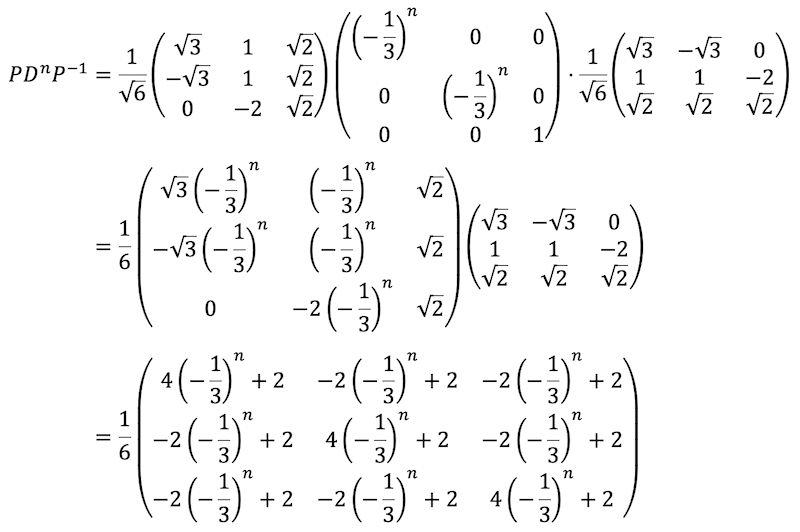
と計算できる。
[検算ポイント3:\( n = 1 \) を代入して \( A^1 = A \) となることを確認]
Step4:\( n \to \infty \) へ
ここで、\( n \to \infty \) のとき、\[
\left( - \frac{1}{3} \right)^n = 0
\]なので、\[ \begin{align*}
\lim_{n \to \infty} A^n & = \frac{1}{6} \left( \begin{array}{ccc} 2 & 2 & 2 \\ 2 & 2 & 2 \\ 2 & 2 & 2 \end{array} \right) \\ & =
\frac{1}{3} \left( \begin{array}{ccc} 1 & 1 & 1 \\ 1 & 1 & 1 \\ 1 & 1 & 1 \end{array} \right)
\end{align*}
\]となる。
[別解]
\( n \to \infty \) を \( D^n \) に適用させると計算が楽になる。
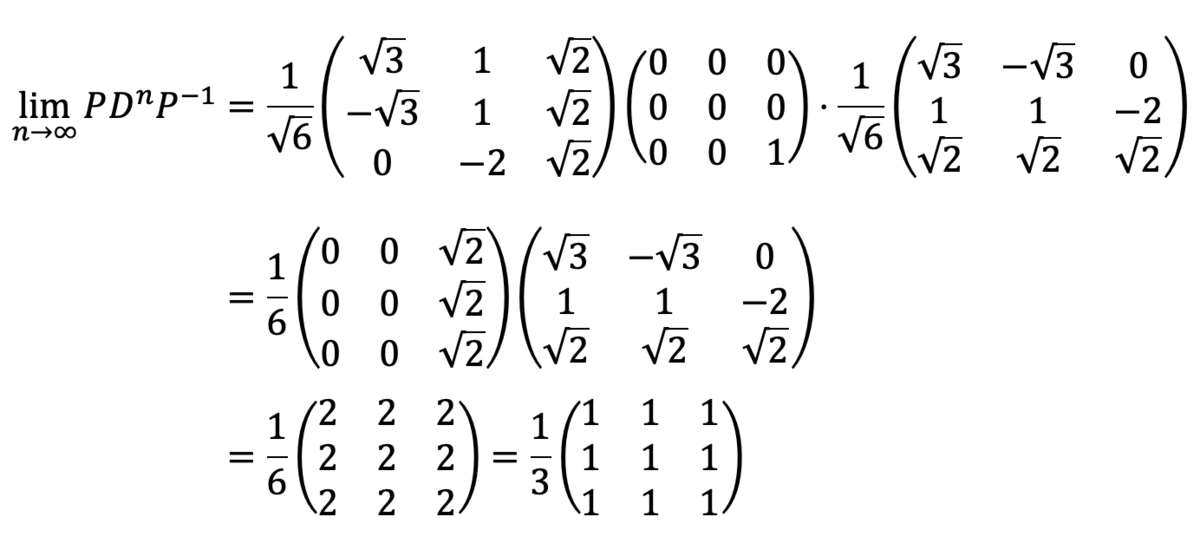
と計算するのもOK。
7.さいごに
今回は、行列のべき乗、\( n \) 乗の求め方および行列の無限乗の求め方を通常の対角化と直交行列を用いた対角化の2つにわけてまとめました。
院試や編入学試験で線形代数を受験する人は、行列の \( n \) 乗は頻出項目なので必ず解けるようにしておきましょう!
今回は対角化可能な行列の \( n \) 乗の求め方でしたが、ジョルダン標準形の場合の \( n \) 乗の求め方も余裕があればやっていきたいと思います。
関連広告・スポンサードリンク