スポンサードリンク
こんにちは、ももうさです。
前回は、瞬時復号可能な符号を作る手法の1つである「ハフマン符号化」についてみていきました。
今回は、瞬時復号可能な符号を作るもう1つの手法である「シャノン・ファノ符号化」の符号化手順について、実際に例題や練習問題を踏まえながら見ていきましょう。
スポンサードリンク
1. まずは例題で確認
まずは、例題でシャノン・ファノ符号化の方法を見ていきましょう。
つぎの表は、とある文字列中(情報源)に出てくる文字の出現確率を表にしたものである。
| 文字(記号) | 符号 (ビット表記) | 出現確率 |
|---|---|---|
| A | (ア) | 12% |
| B | (イ) | 56% |
| C | (ウ) | 4% |
| D | (エ) | 20% |
| E | (オ) | 8% |
(1) この文字列をシャノン・ファノ符号化法によって符号化し、ビット表記の (ア) ~ (オ) に当てはまるビット表記を答えなさい。
(2) (1)で符号化した符号の平均符号長 \( L \) を小数第2位まで答えなさい。(必要であれば小数第3位を四捨五入すること)
Step1. 各文字を出現確率 (回数) の多い順に並べ、全体で1つのグループと仮定
シャノン・ファノ符号化をする際にはまず、与えられた文字(記号・情報)を出現確率が大きい順に並び替えます。
| 文字 | 出現確率 |
|---|---|
| B | 56% |
| D | 20% |
| A | 12% |
| E | 8% |
| C | 4% |
ここからがハフマン符号と方法が変わってくるので、注意してみていきましょう。
シャノン・ファノ符号化では、最初にすべての文字 (記号・情報) を1つのグループと仮定します。
Step2. グループ内の情報を、確率が半分になるように分解していく。(すべてのグループの情報が1つになるまで)
すべてのグループに属する文字が1つになるまで、「2つ以上の文字が属するグループ」を出現確率の和が最も半分に近くなる部分で2分割していきます。
ここで、「出現確率の和が最も半分に近くなる部分」を選んでいく際に、グループ内の各文字の確率を大きい順に足していくことで確認します。(シャノン・ファノ符号化の特徴)
Step2-1. BDAED (100%) を2分割
まずは、BDAED (合計確率: 100%) を2分割します。
ここで、最も半分 (50%) に近くなるように分割するためには、B (56%) とDAEC (44%) に分ければOKですね。
| 文字 | 出現確率 |
|---|---|
| B | 56% |
| D | 20% |
| A | 12% |
| E | 8% |
| C | 4% |
つぎに、分けた2つのグループを下のように二分木で書きます。
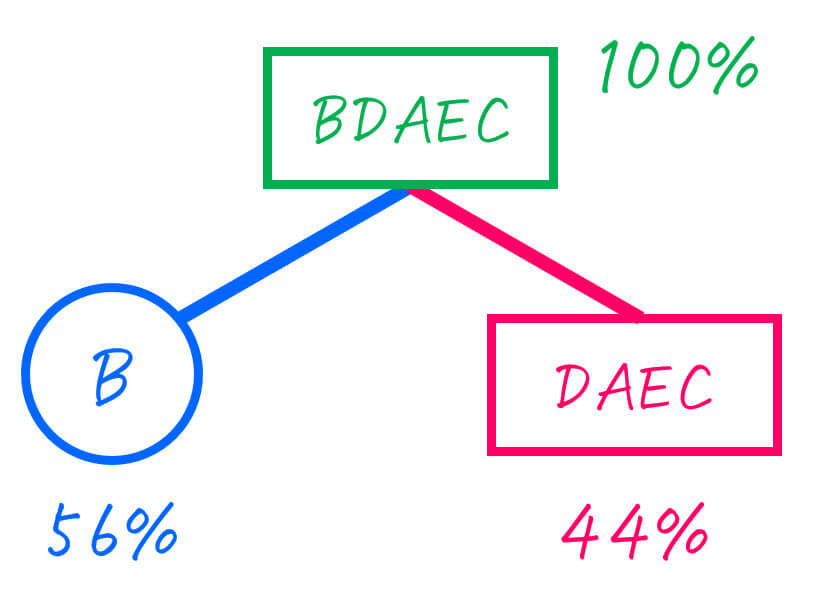
ここで、Bはすでに1つの文字のグループとなったため、これ以上の操作は不要です。一方、ACDEはまだ2つ以上の文字のグループなため、さらに分割をしていきます。
Step2-2. ACDE (44%) を2分割
つぎに、ACDE (合計確率: 44%) を確率が最も半分 (22%) に近くなるところで2分割します。
| 文字 | 出現確率 |
|---|---|
| D | 20% |
| A | 12% |
| E | 8% |
| C | 4% |
ここで、最も半分 (22%) に近くなるように分割するためには、D (20%) とAEC (24%) に分ければOKですね。
さらに、分けた2つのグループを下のように二分木で書きます。
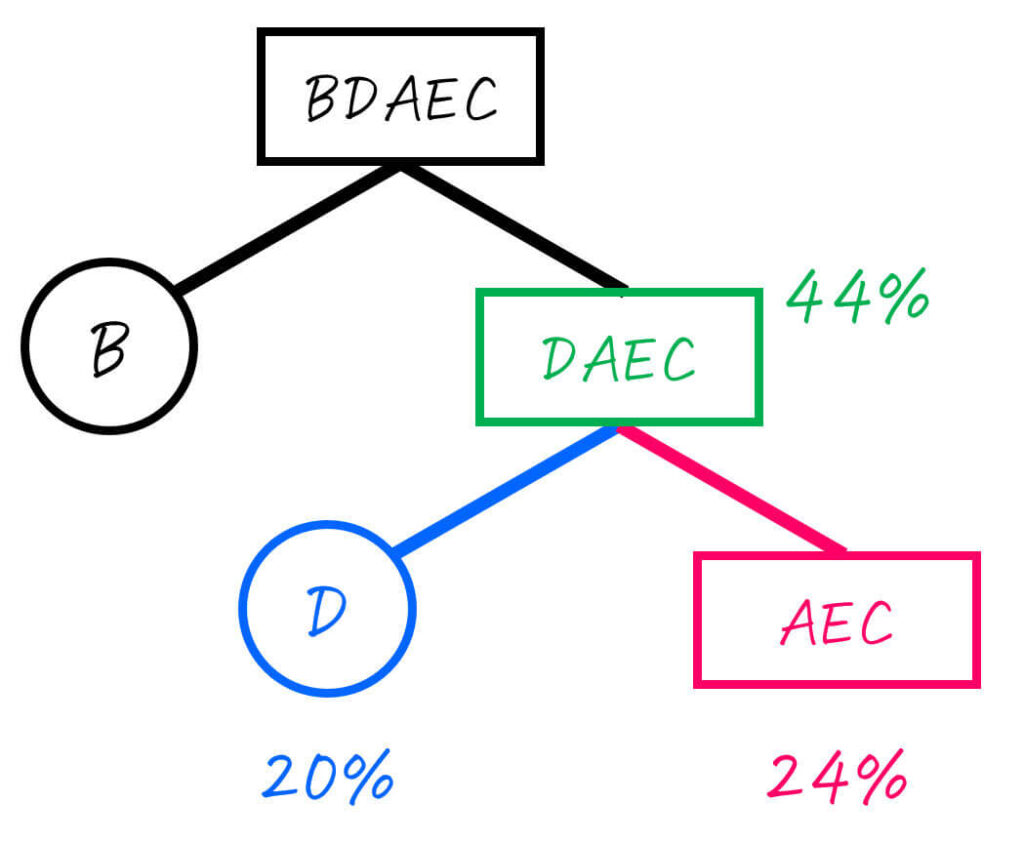
ここで、Dはすでに1つの文字のグループとなったため、これ以上の操作は不要です。一方、AECはまだ2つ以上の文字のグループなため、さらに分割をしていきます。
Step2-3. AEC (24%) を2分割
つぎに、ACDE (24%) を確率が最も半分 (12%) に近くなるところで2分割します。
| 文字 | 出現確率 |
|---|---|
| A | 12% |
| E | 8% |
| C | 4% |
ここで、最も半分 (12%) に近くなるように分割するためには、A (12%) とEC (12%) に分ければOKですね。
さらに、分けた2つのグループを下のように二分木で書きます。
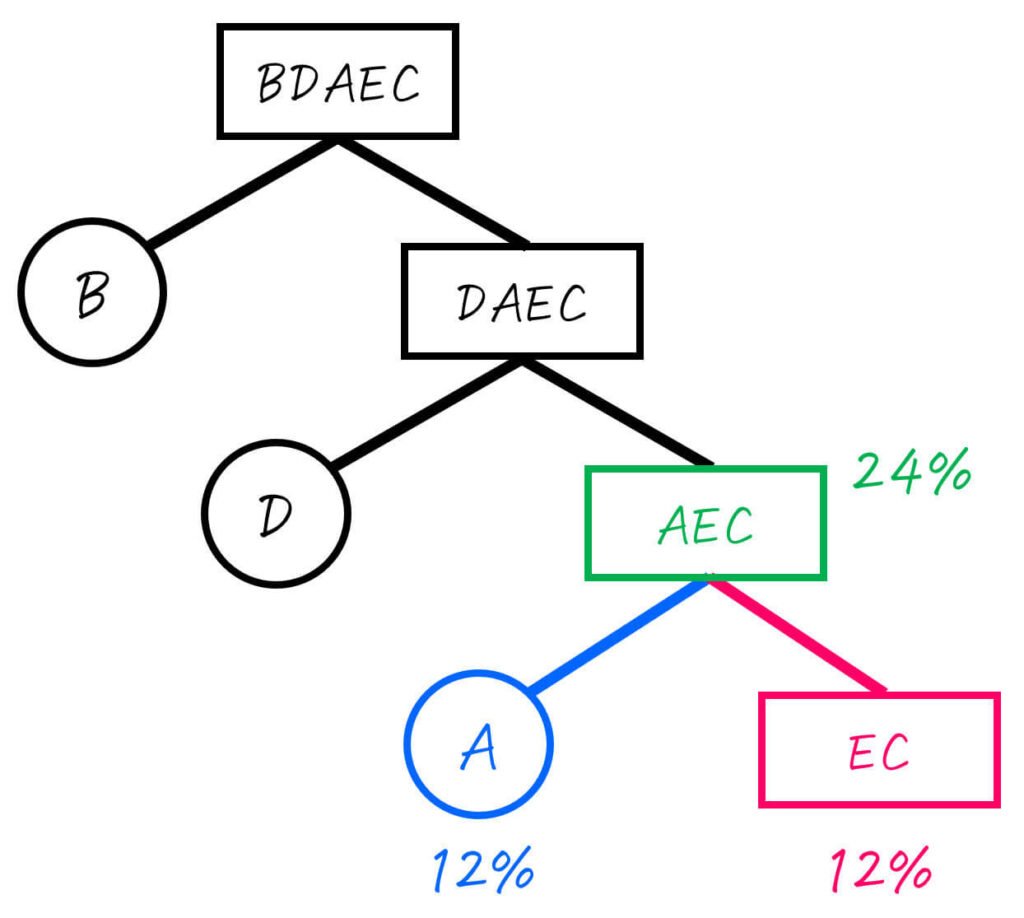
ここで、Aはすでに1つの文字のグループとなったため、これ以上の操作は不要です。一方、ECはまだ2つ以上の文字のグループなため、さらに分割をしていきます。
Step2-4. EC (12%) を2分割
つぎに、EC (合計確率: 12%) を確率が最も半分 (6%) に近くなるところで2分割します。
(とはいっても、グループ内の文字が2つなので、確率に関係なしに1-1に分割するしかありませんが…)
| 文字 | 出現確率 |
|---|---|
| E | 8% |
| C | 4% |
分けた2つのグループを下のように二分木で書きます。
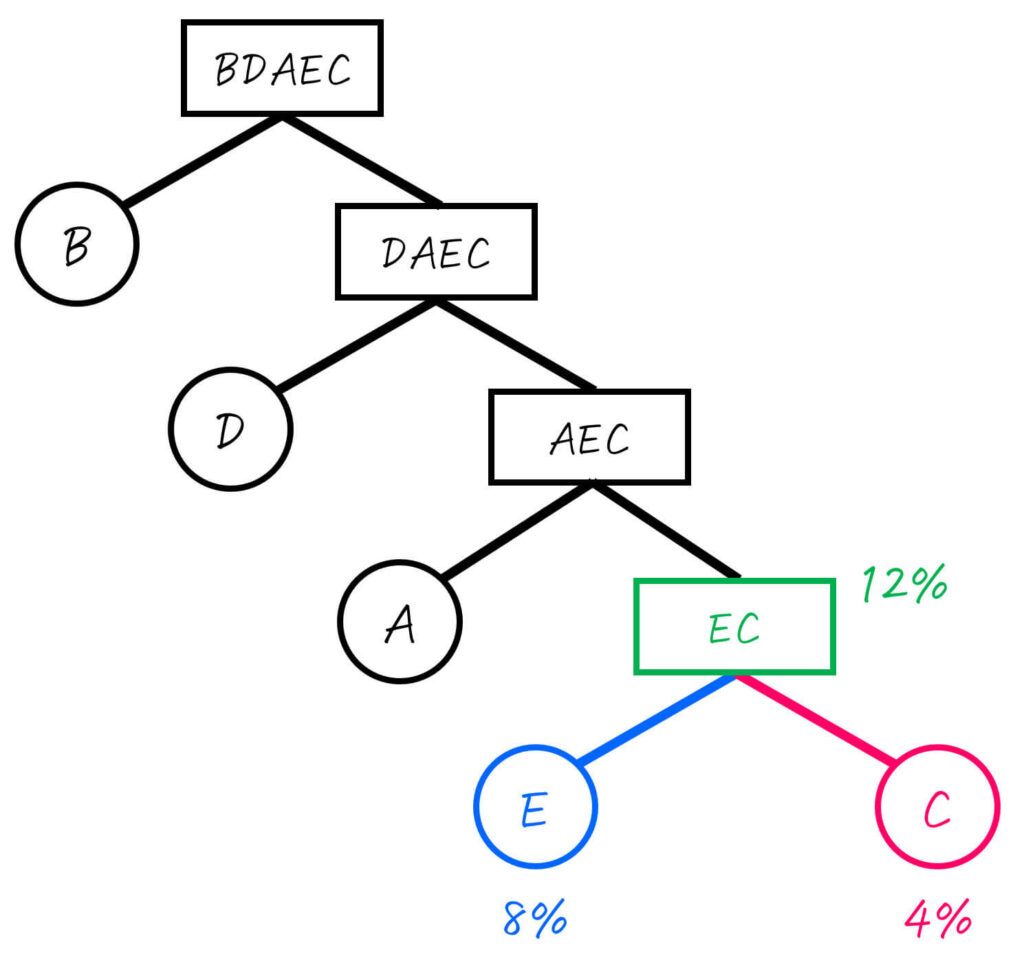
すると、E, C ともに1つの文字のグループとなり、すべてのグループに属する文字が1つとなりましたね。
そのため、Step2の操作はここで完了です。
Step3. 作成した二分木から各文字(情報)ごとの符号を求める
あとは、作成した二分木を見ていくことで、各文字ごとの符号を求めていきましょう。
(※ この部分はハフマン符号化と手順は同じです。)
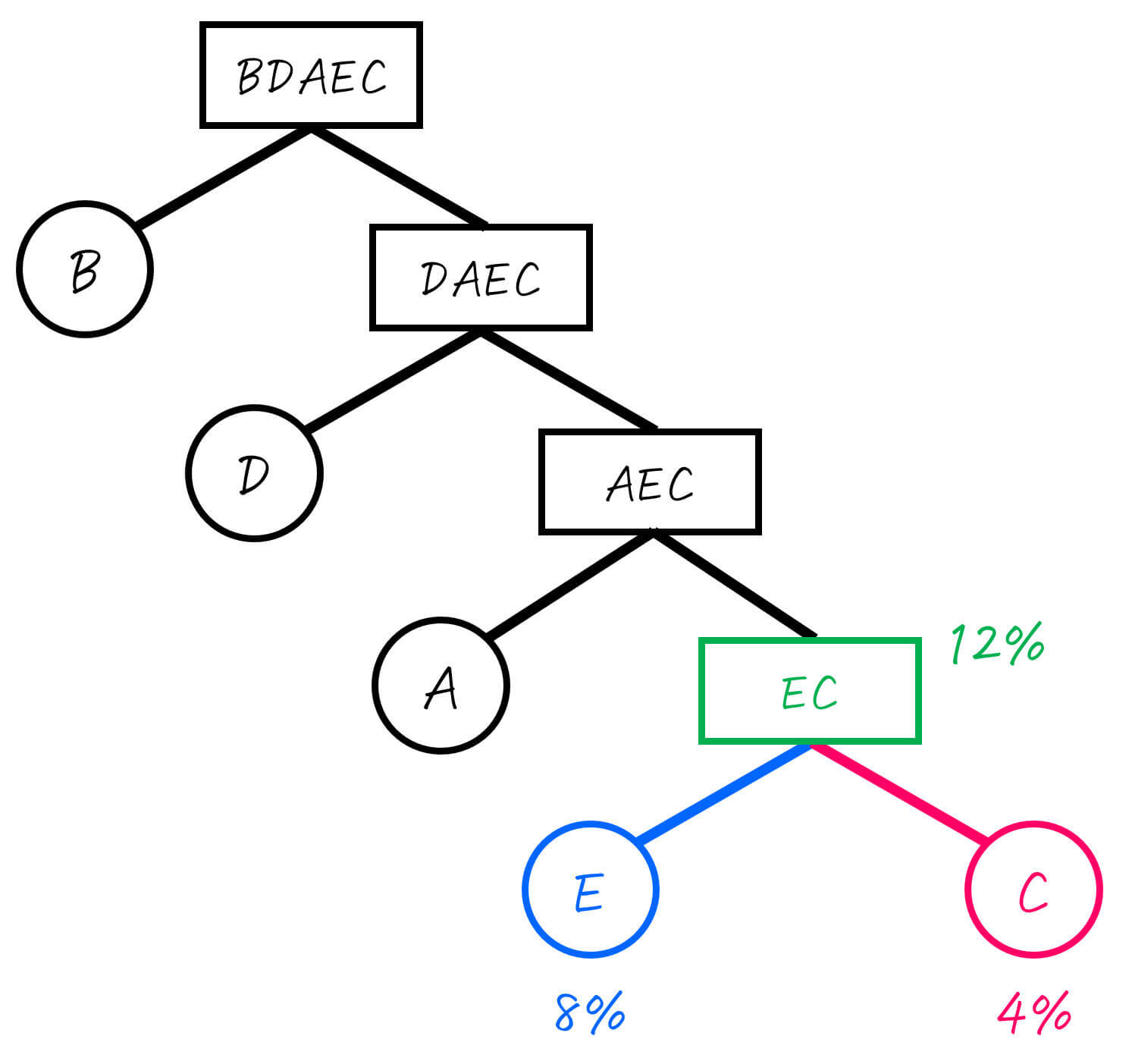
まず、下のように各節(ノード)の左側を0、右側を1として考えます。
(葉となっていないノードの名前は、見やすさのため消しています。)
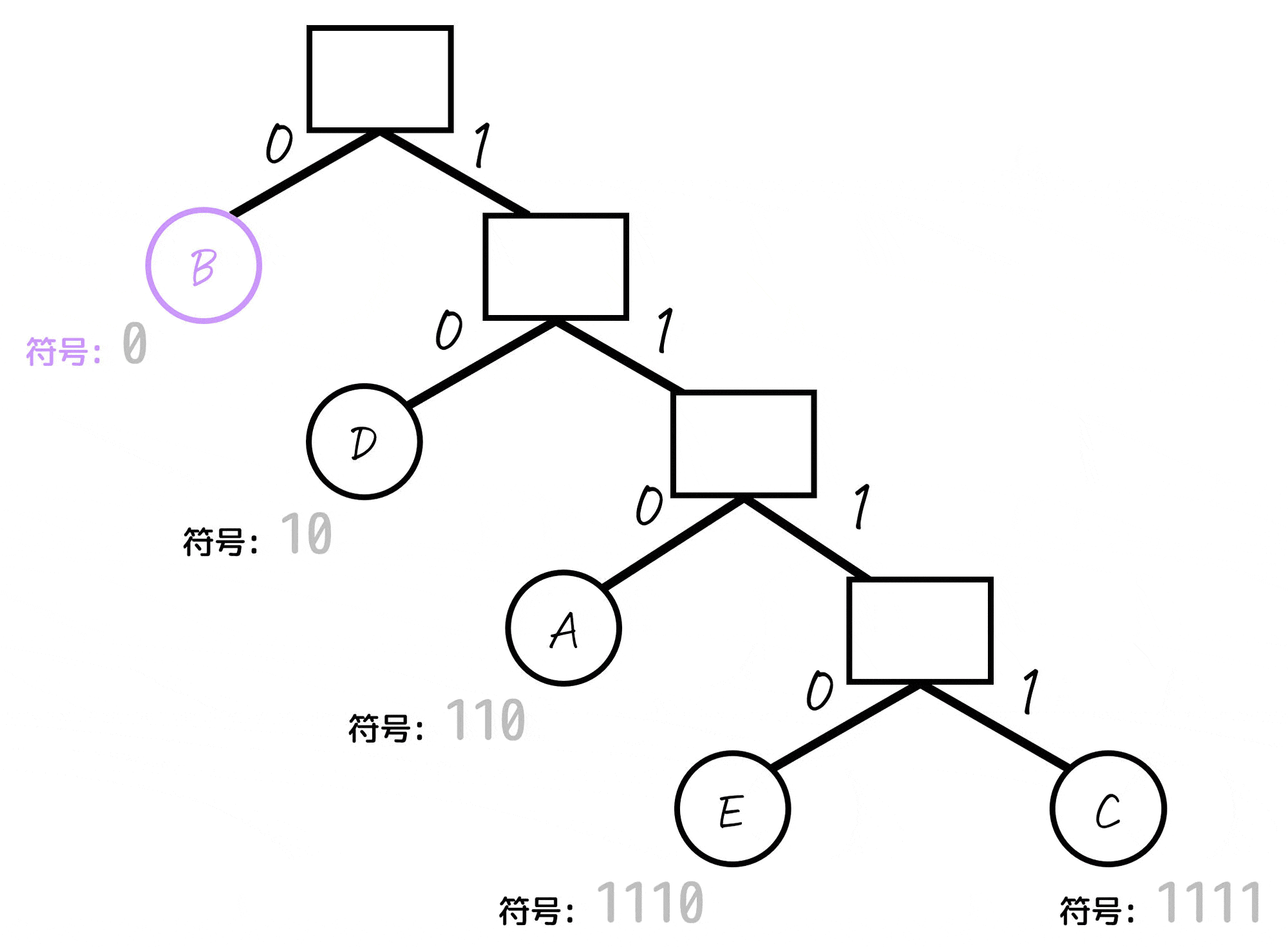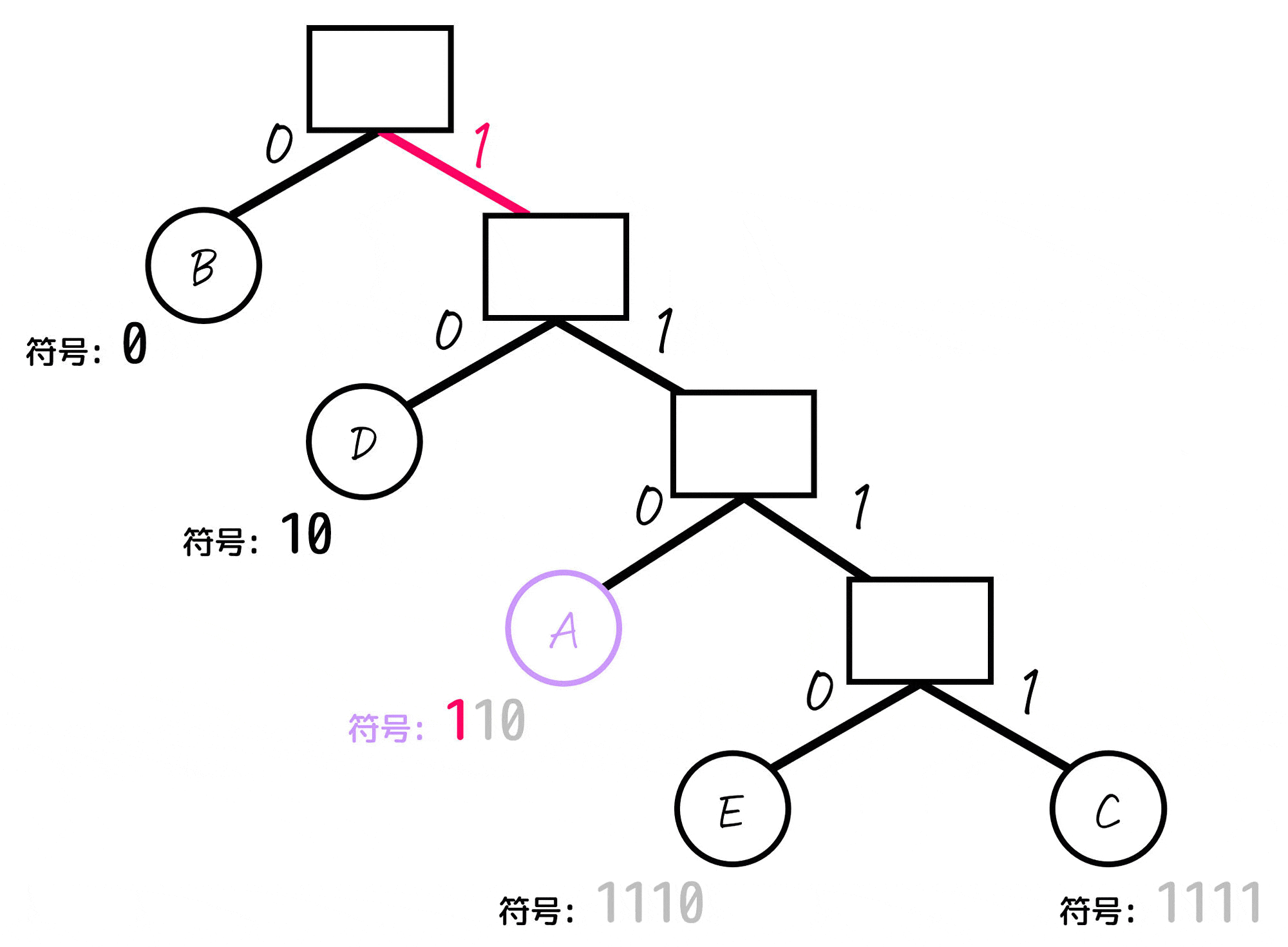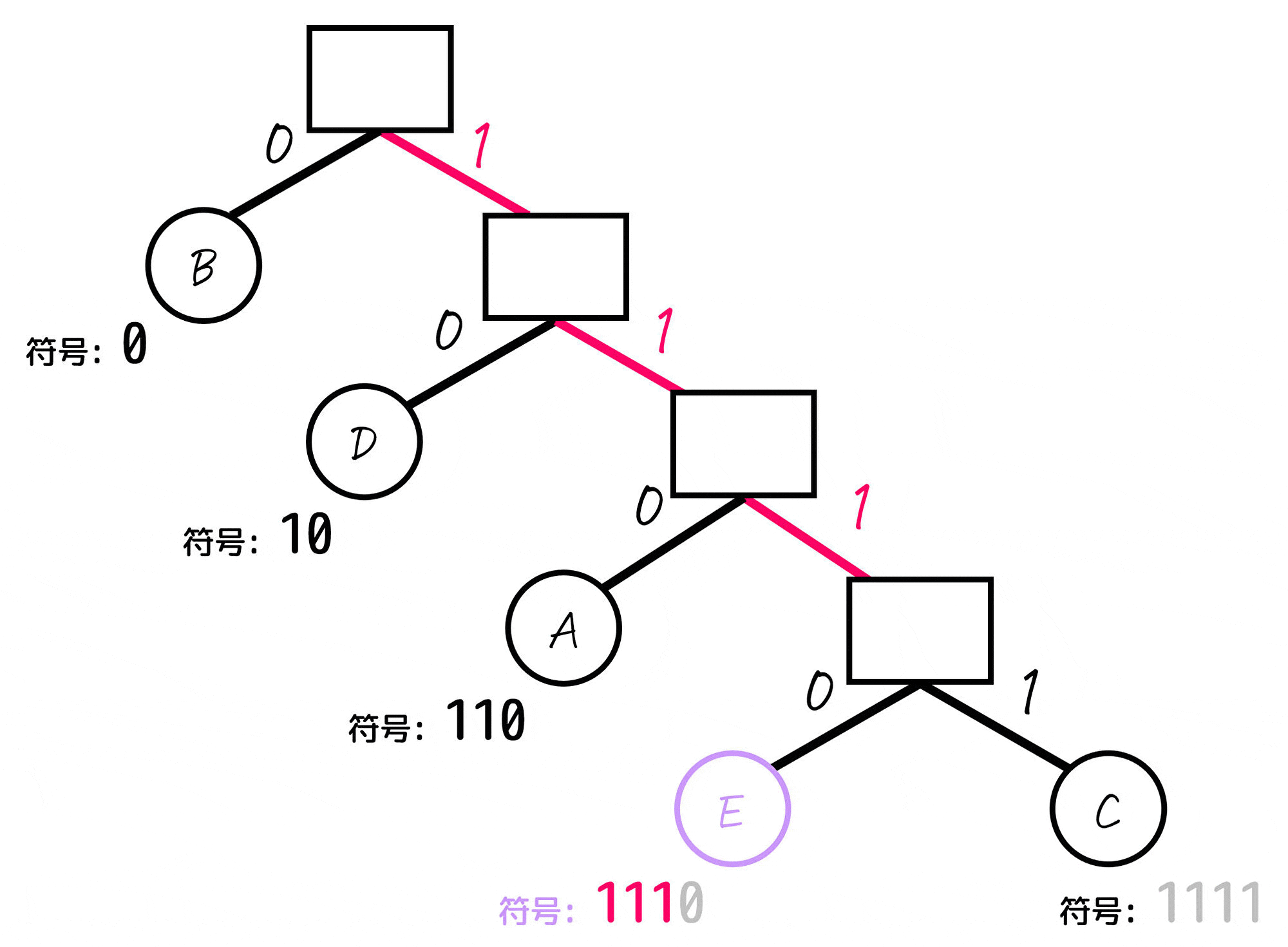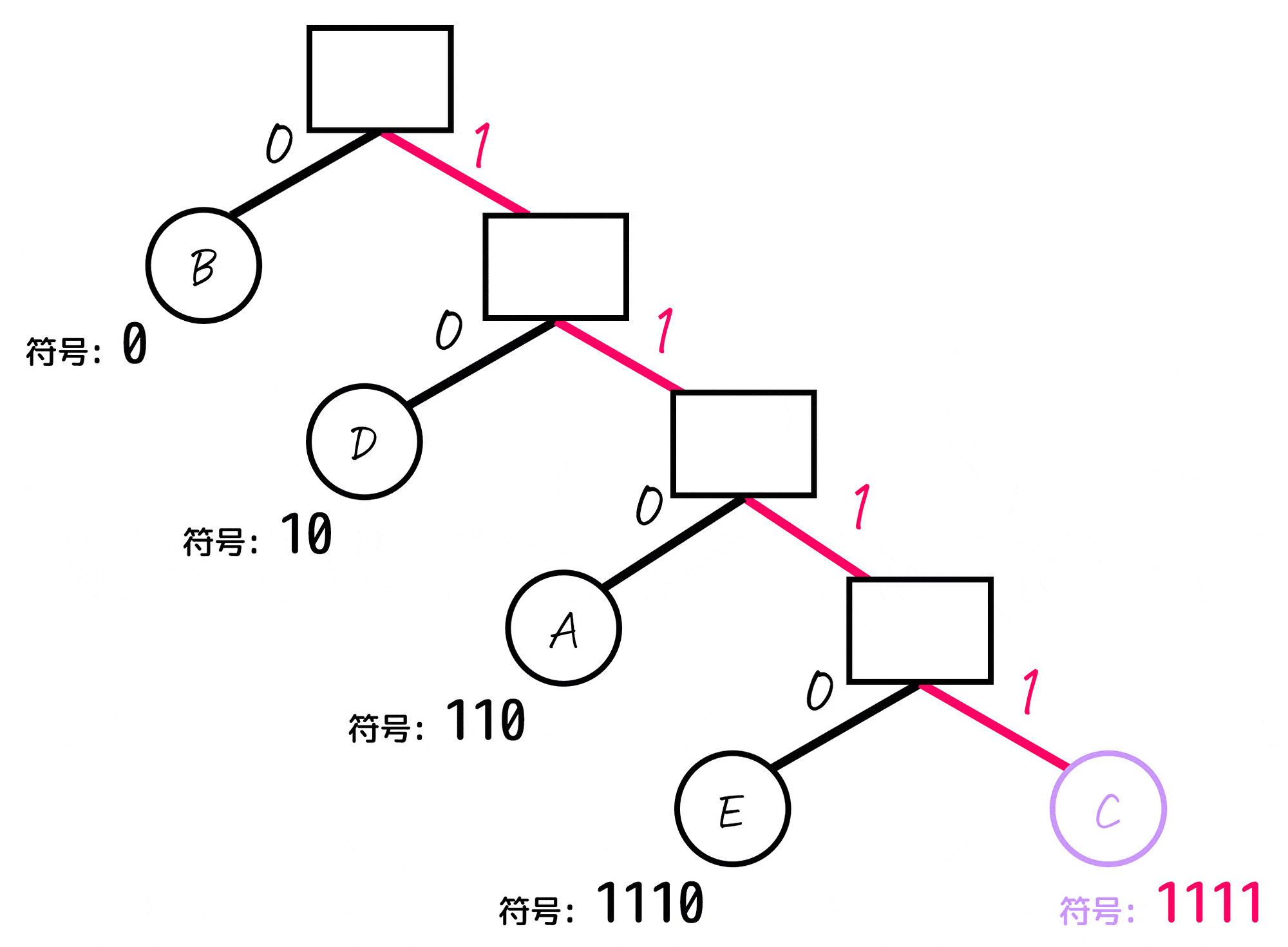
あとは、各文字(A~E)に対応するノードごとに「木構造の一番上の部分から対応するノードまでたどっていく」という操作をし、たどっていく際に通った0, 1を左から順番に並べていったものが符号となります。
よって、各文字A~Eごとの符号は下のように求まります。
| 文字(記号) | 符号 (ビット表記) | 出現確率 |
|---|---|---|
| A | 110 | 12% |
| B | 0 | 56% |
| C | 1111 | 4% |
| D | 10 | 20% |
| E | 1110 | 8% |
結果を見てみると、出現確率が高い符号には短い符号を、出現確率が低い符号には長い符号が付いていることがわかりますね。
このように、シャノン・ファノ符号化も、ハフマン符号化と同じく文字列の平均符号長がなるべく短くなるような符号の決め方を機械的に決めることができるのです!
※ シャノン・ファノ符号化において、二分木を書くことで瞬時復号可能な符号が作成できる理由はこちらに記しています[1] … Continue reading。
(2)
平均符号長は、各文字ごとに「符号長(符号の文字数) × 出現確率」を求め、それらを足すことで求めることができます。
今回の場合は、各文字ごとの「符号長」、および「符号長 × 出現確率」を下のように求めることができます。
| 文字(記号) | 符号 (ビット表記) | 符号長 | 出現確率 | 符号長 × 出現確率 |
|---|---|---|---|---|
| A | 110 | 3 | 12% | 0.36 |
| B | 0 | 1 | 56% | 0.56 |
| C | 1111 | 4 | 4% | 0.16 |
| D | 10 | 2 | 20% | 0.40 |
| E | 1110 | 4 | 8% | 0.32 |
よって、平均符号長 \( L \) は\[\begin{align*}
L & = 0.36 + 0.56 + 0.16 + 0.40 + 0.32
\\ & = 1.80
\end{align*}\]と求まります。
※ ハフマン符号のときと全く同じ平均符号長が得られます。
スポンサードリンク
2. シャノン・ファノ符号化手順まとめ
ある情報 (文字列) をハフマン符号化する場合、次の1-3を順にすればOK。
- 各情報 (文字) を出現確率 (頻度) の大きい順に並び替え、情報全てが同じグループに属していると仮定する
- 2つ以上の情報 (文字) が属しているグループに対し、「グループ内の各情報の確率を大きい順に足していき、グループ全体の確率の和の半分に最も近くなるところ」で2つのグループに分け、二分木を書いていく。
- 2を、全ての情報がそれぞれ異なるグループに属するまで行い、完成した二分木から符号を決める
※ シャノン・ファノ符号化により作成された符号は必ず瞬時復号可能な符号となる。
スポンサードリンク
3. 練習問題
実際に練習問題で、シャノン・ファノ符号化ができるか確認してみましょう。
つぎの表は、とある文字列中(情報源)に出てくる文字の出現回数を表にしたものである。
| 文字(記号) | 符号 (ビット表記) | 出現回数 |
|---|---|---|
| A | (ア) | 5 |
| B | (イ) | 1 |
| C | (ウ) | 6 |
| D | (エ) | 4 |
| E | (オ) | 3 |
| F | (カ) | 1 |
(1) この文字列をシャノン・ファノ符号化法によって符号化し、ビット表記の (ア) ~ (カ) に当てはまるビット表記を答えなさい。
(2) (1)で符号化した符号の平均符号長 \( L \) を小数第2位まで答えなさい。(必要であれば小数第3位を四捨五入すること)
4. 練習問題の答え
(1)を解く前に各文字の出現回数から出現確率を求めましょう。((2)で使うため)
各文字の出現確率は、( 各文字の出現回数 ) ÷ ( 文字全体の出現回数[今回の場合は20] ) で求めることができます。
| 文字(記号) | 符号 (ビット表記) | 出現回数 | 出現確率 |
|---|---|---|---|
| A | (ア) | 5 | 25% |
| B | (イ) | 1 | 5% |
| C | (ウ) | 6 | 30% |
| D | (エ) | 4 | 20% |
| E | (オ) | 3 | 15% |
| F | (カ) | 1 | 5% |
(1) ハフマン符号による符号化
Step1. 各文字を出現確率 (回数) の多い順に並べ、全体で1つのグループと仮定
まず、与えられた文字(記号・情報)を出現確率が大きい順に並び替えます。
| 文字 | 出現確率 |
|---|---|
| C | 30% |
| A | 25% |
| D | 20% |
| E | 15% |
| B | 5% |
| F | 5% |
これら6つの文字をいったん、全て1つのグループに属していると仮定します。
Step2. グループ内の情報を、確率が半分になるように分解していく。(すべてのグループの情報が1つになるまで)
つぎに、すべてのグループに属する文字が1つになるまで、「2つ以上の文字が属するグループ」を出現確率の和が最も半分に近くなる部分で2分割していきます。
(「出現確率の和が最も半分に近くなる部分」を選んでいく際に、グループ内の各文字の確率を大きい順に足していくことで確認します)
Step2-1. CADEBF (100%) を2分割
まずは、CADEBF (合計確率: 100%) を2分割します。
ここで、最も半分 (50%) に近くなるように分割するためには、CA (55%) とDEBF (45%) に分ければOKですね[2]C (30%) とADEBF (70%) だと最も半分に近くなるわけでないのでNG。。
| 文字 | 出現確率 |
|---|---|
| C | 30% |
| A | 25% |
| D | 20% |
| E | 15% |
| B | 5% |
| F | 5% |
分けた2つのグループを下のように二分木で書きます。
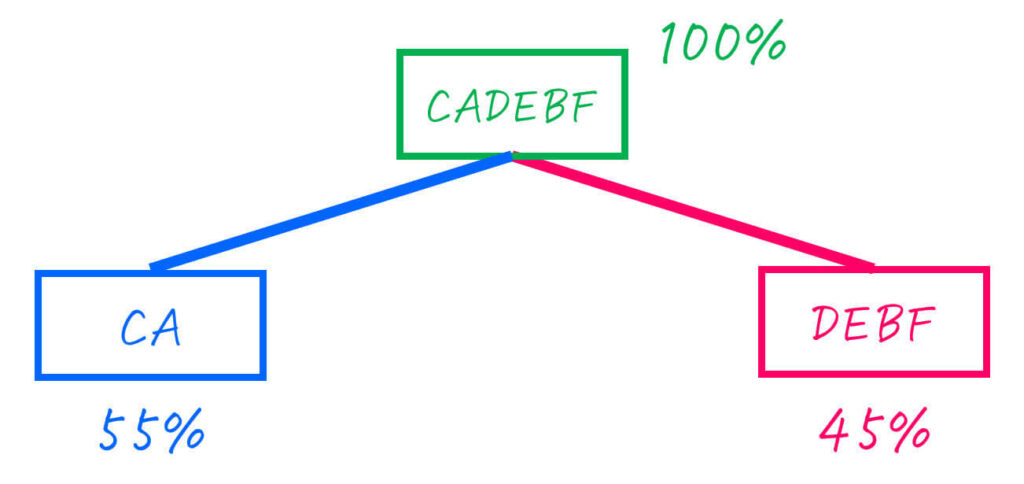
ここで、CA, DEBFの2つのグループともに、まだ2つ以上の文字のグループなため、さらに分割をしていきます。
Step2-2. CA (55%) を2分割
先にCA (合計確率: 55%) からグループを分割していきましょう。
グループ内に2つの文字しかないため、確率を気にせず1つずつに分割すればOKです。
| 文字 | 出現確率 |
|---|---|
| C | 30% |
| A | 25% |
分けた2つのグループを下のように二分木で書きます。
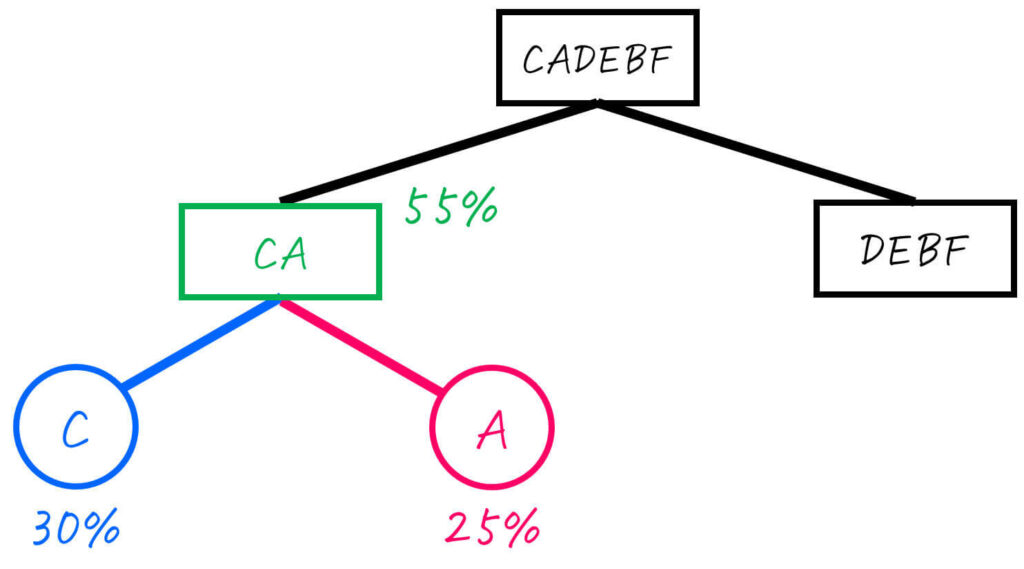
これで、CAのグループは、互いに1つの文字のグループの文字に分割できたため、これ以上の操作は不要です。
なので、ここからはDEBFのグループを分割していきましょう。
Step2-3. DEBF (45%) を2分割
残った、DEBF (合計確率: 45%) を2分割します。
最も半分 (45%) に近くなるように分割するためには、D (20%) とEBF (25%) に分ければOKですね[3]DE (35%) とBF (10%) だと最も半分に近くなるわけでないのでNG。。
| 文字 | 出現確率 |
|---|---|
| D | 20% |
| E | 15% |
| B | 5% |
| F | 5% |
分けた2つのグループを下のように二分木で書きます。
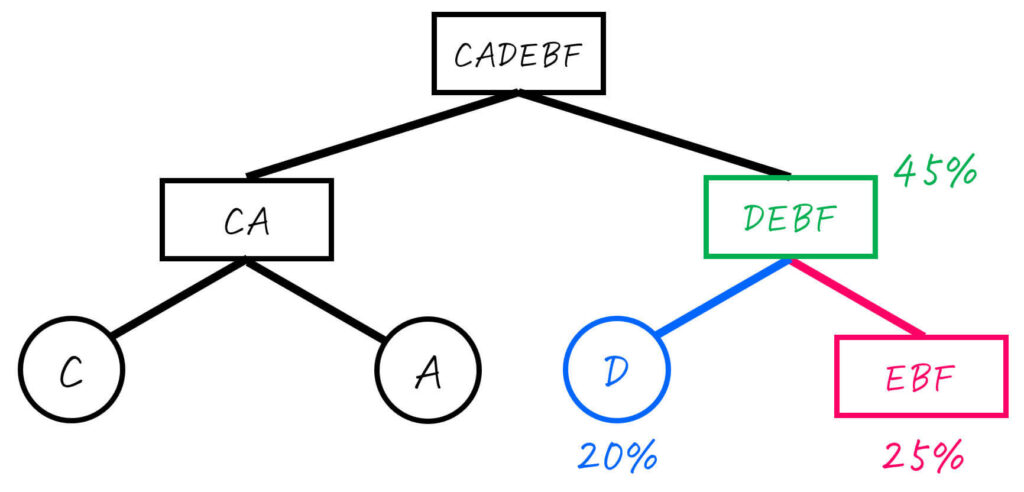
Dはすでに1つの文字のグループとなったため、これ以上の操作は不要です。一方、EBFはまだ2つ以上の文字のグループなため、さらに分割をしていきます。
Step2-4. EBF (25%) を2分割
EBF (合計確率: 25%) を2分割します。
最も半分 (25%) に近くなるように分割するためには、E (15%) とBF (10%) に分ければOKですね。
| 文字 | 出現確率 |
|---|---|
| E | 15% |
| B | 5% |
| F | 5% |
分けた2つのグループを下のように二分木で書きます。
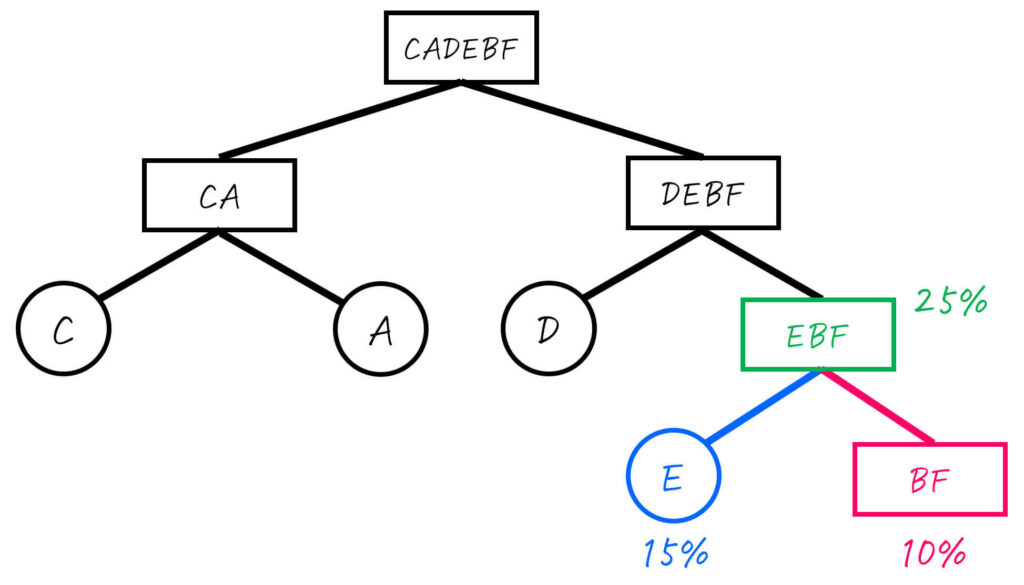
Eはすでに1つの文字のグループとなったため、これ以上の操作は不要です。一方、BFはまだ2つ以上の文字のグループなため、さらに分割をしていきます。
Step2-5. BF (10%) を2分割
最後にBF (合計確率: 10%) からグループを分割していきましょう。
とはいっても、グループ内に2つの文字しかないため、確率を気にせず1つずつに分割すればOKです。
| 文字 | 出現確率 |
|---|---|
| B | 5% |
| F | 5% |
分けた2つのグループを下のように二分木で書きます。
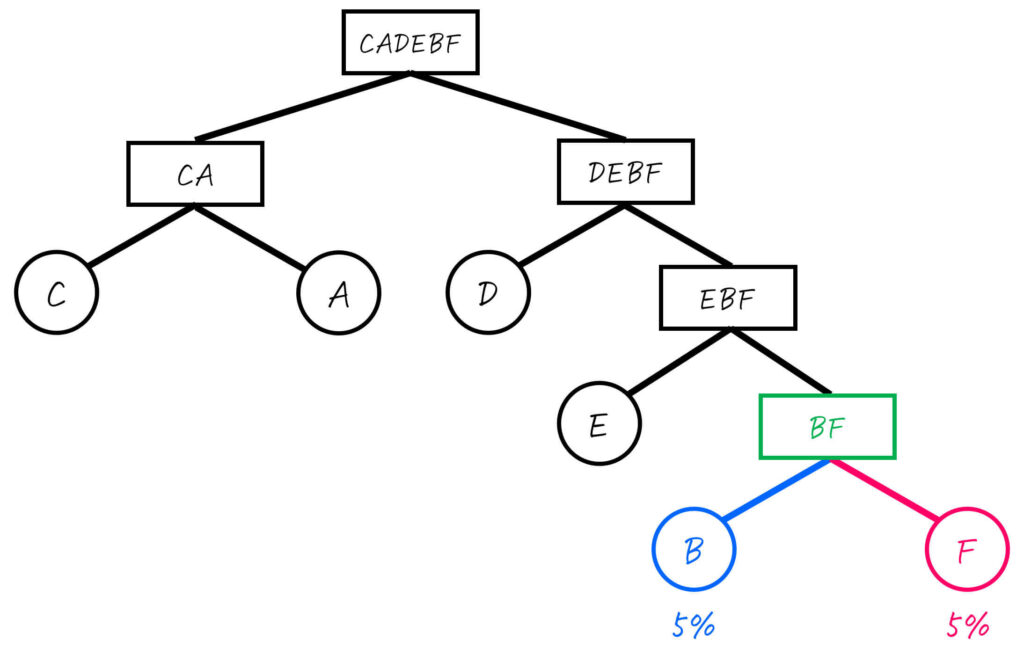
これで、すべてのグループの文字が1つになったため、Step2はクリアです。
Step3. 作成した二分木から各文字(情報)ごとの符号を求める
あとは、各文字(A~E)に対応するノードごとに「木構造の一番上の部分から対応するノードまでたどっていく」という操作をし、たどっていく際に通った0, 1を左から順番に並べていったものが符号となります。
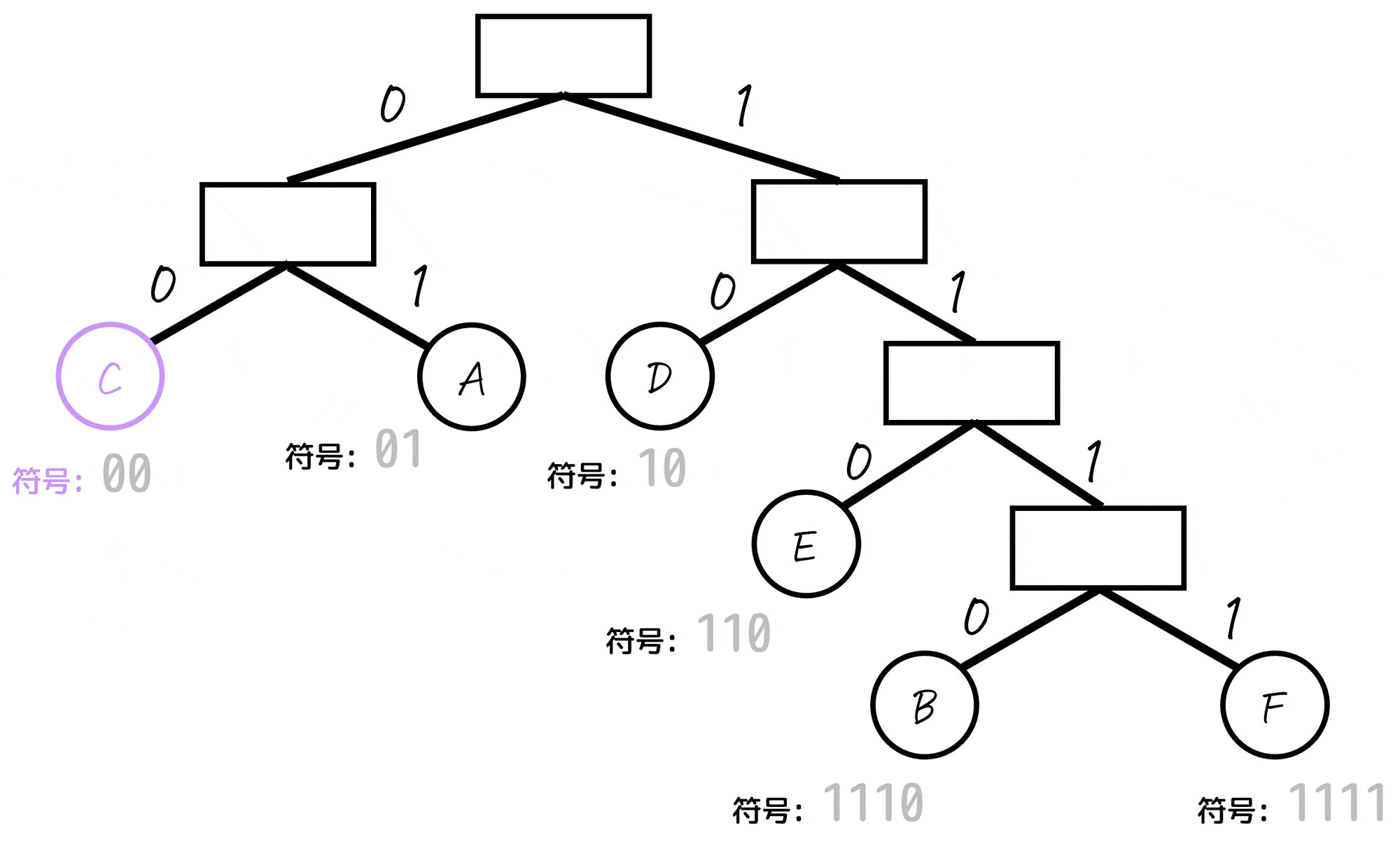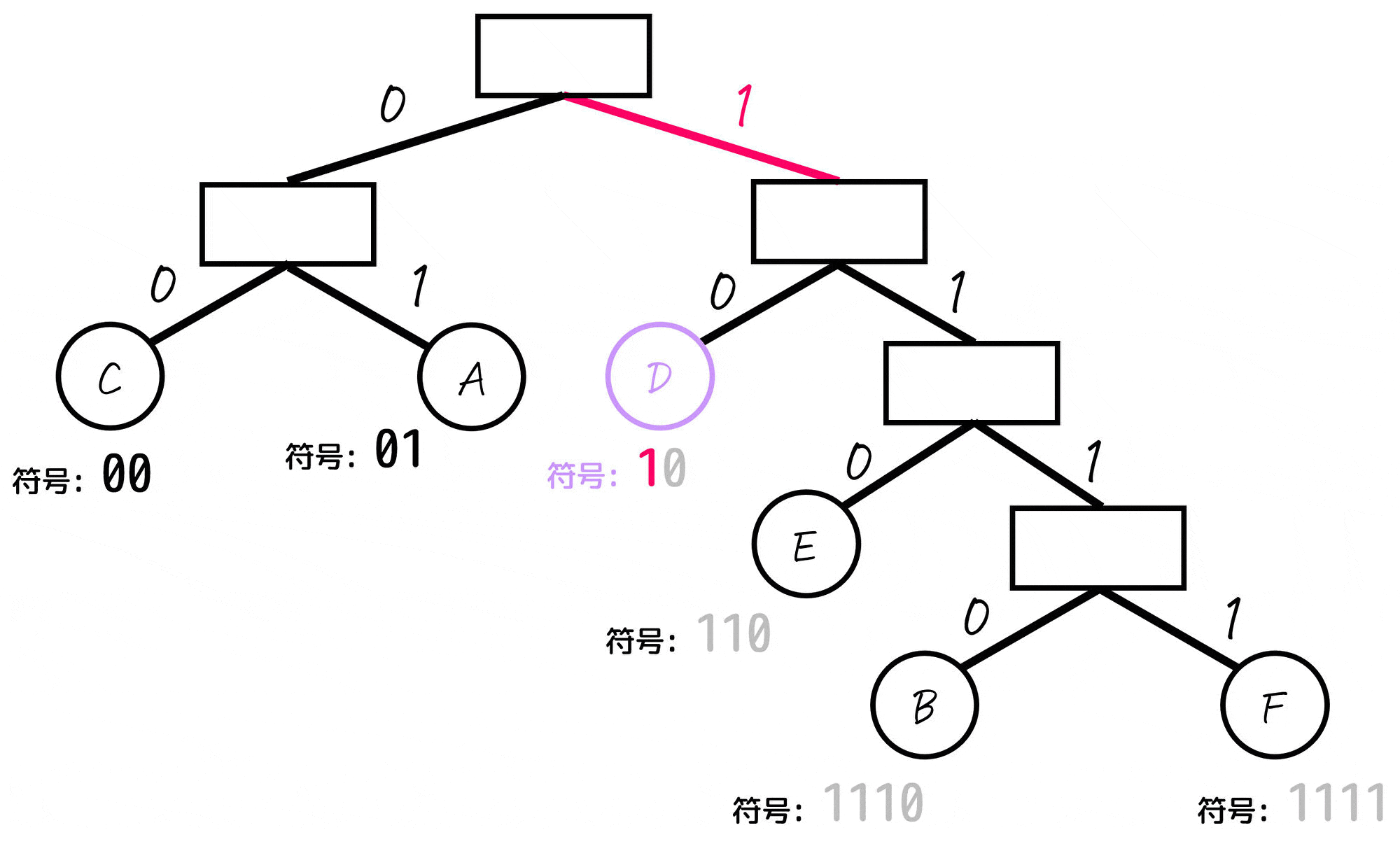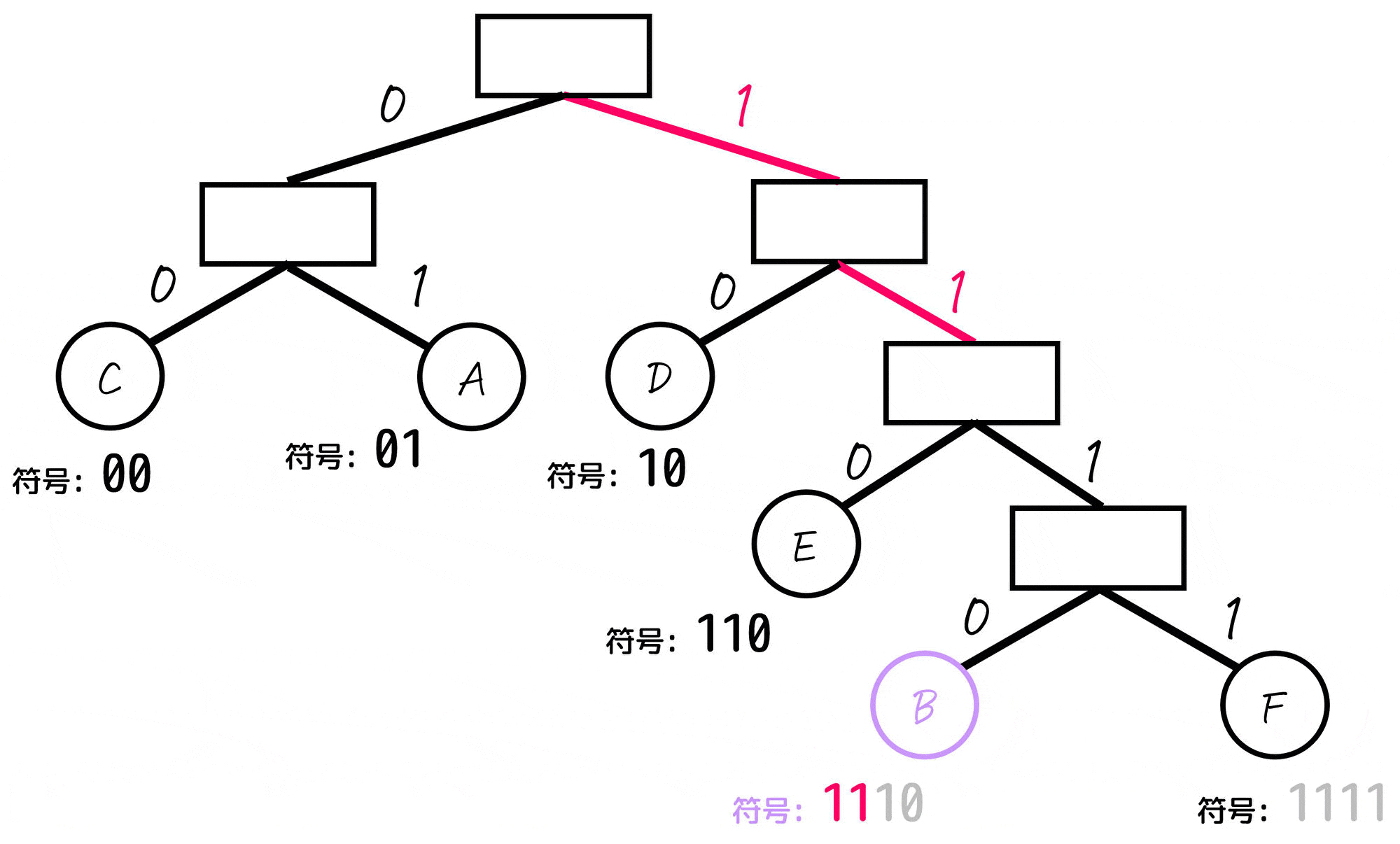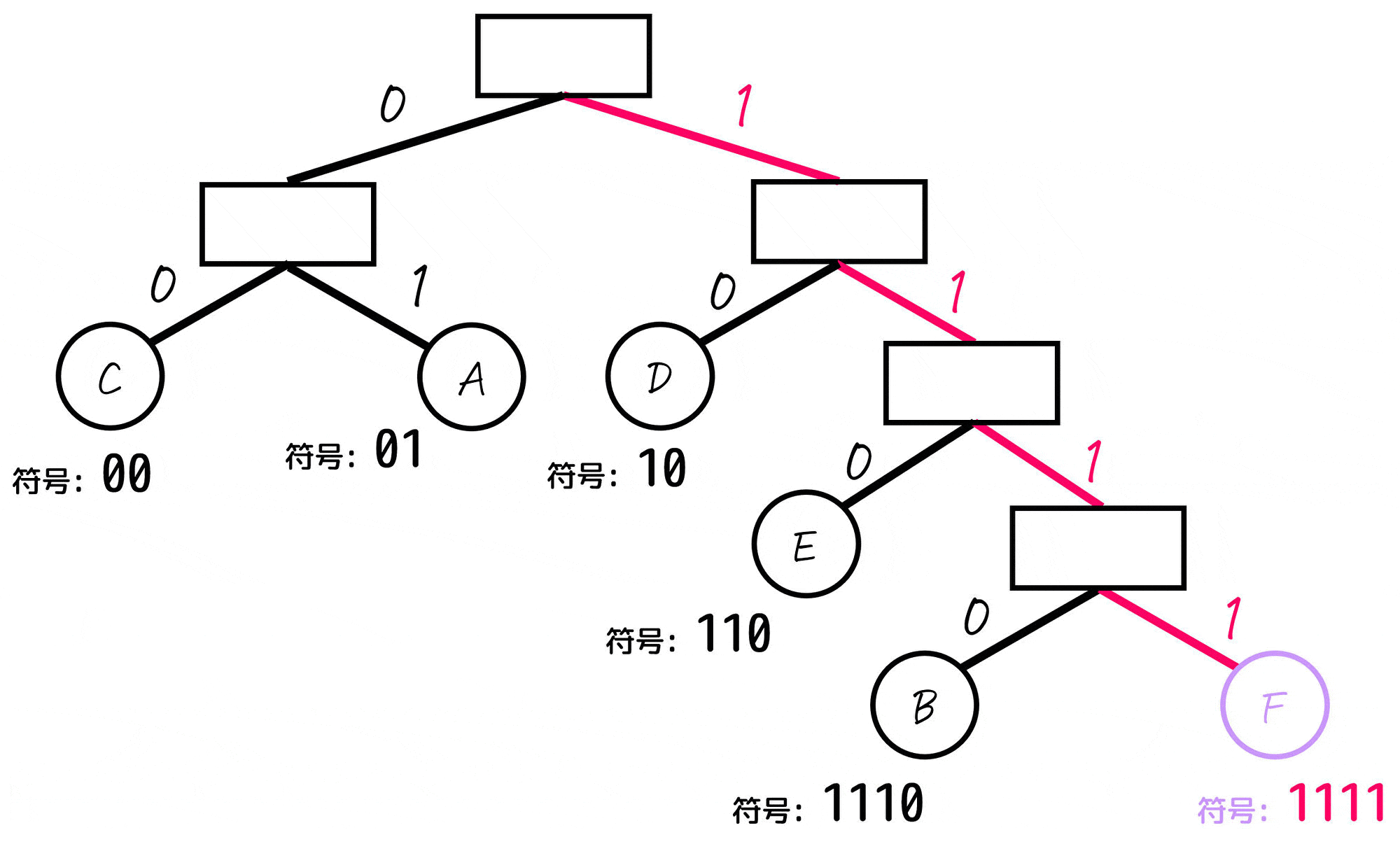
よって、各文字A~Fごとの符号は下のように求まります。
| 文字(記号) | 符号 (ビット表記) | 出現確率 |
|---|---|---|
| A | 01 | 25% |
| B | 1110 | 5% |
| C | 00 | 30% |
| D | 10 | 20% |
| E | 110 | 15% |
| F | 1111 | 5% |
(2) 平均符号長の計算
まず、各文字ごとの「符号長」および「符号長 × 出現確率」を求めましょう。
| 文字(記号) | 符号 (ビット表記) | 符号長 | 出現確率 | 符号長 × 出現確率 |
|---|---|---|---|---|
| A | 01 | 2 | 25% | 0.50 |
| B | 1110 | 4 | 5% | 0.20 |
| C | 00 | 2 | 30% | 0.60 |
| D | 10 | 2 | 20% | 0.40 |
| E | 110 | 3 | 15% | 0.45 |
| F | 1111 | 4 | 5% | 0.20 |
あとは、A~Fごとに求めた「符号長 × 出現確率」をすべて足せば平均符号長 \( L \) があっという間に求まります。\[\begin{align*}
L & = 0.50 + 0.20 + 0.60 + 0.40 + 0.45 + 0.20
\\ & = 2.35
\end{align*}\]※ ハフマン符号で圧縮した場合も同じ平均符号長が求まります。
関連広告・スポンサードリンク







![うさぎでもわかる画像処理 Part02 トーンカーブと画像処理 [Python・MATLABコード付き]](https://www.momoyama-usagi.com/wp-content/uploads/ip1-18-150x150.jpg)