スポンサードリンク
こんにちは、ももやまです。
今日は、確率・統計に出てくる「累積分布関数」についてお勉強していきましょう!
目次 [hide]
スポンサードリンク
1. 確率密度関数の復習
累積分布関数を知るためには、確率密度関数の知識が前提となってきます。
なので、まずは確率密度関数について簡単におさらいしましょう。
(1) 確率分布関数のイメージ
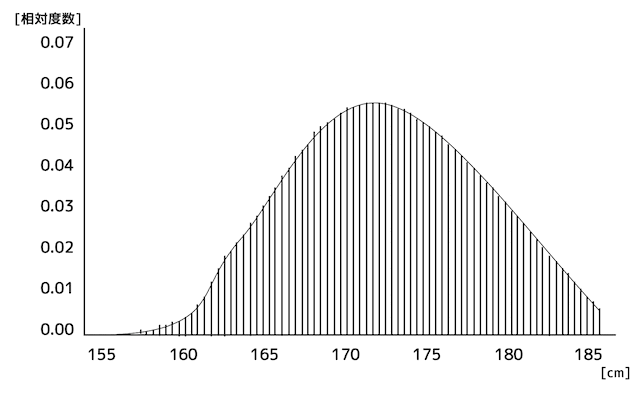
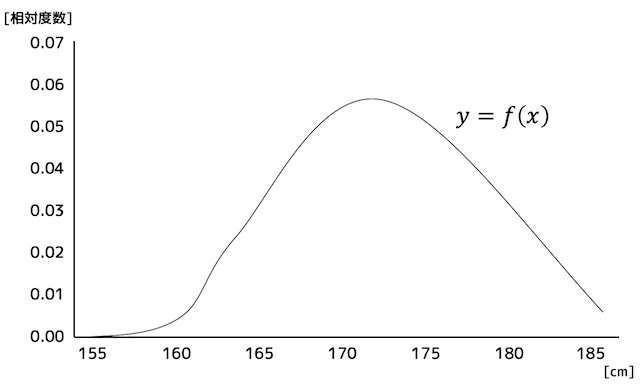
確率密度関数は、ヒストグラムに出てくる相対度数を細かく細かく刻んで、滑らかな曲線になったものを関数にしたものです。
(2) 確率分布関数で重要な6つの性質・公式
確率分布関数
確率密度関数 ( f(x) ) で与えられる確率変数 ( X ) 。ただし、
その1. 確率の密度は、必ず正である。
その2. 確率の密度
※ 確率の密度は、確率とは異なるもの
その3. 確率変数
その4. 確率の和は1であるため、以下の積分式が成立する。
その5. 期待値(平均)
その6. 分散
(1) 2乗した値の期待値 - 期待値の2乗で計算
※ 取りうる値が
(2) 各値とその期待値(平均)の差を2乗したものの期待値(平均)
軽くおさらいしても、「確率密度関数があまりよくわからないなぁ。」という人は、以下の記事にて確率密度関数について解説しているので、リンク先の記事をご覧ください。
スポンサードリンク
2. 累積分布関数のイメージ
(1) 相対度数と累積相対度数
累積分布関数について説明する前に、まずは「相対度数」と「累積相対度数」について復習しましょう。
※ 「累積相対度数」というのが、累積分布関数のベースとなってきます。
[a] 相対度数
相対度数とは、データをある範囲ごとに区切ったときに、その範囲内にどれくらいの割合のデータがあるかを、それぞれの範囲ごと(階級ごと)に表したものです。
式で書くと、
(相対度数)=(各階級ごとの度数)÷(全体の度数)
となります。
例えば、階級「身長170cm以上175cm未満」の相対度数は
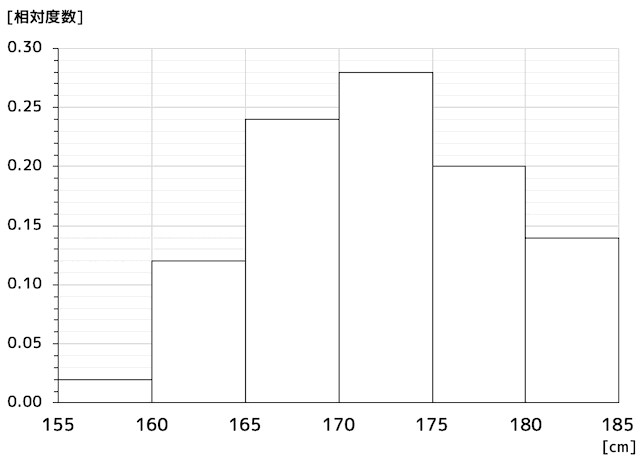
表1. 度数と相対度数の関係
| 身長 | 度数 | 相対度数 |
|---|---|---|
| 155 - 160 | 2 | 0.02 |
| 160 - 165 | 12 | 0.12 |
| 165 - 170 | 24 | 0.24 |
| 170 - 175 | 28 | 0.28 |
| 175 - 180 | 20 | 0.20 |
| 180 - 185 | 14 | 0.14 |
| 合計 | 100 | 1.00 |
[b] 累積相対度数
累積相対度数は、相対度数を累積していったものです。つまり、「(小さい階級から数えていったときに)ある区間までのデータの割合を累積したもの」と言えます。
例えば、先ほどの表1のデータを見てみましょう。
表1の各階級ごとの累積相対度数は、
- 155cm以上160cm未満 → 累積相対度数は、そのまま相対度数0.02。
- 160cm以上165cm未満 → 160cm未満までの累積相対度数0.02に、160cm以上165cm未満の相対度数0.12を足すので、0.02 + 0.12 = 0.14。
- 165cm以上170cm未満 → 165cm未満までの累積相対度数0.14に、165cm以上170cm未満の相対度数0.24を足すので、0.14 + 0.24 = 0.38。
- 170cm以上175cm未満 → 170cm未満までの累積相対度数0.38に、170cm以上175cm未満の相対度数0.28を足すので、0.38 + 0.28 = 0.66。
- 175cm以上180cm未満 → 175cm未満までの累積相対度数0.66に、175cm以上180cm未満の相対度数0.20を足すので、0.66 + 0.20 = 0.86。
- 180cm以上185cm未満 → 180cm未満までの累積相対度数0.86に、180cm以上185cm未満の相対度数0.14を足すので、0.86 + 0.14 = 1.00。
と計算できます。
表2. 相対度数と累積相対度数の関係
| 身長 | 度数 | 相対度数 | 累積相対度数 | 計算式 (累積相対度数) |
|---|---|---|---|---|
| 155 - 160 | 2 | 0.02 | 0.02 | 0.02 |
| 160 - 165 | 12 | 0.12 | 0.14 | 0.02 + 0.12 |
| 165 - 170 | 24 | 0.24 | 0.38 | 0.14 + 0.24 |
| 170 - 175 | 28 | 0.28 | 0.66 | 0.38 + 0.28 |
| 175 - 180 | 20 | 0.20 | 0.86 | 0.66 + 0.20 |
| 180 - 185 | 14 | 0.14 | 1.00 | 0.86 + 0.14 |
| 合計 | 100 | 1.00 | - | - |
(2) 累積相対度数から累積分布関数へ
表2で求めた、各階級ごとの累積相対度数を、下のようなヒストグラムの形にします。
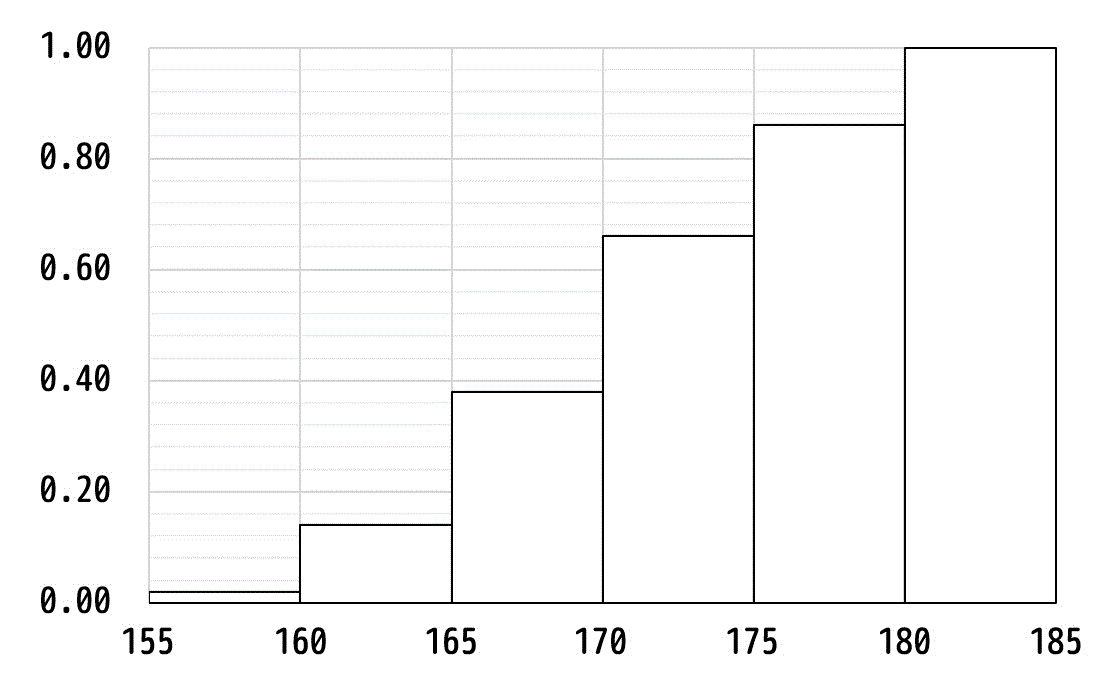
さらに、このヒストグラムの横軸をどんどん細かくしていくことを考えていきます。
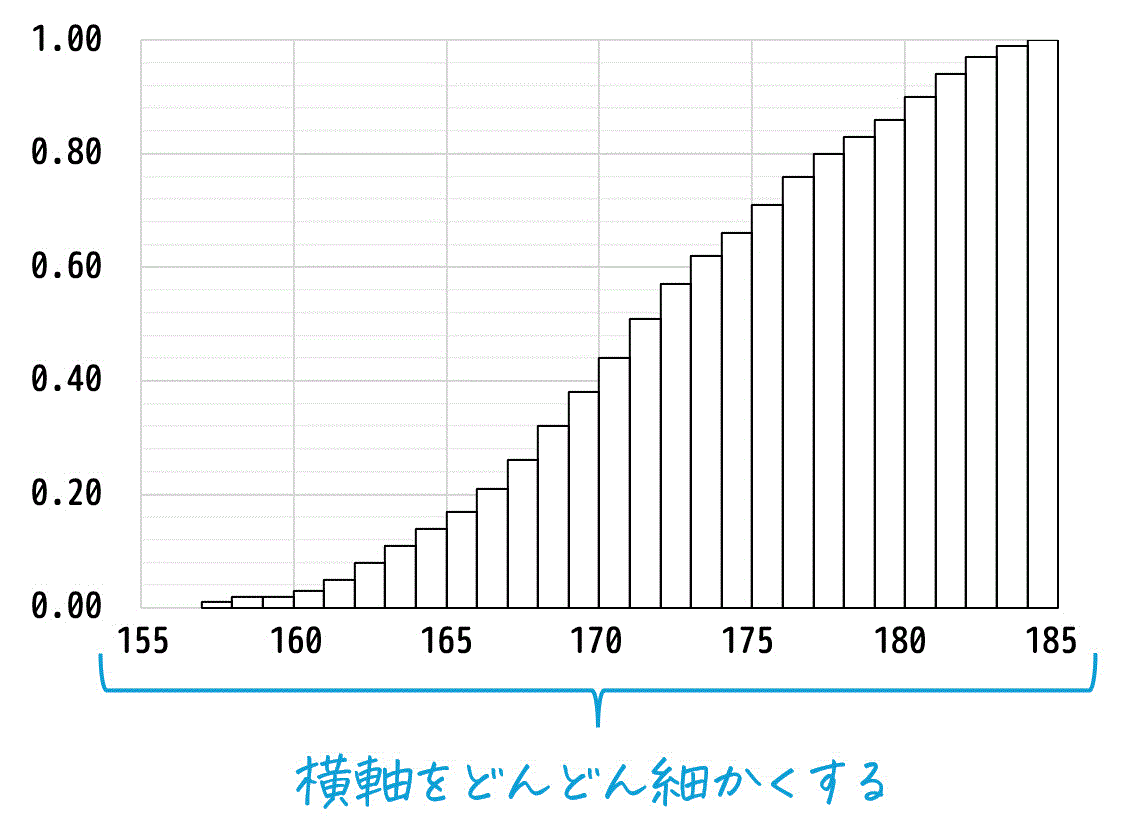
累積分布関数
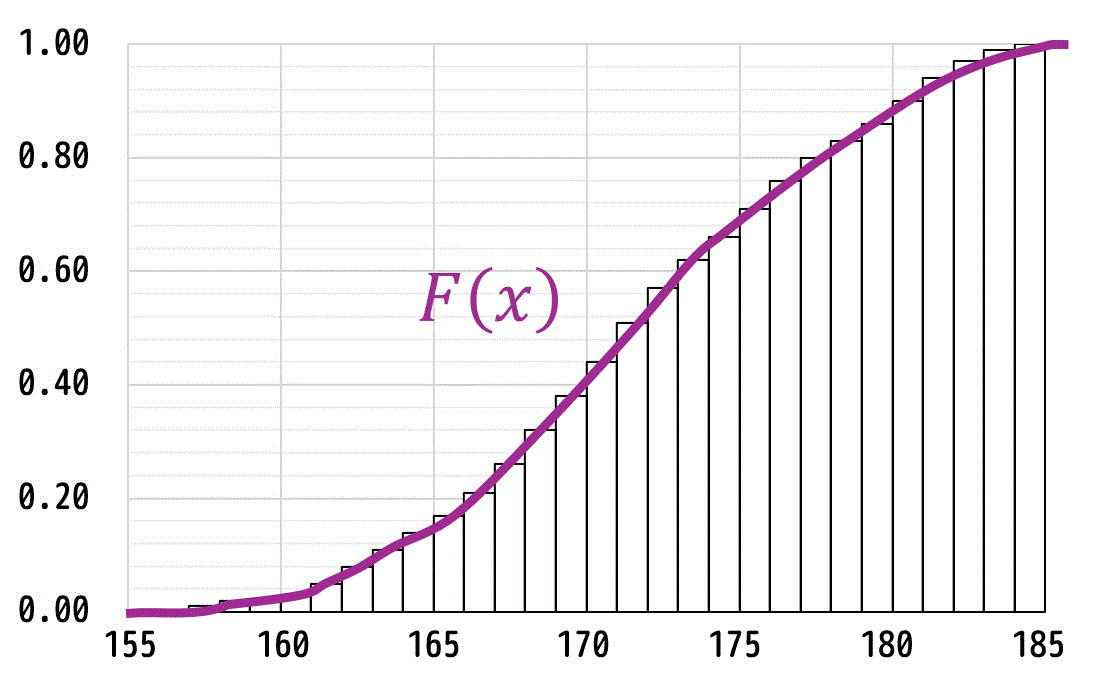
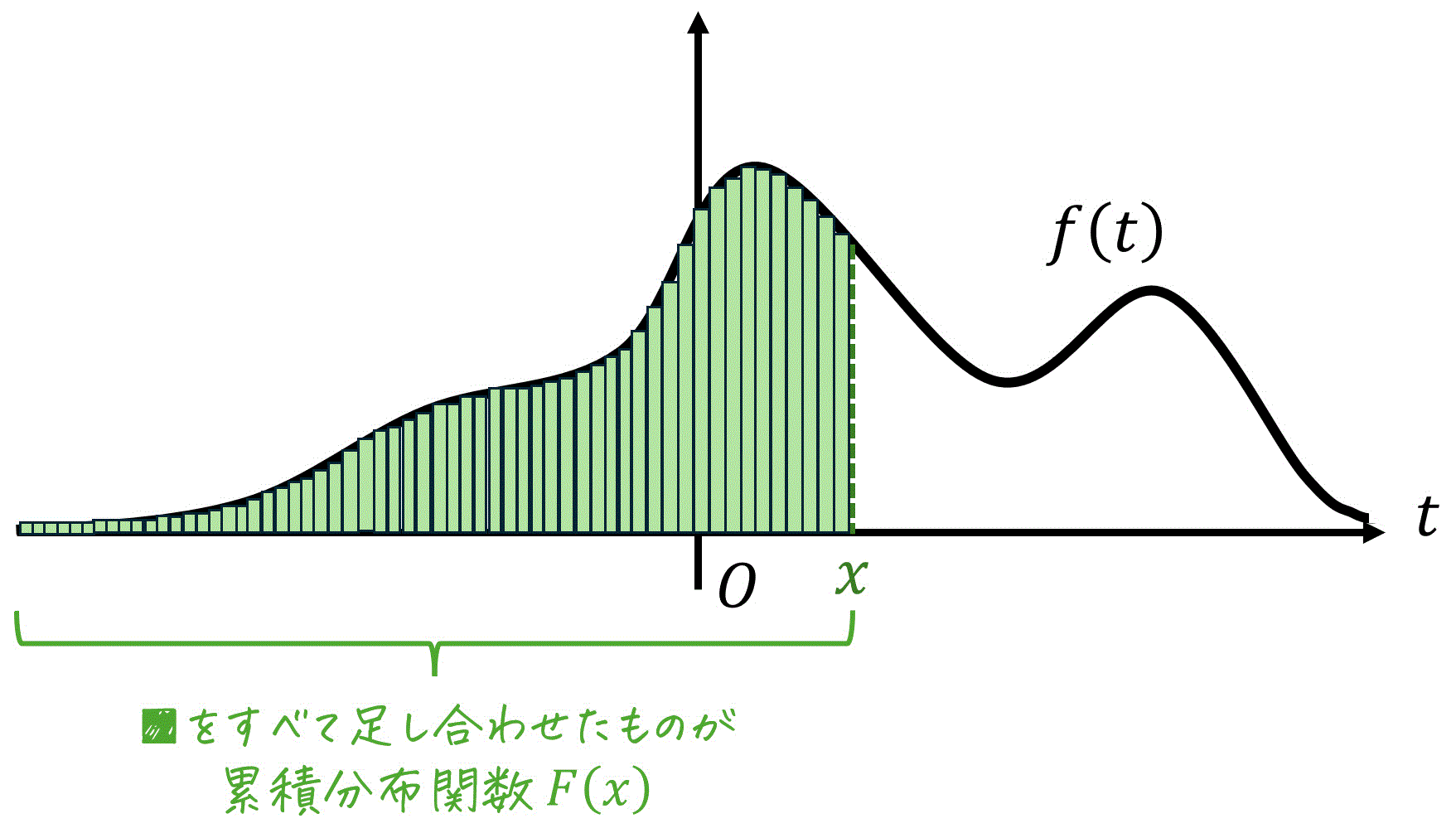
(3) 確率密度関数 f(x) と累積分布関数 F(x) の関係
[a] f(x)からF(x)を求める方法
累積相対度数というのは、ある区間までの相対度数を累積したものでした。
この考えは、累積分布関数でも言えます。つまり、累積分布関数

ここで、確率密度関数
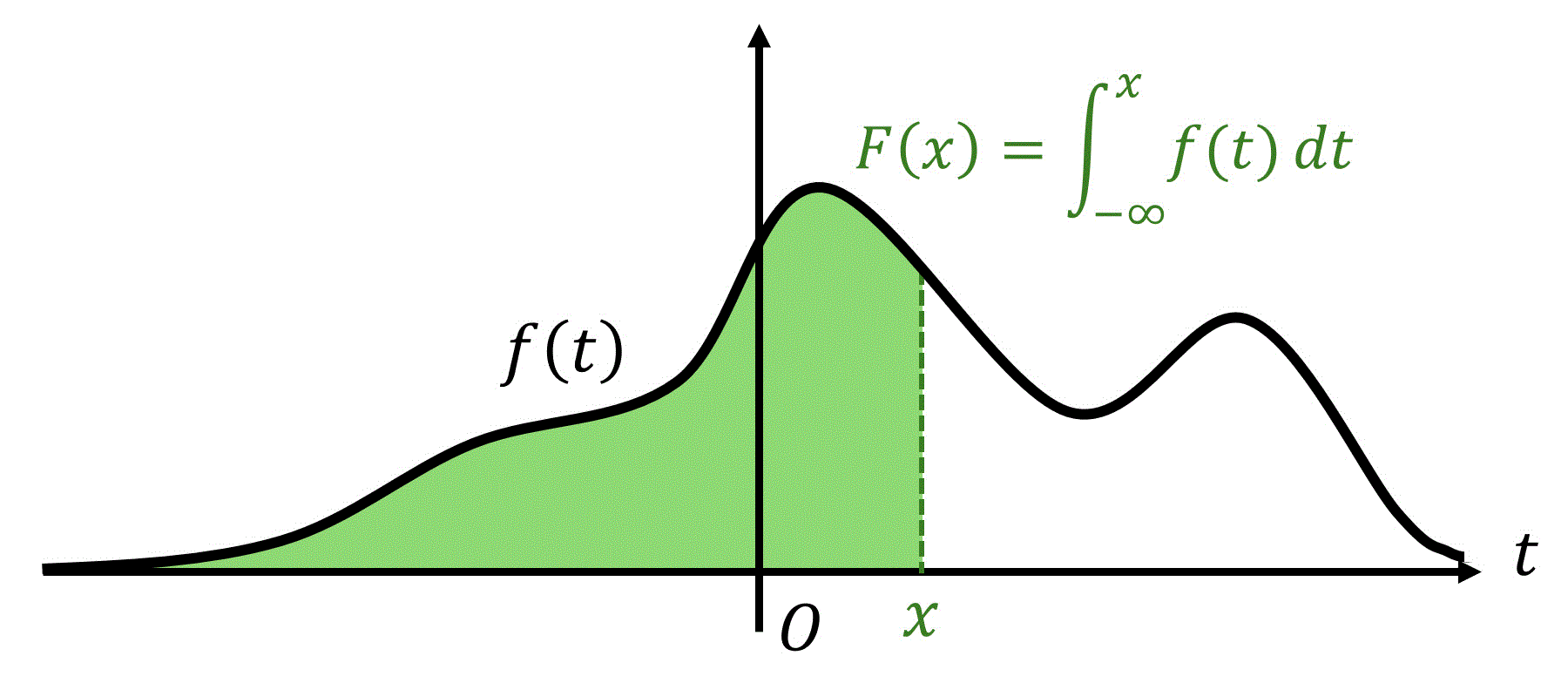
具体的に、ある値
[b] F(x)からf(x)を求める方法
確率密度関数
そのため、累積分布関数
まとめ: f(x)とF(x)の関係
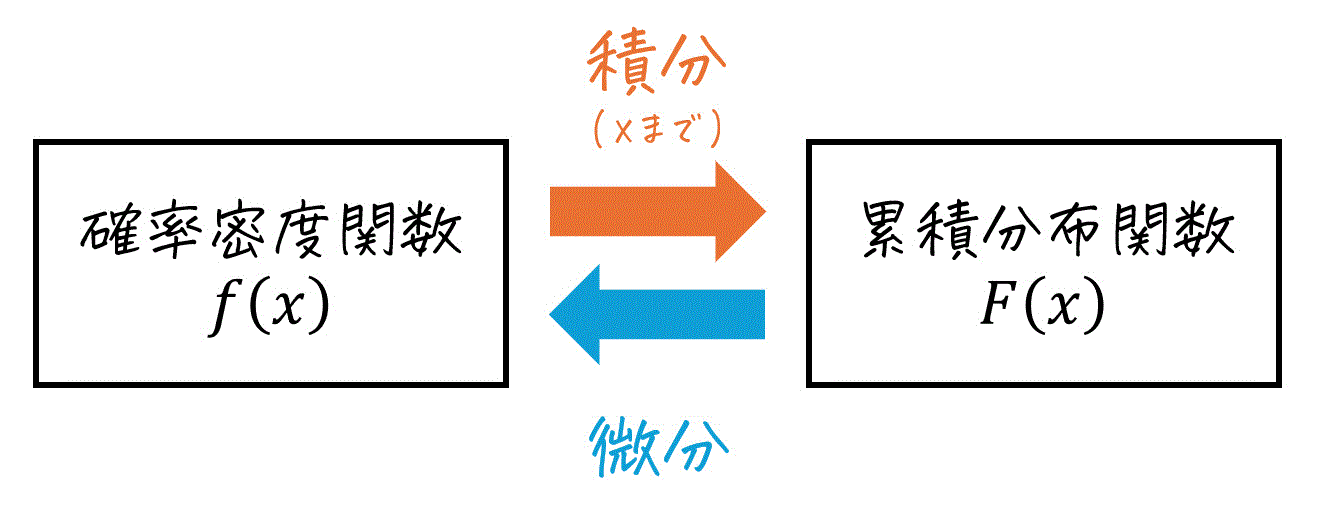
(4) 累積分布関数 F(x)で覚えておきたい3つの性質
つぎに、累積分布関数で覚えておきたい3つの性質を紹介します。
性質1.
累積分布関数
性質2.
累積相対度数では、前の階級値の相対度数をどんどん累積していって求めるため、前の階級値の累積相対度数よりも累積相対度数が小さくなることは絶対にありません。
累積分布関数
数式で書くと、
性質3.
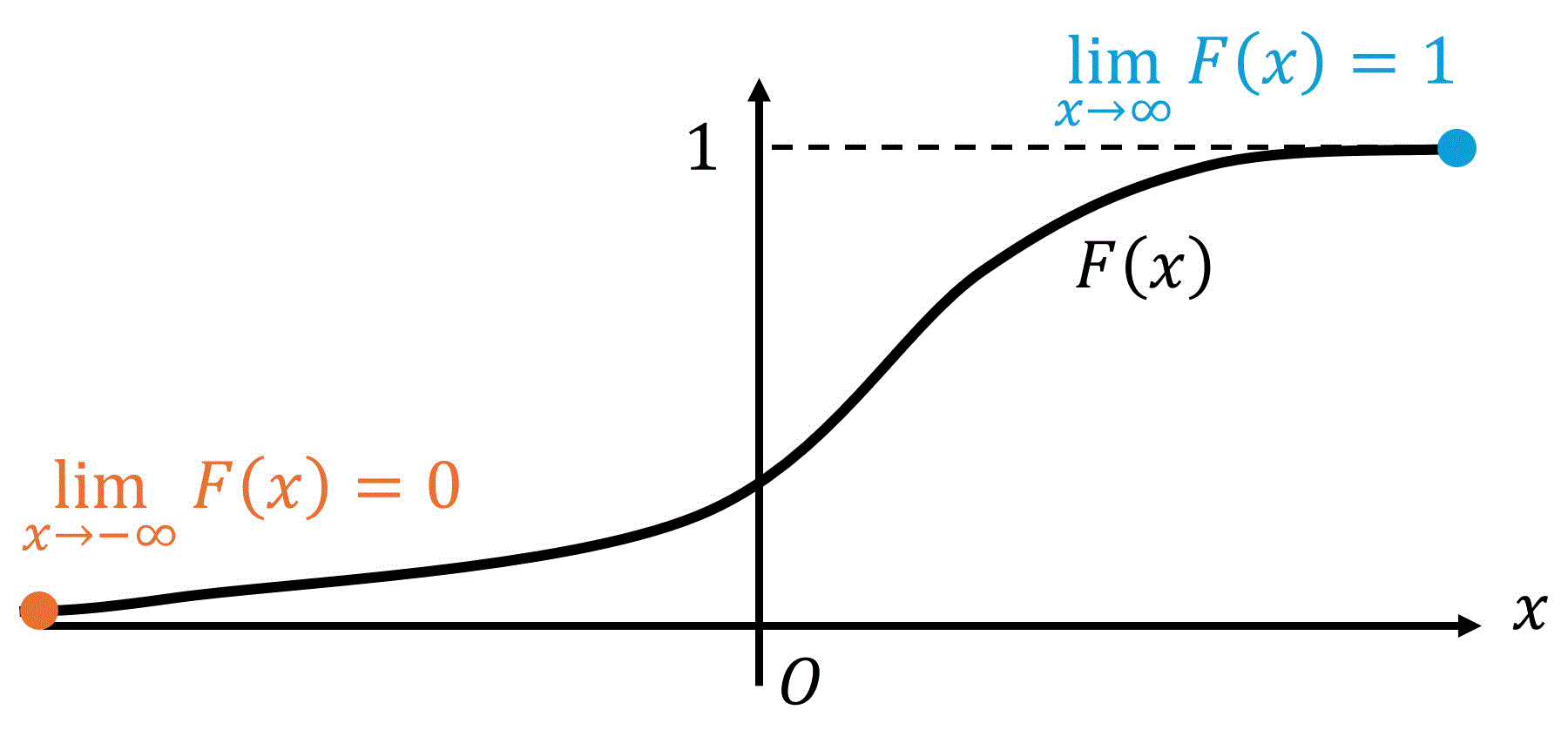
累積分布関数
この2つの性質は、図で見るとより分かりやすくなると思うので、図でも確認しましょう。
スポンサードリンク
3. 例題を解いてみよう
ここからは、実際に例題を解くことで、試験でよく出題される確率密度関数
例題1. 確率密度関数から累積分布関数への変換
確率変数
このとき、累積分布関数
解説1
確率密度関数が
で分かれているので、この4つに場合分けして計算しましょう。
[i]よって、累積分布関数
例題2. 累積分布関数から確率密度関数への変換
確率変数
このとき、確率密度関数
解説2
累積分布関数が
で分かれているので、この4つに場合分けして計算しましょう。
[i]よって、確率密度関数
4. 練習問題にチャレンジ
それでは、累積分布関数の理解が出来ているか、実際に練習問題を解くことで確認しましょう!
練習1.
確率変数
このとき、累積分布関数
練習2.
確率変数
(1) 確率密度関数
(2) 確率変数
(3) 確率変数
5. 練習問題の答え
解答1
確率密度関数が
で分かれているので、この4つに場合分けして計算しましょう。
[i]よって、累積分布関数
※ [i]の積分が合っているか不安な人は、累積分布関数
解答2
(1)
累積分布関数が
で分かれているので、この4つに場合分けして計算する。
[i]よって、確率密度関数
(2)
確率密度関数
実際に計算すると、
(3)
確率密度関数
ここで、
6. まとめ
最後に、累積分布関数
1.累積分布関数
2.累積分布関数
3.累積分布関数は、必ず
4.累積分布関数
5.累積分布関数の極限値について、次の式が成立する。
注釈
| ↑1 | 直接試験で出てくることは少ないですが、求めた累積分布関数 |
|---|
関連広告・スポンサードリンク