スポンサードリンク
こんにちは、ももやまです。
前回のF分布のいろは①では、「F分布とはどんなものなのか」というところから、「F分布を用いて母分散の比率の区間推定」について勉強しました。
今回のF分布のいろは②では、「F分布を使って、2つの標本の母分散が等しいかどうか」を仮説検定する等分散性の検定の方法について学習していきましょう。
スポンサードリンク
1. F分布のおさらい
まずは、F分布について簡単におさらいしておきましょう。
2つの各標本データの変数は、以下の表のように定義されているとする。
| 標本1 | 標本2 | |
|---|---|---|
| カイ2乗値 | \( \chi_1^2 \) | \( \chi_2^2 \) |
| 標本サイズ (既知) | \( n_1 \) | \( n_2 \) |
| 自由度 | \( k_1 = n_1 - 1 \) | \( k_2 = n_2 - 1 \) |
| 不偏分散 | \( s_1^2 \) | \( s_2^2 \) |
| 母分散 | \( \sigma_1^2 \) | \( \sigma_2^2 \) |
(1) F分布の定義
\[F = \frac{ \frac{ \chi_1^2 }{k_1 } }{ \frac{ \chi_2^2 }{k_2 } }\]は、F分布に従う。※ 自由度: \( ( k_1, k_2 ) \)
※ 上の式で計算される \( F \) をF統計量と呼ぶことにしましょう。
(2) F統計量と不偏分散、母分散の関係
\[\begin{align*}
F & = \frac{ \frac{ \chi_1^2 }{k_1 } }{ \frac{ \chi_2^2 }{k_2 } }
\\ & = \frac{ \frac{ \frac{k_1 s_1^2}{\sigma_1^2} }{k_1 } }{ \frac{ \frac{k_2 s_2^2}{\sigma_2^2} }{k_2 } }
\\ & = \frac{ \frac{s_1^2}{\sigma_1^2} }{ \frac{s_2^2}{\sigma_2^2} }
\end{align*}\]
※1 \( F \) の自由度: \( ( k_1, k_2 ) = (n_1 - 1, n_2 - 1) \)
※2 カイ2乗値 \( \chi^2 \) に対して\[\begin{align*}
\chi^2 & = \frac{ (n-1) s^2 }{ \sigma^2 }
\end{align*}\]が成り立つことを変形で使用しています。
※ \( n \): 標本サイズ、\( s^2 \): 不偏分散、\( \sigma^2 \): 母分散
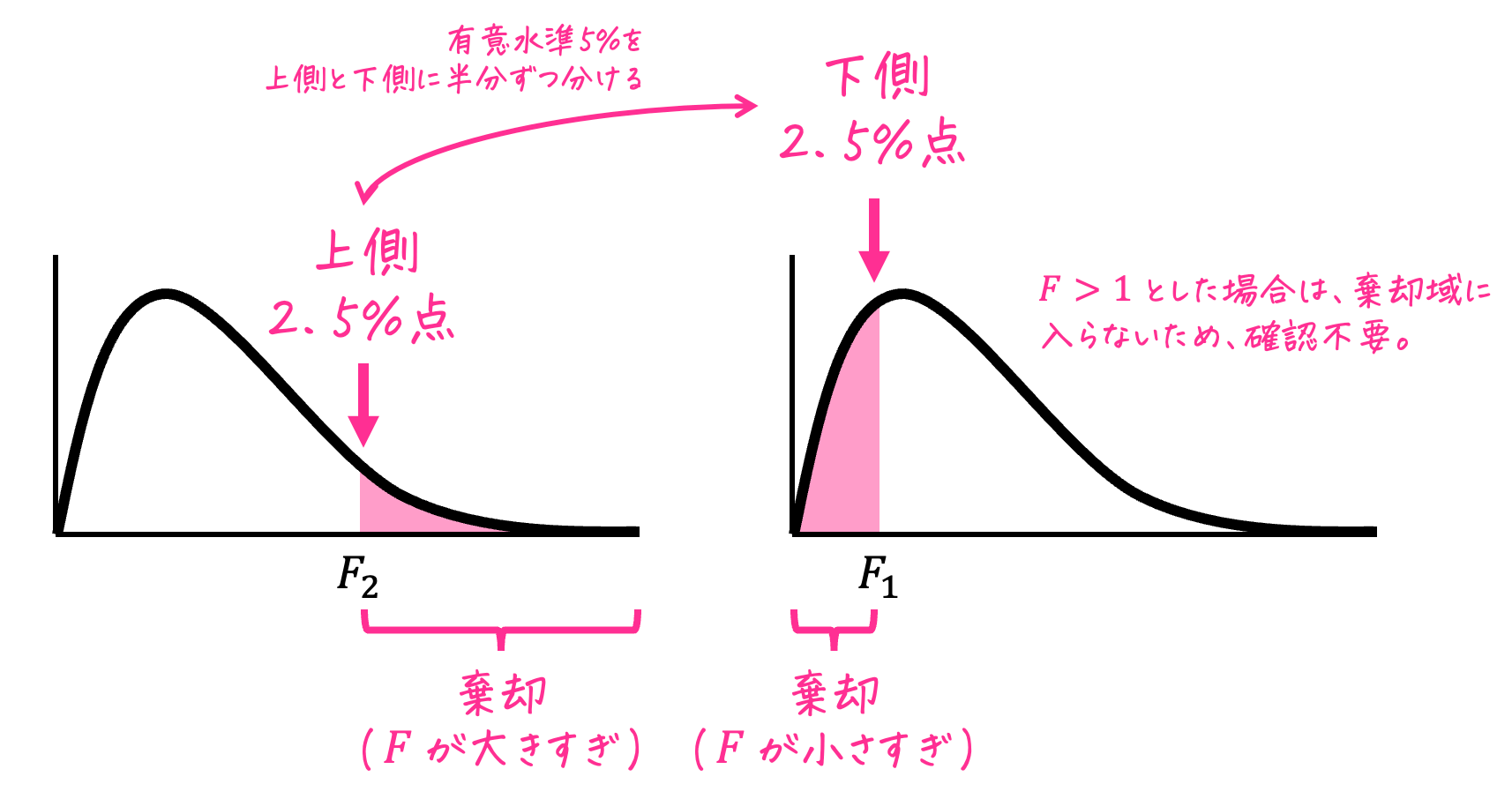
(3) 下側確率をF分布表から読み取る方法
下側確率 \( \alpha \)、自由度 \( (\textcolor{red}{k_1}, \textcolor{blue}{k_2}) \) におけるF値は、以下のStep1〜2の手順で読み取る。
Step1. 上側確率 \( \alpha \)、自由度 \( ( \textcolor{blue}{k_2}, \textcolor{red}{k_1}) \) のときのF値を表から読み取る。(自由度が入れ替わるので注意!)
Step2. 読み取った値の逆数(1/F値)を取る。
スポンサードリンク
2. まずは例題で確認!(等分散性検定の流れ)
実際に、等分散性の検定の流れを例題で確認しましょう。
ある大学では、1年生は1類、2類、3類の3つのクラスに分かれており、桃山先生は1類の1年生の講義「解析学1」の担当をしている。
桃山先生が受け持った1類の「解析学1」の成績分布について、以下のことがわかっている。
| 2024年度 | 2023年度 | |
|---|---|---|
| 履修人数 | 61 | 41 |
| 平均点 | 72 | 75 |
| 不偏分散 | 100 | 50 |
ある日、桃山先生は「解析学1」の点数のばらつき具合について、2023年度と2024年度の変化度合いを調べようとしたが、桃山先生が担当していない2類、3類の「解析学1」の成績データは残っていない。そこで、桃山先生は、つぎの仮説検定を行うことにした。
2024年度の解析学の点数の母分散 \( \sigma_1^2 \) は、2023年度の解析学の点数の母分散 \( \sigma_2^2 \) と等しいといえるか。
この仮説検定を行うために、(1)〜(5)の問いに答えなさい。
(1) 帰無仮説と対立仮説を述べなさい。
(2) この検定に必要な分布を答えなさい。自由度がある分布であれば、自由度も述べること。
(3) 与えられた「解析学1」の成績分布から、この検定で使う統計量を計算しなさい。
(4) 有意水準(危険率)5%で仮説検定を行う。この検定で使う臨界値をすべて求めなさい。(小数の形で表していなくてもよい。)
(5) 有意水準5%で結論を述べなさい。
※ 臨界値:仮説の採択/棄却が変わる境界値のこと。片側検定であれば1つ、両側検定であれば2つある。
※ 必要であれば、こちらからF分布表をダウンロードできます。
解説.
問題を解く前に、与えられたデータから変数をつぎのようにおきます。
※ 母分散 \( \sigma_1^2 \)、\( \sigma_2^2 \) に対応するように変数の添字1, 2をつけています。
| 2024年度 (標本1) | 2023年度 (標本2) | |
|---|---|---|
| 履修人数 | \( n_1 = 61 \) | \( n_2 = 41 \) |
| 不偏分散 | \( s_1^2 = 100 \) | \( s_2^2 = 50 \) |
| 母分散 | \( \sigma_1^2 \) | \( \sigma_2^2 \) |
(1) 帰無仮説と対立仮説
等分散性の検定では、帰無仮説で2標本の母分散が等しいことを仮定し、対立仮説で帰無仮説の否定、つまり2標本の母分散が等しくないことを検定します。
帰無仮説 \( H_0 \): 仮説検定をするための「仮定」
2024年度の解析学の点数の母分散 \( \sigma_1^2 \) と、2023年度の解析学の点数の母分散 \( \sigma_2^2 \) が等しい。つまり、\( \sigma_1^2 = \sigma_2^2 \)
対立仮説 \( H_1 \): 仮説検定を否定することで示したいもの
2024年度の解析学の点数の母分散 \( \sigma_1^2 \) と、2023年度の解析学の点数の母分散 \( \sigma_2^2 \) が等しくない。つまり、\( \sigma_1^2 \not = \sigma_2^2 \)
(2) 必要な分布と自由度の確認
等分散性の検定では、F分布を使用します。また、その自由度は2つの標本の組み合わせによって決まります。
今回は、2024年度のデータ(標本1)に対する自由度を \( k_1 \)、2023年度のデータ(標本2)を \( k_2 \) としましょう。
| 2024年度 (標本1) | 2023年度 (標本2) | |
|---|---|---|
| 履修人数 | \( n_1 = 61 \) | \( n_2 = 41 \) |
| 自由度 | \( k_1 = n_1 - 1 \) | \( k_2 = n_2 - 1 \) |
| 不偏分散 | \( s_1^2 = 100 \) | \( s_2^2 = 50 \) |
| 母分散 | \( \sigma_1^2 \) | \( \sigma_2^2 \) |
すると、自由度の組み合わせは \( (k_1,k_2) \) は \( n_1 = 61 \)、\( n_2 = 41 \) なので、\[\begin{align*}
(k_1,k_2) & = (n_1 - 1, n_2 - 1)
\\ & = (60, 40)
\end{align*}\]となります。
(3) F統計量の計算
今回の検定で使うF統計量を計算していきます。
まず、F値は\[\begin{align*}
F = \frac{ \frac{s_1^2}{\sigma_1^2} }{ \frac{s_2^2}{\sigma_2^2} }
\end{align*}\]で計算できるのでしたね。
ここで、帰無仮説で \( \sigma_1^2 = \sigma_2^2 \) を仮定していましたね。
そのため、F統計量は\[\begin{align*}
F & = \frac{ \frac{s_1^2}{\sigma_1^2} }{ \frac{s_2^2}{\sigma_2^2} }
\\ & = \frac{ \frac{s_1^2}{\sigma_1^2} }{ \frac{s_2^2}{\sigma_1^2} }
\\ & = \frac{ s_1^2 }{ s_2^2 }
\end{align*}\]で計算ができます。
あとは、\( s_1^2 = 100 \)、\( s_2^2 = 50 \) を代入すればF統計量の導出完了です。\[\begin{align*}
F & =\frac{ s_1^2 }{ s_2^2 }
\\ & = \frac{100}{50}
\\ & = 2
\end{align*}\]
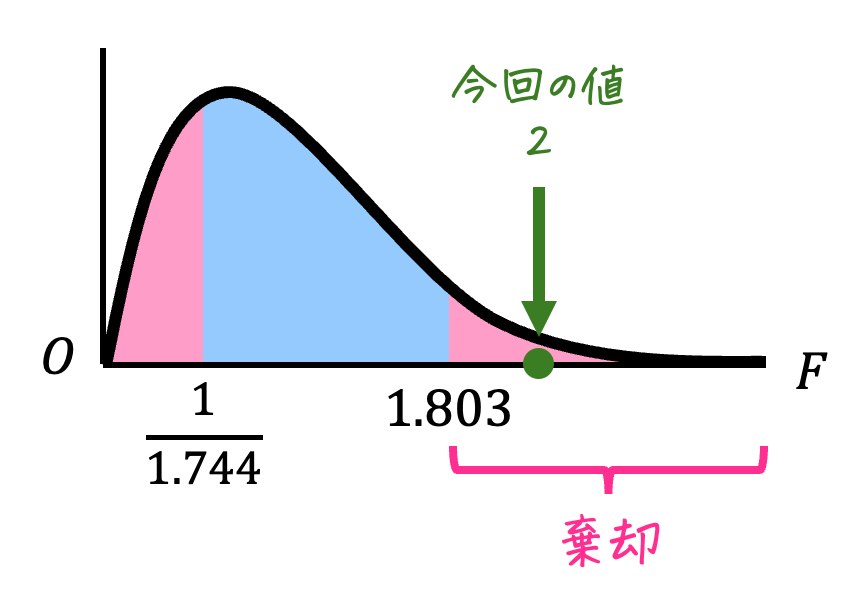
(4) F分布表の読み取り:臨界値(採択/棄却の境界値)の確認
つぎに、有意水準5%に対応する \( F \) の値(=臨界値)を求めていきます。
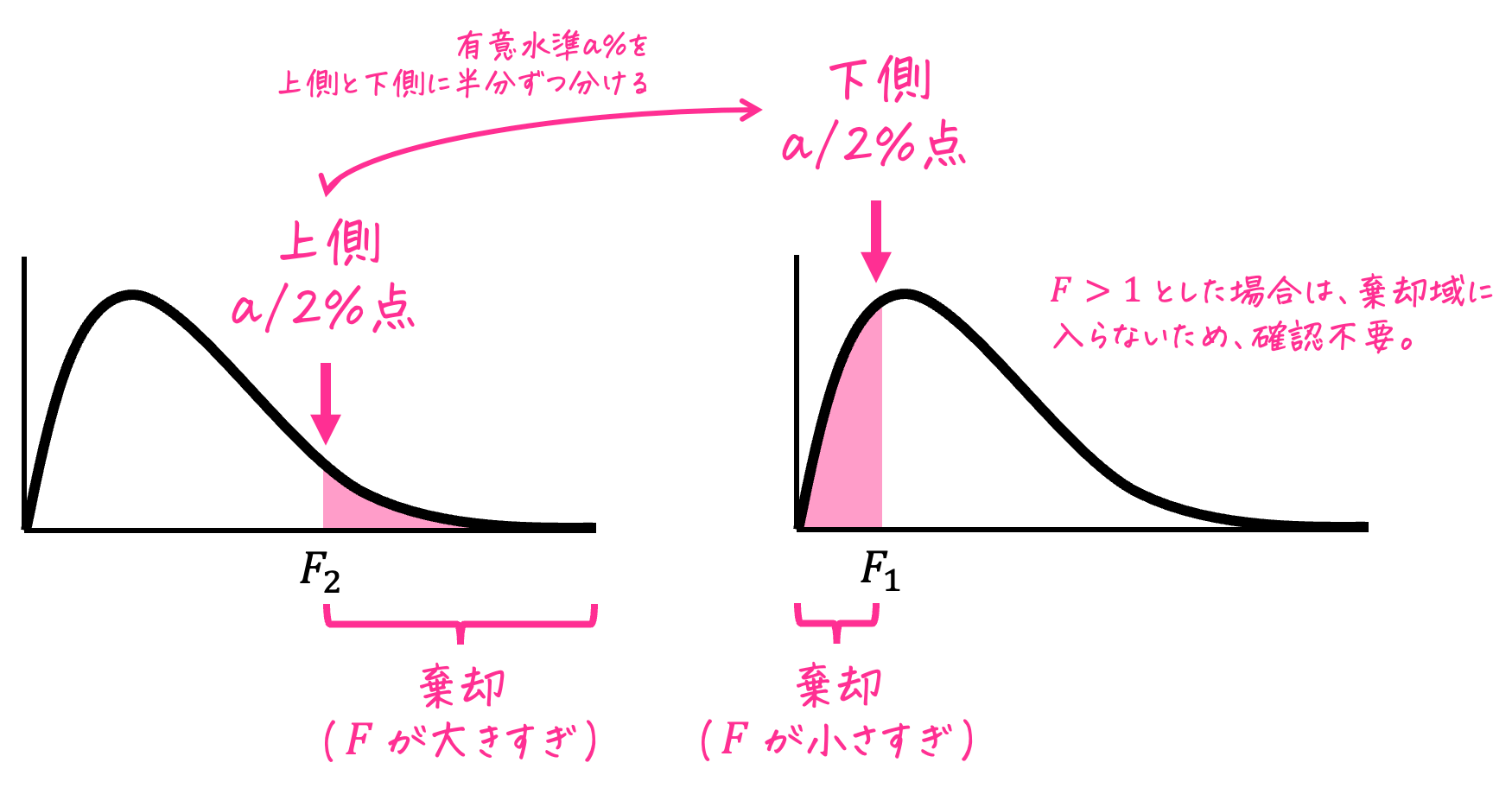
等分散性の仮説検定では、対立仮説が \( \sigma_1^2 \textcolor{red}{\not =} \sigma_2^2 \) なので、母分散の比率が小さすぎる場合、母分散の比率が大きすぎる場合の両方を考慮する必要があります。
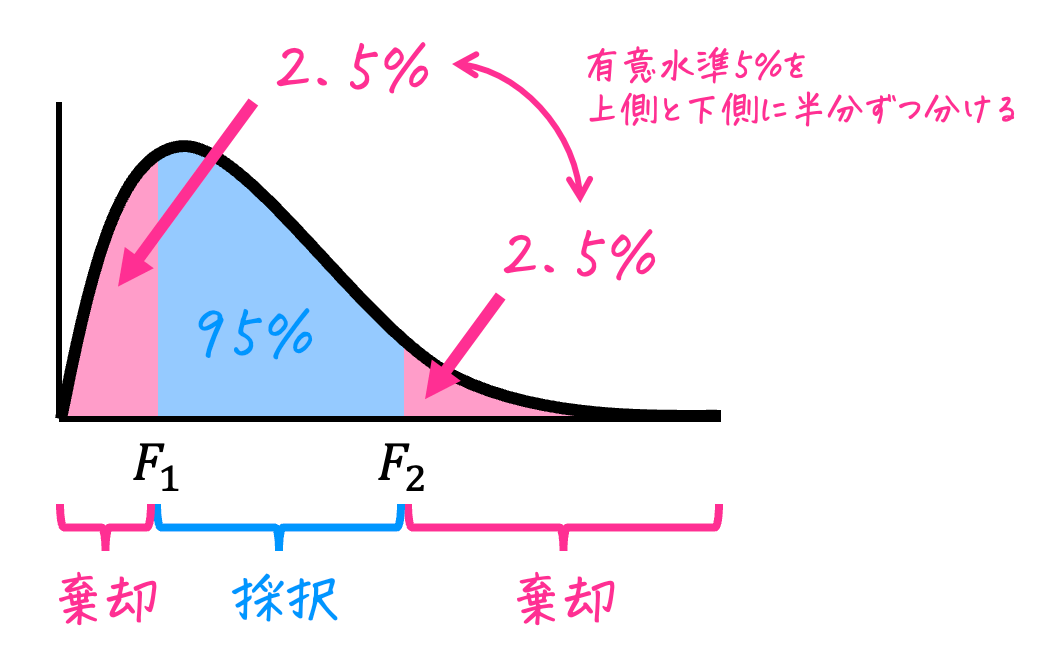
そのため、等分散性の仮説検定は必ず両側検定で実施します。
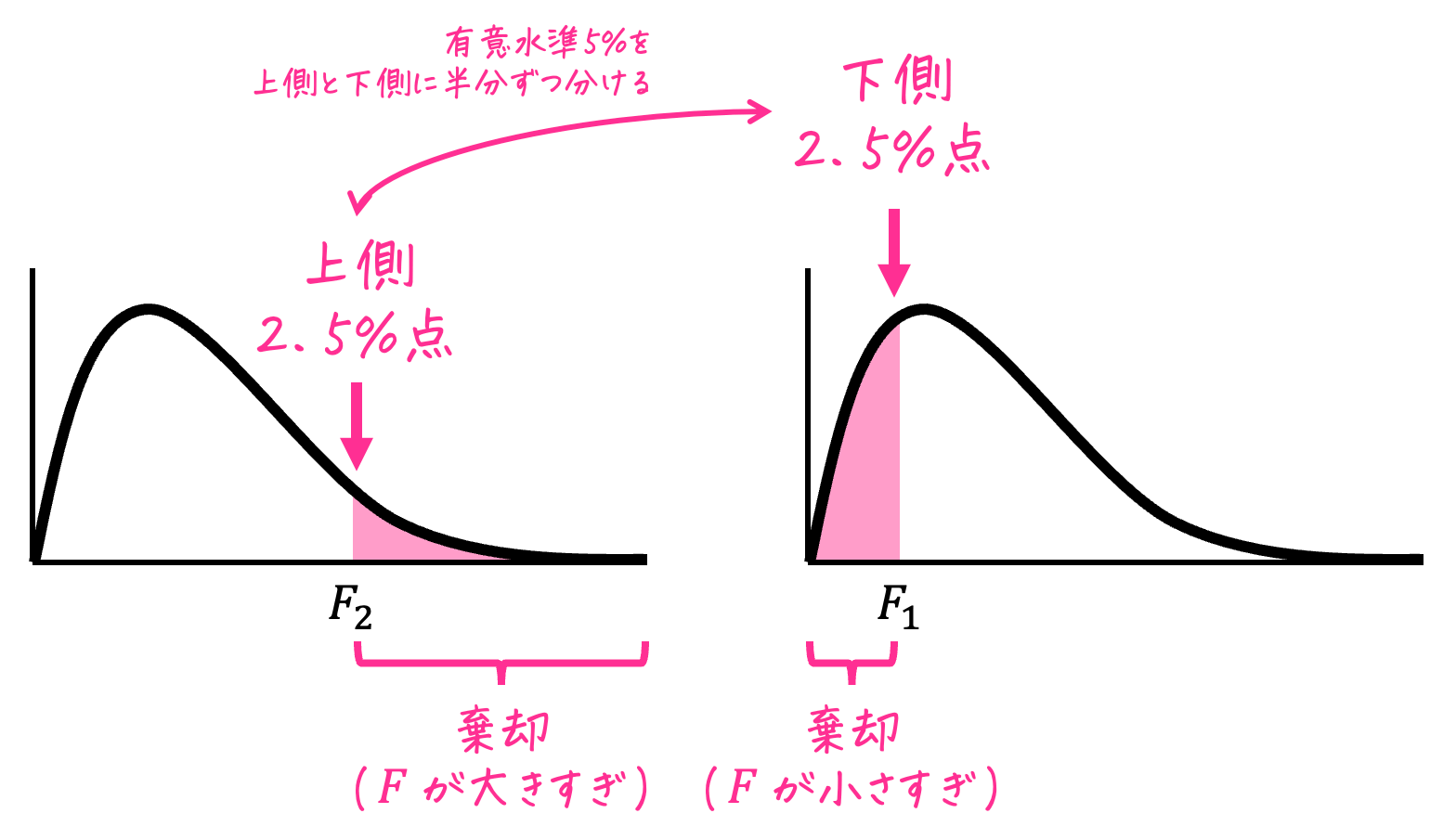
ここで、\( F_1 \)、\( F_2 \) を次のようにおきましょう。
- \( F_1 \) … 母分散の比率が小さすぎる場合の臨界値(下側2.5%点、上側97.5%点)
→ F統計量が、この値よりも小さい場合は仮説が棄却される - \( F_2 \) … 母分散の比率が大きすぎる場合の臨界値(上側2.5%点)
→ F統計量が、この値よりも大きい場合は仮説が棄却される
[i] 母分散の比率が大きすぎる場合の臨界値 \( F_2 \)
\( F_2 \) は上側2.5%点なので、上側確率2.5%に相当する、\( \alpha = 0.025 \) の表を使います。
自由度は \( (k_1,k_2) = (60,40) \) に対応するところを表から読むと、1.803と読み取れます。
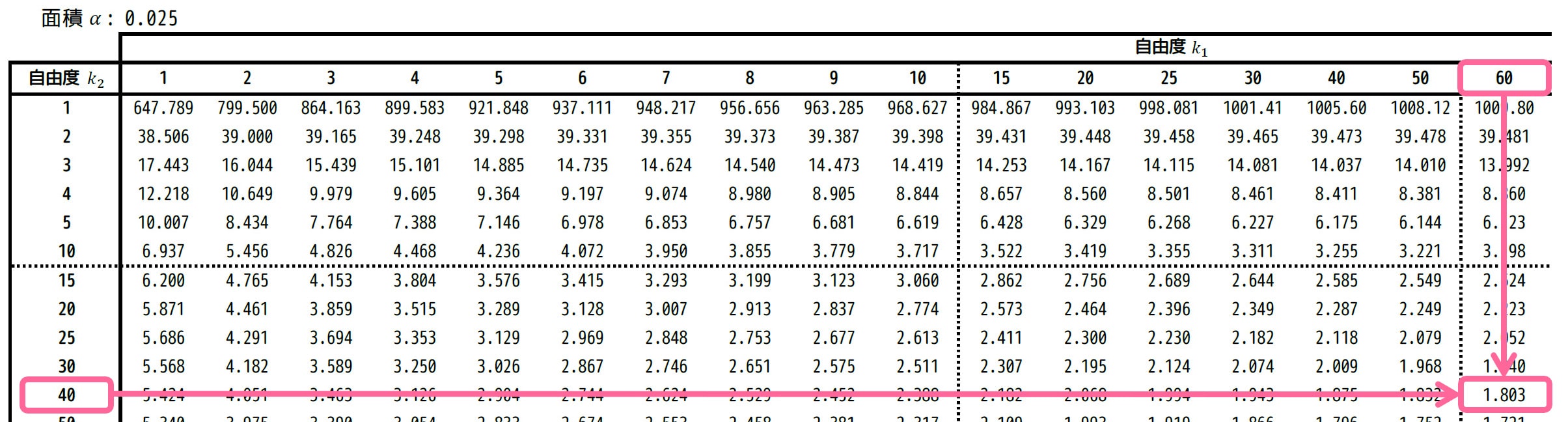
なので、\( F_2 = 1.803 \) ですね。
[ii] 母分散の比率が小さすぎる場合の臨界値 \( F_1 \)
\( F_1 \) は下側2.5%点(上側97.5%点)ですが、\( \alpha = 0.975 \) の表はありません。
なので、次の手順で上側2.5%点 \( F_1 \) の値を読み取ります。
- 上側確率 \( \alpha = 0.025 \)、自由度 \( ( \textcolor{blue}{k_2}, \textcolor{red}{k_1}) \) のときのF値を表から読み取る。
- 読み取った値の逆数(1/F値)を取る。
まず、自由度 \( (k_2,k_1) = (60,40) \)、つまり \( (k_1,k_2) = (40,60) \) に対応するところを表から読むと、1.744と読めます。
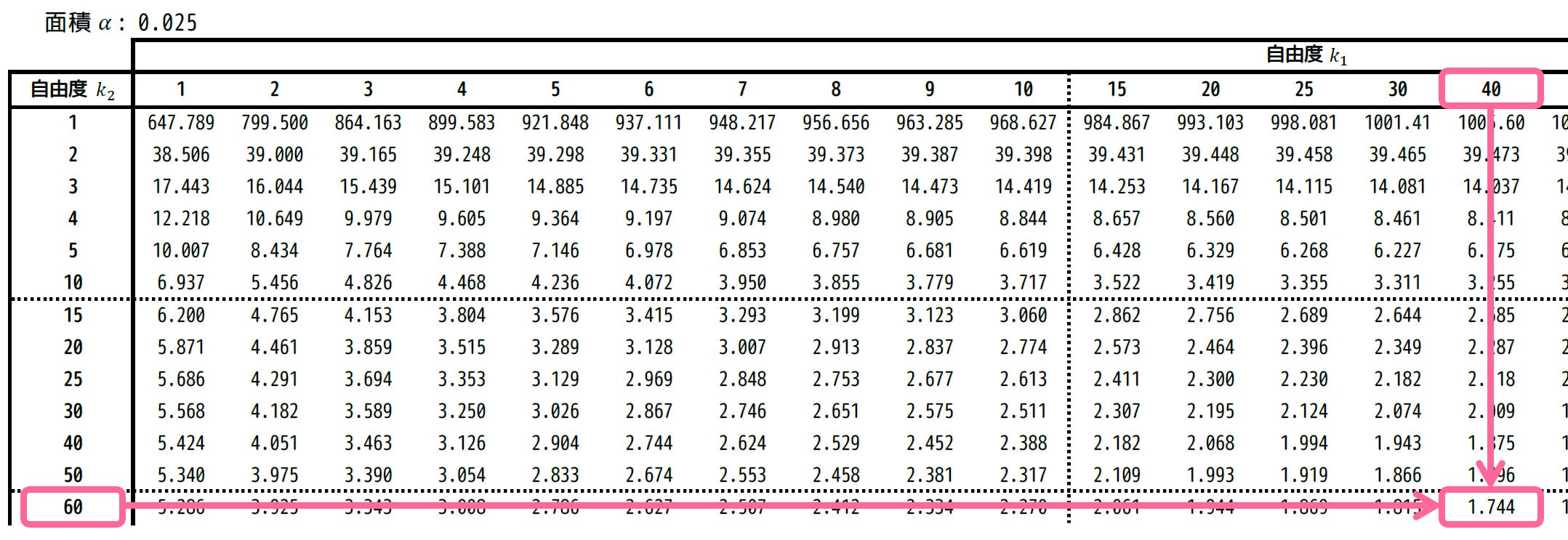
この値 (1.744) の逆数が \( F_1 \) となるので、\[\begin{align*}
F_1 = \frac{1}{1.744}
\end{align*}\]となります。( \( F_1 \) と \( F \) の大小がわかればいいので、1/小数の形のままにします。)
※ 3章で詳しく説明しますが、"[ii] 母分散の比率が小さすぎる場合の臨界値" のステップは省略可能です。
(5) 採択/棄却の判定
あとは、(3)計算したF統計量\[\begin{align*}
F & = \frac{ s_1^2 }{ s_2^2 }
\\ & = 2
\end{align*}\]および、(4)でF分布表から得た臨界値 \( F_1 = \frac{1}{1.744} \)、\( F_2 = 1.803 \) から結論を出します。
【結論の出し方】
- F統計量 \( F \) が2つの臨界値 \( F_1 \), \( F_2 \) におさまっている場合、つまり \( F_1 \leqq F \leqq F_2 \)
→ 仮説は採択:母分散が等しくないとは言えない - F統計量 \( F \) が2つの臨界値 \( F_1 \), \( F_2 \) におさまっていない場合、つまり \( F < F_1 \) もしくは \( F > F_2 \)
→ 仮説は棄却:母分散が等しくないと言える
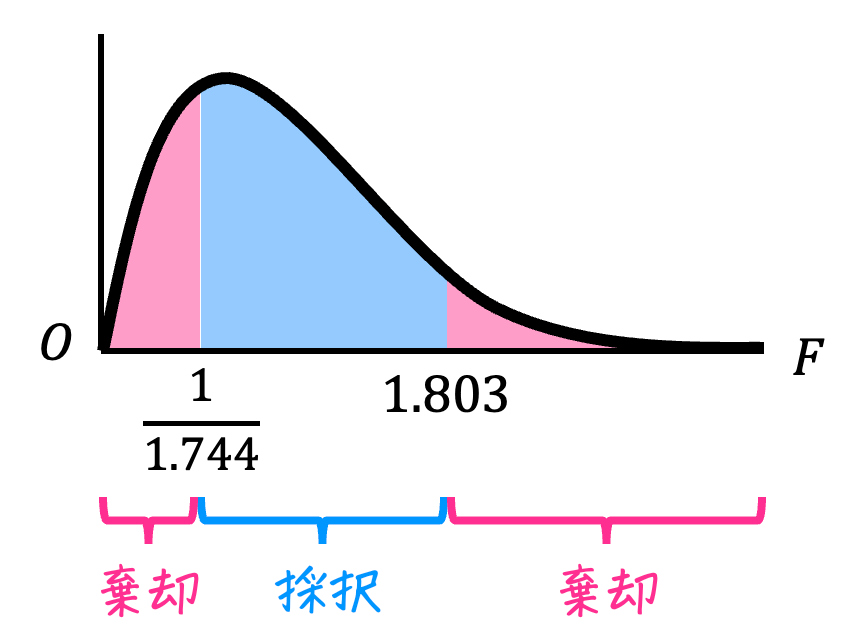
今回は、\( F = 2 \) 、\( F_2 = 1.803 \) なので、\[
F = 2 > 1.803 = F_2
\]ですね。よって、仮説は棄却され、2024年度の解析学の点数の母分散 \( \sigma_1^2 \) は、2023年度の解析学の点数の母分散 \( \sigma_2^2 \) は等しくないと結論付けられます。
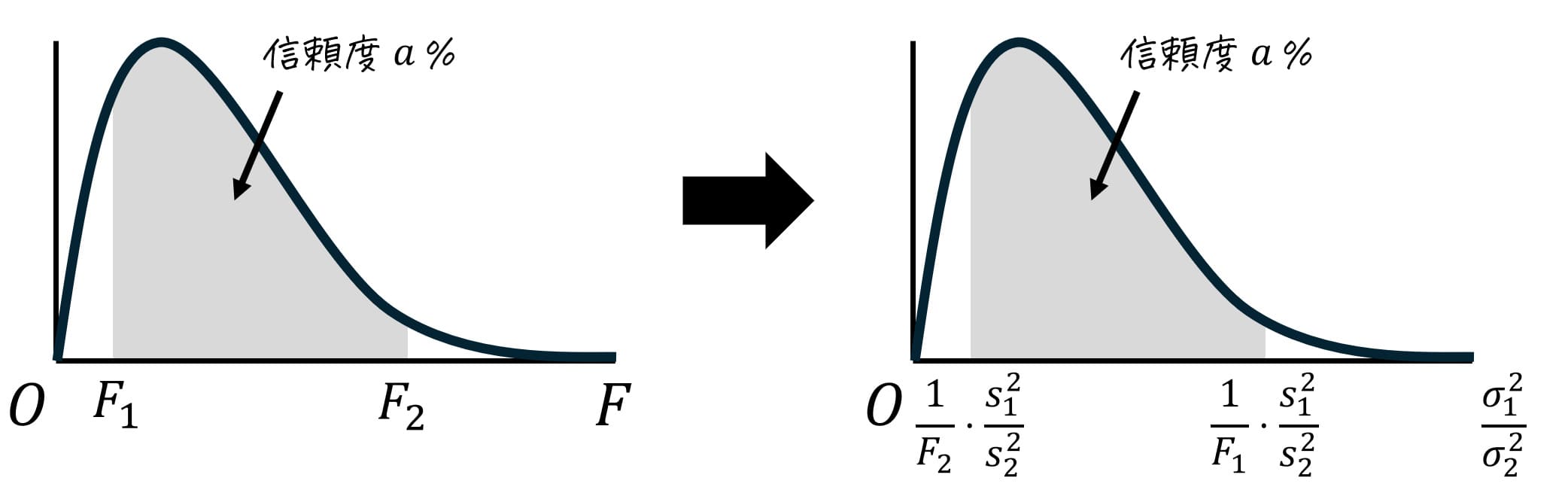
補足.等分散性の仮説検定の結果と母比率の信頼区間の関係
等分散性の検定では、2標本の母分散 \( \sigma_1^2 \), \( \sigma_2^2 \) が等しい(\( \sigma_1^2 = \sigma_2^2 \))という仮定をしてから、\( \sigma_1^2 = \sigma_2^2 \) となる確率が有意水準よりも小さい(棄却)か小さくない(採択)かを判定しています。
ここで、\( \sigma_1^2 = \sigma_2^2 \) というのは、母分散の比 \( \frac{ \sigma_1^2 }{ \sigma_2^2 } \)が\[
\frac{ \sigma_1^2 }{ \sigma_2^2 } = 1
\]と言い換えられますね。
そのため、等分散性の仮説検定の結果と母比率の信頼区間には、以下のような関係があると言えます。
- 有意水準 \( a \) %にて仮説が採択された
→ 信頼度 \( 100 - a \) %での母分散の比の信頼区間に 1 が含まれる - 有意水準 \( a \) にて仮説が棄却された
→ 信頼度 \( 100 - a \) %での母分散の比の信頼区間に 1 が含まれない
※ 実際に、今回の例題で使用した等分散性の検定の問題でも、上の関係は成り立っています。
- 結論 → 棄却
- 母分散の比率の信頼区間:1.11~3.49(信頼区間に1が含まれない)
スポンサードリンク
3. 等分散検定の省略テクニック紹介
ここで、等分散性の計算を少し早くするテクニックを紹介しましょう。
| 標本1 | 標本2 | |
|---|---|---|
| 標本サイズ | \( n_1 \) | \( n_2 \) |
| 自由度 | \( k_1 = n_1- 1 \) | \( k_2 = n_2- 1 \) |
| 不偏分散 | \( s_1^2 = 100 \) | \( s_2^2 = 50 \) |
| 母分散 | \( \sigma_1^2 \) | \( \sigma_2^2 \) |
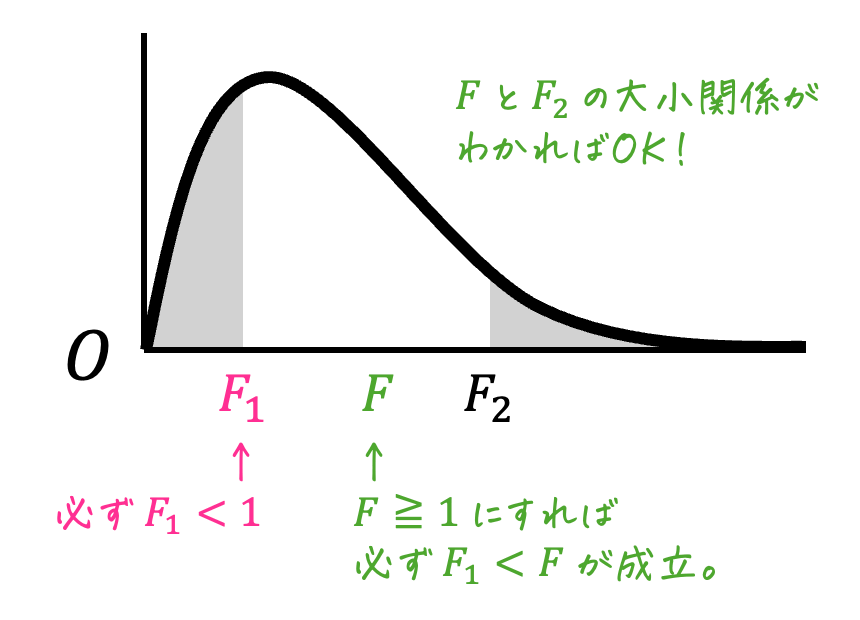
ポイントは、2つの標本のデータのうち、より不偏分散が大きい方を \( s_1^2 \) となるように標本を決めることです。
\( s_1^2 \geqq s_2^2 \) になるように標本1, 標本2を設定することで、\[
F = \frac{ s_1^2 }{ s_2^2 } \geqq 1
\]となります。
ここで下側確率(例: 2.5%、5%、10%、20%など)に対する臨界値 \( F_1 \) は、必ず \( F < 1 \) となる法則があります[1]F分布表に上側確率が書いていると思いますが、全部 \( F>1 \) … Continue reading。
そのため、\( F_1 \) の値を求めなくても、\( F_1 < F \) の関係が成り立ちます。
よって、仮説検定の結果(採択/棄却)を判定する際には、\( F \) と上側の臨界点 \( F_2 \) だけを確認すればOKとなります。
- \( F \leqq F_2 \) のとき
→ 仮説は採択:母分散が等しくないとは言えない - \( F > F_2 \) のとき
→ 仮説は棄却:母分散が等しくないといえる
\( s_1^2 \geqq s_2^2 \) になるように標本1, 標本2を設定することで、採択/棄却の判定を、以下のように省略できる。
具体的には、F統計量\[
F = \frac{ s_1^2 }{ s_2^2 } \geqq 1
\]を、上側確率の臨界点 \( F_2 \) と比べるだけで採択/棄却の結論を出せる。
- \( F \leqq F_2 \) のとき
→ 仮説は採択:母分散が等しくないとは言えない - \( F > F_2 \) のとき
→ 仮説は棄却:母分散が等しくないといえる
※ 下側確率に対する臨界点 \( F_1 \) の計算は不要。\( F > 1 \) かつ \( F_1 \leqq 1 \) なので、\( F_1 \)、\( F \) に対して \( F_1 < F \) が成り立つため。
ただし、どうしても計算したい場合は\[
\frac{1}{ \mathrm{F \ 分布表から読み取った値} } < F
\]と表記することで、\( F_1 < F \) を明示できる。
4. 等分散性の検定手順まとめ
2標本の母分散が等しいかどうかを、標本サイズ \( n_1 \), \( n_2 \)、不偏分散 \( s_1^2 \), \( s_2^2 \) を用いて、有意水準 \( a \) % で検定する流れは以下の通り。
事前準備.(実施するとStep4, Step5の一部計算、処理を省略できる)
標本1の不偏分散 \( s_1^2 \) が標本2の不偏分散 \( s_2^2 \) 以上( \( s_1^2 \geqq s_2^2 \) になるように、標本1、標本2とし、以下のように変数をおく。
| 標本1 | 標本2 | |
|---|---|---|
| 標本サイズ (既知) | \( n_1 \) | \( n_2 \) |
| 自由度 | \( k_1 = n_1- 1 \) | \( k_2 = n_2- 1 \) |
| 不偏分散 (既知) | \( s_1^2 = 100 \) | \( s_2^2 = 50 \) |
| 母分散 (未知) | \( \sigma_1^2 \) | \( \sigma_2^2 \) |
Step1. 帰無仮説と対立仮説を立てる
帰無仮説 \( H_0 \): 仮説検定をするための「仮定」
\( \sigma_1^2 = \sigma_2^2 \)
対立仮説 \( H_1 \): 仮説検定を否定することで示したいもの
\( \sigma_1^2 \not = \sigma_2^2 \)
Step2. 必要な分布、自由度を確認する
使う分布: F分布
自由度: \( (k_1, k_2) = (n_1 - 1, n_2-1) \)
Step3. F統計量の計算
帰無仮説にて、\( \sigma_1^2 = \sigma_2^2 \) としているので、F統計量は以下のように計算できる。\[\begin{align*}
F & = \frac{ \frac{s_1^2}{\sigma_1^2} }{ \frac{s_2^2}{\sigma_2^2} }\\ & = \frac{ \frac{s_1^2}{\sigma_1^2} }{ \frac{s_2^2}{\sigma_1^2} }\\ & = \frac{ s_1^2 }{ s_2^2 }
\end{align*}\]
※ 事前準備で \( s_1^2 \geqq s_2^2 \) としている場合は、必ず \( F \geqq 1 \) となる。
Step4. F分布表の読み取り:臨界値(採択/棄却の境界値)の確認
対立仮説が、\( \sigma_1^2 \textcolor{red}{\not =} \sigma_2^2 \) なので、両側検定を実施する。
- \( F_1 \) … 下側 \( a/2 \) %点 [上側 \( 100 - a \) %点]
- \( F_2 \) … 上側 \( a/2 \) %点
※ 事前準備済の場合は \( F_1 \) の計算不要

[i] \( F_2 \)(上側 \( a \) % 点)
\( F_2 \) は、上側確率 ( \alpha = a / 200 )、自由度 \( ( \textcolor{red}{k_1} , \textcolor{blue}{k_2}) \) のときのF値を表から読み取ったものである。
[ii] \( F_1 \)(下側 \( a/2 \) %点 [上側 \( 100 - a \) %点])
※ 事前準備済の場合は計算不要[2]事前準備で \( s_1^2 \geqq s_2^2 \) としているため、\( F > 1 \) が成り立つ。また、\( F_1 < 1 \) なので、常に\( F_1 < F \) が成り立つ。
\( F_1 \) は次の流れで求められる。
- 上側確率 \( \alpha = a / 200 \)、自由度 \( ( \textcolor{blue}{k_2}, \textcolor{red}{k_1}) \) のときのF値を表から読み取る。
- 読み取った値の逆数(1/F値)を取る。
※ 事前準備をしたが、どうしても \( F_1 \) を計算したい場合は、\[
\frac{1}{ \mathrm{F \ 分布表から読み取った値} }
\]の形まで出してもOK。(この形まで出せば、\( F_1 < 1 \) が自明になるため。)
Step5. F分布表の読み取り:臨界値(採択/棄却の境界値)の確認
★事前準備済の場合( \( \sigma_1^2 \geqq \sigma_2^2 \) としている場合)
- \( F \leqq F_2 \) のとき
→ 仮説は採択:母分散が等しくないとは言えない - \( F > F_2 \) のとき
→ 仮説は棄却:母分散が等しくないといえる
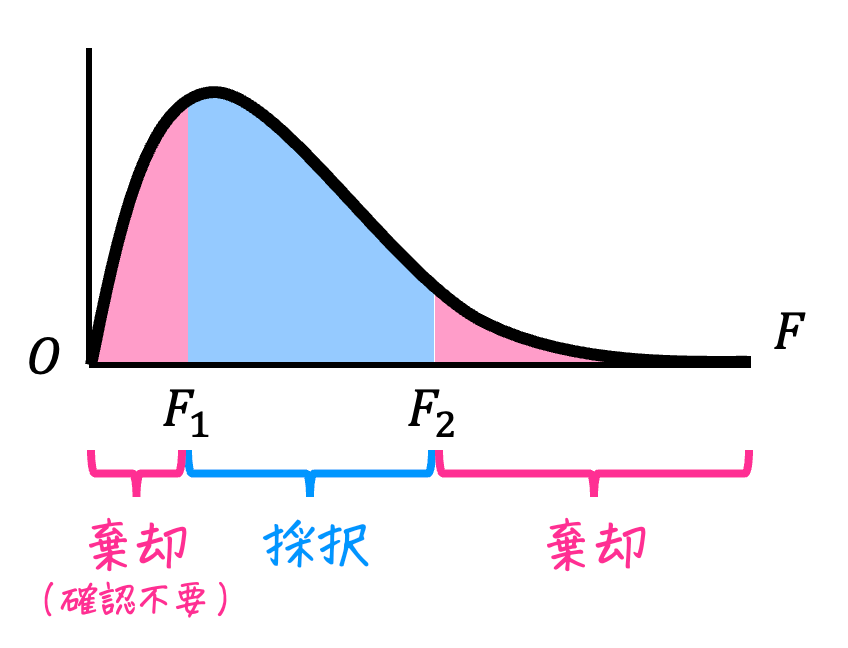
※ \( F_1 < F \) なので、\( F \) と \( F_2 \) に対する不等号を確認すればOK。
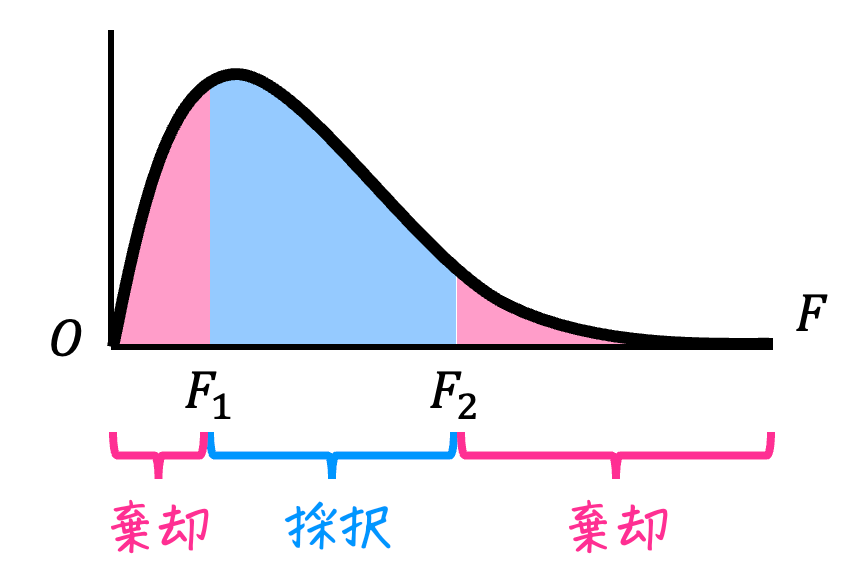
★事前準備をしていない場合
- \( F_1 \leqq F \leqq F_2 \) のとき
→ 仮説は採択:母分散が等しくないとはいえない - \( F < F_1 \) もしくは \( F > F_2 \) のとき
→ 仮説は棄却:母分散が等しくないといえる
5. 練習問題で確認
最後に、今回習った内容が理解できているかを練習問題で確認しましょう。
小問はつけていません。
桃山食堂では、ご飯を自動で一定量盛り付ける機械を導入している。この食堂では、最近、新型の機械を導入し、旧型の機械と比較して盛り付けられるご飯の重さのばらつき具合がどのように変わったかを調査した。
実際に、新しい機械、古い機械からランダムにご飯を盛り付けて、その重さを測定したところ、以下のデータを得ることができた。(ただしお椀の重さは入っていない)
| 新型 | 旧型 | |
|---|---|---|
| サンプル数 | 21 | 16 |
| 平均 [g] | 120 | 118 |
| 不偏分散 [g2] | 20 | 50 |
問題.旧型の機械で盛り付けられるご飯の重さと、新型の機械で盛り付けられるご飯の重さの母分散は、同じとみなしてよいか? 有意水準(危険率)5%で推定しなさい。
※ 必要であれば、こちらからF分布表をダウンロードできます。
6. 練習問題の答え
問題を解く前に、与えられたデータから変数をつぎのようにおきます。
※ \( s_1^2 \geqq s_2^2 \) となるように標本1、標本2を設定しています。
| 旧型 (標本1) | 新型 (標本2) | |
|---|---|---|
| サンプル数 | \( n_1 = 16 \) | \( n_2 = 21 \) |
| 自由度 | \( k_1 = n_1 - 1 \) | \( k_2 = n_2 - 1 \) |
| 不偏分散 [g2] | \( s_1^2 = 50 \) | \( s_2^2 = 20 \) |
| 母分散 [g2] | \( \sigma_1^2 \) | \( \sigma_2^2 \) |
Step1. 帰無仮説、対立仮説を立てる
帰無仮説 \( H_0 \): 仮説検定をするための「仮定」
旧型の機械で盛り付けられるご飯の重さの母分散 \( \sigma_1^2 \) と、新型の機械で盛り付けられるご飯の重さの母分散 \( \sigma_2^2 \) が等しい。つまり、\( \sigma_1^2 = \sigma_2^2 \)
対立仮説 \( H_1 \): 仮説検定を否定することで示したいもの
旧型の機械で盛り付けられるご飯の重さの母分散 \( \sigma_1^2 \) と、新型の機械で盛り付けられるご飯の重さの母分散 \( \sigma_2^2 \) が等しくない。つまり、\( \sigma_1^2 \not = \sigma_2^2 \)
Step2. 使用する分布、自由度の確認
使用する分布: F分布
自由度: \[\begin{align*}
(k_1, k_2) & = (n_1 - 1, n_2-1)
\\ & = (15,20)
\end{align*}\]
Step3. F統計量の計算
帰無仮説にて、\( \sigma_1^2 = \sigma_2^2 \) としているため、F統計量は以下のように計算できる。\[\begin{align*}
F & = \frac{ \frac{s_1^2}{\sigma_1^2} }{ \frac{s_2^2}{\sigma_2^2} }\\ & = \frac{ \frac{s_1^2}{\sigma_1^2} }{ \frac{s_2^2}{\sigma_1^2} }
\\ & = \frac{ s_1^2 }{ s_2^2 }
\\ & = \frac{50}{20}
\\ & = 2.5
\end{align*}\]
Step4. F分布表の読み取り:臨界値(採択/棄却の境界値)の確認
有意水準5%に対応する \( F \) の値(=臨界値)を求めていきます。
等分散性の仮説検定では、母分散の比率が小さすぎる場合、母分散の比率が大きすぎる場合の両方を考慮する必要があります。よって、両側検定を行います。
まず、\( F_1 \)、\( F_2 \) を次のようにおきましょう。
- \( F_1 \) … 母分散の比率が小さすぎる場合の臨界値(上側97.5%点、下側2.5%点)
→ F統計量が、この値よりも小さい場合は仮説が棄却される - \( F_2 \) … 母分散の比率が大きすぎる場合の臨界値(上側2.5%点)
→ F統計量が、この値よりも大きい場合は仮説が棄却される
ここで、事前に \( s_1^2 \geqq s_2^2 \) を仮定しているので、下側確率の臨界点 \( F_1 \) の導出は省略できます[3]どうしても求めたい場合は、\( \alpha = 0.025 \)、自由度は \( (k_1,k_2) = (20,15) \) のF値 2.756 を求めて、\[
F_1 = \frac{1}{2.756} < 1
\]としましょう。。(必ず \( F_1 < F \) となる。)
なので、\( F_2 \) をF分布から求めていきましょう。
[i] 母分散の比率が大きすぎる場合の臨界値 \( F_2 \)
\( F_2 \) は上側2.5%点なので、上側確率2.5%に相当する、\( \alpha = 0.025 \) の表を使います。
自由度は \( (k_1,k_2) = (15,20) \) に対応するところを表から読むと、2.573と読み取れます。
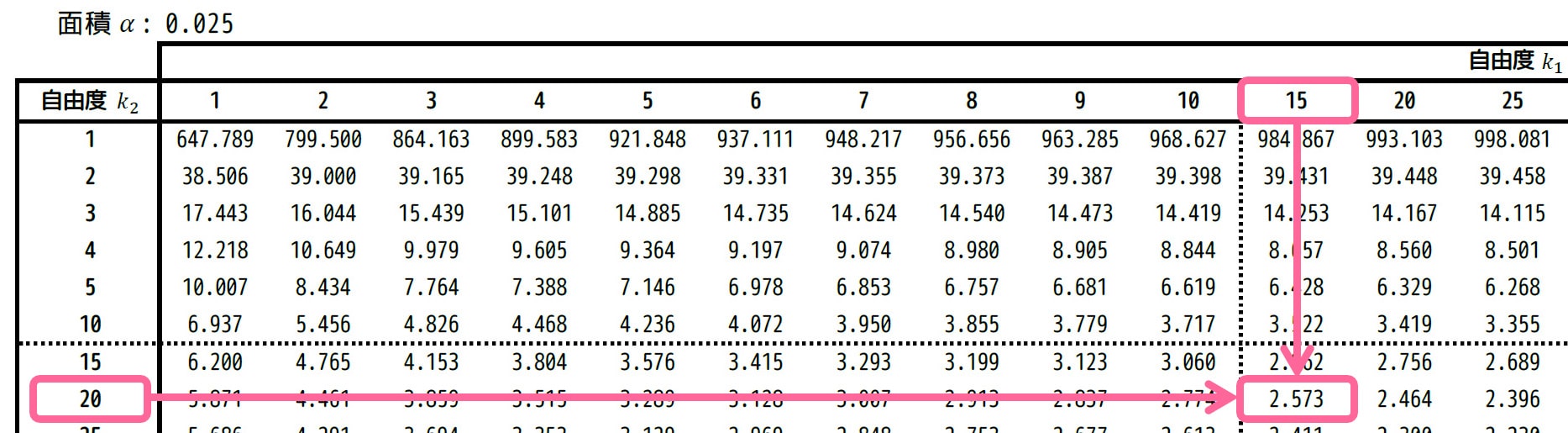
なので、\( F_2 = 2.573 \) ですね。
Step5. F分布表の読み取り:臨界値(採択/棄却の境界値)の確認
あとは、\( F \) と \( F_2 \) の大小関係を確認するだけでOK。(\( F \geqq 1 \) なので、\( F_1 < F \) は明らか)
- \( F \leqq F_2 \) のとき
→ 仮説は採択:母分散が等しくないとはいえない - \( F > F_2 \) のとき
→ 仮説は棄却:母分散が等しくないといえる
今回は、\( F = 2.500 \)、\( F_2 = 2.573 \) なので、\( F \leqq F_2 \) ですね。
よって仮説は採択され、「旧型の機械で盛り付けられるご飯の重さの母分散 \( \sigma_1^2 \) と、新型の機械で盛り付けられるご飯の重さの母分散 \( \sigma_2^2 \) が等しくないとは言えない」と結論付けられます。
注釈
| ↑1 | F分布表に上側確率が書いていると思いますが、全部 \( F>1 \) ですね。下側確率は、上側確率でのF値の逆数となるため、(少なくとも仮説検定で使う範囲の)下側確率におけるF値は \( F<1 \) です。 |
|---|---|
| ↑2 | 事前準備で \( s_1^2 \geqq s_2^2 \) としているため、\( F > 1 \) が成り立つ。また、\( F_1 < 1 \) なので、常に\( F_1 < F \) が成り立つ。 |
| ↑3 | どうしても求めたい場合は、\( \alpha = 0.025 \)、自由度は \( (k_1,k_2) = (20,15) \) のF値 2.756 を求めて、\[ F_1 = \frac{1}{2.756} < 1 \]としましょう。 |
関連広告・スポンサードリンク






![[基本情報・応用情報] うさぎでもわかる情報理論 第3羽 ハフマン符号化](https://www.momoyama-usagi.com/wp-content/uploads/joho3-2-3-150x150.jpg)