スポンサードリンク
回帰分析とは、ある要素を、他の要素を用いて関係を要約するための方法で、統計検定2級では頻出の分野です。
本記事では、回帰分析の中でも最も基本的な「単回帰分析」について勉強していきましょう。
目次
スポンサードリンク
1. 単回帰分析とは
単回帰分析は、ある要素(目的変数と呼びます)を1つの要素(説明変数と呼びます)を使って、目的変数との関係をモデル化する手法です。
実際にどんなものなのかは、見てもらった方がはやいと思うので、実際に見てみましょう。
ここに、20人分の「テストの点数」と「勉強時間」をまとめたデータがあります。
| 学生番号 | 勉強時間 (h) | 点数 (点) | 学生番号 | 勉強時間 (h) | 点数 (点) |
|---|---|---|---|---|---|
| 1 | 2.1 | 48 | 11 | 4.7 | 80 |
| 2 | 3.5 | 76 | 12 | 3.8 | 55 |
| 3 | 1.0 | 34 | 13 | 2.4 | 66 |
| 4 | 4.2 | 70 | 14 | 6.5 | 82 |
| 5 | 5.0 | 72 | 15 | 7.0 | 86 |
| 6 | 6.1 | 80 | 16 | 4.0 | 62 |
| 7 | 2.9 | 60 | 17 | 1.5 | 40 |
| 8 | 3.0 | 53 | 18 | 5.5 | 74 |
| 9 | 7.5 | 79 | 19 | 6.9 | 75 |
| 10 | 5.8 | 80 | 20 | 3.2 | 55 |
このデータをプロットしてみましょう。勉強時間を横軸(X軸)に、テストの点数を縦軸(Y軸)に取って、データポイントを散布図として描きます。
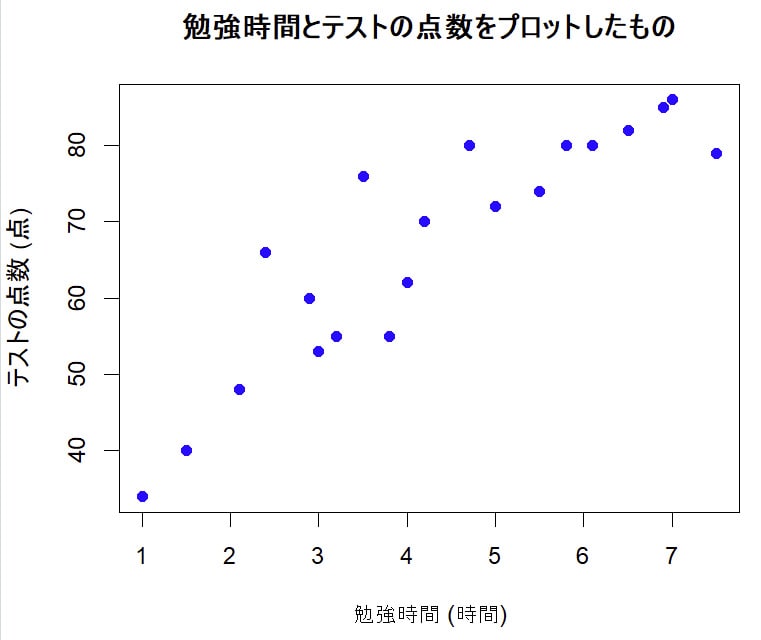
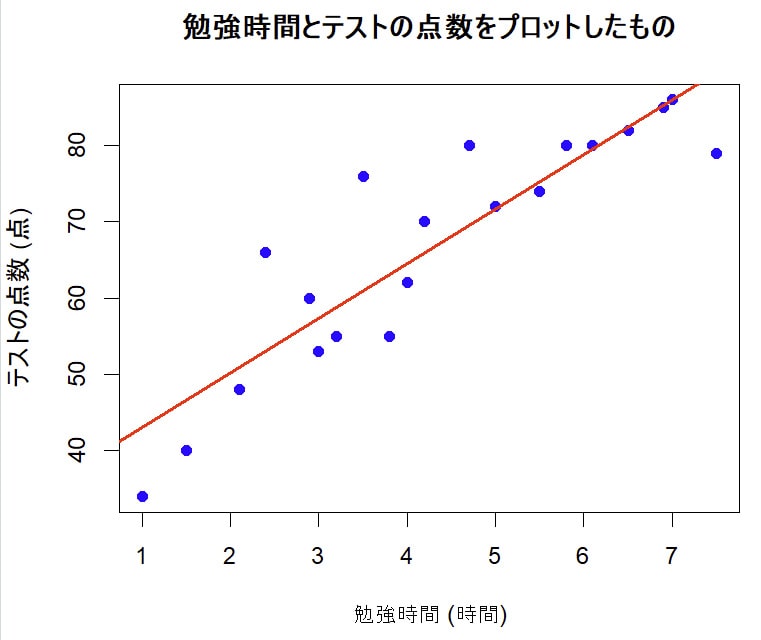
すると、勉強時間とテストの点数に対して、このような直線的な関係が成り立ちそうに見えますね。

このように、「説明変数と目的変数の関係を1本の直線的な関係で要約」するのが単回帰分析なのです。
スポンサードリンク
2. 単回帰分析の数式化(単回帰式)
単回帰分析では、2つの要素を、次のような直線的な関係で表します。
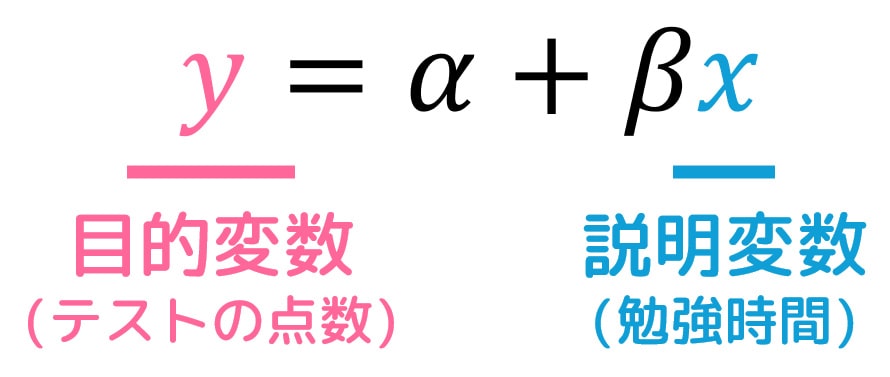
ここで、\( x \) は説明変数と呼ばれ、予測に使用されます。また、\( y \) は目的変数と呼ばれ、説明変数から予測される結果を表します。
また、モデルの式は、説明変数 \( x \) が変わるとどのように目的変数 \( y \) が変わるか示しています。
ここで、式の中の \( \alpha \) は切片(定数項)と呼ばれ、説明変数 \( x \) が0のときの目的変数 \( y \) の値を表します。また、\( \beta \) は回帰係数(傾き)と呼ばれ、説明変数 \( x \) が1変化すると、目的変数 \( y \) がどの程度変化するかを表します。
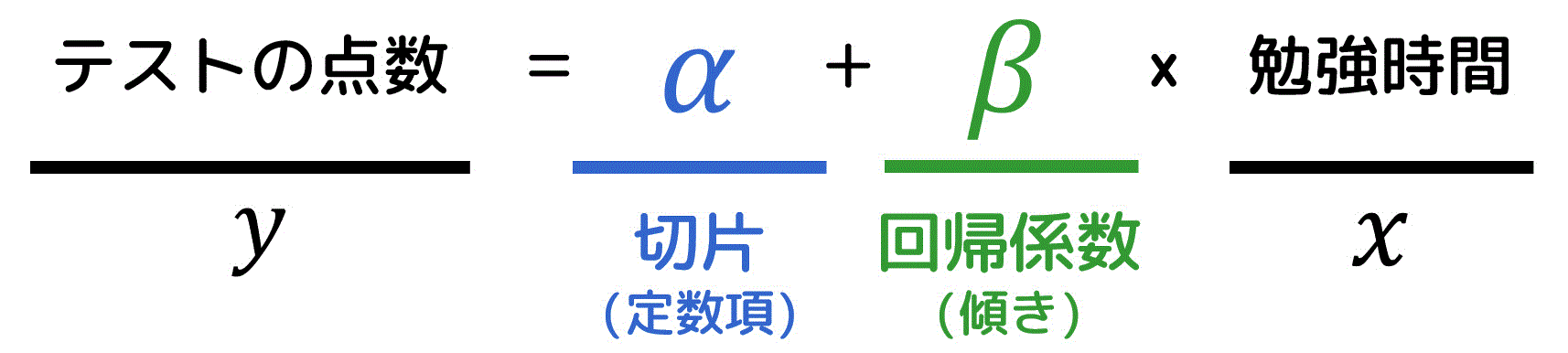
例えば、説明変数を「勉強時間」、目的変数を「テストの点数」とした場合、次のような関係を想定できます。
- 勉強時間が0のとき、テストの点数は \( \alpha \) となる。
- 1時間勉強時間を増やすと、テストの点数は \( \beta \) 増える。
★ 単回帰モデルと誤差
単回帰モデルで2つの要素の関係を完璧に表すことは極めて難しいです。
実際には、直線的な関係で示す際に、実際には観測された値 \( y \) とモデルによって予測された値 \( \alpha + \beta x \) に誤差が生じます。
そこで、直線的な関係に誤差 \( u \) を加えてつぎのように表した形単回帰分析のモデルとなります。\[
y = \alpha + \beta x + u
\]このモデルを単回帰式と呼ぶことにしましょう。
\[
y = \alpha + \beta x + u
\]
【変数の意味】
- \( \alpha \): 切片(定数項)。つまり \( x = 0 \) のときの \( y \) の値。
- \( \beta \): 傾き。説明変数 \( x \) が1増えたときに、\( y \) がどれくらい変化するか。
- \( u \): 誤差。実際の値 \( y \) と推定結果 \( \alpha + \beta x \) との差。
最小2乗法によるαとβの導出
実際に、単回帰式の \( \alpha \), \( \beta \) の値を推定する際には、各データごとの誤差 \( u \) を最小にすることを目指します。
具体的には、観測された値と予測された値との差(残差)の2乗和が最小となる用に、\( \alpha \), \( \beta \) を決定します。この方法を最小2乗法と呼びます。
最小2乗法を用いることで、\( \alpha \), \( \beta \) を次のように求めることが出来ます。
単回帰分析の基本的なモデル\[
y = \alpha + \beta x + u
\]は、最小2乗法を使うことで、次のように求めることが出来る。
\[
\alpha = \overline{y} - \beta \overline{x}
\]
\[\begin{align*}
\beta & = \frac{ \sum^{n}_{k=1} (x_k - \overline{x})(y_k - \overline{y}) }{ \sum^{n}_{k=1} (x_k - \overline{x})^2 }
\\ & = \frac{ s_{xy} }{ s_x^2 }
\end{align*}\]
【変数の意味】
- \( x_k \): 説明変数 \( x \) に関する \( k \) 番目のデータの値
- \( y_k \): 目的変数 \( y \) に関する \( k \) 番目のデータの値
- \( \overline{x} \): 説明変数 \( x \) の平均値
- \( \overline{y} \): 目的変数 \( y \) の平均値
- \( s_x^2 \): 説明変数 \( x \) の標本分散(不偏分散ではない)
- \( s_{xy} \): 説明変数 \( x \) と目的変数 \( y \) の共分散
スポンサードリンク
3. 単回帰分析の結果の見方
統計検定2級などの試験では、表形式やRの出力から単回帰分析の結果を読み取り、それに基づいて問題を解答することが求められます。
Call:
lm(formula = test_scores ~ study_hours, data = data)
Residuals:
Min 1Q Median 3Q Max
-10.5372 -3.9049 -0.3117 2.8181 15.0902
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 35.8608 3.9739 9.024 4.23e-08 ***
study_hours 7.1569 0.8428 8.492 1.04e-07 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 7.037 on 18 degrees of freedom
Multiple R-squared: 0.8003, Adjusted R-squared: 0.7892
F-statistic: 72.12 on 1 and 18 DF, p-value: 1.037e-07
※ e+n は \( 10^n \)、e-n は \(10^{-n} \) を表します。例えば、4.23e-08 は \( 4.23 \times 10^{-8} \) を表しています。
言い換えれば、単回帰分析の結果を正しく解釈できれば、試験で得点を確実に稼ぐことができます。
この章では、Rで出力される単回帰分析の結果の見方について紹介していきます。
Rで出力される内容
回帰分析での出力結果は、つぎの4つに分けることが出来ます。
(1) Call: 結果を出すために使ったコマンド
Call:
lm(formula = test_scores ~ study_hours, data = data)このセクションには、結果を生成するために使用したコマンドが表示されます。
試験においては、解析結果そのものには影響しないため、特に重要視される部分ではありません。
(2) Residuals: 残差の四分位数
Residuals:
Min 1Q Median 3Q Max
-10.5372 -3.9049 -0.3117 2.8181 15.0902 「残差」とは、各データの実際の観測値と回帰式によって予測された値との差のことを指します。
このセクションでは、残差の四分位数(最小値、第一四分位数、中央値、第三四分位数、最大値)が表示され、データのばらつき具合を把握するのに役立ちます。
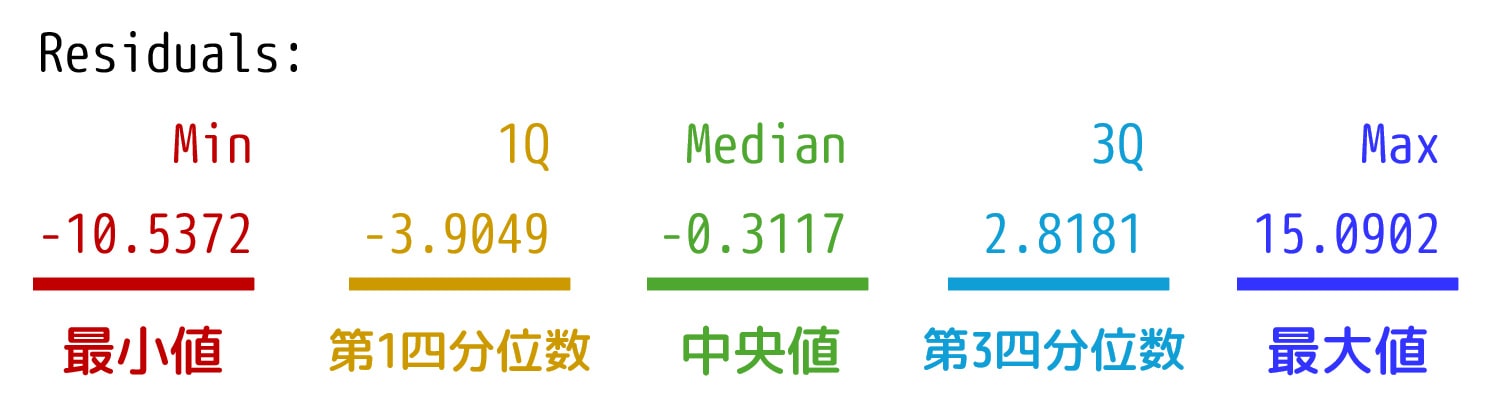
今回の出力結果からは、残差の四分位数を以下にように読み取ることができます。
| 最小値 | 第1四分位数 | 中央値 | 第3四分位数 | 最大値 |
|---|---|---|---|---|
| -10.5372 | -3.9049 | -0.3117 | 2.8181 | 15.0902 |
この結果(四分位数の分布)から、残差のばらつきがどれくらい広がっているかを確認できます。
例えば、今回のデータでは残差が-10.5372から15.0902までの範囲に分布していることが分かります。
補足:残差の平均値は必ず0です。これは、最小二乗法で回帰分析を行った場合、残差が正負で相殺されるためです。
(3) Coefficients: 回帰係数の推定結果
ここでは、切片 \( \alpha \) および回帰係数 \( \beta \) の推定結果が示されています。
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 35.8608 3.9739 9.024 4.23e-08 ***
study_hours 7.1569 0.8428 8.492 1.04e-07 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1[i] Estimate: 推定値
単回帰分析において求められた切片 \( \alpha \)、回帰係数 \( \beta \) の推定値です。
単回帰分析のモデル式\[
y = \alpha + \beta x
\]における \( \alpha \), \( \beta \) を具体的に数値として表しています。

今回の推定結果を見ると、\( \alpha = 35.8608 \)、\( \beta = 7.1569 \) ですね。これらの結果から、以下の2つのことが分かります。
- 勉強時間が0 ( \( x = 0 \) ) のとき、テストの点数は約35.86点となること
- 勉強時間が1単位(1時間)増えると、テストの点数が約7.16点上昇すること
[ii] Std. Error: 標準誤差
標準誤差は、回帰係数の推定値がどの程度の不確かさを持っているかを表す指標です。値が小さいほど、推定値の信頼性が高いことが分かります。
※ 標準誤差の導出式は統計検定2級レベルでは不要なので、覚えなくてOKです。
[iii] t value, Pr(>|t|): t値、p値
t値は、説明変数の回帰係数が0であるかどうかを検証するための統計量です[1]定数項に対するt値も出力されますが、定数項が0ではないかどうかを検証することは、実務的にはあまり意味がない場合が多いです。。
また、p値はt値に基づいて、その結果が偶然生じる確率を示しています。言い換えると、p値は「説明変数の回帰係数が0である確率」を表しています。
t値の出力結果を見ることで、「説明変数が目的変数に有意な影響を与えているか」を確認することができます。
具体的には、単回帰分析では以下の仮説検定が行われます。
- 帰無仮説 \( H_0 \): 仮説検定をするにあたる仮定
→ 説明変数の係数 \( \beta \) が0である。つまり \( \beta = 0 \)。 - 対立仮説 \( H_0 \): 帰無仮説を否定することで示したいもの。
→ 説明変数の係数 \( \beta \) が0ではない。つまり \( \beta \not = 0 \)。
この検定で帰無仮説が棄却されれば、説明変数は目的変数に有意な影響を与えていると考えられます。逆に棄却されなければ、その説明変数は目的変数に有意な影響を与えないため、モデルに含める必要がないと解釈できます。
【今回の例の場合】
勉強時間の回帰係数に対するt値は 8.492、p値は \( 1.04 \times 10^{-7} \) とp値が一般的な有意水準の5%よりも非常に小さい値を示しています。
そのため、帰無仮説「勉強時間の係数 \( \beta \) が0である」という仮説は棄却され、勉強時間はテストの点数に有意に影響を与えていると結論づけられます。
補足:p値の右側に記載の記号は、p値の大小を表しています。

★ t値の自由度
t値の自由度 \( k_t \) は、サンプルサイズ \( n \) からモデルのパラメータ数(切片 \( \alpha \) と回帰係数 \( \beta \))を引いたもので決まります[2]サンプルデータの中で自由に変動できる観測点の数とも言えますね。。
具体的には、以下の式で計算されます。\[
k_t = n - 2
\]
今回のデータの場合、20人のデータから回帰分析を行っているため、自由度 \( k_t \) は次のように計算されます。\[\begin{align*}
k_t & = 20 - 2
\\ & = 18
\end{align*}\]
★ t値の計算方法
t値はつぎの式で計算できます。
※ 帰無仮説で回帰係数を0と仮定しているため、分子に "-0" を記載しています[3]例えば、回帰係数が2であると帰無仮説で仮定した場合、分子の "-0" の部分は "-2" となります。。
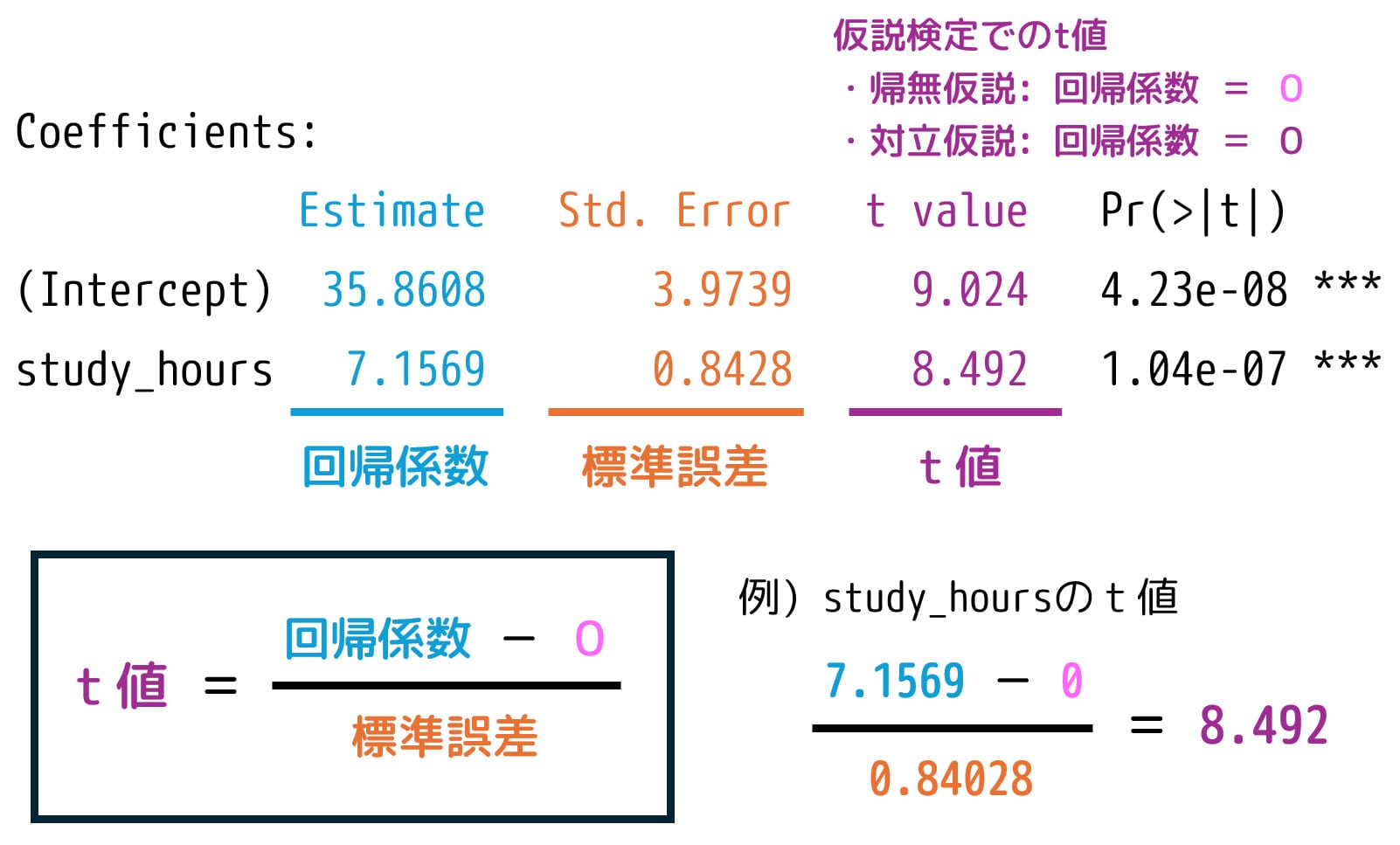
※ 式内の "回帰係数" は、ツールで計算した結果が入ります。
実際に、勉強時間 (study_hours) に対するt値を計算すると、Rで出力されたt値と一致することが分かりますね。
※ t値の自由度、および推定値、標準誤差、t値の関係は統計検定2級で頻出です。頭に入れておきましょう。
(4) 回帰モデルそのものの分析情報
この欄では、単回帰分析全体の結果に対する統計的な分析結果が示されています。
Residual standard error: 7.037 on 18 degrees of freedom
Multiple R-squared: 0.8003, Adjusted R-squared: 0.7892
F-statistic: 72.12 on 1 and 18 DF, p-value: 1.037e-07具体的には、「分析全体のパフォーマンスを評価するための指標」や「単回帰モデルの当てはまりの良さが出力」されています。これらの結果は、回帰モデルそのものがデータをどの程度説明しているか、またモデルが有意であるかを示しています。
★ 分散分析と回帰分析
目的変数の各値 \( y_k \) は、回帰モデルによって予測される値 \( \alpha + \beta x_k \) と回帰モデルでは説明できないズレ \( u_k \) の和で表すことが出来ます。
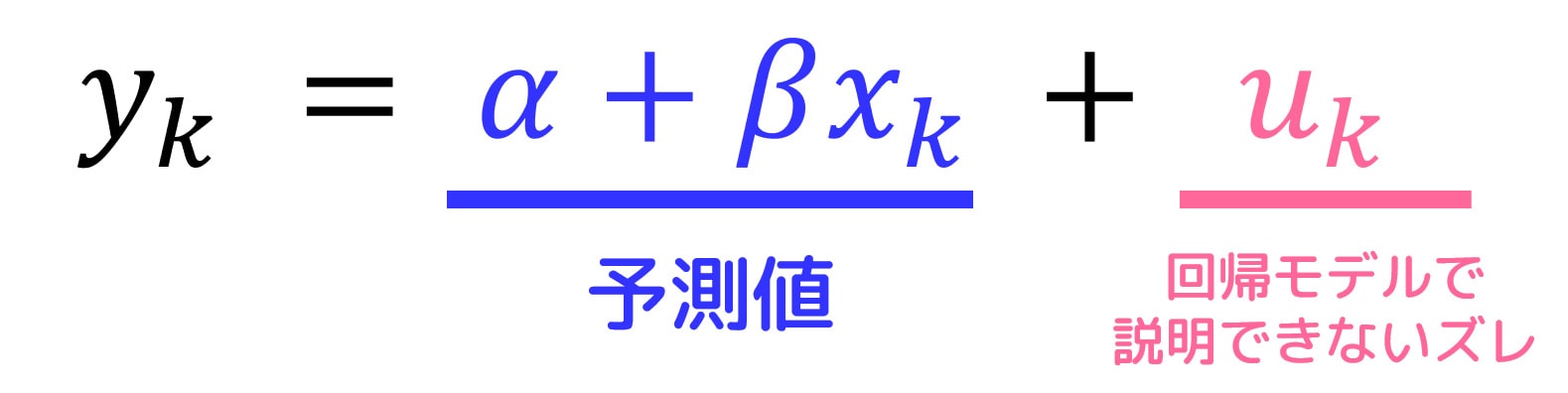
言い換えると、各観測値 \( y_k \) を、「予測値 \( \alpha + \beta x_k \)」と「モデルが説明できない誤差(残差) \( u_k \)」の2つに分解することができる、ということです。
ここで、回帰モデルによって予測される値を \( \hat{y}_k \) としましょう。
すると、回帰モデルでは説明できないズレ \( u_k \) は、目的変数の各値 \( y_k \) から回帰モデルによって予測される値 \( \hat{y}_k \) を引いたものとして表されます。
したがって、式を次のように書き換えることが出来ます。

つぎに、目的変数の各データ値 \( y_k \) というのは、平均 \( \overline{y} \) からのばらついていると考えることが出来ます。
このばらつきを明確にするため、先ほどの式をつぎのように書き換えてみましょう。

この式は、観測 \( y_k \) を、「全体の平均値 \( \overline{y} \)」と「回帰モデルで説明できるズレ(説明変動)」、そして「回帰モデルで説明できないズレ(残差変動)」の3つに分解できることを表しています。
さらに、全体の平均 \( \overline{y} \) を基準に考えるために、両辺から \( \overline{y} \) を引きましょう。

この式は、「目的変数の観測値 \( y_k \) と平均値 \( \overline{y} \) との差(全変動)」が、「回帰による変動(説明変動)」と「回帰モデルで説明できない変動(残差変動)」に分解できることを示しています。
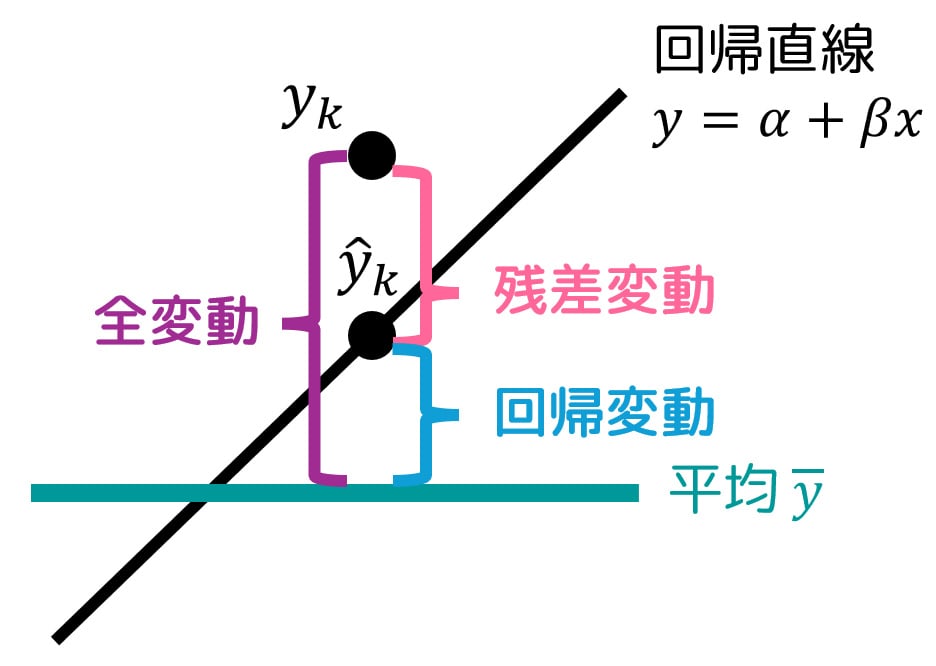
単回帰分析全体の結果を評価する際には、「回帰変動」と「残差変動」の度合いを使ってさまざまな指標を計算します。
ここで、変動を2つに分解して分析する方法と聞いて、何か思い浮かぶ言葉はありませんか?
そう、一元配置分散分析です。
一元配置分散分析を使うことで、各データの「全変動」を、「回帰による変動(説明変動)」と「残差による変動」の2つに分解し、それぞれが全体の変動にどれほど寄与しているかを分析できるのです。
※ 一元配置分散分析がいまいちよくわからない or 一元配置分散分析ってなんだっけ、となった方は以下の記事にて復習しましょう。
★ 回帰分析と一元配置分散分析
実際に、回帰分析における一元配置分散分析のステップを確認しましょう。
ここではデータ全体の変動を「回帰変動」と「残差変動」に分けて評価します。
| 要因 | 平方和 | 自由度 | 平方平均 | \( F \) 値 |
|---|---|---|---|---|
| 回帰変動 | (a) \( S_A \) | \( \phi_A = 1 \) | \( V_A = \frac{ S_A }{ \phi_A } \) | \( \frac{ V_A }{ V_E } \) |
| 残差変動 | (b) \( S_E \) | \( \phi_E = n - 2 \) | \( V_E = \frac{ S_E }{ \phi_E } \) | − |
| 全変動 | (c) \( S_T \) | \( \phi_T = n - 1 \) | − | − |
[i] 平方和
ここで、回帰変動、残差変動、全変動の平方和は次のように計算できます。
(a) 回帰変動:予測値 \( \hat{y}_k \) と平均値 \( \overline{y} \) の差の2乗の総和
(回帰モデルが説明できる部分の変動)
\[\begin{align*}
S_A & = \sum^{n}_{k = 1} \left( \hat{y}_k - \overline{y} \right)^2
\end{align*}\]
(b) 残差変動:観測値 \( y_k \) と予測値 \( \hat{y}_k \) の差の2乗の総和
(回帰モデルが説明できない部分の変動)
\[\begin{align*}
S_E & = \sum^{n}_{k = 1} \left( y_k - \hat{y}_k \right)^2
\end{align*}\]
(c) 全体変動:観測値 \( y_k \) と平均 \( \overline{y} \) の差の2乗の総和
(全データの変動)
\[\begin{align*}
S_T & = \sum^{n}_{k = 1} \left( y_k - \hat{y}_k \right)^2
\end{align*}\]
注意: 全体変動 \( S_T \) は、回帰変動 \( S_A \) と残差変動 \( S_E \) の和に等しくなります。\[
S_T = S_A + S_E
\]
[ii] 自由度
回帰変動の自由度:説明変数の数です。単回帰分析では、説明変数が1つなので常に1です[4]一元配置分散分析では、自由度を「グループ数 - 1」としますが、回帰分析において自由度を「説明変数 - 1 = … Continue reading。\[
\phi_A = 1
\]
残差変動の自由度:データ数からモデルのパラメータ数を引いたもの。単回帰分析では、モデルのパラメータ数は2つ(切片 \( \alpha \) と回帰係数 \( \beta \))なので、常に \( n-2 \) です[5]回帰分析では、切片 \( \alpha \) と回帰係数 \( \beta \) … Continue reading。\[
\phi_E = n - 2
\]
全体変動の自由度:データ数から1を引いたもの。\[
\phi_T = n - 1
\]
注意: 全体変動の自由度 \( k_T \) は、回帰変動の自由度 \( k_A \) と残差変動の自由度 \( k_E \) の和に等しくなります。\[
\phi_T = \phi_A + \phi_E
\]
[iii] 平方平均
平方和を対応する自由度で割ることで、平方平均が求められます。
回帰変動の平方平均\[
V_A = \frac{ S_A }{ \phi_A }
\]
残差変動の平方平均\[
V_E = \frac{ S_E }{ \phi_E }
\]
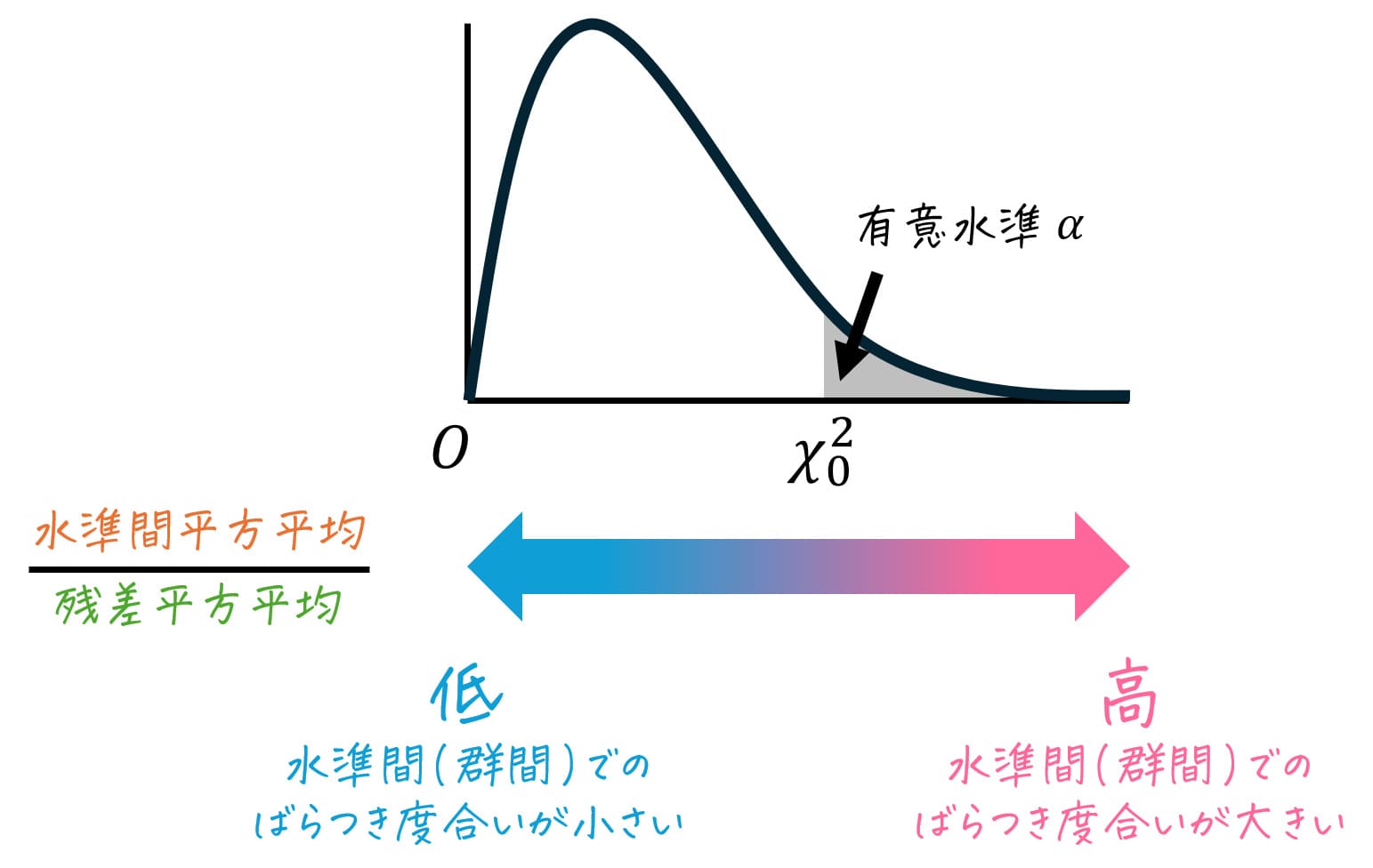
[iv] F値
F値は、回帰変動の平方平均 \( V_A \) を残差変動の平方平均 \( V_E \) で割ったもので計算されます。\[
F = \frac{ V_A }{ V_E }
\]
F値が大きければ、回帰モデルが全体的な変動をうまく説明していることを意味します。
★ それぞれの出力の意味
ここでは、Rの出力で得られた結果が一元配置分散分析のどの結果に対応するかを見ていきます。
Residual standard error: 7.037 on 18 degrees of freedom
Multiple R-squared: 0.8003, Adjusted R-squared: 0.7892
F-statistic: 72.12 on 1 and 18 DF, p-value: 1.037e-07表.回帰変動、残差変動に対する一元配置分散分析の結果
| 要因 | 平方和 | 自由度 | 平方平均 | \( F \) 値 |
|---|---|---|---|---|
| 回帰変動 | \( S_A \) | \( \phi_A = 1 \) | \( V_A = \frac{ S_A }{ \phi_A } \) | \( F = \frac{ V_A }{ V_E } \) |
| 残差変動 | \( S_E \) | \( \phi_E = n- 2 \) | \( V_E = \frac{ S_E }{ \phi_E } \) | − |
| 全体 | \( S_T \) | \( \phi_T = n - 1 \) | − | − |
[i] Residual standard error:残差の標準誤差 (と自由度)
残差変動の平方平均 \( V_E \) を表しており、回帰モデルがデータをどの程度正確に説明できていないかを示します。また、自由度 \( \phi_E \) は残差変動に対する自由度です。

今回の結果は、残差平方平均 \( V_E \) が7.037、残差の自由度 \( \phi_E \) が18であることを意味しています。
[ii] Multiple R-squared: 決定係数
決定係数 \( R^2 \) は、モデルがデータの変動をどれだけ説明できているか(=回帰モデルがデータに上手く当てはまっているか)を0から1の範囲で表します。(1に近いほど、説明力が高いと言えます。)モデルの当てはまりの良さが決定係数だと思っていただけたらOKです。
具体的に、決定係数 \( R^2 \) は全体平方和に対する回帰変動の割合で計算されます。
\[\begin{align*}
R^2 & = \frac{S_A}{S_T}
\\ & = \frac{S_T - S_E}{S_T}
\\ & = 1 - \frac{S_E}{S_T} \ \ ( \because S_A + S_E = S_T )
\end{align*}\]※ \( S_A \) は回帰平方和、\( S_E \) は残差平方和、\( S_T \) は全体平方和を表しています。
決定係数は、単回帰モデル同士でモデルの当てはまり具合を比べる際に利用されます。

例えば、今回のデータの場合、決定係数 \( R^2 \) は 0.8003 です。
つまり、このモデルはデータの80.03%の変動を説明できていると言えます。
★ 相関係数と決定係数の関係
相関係数は、説明変数と目的変数の間の直線的の強さを示す指標です。
実は、相関係数の2乗が決定係数となります。
このため、決定係数は説明変数の目的変数の直線的関係の強さを説明しているとも言えます。
[iii] Adjusted R-squared: 自由度調整済み決定係数
※ この項目は重回帰分析で主に使用されます。
説明変数を増やせば増やすほど、回帰モデルで説明できる変動の割合が増えるため、決定係数 \( R^2 \) は、説明変数を増やしていくと大きくなります。
しかし、すべての説明変数が実際に目的変数に影響を与えるわけではないため、意味のない説明変数をやみくもに追加するのは良くありません。
そこで、やみくもに無関係な説明変数を追加してもモデルの評価が不適切に上昇しないように、自由度調整済み決定係数 \(R^2_f \) が登場しました。
\[\begin{align*}
R^2_f & = 1 - \frac{ \frac{S_E}{n-k-1}}{ \frac{S_T}{n-1} }
\\ & = 1 - \frac{S_E}{S_T} \cdot \frac{n-1}{n-k-1}
\\ & = 1 - \frac{n-1}{n-k-1}\left( 1 - R^2 \right)
\end{align*}\]
※ \( n \) は回帰分析に使用したデータ数です。今回の例の場合、\( n = 20 \) です。
※ \( k \) は説明変数の数を表します。単回帰分析の場合は必ず \( k = 1 \) です。
自由度調整済み決定係数を使うことで、単に説明変数を増やすことでモデルが良くなるように見える現象を防ぐことが出来ます[6]単回帰モデル同士を比較する場合は、説明変数が1つしかないため、自由度調整済み決定係数は使わないことが一般的です。。

今回の出力で示された自由度調整済み決定係数 \( R^2_f \) は 0.7892 ですね。
[iv] F値
F値は、回帰分析において説明変数が目的変数に影響を与えているかどうかを有意であるかどうかを評価するための統計量です。このモデルが信頼できるものかを表していると思っていただけたらOKです。
具体的には、帰無仮説 \( H_0 \) を「説明変数の回帰係数が全て0である」と仮定し、この仮説が成立するかどうかをF値で確認します。
【回帰分析でのF検定】
- 帰無仮説 \( H_0 \): 説明変数の係数が全て0。つまり \( \beta = 0 \)。
(回帰モデルは無意味) - 対立仮説 \( H_1 \): 説明変数の係数に0ではないものがある。つまり \( \beta \not = 0 \)。
(回帰モデルは有意)
この検定の結果が棄却されれば、このモデルが信頼できるものと言えます。一方棄却されなかった場合、このモデル自体が意味ないものだったとも言えてしまいます。
今回のRの出力結果では、次の3つの情報が表示されています。
- F値: 72.12
- F検定で使用する自由度の組 (1,18)
※ 説明変数の自由度が1、残差の自由度が18 - 対応するp値: \( 1.037 \times 10^{-7} \)

この結果から、F値が非常に大きく、p値も極めて小さい(< 0.01)ため、帰無仮説は棄却され、説明変数(勉強時間)と目的変数(テストの点数)に関するこのモデルは信頼できるものと言えます。
★ 単回帰モデルにおけるF値とt値の関係
単回帰分析では、F値と t値 の関係は次の通りです。
(1) 単回帰分析において F値は説明変数 \( \beta \) に対するt値の2乗となります。
→ 実際に今回の例を見ると、説明変数 \( \beta \) に対するt値は 8.492 です。このt値を2乗すると、\( 8.492^2 = 72.12 \) となり、F値と一致しています。
(2) F検定のp値はt検定のp値と等しくなります。
→ 実際に、F検定のp値は \( 1.04 \times 10^{-7} \) と等しくなっています。
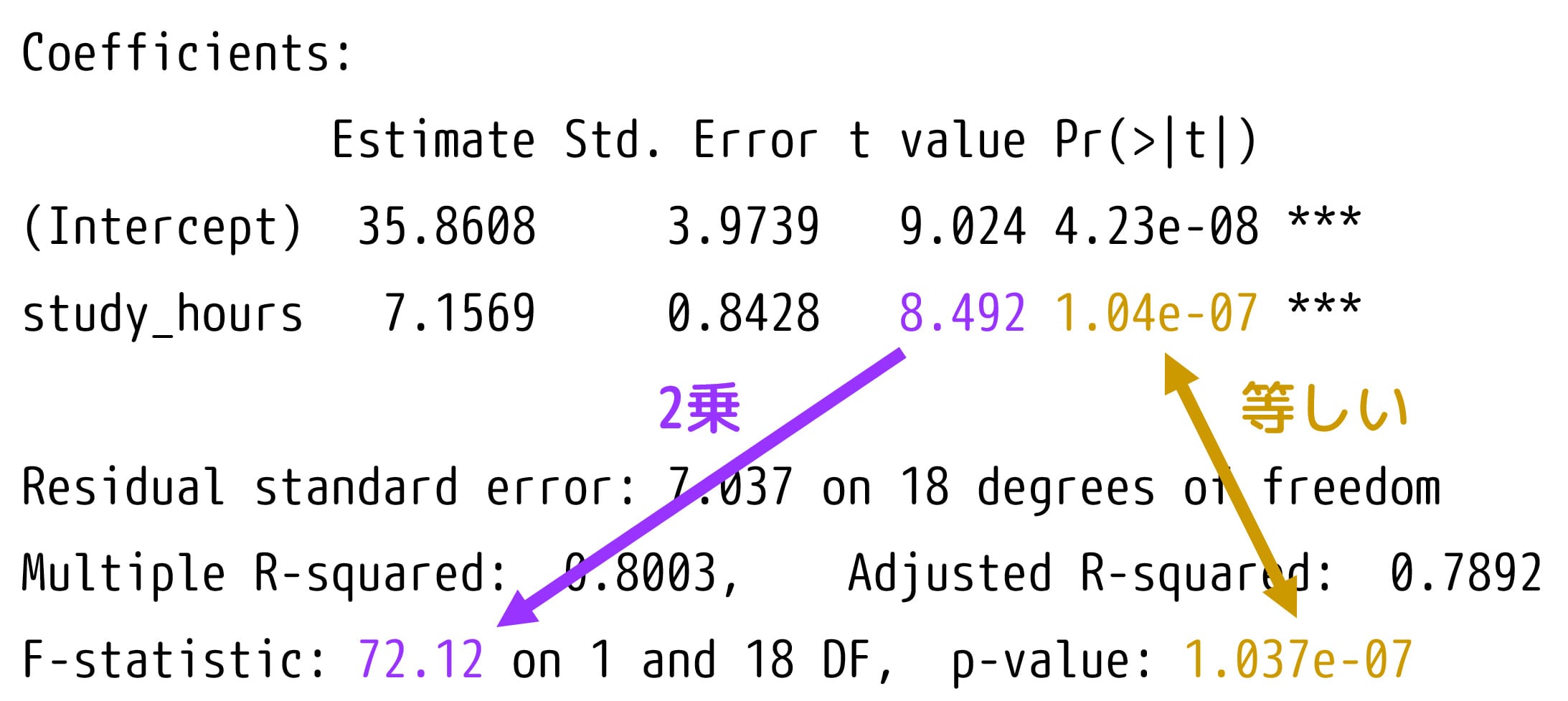
このことから、単回帰分析におけるF検定とt検定の結果は、同じ情報を提供していると言えます。したがって、単回帰分析では、F検定はt検定の結果と同等であるため、あまり独立した役割を果たさないことが多いです。
4. 練習問題にチャレンジ!
では、最後に練習問題にチャレンジしてみましょう!
桃山さんは、ある大学の文化祭の模擬店の売り上げデータを用いて、次の単回帰モデルを推定した。
\[
\mathrm{売上} \ = \alpha + \beta \times \mathrm{部員数}
\]
ここで、「売上」は1日当たりの模擬店の売り上げ(1単位100円)、「部員数」はサークルの部員数を表す。
統計ソフトウェアRを用いて、上記の単回帰モデルを推定したところ、つぎの出力結果を得た。この単回帰モデルをモデル桃山とする。
Call:
lm(formula = sales ~ member, data = data)
Residuals:
Min 1Q Median 3Q Max
-307.17 -113.49 -29.82 112.01 236.44
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 307.135 132.697 [ a ] 0.0363 *
member 10.465 [ b ] 2.293 0.0378 *
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 158.5 on 14 degrees of freedom
Multiple R-squared: 0.2731, Adjusted R-squared: 0.2211
F-statistic:[ c ] on [ d ] and [ e ] DF, p-value: 0.03783ここで、member は部員数を表す変数である。また、出力結果の一部を加工している。つぎの(1)~(6)の問いに答えなさい。
※ 必要であれば、こちらから片側t分布表をダウンロードできます。統計検定受験の方は、こちらの表をお使いください。
※ 必要であれば、こちらから両側t分布表をダウンロードできます。
(1) 出力結果の [ a ] ~ [ e ] に当てはまる数を答えなさい。ただし、[ a ] ~ [ c ] は小数第4位を四捨五入して小数第3位まで、[ d ]、[ e ] は整数で答えること。
(2) 分析に用いたサークル数を答えなさい。
(3) 部員数が50人のサークルの場合、模擬店の売上高は何円と予測されるか。10円単位を四捨五入し、100円単位で答えなさい。
(4) \( \beta \) の値が約20であるという主張が上田さんからあった。この説を検証するため、帰無仮説 \( \beta = 20 \)、対立仮説 \( \beta \not = 20 \) の仮説検定を実施することにした。この仮説検定が棄却される有意水準として、最も小さいものを1~5の中から1つ選びなさい。
- 1%
- 5%
- 10%
- 20%
(5) この単回帰モデルの結果から読み取れることとして、正しいものをつぎの1~5の選択肢から1つ選びなさい。
- 残差の中央値は、平均値よりも大きい。
- 部員数のt値に対応するp値が0.05未満のため、この単回帰モデルはデータの変動をうまく説明できていると言える。
- この回帰分析のF値に対応するp値が0.05未満のため、この単回帰モデルはデータの変動をうまく説明できていると言える。
- 決定係数の値が0.2731なので、この回帰モデルは約27%の確率で売り上げを予測できると言える。
- 部員数が増えると、売上も上がる傾向がある。
(6) 上田さんは、ある大学の文化祭の模擬店の売り上げデータを、桃山さんとは異なる単回帰モデルで推定した。この単回帰モデルをモデル上田とする。
\[
\mathrm{売上} \ = \alpha + \beta \times \mathrm{部員数}
\]
上田さんの方法で、上記の単回帰モデルを推定したところ、つぎの出力結果を得た。
Call:
lm(formula = sales ~ promtime, data = df)
Residuals:
Min 1Q Median 3Q Max
-132.15 -97.53 -13.68 82.99 171.74
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 243.85 59.56 4.094 0.00109 **
promtime 80.96 13.50 5.999 3.26e-05 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 108.3 on 14 degrees of freedom
Multiple R-squared: 0.7199, Adjusted R-squared: 0.6999
F-statistic: 35.98 on 1 and 14 DF, p-value: 3.262e-05ここで、モデル桃山とモデル上田を比較した場合、どちらがより良いモデルと言えるか。結論とその理由について述べた文章のうち、最も適切なものを1つ選びなさい。
- モデル上田の説明変数 promtime の回帰係数が80.96、モデル桃山の説明変数 member の回帰係数 10.465 なので、説明変数の回帰係数が大きいモデル上田を採用すべきである。
- モデル上田の説明変数 promtime の標準誤差が59.56、モデル桃山の説明変数 member の標準誤差が 132.697 なので、説明変数の標準誤差が小さいモデル上田を採用すべきである。
- モデル上田の説明変数 promtime のp値が \( 3.26 \times 10^{-5} \) 、モデル桃山の説明変数 member のp値が 0.0363 なので、説明変数のp値が小さいモデル上田を採用すべきである。
- モデル上田の決定係数 \( R^2 \) が 0.7199、モデル桃山の決定係数 \( R^2 \) が 0.2731 なので、決定係数がより大きいモデル上田を採用すべきである。
- モデル上田のモデルのF検定のp値が \( 3.26 \times 10^{-5} \) 、モデル桃山の説明変数 member のp値が 0.0363 なので、説明変数のp値がより小さいモデル上田がを採用すべきである。
5. 練習問題の答え
Call:
lm(formula = sales ~ member, data = data)
Residuals:
Min 1Q Median 3Q Max
-307.17 -113.49 -29.82 112.01 236.44
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 307.135 132.697 [ a ] 0.0363 *
member 10.465 [ b ] 2.293 0.0378 *
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 158.5 on 14 degrees of freedom
Multiple R-squared: 0.2731, Adjusted R-squared: 0.2211
F-statistic:[ c ] on [ d ] and [ e ] DF, p-value: 0.03783(1)
[a] 解答: 2.315t値の計算公式を使います。
\[\begin{align*}
t & = \frac{ \mathrm{回帰係数} \ - 0}{ \mathrm{標準誤差} }
\\ & = \frac{307.135}{132.697}
\\ & \fallingdotseq 2.3146
\\ & = 2.315
\end{align*}\]したがって、[a]は 2.315 となります。
\[\begin{align*}
t & = \frac{ \mathrm{回帰係数} \ - 0}{ \mathrm{標準誤差} }
\end{align*}\]
したがって、次の式が成り立つような標準誤差を求めればOKです。\[\begin{align*}
2.293 & = \frac{ 10.465 - 0}{ \mathrm{標準誤差} }
\end{align*}\]
この式を変形することで、[b]はつぎのように求められます。
\[\begin{align*}
\mathrm{標準誤差} & = \frac{ 10.465 } { 2.293 }
\\ & = 4.564
\end{align*}\]
つぎの出力結果の [ c ] は回帰分析でのF値、[ d ] は回帰変動の自由度、[ e ] は残差変動の自由度を表しています。
F-statistic:[ c ] on [ d ] and [ e ] DF, p-value: 0.03783解答: [ c ] 5.258
単回帰分析において、F値は回帰係数のt値の2乗に等しいです。
ここで、説明変数 (member) のt値は、member 行の t value 列より、2.293 と読み取れます。
Estimate Std. Error t value Pr(>|t|)
(Intercept) 307.135 132.697 [ a ] 0.0363 *
member 10.465 [ b ] 2.293 0.0378 *
そのため、F値は次のように求められます。\[\begin{align*}
F & = 2.293^2
\\ & = 5.258
\end{align*}\]
したがって、[ c ]には5.258が入ります。
解答: [d] 1
回帰変動の自由度は、説明変数の数に等しいです。
単回帰分析では説明変数は常に1つなので、回帰変動の自由度は1となります。
よって、回帰変動の自由度は1となり、[d]には1が入ります。
ここで、回帰係数のt値は、member 行の t value 列より、2.293 と読み取れます。
解答: [e] 1
残差変動の自由度は、出力結果の on "14" degrees of freedom から読み取れます。

よって、[e] には14が入ります。
(2)
解答: 16
標本サイズ(サークル数)を求める際は、残差変動の自由度の出力に着目します。

出力結果の on "14" degrees of freedom から、残差変動の自由度が 14 と読み取れます。
ここで残差変動の自由度は、標本サイズからモデルのパラメータ数を引くことで求められます。
単回帰分析の場合、モデルのパラメータは切片 \( \alpha \) と回帰係数 \( \beta \) の2つなので、標本サイズ \( n \) と残差の自由度 \( \phi_E \) には次の関係式が成立します。\[
\phi_E = n - 2
\]
出力結果より、残差の自由度が \( \phi_E = 14 \) と読み取れるため、標本サイズ \( n \) はつぎのように計算できます、\[\begin{align*}
n & = \phi_E + 2
\\ & = 14 + 2
\\ & = 16
\end{align*}\]よって、答えは16となります。
(3)
売上の予測値は、単回帰式に部員数を代入して計算できます。
ここで、\( \alpha \), \( \beta \) の値は、出力結果の Estimate から読み取ることができます。

今回の問題の場合、\( \alpha = 307.135 \), \( \beta = 10.465 \) ですね。
よって、以下の方程式に「部員数 = 50」を代入すればOKですね。
\[
\mathrm{売上} \ = 307.135 + 10.465 \times \mathrm{部員数}
\]
実際に代入すると、売上を次のように求めることができます。
\[\begin{align*}
\mathrm{売上} \ & = 307.135 + 10.465 \times 50
\\ & = 830.385
\end{align*}\]
よって、売上高は 830.385 (×100円単位) とわかるので、答えは83,000円となります。
回帰モデルにおける売上の予測値は、回帰方程式に部員数を代入して計算できます。今回の回帰モデルは以下の通りです。
(4)
帰無仮説「回帰係数が20である」という仮定をもとに、t値をつぎの式で計算します。
\[
t = \frac{ \textcolor{deepskyblue}{\mathrm{回帰係数(出力結果)}} -\textcolor{magenta}{20} }{ \textcolor{orange}{\mathrm{標準誤差}} }
\]
ここで、回帰係数(出力結果)、標準誤差 は出力結果の member 行から読み取ります。

よって、t値はつぎのように計算できます。
\[\begin{align*}
t & = \frac{ \textcolor{deepskyblue}{\mathrm{回帰係数(出力結果)}} -\textcolor{magenta}{20} }{ \textcolor{orange}{\mathrm{標準誤差}} }
\\ & = \frac{ \textcolor{deepskyblue}{10.465} -\textcolor{magenta}{20} }{ \textcolor{orange}{4.564} }
\\ & = \frac{- 9.535}{4.564}
\\ & = -2.089
\end{align*}\]
ここで、t値の自由度は、標本サイズから回帰モデルのパラメータ数を引いて求めます。標本サイズは16、単回帰モデルのパラメータは切片 \( \alpha \) と回帰係数 \( \beta \) の2つなので、つぎのようにt値の自由度 \( k_t \) を計算できます。\[\begin{align*}
k_t & = 16 - 2
\\ & = 14
\end{align*}\]
つぎ、t分布表の自由度14に対応するt分布の臨界値 \( t_0 \) をt分布表から確認し、\( -t_0 \leqq t \leqq t_0 \) の範囲にt値 \( t \) が含まれない場合は、仮説を棄却します。
選択肢は1%, 5%, 10%, 20%の4つなので、この4つの有意水準に対応する値をt分布表から読み取ります。
| 有意水準 | 臨界値となる t値 \( t_0 \) | 結論 |
|---|---|---|
| 1% | 2.977 | 棄却されない。 \( - 2.977 \leqq t \leqq 2.977 \) のため。 |
| 5% | 2.145 | 棄却されない。 \( - 2.145 \leqq t \leqq 2.145 \) のため。 |
| 10% | 1.761 | 棄却される。 \( - 1.761 > t \) のため。 |
| 20% | 1.345 | 10%で棄却されるため 確認不要。 |
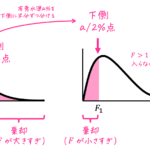
注意: この検定は両側検定です。そのため、片側t分布表から臨界値 \( t_0 \) を調べる場合は、有意水準を半分とした値が \( \alpha \) となる点に注意が必要です。例えば、有意水準5%となるような \( t_0 \) を読み取るときは、下の図のように \( \alpha = 0.100 \) 列に対応するt値を読み取ります。
したがって、有意水準5%では棄却されませんが、有意水準10%で棄却されることが確認できるため、答えは「3. 10%」です。
(5)
選択肢を1つずつ見ていきましょう。
1. 残差の中央値は平均値よりも大きい
誤りです。今回の残差の中央値は、Residuals のMedian から -29.82 と読み取れます。

ここで、残差の平均値は常に0なので、残差の中央値 (-29.82) は平均値 (0) より小さくなります。
2. 部員数のt値に対応するp値が0.05未満のため、この単回帰モデルはデータの変動をうまく説明できていると言える。
誤りです。t値に対応するp値は、回帰係数が0ではない確率を示すもの(=説明変数が目的変数に有意な影響を与えているかどうか)であり、モデルがデータの変動をどの程度うまく説明しているかを直接示すものではありません。
3. この回帰分析のF値に対応するp値が0.05未満のため、この単回帰モデルはデータの変動をうまく説明できていると言える。
誤りです。F値に対応するp値も、回帰モデル全体が有意であるかどうかを示すものであり、モデルがデータの変動をうまく説明しているかを示すものではありません。
4. 決定係数の値が0.2731なので、この回帰モデルは約27%の確率で売り上げを予測できると言える。
誤りです。決定係数の値は、モデルの当てはまり度合い(=データの変動をどれくらいうまく説明しているか)を表しています。予測の正確性を表しているわけではありません。
5. 部員数が増えると、売上も上がる傾向がある。
正しいです。出力結果を見ると、回帰係数 \( beta \) は 10.465 で、正の値を示しています。

そのため、部員数が増えると売上も上がる傾向があると言えます。
(6)
単回帰モデル同士でモデルの良し悪しを比べるときは、決定係数に着目します。
具体的には、決定係数の大小を確認し、より大きい決定係数となるモデルを良いモデルとして選択します。
よって、「4. モデル上田の決定係数 \( R^2 \) が 0.7199、モデル桃山の決定係数 \( R^2 \) が 0.2731 なので、決定係数がより大きいモデル上田が優れていると言える。」が答えとなります。
外挿に注意!
練習問題の(3)にて、算出された単回帰式に、説明変数(勉強時間)を代入して目的変数(テストの点数)を予測することをしました。
このとき、説明変数の観測範囲を超えた範囲で目的変数を予測することを「外挿」と呼びます。一方、説明変数の観測範囲内で目的変数を予測することは内挿と呼びます。
外挿を行う際には、予測の精度が低下する可能性があるため注意が必要です。単回帰式は与えられたデータの範囲内で計算されており、範囲外のデータでも同じ傾向が続くとは限らないからです。
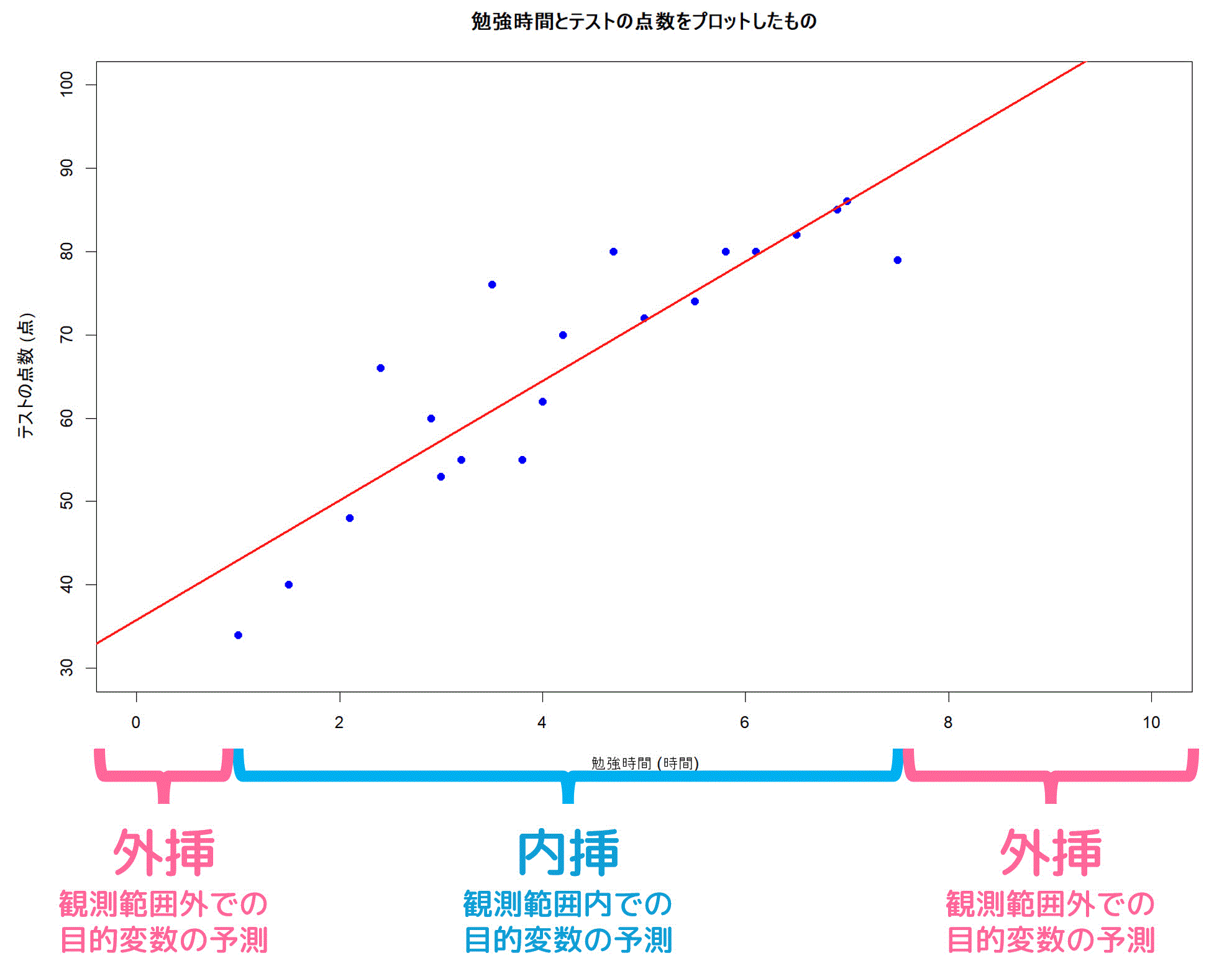
今回紹介した勉強時間とテストの点数の関係の例でいうと、勉強時間が1~8時間のときのデータはありますが、勉強時間が1時間未満の場合や、8時間以上の場合のデータはありません。
そのため、勉強時間が1時間未満の場合や、8時間以上の場合のときにテストの点数を予測することは外挿となります。
注釈
| ↑1 | 定数項に対するt値も出力されますが、定数項が0ではないかどうかを検証することは、実務的にはあまり意味がない場合が多いです。 |
|---|---|
| ↑2 | サンプルデータの中で自由に変動できる観測点の数とも言えますね。 |
| ↑3 | 例えば、回帰係数が2であると帰無仮説で仮定した場合、分子の "-0" の部分は "-2" となります。 |
| ↑4 | 一元配置分散分析では、自由度を「グループ数 - 1」としますが、回帰分析において自由度を「説明変数 - 1 = 0」とするのは誤りです。一元配置分散分析では、「全グループの平均」を求めることで自由度が1失われるため、「グループ数 - 1」としていました。これに対して、回帰分析では、グループごとの平均に相当するものが与えられているわけではなく、説明変数を使って個別の回帰直線をモデル化しています。そのため、回帰分析では説明変数に対する自由度をそのまま使い、自由度から1を引く必要はありません。 |
| ↑5 | 回帰分析では、切片 \( \alpha \) と回帰係数 \( \beta \) の2つのパラメータを使ってモデルをフィットさせるため、これに対応する自由度が2つ失われます。そのため、残差変動の自由度は「観測データ数 - 2」として計算されます。 |
| ↑6 | 単回帰モデル同士を比較する場合は、説明変数が1つしかないため、自由度調整済み決定係数は使わないことが一般的です。 |
関連広告・スポンサードリンク