スポンサードリンク
回帰分析は、ある要素を、他の要素を用いて関係を要約するための方法で、統計検定2級では頻出の分野です。
本記事では、ある要素を、2つ以上の要素を用いて関係を要約する重回帰分析について、学習していきましょう。
※ 本記事は単回帰分析を前提にしているため、事前に単回帰分析について学んでおくことをお勧めします。
↓↓↓単回帰分析の記事はこちら↓↓↓
目次
スポンサードリンク
1. 重回帰分析とは
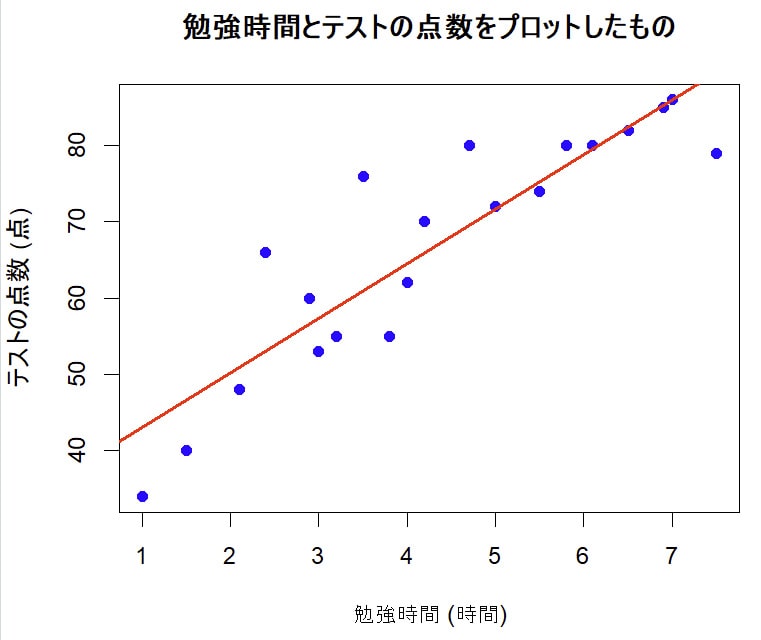
単回帰分析では、下の式のように1つの説明変数から目的変数の値を推測してきました。
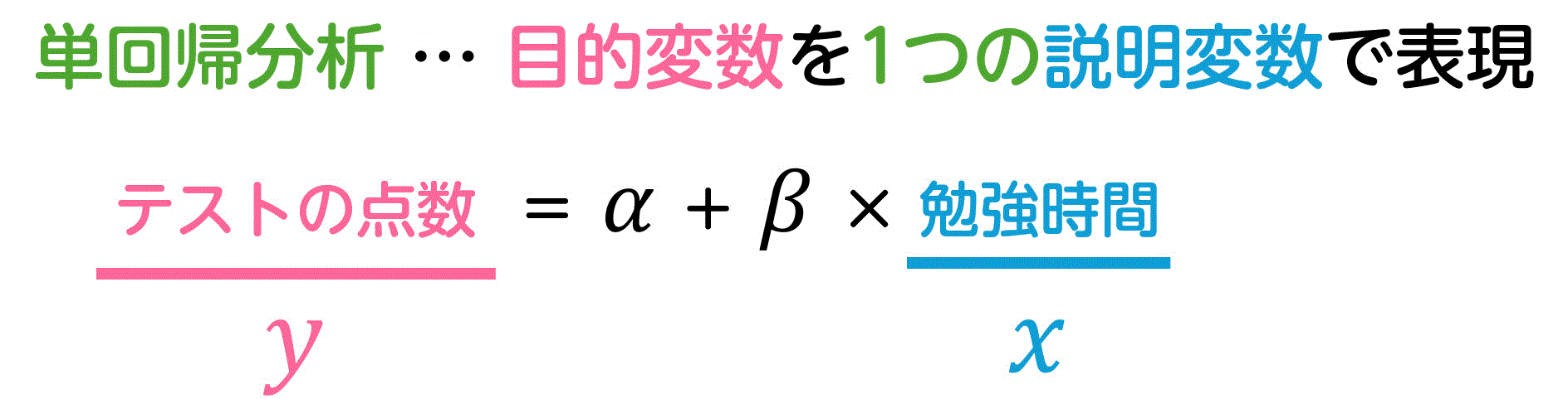
しかし、1つの説明変数だけで目的変数を説明するのは、現実的に十分ではないことが多いです。
例えば、テストの点数が勉強時間だけで決まるとは限りません。他にもさまざまな要因が関与しているはずです。睡眠時間、塾に通っているかなど…。
そこで、下のように単回帰分析で出てくる式を拡張し、複数の説明変数を使って目的変数の関係を表現する方法が考えられました。この方法が重回帰分析です。

スポンサードリンク
2. 用語説明
まずは、重回帰分析で出てくる用語を見ていきましょう。
※ 単回帰分析で既に登場したものもあります。
(1) 目的変数と説明変数 (単回帰分析と同じ)
説明変数は、目的変数を表現する道具となる変数です。記号では \( x_1 \), \( x_2 \), \( x_3 \), … と表記されます。
目的変数は、説明変数から予測される結果を表します。記号では \( y \) と表記します。
例えば、以下の式では、勉強時間、睡眠時間、塾通学有無からテストの点数を予測します。
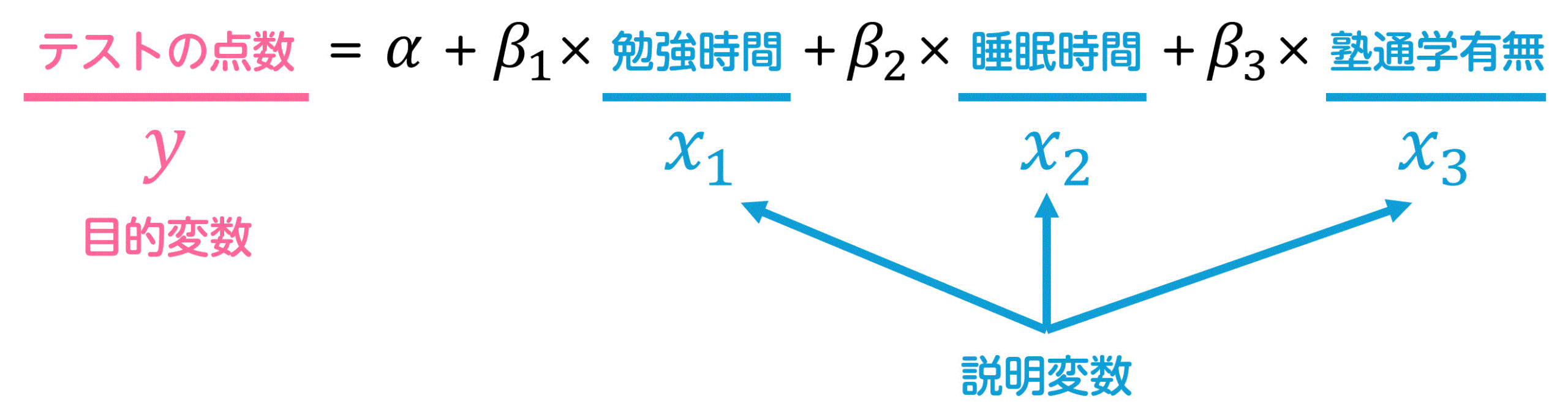
上の例では、説明変数を3つとしていますが、説明変数の数は自由に増減することができます。
参考書などでは、説明変数の数が \( n \) 個と一般化して、重回帰分析モデルの式を次のように表していることが多いです。\[\begin{align*}
y & = \alpha + \beta_1 x_1 + \beta_2 x_2 + \cdots + \beta_n x_n
\\ & = \alpha + \sum^{n}_{k=1} \beta_k x_k
\end{align*}\]
(2) 切片と偏回帰係数
切片(定数項)\( \alpha \) は、説明変数 \( x_1 \), \( x_2 \), \( x_3 \), … が0のときの目的変数 \( y \) の値を表します。
また、\( \beta_1 \), \( \beta_2 \), \( \beta_3 \), … は偏回帰係数(傾き)と呼ばれ、それぞれの説明変数 \( x_1 \), \( x_2 \), …, \( x_n \) が1変化すると、目的変数 \( y \) がどの程度変化するかを表します。
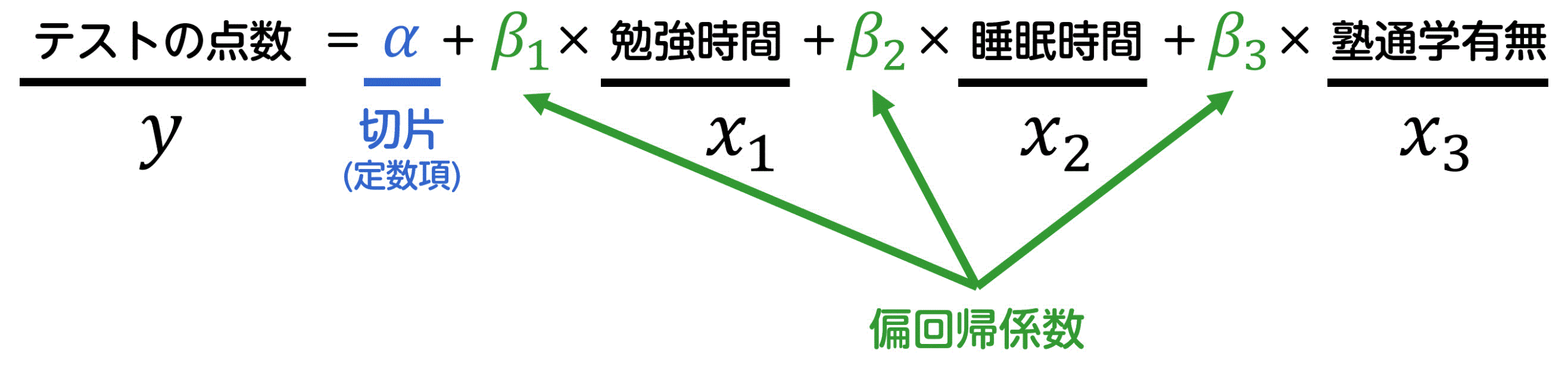
※ 単回帰分析で出てきた回帰係数の重回帰分析バージョンが、偏回帰係数だと思っていただけたらOKです。
※ 偏回帰係数を単に「回帰係数」と記載している参考書もあります。
(3) ダミー変数
説明変数には、時間や重さなどの量的データだけでなく、「塾通学の有無」のような数値でないデータを使うこともできます。
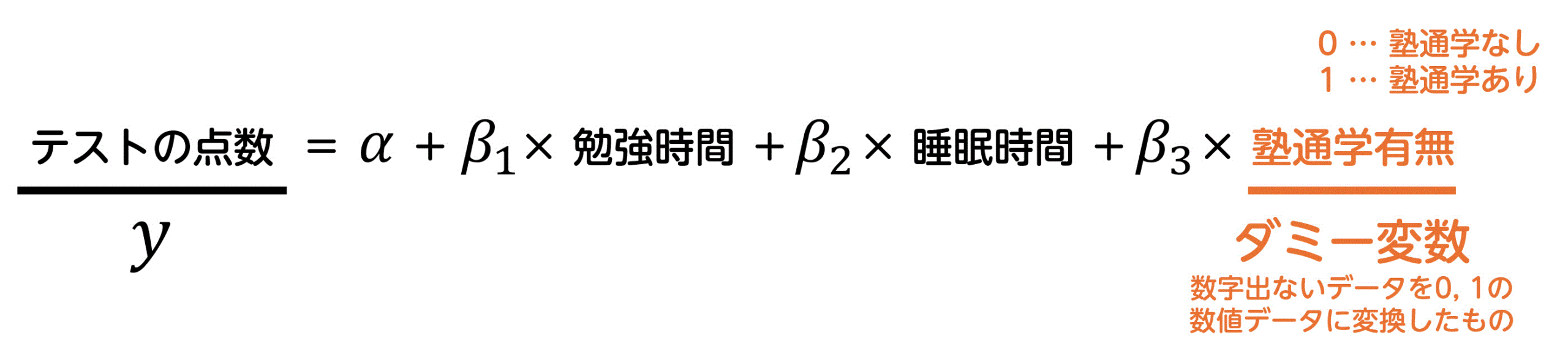
数値でないデータをモデルの式に追加する際には、次のように0と1の2つの値に変換します。
- 0 … 塾通学なし
- 1 … 塾通学あり
このように、数値でないデータを0と1の2つの値に変換して説明変数としたものを、ダミー変数と呼びます。
(4) 重回帰モデルと誤差
重回帰モデルにおいて、説明変数の数を増やしても、目的変数との関係を完全に表現することは非常に難しいです。
実際には、観測された値 \( y \) と、モデルによって予測された値 \( \alpha + \beta_1 x_1 + \beta_2 x_2 + \cdots + \beta_n x_n \) の間には誤差が生じます。
そこで、実際の観測値と予測値の違いを考慮して、以下のような形で重回帰分析のモデルを表現します。\[
y = \alpha + \beta_1 x_1 + \beta_2 x_2 + \cdots + \beta_n x_n + u
\]
ここで \( u \) は誤差項と呼ばれ、モデルによる誤差を表します。
この式を重回帰式と呼ぶことにしましょう。
(5) 最小2乗法による偏回帰係数の導出
※ 重回帰分析の誤差の計算では最小2乗法を使うのですが、この手法の理解には線形代数(行列)の知識が必要です。もし、詳しく勉強したい方は下の記事をご覧ください。なお、統計2級では行列を用いた偏回帰係数の導出はほぼ出題されないため、読み飛ばしてもOKです。
重回帰分析でも、実際に、偏回帰係数 \( \alpha \), \( \beta_1 \), \( \beta_2 \), … \( \beta_n \) の値を推定する際には、各データごとの誤差 \( u \) を最小にすることを目指します。
具体的には、観測された値と予測された値との差(残差)の2乗和が最小となるように、偏回帰係数を決定します。この方法を最小2乗法と呼びます。
最小2乗法を用いることで、\( \alpha \), \( \beta_1 \), \( \beta_2 \), … \( \beta_n \) を次のように求めることが出来ます。
重回帰式は、次のように表される。\[
y = \alpha + \beta_1 x_1 + \beta_2 x_2 + \cdots + \beta_n x_n
\]
このモデルの偏回帰係数 \( \alpha \), \( \beta_1 \), \( \beta_2 \), … \( \beta_n \) は、最小2乗法を使うことで、次のように求めることが出来る。
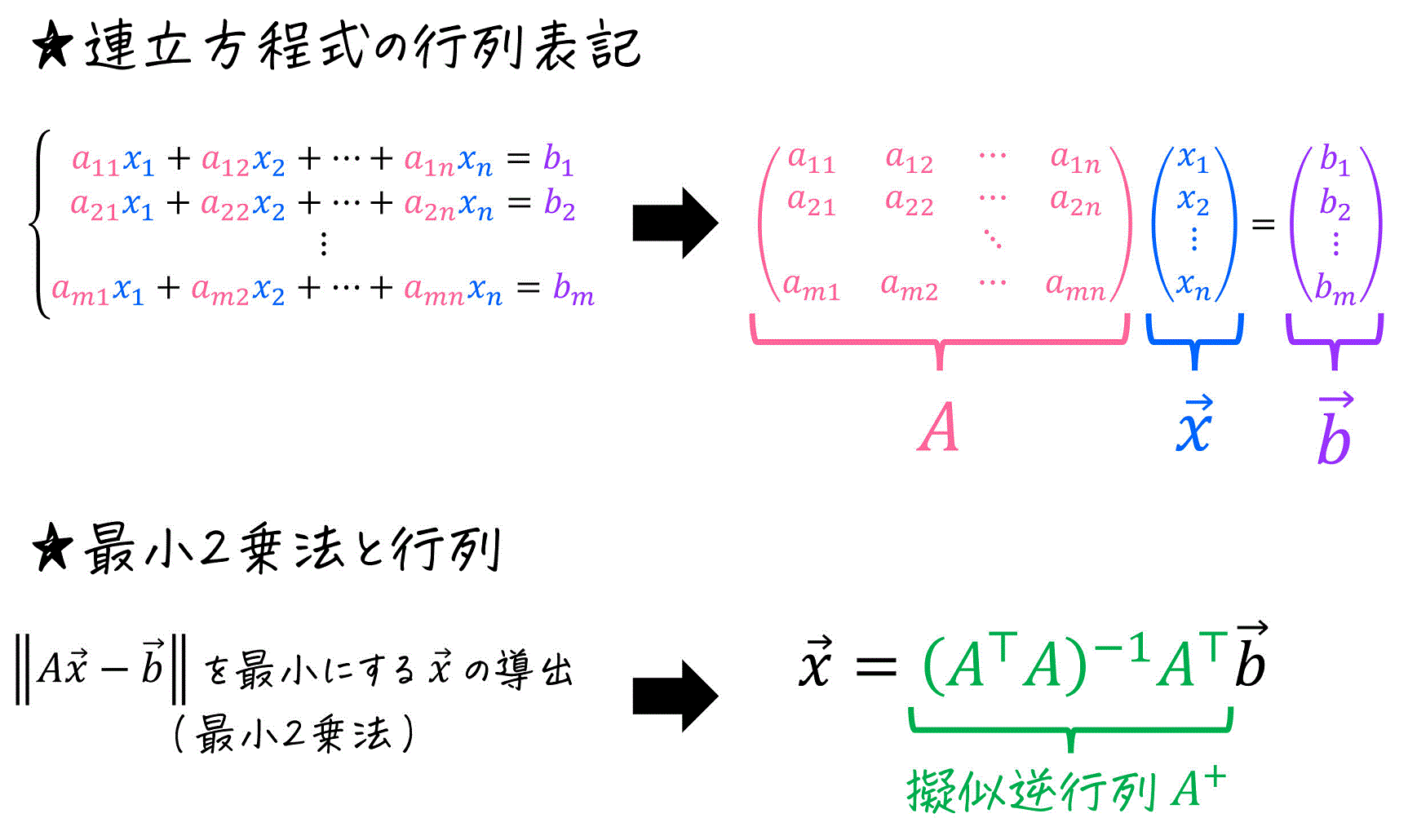
ここで、行列 \( A \) および、ベクトル \( \vec{x} \), \( \vec{b} \) を次のように定義する。\[
A = \left( \begin{array}{cc} 1 & x_{11} & x_{12} & \cdots & x_{1n} \\ 1 & x_{21} & x_{22} & \cdots & x_{2n} \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 1 & x_{m1} & x_{m2} & \cdots & x_{mn} \end{array} \right), \ \ \ \vec{x} = \left( \begin{array}{cc} \alpha \\ \beta_1 \\ \beta_2 \\ \vdots \\ \beta_n \end{array} \right), \ \ \ \vec{b} = \left( \begin{array}{cc} y_1 \\ y_2 \\ \vdots \\ y_m \end{array} \right)
\]
【変数の意味】
- \( x_{pq} \) … \( p \) 番目のデータにおける説明変数 \( x_q \) の値
- \( y_p \) … \( p \) 番目のデータにおける目的変数 \( y \) の真値
【重回帰式の変数と各観測データの対応表】
| 番目 | \( y \) | \( x_1 \) | \( x_2 \) | \( \cdots \) | \( x_n \) |
|---|---|---|---|---|---|
| 1 | \( y_1 \) | \( x_{11} \) | \( x_{12} \) | \( \cdots \) | \( x_{1n} \) |
| 2 | \( y_2 \) | \( x_{21} \) | \( x_{22} \) | \( \cdots \) | \( x_{2n} \) |
| \( \vdots \) | \( \vdots \) | \( \vdots \) | \( \vdots \) | \( \ddots \) | \( \vdots \) |
| \( m \) | \( y_m \) | \( x_{m1} \) | \( x_{m2} \) | \( \cdots \) | \( x_{mn} \) |
例)
- \( x_{12} \): 1番目のデータにおける説明変数 \( x_{2} \) の値を指す。
- \( x_{31} \): 3番目のデータにおける説明変数 \( x_{1} \) の値を指す。
- \( y_4 \): 4番目のデータの目的変数 \( y \) の値を指す
すると、連立方程式 \( A \vec{x} = \vec{b} \) の形に持ち込める。
ここで、誤差 \( \| A \vec{x} - \vec{b} \| \) を最小にするような \( \vec{x} \) は、\( A \) の擬似逆行列 \( A^+ = (A^{\top} A)^{-1} A^{\top} \) で計算できる。\[\begin{align*}
\vec{x} & = (A^{\top} A)^{-1} A^{\top} \vec{b}
\\ & = A^+ \vec{b}
\end{align*}\]
※ \( A^{\top} \) は行列 \( A \) の転置行列を表す。
この \( \vec{x} \) が偏回帰係数となる。
スポンサードリンク
3. 重回帰分析の結果の見方
統計検定2級などの試験では、表形式やRの出力から重回帰分析の結果を読み取り、それに基づいて問題を解答することが求められます。
言い換えれば、重回帰分析の結果を正しく解釈できれば、試験で得点を確実に稼ぐことができます。
基本的なデータの読み取り方は重回帰分析でも単回帰分析と同様ですが、重回帰分析特有のポイントがいくつかありますので、以下ではそれに重点を置いて説明します。\[
\mathrm{売上} \ = \alpha + \beta_1 \times \mathrm{評価} + \beta_2 \times \mathrm{広告費} + \beta_3 \times \mathrm{駅からの距離} + \beta_4 \times \mathrm{オンライン販売の有無}
\]
★ Rの出力結果例
Call:
lm(formula = test_scores ~ study_hours + sleep_hours + attends_cram_school,
data = data)
Residuals:
Min 1Q Median 3Q Max
-4.0632 -1.3898 -0.6929 1.0240 5.8699
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 16.573 6.388 2.594 0.0196 *
study_hours 6.003 1.167 5.143 9.83e-05 ***
sleep_hours 3.364 1.415 2.378 0.0302 *
attends_cram_school 5.189 3.031 1.712 0.1062
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 3.031 on 16 degrees of freedom
Multiple R-squared: 0.9799, Adjusted R-squared: 0.9762
F-statistic: 260.6 on 3 and 16 DF, p-value: 8.651e-14
※ e+n は \( 10^n \)、e-n は \(10^{-n} \) を表します。例えば、4.23e-08 は \( 4.23 \times 10^{-8} \) を表しています。
Rで出力される内容
回帰分析での出力結果は、つぎの4つに分けることが出来ます。
(1) Call: 結果を出すために使ったコマンド
※ 単回帰分析と同じです。
Call:
lm(formula = test_scores ~ study_hours + sleep_hours + attends_cram_school,
data = data)このセクションには、結果を生成するために使用したコマンドが表示されます。
解析結果そのものには影響しないため、特に重要視される部分ではありません。
(2) Residuals: 残差の四分位数
※ 単回帰分析と同じです。
残差の四分位数(最小値、第一四分位数、中央値、第三四分位数、最大値)が表示され、データのばらつき具合を把握するのに役立ちます。
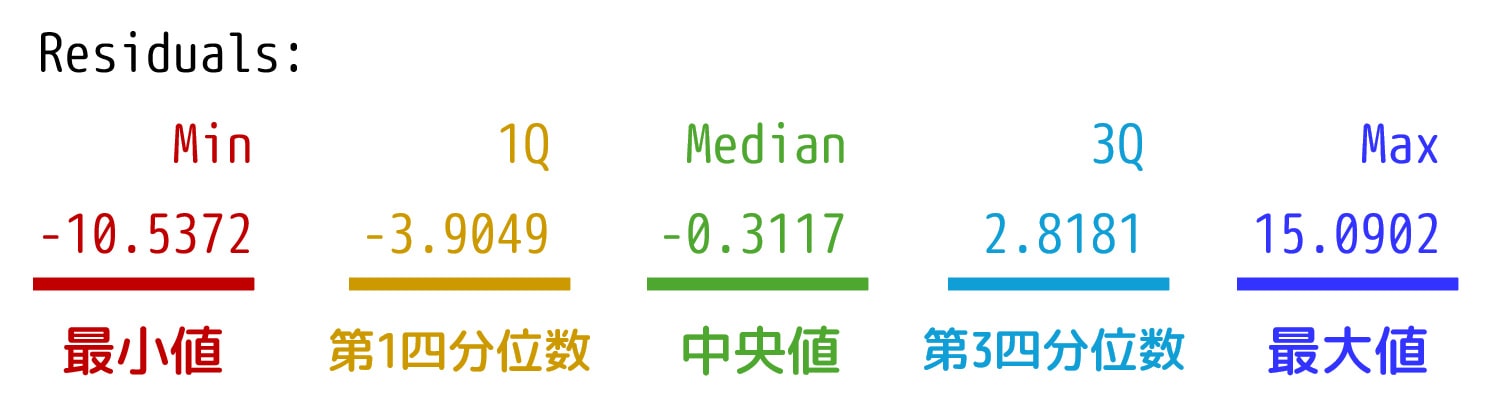
※「残差」とは、各データの実際の観測値と回帰式によって予測された値との差のことを指します。
今回の出力結果からは、残差の四分位数を以下にように読み取ることができます。
| 最小値 | 第1四分位数 | 中央値 | 第3四分位数 | 最大値 |
|---|---|---|---|---|
| -4.0632 | -1.3898 | -0.6929 | 1.0240 | 5.8699 |
補足:残差の平均値は必ず0です。これは、最小二乗法で回帰分析を行った場合、残差が正負で相殺されるためです。
(3) Coefficients: 偏回帰係数の推定結果
切片 \( \alpha \) および偏回帰係数 \( \beta_1 \), \( \beta_2 \), \( \beta_3 \), … の推定結果が示されています。
単回帰分析では説明変数が1つだけですが、重回帰分析では複数の説明変数があるため、表示される偏回帰係数の数が増えています。
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 16.573 6.388 2.594 0.0196 *
study_hours 6.003 1.167 5.143 9.83e-05 ***
sleep_hours 3.364 1.415 2.378 0.0302 *
attends_cram_school 5.189 3.031 1.712 0.1062
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1[i] Estimate: 推定値
重回帰分析において求められた切片 (Intercept) \( \alpha \)、および各説明変数の偏回帰係数 \( \beta_1 \), \( \beta_2 \), \( \beta_3 \), … の推定値です。
これらの推定値は、重回帰モデルの式に具体的に数値として表されます。
重回帰分析のモデル式での、\( \alpha \), \( \beta_1 \), \( \beta_2 \), … を具体的に数値として表しています。\[
y = \alpha + \beta_1 x_1 + \beta_2 x_2 + \beta_3 x_3 + \cdots
\]
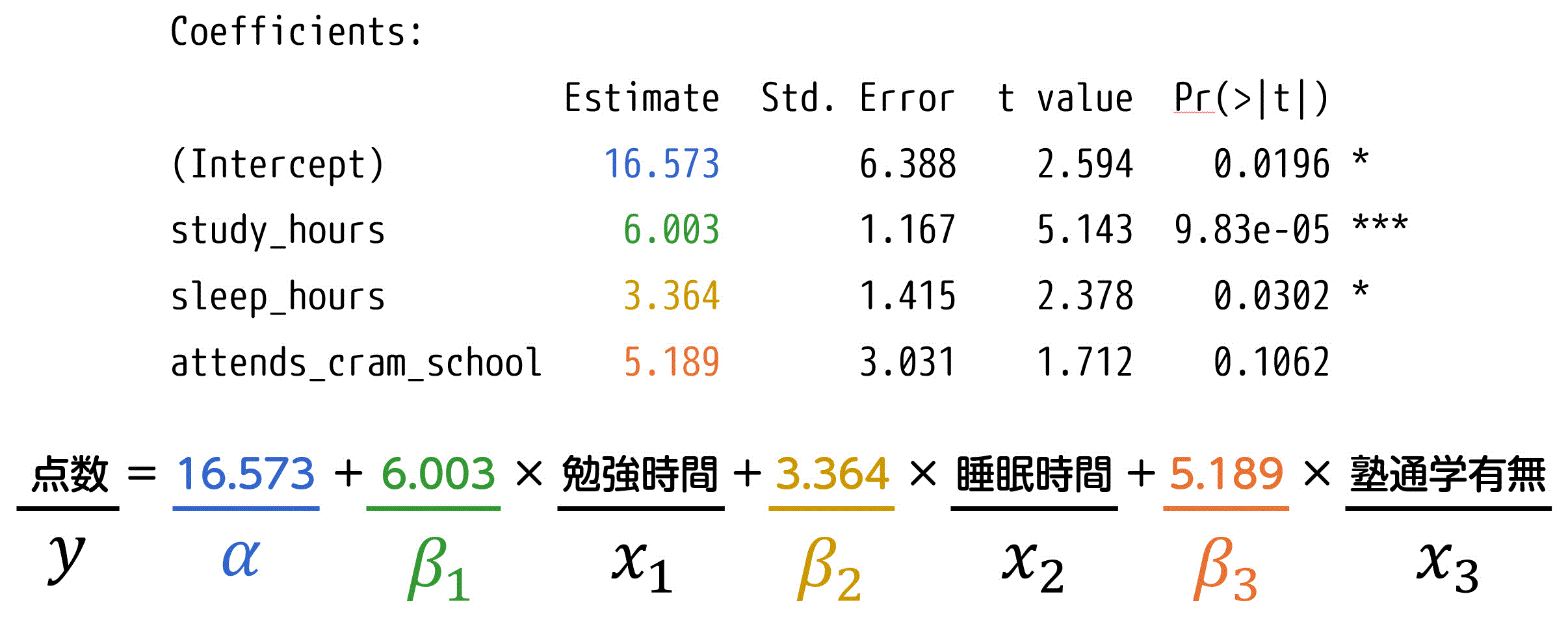
単回帰分析に比べて説明変数が増えるため、モデルの複雑さが増しますが、読み取り方は基本的に同じです。
[ii] Std. Error: 標準誤差
各偏回帰係数の推定値がどの程度の不確かさを持っているかを示す指標です。値が小さいほど、推定値の信頼性が高いことを意味します。
単回帰分析に比べて表示される説明変数が増える点以外は、読み取り方は同じです。
※ 標準誤差の導出式は統計検定2級レベルでは不要なので、覚えなくてOKです。
[iii] t value, Pr(>|t|): t値、p値
t値は、各説明変数の偏回帰係数が0であるかどうかを検証するための統計量です[1]定数項に対するt値も出力されますが、定数項が0ではないかどうかを検証することは、実務的にはあまり意味がない場合が多いです。。
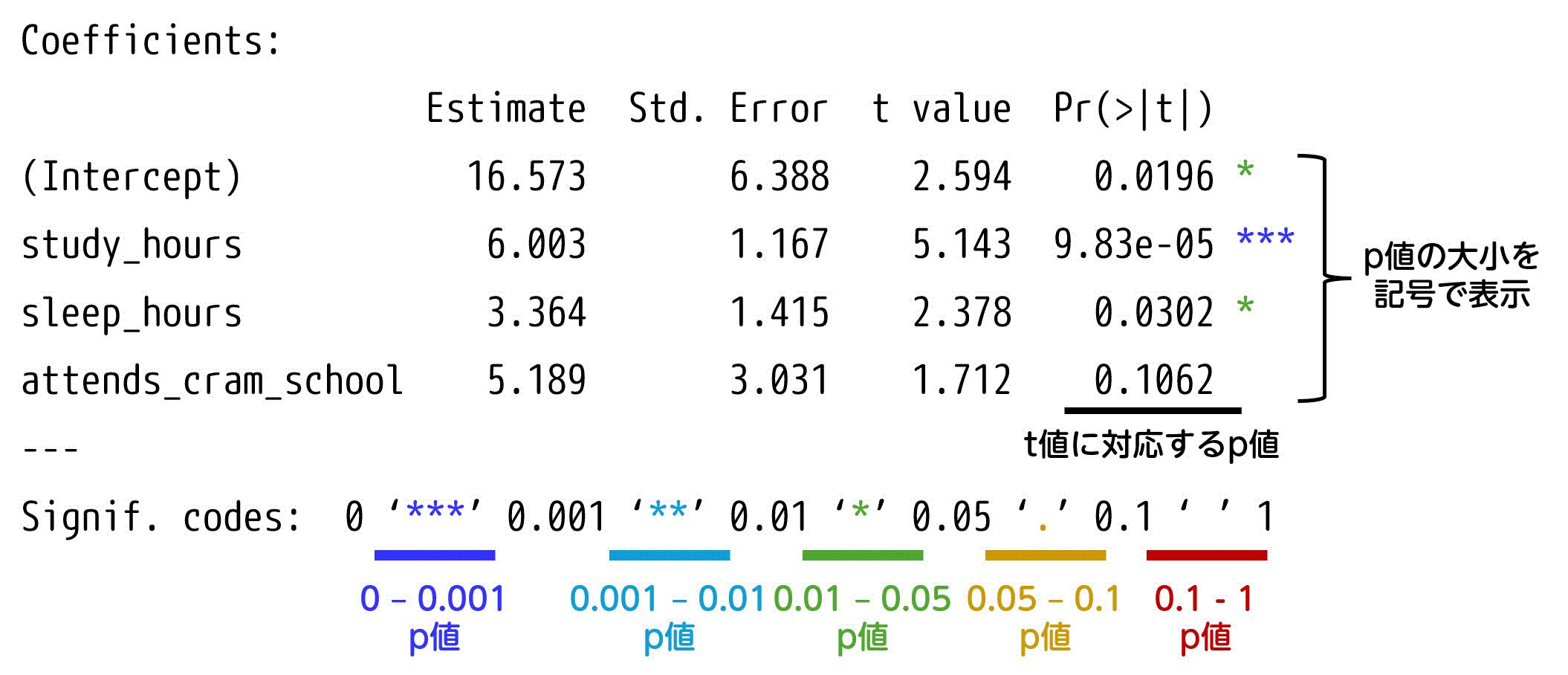
また、p値は各t値に基づいて、その結果が偶然生じる確率を示しています。言い換えると、p値は「各説明変数の偏回帰係数が0である確率」を表しています。
t値の出力結果を見ることで、「説明変数が目的変数に有意な影響を与えているか」を確認できます。
具体的には、重回帰分析では、各説明変数ごとに以下の仮説検定が行われます。
- 帰無仮説 \( H_0 \): 仮説検定をするにあたる仮定
→ \( k \) 番目の説明変数の係数 \( \beta_k \) が0である。つまり \( \beta_k = 0 \)。 - 対立仮説 \( H_1 \): 帰無仮説を否定することで示したいもの。
→ 各説明変数の係数 \( \beta_k \) が0ではない。つまり \( \beta_k \not = 0 \)。
この検定で帰無仮説が棄却された説明変数は、目的変数に有意な影響を与えていると考えられます。逆に棄却されなければ、その説明変数は目的変数に有意な影響を与えないと解釈でき、モデルに含める必要がないとされます。
なお、p値の右側に表示されている記号はp値の大小を表しています。
★ t値の自由度
※ 単回帰分析と自由度が異なることに注意が必要です。
t値の自由度 \( k_t \) は、サンプルサイズ \( \textcolor{green}{n} \) からモデルのパラメータ数(切片 \( \alpha \) と 偏回帰係数 \( \beta_1 \), \( \beta_2 \), …, \( \beta_k \))を引いたもので決まります。この自由度は、サンプルデータの中で自由に変動できる観測点の数を反映しています。
ここで、切片の数は常に1つです。さらに、偏回帰係数の数(つまり説明変数の数)を \( \textcolor{blue}{k} \) 個とすると、自由度 \( k_t \)は次の式で計算されます。\[\begin{align*}
k_t & = \textcolor{green}{n} - (\textcolor{blue}{k} + \textcolor{red}{1})
\\ & = \textcolor{green}{n} - \textcolor{blue}{k} -\textcolor{red}{1}
\end{align*}\]
今回のデータの場合、20人のデータから、説明変数が3つの回帰分析を行っているため、自由度 \( k_t \) は次のように計算されます。\[\begin{align*}
k_t & = \textcolor{green}{20} - \textcolor{blue}{3} - \textcolor{red}{1}
\\ & = 16
\end{align*}\]
★ t値の計算方法
t値は次の式で計算できます。単回帰分析と同様です。
※ 帰無仮説で偏回帰係数を0と仮定しているため、分子に "-0" を記載しています[2]例えば、偏回帰係数が2であると帰無仮説で仮定した場合、分子の "-0" の部分は "-2" となります。。
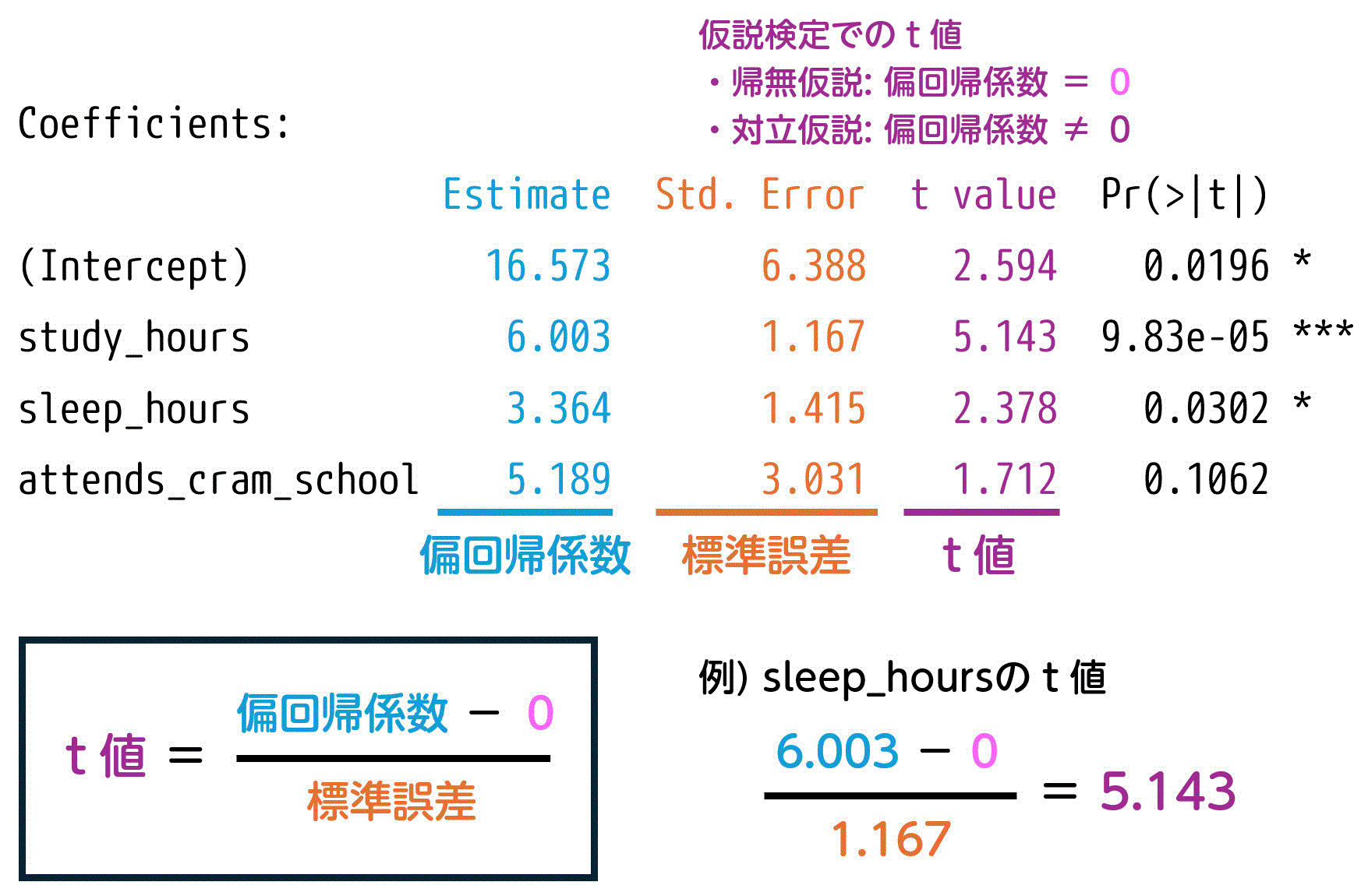
※ 式内の "偏回帰係数" は、ツールで計算した結果が入ります。
実際に、勉強時間 (study_hours) に対するt値を計算すると、Rで出力されたt値と一致することが分かりますね。
※ t値の自由度、および推定値、標準誤差、t値の関係は統計検定2級で頻出です。頭に入れておきましょう。
(4) 回帰モデルそのものの分析情報
この欄では、重回帰分析全体の結果に対する統計的な分析結果が示されています。
表示の見方、および考え方については単回帰分析のときと同様です。
Residual standard error: 3.031 on 16 degrees of freedom
Multiple R-squared: 0.9799, Adjusted R-squared: 0.9762
F-statistic: 260.6 on 3 and 16 DF, p-value: 8.651e-14具体的には、「分析全体のパフォーマンスを評価するための指標」や「重回帰モデルの当てはまりの良さが出力」されています。これらの結果は、回帰モデルそのものがデータをどの程度説明しているか、またモデルが有意であるかを示しています。
★ 分散分析と回帰分析
※ 重回帰分析における分散分析の考え方は、単回帰分析と同じです。
目的変数の各値 \( y_k \) は、回帰モデルによって予測される値 \( \alpha + \beta_1 x_{1k} + \beta_2 x_{2k} + \beta_3 x_{3k} \cdots \) と回帰モデルでは説明できないズレ \( u_k \) の和で表すことが出来ます。
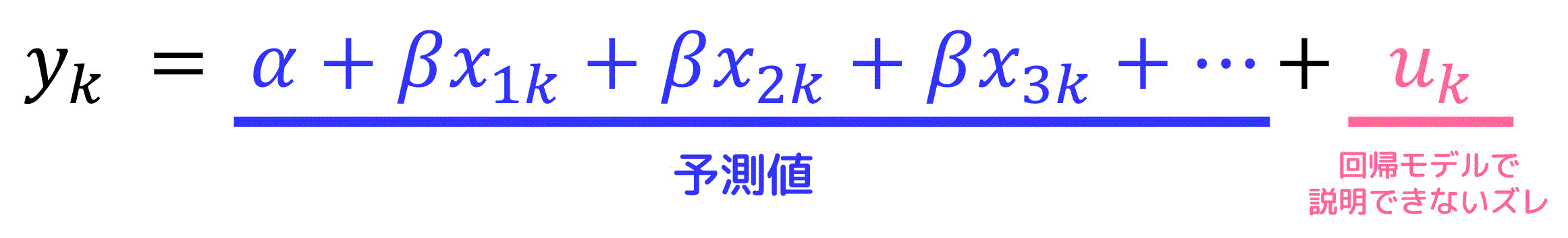
【変数の意味】
- \( x_{pq} \) … \( p \) 番目のデータにおける説明変数 \( x_q \) の値
- \( y_p \) … \( p \) 番目のデータにおける目的変数 \( y \) の真値
これは、各観測値 \( y_k \) を、「予測値 \( \alpha + \beta_1 x_{1k} + \beta_2 x_{2k} + \beta_3 x_{3k} \cdots \)」と「モデルが説明できない誤差(残差) \( u_k \)」の2つに分解することができる、ということです。
ここで、回帰モデルによって予測される値を \( \hat{y}_k \) とすると、
回帰モデルでは説明できないズレ \( u_k \) は、目的変数の各値 \( y_k \) から回帰モデルによって予測される値 \( \hat{y}_k \) を引いたものとして表されます。
したがって、式を次のように書き換えることが出来ます。

つぎに、目的変数の各データ値 \( y_k \) は、平均 \( \overline{y} \) からのばらつきを持つと考えられます。
このばらつきを明確にするため、先ほどの式を以下のように書き換えます。

この式は、観測 \( y_k \) を、「全体の平均値 \( \overline{y} \)」と「回帰モデルで説明できるズレ(説明変動)」、さらに「回帰モデルで説明できないズレ(残差変動)」の3つに分解できることを表しています。
さらに、全体の平均 \( \overline{y} \) を基準に考えるために、両辺から \( \overline{y} \) を引きましょう。

この式は、「目的変数の観測値 \( y_k \) と平均値 \( \overline{y} \) との差(全変動)」が、「回帰による変動(説明変動)」と「回帰モデルで説明できない変動(残差変動)」に分解できることを示しています。
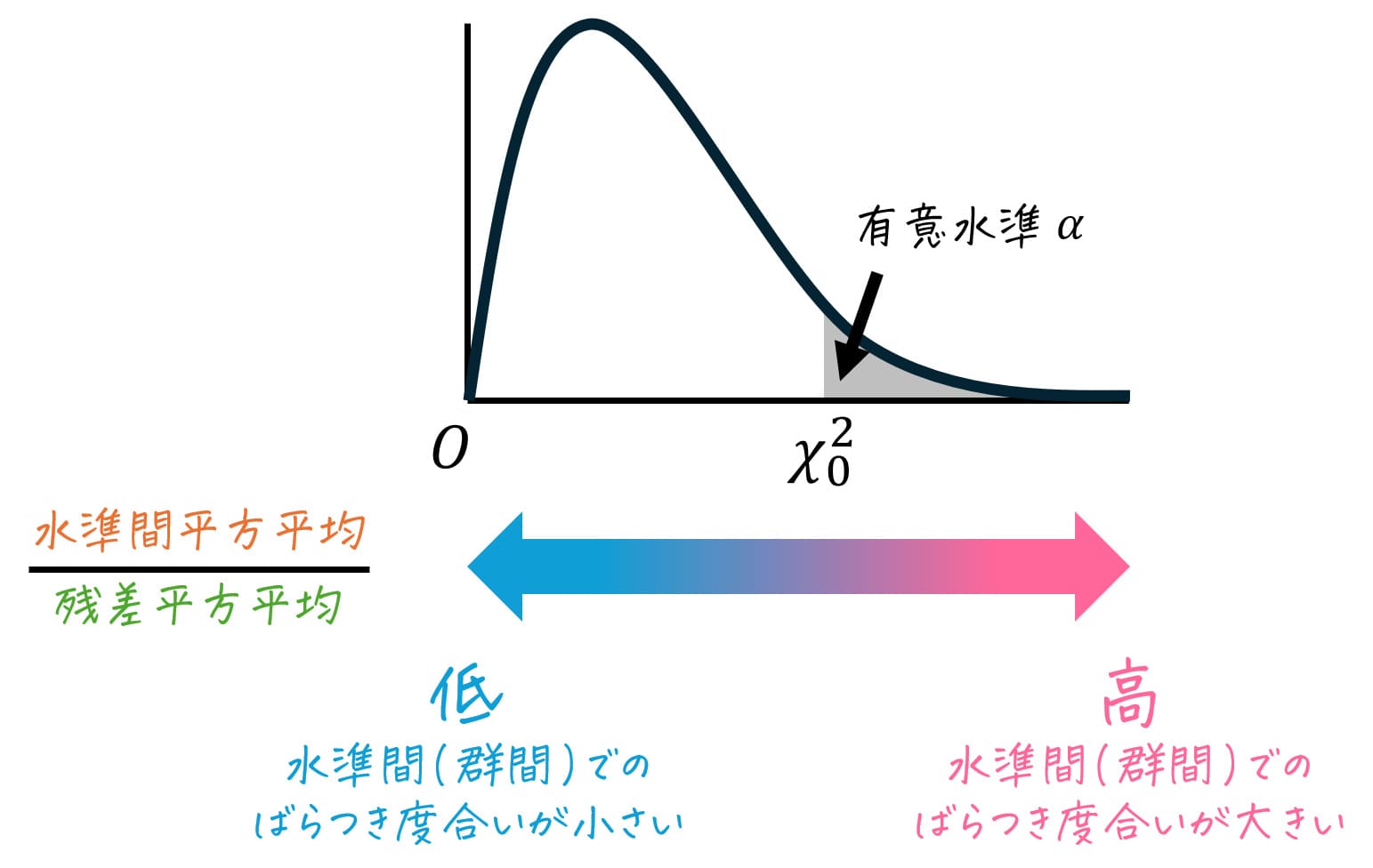
重回帰分析全体の結果を評価する際にも、単回帰分析と同様に「回帰変動」と「残差変動」の度合いを使ってさまざまな指標を計算します。
ここで、変動を2つに分解して分析する方法と聞いて、何か思い浮かぶ言葉はありませんか?
そう、一元配置分散分析です。
一元配置分散分析を使うことで、各データの「全変動」を「回帰による変動(説明変動)」と「残差による変動」の2つに分解し、それぞれが全体の変動にどれほど寄与しているかを分析できます。
※ 一元配置分散分析がいまいちよくわからない or 一元配置分散分析ってなんだっけ、となった方は以下の記事にて復習しましょう。
★ 回帰分析と一元配置分散分析
重回帰分析における一元配置分散分析のステップを確認しましょう。ここではデータ全体の変動を「回帰変動」と「残差変動」に分けて評価します。
※ 単回帰分析と異なる部分を、色をつけて説明しています。
| 要因 | 平方和 | 自由度 | 平方平均 | \( F \) 値 |
|---|---|---|---|---|
| 回帰変動 | (a) \( S_A \) | \( \phi_A = \textcolor{red}{k} \) | \( V_A = \frac{ S_A }{ \phi_A } \) | \( \frac{ V_A }{ V_E } \) |
| 残差変動 | (b) \( S_E \) | \( \phi_E = \textcolor{red}{n - k - 1} \) | \( V_E = \frac{ S_E }{ \phi_E } \) | − |
| 全変動 | (c) \( S_T \) | \( \phi_T = n - 1 \) | − | − |
[i] 平方和
※ 計算方法は、単回帰分析と同様です。
ここで、回帰変動、残差変動、全変動の平方和は次のように計算できます。
(a) 回帰変動:予測値 \( \hat{y}_k \) と平均値 \( \overline{y} \) の差の2乗の総和
(回帰モデルが説明できる部分の変動)
\[\begin{align*}
S_A & = \sum^{n}_{k = 1} \left( \hat{y}_k - \overline{y} \right)^2
\end{align*}\]
(b) 残差変動:観測値 \( y_k \) と予測値 \( \hat{y}_k \) の差の2乗の総和
(回帰モデルが説明できない部分の変動)
\[\begin{align*}
S_E & = \sum^{n}_{k = 1} \left( y_k - \hat{y}_k \right)^2
\end{align*}\]
(c) 全体変動:観測値 \( y_k \) と平均 \( \overline{y} \) の差の2乗の総和
(全データの変動)
\[\begin{align*}
S_T & = \sum^{n}_{k = 1} \left( y_k - \hat{y}_k \right)^2
\end{align*}\]
注意: 全体変動 \( S_T \) は、回帰変動 \( S_A \) と残差変動 \( S_E \) の和に等しくなります。\[
S_T = S_A + S_E
\]
[ii] 自由度
※ 考え方は単回帰分析と同じですが、値が変わります。
回帰変動の自由度:説明変数の数 \( k \) です。[3]一元配置分散分析では、自由度を「グループ数 - 1」としますが、回帰分析において自由度を「説明変数 - … Continue reading。\[
\textcolor{red}{\phi_A = k}
\]
残差変動の自由度:データ数からモデルのパラメータ数を引いたもの。重回帰分析では、モデルのパラメータ数は切片1つ \( \alpha \) と、\( k \) 個の偏回帰係数 \( \beta_1 \), \( \beta_2 \), …, \( \beta_k \) の合計 \( k+1 \) 個です。そのため、自由度はサイズ \( n \) から \( k+1 \) を引いた \( n - k - 1 \) となります。[4]回帰分析では、切片 \( \alpha \) と \( k \) 個の偏回帰係数 \( \beta_1 \), \( \beta_2 \), …, \( \beta_k \) の \( k + 1 \) … Continue reading。\[\begin{align*}
\phi_E & = n - (k+1)
\\ & = n - k - 1
\end{align*}\]
全体変動の自由度:データ数から1を引いたものです。単回帰分析と同様です。\[
\phi_T = n - 1
\]
注意: 単回帰分析と同じく、全体変動の自由度 \( k_T \) は、回帰変動の自由度 \( k_A \) と残差変動の自由度 \( k_E \) の和に等しくなります。\[
\phi_T = \phi_A + \phi_E
\]
[iii] 平方平均
※ 計算方法は、単回帰分析と同様です。
平方和を対応する自由度で割ることで、平方平均が求められます。
回帰変動の平方平均\[
V_A = \frac{ S_A }{ \phi_A }
\]
残差変動の平方平均\[
V_E = \frac{ S_E }{ \phi_E }
\]
[iv] F値
※ 計算方法は、単回帰分析と同様です。
F値は、回帰変動の平方平均 \( V_A \) を残差変動の平方平均 \( V_E \) で割ったもので計算されます。\[
F = \frac{ V_A }{ V_E }
\]
★ それぞれの出力の意味
ここでは、Rの出力で得られた結果が一元配置分散分析のどの結果に対応するかを見ていきます。
Residual standard error: 7.037 on 18 degrees of freedom
Multiple R-squared: 0.8003, Adjusted R-squared: 0.7892
F-statistic: 72.12 on 1 and 18 DF, p-value: 1.037e-07表.回帰変動、残差変動に対する一元配置分散分析の結果
| 要因 | 平方和 | 自由度 | 平方平均 | \( F \) 値 |
|---|---|---|---|---|
| 回帰変動 | (a) \( S_A \) | \( \phi_A = \textcolor{red}{k} \) | \( V_A = \frac{ S_A }{ \phi_A } \) | \( \frac{ V_A }{ V_E } \) |
| 残差変動 | (b) \( S_E \) | \( \phi_E = \textcolor{red}{n - k - 1} \) | \( V_E = \frac{ S_E }{ \phi_E } \) | − |
| 全変動 | (c) \( S_T \) | \( \phi_T = n - 1 \) | − | − |
[i] Residual standard error:残差の標準誤差 (と自由度)
※ 単回帰分析と同様ですが、残差の自由度が単回帰分析とは異なります。
残差変動の平方平均 \( V_E \) を表しており、回帰モデルがデータをどの程度正確に説明できていないかを示します。また、自由度 \( \phi_E \) は残差変動に対する自由度です。

今回の結果は、残差平方平均 \( V_E \) が7.037、残差の自由度 \( \phi_E \) が18であることを意味しています。
表記については単回帰分析のときと同じですが、重回帰では説明変数が複数あるため、残差の自由度は「データ数 - 説明変数の数 - 1」となります。
[ii] Multiple R-squared: 決定係数
※ 単回帰分析と同様ですが、重回帰分析ならではのポイントがあります。
決定係数 \( R^2 \) は、モデルがデータの変動をどれだけ説明できているか(=回帰モデルがデータに上手く当てはまっているか)を0から1の範囲で表します。(1に近いほど、説明力が高いと言えます。)モデルの当てはまりの良さが決定係数だと思っていただけたらOKです。
具体的に、決定係数 \( R^2 \) は全体平方和に対する回帰変動の割合で計算されます。
\[\begin{align*}
R^2 & = \frac{S_A}{S_T}
\\ & = \frac{S_T - S_E}{S_T}
\\ & = 1 - \frac{S_E}{S_T} \ \ ( \because S_A + S_E = S_T )
\end{align*}\]※ \( S_A \) は回帰平方和、\( S_E \) は残差平方和、\( S_T \) は全体平方和を表しています。
決定係数は、単回帰モデル同士でモデルの当てはまり具合を比べる際に利用されます。

例えば、今回のデータの場合、決定係数 \( R^2 \) は 0.9799 です。
つまり、このモデルはデータの97.99%の変動を説明できていると言えます。
ただし、重回帰分析では説明変数の数が増えると決定係数 \( R^2 \) は常に増加するため、モデルの当てはまりが良く見える場合があります。
★ 相関係数と決定係数の関係
相関係数は、説明変数と目的変数の間の直線的関係の強さを示す指標であり、相関係数の2乗が決定係数になります。
したがって、決定係数は説明変数が目的変数に対して持つ直線的関係の強さを示すことができます。
[iii] Adjusted R-squared: 自由度調整済み決定係数
※ 重回帰分析で最も重要なポイントです!
説明変数を増やすほど、回帰モデルで説明できる変動の割合が増加し、決定係数 \( R^2 \) は大きくなります。
しかし、すべての説明変数が目的変数に影響を与えるわけではないため、無関係な説明変数を追加することは避けるべきです。
そこで、自由度調整済み決定係数 \( R^2 \) が登場しました。これは無関係な説明変数を追加してもモデル評価が不適切に上昇しないように調整された指標です。
\[\begin{align*}
R^2_f & = 1 - \frac{ \frac{S_E}{n-k-1}}{ \frac{S_T}{n-1} }
\\ & = 1 - \frac{S_E}{S_T} \cdot \frac{n-1}{n-k-1}
\\ & = 1 - \frac{n-1}{n-k-1}\left( 1 - R^2 \right)
\end{align*}\]
※ \( n \) は回帰分析に使用したデータ数です。今回の例の場合、\( n = 20 \) です。
※ \( k \) は説明変数の数を表します。
重回帰分析でモデルの良し悪しを比べるときには、決定係数ではなく、自由度調整済み決定係数を使います。
自由度調整済み決定係数を使うことで、単に説明変数を増やすことでモデルが良くなるように見える現象を防ぐことが出来ます。

今回の出力で示された自由度調整済み決定係数 \( R^2_f \) は 0.9762 ですね。
[iv] F値
※ 単回帰分析と同様ですが、重回帰分析では複数の説明変数を考慮します。
F値は、回帰式内の説明変数が目的変数に対して有意に影響を与えているかどうかを評価するための統計量です。説明変数の効果が全体として有意かどうかを判断するために使用されます。このモデルが信頼できるものかを表していると思っていただけたらOKです。
具体的には、帰無仮説 \( H_0 \) を「説明変数の偏回帰係数が全て0である」と仮定し、この仮説が成立するかどうかをF値で確認します。
【回帰分析でのF検定】
- 帰無仮説 \( H_0 \): 説明変数の偏回帰係数が全て0。
(回帰モデルは無意味) - 対立仮説 \( H_1 \): 説明変数の偏回帰係数に0ではないものがある。
(回帰モデルは有意)
この検定の結果が棄却されれば、モデルが信頼できるものと見なされます。一方棄却されなかった場合、このモデル自体が意味ないものと見なされる可能性があります。
今回のRの出力結果では、次の3つの情報が表示されています。
- F値: 260.6
- F検定で使用する自由度の組 (3,16)
※ 説明変数の自由度が3、残差の自由度が16 - 対応するp値: \( 8.651 \times 10^{-14} \)

この結果から、F値が非常に大きく、p値も極めて小さい(< 0.01)ため、帰無仮説は棄却され、説明変数(勉強時間)と目的変数(テストの点数)に関するこのモデルは信頼できるものと言えます。
4. 練習問題にチャレンジ!
では、最後に練習問題にチャレンジしてみましょう!
桃山さんは、近隣地域のラーメン屋の売上を分析するために、次の重回帰モデルを考えた。
\[
\mathrm{売上} \ = \alpha + \beta_1 \times \mathrm{評価} + \beta_2 \times \mathrm{広告費} + \beta_3 \times \mathrm{駅からの距離} + \beta_4 \times \mathrm{オンライン販売の有無}
\]
【説明変数の意味】
| 説明変数 | 変数名 | 意味 |
|---|---|---|
| 評価 | review_score | 評価サイトの評価 [点] (※ 満点は5) |
| 広告費 | ad_budget | 1ヶ月当たりに使用する広告費用 [万円] |
| 駅からの距離 | dist_from_station | 最寄り駅から店舗までの距離 [分] |
| オンライン販売の有無 | has_online_store | オンライン販売の有無 (0 … なし、1 … あり) |
統計ソフトウェアRを用いて、上記の重回帰モデルを推定したところ、つぎの出力結果を得た。
Call:
lm(formula = sales ~ review_score + ad_budget + dist_from_station + has_online_store, data = data)
Residuals:
Min 1Q Median 3Q Max
-16.725 -7.675 -3.806 7.473 29.201
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 49.8564 63.1142 0.790 0.438829
review_score 14.4141 3.0033 [ a ] 0.000109 ***
ad_budget 3.3419 [ b ] 5.301 3.45e-05 ***
dist_from_station -3.9179 1.4844 -2.639 0.015724 *
has_online_store 6.9950 5.5595 1.258 0.222808
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 13.56 on 20 degrees of freedom
Multiple R-squared: 0.7657, Adjusted R-squared: 0.7188
F-statistic: 16.34 on [ c ] and [ d ] DF, p-value: 4.322e-06
つぎの(1)~(6)の問いに答えなさい。ただし、出力結果の一部を加工している。
(1) 出力結果の [ a ] ~ [ d ] に当てはまる数を答えなさい。ただし、[ a ], [ b ] は小数第4位を四捨五入して小数第3位まで、[ c ]、[ d ] は整数で答えること。
(2) 分析に用いた店舗数を答えなさい。
(3) 評価サイトの評価が4.1点、1ヶ月当たりに使用する広告費用が5万円、最寄り駅から店舗まで徒歩3分で、オンライン販売を実施している店舗の1ヶ月店舗の売上高は何万円と予測されるか。小数第2位を四捨五入し、小数第1位まで答えなさい。
(4) 有意水準を5%とする。説明変数のうち、「評価」、「広告費」、「駅からの距離」、「オンライン販売の有無」のうち、統計的に有意な説明変数はいくつあるか答えなさい。
(5) この単回帰モデルの結果から読み取れることとして、正しいものをつぎの1~5の選択肢から1つ選びなさい。
- 部員数のF値に対応するp値が0.05未満のため、この重回帰モデルはデータの変動をうまく説明できていると言える。
- 説明変数の中で、「評価」の偏回帰係数が最も大きいため、説明力が最も大きい説明変数は「評価」であると言える。
- 評価サイトの評価が1点上がると、売上高は約14.4万円上がる傾向がある。
- 「オンライン販売の有無」は量的変数ではないため、回帰分析への使用は避けるべきである。
- 最寄り駅から店舗までの距離が長くなると、売上高も増える傾向にある。
近隣地域のラーメン屋の売上を分析するために、評価のみを説明変数とした単回帰モデルで、単回帰分析を行った。
\[
\mathrm{売上} \ = \alpha + \beta \times \mathrm{評価}
\]
結果、つぎの出力結果を得た。
Call:
lm(formula = sales ~ review_score, data = data2)
Residuals:
Min 1Q Median 3Q Max
-37.402 -12.398 -2.752 18.054 34.012
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -38.751 88.007 -0.440 0.66382
review_score 16.837 4.403 3.824 0.00087 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 20.42 on 23 degrees of freedom
Multiple R-squared: 0.3887, Adjusted R-squared: 0.3621
F-statistic: 14.62 on 1 and 23 DF, p-value: 0.0008701ここで、単回帰モデルと重回帰モデルを比較した場合、どちらがより良いモデルと言えるか。結論とその理由について述べた文章のうち、最も適切なものを1つ選びなさい。
- 単回帰モデルの方のF値に対応するp値がより小さい、単回帰モデルの方が良いモデルと言える。
- 重回帰モデルの方のF値に対応するp値がより小さい、単回帰モデルの方が良いモデルと言える。
- 単回帰モデルの方の決定係数がより大きいため、単回帰モデルの方が良いモデルと言える。
- 重回帰モデルの方の決定係数がより大きいため、重回帰モデルの方が良いモデルと言える。
- 単回帰モデルの方の自由度調整済み決定係数がより大きいため、単回帰モデルの方が良いモデルと言える。
- 重回帰モデルの方の自由度調整済み決定係数がより大きいため、重回帰モデルの方が良いモデルと言える。
5. 練習問題の答え
Call:
lm(formula = sales ~ review_score + ad_budget + dist_from_station + has_online_store, data = data)
Residuals:
Min 1Q Median 3Q Max
-16.725 -7.675 -3.806 7.473 29.201
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 49.8564 63.1142 0.790 0.438829
review_score 14.4141 3.0033 [ a ] 0.000109 ***
ad_budget 3.3419 [ b ] 5.301 3.45e-05 ***
dist_from_station -3.9179 1.4844 -2.639 0.015724 *
has_online_store 6.9950 5.5595 1.258 0.222808
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 13.56 on 20 degrees of freedom
Multiple R-squared: 0.7657, Adjusted R-squared: 0.7188
F-statistic: 16.34 on [ c ] and [ d ] DF, p-value: 4.322e-06(1)
[ a ] 解答: 4.779t値を計算するためには、t値の計算公式を使います。具体的には、偏回帰係数を標準誤差で割ればOKです。
\[\begin{align*}
t & = \frac{ \mathrm{偏回帰係数} \ - 0}{ \mathrm{標準誤差} }
\\ & = \frac{14.4141}{3.0033}
\\ & \fallingdotseq 4.799
\end{align*}\]したがって、[a]は 4.779 となります。
\[\begin{align*}
t & = \frac{ \mathrm{偏回帰係数} \ - 0}{ \mathrm{標準誤差} }
\end{align*}\]
したがって、次の式が成り立つような標準誤差を求めればOKです。\[\begin{align*}
5.301 & = \frac{3.3419 - 0}{ \mathrm{標準誤差} }
\end{align*}\]
この式を変形することで、[b]はつぎのように求められます。
\[\begin{align*}
\mathrm{標準誤差} & = \frac{3.3419 } { 5.301 }
\\ & \fallingdotseq 0.630
\end{align*}\]
つぎの出力結果の [ c ] は回帰変動の自由度、[ d ] は残差変動の自由度を表しています。
F-statistic: 16.34 on [ c ] and [ d ] DF, p-value: 4.322e-06[ c ] 解答: 4
回帰変動の自由度は、説明変数の数に等しいです。
今回の説明変数は、以下の4つですね。
| 説明変数 | 変数名 | 意味 |
|---|---|---|
| 評価 | review_score | 評価サイトの評価 [点] (※ 満点は5) |
| 広告費 | ad_budget | 1ヶ月当たりに使用する広告費用 [万円] |
| 駅からの距離 | dist_from_station | 最寄り駅から店舗までの距離 [分] |
| オンライン販売の有無 | has_online_store | オンライン販売の有無 (0 … なし、1 … あり) |
[ c ] 解答: 20
残差変動の自由度は、出力結果の on "20" degrees of freedom から読み取れます。

(2)
解答: 25
標本サイズ(分析に使用した店舗数)を求める際は、残差変動の自由度の出力に着目します。

よって、残差変動の自由度が 20 と読み取れます。
ここで残差変動の自由度は、標本サイズからモデルのパラメータ数を引くことで求められます。
今回のモデルのパラメータは切片 \( \alpha \) と説明変数4つに対応する偏回帰係数 \( \beta_1 \), \( \beta_2 \), \( \beta_3 \), \( \beta_4 \) の合計5つなので、標本サイズ \( n \) と残差の自由度 \( \phi_E \) には次の関係式が成立します。\[
\phi_E = n - 5
\]
出力結果より、残差の自由度が \( \phi_E = 20 \) と読み取れるため、標本サイズ \( n \) はつぎのように計算できます、\[\begin{align*}
n & = \phi_E + 5
\\ & = 20 + 5
\\ & = 25
\end{align*}\]よって、答えは25となります。
(3)
解答: 120.9万円
まず、各パラメータ \( \alpha \), \( \beta_1 \), \( \beta_2 \), \( \beta_3 \), \( \beta_4 \) の値は、出力結果の Estimate から読み取ることができます。
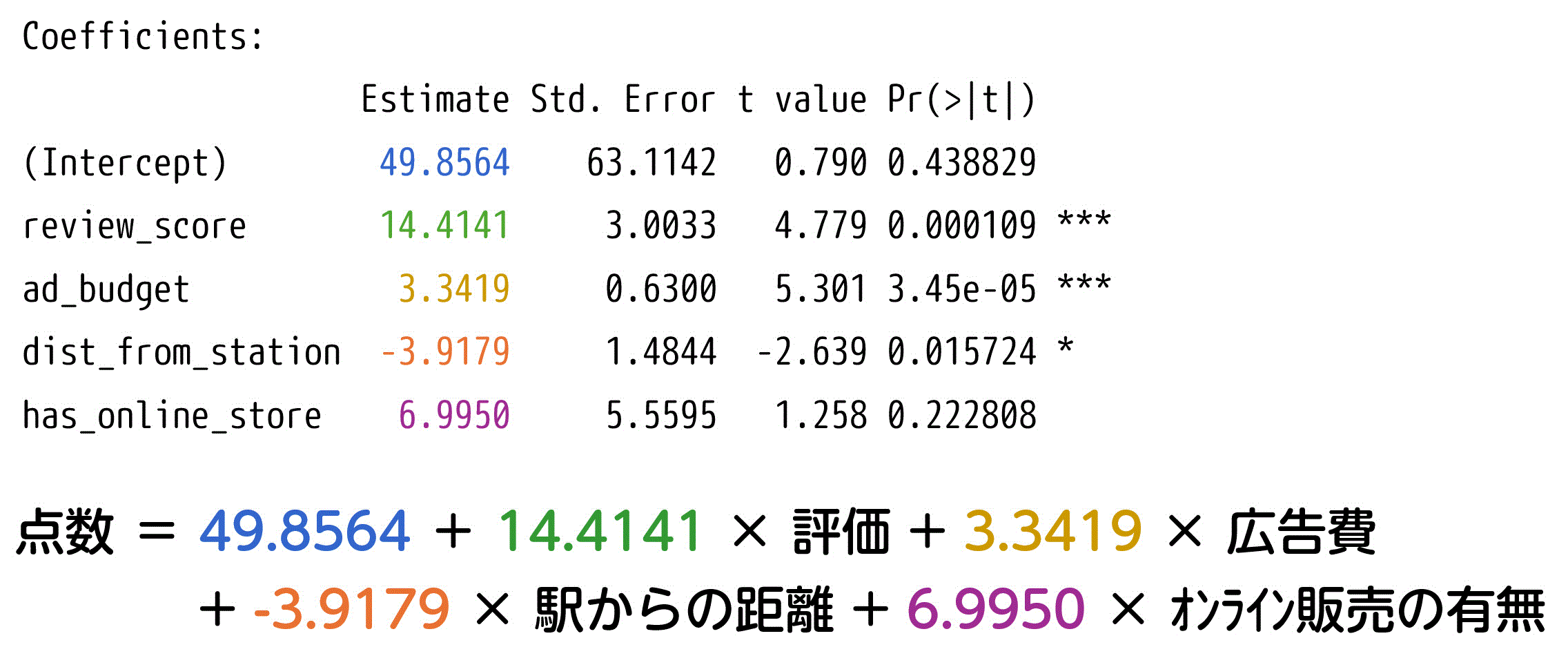
この式に、以下の方程式に与えられたデータと各パラメータの値を代入すればOKです。
- 評価 = 4.1
- 広告費 = 5
- 駅からの距離 = 3
- オンライン販売の有無 = 1 (あり)
実際に代入すると、売上を次のように求めることができます。
\[\begin{align*}
\mathrm{売上} \ & = 49.8564 + 14.4141 \times 4.1 + 3.3419 \times 5 + (- 3.9179) \times 3 + 6.9950 \times 1
\\ & = 49.8564 + 59.09781 + 16.7095 - 11.7537 + 6.9950
\\ & = 120.90501
\end{align*}\]
小数第2位を四捨五入して、答えは 120.9 万円となります。
(4)
解答: 3つ
各説明変数のp値は、出力結果の Pr(>|t|) から読み取ることが出来ます。
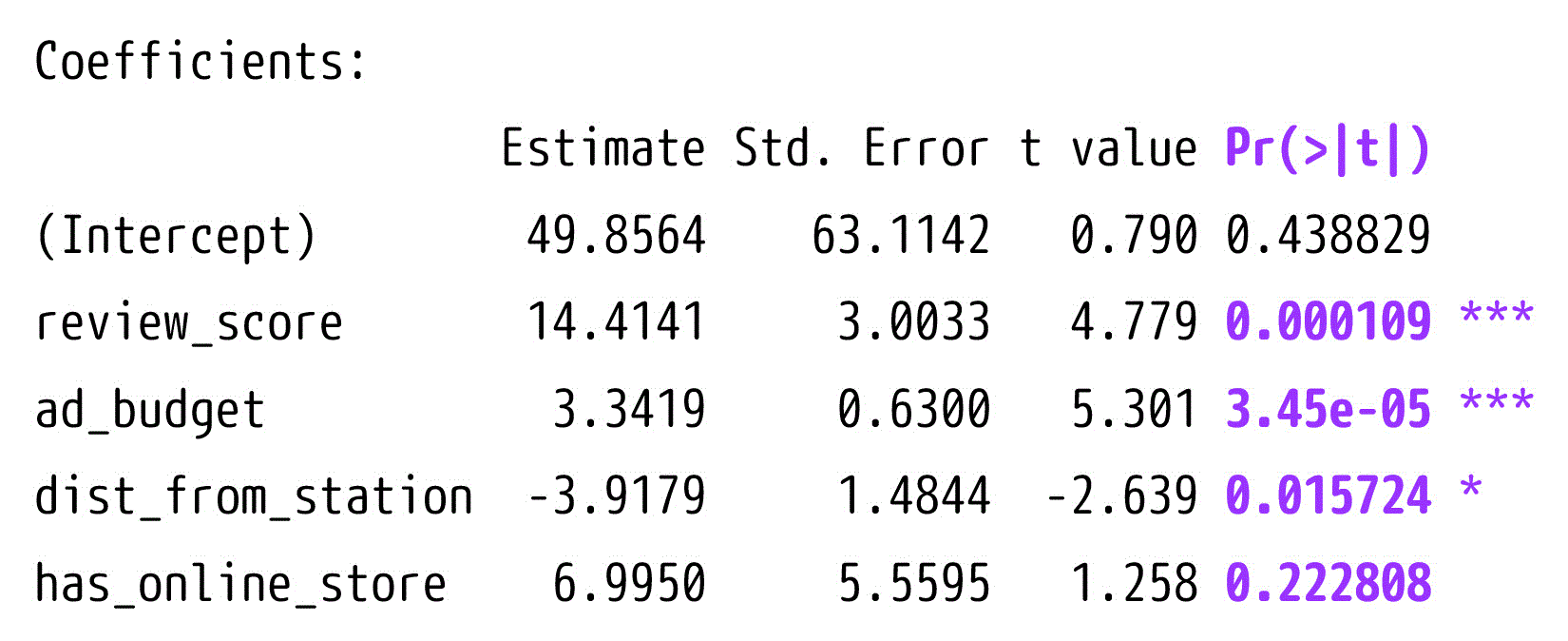
各説明変数が、有意水準5%で有意となる(棄却される)か確かめましょう。
- review_score: 0.000109 < 0.05: 有意(棄却される)
- ad_budget: 3.45e-05 < 0.05: 有意(棄却される)
- dist_from_station: 0.015724 < 0.05: 有意(棄却される)
- has_online_store: 0.222808 ≧ 0.05: 有意でない(棄却されない)
結果、有意な変数は3つであるとわかります。
(5)
解答: 3
選択肢を1つずつ見ていきましょう。
1. 部員数のt値に対応するp値が0.05未満のため、この重回帰モデルはデータの変動をうまく説明できていると言える。
誤りです。F値に対応するp値は、回帰モデル全体が有意であるかどうか(=回帰式内の説明変数が目的変数に対して有意に影響を与えているかどうか)を示すものであり、モデルがデータの変動をうまく説明しているかを示すものではありません。
2. 説明変数の中で、「評価」の偏回帰係数が最も大きいため、説明力が最も大きい説明変数は「評価」であると言える。
誤りです。偏回帰係数の大小は説明力とは関係がありません。
偏回帰係数は、説明変数が1変化すると、目的変数がどれだけ変化するかを示すパラメータです。
3. 評価サイトの評価が1点上がると、売上高は約14.4万円上がる傾向がある。
正しいです。評価(review_score)の偏回帰係数が約14.4であるため、評価が1点上昇すると、売上高は約14.4万円増加することが示されています。
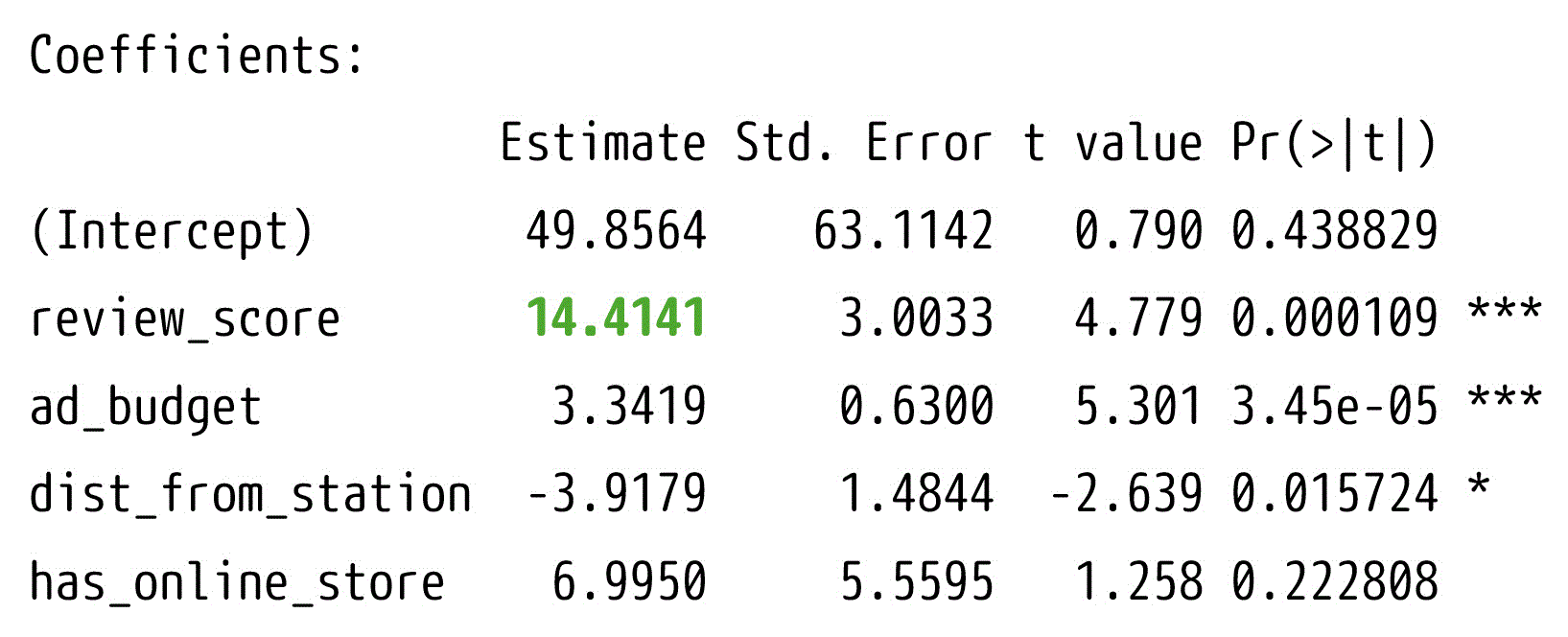
4. 「オンライン販売の有無」は量的変数ではないため、回帰分析への使用は避けるべきである。
誤りです。「オンライン販売の有無」はダミー変数として扱われます。ダミー変数は、質的な情報を数値化する方法で、回帰分析においても適切に使用できます。
この場合、0(オンライン販売なし)または1(オンライン販売あり)で表され、モデル内で他の説明変数と同様に、売上に対する影響を評価することができます。
5. 最寄り駅から店舗までの距離が長くなると、売上高も増える傾向にある。
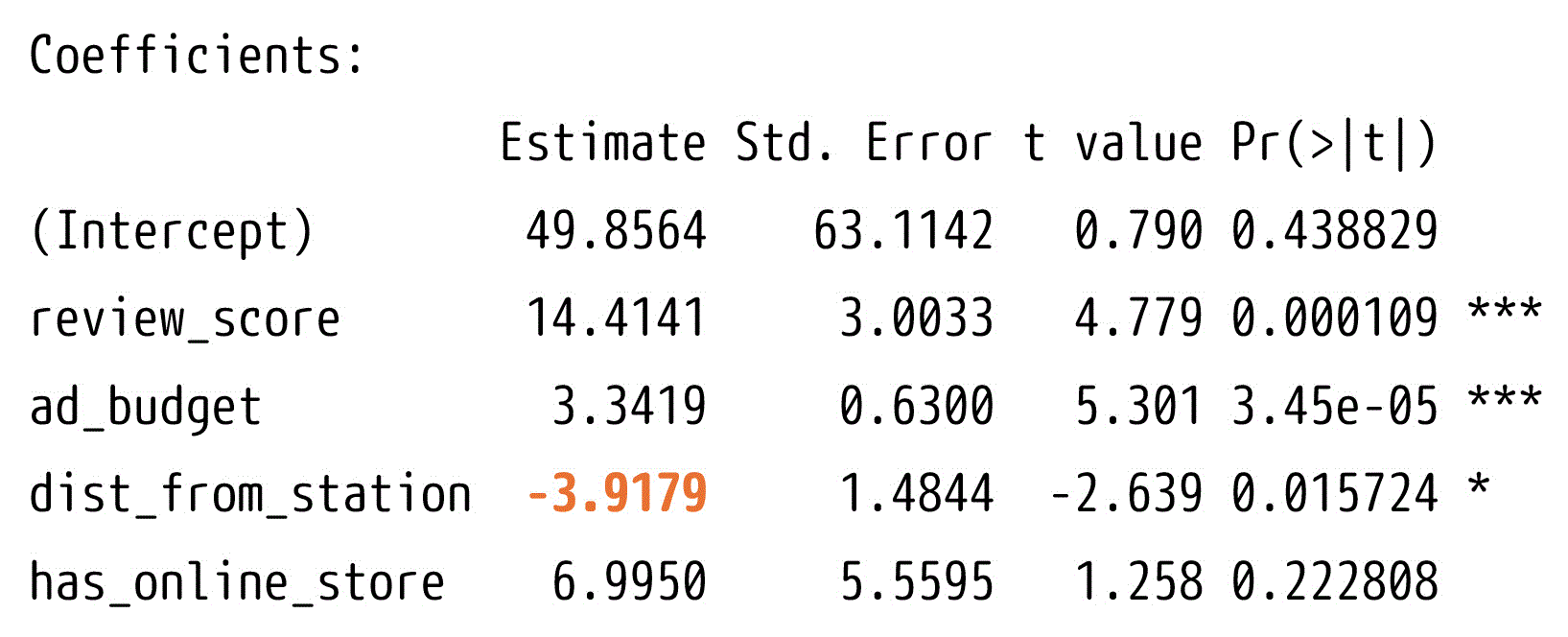
誤りです。回帰モデルの中で「駅からの距離」(dist_from_station)の偏回帰係数は負の値(約-3.92)です。
これは、距離が1分増加するごとに売上高が約3.92万円減少することを意味します。
したがって、最寄り駅からの距離が長くなると、売上高が減少する傾向があると解釈されます。
(6)
解答: 6
重回帰モデルと単回帰モデルのように、説明変数の数が異なるモデルを比較する際には、自由度調整済み決定係数の大小を比べ、より大きいモデルを選択します。
※ 通常の決定係数は説明変数を増やすだけで必ず上昇してしまうため、モデルの真の説明力を評価するには不適切です。
ここで、2つのモデルの自由度調整済み決定係数を比較すると、次の通りとなります。
- 重回帰モデル: 0.7188
- 単回帰モデル: 0.3621
よって、正解は「6. 重回帰モデルの方の自由度調整済み決定係数がより大きいため、重回帰モデルの方が良いモデルと言える。」となります。
注釈
| ↑1 | 定数項に対するt値も出力されますが、定数項が0ではないかどうかを検証することは、実務的にはあまり意味がない場合が多いです。 |
|---|---|
| ↑2 | 例えば、偏回帰係数が2であると帰無仮説で仮定した場合、分子の "-0" の部分は "-2" となります。 |
| ↑3 | 一元配置分散分析では、自由度を「グループ数 - 1」としますが、回帰分析において自由度を「説明変数 - 1」とするのは誤りです。一元配置分散分析では、全グループの平均を求めることで自由度が1失われるため、「グループ数 - 1」としています。これに対して、回帰分析では、説明変数を使って個別の回帰直線をモデル化しています。そのため、自由度は説明変数の数そのものを使います。 |
| ↑4 | 回帰分析では、切片 \( \alpha \) と \( k \) 個の偏回帰係数 \( \beta_1 \), \( \beta_2 \), …, \( \beta_k \) の \( k + 1 \) つのパラメータを使ってモデルをフィットさせるため、これに対応する自由度が \(k+1 \) つ失われます。そのため、残差変動の自由度は「観測データ数 - k - 1」として計算されます。 |
関連広告・スポンサードリンク