スポンサードリンク
こんにちは、ももやまです。
出口調査を理解するためには、統計学の基礎的な知識が必要となります。
そこで、本記事では出口調査を理解するために必要な統計学の基礎的な内容をまとめています。
※ 正規分布については、「出口調査の仕組み」でも解説をしているため、本記事では概念のみの説明となっています。
スポンサードリンク
1. 確率変数
例えば、コインを投げて、表が出たら1点、裏が出たら0点とするゲームを考えてみましょう。
ここで、コインの表が出る確率は1/2、裏が出る確率も1/2です。つまり、1/2の確率で得られる点数は1点、残りの1/2の確率では0点が得られます。

このように、結果がランダムに決まり、その結果に応じて数値(今回の例の場合は点数)が変わる変数を確率変数と呼びます。確率変数は、\( X \) のような大文字で表されることが多いです。
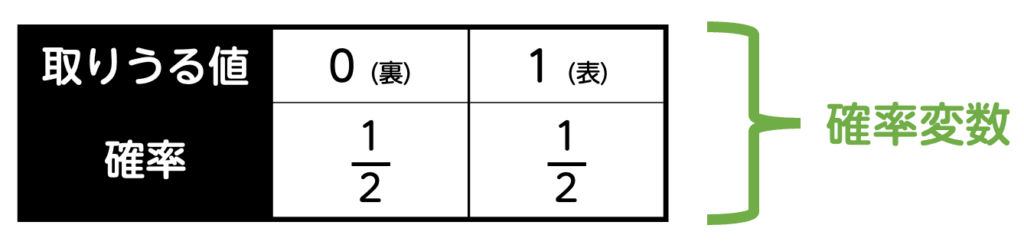
確率変数は、どの値が取られるかは事前には決まっていませんが、それぞれの値が取られる確率はあらかじめ定まっています。
例えば、コイントスの例では、得られる点数は 1 または 0 のどちらかですが、どちらが得られるかは偶然に左右されます。この「偶然性」を確率として扱い、変数に関連づけたものが確率変数です。
スポンサードリンク
2. 平均(期待値)・分散・標準偏差
確率変数 \( X \) がどれくらいの値を取るかを、それぞれの確率で説明するのは大変です。そこで、確率変数が取りうる値の特徴を、1つの数値で簡潔に表す方法として、平均、分散、標準偏差という指標を使います。
[i] 平均 (期待値)
平均とは、確率変数 \( X \) が「平均してどれくらいの値を取るか」を表す指標で、記号では \( E(X) \) などで表します。これは「期待値」とも呼ばれ、確率的な現象における「長期的に見た場合の平均値」を意味します。
平均は、各値にその値が取られる確率を掛けたものの和で計算できます。
では、実際に先ほどのコイントスで得られる点数 \(X \) を例に、平均 \( E(X) \) を求めてみましょう。
実際に平均を求めると次のように計算できます。
\[\begin{align*}
E(X) & = 0 \times \frac{1}{2} + 1 \times \frac{1}{2}
\\ & = \frac{1}{2}
\end{align*}\]
つまり、コイントスで得られる点数の期待値は \( \frac{1}{2} = 0.5 \) 点となります。
[ii] 分散
分散は、確率変数 \( X \) のばらつきの度合い表す指標で、記号では \( V(X) \) や \( \mathrm{Var} (X) \) で表します。
分散は、平均からの距離(偏差)がどれだけ大きいかを測るもので、確率変数の値が平均値の周りにどれくらい散らばっているかを示します。
分散の計算は、各値と平均の差(偏差)を2乗し、その値に確率を掛けたものの和で求めます。偏差を2乗する理由は、正負の符号を消して全ての偏差を正の数に変換し、ばらつきを正確に反映させるためです。
では実際に、先ほどのコイントスで得られる得点 \( X \) について、分散 \( V(X) \) を求めてみましょう。
実際に分散を求めると次のように計算できます。
\[\begin{align*}
V(X) & = \left( 0 - \frac{1}{2} \right)^2 \times \frac{1}{2} + \left( 1 - \frac{1}{2} \right)^2 \times \frac{1}{2}
\\ & = \frac{1}{4} \times \frac{1}{2} + \frac{1}{4} \times \frac{1}{2}
\\ & = \frac{1}{4}
\end{align*}\]
つまり、コイントスで得られる点数 \( X \) の分散は \( \frac{1}{4} = 0.25 \) 点2となります。
[iii] 標準偏差
分散 \( V(X) \) では偏差を2乗しているため、元の単位とずれた形になります。そこで、分散の平方根を取ることで、元の単位に戻した指標が標準偏差です。記号では \( \sigma (X) \) などと表現されます。
標準偏差は、分散と違って「ばらつき度合い」を元のスケールで直感的に理解できるようにしたものです。
標準偏差は、次の式のように、分散の平方根で計算できます。\[
\sigma (X) = \sqrt{ V(X) }
\]
例えば、先程のコイントスで得られる点数 \( X \) の標準偏差 \( \sigma (X) \) は次のように計算できます。\[\begin{align*}
\sigma(X) & = \sqrt{ V(X) }
\\ & = \sqrt{ \frac{1}{4} }
\\ & = \frac{ \sqrt{1} }{ \sqrt{4} }
\\ & = \frac{1}{2}
\end{align*}\]
つまり、コイントスで得られる点数の標準偏差は \( \frac{1}{2} = 0.5 \) 点となります。
確率変数 \( X \) の取りうる値 \( x_1 \), \( x_2 \), … と、各取りうる値となる確率 \( p_1 \), \( p_2 \), … が次のように対応しているとする。
| 取りうる値 | \( x_1 \) | \( x_2 \) | \( \cdots \) | \( x_n \) |
| 確率 | \( p_1 \) | \( p_2 \) | \( \cdots \) | \( p_n \) |
※ 上の表の各列は対応している。例えば、\( x_1 \) となる確率は \( p_1 \)、\( x_2 \) となる確率は \( p_2 \) である。
このとき、平均(期待値)、分散、標準偏差は次のように計算ができる。
(1) 平均(期待値) \( E(X) \)
→ \( X \) が取りうる値の中心的な値を表している。
求め方: 各値にその値が取られる確率を掛けたものの和
\[\begin{align*}
E(X) & = \textcolor{deepskyblue}{x_1} \textcolor{green}{p_1} \textcolor{purple}{+} \textcolor{deepskyblue}{x_2} \textcolor{green}{p_2} \textcolor{purple}{+} \cdots \textcolor{purple}{+} \textcolor{deepskyblue}{x_n} \textcolor{green}{p_n}
\\ & = \textcolor{purple}{\sum^{n}_{k=1}} \textcolor{deepskyblue}{x_k} \textcolor{green}{p_k}
\end{align*}\]
(2) 分散 \( V(X) \)
→ \( X \) のばらつきの度合いを元の単位の2乗単位で表したもの
求め方: 各値に平均の差(偏差)を2乗し、その値に確率を掛けたものの和
※ \( m = E(X) \) とする。\[\begin{align*}
V(X) & = ( \textcolor{deepskyblue}{x_1} - \textcolor{orange}{m} )^2 \textcolor{green}{p_1} \textcolor{purple}{+} ( \textcolor{deepskyblue}{x_2} - \textcolor{orange}{m} )^2 \textcolor{green}{p_2} \textcolor{purple}{+} \cdots \textcolor{purple}{+} ( \textcolor{deepskyblue}{x_n} - \textcolor{orange}{m} )^2 \textcolor{green}{p_n}
\\ & = \textcolor{purple}{\sum^{n}_{k=1}} ( \textcolor{deepskyblue}{x_k} - \textcolor{orange}{m} )^2 \textcolor{green}{p_k}
\end{align*}\]
(3) 標準偏差 \( \sigma (X) \)
→ \( X \) のばらつきの度合いを元の単位で表したもの
求め方: 分散の平方根を取る
\[
\sigma (X) = \sqrt{ V(X) }
\]
[iv] 確率変数の変換
確率変数 \( X \) に定数を加えたり、掛けたりすると、平均、分散、標準偏差はどのように変化するのでしょうか。ここでは、それぞれの変換について説明します。
★ 確率変数Xに定数を掛けた場合
ある確率変数に定数 \( a \) を掛けると、平均、分散、標準偏差は次のように変わります。
| 種類 | 変化の仕方 |
|---|---|
| 平均 | 掛けた定数倍 (\( b \) 倍) となる |
| 分散 | 掛けた定数の2乗倍 ( \( b^2 \) 倍) となる |
| 標準偏差 | 掛けた定数の絶対値倍 (\( |b| \) 倍) となる |
先ほどのコイントスの例で、なぜこのような変化の仕方をするか見て行きましょう。
まず、コイントスの得点ルールを次の通り変化します。
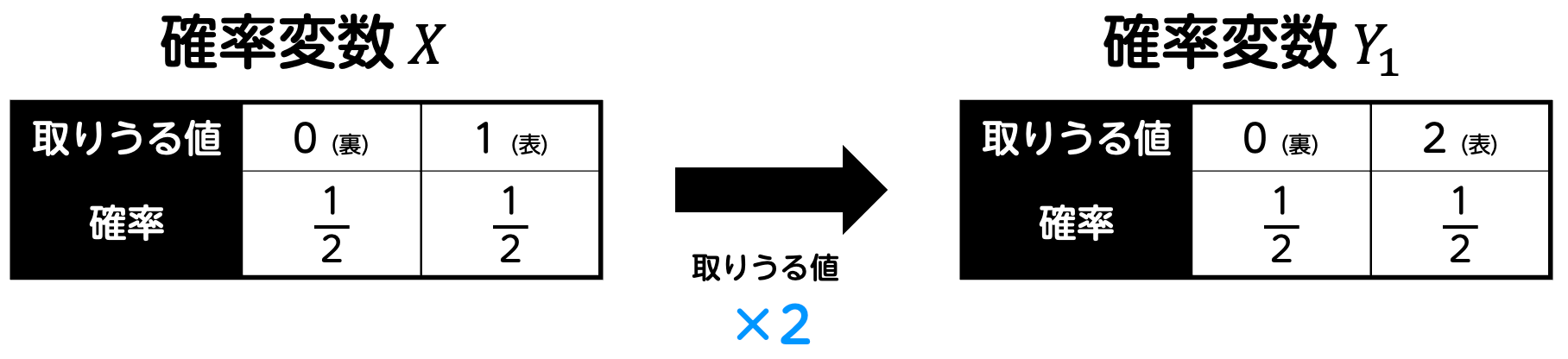
このときに得られる点数の確率変数を \( Y_1 \) とおきましょう。つまり、\( Y_1 = 2X \) ですね。
すると、このルール変更により、表が出た場合も裏が出た場合も、得点は2倍になります。つまり、すべての得点が2倍となっているため、平均 \( E(Y_1) \) も当然元の値 \( E(X) \) の2倍となりますよね。\[\begin{align*}
E(Y_1) & = E(2X)
\\ & = 2 E(X)
\\ & = 2 \times \frac{1}{2}
\\ & = 1
\end{align*}\]
また、ばらつき度合いを表す分散や標準偏差も同様に考えられます。すべての得点が2倍となっているということは、点数の変動も2倍となるため、ばらつき度合いも当然2倍となります。そのため、標準偏差は元の
また、表が出ようが裏が出ようがもらえる点数が2倍になるということは、ばらつき度合いも当然2倍となります。そのため、標準偏差 \( \sigma (Y_1) \) は元の値 \( \sigma(X) \) の2倍となります。\[\begin{align*}
\sigma (Y_1) & = \sigma(2 X)
\\ & = |2| \sigma(X)
\\ & = 2 \times\frac{1}{2}
\\ & = 1
\end{align*}\]
分散については、値のばらつき具合を2乗して考えるため、ばらつきが2倍になったときは、分散は 2乗されて4倍となります。\[\begin{align*}
V(Y_1) & = V(2 X)
\\ & = 2^2 V(X)
\\ & = 4 \times \frac{1}{4}
\\ & = 1
\end{align*}\]
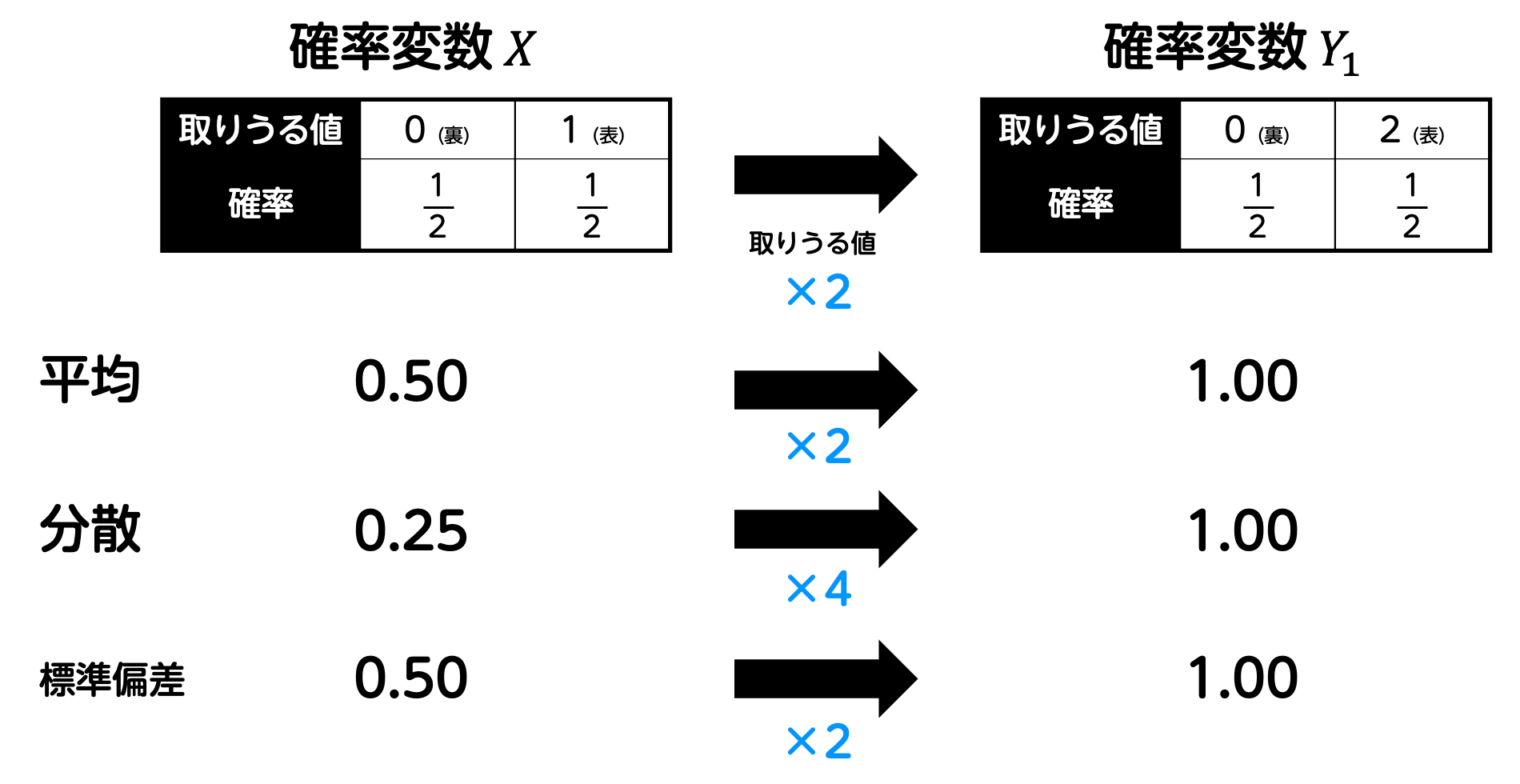
このように、掛け算による変換は、全体のスケールをそのまま拡大するため、平均もばらつき具合も直感的に倍になることが理解できます。
★ 確率変数Xに定数を加えた場合
ある確率変数に定数 \( b \) を足すと、平均、分散、標準偏差は次のように変わります。
| 種類 | 変化の仕方 |
|---|---|
| 平均 | 足した定数 \( b \) 分増加 |
| 分散 | 変化なし |
| 標準偏差 | 変化なし |
先ほどと同じように、なぜこのような変化の仕方をするか見て行きましょう。
ここで、得点のルールを次のように変えたとします。
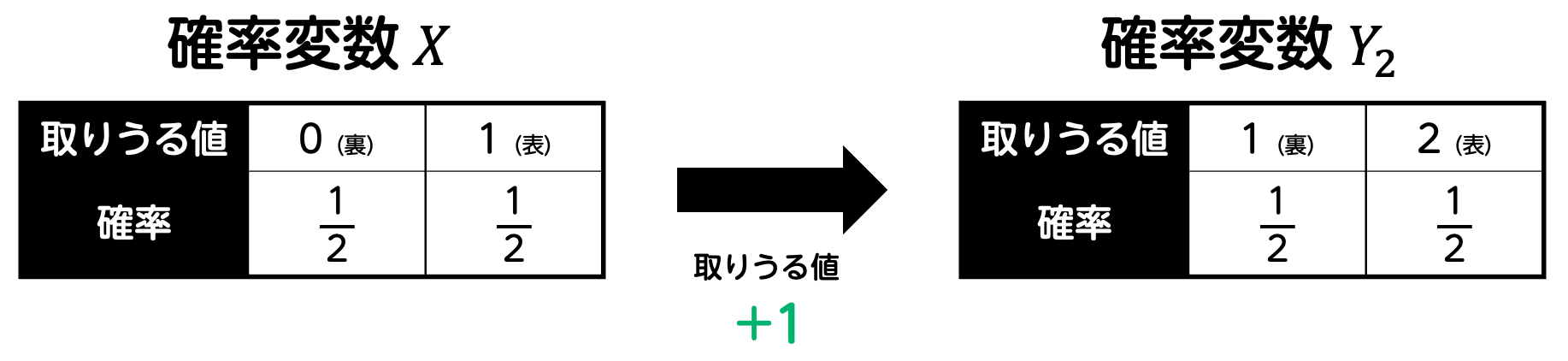
すると、このルール変更により、表が出た場合も裏が出た場合も、もらえる点数は元の値よりも1点増加しています。つまり、すべての得点が1点増えるため、平均 \( E(Y_2) \) も当然元の値 \( E(X) \) より1増えます。\[\begin{align*}
E(Y_2) & = E(X+1)
\\ & = E(X) + 1
\\ & = \frac{1}{2} + 1
\\ & = \frac{3}{2}
\\ & = 1.5
\end{align*}\]
しかし、ばらつき具合(分散や標準偏差)についてはどうでしょうか。ここでは、点数の差(表か裏かによる違い)には全く影響がないことが重要です。得られる点数がすべて1点増えているだけで、点数の「変動の幅」自体は変わりません。したがって、分散や標準偏差は変化しません。
\[
V(Y_2) = V(X)
\]\[
\sigma (Y_2) = \sigma (X)
\]
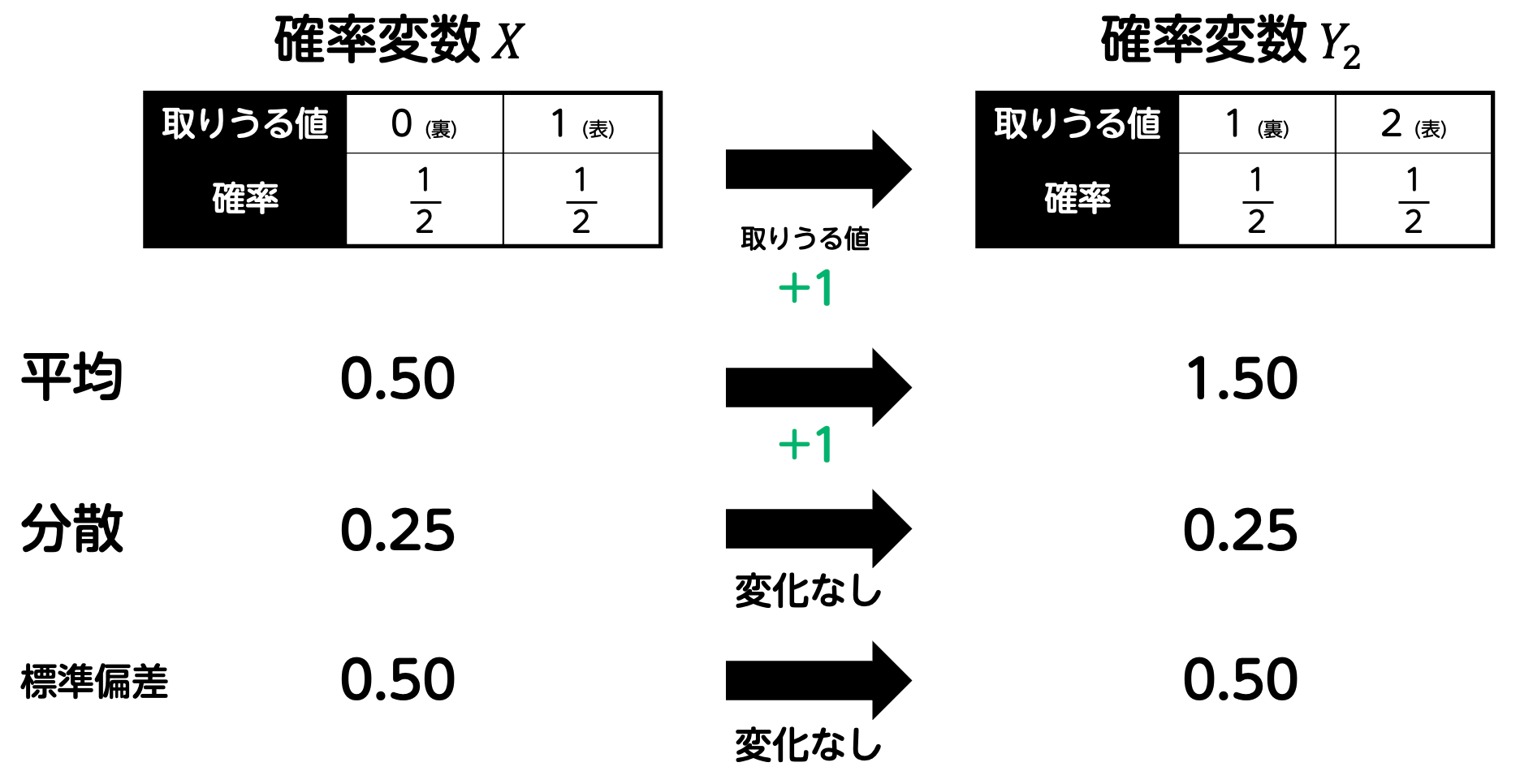
このように、定数を加える変換は、全体の値をシフトするだけで、ばらつきには影響を与えないため、平均だけが変わり、分散や標準偏差は変わらないことが理解できます。
(1) 確率変数 \( X \) を \( a \) 倍して \( aX \) とする。このとき、[1-i], [1-ii], [1-iii] の関係が成り立つ。
[1-i] 平均 \( E(aX) \) … \( a \) 倍となる。\[E(aX) = a E(X)
\] [1-ii] 分散 \( V(aX) \) … \( a^2 \) 倍となる。\[
V(aX) = a^2 E(X)
\] [1-iii] 標準偏差 \( \sigma (aX) \) … \( |a| \) 倍となる。\[
\sigma (aX) = |a| E(X)
\]
(2) 確率変数 \( X \) に \( b \) を足して \( X+b \) とする。このとき、[2-i], [2-ii], [2-iii] の関係が成り立つ。
[2-i] 平均 \( E(X+b) \) … \( b \) 増える \[E(X+b) = E(X) + b
\] [2-ii] 分散 \( V(X+b) \) … 変化しない。\[
V(X+b) = V(X)
\] [2-iii] 標準偏差 \( \sigma (X+b) \) … 変化しない。\[
\sigma (X+b) = \sigma (X)
\]
スポンサードリンク
3. 二項分布
先ほどのコイントスの結果(表と裏)のように、結果が2通りしかない試行を繰り返すことを考えてみましょう。
ここで、結果が2通りしかない試行を繰り返したときに、その片方の事象が起こる回数を \( X \) とします。
このとき、確率変数 \( X \) は特別な分布に従います。この分布を、二項分布と呼びます。
例えば、コイントスを50回行ったときに表が出る回数を \( X_1 \) とおくと、\( X_1 \) は二項分布に従います。
二項分布に従う確率変数は、平均、分散、標準偏差を簡単に求めることができるのが特徴です。
[i] 平均(期待値)の求め方
ある確率変数 \( X \) が二項分布に従うとき、その平均 \( E(X) \) は、試行を行った回数 \( n \) と、片方の事象が起こる確率 \( p \) の積で求めることができます。
\[\begin{align*}
E(X) & = n \times p
\\ & = np
\end{align*}\]
例えば、コイントスを100回行ったとき、表が出る回数 \( X \) の平均 \( E(X) \) は次のように計算ができます。\[\begin{align*}
E(X) & = \underbrace{ n }_{100} \times \underbrace{ p }_{ \frac{1}{2} }
\\ & = 50
\end{align*}\]よって、表が出る回数の平均は50回と求められます。
★ 平均が \( np \) となる理由
1回の試行で、事象が起こる確率を \( p \) としましょう。すると、事象が起こる回数の平均は \( p \) となりますね。
この試行を \( n \) 回繰り返すので、平均 \( p \) が \( n \) 回分足されて、\( np \) となるのです。\[\begin{align*}
E(X) & = \underbrace{ p + p + p + \cdots + p }_{ n \ \mathrm{個} }
\\ & = np
\end{align*}\]
[ii] 分散の求め方
ある確率変数 \( X \) が二項分布に従うとき、その分散 \( V(X) \) は、試行を行った回数 \( n \)、片方の事象が起こる確率 \( p \)、片方の事象が起こらない確率 \( 1-p \) の積で求めることができます。
\[\begin{align*}
V(X) & = n \times p \times (1-p)
\\ & = np (1-p)
\end{align*}\]
例えば、コイントスを100回行ったとき、表が出る回数 \( X \) の分散 \( V(X) \) は次のように計算ができます。\[\begin{align*}
V(X) & = \underbrace{ n }_{100} \times \underbrace{ p }_{ \frac{1}{2} } \times ( 1 - \underbrace{ p }_{ \frac{1}{2} } )
\\ & = 25
\end{align*}\]よって、表が出る回数の分散は25回2と求められます。
★ 分散が \( np(1-p) \) となる理由
1回の試行で、事象が起こる確率を \( p \) としましょう。すると、事象が起こる回数の分散は \( p(1-p) \) となりますね。\[\begin{align*}
(0-p)^2 (1-p) + (1-p)^2 p & = p^2 (1-p) + (1-p)^2 p
\\ & = p (1-p) \left\{ p + (1-p) \right\}
\\ & = p (1-p)
\end{align*}\]
この試行を \( n \) 回繰り返すので、分散 \( p(1-p) \) が \( n \) 回分足されて[1]各試行は独立なときのみ、2つの試行の分散 \( p(1-p) \) を足すことができます。、\( np(1-p) \) となるのです。\[\begin{align*}
E(x) & = \underbrace{ p(1-p) + p(1-p) + p(1-p) + \cdots + p(1-p) }_{ n \ \mathrm{個} }
\\ & = np(1-p)
\end{align*}\]
[iii] 標準偏差の求め方
標準偏差 \( \sigma (X) \) は、分散 \( V(X) \) の平方根で求めることができます。
\[\begin{align*}
\sigma (X) = \sqrt{ V(X) }
\end{align*}\]
例えば、コイントスを100回行ったとき、表が出る回数 \( X \) の標準偏差 \( \sigma (X) \) は、散 \( V(X) = 25 \) を用いてつぎのように計算できます。\[\begin{align*}
\sigma (X) & = \sqrt{ V(X) }
\\ & = \sqrt{25}
\\ & = 5
\end{align*}\]よって、表が出る回数の標準偏差は5回と求められます。
4. 正規分布: 二項分布の近似
これまで、コイントスのように結果が2通りしかない試行を繰り返すと、その片方の事象が起こる回数 \( X \) は二項分布に従うことを説明しました。
次に、試行回数 \( n \) を大きくした場合の二項分布について考えてみましょう。試行回数を増やしていくと、事象の発生回数 \( X \) とその確率をグラフにプロットしたときに、興味深い形が見えてきます。
例えば、コイントスを100回行ったとき、表が出る回数を横軸に、その確率を縦軸にしてグラフを描いてみます。
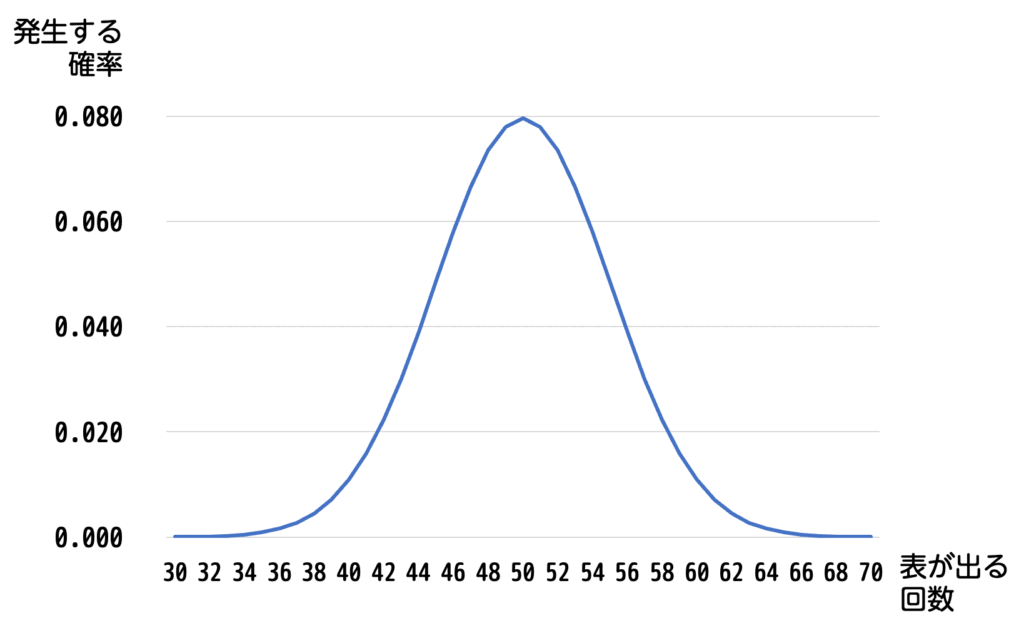
すると、グラフの中央付近に一番高い山ができて、左右対称に広がっていることがわかります。これは偶然ではなく、試行回数が増えると二項分布がこのような形になるのです。
実は、試行回数 \( n \) が十分に大きくなると、この二項分布のグラフは正規分布と呼ばれる特定の形に近づきます。
言い換えると、試行回数が大きいときに、二項分布は正規分布での近似が可能です[2]目安として、試行回数 \( n \)、事象が起こる確率 \( p \) のとき、\( np > 5 \) かつ \( n(1-p) > 5 \) が成り立つ場合に近似ができます。。
関連広告・スポンサードリンク