スポンサードリンク
2020/09/02 コロナウイルスなどの感染者増加と片対数グラフの関係について追加
2022/05/25 改行バグの修正
こんにちは、ももやまです。
実験の基礎シリーズの最終回となる今回は、実験で出てくる片対数・両対数グラフについて説明していきます。
内容としては、
- 片対数グラフ・両対数グラフとは何か
- 対数グラフの読み方
- 片対数グラフが有効な例、プロットの仕方
(なぜコロナの感染者増加を表すグラフは片対数グラフなのか) - 両対数グラフが有効な例、プロットの仕方
- Excelを用いた片対数、両対数グラフの書き方
の5点です。
では、今回も頑張っていきましょう。
目次
スポンサードリンク
1.片対数・両対数グラフとは
(1) 片対数グラフとは
皆さんが今まで使ってきたグラフは、縦の軸の目盛りも、横の軸の目盛りも1, 2, 3… やら 10, 20, 30… と等間隔に振られていますね。
片対数グラフというのは、縦の軸か横の軸の片方の目盛りが等間隔の目盛りではなく「対数の目盛り」になったグラフです。
片方の軸なので、縦と横のどちらを対数にしてもOKですが、縦を対数軸にすることが多い気がします*1。
(2) 両対数グラフとは
両対数グラフというのは、縦の軸か横の軸の片方の目盛りの両方が対数の目盛りになったグラフです。
1年生の実験ではあまりお目にかかる機会はないかもしれません。
片対数グラフ・両対数グラフのグラフ用紙はこちらのホームページに掲載されていたので、確認したい人はぜひ見てください。
(今回片対数グラフの説明をするにあたって、神戸市立工業高等専門学校長谷研究室の片対数グラフを引用しています。[アクセス日:2019年9月29日])
スポンサードリンク
2.対数軸の読み方・プロットの仕方
(1) 対数グラフの1目盛りあたりの単位
片対数や両対数などの対数に関するグラフでまず挫折するのは、目盛りの読み方だと思います。
そこで、対数軸の読み方について少し勉強していきましょう。

一番下の赤矢印の部分では、1目盛りあたり1増えています。
一方、真ん中の青矢印の部分になると増え方が10ずつに変わります。
片対数グラフの1つ上の目盛りが広く、1つ下の目盛りが狭くなっているのが目盛りの間隔の変化のサインを表しています(この部分は必ず値が \( 10^n \) になります)。親切なグラフ用紙なら太線になっているはずです*2。
このサインより上側に行くと1つあたりの目盛りの単位が10倍に、下側にいくと目盛りの単位が 1/10 倍になります。
また、グラフによっては、補助線が書かれていることもあります。
この補助線は、2つの線の真ん中の値を表します。
(例えば、10と20に囲まれた補助線なら15を表す)
(2) 不思議な目盛り間隔の理由
対数目盛を見て、「なんでこんなに目盛りの間隔が違うの?」と思った人もいるかもしれません。
そこで、対数目盛の1から10を表すそれぞれの部分に \( \log_{10} \) をとって方眼紙と比較してみましょう。
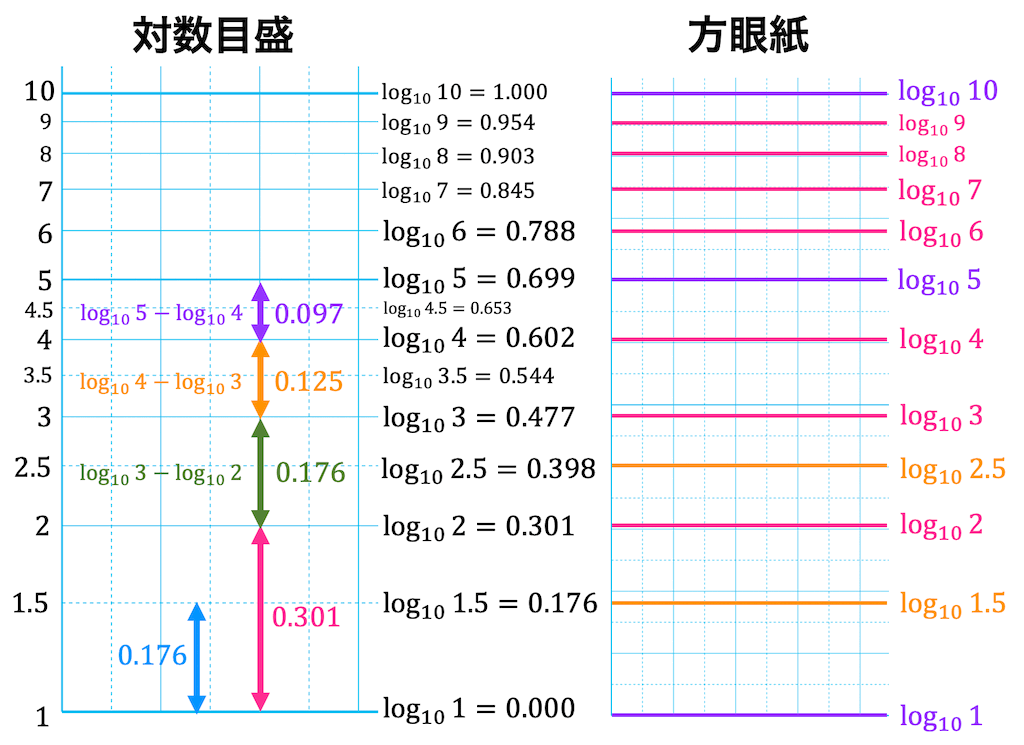
すると、1と2の間隔は \( \log_{10} 1 \) と \( \log_{10} 2 \) の間隔、2と3の間隔は \( \log_{10} 2 \) と \( \log_{10} 3 \) の間隔と等しくなっていますね。
もう1つ、\( 10^n \) を境目に突然値の増え方が10倍になりましたね。この仕組みを図とともにわかりやすく書いてみました。
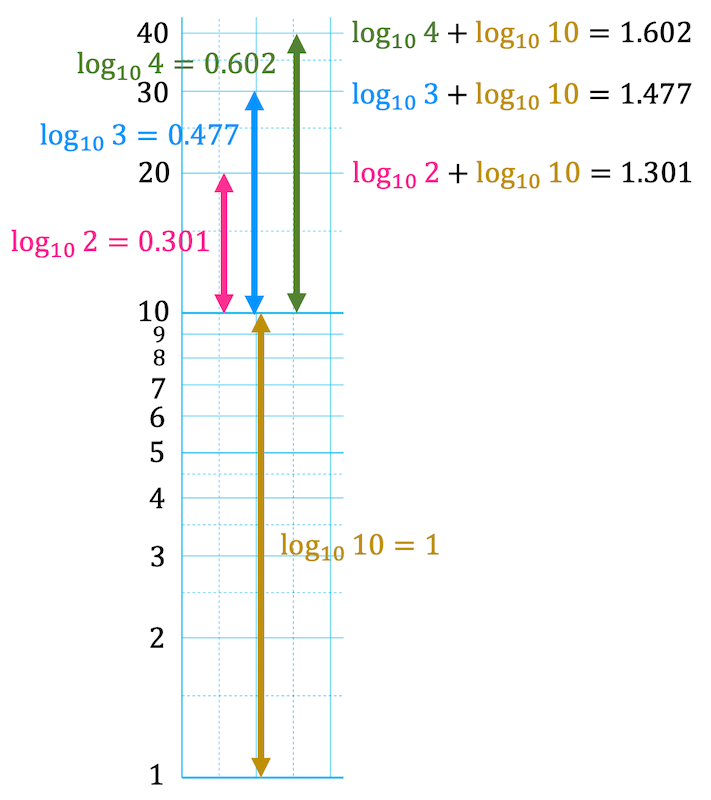
例えば20(つまり \( \log_{10} 20 \) というのは\[
\log_{10} 20 = \log_{10} 2 + \log_{10} 10
\]の2つに分解できますね。
同じ対数の底同士の足し算は真数同士の積で計算できますね。同様に 30, 40の場合も\[
\log_{10} 30 = \log_{10} 3 + \log_{10} 10 \]\[
\log_{10} 40 = \log_{10} 4 + \log_{10} 10
\]のように \( \log_{10} 10 \) が足されていますね。
そのため、\( 10^n \) を境に値が10倍されるのです*3
スポンサードリンク
3.片対数グラフの実用例(なぜ感染者の増加を片対数で表すのか)
ここでは、片対数グラフを使う実用例を1つ紹介したいと思います。
ここ数か月、コロナの話を聞かないことはありません。
感染者が何人だとか、後期も遠隔授業とか、嫌でも耳に流れてきてしまいます。
そんな中、ニュースで突然片対数グラフが出てきました。
(この漫画に出てくるのが片対数グラフ)
新型コロナウイルス感染症について,片対数グラフを見かけたり私自身描いているのですが「対数グラフとはなんぞや」ということを伝えたくて漫画を描きました。
「対数グラフで伝染病を見る」(1/3)
サイトにpdfファイルでアップしたのでまとめて読みたい人はこちらにどうぞhttps://t.co/mwrRCkZ6AD pic.twitter.com/0USW9Eil0a
— かずき@グラフ哲学舎 (@kazukigraph) April 10, 2020
このようなグラフ(片対数)を見た一部の人は「なんだこのグラフ、感染者数を少なく見せるインチキじゃないのか」とわけわからないことを言っていました。
そこで、(コロナに限らず)感染者が急激に増えるシーンで片対数グラフが有効な理由を実際にプロットすることで確かめてみましょう。
(1) 片対数グラフにプロットしてみよう
実際に感染者のデータを使うのもどうかと思ったので、今回はこちらの感染者シミュレーターを使って実験を行いました。
すると、下のような実験結果となりました。
| 経過日数 [日] | 累計感染者 [人] |
| 1 | 9 |
| 2 | 15 |
| 3 | 25 |
| 4 | 43 |
| 5 | 74 |
| 6 | 110 |
| 7 | 157 |
| 8 | 212 |
| 9 | 287 |
| 10 | 369 |
| 11 | 456 |
となりました。
まずは、データに対応する部分に点を打ちましょう。
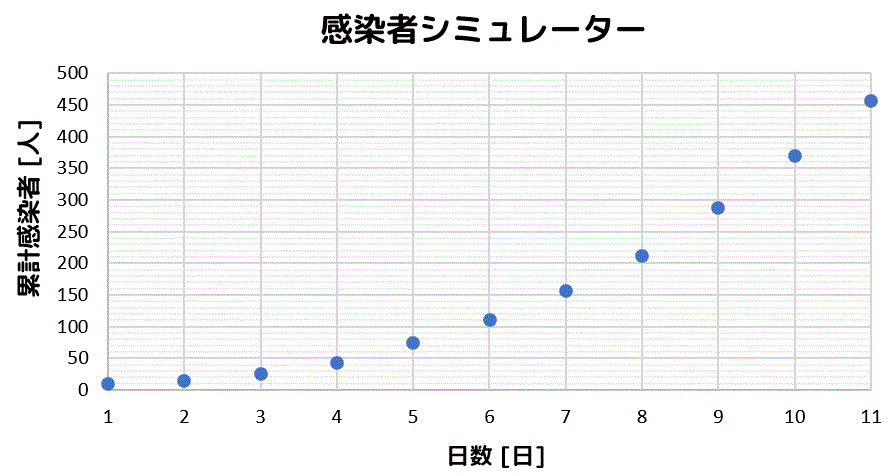
さらに、どの点も近くなるように直線を引いてみましょう。
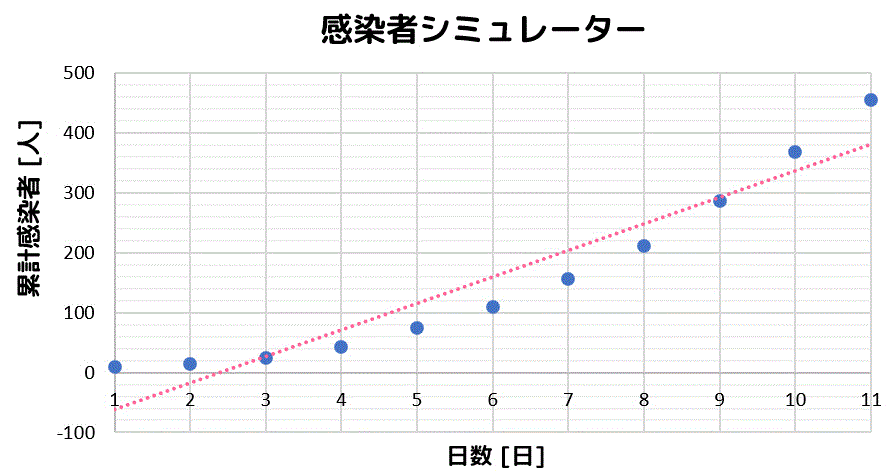
さすがに無理があるグラフになってしまいました。
特に1日目と11日目の点が離れすぎてます。
そこで、人数を対数目盛にしてから、もう1回点を打ってみましょう。
(ここで片対数グラフの登場)
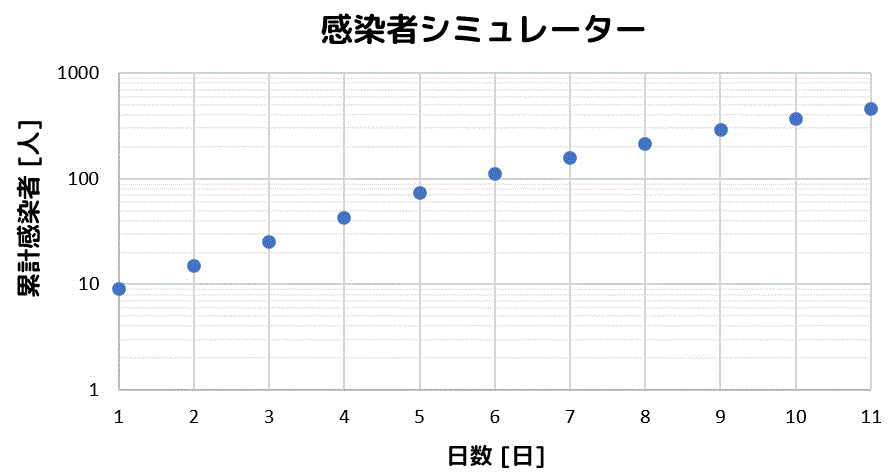
この状態で、先ほどと同じようにどの点も近くなるような直線を引いてみましょう。
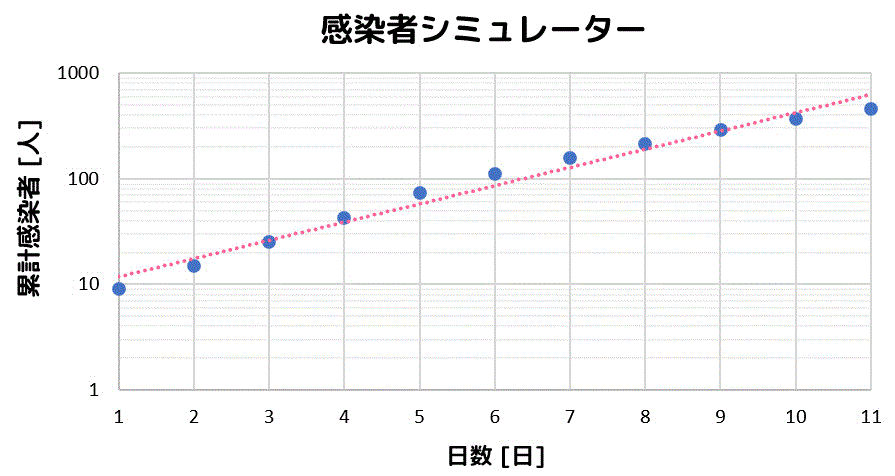
先ほどよりどの点も近くなるような直線が引けましたね。
なぜ対数グラフで直線 = 指数関数的な変化なのか
ところで、対数目盛だと直線になるとはどういうことでしょうか。
少し考えてみましょう。
例えば、\( \log_{10} x = 1 \) となる \( x \) を満たすためには \( x = 10^1 = 10 \) となればOKですね。
同じように \( \log_{10} x = 2 \) であれば \( x = 10^2 = 100 \) で満たしますね。
さらに、
- \( \log_{10} x = 3 \) の場合 \( x = 10^3 = 1000 \)
- \( \log_{10} x = 4 \) の場合 \( x = 10^4 = 10000 \)
- \( \log_{10} x = 5 \) の場合 \( x = 10^5 = 100000 \)
となるように、対数の値が 1, 2, 3, … と等間隔(直線)に増えていく場合、元の数は 1, 10, 100, 1000, … と指数関数(今回は \( 10^x \) 的に)増えていきますね。
そのため、対数目盛で直線になる場合は指数関数的な変化を表すのです。
(2) 片対数グラフと最小2乗法
前回の最小2乗法の記事で、何かしらの変形を行って直線にできるものはなんでも最小2乗法にできると説明しましたね。
そのため、どちらか片方が対数目盛であったとしても、直線になるような変形をすれば最小2乗法が適用できますね。
(a) 式の導出法
まずは、式をどう変形すれば片対数グラフに対する最小2乗法が適用できるかを考えましょう。
片対数グラフで直線になるということは、縦軸である \( y \) 側のデータを対数で変換すれば直線になると言い換えられますね。
これを数式的に表すと、\( Y = \log_{10} y \), \( X = x \) とおきかえることで直線 \( Y = aX + b \) が成立すると言い換えられますね。
ここで、直線 \( Y = aX + b \) に対し、\[
X = x, \ \ \ Y = \log_{10} y
\]を代入し、もとの \( x \), \( y \) の式に戻してあげると\[
\log_{10} y = ax + b
\]となります。
さらに、両辺を\[\begin{align*}
10^{ \log_{10} y } & =10^{ax+b}
\\ & = 10^{b} \cdot 10^{ax}
\\ & = y
\end{align*}\]と変形できます。
ここで、\[
y = 10^{b} \cdot 10^{ax}
\]の \( 10^{b} \) が煩わしいと思った人は \( b' = 10^{b} \) とでもおいて、\[
y = b' 10^{ax}
\]としてもOKです。
(b) 実際のデータに適用
では、先ほど導出した式を実際のデータに適用してみましょう。
| 経過日数 [日] | 累計感染者 [人] |
| 1 | 9 |
| 2 | 15 |
| 3 | 25 |
| 4 | 43 |
| 5 | 74 |
| 6 | 110 |
| 7 | 157 |
| 8 | 212 |
| 9 | 287 |
| 10 | 369 |
| 11 | 456 |
ここからは、「日数」を \( x \) 軸、「感染者数」を \( y \) 軸として説明していきます。
まず、\[
X = x, \ \ \ Y = \log_{10} y
\]に変換した後の各データを表に書いてみましょう。
| X (日数) | Y (感染者数の対数) |
| 1 | 0.954 |
| 2 | 1.176 |
| 3 | 1.398 |
| 4 | 1.633 |
| 5 | 1.869 |
| 6 | 2.041 |
| 7 | 2.196 |
| 8 | 2.326 |
| 9 | 2.458 |
| 10 | 2.567 |
| 11 | 2.659 |
このデータに対し、最小2乗法を適用すると、\[\begin{align*}
Y & = 0.1725X + 0.8992
\\ & = aX + b
\end{align*}\]となります。
この \( a = 0.1725 \), \( b = 0.8992 \) を変換後の式\[
y = 10^{b} \cdot 10^{ax}
\]に代入してあげましょう。
すると、\[\begin{align*}
y & = 10^{0.8992} \cdot 10^{0.1725x}
\\ & = 7.292 \cdot 10^{0.1725x}
\end{align*}\]という関係式が成立します。
この式が、日数と感染者の数に対する近似式となります。
指数関数的な増減をしそうなデータの回帰直線を求める場合、\[
X = x, \ \ \ Y = \log_{10} y
\]と置いてから最小2乗法を適用し、\[
Y = aX + b
\]の \( a \), \( b \) の値を求めると回帰直線\[
y = 10^{b} \cdot 10^{ax}
\]と変形することができる。
4.両対数グラフについて
ここでは、両対数グラフを使う実用例を1つ紹介したいと思います。
とはいっても、両対数グラフが役に立つ場面はあまりありませんが…
(1) 両対数グラフにプロットしてみよう
下の表は、地球を基準(1)としたときの8つの惑星の軌道半径と公転周期を、表したものです。
| 星の名 | 軌道半径 [地球] | 公転周期 [地球] |
| 水星 | 0.387 | 0.240 |
| 金星 | 0.723 | 0.615 |
| 地球 | 1.00 | 1.00 |
| 火星 | 1.52 | 1.88 |
| 木星 | 5.20 | 11.9 |
| 土星 | 9.55 | 29.5 |
| 天王星 | 19.2 | 84.0 |
| 海王星 | 30.1 | 165 |
片対数グラフと同じように、まずは該当するデータを点で打ってみましょう。
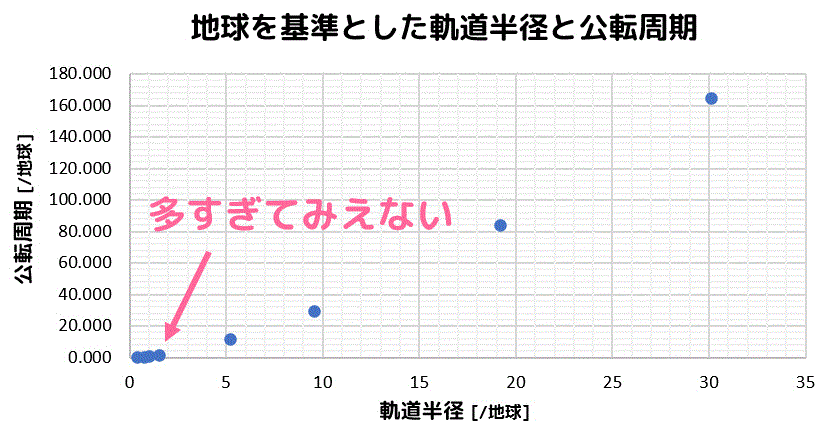
線を引く前から、明らかに直線を引けなさそうなのがわかりますね。
というか、0付近が密集しすぎててもはや見えません。
では、縦軸だけ対数グラフにしてみましょう。
(片対数グラフにプロットした状態)
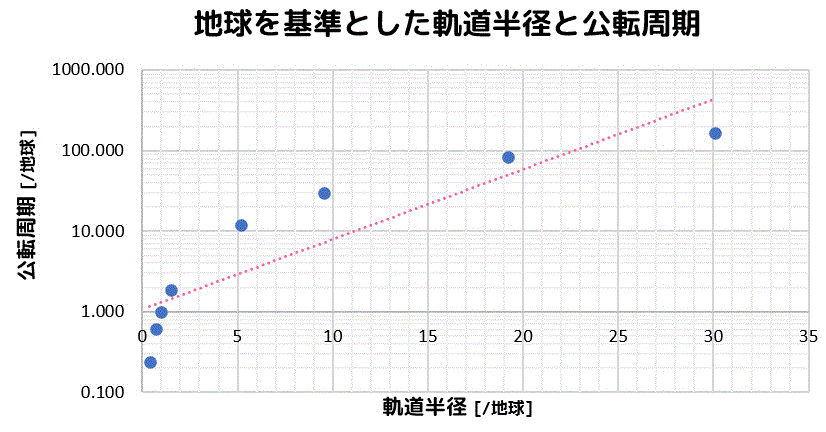
まだまだ直線には遠いですね。
ということで、横軸も対数軸にしてみましょう。
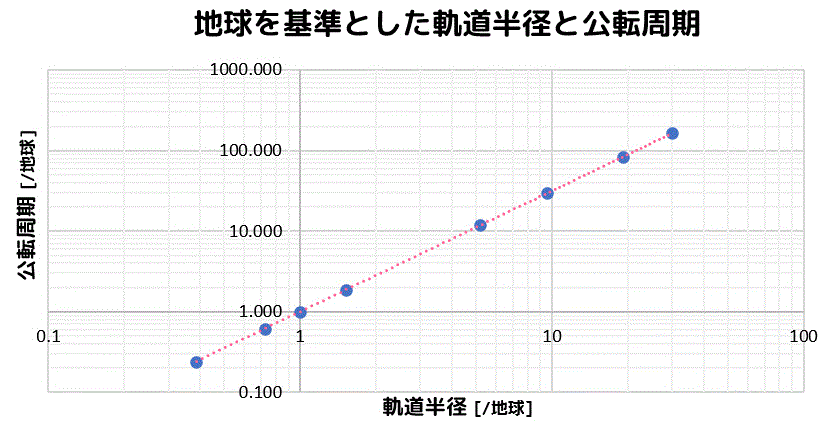
どの点も近くなるような直線が引けましたね。
でもなぜ両方の軸を対数にしたらうまく直線になるのでしょうか。
実際に式を立てて計算してみましょう。
(2) 両対数グラフと最小2乗法
(a) 式の導出法
両対数グラフを書いて直線になるということは、2つの変数 \( x \), \( y\) に対して\[
X = \log_{10} x, \ \ \ Y = \log_{10} y
\]とおいたときに直線 \( Y = aX + b \) となるといいかえられます。
早速、直線の式を変形していきましょう。
まず、直線 \( Y = aX + b \) の式に、\( X = \log_{10} x \), \( Y = \log_{10} y \) を代入します。すると、\[
\log_{10} y = a \log_{10} x + b
\]となりますね。
ここで、\( b = \log_{10} b' \) とおくと、\[\begin{align*}
\log_{10} y & = a \log_{10} x + \log_{10} b'
\\ & = \log_{10} x^a + \log_{10} b'
\\ & = \log_{10} b' x^a
\end{align*}\]となるので、\[
10^{ \log_{10} y } = 10^{ \log_{10} b' x^a } \]\[
y = b' x^a
\]と変形できます。
(\( b = \log_{10} b' \) なので \( b' = 10^b \) となる。)
つまり、データが \( x^2 \), \( x^3 \), … , \( x^a \) のようなべき関数*4な変換をするものに対して、両対数がグラフが有効なものといえます。
(もちろん \( x^{-3} \) のように \( a \) が負でもOK)
(b) 実際のデータに適用してみよう
ということで、先ほどのこちらのデータに、最小2乗法を適用し、近似式を出してみましょう。
| 星の名 | 軌道半径 [地球] | 公転周期 [地球] |
| 水星 | 0.387 | 0.240 |
| 金星 | 0.723 | 0.615 |
| 地球 | 1.00 | 1.00 |
| 火星 | 1.52 | 1.88 |
| 木星 | 5.20 | 11.9 |
| 土星 | 9.55 | 29.5 |
| 天王星 | 19.2 | 84.0 |
| 海王星 | 30.1 | 165 |
今回は、軌道半径を \( x \)、公転周期を \( y \) としましょう。
ここで、\[
X = \log_{10} x, \ \ \ Y = \log_{10} y
\]とおきます。すると、それぞれの星の \( X \), \( Y \) は下のようになります。
| 星の名 | X | Y |
| 水星 | -0.412 | -0.620 |
| 金星 | -0.141 | -0.211 |
| 地球 | 0.000 | 0.000 |
| 火星 | 0.182 | 0.274 |
| 木星 | 0.716 | 1.076 |
| 土星 | 0.980 | 1.470 |
| 天王星 | 1.283 | 1.924 |
| 海王星 | 1.479 | 2.217 |
このデータに対し、最小2乗法を適用すると、\[\begin{align*}
Y & = 1.500X + 5.966 \times 10^{-5}
\\ & = aX + b
\end{align*}\]となります。
この \( a = 1.500 \), \( b = 5.966 \times 10^{-5} \) を変換後の式\[
y = b' x^a \ \ \ ( b' = 10^b )
\]に代入してあげましょう。
すると、\[\begin{align*}
y & = 10^{5.966 \times 10^{-5}} x^{1.500}
\\ & = 1.000 x^{1.500}
\end{align*}\]という関係式が成立します。
つまり、公転周期は軌道半径の1.5乗になるということがわかりますね。
少し言い換えると、公転周期 \( T \) の2乗は軌道半径 \( a \) の3乗に比例することを示せましたね。
これを数式で書くと、定数 \( k \) を用いて\[
\frac{ T^2 }{ a^3} = k
\]となります。
この式、高校物理で見覚えがありませんか…?
実は、この式はケプラーの第3法則そのものなのです!
ということで、両対数グラフを用いてケプラーの第3法則を示せましたとさ、めでたしめでたし。
べき関数的な増減をしそうなデータの回帰直線を求める場合、\[
X = \log_{10} x, \ \ \ Y = \log_{10} y
\]と置いてから最小2乗法を適用し、\[
Y = aX + b
\]の \( a \), \( b \) の値を求めると回帰直線\[
b = \log_{10} b' \ \to \ b' = 10^b \]より、\[\begin{align*}
y & = b' \cdot x^a \\ 10^b \cdot x^a
\end{align*}\]と変形することができる。
5.Excel上で片・両対数版の最小2乗法を計算させる
では、Excelで片対数、両対数の最小2乗法の曲線の傾きと切片を求める方法についてまとめていきます。
まず、求めたい曲線の傾きと切片のデータを選んでから散布図を表示させてから線をクリックし、「近似直線の追加」を選択してください。
↓ここまでは通常の最小2乗法と同じです。わからなければこちらのほうに図を使ってわかりやすく説明しているのでこちらをご覧ください。
(1) 片対数グラフの回帰曲線を求める場合
片対数グラフの回帰曲線 \( y = 10^b \cdot 10^{ax} \) の \( a \), \( b' \) の値を求める場合、近似曲線のオプションで「指数近似」を選びましょう。
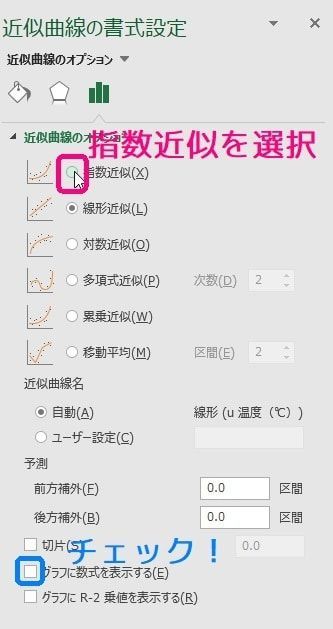
グラフに数式を表示する、にチェックを入れたら無事\[
y = 92.00 e^{-0.08265x}
\]と表示されましたね。(数字の表示桁数は各自で調整しましょう。)
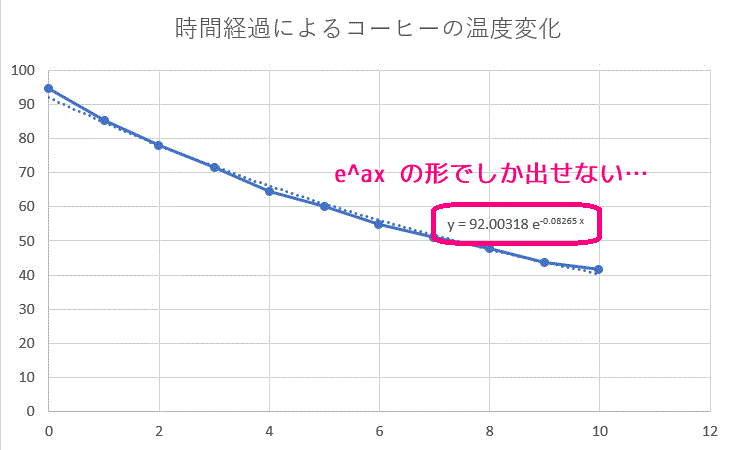
しかし、底が 10 ではなく \( e \) になってしまってます。なので直しましょう。\[
e^{-0.08265x} = 10^{a'}
\]となるような \( a' \) を求めます。\[
\log_{e} e^{-0.08265x} = a' \log_{e} 10 \]\[
-0.08265 x = a' \log_{e} 10
\]となるので、\[
a' = \frac{-0.08265}{\log_{e} 10} = -0.3589
\]となり、\[
y = 92.00 10^{-0.3589x}
\]と求められます。
※出た値に \( \frac{1}{\log_{e} 10} \) 倍すれば \( 10^{a' x} \) の形に直せます。
(2) 両対数グラフの回帰曲線を求める場合
両対数グラフの回帰曲線 \( y = b' \cdot x^a \) の \( a \), \( b' \) の値を求める場合、近似曲線のオプションで「累乗近似」を選びましょう。
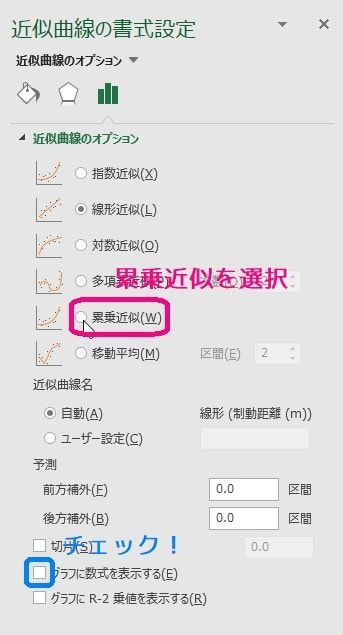
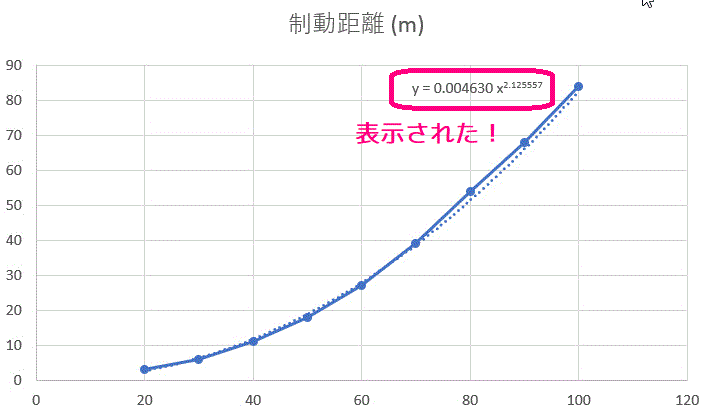
グラフに数式を表示する、にチェックを入れたら無事\[
y = 0.0004630 x^{2.126}
\]と表示されましたね。
(数字の表示桁数は各自で調整しましょう。)
6.さいごに
少し長い記事になってしまいましたが今回は、
- 片対数・両対数グラフの書き方
- 片対数グラフが有効な例(感染者の増加)
- 両対数グラフが有効な例(ケプラーの第3法則)
- Excelで片対数グラフ、両対数グラフを書く方法
について説明していきました。
3回にわたり、「実験の基礎」に関する記事をお読みいただきありがとうございました。
関連広告・スポンサードリンク