スポンサードリンク
こんにちは、ももやまです。
たまには読んだ論文のまとめをしてみることにしてみました。
※注意
あくまでもメモなので誤って解釈をしている部分があるかもしれません。
その場合はコメントなどでご指摘お願いします。
目次
スポンサードリンク
1.読んだ論文
今回はこちらの論文を読みました。2012年に書かれた論文です。
Tensor Displays: Compressive Light Field Synthesis
using Multilayer Displays with Directional Backlighting
Gordon Wetzstein Douglas Lanman Matthew Hirsch Ramesh Raskar
MIT Media Lab
この論文は、メガネなどの特別な装備なしで、映像を立体的に表現する(3Dディスプレイ)方法などについてまとめた論文です。
映像をなるべく鮮明に立体的に表現するために大きく貢献した3つのポイントの紹介、および実際にディスプレイなどの枚数などを変化させて実験し、鮮明さなどの比較をしています。
今回はその論文をまとめたメモのようなものを下に書いていきます。
スポンサードリンク
2.Tensor Displayとは
Tensorディスプレイはメガネを使わずに立体表現が可能な(自称)一般庶民向けのディスプレイです。
このディスプレイはライトフィールドディスプレイの一種であり、ライトフィールドの技術を応用して作られています。
Tensorディスプレイの技術に大きく貢献している3つのポイントとして、「多層パネルディスプレイ」・「指向性バックライト」・「時分割ディスプレイ」が挙げられます。
下のほうで後ほど説明したいと思います。
スポンサードリンク
3-1.ライトフィールドディスプレイ
まずは、テンソルディスプレイの技術の土台となるライトフィールドを使ったライトフィールドディスプレイについて説明します。
ライトフィールドディスプレイは、名前の通りライトフィールドを使ったメガネなどの道具を使うことなしに立体的な表現をすることができるディスプレイです。
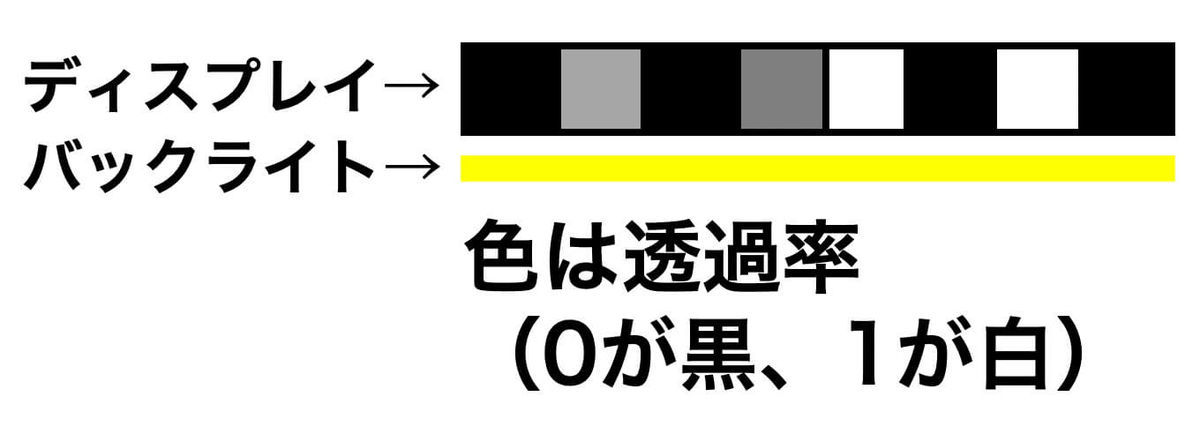
普通のディスプレイは下の画像のように、光源(バックライト)が発する光をディスプレイ部分が部分的に遮る(画素ごとに透過率を調整)ことで映像の再現をしています。
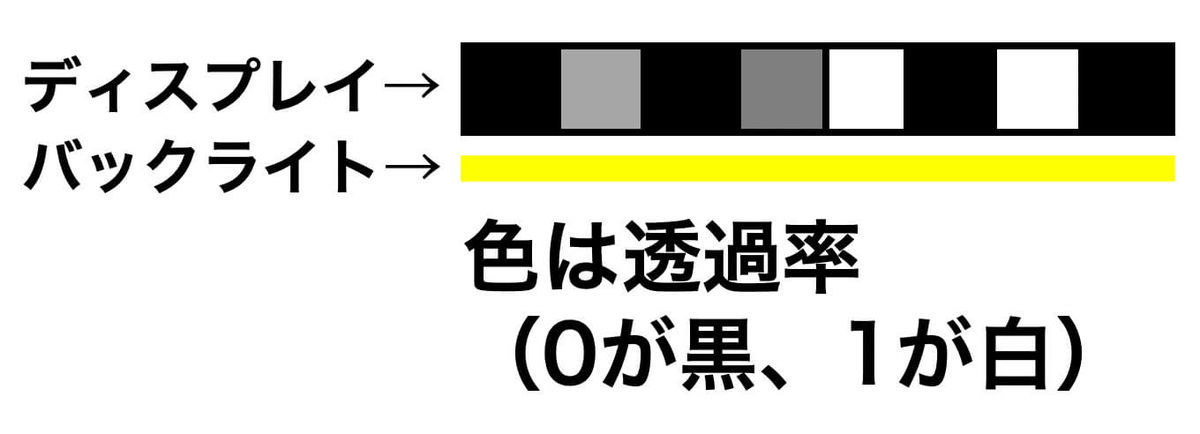
一方、ライトフィールドディスプレイは、物体が放つ光線をディスプレイで再現しています。
また、立体的な表現をするためには、1枚のディスプレイでは表現することができず、どうしても複数枚のディスプレイが必要になります。
2層ディスプレイ
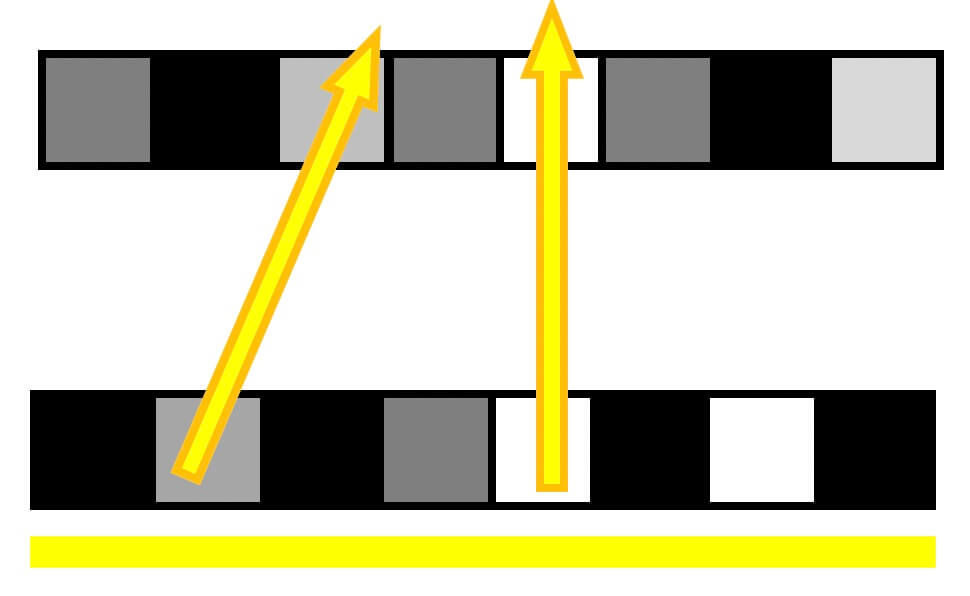
それぞれの光線は、各ディスプレイの透過率の積で表されています。
複数の光線を少ない画素数で表すことができるため、情報量*1を減らすことができます。
理論上は、2枚のディスプレイ(2層)があれば立体的な表現をすることができます。
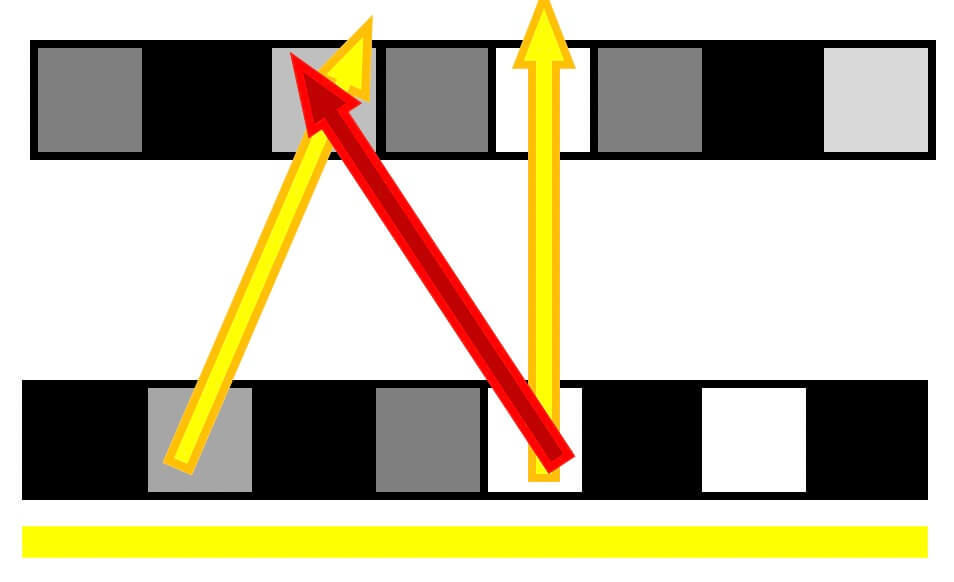
しかし、下のような、誤った光線(赤色の矢印)を表現してしまうことがあるため、テンソルディスプレイにおいては、2層ではなく3層のディスプレイを採用しています。
2層ディスプレイ
3-2.テンソルとは
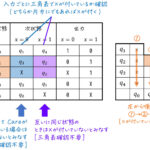
テンソルディスプレイを説明する前に、今回の論文において一番重要な要素であるテンソルについて説明します。
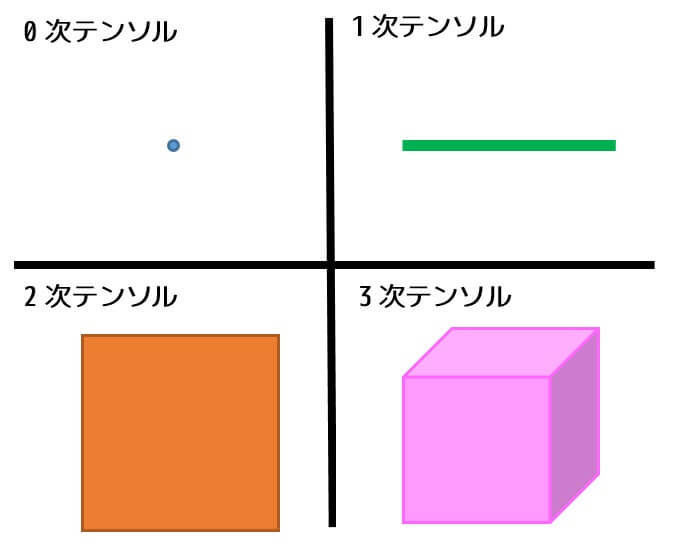
0次~3次のテンソルのイメージ図をこちらに載せておきます。
数学的に表すと0次~3次テンソルはこのような形になります。
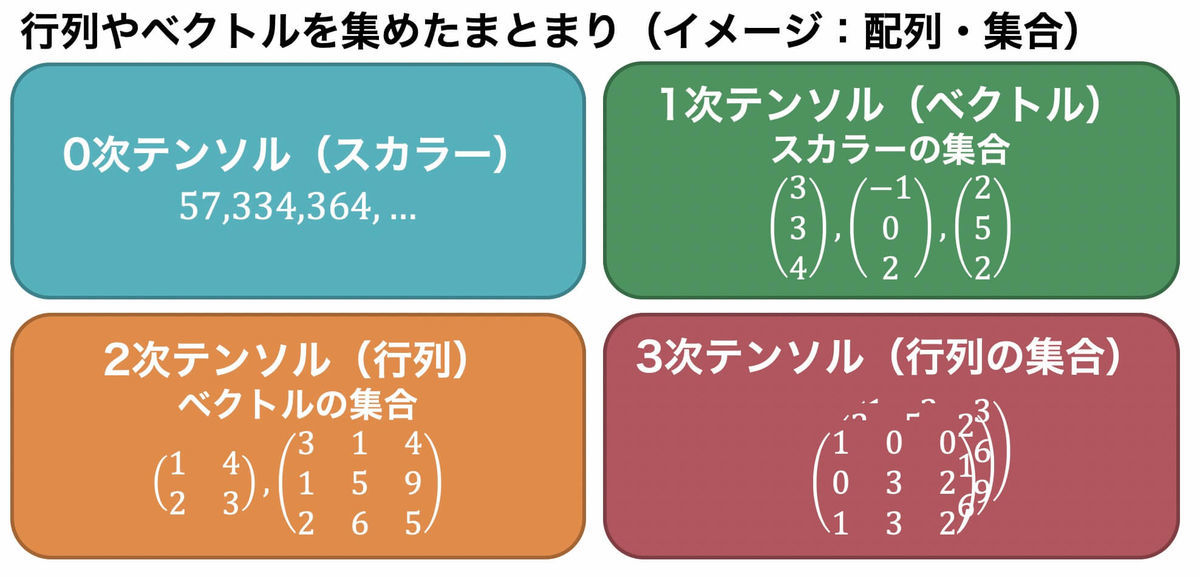
0次テンソル [階数0](スカラー)
0次テンソルは、57, 334, 364 のようなスカラーのことを表します。
イメージは点です。
1次テンソル [階数1](ベクトル)
1次テンソルは、0次テンソル(スカラー)が集まったものを表します。
馴染み深いもので言うと、ベクトルが1次テンソルに該当します。
イメージは線です。
2次テンソル [階数2](行列)
2次テンソルは、1次テンソル(ベクトル)が集まったものを表します。
馴染み深いもので言うと、行列が2次テンソルに該当します。
イメージは長方形です。
3次テンソル [階数3](行列の集まり)
今回テンソル分解で用いるのが3次テンソルです。
3次行列は、2次テンソル(行列)が集まったものを表します。
イメージは直方体です。
3-3.テンソルディスプレイ
いよいよ本題のテンソルディスプレイに入ります。
テンソルディスプレイはディスプレイを3枚重ねることで立体的な表現を実現しています。
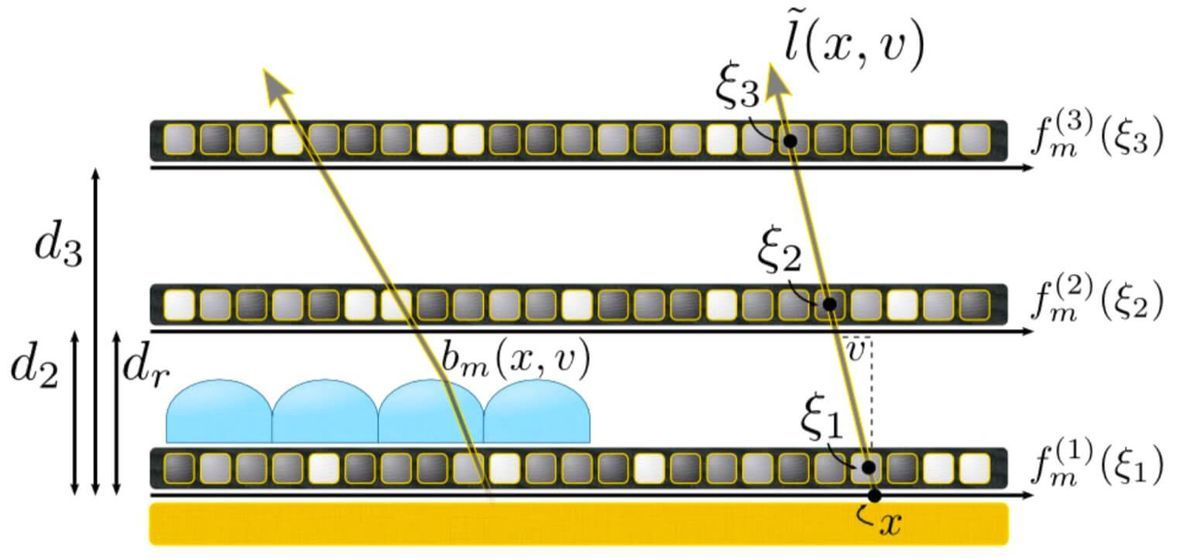
[論文より引用]
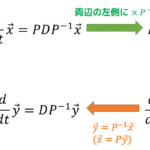
\( N \) 層のディスプレイの光線 \( \tilde{l}(x,y,N) \) は、\[ \tilde{l}(x,y,N) = \prod_{n=1}^N f^{(n)} \left( x + \frac{d_n}{d_r} v \right) \]で表すことができます(透過率の積)。
テンソルディスプレイの光源は3層 (\( N = 3 \)) の透過率の積で表すことができるので、\[\tilde{l}(x,y) = f(\xi_1)g(\xi_2)h(\xi_3) \] と書き換えることができます。
さらに \( \alpha = d_3 - d_2 \), \( \beta = d_1 - d_2 \), \( \gamma = d_2 - d_1 \) のもとで \[ \alpha \xi_1 + \beta \xi_2 + \gamma \xi_3 = 0\] が成立します。
(光線を一直線に通ることから成り立つ数式)
ここで光線の式をテンソル \( \tilde{T} \) を使って表すと、\[ \tilde{T} = \vec{f} \circ \vec{g} \circ \vec{h} \ \mathrm{s.t} \ \tilde{t_{ijk}} = f_i g_j h_k \]となります。ここで \( \circ \) はベクトルの直積(外積・テンソル積)*2を表します。
しかし、問題点が1つあり、様々な要因により光線の向きが変わってしまい、誤差が発生することがあります。
なので、それぞれの点 \( i \), \( j \), \( k \) がライトフィールドで表された光線を通る場合は1、それ以外は0となるようなテンソル \( W \) を定義し、放射光場テンソル \( L \) を求めます。\[\tilde{L} = W \odot \tilde{T} \]ここで \( \odot \) はアダマール積*3を表します。
3-3.時分割ディスプレイ
しかし、いくら3層とはいっても表示できるシーンには限度があります。
ディスプレイの画素数を \( n \) とすると、表現できる光線の数は、2層分の \( n^2 \) 本*4あるにも関わらず、すべてのディスプレイの画素(表現できるシーン)はたった \( 3n \) 個しかないためです。そのため、画像にぼやけが発生してしまいます。
そのぼやけを少なくするために、それぞれの画像を高速に切り替えることで表現できるできるシーンを増やし、ぼやけを減らします。
表示するシーンの数を \( M \) 個(以下 \( M \) フレーム)としたときの光源は、各フレームごとの光源の平均で求めることができます。式にすると、\[ \tilde{l}(x,y,N) = \frac{1}{M} \sum_{m=1}^M \prod_{n=1}^N f^{(n)} \left( x + \frac{d_n}{d_r} v \right) \]となります。
3-4.非負値テンソル因子分解(NFT)
実際に表したいライトフィールド \( l(x,y) \) に対して、3層のディスプレイ上で表されるライトフィールドには限りがあるため、 \( \tilde{l}(x,y) \) の誤差がどうしても発生してしまいます。
これは、\( 0 \leqq f^{(n)}_{m} (\xi) \leqq 1 \) において、\[
\int_{v_{min}}^{v_{max}} \int_{x_{min}}^{x_{max}} \left( l(x,y) - \tilde{l}(x,y) \right)^2 dx \ dv
\]を最小化する問題となります。
これを3つのテンソル \( F,G,H \) を使って表すと、 \( 0 \leqq F,G,H \leqq 1 \) における\[ \| L - W \odot \tilde{T} \|^{2} = \| L - W \odot[\![F,G,H]\!] \|^{2} \]
これは非負値テンソル因子分解(NFT)を使って解くことができます。
非負値テンソル因子分解を使うことで、次数の大きいテンソルを小さいテンソルに分解することができます。
非負値テンソル因子分解についての詳しい説明は、こちらのサイトをご覧ください。
今回は、3次のテンソル(3層ディスプレイだから)なので、3次のテンソルを3つのテンソル \( F \), \( G \), \( H \) の3つに分解をします。
分解した3つのテンソルをそれぞれの層のディスプレイで表示させることで立体的な表現をすることができます。
3-5.指向性バックライト
上で説明した3層ディスプレイは視野が20°しかない欠点を持っています。
その欠点を補うのが指向性バックライトです。
指向性バックライトを用いることで、20°しかないディスプレイの視野を広げることができます。
指向性バックライトは、ディスプレイの中にレンズアレイを入れることで導入をすることができます。

[論文より引用]
この図の水色の部分がレンズアレイに相当します。
レンズアレイを入れたときの光線は、以下の式で表すことができます。\[ \tilde{l}(x,y,N) = \frac{1}{M} \sum_{m=1}^M b_m (x,v) \prod_{n=1}^N f^{(n)} \left( x + \frac{d_n}{d_r} v \right)
\]上記の式をテンソル \( \tilde{T} \) で表すと、\[ \tilde{T}(x,y) = \frac{1}{M} \sum_{m=1}^M \prod_{n=1}^N f^{(n)} \left( x + \frac{d_n}{d_r} v \right) \]ここで表されたテンソル \( \tilde{T} \) も3-4で説明したテンソル分解を用いることで、小さいテンソルに分解し、それぞれのそれぞれの層のディスプレイで表示させることで立体的な表現をすることができます。
4-1.比較その1(3層・2層)vs(指向性ありの2層・1層)
では実際にテンソル分解をして画像を生成したものを見てみましょう。

[論文より引用]
画像は左から順番に「オリジナルのもの」・「2層12フレーム」・「3層1フレーム」・「3層12フレーム」・「指向性バックライトを搭載した1層12フレーム」・「指向性バックライトを搭載した2層12フレーム」を表します。
また、一番上の行では、ライトフィールドを可視化したものが表されています。
またさらに「3層・2層」・「指向性の2層・1層」の被写界深度のグラフもご覧ください。
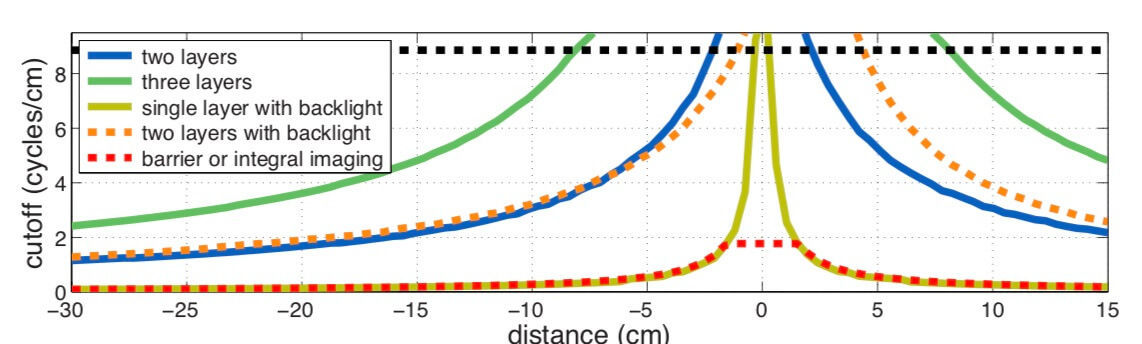
[論文より引用]
3層の場合の被写界深度(ピントが合う位置の範囲)は、他の実験結果(2層や指向性ディスプレイの場合)に比べて圧倒的に広いですね。
4-2.比較その2(指向性の有無による鮮明さの違い)
つぎに層数とフレーム数の条件を固定した上で、指向性バックライトの有無で鮮明さがどれだけ変わるかを比較してみましょう。
鮮明さの比較は、PSNRを使って行います。PSNRの値が小さければ小さいほど劣化していることを表し、大きければ大きいほど鮮明(もとの画像に近い)ことを表します。
PSNRについての説明はこちらの記事が参考になるのでこちらをご覧ください。
40[dB]だと、多くの人が元の画像との見分けがつかなくなるので今回は40[dB]以上であれば合格とします。
\( \beta \) は明るさを表し、\( N \) がディスプレイの層数、\( M \) がフレーム数を表します。
PSNRの出力結果がこちらです。
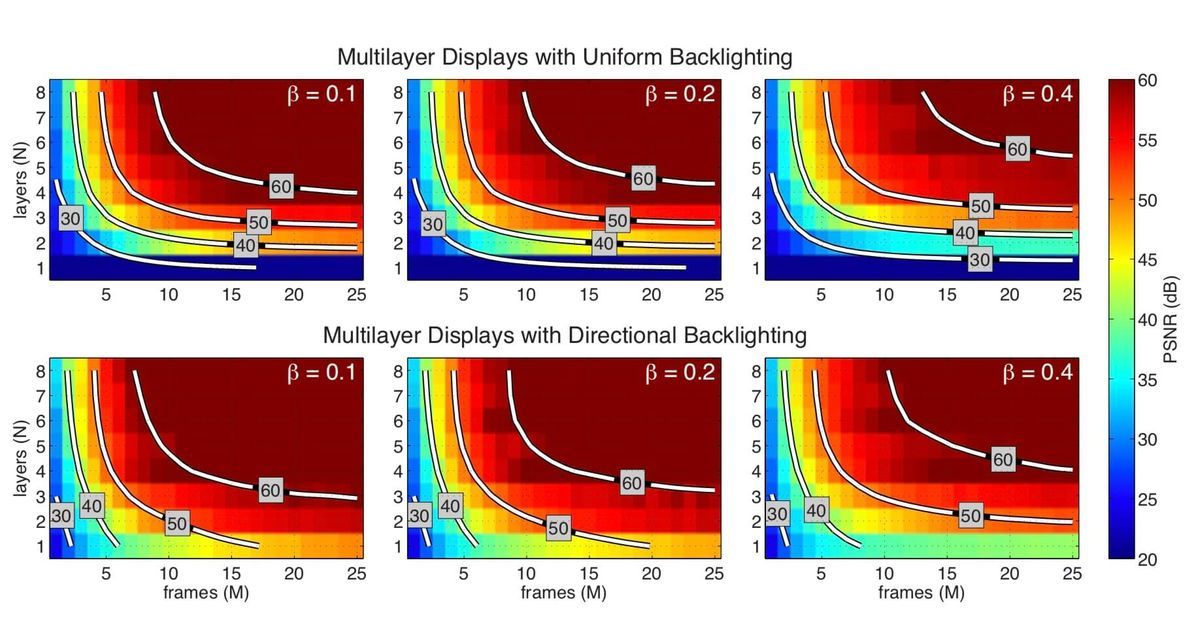
[論文より引用]
結果を見てみると、指向性バックライトを搭載したほうが全体的にPSNRが大きくなっていますね。
特に合格である40[dB]以上の範囲は指向性バックライトの有無で大きく変わります。
4-3.比較その3(3層 vs 指向性1層)
今度は「3層ディスプレイ」と「指向性バックライト有りの1層ディスプレイ」のPSNRを比較してみましょう。
4-2と同じようにPSNRを比較するのですが、今回は明るさとフレーム数に注目してPSNRを比較していきましょう。
4-2と同じく40[dB]を合格ラインとします。
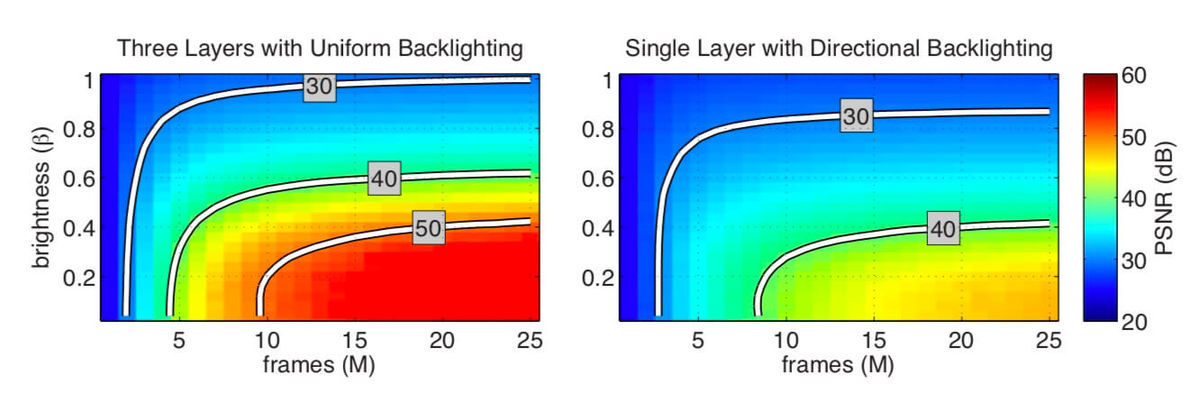
[論文より引用]
実験の結果、1層の指向性バックライトの場合、明るさにかかわらず最低でも8フレームないと40[dB]には届きません。3層の場合は最低4フレームあれば40[dB]に到達するのでこれは不十分ですね。
また、輝度を上げればあげるほどPSNRが減少していることがわかりますね。これは、ディスプレイの層数にかかわらず、輝度と鮮明さはトレードオフの関係であることがわかりますね。
今度は明るさに注目しましょう。1層の指向性バックライトの場合、明るさ \( \beta \) を0.4より大きくしてしまうと、フレーム数をどんなに大きくしてもPSNRが40[dB]を超えませんね。
3層の場合、明るさ \( \beta \) が0.6まで対応しているため、ディスプレイの輝度を求めるのであれば、1層の指向性バックライトは不十分であることがわかります。
5-1.実装
今回は3層ディスプレイと1層+指向性バックライトディスプレイの実装をしてみます。
実装する際のソフトとして、OpenGLとPOV-Rayを使用します。
左側が1層+指向性バックライトディスプレイ、右側が3層ディスプレイとなります。

[論文より引用]
後ほど説明しますが、1層1層を機械的に誤差なく設置する必要があるのがポイントとなります。
実装し、実際に表示させた画像がこちらとなります。

[論文より引用]
よーく見てみるとわかるのですが、1層+指向性バックライトディスプレイの出呂奥には若干のぼけが見られますね。
5-2.細かな比較
今度は指向性の有無だけで鮮やかさの変換を細かく見ていきます。
指向性の有無だけでの比較のため、両者ともディスプレイの層数やフレーム数は統一しています。
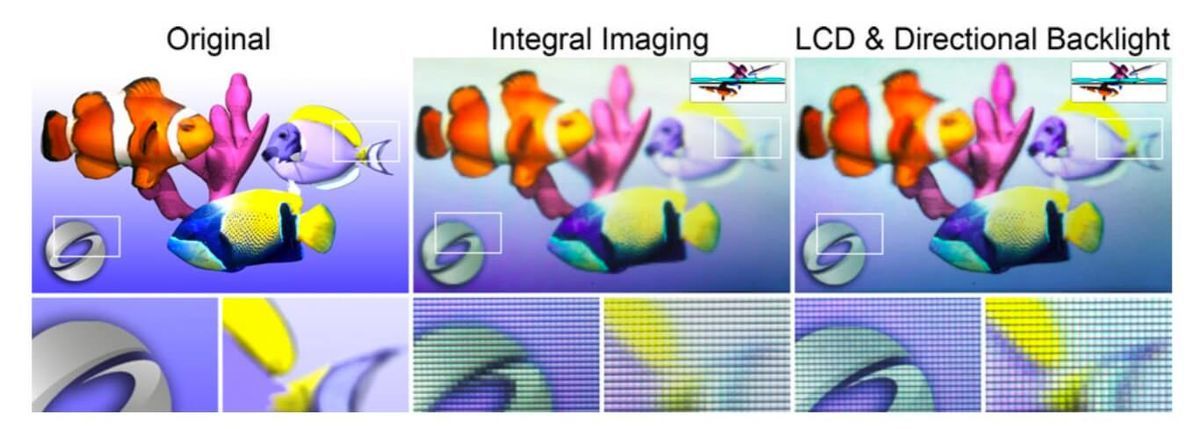
[論文より引用]
画像をよく見ると、指向性ありのほうが鮮やかに見えませんか?
私は鮮やかに見えます。
6-1.まとめなど
最後に少しだけまとめをしたいと思います。
3層ディスプレイで立体を表現するためには、機械などを使ってそれぞれの層ごとの配置をかなり正確にする必要があります。
また、ガンマ補正や、より正確に色を再現するためにキャリブレーションも必要です。
さらに頭部や眼球追跡などの技術と応用することで、視聴者に合わせた画像の投影なども実現できるかもしれません。
6-2.さいごに
今回はTensorディスプレイについてのまとめをしました。
Tensorディスプレイはメガネを使わずに立体表現が可能なライトフィールドの技術を応用してつくられたディスプレイです。
また、テンソルは、ベクトルや行列をまとめた配列、集合のようなものでした。
そして、Tensorディスプレイの技術に大きく貢献しているポイントとして、多層パネル、指向性バックライト、時分割ディスプレイの3つのポイントがありました。
また機会があれば別の論文も紹介してみようかなと思います。
7.参考文献
Qiita 非負値テンソル因子分解の更新式の導出と実装 @drumichiro
[2019年6月24日アクセス]
テンソル分解の基礎と画像・信号処理の応用 Tatsuya Yokota, Assistant Professor at Nagoya Institute of Technology
[2019年6月25日アクセス]
KerasでPSNR(ピーク信号対雑音比)を計算する方法+画像補間アルゴリズムの比較 @koshian
[2019年6月25日アクセス]
3枚の液晶パネルで多視点対応の裸眼3D立体視を実現。SIGGRAPH 2012「Emerging Technologies」展示セクションレポート
[2019年6月25日アクセス]
法政大学 情報科学部 小池 崇文 ライトフィールドディスプレイの研究動向
[2019年6月25日アクセス]
*1:画素数を \( n \) 個とすると、2層を通る光線は全部で \( n^2 \) 個表現することができます。そのときの画素の数は、合計 \( 2n \) 個ですね。なので、\( 2n \) 個の画素数で \( n^2 \) 個の光線を表現することができます。
*2:例えば、3次元ベクトル \( \vec{a} \) と2次元ベクトル \( \vec{b} \) の直積は\[\vec{a} \ {}^t\!\vec{b} = \left( \begin{array}{ccc} a_1 \\ a_2 \\ a_3 \end{array} \right) \left( \begin{array}{ccc} b_1 & b_2 \end{array} \right) = \left( \begin{array}{ccc} a_1 b_1 & a_1 b_2 \\ a_2 b_1 & a_2 b_2 \\ a_3 b_1 & a_3 b_2 \end{array} \right) \]となります。
*3:アダマール積は行列の成分ごとに積を取ったものを表します。具体的には、\[ \left( \begin{array}{ccc} a_{11} & a_{12} & a_{13} \\a_{21} & a_{22} & a_{23} \\a_{31} & a_{32} & a_{33} \end{array} \right) \odot \left( \begin{array}{ccc} b_{11} & b_{12} & b_{13} \\ b_{21} & b_{22} & b_{23} \\ b_{31} & b_{32} & b_{33} \end{array} \right) = \left( \begin{array}{ccc} a_{11} b_{11} & a_{12} b_{12} & a_{13} b_{13} \\ a_{21} b_{21} & a_{22} b_{22} & a_{23} b_{23} \\ a_{31} b_{31} & a_{32} b_{32} & a_{33} b_{33} \end{array} \right) \]のような計算をします。今回は片方が2値テンソル(行列)なので、\[ \left( \begin{array}{ccc} a_{11} & a_{12} & a_{13} \\a_{21} & a_{22} & a_{23} \\a_{31} & a_{32} & a_{33} \end{array} \right) \odot \left( \begin{array}{ccc} 1 & 1 & 0 \\ 0 & 1 & 0 \\ 0 & 1 & 1 \end{array} \right) = \left( \begin{array}{ccc} a_{11} & a_{12} & 0 \\ 0 & a_{22} & 0 \\ 0 & a_{32} & a_{33} \end{array} \right) \]のような計算をしています。
*4:光線は一直線である必要があるため、たとえ3層以上のディスプレイの場合でも表現できる光源の数は \( n^2 \) 個(始点の層と終点の層の2層を通る光線の数)です。
関連広告・スポンサードリンク