スポンサードリンク
こんにちは、ももやまです!
今回は高速なソートアルゴリズムの1つであるヒープソートのアルゴリズムについて分かりやすくまとめたいと思います!
目次
スポンサードリンク
1.ヒープソートってどんなソートなの?
では、ヒープソートはどのようにしてソートしていくのかについて、手順ごとに図を使って丁寧に説明していきたいと思います。
今回は、 a[8] = {14,9,3,12,21,8,1,17} を昇順(1,2,3…)にソートします。
(1) 手順1 配列を木構造にする
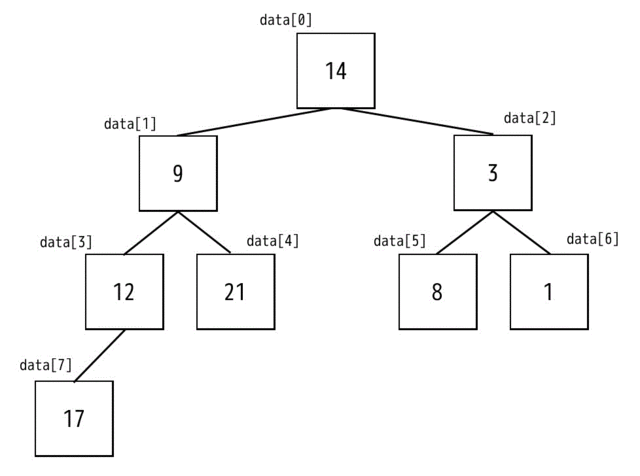
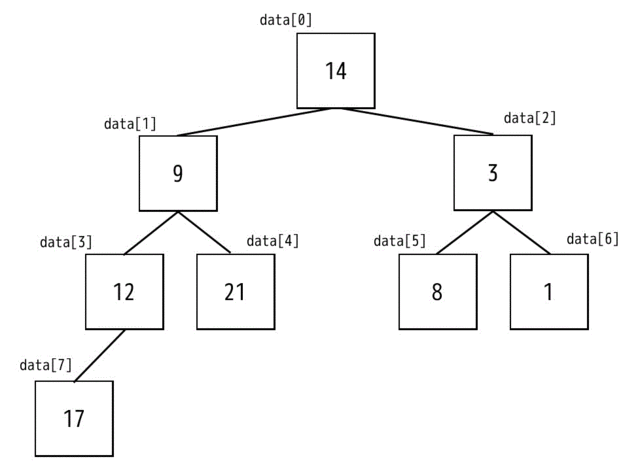
まずは下のように配列を左上から順番に木構造に並べます。
(2) 手順2 木構造をヒープ構造にしていく
つぎに作った配列をヒープ構造にしていきます。
ヒープソートは、後ろから順番にソートするアルゴリズムなため、ヒープ化する際は、昇順ソートの場合はヒープは降順,、降順ソートの場合はヒープは昇順にする必要があるため注意してください。
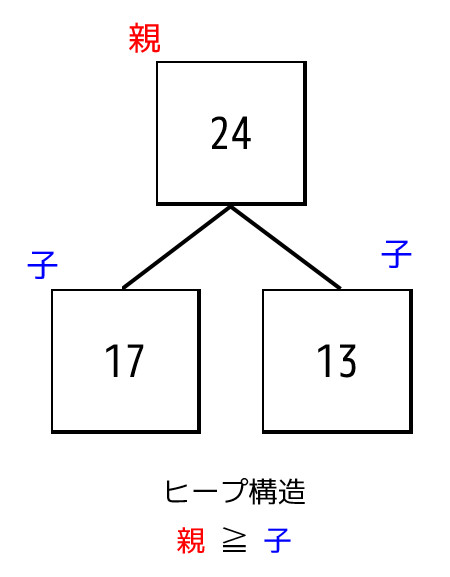
ヒープ構造とは、すべてのノードにおいて「親ノードは、(子ノードが存在すれば)どの子ノードよりも大きい」という条件を満たした構造を表します。 *1
では、ヒープにしていこうと思います。
ヒープかどうかをチェックする必要があるのは、子ノードが存在する親ノードですね。なので、子ノードがないdata[4]とかdata[5]はチェックの必要がありません。
今回子ノードが存在するのは0番目から3番目ですね。なので、3番目、2番目、1番目、0番目の順番にチェックすればいいです。
まずは、3番目のノードを確認します。子ノードには17がありますね。親と子の順番が逆になってるので、3番目と7番目の要素を交換します。
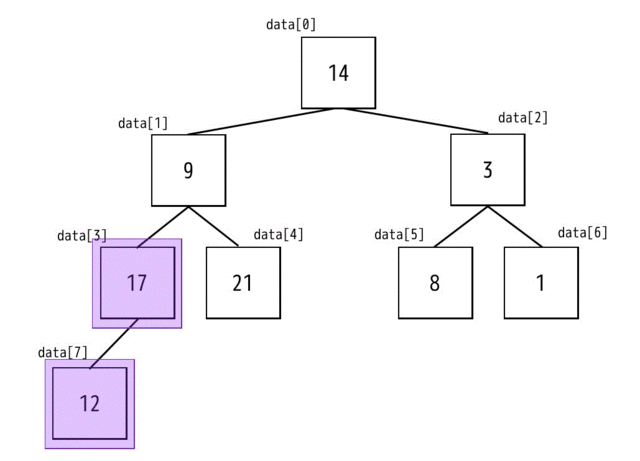
つぎに2番目のノードを確認します。子ノードには8と1がありますね。
このように子ノードが2つ繋がれている場合は、まず子ノード同士で比較を行います。子ノードのうち、大きいのは8ですね。なので、交換する候補は8のほうになります。
2番目の親ノードは3に対し、子ノードの交換候補は8ですね。子ノードのほうが大きいので、親ノードと交換する候補である8と交換します。
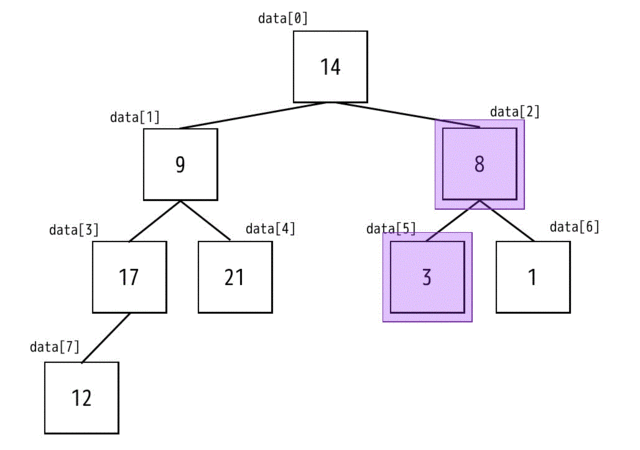
つぎに1番目のノードを確認します。子ノードには17と21がありますね。
大きいのは21なので、21が交換する候補となります。親ノードの9と子ノードの交換候補の21と比べると、21のほうが大きいので交換を行います。*2
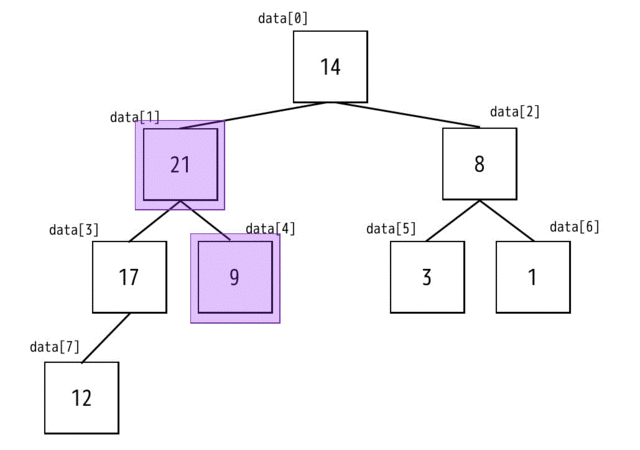
最後に0番目(根)を確認します。子ノードには21と8があります。なので交換候補は21です。親ノードは14なので子ノードの交換候補と交換をします。
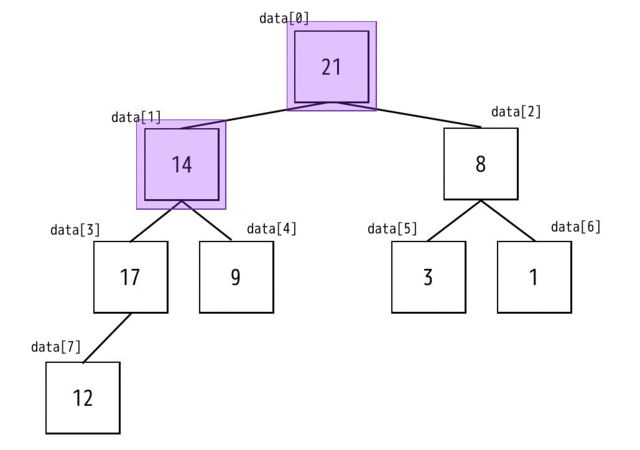
これで終わり! と思いますよね。
でもよーく見てください。入れ替えたノード(1番目のノード)とその子(3番目、4番目の子ノード)がよくみたらヒープになっていませんね。
このように入れ替えた相手のノードに子ノードが繋がれている場合、入れ替えた相手のノードがヒープになっているかの確認が必要になります。
今回はヒープになっていないので再びヒープになるように順番を入れ替えます。
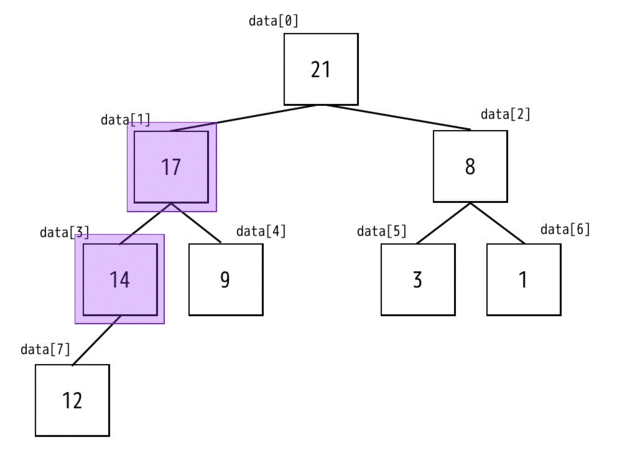
入れ替えた先(3番目)にまた子ノード(7番目)が繋がれていますね。なので入れ替えた先のノードとその子ノードがヒープになっているかを確認します。
今回はヒープになっていますね。なので交換の必要がありません。
(3) 先頭(0番目)と一番うしろのノードを交換する
つぎにヒープ構造になったノードの先頭と一番うしろのノードを交換します。
さらに一番後ろのノードはもう使うことがないので木構造から切り離してしまいます。
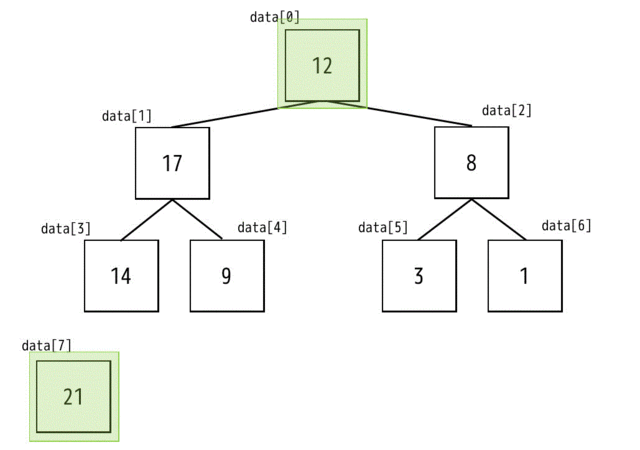
ヒープ構造のノードの先頭は一番大きいので、先頭と一番うしろを交換することで、後ろの値が一番大きくなり、後ろから降順(10,9,8,7…)ソートができますね。後ろから降順ということは、前から数えると昇順になりますね。
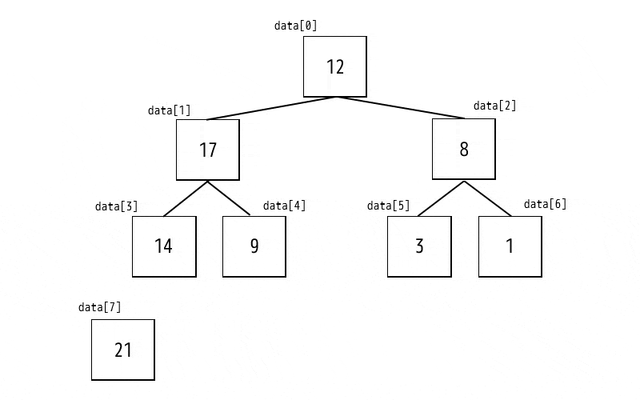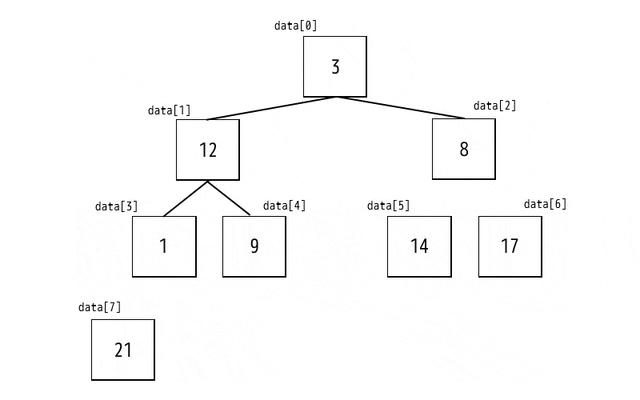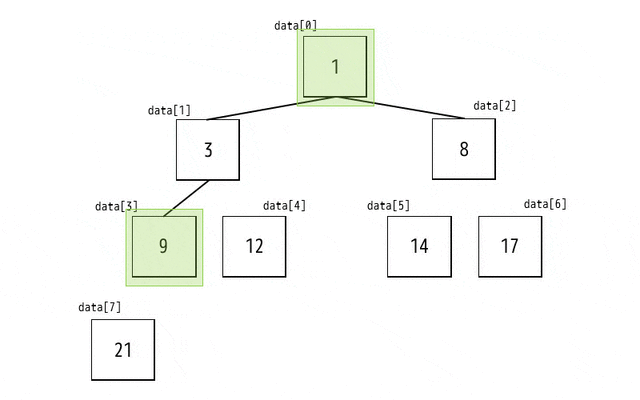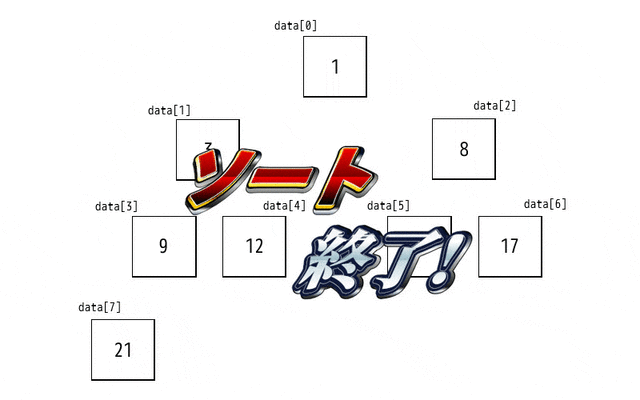
(4) 残ったノードで(2)~(3)を繰り返す
あとは(2)と(3)をソートが終わるまで繰り返すだけです。
繰り返す際には、先頭(0番目)のノード以外はすべてヒープになっているため、先頭の親のノードについてだけヒープの確認を行い、ヒープでなければヒープになおします。
昇順にソートが完了するまでのアニメーションを作ってみたので参考までにどうぞ!
上のアルゴリズムをまとめるとこのようになります
1. 子ノードが存在する親ノード*3を降順にチェック
2-1. 左側と右側の子ノードの値*4を比較する
2-2. 大きかったノードと親ノードの値を比較し、親ノードのほうが小さければ交換
2-3. 交換した場合、交換したノードを親ノードとし、2-1に戻る
交換しなかった場合はつぎの親ノードをチェック
3. 比較終了後、0番目とn番目を交換
4. 今度は0番目とn-1番目からヒープだが、0番目以外はヒープなのでここからは0番目だけをチェックすればOK
ただし、ヒープを交換した場合は交換したノードを親とするのは忘れずに
5. 0番目からn-2番目、0番目からn-3番目、……、0番目から1番目とヒープ化していくとソートが完了する
スポンサードリンク
2.ソート速度の計測
ヒープソートの高速ソートが早い!と実感していただくため、実際にソートさせてみました。
- 使用言語はRuby
- データの範囲が1~10,000の場合(a)と1~100,000,000の場合(b)の2つで測定し、データの範囲による差を調べる
- 要素数 \( n \) は10,000からスタートし、2倍ずつにしていく。
気になる測定結果は…!? ついでに選択ソート(オーダー: \( O(n^{2}) \) )の時間と比較してみました。
| 要素数n | 範囲(a) | 範囲(b) | 選択ソート |
|---|---|---|---|
| 10,000 | 0.034秒 | 0.035秒 | 3.543秒 |
| 20,000 | 0.072秒 | 0.074秒 | 13.286秒 |
| 40,000 | 0.156秒 | 0.160秒 | 48.187秒 |
| 80,000 | 0.332秒 | 0.327秒 | 175.600秒 |
| 160,000 | 0.689秒 | 0.681秒 | 659.002秒 |
| 320,000 | 1.481秒 | 1.433秒 | 2544.051秒 |
| 640,000 | 3.158秒 | 3.085秒 | |
| 1,280,000 | 6.873秒 | 6.586秒 | |
| 2,560,000 | 14.761秒 | 13.986秒 | |
| 5,120,000 | 32.350秒 | 31.913秒 | |
| 10,240,000 | 73.110秒 | 72.049秒 |
さらにグラフ化してみました。 選択ソート部分はグラフには入れていません。
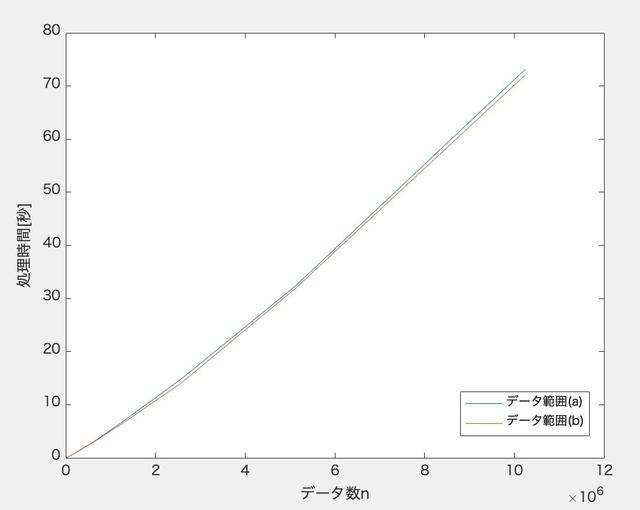
データ数が2倍になると、ソートにかかる時間は2倍ちょいくらいになっていますね。
\( O(n \log n) \) ソートがいかに早いソートかがわかると思います。選択ソートを見てください。ヒープソートなら1秒ちょいでできる要素数320,000のソートを42分かけてやっています。このように高速ソートは要素数が大きくなると爆発的なスピードを発揮します。 要素数1000万でも1分ちょいですよ!! 選択ソートだと何年かかるんでしょうか。
また、ヒープソートはデータ範囲による時間差は見受けられませんね。つまりヒープソートはどのようなデータであっても時間差(ステップ数)はほぼ変わらないアルゴリズムだってこともわかりますね。
スポンサードリンク
3.ソースコード
Rubyでヒープソートを実装してみました。
4.練習
こちらで練習フォームを用意してみたので期末試験などで「ヒープ化せよ」などの問題が出る人はこちらで練習してみてください!
また、配列を「ヒープ化」したものを木構造で可視化するプログラムも作成してみました!
こちらをご覧ください!
5.さいごに
今回はソートアルゴリズムの中でも高速なソートの一種であるヒープソートについてまとめました。
マージソートやクイックソートに比べてはマイナーなソートかもしれませんが、この記事をみてヒープソートのことはたまには思い出してあげてください……。
関連広告・スポンサードリンク