うさぎでもわかる離散数学　番外編2　差分方程式（漸化式）　前編

こんにちは！　ももやまです！

漸化式（差分方程）は数Bで少し習ったと思います。

今回は、

• 高校で習う漸化式の解き方
• 微分方程式っぽく解く別の解き方

の2種類紹介したいと思います。

 

 

スポンサードリンク

１．差分方程式（漸化式）とは

皆さんは高校時代に数学Bで漸化式を習いましたよね。*1

差分方程式（漸化式）とは、ある答えを、少し前の答えとはじめの答えを使って出すような式のことです。

 

例えば、\( a_{n} = 3 a_{n-1} - 2 \) という式があるとします。これは、1つ前の答えを3倍したものに2を引いた値が答えになることを表します。

上の場合はじめの答え（初項）を \( a_0 = 5 \) とすると、1つ先の答え \( a_1 \) は \( 3 a_0 - 2 = 13 \) で出すことができます。 

 

★注意★

• この記事では、初項を \( a_1 \) ではなく \( a_0 \) としてるので気をつけてください
  → 初項が \( a_1 \) だと特殊解は \( a^{n-1} \) のような形で出ますが、\( a_0 \) の場合は \( a^n \) の形で出てきます。
• また、人によっては \( a_n \) という形ではなく、\( f(n) \) を使って表す人もいるので気をつけてください。
  → 例：\( a_{n} = 2 a_{n-1} + 1 \) は \( f(n) = 2f(n-1) + 1 \) と同じ

スポンサードリンク

２．微分方程式っぽく解く解き方の基本

(1) 特性方程式と基本解

例えば\[
a_{n} + p a_{n-1} + q  a_{n-2} = 0
\]のような差分方程式（漸化式）があるとします。

（※このように = 0 になっているタイプの差分方程式は同次方程式と呼ばれます。）

 

ここで、\[
a_n = t^n
\]が解の1つであるとします。

すると、\[\begin{align*}
a_{n} + p a_{n-1} + q  a_{n-2} & = 0 \\
t^{n} + p t^{n-1} + q t^{n-2} & = 0 \\
t^2 + p t + q & = 0 
\end{align*}\]と変形できるので、\[
t^2 + pt + q = 0
\]を満たす \( t \) であればすべて解となることがわかりますね。

 

どんな差分方程式であっても基本解は必ず

• 隣接3項間であれば2個
• 隣接4項間であれば3個
• 隣接n項間であればn-1個

存在します。

(2) 基本解の組み合わせ・定数倍

(1)で、基本解が \( \alpha^n \) と \( \beta^n \) と求まりましたね。

実は、基本解同士を何倍かしたものを足した\[
a_n = C_1 \alpha^n + C_2 \beta^n
\]も同じように解となるのです！

（線形代数用語でいうと、「基本解の1次結合も解となる」といいます。）

 

さらに解を \( C \) 倍した \( C \alpha^n \) も解となります。

 

実際に\[
a_n = C_1 \alpha^n + C_2 \beta^n
\]を代入すると、\[\begin{align*}
a_{n} + p a_{n-1} + q \beta a_{n-2} & = 0 \\
(C_1 \alpha^n + C_2 \beta^n) + p (C_1 \alpha^{n-1} + C_2 \beta^{n-1}) + q (C_1 \alpha^{n-2} + C_2 \beta^{n-2}) & = 0 
\end{align*}\]と変形でき、さらに\[
C_1 ( \alpha^n + p \alpha^{n-1} + q \alpha^{n-2} ) + C_2 ( \beta^n + p \beta^{n-1} + q \beta^{n-2} ) = 0  \tag{1}
\]となります。

 

ここで、\( \alpha^n \), \( \beta^n \) は基本解なので\[
\alpha^n + p \alpha^{n-1} + q \alpha^{n-2} = 0 \\ 
\beta^n + p \beta^{n-1} + q \beta^{n-2} = 0
\]が成立します。

そのため、(1)式の左辺も = 0 となり、等号も成立します。

 

そのため、特性方程式で出した基本解 \( \alpha^n \), \( \beta^n \) から\[
a_n = C_1 \alpha^n + C_2 \beta^n
\]も解であることを示すことができます。

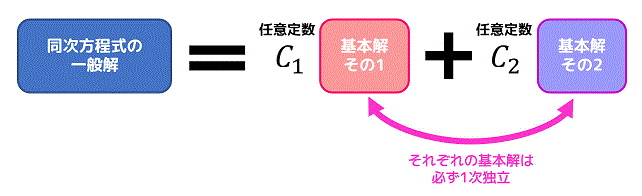
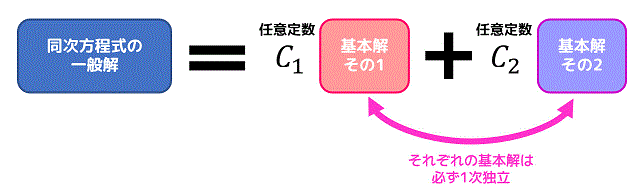
このすべて網羅した解のことを一般解と呼びます。

 

（\( C_1 \), \( C_2 \) はどんな値でもOKな任意定数です。積分定数とかと同じやつだと思ってもらえたらOKです。）

 

(3) 特性方程式に重解が含まれると…

(i) そのままだと解けない理由

いつもうまく特性方程式が解けるとは限りません。

例えば、\[
a_{n} - 4 a_{n-1} + 4  a_{n-2} = 0
\]の場合、特性方程式は\[
t^2 - 4t + 4 = 0 \\
(t-2)^2 = 0
\]となるので、解が \( t = 2 \) の重解となってしまいます。

 

なので、解も\[
a_n = C_1 2^n + C_2 2^n
\]でいいと思いますよね。実はこれがダメなんです。

 

上の式、任意定数 \( C_1, \( C_2 \) を \( A \) とおくと\[
a_n = A 2^n
\ \)と表せちゃいますよね。

基本解が2つ欲しいのに1つしか出てこないため、解をすべて表現することができません。

 

基本解同士で必ず任意定数を打ち消せさない基本解を

• 隣接3項間では2個
• 隣接4項間では3個

持ってくる必要があります。

（線形代数用語で説明すると、それぞれの基本解は必ず1次独立・線形独立である必要がある、となります。）

(ii) 新しい基本解を見つけよう

そこで、新しい基本解を見つける必要があります。

例えば\[
a_{n} - 4 a_{n-1} + 4 \beta a_{n-2} = 0
\]の場合、\( 2^n \) が基本解の1つでしたね。

なるべく \( 2^n \) に近い基本解をもう1つ探しましょう。

 

そんな基本解に \( n 2^n \) があります。実際に代入すると、\[
n 2^n - 4 (n-1) 2^{n-1} + 4 (n-2) 2^{n-2} = 0 \\ 
4n 2^{n-2} + (-8n+8) 2^{n-2} + (4n-8) 2^{n-2} = 0 \\
(4n-8n+4n) 2^{n-2} + (8-8) 2^{n-2} = 0
\]となり、\( n 2^n \) も解になることがわかりますね。

 

なので、任意定数 \( C_1 \), \( C_2 \) を用いて\[
a_n = C_1 2^n + n C_2 2^n
\]と一般解を求めることができます。

スポンサードリンク

３．隣接３項間差分方程式

まずはつぎの漸化式を解いてみましょう。

\[ a_0 = 2, \  a_1 = 7, \  a_{n} - 3a_{n-1} + 2 a_{n-2} = 0 \]

の初期値による特殊解を求めなさい。

(1) 普通に解いてみる

とりあえず、高校のやり方とほぼ同じやり方で解いてみましょう。 
まずは特性方程式を解いてみましょう。
\( t^2-3t+2=0 \) より \( t = 1,2 \) となる。

よって、

\[\left\{ \begin{array}{l} a_n - a_{n-1} = 2(a_{n-1} - a_{n-2}) \\a_n - 2a_{n-1} = (a_{n-1} -2 a_{n-2}) \end{array}\right.\]

となる。この漸化式は、

\( a_{n+1} - a_{n} = 2(a_{n} - a_{n-1}) = 2^2(a_{n-1} - a_{n-2}) =\cdots= 2^n(a_{1} - a_{0})= 5 \cdot 2^n \)
\( a_{n+1} - 2a_{n} = 1(a_{n} - 2a_{n-1}) = 1^2(a_{n-1} - 2a_{n-2}) =\cdots= 1^n(a_{1} - 2a_{0}) = 3 \)

と変形できる。よって、

\( \left\{ \begin{array}{l} a_{n+1} - \ \ a_{n} = 5 \cdot 2^n \ \ \cdots (1) \\a_{n+1} - 2a_{n} = 3 \ \ \ \ \ \ \ \ \   \cdots (2) \end{array}\right. \)

となり、\( a_{n} = 5 \cdot 2^n - 3 \ \ [(1)-(2) \)] と求めることができる。

 

(2) 微分方程式っぽく解く

ここからが本番です。2章で説明したような微分方程式っぽく解き方で解いてみましょう。

特性方程式\[
t^2 - tx + 2 = 0
\]の解は \( t = 1,2 \) でしたよね。

なので、解の形を \( C_1, C_2 \) として、\[ a_n = C_1 \cdot 1^n + 2^n \cdot C_2 = C_1 + 2^n C_2
\]と一般解を求めることができますね。

 

つぎに、与えられた初項から一般解の中から初項に一致する1つを見つけ出す計算をおこないます。

この初項に一致する1つの解のことを特殊解と呼びます。

 

一般解に初項を代入すると、\[
C_1 + 2^0 C_2 = C_1 + C_2 = a_0 = 2
\]となるので、
\[ C_1 + 2^1 C_2 = C_1 + 2 C_2 = a_1 = 7 \]の2つの式が成立する。

\[\left\{ \begin{array}{l} C_1 + \ \ C_2 = 2 \ \ \cdots (1) \\ C_1 + 2C_2 = 7 \ \   \cdots (2) \end{array}\right.\]となります。

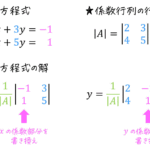
見た瞬間2つの解はわかるけど、今回はあえて逆行列使って解いてみます。
もちろん行列を使わなくても計算は可能です。

 

逆行列を使って連立方程式を解く方法についてはこちらでまとめているので、わからない人は参考までにどうぞ。

www.momoyama-usagi.com

\[\left( \begin{array}{ccc} 1 & 1  \\ 1 & 2  \end{array} \right) \left( \begin{array}{ccc} C_1  \\ C_2  \end{array} \right) =\left( \begin{array}{ccc} 2  \\ 7  \end{array} \right)\]

 

という行列を満たせばいい。ここで逆行列を求める。

 

\[\left( \begin{array}{ccc} 1 & 1  \\ 1 & 2  \end{array} \right)^{-1} =\left( \begin{array}{ccc} 2 & -1  \\ -1 & 1  \end{array} \right)\]

 

なので、

 

\[\left( \begin{array}{ccc} C_1  \\ C_2  \end{array} \right) =  \left( \begin{array}{ccc} 1 & 1  \\ 1 & 2  \end{array} \right)^{-1} \left( \begin{array}{ccc} 2  \\ 7  \end{array} \right)\ =   \left( \begin{array}{ccc} 2 & -1  \\ -1 & 1  \end{array} \right) \left( \begin{array}{ccc} 2  \\ 7  \end{array} \right)\ = \left( \begin{array}{ccc} 3  \\ 5  \end{array} \right)\ \]

となる。（\( A A^{-1} = A^{-1} A = E \) より、元の行列とその行列の逆行列（順番はどっちでもOK）は必ず単位行列）

なので、\( C_1 = -3, C_2 = 5 \) となり、特殊解は\[ a_{n} = 5 \cdot 2^n - 3 \]となる。

 

４．隣接３項間差分方程式（重解あり）

重解があるパターンもやってみましょう。\[ a_0 = 2, \  a_1 = 10, \  a_{n} - 4a_{n-1} + 4 a_{n-2} = 0\]

(1) 普通に解いてみる

\( x^2-4x+4=0 \) より \( x = 2 \) となる。

あれ、重解になる！　式が１つしかでない！

慌てないでください。まずは１つ式をたてて変形しちゃいましょう。

\[\begin{eqnarray}a_{n+1} - 2a_{n} = 2(a_{n} - 2a_{n-1}) = 2^2(a_{n-1} - 2a_{n-2}) = \cdots = 2^n (a_1 - 2 a_0) = 6 \cdot 2^n \end{eqnarray}\]

 となりますよね。つぎに両辺を \( 2^{n+1} \) で割ります。

\[ \frac{a_{n+1}}{2^{n+1}} - \frac{a_{n}}{2^{n}} = 3 \]

さらに \( \frac{a_{n}}{2^n} = b_{n} \) とします。すると、
\[ b_{n} - b_{n-1} = 3 \] となります。\( \frac{a_{0}}{2^0} = b_{0} = 2 \) より、
\[b_{n} = 2 + n \times 3 = 3n + 2\]となる。よって、\( \frac{a_{n}}{2^n} = b_{n} \) より、

\[ a_n = 2^n \times b_{n} = 2^n(3n + 2)\]

と計算でき、特殊解は \(  2^n(3n + 2) \) となる。

意外とめんどいでしょ！　ということで(2)の少し楽なやり方でやってみます。

(2) 微分方程式っぽく解く

特性方程式が重解であった場合は、普通に解くと基本解が欲しい数出てこないのでしたね。

そこで、\( 2^n \) の他に \( n 2^n \) も基本解であると考えて、\[a_n = 2^n (C_1n + C_2)

\]と一般解にするのでしたね。（一般解）（この形は基本変わらない）

すると、\( C_2 = a_0 = 2 \),  \( 2C_1 + 2C_2 = a_1 = 10 \) の2つの式が成立する。

\[\left\{ \begin{array}{l} \ \ \ \ \ \ \ \ \ \ \ C_2 =  \ \ 2 \ \ \cdots (1) \\ 2C_1 + 2C_2 = 10 \ \   \cdots (2) \end{array}\right.\]

さすがにこの式は行列使って計算するまでもないので普通に計算する。すると、\( C_1 = 3, C_2= 2 \) となる。よって特殊解は、

\[a_n = 2^n (3n + 2)\]

となる。

５．隣接４項間差分方程式

４項間の差分方程式も微分方程式チックに解くことができちゃいます。

４項間以上の場合は微分方程式チックに解いたほうが早く特殊解まで出すことができます。

実は隣接４項間は横浜国立大学の入試で出題されています。（もちろん誘導あり）

数列がをみたしているとき，

(1) 3次方程式は異なる3実数解をもつ．の値を求めよ．
(2) を(1)で求めたものとする．とおくとき，をの式で表せ．
さらにとおくとき，をの式で表せ．
(3) のとき，をそれぞれの式で表せ

引用：大学入試から学ぶ高校数学　横浜国立大学

微分方程式チックではない解答はリンク先に用意されてあったのでそちらを参考にしてください。

ではこれを微分方程式っぽく解いてみます。

\[a_{n} - 10a_{n-1} + 31a_{n-2} - 30a_{n-3} =0, \ a_0 = 1, \ a_1 = 2, \ a_2 = 5 \]

の一般解を出します。まずは特性方程式から、(1)の誘導に相当します。

\[\begin{align*}
t^3 - 10t^2 + 31t - 30 & =
(t-2)(t^2-tx+15) \\ & =
(t-2)(t-3)(t-5)=0 \end{align*}\]

より \( t=2,3,5 \) となる。解の形を任意定数 \( C_1,C_2,C_3 \) を用いて、

\[a_n = 2^n \cdot C_1 + 3^n \cdot B_2 + 5^n \cdot C_3 \]

とおく。

これが一般解となる。あとは3つの初期値を使って \( C_1,C_2,C_3 \) の3変数の方程式を作るだけ。

(i) \( n = 0 \) のとき、\( C_1 + C_2 + C_3 = a_0 = 1 \) となる。
(ii) \( n = 1 \) のとき、\( 2C_1 + 3C_2 + 5C_3 = a_1 = 2 \) となる。
(iii) \( n = 2 \) のとき、\( 4C_1 + 9C_2 + 25C_3 = a_2 = 5 \) となる。

 

さて今回も逆行列を使って連立方程式をときます。

\[\left( \begin{array}{ccc} 1 & 1 & 1  \\ 2 & 3 & 5 \\ 4 & 9 & 25  \end{array} \right) \left( \begin{array}{ccc} C_1  \\ C_2 \\ C_3  \end{array} \right) =\left( \begin{array}{ccc} 1  \\ 2 \\ 5  \end{array} \right)\]

となる。

逆行列は、

\[\left( \begin{array}{ccc} 1 & 1 & 1  \\ 2 & 3 & 5 \\ 4 & 9 & 25  \end{array} \right)^{-1} =\frac{1}{6} \left( \begin{array}{ccc} 30 & -16 & 2  \\ -30 & 21 & -3 \\ 6 & -5 & 1  \end{array} \right)\]

となる。

よって、

\[\left( \begin{array}{ccc} C_1  \\ C_2 \\ C_3  \end{array} \right) =  \left( \begin{array}{ccc}1 & 1 & 1  \\ 2 & 3 & 5 \\ 4 & 9 & 25  \end{array} \right)^{-1} \left( \begin{array}{ccc} 1  \\ 2 \\ 5  \end{array} \right)\ = \frac{1}{6}  \left( \begin{array}{ccc} 30 & -16 & 2  \\ -30 & 21 & -3 \\ 6 & -5 & 1  \end{array} \right) \left( \begin{array}{ccc} 1 \\ 2  \\ 5  \end{array} \right)\ = \frac{1}{6} \left( \begin{array}{ccc} 8  \\ -3 \\ 1  \end{array} \right)\ \]

となり、\( C_1 = \frac{4}{3}, C_2 = - \frac{1}{2}, C_3 = \frac{1}{6} \) と求められる。

よって特殊解は、

\[a_n =\frac{4}{3} \cdot 2^n  - \frac{1}{2} \cdot 3^n +  \frac{1}{6} \cdot 5^n =\frac{1}{6}(2^{n+3} - 3^{n+1} + 5^n)\]

と求められる。

６．隣接４項間差分方程式（重解あり）

特性方程式に重解がある場合、予想する式は変化します。

例えば次の問題を解いてみましょう。

\[a_{n} - 5a_{n-1} + 3a_{n-2} + 9a_{n-3} =0 \ a_0 = 0, \ a_1 = -6, \ a_2 = 12 \]

いつものようにまずは特性方程式をときます。

\[\begin{align*} t^3 - 5t^2 + 3t - 9 & = (t+1)(t^2-6t+9) \\ & =(t+1)(t-3)^2=0 \end{align*}\]

よって 1 と 3（2重解）となる。

ここで3が2重解になりましたよね。なので3の部分だけ \( C_1 n + C_2 \) とします。よって一般解は、\( C_1,C_2,C_3 \) は任意の定数として、

\[a_n = (C_1 n+C_2) \cdot 3^n + C_3 \cdot (-1)^n \]

となる。あとは場合分け。

(i) \( n = 0 \) のとき、\( C_2 + C_3 = a_0 = 0 \)
(ii) \( n = 1 \) のとき、\( 3C_1 + 3C_2 - C_3 = a_1 = -6 \)
(iii) \( n = 2 \) のとき、\( 18C_1 + 9C_2 + C_3 = a_2 = 12 \)

今回も逆行列使っちゃいましょう。

\[\left( \begin{array}{ccc} 0 & 1 & 1  \\ 3 & 3 & -1 \\ 18 & 9 & 1  \end{array} \right) \left( \begin{array}{ccc} C_1  \\ C_2 \\ C_3  \end{array} \right) =\left( \begin{array}{ccc} 0  \\ -6 \\ 12  \end{array} \right)\]

となる。

逆行列は、

\[\left( \begin{array}{ccc} 0 & 1 & 1  \\ 3 & 3 & -1 \\ 18 & 9 & 1  \end{array} \right)^{-1} =\frac{1}{48} \left( \begin{array}{ccc} -12 & -8 & 4  \\ 21 & 18 & -3 \\ 27 & -18 & 3  \end{array} \right)\]

となる。

よって、

\[\left( \begin{array}{ccc} C_1  \\ C_2 \\ C_3  \end{array} \right) =  \left( \begin{array}{ccc}0 & 1 & 1  \\ 3 & 3 & -1 \\ 18 & 9 & 1  \end{array} \right)^{-1} \left( \begin{array}{ccc} 0  \\ -6 \\ 12  \end{array} \right)\ = \frac{1}{48}  \left( \begin{array}{ccc}-12 & -8 & 4  \\ 21 & 18 & -3 \\ 27 & -18 & 3  \end{array} \right) \left( \begin{array}{ccc} 0\\ -6  \\ 12  \end{array} \right)\ = \left( \begin{array}{ccc} 2  \\ -3 \\ 3  \end{array} \right)\ \]

となり、\( C_1 = 2, C_2 = -3, C_3 = 3 \) と求められる。

よって特殊解は、

\[a_n = (2n-3) \cdot 3^n + 3 \cdot (-1)^n \]

となる。

 

７．連立差分方程式

連立漸化式を解いたことありますか？

連立漸化式も隣接３項間の差分方程式に書き換えちゃうことができます。

１問解いてみましょう。\( a_0 = 7, \ b_0 = -4 \) とします。

 \[\left\{ \begin{array}{l} a_n = 2a_{n-1} + \ \ b_{n-1}\\ b_n = 2a_{n-1} + 3b_{n-1}  \end{array}\right.\]

まずはこの連立差分方程式を隣接３項間差分方程式に変えます。

\[b_{n-1} = a_n - 2a_{n-1} \\ b_{n} = a_{n+1} - 2a_{n} \] 

なので、これを代入する。

\[a_{n+1} - 2a_{n} = 2a_{n-1} + 3(a_n - 2a_{n-1}) \]\[a_{n+1} - 5a_{n} + 4a_{n-1} = 0\]\[a_{n} - 5a_{n-1} + 4a_{n-2} = 0\]

となる。

あとはいつも通り特性方程式を解くだけ。
\[ t^2 - 5t + 4 = (t-1)(t-4)=0\]

より、解は1と4（重解なし）。よって一般解は、

\[ a_n = C_1 \cdot 4^n + C_2\]

となる。

ここで、\( a_1 = 2a_0 + b_0 = 10 \) となる。

(i) \( n = 0 \) のとき、\( C_1 + C_2 = a_0 = 7 \)
(ii) \( n = 1 \) のとき、\( 4C_1 + C_2 = a_1 = 10 \) となる。

よって、\( C_1 = 1, C_2 = 6 \) となる。

よって特殊解は、

\[ a_n = 1 \cdot 4^n + 6 = 4^n + 6\]

となる。

また、\( b_{n} = a_{n+1} - 2a_{n} \) なので、

\[ b_{n} = 4^{n+1} + 6 - 2(4^n + 6) = 4 \cdot 4^n + 6 - 2 \cdot 4^n - 12 \\ = 2 \cdot 4^n - 6\]

と求められる。

 

８．公式のまとめ

では、今まで説明した公式を確認していきましょう。

 

 

９．練習

では１問練習してみましょう。

問題

\( a_{n} - 6 a_{n-1} + 12 a_{n-2} - 8 a_{n-3} = 0 \) について、

(1) 定数 \( C_1,C_2,C_3 \) を用いて一般解を求めなさい。
(2) \( a_0 = 1, a_1 = 6, a_2 = 4 \) のときの特殊解を求めなさい。

解答

(1) まずは特性方程式をときましょう。

\[t^3-6t^2+12t-8 = (t-2)(t^2-4t+4) = (t-2)^3 \]

となり、なんと2の3重解となる。よって一般解は

\[a_n = (C_1n^2+C_2n+C_3) \cdot 2^n\]

となる。ただし \( C_1, C_2, C_3 \) は任意の定数である。

(2)

\( n = 0 \) のとき、\( C_3 = a_0 = 1 \)
\( n = 1 \) のとき、\( 2C_1+ 2C_2 + 2C_3 = a_1 = 6 \)
\( n = 2 \) のとき、\( 16C_1 + 8C_2 + 4C_3 = a_2 = 4 \)

の3つの方程式が成り立つ。今回も逆行列でやっちゃうよ。

\[\left( \begin{array}{ccc} 0 & 0 & 1  \\ 2 & 2 & 2 \\ 16 & 8 & 4 \end{array} \right) \left( \begin{array}{ccc} C_1  \\ C_2 \\ C_3  \end{array} \right) =\left( \begin{array}{ccc} 1  \\ 6 \\ 4  \end{array} \right)\]

となる。

逆行列は、

\[\left( \begin{array}{ccc} 0 & 0 & 1  \\ 2 & 2 & 2 \\ 16 & 8 & 4   \end{array} \right)^{-1} =\frac{1}{8} \left( \begin{array}{ccc} 4 & -4 & 1  \\ -12 & 8 & -1 \\ 8 & 0 & 0  \end{array} \right)\]

となる。よって、

\[\left( \begin{array}{ccc} C_1  \\ C_2 \\ C_3  \end{array} \right) =  \left( \begin{array}{ccc}0 & 0 & 1  \\ 2 & 2 & 2 \\ 16 & 8 & 4  \end{array} \right)^{-1} \left( \begin{array}{ccc} 1 \\ 6 \\ 4  \end{array} \right)\ = \frac{1}{8}  \left( \begin{array}{ccc} 4 & -4 & 1  \\ -12 & 8 & -1 \\ 8 & 0 & 0  \end{array} \right) \left( \begin{array}{ccc}  1\\ 6  \\ 4  \end{array} \right)\ = \left( \begin{array}{ccc} -2  \\ 4 \\ 1  \end{array} \right)\ \]

となり、\( C_1 = -2, C_2 = 4, C_3 = 1 \) と求められる。よって特殊解は、

\[ a_n = (-2n^2 + 4n + 1) \cdot 2^n \]

と求められる。

 

10．さいごに

今回は、隣接３、４項間差分方程式の解き方、連立差分方程式の解き方をまとめてみました。このように項を予測するやり方でやれば、隣接５項だろうが６項だろうが解くことができるようになります（めんどくさいけど）。

 

この記事から差分方程式、もしくは漸化式の解き方がわかるようになればありがたいです。

 

今回は（右辺）= 0の差分方程式でしたが、次の記事では（右辺）= 0ではない場合の差分方程式の解き方も説明したいと思います。

 

それではまた次回。ばいばーい！

差分方程式後編はこちら！

www.momoyama-usagi.com