本田圭佑のじゃんけんから確率統計を学ぶ

こんにちは、ももやまです！

／
あと2日!
4/19まで #毎日挑戦 #毎日11時start#本田とじゃんけん
＼@pepsi_jpn をフォロー#本田圭佑 とじゃんけん勝負✌
勝てばその場で #ペプシ #ジャパンコーラ
計16万名様にコンビニ無料引換えクーポンがあたる!
あなたは何を出す？
※混みあうと返信が遅くなりますhttps://t.co/HyiM9rLiCt

— Pepsi（ペプシ） (@pepsi_jpn) 2019年4月18日

皆さんは本田圭佑とのじゃんけん勝負に挑戦したことはありますか？
挑戦した人はわかると思うのですが、やけに本田圭佑（ケイスケホンダ）が強くありませんか？

なかなか勝てなくて悔しいですよね…

絶対に謎の力が働いてると思いますよね！？

ということで、実際に本田の勝利確率を求めてみましょう！

スポンサードリンク

１．じゃんけんの試行回数

本当に正確に勝率を求めたり、時間帯ごとの勝率を求めるのであれば3日間くらいの勝負データが必要ですが、そこまでするのはめんどかったので、じゃんけんの思考回数は10,000回にしました。ちなみに10,000回集めるのに30分かかりました。

スポンサードリンク

２．理論値を求めてみよう

まず、10,000回じゃんけんをした場合の平均の勝利回数（勝利回数の期待値）を求めましょう。

今回のじゃんけんでは、あいこはなしなので、勝ちか負けかのどちらかになります。じゃんけんの勝敗に運以外の要素は絡まないとすると勝つ確率も負ける確率もともに 1/2 になりますよね。

つまり、じゃんけんは勝ちか負けかの2パターンの思考しかありませんよね（2パターンの試行しかないことをベルヌーイ試行といいます）。つまり、勝利回数の期待値を求めるのに二項分布を使うことができます。

 

今回の場合は試行回数 \( n \) は10,000
各じゃんけんごとの勝利確率 \( p \) は 1/2

なので、期待値は、

\( 10000 \times \frac{1}{2} = 5000 \)

と求めることができる。よって勝利回数の期待値は5,000回となる。

つぎに分散を求める。公式に代入して、

\( 10000 \times \frac{1}{2} \times (1 - \frac{1}{2}) = 2500 \)

となる。標準偏差は、分散のルートを取るだけなので、

\( \sqrt{2500} = 50 \)

より標準偏差は50回と求めることができる。

標準偏差を求めることで、「データがどれだけばらつきがあるか」がわかるようになります。大きければ大きいほどばらつきが大きく、小さければ小さいほどばらつきが小さいことがわかります。 

ところで、10,000回っていうのはじゃんけんの実施回数としてはかなり多い回数といえますよね。なので、データの分布が正規分布*1（地球上で一番一般的な分布）で近似して「ある回数～ある回数」となる確率を求めることができます。例えば、

平均 ± 標準偏差1つ分の範囲（4,950〜5,050回）：約69.3％ [偏差値40～60]平均 ± 標準偏差2つ分の範囲（4,900〜5,100回）：約95.5％ [偏差値30～70]平均 ± 標準偏差3つ分の範囲（4,850〜5,150回）：約99.7％ [偏差値20～80]

となります。多くの場合において、勝利回数は5,000回から大きく前後しないことがわかりますよね。

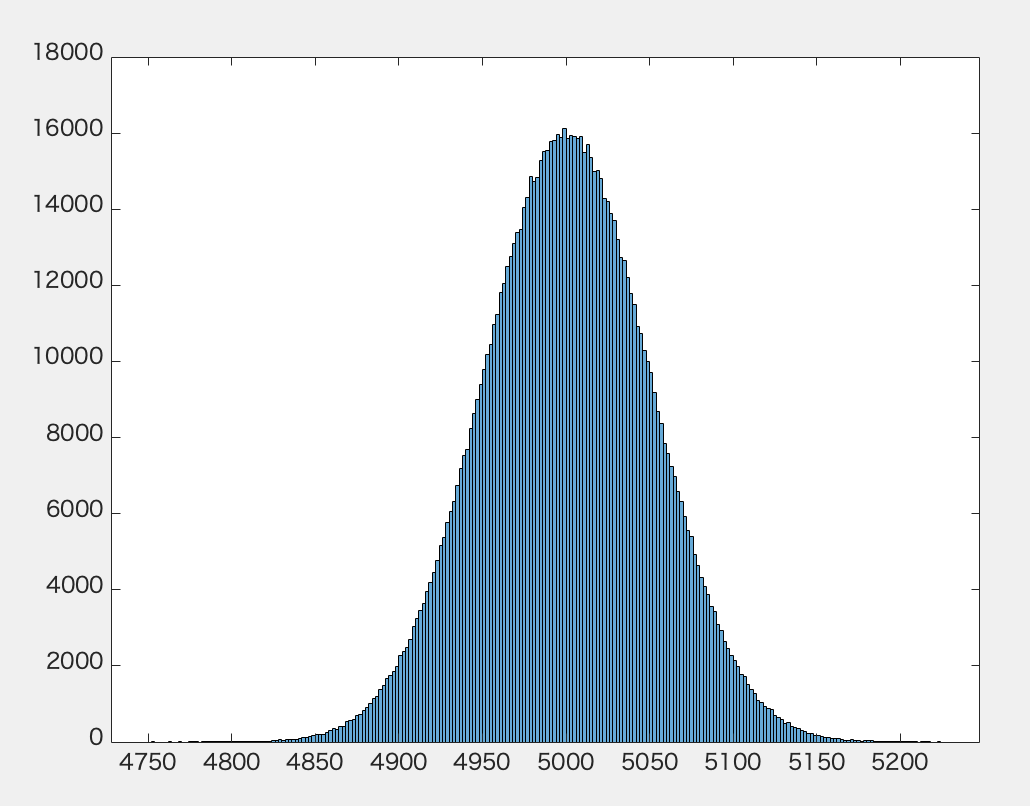
試しに、MATLAB（技術計算用プログラミング言語）を用いて10,000回のじゃんけんを1,000,000セット試行したときの度数分布グラフを下に載せてみます。

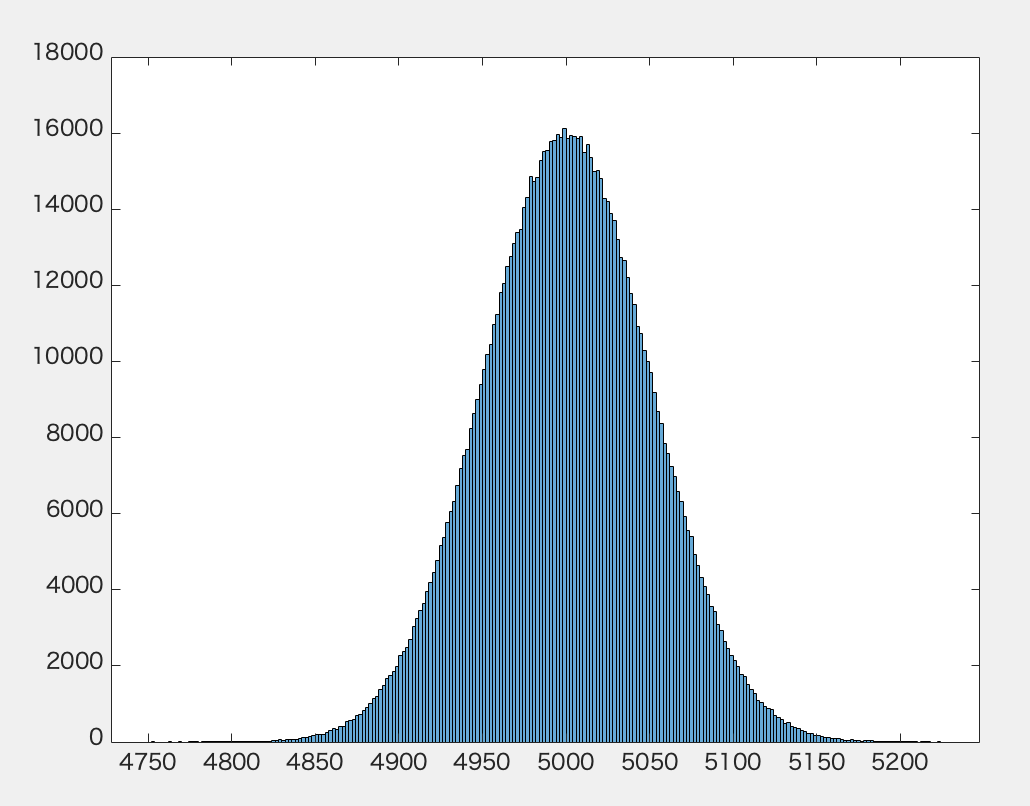
5,000回前後のところのデータ数が多くて、5,000回から遠ざかれば遠ざかるほどデータ数が急に減ってますよね。（まさに正規分布、つまり一般的な分布にそっくりです！）結果出すのに20分かかりました…

 

スポンサードリンク

３．本田圭佑は何回勝利したの？

さていよいよ本題です。TwitterのAPIを使って10,000ツイート分の本田圭佑の勝敗の結果を調べました。「累計No.」というのが累計の試合数カウントを表しています。

敗北回数	累計No.	時間
1	254	12:48:22
2	1026	12:51:33
3	1673	12:52:41
4	1852	12:53:42
5	3386	12:59:01
6	4789	13:03:18
7	5489	13:05:27
8	6265	13:07:36
9	8031	13:12:57
10	8553	13:14:04
11	9191	13:16:10
12	9961	13:18:20

結果、なんと12敗しかしていないのだ！
試合数は 10,000 なので、なんと10,000戦9,988勝、勝率 99.88 ％！

9,988勝は、平均である5,000勝よりも標準偏差 99.76個分も大きい。これを偏差値に換算すると1,047.6となり、並大抵の人間では出せない偏差値であることがわかりあるだろう。

10,000戦して9,988勝以上する確率を計算してみるとなんと \( 3.47 \times 10^{-2164} \) となります。あまりにもすごすぎてわからないと思うので、宝くじで1等当てる確率、2019年センター試験の各科目まぐれで満点になる確率などと比較してみました。

種類	確率	連続回数
ロト6	\( 1.64 \times 10^{-7} \)	318
年末ジャンボ	\( 5.00 \times 10^{-8} \)	296
センター国語	\( 1.79 \times 10^{-25} \)	87
センター英語	\( 6.23 \times 10^{-34} \)	65
センター数1A	\( 2.21 \times 10^{-94} \)	23
センター数2B	\( 6.68 \times 10^{-110} \)	19

※連続回数：例えば、ロト6の場合は連続318回1等を当てる確率がじゃんけんで9,988回以上勝つ確率と同じになる。

10,000回じゃんけんをして12回しか負けない確率というのは、あの大量の選択肢があるセンター試験の数学でさえ、20回前後連続で満点を取ることができるほどの確率とほぼ同じなので、ホンダケイスケが謎の力は本当にやばいことが明らかだろう。宝くじの1等当選確率がかわいく見えてきますよね…。

 

４．さいごに

みなさんわかりましたよね。
本田圭佑はじゃんけんのプロであることが！！

この確率なら、

「俺の勝ち　何で負けたか、明日まで考えといてください。」

と堂々で言っても文句ありませんよね！

「たかがジャンケン、そう思ってないですか？　それやったら明日も俺が勝ちますよ。」

そりゃ10000戦9988勝なら次回も勝てるって自信ありますよね！

ここからは勉強の話になるのですが、「確率・統計分野」は数学Bの「確率分布と統計的な推測」という分野で基礎をやるのですがこの分野はほとんど習わない高校が多いと思います。実はセンター試験の数学2Bの選択問題で「二項分布」・「正規分布」とかは毎年出てます。

高校・大学で「確率・統計」分野を習ってた（もしくは今習ってる）人はぜひ得意になって確率統計の面白さに気づいてくれたらありがたいです。まだ習ってない人はぜひ確率統計分野を勉強してみてください。

 

条件付き確率も結構面白いです、こちらもぜひ見てください！

www.momoyama-usagi.com

それでは、また次回。さようなら。