スポンサードリンク
こんにちは、ももやまです。
「1年前期の解析学の試験まであと1日しかない、あきらめよう。」って思ってる人、諦めないでください!!
試験前日でも数3レベルの知識があれば3時間で総復習ができるように10題の練習問題を作成しました!
こちらでは、積分編の解説記事を記載しております、微分編の解説記事は下のリンクからどうぞ!
- 90分間で問題を解く。答えを回答フォームに入力する。
- 答えを送信後、間違った箇所を確認し、解説を見てどこで間違えたのか(理解ができていないのか)を確認する。
- 間違えた箇所を参考書や記事などで練習する。
- 時間があれば、合っている箇所も確認する。(青色と赤色の枠部分)
- 寝る。
時間がある人はじっくり、時間がない人は素早くこの記事にて1年前期の解析学の復習をしましょう!
それぞれの練習問題の解説では、
- 試験で必要な知識:青色の枠
- 試験で必要な解き方:赤色の枠
- 覚えておくと便利な公式: 緑色の枠
で要点をまとめています。
※ 高校レベルの積分に少し不安がある人は、こちらの記事にて復習することをおすすめします。
目次
スポンサードリンク
問題7. ★ 不定積分
次の(1), (2)の不定積分を計算しなさい。ただし(2)は \( t = \tan \frac{x}{2} \) とおいて積分をすること。また、\( C \) を積分定数とする。(配点 10)
(1)\[ \begin{align*}
\int x^2 \log x \ dx & = \frac{1}{3} x^3 \left[ \ \ 25 \ \ \right] - \frac{1}{3} \int \left[ \ \ 26 \ \ \right] \ dx
\\ & = \frac{1}{3} x^3 \left[ \ \ 25 \ \ \right] - \left[ \ \ 27 \ \ \right] + C
\end{align*} \]
(2) \[\begin{align*}
\int \frac{1}{1 + \sin x + \cos x } \ dx & = \int \left[ \ \ 28 \ \ \right] \ dt
\\ & = \left[ \ \ 29 \ \ \right] + C
\end{align*}\]
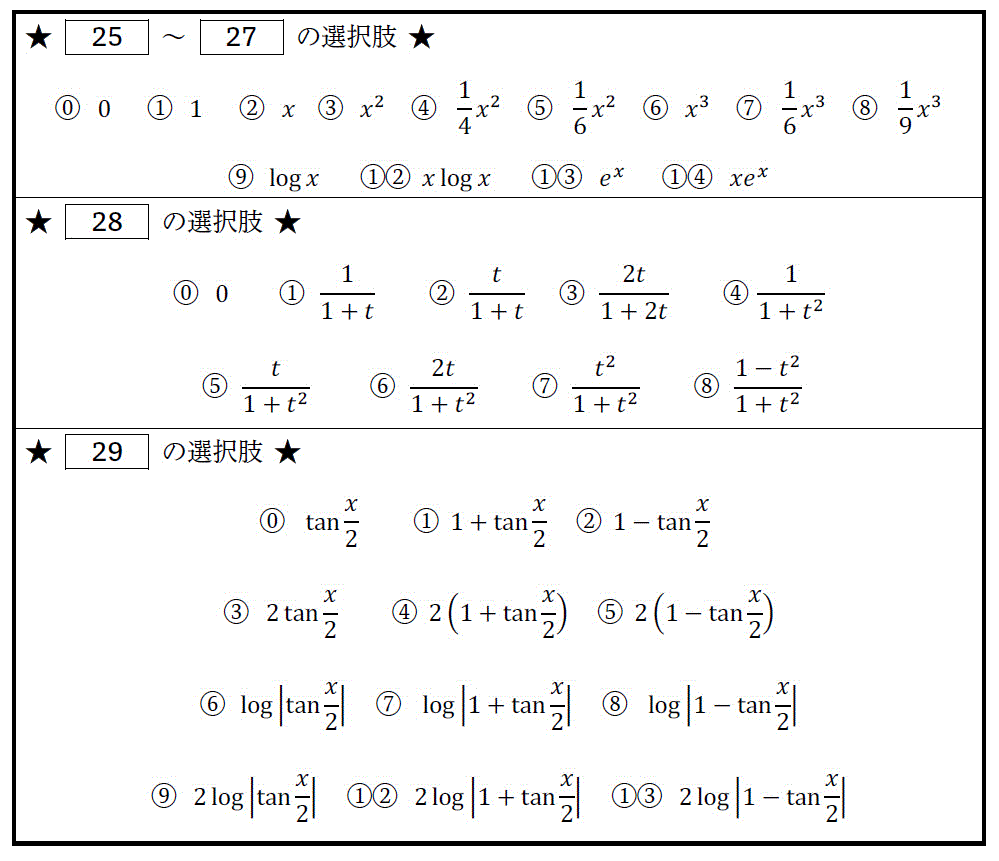
(1) 部分積分
まずは部分積分の公式を確認しましょう。
\[ \int \textcolor{deepskyblue}{f(x)} \textcolor{magenta}{g'(x)} dx = \textcolor{deepskyblue}{f(x)} \textcolor{magenta}{ g(x) } - \int \textcolor{deepskyblue}{f'(x)} \textcolor{magenta}{ g(x) } \ dx \]
※1 積分する関数を微分する関数 \( \textcolor{deepskyblue}{ f(x) } \) と積分する関数 \( \textcolor{magenta}{ g(x) } \) に分ける
※2 微分する関数には、何回も微分したら消える \( x^a \) の形(多項式)や、微分すると \( \frac{1}{x} \) になる \( \log x \) が来ることが多い
\[\begin{align*}
\int \textcolor{magenta}{x^2} \textcolor{deepskyblue}{\log x} \ dx & = \textcolor{magenta}{\frac{1}{3} x^3} \log x - \int \frac{1}{3} x^3 \cdot \textcolor{deepskyblue}{ \frac{1}{x} }
\\ & = \frac{1}{3} x^3 \log x - \frac{1}{3} \int x^2 \ dx
\\ & = \frac{1}{3} x^3 \log x - \frac{1}{9} x^3 + C
\end{align*}\]
(2) t = tan(x/2) とおく積分
\( t = \tan \frac{x}{2} \) とおくことで三角関数が含まれる積分を計算することができます。
三角関数のみで表された積分は、\[
t = \tan \frac{x}{2}
\]とおくことで計算ができる。このとき、\[
\sin x = \frac{2t}{1+t^2} , \ \ \ \cos x = \frac{1 - t^2}{1 + t^2}
\]\[
\tan x = \frac{2t}{1-t^2} , \ \ \ dx = \frac{2}{1+t^2} \ dt
\]となる。
※ この公式は暗記必須(導出過程も必ず確認すること)
※ 導出方法や、計算練習をもっとしたい人はこちらからどうぞ!
よって、\[\begin{align*}
\int \frac{1}{1 + \sin x + \cos x} \ dx & = \int \frac{1}{1 + \frac{2t}{1+t^2} + \frac{1-t^2}{1+t^2}} \cdot \frac{2}{1+t^2} \ dt
\\ & = \frac{1}{ \frac{1+t^2 + 2t + 1-t^2}{1+t^2} } \cdot \frac{2}{1+t^2} \ dt
\\ & = \frac{1+t^2}{2t + 2} \cdot \frac{2}{1+t^2} \ dt
\\ & = \frac{1}{1+t} \ dt
\\ & = \log \left| 1 + t \right| + C
\\ & = \log \left|1 + \tan \frac{x}{2} \right| + C
\end{align*}\]と計算できる。
★ マーク解答 ★
No.25: 9 [2点]
No.26: 3 [1点]
No.27: 8 [2点]
No.28: 1 [3点]
No.29: 7 [2点]
スポンサードリンク
問題8. ★ 定積分
次の(1)~(3)の定積分を計算しなさい。(配点 10)
(1)\[
\int^{3}_{\sqrt{3}} \frac{9}{x^2 + 9} \ dx = \left[ \ \ 30 \ \ \right]
\]
※ 訂正 [2021/08/03]
問題用紙PDFの数式が誤っておりました。申し訳ございません。
(2)\[
\int^{\pi}_{0} x^2 \sin x \ dx = \left[ \ \ 31 \ \ \right]
\]
(3) \[
\int^{1}_{0} \frac{2x+6}{2x^2 - 3x - 2} = \left[ \ \ 32 \ \ \right]
\]

(1) 三角関数への置換積分(or 逆三角関数へ持ち込む)
(i) 置換積分で解く
\( x = 3 \tan t \) とおく。\[
dx = \frac{3}{ \cos^2 t } \ dt
\]また、積分範囲は以下の表のようになる。
| 変数 | 積分範囲 |
|---|---|
| \( x \) | \( \sqrt{3} \to 3 \) |
| \( t \) | \( \frac{\pi}{6} \to \frac{\pi}{4} \) |
\[\begin{align*}
\int^{3}_{\sqrt{3}} \frac{9}{x^2+9} \ dx & = \int^{ \frac{\pi}{4} }_{ \frac{\pi}{6} } \frac{9}{9 + 9 \tan^2 x } \cdot \frac{3}{ \cos^2 t} \ dt
\\ & = \int^{ \frac{\pi}{4} }_{ \frac{\pi}{6} } \frac{1}{1 + \tan^2 t } \cdot \frac{3}{ \cos^2 t} \ dt
\\ & = \int^{ \frac{\pi}{4} }_{ \frac{\pi}{6} } \cos^2 t \cdot \frac{3}{ \cos^2 t} \ dt
\\ & = \int^{ \frac{\pi}{4} }_{ \frac{\pi}{6} } 3 \ dt
\\ & = \left[ 3t \right]^{ \frac{\pi}{4} }_{ \frac{\pi}{6} }
\\ & = \frac{3}{4} \pi - \frac{\pi}{2}
\\ & = \frac{\pi}{4}
\end{align*}\]と計算できる。
(ii) 逆三角関数の形に持ち込む
大学数学で習う逆三角関数の力を借りると、置換なしに計算をすることができます。
ここで、逆三角関数への積分公式を確認しておきましょう。(微分編とはちょっと違った書き方をしています。)
\[
\int \frac{1}{\sqrt{a^2 - x^2} } \ dx = \sin^{-1} \frac{x}{a}
\]\[
\int - \frac{1}{\sqrt{a^2 - x^2} } \ dx = \cos^{-1} \frac{x}{a}
\]\[
\int \frac{a}{a^2 + x^2} \ dx = \tan^{-1} \frac{x}{a}
\]
※ ただし \( a \) は定数
※ 積分定数は省略した
今回の場合、\[\begin{align*}
\ \int^{3}_{\sqrt{3}} \frac{9}{x^2+9} \ dx & = 3 \int^{3}_{\sqrt{3}} \frac{3}{x^2+3^2} \ dx
\\ & = 3 \left[ \tan^{-1} \frac{x}{3} \right]^{3}_{ \sqrt{3} }
\\ & = 3 \left( \tan^{-1} 1 - \tan^{-1} \frac{ \sqrt{3} }{3} \right)
\\ & = 3 \left( \frac{ \pi }{4} - \frac{ \pi }{6} \right)
\\ & = 3 \cdot \frac{ \pi }{ 12 }
\\ & = \frac{ \pi }{ 4}
\end{align*}\]と計算できる。
(2) 部分積分の省略(ブンブン積分)
今回のように被積分関数が「多項式( \( x^a \) の形)」と「三角関数や \( e^x \) の形」となっている場合は、部分積分の省略公式(ブンブン積分)が使えます。
\[\begin{align*}
& \int^{\pi}_{0} x^2 \sin x \ dx
\\ = \ & \left[ x^2 ( -\cos x ) - 2x ( - \sin x ) + 2 ( \cos x ) \right]^{\pi}_{0}
\\ = \ & \left( \pi^2 - 2 \right) - 2
\\ = \ & \pi^2 - 4
\end{align*}\]
部分分数分解の省略公式(ブンブン積分)の練習をもっとしたい人はこちらでどうぞ!
(3) 部分分数分解を用いた積分
(多項式)/(多項式) の分数になっている問題については、部分分数分解を用いて以下の公式に持ち込む。
\[ \int \frac{ f'(x) }{ f(x) } \ dx = \log | f(x) | + C \]
※ 積分定数は \( C \)
分母を\[
2x^2 - 3x - 2 = (2x + 1)(x - 2)
\]と因数分解できる。ここで、\[
\frac{2x+6}{2x^2 - 3x - 2} = \frac{a}{2x+1} + \frac{b}{x-2}
\]の形に分解することを考える。両辺を \( (2x + 1)(x - 2) \) 倍すると、\[
2x + 6 = a (x-2) + b (2x+1)
\]となる。
- \( x = 2 \) を代入 → \( 10 = 5b \) より、\( b = 2 \)
- \( x = -1/2 \) を代入 → \( 5 = - 5a/2 \) より、\( a = -2 \)
つまり、\[
\frac{2x+6}{2x^2 - 3x - 2} = - \frac{2}{2x+1} + \frac{2}{x-2}
\]と部分分数分解できる。
よって、\[\begin{align*}
\int^{1}_{0} \frac{2x+6}{2x^2 - 3x - 2} \ dx & = - \int^{1}_{0} \frac{2}{2x+1} \ dx + 2 \int^{1}_{0} \frac{1}{x-2} \ dx
\\ & = - \left[ \log (2x+1) \right]^{1}_{0} + 2 \left[ \log | x - 2 | \right]^{1}_{0}
\\ & = - \log 3 + 2 \log 1 - \left( \log 1 + 2 \log 2 \right)
\\ & = - 2 \log 2 - \log 3
\end{align*}\]と計算できる。
部分分数分解の積分をもっと練習したい人はこちらから!!
★ マーク解答 ★
No.30: 4 [3点]
No.31: 9 [3点]
No.32: 18 [4点]
スポンサードリンク
問題9. ★媒介変数表示
つぎの媒介変数表示にて表される曲線\[
\left\{ \begin{array}{l} x = \cos t ( 1 + \cos t ) \\ y = \sin t ( 1 + \cos t ) \end{array} \right. \ \ \ \ \left( 0 \leqq t \leqq \pi \right)
\]について、(1), (2)の問いに答えなさい。
※ \( x = ( \cos t ) ( 1 + \cos t ) \), \( y = ( \sin t ) ( 1 + \cos t ) \) です。\( x = \cos \left\{ t (1 + \cos t ) \right\} \) , \( y = \sin \left\{ t (1 + \cos t ) \right\} \) ではないので注意!!
(1) 導関数を計算しなさい。\[
\frac{dy}{dx} = - \frac{ \left[ \ \ 33 \ \ \right] }{ \left[ \ \ 34 \ \ \right] }
\]
(2) 曲線の長さ \( L \) を求めなさい。\[\begin{align*}
L & = \int^{\pi}_{0} \sqrt{ \left[ \ \ 35 \ \ \right] } \ dt
\\ & = \int^{\pi}_{0} \sqrt{ \left[ \ \ 36 \ \ \right] } \ dt
\\ & = \left[ \ \ 37 \ \ \right]
\end{align*}\]
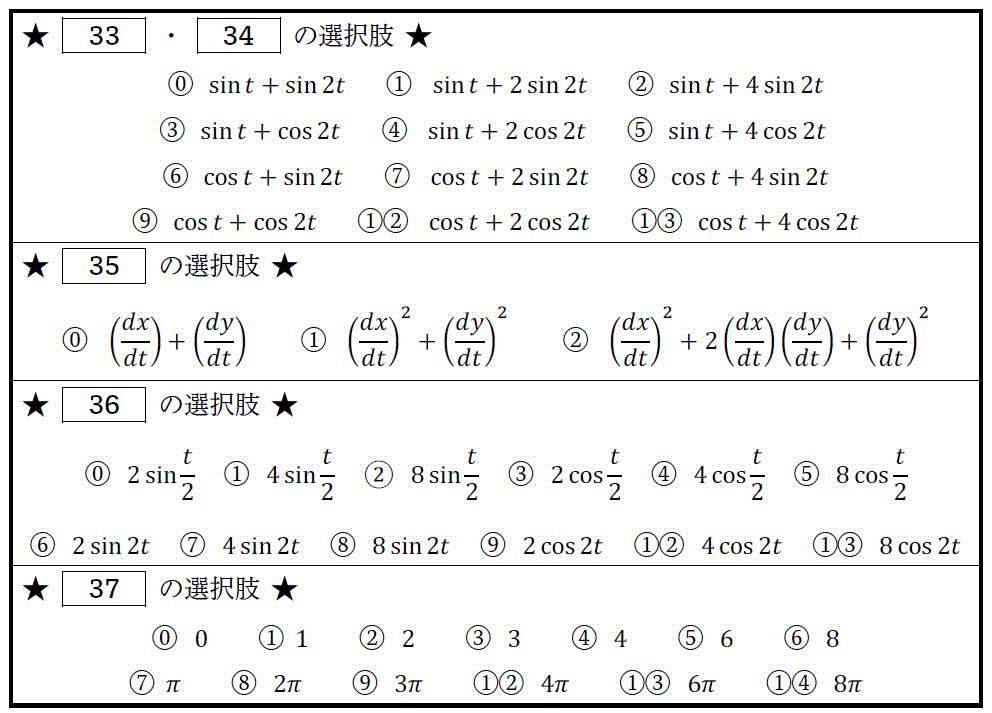
(1) 媒介変数表示の導関数
まずは媒介変数表示の導関数の計算方法を確認しておきましょう。
媒介変数表示\[
\left\{ \begin{array}{l} x = f(t) \\ y = g(t) \end{array} \right.
\]の微分は、\[\begin{align*}
\frac{dy}{dx} & = \frac{ \frac{dy}{dt} }{ \frac{dx}{dt} }
\\ & = \frac{ g'(t) }{ f'(t) }
\end{align*}\]で計算できる。
\( \frac{dx}{dt} \), \( \frac{dy}{dt} \) はそれぞれ\[\begin{align*}
\frac{dx}{dt} & = - \sin t (1 + \cos t) + \cos t \cdot (- \sin t )
\\ & = - \sin t - 2 \sin \cos t
\\ & = - \sin t - \sin 2t
\end{align*}\]\[\begin{align*}
\frac{dy}{dt} & = \cos t (1 + \cos t) + \sin t ( - \sin t )
\\ & = \cos t + \cos^2 t - \sin^2 t
\\ & = \cos t + \cos 2t
\end{align*}\]
となるため、導関数は\[\begin{align*}
\frac{dy}{dx} & = \frac{ \frac{dy}{dt} }{ \frac{dx}{dt} }
\\ & = - \frac{ \cos t + \cos 2t }{ \sin t + \sin 2t }
\end{align*}\]となる。
(2) 曲線の長さ
まずは、曲線の長さの公式を確認しておきましょう。
[媒介変数表示] \[
\left\{ \begin{array}{l} x = f(t) \\ y = g(t) \end{array} \right. \ \ \ ( a \leqq x \leqq b )
\]の曲線の長さ \( L \) は以下のようになる。\[
L = \int^{b}_{a} \sqrt{ \left( \frac{dx}{dt} \right)^2 + \left( \frac{dy}{dt} \right)^2 } \ dt
\]
[陽関数表示]
\[ y = f(x) \ \ \ ( a \leqq x \leqq b ) \] の曲線の長さ \( L \) は以下のようになる。\[\begin{align*}
L & = \int^{b}_{a} \sqrt{ 1 + \left( \frac{dy}{dx} \right)^2 } \ dx
\\ & = \int^{b}_{a} \sqrt{ 1 + \left( f'(x) \right)^2 } \ dx
\end{align*}\]
今回は区間 \( 0 \leqq t \leqq \pi \) の媒介変数表示の曲線の長さ \( L \) を求めればOK。
\[\begin{align*}
L & = \int^{\pi}_{0} \sqrt{ \left( \frac{dx}{dt} \right)^2 + \left( \frac{dy}{dt} \right)^2 } \ dt
\\ & = \int^{\pi}_{0} \sqrt{ \left( - \sin t - \sin 2t \right)^2 + \left( \cos t + \cos 2t \right)^2 }
\\ & = \int^{\pi}_{0} \sqrt{ (\sin^2 t + 2 \sin t \sin 2t + \sin^2 2t) + (\cos^2 t + 2 \cos t \cos 2t + \cos^2 2t ) } \ dt
\\ & = \int^{\pi}_{0} \sqrt{ (\sin^2 t + \cos^2 t) + (\sin^2 2t + \cos^2 2t) + 2 (\cos 2t \cos t + \sin 2t \sin t ) } \ dt
\\ & = \int^{\pi}_{0} \sqrt{ 2 + 2 \cos (2t-t) } \ dt \ \ \left( \because \ \cos \mathrm{の加法定理} \right)
\\ & = \int^{\pi}_{0} \sqrt{ 2(1 + \cos t) } \ dt
\\ & = \int^{\pi}_{0} \sqrt{ 4 \cos^2 \frac{t}{2} } \ dt \ \ \ \left( \because \frac{1 + \cos t}{2} = \cos^2 \frac{t}{2} \right)
\\ & = \int^{\pi}_{0} 2 \cos \frac{t}{2} \ dt \ \ \ \left( \because \cos \frac{t}{2} \geqq 0 \right)
\\ & = \left[ 4 \sin \frac{t}{2} \right]^{\pi}_{0}
\\ & = 4
\end{align*}\]と計算できる。
★ マーク解答 ★
No.33: 9 [2点]
No.34: 0 [2点]
No.35: 1 [3点]
No.36: 3 [1点]
No.37: 4 [2点]
加法定理を逆に適用する部分\[
\cos ( \alpha - \beta ) = \cos \alpha \cos \beta + \sin \alpha \sin \beta
\]\[
\cos ( 2t - t ) = \cos 2t \cos t + \sin 2t \sin t
\]は、1回練習をしておかないと、思いつかない可能性があるので、必ず復習をしておきましょう。
\[
\sin ( \alpha \textcolor{blue}{+} \beta ) = \sin \alpha \cos \beta \textcolor{blue}{+} \cos \alpha \sin \beta
\]\[
\sin ( \alpha \textcolor{red}{-} \beta ) = \sin \alpha \cos \beta \textcolor{red}{-} \cos \alpha \sin \beta
\]\[
\cos ( \alpha \textcolor{blue}{+} \beta ) = \cos \alpha \cos \beta \textcolor{red}{-} \sin \alpha \sin \beta
\]\[
\cos ( \alpha \textcolor{red}{-} \beta ) = \cos \alpha \cos \beta \textcolor{blue}{+} \sin \alpha \sin \beta
\]
※ 符号まで正確に頭にいれておくこと!
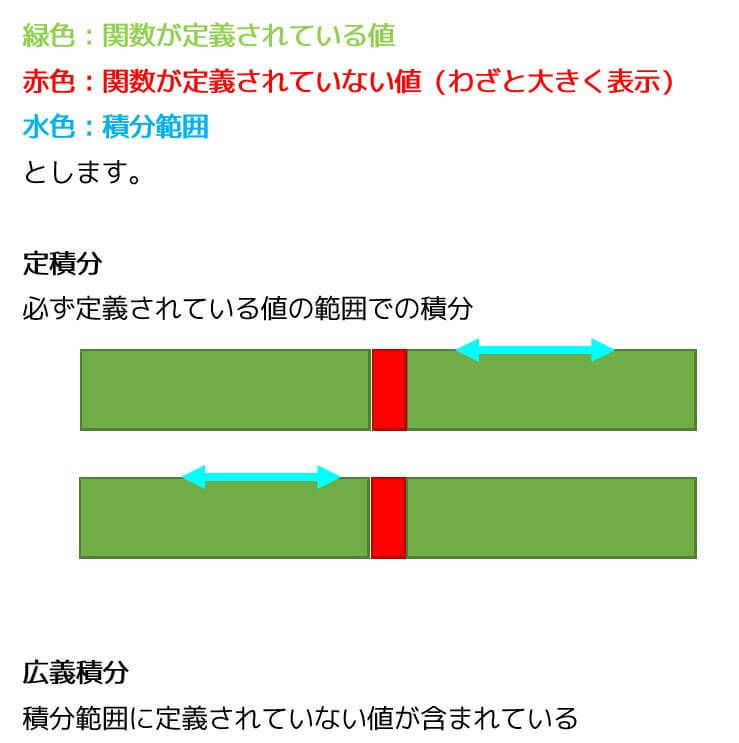
問題10. 広義積分
つぎの(1), (2)の広義積分を計算しなさい。
※ 今回はマークシート式での出題ですが、必ず記述形式の答案作成に慣れておくこと!!
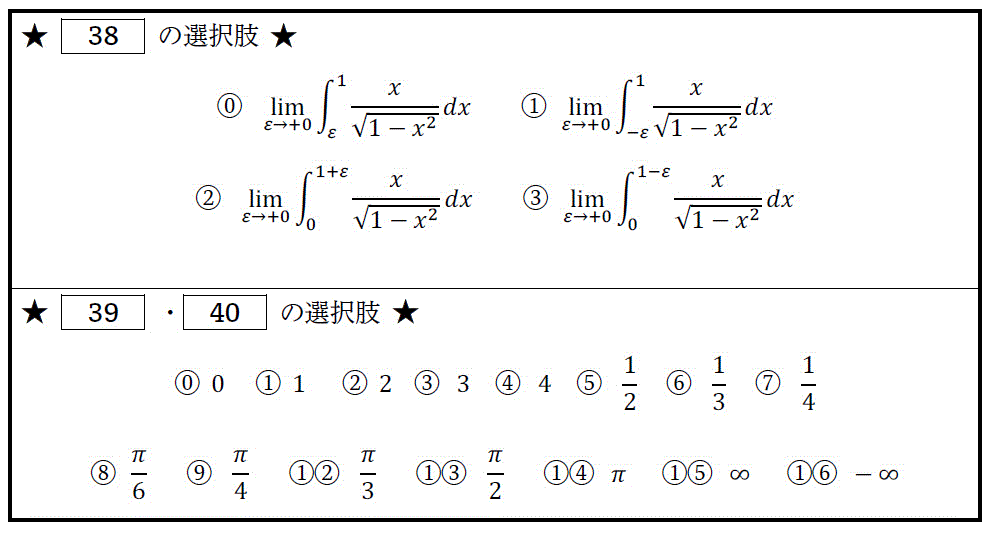
(1) \[\begin{align*}
\int^{1}_{0} \frac{x}{ \sqrt{1-x^2} } \ dx & = \left[ \ \ 38 \ \ \right]
\\ & = \left[ \ \ 39 \ \ \right]
\end{align*}\]
(2) \[\begin{align*}
\int^{\infty}_{0} \frac{1}{(1+x)^3} \ dx = \left[ \ \ 40 \ \ \right]
\end{align*}\]
(1) ある1点で定義されていない関数の積分
積分しようとしている関数は、\( x = 1 \) のとき、分母が0になってしまい定義されませんね。
そこで、1より少し小さい値 \( 1 - \varepsilon \) までを積分し、最後に \( \epsilon \to +0 \) と極限を近づけて計算を行います。
\[\begin{align*}
\int^{1}_{0} \frac{x}{ \sqrt{1 - x^2} } \ dx & = \lim_{ \varepsilon \to + 0 } \int^{1 - \varepsilon}_{0} \frac{x}{ \sqrt{1 - x^2} }
\end{align*}\]
ここで、\[\begin{align*}
& \int^{1 - \varepsilon}_{0} \frac{x}{ \sqrt{1 - x^2} } \ dx
\\ & \ = - \frac{1}{2} \int^{1 - \varepsilon}_{0} \frac{2x}{ \sqrt{1 - x^2} } \ dx
\\ & \ = - \frac{1}{2} \left[ \sqrt{ 1 - x^2} \cdot 2 \right]^{1 - \varepsilon}_{0}
\\ & \ = - \frac{1}{2} \left( 2 ( \sqrt{ (1 - (1- \varepsilon)^2 } - 1 \right)
\\ & \ = 1 - \sqrt{ - \varepsilon^2 + 2 \varepsilon }
\end{align*}\]と計算できるため、\[\begin{align*}
\int^{1}_{0} \frac{x}{ \sqrt{1 - x^2} } \ dx & = \lim_{ \varepsilon \to + 0 } \int^{1 - \varepsilon}_{0} \frac{x}{ \sqrt{1 - x^2} }
\\ & = \lim_{ \varepsilon \to + 0 } 1 - \underbrace{ \sqrt{ - \varepsilon^2 + 2 \varepsilon } }_{ 0 \mathrm{に収束} }
\\ & = 1
\end{align*}\]と計算できる。
(2) 範囲に無限が含まれる積分
積分しようとしている関数の範囲に \( \infty \) が含まれていますね。
この場合、\( R \to \infty \) とおき、積分を行います。つまり、\[
\int^{\infty}_{0} \frac{1}{(1+x)^3} \ dx = \lim_{R \to \infty} \int^{R}_{0} \frac{1}{(1+x)^3} \ dx
\]を求めます。
ここで、\[\begin{align*}
\int^{R}_{0} \frac{1}{(1+x)^3} \ dx & = \int^{R}_{0} (1+x)^{-3} \ dx
\\ & = \left[ - \frac{1}{2} (1+x)^{-2} \right]^{R}_{0}
\\ & = \left[ - \frac{1}{2(1+x)^2} \right]^{R}_{0}
\\ & = - \frac{1}{2} \left( \frac{1}{(1+R)^2} - 1 \right)
\end{align*}\]となる。
よって、\[\begin{align*}
\int^{\infty}_{0} \frac{1}{(1+x)^3} \ dx & = \lim_{R \to \infty} \int^{R}_{0} \frac{1}{(1+x)^3} \ dx
\\ & = \lim_{R \to \infty} - \frac{1}{2} \left( \underbrace{ \frac{1}{(1+R)^2} }_{ 0 \mathrm{に収束} } - 1 \right)
\\ & = \frac{1}{2}
\end{align*}\]と計算できる。
★ マーク解答 ★
No.38: 3 [3点]
No.39: 1 [2点]
No.40: 5 [5点]
広義積分がまだ苦手だなと思った方は、下の記事にて復習をしましょう!
おまけ問題. 広義積分の応用
うさぎ模試のPDFにはありませんが、余裕がある方はぜひチャレンジしてみてください。
次の広義積分\[
\int^{\infty}_{0} \frac{\sin^3 x}{(1+x)^3} \ dx
\]は収束するか?
解答
今回の問題のように、
- 普通に積分するのが難しそう
- 広義積分の収束だけを確認すればいい(具体的に何に収束するかを求めなくてよい)
の場合、優関数の原理を使うことを疑ってください。
広義積分\[
\int^{b}_{a} g(x) \ dx
\]が収束し、かつ \( g(x) \) の積分範囲で常に \( | f(x) | \leqq g(x) \) となる場合、広義積分の値を計算せずに\[
\int^{b}_{a} f(x) \ dx
\]が収束することを示すことができる。
優関数の原理を使いそうだなと思ったら、まずは(積分範囲内で常に)被積分関数よりも大きくなり、なおかつ広義積分が簡単に出せそうなものを探しましょう。
今回の場合、問題10の(2)の答え\[
\int^{\infty}_{0} \frac{1}{(1+x)^3} \ dx = \frac{1}{2}
\]を使うのが一番いいでしょう。
ここで、\( | \sin x | \leqq 1 \) なので当然 \( | \sin^3 x | \leqq 1 \) となり、当然\[
\left| \frac{ \sin^3 x }{ (1+x)^3 } \right| \leqq \frac{1}{(1+x)^3}
\]が成立しますよね。
よって\[
\int^{\infty}_{0} \frac{1}{(1+x)^3} \ dx
\]が \( \frac{1}{2} \) に収束するため、優関数の原理より、\[
\int^{\infty}_{0} \frac{\sin^3 x}{(1+x)^3} \ dx
\]も収束する。
さいごに
今回は、微分編・積分編の2つの記事で1年前期で習う解析学の総復習記事を作成いたしました。
1年前期大学で習う解析学は、1年生後期で習う「2変数関数の微積分」、およびその後の「複素解析」、「フーリエ変換」など様々な場面で使うこととなるので、必ず計算できるようになっておきましょう。
関連広告・スポンサードリンク