スポンサードリンク
こんにちは、ももやまです。
動的計画法は、アルゴリズムでもかなり重要な内容です。AtCoderやらプログラミングコンテストとかでもよく出てきます。
ですが、動的計画法は「アルゴリズムを学ぶ上での壁・登竜門」とも呼ばれるとおり、かなり難易度の高いアルゴリズムとなっています。どの参考書を見てもなかなかわかりやすくは書かれていません。
そんな動的計画法を今回はうさぎでもわかるようにわかりやすくかみ砕いて説明したいと思います。
目次
スポンサードリンク
1.動的計画法とは
動的計画法とは、
- 問題をいくつかの簡単で小さな問題に分割
- それぞれの問題の計算結果を表に記録
- 同じ問題に対しては表から計算結果を参照する
の3つの特徴を持ったアルゴリズムです。
といきなり言われてもわけがわからないと思うので、動的計画法のイメージを説明しましょう。
動的計画法のイメージ
例えば、\[
28 \times 37
\]の計算を解きなさい。
という問題があったとします。そうしたとき、皆さんは普通に筆算をすることで 1036 と求められますね。
その問題のすぐ下に\[
28 \times 37 \times 4
\]を解きなさい。
という問題があったとします。おそらく、ほとんどの皆さんは、先程の計算けっか「28×37=1036」を使い、\[\begin{align*}
& 28 \times 37 \times 4 \\ = \ & 1036 \times 4 \\ = \ & 4144
\end{align*}\]と求めると思います。
このように、我々人間は「1回求めた答えを」再利用してより難しい問題を簡単に解くことができますね。
しかし、コンピュータはただプログラミングしただけでは勝手に答えを再利用してはくれません。
28*37 = 1036 28*37*2 = 2072 28*37*5 = 5180 28*37*10 = 10360
のように我々人間なら明らかに「28×37=1036」を使いまわすような問題であっても、1つずつごり押しで解いていってしまいます。
このように(コンピュータ)にとって量が少なければいいんですが、もっと量が増えるとどうでしょうか。
もしかしたらごり押してたら100年かかるような問題に出会うかもしれません。
そこで我々人間が「1回出した答えはどこかに記憶して次回に活かすよう賢い計算方法で解くアルゴリズム」を組む必要が出てきます。
この「賢い計算方法で解くアルゴリズム」こそがまさに動的計画法なのです!
スポンサードリンク
2.動的計画法の例1(フィボナッチ数列)
まずは、フィボナッチ数列\[
f(n) = f(n-1) + f(n-2)
\]を解くプログラムを考えましょう。
(1) 動的計画法を使わない場合(再帰法)
まず、何も考えずに再帰法を使った場合のプログラムを見てみましょう。
なお、再帰法についての詳しい解説は下の記事で行っているので、もし再帰法がわからないという人がいれば下の記事をご覧ください。
ソースコード(再帰法)
C言語
int fib1(int n) {
if(n <= 1) {
return 1; // 初期値
}
else {
return fib1(n-1) + fib1(n-2); // a_n = a_{n-1} + a_{n-2}
}
}
int main() {
int n = 30;
printf("再帰:n = %d のとき %2d\n",n,fib1(n));
return 0;
}
Python
def fib1(n):
if n <= 1:
return 1
else:
return fib1(n-1) + fib1(n-2)
print(fib1(30)) # 1346269
しかし、再帰法でプログラムを書いた場合、n を大きくすればするほど計算時間は指数関数的に増加してしまいます。
オーダー表記で計算量を表すと、*1\[
O \left( \frac{1 + \sqrt{5} }{ 2 } \right)^{n} \fallingdotseq O(1.618^{n})
\]となり、確かに指数関数的に計算時間が増えることがわかると思います。
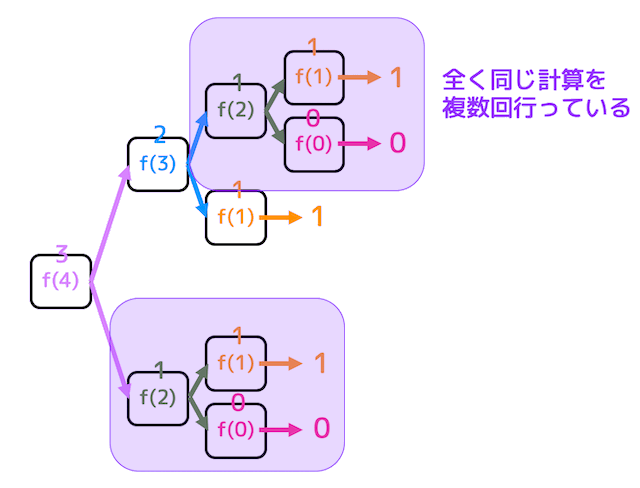
計算量が大幅に増えてしまう理由として、下の図の紫色部分のように全く同じ計算を何度も何度も繰り返していることが挙げられます。
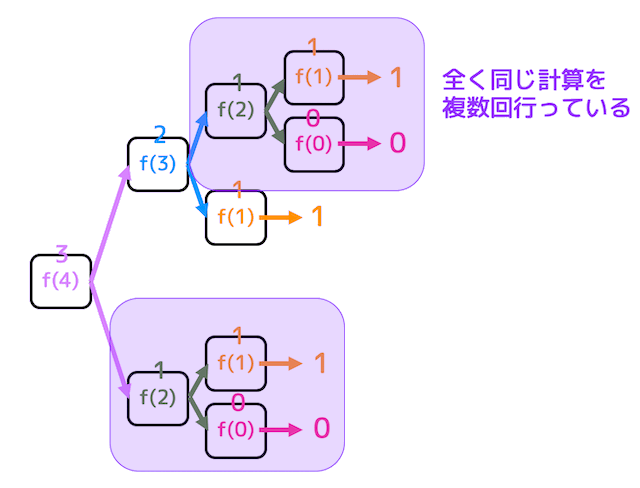
答えがわかっている問題を何回も何回も解くのは時間の無駄ですよね。
ということで、同じ問題を2回以上解かないもっとよいアルゴリズムを考えましょう。
(2) 答えをメモしていこう(メモ化再帰)
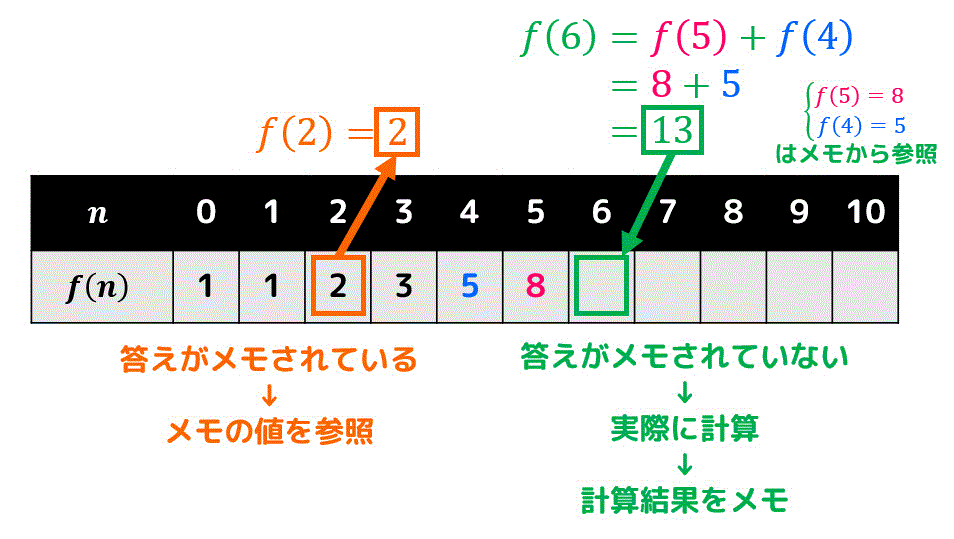
やみくもに再帰を使う場合、同じ計算結果を何回も何回も計算するため、時間の無駄になってしまうのでしたね。そこで、
- 初めて計算するときに再帰呼び出しの計算結果を変数にメモ
- 1回求めた値はメモから参照
することで、同じ計算の結果はメモから参照されるため、同じ値を2回以上計算することなく結果が求められますね!
この方法はメモ化再帰と呼ばれ、動的計画法の入り口*2となっています。
ソースコード(メモ化再帰)
実際にメモ化再帰を用いたフィボナッチ数列の計算プログラムをCとPythonの2つで見ていきましょう。
C言語
#include<stdio.h>
#define N 101 // 配列の大きさ 余裕をもって定義
int memo[N] = {0}; // 結果をメモ(グローバル変数で宣言)
// 実は、上の1行で配列の要素すべてを0に初期化できて便利なので参考までに
int fib2(int n) {
int ans;
if(n <= 1) {
return 1;
}
else {
// メモされていなければ、計算し、結果をメモする
if(memo[n] == 0) {
memo[n] = fib2(n-1) + fib2(n-2);
}
return memo[n]; // メモされたものを返す
}
}
int main() {
int n = 30;
printf("メモ:n = %d のとき %2d\n",n,fib2(n));
return 0;
}
Python
memo = [0] * (50) # 結果をメモ(グローバル変数で宣言!)
def fib2(n):
if n <= 1:
return 1
else:
if memo[n] == 0:
memo[n] = fib2(n-1) + fib2(n-2)
return memo[n]
print(fib2(30)) # 1346269
なおメモ化再帰の場合、グローバル変数(外部変数)を用いた定義が必要になるので、注意しましょう。
(3) 動的計画法を使ってみよう
では、フィボナッチ数列\[
f(n) = f(n-1) + f(n-2)
\]を動的計画法で解いてみましょう。
まず、答えをメモしていくための表(配列)を用意します。
つぎに、簡単な問題の答え(左側)から順に答えをどんどん埋めていきます。
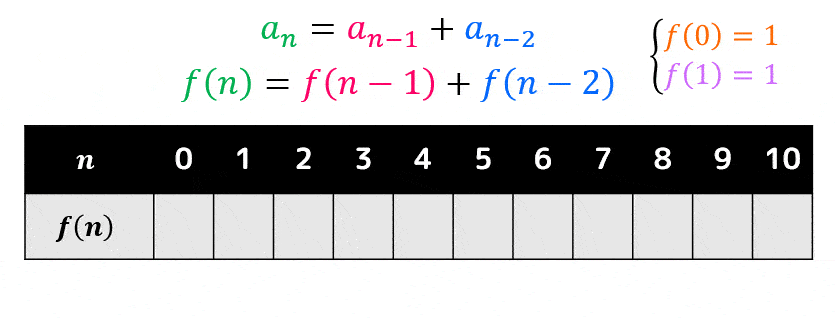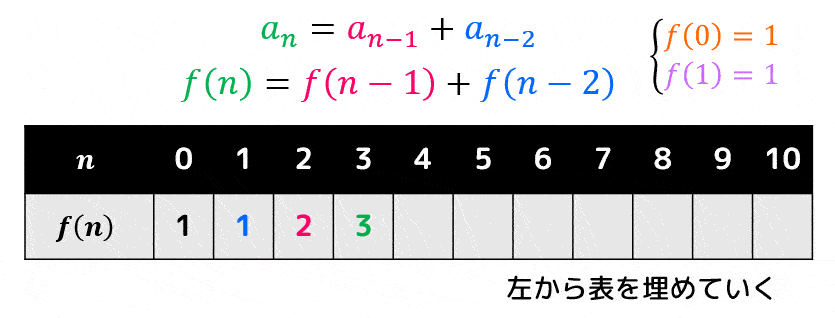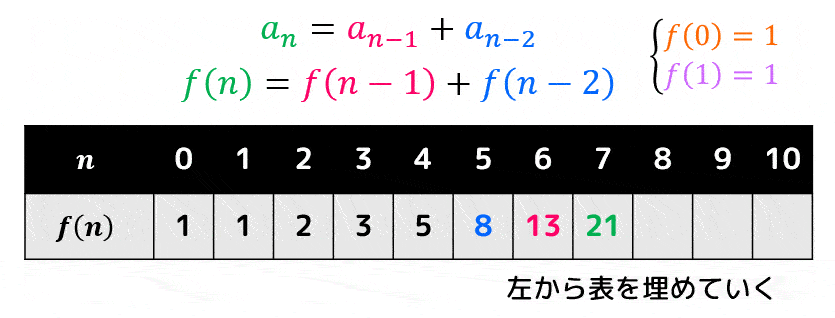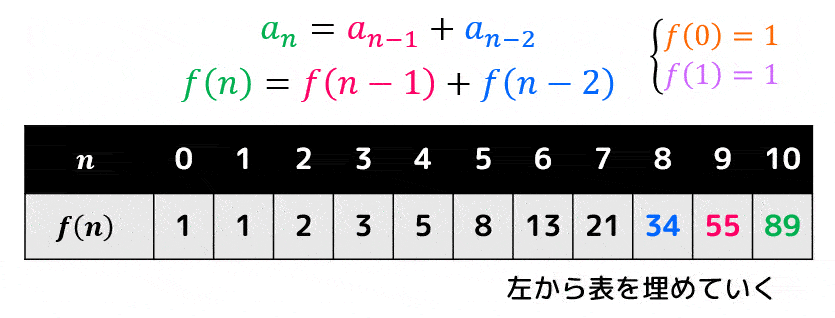
求めたい答えが出るまで表を埋めていくことで、あっという間に答えを出すことができます。

動的計画法でフィボナッチ数列の第 \( n \) 項を求める場合、\( n+1 \) 回計算結果を表に入れる操作をするだけで答えが出せるため、なんとオーダー \( O(n) \) で計算することができちゃいます!
再帰の場合に比べて驚くほど早く答えが出せちゃいます!
ただし、答えをメモするためのメモリ領域が必要なので注意しましょう*3。
ソースコード(動的計画法によるフィボナッチ数列の計算)
実際に動的計画法を用いたフィボナッチ数列の計算プログラムをCとPythonの2つで見ていきましょう。
C言語
#include<stdio.h>
#define N 101 // 配列の大きさ 余裕をもって定義
int fib3(int n) {
int a[N]; // 表に相当
// 初期値代入
a[0] = 1;
a[1] = 1;
// a[2] 以降の導出
for(int i = 2; i <= n; i += 1) {
a[i] = a[i-1] + a[i-2];
}
return a[n];
}
int main() {
int n = 30;
printf("動的:n = %d のとき %2d\n",n,fib3(n));
return 0;
}
Python
def fib3(n):
a = [1] * (n+1) # a[0] = 1, a[1] = 1
# a[2] 以降の導出
for i in range(2,n+1):
a[i] = a[i-1] + a[i-2]
return a[n]
スポンサードリンク
3.動的計画法の例2(部分和問題)
もう少し難しい部分和問題にチャレンジしてみましょう。
部分和問題とは、以下のような問題です。
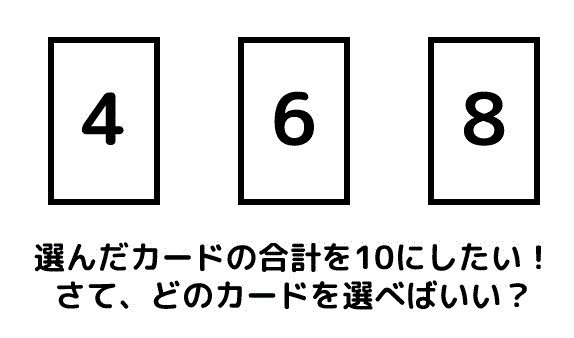
4, 6, 8の3枚のカードがある。
この3枚のカードから何枚か選んで、合計を10にすることができるだろうか。
10にできるのであれば 10 を、できないのであれば10以下でできる最大の自然数を答えなさい。
(1) とりあえず全探索
まず、動的計画法を使わず、全探索(すべてのパターンを列挙)することで答えを求めてみましょう。
今回の場合、下のように列挙することで合計8パターン(\( 2^{3} \) パターン)列挙すれば答えを求められますね。
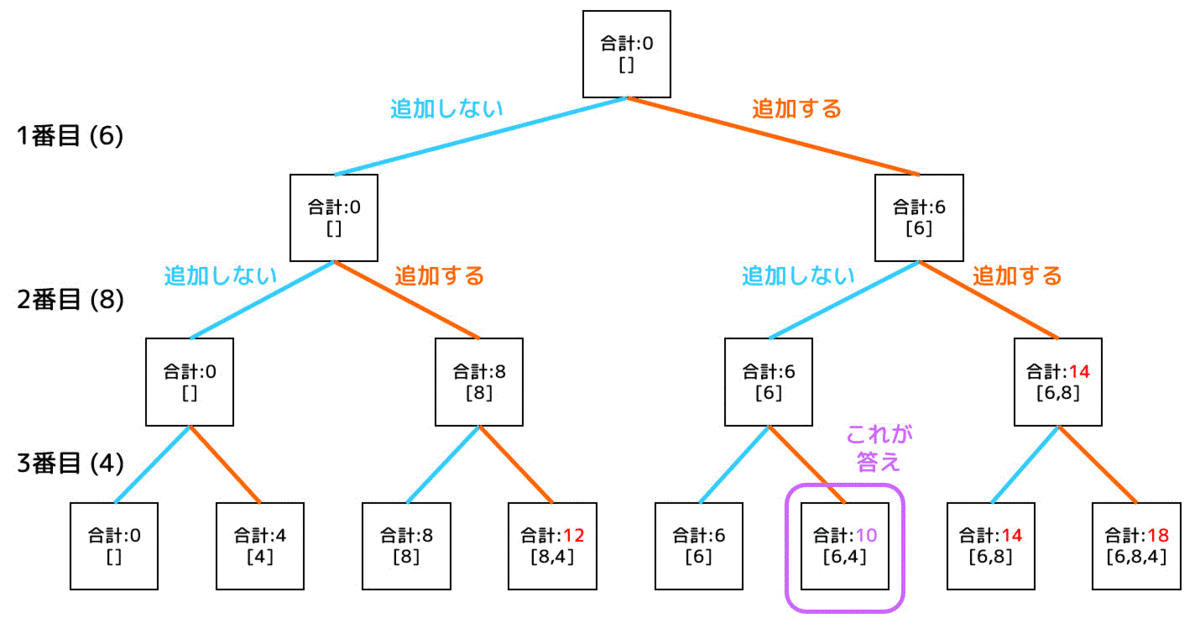
しかし、パターン数が増えたときはどうなるでしょうか。
例えば100個カードがあったときはなんと \( 2^{100} \) パターン… 恐ろしいくらい計算時間がかかりそうですね。
オーダー表記すると \( O(2^{n}) \) となり、指数関数的に計算時間が増えてしまうことがわかりますね。
ソースコード(全探索)
全探索を行うプログラムは下に示すので参考までにご覧ください。
なお、やみくもに全探索を行うのはちょっと頭が悪いので、合計値をオーバーするなどで解ではないことが確定した瞬間にカットし、計算量を少し削減しています。
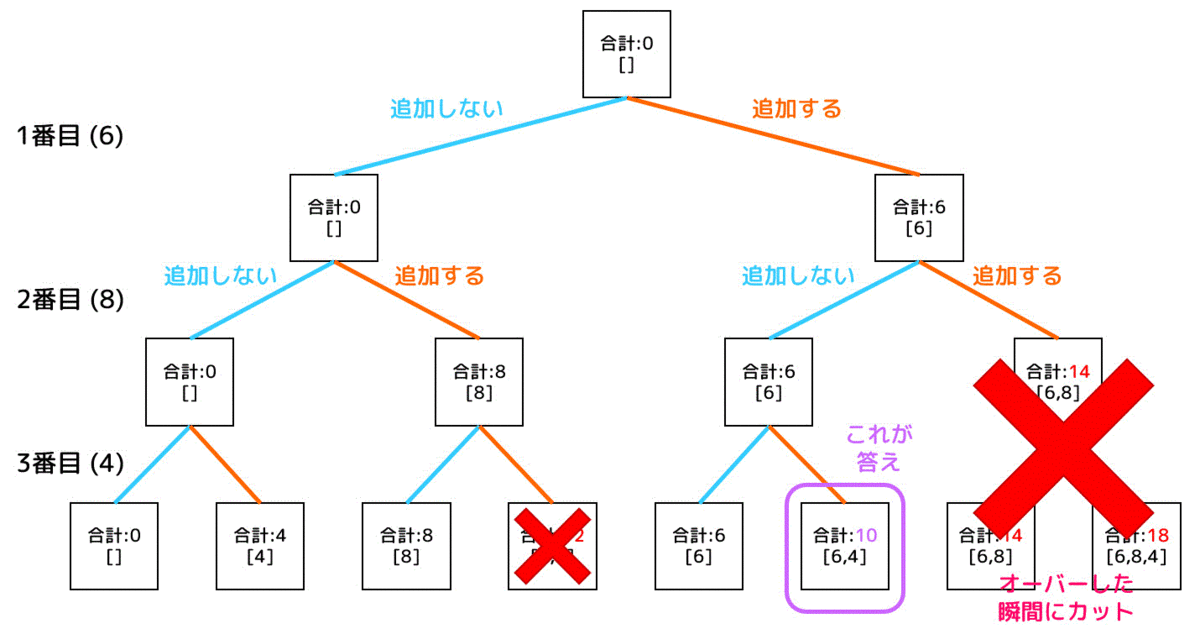
C言語
#include<stdio.h>
#define N 3 // カードの枚数
#define MAX_NUM 10 // 合計が MAX_NUM になるか
int find_max_saiki(int num_list[N],int now,int limit) {
int tmp_choice,tmp_not_choice;
if(now >= N || limit < 0) {
return 0; // これ以上追加できないとき or リストの最後尾まで探索終了
}
else {
// 追加 / 追加しない ときの2パターンを考える
tmp_not_choice = find_max_saiki(num_list,now+1,limit);
if(num_list[now] > limit) {
return tmp_not_choice; // now番目を追加できるようなコストがないとき
}
else {
tmp_choice = find_max_saiki(num_list,now+1,limit - num_list[now]) + num_list[now];
if(tmp_choice > tmp_not_choice) {
return tmp_choice;
}
else {
return tmp_not_choice;
}
}
}
}
int main() {
int num_list[N] = {4,8,6};
ans = find_max_saiki(num_list,0,MAX_NUM); // 先頭から順に探すので now は0スタート
printf("%2dに最も近い選び方1:%2d\n",MAX_NUM,ans);
return 0;
}
Python
def find_max_saiki(num_list,now,limit):
list_len = len(num_list)
if now >= list_len or limit <= 0:
return 0 # これ以上追加できないとき or リストの最後尾まで探索終了
else:
tmp_not_choice = find_max_saiki(num_list,now + 1,limit)
if num_list[now] > limit:
return tmp_not_choice # now番目を追加できるようなコストがないとき
else:
tmp_choice = find_max_saiki(num_list,now + 1,limit - num_list[now]) + num_list[now]
return max(tmp_choice,tmp_not_choice) # 追加 / 追加しない ときの2パターンを考える
(2) 動的計画法を使う場合
動的計画法では、表(配列)に計算結果を記録しながら答えを求めていきます。
ですが1次元の表ではメモする内容が不足するので、2次元の表を使います。
具体的には、
- i 番目まで追加 or 追加しないか検討したとき(縦方向)
- 合計がj以下となる最大の自然数(横方向:以下制限 j と呼びます)
を2次元の表に格納します。
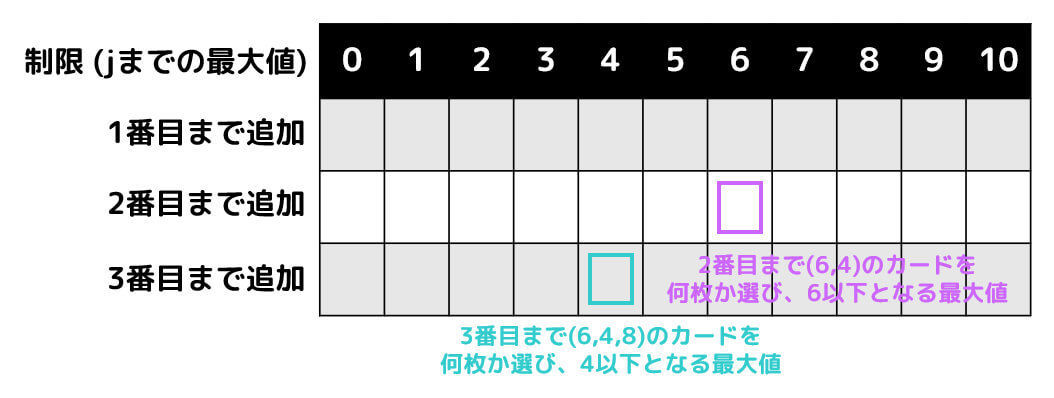
今回欲しい答え*4は、上の図の右下部分(水色で囲われた部分)となります。
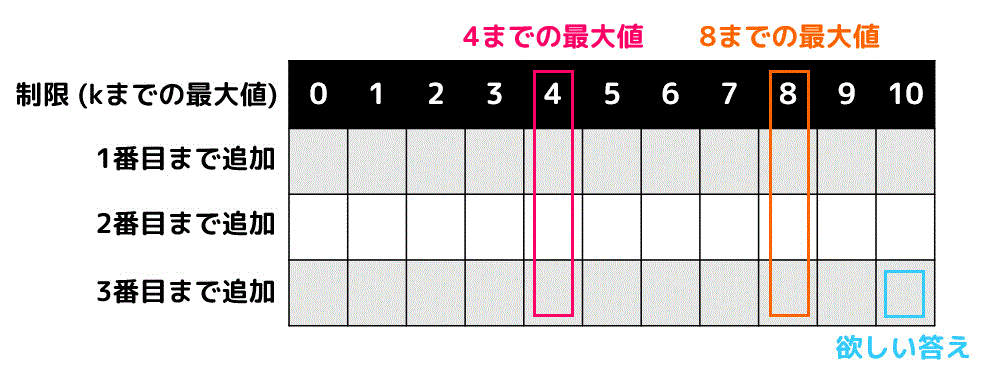
処理の流れ
動的計画法で部分和問題を求めるアルゴリズムは少し複雑なので、丁寧に解説していきたいと思います。
Step1. 1番目までのカード
まず、1番目のカードについて考えます。
1番目のカードは6なので、「制限が6以上」のときは1番目のカードを追加することができ、合計は6となります。
逆に制限が6未満であれば、1番目のカードは追加できないので、合計は0(何も追加していない状態)となります。
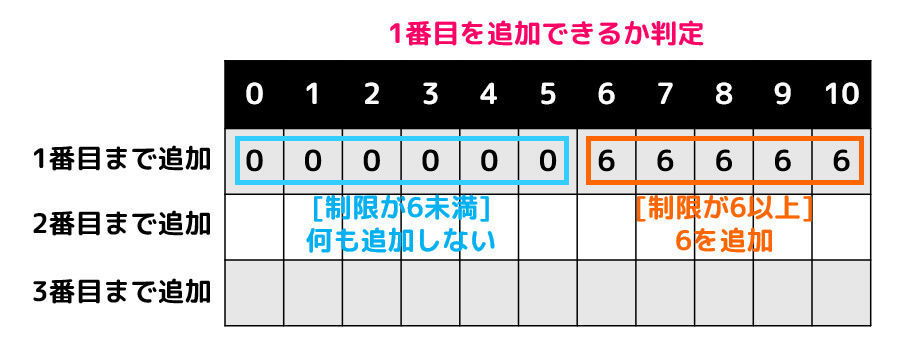
Step2. 2番目までのカード
2番目以降のカードについては、1つ前の状態(2番目であれば1番目、3番目であれば2番目)を用いて考えます。
2番目のカードは8なので、「制限が8未満」であれば2番目を追加することができませんね。
そのため、2番目まで追加したときの合計は1番目と同じになりますね。
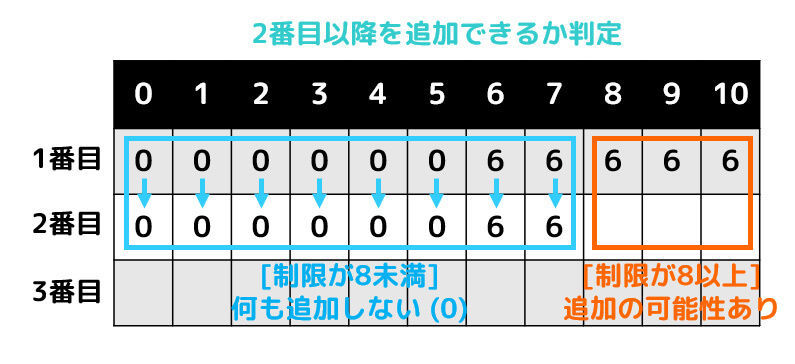
一方、「制限が8以上」であれば、2番目を追加することができますね。
この場合、
- 追加しない場合
- (1番目の状態から)コスト8を使って追加した場合
の2つを考えます。
例えば、制限が8であれば、「1番目のコスト(制限)0のときに8を追加したとき」と、「1番目の制限8のときに何も追加しなかった場合」の2つを比べます。
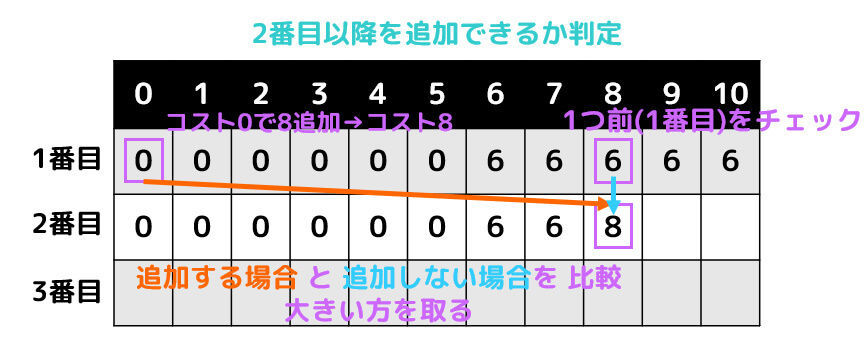
今回の場合、追加したときのほうが大きいので、2番目の制限(コスト)8には「8」が入ります。
同じように制限9, 10のときも埋めていくと、下のようになります。
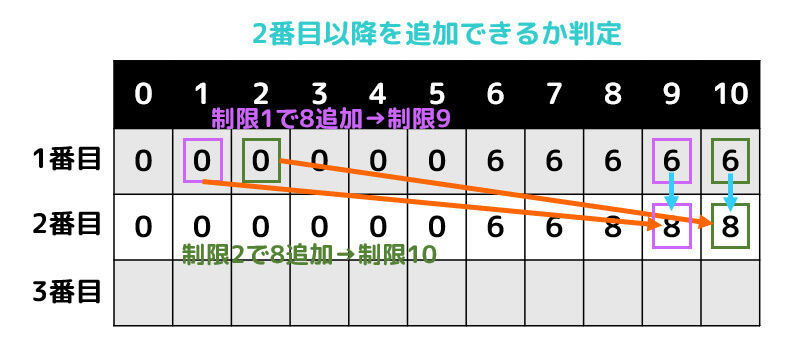
なお、2列目以降の表を埋めていく部分をプログラム(Python)で書くと、下のようになります。
# dp_table[i][j] → i番目のカードの中から何枚か選んだとき、制限j以下で作れる最大の整数
tmp_not_choice = dp_table[i-1][j] # 追加しない場合
if num_list[i] > j: # 制限オーバー(強制的に追加しない)
dp_table[i][j] = tmp_not_choice
else:
tmp_choice = dp_table[i-1][j - num_list[i]] + num_list[i] # 追加する場合
dp_table[i][j] = max(tmp_choice,tmp_not_choice)
3番目までのカード
同じように3番目についてもやっていきましょう。
とはいっても、2番目以降は同じ処理の繰り返しです。
3番目のカードは4なので、制限が4以下であれば何も追加できません。
そのため、強制的に追加しない場合が答えとなります。
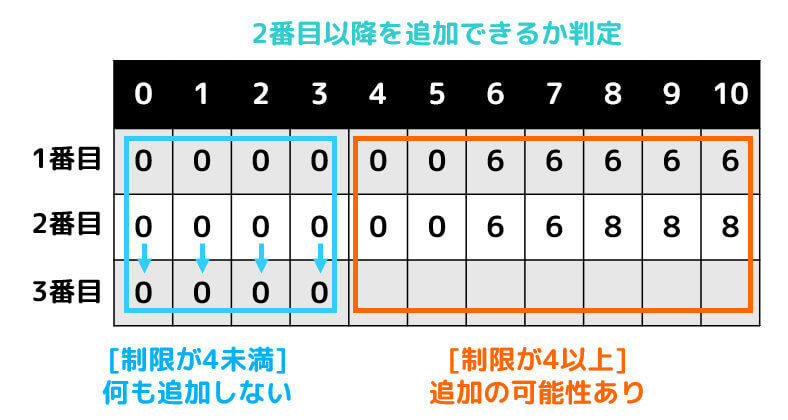
追加できる場合は、
- コスト4を使って追加する場合
- 追加しない場合
の2パターンを考え、大きい方を追加していきます。
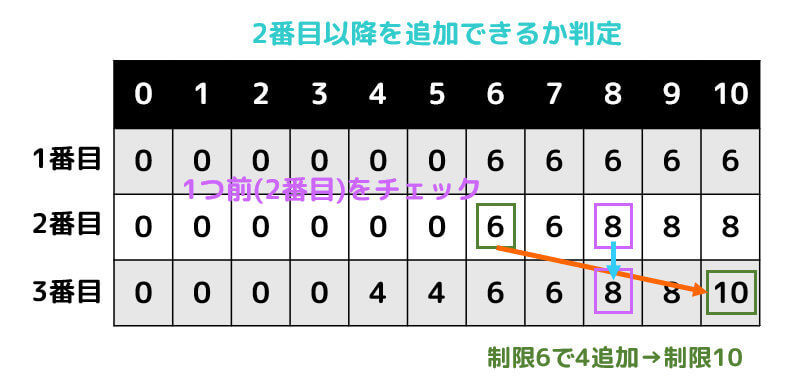
表を埋め終わったら表の右下を確認します。
表の右下は10となっているので、3枚のカード 6, 8, 4 を使って合計10を作れることがわかりますね。
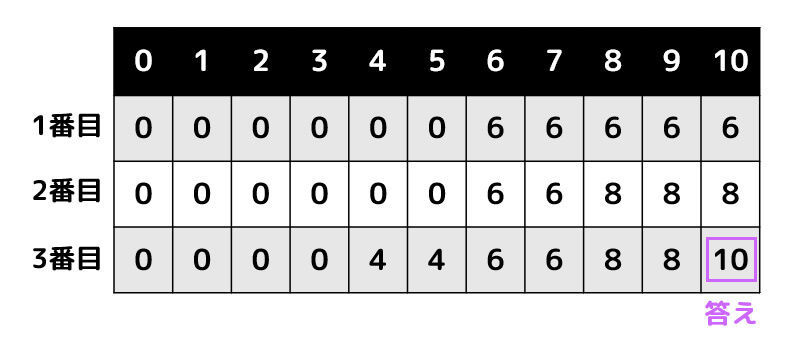
(3) ソースコード(動的計画法を用いた部分和問題)
では、部分和問題を動的計画法を用いて解くソースコードをCとPythonにわけて紹介したいと思います。
アルゴリズムの参考にどうぞ。
C言語
#include<stdio.h>
#define N 3 // 配列 num_list の要素数
#define MAX_NUM 10 // MAX_NUM 以内の最大値を求める
int find_max_dp(int num_list[N]) {
int tmp_choice, tmp_not_choice;
int table[N][MAX_NUM+1];
// DP表の一番上(i = 0)を初期化
for(int j = 0; j <= MAX_NUM; j += 1) {
if(num_list[0] > j) {
table[0][j] = 0; // 何も入れられないとき
}
else {
table[0][j] = num_list[0]; // 0番目の数字を足せるとき
}
}
for(int i = 1; i < N; i += 1) {
for(int j = 0; j <= MAX_NUM; j += 1) {
tmp_not_choice = table[i-1][j];
if(num_list[i] > j) {
table[i][j] = tmp_not_choice;
}
else {
tmp_choice = table[i-1][j - num_list[i]] + num_list[i];
if(tmp_choice >= table[i-1][j])
table[i][j] = tmp_choice;
else
table[i][j] = tmp_not_choice;
}
}
}
return table[N-1][MAX_NUM];
}
int main() {
int num_list[N] = {4,8,6};
int ans = find_max_saiki(num_list,0,MAX_NUM);
printf("%2dに最も近い選び方1:%2d\n",MAX_NUM,ans);
return 0;
}
Python
def find_max_dp(num_list, limit):
list_len = len(num_list)
dp_table = [[0 for j in range(limit + 1)] for i in range(list_len)]
# 1番目のカード
for j in range(limit + 1):
if num_list[0] <= j:
dp_table[0][j] = list[0] # 1番目のカードを追加
# 2番目以降のカード
for i in range(list_len):
for j in range(limit + 1):
tmp_not_choice = dp_table[i-1][j]
if num_list[i] > j: # コスト不足のとき
dp_table[i][j] = tmp_not_choice
else:
tmp_choice = dp_table[i-1][j - num_list[i]] + num_list[i]
dp_table[i][j] = max(tmp_choice,tmp_not_choice)
return dp_table[list_len - 1][limit]
list = [4,8,6]
print(find_max_dp(list,10))
(4) 動的計画法による部分和問題の計算量
動的計画表で部分和問題を求めていくときの計算時間を考えましょう。
部分和問題を求める際には、
- 縦が与えられた数字の個数である \( n \) 個
- 横が0から容量 \( l \) までの \( l+1 \) 個
の表を埋めることで結果を求めることができます。

そのため、処理ステップ数は\[
n(l+1) = nl + n
\]となり、\( nl + n \) ステップ数と求められます。
よって、計算量をオーダーで表すと \( O(nl) \) となります。
動的計画法の計算量は、表を埋めるために必要な計算量と思っていただけたらOKです!
(空間計算量も、表を記憶する分だけかかると考えてもらえたらOKです! 今回の場合は \( O(nl) \) となります。)
4.動的計画法でナップサック問題を解いてみよう!
(1) ナップサック問題とは
2と3で動的計画法も慣れてきたと思うので、そろそろ動的計画法で出てくる超有名問題「ナップサック問題」を解いてみましょう。
まず、ナップサック問題とはどのような問題なのかを説明します。
ナップサック問題(ナップサックもんだい、Knapsack problem)は、計算複雑性理論における計算の難しさの議論の対象となる問題の一つで、「容量 \( C \) のナップサックが一つと、\( n \) 種類の品物(各々、価値 \( p_i \), 容積 \( c_i \))が与えられたとき、ナップサックの容量 \( C \) を超えない範囲でいくつかの品物をナップサックに詰め、ナップサックに入れた品物の価値の和を最大化するにはどの品物を選べばよいか」という整数計画問題である。
[引用元:ナップサック問題-wikipedia]
つまり、何種類かあるものの中から「ある一定の容量を超えないように」選んでいき、選んだものの合計金額が最大になるような選び方を求めるような問題がナップサック問題となっています。
(2) ナップサック問題にチャレンジ!
とはいっても普通のナップサック問題では、面白くないのでちょっと変わったナップサック問題を持ってきました。
問題 寿司屋の食べ放題
とある男は「寿司屋も〇やま*5」で、寿司屋の食べ放題コースでたくさん寿司を食べていた。
すると、彼女から「あんた明日から痩せるって言ったじゃない! 寿司はあと300kcalにしなさい!」と言われてしまいました*6。
ここで問題。1円でも得をしたい男が「食べたいと思っている寿司1~5」の中から300kcal以内に収まるように何種類か選んだとき、寿司の合計金額の最大値(最も元が取れるときの合計金額)を求めなさい。
ただし、男はいろんなネタが楽しみたいため、同じ寿司は2種類以上選ばないこと。
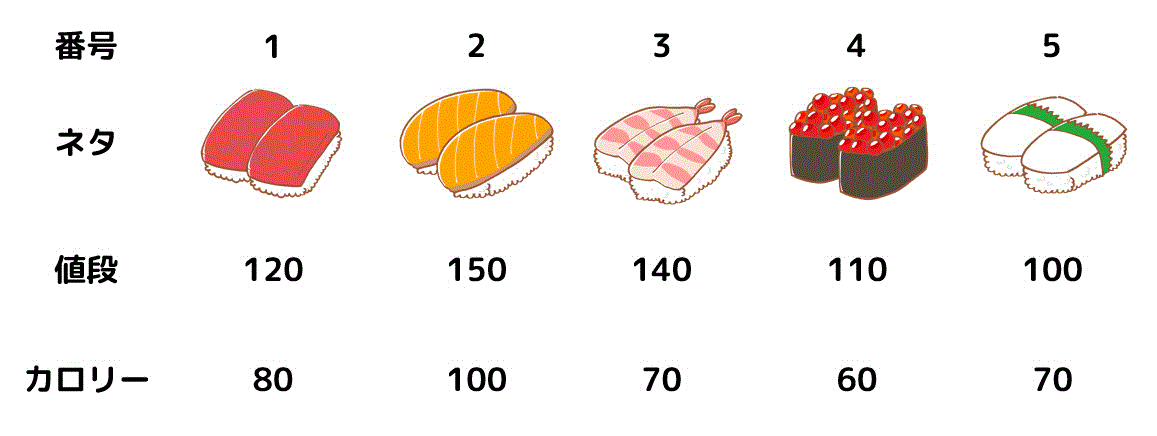
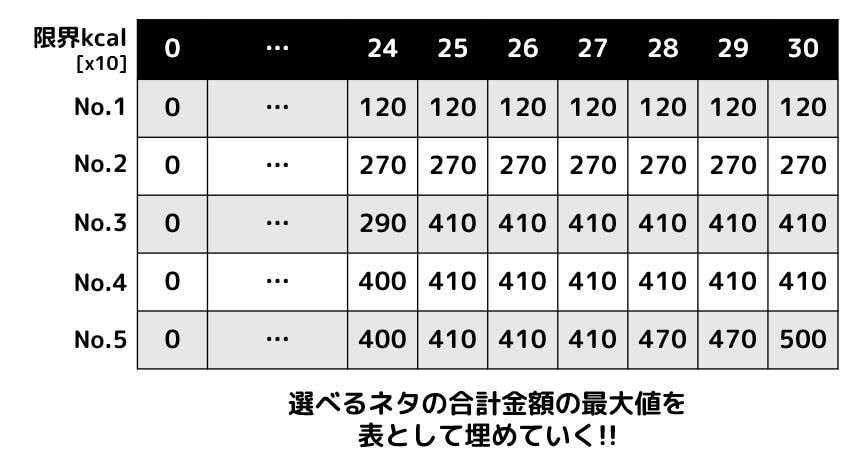
この問題を動的計画法を用いて解くときも、
- 縦が数字の個数 \( n \)
- 横が0から限界カロリー \( l \) までの限界カロリー
からなる2次元配列の表を埋めていくことで結果を求めることができます。
ですが、
- 表に埋めるのはカロリーの最大値ではなく、金額の最大値
(求めたいのはそれぞれの限界kcal以内で食べれる寿司の最大金額なため) - 5つの寿司ともカロリーが10kcal単位なので、表に埋めるのも10kcal単位にする
(計算ステップ数が1/10になるので10倍早く結果が出せる)
の2つが違うポイントとなります。
(3) ナップサック問題のソースコード
というわけで、実際にナップサック問題を動的計画法で解くプログラムをCとPythonに分けて下に載せたいと思います。
C言語
#include<stdio.h>
#define N 5 // 寿司の種類
#define KCAL_MAX 30 // 限界カロリー [×10]
int sushi_choice(int cost_list[N],int kcal_list[N]) {
int tmp_choice, tmp_not_choice;
int table[N][KCAL_MAX+1];
// DP表の一番上(i = 0)を初期化
for(int j = 0; j <= KCAL_MAX; j += 1) {
if(kcal_list[0] > j) {
table[0][j] = 0; // 1品目を食べられない
}
else {
table[0][j] = cost_list[0]; // 1品目を食べられる
}
}
for(int i = 1; i < N; i += 1) {
for(int j = 0; j <= KCAL_MAX; j += 1) {
tmp_not_choice = table[i-1][j]; //i品目を食べないとき
if(kcal_list[i] > j) {
table[i][j] = tmp_not_choice; // カロリーオーバー
}
else {
tmp_choice = table[i-1][j - kcal_list[i]] + cost_list[i];
if(tmp_choice >= table[i-1][j])
table[i][j] = tmp_choice;
else
table[i][j] = tmp_not_choice;
}
}
}
return table[N-1][KCAL_MAX];
}
int main() {
int cost_list[N] = {120,150,140,110,100}; // それぞれのネタの値段
int kcal_list[N] = {8,10,7,6,7}; // それぞれの値段のカロリー [×10]
int max_cost = sushi_choice(cost_list,kcal_list);
printf("%2dkcal以内で食べられる金額の最大:%3d円\n",KCAL_MAX * 10,max_cost);
return 0;
}
Python
def sushi_choice(cost_list,kcal_list,limit):
list_len = len(kcal_list)
dp_table = [[0 for j in range(limit + 1)] for i in range(list_len)]
# 1品目を食べるか食べないか
for j in range(limit + 1):
if kcal_list[0] <= j:
dp_table[0][j] = cost_list[0] # 食べるとき
# 2品目以降を食べるか食べないか
for i in range(1,list_len):
for j in range(limit + 1):
tmp_not_choice = dp_table[i-1][j]
if kcal_list[i] > j: # カロリーオーバー
dp_table[i][j] = tmp_not_choice # 食べられない
else:
tmp_choice = dp_table[i-1][j - kcal_list[i]] + cost_list[i]
dp_table[i][j] = max(tmp_choice,tmp_not_choice)
return dp_table[list_len - 1][limit]
cost = [120,150,140,110,100] # それぞれの寿司の値段
kcal = [8,10,7,6,7] # それぞれの寿司のカロリー [×10]
ans = sushi_choice(cost,kcal,30)
print(ans)
(4) 動的計画法によるナップサック問題の計算量
動的計画表でナップサック問題を求めていくときの計算時間を考えましょう。
ナップサック問題を求める際には
- 縦が商品の個数分(\( n \) 個)
- 横が0からカロリー \( l \) までの \( l+1 \) 個
の表を埋めることで結果を求めることができます。

そのため、処理ステップ数は部分和問題と同じく\[
n(l+1) = nl + n
\]となり、\( nl + n \) ステップ数と求められます。
よって、計算量をオーダーで表すと \( O(nl) \) となります。
(空間計算量も、表を記憶する分だけかかると考えてもらえたらOKです! 今回の場合は \( O(nl) \) となります。)
動的計画法の計算量は、表を埋めるために必要な計算量!!
5.さいごに
今回は、アルゴリズムの中でも非常に重要な動的計画法について説明しました。
動的計画法を使うことで、
- 一定金額以内なら食べ放題のとき、どんなメニューで頼めばちょうどの金額で食べられるか
- ある商品の中から何品か選んだときにちょうど1,000円となるような組み合わせは何通りあるか
のような応用問題も求めることができるので、興味がある人はぜひプログラミングしてみましょう!
需要があれば、動的計画法の応用問題についてもいつか別記事で解説したいと思います!
*1:導出の際には差分方程式を解きます。実際に、\[
a_{n} = a_{n-1} + a_{n-2}, \ \ a_{0} = 0, \ \ a_{1} = 1
\]の漸化式(差分方程式)を解くと、\[
a_n = \frac{1}{ \sqrt{5} } \left( \left( \frac{1 + \sqrt{5} }{ 2 } \right)^{n} - \left( \frac{1 - \sqrt{5} }{ 2 } \right)^{n} \right)
\]となるので、大きい項である\[
\frac{1}{ \sqrt{5} } \left( \frac{1 + \sqrt{5} }{ 2 } \right)^{n}
\]を取ることでオーダーが求められます。
もし差分方程式の解き方に興味がある人はこちらの記事を御覧ください。
*2:中には1度計算した内容を表(配列)に記録し、記録した内容から呼び出しているため動的計画法の解法の1つと考えることもできますが、動的計画法とメモ化再帰は区別して(違う解法として)いる先生、参考書も多いので、本サイトでは動的計画法とメモ化再帰を別のものとして扱っていきたいと思います。
*3:空間計算量 \( O(n) \) 相当
*4:全部(3番目まで)のカードの中から何枚か選び合計が10以下となる最大の自然数
*5:架空の店です
*6:実際にこんなこと言ってくる人は絶対いないとおもってます。
関連広告・スポンサードリンク