スポンサードリンク
こんにちは、ももやまです。
コンピュータの世界では、あらゆるもの(命令・データ)が2進数(0 or 1)で管理されているのでしたね。
このあらゆるもの、データというのは文書ファイルにとどまらず、皆さんが普段目にする画像も含まれます。
しかし、写真などの画像データを2進数で表現するためにはちょっとした工夫が必要です。
今回は、コンピュータ上で画像が取り扱うための工夫について見ていきたいとおもいます!
※ 今回の分野を理解するためには、2進数に関する知識が必須です。もし「2しんすうってなんだ?」と思った方は、下の記事にて2進数に関する理解をしておきましょう。
目次
スポンサードリンク
1. 画像の最小単位・ピクセル(画素)
2進数というのは、「0か1で管理する世界」でしたね。
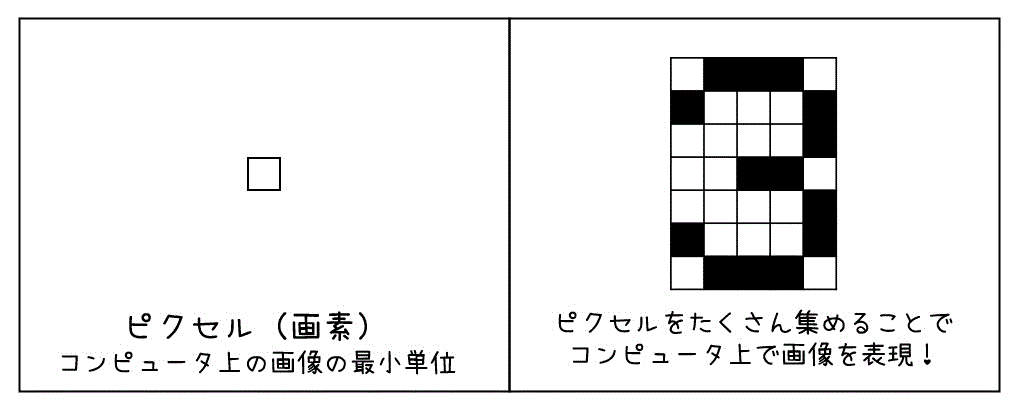
この0か1というのを小さい四角を使って表現してみることにしましょう。具体的には、この四角が塗りつぶされていない状態を0、塗りつぶされている状態を1とします。

この小さい四角1つでは何も表すことができません。しかし、この小さい四角を集めてあげると…

意味がありそうな画像が見えてきましたね…!
このようにコンピュータ上では、上のように小さい四角をたくさん集めることで画像を表現しているのです。また、この小さい四角のことをピクセル、もしくは画素と呼び、コンピュータの世界における画像データの最小単位となります。

スポンサードリンク
2. 明るさを表す単位・画素値
白か黒かの2色では、表現できる画像にかなり限りがあります。
そこで、ピクセルに対して8ビット(1バイト)を用いて白から黒の間の色を表現することを考えましょう。
まず、真っ暗なピクセルを0、真っ白なピクセルを255と定めます。
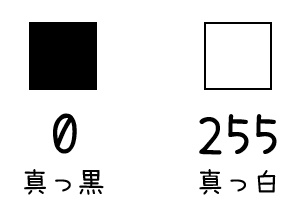
さらに、その中間の色(グレー)を0~255の数値で表すことを考えます。この明るさのことを画素値、もしくは輝度値と呼びます。
画素値が0に近ければ近いほど暗く(黒に近く)、255に近ければ近いほど明るく(白に近く)なります。
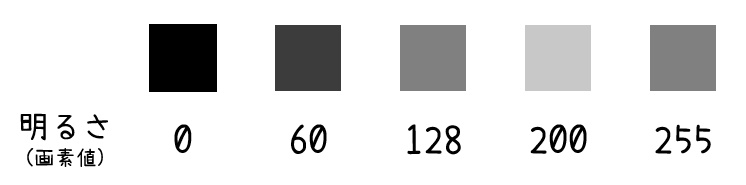
このように、1つのピクセルを表現するために8ビット[1]nビットで表せる数の総数は \( 2^n \) 個のため。今回は8ビットなので \( 2^8 = 256 \) 通りの表現が可能となる。を使うことで、256色のグレーをつくることができるのです。

スポンサードリンク
3. カラー画像をコンピュータ上で扱うためには
普段皆さんが目にする画像、写真はほとんどがカラー画像ですよね。そこで、コンピュータ上でカラー画像を表す方法も見ていきましょう。
皆さんは小学校のころ、絵の具で色を混ぜ合わせて新しい色を作り出すといったことをしましたね。
コンピュータ上でも同じように、色を混ぜ合わせることで様々な色のピクセルを作り出します。このときに使われる色が赤・緑・青の3色です。光の3原色とも呼ばれます。

この光の3原色の混ぜる量を0 ~ 255で調整することでいろんな色が作れます[2] … Continue reading。
その数、なんと16,777,216色[3]赤、緑、青それぞれで \( 2^8 \) パターンの色の調整が可能なので、合計で \( \( (2^8)^3 = 2^{24} \) 通りの色が表現できます。!
下に混ぜ合わせてできる色の例を載せてみたので、ご覧ください。
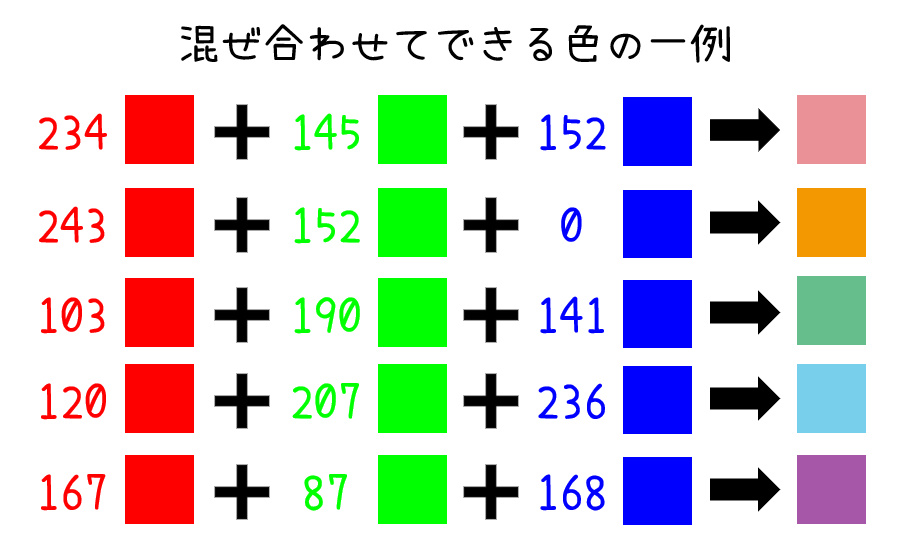
カラーコードでモノクロ色を表現する
「光の3原色を使って白色や黒色も表現できるの?」と思った人もいるかもしれません。
実は、白色や黒色も光の3原色から作り出すことができるのです。
具体的には、何も混ぜない場合(赤0・緑0・青0)は黒色、全部をフルに入れた(赤255・緑255・青255)場合は白色が作られます[4] … Continue reading。

絵の具で、色々な色を混ぜて黒色を作ったことがある人から見ると、少し不思議な感覚になるかもしれません。
余談 カラーコードとは
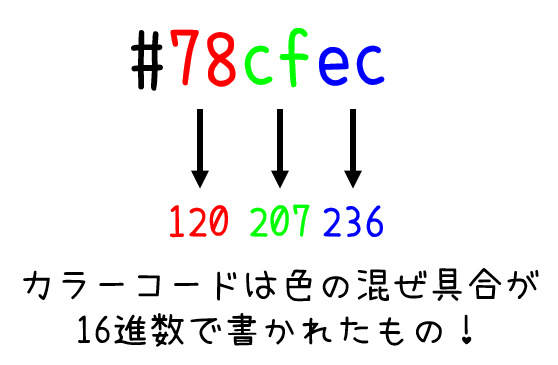
プログラミング(特にhtml)をしていると、色の指定を #78cfec のように6桁の英数字を使って指定することがあります。
このカラーコードは、2桁ごとに赤・緑・青の画素値が16進数で表されたものとなっています。
4. 画像のデジタル化・アナログからデジタルへ
1~3章では、コンピュータ上で画像がどのように表現されるかについて説明していきました。
この4章では、普段皆さんが目にする景色(アナログ世界)がどのようにしてコンピュータ上で表現できる形(デジタル世界)に変換されるのかを見ていきましょう。
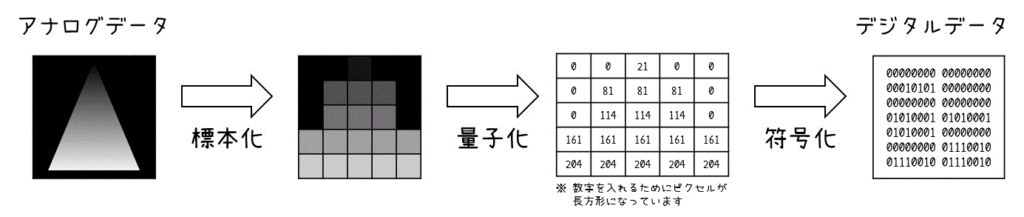
Step1. 標本化
まず、コンピュータ上で画像を表現するために、画像を細かく細かく刻みます。
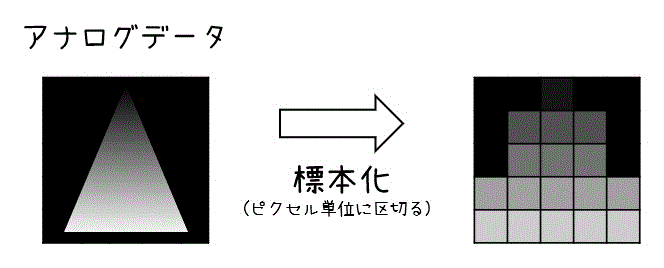
この細かく刻んだものが先ほど説明した画像データの最小単位であるピクセル・画素となります。
Step1の刻む段階で細かく刻めば刻むほど、より鮮明にコンピュータ上で画像を表すことができます。
余談 画素数とカメラのスペック
なおコンピュータの世界では、どれくらい鮮明に刻んだのかを画像内のすべてのピクセル・画素の数で表現します。例えば、横300、縦200で刻んだ場合、画素数は300×200=60,000となります。
この画素数は、スマートフォンや一眼に搭載されているカメラの性能を表す際によく使われます。例えば、2021年最新のiPhone(iPhone13)の場合、横4,032、縦3,024で刻まれており、画素数は約1,200万画素[5]正確には1219万2768画素です。となります。
Step2. 量子化
次に、細かく刻んだもの明るさを(画素値)0~255の256段階で数値化します。
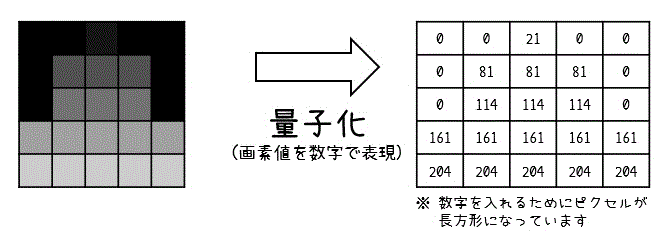
なお、カラー画像の場合、赤色・緑色・青色の明るさ(色の混ぜ具合)をそれぞれ0~255で数値化します。
Step3. 符号化
最後に画像の刻み具合(横と縦のピクセル数)と、それぞれの画素値を2進数にしてデータに書き込みます。
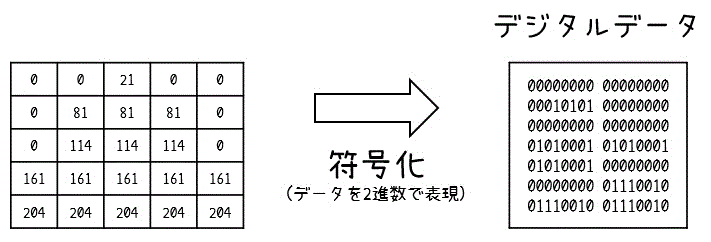
上の3ステップで、画像をコンピュータの世界で表現できるような形にすることができます。
なお、標本化→量子化→符号化の流れは画像だけでなく、音をコンピュータ上で表現する際にも使われます[6]ITパスポートや基本情報では画像ではなく、音を用いて標本化、符号化、量子化に関する問題が出ることが多い。。
国家試験(基本情報技術者)の問題を解いてみよう!
実際に国家試験の1つである基本情報技術者には、このような問題が出題されています。
標本化、符号化、量子化の三つの工程で、アナログをディジタルに変換する場合の順番として、適切なものはどれか。
ア:標本化,量子化,符号化
イ:符号化,量子化,標本化
ウ:量子化,標本化,符号化
エ:量子化,符号化,標本化
解答:ア
このような問題を解く際、順番を丸暗記するのではなく、デジタル化の流れを頭に入れておくことでど忘れを減らすことができるので、この際にデジタル化の流れを理解しておきましょう。
5. 画像のサイズ計算
最後に、コンピュータ上に画像を保存するためにはどのくらいの容量を使うのかを計算してみましょう。
(1) 1ピクセルあたりのデータ量
まずは、1ピクセルあたりに使われるデータ量を、「白黒」・「グレースケール」・「カラー」の3つに分けて計算してみましょう。
| 種類 | 表現可能な色の数 | 1ピクセルあたりのデータ量 |
|---|---|---|
| 白黒 | \( 2^1 \) 色 | 1ビット |
| グレースケール | \( 2^8 \) 色 | 8ビット=1バイト |
| カラー | \( 2^{24} \) 色 | 24ビット=3バイト |
(2) あとは画素数を掛けるだけ
1ピクセル当たりの容量が分かってしまえば、あとは
(容量) = (1ピクセルあたりのデータ量) × (総画素数)
で簡単に計算ができます。
試しに計算の練習をしてみましょう。
iPhoneで撮影できる画像の大きさは横4,032画素、縦3,024画素のカラー画像である。
このカラー画像1枚を保存するために必要な容量を計算しなさい。
※1 画像は圧縮されていないものとする。
※2 お手元に電卓をご用意ください。
[解答]
必要な容量は\[\begin{align*}
3 \times 4032 \times 3024 & = 36578304 \mathrm{[byte]}
\\ & \fallingdotseq 35721 \mathrm{[KB]}
\\ & \fallingdotseq 34.88 \mathrm{[MB]}
\end{align*}\]となり、容量が約34.9MBであることがわかります。
(3) 画質の名前・画素数・容量一覧表
フルHD、4Kのような画像のきれいさを表す単語を聞いたことがあるかと思います。
下に、画質のきれいさを表す名前と、その大きさ、画素数、1枚あたりの容量を表にしたものをおいておくので参考までにどうぞ。
| 画質名 | 大きさ | 画素数 | 容量 [カラー] | 容量 [モノクロ] |
|---|---|---|---|---|
| SD | 720×480 | 34.6万 | 0.989 [MB] | 338 [KB] |
| HD | 1,280×720 | 92.2万 | 2.63 [MB] | 900 [KB] |
| フルHD | 1,920×1,080 | 207万 | 5.93 [MB] | 1.98 [MB] |
| 2K | 2,560×1,440 | 369万 | 10.5 [MB] | 3.52 [MB] |
| 4K | 3,840×2,160 | 830万 | 23.7 [MB] | 7.91 [MB] |
| 8K | 7,680×4,320 | 3318万 | 94.9 [MB] | 31.6 [MB] |
(4) 画像の圧縮技術
先ほど、iPhoneの撮影画像1枚を保存するために34.9MB必要であると説明しました。
しかし、1枚保存するのに34.9MBかかってしまうと、あっという間にiPhoneの容量を食いつくしてしまいます。
そこで使われるのが画像の圧縮技術です。
簡単に説明すると省略できる無駄な部分を削除したりするなどで、容量を減らす技術のことを表します。
この画像圧縮技術のおかげで、1枚あたり34.9MB必要なiPhoneの写真データが2MB~3MB程度まで小さくできるのです!
※ 圧縮技術については、機会があれば記事にしたいと思います。
国家試験(ITパスポート)の問題を解いてみよう!
画像のサイズに関する計算は、ITパスポートでも出てきます。さっそく過去問を見てみましょう。
300×600ドットで構成され、1画素の情報を記録するのに24ビットを使用する画像データがある。これを150×300ドットで構成され、1画素の情報を記録するのに8ビットを使用する画像データに変換した。必要な記憶容量は何倍になるか。
ア:1 / 12
イ:1 / 6
ウ:1 / 4
エ:1 / 2
[ITパスポート平成28年秋期 問78]
正解:ア
このように2つの画像の記憶容量を比較するタイプの問題の場合、「2つの記憶容量をすべて計算して最後に割る」計算をしてしまうと計算量が増えてしまい、ミスが増加します。
ではどのような方法がおすすめかと言いますと、それぞれの画像の記憶容量を計算する式を立ててから、分数の掛け算を計算するように途中で約分する方法です。
具体的には、\[\begin{align*}
\frac{\mathrm{変換後}}{ \mathrm{変換前} } & = \frac{150 \times 300 \times 8}{300 \times 600 \times 24}
\\ & = \frac{ \cancel{ 150 } \times \cancel{300} \times \cancel{ 8 } }{ \cancel{ 300 }^{ \ 2} \times \cancel{600}^{ \ 2} \times \cancel{ 24 }^{ \ 3} }
\\ & = \frac{1 \times 1 \times 1}{ 2 \times 2 \times 3}
\\ & = \frac{1}{12}
\end{align*}\]と計算します。
よって、答えはアの 1/12 となります。
国家試験(基本情報)の問題を解いてみよう!
ITパスポートよりワンランク上の基本情報でも、同じような問題が出題されます。
ただし、ITパスポートよりは若干計算量が増加するため、計算ミスに注意が必要です。
横1,600画素、縦1,200画素で、24ビットのカラー情報をもつ画像が撮影できるディジタルカメラがある。このカメラに8Mバイトの記録用メモリを使用すると、何枚の画像が記録できるか。ここで、画像は圧縮しないものとする。
ア:1
イ:4
ウ:11
エ:15
[基本情報技術者平成18年秋期 午前問26]
正解:ア
まず、1枚あたりに必要な画像を計算しましょう。
なお、本来は 1[KB] = 1,024[byte]、1[MB] = 1,024[KB] なのですが、4択の問題なので多少横着をして、1[KB] = 1,000[byte]、1[MB] = 1,000[KB] で計算をします[7]計算を横着することで、計算ミスを減らすことと、問題を解くスピードが両方上がるので、選択肢があるタイプの問題では横着を絶対しましょう。。また、24ビット=3バイトとしてから計算することをおすすめします。
\[\begin{align*}
3 \times 1600 \times 1200 & = 5760000 \mathrm{[byte]}
\\ & \fallingdotseq 5760 \mathrm{[KB]}
\\ & \fallingdotseq 5.76 \mathrm{[MB]}
\end{align*}\]
となり、1枚当たり約5.76MBの容量を食うことがわかります。
カメラに設定されているのは8MBのメモリなので、2枚目を取ろうとした時点で明らかに8MBを超えてしまいますね。
なので、記録できるのは1枚だけとなり、答えはアとなります。
6. さいごに
今回は、画像処理の最初の1歩として画像がコンピュータ上でどのように表されるのかについて説明していきました。
この部分は、ITパスポートや基本情報のような国家試験においても頻出な分野なので、これから画像処理を勉強しない人も理解をしておきましょう!
注釈
| ↑1 | nビットで表せる数の総数は \( 2^n \) 個のため。今回は8ビットなので \( 2^8 = 256 \) 通りの表現が可能となる。 |
|---|---|
| ↑2 | 大学で習う線形代数の用語を使って難しく言うと、「任意の色を赤・緑・青の線形結合で表現できる」や「赤・緑・青を基底として任意の色が作られる」と表現することができます。 |
| ↑3 | 赤、緑、青それぞれで \( 2^8 \) パターンの色の調整が可能なので、合計で \( \( (2^8)^3 = 2^{24} \) 通りの色が表現できます。 |
| ↑4 | 赤・緑・青の量を同じにすることでグレースケールの色を表現することができます。例えば、赤128・緑128・青128はグレースケールの画素値128の色と全く同じです。 |
| ↑5 | 正確には1219万2768画素です。 |
| ↑6 | ITパスポートや基本情報では画像ではなく、音を用いて標本化、符号化、量子化に関する問題が出ることが多い。 |
| ↑7 | 計算を横着することで、計算ミスを減らすことと、問題を解くスピードが両方上がるので、選択肢があるタイプの問題では横着を絶対しましょう。 |
関連広告・スポンサードリンク