スポンサードリンク
こんにちは、ももうさです。
今回から2回にわたって、画像の幾何学的変換について説明していきます!
※ 大学1年生で習った線形代数の内容を使います。もし忘れてしまったよ(or まだ習ってないよ)という方は、より詳細な説明があるリンクを適宜貼っているため、そちらをご覧ください。
目次
スポンサードリンク
0. 線形変換と画像の関係
まずは、今回の画像の幾何学的変換で使う「線形変換(線形写像)」について軽く説明していきます。
なお、線形写像や線形変換についてのより詳しい内容は下の記事にて説明していますので、必要な方はご覧ください。
(1) 関数と線形写像
皆さんは中学、そして高校の数学で関数 \( f(x) \) について習ってきましたね。
関数というのは、ある(1つの数字)を入れると、ある規則に従って決まった値 \( f(x) \) を出力する魔法の箱みたいなものでした。
下の例の場合、入力した値 \( x \) を2倍にして出力する関数 \( f(x) = 2x \) を表しています。
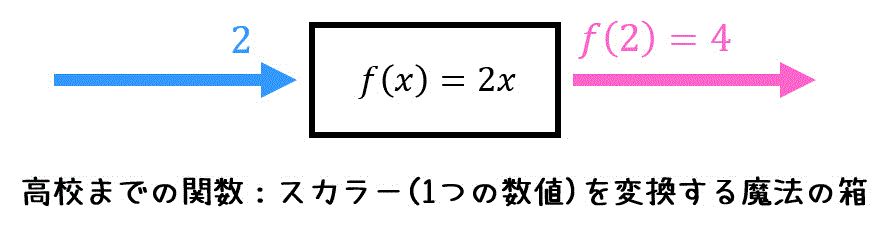
大学に入ると、「線形代数」という科目で、線形写像という関数を拡張したものを習います。
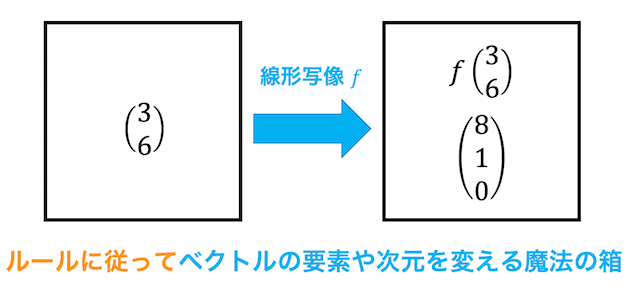
線形写像とは、下のようにある1つのベクトル \( \vec{x} \) を入力すると、行列で表されるある変換規則 \( A \) に従って決まったベクトル \( f( \vec{x} ) = A \vec{x} \) を出力する魔法の箱のようなものです。
また、線形写像に登場する変換規則 \( A \) のことを、表現行列と呼ばれます。この表現行列 \( A \) のサイズによっては、入力するベクトルと出力されるベクトルの次元を変えることもできます。

線形写像(線形変換)の変換規則を表す表現行列 \( A \) は、最も単純なベクトルである単位基本ベクトル \( \vec{e}_1 \), \( \vec{e}_2 \), … の変換先を並べたもので構成されています。
つまり、最も単純な単位基本ベクトルに対しての変換先がわかれば、すべてのベクトルに対しての変換先を \( A \vec{x} \) で求めることができるのです!
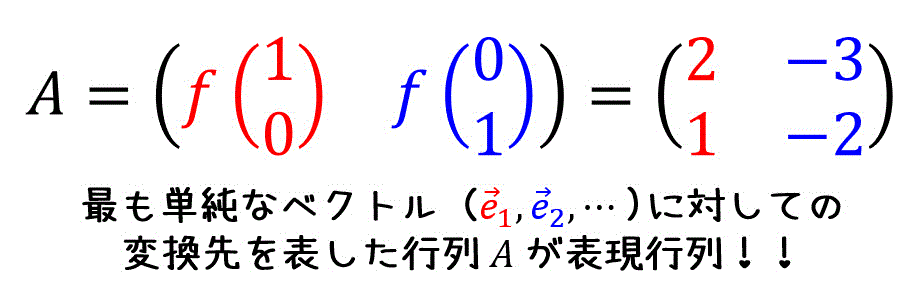
(2) 線形変換と幾何学的変換
線形写像 \( f \) の中でも、入力と出力でベクトルの次元が変わらない線形写像のことを、線形変換と呼びます。
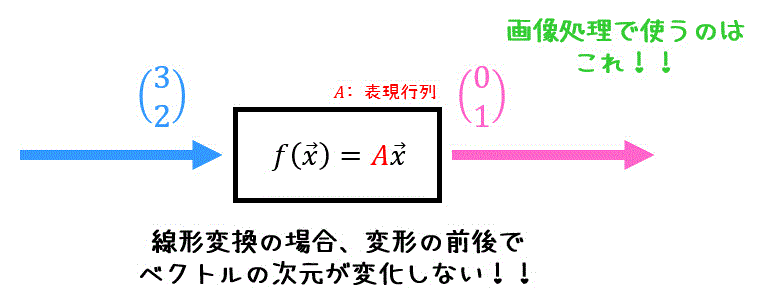
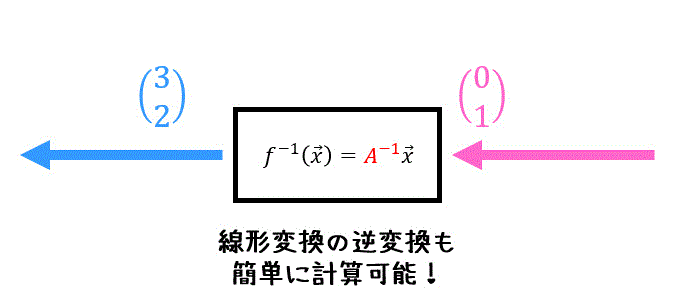
線形変換の大きな特徴として、1回行った変換を元に戻す逆変換 \( f^{-1} \) を \( f^{-1} ( \vec{x} A^{-1} \vec{x} \) と簡単に計算することができます。
※ ただし表現行列 \( A \) が \( |A| = 0 \) のときは逆行列 \( A^{-1} \) をもたないため、逆変換を計算することができません。
画像の幾何学的変換では、画像内の画素に対し、どのように線形変換 \( f \) を行えば、思った通りの幾何学的変換が実現できるかを表現します。ここで、画像内の変換前の画素 (x,y) と変換後の画素 (x', y' ) を、2次元ベクトル\[
\vec{x} = \left( \begin{array}{ccc} x' \\ y' \end{array} \right) , \ \ \ \vec{x}' = \left( \begin{array}{ccc} x' \\ y' \end{array} \right)
\]を用いて表すとします。
ここで、変換 \( f \) の表現行列を \( A \) とすると、変換前の画素 \( \vec{x} \)、変換後の画素 \( \vec{x}' \) の関係は\[\begin{align*}
\vec{x}' & = f( \vec{x})
\\ & = A \vec{x}
\end{align*}\]となりますね。
今回は、この線形変換 \( f \) の表現行列 \( A \) をどのようにすれば、画像の回転、拡大縮小などの様々な幾何学的変換を表現できるかについて説明していきます!
スポンサードリンク
1. 線形変換を考えるときのコツ
線形変換 \( f \) の表現行列 \( A \) は、最も単純ベクトル(基本ベクトル)である\[
\vec{e}_1 = \left( \begin{array}{ccc} 1 \\ 0 \end{array} \right) , \ \ \
\vec{e}_2 = \left( \begin{array}{ccc} 0 \\ 1 \end{array} \right)
\]に対して変換 \( f \) を適用した際の変換先のベクトルを並べた行列となっているのでしたね。\[
A = \left( \vec{e}_1, \vec{e}_2 \right)
\]
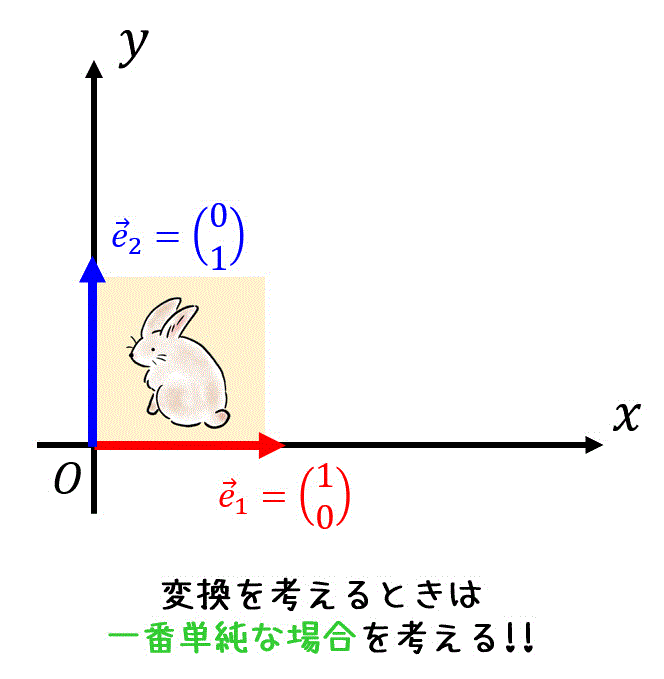
そのため、画像の線形変換 \( f \) を行う表現行列 \( A \) を考える際には、これらの基本ベクトルがどこに移動するのかを考えると、どうしてそのような変換式(変換行列/表現行列)になるのかがわかると思います。
スポンサードリンク
2. 画像の拡大・縮小
ある画像を \( x \) 軸方向、もしくは \( y \) 軸方向に引き延ばしたり縮めたりする変換を表します。
(1) \( x \) 軸方向への拡大・縮小
\( x \) 軸方向に \( s_x \) 倍拡大する変換 \( f \)を考えましょう。
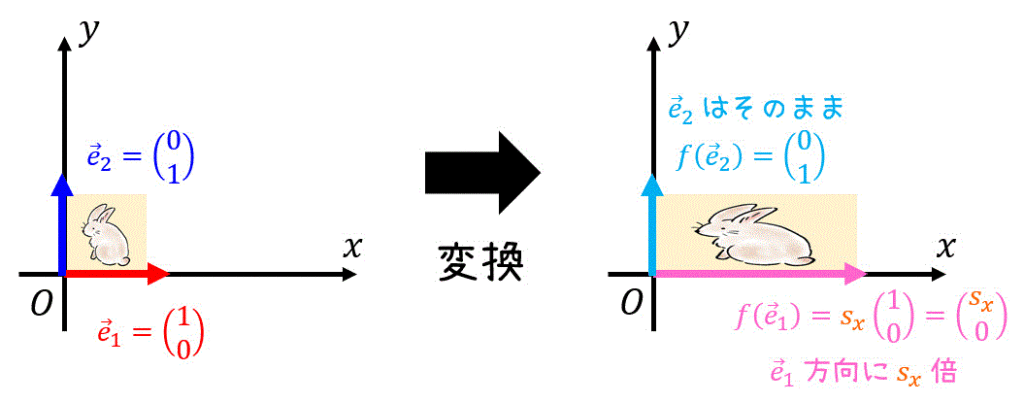
このとき、\( x \) 軸方向への基本ベクトル \( \vec{e}_1 \) は \( s_x \) 倍されるので、\[\begin{align*}
f( \vec{e}_1) & = s_x \vec{e}_1
\\ & = \left( \begin{array}{ccc} s_x \\ 0 \end{array} \right)
\end{align*}\]となります。
一方 \( y \) 軸方向への基本ベクトル \( \vec{e}_2 \) はそのままなので、\[
f( \vec{e}_2) = \left( \begin{array}{ccc} 0 \\ 1 \end{array} \right)
\]のままです。
よって、\( x \) 軸方向に \( s_x \) 倍するための変換行列 \( A \) は\[\begin{align*}
A & = \left( \textcolor{magenta}{ f( \vec{e}_1 ) } , \textcolor{deepskyblue}{ f( \vec{e}_2 ) } \right)
\\ & = \left( \begin{array}{ccc} \textcolor{magenta}{ s_x } & \textcolor{deepskyblue}{ 0 } \\ \textcolor{magenta}{ 0 } & \textcolor{deepskyblue}{ 1 } \end{array} \right)
\end{align*}\]となります。
(2) \( y \) 軸方向への拡大・縮小
今度は \( y \) 軸方向に \( s_y \) 倍拡大することを考えましょう。
このとき、\( y \) 軸方向への基本ベクトル \( \vec{e}_2 \) は \( s_y \) 倍されるので、\[\begin{align*}
f( \vec{e}_2) & = s_y \vec{e}_2
\\ & = \left( \begin{array}{ccc} 0 \\ s_y \end{array} \right)
\end{align*}\]となります。
一方 \( x \) 軸方向への基本ベクトル \( \vec{e}_1 \) はそのままなので、\[
f( \vec{e}_2) = \left( \begin{array}{ccc} 1 \\ 0 \end{array} \right)
\]のままです。

よって、\( y \) 軸方向に \( s_y \) 倍するための変換行列 \( A \) は\[\begin{align*}
A & = \left( \textcolor{magenta}{ f( \vec{e}_1 ) } , \textcolor{deepskyblue}{ f( \vec{e}_2 ) } \right)
\\ & = \left( \begin{array}{ccc} \textcolor{magenta}{ 1 } & \textcolor{deepskyblue}{ 0 } \\ \textcolor{magenta}{ 0 } & \textcolor{deepskyblue}{ s_y } \end{array} \right)
\end{align*}\]となります。
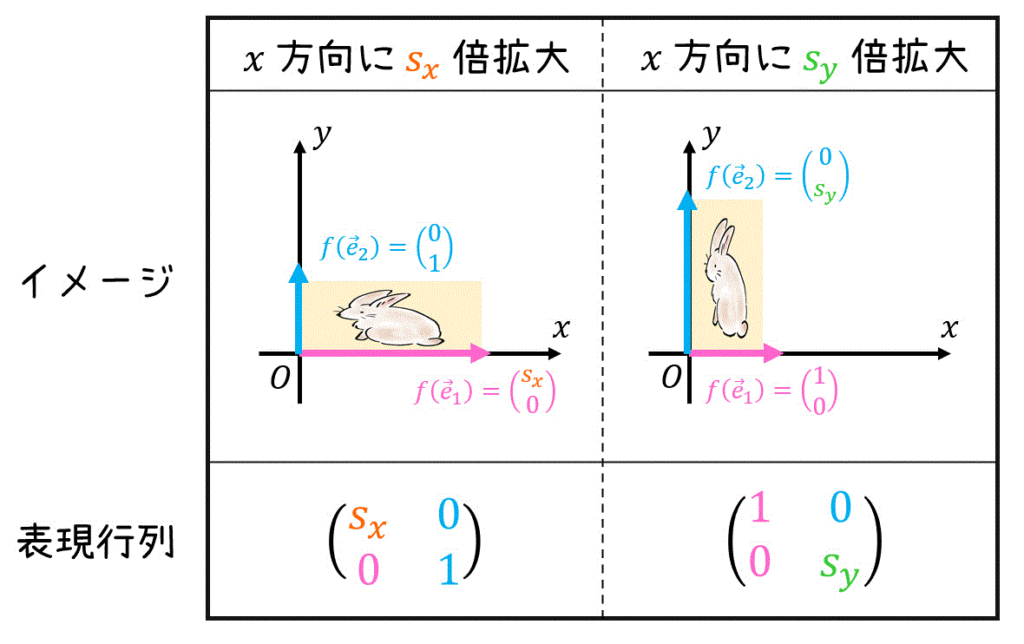
なお、実際には \( x \) 軸方向へ \( \textcolor{orange}{s_x} \) 倍拡大と \( y \) 軸方向へ \( \textcolor{green}{s_y} \) 倍変換するのを合わせて、表現行列を\[
\left( \begin{array}{ccc} \textcolor{orange}{s_x} & 0 \\ 0 & \textcolor{green}{s_y} \end{array} \right)
\]とすることがほとんどです。
変換前の画素を \( (x,y) \)、変換後の画素を \( (x' , y' ) \) とする。
このとき、\( x \) 軸方向に \( \textcolor{orange}{s_x} \) 倍拡大、\( y \) 軸方向に \( \textcolor{green}{s_y} \) 倍拡大する変換式は、下のように表せる。\[
\left( \begin{array}{ccc} x' \\ y' \end{array} \right) = \left( \begin{array}{ccc} \textcolor{orange}{s_x} & 0 \\ 0 & \textcolor{green}{s_y} \end{array} \right) \left( \begin{array}{ccc} x \\ y \end{array} \right)
\]
3. 鏡映変換
鏡映変換とは、ある直線に対して対称な位置に移動させる変換を表します。
ここでは、よく使う \( x \) 軸、\( y \) 軸、直線 \( y = x \) に対して対称な位置に移動させる変換を見ていきましょう。
(1) \( x \) 軸に対して対称な位置に移動
\( x \) 軸に対して対称に移動させる変換 \( f \ )を考えましょう。
\( x \) 軸の正の方向を向いている \( \vec{e}_1 \) は、対称移動をさせても位置が変わりませんね。そのため、\[
f( \vec{e}_1) = \left( \begin{array}{ccc} 1 \\ 0 \end{array} \right)
\]のままですね。
一方 \( y \) 軸の正の方向を向いている \( \vec{e}_2 \) は、対称移動をさせるとベクトルの向きが反転します。そのため、\[
f( \vec{e}_2) = \left( \begin{array}{ccc} 0 \\ -1 \end{array} \right)
\]となります。
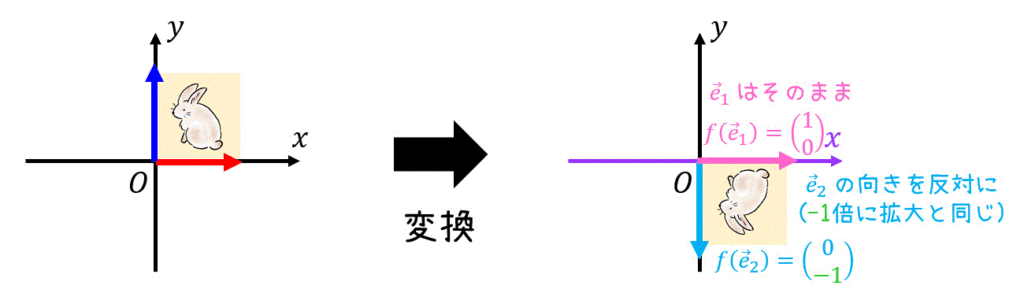
よって、\( x \) 軸に対して対称に移動させる変換を表す変換行列 \( A \) は\[\begin{align*}
A & = \left( \textcolor{magenta}{ f( \vec{e}_1 ) } , \textcolor{deepskyblue}{ f( \vec{e}_2 ) } \right)
\\ & = \left( \begin{array}{ccc} \textcolor{magenta}{ 1 } & \textcolor{deepskyblue}{ 0 } \\ \textcolor{magenta}{ 0 } & \textcolor{deepskyblue}{ -1 } \end{array} \right)
\end{align*}\]となります。
なお、この変換は(1-ii)で出てきた拡大縮小変換を用いて、「\( y \) 軸方向に-1倍拡大する変換」と解釈することもできます。
(2) \( y \) 軸に対して対称な位置に移動
今度は、\( y \) 軸に対して対称に移動させる変換 \( f \ )を考えましょう。
\( y \) 軸の正の方向を向いている \( \vec{e}_2 \) は、対称移動をさせても位置が変わりませんね。そのため、\[
f( \vec{e}_2) = \left( \begin{array}{ccc} 0 \\ 1 \end{array} \right)
\]のままですね。
一方 \( x \) 軸の正の方向を向いている \( \vec{e}_1 \) は、対称移動をさせるとベクトルの向きが反転します。そのため、\[
f( \vec{e}_2) = \left( \begin{array}{ccc} -1 \\ 0 \end{array} \right)
\]となります。
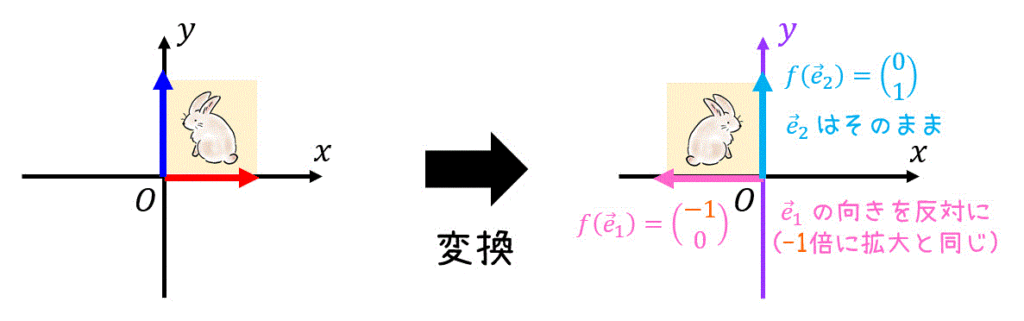
よって、\( x \) 軸に対して対称に移動させる変換を表す変換行列 \( A \) は\[\begin{align*}
A & = \left( \textcolor{magenta}{ f( \vec{e}_1 ) } , \textcolor{deepskyblue}{ f( \vec{e}_2 ) } \right)
\\ & = \left( \begin{array}{ccc} \textcolor{magenta}{ -1 } & \textcolor{deepskyblue}{ 0 } \\ \textcolor{magenta}{ 0 } & \textcolor{deepskyblue}{ 1 } \end{array} \right)
\end{align*}\]となります。
なお、この変換は(1-i)で出てきた拡大縮小 変換 を用いて、「\( x \) 軸方向に-1倍拡大する変換」と解釈することもできます。
(3) 直線 \( y=x \) に対して対称な位置に移動
さらに、直線 \( y = x \) に対して対称に移動させる変換 \( f \ )を考えましょう。
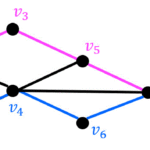
この変換を行うと、基本ベクトル \( \vec{e}_1 \)、\( \vec{e}_2 \) は、下の図のような向きに変換されます。
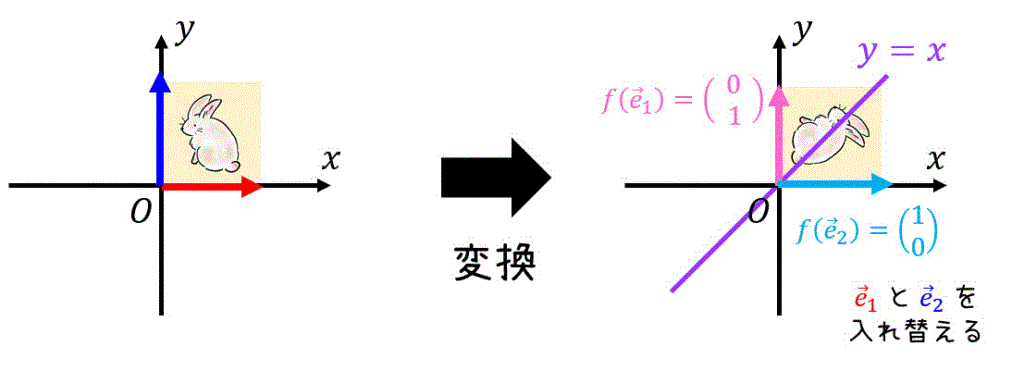
よって、直線 \( y = x \) に対して、対称に移動させる変換を表す変換行列 \( A \) は\[\begin{align*}
A & = \left( \textcolor{magenta}{ f( \vec{e}_1 ) } , \textcolor{deepskyblue}{ f( \vec{e}_2 ) } \right)
\\ & = \left( \begin{array}{ccc} \textcolor{magenta}{ 0 } & \textcolor{deepskyblue}{ 1 } \\ \textcolor{magenta}{ 1 } & \textcolor{deepskyblue}{ 0 } \end{array} \right)
\end{align*}\]となります。
今まで出てきた対称変換をまとめると、下のようになります。
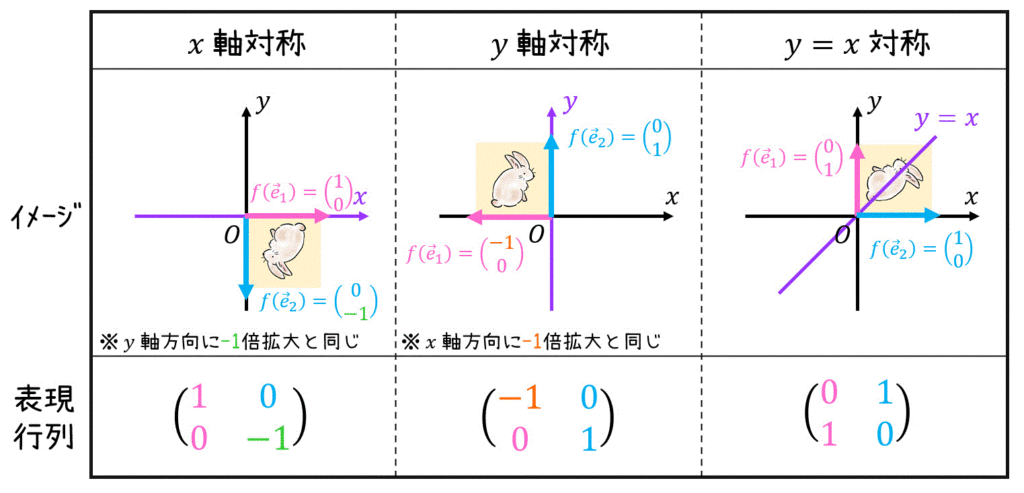
変換前の画素を \( (x,y) \)、変換後の画素を \( (x' , y' ) \) とする。
このとき、\( x \) 軸、\( y \) 軸、直線 \( y = x \) に対して対称な位置に移動する変換式は、下のように表せる。
(1) \( x \) 軸対称\[
\left( \begin{array}{ccc} x' \\ y' \end{array} \right) = \left( \begin{array}{ccc} 1& 0 \\ 0 & \textcolor{green}{-1} \end{array} \right) \left( \begin{array}{ccc} x \\ y \end{array} \right)
\]
(2) \( y \) 軸対称\[
\left( \begin{array}{ccc} x' \\ y' \end{array} \right) = \left( \begin{array}{ccc} \textcolor{orange}{-1} & 0 \\ 0 & 1 \end{array} \right) \left( \begin{array}{ccc} x \\ y \end{array} \right)
\]
(3) 直線 \( y = x \) 対称\[
\left( \begin{array}{ccc} x' \\ y' \end{array} \right) = \left( \begin{array}{ccc} 0 & 1 \\ 1 & 0 \end{array} \right) \left( \begin{array}{ccc} x \\ y \end{array} \right)
\]
4. 回転変換
原点中心に \( \theta \) だけ反時計回りに回転させる変換を考えましょう。
このとき、ベクトル \( \vec{e}_1 \) の変換先は単位円を見ると \[
f( \vec{e}_1) = \left( \begin{array}{ccc} \cos \theta \\ \sin \theta \end{array} \right)
\]となることがわかりますね。
また、ベクトル \( \vec{e}_2 \) は、単位円を見ると、\( \vec{e}_1 \) を90°回転させたベクトルであることがわかりますね。
そのため、ベクトル \( \vec{e}_2 \) の変換先は\[\begin{align*}
f ( \vec{e}_2) & = \left( \begin{array}{ccc} \cos ( \theta + 90^{\circ} ) \\ \sin ( \theta + 90^{\circ} ) \end{array} \right)
\\ & = \left( \begin{array}{ccc} - \sin \theta \\ \cos \theta \end{array} \right)
\end{align*}\]と計算できますね。
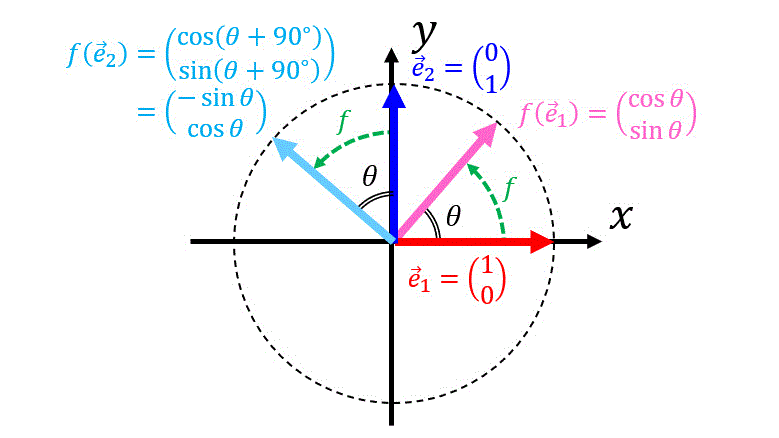
よって、回転変換 \( f \) の変換行列は\[
\left( f ( \textcolor{red}{\vec{e}_1} ) , f ( \textcolor{blue}{\vec{e}_2} ) \right) =
\left( \begin{array}{ccc} \textcolor{magenta}{\cos \theta} & \textcolor{deepskyblue}{- \sin \theta} \\ \textcolor{magenta}{ \sin \theta } & \textcolor{deepskyblue}{ \cos \theta } \end{array} \right)
\]となります。
変換前の画素を \( (x,y) \)、変換後の画素を \( (x' , y' ) \) とする。
このとき、原点を中心に \( \theta \) だけ反時計回りに回転させる変換は、下のように表せる。\[
\left( \begin{array}{ccc} x' \\ y' \end{array} \right) = \left( \begin{array}{ccc} \cos \theta & - \sin \theta \\ \sin \theta & \cos \theta \end{array} \right) \left( \begin{array}{ccc} x \\ y \end{array} \right)
\]
5. スキュー変換
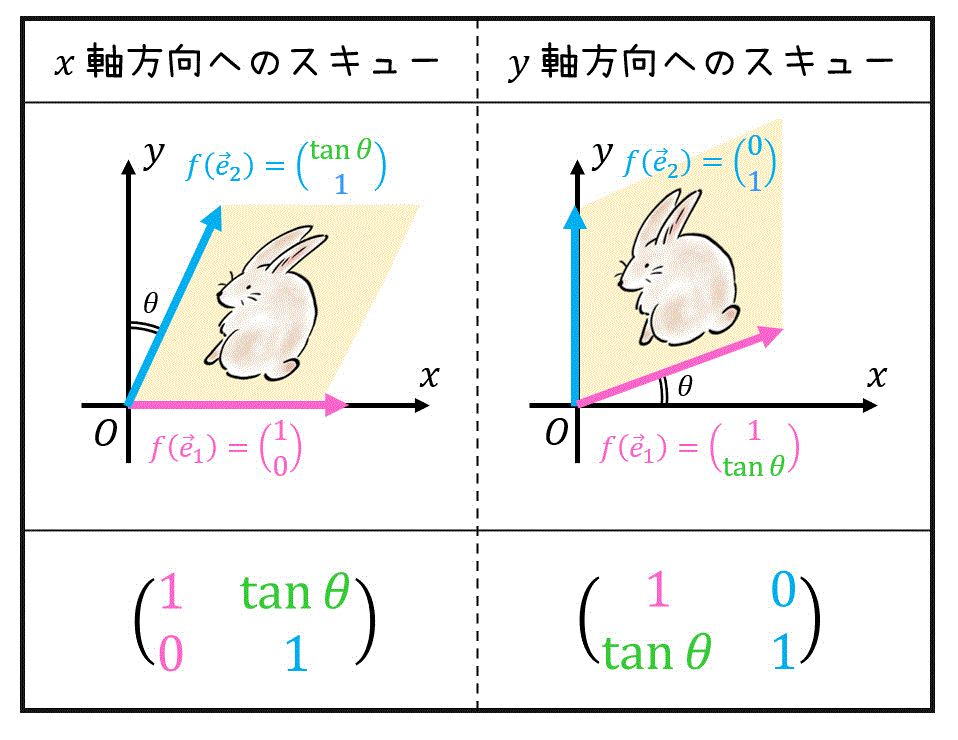
スキューとは、下のように長方形の画像を平行四辺形に傾けることを表します。。
ここで問題です。青い辺の ? の長さを \( \theta \) を用いて表してみましょう。

三角比を使うと、青い辺の長さは \( \tan \theta \) であることがわかりますね。
これを踏まえて、変換の式を見ていきましょう。
(1) \( x \) 軸方向へのスキュー
\( x \) 軸方向へのスキュー変換 \( f \) を考えましょう。
\( x \) 軸の正の方向を向いている \( \vec{e}_1 \) は、スキュー変換を行っても何も動きません。そのため、\[
f( \vec{e}_1) = \left( \begin{array}{ccc} 1 \\ 0 \end{array} \right)
\]のままですね。
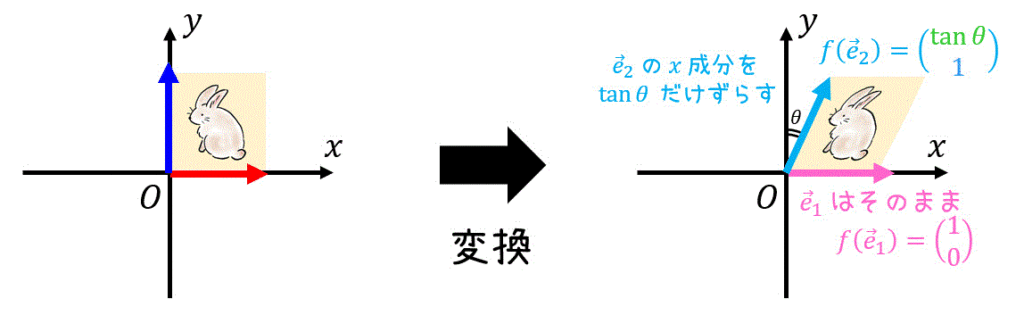
一方 \( y \) 軸の正の方向を向いている \( \vec{e}_2 \) は、スキュー変換を行うと、\( \vec{e}_2 \) の \( x \) 成分が \( \tan \theta \) だけずれます。ただし、傾ける際に \( \vec{e}_2 \) の \( y \) 成分は変化しない点に要注意です。よって、\[
f( \vec{e}_2) = \left( \begin{array}{ccc} \tan \theta \\ 1 \end{array} \right)
\]となります。
よって、\( x \) 軸方向へ \( \theta \) だけ傾けてスキュー変換を行う変換行列 \( A \) は\[\begin{align*}
A & = \left( \textcolor{magenta}{ f( \vec{e}_1 ) } , \textcolor{deepskyblue}{ f( \vec{e}_2 ) } \right)
\\ & = \left( \begin{array}{ccc} \textcolor{magenta}{ 1 } & \textcolor{deepskyblue}{ \tan \theta } \\ \textcolor{magenta}{ 0 } & \textcolor{deepskyblue}{ 1 } \end{array} \right)
\end{align*}\]となります。
(2) \( y \) 軸方向へのスキュー
同じように \( y \) 軸方向へののスキュー変換 \( f \) を考えましょう。
\( y \) 軸の正の方向を向いている \( \vec{e}_2 \) は、スキュー変換を行っても何も動きません。そのため、\[
f( \vec{e}_2) = \left( \begin{array}{ccc} 0 \\ 1 \end{array} \right)
\]のままですね。
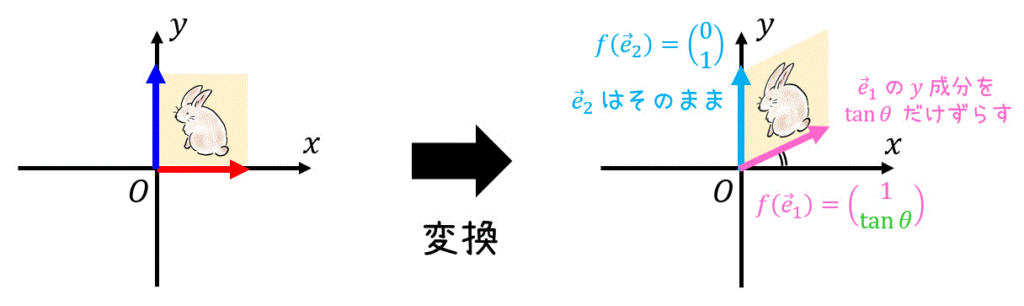
一方 \( x \) 軸の正の方向を向いている \( \vec{e}_1 \) は、スキュー変換を行うと、\( \vec{e}_1 \) の \( y \) 成分が \( \tan \theta \) だけずれます。ただし、傾ける際に \( \vec{e}_1 \) の \( x \) 成分は変化しません。よって、\[
f( \vec{e}_1) = \left( \begin{array}{ccc} 1 \\ \tan \theta \end{array} \right)
\]となります。
よって、\( y \) 軸方向へ \( \theta \) だけ傾けてスキュー変換を行う変換行列 \( A \) は\[\begin{align*}
A & = \left( \textcolor{magenta}{ f( \vec{e}_1 ) } , \textcolor{deepskyblue}{ f( \vec{e}_2 ) } \right)
\\ & = \left( \begin{array}{ccc} \textcolor{magenta}{ 1 } & \textcolor{deepskyblue}{ 0 } \\ \textcolor{magenta}{ \tan \theta } & \textcolor{deepskyblue}{ 1 } \end{array} \right)
\end{align*}\]となります。
変換前の画素を \( (x,y) \)、変換後の画素を \( (x' , y' ) \) とする。
このとき、 \( x \) 軸方向 もしくは \( y \) 軸方向へ \( \theta \) だけ傾けてスキュー変換を行う変換は下のように表せる。
\( x \) 軸方向へ \( \theta \) 傾けたスキュー\[
\left( \begin{array}{ccc} x' \\ y' \end{array} \right) = \left( \begin{array}{ccc} 1 & \textcolor{green}{ \tan \theta } \\ 0 & 1 \end{array} \right) \left( \begin{array}{ccc} x \\ y \end{array} \right)
\]
\( y \) 軸方向へ \( \theta \) 傾けたスキュー \[
\left( \begin{array}{ccc} x' \\ y' \end{array} \right) = \left( \begin{array}{ccc} 1 & 0 \\ \textcolor{green}{ \tan \theta } & 1 \end{array} \right) \left( \begin{array}{ccc} x \\ y \end{array} \right)
\]
6. 例題で確認!(幾何学的変換)
では、ここまでの幾何学変換を理解しているかを、例題で確認してみましょう!
次の(1)~(4)の変換を行うための変換行列を書きなさい。
(1) ある画像を \( x \) 軸方向に3倍、\( y \) 軸方向に2倍する変換 \( f_1 \)
(2) ある画像を \( y \) 軸対称に移動させるための変換 \( f_2 \)
(3) ある画像を原点中心に \( 30^{\circ} \) 反時計回りに回転する変換 \( f_3 \)
(4) ある画像を \( x \) 軸方向へ \( 60^{\circ}\) 傾けるスキュー変換 \( f_4 \)
[解答]
(1) \( s_x = 3 \), \( s_y = 2 \) のときの拡大縮小変換である。\[
\left( \begin{array}{ccc} 3 & 0 \\ 0 & 2 \end{array} \right)
\]
(2) \( y \) 軸対称なので、\( y \) 方向そのまま、\( x \) 方向の向きが反対になる変換である。\[
\left( \begin{array}{ccc} -1 & 0 \\ 0 & 1 \end{array} \right)
\]
(3) \( \theta = 30^{\circ} \) のときの回転変換である。\[\begin{align*}
\left( \begin{array}{ccc} \cos 30^{\circ} & - \sin 30^{\circ} \\ \sin 30^{\circ} & \cos 30^{\circ} \end{array} \right) & =
\left( \begin{array}{ccc} \frac{\sqrt{3}}{2} & - \frac{1}{2} \\ \frac{1}{2} & \frac{\sqrt{3}}{2} \end{array} \right)
\\ & = \frac{1}{2} \left( \begin{array}{ccc} \sqrt{3} & - 1 \\ \ 1 & \sqrt{3} \end{array} \right)
\end{align*}\]
(4) \( \theta = 60^{\circ} \) のときの \( x \) 軸方向へのスキュー変換である。 \[\begin{align*}
\left( \begin{array}{ccc} 1 & \tan 60^{\circ} \\ 0 & 1 \end{array} \right) =
\left( \begin{array}{ccc} 1 & \sqrt{3} \\ 0 & 1 \end{array} \right)
\end{align*}\]
7. 幾何学変換の合成変換
1で、様々な幾何学変換を説明していきました。
ここからはこれらの幾何学変換を組み合わせることを考えていきましょう。
(1) 合成変換の表現行列
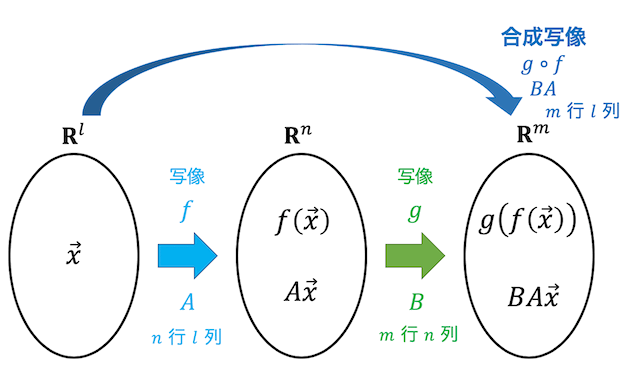
ある変換 \( f \) の表現行列が \( A \)、さらに別の変換の \( g \) の表現行列が \( B \) であるとします。
このとき、\( f \) → \( g \) の順で変換を適用することを考えましょう。
まず、変換 \( f \) を行うと、\( \vec{x}' = A \vec{x} \) で変換 \( f \) を適用した後のベクトル \( \vec{x}' \) を求めることができます。続けて変換 \( g \) を行うと、\( \vec{x}'' = B \vec{x}' \) で変換 \( g \) を適用した後のベクトル \( \vec{x}'' \) が求まりますね。
この2つを合わせると、\[\begin{align*}
\vec{x}'' & = g( f ( \vec{x} ) )
\\ & = g ( \vec{x}' )
\\ & = B \vec{x}'
\\ & = BA \vec{x}
\end{align*}\]となりますね。
よって、変換 \( f \) の後に変換 \( g \) を適用する合成変換の表現行列は、\( BA \) となることがわかりますね。
(2) 変換の順序を変えると…?
では、次に変換の順序を変えて、変換 \( g \) → 変換 \( f \) の順で計算をしてみましょう。
まず、変換 \( g \) を行うと、\( \vec{x}' = B \vec{x} \) で変換 \( g \) を適用した後のベクトル \( \vec{x}' \) を求めることができます。続けて変換 \( f \) を行うと、\( \vec{x}'' = A \vec{x}' \) で変換 \( f \) を適用した後のベクトル \( \vec{x}'' \) が求まりますね。
この2つを合わせると、\[\begin{align*}
\vec{x}'' & = f( g ( \vec{x} ) )
\\ & = f ( \vec{x}' )
\\ & = A \vec{x}'
\\ & = AB \vec{x}
\end{align*}\]となりますね。
よって、変換 \( g \) の後に変換 \( A \) を適用する合成変換の表現行列は、\( AB \) となることがわかりますね。
ここで、行列の積は順番を変えても答えが一致するとは限らないことを思い出してください。実際に、行列の積の順番を変えると答えが変化することを画像を通じて確認してみましょう。
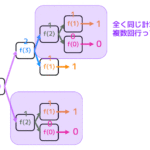
(3) 変換の順序によって結果が変わることを画像で体感してみよう
実際に変換の順番を入れ替えると、結果が変わることを下の画像にて体感してもらいましょう。
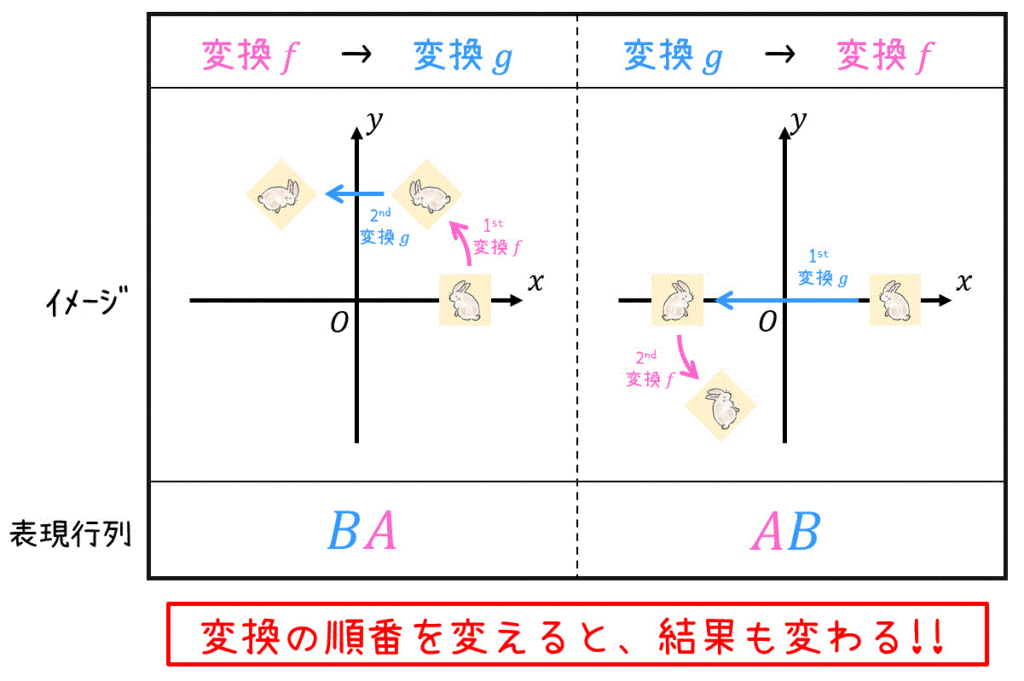
ある幾何学変換 \( f \) の変換行列を \( A \)、幾何学変換 \( g \) の変換行列を \( B \) とする。
このときの合成変換の変換行列は、以下のようになる。
(1) 変換 \( f \) → 変換 \( g \) の順に適用する場合: \( BA \)
(2) 変換 \( g \) → 変換 \( f \) の順に適用する場合: \( AB \)
※ 変換の順番を変えると、結果が変わるので要注意!!
8. 幾何学変換の逆変換
一旦行った線形変換 \( f \) を元に戻すときの変換を逆変換 \( f^{-1} \) とよびます。
逆変換の変換行列は、元の変換行列 \( A \) の逆行列 \( A^{-1} \) で簡単に求めることができます。
せっかくなので、例を出してみましょう。
例えば、ある点 (2,-1) に対して \( x \) 軸方向に3倍、\( y \) 軸方向に2倍する変換を適用すると、変換後の座標は\[\begin{align*}
\left( \begin{array}{ccc} x' \\ y' \end{array} \right) & =
\left( \begin{array}{ccc} 3 & 0 \\ 0 & 2 \end{array} \right) \left( \begin{array}{ccc} 2 \\ -1 \end{array} \right) \\ & = \left( \begin{array}{ccc} 6 \\ -2 \end{array} \right)
\end{align*}\]より、(6,-2) となりますね。
次に、行った変換を元に戻してあげましょう。ここで、変換行列\[
A = \left( \begin{array}{ccc} 3 & 0 \\ 0 & 2 \end{array} \right)
\]の逆行列は、\[\begin{align*}
A^{-1} & = \frac{1}{6} \left( \begin{array}{ccc} 2 & 0 \\ 0 & 3 \end{array} \right)
\end{align*}\]と計算できますね。実際に計算してみると、\[\begin{align*}
\left( \begin{array}{ccc} x \\ y \end{array} \right) & = A^{-1} \left( \begin{array}{ccc} x' \\ y' \end{array} \right)
\\ & = \frac{1}{6} \left( \begin{array}{ccc} 2 & 0 \\ 0 & 3 \end{array} \right) \left( \begin{array}{ccc} 6 \\ -2 \end{array} \right)
\\ & = \left( \begin{array}{ccc} 2 \\ -1 \end{array} \right)
\end{align*}\]となり、確かに元に戻りますね。
ある幾何学変換 \( f \) の変換行列を \( A \) とする。
このとき、変換 \( f \) の逆変換 \( f^{-1} \)、つまり一度変換 \( f \) を適用したベクトル(画素)を元に戻す変換行列は \( A^{-1} \) となる。
※ ただし、逆行列 \( A^{-1} \) が存在しない場合、つまり行列式 \( |A| = 0 \) のときは計算ができないため注意。
なお、合成変換と逆変換について、もう少し数学的に勉強したいよという方は、下の記事をぜひご覧ください。
9. 例題で確認!(合成変換・逆変換)
それでは、合成変換と逆変換を理解しているかを、例題で確認してみましょう!
次の(1), (2)の処理を行う変換行列を答えなさい。
(1) \( x \) 軸に2倍、\( y \) 軸に4倍拡大した後に、\( x \) 軸対称の鏡映変換を行う。
(2) \( y \) 軸対称の鏡映変換を行った後に、原点中心に \( 45^{\circ} \) 回転する。
[解答]
(1)
\( x \) 軸2倍、\( y \) 軸4倍に拡大する変換行列 \( A \) は\[
A = \left( \begin{array}{ccc} 2 & 0 \\ 0 & 4 \end{array} \right)
\]となり、\( x \) 軸対称の鏡映変換を行う変換行列 \( B \) は\[
B = \left( \begin{array}{ccc} 1 & 0 \\ 0 & -1 \end{array} \right)
\]となる。よって、変換行列 \( X \) は、\[\begin{align*}
X & = BA
\\ & = \left( \begin{array}{ccc} 1 & 0 \\ 0 & -1 \end{array} \right) \left( \begin{array}{ccc} 2 & 0 \\ 0 & 4 \end{array} \right)
\\ & = \left( \begin{array}{ccc} 2 & 0 \\ 0 & -4 \end{array} \right)
\end{align*}\]となる。
(2)
\( y \) 軸対称の鏡映変換を行う変換行列 \( A \) は\[
A = \left( \begin{array}{ccc} -1 & 0 \\ 0 & 1 \end{array} \right)
\]となり、原点中心に \( 45^{\circ} \) 回転する変換行列 \( B \) は\[\begin{align*}
B & = \left( \begin{array}{ccc} \cos 45^{\circ} & - \sin 45^{\circ} \\ \sin 45^{\circ} & \cos 45^{\circ} \end{array} \right)
\\ & = \left( \begin{array}{ccc} \frac{\sqrt{2}}{2} & - \frac{ \sqrt{2} }{2} \\ \frac{ \sqrt{2} }{2} & \frac{\sqrt{2}}{2} \end{array} \right)
\\ & = \frac{1}{2} \left( \begin{array}{ccc} \sqrt{2} & - \sqrt{2} \\ \ \sqrt{2} & \sqrt{2} \end{array} \right)
\end{align*}\]となる。
よって、変換行列 \( X \) は、\[\begin{align*}
X & = BA
\\ & = \frac{1}{2} \left( \begin{array}{ccc} \sqrt{2} & - \sqrt{2} \\ \ \sqrt{2} & \sqrt{2} \end{array} \right) \left( \begin{array}{ccc} -1 & 0 \\ 0 & 1 \end{array} \right)
\\ & = \frac{1}{2} \left( \begin{array}{ccc} - \sqrt{2} & - \sqrt{2} \\ - \sqrt{2} & \sqrt{2} \end{array} \right)
\end{align*}\]となる。
ある座標に対して、\( x \) 軸対称の鏡映変換を行い、さらに \( y \) 軸方向に2倍拡大する変換を行ったところ、座標が(3,2)に移動した。
変換元の座標を求めなさい。
\( x \) 軸対称の鏡映変換を行う変換行列 \( A \) は\[
A = \left( \begin{array}{ccc} 1 & 0 \\ 0 & -1 \end{array} \right)
\]となる。また、\( y \) 軸方向に2倍拡大する変換行列 \( B \) は\[
B = \left( \begin{array}{ccc} 1 & 0 \\ 0 & 2 \end{array} \right)
\]となる。
よって、題意の変換(合成変換)は、\[\begin{align*}
X & = BA
\\ & = \left( \begin{array}{ccc} 1 & 0 \\ 0 & 2 \end{array} \right) \left( \begin{array}{ccc} 1 & 0 \\ 0 & -1 \end{array} \right)
\\ & = \left( \begin{array}{ccc} 1 & 0 \\ 0 & -2 \end{array} \right)
\end{align*}\]となる。
ここで求めたいのは変換元の座標なので、変換後の座標に対して逆変換を行うことで、変換前の座標を出す。
ここで、\( X \) の逆行列は\[
X^{-1} = \frac{1}{2} \left( \begin{array}{ccc} 2 & 0 \\ 0 & -1 \end{array} \right)
\]なので、変換前の座標は、\[\begin{align*}
\left( \begin{array}{ccc} x \\ y \end{array} \right) & = X^{-1} \left( \begin{array}{ccc} 3 & 0 \\ 0 & 2 \end{array} \right)
\\ & = \frac{1}{2} \left( \begin{array}{ccc} 2 & 0 \\ 0 & -1 \end{array} \right) \left( \begin{array}{ccc} 3 & 0 \\ 0 & 2 \end{array} \right)
\\ & = \left( \begin{array}{ccc} 3 & 0 \\ 0 & -1 \end{array} \right)
\end{align*}\]となるため、変換前の座標は (3,-1) と求められる。
10. まとめ
今回は、線形変換を利用した画像の幾何学変換についてのまとめを行っていきました。
最後に、次回予告として「画像の平行移動を行うための変換」について少し考えましょう。
この線形変換は、下のように行列を使って表すことができます。(\( x \) 軸方向に \( t_x \)、\( y \) 軸方向に \( t_y \) 移動した場合の変換式です)
しかし、\( \vec{x}' = A \vec{x} \) のような変換行列 \(A \) を使った形ではどう頑張っても表すことができません。

そこで、次回は平行移動などのような、そのままでは変換行列 \( \vec{x}' = A \vec{x} \) で表すのが難しい変換を、一工夫して線形変換で表すための方法(アフィン変換)について説明します!
関連広告・スポンサードリンク