スポンサードリンク
こんにちは、ももやまです。
オートマトンの理解度確認や復習をするための記事はまだ(ほとんど)ないと思います。
そこで4時間で復習が可能な、オートマトンと言語理論の総復習問題(うさぎ模試)を作成いたしました!
- 90分間で問題を解く。問題3, 問題4についてはを回答フォームに入力する。
- 答えを送信後、間違った箇所を確認し、解説を見てどこで間違えたのか(理解ができていないのか)を確認する。
- 間違えた箇所を参考書や記事などで練習する。
- 時間があれば、合っている箇所も確認する。
- 寝る。
目次
スポンサードリンク
1. オートマトンの演算
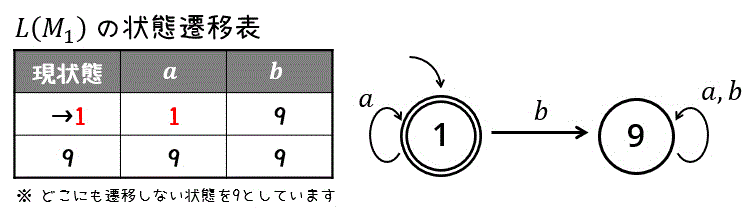
\( \Sigma = \{ a, b \} \) 上の非決定性有限オートマトン(NFA) \( M_1 \) と、決定性有限オートマトン(DFA) \( M_2 \) が以下のような状態遷移図で与えられている。
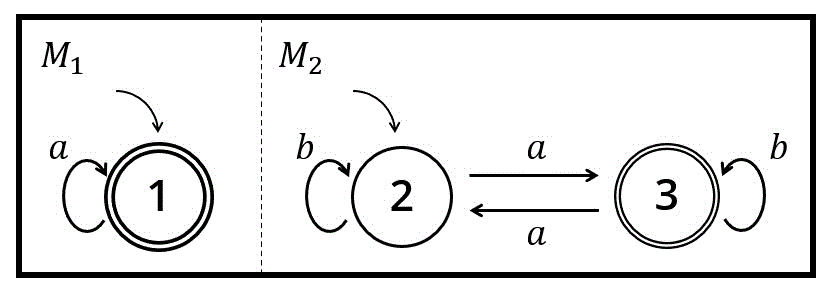
このとき、(1)~(5)の問いに答えなさい。
(1) \( M_1 \) を完全決定性有限オートマトン(DFA)にし、さらに最簡形でなければ最簡形の決定性有限オートマトンに変換し、状態遷移図を書きなさい。
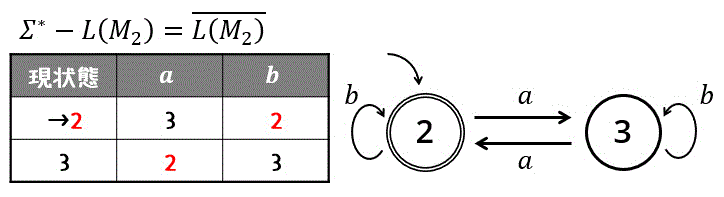
(2) \( \Sigma^* - L(M_2) \) を認識(受理)する最簡形の完全決定性有限オートマトン(最小状態DFA)を求め、状態遷移図で答えなさい。
(3) \( L(M_1) \cup L(M_2) \) を受理する最簡形の完全決定性有限オートマトン(最小状態DFA)を求め、状態遷移図で答えなさい。
(4) \( L(M_1) - L(M_2) \) を受理する最簡形の完全決定性有限オートマトン(最小状態DFA)を求め、状態遷移図で答えなさい。
(5) \( L(M_1) \cdot L(M_2) \) を受理する最簡形の完全決定性有限オートマトン(最小状態DFA)を求め、状態遷移図で答えなさい。
配点:各6点×5=30点
部分点1:結果は正しいが最簡形の状態遷移図になっていない。[2点減点で4点]
部分点2:(5)において、非完全形オートマトンがかけている [2点]
解説
(1) 非決定性(NFA) → 決定性(DFA)への変換
該当するうさぎ塾の記事はこちら↓↓↓
状態遷移図を書きながら、完全決定性(有限)オートマトンへ変換しましょう。
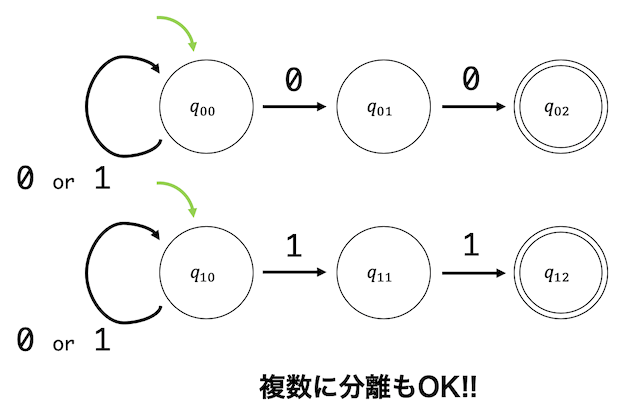
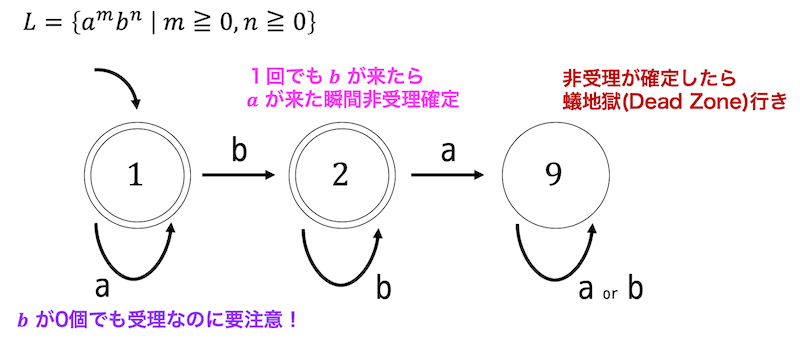
ここで、どこにも遷移しない状態は「状態9[1]状態の名前は自由につけてOKです。私は、空集合と9集合の響きが似ているので、どこにも遷移しない状態を9とつけています。」としています。
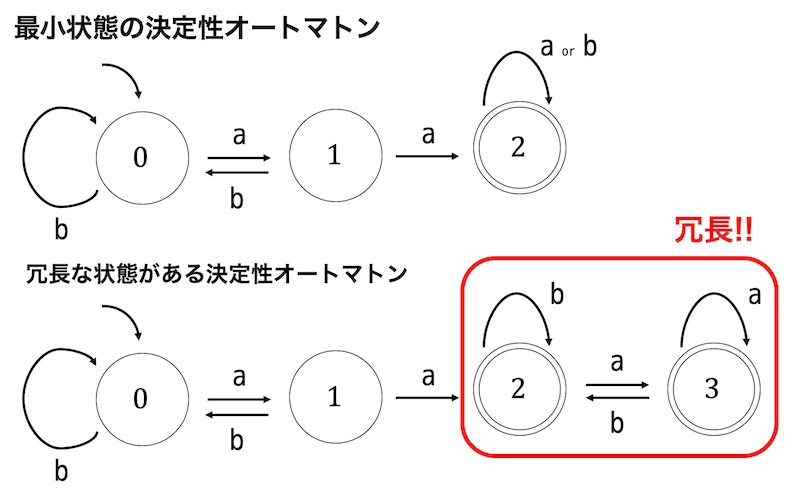
※ 最小化の確認ですが、受理状態と非受理状態に分けた段階で、全グループがバラバラになるため、明らかに最小状態であることがわかります。
※ \( L(M_1) \) は、直感的には「\( a \) のみの文字列を認識、受理するオートマトン」となります。この直感は検算をするときに少し使うことができます。
Step1. 初期状態から遷移可能な状態をすべての文字 \( \Sigma = \{ a, b \} \) に対して列挙していく。
Step2. 遷移先が未知の状態が出てこなくなるまでStep1を繰り返す。
※ 遷移可能な状態が複数あれば、複数をすべて書く。
※ 遷移可能な状態がなければ、遷移可能な状態がない(非受理の)状態(9)を作る。
(2) 決定性オートマトンの補集合は…?
(2)~(4)の該当するうさぎ塾の記事はこちら↓↓↓
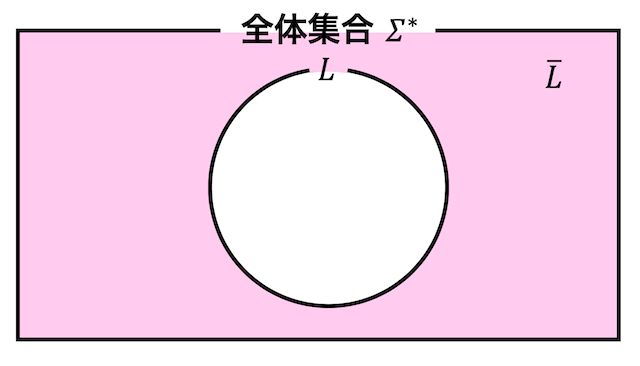
\( \Sigma^* \) とは、すべての文字列を指します。
つまり、\( \Sigma^* - L(M_2 ) \) を認識する言語は、\( L(M_2) \) の補集合 \( \overline{L(M_2)} \) を求めればOK。
ここで、決定性オートマトンの最大の特徴、受理状態◎と非受理状態○を入れ替えたものは必ず補集合になる特徴を利用すれば、答えの状態遷移図をあっという間に書けます。

※ 最小化の確認ですが、受理状態と非受理状態に分けた段階で、全グループがバラバラになるため、明らかに最小状態であることがわかります。
ある言語 \( L \) の補集合 \( \overline{L} \) は、完全決定性有限オートマトン(DFA)であれば、状態遷移図の受理状態◎と非受理状態○を入れ替えることで簡単に作成できる。
(3) オートマトンの演算(和集合)
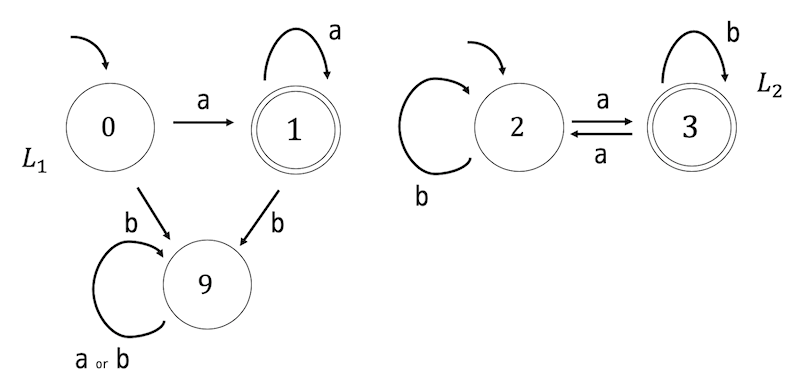
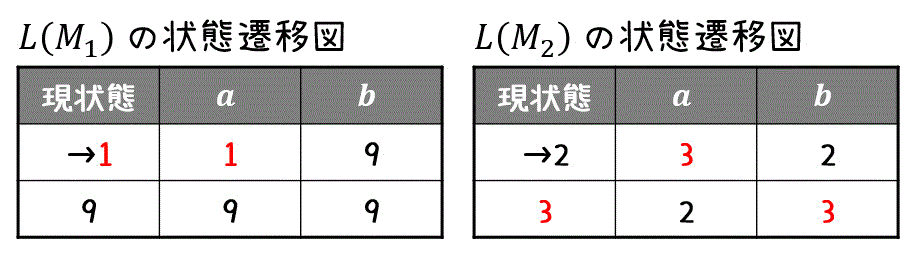
2つのオートマトン \( L(M_1) \), \( L(M_2) \) の演算を行うときは、演算を行う2つのオートマトンを同時に読んでいきます。
そのため、まずは演算を行う状態遷移図を並べてかきましょう。
※ 受理状態は、赤色などで色わけしておくと後ほど図を書くときに助けとなります。
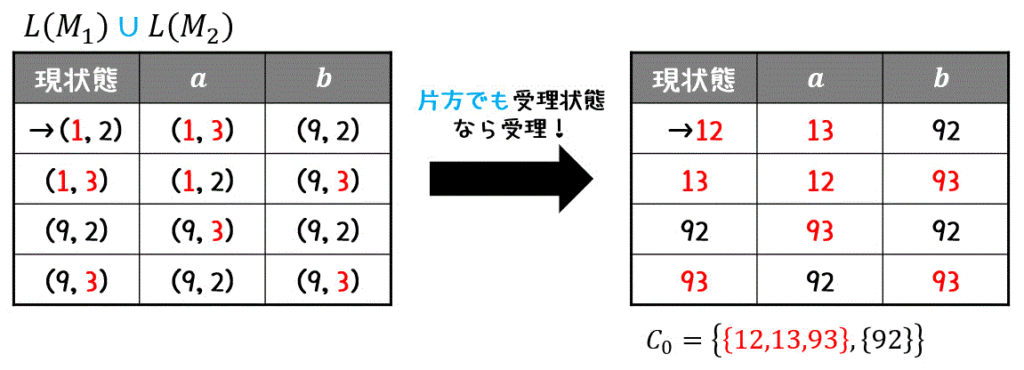
準備が出来たら、(L1の初期状態, L2の初期状態) を初期状態として、お互いの状態遷移を未知の状態遷移がなくなるまで読み取っていきます。
全部読み取れたら、受理状態を考えます。
今回は、和集合 \( \cup \) なので、2つの状態のうち片方でも受理状態であれば受理状態となります。
最小化かどうかの確認
最小化についての詳しい内容はこちら↓↓↓
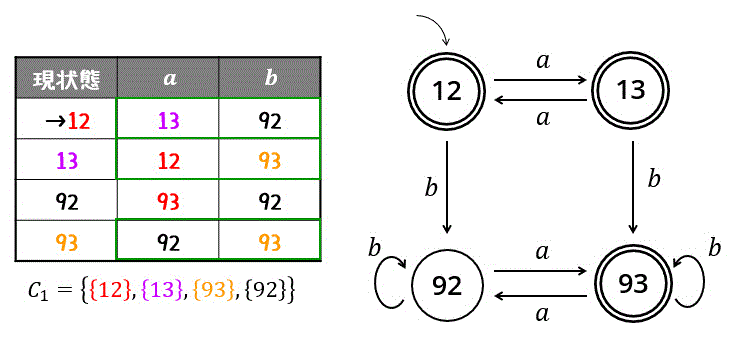
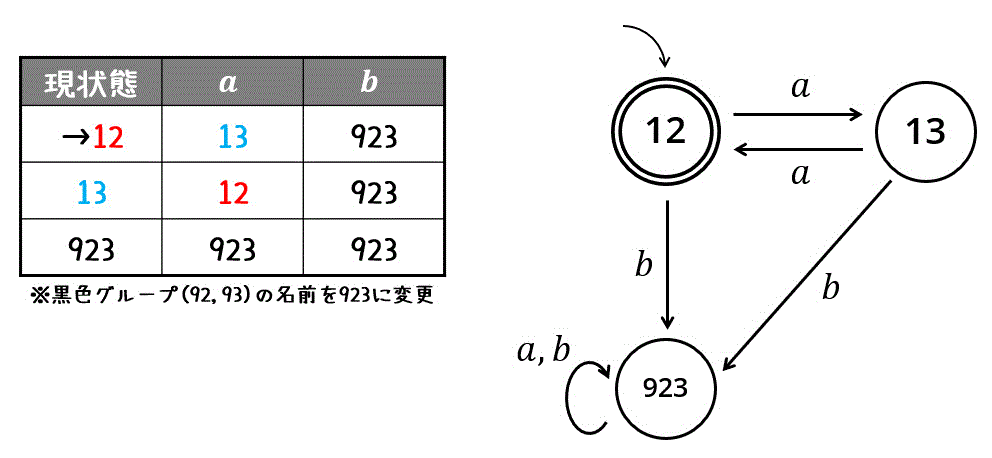
まず、状態を受理状態のグループ(12,13,93)と受理状態ではないグループ(92)にわけます。\[
C_0 = \left\{ \textcolor{red}{ \{ 12,13,93 \} }, , \{ 92 \} \right\}
\]次に、同じグループ (12,13,93) 内で異なるグループに遷移する状態があるか確認します。
すると今回は、12, 13, 93の3種類とも、受理状態が異なるグループに遷移しますね。
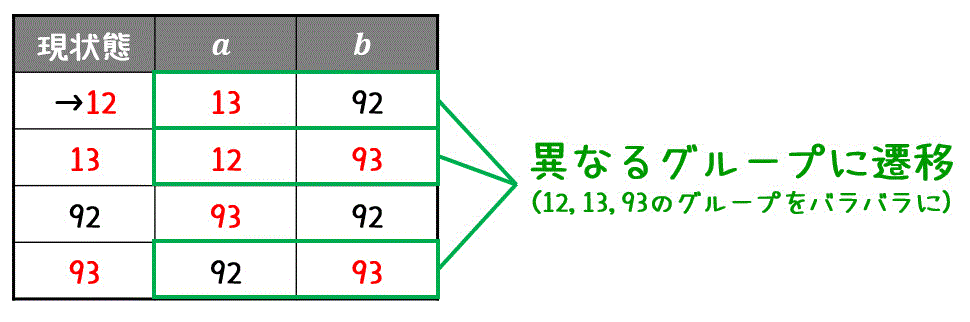
異なるグループに遷移するということは、等価なグループとは言えないため、12, 13, 93はすべて異なるグループに分離します。(このときにグループごとに色を分けるのがおすすめです。)\[
C_1 = \left\{ \textcolor{red}{ \{ 12 \} }, \textcolor{magenta}{ \{ 13 \} }, \textcolor{orange}{ \{ 93 \} } , \{ 92 \} \right\}
\]
[修正] 2021/12/05 … 状態遷移図が滅茶苦茶なものになっていたため、正しいものに差し替えております。申し訳ございません。
すべてのグループが異なる状態になったため、今回の答えは元々最小状態決定性オートマトンであると言えますね。
オートマトンの状態の中で、等価な状態のグループを見つかればそれを1つまとめることができる。
等価な状態のグループは、以下のStepで発見可能。
Step1. 受理◎グループ(赤)と、非受理グループ(黒)に分ける。
Step2. それぞれのグループごとに、遷移先が異なるグループとなっている仲間はずれを探す。
Step3. 仲間はずれが見つかれば、その状態を別グループ(の色)にしてあげ、Step2に戻る。見つからなければ、Step2には戻らない。
Step4. 同じグループの状態は等価であるといえるため、ひとまとめにすることができる。
※1 最小化の際は5色くらいの色ペンを使うと、それぞれの状態がどのグループに属するかが一目瞭然です!
※2 私はグループを色で分けるときに、受理状態は暖色系の色、非受理状態は寒色系の色を使うと決めています。そうすることで、どの状態が受理状態なのかがわかりやすくなります。
(4) オートマトンの演算(差集合)
離散数学で習ったとおり、集合演算 \( L_1 - L_2 \) は、\( L_1 \) の集合から \( L_2 \) の補集合、つまり \( L_1 \cap \overline{L_2} \) を表します。
ここで、\( \overline{L(M_2)} \) の状態遷移表を確認しておきましょう。
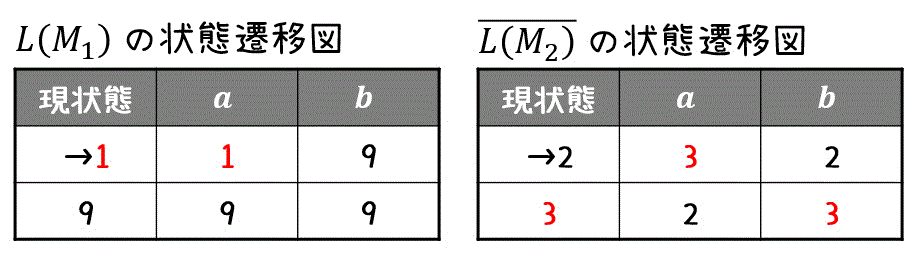
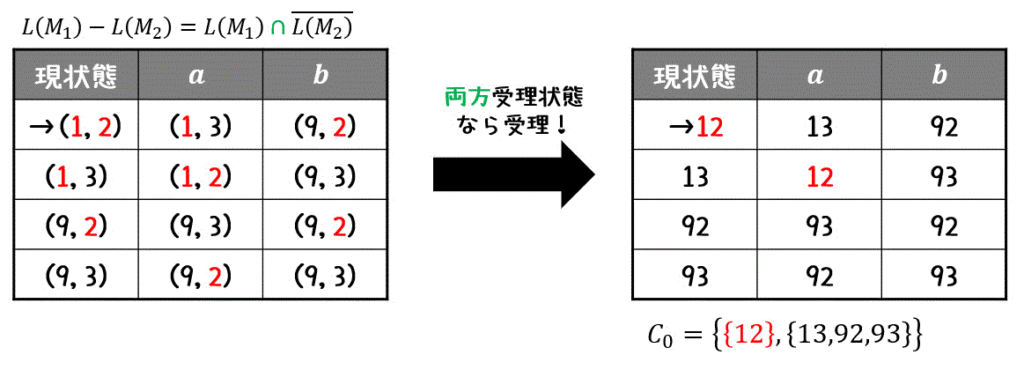
準備が出来たら、(\( L_1 \) の初期状態, \( \overline{L_2} \) の初期状態) を初期状態として、お互いの状態遷移を未知の状態遷移がなくなるまで読み取っていきます。
全部読み取れたら、受理状態を考えます。
今回は、積集合 \( \cap \) なので、2つの状態のうち両方が受理状態であれば受理状態となります。
最小化の確認
まず、状態を受理状態のグループ(12,13,93)と受理状態ではないグループ(92)にわけます。\[
C_0 = \left\{ \textcolor{red}{ \{ 12 \} }, \{ 13,92,93 \} \right\}
\]次に、同じグループ (12,92,93) 内で互いに異なるグループに遷移する状態があるか確認します。
すると今回は、12, 92, 93 のうちの13が、異なるグループに遷移することがわかりますね。
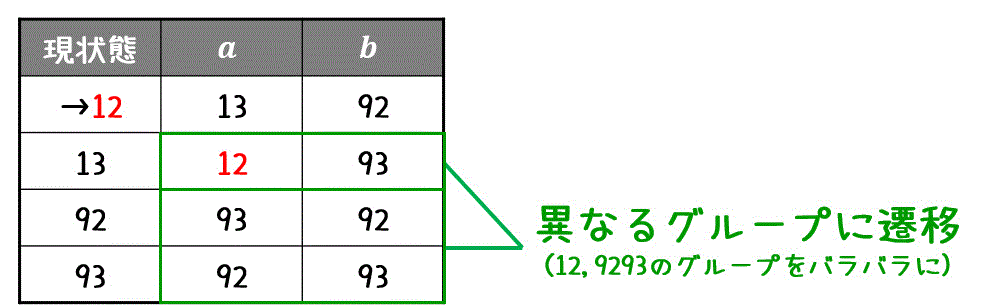
なので、13だけを分離します。\[
C_1 = \left\{ \textcolor{red}{ \{ 12 \} }, \textcolor{deepskyblue}{ \{ 13 \} } , \{ 92,93 \} \right\}
\]
1つでもグループの分離に成功した場合、再び同じグループ内なのに互いに異なるグループに遷移する状態を探します。
すると、92, 93はともに同じグループに遷移していますね。なので、これ以上分離ができません。

そのため、92, 93は等価な状態といえ、1つの状態にまとめることができます。
この同じ状態を923と名前付けて、状態遷移表を書き換えれば最小化の完了です。
和集合 \( L_1 \cup L_2 \)、積集合 \( L_1 \cap L_2 \)、差集合 \( L_1 - L_2 \) の演算の種類に関係なく、2つのオートマトンの演算の際は、2つの状態遷移表を同時に読んでいき、新たな状態遷移表を書いていく。
和集合、積集合、差集合で異なる部分は、受理状態のみである。
和集合 \( L_1 \cup L_2 \)
→ \( L_1 \), \( L_2 \) のうち、片方でも受理状態であれば受理状態となる。
積集合 \( L_1 \cap L_2 \)
→ \( L_1 \), \( L_2 \) のうち、両方とも受理状態であれば受理状態となる。
差集合 \( L_1 - L_2 = L_1 \cap \overline{L_2} \)
→ \( L_1 \), \( \overline{L_2} \) のうち、両方とも受理状態であれば受理状態となる。
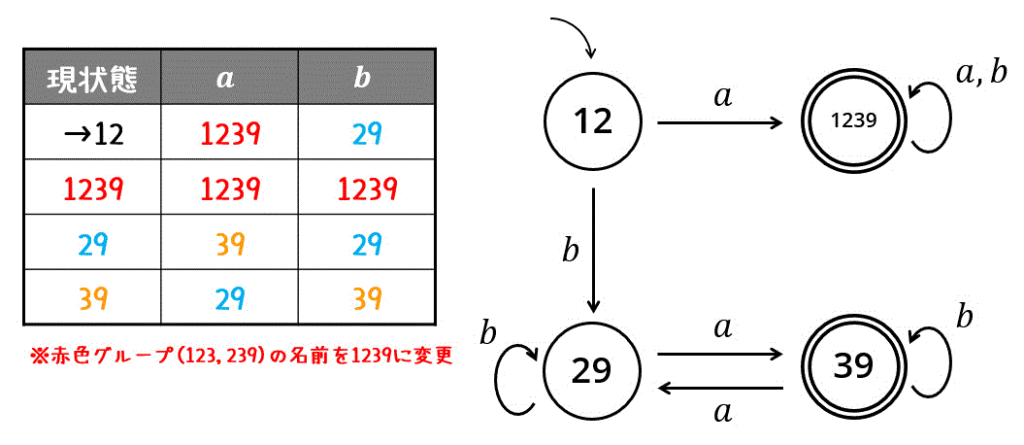
(5) オートマトンの連接
オートマトンの連接についての詳しい記事はこちら↓↓↓
2つのオートマトンを連接する場合、以下の3つの処理を同時に行うことで、連接 \( L (M_1) \cdot L(M_2 )\) の非決定性有限オートマトンが作成できます。
- 連接元の受理状態に向いている矢印を探し、それを連接先の初期状態にも向ける
- 連接元の受理状態を非受理状態へ
- 連接元のオートマトンが空文字を受理しない場合は連接先の初期状態を削除
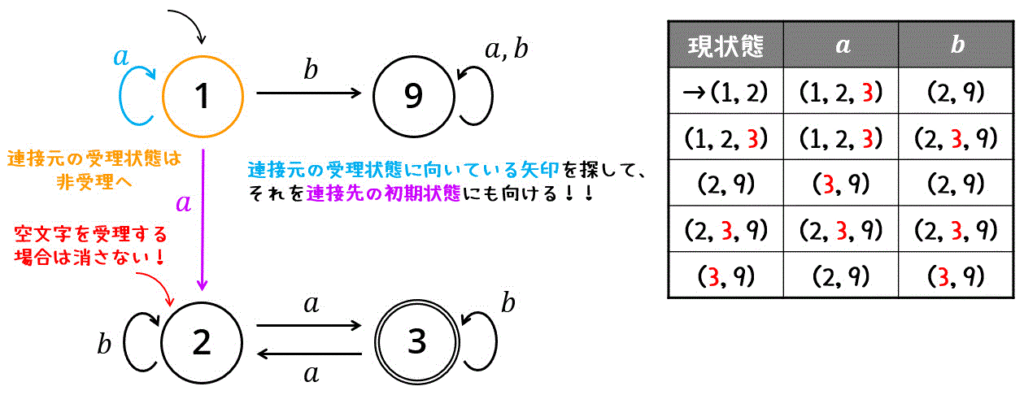
次に、作成した非決定性オートマトンを決定性オートマトンに変換します。

最小化の確認
作成したオートマトンが最小状態かどうかを確認します。
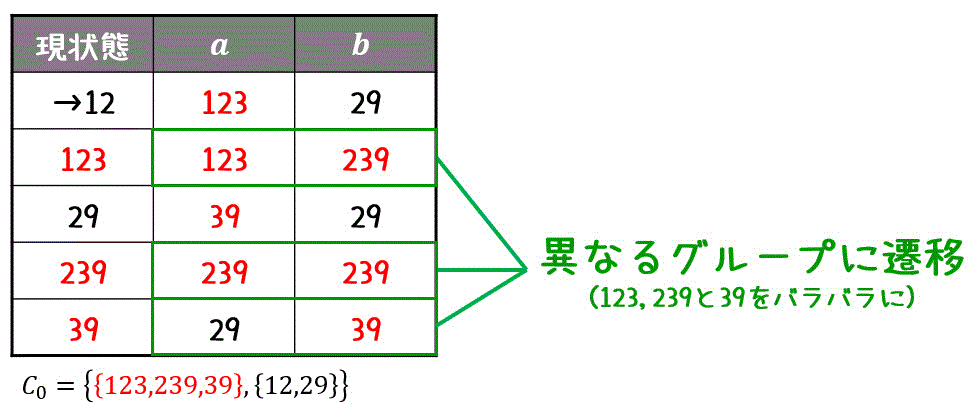
まず、受理状態 (123, 239, 39) とそれ以外 (12,29) のグループにわけます。\[
C_0 = \left\{ \textcolor{red}{ \{ 123, 239, 39 \} }, \{ 12, 29\} \right\}
\]次に、同じグループ (123, 239, 39), (12,29) 内で互いに異なるグループに遷移する状態があるか確認します。
すると、今回は(123, 239, 39)のグループのうち、39だけが遷移先が異なるため仲間はずれです。
なので39を分離しましょう。\[
C_1 = \left\{ \textcolor{red}{ \{ 123, 239 \} }, \textcolor{orange}{ \{ 39 \} } , \{ 12, 29\} \right\}
\]
引き続き、同じグループ内で遷移先が異なる仲間はずれを探します。すると、黒グループ(12, 29)の遷移先がバラバラですね。
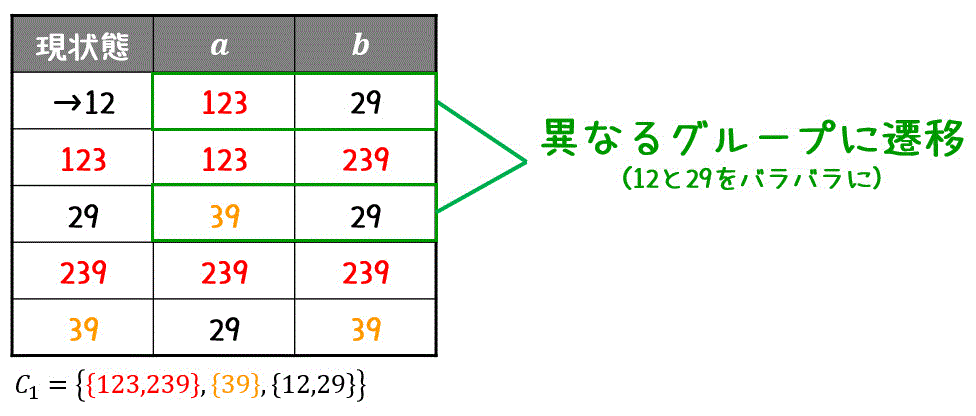
なので、12, 29はバラバラなグループとなります。\[
C_2 = \left\{ \textcolor{red}{ \{ 123, 239 \} }, \textcolor{orange}{ \{ 39 \} } , \textcolor{deepskyblue}{ \{ 29 \} }, \{ 12\} \right\}
\]
(1つでもグループをバラバラに出来たため、) 再びグループ分離出来ないか探します。
しかし、123, 239はともに同じグループに遷移することと、残りのグループはすでにバラバラになっているため、これ以上グループ分離をすることができません。

そのため、赤色グループ(123, 239)はひとまとめにすることができます。
このグループに1239と名付け、状態遷移表から状態遷移図を書けばOKです。
スポンサードリンク
2. 正規言語の記述・マイヒルネロードの定理
\( \Sigma = \{ a, b \} \) とする。次の言語 \( L_1 \), \( L_2 \) は正規言語(正則)か正規言語でないか答えなさい。
さらに正規言語であれば、与えられた言語を認識する最簡形の完全決定性有限オートマトン(DFA)の状態遷移図を、正規言語でなければ正規言語でないことをマイヒルネロード(Myhill-Nerode)の定理を用いて示しなさい。ただし、\( i, j \) は0以上の整数とする。
(1) \[
L_1 = \left\{ a^i a^i b^j \middle| \ i \geqq 0, j \geqq 0 \right\}
\]
(2) \[
L_2 = \left\{ a^i b^j a^i \middle| \ i \geqq 0, j \geqq 0 \right\}
\]
(1) 結果に3点、状態遷移図に7点。
→ 図は正しいが、最小状態の決定性オートマトンでなければ-3点(状態遷移図に4点)
→ 非決定性オートマトンしかかけていなければ-5点(状態遷移図に2点
(2) 結果に3点、証明に7点。
(1)
正規言語である。[3点]
ポイントは、\( a^i a^i = a^{2i} \) となる点です。これを使うと \( a^i a^i b^j = a^{2i} b^j \) となりますね。
ここで、\( a^{2i} \)(\( a \) だけが偶数個ある文字列)を受理する有限オートマトンは、「偶数状態」、「奇数状態」、「a以外の文字列が来た状態」の3状態を用いて書くことができますね。(つまり正規言語)
また、(\( b^j \)(\( b \) だけの文字列)を受理する有限オートマトンも「bだけの文字列来ている状態」、「b以外の文字が来た状態」の2状態で表すことができます。 (つまり正規言語)
ここで、正規言語同士の言語を連接させても正規言語になるため、\( a^{2i} b^{j} \) も正規言語となることがわかりますね。
なので、どんな有限オートマトンをかけば、条件にあう言語だけを認識することができるかを考えていきましょう。
解き方1 いきなり決定性オートマトンを書いてしまう [慣れている人向け]
慣れている人であれば、いきなり決定性オートマトンを書いてしまいましょう。
今回の場合、
- \( a \) が偶数回続いている状態
- \( a \) が偶数回続いた後に \( b \) が続いている状態
- 条件に反する文字が来ている状態
の3つに分解してから考えると書きやすいかと思います。
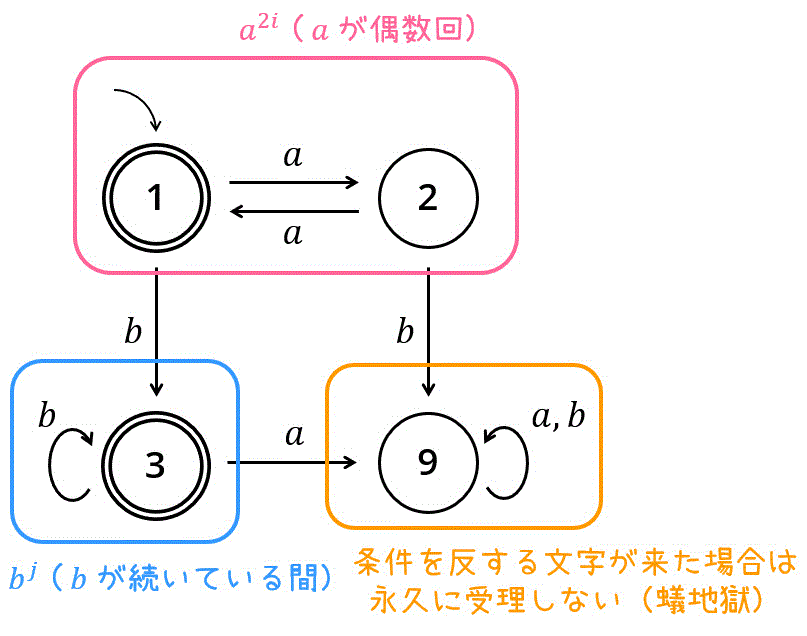
※ \( i \geqq 0 \), \( j \geqq 0 \) なので、空文字の状態や、\( a \) だけが偶数個ある文字列も認識する点に注意です。
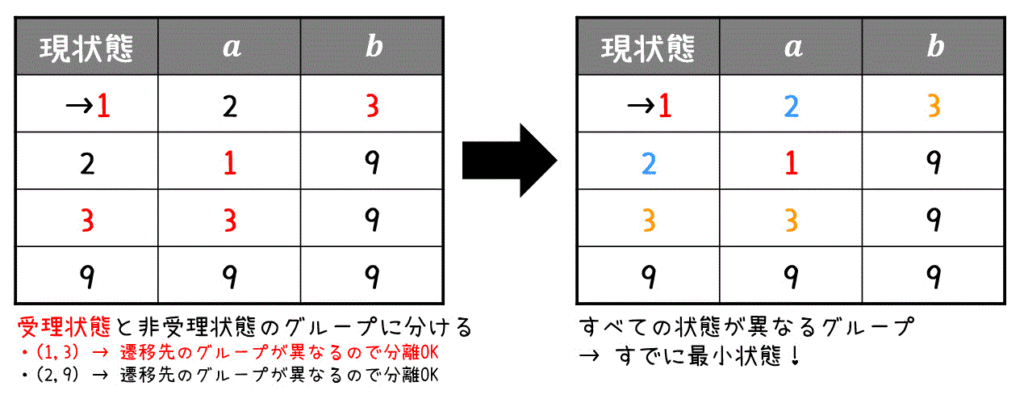
実際に書いた有限オートマトンが最小化状態か確認すると、下のように全部の状態が異なるグループになるため、本当に最小化状態であることを確認できます。
解き方2 非決定性オートマトンを書いてから決定性に変換する
慣れていない人は、直感的に書ける非決定性オートマトンを書いてから、それを決定性オートマトンに書き換える方法をおすすめします。
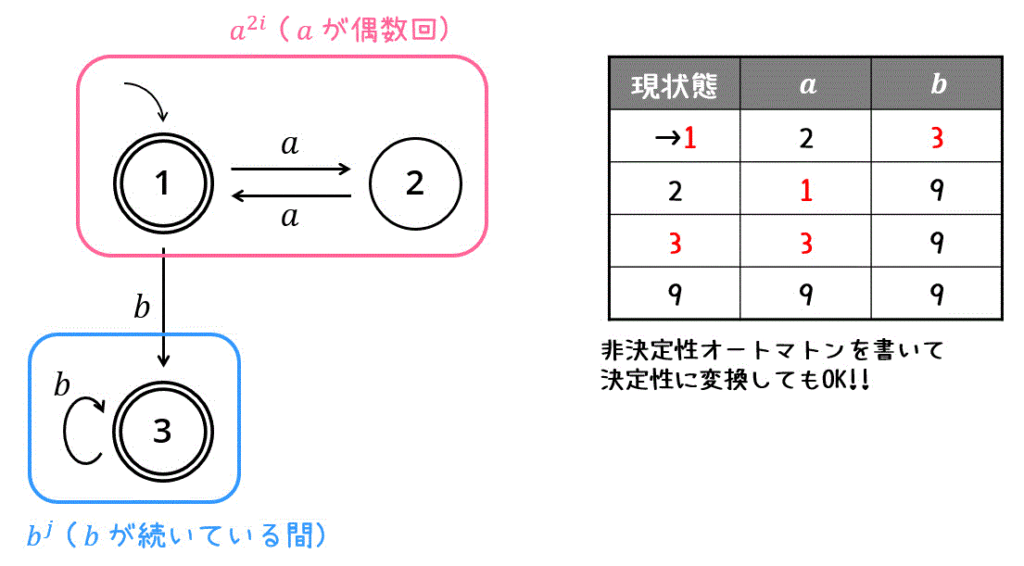
状態遷移図を書いたあとは、決定性オートマトンを記述するだけです。

解き方3 2つの非決定性オートマトンを連接する
最初に、\[
L_3 = \left\{ a^i a^i b^j \middle| \ i \geqq 0 \right\}
\]\[
L_4 = \left\{ b^j \middle| \ j \geqq 0 \right\}
\]の2つに分解し、それを連接 \( L_3 \cdot L_4 \) して記述する方法もあります。

連接の処理をすると、下のような非決定性オートマトンが出来るので、それを決定性オートマトンに変換してください。
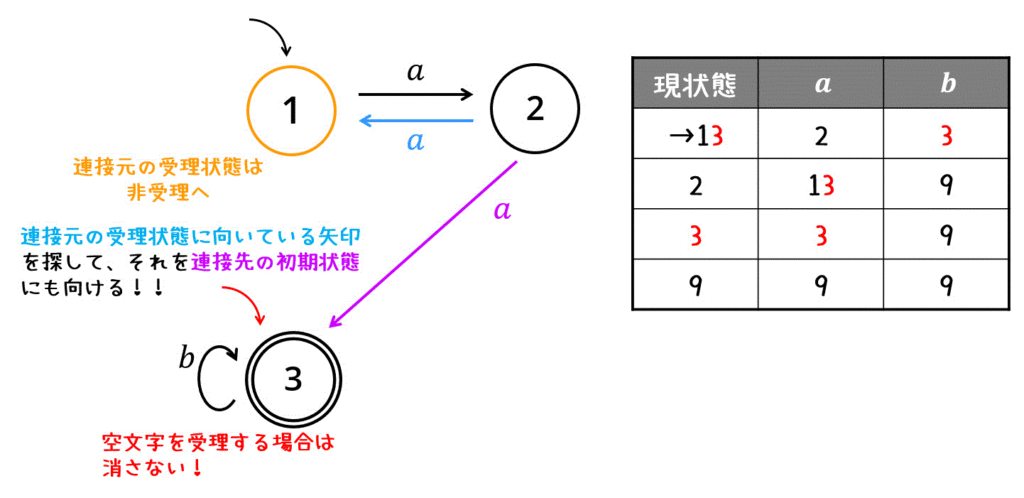
状態13を状態1に書き換えると、解き方1、解き方2と全く同じ状態遷移図が完成します。

(2)
正規言語でない。[3点]
\( \textcolor{red}{a^i} b^j \textcolor{blue}{a^i} \)と、\( \textcolor{red}{a^i} \) と \( \textcolor{blue}{a^i} \) の間に \( b^j \) が入っていますね。
そのため、(無限に来るかもしれない)\( a \) の個数を記憶してあげないと、
[証明]\( L_2 \) が正規言語であると仮定する。すると、 関係 \( R_{L_2} \) は右不変かつ有限指数の同値関係 \( R_{L_2} \) となる。
(i) \( R_{L_2} \) は有限指数なので、\( a^i R_{L_2} a^j \) を満たす自然数(ただし \( i \not = j \) )が存在する[2]\( i > j \) や \( i < j \) でもOKです。。
(ii) \( R_{L_2} \) は右不変なので、 \( a^i \textcolor{red}{b^{j} a^{i}} R_{L_2} a^j \textcolor{red}{b^{j} a^{i}} \) が成り立つ。
ここで、\( a^i b^j a^i \in L_2 \) なので、\( R_{L_2} \) の定義より \( a^j b^j a^i \) となる。しかし、これは言語 \( L_2 \) の定義に矛盾。
よって、\( L_2 \) は正規言語ではないことが示され、題意は満たされた。
ある言語 \( L \) が正規言語(正則)でないことを示すには、\( L \) が正規言語であることを仮定して、以下の流れて背理法で示す。
Step1. \( L \) が正規言語であるならば、右不変かつ有限指数の同値関係 \( R_{L} \) が成立する。
Step2. 有限指数なので \( x^i R_{L} x^j \) を満たす自然数 \( i \), \( j \) が成立する。(ただし \( i \not = j \) or \( i > j \) or \( i < j \) )
※ \( x \) は任意の文字列 ( \( x \in \Sigma^* \) ) を入れることが可能。だいたい \( a^i R_{L} a^j \) や \( b^i R_{L} b^j \) が入る。
Step3. 右不変なので \( x^i \textcolor{red}{y} R_{L} x^j \textcolor{red}{y} \) が成り立つ。
※ \( y \) は任意の文字列 ( \( y \in \Sigma^* \) ) を入れることが可能。
Step4. ここで題意より、\( x^i y \in L \) が成立するので、\( R_{L} \) の定義より \( x^j y \in L \) となるが、これは題意に矛盾。
( \( x^i y \) を成立させた上で \( x^j y \) を常に成立させないようにする)
Step5. よって、\( L \) は正規言語ではないことが示され、題意は満たされた。
スポンサードリンク
3. 正規言語の判定
\( \Sigma = \{ a, b \} \) とする。次の(1)~(10)それぞれにある[X], [Y]の文章について、その正誤の組み合わせとして正しいものを下の選択肢①~④から1つ選びなさい。ただし、\( i \), \( j \), \( k \) は自然数(1以上の整数)、\( x^R \) は語 \( x \) の反転とし、言語は \( \Sigma \) 上の言語を表す。
[Y] 言語 \( \{ \ a^i b^i \ \mid \ i \geqq 1000 \} \) は正規言語である。
- [X] 正 [Y] 正
- [X] 正 [Y] 誤
- [X] 誤 [Y] 正
- [X] 誤 [Y] 誤
解答: 2 [3点] [X] \( a \) が来たあとに同じ回数の \( b \) が来るかどうかを判定するために、\( a \) の個数を記憶する必要があります。しかし、今回は \( i \leqq 1000 \) なので、\( a \) が1001個来た瞬間に非受理が確定する。1000個(有限)の記憶で判定できるため、正規言語である。(正しい)
[Y] [X]と異なり、1001個以上のときに同じ回数の \( b \) が来ているかを判定するために、1001以上(無限)の \( a \) の個数を記憶する必要がある。よって、正規言語ではない。(誤り)有限オートマトンを書くことができる言語は、正規言語である。
つまり、有限の記憶で受理するかを判定することができれば正規言語といえる。
[Y] 言語 \( \{ \ a^i b^j \ \mid \ i \geqq 1000, j \geqq 1000 \} \) は正規言語である。
- [X] 正 [Y] 正
- [X] 正 [Y] 誤
- [X] 誤 [Y] 正
- [X] 誤 [Y] 誤
解答:1 [3点]
\( a^i b^j \) は、\[ \{ \ a^i \ \mid \ i \leqq 1000 \} \]\[ \{ b^j \ \mid \ j \leqq 1000 \} \]の連接である。
[X] \( a^i \) は \( a \) の個数が0~999、1,000以上の1,001状態(有限)の記憶で判定することができる。 \( b^i \) も \( b \) の個数が0~999、1,000以上の1,001状態(有限)の記憶で判定することができる。 よって、この連接も正規言語である。[Y] 条件が1,000以上なので、無限の記憶が必要そうに見えますが、\( a^i \) も \( b^j \) も文字数が1,000以上のときは \( a \)(もしくは \( b \))だけの文字列かどうかを判定し続ければOKなため、1,001個以上のときの状態は記憶させる必要がない。よって、有限の記憶による判定が可能なので[Y]も正規言語である。
[Y] 言語 \( \{ \ x \ \mid \ x \in \Sigma^*, |x|_a - |x|_b \leqq 334 \} \) は正規言語である。
- [X] 正 [Y] 正
- [X] 正 [Y] 誤
- [X] 誤 [Y] 正
- [X] 誤 [Y] 誤
解答: 2 [3点]
[X] \( |x|_a + |x|_b \) は、\( x \) の \( a \) と \( b \)の文字数、つまり \( x \) の文字列の長さを表す。今回は \( \geqq 334 \) なので、文字列0文字~333文字の状態と、334文字以上の状態[3]334文字以上のときは、必ず受理するため文字数を記憶する必要はないだけで判定が可能。よって、有限の記憶による判定が可能なため、正規言語といえる。 [Y] \( |x|_a - |x|_b \leqq 334 \) のマイナスがミソ。無限に続く文字列の中から、\( a \) の文字数と \( b \) の文字数をカウントし、\( |x|_a - |x|_b \) が334以下になっているかを確認する必要がある。そのため、有限の記憶では判定できないため、正規言語ではない。[Y] 言語 \( \{ \ x \ \mid \ x \in \Sigma^*, |x|_a \times |x|_b = 2k \} \) は正規言語である。
- [X] 正 [Y] 正
- [X] 正 [Y] 誤
- [X] 誤 [Y] 正
- [X] 誤 [Y] 誤
解答: 1 [3点]
[X] \( |x|_a + |x|_b = 2k \) ということは、「\( a \) の文字列が偶数 and \( b \) の文字列が偶数」もしくは 「\( b \) の文字列が奇数 and \( b \) の文字列が奇数」であればOK。ここで、どんなに無限に続く文字列であろうが、 文字列の長さは「偶数」か「奇数」かの2通りですね。そのため、「\( a \) の偶奇(2通り) ×\( b \) の偶奇(2通り)=4通り」と、有限の状態数による記憶で判定が可能。よって、正規言語である。 [Y] \( |x|_a \times |x|_b = 2k \) ということは、「\( a \) の文字列が奇数 and \( b \) の文字列が奇数」以外であればOK。[X]と同じく、文字列の長さは「偶数」か「奇数」かの2通りですね。そのため、「\( a \) の偶奇(2通り) ×\( b \) の偶奇(2通り)=4通り」と、有限の状態数による記憶で判定が可能。よって、正規言語である。[Y] 言語 \( \{ \ xbx \ \mid \ x \in \Sigma^* \} \) は正規言語である。
- [X] 正 [Y] 正
- [X] 正 [Y] 誤
- [X] 誤 [Y] 正
- [X] 誤 [Y] 誤
解答: 4 [3点]
[X] \( x = x^R \) ということは、\( x \) の文字列を反転させても同じ文字列(回文)かどうかの判定が必要ですね。突然ですが皆さんに質問ですね。「たけやぶやけた」は回文ですか?
答えは、回文なのですが、回文かどうかを判定するときに皆さんは後ろから実際に後ろから文字列を読んで確認していきましたね。
オートマトンでも同じように、回文かどうかを判定する際には、無限に続く文字列の文字を記憶してから、後ろから読んでも一致するかどうかを確認する必要があります。よって、正規言語ではありません。
★ [X]が正規言語とはならない簡単な証明 ★
有限指数: \( a^i R_{L} a^j \) (ただし \( i \not = j \)
右不変: \( a^i \textcolor{red}{b a^i} R_{L} a^j \textcolor{red}{b a^j} \)
ここで、\( a^i b a^i \in L \) だから \( R_{L} \) の定義より \( a^i b a^j \) だが、大嘘。
★ [Y]が正規言語とはならない簡単な証明 ★
有限指数: \( a^i R_{L} a^j \) (ただし \( i \not = j \)
右不変: \( a^i \textcolor{red}{b a^i} R_{L} \textcolor{red}{b a^j} \)
ここで、\( a^i b a^i \in L \) だから \( R_{L} \) の定義より \( a^i b a^j \) だが、大嘘。
[Y] 言語 \( \{ \ x a^i b^i y \ \mid \ x \in \Sigma^* \} \) は正規言語である。
- [X] 正 [Y] 正
- [X] 正 [Y] 誤
- [X] 誤 [Y] 正
- [X] 誤 [Y] 誤
解答: 3 [3点]
[X] \( x a^i b^i \) なので、無限に続く \( a^i \) の \( i \) の数を記憶する必要がある。そのため、正規言語ではない。★ [X]が正規言語とはならない簡単な証明 ★
有限指数: \( a^i R_{L} a^j \) (ただし \( i > j \)[4]ここで \( i \not = j \) にしてしまうと、右不変で \( a^j b^i \) としたときに \( aaaabbb \) などが受理してしまう。( \( i = 3, x = a \) で成立))
右不変: \( a^i \textcolor{red}{b^i} R_{L} a^j \textcolor{red}{b^i} \)
ここで、\( a^i b^i\in L \) だから \( R_{L} \) の定義より \( a^j b^i \) だが、大嘘。
[Y] 任意の言語 \( L \) に対し、\( L_1 - L_2 \) が正規言語ならば、\( L_1 \cap L_2 \) も正期言語である。
- [X] 正 [Y] 正
- [X] 正 [Y] 誤
- [X] 誤 [Y] 正
- [X] 誤 [Y] 誤
解答: 2 [3点]
[X] \( \Sigma^* - L = \overline{L} \)(\( L \) の補集合)を表します。ここで、ある言語 \( L \) の補集合は、完全決定性オートマトンの受理◎と非受理○を入れ替えるだけでしたね。なので、\( \overline{L} \) が正規言語であれば当然 \( \overline{\overline{L}} \) も正規言語となります。よって正しい。ある言語 \( L \) が正規言語であるとする。
すると、\( L \) の補集合 \( \overline{L} \) も正規言語である。
また、\( \overline{L} \) の補集合 \( \overline{\overline{L}} = L \) も正規言語となる。
ある言語 \( L_1 \)、\( L_2 \) がともに正規言語であるとする。
すると、\( L_1 \cup L_2 \)、\( L_1 \cap L_2 \)、\( L_1 - L_2 \)、\( L_1 \cdot L_2 \) はすべて正規言語となる。
※ ただし逆(例: \( L_1 \cup L_2 \) ならば \( L_1 \)、\( L_2 \) は正規言語)は成り立つとは限らないため注意
反例を探す際には、極端な例を考えると簡単に見つかる。
例えば、「どんな文字列でも認識する言語」、「どんな文字列でも認識しない言語」を考えると良い。(両方とも正規言語です)
[Y] 任意の言語 \( L \) に対し、\( L_1 \), \( L_2 \) が両方とも正規言語ではないならば、\( L_1 \cup L_2 \) は正規言語ではない。
- [X] 正 [Y] 正
- [X] 正 [Y] 誤
- [X] 誤 [Y] 正
- [X] 誤 [Y] 誤
解答: 2 [3点]
[X] 命題の対偶をとると「\( L_1 \), \( L_2 \) が両方とも正規言語ならば \( L_1 \cup L_2 \) も正規言語である」となり、定義と一致する。よって正しい。 [Y] 例えば、\( L_1 \) が正規言語でない言語、\( L_2 \) を \( L_1 \) の補集合とする。すると、\( L_1 \cup L_2 = L_1 \cup \overline{L_1} = \Sigma^* \) となり、正規言語となり、反例となる。よって誤り。最後に、今回は出題していませんが、念の為「正規言語とスター閉包の性質」についても確認しましょう。
ある言語 \( L \) が正規言語であるとする。
すると、\( L \) のスター閉包 \( L^* \) も正規言語である。
(逆に \( L^* \) が正規言語だからと言って、\( L \) が正規言語であるとは限らないため注意)
[Y] 任意の言語 \( L \) に対し、\( L \) が正規言語ならば、\( L \) を生成する文脈自由文法が必ず存在する。
- [X] 正 [Y] 正
- [X] 正 [Y] 誤
- [X] 誤 [Y] 正
- [X] 誤 [Y] 誤
解答: 3 [3点] [X] 文脈自由文法で生成できる言語は、有限オートマトンで表せる言語(正規言語)よりも遥かに大きい。よって誤り。
[Y] 正規言語 \( L \) で表せる言語は、正規文法(文脈自由文法よりも縛りが厳しい文法)で表すことができる。当然文脈自由文法で表すことができるため、正しい。正規言語な言語は、正規文法と呼ばれる文脈自由文法より縛りが厳しい文法で表すことができる。そのため、正規言語である言語は必ず文脈自由文法で表すことができる。
一方、文脈自由文法は正規言語よりも縛りがゆるいため、文脈自由文法な言語は必ずしも正規言語であるとは限らない。
[Y] 任意の文脈自由文法で生成できる言語 \( L \) に対し、チョムスキー標準形に変換できない言語 \( L \) が存在する。
- [X] 正 [Y] 正
- [X] 正 [Y] 誤
- [X] 誤 [Y] 誤
- [X] 正 [Y] 誤
解答: 4 [3点] [X] \( L_1 = \Sigma^* \)(なんでも受理する言語)、\( L_2 \) を文脈自由文法で生成できる正規言語ではない言語とする。すると、\( L_1 \cap L_2 = L_2 \) となるため、これが反例となる。誤り。
[Y] 文脈自由文法で生成できる言語 \( L \) はどんな言語であろうと、必ずチョムスキー標準形に変換することができる。よって誤り。正規言語の判定をもっと練習したい人の記事はこちら ↓↓↓
問題4. 文脈自由文法
次の形式文法 \( G_1 \), \( G_2 \) がある。次の(1)~(7)の問いに答えなさい。ただし、(2), (3)は個数を回答欄に入力すること。\[
G_1 = \left( \{ S_1 , A \} , \{ a, b \}, \{ S_1 \to aA, A \to a, A \to aA \}, S_1 \right)
\]\[
G_2 = \left( \{ S_2 , A, B \} , \{ a, b \}, \{ S_2 \to AB, A \to a, B \to b, A \to aAB \}, S_2 \right)
\]
(1) 次の(i)~(iii)それぞれにある[X], [Y]の文章について、その正誤の組み合わせとして正しいものを下の選択肢1~4から1つ選びなさい。
(i)
[X] \( G_1 \) は正規文法である。
[Y] \( G_1 \) はグライバッハ標準形である。
(ii)
[X] \( G_2 \) は文脈自由文法である。
[Y] \( G_2 \) はチョムスキー標準形である。
(iii)
[X] \( G_1 \) を認識するプッシュダウンオートマトンが存在する。
[Y] \( G_2 \) を認識するプッシュダウンオートマトンが存在する。
- [X] 正 [Y] 正
- [X] 正 [Y] 誤
- [X] 誤 [Y] 誤
- [X] 正 [Y] 誤
(2) \( G_1 \) が生成する言語 \( L(G_1 ) \) の要素のうち、長さが6以下のものは何個あるか。
(3) \( G_2 \) が生成する言語 \( L(G_2 ) \) の要素のうち、長さが6以下のものは何個あるか。
(4) \( G_1 \) が生成する言語 \( L(G_1) \) はどれか。下の1~6から1つ選びなさい。
- \( \{ \ x \ \mid \ x \in \Sigma^* , |x|_a \geqq 0 \} \)
- \( \{ \ x \ \mid \ x \in \Sigma^* , |x|_a \geqq 1 \} \)
- \( \{ \ x \ \mid \ x \in \Sigma^* , |x|_a \geqq 2 \} \)
- \( \{ \ a^i \ \mid \ i \geqq 0 \} \)
- \( \{ \ a^i \ \mid \ i \geqq 1 \} \)
- \( \{ \ a^i \ \mid \ i \geqq 2 \} \)
(5) \( G_2 \) が生成する言語 \( L(G_2) \) はどれか。下の1~8から1つ選びなさい。
- \( \{ \ a^i b^j \ \mid \ i = j \} \)
- \( \{ \ a^i b^j \ \mid \ i \not = j \} \)
- \( \{ \ a^i b^j \ \mid \ i > j \} \)
- \( \{ \ a^i b^j \ \mid \ i < j \} \)
- \( \{ \ a^i b^j \ \mid \ i+1 = j \} \)
- \( \{ \ a^i b^j \ \mid \ i+1 \not = j \} \)
- \( \{ \ a^i b^j \ \mid \ i+1 > j \} \)
- \( \{ \ a^i b^j \ \mid \ i+1 < j \} \)
(6) \( L_3 = L(G_1) \cup L(G_2) \)、\( L_4 = L(G_1) \cap L(G_2) \) とする。\( L_3 \), \( L_4 \) は正規言語か。正しいものを1~4から選びなさい。
- \( L_3 \) も \( L_4 \) も正規言語である。
- \( L_3 \) は正規言語であるが、\( L_4 \) も正規言語でない。
- \( L_3 \) は正規言語でないが、\( L_4 \) も正規言語である。
- \( L_3 \) も \( L_4 \) も正規言語でない。
(7) (6)と同じく \( L_3 = L(G_1) \cup L(G_2) \)、\( L_4 = L(G_1) \cap L(G_2) \) とする。\( L_3 \), \( L_4 \) は文脈自由文法で表現することができるか。正しいものを1~4から選びなさい。
- \( L_3 \) も \( L_4 \) も可能。
- \( L_3 \) は可能だが、\( L_4 \) は不可能。
- \( L_3 \) は不可能だが、\( L_4 \) は可能。
- \( L_3 \) も \( L_4 \) も不可能。
文脈自由文法に関する記事はこちら↓↓↓
(1)
★解答★
(i) 1 [1点], (ii) 2 [1点], (iii) 1 [1点]
(i) 正規文法と、グライバッハ標準形の確認をしましょう。
[X], [Y]とも条件にあっているため、答えは1。次の(1)もしくは(2)の生成規則だけで構成されている文脈自由文法を、正規文法と呼ぶ。
(1) [右正規文法]
- \( A \to a \)(非終端記号 → 終端記号1文字)
- \( A \to aB \) (非終端記号 → 終端記号+非終端記号)
- \( A \to \varepsilon \)(非終端記号→空文字)
(2) [左正規文法]
- \( A \to a \)(非終端記号 → 終端記号1文字)
- \( A \to Ba \) (非終端記号 → 非終端記号+終端記号)
- \( A \to \varepsilon \)(非終端記号→空文字)
※1 \( A \to aB \) と \( A \to Ba \) を同時に使ってしまうと正規文法とはいえない。
※2 正規文法で表せる言語は、必ず有限オートマトンでの表現が可能。(正規言語である)
生成規則が以下のものだけの文脈自由文法をグライバッハ標準形と呼ぶ。
- \( A \to aX \)(非終端記号 → 終端記号1文字+非終端記号0文字以上)
- \( S \to \varepsilon \) (開始記号 → 空文字)
※ \( X \) には、下のように非終端記号が2つ以上入っていたり、空文字でもOKである。\[
A \to aBCD, \ \ \ A \to b
\]
※ 任意の文脈自由文法は、グライバッハ標準形への変換が可能である。
(ii) [X]の文脈自由文法は当然正しいですが、[Y]のチョムスキー標準形には要注意です。
確かにチョムスキー標準形特有の \( S_2 \to AB \) はありますが、チョムスキー標準形に反する生成規則 \( A \to aAB \) が含まれているため、チョムスキー標準形とは言えません。
よって、[X]は正しく、[Y]は誤りなので2。
生成規則が以下のものだけの文脈自由文法をチョムスキー標準形と呼ぶ。
- \( A \to a \)(非終端記号 → 終端記号1文字)
- \( A \to BC \) (非終端記号 → 非終端記号2文字)
- \( S \to \varepsilon \)(開始記号 → 空文字)
※ 任意の文脈自由文法は、チョムスキー標準形への変換が可能である。
※ 終端記号への変換は、単独1文字 \( A \to a \) でしか登場しないのもポイント。
(iii) 文脈自由文法で表せる文法は、必ずプッシュダウンオートマトンで表すことができます。なので、[X], [Y] とも正しく、答えは1。
文脈自由文法で表せる言語は、必ずプッシュダウンオートマトンで表すことができる。
また、プッシュダウンオートマトンで表せる言語は、必ず文脈自由文法で表せる。
(2) [2点]
下のように、樹形図を書いて探していきましょう。
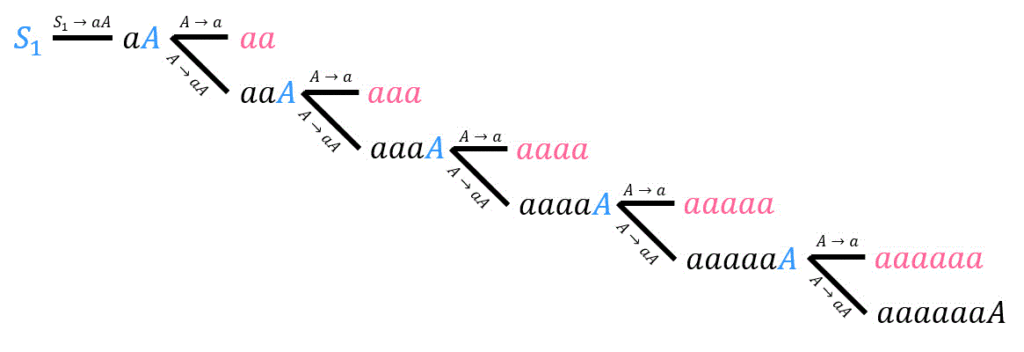
よって、\( aa \), \( aaa \), \( aaaa \), \( aaaaa \), \( aaaaaa \) の5個なので、答えは5。
(3) [3点]
樹形図を書いて探していきましょう。
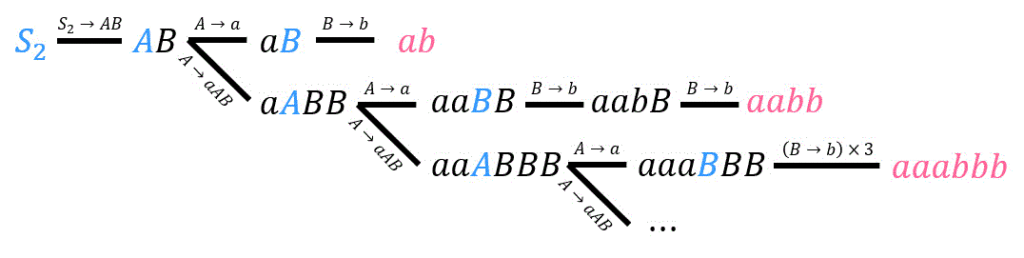
(4) [3点]
(2)で列挙した結果から、\( a \) だけが2文字以上続く文字列を認識する言語でありそうなことがわかりますね。その感覚は正しいです。よって、答えは6ですね。
※ 3とひっかからないように注意!
(5) [3点]
(3)で列挙した結果から、\( a \) の連続の後に同じ文字だけ \( b \) が続く言語であることがわかりますね。よって、答えは1です。
(6) [4点]
\( L_3 = L(G_1) \cup L(G_2) \) を考えると、次の1, 2のうちどちらかを満たせば受理する言語であることがわかりますね。
- \( a \) だけの文字列
- (1文字以上の) \( a \) の連続の後に、同じ文字だけ \( b \) が続く
しかし、2を実現するためには無限に続く文字列に対して、(無限かもしれない)\( a \) の文字数を記憶する必要がありますね。なので、\( L_3 \) は正規言語ではありません。
一方、\( L_4 = L(G_1) \cap L(G_2) \) は、上で出てきた1, 2を両方満たして初めて受理する言語ですね。しかし、\( a \) だけの文字列しか受理しない1と、\( b \) が最低1文字は含まれる2を両方とも満たす文字列は1つもありません。
そのため、\( L_3 \cap L_4 = \cap \) となりますね。何も受理しない言語は正規言語なので、\( L_4 \) は正規言語となります。
よって、\( L_3 \) は正規言語ではなく、\( L_4 \) は正規言語なため、答えは3。
(7) [2点]
まず、\( L_4 \) は正規言語なため、当然文脈自由文法で表すことができます。
つぎに、\( L_3 \) ですが、例えば次のような文脈自由文法\[
G_3 = \left( \{ S_3 , A,B \} , \{ a, b \}, \{ S_3 \to A, S_3 \to B, A \to a, A \to aA, B \to \varepsilon, B \to a B b \}, S_3 \right)
\]とすることで、\( L_3 \) と同等な文脈自由文法となります。
よって、\( L_3 \), \( L_4 \) ともに文脈自由文法となるため、答えは1。
関連広告・スポンサードリンク