うさぎ塾　微積分総復習　Part3　積分編

こんにちは、ももやまです。

「うさぎ塾　微積分総復習」では、数3の中で特に重要な

• 極限（Part1）
• 微分（Part2）
• 積分（Part3）

の総復習問題を用意しています。

最終回であるPart3は、積分に関する総復習問題を厳選して用意しました。

• 数3で極限を一通り習った人
• 模試・試験・入試前の直前演習
• 大学で解析学を学ぶ前のリハビリ

などにご使用ください。

なお、問題のPDFはこちらからダウンロードできます。

解答は、この記事の後ろにまとめて用意しています。

※ \( \log x \) は、\( \log_{e} x \)（底が \( e \) の対数、自然対数）を表します。

スポンサードリンク

問題１．不定積分総復習

つぎの(1)～(7)の不定積分を計算しなさい。（配点　35）

(1)\[
\int (x-1)(x^2 + x + 1) \ dx
\]

(2)\[
\int \frac{1}{(2x+1)^2} \ dx
\]

(3)\[
\int \sin x \cos x \ dx
\]

(4) \[
\int 3^x \ dx
\]

(5) \[
\int x \log x \ dx
\]

(6)\[
\int x^2 e^x \ dx
\]

(7)\[
\int \frac{1}{3x+34} \ dx
\]

スポンサードリンク

解答１．

[5点×7=35点]

(1)

まず、式を展開しましょう。\[\begin{align*}
(x-1)(x^2 + x + 1) & = x^3 + x^2 + x - x^2 - x - 1
\\ & = x^3 - 1
\end{align*} \]なので、積分定数 \( C \) を用いて\[\begin{align*}
\int (x-1)(x^2 + x + 1) \ dx & = \int x^3 - 1 \ dx
\\ & = \frac{1}{4} x^4 - x + C
\end{align*}\]となる。

この公式は、数2で習う\[
\int x^4 \ dx = \frac{1}{5} x^5 + C
\]のような多項式・整式だけでなく、\[\begin{align*}
\int \frac{1}{x^3} \ dx & = \int \ x^{-3} \ dx
\\ & = - \frac{1}{2} x^{-2} + C
\\ & = - \frac{1}{2x^2} + C
\end{align*} \]や、\[\begin{align*}
\int \sqrt{x} \ dx & = x^{ \frac{1}{2} } \ dx
\\ & = \frac{2}{3} x^{ \frac{3}{2} }
\\ & = \frac{2}{3} x \sqrt{x}
\end{align*} \]のように、分数やルートの式でも使うこともできます！

ただし、\( n = -1 \) のとき、つまり\[
\int x^{-1} \ dx = \int \frac{1}{x} \ dx
\]には注意が必要です。

そのまま公式に当てはまめると、\[
\int x^{-1} \ dx = x^0 \ dx + C = C
\]とわけがわからないことになってしまいます。

ところで、前回の微分編で\[
\left( \log |x| \right)' = \frac{1}{x}
\]となることを説明しましたね。

積分は、微分の逆の操作をしているので、\( n = -1 \) のときは、\[\begin{align*}
\int x^{-1} \ dx & = \int \frac{1}{x} \ dx
\\ & = \log |x| + C
\end{align*} \]となるので注意が必要です。

(2)

やり方は2通りあります。

[その1：素直に置換積分]

複雑な積分を計算する方法の1つに、いったん他の文字に置き換えてから積分する方法があります。

しかし、置き換えた場合は、積分する文字も変化するため注意が必要です。

今回の場合、\( t = 2x + 1 \) とおく。すると、\( dt = 2 dx \) より、\( dx = \frac{1}{2} \ dt \) となる。

つまり、\[\begin{align*}
\int \frac{1}{(2x+1)^2} \ dx & = \int \frac{1}{t^2} \cdot \frac{1}{2} \ dt
\\ & = \frac{1}{2} \int \frac{1}{t^2} \ dt
\\ & = \frac{1}{2} \cdot \left( - \frac{1}{t} \right) + C
\\ & = - \frac{1}{2t} + C
\\ & = - \frac{1}{2(2x+1)} + C
\end{align*} \]と計算できます。

[その2：置換積分の省略公式]

実は、カッコ・ルートの中身を微分した結果が被積分関数内に含まれている場合、簡単に積分することができます。

詳しい方法については、こちらの記事で説明しているので、ぜひご覧ください。

今回の場合、\( (2x+1)^{-2} \) の括弧の中身は \( 2x+1 \) なので、微分した結果は2となります。

そこで、\[\begin{align*}
\int \frac{1}{(2x+1)^2} \ dx & = \int (2x+1)^{-2} \ dx
\\ & = \frac{1}{2} \int 2 (2x +1)^{-2} \ dx
\end{align*}\]とすることで、\[\begin{align*}
\int \frac{1}{(2x+1)^2} \ dx = \int (2x+1)^{-2} \ dx
\\ & = \frac{1}{2} \int 2 (2x +1)^{-2} \ dx
\\ & = \frac{1}{2} \int (2x+1)' (2x +1)^{-2} \ dx
\\ & = \frac{1}{2} \cdot (2x+1)^{-1} \cdot (-1) + C
\\ & = - \frac{1}{2(2x+1)} + C
\end{align*}\]と計算することができるのです！

このタイプの積分には、他にも\[
\int x \sqrt{1-x^2} \ dx, \ \ \ \int  xe^{x^2} \ dx
\]のようなものにも適用することができます。

2つとも実際に計算してみると、\[\begin{align*}
\int x \sqrt{1-x^2} \ dx & = - \frac{1}{2} (-2x) \sqrt{1-x^2} \ dx
\\ & = - \frac{1}{2} (1-x^2)' \sqrt{1-x^2} \ dx
\\ & = - \frac{1}{2} \cdot (1-x^2)^{ \frac{3}{2} } \cdot \frac{2}{3}
\\ & = - \frac{1}{3} \sqrt{1-x^2} (1-x^2) + C
\end{align*} \]

\[\begin{align*}
\int xe^{x^2}\ dx & = \frac{1}{2} \int 2x e^{x^2} \ dx
\\ & = \frac{1}{2} \int (x^2)' e^{x^2} \ dx
\\ & = \frac{1}{2} e^{x^2} + C
\end{align*} \]

のように計算することができます。

(3)

三角関数の公式を使うタイプの積分です。

まず、三角関数の積分の公式を確認しましょう。

微分のときと同じように \( a \) を付けた形にしています。

注意点としては、他の積分公式でも言えますが、\[
\int \cos x \ dx = \sin x + C
\]などの公式の \( x \) の部分を他の文字に書き換えても成立しません。

つまり、公式と全く同じ形であったときのみ公式を適用することができます。

例えば、\[
\int \cos 2x \ dx = \sin 2x + C
\]とするのはダメです。（正しくは \( \frac{1}{2} \sin 2x + C \)）

公式ではない形の場合、置換積分を行い、公式の形に直してから計算をする必要があります。

例えば、上の例の場合、\( 2x = t \) と置き換え、\( 2 dx = dt \), \( dx = \frac{1}{2} dt \) としてから、\[\begin{align*}
\int \cos 2x \ dx & = \frac{1}{2} \int \cos t \ dt
\\ & = \frac{1}{2} \sin t + C
\\ & = \frac{1}{2} \sin 2x + C
\end{align*} \]と計算する必要があります。

なお、三角関数の積分では倍角、3倍角、加法定理、積和の公式など様々な公式を使います。

忘れてしまった人は、こちらの記事で復習しましょう。

www.momoyama-usagi.com

特に2倍角の定理に関する積分はかなり頻繁に出るので、できるかぎり公式を頭の中に入れておきましょう。今回の場合、\[
\sin x \cos x = \frac{1}{2} \sin 2x
\]となるため、\[\begin{align*}
\int \sin x \cos x \ dx & = \frac{1}{2} \int \sin 2x \ dx
\\ & = - \frac{1}{4} \cos 2x
\end{align*} \]と計算できます。

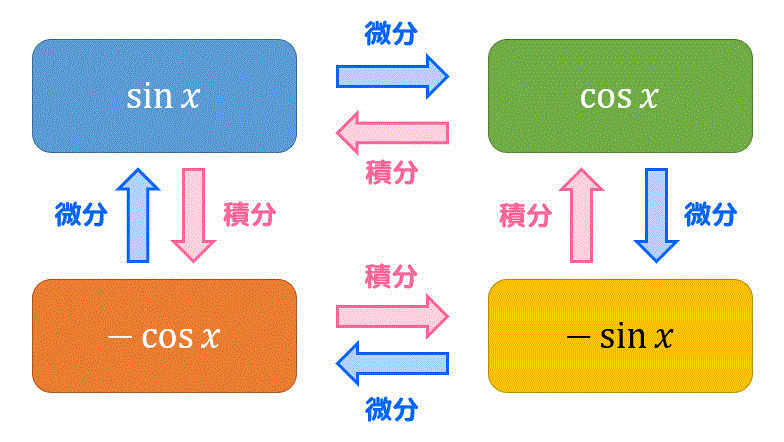
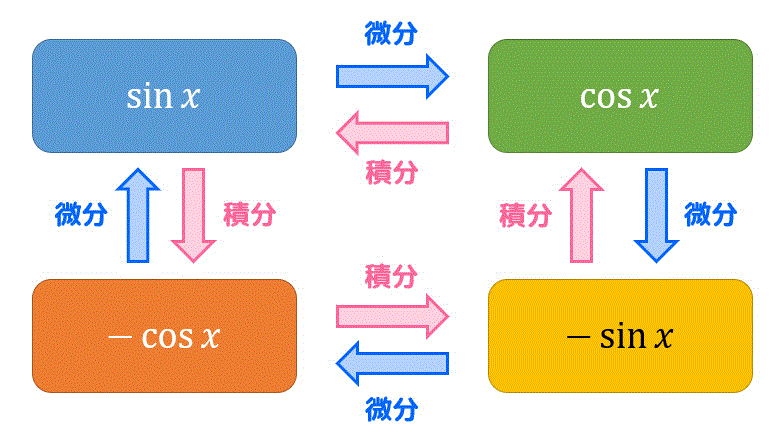
前回も説明しましたが、三角関数の微分積分の関係は、下のような図の関係になっていることを頭に入れておくと公式を忘れにくいかと思います。

(4)

指数関数の \( e^x \) 以外の微分を行う問題です。

公式の導出方法は2パターンです。

[その1：微分の公式から導き出す]

前回の微分編で、対数微分法を用いて\[
\left( a^x \right)' = a^x \log a
\]と微分できることを示しました。

つまり、\( \log a \) を割って\[
\left( \frac{a^x}{\log a} \right)' = a^x
\]としても成立しますね。

よって、\[
\int a^x \ dx = \frac{a^x}{\log a} + C
\]と導くことができます。

[その2：頑張って積分する]\[\begin{align*}
\int a^x \ dx & = \int e^{x \log a} \ dx
\\ & = \frac{1}{\log a} e^{x \log a}
\\ & = \frac{1}{\log a} a^x + C
\end{align*} \]と計算できます。

\( a^x = e^{x \log a} \) とするのがコツ！

今回の場合、\( a = 3 \) のパターンなので、積分定数 \( C \) を用いて\[
\int 3^x \ dx = \frac{3^x}{\log 3} + C
\]と求められます。

(5)

部分積分を使うパターンです。 \( \log x \) が出てきた場合は部分積分をすることが多いです。（たまに例外がありますが…）

念のため、公式を確認しておきましょう。

部分積分について詳しくはこちらの記事をご覧ください。

次の(6)で使える部分積分の連鎖公式も下の記事で説明しています。

www.momoyama-usagi.com

今回の場合は、積分定数 \( C \) を用いて\[\begin{align*}
\int x \log x \ dx & = \frac{1}{2} x^2 \log x - \int \frac{1}{2} x^2 \cdot \frac{1}{x} \ dx
\\ & =  \frac{1}{2} x^2 \log x - \frac{1}{2} \int  x \ dx
\\ & =  \frac{1}{2} x^2 \log x - \frac{1}{4} x^2 + C
\end{align*} \]と計算することができます。

(6)

\( e^x \) ×（多項式）のパターンは、部分積分を連鎖的に適用させることで、あっという間に計算をすることができます。

普通に積分する場合、積分定数 \( C \) を用いて\[\begin{align*}
\int x^2 e^x \ dx & = x^2 e^x - \int 2x e^x \ dx
\\ & = x^2 e^x - \left( 2x e^x  - \int 2 e^x \ dx \right)
\\ & = x^2 e^x - 2x e^x + 2 \int  e^x \ dx
\\ & = (x^2 - 2x + 2) e^x + C
\end{align*} \]と計算します。

しかし、連鎖公式を適用させることで、\[\begin{align*}
\int x^2 e^x \ dx & = x^2 e^x - 2x e^x + 2e^x
\\ & = (x^2 - 2x + 2) e^x + C
\end{align*}\]とあっという間に計算ができます。

余計なインテグラルも書く必要がないので時間短縮につながります。

(7)

分子が、分母の微分したものを表すタイプの関数は、下の公式により簡単に積分することができます。

今回は、「分子が分母を微分した形であること」が見分けやすいですが、問題によっては少し見分けにくい（知ってないと解けない）ようなタイプもあるので注意してください。

今回の場合、積分定数 \( C \) を用いて\[\begin{align*}
\int \frac{1}{3x+34} \ dx & = \frac{1}{3} \frac{3}{3x+34}
\\ & = \frac{1}{3} \log | 3x + 34 | + C
\end{align*}\]計算できます。（絶対値付けてね！！）

スポンサードリンク

問題２．定積分総復習

つぎの(1)～(5)の定積分を計算しなさい。（配点　25）

(1)\[
\int^{3}_{0} \sqrt{9-x^2} \ dx
\]

(2)\[
\int^{e^3}_{e} \frac{1}{x \log x} \ dx
\]

(3)\[
\int^{3}_{2} \frac{1}{(x+3)(x+4)} \ dx
\]

(4)\[
\int^{e}_{0} \frac{2x+4}{x^2+4x+12} \ dx
\]

(5)\[
\int^{ \frac{1}{2} }_{0} \frac{1}{1+4x^2} \ dx
\]

解答２．

[5点×5=25点]（結果が違う場合、不定積分（原始関数）が正しければ3点）

(1)

いきなり特殊なパターンの定積分です。

今回の場合、\( a = 3 \) のパターンなので、\( x = 3 \sin t \) とする。

すると、\( dx = 3 \cos t \ dt \) となる。

また、積分範囲は \( 0 \to 3 \) から \( 0 \to \frac{\pi}{2} \) に変わる。

（慣れないうちは積分範囲の変換は頭でやらず、必ず書くこと！！）

よって、\[\begin{align*}
\int^{3}_{0} \sqrt{ 9 - x^2 } \ dx & = \int^{ \frac{\pi}{2} }_{0} \sqrt{ 9 -  9\sin^2 t} \cdot 3 \cos t \ dt
\\ & = \int^{ \frac{\pi}{2} }_{0} \sqrt{ 9 \cos^2 t} \cdot 3 \cos t \ dt
\\ & = 9  \int^{ \frac{\pi}{2} }_{0} \cos^2 t \ dt
\\ & = \frac{9}{2}  \int^{ \frac{\pi}{2} }_{0}  \cos 2t + 1 \ dt
\\ & = \frac{9}{2} \left[ \frac{1}{2} \sin 2t + t \right]t^{ \frac{\pi}{2} }_{0}
\\ & = \frac{9}{2} \cdot \frac{\pi}{2} = \frac{9}{4} \pi
\end{align*}\]となる*1。

なお、倍角公式\[
\cos^2 x = \frac{1}{2} ( \cos 2x + 1 )
\]を忘れた or 導出できないという人はこちらで確認しましょう。

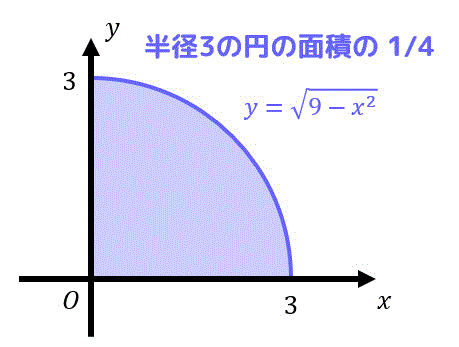
[別解]

定積分\[ y = \sqrt{9 - x^3}\]は半径3の円の面積\[
3^2 \pi = 9 \pi
\]の 1/4 を表しているので、\[
\int^{3}_{0} \sqrt{ 9 - x^2 } \ dx = \frac{1}{4} 3^2 \pi = \frac{9}{4} \pi
\]と計算するのもあり。

(2)

積分公式\[ \frac{ f'(x)}{f(x)} = \log | f(x) | + C \]を難しくしたバージョン。

\[\begin{align*}
\int^{e^3}_{e} \frac{1}{x \log x} \ dx & = \int^{e^3}_{e} \frac{ \frac{1}{x} }{\log x} \ dx
\\ & = \int^{e^3}_{e} \frac{ ( \log x )' }{ \log x } \ dx
\\ & =  \left[ \log | \log | x | | \right]^{e^3}_{e}
\\ & = \log 3 - \log 1 = \log 3
\end{align*} \]

(3)

部分分数分解をして和の形に分離してから計算するパターン\[\begin{align*}
\int^{3}_{2} \frac{1}{(x+3)(x+4)} \ dx & = \int^{3}_{2} \left( \frac{1}{x+3} - \frac{1}{x+4} \right) \ dx
\\ & = \int^{3}_{2} \frac{1}{x+3} \ dx - \int^{3}_{2} \frac{1}{x+4} \ dx
\\ & = \left[ \log |x+3| \right]^{3}_{2} - \left[ \log |x+4| \right]^{3}_{2}
\\ & = \log 6 - \log 5 - \left( \log 7 - \log 6 \right)
\\ & = 2 \log 6 - \log 5 - \log 7
\\ & = \log \frac{36}{35}
\end{align*} \]と計算できる。

このパターンの積分練習はこちらの記事をご覧ください。

（1つ前の式で止めてOKです。）

(4)

再び積分公式\[ \frac{ f'(x)}{f(x)} = \log | f(x) | + C \]のパターンです。\[\begin{align*}
\int^{e}_{0} \frac{2x+4}{x^2 + 4x + 12} \ dx & = \int^{e}_{0} \frac{ ( x^2 + 4x + 12 )' }{x^2 + 4x + 12} \ dx
\\ & = \left[ \log | x^2 + 4x + 12 | \right]^{e}_{0}
\\ & = \log \left( e^2 + 4e + 12 \right) - \log 12
\\ & = \log \frac{e^2 + 4e + 12}{12}
\end{align*} \]となる。

（1つ前の式で止めてOKです。）

(5)

三角関数の置き換えを行う特殊パターンです。\[
\int^{\beta}_{\alpha} \frac{1}{a^2 + x^2} \ dx
\]の \( a = 1/2 \) のパターンなので、\( x = \frac{1}{2} \tan t \) とおきます。

すると、\( dx = \frac{1}{2 \cos^2 t} \) となり、積分範囲は \( 0 \to 1/2 \) から \( 0 \to \pi/4 \) となります。

よって、\[\begin{align*}
\int^{\frac{1}{2}}_{0} \frac{1}{1 + 4x^2} \ dx & = \int^{\frac{\pi}{4}}_{0} \frac{1}{1 + \tan^2 t} \cdot \frac{1}{2 \cos^2 t} \ dt
\\ & = \frac{1}{2} \int^{\frac{\pi}{4}}_{0} 1 \ dt
\\ & = \frac{1}{2} \left[  t \right]^{\frac{\pi}{4}}_{0}
\\ & = \frac{1}{2} \cdot \frac{\pi}{4}
\\ & = \frac{\pi}{8}
\end{align*} \] となる。

問題３．定積分関数の微分

つぎの関数の導関数 \( G'(x) \) を求めなさい。（配点　 5）\[
G(x) = \int^{x}_{0} (x-t) \cos t \ dt
\]

解答３．

[5点]

定積分関数で表された関数を微分する問題です。

次の2つの公式を頭に入れておきましょう。

計算すると、\[\begin{align*}
G'(x) & = \frac{d}{dx} \int^{x}_{0} (x - t) \cos t \ dt
\\ & = \frac{d}{dx} x \int^{x}_{0} \cos t \ dt - \int^{x}_{0} t \cos t \ dt
\\ & = \color{blue}{ \int^{x}_{0} \cos t \ dt  + x \cos x } - x \cos x
\\ & = \left[ \sin t \right]^{x}_0
\\ & = \sin x
\end{align*} \]となります。

ポイントとしては、

• 2行目で2つの積分式に分解
• 3行目の青色部分は積の微分公式を適用

していることです。

せっかくなので公式2を使う類題を解いてみましょう。

[類題]\[
f(x) = \int^{x^2}_{x} \frac{t}{1+t^2} \ dt
\]のとき、導関数 \( f'(x) \) を求めなさい。

[解答]\[\begin{align*}
f'(x) & = \frac{x^2}{1+ \left( x^2 \right)^2 } \cdot \left( x^2 \right)' - \frac{x}{1+x^2} \cdot (x)'
\\ & = \frac{2x^3}{1+x^4} - \frac{x}{1+x^2}
\end{align*} \]と計算できる。

問題４．面積・体積計算

曲線 \( y = 1-x^2 \) (\( 0 \leqq x \leqq 1 \)) と \( x \) 軸、\( y \) 軸で囲まれた部分の領域を \( D \) とする。

(1) \( D \) の面積 \( S \) を求めなさい。
(2) \( D \) を \( x \) 軸のまわりに1回転してできる立体の体積 \( V_1 \) を求めなさい。
(3) \( D \) を \( y \) 軸のまわりに1回転してできる立体の体積 \( V_2 \) を求めなさい。

解答４．

[5点×3=15点]（5点の配点→立式に3点、積分結果に2点）

[参考] 領域 \( D \) は、図の部分となる。

(1)

曲線で囲まれた部分の面積計算の公式を確認しておきましょう。

今回の場合、面積 \( S \) は、曲線 \( y = 1 - x^2 \) と \( x = 0 \), \( x = 1 \) に囲まれた部分の面積に相当するので、\[\begin{align*}
S & = \int^{1}_{0} 1-x^2 \ dx
\\ & = \left[ x - \frac{1}{3} x^3 \right]^{1}_{0}
\\ & = 1 - \frac{1}{3}
\\ & = \frac{2}{3}
\end{align*}\]で計算できる。

(2)

\( x \) 軸まわりに1回転してできる回転体の体積の公式を確認しておきましょう。

今回の場合、体積 \( V_1 \) は、曲線 \( y = 1 - x^2 \) と \( x = 0 \), \( x = 1 \) に囲まれた部分の面積に相当するので、\[\begin{align*}
V_1 & = \pi \int^{1}_{0} (1-x^2)^2 \ dx
\\ & = \pi \int^{1}_{0} 1 - 2x^2 + x^4 \ dx
\\ & = \pi \left[ x - \frac{2}{3} x^3 + \frac{1}{5} x^5 \right]^{1}_{0}
\\ & = \pi \left( 1 - \frac{2}{3} + \frac{1}{5} \right)
\\ & = \frac{8}{15} \pi
\end{align*}\]で計算できる。

(3)

\( y \) 軸まわりに1回転してできる回転体の体積の公式を確認しておきましょう。

曲線 \( y = 1 - x^2 \) を x = の形で表すと、\( x \gt 0 \) より、\( x = \sqrt{1-y} \) となる。

また、体積 \( V_2 \) は、曲線 \( x=\sqrt{1-y} \) と \( y = 0 \), \( y = 1 \) に囲まれた部分*2の面積に相当する。

よって、

\[\begin{align*}
V_2 & = \pi \int^{1}_{0} (\sqrt{1-y})^2 \ dy
\\ & = \pi \int^{1}_{0} 1-y \ dy
\\ & = \pi \left[ y - \frac{1}{2} y^2 \right]^{1}_{0}
\\ & = \pi \left( 1 - \frac{1}{2} \right)
\\ & = \frac{\pi}{2}
\end{align*}\]で計算できる。

[別解：バームクーヘン積分]

\( y \) 軸周りの立体の体積は、下のように計算する手もある。

（通称バームクーヘン積分）

今回の問題の場合、\[\begin{align*}
V & = 2 \pi \int^{1}_{0} x(1-x^2) \ dx
\\ & = 2 \pi \int^{1}_{0} x - x^3 \ dx
\\ & = 2 \pi \left[ \frac{1}{2} x^2 - \frac{1}{4} x^4 \right]^{1}_{0}
\\ & = 2 \pi \cdot \frac{1}{4}
\\ & = \frac{\pi}{2}
\end{align*}\]と計算できる。

※ただし、素直に x = の形にしたほうが解きやすい問題も多いので、うかつにバームクーヘン積分をするのはあまりおすすめできません…

問題５．曲線の長さ

つぎの(1), (2)の問いに答えなさい。（配点　10）

(1) 曲線\[
y = \frac{e^x + e^{-x} }{2}
\]の \( -1 \leqq x \leqq 1 \) 部分の曲線の長さ \( L_1 \) を求めなさい。

(2) 媒介変数\[
\left\{ \begin{array}{l} x = t - \sin t  \\ y = 1 - \cos t  \end{array}\right. \ \ \left( 0 \leqq t \leqq \pi \right)
\]で表される曲線の長さ \( L_2 \) を求めなさい。

解答５．

[5点×2=10点]（5点の配点→立式に3点、積分結果に2点）

(1)

まずは、\( y = f(x) \) で表される関数の曲線の長さ \( L \) を出す公式を確認しておきましょう。

今回は、曲線\[
y = \frac{ e^{x} + e^{-x} }{2}
\]の長さ \( L_1 \) を求めればよい。

（参考：曲線の図は下のようになる）

ここで、\[
\frac{dy}{dx} = \frac{ e^{x} - e^{-x} }{2}
\]となるので、長さ \( L_1 \) は\[\begin{align*}
L_1 & = \int^{1}_{-1} \sqrt{ 1 + \left( \frac{dy}{dx} \right)^2 } \ dx
\int^{1}_{-1} \sqrt{ 1 + \left( \frac{ e^{x} - e^{-x} }{2} \right)^2 } \ dx
\\ & = \int^{1}_{-1} \sqrt{ 1 + \frac{e^{2x} - 2 + e^{-2x}}{4} } \ dx
\\ & = \int^{1}_{-1} \sqrt{ \frac{e^{2x} + 2 + e^{-2x}}{4} } \ dx
\\ & = \int^{1}_{-1} \sqrt{ \left( \frac{e^{x}+e^{-x}}{2} \right)^2 } \ dx
\\ & = \int^{1}_{-1} \frac{ e^{x}+e^{-x} }{2} \ dx
\\ & = \left[ \frac{ e^{x} - e^{-x} }{2} \right]^{1}_{-1}
\\ & = \frac{1}{2} \left( e - \frac{1}{e} \right) - \frac{1}{2} \left( \frac{1}{e} - e \right)
\\ & = e - \frac{1}{e}
\end{align*}\]と計算できる。

(2)

媒介変数表示で表される曲線の長さの公式も確認しましょう。

今回は\[
\left\{ \begin{array}{l} x = t - \sin t  \\ y = 1 - \cos t  \end{array}\right. \ \ \left( 0 \leqq t \leqq \pi \right)
\]で表される曲線の長さ \( L_2 \) を求めればよい。

（参考：曲線の図は下のようになる）

ここで、\[
\frac{dx}{dt} = 1 - \cos t , \ \ \ \frac{dy}{dt} = \sin t
\]なので、

\[\begin{align*} L_2 = \ &
\int^{\pi}_{0} \sqrt{ \left( \frac{dx}{dt} \right)^2 + \left( \frac{dy}{dt} \right)^2 } \ dt
\\ = \ & \int^{\pi}_{0} \sqrt{ \left( 1 - \cos t \right)^2 + \left( \sin t \right)^2 } \ dt
\\ = \ & \int^{\pi}_{0} \sqrt{ \cos^2 t - 2 \cos t + 1 + \sin^2 t } \ dt
\\ = \ & \int^{\pi}_{0}  \sqrt{ \sin^2 t + \cos^2 t - 2 \cos t + 1 } \ dt
\\ = \ & \int^{\pi}_{0}  \sqrt{ 1 - 2 \cos t + 1 } \ dt
\\ = \ & \int^{\pi}_{0}  \sqrt{ 2 ( 1- \cos t ) }  \ dt
\\ = \ & \int^{\pi}_{0}  \sqrt{ 2 \cdot 2 \sin^2 \frac{t}{2} }  \ dt \ \ \left( \because \sin^2 t = \frac{1 - \cos 2t}{2} \right)
\\ = \ & \int^{\pi}_{0}  \sqrt{ 4 \sin^2 \frac{t}{2} }  \ dt
\\ = \ & \int^{\pi}_{0} 2 \sin \frac{t}{2}  \ dt \ \ \left( \because \sin \frac{t}{2} \geqq 0 \right)
\\ = \ & \left[ - 4 \cos \frac{t}{2} \right]^{\pi}_{0}
\\ = \ &  4
\end{align*} \]と求められる。

問題６．

\( n \geqq 2 \) において、\[
I_n = \int^{ \frac{\pi}{2} }_{0} \sin^n x \ dx
\]であるとき、\( I_n \) を \( I_{n-2} \) を用いて表しなさい。（配点　10）

解答６．

[10点]

最後は漸化式を作って解くタイプの積分です。

あまりパターンはないので、やり方を頭に入れておくことをおすすめします。\[\begin{align*}
I_n & = \int^{ \frac{\pi}{2} }_{0} \sin^n x \ dx
\\ & = \int^{ \frac{\pi}{2} }_{0} \sin^{n-1} x \cdot \sin x \ dx
\\ & = \left[ - \sin^{n-1} \cdot \cos x \right]^{ \frac{\pi}{2} }_{0} - \int^{ \frac{\pi}{2} }_{0} (1-n) \sin^{n-2} \cdot \cos^2 x \ dx
\\ & = 0 + (n-1) \int^{ \frac{\pi}{2} }_{0} \sin^{n-2} x \left( 1 - \sin^2 x \right) \ dx
\\ & = (n-1) \int^{ \frac{\pi}{2} }_{0} \sin^{n-2} x - \sin^{n} x \ dx
\\ & = (n-1) \int^{ \frac{\pi}{2} }_{0} \sin^{n-2} x \ dx - (n-1) \int^{ \frac{\pi}{2} }_{0} \sin^{n} x \ dx
\\ & = (n-1) I_{n-2} - (n-1) I_n
\end{align*} \]となるので、\[
I_n = (n-1) I_{n-2} - (n-1) I_n
\\ n I_n = (n-1) I_{n-2}
\]となり、\[
I_n = \frac{n-1}{n} I_{n-2}
\]の関係式が成り立つ。

さいごに

今回は、微積分の総復習として、積分の計算演習問題を19問用意しました。

練習で間違えた問題は、必ず復習して解けるようにしておきましょう。

これで、全3回にわたる微積分総復習はすべて終了です！

おつかれさまでした！