スポンサードリンク
※ ディジタルシステムではなく、動的システムの極や安定性について知りたい人は、こちらの記事ではなく、下のリンク先の記事をご覧ください。
こんにちは、ももやまです。
前回(第03羽)はディジタルシステムのいろはとして、
- ディジタルシステムとはなにか
- 伝達関数について
- インパルス応答について
- 任意の入力から出力を求める方法
の4種類についてお話しました。
今回は、ディジタルシステムのお話の続きとして、
- 極と零点
- ディジタルシステムの安定性
の2つについて説明していきます。
スポンサードリンク
1. 伝達関数の極と零点
伝達関数 \( H(z) \) は、\[
H(z) = \frac{\textcolor{blue}{N (z)}}{\textcolor{red}{D (z)}}
\]のように、分子と分母の形で表されることがほとんどです[1]\( N (z) \), \( D (z) \) にした理由は、分子・分母をそれぞれ英語で "numerator", "denominator" というからです。。
この分子部分が0になるときを零点、分母部分が0になるときを極と呼びます。
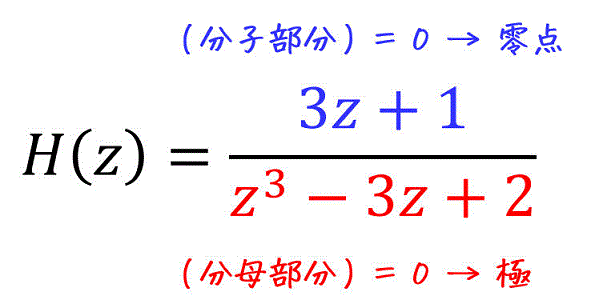
伝達関数 \( H(z) \) において、
- 分子部分 \( N (z) \) が0になる \( z \) → 零点
- 分母部分 \( D (z) \) が0になる \( z \) → 極
と呼ばれる。
※ \( z = 0 \) を見逃さないために、分子分母に \( z^k \) 倍するなどして、\( z^{-1} \) のようなマイナスn乗を消してから計算すること!
零点は、名前の通り \( H(z) = 0 \) となるz、極は分母部分が0になってしまうために定義されないzを表しているんだな程度の理解でOKです。
実際に例題で、零点と極を求めてみましょう。
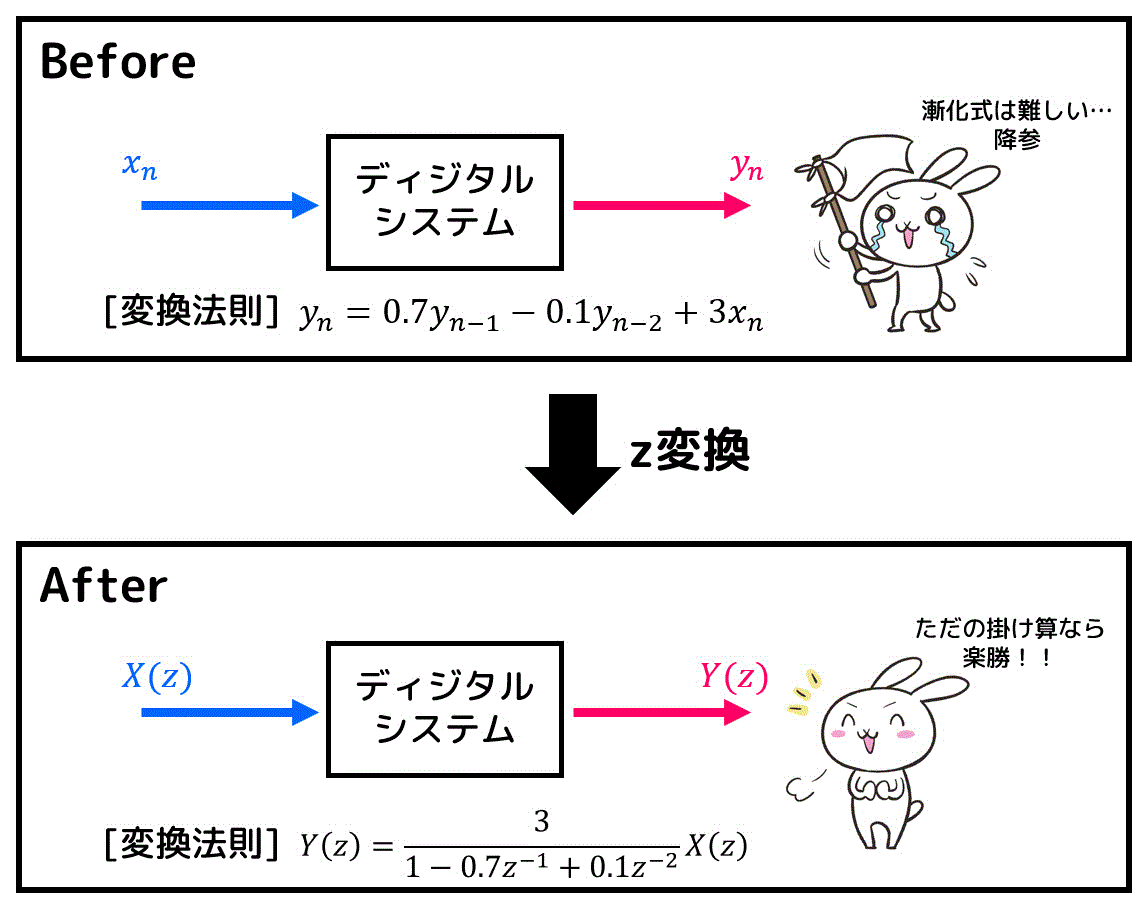
次の伝達関数\[
H(z) = \frac{3}{1 - 0.7z^{-1} + 0.1z^{-2}}
\]の極と零点があれば求めなさい。複数あればすべて求めること。
そのままの形で考えてもいいですが、\( z = 0 \) のときを見逃さないために分子分母をともに \( z^2 \) 倍して\[
\frac{3}{1 - 0.7z^{-1} + 0.1z^{-2}} = \frac{3z^2}{10z^2 - 7z + 1}
\]にしてから考えましょう[2]\( z = 0 \) のとき、\( z^{-1} = \frac{1}{0} \) でおかしなことになる。。
[極]
分母が0となる点。つまり\[\begin{align*}
(10z^2 - 7z + 1) & = (5z - 1)(2z - 1)
\\ & = 0
\end{align*}\]を満たす点。
よって、\( z = 0.2 , 0.5 \) が極。
[零点]
分子が0となる点。つまり \( 3z^2 = 0 \) を満たす点。
よって、\( z = 0 \) が零点。
伝達関数 \( H(z) \) が\[
H(z) = \frac{H_N (z)}{(1 - r_1 z^{-1})(1 - r_2 z^{-1})(1 - r_3 z^{-1}) \cdots}
\]の形で表されている場合、\( z = r_1, r_2, r_3 , \cdots \) が極となる。
※ この形にできればわざわざ (分母) = 0 を解く必要はなし!
スポンサードリンク
2. システムの安定性
(1) システムが安定しているとは
安定という言葉は日常生活でもよくつかいますね。
- やっぱ「安定」のマックだよな。
- 最近メンタルが「安定」してるな〜
- 患者の容体は「安定」している。
信号処理・制御数学の世界でも「安定」という言葉はよくつかいます。
では、「システムが安定している」とはどういう状態なのでしょうか…?
答えは、簡単です。
インパルス応答のnを十分大きくしても出力値が0に収束することを「システムが安定している」と呼びます。
(2) 伝達関数からシステムの安定性を判定してみよう
インパルス関数を入力したときの出力値を \( n \to \infty \) に飛ばせば、システムが安定しているかどうかを判定することはできます。
しかし、わざわざ逆z変換をしてシステムの安定性を調べるのは少しめんどくさいです。
そこで、伝達関数 \( H(z) \) の形からシステムの安定性を調べる方法を考えてみましょう。
(i) \( h_n \) が収束する条件を考えてみよう
(試験に出てくる)インパルス応答は\[
h_n = c_1 \alpha^n + c_2 \beta^n + \cdots
\]のように、(定数倍)×(指数関数のn乗)の和の形で表されることがほとんどです。
このインパルス応答 \( h_n \) が0に収束する条件、つまり\[
\lim_{n \to \infty} h_n = 0
\]が成立する条件はどんなときかを考えてみましょう。
まず、指数関数 \( r^n \) を \( n \to \infty \) にしたときに0に収束する状態、つまり\[
\lim_{n \to \infty} r^n = 0
\]を成立させるためには、\( |r| < 1 \) であることが条件でしたね。
次に、インパルス応答で出てくるすべての項が0に収束する必要がありますね。
例えば\[
h_n = \underbrace{3 \cdot (0.3)^n}_{0 \mathrm{に収束} } - \underbrace{7 \cdot (0.9)^n}_{0 \mathrm{に収束} }
\]であれば \( h_n \) に収束します。一方\[
h_n = \underbrace{3 \cdot (0.3)^n}_{0 \mathrm{に収束} } - \underbrace{7 \cdot (0.9)^n}_{0 \mathrm{に収束} } + \underbrace{0.2 \cdot (1.2)^n}_{\mathrm{無限大に発散}}
\]であれば1つ収束しない項 \( 0.2 \cdot (1.2)^n \) があるため、\( h_n \) も収束しません。
この2つをまとめると、\( h_n \) を収束させるためのポイントは以下の2つになりますね。
- \( h_n \) に出てくるすべての項が収束する
- 各項に出てくる指数関数 \( r^n \) は、\( |r| < 1 \) のときに収束する
(2) z変換の世界上で収束する条件を書き換えてみよう
z変換で出てくる伝達関数 \( H(z) \) が\[
H(z) = \frac{ H_N(z) }{(1 - r_1 z^{-1}) (1 - r_2 z^{-1})(1 - r_3 z^{-1}) \cdots }
\]の形で表せるとします。
\( H(z) \) に部分分数分解を行うと、\[\begin{align*}
H(z) & = \frac{ H_N(z) }{(1 - r_1 z^{-1}) (1 - r_2 z^{-1})(1 - r_3 z^{-1}) \cdots }
\\ & = \frac{c_1}{1- r_1 z^{-1}} + \frac{c_2}{1- r_2 z^{-1}} + \frac{c_3}{1- r_3 z^{-1}} + \cdots
\end{align*}\]と変形できます[3]方程式 (伝達関数の分母) = 0 が重解をもたないとき。重解を保つ場合は後ほど補足で説明します。。
この \( H(z) \) を逆z変換し、インパルス応答 \( h_n \) を求めると\[
h_n = c_1 r_1^n + c_2 r_2^n + c_3 r_3^n + \cdots
\]の形になりますね。
ここで、\( c_1 \), \( c_2 \), \( c_3 \), … の定数項はたかが定数のちっぽけな値なので、\( n \to \infty \) をする際には無視して考えることができます。
そのため、指数関数部分の \( r_1^n \), \( r_2^n \), \( r_3^n \), … がすべて0に収束すれば、言い換えると \( |r_1| < 1 \), \( |r_2| < 1 \), \( |r_3| < 1 \), … をすべて満たせば \( h_n \) は0に収束します。
信号処理の用語で説明すると、極となる \( z \) がすべて \( |z| < 1 \) にあればシステムが安定であるといえますね。
これは、伝達関数 \( H(z) \) の分母を因数分解するだけで、システムの安定性を判定することができることを意味しています!
インパルス応答 \( h_n \) が0に収束するとき、つまり\[
\lim_{n \to \infty} h_n = 0
\]が成立するとき、システムが安定であると言える。
また、システムの安定性は \( h_n \) を求めなくても判定ができる。
具体的には伝達関数 \( H(z) \) のすべての極が \( |z| < 1 \) であればシステムが安定であると言える。
★余談:伝達関数の極が重解をもつとき★
上の説明のときは「伝達関数 \( H(z) \) の (分母) = 0 が重解を持つとき」、つまり伝達関数の極が重解になるときを考慮していませんでした。
補足として、2重解を持つときも説明しましょう。2重解を持つということは、部分分数分解が\[
\frac{H_N(z)}{(1 - r_1 z^{-1})^n \cdots} = \frac{c_1}{1 - r_1 z^{-1}} + \frac{ c_2 z^{-1} }{ ( 1 - r_1 z^{-1} )^2 } + \cdots
\]のような形になりますね。
ここで、2番目の項\[
\frac{ c_2 z^{-1} }{ ( 1 - r_1 z^{-1} )^2 }
\]を逆z変換公式\[
\mathcal{Z}^{-1} \left[ \frac{\textcolor{red}{a} z^{-1}}{(1 - \textcolor{red}{a} z^{-1})^2 } \right] = n \textcolor{red}{a}^n
\]に当てはめると、\[\begin{align*}
\mathcal{Z}^{-1} \left[ \frac{ c_2 z^{-1} }{ ( 1 - r_1 z^{-1} )^2 } \right]
& = \frac{c_2}{r_1}\mathcal{Z}^{-1} \left[ \frac{ r_1 z^{-1} }{ ( 1 - r_1 z^{-1} )^2 } \right]
\\ & = \frac{c_2}{r_1} n r_1^n
\end{align*}\]となります。
ここで、\( \frac{c_2}{r_1} \) は定数なので無視できますね。さらに \( n r_1^n \) は、\( |r_1| < 1 \) のとき\[\begin{align*}
\lim_{n \to \infty} n r_1^n & = \lim_{n \to \infty} \frac{n}{r_1^{-n}}
\\ & = \lim_{n \to \infty} \frac{1}{- r_1^{-n} \log r_1}
\\ & = \lim_{n \to \infty} - \frac{1}{\log r_1} r_1^n
\\ & = 0
\end{align*} \]とロピタルの定理を使って変形できます。
よって、\[
\frac{H_N(z)}{(1 - r_1 z^{-1})^n \cdots} = \frac{c_1}{1 - r_1 z^{-1}} + \frac{ c_2 z^{-1} }{ ( 1 - r_1 z^{-1} )^2 } + \cdots
\]も0に収束し、2重解のときも重解がないときと同じように「すべての極が \( |z| < 1 \) であればシステムが安定である」ことがいえますね。
※ 3重解以上のときも同じ要領で確かめることができます
(3) 例題で確認!
次の伝達関数\[
H(z) = \frac{3}{1 - 0.7z^{-1} + 0.1z^{-2}}
\]で表されるシステムの安定性を調べなさい。
伝達関数 \( H(z) \) を変形すると\[
H(z) = \frac{3}{(1 - 0.5 z^{-1})(1 - 0.2 z^{-1}) }
\]となる。よって、極は \( z = 0.2 , 0.5 \) となる。
すべての極が \( |z| < 1 \) にあるため、システムは安定である。
※実際に \( H(z) \) を逆ラプラス変換し、インパルス応答 \( h_n \) を求めると\[
h_n = 5 \cdot 0.5^n + 2 \cdot 0.2^n \ \ (n \geqq 0)
\]となるため、\( n \to \infty \) のときに \( h_n = 0 \) となる(つまり安定)。
スポンサードリンク
3. 練習問題
では、今回習った内容が定着できているかを練習問題で確認しましょう!
次の漸化式\[
y_n = \frac{9}{4} y_{n-1} - \frac{9}{8} y_{n-2} + x_n + \frac{3}{2} x_{n-1}
\]で表されるシステムがある。
(1) 伝達関数 \( H(z) \) を求めなさい。(第03羽の練習問題と同じ)
(2) 伝達関数の極、零点があれば求めなさい。複数あればすべて答えること。
(3) 伝達関数からシステムの安定性を判定しなさい。
(1)
※ 伝達関数の詳細な計算方法、公式については前回の記事を確認すること。
両辺をz変換し、\[
Y(z) = \textcolor{green}{H(z)} X(z)
\]の形に持ち込めばOK。
両辺を \( z \) 変換すると、\[
Y(z) = \frac{9}{4} z^{-1} Y(z) - \frac{9}{8} z^{-2} Y(z) + X(z) + \frac{3}{2} z^{-1} X(z)
\]となるので、\[
\left( 1 - \frac{9}{4} z^{-1} + \frac{9}{8} z^{-2} \right) Y(z) = \left( 1 + \frac{3}{2} z^{-1} \right) X(z)
\]\[\begin{align*}
Y(z) & = \frac{ 1 + \frac{3}{2} z^{-1} }{ 1 - \frac{9}{4} z^{-1} + \frac{9}{8} z^{-2} } X(z) \\
Y(z) & = \textcolor{green}{ \frac{ 8 + 12 z^{-1} }{8 - 18z^{-1} + 9 z^{-2}} } X(z)
\end{align*}\]より、伝達関数は\[
H(z) = \frac{ 8 + 12 z^{-1} }{8 - 18z^{-1} + 9 z^{-2}}
\]となる。
(もちろん分子分母を \( z^2 \) 倍して\[
H(z) = \frac{8z^2 + 12z}{8z^2 - 18z + 9}
\]と答えてもOK)
(2)
分子分母を \( z^2 \) 倍して\[
\frac{8z^2 + 12z}{8z^2 - 18z + 9} = \frac{4z(2z+3)}{(2z-3)(4z-3)}
\]としてから考える。
極は (分母) = 0 となる \( z \) なので、\[
(2z-3)(4z-3) = 0
\]より、\( z = 1.5 \), \( z = 0.75 \) が極。
零点は (分子) = 0 となる \( z \) なので、\[
4z(2z+3)=0
\]より \( z = 0 \), \( z = -1.5 \) が零点。
(3)
伝達関数の極に \( z = 1.5 \) と、\( |z| \geqq 1 \) のものが含まれる。
よって、このシステムは安定ではない。(つまり、\( n \to \infty \) のとき、インパルス応答 \( h_n \) は無限大に発散する)
※実際にインパルス応答 \( h_n \) を計算すると、\[
4 \cdot \textcolor{red}{1.5}^n - 3 \cdot 0.75^n
\]となるため、確かに \( n \to \infty \) のときに無限大に発散することがわかる。
4. さいごに
ということで、前回に引き続き今回もディジタルシステムの理論について説明していきました。
次回は最終回として、ディジタルシステムの特性(周波数特性・振幅特性・位相特性)についてみていきましょう!
関連広告・スポンサードリンク