スポンサードリンク
こんにちは、ももやまです。
今回から2階以上の線形微分方程式(基本は2階)の解き方や仕組みについて説明していきたいと思います。
今回は、2階線形微分方程式の解き方を説明する前段階として、
- 2階線形微分方程式とはどんなものなのか
- 非同次微分方程式における同次解と特殊解の関係
- 同次方程式(同次解)における基本解と一般解の関係
- ロンスキアン(ロンスキー行列式)
について説明していきたいと思います。
前回の微分方程式の記事を下に載せておくので、まだ見ていない方はぜひご覧ください。
目次
スポンサードリンク
1.2階線形微分方程式とは
2階線形微分方程式とは、\[
\frac{d^2 y}{dx^2} + P(x) \frac{dy}{dx} + Q(x) y = R(x)
\]の形をした微分方程式のことを表します。
( \( P(x) \), \( Q(x) \), \( R(x) \) は \( x \) だけの関数)
さらに \( R(x) = 0 \) のとき、つまり\[
\frac{d^2 y}{dx^2} + P(x) \frac{dy}{dx} + Q(x) y = 0
\]の形の場合、同次式の2階線形微分方程式となります。
スポンサードリンク
2.非同次方程式における同次式と特殊解の関係
非同次の2階線形微分方程式\[
\frac{d^2 y}{dx^2} + P(x) \frac{dy}{dx} + Q(x) y = R(x)
\]の一般解は、
- 同次方程式の一般解
- 非同次方程式を満たす1つの特殊解(なんでもいい)
の和で構成されています。

つまり、同次方程式\[
\frac{d^2 y}{dx^2} + P(x) \frac{dy}{dx} + Q(x) y = 0
\]の一般解を求め、さらに\[
\frac{d^2 y}{dx^2} + P(x) \frac{dy}{dx} + Q(x) y = R(x)
\]を満たすような特殊解 \( y \) を1つ求めることで非同次方程式の一般解を求めることができます。
微分方程式\[
\frac{d^2 y}{dx^2} + P(x) \frac{dy}{dx} + Q(x) y = R(x)
\]の特殊解が \( y_0 \)、同次式の2階線形微分方程式\[
\frac{d^2 y}{dx^2} + P(x) \frac{dy}{dx} + Q(x) y = 0
\]の一般解が \( Y \) のとき、\[
\frac{d^2 y}{dx^2} + P(x) \frac{dy}{dx} + Q(x) y = R(x)
\]が \( y = Y + y_0 \) となることを示します。
一般解が \( y \) のとき、\[
y'' + P(x) y' + Q(x) = R(x) \tag{1}
\]が成立します。
また、\( y_0 \) は特殊解の1つなので、\[
y_0'' + P(x) y_0' + Q(x) = R(x) \tag{2}
\]が成立します。
(1) - (2)より、\[
y'' - y_0'' + P(x) (y' - y_0') + Q(x) (y - y_0) = 0 \]\[
(y - y_0)'' + P(x) (y - y_0)' + Q(x) (y - y_0) = 0 \tag{3}
\]が成立します。
また、同次方程式の一般解が \( Y \) なので、\[
Y'' + P(x) Y' + Q(x) Y = 0 \tag{4}
\]が成立します。
ここで、\( Y = y - y_0 \) を(4)に代入すると、\[
(y - y_0)'' + P(x) (y-y_0)' + Q(x) (y - y_0) = 0
\]となり、(3)式と等しくなるので、確かに
- 同次方程式の一般解
- 非同次方程式を満たす1つの特殊解(なんでもいい)
の和で非同次方程式の一般解を求めることができることが示されました。
なお、非同次方程式の特殊解の見つけ方には、
があります。
それぞれの方法に長所・短所があるので「自分の特異不得意や問題によって使い分ける」ことをおすすめします。
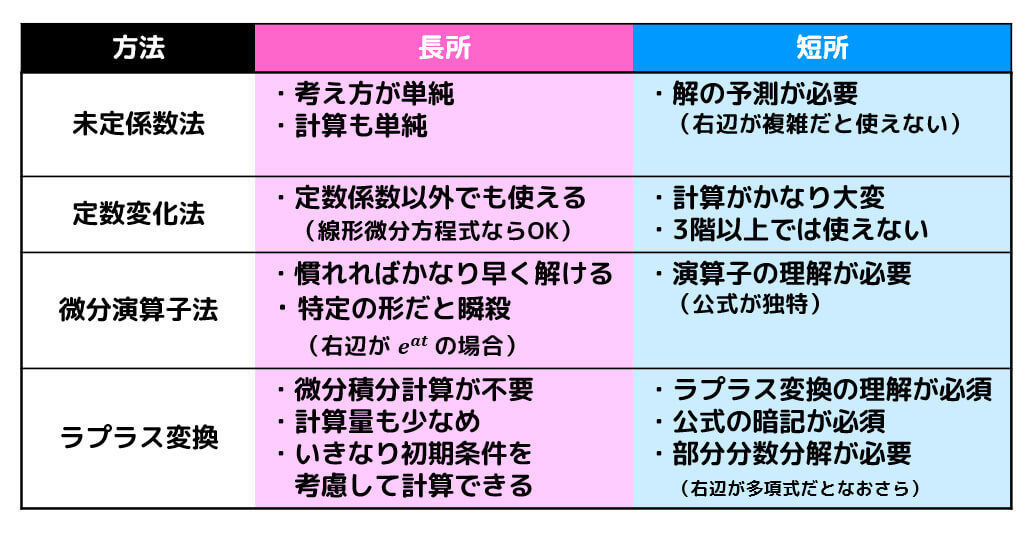
(〇〇法を使って解けと指定されたら、おとなしく指定された方法で解きましょう…)
スポンサードリンク
3.基本解と一般解
(1) 基本解と一般解の関係
同次式の2階線形微分方程式\[
\frac{d^2 y}{dx^2} + P(x) \frac{dy}{dx} + Q(x) y = 0
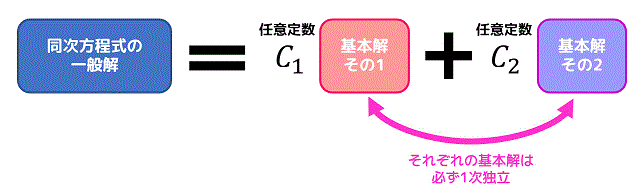
\]の一般解は、必ず一番単純な解 \( y_1 \), \( y_2 \) を用いて\[
y = C_1 y_1 + C_2 y_2
\]の形で表すことができます。
この最も単純な2つの解のことを基本解と呼びます。
ただし、基本解となるためには2つの条件
- 解が微分方程式を満たすこと
- 2つの解が1次独立(後ろで説明します)
を満たす必要があります。
つまり、微分方程式の解が \( y = y_1 \), \( y = y_2 \) のとき、2つの解を定数倍し、それぞれを足した\[
y = C_1 y_1 + C_2 y_2
\]も解となります。
実際に示してみましょう。微分方程式\[
\frac{d^2 y}{dx^2} + P(x) \frac{dy}{dx} + Q(x) y = 0
\]の基本解が \( y_1 \), \( y_2 \) のとき、\[
y = C_1 y_1 + C_2 y_2
\]も解になることを示します。
\[
\frac{dy}{dx} = C_1 y_1' + C_2 y_2' , \ \ \
\frac{d^2 y}{dx^2} = C_1 y_1'' + C_2 y_2'' \]\[
\]となるので、微分方程式に代入すると\[
\left ( C_1 y_1'' + C_2 y_2'' \right) + P(x) \left( C_1 y_1' + C_2 y_2' \right) + Q(x) \left( C_1 y_1 + C_2 y_2 \right) = 0 \]\[
C_1 \left( y_1'' + P(x) y_1' + Q(x) y_1' \right) + C_2 \left( y_2'' + P(x) y_2' + Q(x) y_2' \right) = 0
\]とります。
ここで、\( e^{k_1} \), \( e^{k_2} \) は解なので、\[
y_1'' + a y_1' + b y_1 = 0 \]\[
y_2'' + a y_2' + b y_2 = 0
\]を満たします。よって、\[
C_1 \left( y_1'' + P(x) y_1' + Q(x) y_1' \right) + C_2 \left( y_2'' + P(x) y_2' + Q(x) y_2' \right) = 0
\]も成立し、\[
y = C_1 y_1 + C_2 y_2
\]も解となることがわかりますね。
(2) 一般解は2つの解の1次結合
先程、(定数係数)2階線形微分方程式の基本解が \( C_1 y_1 \), \( C_2 y_2 \) のときの一般解は\[
y = C_1 y_1 + C_2 y_2
\]のような形になると説明しましたね。
この形を少し線形代数っぽく説明すると、同次式の2階線形微分方程式の一般解は2つの基本解 \( y_1 \), \( y_2 \) の1次結合(線形結合)\[
y = C_1 y_1 + C_2 y_2
\]で表せると説明できますよね。
もし、1次結合(線形結合)・1次独立(線形独立)・1次従属(線形従属)などの言葉を忘れてしまった人はこちらの記事で復習することをおすすめします。
もう少し難しい説明をすると、定数係数に限らず、同次式の2階線形微分方程式\[
\frac{d^2 y}{dx^2} + P(x) \frac{dy}{dx} + Q(x) = 0
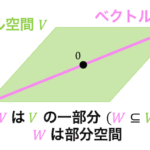
\]の解集合 \( V \)、つまり\[
V = \left\{ y \ \middle| \ \frac{d^2 y}{dx^2} + P(x) \frac{dy}{dx} + Q(x) = 0 \right\}
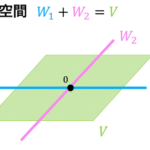
\]は、1つのベクトル空間(線形空間)となります。
余談ですが、2階に限らず、\( n \) 階の線形微分方程式の一般解は、\( n \) 個の基本解 \( y_1 \), \( y_2 \), …, \( y_n \) の線形結合\[
y = C_1 y_1 + C_2 y_2 + \cdots + C_n y_n
\]で表すことができ、解集合もベクトル空間となります。
(3) 基本解は1次独立
少し線形代数の復習をしましょう。
2つのベクトル \( \vec{a}_1 \), \( \vec{a}_2 \) がどうゆう条件を満たすときは1次独立(線形独立)であると言うことができたでしょうか。
方程式\[
c_1 \vec{a}_1 + c_2 \vec{a}_2 = \vec{0}
\]を満たす定数 \( c_1 \), \( c_2 \) が \( c_1 = c_2 = 0 \) しかないとき、1次独立というのでしたね。
微分方程式の場合、同次式の2階線形微分方程式の2つの基本解は1次独立な解である必要があります*1。
数式で表すと、2つの基本解 \( y_1 \), \( y_2 \) に対し、\[
C_1 y_1 + C_2 y_2 = 0
\]を満たすような \( C_1 \) ,\( C_2 \) が \( C_1 = C_2 = 0 \) しか存在しないような \( y_1 \), \( y_2 \) である必要があります。
余談ですが、2階に限らず、\( n \) 階線形微分方程式の場合、\( n \) 個の1次独立な基本解が出てきます。
なんで1次独立じゃないとダメなの
2階線形微分方程式の一般解には必ず \( C_1 \), \( C_2 \) のように2つの任意定数が出てきて\[
y = C_1 y_1 + C_2 y_2
\]と表せます。
しかし、もし基本解 \( y_1 \), \( y_2 \) が1次従属であった場合、\( C_1 \), \( C_2 \) が0でなくても、\[
C_1 y_1 + C_2 y_2 = 0 \]\[
y_1 = - \frac{C_2}{C_1} y_2
\]が成立してしまうので、任意定数が1つになってしまいます。
例えば、基本解が \( e^{2x} \), \( 2e^{2x} \) のような1次従属な*2組み合わせを許してしまうと、\[
y = C_1 e^{2x} + 2C_2 e^{2x}
\]というのは、\[
y = (C_1 + 2C_2) e^{2x} = A e^{2x}
\]のように1つの(基本解の個数以下の)任意定数にできてしまうため、2つ任意定数があるはずなのに1つしかないというおかしい状況になってしまいます。
そのため、2階線形微分方程式には必ず2つの1次独立な解が必要なのです。
(n階の場合は、n個の1次独立な解が必要)
\frac{d^2 y}{dx^2} + P(x) \frac{dy}{dx} + Q(x) = 0
\]には、必ず2つの1次独立な解 \( y_1 \), \( y_2 \) が存在し、その2つの解のことを基本解と呼ぶ。
(3) ロンスキアン(ロンスキー行列式)
求めてきた2つの基本解 \( y_1 \), \( y_2 \) が本当に1次独立かを定義\[
C_1 y_1 + C_2 y_2 = 0 \tag{1}
\]に従って確認するのは少し大変ですよね。
そこで、行列式を使って基本解が1次独立になるかどうかを確認してみましょう。
2つの変数 \( C_1 \), \( C_2 \) に対し、式が1つしかないので \( x \) で微分することにより、式を1つ増やしましょう。
(1)を微分すると、\[
C_1 y_1' + C_2 y_2' = 0
\]となり、2つ合わせて\[
\left\{ \begin{array}{l} \ \ C_1 y_1 + C_2 y_2 = 0 \\ C_1 y_1' + C_2 y_2' = 0 \end{array}\right.
\]と2つの式が出てきます。
これを行列を用いて表すと、\[
\left( \begin{array}{ccc} y_1 C_1 + y_2 C_2 \\ y_1' C_1 + y_2' C_2 \end{array} \right) = \left( \begin{array}{ccc} 0 \\ 0 \end{array} \right)
\]となるので、\[
\left( \begin{array}{ccc} y_1 + y_2 \\ y_1' + y_2' \end{array} \right) \left( \begin{array}{ccc} C_1 \\ C_2 \end{array} \right) = \left( \begin{array}{ccc} 0 \\ 0 \end{array} \right)
\]と表現、つまり\[
A \vec{x} = \vec{0}
\]の形にすることができます。
ここで、\( y_1 \), \( y_2 \) が1次独立になるということは、\( \vec{x} \)、つまり\[
\left( \begin{array}{ccc} C_1 \\ C_2 \end{array} \right)
\]が自明な解\[
\left( \begin{array}{ccc} C_1 \\ C_2 \end{array} \right) = \left( \begin{array}{ccc} 0 \\ 0 \end{array} \right)
\]以外の解をもたないと言い換えられますね。
つまり、行列式 \( |A| \not = 0 \)、つまり\[
\left| \begin{array}{ccc} y_1 & y_2 \\ y_1' & y_2' \end{array} \right| \not = 0
\]が成立しますね。
(忘れてしまった人はこちらで確認をしましょう。)
この行列式\[
W(y_1, y_2 ) = \left| \begin{array}{ccc} y_1 & y_2 \\ y_1' & y_2' \end{array} \right|
\]のことをロンスキアン(ロンスキー行列式)と呼び、\[
W(y_1, y_2 ) \not = 0
\]のとき、\( y_1 \), \( y_2 \) は1次独立(線形独立)と言うことができます。
W(y_1, y_2 ) = \left| \begin{array}{ccc} y_1 & y_2 \\ y_1' & y_2' \end{array} \right| \not = 0
\]を示せばよい。
なお、基本解であることを示すときは、ロンスキアンが0以外になることの他に、実際に \( y_1 \) ,\( y_1' \), \( y_1'' \), \( y_2 \), \( y_2' \), \( y_2'' \) を代入して微分方程式を満たすかどうかの確認も必要です。
では、実際にロンスキアンを使った例題を解いてみましょう。
例題1
微分方程式\[
\frac{d^2 y}{dx^2} - 4 \frac{dy}{dx} + 4 y = 0
\]において、\( y_1 = e^{2x} \), \( y_2 = xe^{2x} \) が微分方程式の基本解となることを示しなさい。
解説1
微分方程式の基本解となることを示すためには、
- 2つの解が微分方程式を満たすこと … (i)
- 2つの解が1次独立であること … (ii)
を示せばよい。
まず、2つの解が微分方程式を満たすことを示す。\[
\frac{dy_1}{dx} = 2e^{2x}, \ \ \ \frac{d^2 y_1}{dx^2} = 4e^{2x}
\]となるので、\[
4e^{2x} - 4 \cdot 2 e^{2x} + 4 e^{2x} = 0 \]\[
4e^{2x} - 8 e^{2x} + 4 e^{2x} = 0
\]となり、\( y_1 \) は微分方程式の解となる。
また、\[\begin{align*}
\frac{dy_2}{dx} & = e^{2x} + 2xe^{2x} \\
\frac{d^2 y_2}{dx^2} & = 2e^{2x} + 2e^{2x} + 4xe^{2x}
\\ & = 4x e^{2x} + 4e^{2x}
\end{align*} \]となるので、\[
4x e^{2x} + 4e^{2x} - 4 \left( e^{2x} + 2xe^{2x} \right)+ 4xe^{2x} = 0 \]\[
xe^{2x} \left( 4 - 8 + 4 \right) + e^{2x} ( 4 - 4 ) = 0
\]となり、\( y_2 \) は微分方程式の解となる。
よって、\( y_1 \), \( y_2 \) の解は微分方程式を満たし、(i) が示された。
さらに、ロンスキアン \( W(y_1, y_2) \) が\[\begin{align*}
W(y_1, y_2 ) & = \left| \begin{array}{ccc} e^{2x} & xe^{2x} \\ 2e^{2x} & e^{2x} + 2x e^{2x} \end{array} \right|
\\ & = e^{2x} \left( e^{2x} + 2x e^{2x} \right) - x e^{2x} \cdot 2e^{2x}
\\ & = e^{4x} + 2x e^{4x} - 2x e^{4x}
\\ & = e^{4x} \not = 0
\end{align*} \]となるので、\( y_1 \), \( y_2 \) は1次独立な解であることが示されたので、(ii) も示された。
よって、(i), (ii) より、\( y_1 = e^{2x} \), \( y_2 = xe^{2x} \) が微分方程式の基本解であることが示された。
4.練習問題
では、3問ほど練習してみましょう。
練習1
微分方程式\[
\frac{d^2 y}{dx^2} + y = 0
\]において、\( y_1 = \cos x \), \( y_2 = \sin x \) が微分方程式の基本解となることを示しなさい。
練習2
微分方程式\[
\frac{d^2 y}{dx^2} - \frac{2}{x^2} y = x^2
\]について、つぎの(1)~(3)の問いに答えなさい。
(1) 同次式\[
\frac{d^2 y}{dx^2} - \frac{2}{x^2} y = 0
\] において、\( y_1 = x^2 \), \( y_2 = \frac{1}{x} \) が微分方程式の基本解となることを示しなさい。
(2) \( y = \frac{1}{10} x^4 \) が特殊解となることを確認しなさい。
(3) 一般解を求めなさい。
練習3
微分方程式\[
\frac{d^2 y}{dx^2} - \frac{1}{x} \frac{dy}{dx} + \frac{1}{x^2} y = \frac{1}{x^2}
\]について、つぎの(1)~(3)の問いに答えなさい。
(1) 同次式\[
\frac{d^2 y}{dx^2} - \frac{1}{x} \frac{dy}{dx} + \frac{1}{x^2} y = 0
\] において、\( y_1 = x \), \( y_2 = x \log x \) が微分方程式の基本解となることを示しなさい。
(2) \( y = 1 \) が特殊解となることを確認しなさい。
(3) 一般解を求めなさい。
5.練習問題の答え
解答1
微分方程式の基本解となることを示すためには、
- 2つの解が微分方程式を満たすこと … (i)
- 2つの解が1次独立であること … (ii)
を示せばよい。
まず、2つの解が微分方程式を満たすことを示す。\[
\frac{dy_1}{dx} = - \sin x, \ \ \ \frac{d^2 y_1}{dx^2} = - \cos x
\]となるので、\[
- \cos x + \cos x = 0
\]となり、\( y_1 = \cos x \) は微分方程式の解となる。
また、\[\begin{align*}
\frac{dy_2}{dx} = \cos x, \ \ \ \frac{d^2 y_2}{dx^2} = - \sin x
\end{align*} \]となるので、\[
- \sin x + \sin x = 0
\]となり、\( y_2 = \sin x \) は微分方程式の解となる。
よって、\( y_1 \), \( y_2 \) の解は微分方程式を満たし、(i) が示された。
さらに、ロンスキアン \( W(y_1, y_2) \) が\[\begin{align*}
W(y_1, y_2 ) & = \left| \begin{array}{ccc} \cos x & \sin x \\ - \sin x & \cos x \end{array} \right|
\\ & = \cos^2 x + \sin^2 x
\\ & = 1 \not = 0
\end{align*} \]となるので、\( y_1 \), \( y_2 \) は1次独立な解であることが示されたので、(ii) も示された。
よって、(i), (ii) より、\( y_1 = \cos x \), \( y_2 = \sin x \) が微分方程式の基本解であることが示された。
解答2
(1)
まず、2つの解が微分方程式\[
\frac{d^2 y}{dx^2} - \frac{2}{x^2} y = 0
\]を満たすことを示す。\[
\frac{dy_1}{dx} = 2x , \ \ \ \frac{d^2 y_1}{dx^2} = 2
\]となるので、\[
2 - \frac{2}{x^2} \cdot x^2 = 0 \]\[
2 - 2 = 0
\]となり、\( y_1 = x^2 \) は微分方程式の解となる。
また、\[\begin{align*}
\frac{dy_2}{dx} = - \frac{1}{x^2}, \ \ \ \frac{d^2 y_2}{dx^2} = \frac{2}{x^3}
\end{align*} \]となるので、\[
\frac{2}{x^3} - \frac{2}{x^2} \cdot \frac{1}{x} = 0 \]\[
\frac{2}{x^3} - \frac{2}{x^3} = 0
\]となり、\( y_2 = \frac{1}{x} \) は微分方程式の解となる。
よって、\( y_1 \), \( y_2 \) の解は微分方程式を満たし、(i) が示された。
さらに、ロンスキアン \( W(y_1, y_2) \) が\[\begin{align*}
W(y_1, y_2 ) & = \left| \begin{array}{ccc} x^2 & \frac{1}{x} \\ 2x & - \frac{1}{x^2} \end{array} \right|
\\ & = x^2 \cdot \left( - \frac{1}{x^2} \right) - 2x \cdot \frac{1}{x}
\\ & = -1 -2
\\ & = -3 \not = 0
\end{align*} \]となるので、\( y_1 \), \( y_2 \) は1次独立な解であることが示されたので、(ii) も示された。
よって、(i), (ii) より、\( y_1 = x^2 \), \( y_2 = \frac{1}{x} \) が微分方程式の基本解であることが示された。
(2)
微分方程式\[
\frac{d^2 y}{dx^2} - \frac{2}{x^2} y = x^2
\]に\[
y = \frac{1}{10} x^4
\]を代入して満たすかどうかを確認する。\[
\frac{dy}{dx} = \frac{2}{5} x^3, \ \ \ \frac{d^2 y}{dx^2} = \frac{6}{5} x^2
\]なので、\[\begin{align*}
\frac{6}{5} x^2 - \frac{2}{x^2} \cdot \frac{1}{10} x^4 & =
\frac{6}{5} x^2 - \frac{1}{5} x^2 \\ & = x^2
\end{align*} \]となるので、確かに\[
y = \frac{1}{10} x^4
\]は特殊解となる。
(3)
微分方程式の一般解は、
- 同次方程式の一般解
- 非同次方程式を満たす1つの特殊解(なんでもいい)
の和で求めることができる。
ここで、基本解は \( x^2 \), \( \frac{1}{x} \) なので、同次方程式の一般解は任意定数 \( C_1 \), \( C_2 \) を用いて\[
y = C_1 x^2 + C_2 \frac{1}{x}
\]となる。
さらに非同次方程式の特殊解は(2)より\[
y = \frac{1}{10} x^4
\]となる。よって、この2つの和\[
y = C_1 x^2 + C_2 \frac{1}{x} + \frac{1}{10} x^4
\]が一般解となる。
解答3
まず、2つの解が微分方程式\[
\frac{d^2 y}{dx^2} - \frac{1}{x} \frac{dy}{dx} + \frac{1}{x^2} y = 0
\]を満たすことを示す。\[
\frac{dy_1}{dx} = 1 , \ \ \ \frac{d^2 y_1}{dx^2} = 0
\]となるので、\[
0 - \frac{1}{x} + \frac{1}{x^2} \cdot x = 0 \]\[
- \frac{1}{x} + \frac{1}{x} = 0
\]となり、\( y_1 = x \) は微分方程式の解となる。
また、\[\begin{align*}
\frac{dy_2}{dx} = \log x + 1, \ \ \ \frac{d^2 y_2}{dx^2} = \frac{1}{x}
\end{align*} \]となるので、\[
\frac{1}{x} - \frac{1}{x} ( \log x + 1 ) + \frac{1}{x^2} \cdot x \log x = 0 \]\[
\frac{1}{x} - \frac{\log x}{x} - \frac{1}{x} + \frac{\log x}{x} = 0
\]となり、\( y_2 = x \log x \) は微分方程式の解となる。
よって、\( y_1 \), \( y_2 \) の解は微分方程式を満たし、(i) が示された。
さらに、ロンスキアン \( W(y_1, y_2) \) が\[\begin{align*}
W(y_1, y_2 ) & = \left| \begin{array}{ccc} x & x \log x \\ 1 & \log x + 1 \end{array} \right|
\\ & = x ( \log x + 1 ) - x \log x
\\ & = x \log x + x - x \log x
\\ & = x \not = 0
\end{align*} \]となるので、\( y_1 \), \( y_2 \) は1次独立な解であることが示されたので、(ii) も示された。
よって、(i), (ii) より、\( y_1 = x \), \( y_2 = x \log x \) が微分方程式の基本解であることが示された。
(2)
微分方程式\[
\frac{d^2 y}{dx^2} - \frac{1}{x} \frac{dy}{dx} + \frac{1}{x^2} y = \frac{1}{x^2}
\]に\[
y = 1
\]を代入して満たすかどうかを確認する。\[
\frac{dy}{dx} = 0, \ \ \ \frac{d^2 y}{dx^2} = 0
\]なので、\[\begin{align*}
0 - 0 + \frac{1}{x^2} \cdot 1 = \frac{1}{x^2}
\end{align*} \]となるので、確かに\[
y = 1
\]は特殊解となる。
(3)
微分方程式の一般解は、
- 同次方程式の一般解
- 非同次方程式を満たす1つの特殊解(なんでもいい)
の和で求めることができる。
ここで、基本解は \( x \), \( x \log x \) なので、同次方程式の一般解は任意定数 \( C_1 \), \( C_2 \) を用いて\[
y = C_1 x + C_2 x \log x
\]となる。
さらに非同次方程式の特殊解は(2)より\[
y = 1
\]となる。よって、この2つの和\[
y = C_1 x + C_2 x \log x + 1
\]が一般解となる。
6.さいごに
今回は、2階線形微分方程式の解き方を説明する準備段階として、
- 2階線形微分方程式とはどんなものなのか
- 非同次微分方程式における同次解と特殊解の関係
- 同次方程式(同次解)における基本解と一般解の関係
- ロンスキアン(ロンスキー行列式)
の4つについてまとめていきました。
次回からは実際に2階線形微分方程式を解き方について説明していきたいと思います。
関連広告・スポンサードリンク