うさぎでもわかる微分方程式　Part00　微分方程式ってなに？

2020年3月28日 2023年10月5日 35分6秒

ももうさ

スポンサードリンク

こんにちは、ももやまです。

今回から数回にわけて微分方程式についての記事を書いていきたいと思います。

Part00では、実際に微分方程式の解法を説明する前段階として

微分方程式ってなに？
微分方程式の大まかな種類
簡単な微分方程式を解いてみよう（直接積分形）
一般解と特解の違い
微分方程式の応用例

について説明していきたいと思います。

微分方程式では、微分・積分を頻繁に行うため、ある程度の解析学の知識（1変数関数の微積）があることが望ましいです。

特に、

などを忘れてしまっている人は上のリンクから復習することをおすすめします。

スポンサードリンク

１．微分方程式とは

皆さんが今まで解いてきた方程式というのは、解が必ず数値となります。

例えば、2次方程式 $x^{2} - 5 x + 6 = 0$ の解は $x = 2$ と $x = 3$ の2つの数値になりますね。

上のように、等式を満たすような値を見つけることができれば、方程式が解けたといえます。

一方、微分方程式では解が数値ではなく関数となります。

つまり、等式を満たすような関数を見つけることができれば微分方程式が解けたといえます。

例えば $y$ が $x$ の関数（つまり $y (x)$ ）のときの $y^{'} = \frac{d y}{d x} = 2 x + 3$ のときの解は任意定数 $C$ を用いて $y = x^{2} + 3 x + C$ と表されます*1。

上のように、等式を満たすような方程式を見つけることができれば、微分方程式が解けたといえます。

普通の（微分方程式ではない）方程式は、等式を満たすような値を求めるだけなので、1次方程式なら簡単に解け、2次方程式でも解の公式を使って簡単に解くことができます。

しかし、微分方程式は等式を満たすような関数を求める必要があります。関数はただの値に比べたら複雑な形になるので、方程式に比べて解くのが圧倒的に難しいです。

大学や高専などである「微分方程式」という科目、分野、数検1級で問われる問題、院試では、おもに

微分方程式の中でも特定のパターンに当てはめれば解ける微分方程式
初等物理などの工学系の科目で使う微分方程式

が取り扱われる場合がほとんどです。

そのため、大学の初等物理（力学や電磁気）で出てくる微分方程式の9割以上は、特定のパターンに当てはめることで解くことができます。

スポンサードリンク

２．様々な微分方程式

微分方程式には、様々な種類が出てきます。

具体的にどう分類されるのかを見ていきましょう。

(1) 常微分 or 偏微分

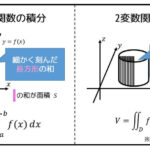
微分方程式の解が1変数関数 $y = y (x)$ となる微分方程式のことを常微分方程式と呼びます。

一方、2変数の関数 $u = u (x, y)$ 、あるいはそれ以上の多変数関数となる微分方程式のことは偏微分方程式と呼びます。

偏微分が関係しない微分方程式が常微分方程式、偏微分が関係する微分方程式が偏微分方程式だと頭の中で思っておけばOKです。

常微分方程式と偏微分方程式

y

が

x

の1変数関数

y (x)

のとき、

x

y

および

\frac{d y}{d x}

\frac{d^{2} y}{d x^{2}}

, …

\frac{d^{n} y}{d x^{n}}

で表される関係式を常微分方程式と呼ぶ。

（ $\frac{d y}{d x}$ を $y^{'}$ 、 $\frac{d^{2} y}{d x^{2}}$ を $y^{″}$ と書かれることもある）

偏微分方程式 $u$ が $x$ , $y$ , … の2変数以上の関数 $u (x, y, \dots)$ のとき、 $u$ , $x$ , $y$ , … および $\frac{\partial u}{\partial x}$ , $\frac{\partial u}{\partial y}$ , $\frac{\partial^{2} u}{\partial x^{2}}$ , $\frac{\partial^{2} u}{\partial y^{2}}$ , $\frac{\partial^{2}}{\partial y \partial x}$ で表される関係式を偏微分方程式と呼ぶ。

（ $\frac{\partial u}{\partial x}$ を $u_{x}$ 、 $\frac{\partial^{2} u}{\partial x^{2}}$ を $u_{x x}$ 、 $\frac{\partial^{2} u}{\partial y \partial x}$ を $u_{x y}$ と書かれることもある）

力学などの初等物理に出てくる微分方程式のほとんどが常微分方程式です。

また、大学や高専の期末試験、数検1級、院試では、常微分方程式を解く問題しか出題されないことがほとんどです。

そのため、偏微分方程式のことは今は忘れてもらってOKです。

普通の微分（常微分）のことだけを考えましょう。

（これより先、単に微分方程式と書いてあった場合は常微分方程式のことを指していると思ってください。）

[超余談]

常微分方程式は英語でOrdinary Differential Equationsと呼び、ODEと略されることがあります。本記事のURLのodeXX*2のodeは常微分方程式の英略からとっています。

(2) 線形 or 非線形

微分しようとする変数 $y$ と、導関数 $\frac{d y}{d x}$ , $\frac{d^{2} y}{d x^{2}}$ , … などがすべて1次式となっている微分方程式のことを線形微分方程式と呼びます。

つまり、微分項同士の掛け算を含まない微分方程式が線形微分方程式です。

例えば、 $\frac{d^{2} y}{d x^{2}} - 5 \frac{d y}{d x} + 6 y = 0$ $\frac{d y}{d x} - x y = 6 x^{2} + 3 x$ $x^{2} \frac{d y}{d x} - 2 y = 0$ などは線形な項*3しか含まれないので線形微分方程式です。

一方 $y \frac{d y}{d x} = 3 x + 4$ $\frac{d y}{d x} - y^{2} = 0$ ${(\frac{d y}{d x})}^{2} - 3 \frac{d y}{d x} = 0$ では、 $y \frac{d y}{d x}$ , $y^{2}$ , ${(\frac{d y}{d x})}^{2}$ のように微分項同士の掛け算が含まれているので、線形微分方程式とは言えません。

このような方程式は非線形微分方程式と呼ばれます。

線形 or 非線形？

y

\frac{d y}{d x}

\frac{d^{2} y}{d x}

\frac{d^{n} y}{d x^{n}}

のような微分項同士の掛け算が含まれていない微分方程式を線形微分方程式と呼ぶ。

一方、 $y \frac{d y}{d x}$ , $y^{2}$ , $(\frac{d y}{d x})$ のように微分項同士の掛け算が含まれている微分方程式を非線形微分方程式と呼ぶ。

非線形微分方程式は、線形微分方程式に比べて解く難易度が高いものが多く、 ${(\frac{d y}{d x})}^{2}$ , $\frac{d y}{d x} \frac{d^{2} y}{d x^{2}}$ のように微分したもの同士の積が含まれる項が含まれると、さらに難易度が上がります。

カオス理論と呼ばれるほどです。

大学や高専の期末試験、数検1級、院試では、簡単なパターンで解けないような非微分方程式を求める問題は出てこない場合がほとんどなので、安心してください。

(3) 微分方程式の階数

(i) 各項の階数

それぞれの項で微分されている回数が各項の階数となります。

[例]

$\frac{d y}{d x}$ → 1階
$4 \frac{d y}{d x}$ → 1階
$4 {(\frac{d y}{d x})}^{2}$ → 1階
$\frac{d^{2} y}{d x^{2}}$ → 2階
$3 x^{5} \frac{d^{2} y}{d y^{2}}$ → 2階
$\frac{d^{n} y}{d y^{n}}$ → n階

(ii) 微分方程式の階数

微分方程式内で出てくる項の中で、一番大きい階数が微分方程式の階数となります。

[例1]

\frac{1}{x^{2}} \frac{d y}{d x} = - x^{3}

は

\frac{1}{x^{2}} \frac{d y}{d x}

が一番大きい階の項（1階）なので、1階微分方程式です。

[例2]

\frac{d^{2} y}{d x^{2}} - 5 \frac{d y}{d x} + 6 y = 0

は、

\frac{d^{2} y}{d x^{2}}

が一番大きい階の項（2階）なので、2階微分方程式です。

[例3]

a_{n} \frac{d^{n} y}{d x^{n}} + a_{n - 1} \frac{d^{n - 1} y}{d x^{n - 1}} + \dots + a_{1} \frac{d y}{d x} + a_{0} y = f (x)

は、

a_{n} \frac{d^{n} y}{d x^{n}}

が一番大きい階の項（n階）なので、n階微分方程式です。

微分方程式の階数微分方程式内の項の中で、一番大きい階数の項が微分方程式の階数となる。

例えば、 $a_{n} \frac{d^{n} y}{d x^{n}} + a_{n - 1} \frac{d^{n - 1} y}{d x^{n - 1}} + \dots + a_{1} \frac{d y}{d x} + a_{0} y = f (x)$ であれば $n$ 階微分方程式となる。

大学や高専の期末試験、数検1級、院試では、

1階微分方程式
一部の2階微分方程式
公式に当てはめられる3階以上の微分方程式

を中心に聞かれることが多いです。

(4) 同次（斉次） or 非同次（非斉次）

微分方程式の中でも、 $a_{n} \frac{d^{n} y}{d x^{n}} + a_{n - 1} \frac{d^{n - 1} y}{d x^{n - 1}} + \dots + a_{1} \frac{d y}{d x} + a_{0} y = 0$ のように、 $y$ に関係ない項がないものを同次微分方程式・斉次微分方程式と呼びます。

例えば、 $\frac{d^{2} y}{d x^{2}} - 5 \frac{d y}{d x} + 6 y = 0$ や $\frac{1}{x^{2}} \frac{d y}{d x} = 0$ は、 $y$ に関係ない項が一切ないので同次微分方程式です。

一方、 $a_{n} \frac{d^{n} y}{d x^{n}} + a_{n - 1} \frac{d^{n - 1} y}{d x^{n - 1}} + \dots + a_{1} \frac{d y}{d x} + a_{0} y = f (x)$ のように、 $y$ に関係ない $f (x)$ が含まれているような式のことを非同次微分方程式・斉次微分方程式と呼びます。

例えば、 $\frac{d^{2} y}{d x^{2}} - 5 \frac{d y}{d x} + 6 y = e^{3 x}$ や $\frac{1}{x^{2}} \frac{d y}{d x} = - x^{3}$ は、 $y$ に関係ない項が含まれているので、非同次微分方程式です。

同次 or 非同次微分方程式

a_{n} \frac{d^{n} y}{d x^{n}} + a_{n - 1} \frac{d^{n - 1} y}{d x^{n - 1}} + \dots + a_{1} \frac{d y}{d x} + a_{0} y = f (x)

で、

f (x) = 0

となっている微分方程式（

y

に関係ない項が一切ない）を同次微分方程式、それ以外の方程式（

y

に関係ない項が含まれている）を非同次微分方程式と呼ぶ。

スポンサードリンク

３．最も基本的な微分方程式（直接積分形）

まずは、最も基本的かつ簡単に解くことができる直接積分形の微分方程式を解いていきましょう。

直接積分形1階の微分方程式が

\frac{d y}{d x} = f^{'} (x)

の形をしている微分方程式を直接積分形と呼び、一般解は任意定数

C

を用いて、

y = \int f^{'} (x) d x = f (x) + C

と解くことができる。

$y$ を $x$ で微分したものが $f^{'} (x)$ なので、当然 $y$ は $f^{'} (x)$ を積分した $f (x) + C$ となります！

このように、任意定数 $C$ を含んだ解のことを一般解と呼びます。

思ったより簡単ですよね！

でも任意定数（積分定数） $C$ 忘れに注意しましょう*4。

1問例題を解いてみましょう。

例題1

微分方程式 $\frac{d y}{d x} = x^{3} - 3 x^{2} + 6 x - 5$ の一般解を求めなさい。

解説1

直接積分形の微分方程式なので、一般解は任意定数 $C$ を用いて $\begin{aligned} y & = \int x^{3} - 3 x^{2} + 6 x - 5 d x \\ = \frac{1}{4} x^{4} - x^{3} + 3 x^{2} - 5 x + C \end{aligned}$ となる。

（答案には「直接積分形」などと書く必要は基本的にはありません。）

４．一般解と特解と特異解

(1) 一般解に出てくる任意定数の数

任意定数 $C$ を含んだ解のことを一般解と呼ぶことを先ほど学びました。

一般解の任意定数の数は、積分をした回数、つまり微分方程式の階数によって決まります。

例えば、

1階微分方程式では、1回積分を行うので、一般解の任意定数の数は1個
2階微分方程式では、2回積分を行うので、一般解の任意定数の数は2個
n階微分方程式では、n回積分を行うので、一般解の任意定数の数はn個

となります。

(2) 特解（特殊解）の求め方

任意定数の値を求めるためには、微分方程式とは別に初期条件（もしくは境界条件）と呼ばれる条件を与える必要があります*5。

初期条件や境界条件などによって求まる解のことを特解（特殊解）と呼びます。

実際に例題を見てみましょう。

例題2

微分方程式 $\frac{d y}{d x} = x^{3} - 3 x^{2} + 6 x - 5$ の一般解は任意定数 $C$ を用いて、 $y = \frac{1}{4} x^{4} - x^{3} + 3 x^{2} - 5 x + C$ と求められた。

初期条件 $y (2) = 0$ を満たす特解を求めなさい。

解説2

初期条件 $y (2) = 0$ は、 $x = 2$ のとき $y = 0$ を満たすことを表している。

ここで、 $x = 2$ を代入すると、 $\begin{aligned} y & = \frac{1}{4} 2^{4} - 2^{3} + 3 \cdot 2^{2} - 5 \cdot 2 + C \\ = 4 - 8 + 12 - 10 + C \\ = - 2 + C \\ = 0 \end{aligned}$ となるので、 $C = 2$ となる。

よって、特解は $y = \frac{1}{4} x^{4} - x^{3} + 3 x^{2} - 5 x + 2$ となる。

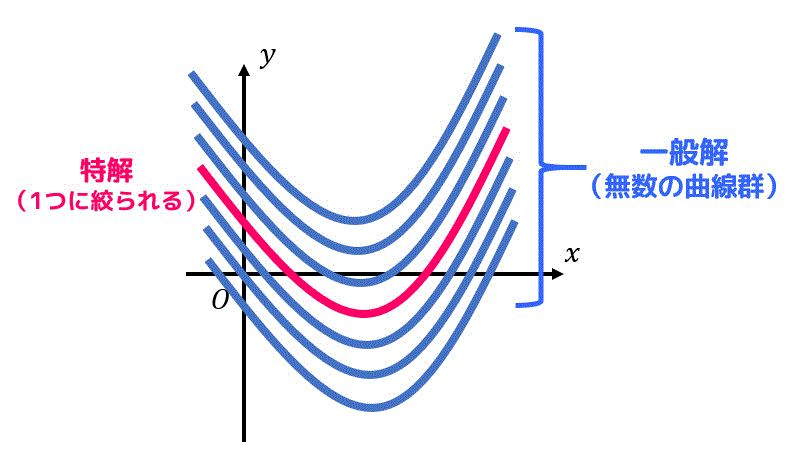
一般解は、無数にある曲線（解）を表しております。

初期条件（境界条件）をあてはめ、特解を求めることで、無数にある曲線の中から1つに絞ることができます。

(3) 特異解

一般解は、無数にある解を示していますが、中には一般解では表せないけど微分方程式の解となっているものがあります。このような解を特異解と呼びます。

例えば、 $\frac{d y}{d x} = y^{2} - y$ の解は、次回説明する変数分離形に変形してから*6解くことで、一般解を任意定数 $C$ を用いて $y = \frac{1}{1 - C e^{x}}$ と求めることができます*7。[脚注へのリンクが出来なかったため、恐れ入りますが手動にて一番下までスクロールいただけますと幸いです。]

しかし、 $y = 0$ のとき、微分方程式の「(左辺) = (右辺) = 0」が成立するので、 $y = 0$ も解といえますよね。

しかし、一般解 $y = \frac{1}{1 + C e^{x}}$ では、任意定数 $C$ がどんな値であったとしても、 $y = 0$ を表現することはできません。

そのため、 $y = 0$ は一般解では表せない解、つまり特異解となります。

なお、次回以降の「うさぎでもわかる微分方程式」では、あくまでも微分方程式の解き方をメインに説明するので、特異解については考えないこととします。

なので、「一般解ですべての微分方程式の解を表現できないこともあるんだな～」って頭に入れておけばOKです。

（この記事では一般解と特解の出し方のみ解説していきます。）

５．直接積分形の応用

せっかく微分方程式をお勉強したので、実際に初等物理に応用してみましょう。

ある物体が動いた距離を $x$ とすると、物体の速度 $v$ は時間 $t$ で微分した $v = \frac{d x}{d t}$ で表すことができます。

さらに、物体の加速度 $a$ は、さらに時間 $t$ で微分して $a = \frac{d v}{d t} = \frac{d}{d t} \frac{d x}{d t} = \frac{d^{2} x}{d t^{2}} (= \frac{d (d x)}{(d t)^{2}})$ となりますね。

では、ここである物体を空に向かって真上に投げたらどれくらいまでの高さまで上がるかを微分方程式を使って計算してみましょう。

地球には重力加速度 $g$ が働くので、 $\frac{d v}{d t} = - g$ が成立しますね。

よって、ある時刻 $t$ における物体の速度 $v$ は、任意定数 $V_{0}$ を用いて $\begin{aligned} v & = \int - g d t \\ = - g t + V_{0} \end{aligned}$ と求めることができます。（任意定数 $V_{0}$ は初速度に相当します。）

さらに、速度が分かったので、変位 $x$ を求めてみましょう。

時刻 $t$ における速度は $- g t + V_{0}$ なので、微分方程式 $\frac{d x}{d t} = - g t + V_{0}$ が成立しますね。

よって、変位 $x$ は任意定数 $h$ を用いて $\begin{aligned} x & = \int - g t + V_{0} d t \\ = - \frac{1}{2} g t^{2} + V_{0} t + h \end{aligned}$ と求めることができます。

任意定数 $h$ は初めの変位 $h$ （初めの物体の高さ）に相当します。

つまり、高さ $h$ から初速度 $V_{0}$ で真上に物体を上げたとき、時刻 $t$ のときの高さ $x$ は、 $x = - \frac{1}{2} g t^{2} + V_{0} t + h$ となることが微分方程式から求められるのです！

ついでに特解を求める練習をしてみましょう。

例えば、はじめの物体の高さ $h = 0$ [m] から、真上に初速度 $V_{0} = 50$ [m/s] で物体を上げたとします。

このときの $t = 5$ 秒後の高さ $x$ は重力加速度を 9.8 $[m / s^{2}]$ とすると、 $\begin{aligned} x & = - \frac{1}{2} g t^{2} + V_{0} t + h \\ = - \frac{1}{2} \cdot 9.8 \cdot 5^{2} + 50 \cdot 5 + 0 \\ = 127.5 \\ ≒ 1.3 \times 10^{2} \end{aligned}$ と計算することができます。

（有効数字2桁を守っています）

６．練習問題

では、微積分のリハビリをかねて、4問ほど練習してみましょう。

ただし、1問は微分方程式の種類分け（線形微分方程式の判別、それぞれの微分方程式が何階の微分方程式なのか）に関する問題となっています。

練習1

つぎの(a)～(d)の微分方程式の中から、

線形微分方程式
2階微分方程式

をすべて選びなさい。

(a) $\frac{d y}{d x} - 5 x^{2} = 0$

(b) ${(\frac{d y}{d x})}^{2} - 6 \frac{d y}{d x} + 9 y = 0$

(d) $(x + 2) (y + 2) \frac{d y}{d x} = x y$

練習2

微分方程式 $\frac{d y}{d x} = \frac{x}{x^{2} + 3}$ について、(1), (2)の問いに答えなさい。

(1) 一般解を求めなさい。
(2) 初期条件 $y (1) = 0$ を満たす特解を求めなさい。

練習3

微分方程式 $\frac{d y}{d x} = \frac{x^{2}}{x^{2} + 1}$ について、(1), (2)の問いに答えなさい。

(1) 一般解を求めなさい。
(2) 初期条件 $y (1) = 1$ を満たす特解を求めなさい。

練習4

微分方程式 $\frac{d y}{d x} = x^{2} e^{x}$ について、(1), (2)の問いに答えなさい。

(1) 一般解を求めなさい。
(2) 初期条件 $y (1) = e$ を満たす特解を求めなさい。

７．練習問題の解答

解答1

線形：(a), (c)
２階：(c)

(a) $\frac{d y}{d x} - 5 x^{2} = 0$ 微分項 $y$ の掛け算となっていないので線形。

一番階数が多い項は $\frac{d y}{d x}$ の1階なので、1階微分方程式。

(b) ${(\frac{d y}{d x})}^{2} - 6 \frac{d y}{d x} + 9 y = 0$

${(\frac{d y}{d x})}^{2}$ の部分が微分項の掛け算になっているので非線形。

一番階数が多い項は ${(\frac{d y}{d x})}^{2}$ , $\frac{d y}{d x}$ の1階なので1階微分方程式。

微分項 $y$ の掛け算となっていないので線形。

一番階数が多い項は $\frac{d^{2} y}{d x^{2}}$ の2階なので2階微分方程式。

(d) $(x + 2) (y + 2) \frac{d y}{d x} = x y$

$(x + 2) (y + 2) \frac{d y}{d x}$ の項が $\frac{d y}{d x}$ と $y$ の掛け算となっているので非線形。

一番階数が多い項は $(x + 2) (y + 2) \frac{d y}{d x}$ の1階なので1階微分方程式。

解答2

(1)

直接積分形の微分方程式なので、一般解は任意定数 $C$ を用いて $\begin{aligned} y & = \int \frac{x}{x^{2} + 3} d x \\ = \frac{1}{2} \int \frac{2 x}{x^{2} + 3} d x \\ = \frac{1}{2} \log (x^{2} + 3) + C \end{aligned}$ となる。

(2)

初期条件 $y (1) = 0$ なので、 $x = 1$ のとき $y = 0$ を満たす。

ここで、 $x = 1$ を代入すると、 $\begin{aligned} y & = \frac{1}{2} \log (x^{2} + 3) + C \\ = \frac{1}{2} \log 4 + C \\ = \frac{1}{2} \log 2^{2} + C \\ = \log 2 + C \\ = 0 \end{aligned}$ となるので、 $C = - \log 2$ となる。

よって、特解は $y = \frac{1}{2} \log (x^{2} + 3) - \log 2$ となる。

解答3

(1)

直接積分形の微分方程式なので、一般解は任意定数 $C$ を用いて $\begin{aligned} y & = \int \frac{x^{2}}{x^{2} + 1} d x \\ = \int (1 - \frac{1}{x^{2} + 1}) d x \\ = \int 1 d x - \int \frac{1}{1 + x^{2}} d x \\ = x - \tan^{- 1} x + C \end{aligned}$ となる。

(2)

初期条件 $y (1) = 1$ なので、 $x = 1$ のとき $y = 1$ を満たす。

ここで、 $x = 1$ を代入すると、 $\begin{aligned} y & = x - \tan^{- 1} x + C \\ = 1 - \tan^{- 1} 1 + C \\ = 1 - \frac{π}{4} + C \\ = 1 \end{aligned}$ となるので、 $C = \frac{π}{4}$ となる。

よって、特解は $y = x - \tan^{- 1} x + \frac{π}{4}$ となる。

解答4

(1)

直接積分形の微分方程式なので、一般解は任意定数 $C$ を用いて $\begin{aligned} y & = \int x^{2} e^{x} d x \\ = x^{2} e^{x} - 2 x e^{x} + 2 e^{x} + C \\ = (x^{2} - 2 x + 2) e^{x} + C \end{aligned}$ となる。

部分積分については、連鎖公式（ブンブン）を使って計算式を省略しております。

ブンブン積分について詳しくは下の記事をご覧ください。

www.momoyama-usagi.com

(2)

初期条件 $y (1) = e$ なので、 $x = 1$ のとき $y = e$ を満たす。

ここで、 $x = 1$ を代入すると、 $\begin{aligned} y & = (x^{2} - 2 x + 2) e^{x} + C \\ = e + C \\ = e \end{aligned}$ となるので、 $C = 0$ となる。

よって、特解は $y = (x^{2} - 2 x + 2) e^{x} + C$ となる。

８．さいごに

今回は、様々な微分方程式を解く前段階として、

微分方程式ってなに？
微分方程式の種類について
簡単な微分方程式を解いてみよう！

などについてまとめていきたいと思います。

次回からは、実際に様々な微分方程式のパターン、解き方をまとめていきたいと思います。

ではまた次回。

*1:この微分方程式は、直接積分形なので、任意定数 $C$ を用いて $\begin{aligned} y & = \int 2 x + 3 d x \\ = x^{2} + 3 x + C \end{aligned}$ と簡単に解くことができます。直接積分形については、本記事の第3章をご覧ください。

*2:XXはPartXXのXXが入ります。今回の場合はPart00なので、ode00

*3: $y$ , $\frac{d y}{d x} = y^{'}$ , $\frac{d^{2} y}{d x^{2}} = y^{″}$ , … が線形な項である。

*4:念のため、なぜ任意定数が必要なのかを説明すると、例えば $f (x)$ を微分して $\frac{d y}{d x} = 2 x$ になるような関数としては、 $f (x) = x^{2}$ のほかに、 $f (x) = x^{2} + 1$ や $f (x) = x^{2} + 114514$ など様々な数があります。そのような数は無限にあるのでいちいち書いていたらキリがありませんですね。そこで、任意定数 $C$ を用いて、 $f (x) = x^{2} + C$ のようにあらわすことですべての解を表現しているのです。

*5:初期条件は、ある1点の条件 $y (x) = y$ を指します。例えば、 $y (2) = 3$ であれば、 $x = 2$ のとき、 $y$ の値は $y = 3$ となることを指します。一方、境界条件は、2点 $y (x_{1}) = y_{1}$ , $y (x_{2}) = y_{2}$ 、あるいは2点以上の条件を指します。境界条件という言葉は、どちらかというと常微分方程式よりも偏微分方程式を解く場合によく使われます。

*6:「直接積分形っぽくない？」と思う人もいるかもしれませんが、右辺が $f (x)$ ではなく、 $f (y)$ になっているので直接積分形ではありません。

*7: 途中計算式を以下に記します。まず、 $\frac{1}{y^{2} - y} \frac{d y}{d x} = 1$ のように変形してから、両辺に $d x$ をかけて $\int \frac{1}{y^{2} - y} d y = \int 1 d x$ の積分計算の形にします。 $\begin{aligned} \int \frac{1}{y^{2} - y} \frac{d y}{d x} & = \int \frac{1}{y^{2} - y} d y \\ = \int \frac{1}{y - 1} - \frac{1}{y} \\ = \log | y - 1 | - \log | y | \\ = \log | \frac{y - 1}{y} | \end{aligned}$ $x$ に関する積分計算。 $\int 1 d x = x$ あとはお互いの積分結果を等号で結び、形をきれいにすればOK。 $\begin{aligned} \log | \frac{y - 1}{y} | & = x + C^{'} \\ | \frac{y - 1}{y} | & = C^{'} e^{x} \\ \pm \frac{y - 1}{y} & = C^{'} e^{x} \\ \frac{y - 1}{y} & = C e^{x} \\ 1 - \frac{1}{y} & = C e^{x} \\ \frac{1}{y} & = 1 - C e^{x} \\ y & = \frac{1}{1 - C e^{x}} \end{aligned}$ ※途中で $C = \pm e^{C^{'}}$ とおいた。