うさぎでもわかる信号処理・制御工学　第14羽　高速フーリエ変換(FFT)

2022年5月7日 2023年5月30日 50分30秒

ももうさ

スポンサードリンク

こんにちは、ももやまです！

今回は離散フーリエ変換を工夫して早く解くアルゴリズム、高速フーリエ変換(FFT / Fast Fourier Transform)について見ていきましょう！

※ この記事は離散フーリエ変換(DFT)の知識が必須になってきます。もしまだ離散フーリエ変換(DFT)があやふやな人や、よくわからないなぁという人は、下の記事にて離散フーリエ変換(DFT)の復習をしてから、こちらの記事に戻ってください。

1. 離散フーリエ変換と行列 [復習]
2. 高速フーリエ変換(FFT)の仕組み
3. 高速フーリエ変換の練習問題
4. バタフライ演算（計算の可視化）
5. プログラム

スポンサードリンク

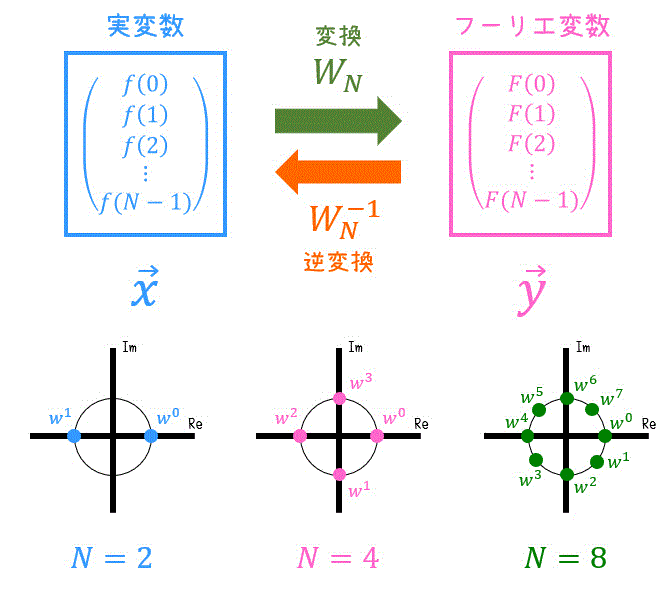
1. 離散フーリエ変換と行列 [復習]

まず、実変数 \( f(n) \) をフーリエ変数 \( F(k) \) に変換する \( N \) 点離散フーリエ変換の公式を確認しましょう。

\[\begin{align*}
F(k) & = \sum^{N-1}_{n = 0} f(n) e^{- i \frac{2 \pi k}{N} n }
\end{align*}\]

この式を簡単にするためには、 \( w = e^{- \frac{2 \pi}{N} i } \) と呼ばれる回転因子とおけばOKでしたね。

実際に回転因子 \( w = e^{- \frac{2 \pi}{N} i } \) を用いて変形すると、下のような式に変形することができます。\[
F(k) = \sum^{N-1}_{n = 0} f(n) w^{kn}
\]さらにこの式を行列で表すことを考えましょう。

\( N \) 点の実変数 \( f(0) \), \( f(1) \), … \( f(N-1) \) を離散フーリエ変数 \( F(0) \), \( F(1) \), … \( F(N-1) \) へ変換するための式は、下のように行列を用いた連立方程式の形で表すことができますね。

\[
\left( \begin{array}{ccc} F(\textcolor{magenta}{0}) \\ F(\textcolor{magenta}{1}) \\ F(\textcolor{magenta}{2}) \\ \vdots \\ F( \textcolor{magenta}{N-1} ) \end{array} \right) =

\underbrace{ \left( \begin{array}{ccc} w^{\textcolor{magenta}{0} \cdot \textcolor{deepskyblue}{0}} & w^{\textcolor{magenta}{0} \cdot \textcolor{deepskyblue}{1}} & w^{\textcolor{magenta}{0} \cdot \textcolor{deepskyblue}{2}} & \cdots & w^{\textcolor{magenta}{0} \cdot \ ( \textcolor{deepskyblue}{N-1} )}
\\ w^{\textcolor{magenta}{1} \cdot \textcolor{deepskyblue}{0}} & w^{\textcolor{magenta}{1} \cdot \textcolor{deepskyblue}{1}} & w^{\textcolor{magenta}{1} \cdot \textcolor{deepskyblue}{2}} & \cdots & w^{\textcolor{magenta}{1} \cdot ( \textcolor{deepskyblue}{N-1} )} \\ w^{\textcolor{magenta}{2} \cdot \textcolor{deepskyblue}{0}} & w^{\textcolor{magenta}{2} \cdot \textcolor{deepskyblue}{1}} & w^{\textcolor{magenta}{2} \cdot \textcolor{deepskyblue}{2}} & \cdots & w^{\textcolor{magenta}{2} \cdot ( \textcolor{deepskyblue}{N-1} )}
\\ & & & \ddots & \\
w^{( \textcolor{magenta}{N-1} ) \cdot \textcolor{deepskyblue}{0}} & w^{( \textcolor{magenta}{N-1} ) \cdot \textcolor{deepskyblue}{1}} & w^{( \textcolor{magenta}{N-1} ) \cdot \textcolor{deepskyblue}{2}} & \cdots & w^{( \textcolor{magenta}{N-1} ) \cdot ( \textcolor{deepskyblue}{N-1} )}
\end{array} \right) }_{{\mathrm{DFT行列 (変換行列)} \ W_N}}
\left( \begin{array}{ccc} f(\textcolor{deepskyblue}{0}) \\ f(\textcolor{deepskyblue}{1}) \\ f(\textcolor{deepskyblue}{2}) \\ \vdots \\ f( \textcolor{deepskyblue}{N-1} ) \end{array} \right)
\]

しかし、この行列計算を行うためには、「\( N \) 次正方行列であるDFT行列の各成分と対応するベクトルの成分を掛け、その結果を足す」操作を \( N^2 \) 回行う必要があります^[1]\( N \) 次正方行列の成分の数はN×N個あるため。。

つまり、計算量が \( O(N^2) \) と少し重たいものになってしまいます。

そこで、離散フーリエ変換の法則性に着目し、より早く離散フーリエ変換を行うアルゴリズム、高速フーリエ変換を紹介していきましょう！

スポンサードリンク

2. 高速フーリエ変換(FFT)の仕組み

実際に \( N = 8 \) のときの離散フーリエ変換(DFT)を使って、高速フーリエ変換の仕組みを説明していきましょう。

FFTをする前の下準備

\( N = 8 \) のときの離散フーリエ変換の変換式は、変換行列 \( W_8 \) を用いて下のようにかけますね。

\[
\underbrace{ \left( \begin{array}{ccc} F_8 (0) \\ F_8 (1) \\ F_8 (2) \\ F_8 (3) \\ F_8 (4) \\ F_8 (5) \\ F_8 (6) \\ F_8 (7) \end{array} \right) }_{\vec{y}_8} =
\underbrace{ \left( \begin{array}{ccc}
w_8^{\textcolor{magenta}{0} \cdot \textcolor{deepskyblue}{0}} & w_8^{\textcolor{magenta}{0} \cdot \textcolor{deepskyblue}{1}} & w_8^{\textcolor{magenta}{0} \cdot \textcolor{deepskyblue}{2}} & w_8^{\textcolor{magenta}{0} \cdot \textcolor{deepskyblue}{3}} & w_8^{\textcolor{magenta}{0} \cdot \textcolor{deepskyblue}{4}} & w_8^{\textcolor{magenta}{0} \cdot \textcolor{deepskyblue}{5}} & w_8^{\textcolor{magenta}{0} \cdot \textcolor{deepskyblue}{6}} & w_8^{\textcolor{magenta}{0} \cdot \textcolor{deepskyblue}{7}} \\
w_8^{\textcolor{magenta}{1} \cdot \textcolor{deepskyblue}{0}} & w_8^{\textcolor{magenta}{1} \cdot \textcolor{deepskyblue}{1}} & w_8^{\textcolor{magenta}{1} \cdot \textcolor{deepskyblue}{2}} & w_8^{\textcolor{magenta}{1} \cdot \textcolor{deepskyblue}{3}} & w_8^{\textcolor{magenta}{1} \cdot \textcolor{deepskyblue}{4}} & w_8^{\textcolor{magenta}{1} \cdot \textcolor{deepskyblue}{5}} & w_8^{\textcolor{magenta}{1} \cdot \textcolor{deepskyblue}{6}} & w_8^{\textcolor{magenta}{1} \cdot \textcolor{deepskyblue}{7}} \\
w_8^{\textcolor{magenta}{2} \cdot \textcolor{deepskyblue}{0}} & w_8^{\textcolor{magenta}{2} \cdot \textcolor{deepskyblue}{1}} & w_8^{\textcolor{magenta}{2} \cdot \textcolor{deepskyblue}{2}} & w_8^{\textcolor{magenta}{2} \cdot \textcolor{deepskyblue}{3}} & w_8^{\textcolor{magenta}{2} \cdot \textcolor{deepskyblue}{4}} & w_8^{\textcolor{magenta}{2} \cdot \textcolor{deepskyblue}{5}} & w_8^{\textcolor{magenta}{2} \cdot \textcolor{deepskyblue}{6}} & w_8^{\textcolor{magenta}{2} \cdot \textcolor{deepskyblue}{7}} \\
w_8^{\textcolor{magenta}{3} \cdot \textcolor{deepskyblue}{0}} & w_8^{\textcolor{magenta}{3} \cdot \textcolor{deepskyblue}{1}} & w_8^{\textcolor{magenta}{3} \cdot \textcolor{deepskyblue}{2}} & w_8^{\textcolor{magenta}{3} \cdot \textcolor{deepskyblue}{3}} & w_8^{\textcolor{magenta}{3} \cdot \textcolor{deepskyblue}{4}} & w_8^{\textcolor{magenta}{3} \cdot \textcolor{deepskyblue}{5}} & w_8^{\textcolor{magenta}{3} \cdot \textcolor{deepskyblue}{6}} & w_8^{\textcolor{magenta}{3} \cdot \textcolor{deepskyblue}{7}} \\
w_8^{\textcolor{magenta}{4} \cdot \textcolor{deepskyblue}{0}} & w_8^{\textcolor{magenta}{4} \cdot \textcolor{deepskyblue}{1}} & w_8^{\textcolor{magenta}{4} \cdot \textcolor{deepskyblue}{2}} & w_8^{\textcolor{magenta}{4} \cdot \textcolor{deepskyblue}{3}} & w_8^{\textcolor{magenta}{4} \cdot \textcolor{deepskyblue}{4}} & w_8^{\textcolor{magenta}{4} \cdot \textcolor{deepskyblue}{5}} & w_8^{\textcolor{magenta}{4} \cdot \textcolor{deepskyblue}{6}} & w_8^{\textcolor{magenta}{4} \cdot \textcolor{deepskyblue}{7}} \\
w_8^{\textcolor{magenta}{5} \cdot \textcolor{deepskyblue}{0}} & w_8^{\textcolor{magenta}{5} \cdot \textcolor{deepskyblue}{1}} & w_8^{\textcolor{magenta}{5} \cdot \textcolor{deepskyblue}{2}} & w_8^{\textcolor{magenta}{5} \cdot \textcolor{deepskyblue}{3}} & w_8^{\textcolor{magenta}{5} \cdot \textcolor{deepskyblue}{4}} & w_8^{\textcolor{magenta}{5} \cdot \textcolor{deepskyblue}{5}} & w_8^{\textcolor{magenta}{5} \cdot \textcolor{deepskyblue}{6}} & w_8^{\textcolor{magenta}{5} \cdot \textcolor{deepskyblue}{7}} \\
w_8^{\textcolor{magenta}{6} \cdot \textcolor{deepskyblue}{0}} & w_8^{\textcolor{magenta}{6} \cdot \textcolor{deepskyblue}{1}} & w_8^{\textcolor{magenta}{6} \cdot \textcolor{deepskyblue}{2}} & w_8^{\textcolor{magenta}{6} \cdot \textcolor{deepskyblue}{3}} & w_8^{\textcolor{magenta}{6} \cdot \textcolor{deepskyblue}{4}} & w_8^{\textcolor{magenta}{6} \cdot \textcolor{deepskyblue}{5}} & w_8^{\textcolor{magenta}{6} \cdot \textcolor{deepskyblue}{6}} & w_8^{\textcolor{magenta}{6} \cdot \textcolor{deepskyblue}{7}} \\
w_8^{\textcolor{magenta}{7} \cdot \textcolor{deepskyblue}{0}} & w_8^{\textcolor{magenta}{7} \cdot \textcolor{deepskyblue}{1}} & w_8^{\textcolor{magenta}{7} \cdot \textcolor{deepskyblue}{2}} & w_8^{\textcolor{magenta}{7} \cdot \textcolor{deepskyblue}{3}} & w_8^{\textcolor{magenta}{7} \cdot \textcolor{deepskyblue}{4}} & w_8^{\textcolor{magenta}{7} \cdot \textcolor{deepskyblue}{5}} & w_8^{\textcolor{magenta}{7} \cdot \textcolor{deepskyblue}{6}} & w_8^{\textcolor{magenta}{7} \cdot \textcolor{deepskyblue}{7}}
\end{array} \right) }_{\mathrm{変換行列} \ W_8}
\underbrace{ \left( \begin{array}{ccc} f_8 (0) \\ f_8 (1) \\ f_8 (2) \\ f_8 (3) \\ f_8 (4) \\ f_8 (5) \\ f_8 (6) \\ f_8 (7) \end{array} \right) }_{\vec{x}_8}
\]

さらに、\( w_8^8 = 1 \) を代入することによりより、変換行列を下のように変形することができますね。

成分内の \( w^a \) の \( a \) の部分を \( 0 \leqq a < 8 \) になるように書き換えたら、いよいよ高速フーリエ変換アルゴリズムの開始です。

高速フーリエ変換は分割統治法！

高速フーリエ変換のアルゴリズムを簡単に説明すると、下の1-4と図で表されます。

離散フーリエ変換の連立方程式を、変換行列 \( W_N \) の偶数行、奇数行の2種類に分割する。（分割時には実変数ベクトル \( \vec{x}_N \) の値が変わる）
偶数行、奇数行に分割する作業を \( N = 1 \) になるまで繰り返す
各行ごとに \( N = 1 \) のときの実変数 \( \vec{x}_1 \) の値をそのままフーリエ変数とする
3をまとめたものが高速フーリエ変換の結果となる

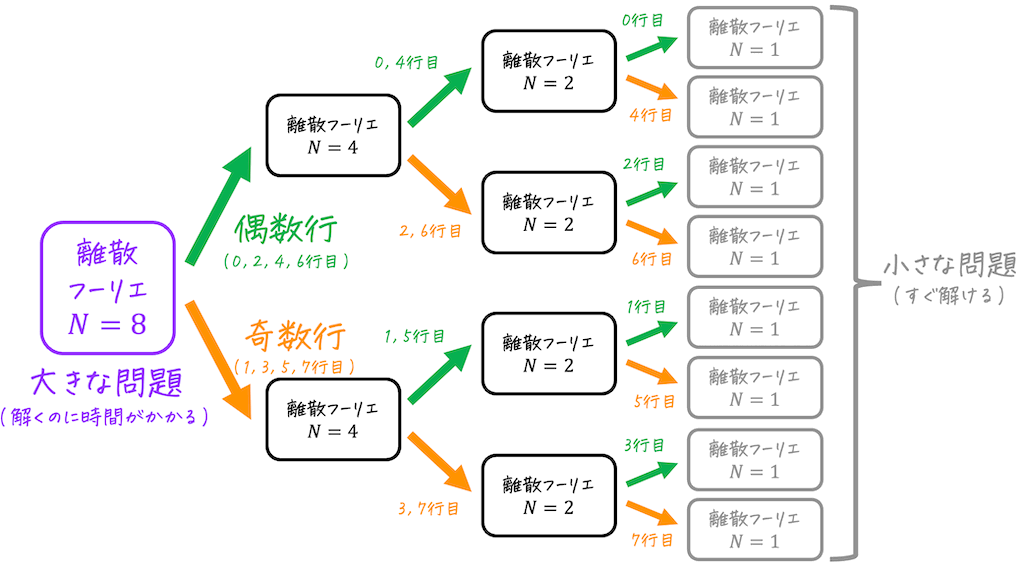
このように、解くのに時間がかかる大きな問題を、すぐ解ける小さな問題に分割し、小さな問題を全て解くことで最終的に元の大きな問題を解く方法を分割統治法と呼びます。

[注意] この高速フーリエ変換の記事では、行列の行数（列数）を数える際に1行目からではなく、0行目からカウントすることにします。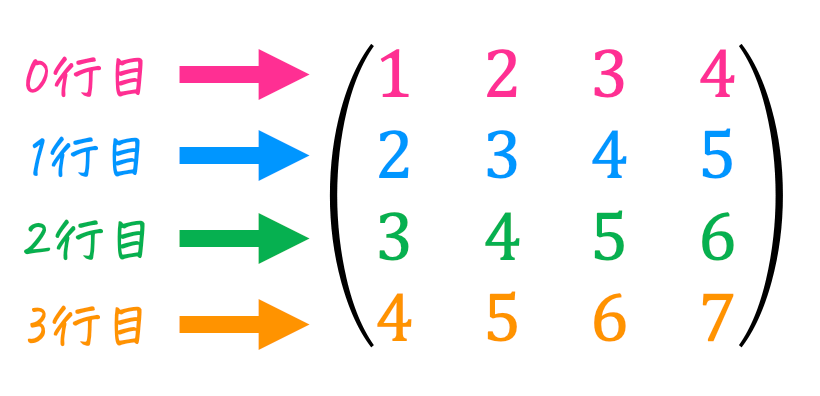

具体例で高速フーリエ変換のアルゴリズムを確認

ここからは、\( N = 8 \) の離散フーリエ変換を使って「高速フーリエ変換のアルゴリズム」を確認していきましょう。

なお、ここからは、\( N \) 点離散フーリエ変換の変数を次のように定義します。

実変数 \( f_N (k) \)
フーリエ変数(計算結果) \( F_N (k) \)
回転因子 \( w_N = e^{ - \frac{2 \pi }{N} i } \)

\( N = 8 \) → \( N = 4 \) への分割

[Step1] 偶数行と奇数行に分ける

まずは、変換行列 \( W_8 \) の偶数行（0, 2, 4,… 行目）、奇数行（1, 3, 5,… 行目）ごとに着目します。

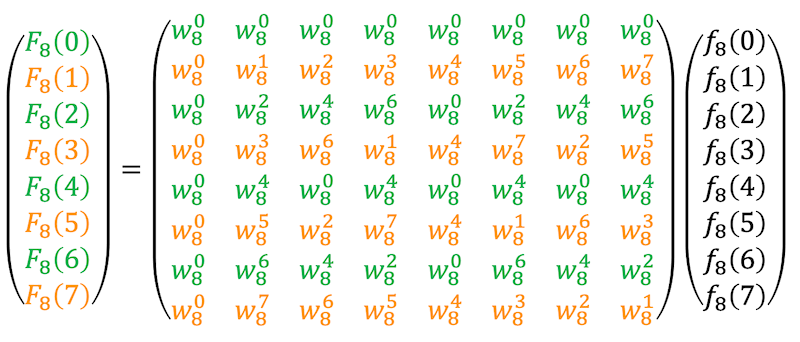
次に連立方程式を

\( W_8 \) の偶数行だけ集めた連立方程式
\( W_8 \) の奇数行だけ集めた連立方程式

の2つに分割します。

すると、次の2つの連立方程式に分割ができますね。

[Step2] 偶数行の変形

偶数行の連立方程式は、緑枠の部分に共通点が見られますね。

なので、連立方程式を4次正方行列が出てくる形に書き換えることができますね。

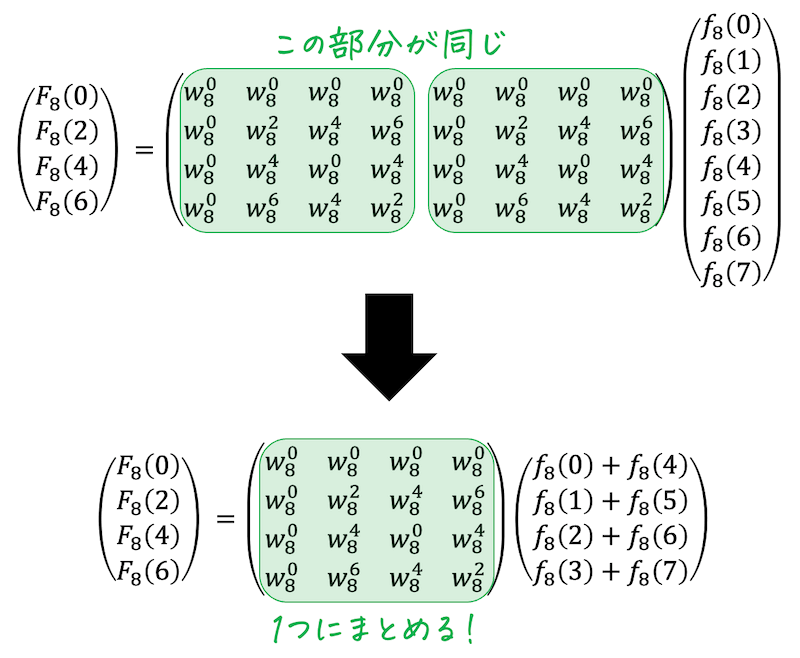
この計算結果を、\( N = 4 \) の離散フーリエ変換に代入し、さらに回転因子を \( w_4 \) バージョンに書き換えます。

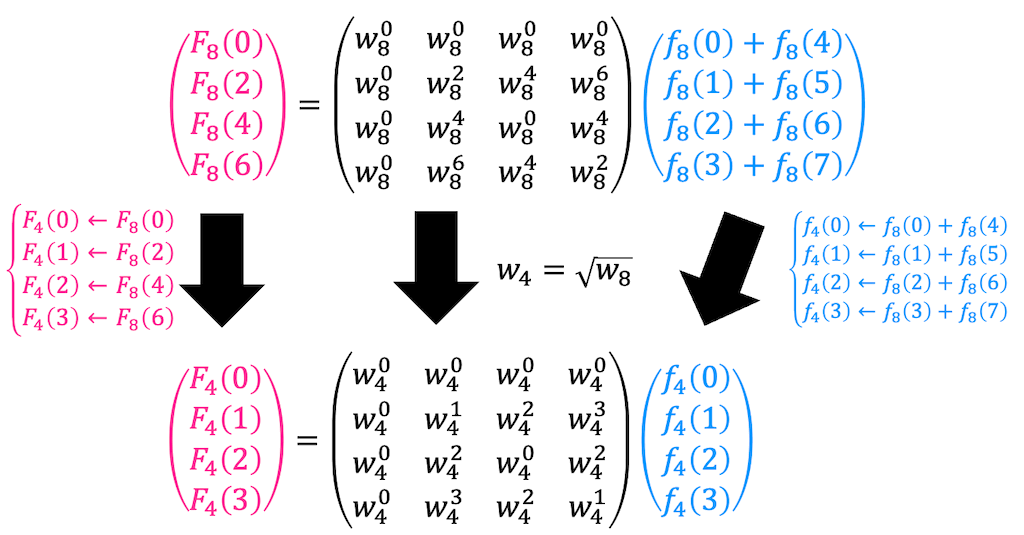
すると、\( N = 4 \) の離散フーリエ変換を解く問題となりますね。

[Step3] 奇数行の変形

奇数行は、そのままだと係数行列（4行8列の行列）の法則性を見つけることができません。

そこで、右側4列（青枠部分）に \( w_8^4 = -1 \) を適用してあげましょう。

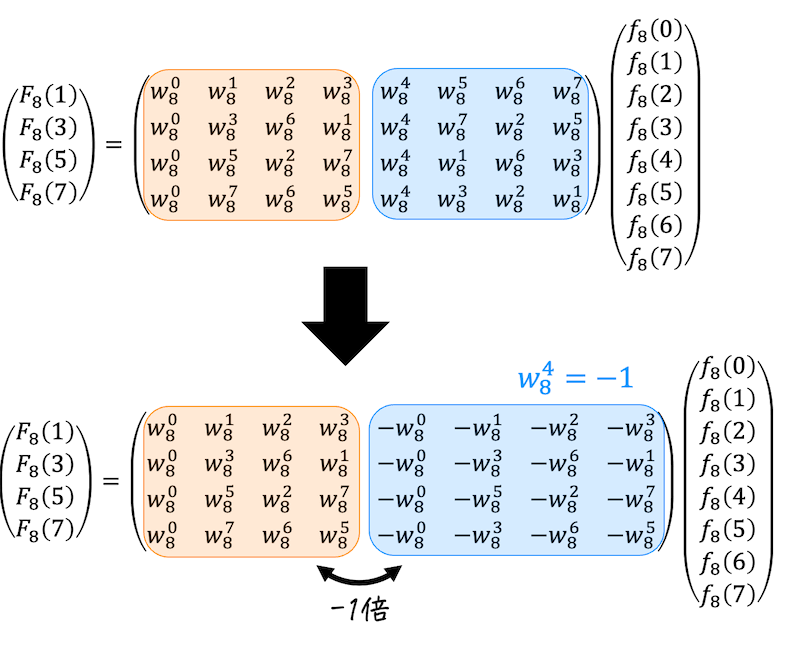
すると、オレンジ色の枠部分を-1倍したものがそのまま青色の枠部分となっていますね。

なので、Step2と同じように連立方程式を4次正方行列が出てくる形に書き換えることができますね。

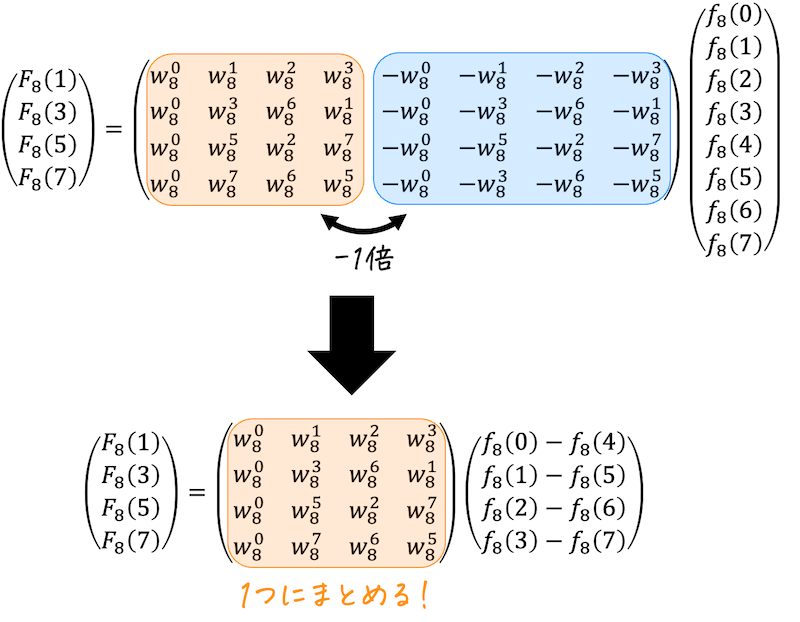
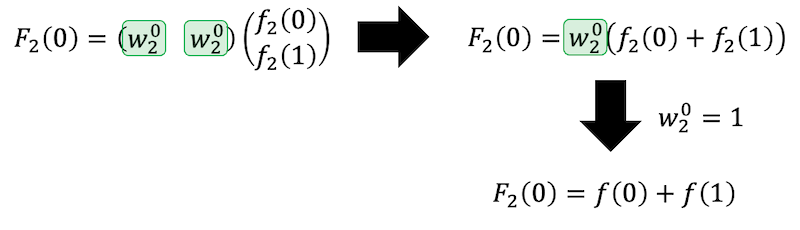
さらに、紫で囲った部分（行列の0行目）がすべて \( w_8^0 \) になるように変形を行います。

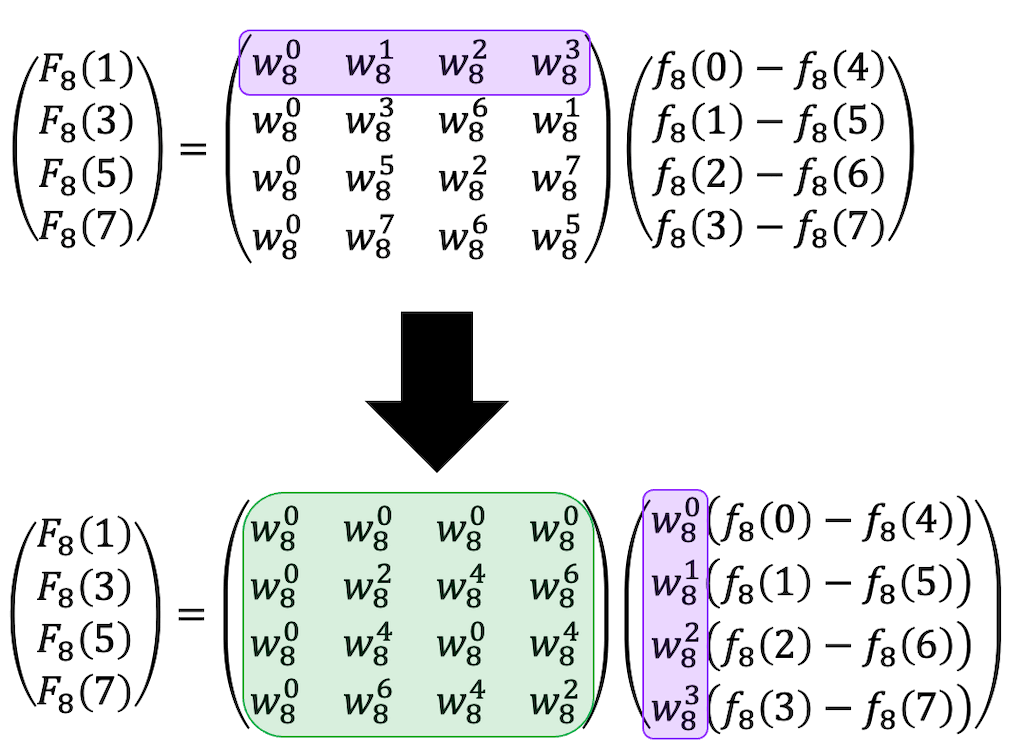
すると、4次正方行列がStep2（偶数行）のときと同じになりますね。

あとは、Step2と同じように、計算結果を、\( N = 4 \) の離散フーリエ変換に代入し、回転因子を \( w_4 \) バージョンに書き換えればOKです。

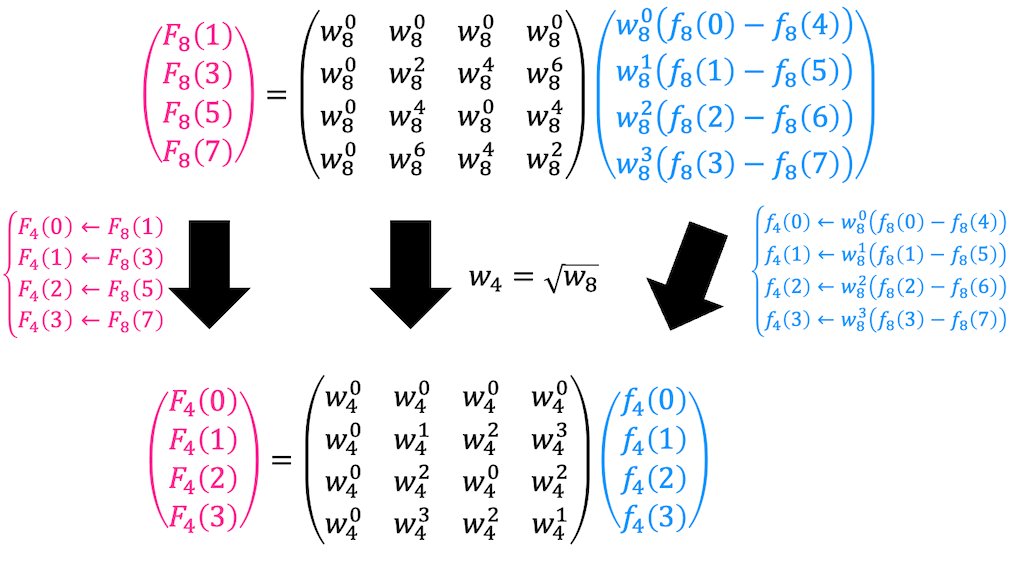
これで、奇数行の連立方程式も、\( N = 4 \) の離散フーリエ変換を解く問題になりましたね。

\( N = 4 \) → \( N = 2 \) への分割

[Step1] 偶数行と奇数行に分ける

\( N = 8 \) の離散フーリエ変換の偶数行と奇数行（の行列）に着目することにより、\( N = 4 \) の離散フーリエ変換2つの式に変形することができましたね。

この \( N = 4 \) の離散フーリエ変換も、偶数行と奇数行に着目して2つに分解してあげましょう。

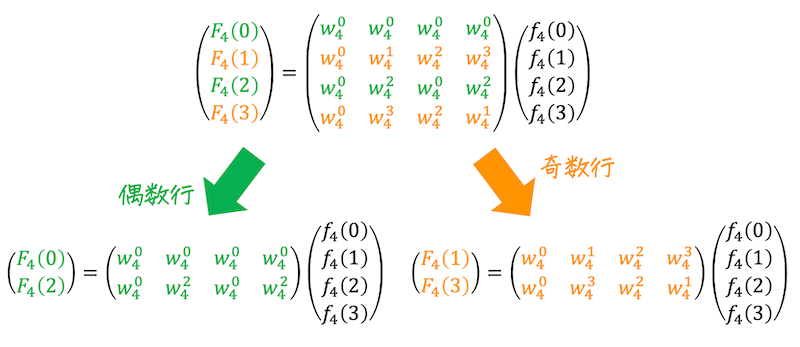
[Step2] 偶数行の変形

\( N = 8 \) のときと同じように、緑色の枠部分に着目し、行列部分を2次の正方行列に書き換えます。

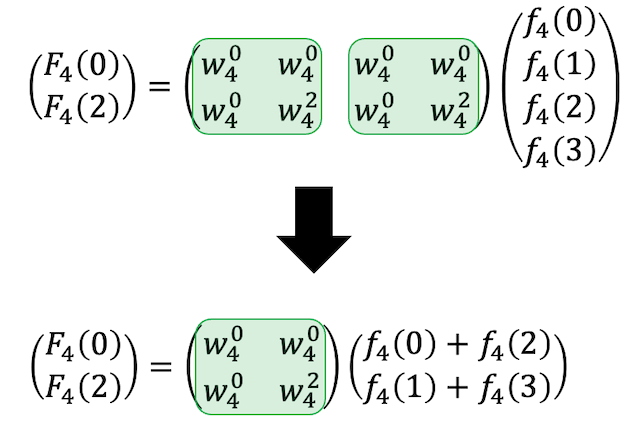
[Step3] 奇数行の変形

奇数行の変形も、\( N = 8 \) のときと同じように1, 2を適用し、偶数行の変形で出てきた緑色の枠と同じ形にしましょう。

行列の右半分部分（青色の枠）に \( w_4^2 = -1 \) を適用
行列の0行目（紫色の枠）の成分を \( w_4^0 \) にするように変形

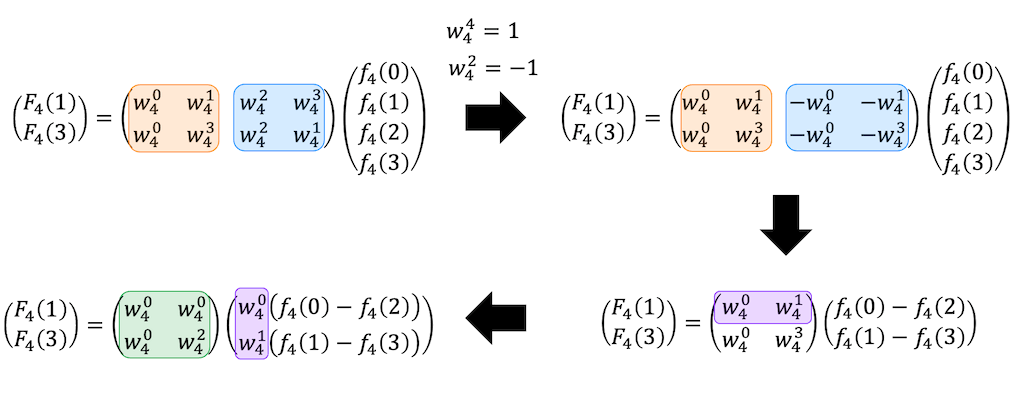
変形ができたら、あとは偶数行、奇数行それぞれ代入をすればOKです。

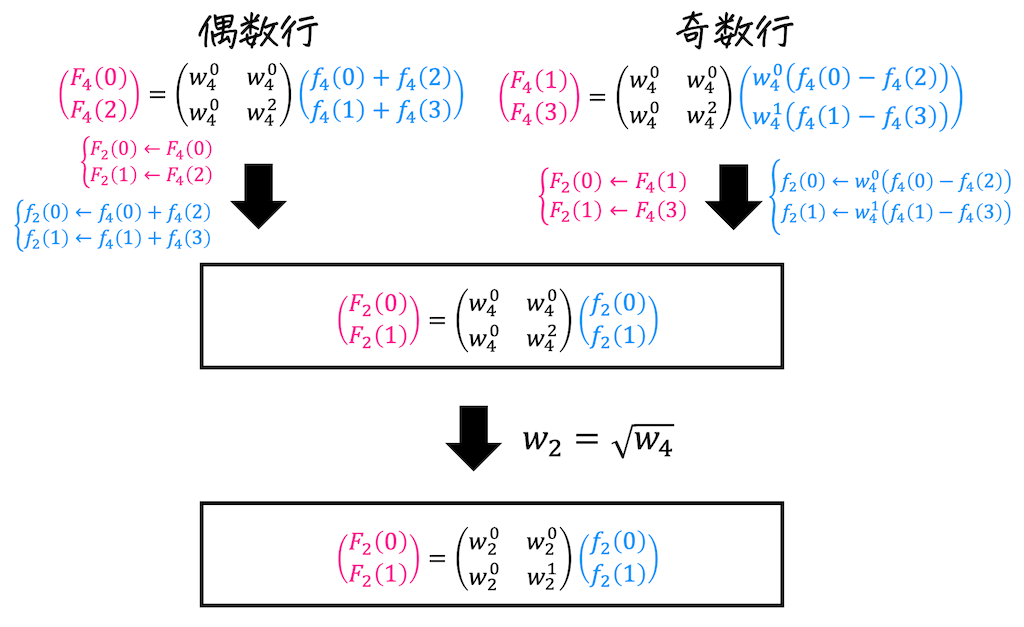
すると、\( N = 8 \) の離散フーリエ変換が4つの \( N = 2 \) の離散フーリエ変換の式に変形できましたね。

\( N = 2 \) → \( N = 1 \) への分割

4つの離散フーリエ変換の変換式を、それぞれの式（行列）ごとに偶数行と奇数行の2種類に分けましょう。すると \( N = 1 \) の離散フーリエ変換式が8種類になりますね。

[Step1] 偶数行と奇数行に分ける

これまでと同じように偶数行と奇数行に分けます。

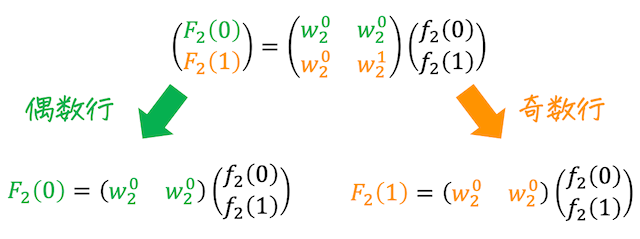
[Step2] 偶数行の変換

[Step3] 奇数行の変換

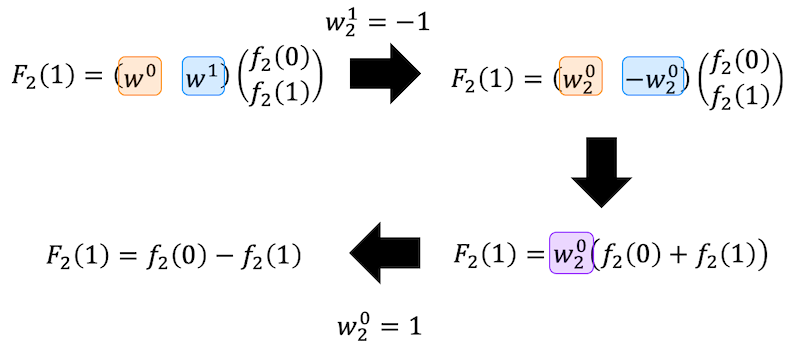
これで、\( N = 1 \) の離散フーリエ変換に分解することができましたね。

あとは、それぞれの \( N = 1 \) の離散フーリエ変換をあわせることで \( N = 8 \) の離散フーリエ変換を求めることができます。

これが高速フーリエ変換のアルゴリズムです！

高速フーリエ変換が使える条件

高速フーリエ変換(FFT)では偶数行と奇数行に半分ずつ分割していき、最終的に1行の式にしていく処理を行います。

そのため、この処理(FFT)を行えるのは、\( N \) が2のべき乗（1, 2, 4, 8, 16, 32, 64, …）のときのみです。

（2のべき乗以外の場合、分解の途中で偶数行と奇数行でちょうど半分ずつ分割することができないため^[2]例えば \( N = 5 \) だとすると、偶数行が0, 2, 4行目の3行分、奇数行が1, … Continue reading。）

高速フーリエ変換アルゴリズム

\( N \) 個の実変数の成分からなるベクトルを \( \vec{x}_0 \), \( \vec{x}_1 \) と2つのベクトルに分解する。
（つまり2つのベクトルの要素数は \(N/2\) 個になる。）

\( \vec{x}_0 \) に対して、次の計算を行う。\[\vec{x}_{0} = \left( \begin{array}{ccc} f(0) + f(N/2) \\ f(1) + f(N/2+1) \\ \vdots \\ f(N/2-1) + f(N-1) \end{array} \right)\]

\( \vec{x}_1 \) に対して、次の計算を行う。ただし、\( w_N = e^{ - \frac{2 \pi}{N} i } \) である。
\[\vec{x}_{1} = \left( \begin{array}{ccc} w_N^0 \left\{ f(0) - f(N/2) \right\} \\ w_N^1 \left\{ f(1) + f(N/2+1) \right\} \\ \vdots \\ W_N^{ \frac{N}{2} - 1 } \left\{ f(N/2-1) + f(N-1) \right\} \end{array} \right)\]

分けたベクトルの要素数が1（つまり \( N = 1 \)）でなければ、1に戻って再び分解をする

最後に、\( N = 1 \) になったベクトルの要素を順番に合わせることで、離散フーリエ変換の結果となる。

\( N \) が2のべき乗（1, 2, 4, 8, 16, 32, 64, …）の場合のみ、高速フーリエ変換を行うことができる。

高速フーリエ変換の計算量

ここで、高速フーリエ変換の計算量を確認しましょう。

高速フーリエ変換の処理内容は、次の3つに分けることができますね。

\( N = 1 \) になるまで \( N \) 点離散フーリエ変換を \( N/2 \) 点離散フーリエ変換に分解する
各分解ごとに \( N \) 回足し算 or 引き算を行う
（偶数行、奇数行に関わらず必ず加減算はするため）
各分解ごとに \( N/2 \) 回掛け算を行う
（掛け算は奇数行のみに行うため。）

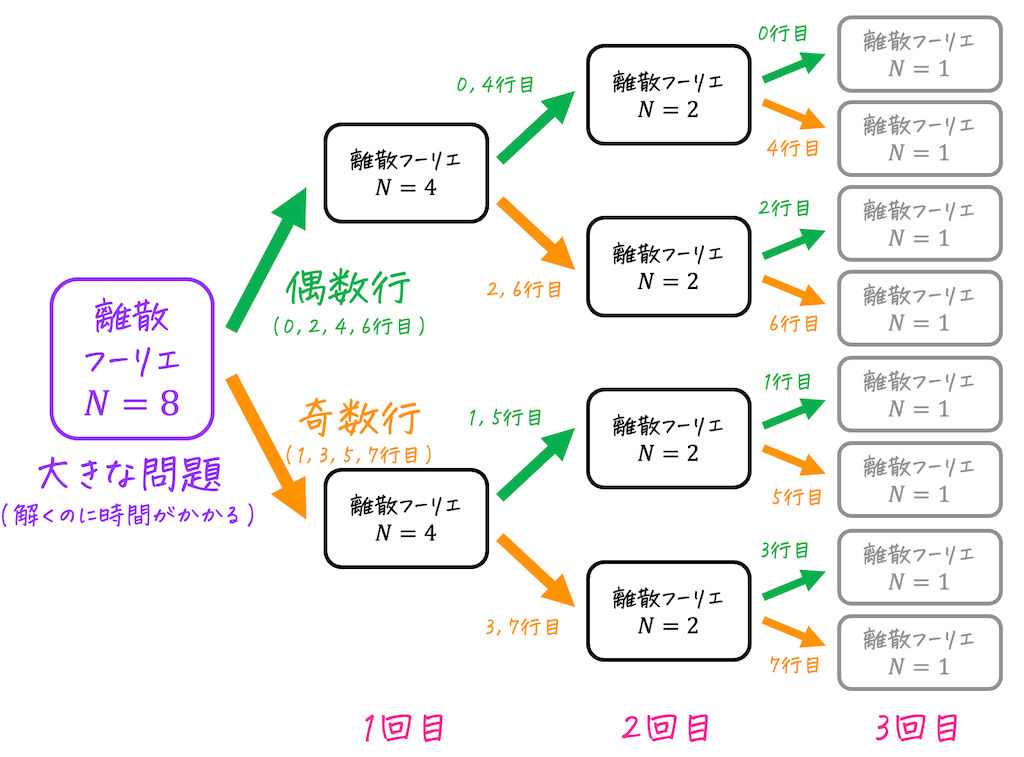
まず、分解処理ですが、分解のたび、\( N \) が1/2になるのですがら、\( N \) が1になるまでの分解回数は \( \log_2 N \) 回^[3]\( \log_2 N = A \) は \( 2^A = N \) を満たすような \( A \) を求めるのと同じ計算になります。となりますね。

例えば、\( N = 8 \) であれば、8→4、4→2、2→1と3回で分解でき、たしかに \( \log_2 8 = 3 \) の計算と一致していますね。

次に、各分解ごとの計算ですが、行数の偶奇に関わらず、必ず足し算か引き算は行います。そのため、各分解ごとの加減算の回数は \( N \) 回となります。

さらに、奇数行（オレンジ色の矢印）に対しては加減算（正確には引き算のみ）後に回転因子を掛けますね。奇数は全体の半分なので、各処理ごとに \( N/2 \) 回の掛け算が行われます。

よって、高速フーリエ変換の計算回数は次のように求めることができます！

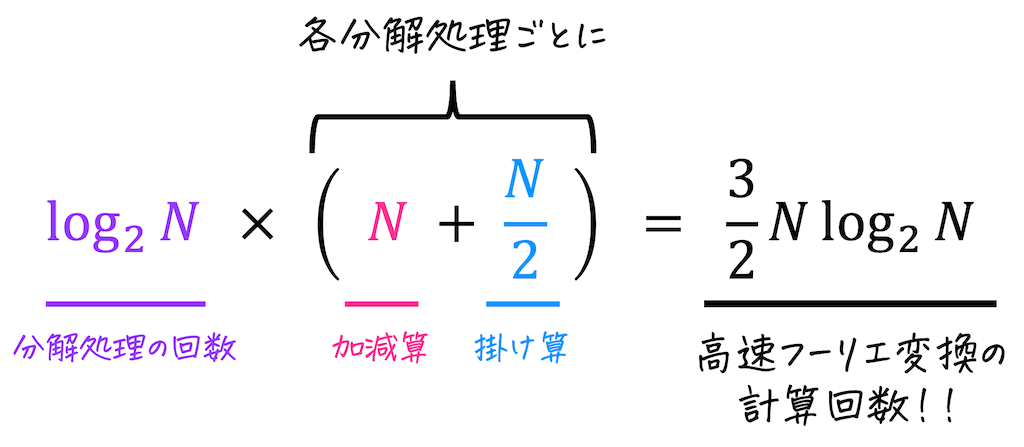
オーダー表記をすると \( O ( \log N ) \) なので、通常の離散フーリエ変換の計算量 \( O(N^2) \) よりも高速なことがわかりますね！

スポンサードリンク

3. 高速フーリエ変換の練習問題

では、実際に高速フーリエ変換のアルゴリズムを、手計算をすることで脳に叩き込みましょう。

練習問題

実変数\[
\vec{x} = \left( \begin{array}{ccc} 1 \\ 0 \\ 0 \\ 1 \\ 0 \\ 0 \\ 0 \\ 1 \end{array} \right)
\]を高速フーリエ変換しなさい。

[解答]

\( N = 8 \) → \( N = 4 \)

[偶数行に対して]

\[\begin{align*}
\left( \begin{array}{ccc} F_8(0) \\ F_8(2) \\ F_8(4) \\ F_8(6) \end{array} \right) & = \left( \begin{array}{ccc} f_8(0) + f_8(4) \\ f_8(1) + f_8(5) \\ f_8(2) + f_8(6) \\ f_8(3) + f_8(7) \end{array} \right)
\\ & = \left( \begin{array}{ccc} 1 \\ 0 \\ 0 \\ 2 \end{array} \right)
\\ & = \left( \begin{array}{ccc} f_4 (0) \\ f_4(1) \\ f_4(2) \\ f_4(3) \end{array} \right)
\end{align*}\]

[奇数行に対して]

\[\begin{align*}
\left( \begin{array}{ccc} F_8(1) \\ F_8(3) \\ F_8(5) \\ F_8(7) \end{array} \right) & = \left( \begin{array}{ccc} W_8^0 \left\{ f_8(0) - f_8(4) \right\} \\ W_8^1 \left\{ f_8(1) + f_8(5) \right\} \\ W_8^2 \left\{ f_8(2) + f_8(6) \right\} \\ W_8^3 \left\{ f_8(3) + f_8(7) \right\} \end{array} \right)
\\ & = \left( \begin{array}{ccc} 1 \\ 0 \\ 0 \\ 0 \end{array} \right)
\\ & = \left( \begin{array}{ccc} f_4 (4) \\ f_4(5) \\ f_4(6) \\ f_4(7) \end{array} \right)
\end{align*}\]

\( N = 4 \) → \( N = 2 \)

[偶数行→偶数行]

\[\begin{align*}
\left( \begin{array}{ccc} F_8(0) \\ F_8(4) \end{array} \right) & = \left( \begin{array}{ccc} f_4(0) + f_4(2) \\ f_4(1) + f_4(3) \end{array} \right)
\\ & = \left( \begin{array}{ccc} 1 \\ 2 \end{array} \right)
\\ & = \left( \begin{array}{ccc} f_2 (0) \\ f_2(1) \end{array} \right)
\end{align*}\]

[偶数行→奇数行]

\[\begin{align*}
\left( \begin{array}{ccc} F_8(2) \\ F_8(6) \end{array} \right) & = \left( \begin{array}{ccc} W_4^0 \left\{ f_4(0) - f_4(2) \right\} \\ W_4^1 \left\{ f_4(1) - f_4(3) \right\} \end{array} \right)
\\ & = \left( \begin{array}{ccc} 1 \\ -i \cdot (-2) \end{array} \right)
\\ & = \left( \begin{array}{ccc} 1 \\ 2i \end{array} \right)
\\ & = \left( \begin{array}{ccc} f_2 (2) \\ f_2(3) \end{array} \right)
\end{align*}\]

[奇数行→偶数行]

\[\begin{align*}
\left( \begin{array}{ccc} F_8(1) \\ F_8(5) \end{array} \right) & = \left( \begin{array}{ccc} f_4(4) + f_4(6) \\ f_4(5) + f_4(7) \end{array} \right)
\\ & = \left( \begin{array}{ccc} 1 \\ 0 \end{array} \right)
\\ & = \left( \begin{array}{ccc} f_2 (4) \\ f_2(5) \end{array} \right)
\end{align*}\]

[奇数行→奇数行]

\[\begin{align*}
\left( \begin{array}{ccc} F_8(3) \\ F_8(7) \end{array} \right) & = \left( \begin{array}{ccc} w_4^0 \left\{ f_4(4) - f_4(6) \right\} \\ w_4^1 \left\{ f_4(5) - f_4(7) \right\} \end{array} \right)
\\ & = \left( \begin{array}{ccc} 1 \\ 0 \end{array} \right)
\\ & = \left( \begin{array}{ccc} f_2 (6) \\ f_2(7) \end{array} \right)
\end{align*}\]

\( N = 2 \) → \( N = 1 \)

[偶数行→偶数行]

\[\begin{align*}
F_8(0) & = f_2 (0)+ f_2(1)
\\ & = 1 + 2
\\ & = 3
\end{align*}\]

\[\begin{align*}
F_8(4) & = f_2 (0) - f_2(1)
\\ & = 1 - 2
\\ & = -1
\end{align*}\]

[偶数行→奇数行]

\[\begin{align*}
F_8(2) & = f_2 (2) + f_2(3)
\\ & = 1 + 2i
\end{align*}\]

\[\begin{align*}
F_8(6) & = f_2 (2) - f_2(3)
\\ & = 1 - 2i
\end{align*}\]

[奇数行→偶数行]

\[\begin{align*}
F_8(1) & = f_2 (4)+ f_2(5)
\\ & = 1 + 0
\\ & = 1
\end{align*}\]

\[\begin{align*}
F_8(5) & = f_2 (4) - f_2(5)
\\ & = 1 - 0
\\ & = 1
\end{align*}\]

[奇数行→奇数行]

\[\begin{align*}
F_8(3) & = f_2 (6)+ f_2(7)
\\ & = 1 + 0
\\ & = 1
\end{align*}\]

\[\begin{align*}
F_8(7) & = f_2 (6) - f_2(7)
\\ & = 1 - 0
\\ & = 1
\end{align*}\]

よって、高速フーリエ変換した結果は\[
\left( \begin{array}{ccc} F_8(0) \\ F_8(1) \\ F_8(2) \\ F_8(3) \\ F_8(4) \\ F_8(5) \\ F_8(6) \\ F_8(7) \end{array} \right) = \left( \begin{array}{ccc} 3 \\ 1 \\ 1+2i \\ 1 \\ -1 \\ 1 \\ 1-2i \\ 1 \end{array} \right)
\]と求められる。

4. バタフライ演算（計算の可視化）

高速フーリエ変換を計算する際に加算や掛け算を繰り返すため、何を計算しているのかがわからなくなってきます。

そこで、計算の過程を図で示すような方法が開発されました。これをバタフライ演算と呼びます。

(1) バタフライ演算の読み方

まずはバタフライ演算の読み方を勉強していきましょう。

※ バタフライ演算を読む際には、左から右に向けて読んでいきます。

(a) 足し算

バタフライ演算では、2つの線が合流することで値を足されることを直感的に表現します。

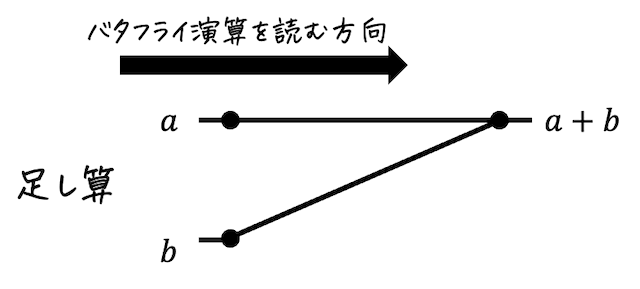
(b) 引き算

引き算を行う場合は、引く方の線の途中に-1を書きましょう。

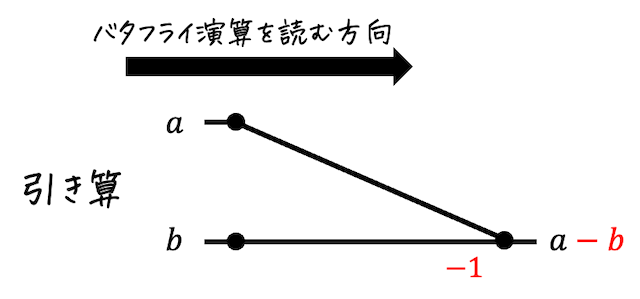
※ -1 は、- とだけ書かれることもあります。

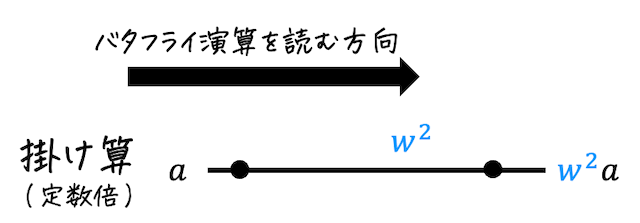
(c) 掛け算（定数倍）

線の途中に数字が書くことで、値が定数倍されることを表現することができます。

(2) バタフライ演算の例（2点離散フーリエ変換）

例えば、2点離散フーリエ変換を高速フーリエ変換を用いた際の計算過程\[
\left\{ \begin{array}{l} f_2(0)+f_2(1) = F_2(0) \\ f_2(0) - f_2(1) = F_2(1) \end{array} \right.
\]をバタフライ演算で表すと、下のように書くことができます。

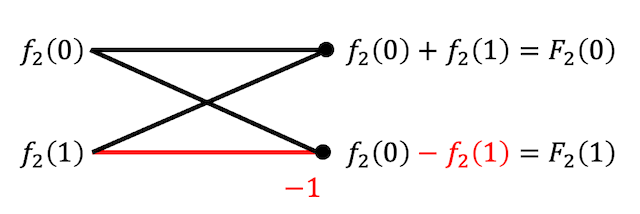
※ わかりやすくするために、引き算をしている線のみ赤色で書きました。

(3) バタフライ演算を読む練習

まずは、バタフライ演算を読む練習をしましょう。

練習

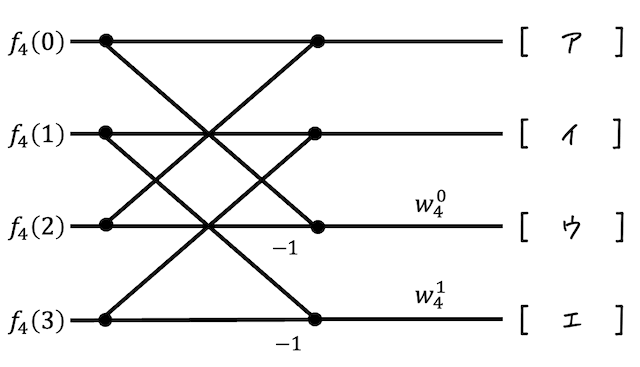
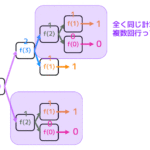
次の図は、4点離散フーリエ変換を高速フーリエ変換した際の計算過程の一部をバタフライ演算で示したものである。[ ア ] 〜 [ エ ] の計算結果を、\( f_4 (k) \), \( w_4 \) を用いて表しなさい。
（※ \( k \) には0〜3の数字が入る）

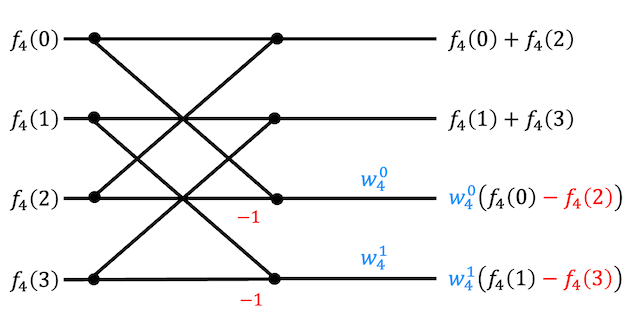
[解答]

\( f_4 (2) \), \( f_4(3) \) のラインは、引き算をしたあとに定数倍として \( w_4^0 \), \( w_4^1 \) が入るのがポイントです。

(4) バタフライ演算を美しく見せる技法（ビットリバース）

(i) 入力と出力の順番が違う!?

ここからは、バタフライ演算（高速フーリエ変換の計算過程）を美しく見せるための技を見ていきましょう。

例えば、\( N = 4 \) 点離散フーリエ変換を高速フーリエ変換を用いたときの計算過程は次のように書くことができます。

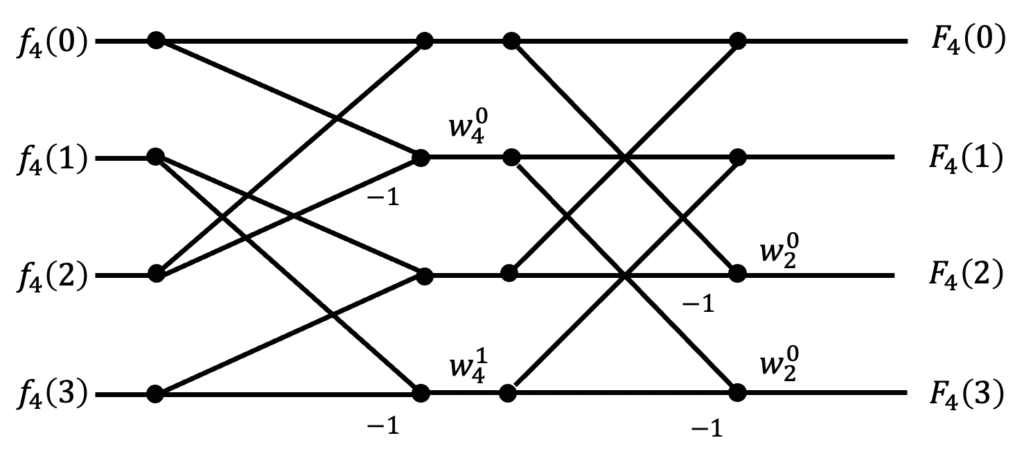
しかし、右側の方が特にぐちゃぐちゃしてしまっていて少し見にくいです。

そこで、出力の順番を入れ替えてみましょう。

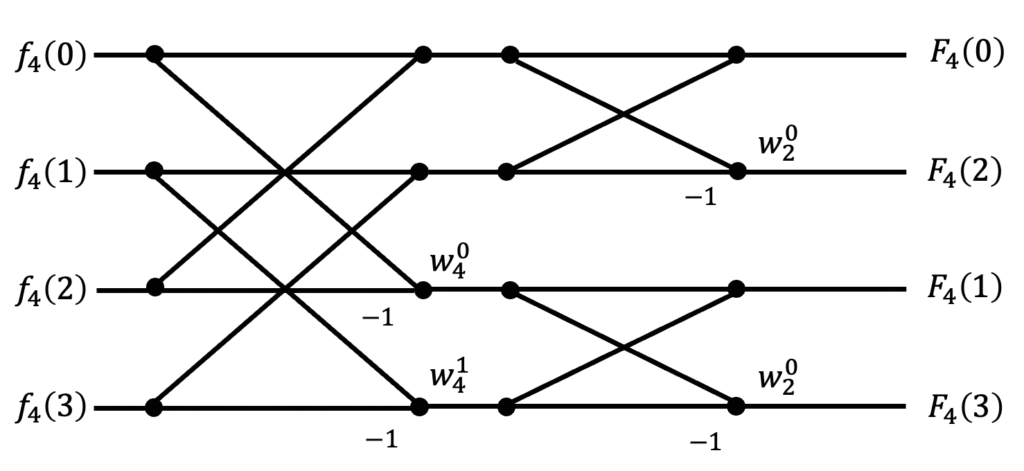
このように出力の順番を入れ替えることで、バタフライ演算が少しきれいになりますね。

さらに、どこでどの高速フーリエ変換をしているかもわかりやすくなりますね！

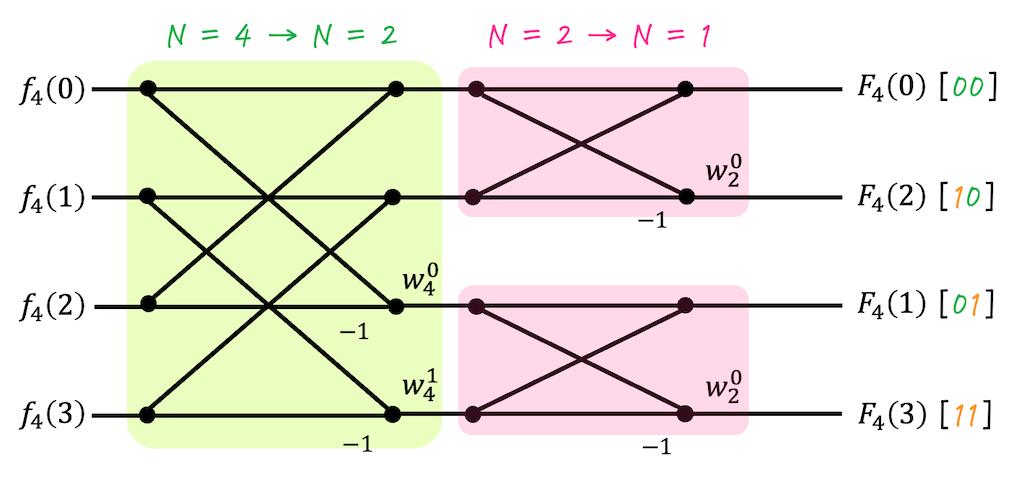
(ii) 出力順序とビットリバース

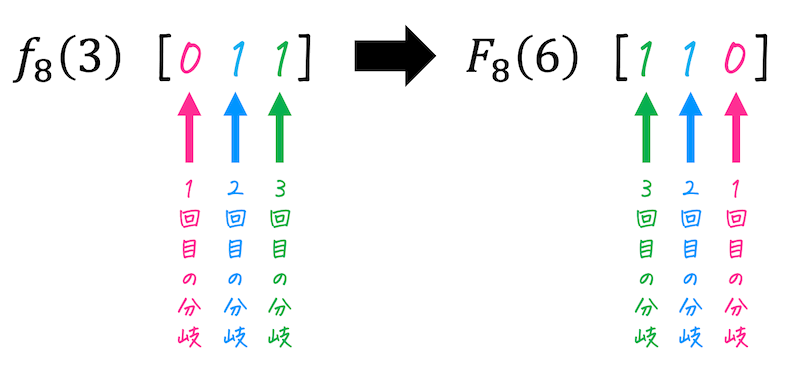
先に結論を言うと、バタフライ演算の出力は、入力順をビットリバースしたものを出力順することできます^[4]多くの参考書やスライドでは出力順は入力順のビットリバースとだけ書かれていることが多いです。。

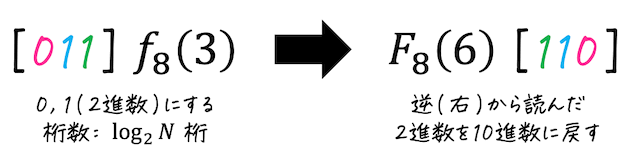
ビットリバースの手順は、次の1-3で行うことができます。

元の入力順を2進数に直す（桁数は \( \log_2 N \) 桁）
2進数を右から読む（ビット反転）
右から読んだものを10進数に直す

下に、例として \(N = 4 \), \( N = 8 \) のときに入力順をビットリバースしたもの（出力順）を載せています。

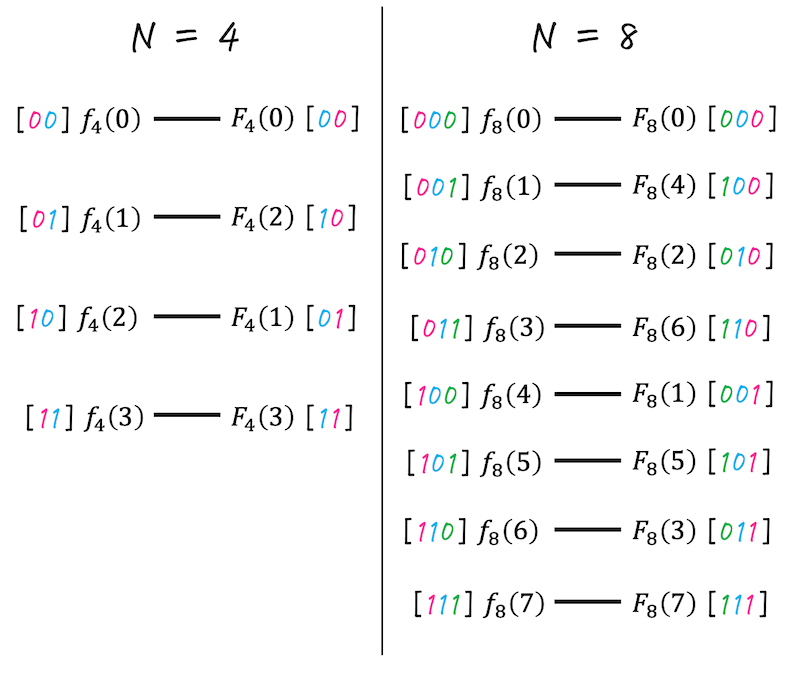
[補足] なぜビットリバースするだけできれいになるか

ビットリバースがきれいに見えるのは、「偶数行の処理(2章のStep2)を上側半分、奇数行の処理(2章のStep3)を下側半分」に分けているからです。

例えば、\( N = 4 \to N = 2 \) の変換を見てみると、偶数行への分解処理は上2行、奇数行への分解処理は下2行になっていますよね。

ここで、入力順を2進数にしたものに着目すると、

\( f_4 (0) \) → [00] (偶数行 → 偶数行)
\( f_4 (1) \) → [01] (偶数行 → 奇数行)
\( f_4 (2) \) → [10] (奇数行 → 偶数行)
\( f_4 (3) \) → [11] (奇数行 → 奇数行)

と「左から順に偶数行(0)、奇数行(1)のどちらを適用したか」を表していますね。

一方出力されるものは、

\( F_4 (0) \) → [00] (偶数行 → 偶数行)
\( F_4 (2) \) → [10] (偶数行 → 奇数行)
\( F_4 (1) \) → [01] (奇数行 → 偶数行)
\( F_4 (3) \) → [11] (奇数行 → 奇数行)

と、「右から順に偶数行(0)、奇数行(1)のどちらを適用したか」を表されていることがわかります。

そのため、「左から順に偶奇を表している入力順のビットリバース（し、右から順に変更）をする」ことできれいなバタフライ演算の図が描ける！

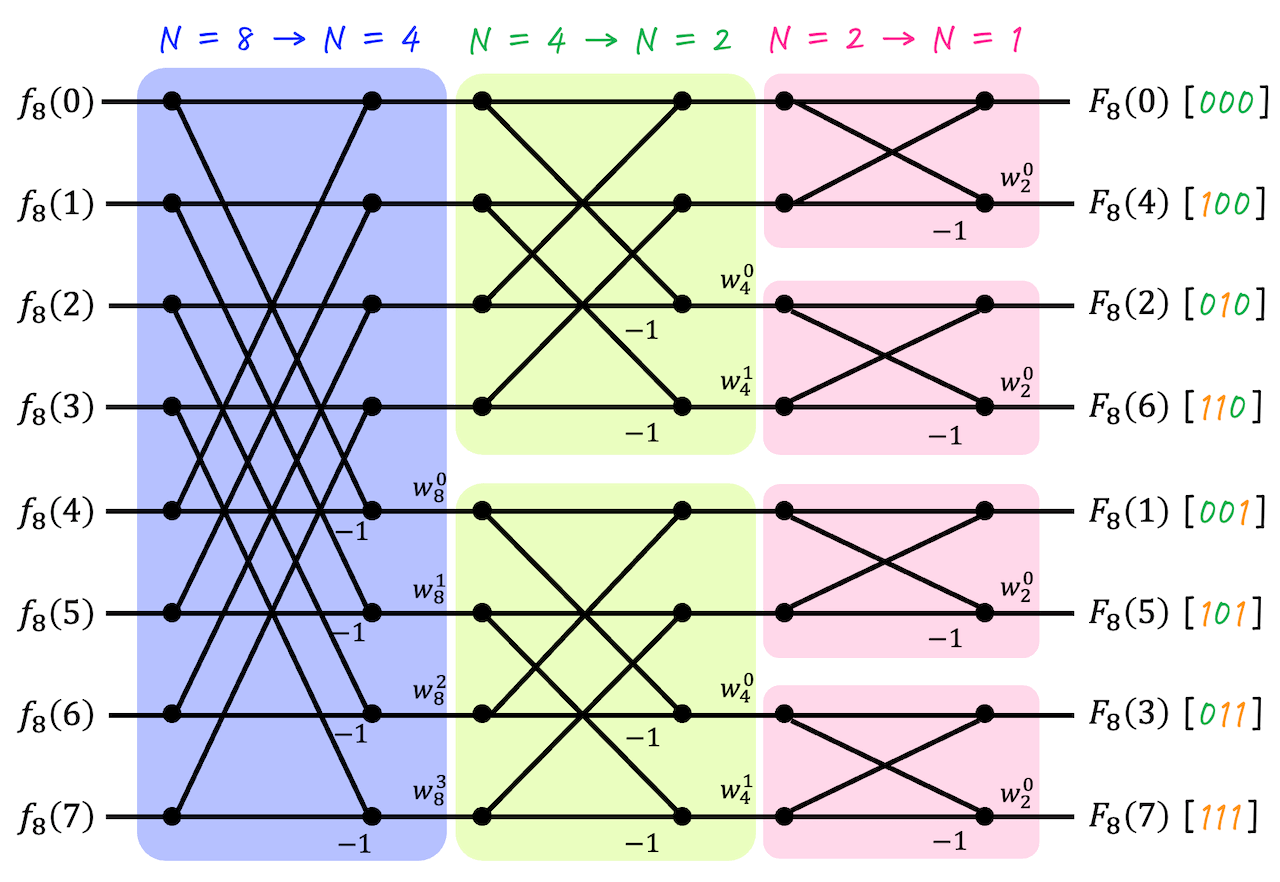
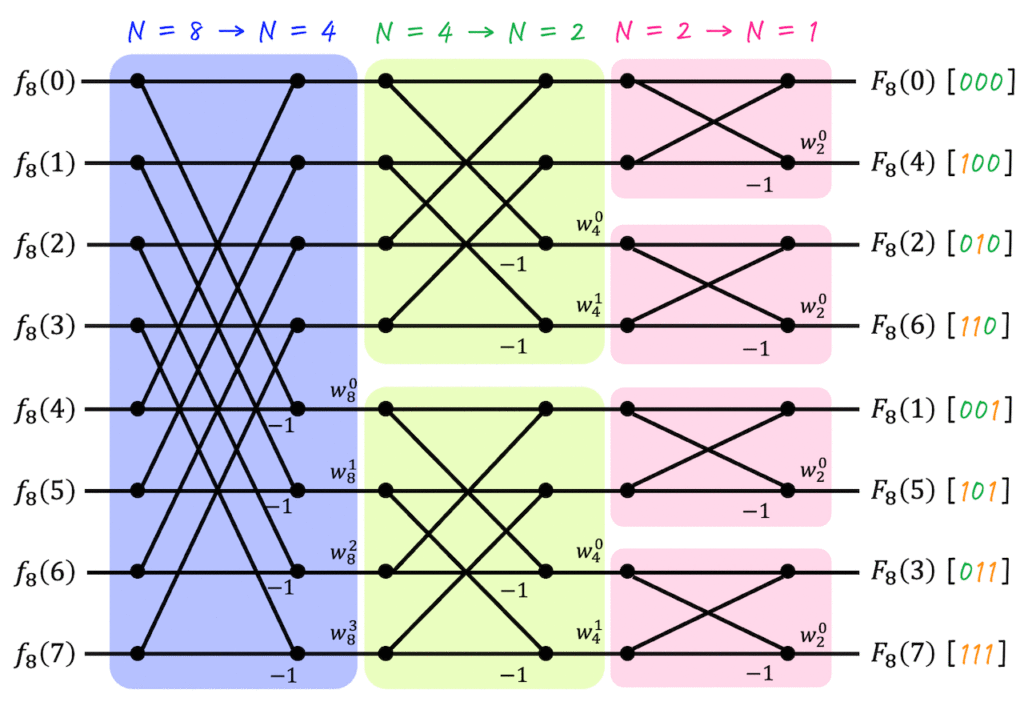
(iii) N = 8 の高速フーリエ変換のバタフライ演算

最後に \( N = 8 \) の高速フーリエ変換の計算過程を、バタフライ演算で見てみましょう。

5. プログラム

最後に高速フーリエ変換を行う自作のPython, MATLABプログラムをお見せします。

アルゴリズムの理解の参考に御覧ください。

※1 再帰を使っています。
※2 Pythonは複素数がj、MATLABは複素数がiなので要注意！

Python

要素数を2で割る際に n / 2 ではなく、n // 2 としているのは、n / 2 の計算結果を整数型で出してもらうためです^[5]配列の添字が整数型でない場合、エラーが発生する。。

import math # math.pi を使うため
import numpy as np # 行列, ベクトル計算をするため

def myFFT(realVec,n):
    if n == 1:
        return realVec # N = 1 のときは入力 = 出力
    else:
        fourierVec = np.zeros(n, dtype=np.complex128) # 成分が複素数のため

        # 偶数行成分
        nextEvenInput = realVec[0:n//2] + realVec[n//2:n] 
        fourierVec[0:n:2] = myFFT(nextEvenInput,n//2)

        # 奇数行成分
        exp_part = -1 * np.array(np.array(range(n//2))) * 2 / n * math.pi * 1j
        w_factor = np.exp(exp_part)
        nextOddInput = w_factor * (realVec[0:n//2] - realVec[n//2:n])
        fourierVec[1:n:2] = myFFT(nextOddInput,n//2)
        
        return fourierVec

realVec = np.array([1,0,0,1,0,0,0,1]) # 入力(実変数のベクトル)

fourierVec = myFFT(realVec,8) # 出力(フーリエの変数ベクトル)
print(fourierVec)

MATLAB

realVec = [1,0,0,1,0,0,0,1]; % 入力(実変数のベクトル)

fourierVec = myFFT(realVec,numel(realVec)) % 出力(フーリエ変数のベクトル) 

function [res] = myFFT(rVec,n)
    if n == 1
        res = rVec; % N = 1のときは入力 = 出力
    else
        res = zeros(n,1);

        % 偶数行成分
        nextEvenInput = rVec(1:n/2) + rVec(n/2+1:n);
        res(1:2:n) = myFFT(nextEvenInput,n/2);
    
        % 奇数行成分
        exp_part = -1 * (0:(n/2-1)) * 2 / n * pi * i; 
        w_factor = exp(exp_part).';
        nextOddInput = w_factor .* (rVec(1:n/2) - rVec(n/2+1:n));
        res(2:2:n) = myFFT(nextOddInput,n/2);
    end
end

実行結果

先程の練習問題と同じ実変数ベクトルを入力したときの実行結果です。

Python

[ 3.+0.j  1.+0.j  1.+2.j  1.+0.j -1.+0.j  1.+0.j  1.-2.j  1.+0.j]

MATLAB

ans =

  1 列から 5 列

   3.0000 + 0.0000i   1.0000 + 0.0000i   1.0000 + 2.0000i   1.0000 + 0.0000i  -1.0000 + 0.0000i

  6 列から 8 列

   1.0000 + 0.0000i   1.0000 - 2.0000i   1.0000 + 0.0000i

注釈[+]

注釈
↑1	\( N \) 次正方行列の成分の数はN×N個あるため。
↑2	例えば \( N = 5 \) だとすると、偶数行が0, 2, 4行目の3行分、奇数行が1, 3行の2行分と、最初の分解で偶数行と奇数行でちょうど半分ずつわかれていませんね。
↑3	\( \log_2 N = A \) は \( 2^A = N \) を満たすような \( A \) を求めるのと同じ計算になります。
↑4	多くの参考書やスライドでは出力順は入力順のビットリバースとだけ書かれていることが多いです。
↑5	配列の添字が整数型でない場合、エラーが発生する。