スポンサードリンク
こんにちは、ももやまです。
今回は、数Bの「確率分布と統計的な推測」に出てくる標本調査について、そして「確率・統計」分野で重要な中心極限定理について説明していきたいと思います。
今回の範囲は、共通テスト(センター試験)で直接的に聞かれることは少ないですが、次回説明する「母平均の推定」で必要な知識となるので、頭にいれておきましょう。
前回の「うさぎでもわかる確率分布と統計的な推測」4日目はこちら↓
目次
スポンサードリンク
1.標本調査
(1) 標本調査とは
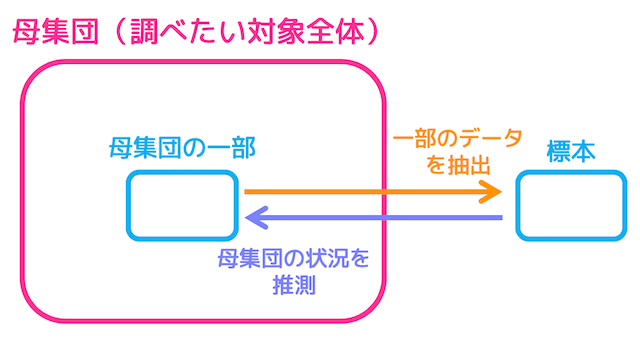
大量のデータの情報を調べるときに、いちいち全部のデータ(母集団)を調べていたらきりがありません。
そこで、実際には全部のデータの中から何個かをランダムに*1抽出(抽出したデータのことを標本と呼びます)し、抽出したデータを調べてから母集団のデータを予測するという手法を用います。この手法のことを標本調査と呼びます。
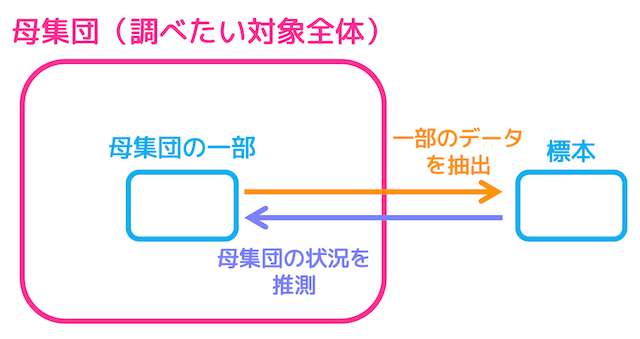
(一方全部のデータを調べてから母集団のデータを調べる方法を全数調査と呼びます*2。)
(2) 標本調査の例
標本調査の例をいくつか紹介していきましょう。
例えば、テレビ番組の人気を示す「視聴率」がありますね。しかし、今までで「視聴率の調査、つまりどの番組を見ていましたか?」の調査を受けたことがある人はほとんどいないかと思います。
視聴率を調べるためにいちいち全国の人にアンケートをとってたらキリがないし、時間の無駄です。そのため、視聴率を調べる際には、「一部の世帯だけを偏りなく調査」する標本調査が用いられます。
他にも標本調査の例として、
- 選挙の開票速報
(一部の人からどこに投票したのかを聞き、選挙情勢を予測) - 製品などの重さ・長さチェック
(いちいち全部の製品を測っていたらキリがない)
などがあります。
余談 標本調査と測定
余談ですが、理系大学生になる人(もしくは今なっている人)は1年生の実験で、「ある物体(の重さ・長さなど)を何回か測定して」から測定結果とその誤差を計算することをするかもしれません。
実験で得る測定値は、自然科学という母集団から抽出された標本の中の1つなので、全数調査で結果を調べるためには無限回の測定が必要となってしまい、測定が終わりません。
そのため、何回か測定してから結果を予測する標本調査が用いられます。
スポンサードリンク
2.標本調査の用語
(1) 母平均・母分散・母標準偏差とは
母集団、つまり調べたい対象全体の平均、分散、標準偏差のことをそれぞれ母平均、母分散、母標準偏差と呼びます。
(平均、分散、標準偏差の計算方法は数1「データの分析」と同じです)
例えば、母集団5人の身長が 162cm, 164cm, 166cm, 168cm, 170cm だった場合の母平均 \( m \) は、\[\begin{align*}
m & = \frac{1}{5} (162 + 164 + 166 + 168 + 170)
\\ & = 166
\end{align*}\]となり、母分散 \( \sigma^2 \) は、\[\begin{align*}
\sigma^2 & = \frac{1}{5} \left( (162-166)^2 + (164-166)^2 + (166-166)^2 + (168-166)^2 + (170-166)^2 \right)
\\ & = \frac{1}{5} ( 16 + 4 + 0 + 4 + 16)
\\ & = 8
\end{align*}\]となり、母標準偏差 \( \sigma \) は、\[\begin{align*}
\sigma & = \sqrt{ \sigma^2 }
\\ & = 2 \sqrt{2}
\end{align*}\]となります。
(2) 標本の大きさ・標本数
標本にあるデータの数のことを標本の大きさ(サンプルサイズ)と呼びます。
標本数(サンプル数)と呼びたくなる気持ちもわかるのですが、標本数は「標本自体の数」を表しているため、標本数と標本の大きさは別物となってしまいます。

(3) 標本平均・標本分散・標本標準偏差とは
標本(母集団からランダムに選んだいくつかのデータ)の平均、分散、標準偏差のことをそれぞれ標本平均、標本分散、標本標準偏差と呼びます。
(平均、分散、標準偏差の計算方法は数1「データの分析」と同じです)
例えば、母集団5人から3人選んだところ、身長が 162cm, 164cm, 166cm だった場合の標本平均 \( \bar{X} \) は、\[\begin{align*}
\bar{X} & = \frac{1}{3} (162 + 164 + 166)
\\ & = 164
\end{align*}\]となり、標本分散 \( s^2 \) は、\[\begin{align*}
s^2 & = \frac{1}{5} \left( (162-166)^2 + (164-166)^2 + (166-166)^2 \right)
\\ & = \frac{1}{5} ( 16 + 4 + 0 + 4 + 16)
\\ & = 8
\end{align*}\]となり、標本標準偏差 \( s \) は、\[\begin{align*}
s & = \sqrt{ \sigma^2 }
\\ & = 2 \sqrt{2}
\end{align*}\]となります。
(今回の場合、偶然「標本分散=母分散」、「標本標準偏差=母標準偏差」が成立しています)
標本の選び方によって、標本平均、標本分散、標本標準偏差は、標本の選び方によって値が変化します。
また、「母平均 ≠ 標本平均」、「母分散 ≠ 標本分散」、「母標準偏差 ≠ 標本標準偏差」な点に注意しましょう。
おまけ:不偏分散(数B範囲外です)
数Bの範囲外なので、ここは高校生の皆さんは見なくてもOKです。
標本の選び方によって、標本分散 \( s \) は変化します。
実は、標本分散 \( s \) の平均 \( E(s) \)(つまり、標本分散 \( s \) がどれくらいの値になるのか)は母分散 \( \sigma^2 \) よりも少し大きな値となってしまいます。
そこで、標本分散の公式\[
s^2 = \frac{1}{n} \sum^{n}_{k = 1} (X_k - \overline{X})^2
\]の \( n \) で割る部分を \( n -1 \) で割る、つまり\[
u^2 = \frac{1}{n-1} \sum^{n}_{k = 1} (X_k - \overline{X})^2
\]としたものを不偏分散 \( u^2 \) と定義することで母分散 \( \sigma^2 \) と \( u^2 \) の平均 \( E(u^2) \) を等しくすることができます。
スポンサードリンク
3.標本平均の関係
「確率分布と統計的な推測」で重要な項目の1つに、標本平均から母平均を推定するというのがあります。
そのために必要な標本平均の関係式をここで説明していきましょう。
(1) 標本平均の平均 / 分散
標本の選び方によって、標本平均 \( \bar{X} \) は変化します。
そこで、標本平均 \( \overline{X} \) がだいたいどれくらいの値を取るか、つまり標本平均の平均 \( E(\overline{X}) \) と、標本平均 \( \overline{X} \) の値がどれくらいばらつくのか、つまり標本平均の分散 \( V( \overline{X} ) \) を考えてみましょう。
例題
箱の中に大量のカードが入っており、中身の 3/4 には2、1/4 には1が書かれている。
無作為に2枚のカードを取り出し、取り出したときに書かれているカードの数字を順に \( X_1 \), \( X_2 \) とする(つまり標本は \( X_1 \), \( X_2 \) の2つ)。
このとき標本平均 \( \bar{X} \) の平均 \( E( \overline{X}) \)、および分散 \( V ( \overline{X} ) \) はどうなるか。
解答
まず、\( X_1 \), \( X_2 \) の取りうる値とそのときの標本平均 \( \overline{X} \)、とそうなる確率を求める。
| \( X_1 \) | \( X_2 \) | 標本平均 \( \overline{X} \) | 確率 |
| 1 | 1 | 1 | \( \frac{1}{4} \cdot \frac{1}{4} = \frac{1}{16} \) |
| 1 | 2 | \( \frac{3}{2} \) | \( \frac{1}{4} \cdot \frac{3}{4} = \frac{3}{16} \) |
| 2 | 1 | \( \frac{3}{2} \) | \( \frac{3}{4} \cdot \frac{1}{4} = \frac{3}{16} \) |
| 2 | 2 | 2 | \( \frac{3}{4} \cdot \frac{3}{4} = \frac{9}{16} \) |
よって、\( \overline{X} \) の確率分布は、下の表のようになる。
| 標本平均 | 確率 |
| 1 | \( \frac{1}{16} \) |
| \( \frac{3}{2} \) | \( \frac{6}{16} \) |
| 2 | \( \frac{9}{16} \) |
表より、標本平均 \( \overline{X} \) の平均 \( E( \overline{X} ) \) は、\[\begin{align*}
E( \overline{X} ) & = 1 \cdot \frac{1}{16} + \frac{3}{2} \cdot \frac{6}{16} + 2 \cdot \frac{9}{16}
\\ & = \frac{28}{16}
\\ & = \frac{7}{4}
\end{align*} \]となる。
また、標本平均の2乗平均 \( E( \overline{X}^2 ) \) は\[\begin{align*}
E( \overline{X}^2 ) & = 1^2 \cdot \frac{1}{16} + \left( \frac{3}{2} \right)^2 \cdot \frac{6}{16} + 2^2 \cdot \frac{9}{16}
\\ & = 1 \cdot \frac{1}{16} + \frac{9}{4} \cdot \frac{3}{8} + 4 \cdot \frac{9}{16}
\\ & = \frac{101}{32}
\end{align*} \]となるので、標本平均の分散 \( V ( \overline{X} ) \) は、\[\begin{align*}
V ( \overline{X} ) & = E( \overline{X}^2 ) - \left\{ E( \overline{X} ) \right\}^2
\\ & = \frac{101}{32} - \left( \frac{7}{4} \right)^2
\\ & = \frac{101}{32} - \frac{49}{16}
\\ & = \frac{3}{32}
\end{align*} \]と求めることができます。
(2) 標本平均の平均と母平均・標本平均の平均と母分散の関係
母平均と標本平均の平均 \( E( \overline{X} ) \) の関係、および母分散と標本平均の分散 \( V ( \overline{X} ) \) の関係を見ていきましょう。
先程の例題のつづき
箱の中に大量のカードが入っており、中身の 3/4 には2、1/4 には1が書かれている。
このとき、カードにかかれている数字の母平均 \( m \)、および母分散 \( \sigma^2 \) を求め、標本平均の平均 \( E( \overline{X} ) \)、標本平均の分散 \( V( \overline{X} ) \) の関係を推測してみよう。
先程の例題のつづきの解説
母集団は、箱の中にあるカードすべてである。
つまり、母平均は、箱の中にある全部のカードの数字の平均値、母分散は、箱の中にある全部のカードの数字の分散を求めればよい。
よって、母平均 \( m \) は、\[ \begin{align*}
m & = \frac{3}{4} \cdot 2 + \frac{1}{4} \cdot 1
\\ & = \frac{7}{4}
\end{align*} \]となり、母分散 \( \sigma^2 \) は、\[ \begin{align*}
\sigma^2 & = 1^2 \cdot \frac{1}{4} + 2^2 \cdot \frac{3}{4} - \left( \frac{7}{4} \right)^2
\\ & = \frac{1}{4} + 3 - \frac{49}{16}
\\ & = \frac{3}{16}
\end{align*} \]と求まる。
ここで、無作為に2枚取り出したときの標本平均の平均 \( E( \overline{X} ) \)、標本平均の分散 \( V( \overline{X} ) \) はそれぞれ\[
E( \overline{X} ) = \frac{7}{4} , \ \ \ V( \overline{X} ) = \frac{3}{32}
\]でしたね。
ここで、\[
E( \overline{X} ) = \frac{7}{4} =m \\
V( \overline{X} ) = \frac{3}{32} = \frac{\sigma^2}{2} = \frac{\sigma^2}{n}
\]なので、
- (標本平均の平均)=(母平均)
- (標本平均の分散)=\( \left( \frac{母分散}{標本の大きさ} \right) \)
が成り立ちそうですね。
本当に成り立つか少し証明してみましょう。
関係式の証明(余裕ない人は飛ばしてもOK)
母平均 \( m \)、母分散 \( \sigma^2 \) の母集団から大きさが \( n \) の標本を選び、それぞれの標本の値が \( X_1 \), \( X_2 \), …, \( X_n \) とします。
すると、それぞれの標本 \( X_i \) の平均 \( X_i \) は母平均 \( m \) に、\( X_i \) の分散 \( V (X_i) \) は母分散 \( \sigma^2 \) と等しくなります。なので、\[
E(X_i) = m , \ \ \ V(X_i) = \sigma^2 \ \ \ (i = 1, 2, \cdots, n)
\]が成立します。
ここで、標本平均 \( \overline{X} \) は\[
\overline{X} = \frac{1}{n} (X_1 + X_2 + \cdots + X_n)
\]と計算できますね。
よって、標本平均の平均 \( E( \overline{X} ) \) は、\[ \begin{align*}
E ( \overline{X} ) & = E \left( \frac{1}{n} (X_1 + X_2 + \cdots + X_n) \right)
\\ & = \frac{1}{n} E ( X_1 + X_2 + \cdots + X_n ) \ \ \ \left( \because E(aX) = aE(X) \right)
\\ & = \frac{1}{n} \left( E(X_1) + E(X_2) + \cdots + E(X_n) \right) \ \ \ \left( \because E(X+Y) = E(X) + E(Y) \right)
\\ & = \frac{1}{n} (m + m + \cdots + m)
\\ & = \frac{1}{n} (nm)
\\ & = m
\end{align*} \]と求められる。
また、標本の大きさが十分に大きいと仮定しているため、\( X_1 \), \( X_2 \), …, \( X_n \) は互いに独立となる。
よって、標本平均の分散 \( V( \overline{X} ) \) は、\[ \begin{align*}
V ( \overline{X} ) & = V \left( \frac{1}{n} (X_1 + X_2 + \cdots + X_n) \right)
\\ & = \frac{1}{n^2} V ( X_1 + X_2 + \cdots + X_n ) \ \ \ \left( \because V(aX) = a^2 V(X) \right)
\\ & = \frac{1}{n^2} \left( V(X_1) + V(X_2) + \cdots + V(X_n) \right) \ \ \ \left( \because V(X+Y) = V(X) + V(Y) \right)
\\ & = \frac{1}{n^2} (\sigma^2 + \sigma^2 + \cdots +\sigma^2)
\\ & = \frac{1}{n^2} (n \sigma^2)
\\ & = \frac{\sigma^2}{n}
\end{align*} \]となり、たしかに成り立ちますね。
関係式の意味
標本平均 \( \overline{X} \) に成り立つ2つの関係式\[
E( \overline{X} ) = m , \ \ \ V( \overline{X} ) = \frac{\sigma^2}{n}
\]の意味を説明していきましょう。
母集団の母平均を \( m \)、母分散を \( \sigma^2 \) とし、十分大きい母集団から大きさ \( n \) の標本を取るとする。
すると、標本平均 \( \overline{X} \) の平均 \( E( \overline{X} ) \) と分散 \( V( \overline{X} ) \) に\[
E( \overline{X} ) = m , \ \ \ V( \overline{X} ) = \frac{\sigma^2}{n}
\]の関係式が成立する。
つまり、
- 標本平均 \( \overline{X} \) の平均は母平均と一致する
- 標本を増やせば増やすほど、標本平均の分散は小さくなる
ことがわかる。
4.中心極限定理
先程、十分に大きい母集団から大きさ \( n \) の標本を選び、その標本平均を \( \overline{X} \) とすると、\[
E( \overline{X} ) = m , \ \ \ V( \overline{X} ) = \frac{\sigma^2}{n}
\]が成立することを確認しましたね。
実は、標本数 \( n \) を大きくしていくと、\( \overline{X} \) は正規分布に近似的に従うのです!
言い換えると、母集団がどんな分布であっても*3、母集団から多くのデータを集めた標本の標本平均 \( \overline{X} \) は正規分布に従うと言えますね!
これが中心極限定理です。
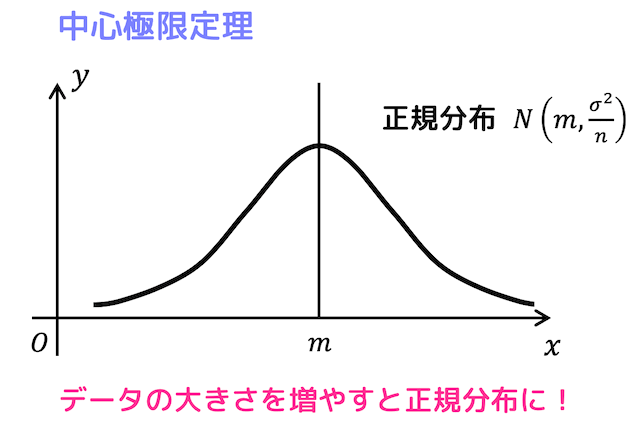
母集団の母均を \( m \)、母分散を \( \sigma^2 \) とし、十分大きい母集団から十分大きい大きさ \( n \) の標本を選び、標本平均を \( \overline{X} \) とする。
このとき、\( \overline{X} \) は平均 \( m \)、分散 \( \frac{\sigma^2}{n} \) の正規分布 \( N(m, \frac{\sigma^2}{n}) \) に近似的に従う。
つまり、標本の大きさ \( n \) を増やせば増やすほど分散は0に近づき、より平均 \( m \) 付近の値を取るような正規分布となります。
5.(簡単に)練習問題
では、練習(共通テスト対策)をしてみましょう!
必要であればこちらから正規分布表をダウンロードし、使用してください。
※注意
小数の形で解答する場合、指定された桁数の1つ下の桁を四捨五入して解答してください。また、必要に応じて、確定された桁まで⓪をマークしてください。
例えば、[ ア ] . [ イウ ] に 2.5 と答えたいとき → 2.50 とする。
あるテストの点数の母平均は60、母分散は2500だった。
このとき、100人の生徒(標本)を無作為に選び、その標本平均を \( \overline{X} \) とする。
\( \overline{X} \) の平均は [ アイ ]、分散は [ ウエ ]、標準偏差は [ オ ] となる。
ここで、標本の大きさ100は十分に大きいとみなせるので、\( \overline{X} \) は正規分布に従うと仮定できる。
正規分布と仮定したとき、標本平均 \( \overline{X} \) が50点以上70点以下に収まる確率は 0.[ カキ ] となる。
6.練習問題の答え
生徒数(標本の大きさ)が100、母平均 \( m \) が60、母分散 \( \sigma^2 \) が2500なので、標本平均 \( \overline{X} \) の平均 \( E( \overline{X} ) \) は、\[
E( \overline{X} ) = m = 60
\]となる。(アイ:60)
また、分散 \( V( \overline{X} ) \) は\[\begin{align*}
V( \overline{X} ) & = \frac{ \sigma^2 }{n}
\\ & = \frac{2500}{100}
\\ & = 25
\end{align*} \]となる。(ウエ:25)
また、標準偏差 \( \sigma( \overline{X} ) \) は\[\begin{align*}
\sigma( \overline{X} ) & = \sqrt{25}
\\ & = 5
\end{align*} \]となる。(オ:5)
ここで、\( \overline{X} \) が50点以上70点以下というのは、
- \( \overline{X} \) が「平均 (60点) - 標準偏差2個分 (5×2 = 10点) 以上」
- \( \overline{X} \) が「平均 (60点) + 標準偏差2個分 (5×2 = 10点) 以下」
となる確率、つまり\[
Z = \frac{X - m}{\sigma}
\]とおいたときの \( -2 \leqq Z \leqq 2 \) となる確率と同じである。
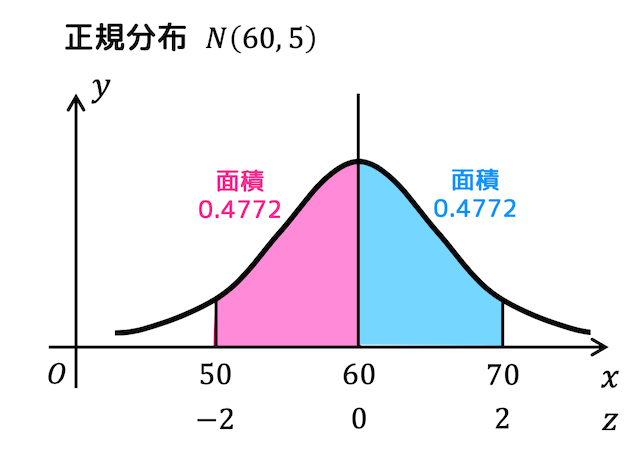
\( -2 \leqq Z \leqq 0 \) となる確率は、\( 0 \leqq Z \leqq 2 \) となる確率と同じなので、
標準正規分布表から \( 0 \leqq Z \leqq 2 \) を読み取って値を2倍にすればよい。
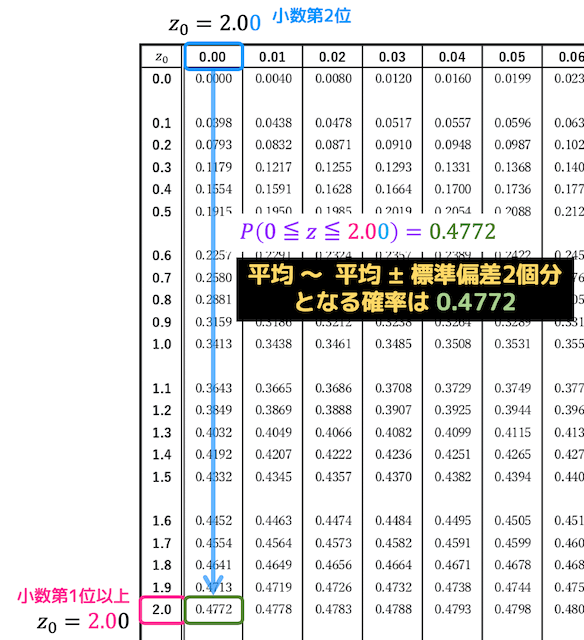
よって、平均 〜 平均 ± 標準偏差2個分となる確率(\( 0 \leqq Z \leqq 2 \))が0.4772となるので、2倍した0.9544が \( -2 \leqq Z \leqq 2 \) となる確率となる。
よって、小数第3位を四捨五入した0.95が答え(カキ:95)。
なお、実際には母集団から標本平均を推定する問題よりも、標本から母平均を推定する問題が頻出します。
7.さいごに
今回は、「確率分布と統計的な推測」の分野の中の「標本調査」と「中心極限定理」についてまとめていきました。
次回は、今回習った「標本調査」や「中心極限定理」などを生かして、実際に標本から「母平均」などを推定する方法についてまとめていきたいと思います!
(母平均の推定は共通テスト頻出項目です!)
復習(中心極限定理)
今回は中心極限定理について復習すればOKです。
母集団がどんな分布(ただし分散が0以外の)であっても、 母集団から多くのデータを集めた標本の標本平均 \( \overline{X} \) は平均 \( m \)、分散 \( \frac{\sigma^2}{n} \) の正規分布 \( N(m, \frac{\sigma^2}{n}) \) に近似的に従う。
関連広告・スポンサードリンク