1週間で完成！　うさぎでもわかる確率分布と統計的な推測　4日目　正規分布

こんにちは、ももやまです。

今回は、数Bの「確率分布と統計的な推測」で最も重要な分野の1つである「正規分布」についてうさぎでもわかるようにわかりやすく説明していきたいと思います。

 

 

特に後ろのほうで説明する「二項分布と正規分布」は共通テスト（センター試験）でも頻出する項目なので必ず頭にいれておきましょう。

 

前回の「うさぎでもわかる確率分布と統計的な推測」3日目はこちら↓

www.momoyama-usagi.com

スポンサードリンク

１．正規分布ってなに？

(1) コイントスと正規分布

突然ですが、復習です。

復習問題

コイントスを100回やって表が出た回数を \( X \) としたとき、\( X \) の平均 \( E(X) \) はいくらになるでしょうか？

復習解答

コインを投げる試行は「表が出る」か「表が出ない（裏が出る）」かの2パターンの結果しか起こりません。

ということは、表が出る回数 \( X \) は二項分布に従うことがわかりますね。

表が出る確率は、1/2 なので、平均 \( E(X) \) は、\[\begin{align*}
E(X) & = 100 \cdot \frac{1}{2}
\\ & = 50
\end{align*} \]となるので、「100回コインを投げるとだいたい表が50回でる」ことがわかりますね。

コインを100回投げる操作を繰り返すと……

では、「コインを100回投げる操作」を何セットか試して、表が出た回数の頻度（相対度数）をヒストグラムにしてみましょう*1。

1,000セット行ったとき

まずは1,000セット試したときのヒストグラムを見てみましょう。

縦軸が相対度数、横軸が表が出る回数を示しています。

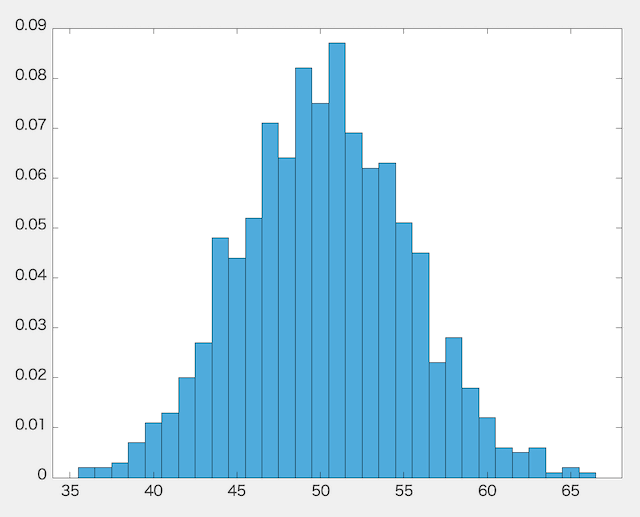
ヒストグラムが山のような形となりましたね。

では、セット数を100倍の100,000セットにしてみましょう。

100,000セット行ったとき

つぎに100,000セット試したときのヒストグラムを見てみましょう。

先程と同じく縦軸が相対度数、横軸が表が出る回数を示しています。

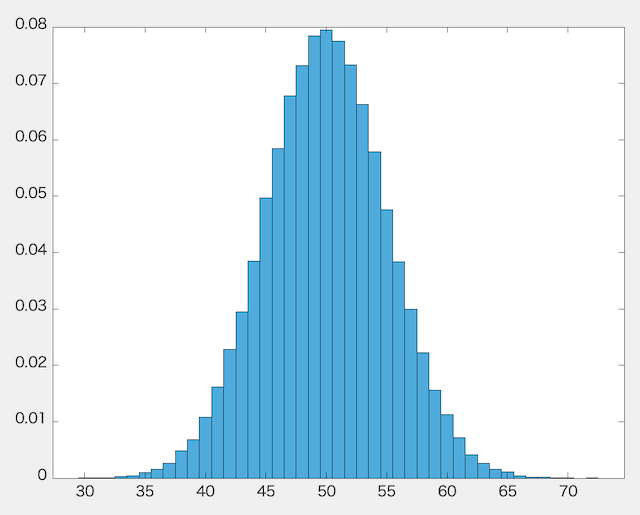
先程よりもきれいな山の形となりましたね。

もう少し回数を増やして、100万セットにしてみましょう。

1,000,000セット行ったとき

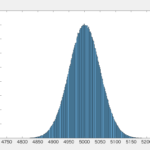
下が100万セットの場合の結果です。

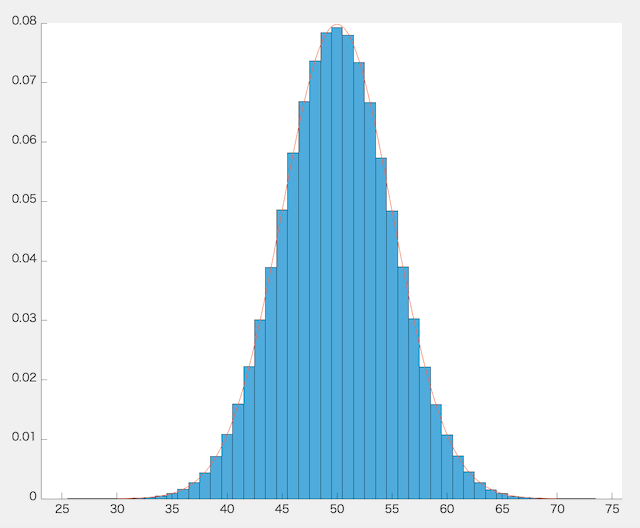
このヒストグラムの縦の区切り線を消すと……、

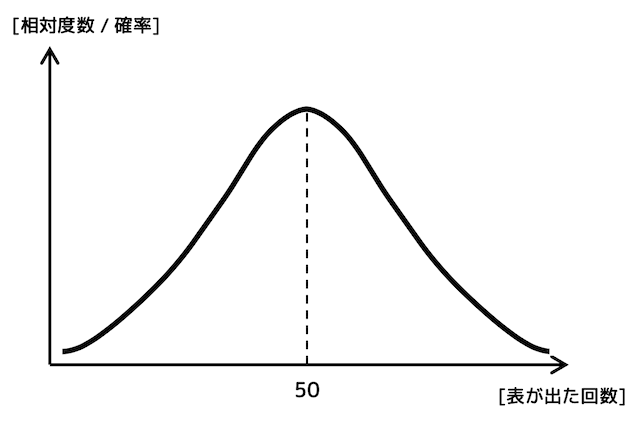
このような平均付近は大きく、平均から離れれば離れるほど確率が減っていくような山になりますね。

実は、この山のような分布こそが正規分布なのです！

 

スポンサードリンク

２．正規分布と標準正規分布

(1) 標準正規分布とは

正規分布のグラフの形（分布の仕方）は、平均 \( m \) と標準偏差 \( \sigma \) の2つによって決まります。

平均 \( m \)、標準偏差 \( \sigma \)（分散 \( \sigma^2 \)）の正規分布のことを記号で \( N(m, \sigma^2) \) とあらわします。

 

正規分布の中でも平均が0で、標準偏差が1の正規分布を標準正規分布 \( N(0,1) \) と呼び、正規分布の一番基本的な形となります。

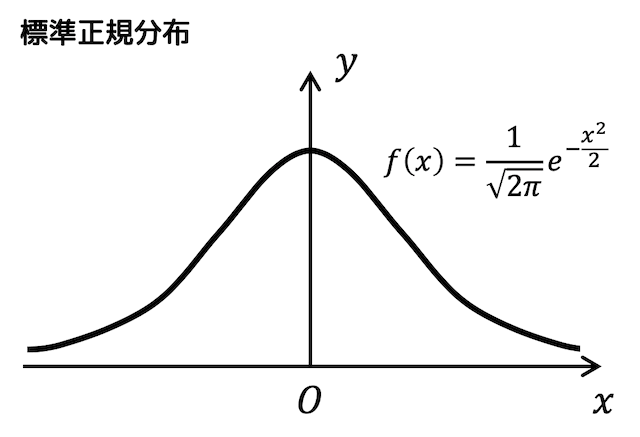
標準正規分布は、前回説明した確率密度関数の1つです。

数式で表すと標準正規分布の確率密度関数 \( f(x) \) は\[
f(x) = \frac{1}{\sqrt{2 \pi} } e^{- \frac{ x^2 }{2} }
\]で表されます。（※数式自体は覚えなくていいです）

 

確率密度関数 \( f(x) \) で表される確率変数 \( X \) が \( a \leqq X \leqq b \) になる確率は、\[
\int^{b}_{a} f(x) \ dx
\]を計算することで求められることを前回説明しましたね。

つまり、正規分布に従う確率変数 \( X \) が\( a \leqq X \leqq b \) になる確率は、\[
\int^{b}_{a} \frac{1}{\sqrt{2 \pi} } e^{- \frac{ x^2 }{2} } \ dx
\]を計算すれば求められるのですが、この積分は文系はおろか、理系でもできないタイプの積分です*2。

（大学で習う2重積分を使えば解くことができますが、それでもめんどい積分です。）

 

そのため、共通テストなどの入試や資格試験などでは、計算結果があらかじめ表で与えられています。

具体的には、正規分布に従う確率変数 \( X \) が\( 0 \leqq X \leqq z_0 \) になる確率が下のような表で与えられています。

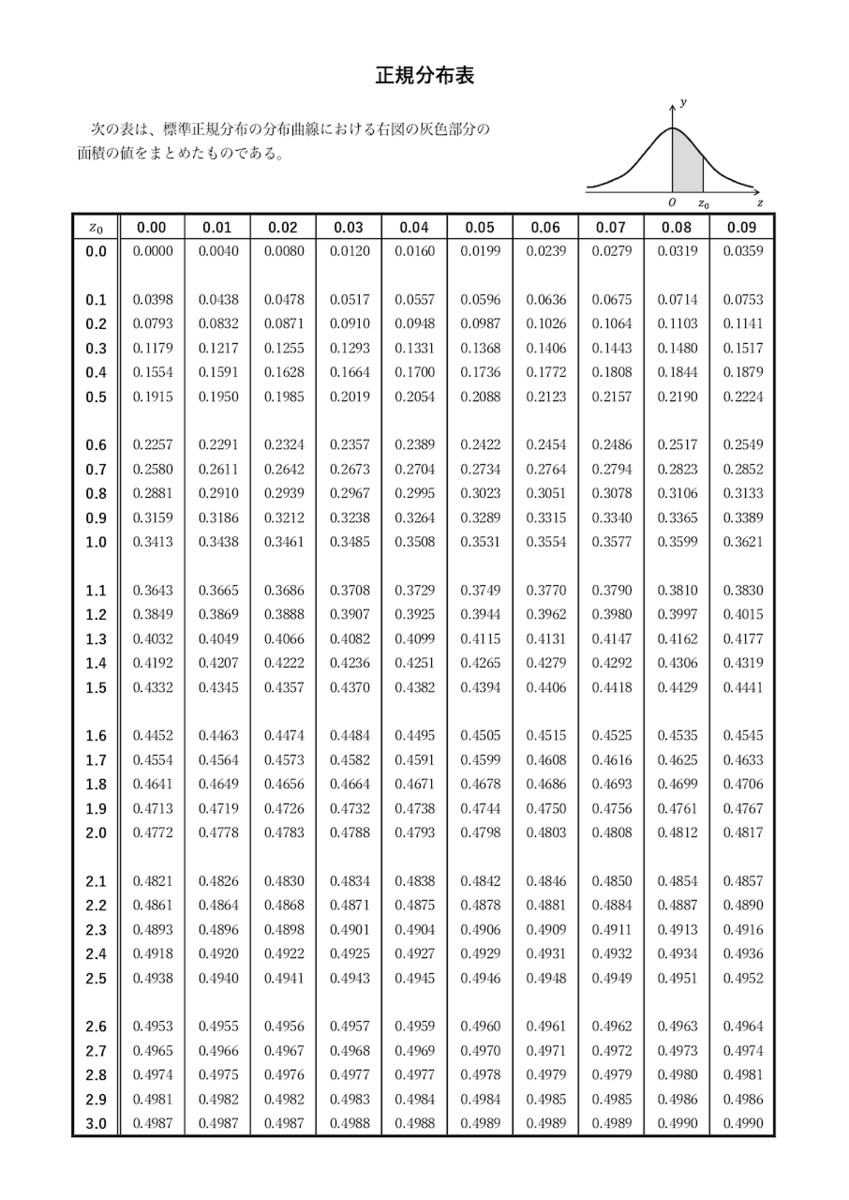
正規分布表は、こちらからダウンロードできるので練習問題などを解く際にぜひご利用ください。

(2) 正規分布表の読み方

では、共通テストで重要な正規分布表の読み方について、いくつかパターンわけして紹介していきたいと思います。

パターン1　xが 0 以上 z0 以下になる確率（基本パターン）

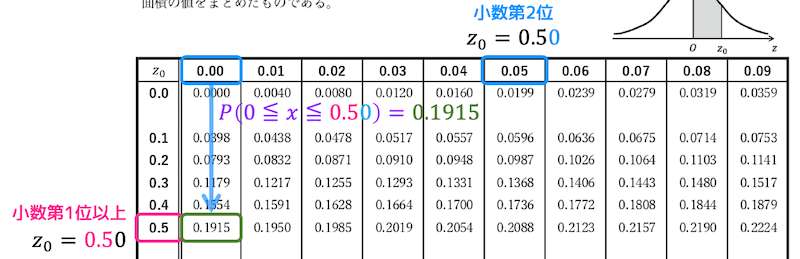
上の表の \( z_0 \) の縦側で「整数部分・小数第1位」を表し、横側で「小数第2位」を表します。

例えば、\( x \) が \( 0 \leqq x \leqq 0.50 \) となる確率 \( P(0 \leqq x \leqq 0.50) \) は、

• 整数＋小数第1位は0.5なので、縦は0.5の部分
• 小数第2位は0なので、横は0.00の部分

を見ることで、\[
P(0 \leqq x \leqq 0.50) = 0.1915
\]と読み取ることができ、確率が 0.1915 であることがわかります。

パターン2　xが -z0 以上 0 以下になる確率（負の場合）

標準正規分布は \( y \) 軸に対して対称です。

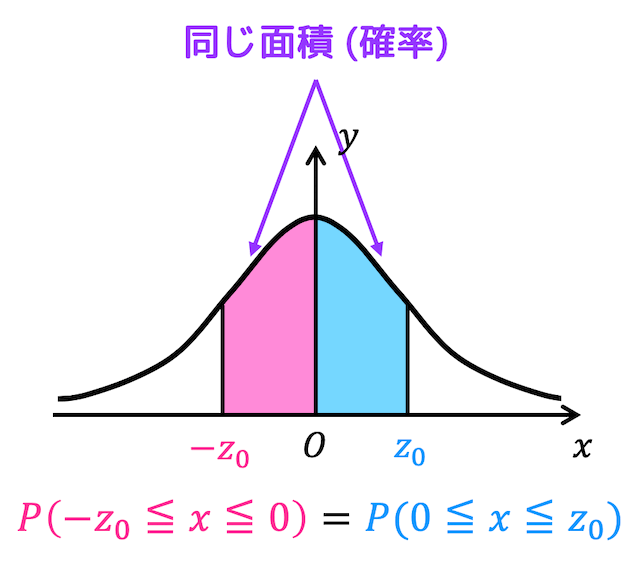
そのため、\( 0 \leqq x \leqq z_0 \) となる確率と \( - z_0 \leqq x \leqq 0 \) は同じになります。（上の図がイメージ）

正規分布表に \( z_0 \) が負になる場合が書かれていないのは正の値の場合を見れば \( y \) 軸が対称なのを利用して負の値を求めることができるからです。

 

例えば、\( -1.25 \leqq x \leqq 0 \) となる確率 \( P(-1.25 \leqq x \leqq 0) \) は、正の場合 \( P(0 \leqq x \leqq 1.25) \) を用いることで求められます。

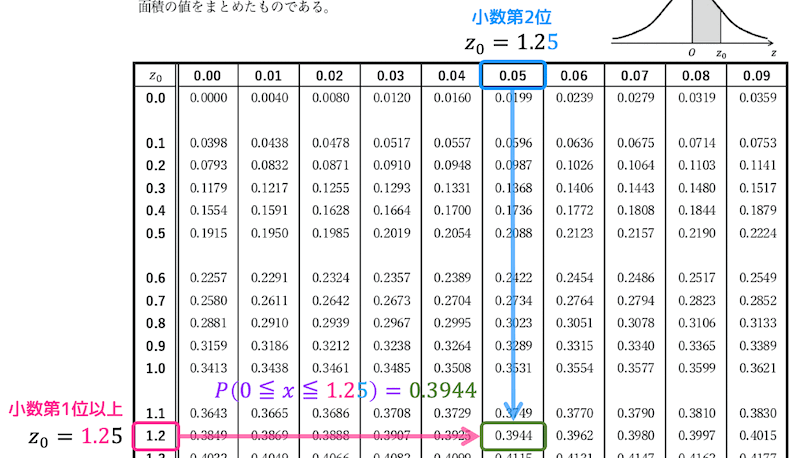
よって、\[\begin{align*}
P(-1.25 \leqq x \leqq 0) & = P(0 \leqq x \leqq 1.25) 
\\ & = 0.3944
\end{align*}\]となり、確率は 0.3944 となります。

パターン3　xが -z0 以上 z1 以下になる確率（2つの面積の足し合わせ）

範囲が負〜正まで入っている場合です。

この場合は、マイナス〜0、0〜プラスの2つに分けてから足し合わせたものが確率となります。

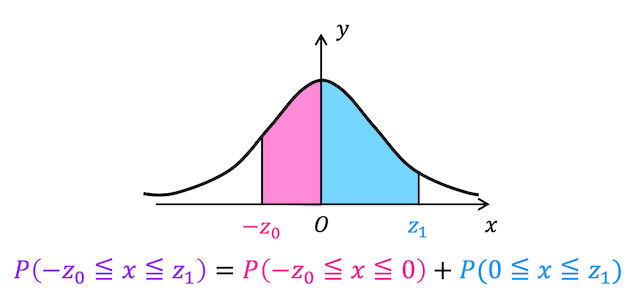
例えば、\( -1.25 \leqq x \leqq 0.5 \) となる確率 \( P(-1.25 \leqq x \leqq 0.5) \) は、負の面積部分\( P(-1.25 \leqq x \leqq 0) \) と正の面積部分 \( P(0 \leqq x \leqq 0.5) \) を足すと求められます。つまり、\[\begin{align*}
P(-1.25 \leqq x \leqq 0.5) & = P(-1.25 \leqq x \leqq 0)+ P(0 \leqq x \leqq 0.5)
\\ & = P(0 \leqq x \leqq 1.25)+ P(0 \leqq x \leqq 0.5)
\\ & = 0.3944 + 0.1915
\\ & = 0.5859
\end{align*}\]となるので、確率は 0.5859 と求められます。

パターン4　xが z0 以上 z1 以下になる確率（2つの面積の引き算）

つぎに引き算をするパターンです。

この場合、0 から \( z_1 \) までの面積を求めてから \( z_0 \) の面積を引くことで確率を求めます。

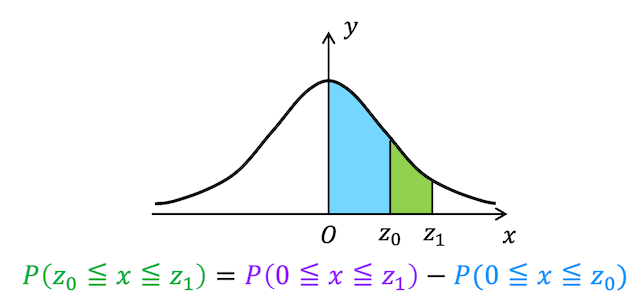
例えば、\( 0.5 \leqq x \leqq 1.25 \) となる確率 \( P(0.5\leqq x \leqq 1.25) \) は、大きい面積部分\( P(0 \leqq x \leqq 1.25) \) から小さい面積部分 \( P(0 \leqq x \leqq 0.5) \) を引くと求められます。つまり、\[\begin{align*}
P(0.5 \leqq x \leqq 1.25) & = P(0 \leqq x \leqq 1.25) - P(0 \leqq x \leqq 0.5)
\\ & = 0.3944 - 0.1915
\\ & = 0.2029
\end{align*}\]となるので、確率は 0.2029 と求められます。

 

なお、負の場合（例：\( - z_1 \leqq x \leqq - z_0 \) となる確率）も、パターン2を組み合わせる（正に変換してから確率を出す）ことで簡単に求めることができます。

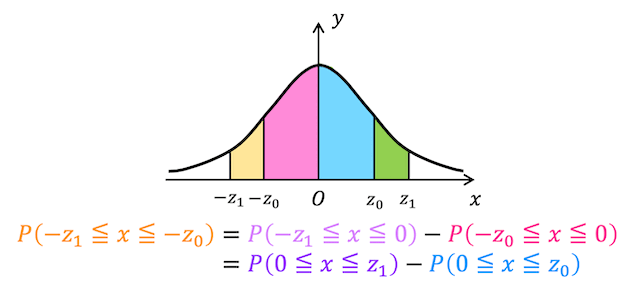
例えば、\( -1.25 \leqq x \leqq -0.5 \) となる確率 \( P(-1.25 \leqq x \leqq 0.5) \) であれば、\[\begin{align*}
P(-1.25 \leqq x \leqq -0.5) & = P(-1.25 \leqq x \leqq 0) - P(-0.5 \leqq x \leqq 0)
\\ & = P(0 \leqq x \leqq 1.25) - P(0 \leqq x \leqq 0.5)
\\ & = 0.3944 - 0.1915
\\ & = 0.2029
\end{align*}\]と計算でき、確率は 0.2029 と求められます。

パターン5　xが正 / 負になる確率 = 0.5 を使うパターン

最後に、\( x \) が \( z_0 \) 以上になる場合も説明していきましょう。

 

確率密度関数は \( y \) 軸対称でしたね。

そのため、\( x \) が0以上になる確率（青色面積部分）と \( x \) が0以下になる確率（赤色面積部分）はともに等しくなりますよね。

 

全体の面積は1（確率の合計は1）なので、青色面積部分、赤色面積部分の面積は半分ずつの0.5になりますね。

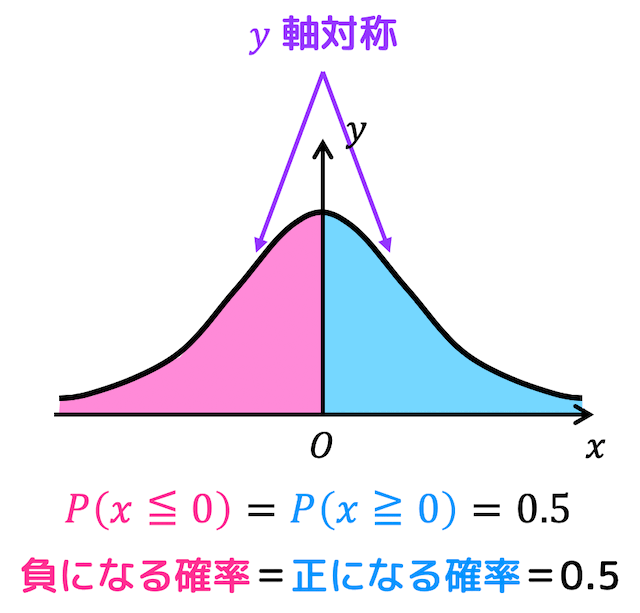
つまり、正になる確率と負になる確率はともに0.5になることがわかりますね。

 

これを使うことで、\( x \) が \( z_0 \) 以上になる確率 \( P (z_0 \leqq x) \) を下の図のように求めることができます。

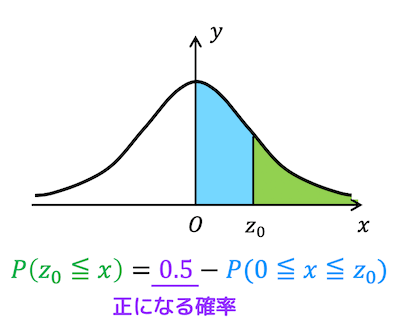
例えば、\( 1.25 \leqq x \) となる確率 \( P(1.25 \leqq x) \) は、正となる確率0.5から、\( 0 \leqq x \leqq 1.25 \) となる確率を引くことで求めることができます。

よって、\[\begin{align*}
P(1.25 \leqq x) & = 0.5 - P(0 \leqq x \leqq 1.25) 
\\ & = 0.5 - 0.3944
\\ & = 0.1056
\end{align*}\]となります。

（\( x \) が \( 0 \leqq x \leqq 1.25 \) となる確率はパターン2で求めているので読み取り方を省略しています。）

 

また、パターン2を組み合わせて \( x \) が \( -z_0 \) 以下になる確率 \( P (x \leqq - z_0) \) を下の図のように求めることができます。

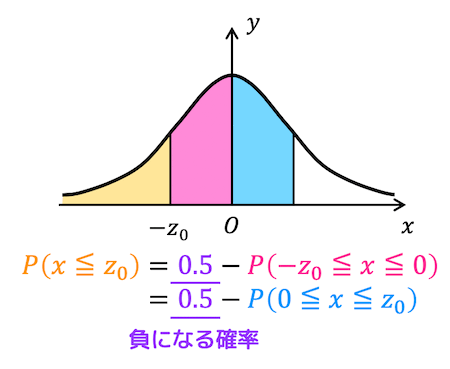
例えば、\( x \leqq -0.5 \) となる確率 \( P(x \leqq -0.5) \) は、正となる確率0.5から、\( -0.5 \leqq x \leqq 0 \) となる確率を引くことで求めることができるので、\[\begin{align*}
P(x \leqq -0.5) & = 0.5 - P(-0.5 \leqq x \leqq 0) 
\\ & = 0.5 - P(0 \leqq x \leqq 0.5) 
\\ & = 0.5-0.1915
\\ & = 0.3085
\end{align*}\]となります。

(3) 標準正規分布 → 正規分布の変換

共通テストなどで出てくる正規分布は、平均0、標準偏差1の標準正規分布 \( N(0,1) \) ではない場合がほとんどです。

しかし、試験では標準正規分布以外の確率は事前に与えられません。

 

そこで、平均 \( m \) 、標準偏差 \( \sigma \) の正規分布 \( N(m,\sigma^2) \) を標準正規分布の形になおす方法をここでは紹介したいと思います。

(i) 平均を0に補正する

まず、平均を0に補正する必要があります。

平均が \( m \) の確率分布を平均 0 にするためには、\( x \) から \( m \) を引いてあげる必要がありますね*3。

 

つまり、\( t = x - m \) とすることで、\( t \) の平均を0にすることができますね。

(ii) 標準偏差を1に補正する

平均を0にしたあとは、標準偏差を1に補正する必要があります。

標準偏差が \( \sigma \) の確率分布を標準偏差 \( 1 \) にするためには、\( t \) を \( \sigma \) で割ってあげればいいですね*4。

 

つまり、\( z = \frac{t}{\sigma} = \frac{x-m}{\sigma} \) とすることで、\( z \) の標準偏差を1にすることができますね。

また、\( t \) の平均は0に補正されているので、割っても平均は0のまま変わりませんね。

 

(i), (ii) の操作、つまり平均 \( m \)、標準偏差 \( \sigma \) で表される正規分布で表される確率変数 \( x \) を\[
z = \frac{x-m}{\sigma}
\]とおくことで、\( z \) は平均0、標準偏差1の標準正規分布に従うので、正規分布表を用いて確率を求めることができるようになります。 

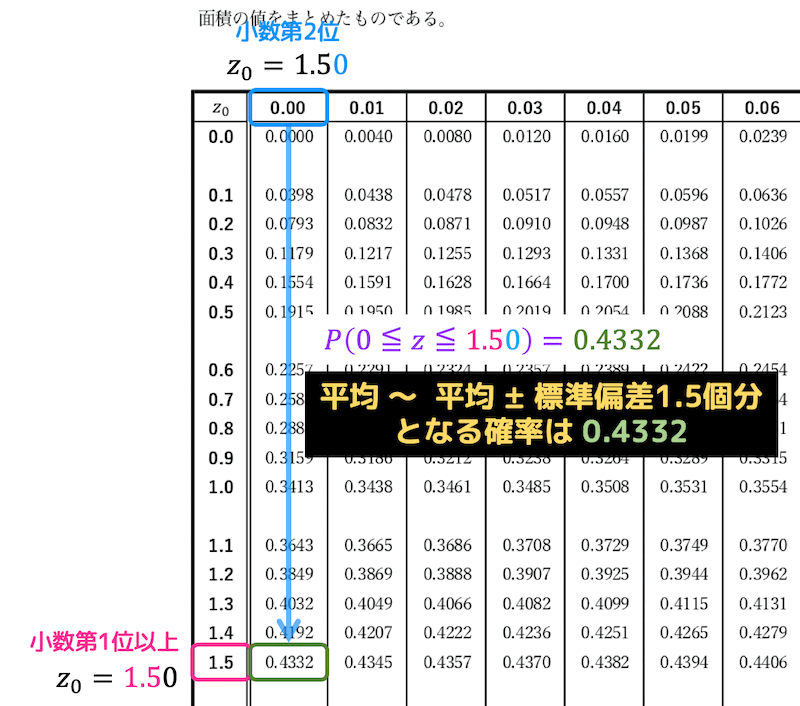
(4) 正規分布表の日本語的な意味

なお、確率変数 \( z \) は、平均より標準偏差何個分大きい or 小さいかを示す確率変数となっています。

そのため、正規分布表を日本語でわかりやすく説明すると、正規分布に従う確率変数が『平均 〜 平均 ± 標準偏差 \( z_0 \) 個分』の範囲に入る確率を示した表と言えます！

 

例えば、\( P(0 \leqq z \leqq 0.5) \) となる確率は、ある確率変数が、「平均」〜「平均 ± 標準偏差0.5個分」となる確率を表しています。

この確率は、正規分布表から下のように読み取れますね。

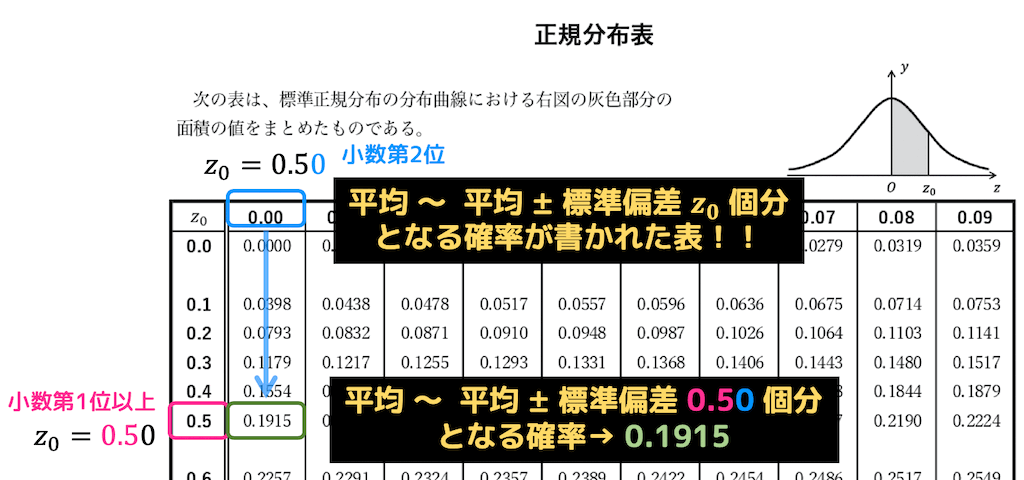
このように、正規分布表は平均から標準偏差 \( z_0 \) 個分ずれる確率を示した表となっています。

 

スポンサードリンク

３．二項分布と正規分布

最初に、「コインを100回投げて表が出る回数を記録する」セット数を増やせば増やすほどきれいな山の形になり、そのきれいな形が正規分布であると説明しましたね。

 

実は、「コインを100回投げて表が出る回数」のような二項分布に従う確率分布は、セット数 \( n \) を増やせば増やすほど正規分布に近づいていくのです！

 

そこで、\( n \) が十分に大きいとき*5は、正規分布と近似することで、少ない計算量で「ある範囲内の結果となる確率」を求めることができます。

 

例えば、「コインを100回投げて表が50回以上60回以下出る回数」を求めたい場合、二項分布だけであれば\[
\sum^{60}_{k = 50} {}_{100} \mathrm{C} _{k} \left( \frac{1}{2} \right)^{k} \left( \frac{1}{2} \right)^{100-k}
\]を出す必要があってめんどくさいですが、正規分布と仮定することで正規分布表を用いて少し簡単な計算をするだけで確率を出せるので、かなり計算が楽になります。

 

この流れをつかむために、練習問題で実際に練習してみましょう！

４．練習問題（共通テスト練習）

では、練習（共通テスト対策）をしてみましょう！

必要であればこちらから正規分布表をダウンロードしてください。

※注意

小数の形で解答する場合、指定された桁数の1つ下の桁を四捨五入して解答してください。また、必要に応じて、確定された桁まで⓪をマークしてください。

例えば、[　ア　] . [　イウ　] に 2.5 と答えたいとき → 2.50 とする。

 

５．練習問題の答え

(1)

サイコロを1回投げたときに出る目は 1, 2, 3, 4, 5, 6 のいずれかである。そのなかで 3, 6が出ればいいので確率は\[
\frac{2}{6} = \frac{1}{3}
\]となる。（ア：1　イ：3）

 

(2)

サイコロを投げたときに、「3の倍数が出る」か「3の倍数が出ないか」なので、\( X \) は二項分布に従う。（ウ：2）

そのため、平均 \( m \) は、\[\begin{align*}
m & = 162 \cdot \frac{1}{3}
\\ & = 54
\end{align*}\]となる。（エオ：54）

また、分散 \( \sigma^2 \) が[\begin{align*}
\sigma^2 & = m \cdot \left( 1 - \frac{1}{3} \right)
\\ & = 54 \cdot \frac{2}{3}
\\ & = 36
\end{align*}\]と求められるので、標準偏差 \( \sigma \) は、[\begin{align*}
\sigma & = \sqrt{ 36 }
\\ & = 6
\end{align*}\]となる。（カ：6）

 

ここで、標準正規分布になおすために、\[\begin{align*}
Z = \frac{X - m}{\sigma} = Z = \frac{X - 54}{6}
\end{align*} \]とおく。

（標準正規分布表を使える形にするために、は平均から標準偏差何個分ずれているかを表す確率変数 \( Z \) に変換する）

\( X \) が48以上となる確率というのは、\( X \) が「平均 (54) - 標準偏差1個分 (6)」以上となる確率と等しいので、\[
P(X \geqq 48) = P (Z \geqq -1.00)
\]となる。（キ . クケ： 1.00）

 

[念の為]  \( X \) から \( Z \) の変換を真面目にしてみる

\[\begin{align*}
X \geqq 48 & \Leftrightarrow X - 54 \geqq -6
\\ & \Leftrightarrow \frac{X-54}{6} \geqq -1
\\ & \Leftrightarrow Z \geqq -1
\end{align*}\]と変形できる。

（共通テストはマーク式なので途中式を見られません。なので、「平均から標準偏差何個分ずれているか」を求めるという考えでOKです。）

 

また、\( X \) が54回以上となる確率、つまり「平均以上になる確率」というのは、下の図の青色部分に相当する。そのため、確率は0.5となる。（コ . サシ：0.50）

※ 正規分布での平均以上 / 平均以下になる確率は0.5になることは必ず頭に入れておこう！

よって、\( X \) が「平均 (54) - 標準偏差1個分 (6)」以上となる確率「\( P(Z \geqq -1.00) \) は、下の図の赤色面積＋青色面積となる部分となる。

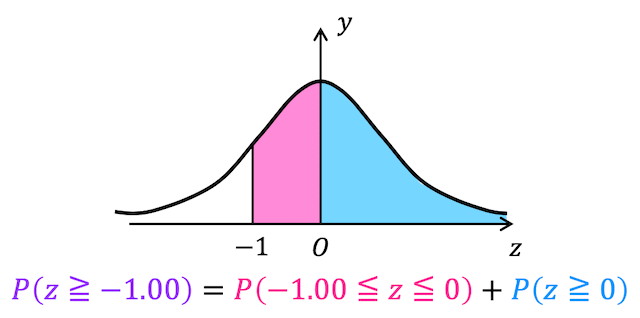
日本語に直すと、

• 「平均 (54) - 標準偏差1個分 (6)」〜「平均 (54)」となる確率
  →「平均」〜「平均 ± 標準偏差1個分」になる確率を正規分布表から読み取る
  → 0.3413
• 「平均 (54) 以上となる確率」
  → 0.5

の2つの和で計算できる。

 

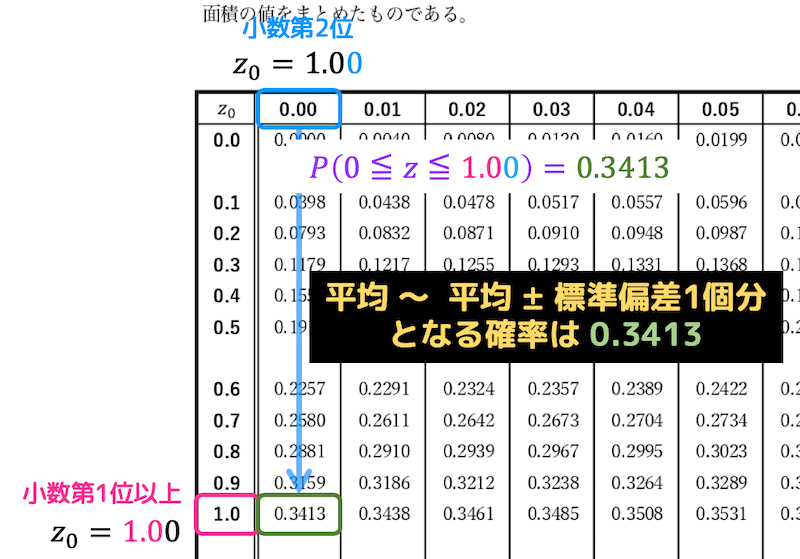
よって、\( X \) が「平均 (54) - 標準偏差1個分 (6)」以上となる確率「\( P(Z \geqq -1.0) \) は、\[\begin{align*}
P(Z \geqq -1.00) & = P(-1.00 \leqq z \leqq 0) + P(z \geqq 0)
\\ & = 0.3413 + 0.5
\\ & = 0.8413
\end{align*}\]となるので小数第3位を四捨五入した 0.84 が答えとなる

（スセ：84）

 

(4)

(3) と同じように \( X \) が45以上48以下となる確率を求めていこう。

まず、45, 48がそれぞれ平均から標準偏差何個分ずれているかを求める。
（先程の \( z \) に相応するものを求めています）

• \( X \) が45以上
  → \( X \) が「平均 (54) - 標準偏差1.5個分 (6 × 1.5 = 9) 」以上となる確率
• \( X \) が48以下
  → \( X \) が「平均 (54) - 標準偏差1個分 (6) 」以下となる確率

なので、「平均 (54) - 標準偏差1.5個分 (6 × 1.5 = 9) 」〜「平均 (54) - 標準偏差1個分 (6) 」の範囲になる確率、つまり下の図の黄色部分の面積を求めればOK。

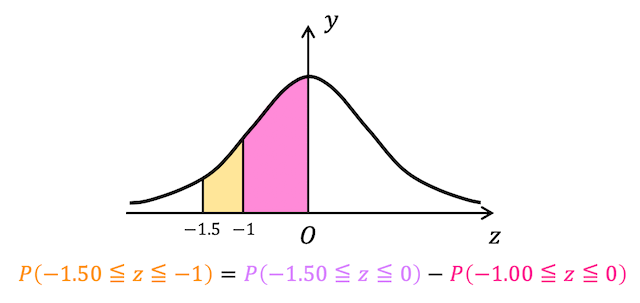
黄色部分の面積を日本語で表すと、

• 「平均 (54) - 標準偏差1.5個分 (9)」〜「平均 (54)」となる確率
  →「平均」〜「平均 ± 標準偏差1.5個分」になる確率を正規分布表から読み取る
  → 0.4332 [赤色＋黄色部分]
• 「平均 (54) - 標準偏差1個分 (6)」〜「平均 (54)」となる確率
  →「平均」〜「平均 ± 標準偏差1個分」になる確率を正規分布表から読み取る
  → 0.3413 [赤色部分]
  ※ (3)で読み取っているので新たに読み取らなくてOK

の差（赤色＋黄色部分 - 赤色部分）となる。

よって、\( X \) が「平均 (54) - 標準偏差1.5個分 (9)」以上「平均 (54) - 標準偏差1個分 (6)」となる確率「\( P(-1.5 \leqq Z \leqq -1.0) \) は、\[\begin{align*}
P(-1.5 \leqq Z \leqq -1.0) & = P(-1.5 \leqq Z \leqq 0) - P(-1.00 \leqq z \leqq 0) 
\\ & = 0.4332 - 0.3413 
\\ & = 0.0919
\end{align*}\]となるので小数第3位を四捨五入した 0.09 が答えとなる。

（ソタ：09）

 

６．さいごに

今回は、

• 正規分布・標準正規分布とはどんな分布なのか
• 正規分布を基本的な形である標準正規分布に直す方法
• 正規分布表の読み方・正規分布表の意味
• 二項分布と合わさった問題の解き方

についてまとめていきました。

正規分布表を使いこなせるようになれば、「確率分布と統計的な推測」のゴールが近づいてきたと言えるのでぜひ使いこなせるようになりましょう！

 

次回からはいよいよ「推定」に関するお話に入っていきます。

では、また次回。

（今回は復習コーナーはありません。正規分布表を用いて問題が解けるように練習しましょう。）