スポンサードリンク
こんにちは、
「うさぎでもわかる線形代数 第16羽」では正則な行列 \( P \) を用いて、行列 \( A \) を \( P^{-1} AP \) と対角化(対角行列を作成)する方法についてお勉強しました。
また、第17羽では直交行列 \( P \) を用いて、行列 \( A \) を \( P^{-1} AP \) と対角化する方法も学習しましたね。
しかし、対角化は
- 正方行列しか対角化できない。
- 正方行列であっても対角化できない行列がある。
- 直交行列による対角化は条件が非常に厳しい(実対称行列のみ可能)
そこで、今回はこれら3つの欠点をカバーした、対角化の上位互換である「特異値分解」について説明していきます!
特異値分解を使うことで、すべての行列[1]行列の成分に複素数が含まれる場合は、転置行列 \( V^{\top} \) を随伴行列 \( V^* \) に変えればOKです。 \( A \) を行列 \( U \), \( V \) および対角行列 \( \Sigma \) を用いて\[
A = U \Sigma V^{\top}
\]と分解することができます!
※ 特異値分解の方法には何種類かあるのですが、今回は特異値分解の中でも最も手計算が簡単なエコノミーサイズの特異値分解で説明をしています。
(エコノミーサイズの特異値分解とフルサイズの特異値分解の違いは3章で説明しています)
目次
スポンサードリンク
[復習] 行列の対角化
特異値分解の仕組みを説明する前に、軽く行列の対角化について復習問題を用いて復習しましょう。
対角化で使う固有値、固有ベクトルの計算方法は、特異値分解を計算する際に使用するので、計算方法を忘れてしまった人は、下の記事にて確認しましょう。
(1) 正則行列を用いた対角化
行列 \( A \) を、正則行列 \( P \) を用いて \( P^{-1} A P \) を対角行列にすることを対角化と呼びます。
ここで、実際に復習問題で、対角化の方法を復習しましょう。
正則行列 \( P \) を用いて、次の行列 \( A \) を対角化しなさい。\[
A = \left( \begin{array}{ccc} 0 & 3 \\ -2 & 7 \end{array} \right)
\]
[Step1] 固有値を求める
固有値は \( | A - tE | = 0 \) で求めることができます。
\[\begin{align*}
|A - tE| & = \left| \begin{array}{ccc} -t & 3 \\ -2 & 7-t \end{array} \right|
\\ & = -t(7-t) - (-6)
\\ & = t^2 - 7t + 6
\\ & = (t-1)(t-6)
\\ & = 0
\end{align*}\]より、固有値は1, 6です。
[Step2] 固有ベクトルを求める
固有ベクトルは、各固有値ごとに連立方程式 \( (A-tE) \vec{p} = \vec{0} \) を満たすような \( \vec{p} \) を固有値の数だけ求めることで求められます[2] … Continue reading。
(i) 固有値1のときの固有ベクトル \( \vec{p}_1 \)
\[\begin{align*}
A - 1E & = \left( \begin{array}{ccc} -1 & 3 \\ -2 & 6 \end{array} \right)
\\ & = \left( \begin{array}{ccc} 1 & -3 \\ 0 & 0 \end{array} \right)
\end{align*}\]より、固有ベクトル \( \vec{p}_1 \) は\[
\vec{p}_1 = \left( \begin{array}{ccc} 3 \\ 1 \end{array} \right)
\]
(ii) 固有値6のときの固有ベクトル \( \vec{p}_2 \)
\[\begin{align*}
A - 6E & = \left( \begin{array}{ccc} -6 & 3 \\ -2 & 1 \end{array} \right)
\\ & = \left( \begin{array}{ccc} 2 & -1 \\ 0 & 0 \end{array} \right)
\end{align*}\]より、固有ベクトル \( \vec{p}_2 \) は\[
\vec{p}_2 = \left( \begin{array}{ccc} 1 \\ 2 \end{array} \right)
\]
[Step3] 対角化
ここで、正則行列 \( P = ( \vec{p}_1 , \vec{p}_2) \) とします。
すると、固有値の定義 \( A \vec{p} = t \vec{p} \) より、\( A \vec{p}_1 = 1 \vec{p}_1 \), \( A \vec{p}_2 = 6 \vec{p}_2 \) が成立しますね。
よって、次のような変形をすることができます。\[\begin{align*}
A P & = A ( \vec{p}_1 , \vec{p}_2 )
\\ & = ( A \vec{p}_1, A \vec{p}_2 )
\\ & = ( 1 \vec{p}_1 , 6 \vec{p}_2 )
\\ & = ( \vec{p}_1, \vec{p}_2 ) \left( \begin{array}{ccc} 1 & 0 \\ 0 & 6 \end{array} \right)
\\ & = PD
\end{align*}\]
両辺の左側に \( P ^{-1} \) を掛けることで、\[\begin{align*}
P^{-1} A P & = P^{-1} P D
\\ & = D
\end{align*}\]となりますね。※ \( D \) は対角行列
よって、行列 \( A \) は、以下の正則行列 \( P \) を用いて、\( P^{-1} AP \) を対角行列にすることができます。\[
P = \left( \begin{array}{ccc} 3 & 1 \\ 1 & 2 \end{array} \right) , \ \ \ D = \left( \begin{array}{ccc} 1 & 0 \\ 0 & 6 \end{array} \right)
\]
(2) 直交行列を用いた対角化
行列 \( A \) が実対称行列(\( A = A^{\top} \) を満たす)のときは、直交行列 \( P \) を用いて \( P^{-1} AP \) を対角行列にすることができます。
こちらも手順を復習問題にて、確認しましょう。
直交行列 \( P \) を用いて、次の行列 \( A \) を対角化しなさい。\[
A = \left( \begin{array}{ccc} 1 & 2 \\ 2 & 1 \end{array} \right)
\]
[Step1] 固有値を求める
固有値は \( | A - tE | = 0 \) で求めることができます。
※ここまでは正則行列のときと同じです
\[\begin{align*}
|A - tE| & = \left| \begin{array}{ccc} 1-t & 2 \\ 2 & 1-t \end{array} \right|
\\ & = (1-t)^2 - 4
\\ & = t^2 -2t + 1 - 4
\\ & = t^2-2t-3
\\ & = (t-3)(t+1)
\\ & = 0
\end{align*}\]より、固有値は3, -1です。
[Step2] 大きさ1の固有ベクトルを求め、同じ固有値に対する固有ベクトルを直交化させる
連立方程式 \( (A-tE) \vec{p} = \vec{0} \) を解くことで固有ベクトル \( \vec{p} \) を求めることができるのですが、直交行列により対角化を行う際には次の注意が必要です。
- \( \vec{p} \) の大きさを1に正規化すること
- 重解の場合、同じ固有値に対する固有ベクトルをグラムシュミットの直交化法により、直交化する必要があること
(i) 固有値3のときの固有ベクトル \( \vec{p}_1 \)
\[\begin{align*}
A - 3E & = \left( \begin{array}{ccc} -2 & 2 \\ 2 & -2 \end{array} \right)
\\ & = \left( \begin{array}{ccc} 1 & -1 \\ 0 & 0 \end{array} \right)
\end{align*}\]より、大きさ1の固有ベクトル \( \vec{p}_1 \) は\[
\vec{p}_1 = \frac{1}{ \sqrt{2} } \left( \begin{array}{ccc} 1 \\ 1 \end{array} \right)
\]
(ii) 固有値-1のときの固有ベクトル \( \vec{p}_2 \)
\[\begin{align*}
A + 1E & = \left( \begin{array}{ccc} 2 & 2 \\ 2 & 2 \end{array} \right)
\\ & = \left( \begin{array}{ccc} 1 & 1 \\ 0 & 0 \end{array} \right)
\end{align*}\]より、大きさ1の固有ベクトル \( \vec{p}_2 \) は\[
\vec{p}_2 = \frac{1}{ \sqrt{2} } \left( \begin{array}{ccc} 1 \\ -1 \end{array} \right)
\]
[Step3] 直交行列による対角化
ここで、直交行列 \( P = ( \vec{p}_1 , \vec{p}_2) \) とします。
すると、固有値の定義 \( A \vec{p} = t \vec{p} \) より、\( A \vec{p}_1 = 3 \vec{p}_1 \), \( A \vec{p}_2 = -1 \vec{p}_2 \) が成立しますね。
よって、次のような変形をすることができます。\[\begin{align*}
A P & = A ( \vec{p}_1 , \vec{p}_2 )
\\ & = ( A \vec{p}_1, A \vec{p}_2 )
\\ & = ( 3 \vec{p}_1 , -1 \vec{p}_2 )
\\ & = ( \vec{p}_1, \vec{p}_2 ) \left( \begin{array}{ccc} 3 & 0 \\ 0 & -1 \end{array} \right)
\\ & = PD
\end{align*}\]※ \( D \) は対角行列
よって、両辺に \( P^{-1} \) を掛けると \( P^{-1} AP = D \) となるため、直交行列 \( P \) を用いて、以下のように対角化ができます。\[
P = \frac{1}{ \sqrt{2} } \left( \begin{array}{ccc} 1 & 1 \\ 1 & -1 \end{array} \right), \ \ \ P^{-1}AP = \left( \begin{array}{ccc} 3 & 0 \\ 0 & -1 \end{array} \right)
\]
※ 直交行列の場合、\( P^{-1} = P^{\top} \) なため、\( P^{\top} AP = D \) としてもOK。(\( P^{\top} \) は行列 \( P \) の転置行列、\( {}^t \! P \) と表記することもあり。)
特異値分解の計算は、直交行列による対角化の計算に似ている部分が結構あります。
そのため、直交行列による対角化が怪しい人は、必ずこちらの記事にて復習をしてから特異値分解の勉強をしましょう。
スポンサードリンク
1. 特異値・特異ベクトル
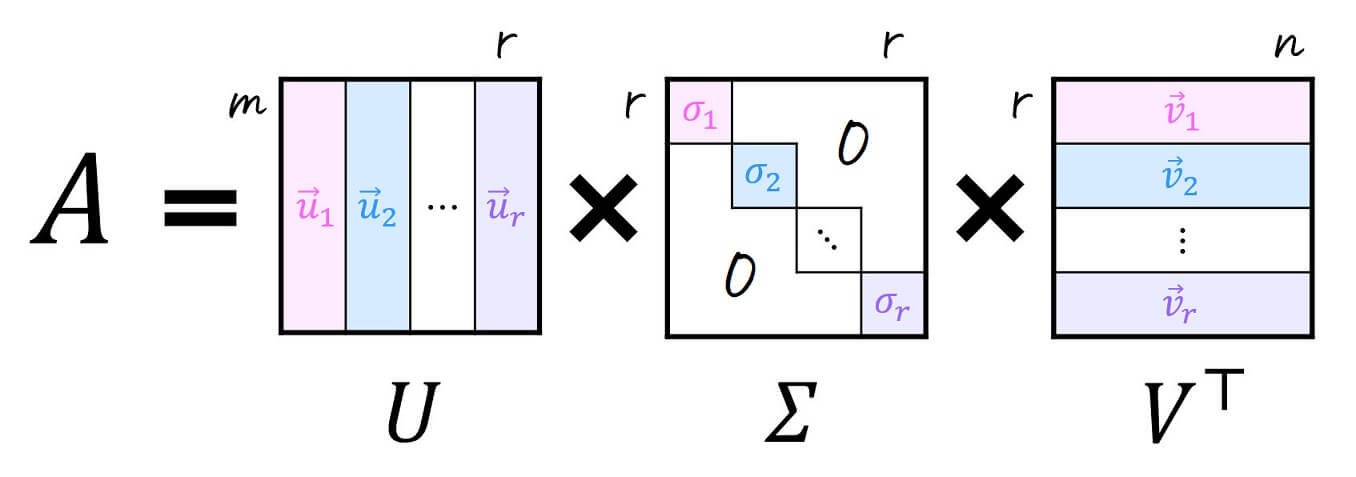
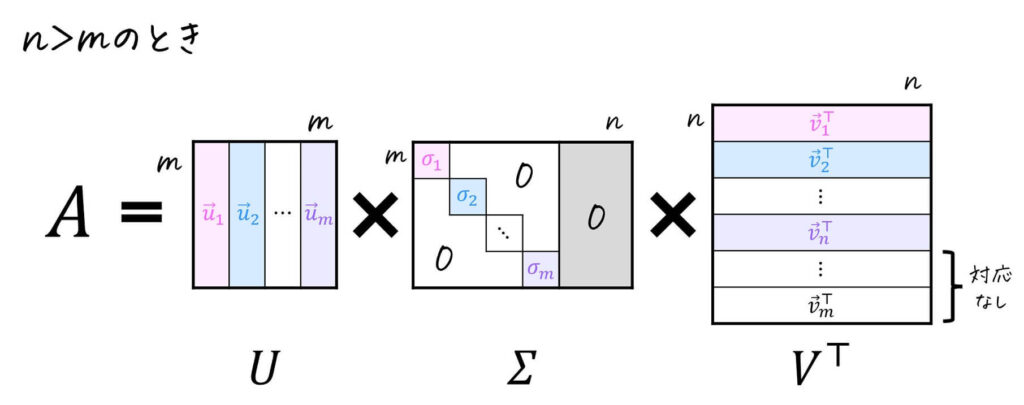
特異値分解は、\( m \) 行 \( n \) 列の行列 \( A \) を下のように、行列 \( U \), \( V \) および対角行列 \( \Sigma \) で分解することを指します。

※ \( r = \min (m,n) \) です。つまり \( m \), \( n \) のうち、小さい方が \( r \) になります。
この特異値分解を計算する際に必要なのが、
- 行列 \( A \) の特異値 \( \sigma \)
- 各特異値に対する左特異ベクトル \( \vec{u} \)
- 各特異値に対する右特異ベクトル \( \vec{v} \)
の3つです[3]左特異ベクトル、右特異ベクトルの左右ってなんだよって思った人もいるかもしれませんが、\( \Sigma \) の左側にある行列 \( U \) … Continue reading。
まずは、特異値分解を計算する際に使う特異値 \( \sigma \)、左特異ベクトル \( \vec{u} \)、および右特異ベクトル \( \vec{v} \) についてみていきましょう。
※ この先左特異ベクトル、右特異ベクトルを合わせて特異ベクトルと呼ぶことがあります。
(1) 特異値・特異ベクトルの定義
\( m \) 行 \( n \) 列行列 \( A \) に対し、\( A \vec{v} = \sigma \vec{u} \) および \( A^{\top} \vec{u} = \sigma \vec{v} \) を満たすような \( \sigma \) および、ベクトル \( \vec{u} \), \( \vec{v} \) を考えます。
このときの、
- \( \sigma \) が特異値の定義
- \( \vec{u} \) が左特異ベクトル
- \( \vec{v} \) が右特異ベクトル
が特異値、(左/右)特異ベクトルの定義となります。
ここで、\( A \vec{v} \) の計算をするためには、\( \vec{v} \) は \( n \) 次元ベクトルである必要がありますね。
つぎに、\( A \vec{v} \) の計算結果 \( \sigma \vec{u} \) は \( m \) 次元ベクトルになりますね。よって、\( \vec{u} \) は \( m \) 次元ベクトルである必要がありますね。
また、特異値の数は \( m \), \( n \) のうち、小さい数(つまり \( \min (m,n) \) 個)だけあります。
\( m \) 行 \( n \) 列の行列 \( A \) に対し、\[\begin{align*}
A \vec{v} & = \sigma \vec{u} \\
A^{\top} \vec{u} & = \sigma \vec{v}
\end{align*}\]の両方を満たすような \( \sigma \) を特異値、\( m \) 次元ベクトル \( \vec{u} \) を左特異ベクトル、\( n \) 次元ベクトル \( \vec{v} \) を右特異ベクトルと呼ぶ。
※1 特異値の数は \( \min (m,n) \) 個ある。
※2 \( | \vec{u} | = | \vec{v} | = 1 \)、\( \sigma > 0 \) とする。
※3 \( A^{\top} \) は行列 \( A \) の転置を表す。(\( {}^t \! A \) と表されることもあり。)
(2) 特異値の求め方
(i) 特異値を出す仕組み
まずは特異値 \( \sigma \) を求めてみましょう。
行列 \( A \vec{v} = \sigma \vec{u} \) の両辺に \( A^{\top} \) を左側から掛けます。すると、\[\begin{align*}
A^{\top} A \vec{v} & = A^{\top} \sigma \vec{u}
\\ & = \sigma (A^{\top} \vec{u})
\\ & = \sigma ( \sigma \vec{v} )
\\ & = \sigma^2 \vec{v}
\\ & = \sigma^2 E \vec{v}
\end{align*}\]とできますね。
ここで、\( B = A^{\top} A \) とし、さらに変形していくと\[\begin{align*}
A^{\top} A \vec{v} & = \sigma^2 E \vec{v} \\
B \vec{v} & = \sigma^2 E \vec{v} \\
B \vec{v} - \sigma^2 E \vec{v} & = \vec{0} \\
(B - \sigma^2 E ) \vec{v} & = \vec{0}
\end{align*}\]と行列を用いた連立方程式の形に変形できますね。
ここで、ベクトル \( \vec{v} \) を用いて作られる行列 \( V \) を正規直交基底のベクトルを並べることで作れる行列にするため、\( \vec{v} \) が \( \vec{0} \) 以外の解を持つことを考えましょう。
もし、\( C = B - \sigma^2 E \) が正則だとすると、\( C \) には逆行列 \( C^{-1} \) が存在します。そのため、\[\begin{align*}
C \vec{v} & = \vec{0} \\
C^{-1} C \vec{v} & = C^{-1} \vec{0} \\
\vec{v} & = \vec{0}
\end{align*}\]となり、\( \vec{v} = \vec{0} \) 以外の解をもちません。
そのため、行列 \( B - \sigma^2 E \) は非正則である必要があります。言い換えると、\( |B - \sigma^2 E| = 0 \) の関係式が成立する必要があります。
よって、特異値を求める際には \( | B - \sigma^2 E | = 0 \)、つまり\[
|A^{\top} A - \sigma^2 E | = 0
\]を満たすような \( \sigma \) を求めればOKですね!
(ii) 特異値と固有値の関係
なお、\( B = A^{\top} A \)、\( t = \sigma^2 \) とすることで、特異値 \( \sigma^2 \) を求める式 \( A^{\top} A - \sigma^2 E \) を固有値 \( t \) を求める式に書きかえることができます。

日本語だと「行列 \( A^{\top} A \) の固有値の平方根 \( \sqrt{t} \) が特異値 \( \sigma \) となる」と言えますね。
※ \( A^{\top} A \) は必ず実対称行列となります。そのため、\( A^{\top} A \) の固有値 \( t \) は必ず実数になり、さらに \( \sqrt{t} > 0 \) なので \( A \) の特異値は正となります。
(iii) もう1つの特異値の求め方
\( A \vec{v} = \sigma \vec{u} \) ではなく、\( A^{\top} \vec{u} = \sigma \vec{v} \) に着目して特異値 \( \sigma \) を求めることもできます。
この場合、両辺に \( A \) を左側から掛けて、\[\begin{align*}
AA^{\top} \vec{u} & = A \sigma \vec{v}
\\ & = \sigma ( A \vec{v} )
\\ & = \sigma ( \sigma \vec{u} )
\\ & = \sigma^2 \vec{u}
\\ & = \sigma^2 E \vec{u}
\end{align*}\]ができますね。
つぎに、連立方程式の形を作ります。\[\begin{align*}
A A^{\top} \vec{u} & = \sigma^2 E \vec{u} \\
AA^{\top} \vec{u} - \sigma^2 E \vec{u} & = \vec{0} \\
(AA^{\top} - \sigma^2 E ) \vec{u} & = \vec{0}
\end{align*}\]と
ここで、正規直交基底を成すベクトル \( \vec{u} \) を並べた行列 \( U \) を作るためには \( \vec{u} \) が \( \vec{0} \) 以外である必要があります。
そのため、\( AA^{\top} - \sigma^2 E \) が正則とならないような \( \sigma \) を\[
| A^{\top} A - \sigma^2 E | = 0
\]で求めればOKですね。

こちらも、\( A A^{\top} = B \), \( t = \sigma^2 \) とおくことで、固有値を求める式に変形することができます。
つまり、「行列 \( AA^{\top} \) の固有値の平方根 \( \sqrt{t} \) が特異値 \( \sigma \) となる」と言えますね。
※ \( A^{\top} A \) と同じく、\( A A^{\top} \) も必ず実対称行列となります。
(iv) どっちの公式を使うのか
特異値 \sigma の導出公式として、下の2つを紹介しました。
- \( | A A^{\top} - \sigma^2 E | = 0 \)
- \( | A^{\top} A - \sigma^2 E | = 0 \)
どちらを使っても計算は出来ますが、手計算をする場合は計算量が少なくなる方を選んでください。
言い換えると、\( A A^{\top} \) と \( A^{\top} A \) のうち、より行列のサイズが小さくなる方を選べばOKです。
例えば、\( A \) が下のような2行3列の行列だとします。
すると、\( A A^{\top} \) は2行2列、\( A^{\top} A \) は3行3列となるため、より行列のサイズが小さくなるのは \( A A^{\top} \) ですね。
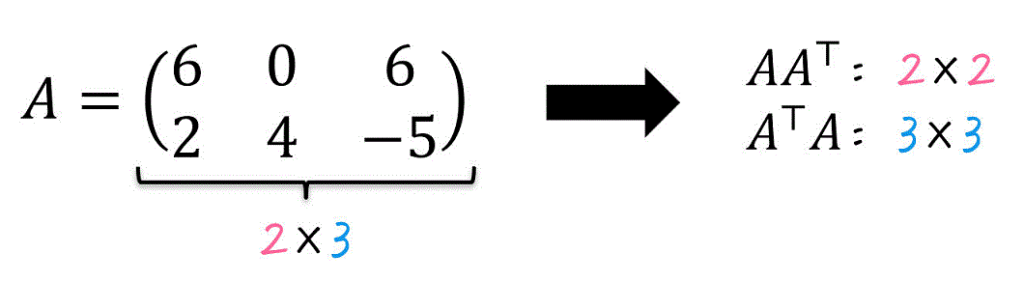
なので、この行列 \( A \) の特異値 \( \sigma \) を計算する際には、\( A A^{\top} \) が出てくる \( | A A^{\top} - \sigma^2 E | = 0 \) を使うことになります。
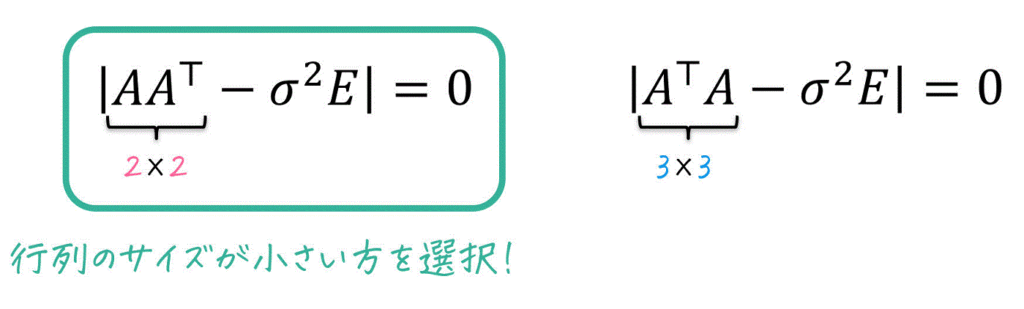
行列 \( A \) の特異値 \( \sigma \) は次の2つの方程式のうち、いずれか1つを解くことで求めることができる。
\( | A A^{\top} - \sigma^2 E | = 0 \) → \( A A^{\top} \) の固有値の平方根と同じ
\( | A^{\top} A - \sigma^2 E | = 0 \) → \( A^{\top} A \) の固有値の平方根と同じ
いずれか1つを解けばOKなので、計算量を少なくするために出てくる行列のサイズが小さくなる方を選択するのがおすすめ。
[注意]- サイズが大きくなる公式を使ってしまった場合でも特異値は求められるが、\( \sigma = 0 \) という余分な解が出てくる。この \( \sigma = 0 \) は特異値に含めない。
- どちらの公式を選んだかによって、特異ベクトルの求める手順が変わるため注意。
- \( m \) 行 \( n \) 列の行列 \( A \) の特異値の個数(重解も別々にカウント[4]例えば、特異値が4, 4, 3だった場合は3個とカウントする。)は、\( \min (m,n) \) 個存在する。例えば、2行3列の行列であれば、特異値は2個ある。
(\( m \) と \( n \) のうち、より小さい方が特異値の個数となる)
(3) 特異ベクトルの求め方
(i) まずは片方の特異ベクトルを求める
次に、求められた各特異値ごとに連立方程式
- \( (A^{\top} A - \sigma^2 E) \vec{v} = \vec{0} \)
- \( (AA^{\top} - \sigma^2 E ) \vec{u} = \vec{0} \)
のどちらかを解くことで、左特異ベクトル \( \vec{u} \)、右特異ベクトル \( \vec{v} \) のうちの片方を求めます。
※ 特異ベクトルを計算する際も、(特異値のときと同じように)計算で出てくる行列のサイズがより小さくなる方を選びましょう。
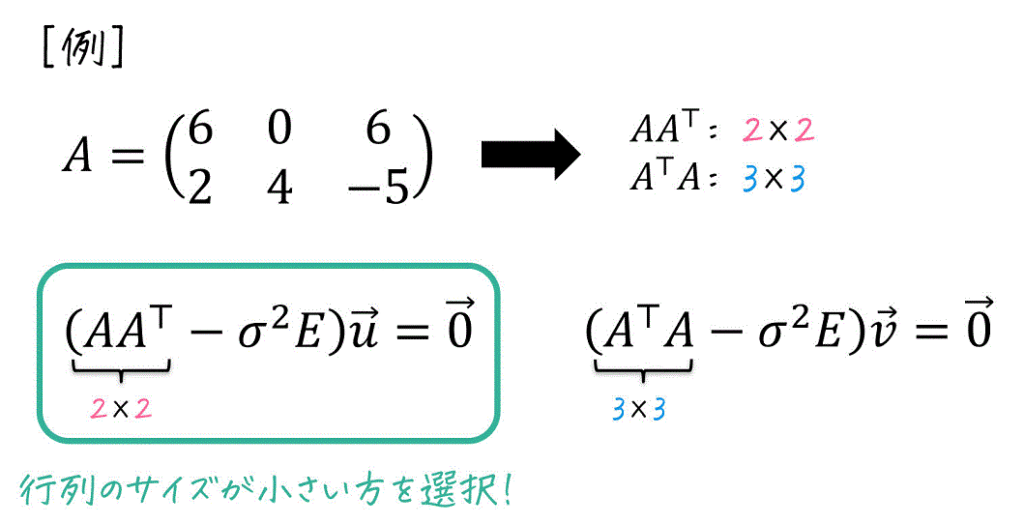
ただし、特異ベクトル \( \vec{u} \), \( \vec{v} \) を求める際には各特異ベクトルを直交化させることで、\( U U^{\top} = E \), \( U^{\top} U = E \), \( V V^{\top} = E \), \( V^{\top} V = E \) が成立するように、次の2つに注意して求めましょう。
[注意]- 特異ベクトルの大きさを1になるように正規化すること。
- 重解が発生した場合、同じ特異値に対する特異ベクトルが複数出てくる。この場合は、グラムシュミットの直交化法により、同じ特異値に対する特異ベクトルを直交化させること。
(異なる特異値に対する特異ベクトル同士は、もともと直交化しているので直交化させる必要なし)
なお、左特異ベクトル \( \vec{u} \) は \( AA^{\top} \) の固有ベクトルに、右特異ベクトル \( \vec{v} \) は \( A^{\top} A \) の固有ベクトルに等しくなります[5] \( A A^{\top} = B \) もしくは \( A^{\top} = B \) とすると、固有ベクトルの計算公式 \( (A - tE) \vec{p} = \vec{0} \) とそっくりな形になりますね。。
(ii) もう片方の特異ベクトルを定義式から求める
地道に(i)の連立方程式を2つ解いて特異ベクトルを求めるのもありですが少し計算がめんどくさいです。
そこで、左特異ベクトル \( \vec{ u } \)、右特異ベクトル \( \vec{v} \) のうち、片方が求まってしまえばもう片方を特異値、特異ベクトルの定義式
- \( A \vec{v} = \sigma \vec{u} \)
- \( A^{\top} \vec{u} = \sigma \vec{v} \)
から求めましょう。
左特異ベクトルが \( \vec{u} \) がわかっている場合は、\( A^{\top} \vec{u} = \sigma \vec{v} \) を変形し、\[
\vec{v} = \frac{1}{\sigma} A^{\top} \vec{u}
\]を計算することで \( \vec{v} \) を求めます。
右特異ベクトル \( \vec{v} \) がわかっている場合は、\( A \vec{v} = \sigma \vec{u} \) を変形し、\[
\vec{u} = \frac{1}{\sigma} A \vec{v}
\]を計算することで \( \vec{u} \) を求めます。
- \( (A^{\top} A - \sigma^2 E) \vec{v} = \vec{0} \) → 固有値 \( \sigma^2 \) の \( A^{\top} A \) の固有ベクトルと同じ
- \( (AA^{\top} - \sigma^2 E ) \vec{u} = \vec{0} \) → 固有値 \( \sigma^2 \) の \( A A^{\top} \) の固有ベクトルと同じ
※1 \( \vec{u} \), \( \vec{v} \) の大きさを1にすること
※2 各特異値ごとに求められる特異ベクトルは重解の数だけある
※3 特異値が重解の時は、同じ特異値に対する特異ベクトルを直交化させること
\\ \vec{v} & = \frac{1}{\sigma} A^{\top} \vec{u}
\end{align*}\]
※ \( \vec{v} \) もしくは \( \vec{u} \) を求めた後にベクトルの正規化をする必要があると思われるかもしれませんが、\( \vec{u} \) から \( \vec{v} \) に変換する際に大きさは1のまま変わらないため(直交変換となっているため)、不要です[6]\( \vec{u} \) から \( \vec{v} \) を求める場合のみですが、本当に大きさが変わらないことを確認します。定義より、\( A^{\top} \vec{u} = \sigma \vec{v} \) … Continue reading。また、ベクトルの大きさが変わらない変換(直交変換)を適用した場合は、各特異ベクトル同士の直交性は満たしたままなので正規直交化もする必要がありません。
(4) 例題で確認
実際に特異値、特異ベクトルの求め方を例題で確認してみましょう。
次の行列 \( A \) の特異値、特異ベクトルを求めたい。\[
A = \left( \begin{array}{ccc} 6 & 0 & 6 \\ 2 & 4 & -5 \end{array} \right)
\]つぎの(1)~(4)の問いに答えなさい。
(1) 行列 \( A A^{\top} \) の固有値、大きさ1の固有ベクトルを求めなさい。
(2) 行列 \( A \) の特異値を求めなさい。
(3) 行列 \( A \) の各特異値ごとに対応する左特異ベクトル \( \vec{u} \) を求めなさい。
(4) (3)の結果を用いて、行列 \( A \) の各特異値ごとに対応する右特異ベクトル \( \vec{v} \) を求めなさい。
[解説1]
(1)
(i) 固有値計算
まずは \( A A^{\top} \) を計算する。\[\begin{align*}
A A^{\top} & = \left( \begin{array}{ccc} 6 & 0 & 6 \\ 2 & 4 & -5 \end{array} \right) \left( \begin{array}{ccc} 6 & 2 \\ 0 & 4 \\ 6 & -5 \end{array} \right)
\\ &= \left( \begin{array}{ccc} 36 + 0 + 36 & 12 + 0 - 30 \\ 12 + 0 - 30 & 4 + 16 + 25 \end{array} \right)
\\ & = \left( \begin{array}{ccc} 72 & -18 \\ -18 & 45 \end{array} \right)
\end{align*}\]※必ず実対称行列になります。
ここで、\( A A^{\top} \) の固有値を \( t \) とすると、\[\begin{align*}
|A A^{\top} - tE| & = \left| \begin{array}{ccc} 72 & -18 \\ -18 & 45 \end{array} \right|
\\ & = \left| \begin{array}{ccc} 72-t & -18 \\ -18 & 45-t \end{array} \right|
\\ & = (72-t)(45-t) - (-18) \cdot (-18)
\\ & = t^2 - 117t + 3240 - 324
\\ & = t^2 - 117t + 2^3 \cdot 3^5 \cdot 5
\\ & = (t-36)(t-81)
\\ & = 0
\end{align*}\]となるため、固有値は36, 81。
(ii) 固有ベクトル計算
(a) 固有値81に対する固有ベクトル \( \vec{p}_1 \)
\[\begin{align*}
(A A^{\top} -81E) & = \left( \begin{array}{ccc} -9 & -18 \\ -18 & -36 \end{array} \right)
\\ & = \left( \begin{array}{ccc} 1 & 2 \\ 0 & 0 \end{array} \right)
\end{align*}\]より、連立方程式 \( (A A^{\top} - 81E) \vec{p}_1 = \vec{0} \) の解は任意定数 \( k \) を用いて\[
\vec{p}_1 = k \left( \begin{array}{ccc} 2 \\ -1 \end{array} \right)
\]となる。
このうち、大きさ1の固有ベクトルは\[
\vec{p}_1 = \frac{1}{\sqrt{5}}\left( \begin{array}{ccc} 2 \\ -1 \end{array} \right)
\]と求められる。(※ \( k = 1 \) を代入してから正規化するのがおすすめです)
(b) 固有値36に対する固有ベクトル \( \vec{p}_2 \)
\[\begin{align*}
(A A^{\top} -36E) & = \left( \begin{array}{ccc} 36 & -18 \\ -18 & 9 \end{array} \right)
\\ & = \left( \begin{array}{ccc} 2 & -1 \\ 0 & 0 \end{array} \right)
\end{align*}\]より、連立方程式 \( (A A^{\top} - 81E) \vec{p}_2 = \vec{0} \) の解は任意定数 \( k \) を用いて\[
\vec{p}_2 = k \left( \begin{array}{ccc} 1 \\ 2 \end{array} \right)
\]となる。
このうち、大きさ1の固有ベクトルは\[
\vec{p}_2 = \frac{1}{\sqrt{5}} \left( \begin{array}{ccc} 1 \\ 2 \end{array} \right)
\]と求められる。
(※ \( k = 1 \) を代入してから正規化するのがおすすめです)
(2)
行列 \( A \) の特異値 \( \sigma \) は、\( A A^{\top} \) の固有値の平方根に等しい、つまり \( \sigma = \sqrt{t} \) である。
よって、特異値は9, 6である。
(3)
行列 \( A \) の各特異値 \( \sigma \) に対応する左特異ベクトル \( \vec{u} \) は、\( A A^{\top} \) の固有値 \( \sqrt{t} \) に対する固有ベクトル \( \vec{p} \) に等しい。
よって、特異値9に対する左特異ベクトル \( \vec{u}_1 \) は、\( A A^{\top} \) の固有値81に対する固有ベクトル \( \vec{p}_1 \) と等しくなるので、\[
\vec{u}_1 = \frac{1}{\sqrt{5}}\left( \begin{array}{ccc} 2 \\ -1 \end{array} \right)
\]となる。
また、特異値6に対する左特異ベクトル \( \vec{u}_1 \) は、\( A A^{\top} \) の固有値36に対する固有ベクトル \( \vec{p}_2 \) と等しくなるので、\[
\vec{u}_2 = \frac{1}{\sqrt{5}}\left( \begin{array}{ccc} 1 \\ 2 \end{array} \right)
\]となる。
(4)
特異値ごとに、右特異ベクトル \( \vec{v} \) を対応する特異値 \( \sigma \) および左特異ベクトル \( \vec{u} \) を用いて表される公式\[
\vec{v} = \frac{1}{\sigma} A^{\top} \vec{u}
\]で求めればOK。
(i) 特異値9に対応する右特異ベクトル \( \vec{v}_1 \)\[\begin{align*}
\vec{v}_1 & = \frac{1}{9} A^{\top} \vec{u}_1
\\ & = \frac{1}{9} \left( \begin{array}{ccc} 6 & 2 \\ 0 & 4 \\ 6 & -5 \end{array} \right) \cdot \frac{1}{\sqrt{5}} \left( \begin{array}{ccc} 2 \\ -1 \end{array} \right)
\\ & = \frac{1}{ 9 \sqrt{5} } \left( \begin{array}{ccc} 10 \\ -4 \\ 17 \end{array} \right)
\end{align*}\]
(ii) 特異値6に対応する右特異ベクトル \( \vec{v}_2 \)\[\begin{align*}
\vec{v}_2 & = \frac{1}{6} A^{\top} \vec{u}_2
\\ & = \frac{1}{6} \left( \begin{array}{ccc} 6 & 2 \\ 0 & 4 \\ 6 & -5 \end{array} \right) \cdot \frac{1}{\sqrt{5}} \left( \begin{array}{ccc} 1 \\ 2 \end{array} \right)
\\ & = \frac{1}{ 6 \sqrt{5} } \left( \begin{array}{ccc} 10 \\ 8 \\ -4 \end{array} \right)
\\ & = \frac{1}{ 3 \sqrt{5} } \left( \begin{array}{ccc} 5 \\ 4 \\ -2 \end{array} \right)
\end{align*}\]
スポンサードリンク
2. 特異値分解の式導出
特異値 \( \sigma \) 、特異ベクトル \( \vec{u} \), \( \vec{v} \) の求め方を学習したので、いよいよこれらを使って特異値分解の式\[
A = U D V^{\top}
\]を導出していきましょう。
まず、特異値、特異ベクトルの公式には \( A \vec{v} = \sigma \vec{u} \) がありましたね。
ここで、\( m \) 行 \( n \) 列の特異値、特異ベクトルの個数は \( m \), \( n \) のうちより小さい方の数だけあるのでしたね。なので、個数を \( r \) とし、\( r = \min (m,n) \) とします。
さらに、\( r \) 個中 \( k \) 番目の特異値 \( \sigma_k \) に対応する左特異ベクトル、右特異ベクトルをそれぞれ \( \vec{u}_k \), \( \vec{v}_k \) とします。
すると、ある行列 \( A \) に対して、\( r \) 個の関係式\[\begin{align*}
A \vec{v}_1 & = \sigma_1 \vec{u}_1 \\
A \vec{v}_2 & = \sigma_2 \vec{u}_2 \\
A \vec{v}_3 & = \sigma_3 \vec{u}_3 \\
& \vdots \\
A \vec{v}_r & = \sigma _r \vec{u}_r
\end{align*}\]が成り立ちます。
さらに、行列 \( U \), \( V \) を正規直交基底を成すベクトルからなる以下のような行列とします。\[\begin{align*}
U & = ( \vec{u}_1, \vec{u}_2, \cdots, \vec{u}_r ) \\
V & = ( \vec{v}_1 , \vec{v}_2 , \cdots, \vec{v}_r)
\end{align*}\]
すると、\[\begin{align*}
AV & = A ( \vec{v}_1, \vec{v}_2 , \cdots , \vec{v}_n )
\\ & = ( A \vec{v}_1, A \vec{v}_2 , \cdots , A \vec{v}_r )
\\ & = ( \sigma_1 \vec{u}_1, \sigma_2 \vec{u}_2, \cdots , \sigma_r \vec{u}_r )
\\ & = ( \vec{u}_1, \vec{u}_2 , \cdots , \vec{u}_r ) \underbrace{ \left( \begin{array}{ccc} \sigma_1 & 0 & \cdots & 0 \\ 0 & \sigma_2 & \cdots & 0 \\ & & \ddots & \\ 0 & 0 & \cdots & \sigma_r \end{array} \right) }_{\Sigma}
\\ & = U \Sigma
\end{align*}\]より、関係式 \( A V = U \Sigma \) が導出できますね。
ここで、\( V \) は正規直交基底となるベクトルを並べた行列なので \( VV^{\top} = E \) が成り立ちます[7]正規直交基底をベクトルの次元の数だけ並べることで作れる正方行列(つまり直交行列) \( U \) が \( U U^{\top} = U^{\top} U = E \) … Continue reading。
両辺に右端から \( V^{\top} \) を掛けると、\[\begin{align*}
A V V^{\top} & = U \Sigma V^{\top} \\
A E & = U \Sigma V^{\top} \\
A & = U \Sigma V^{\top}
\end{align*}\]となり、確かに特異値分解の式 \( A = U \Sigma V^{\top} \) が導出できましたね。
実際に試験やレポートなどで特異値分解をする際には、下のように各特異値 \( \sigma_k \) と左特異ベクトル \( \vec{u}_k \) が列ごとに対応していること、および各特異値 \( \sigma_k \) と右特異ベクトルの転置 \( \vec{v}_k^{\top} \) が行ごとに対応していることを頭に入れておきましょう。わざわざ公式を導出しなくてもすみます。
※1 いざという時のため、導出方法は知っておくことをおすすめします。
※2 今回の記事では、例題や練習問題の解説において、\( A = U \Sigma V^{\top} \) を導出しています。
次の行列 \( A \) を行列 \( U \), \( V \) および対角行列 \( \Sigma \) を用いて特異値分解 \( A = U \Sigma V^{\top} \) を行いたい。\[
A = \left( \begin{array}{ccc} 6 & 0 & 6 \\ 2 & 4 & -5 \end{array} \right)
\]\( A = U \Sigma V^{\top} \) を満たす行列 \( U \), \( V \) および対角行列 \( \Sigma \) を求めなさい。
(a) 行列 \( A \) の特異値は9, 6。
(b) 行列 \( A \) の特異値9に対応する左特異ベクトル \( \vec{u}_1 \)、特異値6に対応する左特異ベクトル \( \vec{u} \) は次の通りである。\[ \vec{u}_1 = \frac{1}{\sqrt{5}}\left( \begin{array}{ccc} 2 \\ -1 \end{array} \right)
, \ \ \ \vec{u}_2 = \frac{1}{\sqrt{5}} \left( \begin{array}{ccc} 1 \\ 2 \end{array} \right)
\]
(c) 行列 \( A \) の特異値9に対応する右特異ベクトル \( \vec{v}_1 \)、特異値6に対応する右特異ベクトル \( \vec{v}_2 \) は次の通りである。\[
\vec{v}_1 = \frac{1}{ 9 \sqrt{5} } \left( \begin{array}{ccc} 10 \\ -4 \\ 17 \end{array} \right) , \ \ \ \vec{v}_2 = \frac{1}{ 3 \sqrt{5} } \left( \begin{array}{ccc} 5 \\ 4 \\ -2 \end{array} \right)
\]
[解説2]
行列 \( U \), \( V \) をそれぞれ\[\begin{align*}
U & = ( \vec{u}_1, \vec{u}_2 )
\\ & = \frac{1}{\sqrt{5}} \left( \begin{array}{ccc} 2 & 1 \\ -1 & 2 \end{array} \right)
\end{align*}\]\[ \begin{align*}
V & = ( \vec{v}_1 , \vec{v}_2)
\\ & = \frac{1}{ 9 \sqrt{5} } \left( \begin{array}{ccc} 10 & 15 \\ -4 & 12 \\ 17 & -6 \end{array} \right)
\end{align*}\]とします。
すると、行列 \( A \) に対して、関係式\[\begin{align*}
A \vec{v}_1 & = 9 \vec{u}_1 \\
A \vec{v}_2 & = 6 \vec{u}_2
\end{align*}\]が成り立ちます。
よって、\[\begin{align*}
AV & = A ( \vec{v}_1, \vec{v}_2)
\\ & = ( A \vec{v}_1, A \vec{v}_2 )
\\ & = ( 9 \vec{u}_1, 6 \vec{u}_2 )
\\ & = ( \vec{u}_1, \vec{u}_2 ) \underbrace{ \left( \begin{array}{ccc} 9 & 0 \\ 0 & 6 \end{array} \right) }_{\Sigma}
\\ & = U \Sigma
\end{align*}\]と変形でき、関係式 \( AV = U \Sigma \) が導出できます。
ここで、\( V \) は正規直交基底となるベクトルを並べた行列なので \( VV^{\top} = E \) が成り立ちます。
よって、両辺の右端に \( V^{\top} \) を掛けることで\[\begin{align*}
A V & = U \Sigma \\
A V V^{\top} & = U \Sigma V^{\top} \\
A E & = U \Sigma V^{\top} \\
A & = U \Sigma V^{\top}
\end{align*}\]と変形ができます。
よって、行列 \( A \) は、\[\begin{align*}
A = \underbrace{ \frac{1}{\sqrt{5}} \left( \begin{array}{ccc} 2 & 1 \\ -1 & 2 \end{array} \right) }_{U} \cdot \underbrace{\left( \begin{array}{ccc} 9 & 0 \\ 0 & 6 \end{array} \right) }_{\Sigma} \cdot \underbrace{ \frac{1}{ 9 \sqrt{5} } \left( \begin{array}{ccc} 10 & -4 & 17 \\ 15 & 12 & -6 \end{array} \right) }_{V^{\top}}
\end{align*}\]と特異値分解ができる。
つまり、それぞれの行列 \( U \), \( V \), \( \Sigma \) は\[\begin{align*}
U & = \frac{1}{\sqrt{5}} \left( \begin{array}{ccc} 2 & 1 \\ -1 & 2 \end{array} \right) \\
\Sigma & = \left( \begin{array}{ccc} 9 & 0 \\ 0 & 6 \end{array} \right) \\
V & = \frac{1}{ 9 \sqrt{5} } \left( \begin{array}{ccc} 10 & 15 \\ -4 & 12 \\ 17 & -6 \end{array} \right)
\end{align*}\]となる。
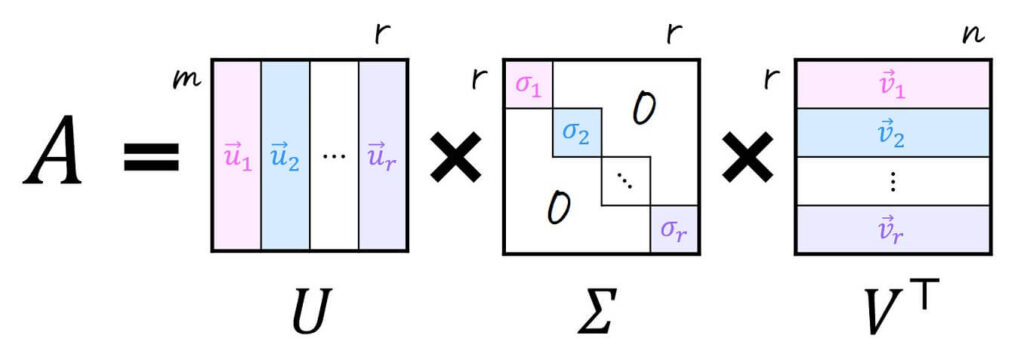
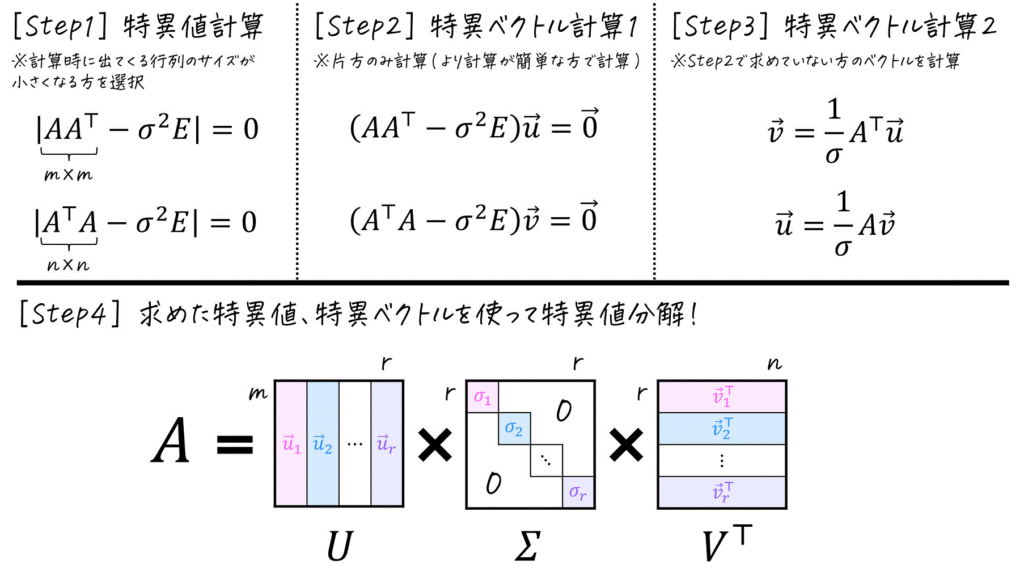
\( m \) 行 \( n \) 列で出てくる行列 \( A \) の \( r = \min (m,n) \) 個の特異値を大きい順に \( \sigma_1 \), \( \sigma_2 \), …, \( \sigma_r \) とする。
また、\( \sigma_k \) に対応する左特異ベクトルを \( \vec{u}_k \)、右特異ベクトルを \( \vec{v}_{k} \) とする。
このとき、行列 \( A \) は、下の行列 \( U \), \( \Sigma \), \( V \) を用いて \( A = U \Sigma V^{\top} \) と特異値分解をすることができる。
\[\begin{align*}
U & = \underbrace{ \left( \begin{array}{ccc} \textcolor{magenta}{\vec{u}_1}, \textcolor{deepskyblue}{\vec{u}_2} , \cdots , \textcolor{purple}{ \vec{u}_r } \end{array} \right) }_{m \times r \mathrm{行列} } \\
\Sigma & = \underbrace{ \left( \begin{array}{ccc} \textcolor{magenta}{\sigma_1} & 0 & \cdots & 0 \\ 0 & \textcolor{deepskyblue}{\sigma_2} & \cdots & 0 \\ & & \ddots & \\ 0 & 0 & \cdots & \textcolor{purple}{\sigma_r} \end{array} \right) }_{r \times r \mathrm{行列}} \\
V & = \underbrace{ \left( \begin{array}{ccc} \textcolor{magenta}{\vec{v}_1}, \textcolor{deepskyblue}{\vec{v}_2} , \cdots , \textcolor{purple}{ \vec{v}_r } \end{array} \right) }_{r \times n \mathrm{行列} }
\end{align*}\]となる。
3. エコノミーサイズ・フルサイズの特異値分解の違い
(1) エコノミーサイズの特異値分解 [今回説明したVer]
今回の特異値ベクトルでは、下のように \( m \) 行 \( n \) 列の行列 \( A \) を行列 \( U \), \( V \) および対角行列 \( \Sigma \) を用いて分解しました。
このように、\( \Sigma \) を(なるべく小さい)対角行列になるように特異値分解する方法を、エコノミーサイズの特異値分解と呼びます。

この方法のメリットは、
- 手計算が簡単
- \( U \), \( \Sigma \), \( V \) のサイズが小さくなるのでコンピュータ上で扱う際に容量を減らすことができる
の2つがあります。
一方、\( U \) , \( V \) が正方行列ではないため、\( U \), \( V \) を使ってベクトルを変換(\( U \vec{x} \), \( V \vec{x} \) などを計算)する際にベクトルの次元が変わってしまう欠点もあります。
(2) フルサイズの特異値分解
一方、下のように \( \Sigma \) が元の行列 \( A \) と同じサイズになるように特異値分解する方法もあります。

この方法で分解する最大のメリットは \( U \), \( V \) が直交行列(正方行列)となるため、直交行列の特徴(変換の前後で内積が変わらないなど)を活かすことができます[8]例えば、行列2ノルム \( \| A \|_2 \) が \( A \) の最大特異値の平方根に一致することの証明は、「\( U \), \( V \) … Continue reading。
一方、左特異ベクトル \( \vec{u} \) と右特異ベクトル \( \vec{v} \) の数が等しくなくなるので、対応しない特異ベクトルに関しては連立方程式を解きなおす必要があります。
具体的に、\( m > n \) のときは、\( m - n \) 個の左特異ベクトル \( \vec{u} \) が右特異ベクトル \( \vec{v} \) に対応していないため、対応していない左特異ベクトルを \( ( A A^{\top} - \textcolor{red}{0}E ) \vec{u} = \vec{0} \) で計算します。
※ 赤色部分が0なのは、対応していない左特異ベクトルに関する必ず特異値は0になるため。
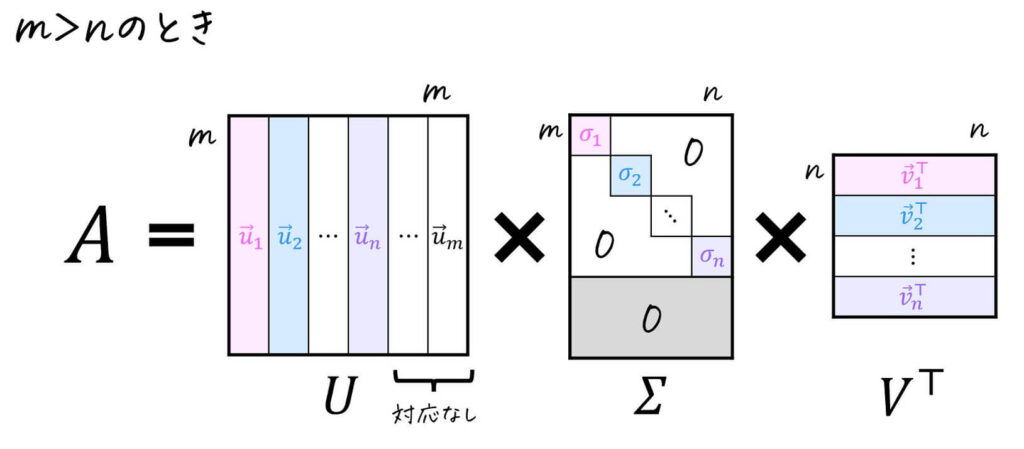
同様に \( m < n \) のときは、\( n-m \) 個の右特異ベクトル \( \vec{v} \) が左特異ベクトル \( \vec{u} \) に対応していないため、対応していない右特異ベクトルを \( ( A^{\top} A - \textcolor{red}{0}E ) \vec{v} = \vec{0} \) で計算します。
※ 赤色部分が0なのは、対応していない右特異ベクトルに関する必ず特異値は0になるため。
4. 練習問題
それでは、2問ほど特異値分解を計算する練習をしてみましょう。
次の(1), (2)の行列を特異値分解し、\( A = U \Sigma V^{\top} \), \( B = U \Sigma V^{\top} \) の形で表しなさい。
(1)\[
A = \left( \begin{array}{ccc} 4 & 1 \\ 1 & -4 \\ -3 & -7 \end{array} \right)
\]※ (1)は途中計算が少ししんどいので、計算が苦手な方は関数電卓などを使うことをおすすめします。
(2)\[
B = \left( \begin{array}{ccc} -3 & 4 & -5 & 2 \\ -2 & -3 & 4 & -5 \end{array} \right)
\]
5. 練習問題の答え
(1) 3×2行列の特異値分解
[Step1] 行列の特異値を求める。
今回は、行列が3行2列なので、\( |A^{\top} A - \sigma^2 E| = 0 \) を解くほうが計算量が少なくなる。
\( A^{\top} A \) を計算すると、\[\begin{align*}
A^{\top} A & = \left( \begin{array}{ccc} 4 & 1 & -3 \\ 1 & -4 & -7 \end{array} \right)
\left( \begin{array}{ccc} 4 & 1 \\ 1 & -4 \\ -3 & -7 \end{array} \right)
\\ & = \left( \begin{array}{ccc} 26 & 21 \\ 21 & 66 \end{array} \right)
\end{align*}\]と計算できる。(計算結果が実対称行列となっているか確認!)
ここで、行列 \( A \) の特異値を \( \sigma \) とし、\( t = \sigma^2 \) とすると\[\begin{align*}
|A^{\top} A - \sigma^2 E| & = \left| \begin{array}{ccc} 26 - t & 13 \\ 13 & 66-t \end{array} \right|
\\ & = (26-t)(66-t) - 13 \cdot 13
\\ & = t^2 - 92 + 1275
\\ & = (t-17)(t-75)
\\ & = 0
\end{align*}\]が成立する。
よって、\( t = 75, 17 \) となるため、特異値は \( \sigma = 5 \sqrt{3}, \sqrt{17} \) となる。
[Step2] 右特異ベクトルを求める。
今回は、\( A^{\top} A \) の方が行列のサイズが小さく計算量が少ないため、先に連立方程式 \( (A^{\top} A - \sigma^2 E) \vec{v} = \vec{0} \) を解き、右特異ベクトル \( \vec{v} \) を求める。
※ \( A A^{\top} \) の方が行列のサイズが小さい場合は、\( (AA^{\top} - \sigma^2 E ) \vec{u} = \vec{0} \) を計算し、左特異ベクトル \( \vec{u} \) を先に計算する。
(1) 特異値 \( 5 \sqrt{3} \) に対する左特異ベクトル \( \vec{v}_1 \)
\( (A^{\top} A - \sigma^2 E) \vec{v}_1 = \vec{0} \) を解く。
\[\begin{align*}
A^{\top} A - 75 E & = \left( \begin{array}{ccc} -49 & 21 \\ 21 & -49 \end{array} \right)
\\ & = \left( \begin{array}{ccc} 7 & -3 \\ 0 & 0 \end{array} \right)
\end{align*}\]となるため、\( \vec{v}_1 \) の解は任意定数 \( k \) を用いて\[
\vec{v}_1 = k \left( \begin{array}{ccc} 3 \\ 7 \end{array} \right)
\]となる。よって、大きさ1の左特異ベクトル \( \vec{v}_1 \) は\[
\vec{v}_1 = \frac{1}{\sqrt{58}} \left( \begin{array}{ccc} 3 \\ 7 \end{array} \right)
\]と計算できる。
(2) 特異値 \( \sqrt{17} \) に対する左特異ベクトル \( \vec{v}_2 \)
\( (A^{\top} A - \sigma^2 E) \vec{v}_2 = \vec{0} \) を解く。
\[\begin{align*}
A^{\top} A - 17 E & = \left( \begin{array}{ccc} 9 & 21 \\ 21 & 9 \end{array} \right)
\\ & = \left( \begin{array}{ccc} 3 & 7 \\ 0 & 0 \end{array} \right)
\end{align*}\]となるため、\( \vec{v}_2 \) の解は任意定数 \( k \) を用いて\[
\vec{v}_2 = k \left( \begin{array}{ccc} 7 \\ -3 \end{array} \right)
\]となる。よって、大きさ1の左特異ベクトル \( \vec{v}_2 \) は\[
\vec{v}_2 = \frac{1}{\sqrt{58}} \left( \begin{array}{ccc} 7 \\ -3 \end{array} \right)
\]と計算できる。
[Step3] 左特異ベクトルを求める
左特異ベクトル \( \vec{u} \) は、特異値 \( \sigma \) および右特異ベクトル \( \vec{v} \) を用いて表される公式\[
\vec{u} = \frac{1}{\sigma} A \vec{v}
\]で計算できる。
(1) 特異値 \( 5 \sqrt{3} \) に対する右特異ベクトル \( \vec{u}_1 \)
\[\begin{align*}
\vec{u}_1 & = \frac{1}{ 5 \sqrt{3} } \left( \begin{array}{ccc} 4 & 1 \\ 1 & -4 \\ -3 & -7 \end{array} \right) \cdot \frac{1}{\sqrt{58}} \left( \begin{array}{ccc} 3 \\ 7 \end{array} \right)
\\ & = \frac{1}{ 5 \sqrt{174} } \left( \begin{array}{ccc} 19 \\ -25 \\ -58 \end{array} \right)
\end{align*}\]
(2) 特異値 \( \sqrt{17} \) に対する右特異ベクトル \( \vec{u}_2 \)
\[\begin{align*}
\vec{u}_2 & = \frac{1}{ \sqrt{17} } \cdot \left( \begin{array}{ccc} 4 & 1 \\ 1 & -4 \\ -3 & -7 \end{array} \right) \cdot \frac{1}{\sqrt{58}} \left( \begin{array}{ccc} 7 \\ -3 \end{array} \right)
\\ & = \frac{1}{ \sqrt{986} } \left( \begin{array}{ccc} 25 \\ 19 \\ 0 \end{array} \right)
\end{align*}\]
[Step4] 特異値分解の形に持ち込む
行列 \( U \), \( V \) をそれぞれ\[\begin{align*}
U & = ( \vec{u}_1, \vec{u}_2 )
\\ & = \frac{1}{\sqrt{58}} \left( \begin{array}{ccc} 3 & 7 \\ 7 & -3 \end{array} \right)
\end{align*}\]\[ \begin{align*}
V & = ( \vec{v}_1 , \vec{v}_2)
\\ & = \left( \begin{array}{ccc} \frac{19}{ 5 \sqrt{174} } & \frac{25}{ \sqrt{986} } \\ - \frac{5}{ \sqrt{174} } & \frac{19}{ \sqrt{986} } \\ - \frac{58}{ 5 \sqrt{174} } & 0 \end{array} \right)
\end{align*}\]とする。
また、行列 \( A \) に対して、関係式\[\begin{align*}
A \vec{v}_1 & = 5 \sqrt{3} \vec{u}_1 \\
A \vec{v}_2 & = \sqrt{17} \vec{u}_2
\end{align*}\]が成り立つ。
よって、\[\begin{align*}
AV & = A ( \vec{v}_1, \vec{v}_2)
\\ & = ( A \vec{v}_1, A \vec{v}_2 )
\\ & = ( 5 \sqrt{3} \vec{u}_1, \sqrt{17} \vec{u}_2 )
\\ & = ( \vec{u}_1, \vec{u}_2 ) \underbrace{ \left( \begin{array}{ccc} 5 \sqrt{3} & 0 \\ 0 & \sqrt{17} \end{array} \right) }_{\Sigma}
\\ & = U \Sigma
\end{align*}\]と変形でき、関係式 \( AV = U \Sigma \) が導出できます。
ここで、\( V \) は正規直交基底となるベクトルを並べた行列なので \( VV^{\top} = E \) が成り立つ。
よって、両辺の右端に \( V^{\top} \) を掛けることで\[\begin{align*}
A V & = U \Sigma \\
A V V^{\top} & = U \Sigma V^{\top} \\
A E & = U \Sigma V^{\top} \\
A & = U \Sigma V^{\top}
\end{align*}\]と変形ができる。
よって、行列 \( A \) は、\[\begin{align*}
A = \underbrace{ \frac{1}{\sqrt{58}} \left( \begin{array}{ccc} 3 & 7 \\ 7 & -3 \end{array} \right)}_{U} \cdot \underbrace{\left( \begin{array}{ccc} 5 \sqrt{3} & 0 \\ 0 & \sqrt{17} \end{array} \right) }_{\Sigma} \cdot \underbrace{ \left( \begin{array}{ccc} \frac{19}{ 5 \sqrt{174} } & - \frac{5}{ \sqrt{174} } & - \frac{58}{ 5 \sqrt{174} } \\ \frac{25}{ \sqrt{986} } & \frac{19}{ \sqrt{986} } & 0 \end{array} \right) }_{V^{\top}}
\end{align*}\]と特異値分解ができる。
(2) 2×4行列の特異値分解
[Step1] 行列の特異値を求める。
今回は、行列が2行4列なので、\( | B B^{\top} - \sigma^2 E| = 0 \) を解くほうが計算量が圧倒的に少なくなる。
\( B B^{\top} \) を計算すると、\[\begin{align*}
B B^{\top}& = \left( \begin{array}{ccc} -3 & 4 & -5 & 2 \\ -2 & -3 & 4 & -5 \end{array} \right) \left( \begin{array}{ccc} -3 & -2 \\ 4 & -3 \\ -5 & 4 \\ 2 & -5 \end{array} \right)
\\ & = \left( \begin{array}{ccc} 54 & -36 \\ -36 & 54 \end{array} \right)
\end{align*}\]と計算できる。(計算結果が実対称行列となっているか確認!)
ここで、行列 \( B \) の特異値を \( \sigma \) とし、\( t = \sigma^2 \) とすると\[\begin{align*}
|BB^{\top} - \sigma^2 E| & = \left| \begin{array}{ccc} 54 - t & -36 \\ -36 & 54-t \end{array} \right|
\\ & = (54-t)(54-t) - (-36) \cdot (-36)
\\ & = t^2 - 108 + 1620
\\ & = (t- 18)(t-90)
\\ & = 0
\end{align*}\]が成立する。
よって、\( t = 90, 18 \) となるため、特異値は \( \sigma = 3 \sqrt{10}, 3 \sqrt{2} \) となる。
[Step2] 左特異ベクトルを求める。
今回は、\( BB^{\top} \) の方が行列のサイズが小さく計算量が少ないため、先に連立方程式 \( (B B^{\top} - \sigma^2 E) \vec{u} = \vec{0} \) を解き、左特異ベクトル \( \vec{u} \) を求める。
(1) 特異値 \( 3 \sqrt{10} \) に対する左特異ベクトル \( \vec{u}_1 \)
\( (B^{\top} B - \sigma^2 E) \vec{u}_1 = \vec{0} \) を解く。
\[\begin{align*}
B^{\top} B - 90 E & = \left( \begin{array}{ccc} -36 & -36 \\ -36 & -36 \end{array} \right)
\\ & = \left( \begin{array}{ccc} 1 & 1 \\ 0 & 0 \end{array} \right)
\end{align*}\]となるため、\( \vec{v}_1 \) の解は任意定数 \( k \) を用いて\[
\vec{v}_1 = k \left( \begin{array}{ccc} 1 \\ -1 \end{array} \right)
\]となる。よって、大きさ1の右特異ベクトル \( \vec{v}_1 \) は\[
\vec{v}_1 = \frac{1}{\sqrt{2}} \left( \begin{array}{ccc} 1 \\ -1 \end{array} \right)
\]と計算できる。
(2) 特異値 \( 3 \sqrt{2} \) に対する左特異ベクトル \( \vec{u}_2 \)
\( (B^{\top} B - \sigma^2 E) \vec{u}_2 = \vec{0} \) を解く。
\[\begin{align*}
B^{\top} B - 18 E & = \left( \begin{array}{ccc} 36 & -36 \\ -36 & 36 \end{array} \right)
\\ & = \left( \begin{array}{ccc} 1 & -1 \\ 0 & 0 \end{array} \right)
\end{align*}\]となるため、\( \vec{v}_1 \) の解は任意定数 \( k \) を用いて\[
\vec{v}_2 = k \left( \begin{array}{ccc} 1 \\ 1 \end{array} \right)
\]となる。よって、大きさ1の右特異ベクトル \( \vec{v}_2 \) は\[
\vec{v}_2 = \frac{1}{\sqrt{2}} \left( \begin{array}{ccc} 1 \\ 1 \end{array} \right)
\]と計算できる。
[Step3] 右特異ベクトルを求める
右特異ベクトル \( \vec{v} \) は、特異値 \( \sigma \) および左特異ベクトル \( \vec{u} \) を用いて表される公式\[
\vec{v} = \frac{1}{\sigma} B^{\top} \vec{u}
\]で計算できる。
(1) 特異値 \( 3 \sqrt{10} \) に対する左特異ベクトル \( \vec{v}_1 \)
\[\begin{align*}
\vec{v}_1 & = \frac{1}{ 3 \sqrt{10} } \cdot \left( \begin{array}{ccc} -3 & -2 \\ 4 & -3 \\ -5 & 4 \\ 2 & -5 \end{array} \right) \cdot \frac{1}{\sqrt{2}} \left( \begin{array}{ccc} 1 \\ -1 \end{array} \right)
\\ & = \frac{1}{ 6 \sqrt{5} } \left( \begin{array}{ccc} -1 \\ 7 \\ -9 \\ 7 \end{array} \right)
\end{align*}\]
(2) 特異値 \( 3 \sqrt{2} \) に対する右特異ベクトル \( \vec{v}_2 \)
\[\begin{align*}
\vec{v}_2 & = \frac{1}{ 3 \sqrt{2} } \cdot \left( \begin{array}{ccc} -3 & -2 \\ 4 & -3 \\ -5 & 4 \\ 2 & -5 \end{array} \right) \cdot \frac{1}{\sqrt{2}} \left( \begin{array}{ccc} 1 \\ 1 \end{array} \right)
\\ & = \frac{1}{ 6 } \left( \begin{array}{ccc} -5 \\ 1 \\ -1 \\ -3 \end{array} \right)
\end{align*}\]
[Step4] 特異値分解の形に持ち込む
行列 \( U \), \( V \) をそれぞれ\[\begin{align*}
U & = ( \vec{u}_1, \vec{u}_2 )
\\ & = \frac{1}{\sqrt{2}} \left( \begin{array}{ccc} 1 & 1 \\ -1 & 1 \end{array} \right)
\end{align*}\]\[ \begin{align*}
V & = ( \vec{v}_1 , \vec{v}_2)
\\ & = \frac{1}{ 6 \sqrt{5} } \left( \begin{array}{ccc} -1 & -5 \sqrt{5} \\ 7 & \sqrt{5} \\ -9 & - \sqrt{5} \\ 7 & - 3 \sqrt{5} \end{array} \right)
\end{align*}\]とする。
また、行列 \( B \) に対して、関係式\[\begin{align*}
B \vec{v}_1 & = 3 \sqrt{10} \vec{u}_1 \\
B \vec{v}_2 & = 3 \sqrt{2} \vec{u}_2
\end{align*}\]が成り立つ。
よって、\[\begin{align*}
BV & = B ( \vec{v}_1, \vec{v}_2)
\\ & = ( B \vec{v}_1, B \vec{v}_2 )
\\ & = ( 3 \sqrt{10} \sqrt{3} \vec{u}_1, 3 \sqrt{2} \vec{u}_2 )
\\ & = ( \vec{u}_1, \vec{u}_2 ) \underbrace{ \left( \begin{array}{ccc} 3 \sqrt{10} & 0 \\ 0 & 3 \sqrt{2} \end{array} \right) }_{\Sigma}
\\ & = U \Sigma
\end{align*}\]と変形でき、関係式 \( AV = U \Sigma \) が導出できます。
ここで、\( V \) は正規直交基底となるベクトルを並べた行列なので \( VV^{\top} = E \) が成り立つ。
よって、両辺の右端に \( V^{\top} \) を掛けることで\[\begin{align*}
B V & = U \Sigma \\
B V V^{\top} & = U \Sigma V^{\top} \\
B E & = U \Sigma V^{\top} \\
B & = U \Sigma V^{\top}
\end{align*}\]と変形ができる。
よって、行列 \( B \) は、\[\begin{align*}
B = \underbrace{ \frac{1}{\sqrt{2}} \left( \begin{array}{ccc} 1 & 1 \\ -1 & 1 \end{array} \right)}_{U} \cdot \underbrace{\left( \begin{array}{ccc} 3 \sqrt{10} & 0 \\ 0 & 3 \sqrt{2} \end{array} \right) }_{\Sigma} \cdot \underbrace{ \frac{1}{ 6 \sqrt{5} } \left( \begin{array}{ccc} -1 & 7 & -9 & 7 \\ -5 \sqrt{5} & \sqrt{5} & - \sqrt{5} & -3 \sqrt{5} \end{array} \right) }_{V^{\top}}
\end{align*}\]と特異値分解ができる。
6. さいごに
では、特異値分解(エコノミーサイズ)の計算方法を1枚の画像で振り返ってみましょう。
実際に特異値分解を手計算する機会は、試験以外では少ないと思いますが、研究やプログラミングなどで特異値分解を使う機会は出てくると思うので、特異値分解の仕組みは理解しておくと将来役に立つかもしれません。
注釈
| ↑1 | 行列の成分に複素数が含まれる場合は、転置行列 \( V^{\top} \) を随伴行列 \( V^* \) に変えればOKです。 |
|---|---|
| ↑2 | 今回の復習例題ではありませんが、重解の固有値に対する固有ベクトルを求める際には、必ず同じ固有値に対する固有ベクトルが線形独立(1次独立)になるように求めましょう。 |
| ↑3 | 左特異ベクトル、右特異ベクトルの左右ってなんだよって思った人もいるかもしれませんが、\( \Sigma \) の左側にある行列 \( U \) を作るために並べるベクトルが \( \vec{u} \) なので、左特異ベクトルと呼ばれます。同じように \( \Sigma \) の右側にある行列 \( V \) を作るために並べるベクトルが \( \vec{v} \) なので、右特異ベクトルと呼ばれます。 |
| ↑4 | 例えば、特異値が4, 4, 3だった場合は3個とカウントする。 |
| ↑5 | \( A A^{\top} = B \) もしくは \( A^{\top} = B \) とすると、固有ベクトルの計算公式 \( (A - tE) \vec{p} = \vec{0} \) とそっくりな形になりますね。 |
| ↑6 | \( \vec{u} \) から \( \vec{v} \) を求める場合のみですが、本当に大きさが変わらないことを確認します。定義より、\( A^{\top} \vec{u} = \sigma \vec{v} \) が成立するので、\( |A^{\top} \vec{u}| = |\sigma \vec{v}| = \sigma | \vec{v} | \) が成立します。そのため、\[\begin{align*} | \vec{v}| & = \left| \frac{1}{\sigma} \cdot \sigma \vec{v} \right| \\ & = \frac{1}{\sigma} | \sigma \vec{v} | \\ & = \frac{1}{\sigma} | A^{\top} \vec{u} | \\ & = \left| \frac{1}{\sigma} A^{\top} \vec{u} \right| \end{align*}\]と変形することにより、変形\[ \vec{v} = \frac{1}{\sigma} A^{\top} \vec{u} \]の前後で大きさが変わっていないことがわかりますね。\( \vec{v} \) から \( \vec{u} \) のときも同じように確認できます。 |
| ↑7 | 正規直交基底をベクトルの次元の数だけ並べることで作れる正方行列(つまり直交行列) \( U \) が \( U U^{\top} = U^{\top} U = E \) を満たすことは有名ですが、正方行列でなくても正規直交基底となるベクトルを並べた行列 \( V \) であれば、\( VV^{\top} = E \) および \( V^{\top} V = E \) をしっかり満たします(ただし行列のサイズが違うので \( V V^{\top} \not = V^{\top} V \))。実際に計算をしてみると、\[\begin{align*} VV^{\top} & = ( \vec{v}_1 , \vec{v}_2 , \cdots, \vec{v}_r) \left( \begin{array}{ccc} \vec{v}_1^{\top} \\ \vec{v}_2^{\top} \\ \vdots \\ \vec{v}_r^{\top} \end{array} \right) \\ & = \left( \begin{array}{ccc} | \vec{v}_1 |^2 & \vec{v}_1 \cdot \vec{v}_2 & \cdots & \vec{v}_1 \cdot \vec{v}_r \\ \vec{v}_2 \cdot \vec{v}_1 & | \vec{v}_2 |^2 & \cdots & \vec{v}_2 \cdot \vec{v}_r \\ & & \ddots & \\ \vec{v}_r \cdot \vec{v}_1 & \vec{v}_r \cdot \vec{v}_2 & \cdots & | \vec{v}_r |^2 \end{array} \right) \\ & = \left( \begin{array}{ccc} 1 & 0 & \cdots & 0 \\ 0 & 1 & \cdots & 0 \\ & & \ddots & \\ 0 & 0 & \cdots & 1 \end{array} \right) \\ & = E \end{align*}\]となり、確かに単位行列になることがわかります。 |
| ↑8 | 例えば、行列2ノルム \( \| A \|_2 \) が \( A \) の最大特異値の平方根に一致することの証明は、「\( U \), \( V \) が直交行列のため、変換の前後で内積(ベクトルの2ノルム)が変わらない」ことが言えるフルサイズの特異値分解の方が簡単です。 |
関連広告・スポンサードリンク