プログラムの計算量、オーダー表記 O( ) の求め方のまとめ

記事修正　2019/05/25　一部極限式やオーダーの \( n \) が \( x \) になっていたのを修正

こんにちは、ももやまです。
今日は久しぶりに情報系のまとめです。

皆さん、効率のよいアルゴリズムってどんなアルゴリズムだと思いますか？
時間がかからない、メモリを食わない、などなど様々な評価の仕方があると思います。

今回は「どうやってアルゴリズムの良し悪しを評価するか」、そして「アルゴリズムの評価でよく使われるオーダー表記 O( )」についてまとめてみようと思います。

スポンサードリンク

１．計算量ってなに…？

何人かが作ったアルゴリズムの良し悪しを評価したいとします。
評価の方法には様々な方法があるのですが今回は、かかった時間で評価してみるとします。

例えば、Aさんの作ったアルゴリズムは実行に30秒かかりました。
しかしBさんの作ったアルゴリズムはたったの10秒で計算できちゃいました。

あ、Bさんのほうが速度が3倍だからBさんのアルゴリズムのほうが良い！と思うのは実は問題点があります。

極端な例ですが、Aさんのアルゴリズムの実行時間を評価するのにCeleron*1のCPUが入っている計算機(PC)を使い、Bさんのアルゴリズムを評価するときにスーパーコンピューターレベルの計算機を使っていたら計算機の性能の良し悪しが実行時間の差に影響してしまいます。このように、かかった時間で評価する場合は実行する場所（環境）がわからないため明確にアルゴリズムの良し悪しが判別できません。

こんなときに使うのが計算量です。計算量には時間計算量と空間計算量の2つがあります。
時間計算量は、実行が始まってから実行が終わるまでの命令が実行された回数（ステップ数）を表します。
一方、空間計算量は、アルゴリズムを解くときにどれほどの空間（メモリ）を使うかを表します。
今回は時間計算量だけについて考えたいと思います。
時間がかかったかどうかは入力されたデータ数 \( n \) のときのステップ数を基準に性能の良し悪しを決めます。例えば、こんなアルゴリズム（関数）があるとします。

// アルゴリズム1
int findMod(int n) {
    // 下のfor文はどちらが実行されても1ステップ
    if(n % 3 == 0) { 
        return 1; // ここで1ステップ
    }
    else {
        return 0; // ここで1ステップ
    } 
}

このアルゴリズムの場合はどちらのfor文が実行されても1ステップですね。なのでこのアルゴリズムは1ステップとなります。

// アルゴリズム2
int calcSum(int data[], int n) {
    int sum = 0;  // ここで1ステップ
    for(int i = 0; i < n; i += 1) {
        sum += data[i]; // ここでnステップ
    }
    return sum; // ここで1ステップ
} 

このプログラムは定義(int sum = 0;)で1ステップ、結果(return sum;)で1ステップ、結果の格納でnステップとなり、合計 n+2 ステップとなりますね。
ステップ数ならどの環境で実行した場合でも変わりませんよね。

スポンサードリンク

２．最悪計算量と平均計算量

計算量には、最悪計算量と平均計算量というものがあります。

(1) 最悪計算量

まずは、最悪計算量の場合です。例えば、つぎのようなプログラムがあるとします。

// 
int f1(int,data[], int n) {
    if(n % 2 == 0) {
        // 偶数なら n^2 ステップの処理: O(n^2)
    }
    else {
        // 奇数ならn^3 ステップの処理: O(n^3)
    }
}

最悪計算量は、名前の通り最悪な場合、つまり一番ステップ数が多い条件の場合を考えるので、上の場合だと、奇数である \( n^{3} \) ステップの方を採用します。
最悪計算量で考えるメリットは、

• for文の場合はとにかく一番多くループする場合、if文の場合は一番ループする条件を考えればいいだけなので計算が楽
• 最悪計算量は、これ以上計算がかからない時間を保証するものなので、経験などに基づく推測などが不要

があります。もう1つアルゴリズムの例を出しましょう。

// 昇順ソート
void aSort(int data[],int n) {
    int tmp;
    for(int i = 0; i < n - 1; i += 1) { // n - 1 ステップ
        for(int j = i + 1; j < n; j += 1) { // n - 1 ステップと近似OK
            if (data[i] > data[j]) { // 最悪のケースなので全部通ると仮定
                tmp = data[i];
                data[i] = data[j];
                data[j] = tmp;
            }
        }
    }
}

このアルゴリズムの場合、for文が2つありますね。このアルゴリズムは最悪の計算量を計算する際には、

1. 最初のfor文はn-1ステップ（これはわかりやすい）
2. つぎのfor文は、iの値によってループ回数が変わる、でも最悪のケースなのでnステップとする
3. 2重for文の中にあるif文はすべて中を通ると仮定

します。すると、\( n^{2} - 2n + 1 \) ステップ*2となりますね。このように最悪のケースで計算量を求めるのは結構簡単なことがわかりますね。

(2) 平均計算量

しかし、最悪の計算量だけでは計算量の予測ができない場合もあります。例えば、「if文をほとんど通らないケース」や、「for文をほとんど回らない」場合は、最悪計算量でステップ数を求めると、実際の計算時間とはかなり異なった結果が出てしまいます。

最悪なパターンというものがまず起こらないようなアルゴリズム、例えば、クイックソートアルゴリズムはその典型的な例となります。クイックソートは、多くの場面においては理想的なソートアルゴリズムであり、その平均計算量のオーダー（計算量を予測したもの、下で紹介します）は、 \( O(n \log n) \) です。しかし、最悪のケースを想定してしまうと、\( O(n^{2} ) \) となってしまい、バブルソートなどの素朴なソート（人間が容易にできるソート）と一緒になってしまいます。

このように、場合によっては最悪計算量だけでなく、平均計算量も計算してあげなければならないこともあります。

スポンサードリンク

スポンサードリンク

３．オーダーってなに…？

上のような単純なプログラムの場合は問題ないのですが、ステップ数が \( 3n + 5 \) ステップ、\( n^{2} + 6n + 3 \) ステップ、\( 4n^{3} + 3n^{2} + 5n + 9 \) ステップのように複雑な関数になってくると比較がめんどくさくなってきますね。

そんなときに使われるのがオーダー記法です。オーダー記法では、入力数 \( n \) が十分に大きいときのステップ数を大雑把に見積もることができます。オーダー表記では、

1. 一番大きい項以外は無視（例：\( 4n^{3} + 3n^{2} + 5n + 9 \) は \( 4n^{3} \) と考える）
2. 定数倍の違いは無視 （例： \( 4n^{3} \) は \( n^{3} \) と考える）
3. 計算結果をビックオー表記にする（例： 1と2の結果が \( n^{3} \) の場合は \( O(n^{3}) \) ）

して考えます。nが十分に大きいときは、\( n^{2} \) の項は \( n^{3} \) の項に比べたら微々たる差ですよね。
理系の人は高校でこんな極限を習っていると思います（数3） \[ \lim_ {n \to \infty} \frac{3n^{2}}{4n^{3}} = \lim_{n \to \infty} \frac{3}{4n} =0 \]
分母にある \( n^{3} \) の項のほうが分子の \( n^{2} \) の項に比べてはるかに大きいので極限は0となることがわかりますね。

また、定数倍の違いは無視します。\( 4n^{3} \) も \( n^{3} \) もデータの増え方は同じですよね。先ほどと同じように極限を取ると、\[ \lim_ {n \to \infty} \frac{4n^{3}}{n^{3}} = 4 \]とたかが4倍の違いであることがわかりますね。十分大きい数 \( n \) に比べたら4倍なんてちっぽけなものです。

1,2の結果をした結果、 \( 4n^{3} + 3n^{2} + 5n + 9 \) ステップのアルゴリズムは計算量が \( O(n^{3}) \) のアルゴリズムと言うことができますね。
実際にオーダー表記の \( O(n^{3}) \) とステップ数の \( 4n^{3} + 3n^{2} + 5n + 9 \) の極限をとってみると、\[ \lim_ {n \to \infty} \frac{4n^{3} + 3n^{2} + 5n + 9}{n^{3}} = 4 \]とたかが4倍程度、つまり定数倍の違いしかないことがわかりますね。

４．項の強さ

※今回は、より結果が大きくなる方を「項が強い」と表記します。
オーダー表記にする際にどの項が強いのかを理解する必要があります。
例えば、\( n^{2} \) と \( n^{3} \) の場合は \( n^{3} \) のほうが大きいことはわかりやすいと思います。
しかし、\( n^{2} \)、\( 2^{n} \) 、\( \log_2 n \) 、 \( n! \)、 \( n^{n} \) のようにパッと見ただけでは少しわかりにくいものもあるかもしれません。
下に主なオーダーの強さの一覧をまとめてみたので参考にしてください。
細かい項の強さの比較や項の比較の仕方はこちらのブログにまとめました。

www.momoyama-usagi.com

\( a \) を \( n \) より小さい十分に大きな数とします。
\[\begin{align*}
O(1) < & O(\log n) < O(\sqrt{n}) < O(n) \\ < & O(n \log n) < O(n^{2}) < O(n^{3}) < \cdots < O(n^{a}) \\ < & O(2^{n}) < O(3^{n}) < \cdots < O(a^{n}) < O(n !)
\end{align*} \]
となります。簡単に言うと (定数) < (対数関数) < (多項式) < (指数関数) < (階乗) です*3。

５．オーダー一覧とその解説

最後に主に使われるオーダーについてまとめみました。
まとめるにあたって、以下のサイトを参考にさせていただきました。

qiita.com

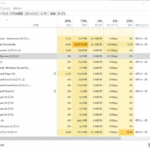
下の表は、\( n \) の値を変えたときに他の関数がどれくらいの値になるのかを示しています。
1秒間に1億ステップ (100,000,000) 実行できるものとして考え、1秒（1億ステップ）を超えてしまうものは計算にかかる時間を載せています。
参考までに、宇宙の年齢は約138億歳らしいです。

\( O(n \log n) \) までなら、データ数が増えてもあまり処理時間が変わりませんよね。
下でも説明するのですが、高度なソートアルゴリズム \( O(n \log n) \) と素朴なソート \( O(n^{2}) \) では \( n \) が小さいときには差が小さいですが、 \( n \) が大きくなればなるほど差がとんでもないことになるので、いかにオーダーの項を小さくするか（\( n^{2} \) を \( \log n \) にする以外にも ）が良いアルゴリズムをつくるポイントの1つになりますよね。

また、多項式時間 \( O(n^{a}) \) と指数時間 \( O(a^{n}) \) には見えない大きな壁があるレベルで差があります。 \( n = 20 \) 程度のプログラムであれば指数時間でもOKなのですが、\( n \) を20から少し増やすだけでもう使い物にならなくなってしまいます。
指数時間のアルゴリズムは、\( n \) を少し増やすだけでステップ数が爆発的に増加するので、組み合わせ爆発と呼ばれます。
階乗 \( O(n!) \) なんか恐ろしいですよね、たったの \( n = 50 \) でも9阿僧祇（\( 10^{56} \)）年かかるんですよ。

組み合わせ爆発については、非常におもしろい動画があるので紹介したいと思います。
『フカシギの数え方』 おねえさんといっしょ！ みんなで数えてみよう！

いかに効率的なアルゴリズムを作るかが大切なのかをおねえさんが教えてくれます……

(1) O(1)　定数時間

データ数 \( n \) がどんな大きさであっても必ず同じステップ数で実行できるアルゴリズムです。
例えば、ハッシュ探索などがO(1)（定数時間）に値します。

(2) O(log n)　対数時間

データ数 \( n \) とステップ数が対数 log に比例するアルゴリズムです。
ここで、「なんで対数の底が省略されているの？」と思った人もいるかもしれません。
では \( \log_{10} n \) は \( \log_{2} n \) がどれほど違うのかを計算してみましょう。\[ \log_{10} n = \frac{ \log_{2} n}{ \log_{2} 10} \]となり、\( \log _{10} n \) は \( \log_2 n \) と比べてたかが \( \frac{1}{ \log_{2} 10} \) 倍、つまり定数倍なので項の強さとしては同じことがわかりますね。対数の底がいくらだろうと項の強さが同じなのでオーダーで書く際には底を省略することが多いです。
対数時間のアルゴリズムの例としては、二分探索*4などがあります。
二分探索は、 データ数が1億あったとしてもたったの27回でデータを見つけ出すことができるすごく優秀なアルゴリズムです。それくらい \( O(\log n) \) のアルゴリズムは優秀なアルゴリズムです。
再帰関数の場合は、下のように \( n \) の範囲が1/2ずつしぼられていくような関数が \( O(\log n) \) 時間で終わるアルゴリズムとなります（再起関数の初期値は省略しています）。\[ f(n) = f(n/2) + 2 \]この再帰関数のステップ数は、以下の差分方程式（漸化式）を解くことで得られます。

(3) O(sqrt(n))

データ数 \( n \) が \( \sqrt{n} \) に比例するアルゴリズムです。
\( O(\sqrt{n}) \) となるアルゴリズムは例えばこのようなものがあります。

// 素数判定アルゴリズム
int isPnumber(int n) {
    // ステップ数 sqrt(n) - 1 
    for(int i = 2; i <= sqrt(n); i += 1) {
        if(n % i == 0) {
            return 0; // 素数でないと確定
        }
    }
    return 1;
}

このように素数を判定する場合、\( \sqrt{n} \) までを調べればよいのですが、これを n/2 や n までfor文をループさせてしまうと、\( O(n) \) のプログラムになってしまい、あまり良いアルゴリズムではなくなってしまいます。

(4) O(n) 定数時間

定数時間の名前の通り、データ数 \( n \) に比例してステップ数も \( n \) 倍になるアルゴリズムです。
for文によるn回（もしくはnに比例する回数、例えば3nとか）ループだけで処理が終わるアルゴリズムが該当します。

(5) O(n log n) 定数時間

\( O(n) \) 相当のループと \( O(\log n) \) 相当のループの2つが合わさっているアルゴリズムです。
マージソートやヒープソートなどの高速ソートアルゴリズムがこの \( O(\log n) \) に該当します。

(6) O(n²) 二乗時間

\( O(n) \) 相当のforループを2重にしたようなアルゴリズム。
バブルソート、挿入ソートなどの素朴なソートアルゴリズムは \( O(n^{2}) \) となります。

超えられない壁

(7) O(2ⁿ) 指数時間

例えば、「\( n \) 個の部分集合のパターンを素直に全部列挙する」とか「\( n \) 品ある食堂メニューから1000円以内で買える組み合わせをすべて列挙する」など、素直にパターンを列挙するとこのような時間になります。

(8) O(n!) 階乗時間

今回紹介するオーダーの中で、一番計算時間がかかてしまうものです。
例えば、巡回セールスマン問題*5などはこの \( O(n!) \) に相当します。
\( n = 10 \) 程度のものであれば計算可能だが、10を超えてしまうともう使い物にならないアルゴリズムになってしまいます。
ちなみに、\( n! \) に比べたらたったの \( n \) 倍しか違わないので無視できるので、\( O((n-1)! \) のことを \( O(n!) \) と書く人もかなりいます。

６．さいごに

今回はアルゴリズムの（時間）計算量について、とくにオーダーについての説明でした。
アルゴリズムを組み立てる際には、「ただ動けばいいや」だけでなく、「どうやったら効率よく計算できるんだろう」、「どうやったらもうちょっと早くなるんだろう」というのを考えながらアルゴリズムを組み立てるといいかもしれません。

計算量、オーダー表記が理解できてるかの確認チェック問題を作ったので参考までにしてください……
期末試験っぽく全部マーク形式です。

おねえさんに（効率の良いアルゴリズムを）教えてあげたい……