スポンサードリンク
こんにちは、ももやまです。
今回は前回の基本3ソートアルゴリズムに引き続き、基本ソートよりもより実用的で高速な応用4ソートアルゴリズム(クイックソート・マージソート・シェルソート・ヒープソート)について説明していきたいと思います。
なお、応用4ソートのうち、クイックソート・シェルソート・ヒープソートの3つは基本情報に頻繁に出てくるので基本情報を受ける人はそれぞれのソートの仕組みを頭に入れておきましょう。
残りのマージソートも応用情報に出てくるので、応用情報まで目指している人はマージソートについても軽く理解しておくといいかもしれません。
前回の基本3ソートアルゴリズムについては、下の記事をご覧ください。
スポンサードリンク
1.クイックソート
(1) クイックソートのしくみ
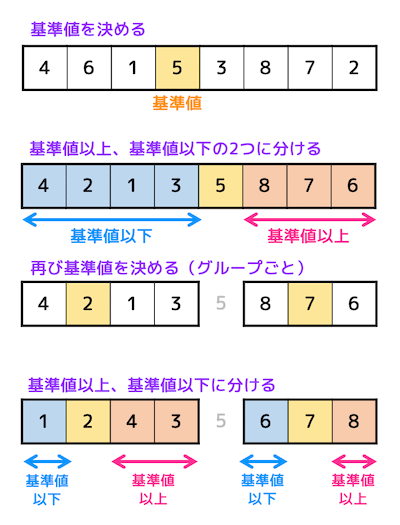
クイックソートでは、あるデータの中から1つ基準値を決め、基準値より小さいグループと基準値より大きいグループの2つに振り分けます。
振り分けたそれぞれのグループにも同じように「基準値より小さい」・「基準値より大きい」の2つに振り分けていきます。
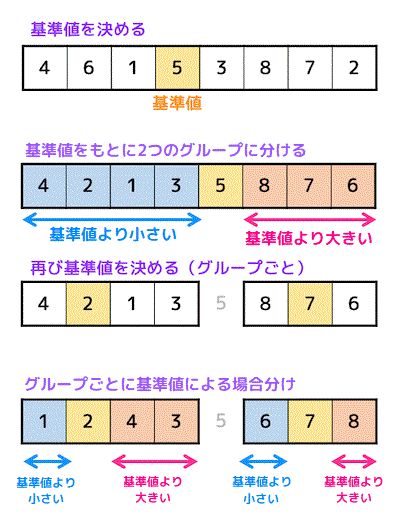
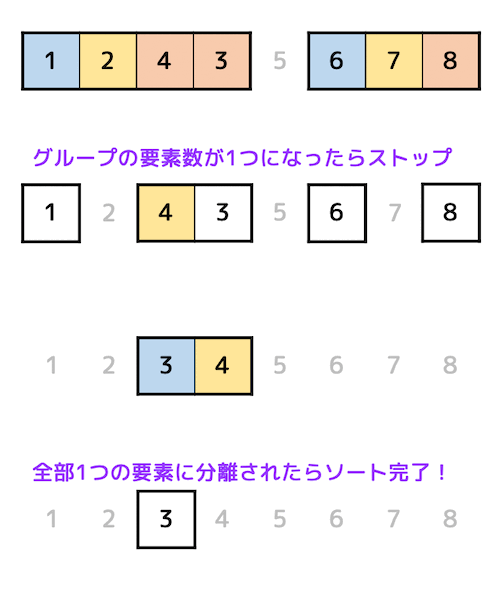
振り分ける操作を各グループの要素数が1つになるまで繰り返すとすべてのデータが順番通りになり
ソートが完了します。
(2) クイックソートのアルゴリズム・プログラム
要素数が n (つまり left = 0, right = n - 1)の配列 data を昇順にクイックソートする関数、およびピボットを決める関数は下のように書くことができます。
// ピボット(基準値)を決める関数
int find_pivot(int data[], int left, int right) {
return data[(left + right) / 2];
}
// クイックソートを行う関数
void quick_sort(int data[],int left, int right) {
int i, j, pivot, tmp;
// グループ内の要素が1つになれば終了
if(left >= right) {
return;
}
// ピボットを決定する
pivot = find_pivot(data,left,right);
i = left; // ソート対象の始点
j = right; // ソート対象の終点
// データを「pivotより小さいグループ」と「pivotより大きいグループ」にわける
while(1) {
// pivotより大きいデータを探す
while(data[i] < pivot) {
i += 1;
jikkou_i += 1;
}
// pivotより小さいデータを探す
while(data[j] > pivot) {
j -= 1;
jikkou_j += 1
}
if(i >= j) {
break; // 「pivotより小さい」と「pivotより大きい」の2つ分けられたらおわり
}
// data[i] と data[j] を交換
tmp = data[i];
data[i] = data[j];
data[j] = tmp;
// 交換終わり
i += 1;
j -= 1;
}
quick_sort(data, left, i - 1); // pivot以下のグループ
quick_sort(data, j + 1, right); // pivot以上のグループ
}
上の関数 quick_sort の仕組みとしては、
- まず
pivotを決定 - 始点
leftからpivot以上のデータを探す(iを右に動かす) - 終点
rightからpivot以下のデータを探す(jを左に動かす) - 2と3のデータを入れ替える
leftからの探索とrightからの探索が交差するまで2〜4をループ- 交差したら「pivot以下のグループ」と「pivot以上のグループ」の2つに分けて再帰的*1に解いていく
となります。
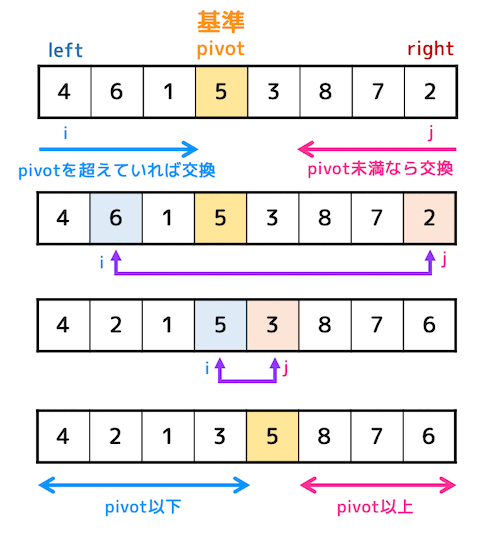
なお、クイックソートでは配列をいくつもの「要素数が少ないグループ」にわけてソートを行うため、分割統治法を用いたソートアルゴリズムといえます。
(3) クイックソートの特徴(計算量・安定性など)
(i) 平均計算量・最悪計算量
クイックソートは、「pivot以下のグループ」と「pivot以上のグループ」の2つのデータにわけるまでに最大で n ステップ、さらに再帰部分で配列を半分にわけていくので約 \log n ステップかかるので、全体の平均計算量は \( O( \log n ) \) となります。
ただし、ピボットが非常に偏り(左側が0個、右側が残り全部)続けてしまった場合は、配列をわけていくのに n ステップかかってしまうので最悪計算量は \( O( n^{2} ) \) となります。
ただし、ピボットの選び方を工夫することで \( O(n^{2} ) \) になるのを防ぐことができます。
例えば、基準値(ピボット)を単純に「配列の中央」にするのではなく、「配列の先頭」・「配列の中央」・「配列の最後尾」の3つの中の中央値を取るようにするとピボットが偏るのを防ぐことができます。
なお、ピボットを先頭・中央・最後尾の中央値にするような関数 find_pivot は下のように書くことができます。
// ピボットを先頭・中央・最後尾の中央の値にする関数
int find_pivot(int data[], int left, int right) {
int pivot_kouho[3] = {data[left], data[(left + right) / 2],data[right]};
insertion_sort(pivot_kouho,3);
return pivot_kouho[1]; // ソートしたデータの真ん中が中央値
}
(ii) 安定性・内部ソートかどうか
クイックソートは、非常な高速でソートである一方、同じ値の順序関係が崩れてしまうデメリット(安定ソートではない)があります。
また、クイックソートは外部メモリ(作業用配列)を使わずにソートできるため、内部ソートです。
スポンサードリンク
2.マージソート
(1) マージソートのしくみ
マージソートでは、まず下のようにデータを半分ずつに分割していきます。
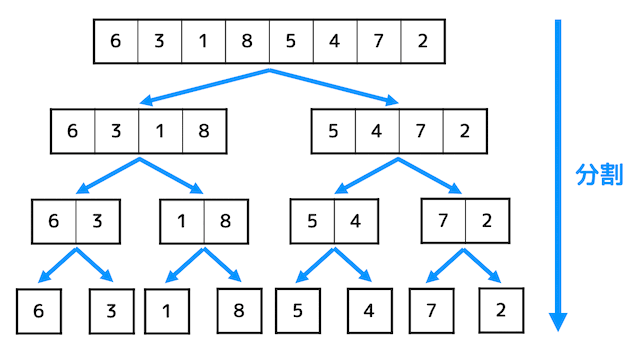
つぎに、分割した各データを少しずつ整列(マージ)していきます。
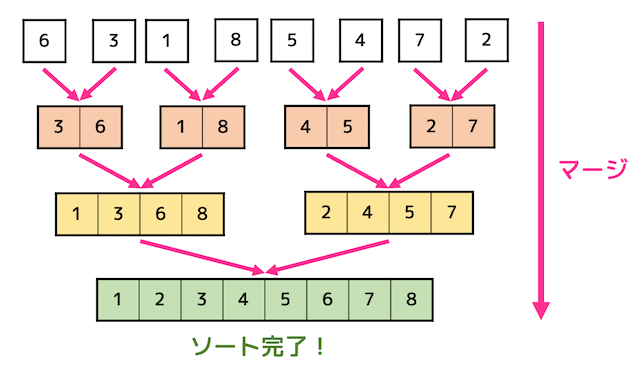
上の2つの過程でソートを行うのがマージソートです。
(2) マージソートのアルゴリズム
(i) 分割部分
分割部分は配列の中央よりも左側にあるデータ(左半分)と配列の中央よりも右側にあるデータ(右半分)の2つにわけて再帰的に分割していきます。
なおマージソートは、全体の配列を小さく分けてから徐々にソートしていくため、クイックソートと同じく分割統治法を用いたソートといえます。
(ii) マージ部分
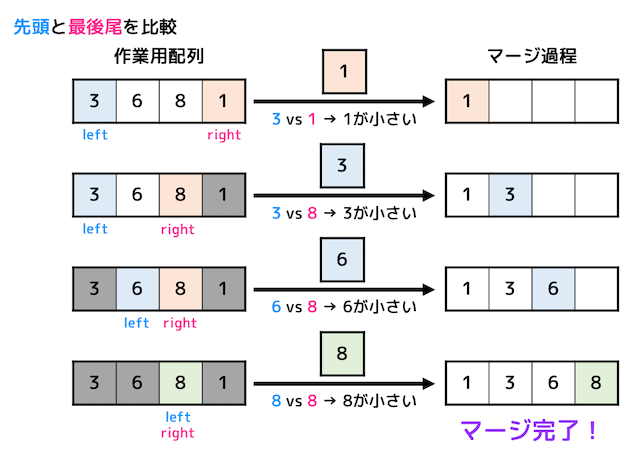
マージ部分は、作業用配列をうまく使うことで表現ができます。
まず、左半分のデータをそのまま作業用配列にコピーします。
つぎに右半分のデータはもとの配列の逆順にコピーします。
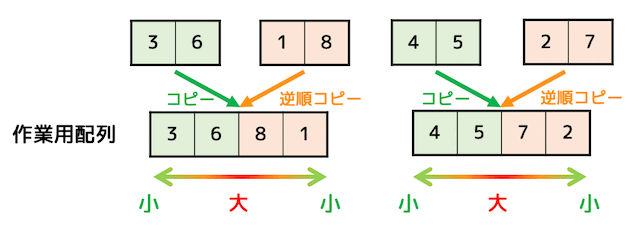
すると、作業用配列の両端が小さい値に、真ん中が大きい値となりますね。
あとは、両端の「先頭」と「最後尾」のどちらか小さい値の方を元のデータ配列に値を入れていく操作を作業用配列のすべてのデータがコピーされるまで続ければマージ完了です。
(iii) マージソートのプログラム
作業用配列 tmp を用いた要素数が n (つまり left = 0, right = n - 1)配列 data のマージソートを行うプログラムは下のように書くことができます。
void merge_sort(int data[], int tmp[], int left, int right) {
int i, j, mid;
// 要素数が1になったらストップ
if(left >= right) {
return;
}
// 配列の分割
mid = (left + right) / 2;
merge_sort(data,tmp,left, mid); // 配列の前半部分
merge_sort(data,tmp,mid + 1,right); // 配列の後半部分
// 分割終了、ここからはすべてマージの過程
// 配列の前半をそのまま作業用配列にコピー
for(i = left; i <= mid; i += 1) {
tmp[i] = data[i];
}
// 配列の後半を逆順に作業用配列にコピー
for(i = mid + 1, j = right; i <= right; i += 1, j -= 1) {
tmp[i] = data[j];
}
i = left;
j = right;
// 作業用配列からもとのデータが入った配列にコピー
for(int k = left; k <= right; k += 1){
if(tmp[i] <= tmp[j]) {
// 先頭が小さければ作業用配列の先頭をコピー
data[k] = tmp[i];
i += 1;
}
else {
// 最後尾が小さければ作業用配列の最後尾をコピー
data[k] = tmp[j];
j -= 1;
}
}
}
(3) マージソートの特徴(計算量・安定性など)
(i) 平均計算量・最悪計算量
マージソートは、配列を半分ずつに分割、分割した配列を元に戻す操作で 約 \( \log n \) ステップ、1ステップあたりの配列をマージするために約 \( 2n \) ステップかかるのでオーダーは \( O( n \log n ) \) となります。
クイックソートと異なるのは平均計算量だけでなく、最悪計算量も \( O( n \log n) \) となるところです。
(ii) ソートの安定性・内部ソートか
マージソートのメリットの1つに安定ソートである点があります。つまり、同じ値の順序関係を維持しながらソートを行うことができます。
しかし、ソートに外部メモリ(作業用配列)を使う必要があるため、内部ソートとはなりません(外部ソートです)。
スポンサードリンク
3.シェルソート
(1) シェルソートの仕組み
挿入ソートは、昇順(降順)に近ければ近いほど早くソートできるアルゴリズムでした。
シェルソートは、挿入ソートを改良したソート方法です。
具体的には少しずつ「昇順(降順)」に近づけながらソートを行うアルゴリズムです。
まず、ある一定間隔に要素を取り出し、挿入ソートを行います。
(下の図の間隔:4つごと)
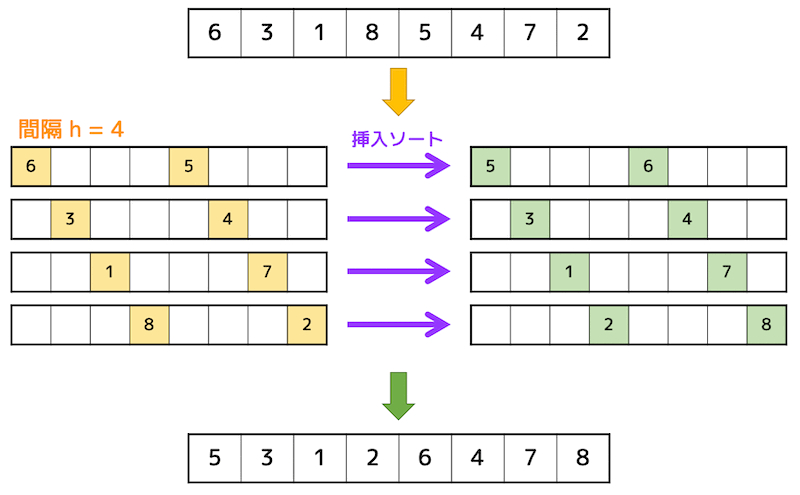
つぎに、間隔を詰めて要素を取り出し、挿入ソートを行います。
(下の図の間隔:2つごと)
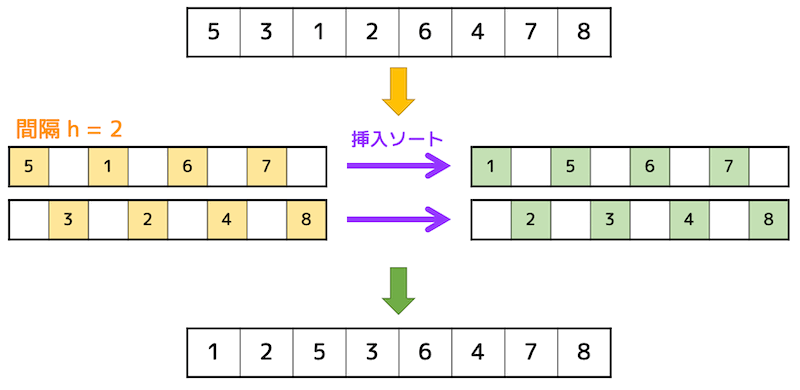
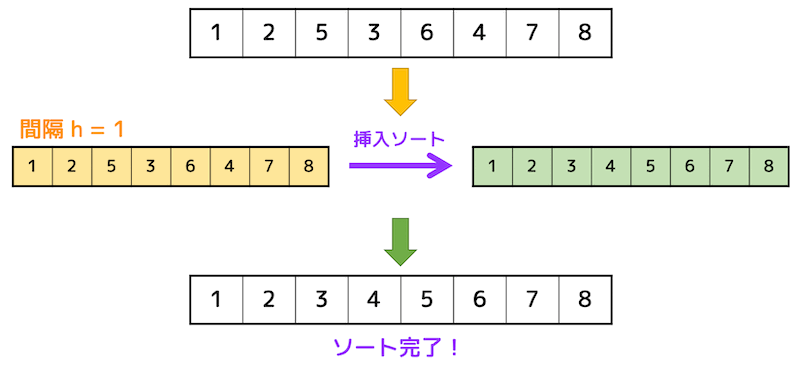
間隔が1になるまで繰り返し挿入ソートを行います。
間隔が1のとき(つまり普通の挿入ソートと同じ)にソートを行うことでソートが完了します。
(2) シェルソートのアルゴリズム
要素数が n 、配列 data のマージソートを行う関数 shell_sort は下のように書くことができます。
void shell_sort(int data[], int n) {
int j,tmp, h = n / 2; // h は間隔(初期値は全体の半分)
// 間隔が1のときまでソート
while(h >= 1) {
for(int i = h; i < n; i += 1) {
j = i;
// 正しい順番になるまで左へ
while( (j >= h) && (data[j-h] > data[j]) ) {
// data[j-h] と data[j] を入れ替え
tmp = data[j-h];
data[j-h] = data[j];
data[j] = tmp;
// 入れ替え終わり
j -= h; // 間隔ごとに見ていく
}
}
h /= 2; // 間隔を半分に
}
}
(3) シェルソートの特徴(計算量・安定性など)
(i) 間隔 h の選び方
上のプログラムでは、間隔 h の初期値をデータ数の半分とし、徐々に間隔を半分にしていきましたね。
ですが実際にはより「ステップ数が少なくかつ整列済みに近い状態にするために」漸化式\[
h_{n+1} = 3 h_{n} + 1
\]で選び出された数列「1, 4, 13, 40, 121……」を大きい順に*2適用させています。
さらに、初期値の段階で適切な間隔になるように、h の値は上の漸化式を満たし、かつ(データ数 / 9)を超えない最も大きな値に設定することでより早くシェルソートを行うことができます。
これらの条件を満たすように h の値を設定しながら要素数が n 、配列 data のシェルソートを行う関数 shell_sort は、下のように書くことができます。
void shell_sort(int data[], int n) {
int j,tmp, h = 1; // h は間隔
// h_{n+1} = 3 * h_{n} + 1 を満たし、かつ n / 9 を超えない最も大きい h を求める
while(3 * h + 1 <= n / 9) {
h = 3 * h + 1;
}
// 間隔が1のときまでソート
while(h >= 1) {
for(int i = h; i < n; i += 1) {
j = i;
// 正しい順番になるまで左へ
while( (j >= h) && (data[j-h] > data[j]) ) {
// data[j-h] と data[j] を入れ替え
tmp = data[j-h];
data[j-h] = data[j];
data[j] = tmp;
// 入れ替え終わり
j -= h; // 間隔ごとに見ていく
}
}
h /= 3; // 間隔を詰める
}
}
(ii) 最悪計算量・平均計算量
シェルソートの正しい計算量は未だに未解決となっています。
最初に紹介した h = ……, 4, 2, 1 と設定していく方法では最悪計算量が \( O(n^{2}) \)、平均計算量は \( O(n^{1.5}) \) となります。
一方 \( h_{n+1} = 3 h_{n} + 1 \) の漸化式を用いて h を設定していく方法では、最悪計算量が \( O(n^{2}) \)と変わりませんが、平均計算量を約 \( O(n^{1.25}) \) まで減らすことができます。
(iii) 安定性・内部ソートか
シェルソートは挿入ソートとは異なり、隣り合ったデータ以外でデータを交換しまくるため、同じ値の順序関係が崩れてしまうことがあり、安定ソートとはいえません。
また、シェルソートは外部メモリ(作業用配列)を使わずにソートできるため、内部ソートです。
4.ヒープソート
(1) ヒープソートの仕組み
ヒープソートは、データを「順序木*3」と呼ばれる木構造に構成し、最大値(最小値)を取り出して整列済みにしていくことでソートを行うアルゴリズムです。
まず、データを木構造にし、順序木(ヒープ)にします。
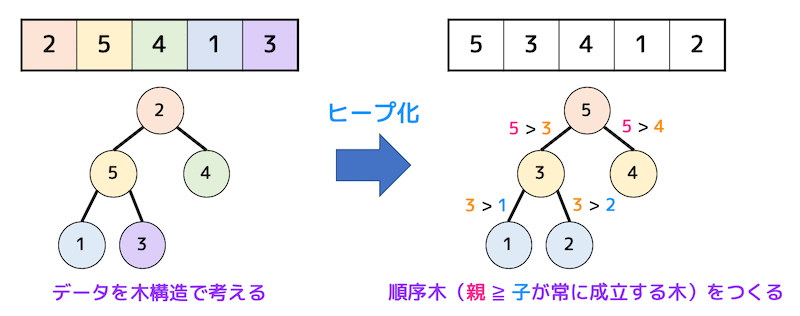
すると、木構造の根が一番大きい値となるので先頭と未確定列の最後尾を交換し、データ「5」の位置が確定します。
確定したら再び順序木をつくります。
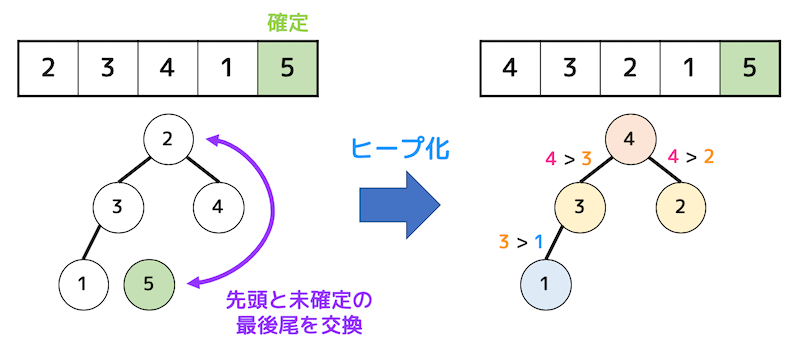
これをすべてのデータが確定するまで繰り返します。
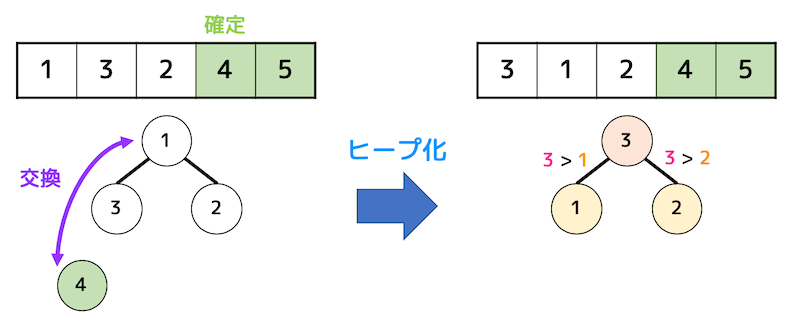
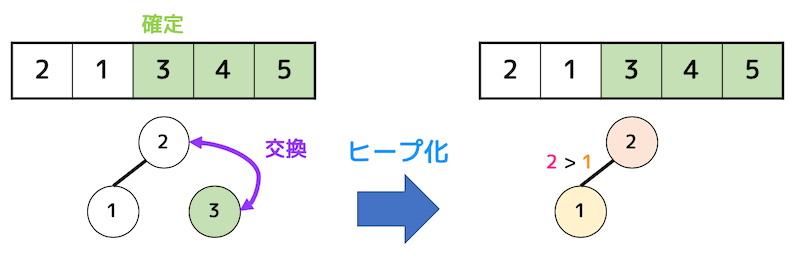
(2) ヒープソートの詳しいアルゴリズムなど
ヒープソートについては、こちらの記事に詳しい内容が書いてあるので興味がある方はぜひご覧ください!
5.応用4ソートのまとめ
では、今回説明した4つのソートを簡単にですがまとめていきましょう。
(1) 応用4ソートの性質
クイックソート:基準値以上のデータと基準値以下のデータの2つにわけるのを再帰的に繰り返すことでソートしていく。
分割統治法を用いたソート方法。
マージソート:配列を2分割ずつしていき、分割したデータをマージしていくことでソートを行う。
分割統治法を用いたソート方法。
シェルソート:一定間隔おきにデータを取り出したものをソートしていき、徐々に取り出す間隔を狭めながらソートしていく。
ヒープソート:未整列のデータを順序木にし、木構造の根からデータを取り出し、整列済にするのを未整列のデータがなくなるまで繰り返してソートを行う。
(2) 計算量・安定性
| ソート名 | 最悪計算量 | 平均計算量 | 安定? | 内部? |
|---|---|---|---|---|
| クイック | \( O(n^{2}) \) | \( O(n \log n) \) | No | Yes |
| マージ | \( O(n \log n) \) | \( O(n \log n) \) | Yes | No |
| シェル | \( O(n^{2}) \) | \( O(n^{1.25}) \) | No | Yes |
| ヒープ | \( O(n \log n) \) | \( O(n \log n) \) | No | Yes |
※1:安定性は、同じ値のデータをソートしたときに順序関係が保存されるかどうかを表す。
※2:内部(ソート)は、ソートの際に外部メモリ(作業用配列など)が不要かどうかを表す。
6.練習問題
では、基本情報や応用情報の問題で何問か練習してみましょう。
今回は応用情報の問題が多めです。
練習1
整列アルゴリズムの一つであるクイックソートの記述として、適切なものはどれか。
[基本情報技術者平成27年秋期 午前問7]ア:対象集合から基準となる要素を選び、これよりも大きい要素の集合と小さい要素の集合に分割する。この操作を繰り返すことで、整列を行う。
イ:対象集合から最も小さい要素を順次取り出して、整列を行う。
ウ:対象集合から要素を順次取り出し、それまでに取り出した要素の集合に順序関係を保つよう挿入して、整列を行う。
エ:隣り合う要素を比較し、逆順であれば交換して、整列を行う。
練習2
分割統治法を適用した整列(ソート)アルゴリズムはどれか。
[ソフトウェア開発技術者平成18年春期 午前問12]ア:クイックソート
イ:選択ソート
ウ:挿入ソート
エ:ヒープソート
練習3
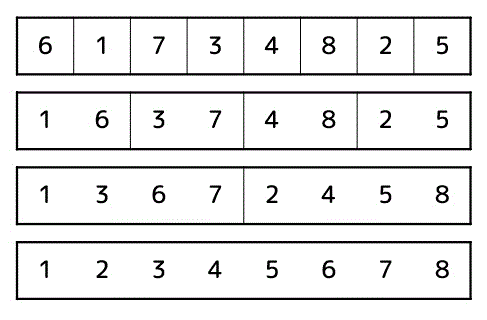
データ列が整列の過程で図のように上から下に推移する整列方法はどれか。ここで、図中のデータ列中の縦の区切り線は、その左右でデータ列が分割されていることを示す。
ア:クイックソート
イ:シェルソート
ウ:ヒープソート
エ:マージソート
練習4
次の手順はシェルソートによる整列を示している。データ列7, 2, 8, 3, 1, 9, 4, 5, 6を手順1~4に従って整列するとき、手順(3)を何回繰り返して完了するか。ここで、[ ]は小数点以下を切り捨てた結果を表す。
[応用情報技術者平成24年春期 午前問7]〔手順〕
- [データ数÷3] → H とする。
- データ列を、互いにH要素分だけ離れた要素の集まりからなる部分列とし、それぞれの部分列を、挿入法を用いて整列する。
- [H÷3] → H とする。
- Hが0であればデータ列の整列は完了し、0でなければ(2)に戻る。
ア:2
イ:3
ウ:4
エ:5
7.練習問題の答え
解答1
解答:ア
それぞれの選択肢ごとの解説
ア:大正解! クイックソートの説明です。
イ:選択ソート(基本3ソート)の説明です。
ウ:挿入ソート(基本3ソート)の説明です。
エ:バブルソート(基本3ソート)の説明です。
解答2
解答:ア
分割統治法とは、そのまま解くのが難しい問題を、いくつかの小さくて簡単な問題にして解き、最後にもとの問題にまとめることで問題を解いていく方法です。
選択肢の4つの中で、分割統治法を用いているソート法はクイックソートなので、答えはアとなります。
(クイックソートはデータ列を「基準値以下」と「基準値以上」の2つのグループ分けていき、さらにわけたグループでもどんどん「基準値以下」・「基準値以上」と細かくしていくことでソートしていく分割統治法を用いたアルゴリズムです。)
解答3
解答:エ
各データの隣り合う同士でソートされてそれぞれ要素数2のグループとなり、要素数2のグループ同士でソートされ要素数4に……、となるソートはマージソートである。
よって答えはエ。
★各選択肢の解説★
ア:クイックソートであればある基準値を基準にデータを分ける操作があるはずだがそんな操作はない。よって誤り。
イ:シェルソートであれば一定間隔ごとの部分列ごとにソートされるはずだがそんな操作はない。よって誤り。
ウ:後ろから(前から)ソートされるが、そんな気配はないのでこれもダメ。
エ:大正解。
解答4
解答:ア
この問題で大切なのは、データの中身よりも要素数である。
Hの数が変動するのは操作1([データ数÷3] → H)と操作3([H÷3] → H)だけである。そのため、データの中身は一切関係がない。
今回は、要素数が9のデータをシェルソートする。
そのため、最初のHは3、1回目操作3でHは1、2回目の走査3でHは0となるので答えはアの「2」となる。
8.さいごに
今回は前回の基本3ソートアルゴリズムに引き続き、4つの応用ソートアルゴリズムについてまとめていきました。
応用ソートアルゴリズムはプログラムこそ書ける必要はありませんが、少なくとも仕組みは頭にいれておきましょう。
今回でアルゴリズム関連の記事は一旦中断したいと思います。
今まで見ていただきありがとうございました!
関連広告・スポンサードリンク