![うさぎでもわかる計算機システム Part01 2進数 [基本情報対応]](https://www.momoyama-usagi.com/wp-content/uploads/2021/05/20190612102246-1.gif)
スポンサードリンク
こんにちは、ももやまです!
今回からしばらく計算機システム、つまり計算機のハードウェアについてまとめていきたいと思います。
今回は2進数で0以上の数を表す方法を考えます。
負の数を2進数で表す方法については次回まとめたいと思います(2の補数)。
2進数をすでに理解している人は最後に演習問題を用意したのでそちらに挑戦してみてください!(基本情報の過去問も用意しています)
目次
スポンサードリンク
1.10進数と2進数
(1) 10進数 [decimal number]
まずは、皆さんがなじみの深い10進数を改めて紹介したいと思います。
たとえば、19.625という数を思い浮かんでください。
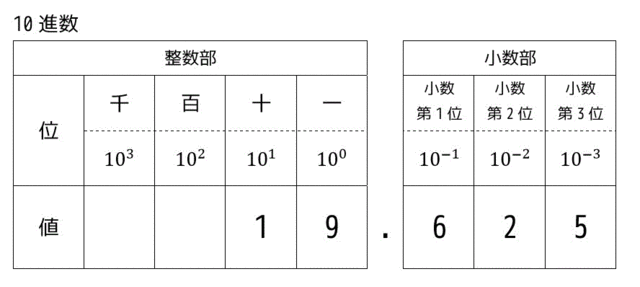
19.625の整数部分は19(整数部)、小数の部分は0.625(小数部)と分けることができます。
整数部の位は順番に1の位、10の位、100の位……と10倍ずつ大きくなり、小数部の位は順番に1/10の位、1/100の位、1/1000の位……と1/10倍ずつ小さくなりますね。
また、1つの位には0~9の値が入ります。
また、あえて10進数と強調するため、数字の最後にdをつけることがあります(dec)。
たとえば13という数字が10進数と強調したいときは13dとします。
dは、decimal [dec] からきています。
(2) 2進数 [binary number]
では2進数の場合はどうなるでしょうか。
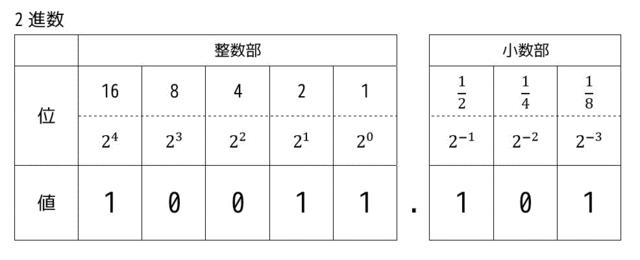
10進数と同じように整数部、小数部がありますね。
ですが、位のところに注目してください。順番に1の位、2の位、4の位……と、位が1つ上がるにつれて10倍ではなく2倍になっていますね。 ここが2進数の最大の違いです。また、小数部も1/2の位、1/4の位……と1/2倍になっていますね。
また、それぞれの位には0か1しか入りませんね。
以上2つが10進数と2進数の違いです。
2進数の数を表すときは、10進数と間違われないように次のような記号を数字の前やあとにつけます。例えば2進数の1001の場合、
- 1001b
- 0b1001
- \( (1001)_2 \)
bは、binary [bin] からきています。
スポンサードリンク
2.2進数⇔10進数の変換
(1) 2進数→10進数
まずは、2進数→10進数にする方法を説明します。
上の例で説明した10011.101bを10進数になおしてみましょう。
2進数を10進数に直すためには、それぞれの位が1のところの位の値を足しこみます。
今回の場合、\( 2^4 \), \( 2^1 \), \( 2^0 \), \( 2^{-1} \), \( 2^{-3} \) の位が1ですね。なので、値は\[ 2^4 + 2^1 + 2^0 + 2^{-1} + 2^{-3} = 19 + \frac{1}{2} + \frac{1}{8} = 19.625\]となります。
(2) 10進数→2進数
つぎに10進数→2進数にする方法を説明します。
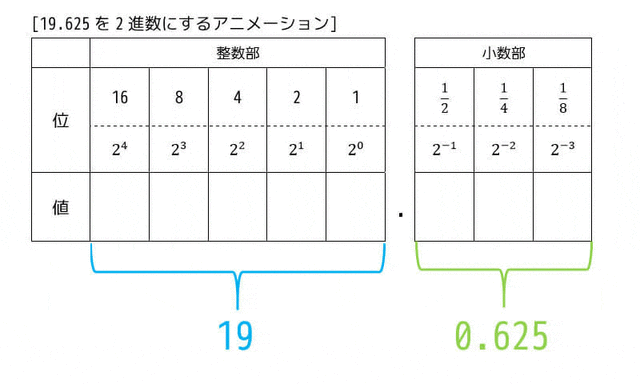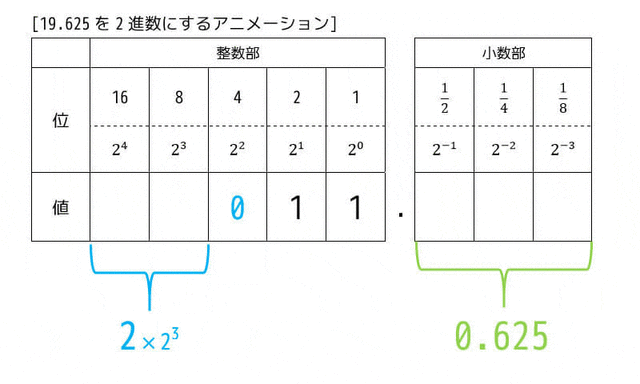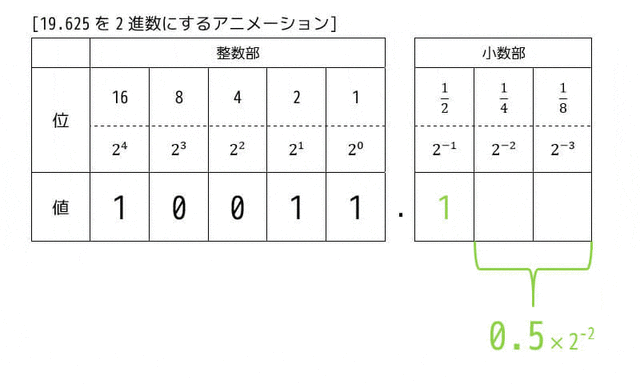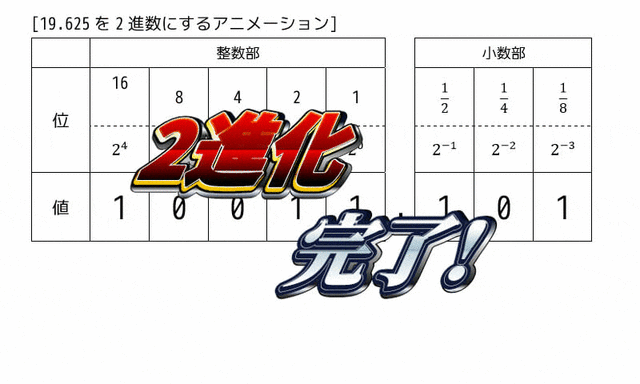
では、19.625を2進数になおしてみましょう。
10進数から2進数に直す際には、整数部分と小数部分にわけて考えます。
(i) 整数部分
まずは整数部分の19を2進数にしていきましょう。
整数部分を2進数にしていくためには、はじめに整数部分を2で割ったときの商と余りを求めます。得られた商を更に2で割っていき、これを商が1になるまで続けます*1。
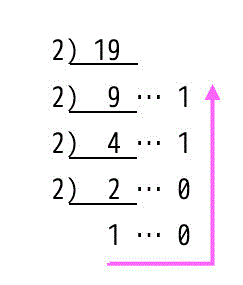
計算後、あまりを左下から上の方向に読んだのが整数部の2進数となります。
数式で表すと、\[
\begin{align*}
19 & = 2 \cdot 9 + 1
\\ & = 2 (2 \cdot 4 + 1) + 1
\\ & = 2 (2 (2 \cdot 2 + 0) + 1) + 1
\\ & = 2 (2 (2 (2 \cdot 1 + 0) + 0) + 1) + 1
\\ & = 2^4 + 2^1 + 2^0
\end{align*}
\]となります。
(ii) 小数部分
次に小数部分の0.625を2進数にしていきましょう。
小数部分を2進数にしていくためには、小数部分を2で掛けていきます。2で掛けた値を整数部分と小数部分にわけ、小数部分だけ2でまた掛けていきます(掛ける際には小数点無視)。これを小数部分が0になるまで続けます。
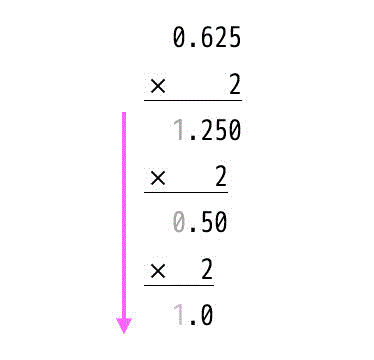
数式で表すと、\[
\begin{align*}
0.625 & = 2^{-1} \cdot (1 + 0.25)
\\ & = 2^{-1} \cdot (1 + 2^{-1} \cdot (0 + 0.5) )
\\ & = 2^{-1} \cdot (1 + 2^{-1} \cdot (0 + 2^{-1} \cdot 1) )
\\ & = 2^{-1} + 2^{-3}
\end{align*}
\]となります。
しかし、小数によっては永久に続く無限小数となることもあります。
例えば、0.4を2進数になおしてみましょう。
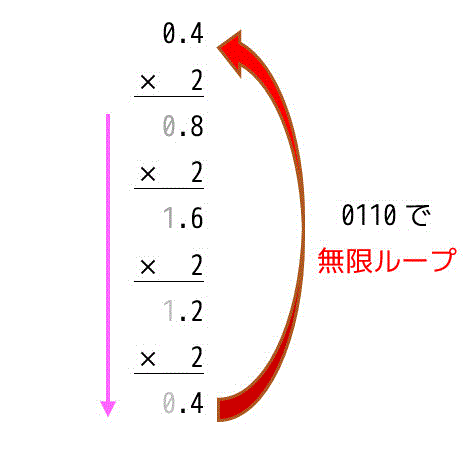
0.4を2進数にすると、0.0110 0110 0110 と無限ループします。
このような場合、「計算を途中で打ち切る方法」と「循環する部分を点で示す方法」の2つがあります。
計算を途中で打ち切る場合は、無限ループはしませんが、計算結果に誤差が出てしまいます。例えば、小数第4位で打ち切ると、0.0110b となりますが、\[ 0.0110_{2} = 2^{-2} + 2^{-3} = \frac{1}{4} + \frac{1}{8} = \frac{3}{8} = 0.375 \]となり、0.025 (1/40)の誤差が発生してしまいます。
計算機上では、こちらの「計算を途中で打ち切る方法」が使われます。そのため、小数の計算を繰り返すと誤差が発生することがあります*2。
循環する部分を点で示す方法の場合は、循環する部分の始まりと終わりを下のように上つきの点で表します。\[ 0.4 = 0.0110 \ 0110 \ 0110 \cdots = 0. \dot{0} 11 \dot{0}_{2} \]
10進数→2進数の変換をアニメーションにしてみました。
スポンサードリンク
3.2進数同士の四則演算
2進数同士でも10進数と同じように四則演算を行うこともできます。
ただし、繰り上がりが10ではなく、2で行われることに注意してください。
(1) 足し算
110100.10, 100010.11の2つの数の足し算をしてみましょう。10進数に直すとそれぞれ52.50, 34.75となります。
10進数の場合と同じように筆算をすることで求めることができます。
暗算だとわけわからくなるのでやめましょう。

繰り上がりが2で起こることに注意してください。繰り上がりをした箇所を青色で示しています。繰り上がりを処理したら足し算の完了です。結果は1010111.01となります。これを10進数に直すと87.25となり、確かにうまく計算ができていることがわかります。
(2) 引き算
引き算も10進数と同様に計算が出来ます。
2進数の正負を入れ替える際に使います。
10000b - 1001b (10進数:16 - 9) の計算をしてみましょう。
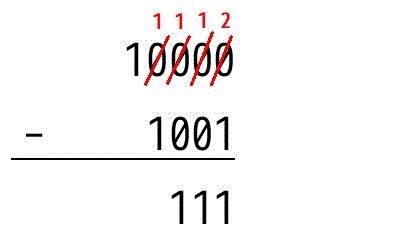
計算結果は111b、つまり10進数でいう7となり、計算結果が10進数でそのまま計算した場合と一致しますね。
10進数と同じように小さい位から順番に1桁ずつ引き算をしていきます。
もし、引き算の際に足りなくなった場合は、10進数と同じように桁借りをします。
10進数の場合、1つの上の桁から10を借りますが、2進数の場合は、借りるのは10ではなく2となるところに要注意です。
(3) 掛け算
掛け算の場合も10進数と同様に筆算で計算ができるのですが、桁数が増えると繰り上がりの箇所が増えて計算ミスが発生しやすくなるので注意してください。
足し算の例と同じ52.50, 34.75で試してみたいと思います。
10進数の掛け算の筆算の場合と同じようにまずは小数点を無視します。

繰り上がりを処理したら最後に小数点を付けます。110100.10b, 100010.11bはともに小数第2位までなので、小数点は第4位までつきます*3。よって答えは111 0010 0000.0110bとなります。10進数に直すと1824.375となり、確かに計算が正しいことがわかります。
(4) 割り算
割り算も同様に計算ができます。
引き算を繰り返すので計算ミスに注意してください。
110111b ÷ 101b の計算をしてみましょう(10進数:55÷5)。
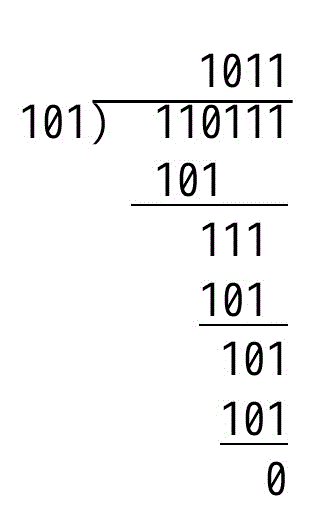
計算結果は1011b、10進数にすると11となり、確かに10進数でそのまま計算した結果と一致します。
4.ビット・バイトなどの情報単位
(1) ビットについて
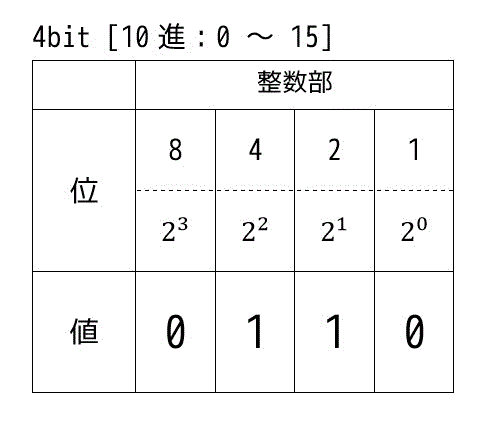
計算機では、計算できる桁数の限界をビットで表します。
例えば、4bitの場合は、図のように4桁まで格納することができます。
(10進数の場合:0〜15まで格納可)
計算できる桁数の限度を超えてしまったものはすべて無視されます。
4bitの例でいくと、10010などが来た場合は、一番上の桁が無視され、0010となります。上の桁が無視され、実際に表したい数とは異なる数値になってしまう現象をオーバーフローと言います。
ゲームなどのバグの原因の1つにオーバーフローがあります。
あまりにもプレイヤーが強くなりすぎて桁があふれ、1周回って弱体化するバグなどはステータスのオーバーフローが原因です。
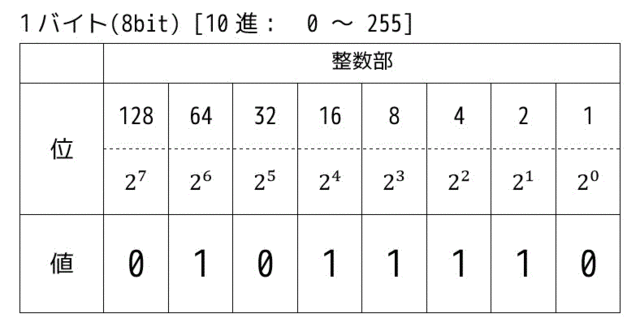
計算機上では、8bitのひとまとまりを1バイトと表します。
(2) バイト以上の単位
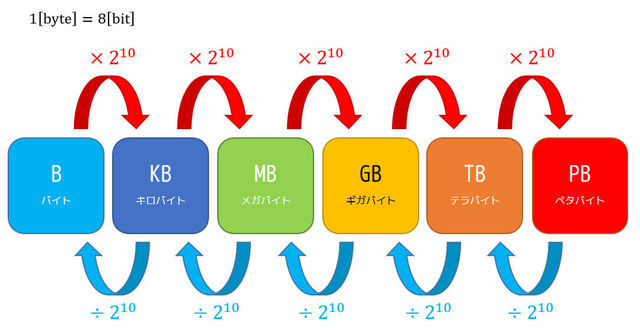
さらに1024 (\( 2^{10} \))バイトをひとまとまりにしたものを1キロバイト[KB]と言います。それ以降は、
- 1024キロバイト[KB] → 1メガバイト[MB]
- 1024メガバイト[MB] → 1ギガバイト[GB]
- 1024ギガバイト[GB] → 1テラバイト[TB]
- 1024テラバイト[TB] → 1ペタバイト[PB]
と徐々に1024をひとまとまりにして名前が変わっていきます。
ハードディスクやSSD、RAM(メモリ)などのGB,TBなどはすべてこの情報量の単位です。
また、皆さんが通信量が足りないときに言う、ギガが足りないのギガは[GB]も同じように情報量の単位です。
5.2進数の論理演算
2進数はそれぞれの桁が0(False)か1(True)で表現されていますね。
なので、通常の演算の他にもビットごとの論理和、論理積、排他的論理和などの計算を行うこともできます。
論理和、論理積、排他的論理和がうーんという人はこちらにまとめていますのでぜひご覧ください。
(1) 論理和
同じ桁数同士で論理和を求めることができます。
例:0110 or 0011 の演算
図のようにそれぞれのビットごとのorを取ると、
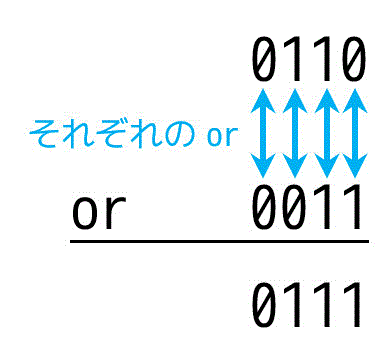
0111となります。
(2) 論理積
同じように論理積も求めることが出来ます。
例:0110 and 0011 の演算
図のようにそれぞれのビットごとのandを取ると
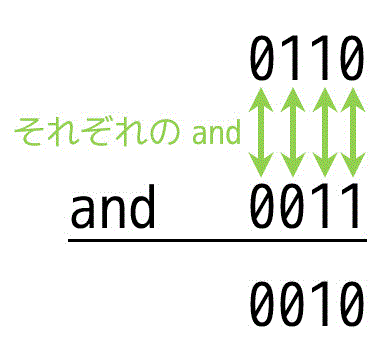
0010となります。
(3) 排他的論理和
排他的論理和も求めることができます。
例:0110 xor 0011 の演算
それぞれのビットごとのxorを取ると
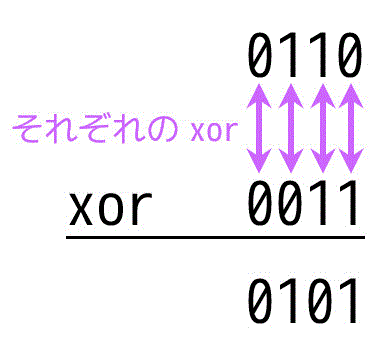
0101となります。
6.2進数の論理シフト
2進数では、論理シフト演算ができます。
シフト演算では、桁を左にずらす場合と右にずらす場合の2パターンがあります。
それぞれのパターンを説明していきたいと思います。
今回は整数部のみとし、8桁(8ビット、1バイト)と仮定します。
この桁からあふれ出たものはすべて無視することにします。
(1) 左にシフトする場合
図のように左に1つ桁をシフトする場合を考えます。
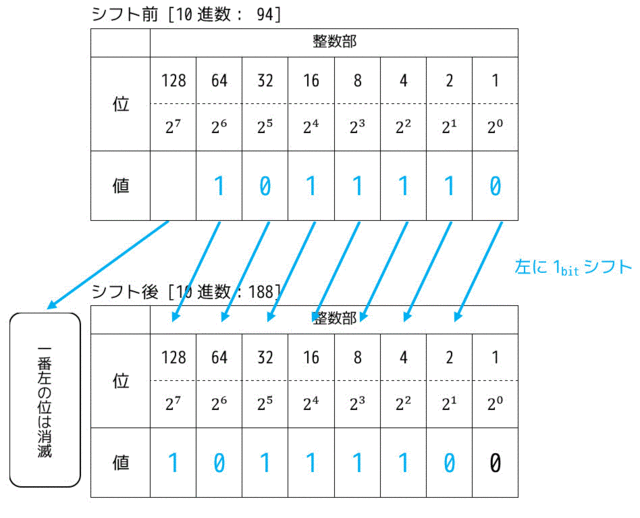
この場合1つずつ値が左にずれていますね。
さらに、空いた箇所には0が挿入されています。
また、一番左にある桁は消滅します。
この操作は、値の大きさを2倍にする操作に相当します。
(一番左の桁が消滅した場合を除く)
(2) 右にシフトする場合
つぎに図のように右に1つ桁をシフトする場合を考えます。
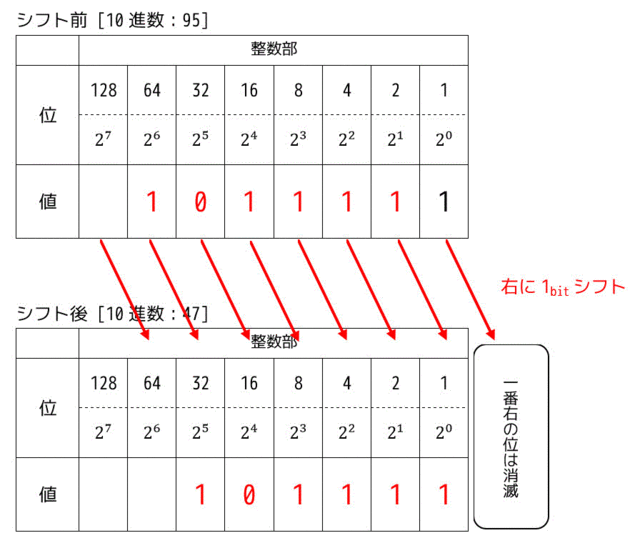
この場合1つずつ値が右にずれていますね。
(1)の場合と同じく、空いた場所には0(空欄)が入っていますね。
また、一番右の桁はシフトする際に消えてしまいます。
この操作は、値の大きさを1/2倍にする操作に相当します。
(小数点以下切り捨て)
今の2つの操作をまとめると、
- 左に \( n \) bitシフト → 値は \( 2^n \) 倍する操作
- 右に \( n \) bitシフト → 値は \( 1/2^n \) 倍する操作
になります(オーバーフローなどがなければ)。
7.8進数、16進数
2進数で100100101110101… と長い数を読むのは計算機くんは簡単でも人間だと読みにくくて大変です。
なので、人間が読みやすくするために2進数を何個かひとまとまりにします。
このとき用いられるのが8進数、16進数です。
(1) 8進数 [octal number]
8進数は、2進法を3桁区切りにしていき、読んでいきます。
つまり、1つの位には0~7までの数が入ります。
8進数を表す際は、何進数かわかるように、次のような記号や数字を書きます。
oは、octal [oct] からきています(オクトパスが語源、あしが8本なので)。
- 435o
- 0o435
- \( (435)_8 \)
たとえば、2進数の(100 011 .101)bを8進数に直してみましょう。
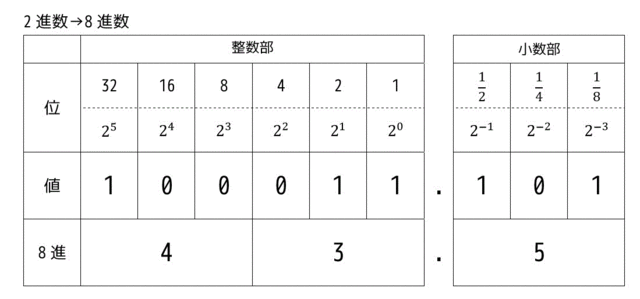
3桁区切りにすると、100 011 . 101 の3つに分解できますね。
つぎにそれぞれ分解したところがいくらになるのかを計算していきます。例えば、100は、\( 2^2 \) の位だけが1なので、\( 2^2 = 4 \)、011は \( 2^1 \)、\( 2^0 \) の位が1なので \( 2^1 + 2^0 = 3 \) 、小数部である101は \( 2^2 \) の位と \( 2^0 \) の位が1なので \( 2^2 + 2^0 = 5 \) となります
よって100011.101bは8進数だと43.5oと表すことができます。
(2) 16進数 [hexadecimal number]
16進数は、2進法を4桁区切りにしていきます。
つまり、1つの位には0~15までの数が入ります。
ですが、1桁で10~15をアラビア数字で表すことはできませんね…。
16進数では、10~15に相当する数をA~Fのアルファベット(大文字でも小文字でもOK)で表します。
| 10進 | 16進 |
| 10 | A |
| 11 | B |
| 12 | C |
| 13 | D |
| 14 | E |
| 15 | F |
16進数を表す際も、何進数かわかるように、次のような記号や数字を書きます。
- 5EBh
- 0x5EBh
- \( (\mathrm{5EB})_16 \)
hやxは、hexadecimal [hex] からきています。
では実際に1つ例として (1011 1110.1011)b を16進数になおしてみましょう。
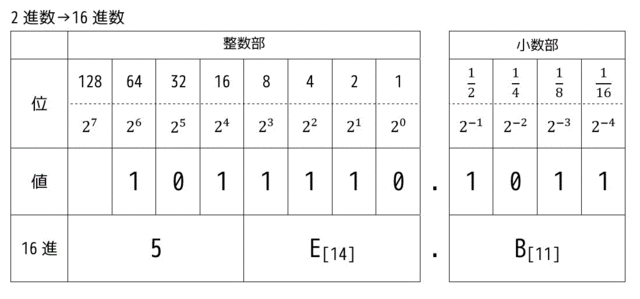
4桁区切りにすると、整数部は 101,1110の2つ、小数部は1011の合計3つに分解できますね。位が小さいほうから区切っていくことに注意してください。
つぎに8進数のときと同じようにそれぞれ分解したところがいくらになるのかを計算していきます。例えば、101は、\( 2^2 \), \( 2^0 \) の位が1なので、\( 2^2 + 2^0 = 5 \)、1110は \( 2^3 \), \( 2^2 \), \( 2^1 \) の位が1なので \( 2^3 + 2^2 + 2^1 = 14 \)、となりE、小数部である1011は \( 2^3 \), \( 2^1 \), \( 2^0 \) の位が1なので \( 2^3 + 2^1 + 2^0 = 11 \) となり、Bとなります。
よって100011.101bは8進数だと5E.Bhと表すことができます。
整数部は桁が小さいほう(右から順に)から3桁or4桁区切り、余った場合は桁が余った部分を0扱い、小数部は桁が大きいほう(左から順に)から3桁、4桁区切りをし、余った場合は桁が余った部分を0扱いすることがポイントです。
8.練習問題
(1) 練習1
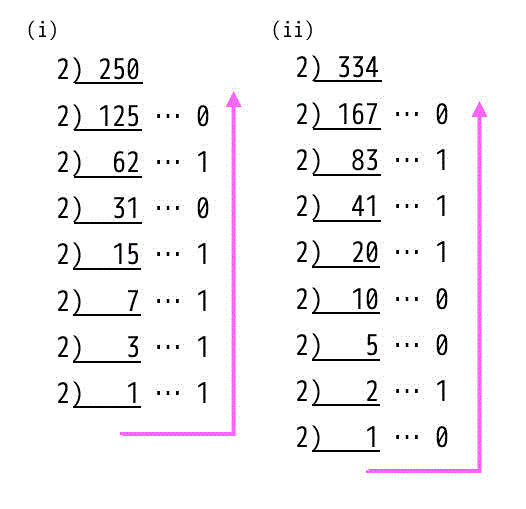
つぎの10進数を2進数に直しなさい。
(i) 250 (ii) 334
(2) 練習2
つぎの2進数を10進数に直しなさい。
(i) (1 1001)b (ii) (101 0110)b
(3) 練習3
1バイトのデータで0のビット数と1のビット数が等しいもののうち,符号なしの2進整数として見たときに最大になるものを,10進整数として表したものはどれか。
(基本情報技術者平成18年秋季 午前問1)
ア:120
イ:127
ウ:170
エ:240
(4) 練習4
10進数の分数1/32を16進数の小数で表したものはどれか。
(基本情報技術者平成20年春期 午前問2)
ア:0.01
イ:0.02
ウ:0.05
エ:0.08
(5) 練習5
11.2を2進数に直しなさい。
ただし、小数第5位以下を切り捨て(無視し)、小数第4位まで答え、そのとき発生する誤差を10進数で答えなさい。
(6) 練習6
つぎの問いに答えなさい。
(i) 10進数の数102, 57をそれぞれ2進数に直しなさい。
(ii) 2進数に直した状態で102+57, 102×57を計算しなさい。
(iii) 計算結果を10進数に直し、正しいかどうかを確認しなさい。
9.練習問題の解答
(1) 解答1
250 → (1111 1010)b 334 → (1 0100 1110)b
(2) 解答2
(i) \[2^4 + 2^3 + 2^0 = 16 + 8 + 1 = 25 \](ii) \[2^6 + 2^4 + 2^2 + 2^1 = 64 + 16 + 4 + 2 = 86\]
(3) 解答3
ア、イ、ウ、エそれぞれの選択肢を2進数に直す。
ア:120 → 0111 1000
イ:127 → 0111 1111
ウ:170 → 1010 1010
エ:240 → 1111 0000
より、ウ、エが0と1のビット数が等しい。
よって答えはより大きい数であるエとなる。
(4) 解答4
まずは、1/32を2進数に直す。\[ \frac{1}{32} = 2^{-5}\]なので、2進数に直すと、0.00001となる。
2進数から16進数に直すためには図のように4桁区切りをすればいい。
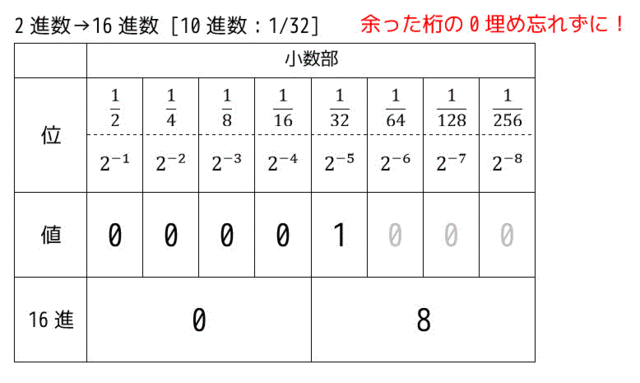
すると、0. 0000 1000 (2区切り目は余った桁を0で埋める)となり、小数の区切りは 0000 と 1000 となる。1000は、\( 2^3 \) の桁だけが1なので、答えは0.08となりエが答え。
(5) 解答5
このような計算は10進数と2進数にわけて計算をする。
まずは整数部の11を2進数に直す。
11 → 1011
次に0.2の小数部を2進数に直し、第4位まで求める。
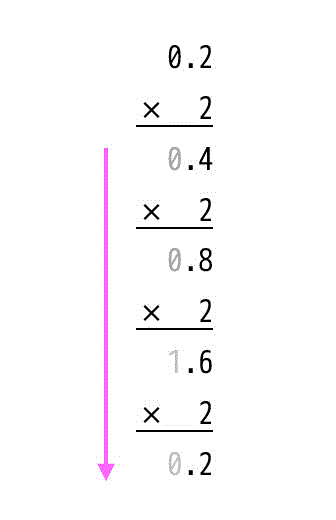
よって小数部は0.0010となる。
よって、整数部+小数部=1011.0010bが答え。
また、答えの2進数を10進数に戻すと、\[2^3+2^1+2^0+2^{-3} = 11 + \frac{1}{8} = 11.125\]となる。これを11.2から引くと誤差は0.075と求まる。
(6) 解答6
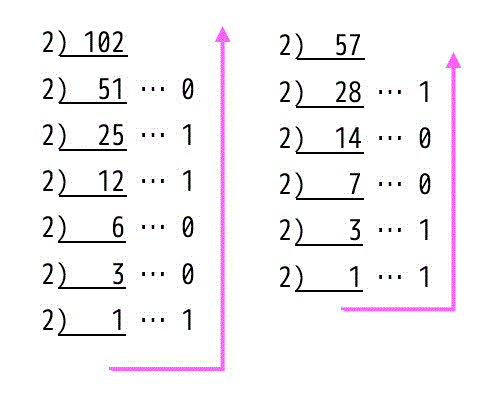
(i)
102:1100110b 57:111001b
(ii)
足し算の結果:1001 1111b
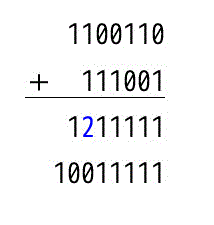
掛け算の結果:1 0110 1011 0110

(iii)
(1001 1111)b = 159, (1 0110 1011 0110)b = 5814 となる。
また、102+57 = 159, 102×57 = 5814 より確かに計算結果は正しいこともわかる。
10.さいごに
今回は、計算機上における数値の表現方法である2進数について、2進数と10進数の変換方法、2進数同士の演算、2進数をより見やすくするための表記法である8進数、16進数、さらには計算機上で表現できる数を表すビット、バイトなどの単位などについてまとめました。
2進数は計算機のシステムを理解する上での基礎中の基礎なので必ず理解を深めてください!
次回は2の補数(2進数で負の数を表現する方法)を紹介します。
Part02:負の数と2の補数編はこちら↓
関連広告・スポンサードリンク