うさぎでもわかる計算機システム　Part04　桁落ち・情報落ち・丸め誤差・打ち切り誤差について [基本情報対応]

2019年6月21日 2021年7月2日 38分54秒

ももうさ

スポンサードリンク

こんにちは、ももやまです。
今回は2進数の小数点表記で発生する誤差である桁落ち・情報落ち・丸め誤差の3つについてのまとめました。

２進数の小数点表記についての記事はこちらにまとめているため、まだ小数点表記についてよくわかっていない人はこちらの記事をご覧ください。

www.momoyama-usagi.com

実際に誤差が発生する例をプログラムを書きながら紹介しているため、かなり長い記事となっています。

桁落ち、情報落ち、丸め誤差がどのようなときに起こるかだけを知りたい人や演習をしたい人は目次から「４．まとめ」、「５．練習問題」を選んでください。

スポンサードリンク

１．桁落ち

(1) 概要

まずは、桁落ちです。
桁落ちは、ほぼ等しい2つの数の引き算をすることで、有効数字が減る現象を表します。

まずはわかりやすく10進数で考えてみましょう。ほぼ等しい2つの数として、\( 8.31 \times 10^{3} \), \( 8.30 \times 10^{3} \) をもってきました。これを計算してみると、\[ 8.31 \times 10^{3} - 8.30 \times 10^{3} = 0.01 \times 10^{3} \]となってしまい、有効数字が1桁になってしまいました。

\( 0.01 \times 10^{3} \) を、 \( 1.00 \times 10^{1} \) に直す際に発生した1.00の00は無理やり埋めただけで有効数字といえる正確な値ではありませんよね。

2進数の浮動小数点表記においても、10進数の場合と同様に桁落ちが発生します。
2進数の有効数字は、浮動小数点の仮数部となります。

桁落ちは、仮数部（有効数字）がある浮動小数点でのみ発生するため、有効数字の概念がない固定小数点表記では発生しません。

(2) 具体例1　２次方程式の解の算出

桁落ちが発生する有名な例に「二次方程式」があるので紹介します。2次方程式\[ ax^{2} + bx + c = 0\]の2つの解は、解の公式で\[x = \frac{-b \pm \sqrt{b^{2} -4 ac}}{2a} \]となるので早速プログラムして求めてみます。

今回は2つの解 \( x \) のうち、小さい解を \( x_{1} \), 大きい解を \( x_{2} \) とし、\[x^{2} + 1000.001x + 1 = 0\]の解をもとめます。

2つの解は、理論的には\[x^{2} + 1000.001x + 1 = (x + 1000)(x + 0.001) = 0\]となり、\( x_{1} = -1000 \), \( x_{2} = -0.001 \) となります。

実際に理論値通りになるのかをプログラム（C言語）で調べてみたいと思います。

プログラム

#include<stdio.h>
#include<math.h>


int main() {
    double a = 1, b = 1000.001, c = 1; // ax^2 + bx + c = 0 の入る (ここを書き換え)
    double d = pow(b,2) - 4.0 * a * c; // sqrt(b^2 - 4ac) の部分
    double ans_small = ^[1]-1.0 * b) - sqrt(d / (2.0 * a); // 小さい解
    double ans_big = ^[2]-1.0 * b) + sqrt(d / (2.0 * a); // 大きい解

    printf("☆解の公式で求めた解☆\n");
    printf("1つ目 … %27.20f\n",ans_small);
    printf("2つ目 … %27.20f\n\n",ans_big);

    return 0;
}

実行結果

☆解の公式で求めた解☆
1つ目 …  -1000.00000000000000000000
2つ目 …     -0.00099999999997635314

大きい解(理論値：-0.001)を求めるときに誤差が発生していますね。
ここで公式の分子を思い出してみましょう。\( b = 1000.001 \), \( c = 1 \) を代入し、 \[ -1000.001 \pm \sqrt{1000.001^{2} - 4} \] となります。さらに\[ \sqrt{1000.001^{2} - 4} \fallingdotseq 1000.001 \] ですね。よって、\[ -1000.001 + \sqrt{1000.001^{2} - 4}\] の計算時にほぼ同じ2つの値の減算を行っているため桁落ちが発生します*1。

\( b \) が負となるバージョンもやってみましょう。
\[x^{2} - 1000.001x + 1 = 0\]の解をもとめます。

2つの解は、理論的には\[x^{2} - 1000.001x + 1 = (x - 0.001)(x - 1000) = 0\]となり、\( x_{1} = 0.001 \), \( x_{2} = 1000 \) となります。

（ここを書き換え）の行の部分を double a = 1, b = -1000.001, c = 1; と書き換えると、以下の実行結果を得られます。

☆解の公式で求めた解☆
1つ目 …      0.00099999999997635314
2つ目 …   1000.00000000000000000000

小さい解(理論値：0.001)を求めるときに誤差が発生していますね。
また公式の分子を思い出してみましょう。\( b = -1000.001 \), \( c = 1 \) を代入し、 \[ 1000.001 \pm \sqrt{1000.001^{2} - 4} \] となります。さらに\[ \sqrt{1000.001^{2} - 4} \fallingdotseq 1000.001 \] ですね。よって、\[ 1000.001 - \sqrt{1000.001^{2} - 4}\] の計算時にほぼ同じ2つの値の減算を行っているため桁落ちが発生します*2。

これをまとめると、つぎのようになります。

2次方程式の解の公式適応時の桁落ち条件

2次方程式 \[ a x^{2} + b x + c =0 \]の解 \( x_{1} \), \( x_{2} \), \( (x_{1} \lt x_{2} ) \) を解の公式 \[x = \frac{-b \pm \sqrt{b^{2} -4 ac}}{2a} \] で求める場合

\( b \gt 0 \) のとき
\[ b \fallingdotseq \sqrt{b^{2} -4 ac} \] のとき、大きい解である \( x_{2} \) で誤差発生。

\( b \lt 0 \) のとき
\[ b \fallingdotseq - \sqrt{b^{2} -4 ac} \] のとき、小さい解である \( x_{1} \) で誤差発生。

桁落ちをなくすためには

二次方程式の解の計算の際に桁落ちの誤差をなくすためには、解と係数の関係を使って解を算出する方法が考えられます。

2次方程式の解と係数の関係

2次方程式 \[ a x^{2} + b x + c =0 \]の解 \( x_{1} \), \( x_{2} \), \( (x_{1} \lt x_{2} ) \) とすると、\[ x_{1} + x_{2} = - \frac{b}{a} \ \ \ x_{1} x_{2} = \frac{c}{a}\]が成立する。

和の解と係数の関係を用いると、再び桁落ちが起こる可能性があるため、積の解と係数の関係を用いて誤差の発生を防ぎます。

\( b > 0 \) のとき
桁落ちが発生する可能性があるのは、大きい解の \( x_{2} \) であるので、小さい解 \( x_{1} \) を解の公式で算出後、大きい解 \( x_{2} \) を次の式で求めます。\[x_{2} = \frac{c}{a x_{1}}\]

\( b \lt 0 \) のとき
桁落ちが発生する可能性があるのは、小さい解の \( x_{1} \) であるので、大きい解 \( x_{2} \) を解の公式で算出後、小さい解 \( x_{1} \) を次の式で求めます。\[x_{1} = \frac{c}{a x_{2}}\]

以上を改良して2つの解を求めるプログラムを下に記しました。

#include<stdio.h>
#include<math.h>


int main() {
    double a = 1, b = 1000.001, c = 1;  // ax^2 + bx + c = 0 の入る (ここを書き換え)
    double d    = pow(b,2) - 4.0 * a * c; // 判別式
    double ans_small = ^[3]-1.0 * b) - sqrt(d / (2.0 * a);
    double ans_big = ^[4]-1.0 * b) + sqrt(d / (2.0 * a);
    printf("☆解の公式で求めた解☆\n");
    printf("1つ目 … %27.20f\n",ans_small);
    printf("2つ目 … %27.20f\n\n",ans_big);
    double ans2;
    if(b >= 0) {
        ans2 = c / (a *ans_small);
        printf("☆解と係数の関係から求めた解☆\n");
        printf("1つ目 … %27.20f\n",ans_small);
        printf("2つ目 … %27.20f\n",ans2);
    }
    else {
        ans2 = c / (a *ans_big);
        printf("☆解と係数の関係から求めた解☆\n");
        printf("1つ目 … %27.20f\n",ans2);
        printf("2つ目 … %27.20f\n\n",ans_big);
    }

    return 0;
}

実行結果： \( b = 1000.001 \gt 0 \) の場合（他の変数はプログラム通り）

☆解の公式で求めた解☆
1つ目 …  -1000.00000000000000000000
2つ目 …     -0.00099999999997635314
☆解と係数の関係から求めた解☆
1つ目 …  -1000.00000000000000000000
2つ目 …     -0.00100000000000000000

実行結果： \( b = -1000.001 \lt 0 \) の場合（他の変数はプログラム通り）

☆解の公式で求めた解☆
1つ目 …      0.00099999999997635314
2つ目 …   1000.00000000000000000000
☆解と係数の関係から求めた解☆
1つ目 …      0.00100000000000000000
2つ目 …   1000.00000000000000000000

このように解と係数の関係で求めると正しく解を求めることができますね。

(2) 具体例2　数値微分

もう少し具体例を出してみましょう。
例えば、\( f(x) = \sin x \) の \( x = 1 \) における微分係数 \( f'(1) \) を計算機上で求めてみます。

\( x = x_{0} \) における微分係数微分の定義式は \[ \lim_{h \to 0} \frac{f(x_{0}+h) - f(x_{0})}{h} \] ですね。

プログラムをすることによって求めた微分係数と、解析的（実際に導関数を求め、 \( x = 1 \) を代入、今回の場合は \( f'(x) = \cos x \) に \( x = 1 \) を代入）に求めたプログラムの誤差を調べます。

ただしプログラムの場合、解析的に \( h \to 0 \) を考えるのは難しいため、\( h \) を有限の範囲内で限りなく小さくして考えます*3。

プログラム

#include<stdio.h>
#include<math.h>

int main() {
    float x = 1;
    float d1;
    double d0 = cos(x); // cos(1) の理論値
    float y0 = sin(x),h,y1;
    for(int i = 0; i <= 20; i += 1) {
        h = pow(2,-1 * i); //2^-i
        y1 = sin(x + h);
        d1 = (y1 - y0) / h; // sin(1) を微分した結果の値
        printf("h = 2^(-%2d) -> %2.8f\n",i,fabs(d1 - d0));
    }
}

実行結果

h = 2^(- 0) -> 0.47247586
h = 2^(- 1) -> 0.22825423
h = 2^(- 2) -> 0.11024764
h = 2^(- 3) -> 0.05392936
h = 2^(- 4) -> 0.02663901
h = 2^(- 5) -> 0.01323321
h = 2^(- 6) -> 0.00659564
h = 2^(- 7) -> 0.00329211
h = 2^(- 8) -> 0.00163653
h = 2^(- 9) -> 0.00081256
h = 2^(-10) -> 0.00038531
h = 2^(-11) -> 0.00014117
h = 2^(-12) -> 0.00001910
h = 2^(-13) -> 0.00022504
h = 2^(-14) -> 0.00071332
h = 2^(-15) -> 0.00071332
h = 2^(-16) -> 0.00266644
h = 2^(-17) -> 0.00657269
h = 2^(-18) -> 0.00657269
h = 2^(-19) -> 0.02219769
h = 2^(-20) -> 0.02219769

hが大きくなれば誤差が小さくなると皆さん思いますよね。

確かに、hが小さいうちは、h を小さくすればするほど誤差は小さくなっていますね。しかし、\( h \gt 12 \) からはhが小さくなればなるほどなぜか誤差が逆に大きくなっています。なぜでしょうか？

このプログラムの誤差の原因は2つ考えられます。

(1) 打ち切り誤差

打ち切り誤差とは、本来無限に続く計算を有限回で止めてしまうことで発生する誤差です。
打ち切り誤差についての詳しい説明は、下のほうで説明してあります。

本来は0に限りなく近いhの値*4をhの値を有限のh値で打ち切る*5ことにより発生するものです。

最初のうちは、hの値を 1/2 にするたびに誤差が約 1/2 になっていますね。hをより0に近づければ近づけるほど、「0に限りなく近づけた値」に近づき、打ち切り誤差は減少します。

(2) 桁落ち

しかし、hが12を超えたあたりから逆に誤差は大きくなりましたね。

ここで桁落ちの条件を思い出してみましょう。

ほぼ等しい2つの数の引き算をすることで桁落ちは発生しますね。

\( h \) を小さくすればするほど \( f(x_{0}+h) \), \( f(x_{0}) \) の差は小さくなっていきますね。

小さくなった状態で \( f(x_{0}+h) - f(x_{0}) \) を計算すると、ほぼ等しい2つの数の減算を行うことで計算結果の有効数字が減少し、誤差の原因となります。

以上2つが、数値微分における誤差の原因となります。
数値微分をする場合、結果との誤差が小さくなり続けてる中で最も小さい \( h \) の値を採用するのが数値微分における誤差を小さくするコツといえます。
今回の場合だと \( h = 12 \) のときとなります。

また、実際に数値微分をする際には、\( \sin x \) のような解析的な微分結果が自明なものではなく、複雑な関数で解析的に微分ができないようなものに行います。

そのような場合には、\[\lim_{h \to 0} \frac{f(x+2h) - f(x)}{2h} \] など、\( h \) の値を変えて計算を行い、上で行った\[ \lim_{h \to 0} \frac{f(x+h) - f(x)}{h} \] との差を比べ、差が小さくなり続けてる中で最も小さい \( h \) の値を採用するのがただしい数値微分の結果を得るコツとも言えます。

スポンサードリンク

２．情報落ち

(1) 概要

情報落ちは、差が極端にある大きい数と小さい数の加算/減算のときに小さい数の計算が反映されない現象を表します。

10進数の場合で例を出してみましょう。\[ 3.0453 \times 10^{15} + 8.1019 \times 10^{-3} \]このような計算をするとき、皆さんは大きい方の指数部にそろえて計算しますよね。しかし、揃えようとすると、\[ 3.0453 \times 10^{15} + 0.0000 \times 10^{15} \]となってしまい、\( 8.1019 \times 10^{-3} \) の有効数字がなくなってしまい、消えてしまいますね。

計算機上でも差が極端にあるもの同士を計算すると、有効数字がなくなってしまい、小さい数が反映されなくなってしまうのです。

(2) 実例1

では情報落ちが起こる例をご覧いただきましょう。
大きい数を1としたとき、どこまで小さい値にしたときに情報落ちが発生するかを単精度の場合と倍精度の場合の2つを比較してみましょう。

(1) 単精度

プログラム

#include<stdio.h>
#include<math.h>

// 単精度(float)の場合
int main(){
    float a = 1;
    float b,sum;
    for(int i = 0; i >= -10; i -= 1) {
        b = pow(10,i);
        sum = a + b;
        if(a == sum) {
            printf("b = 10^(%3d) Yes: %.10f\n",i,sum);
        }
        else {
            printf("b = 10^(%3d) No : %.10f\n",i,sum);
        }
    }
}

実行結果

b = 10^(  0) No : 2.0000000000
b = 10^( -1) No : 1.1000000238
b = 10^( -2) No : 1.0099999905
b = 10^( -3) No : 1.0010000467
b = 10^( -4) No : 1.0001000166
b = 10^( -5) No : 1.0000100136
b = 10^( -6) No : 1.0000009537
b = 10^( -7) No : 1.0000001192
b = 10^( -8) Yes: 1.0000000000
b = 10^( -9) Yes: 1.0000000000
b = 10^(-10) Yes: 1.0000000000

(2) 倍精度

プログラム（単精度で誤差が発生した i = -8からチェックしています）

#include<stdio.h>
#include<math.h>
// 倍精度の場合
int main(){
double a = 1;
double b,sum;
for(int i = -8; i >= -20; i -= 1) {
b = pow(10,i);
sum = a + b;
if(a == sum) {
printf("b = 10^(%3d) Yes: %.20f\n",i,sum);
}
else {
printf("b = 10^(%3d) No : %.20f\n",i,sum);
}
}
}

実行結果

b = 10^( -8) No : 1.00000000999999990000
b = 10^( -9) No : 1.00000000100000010000
b = 10^(-10) No : 1.00000000010000000000
b = 10^(-11) No : 1.00000000001000000000
b = 10^(-12) No : 1.00000000000100010000
b = 10^(-13) No : 1.00000000000009990000
b = 10^(-14) No : 1.00000000000001000000
b = 10^(-15) No : 1.00000000000000110000
b = 10^(-16) Yes: 1.00000000000000000000
b = 10^(-17) Yes: 1.00000000000000000000
b = 10^(-18) Yes: 1.00000000000000000000
b = 10^(-19) Yes: 1.00000000000000000000
b = 10^(-20) Yes: 1.00000000000000000000

(3) 実例2

情報落ちは、差が大きい2つの数（大きい数と小さい数）の足し算や引き算で発生します。

ということで、今度はより実践的な例で情報落ちが発生する例と情報落ちが防ぐ方法を紹介していきたいとおもいます。

例えば、等比級数\[ \sum_{k=1}^{n} \frac{1}{3^{k}} = \frac{1}{3} + \frac{1}{9} + \cdots + \frac{1}{3^{n}} \]の値を求めてみます。

理論値 \( n = \infty \) の場合、 \[ \sum_{k=1}^{\infty} \frac{1}{3^{k}} = \frac{\frac{1}{3}}{1 - \frac{1}{3}} = \frac{1}{2}
\]となります。

今回は \( n = 20 \) までとして、昇順 \( n = 1,2,3 \) と加算した場合と、降順 \( n = 20,19,18 \) と加算した場合とで値がどう変わるかを比較します。

\( n = 20 \) までしか計算を行わないため、打ち切り誤差が昇順の場合と降順の場合で発生しますが、両者とも誤差の量は同じ*6になるはずなので今回は考えないことにします。

プログラム

#include<stdio.h>
#include<math.h>

// 倍精度の場合
int main(){
    double a = 1;
    double b,sum;
    for(int i = -8; i >= -20; i -= 1) {
        b = pow(10,i);
        sum = a + b;
        if(a == sum) {
            printf("b = 10^(%3d) Yes: %.20f\n",i,sum);
        }
        else {
            printf("b = 10^(%3d) No : %.20f\n",i,sum);
        }
    }
}

実行結果

ascend : 0.49999997019767761230
descend: 0.50000000000000000000

このように、降順から足していく場合よりも昇順から足していく方法のほうが誤差が大きくなっていますね。

昇順（大きい値）から足す場合は、\[\frac{1}{3} + \frac{1}{9} + \frac{1}{27} + \cdots\]と計算していくため、足していくにつれて、和に対して加算する \( 1/3^{n} \) があまりにも小さくなるため、情報落ちが発生してしまいます。

一方降順（小さい値）から足した場合は、小さい数から大きい数と計算していくため、足していった和と加算する \( 1/3^{n} \) の差が大きくないため、情報落ちは発生しません*7。

なので、浮動小数点を用いて和の計算をする際には、大きい数から順番に足すのではなく、小さい数から順番に足していくと情報落ちを防ぐことができます。

スポンサードリンク

３．丸め誤差

(1) 概要

丸め誤差は、途中の桁で四捨五入や切り捨て、切り上げを行うことで発生する誤差です。
以下四捨五入、切り捨て、切り上げをすることを丸めると表記します。

まずは10進数の場合を考えてみましょう。
たとえば、変数aの値が810.364364 という結果だとします。これを小数第3位で四捨五入して \( a = 810.36 \) と計算するとします。

例えば、\( 100a \) の値を小数第2位まで求めるとします。このとき丸めずに計算した場合は、81036.44 と求めることができます。しかし、途中で四捨五入した \( a = 810.36 \) で計算すると、81036.00 となってしまい、0.44の誤差が発生してしまいます。

このように、途中で四捨五入などにより丸めたものを他の計算の用いると、その誤差が次第に大きくなってしまいます。
計算を複数回行うことで、さらにその誤差が大きくなってしまいます。

計算機の場合、0.4や0.7などの小数を2進数に直すと有限小数ではなく、無限小数になってしまいますね。そのため、小数を2進数にする際に一定桁数で丸められてしまいます。これが丸め誤差の原因です。

丸められた状態の小数で様々な計算を行うことにより、誤差がさらに大きくなってしまい、無視できない誤差になってしまいます。

(2) 具体例

小数0.1を100回足したものをsum1（理論値：10）、0.5を100回足したものをsum5（理論値：50）とし、それぞれの合計を表示させてみます。

プログラム

#include<stdio.h>
#include<math.h>

#define N 20

int main() {
    float sum_asc = 0; // floatは単精度
    float sum_des = 0; 
    for(int i = 1; i <= N; i += 1) {
        sum_asc += 1.0 / pow(3,i);     // 3^(-1) + 3^(-2) + 3^(-3) ...
        sum_des += 1.0 / pow(3,N-i+1); // 3^(-20) + 3^(-19) + 3^(-18) ...
    }
    printf("ascend : %.20f\n",sum_asc); // 大きい値から加算
    printf("descend: %.20f\n",sum_des); // 小さい値から加算
}

実行結果

sum0.1:  9.99999999999998050000
sum0.5: 50.00000000000000000000

0.1を加算したほうは10より少し小さい値になっていますね。一方0.5のほうは理論値通りの50ですね。

ここで、0.1を2進数に直して見ましょう。すると 0.0001 1001 1001 1001… と無限小数になりますね。
なので、とある桁で丸められ（切り捨てられ）、誤差が発生してしまいます。

同じように0.5も2進数になおしてみましょう。すると、0.1b と有限小数になります。
なので、桁が丸められることなく、理論値である50が計算できます。

(3) 打ち切り誤差との違い

打ち切り誤差と丸め誤差は混合する人が多いので打ち切り誤差についても説明をします。

上にも出てきましたが、打ち切り誤差は、本来無限に続く計算（例：無限等比級数の計算、極限の計算）を有限回で止めたことで発生する誤差です。

例えば、\[ \sum_{k=1}^{\infty} \frac{1}{3^{k}} = \frac{1}{2} \]は、無限回計算した場合に得られる答えですが、計算機上では無限回足せないため、\[ \sum_{k=1}^{100} \frac{1}{3^{k}} \]のような有限回の加算となってしまい、誤差が発生してしまいます。

また、\[\lim_{h \to 2} \frac{2x^{2} - 3x - 2}{3x^{2} - 2x - 8} \] のような極限を考えるときでも、 \( h \) を2に近づける操作を有限の値で打ち切ってしまう*8必要があるため、打ち切り誤差が発生してしまいます。

ただし、打ち切り誤差は、足す回数 \( n \) （極限の場合はよりその値に近づける）などを増やせば増やすほどより無限回の場合（理論値）に近づくので、打ち切り誤差をへらすことができます。

４．2進数の小数表記の際の誤差まとめ

今までかなり長い説明をしましたが、今まで紹介した誤差を簡単にまとめたいと思います。

桁落ち（浮動小数点のみ）

ほぼ等しい2つの数の減算で発生する誤差。
（例1：20190621.364364 - 20190621.364363）
（例2：- 1000.001 + 1000.000）

情報落ち（浮動小数点のみ）

差が極端にある大きい数と小さい数の加減算時に小さい数の計算が反映されない誤差。
（例：1919894334 - 0.000003）

丸め誤差（固定・浮動小数点両方）

丸め誤差は、途中の桁で四捨五入や切り捨て、切り上げを行うことで発生する誤差。
2進数の場合は、0.2など、2進数に直すと無限に続く小数などを一定のビット数で切り捨て（四捨五入など）る際に生じる。

打切り誤差（固定・浮動小数点両方）

無限に続く計算（無限級数）などを途中で計算を止めた際に発生する誤差。
無限等比級数の計算や、極限計算で発生する。

５．練習問題

では実際に何問か練習してみましょう。

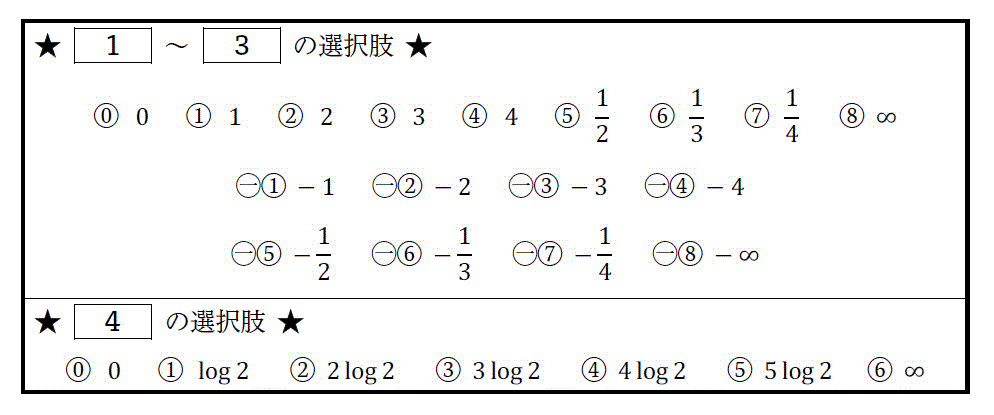
練習1

けた落ちの説明として、適切なものはどれか。
[基本情報技術者平成22年秋期　午前問2]

ア：値がほぼ等しい浮動小数点同士の減算において，有効けた数が大幅に減ってしまうことである。
イ：演算結果が，扱える数値の最大値を超えることによって生じる誤差のことである。
ウ：数表現のけた数に限度があるとき，最小のけたより小さい部分について四捨五入，切上げ又は切捨てを行うことによって生じる誤差のことである。
エ：浮動小数点の加算において，一方の数値の下位のけたが結果に反映されないことである。

練習2

数多くの数値の加算を行う場合、絶対値の小さなものから順番に計算するとよい。これは、どの誤差を抑制する方法を述べたものか。
[基本情報技術者平成17年春期　午前問4]

ア：アンダフロー
イ：打切り誤差
ウ：けた落ち
エ：情報落ち

練習3

浮動小数点形式で表現された数値の演算結果における丸め誤差の説明はどれか。
[基本情報技術者平成19年秋期　午前問4]

ア：演算結果がコンピュータの扱える最大値を超えることによって生じる誤差である。
イ：数表現のけた数に限度があるので，最下位けたより小さい部分について四捨五入や切上げ，切捨てを行うことによって生じる誤差である。
ウ：乗除算において，指数部が小さい方の数値の仮数部の下位部分が失われることによって生じる誤差である。
エ：絶対値がほぼ等しい数値の加減算において，上位の有効数字が失われることによって生じる誤差である。

練習4

浮動小数点数の加減算を実行したとき、けた落ちが発生する演算はどれか。ここで、有効けたは、仮数部3けたに対して，演算は6けたで行われるものとする。
[第2情報処理技術者試験　平成12年度秋期（旧）]

ア：\( 0.123 \times 10^{2} + 0.124 \times 10^{-2} \)
イ：\( 0.234 \times 10^{5} - 0.221 \times 10^{2} \)
ウ：\( 0.556 \times 10^{6} +0.552 \times 10^{4} \)
エ：\( 0.556 \times 10^{7} - 0.552 \times 10^{7} \)