スポンサードリンク
こんにちは、ももやまです。
今回は組み合わせ回路、順序回路について代表的なパーツを紹介しながらまとめていきたいと思います。
目次
スポンサードリンク
1.組み合わせ回路
組み合わせ回路は、出力が現在の入力だけによって決まる回路です。
言い換えると現在の入力以外(過去のの入力など)には出力は左右されません。
では、いくつか組み合わせ回路の例を紹介しましょう。
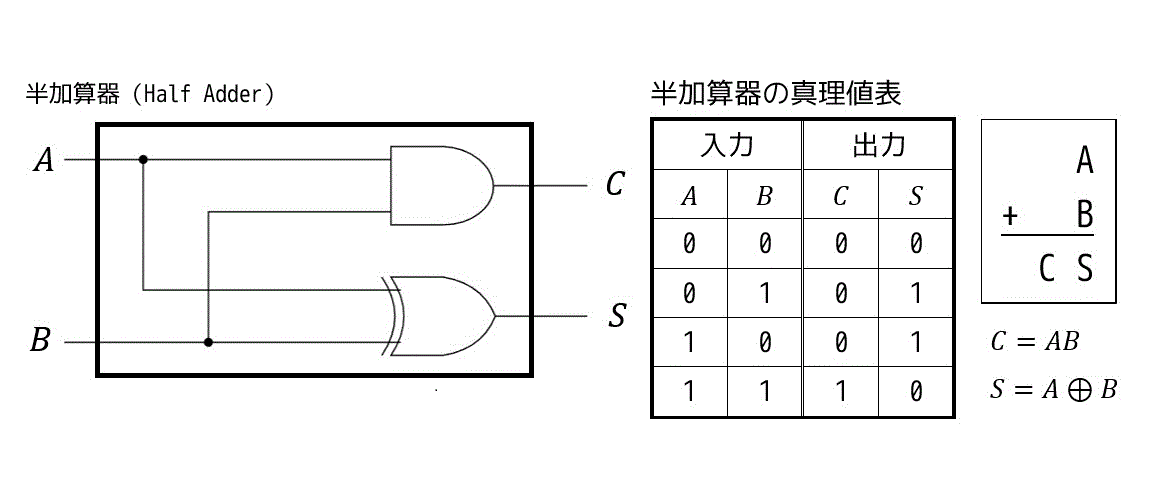
(1) 半加算器 (Half Adder)
半加算器は2つの入力 \( A,B \) の加算をするものを表します。
半加算器を使うことで、2進数を用いた加算(2の補数を使うことで減算も可能)を表現することができます。
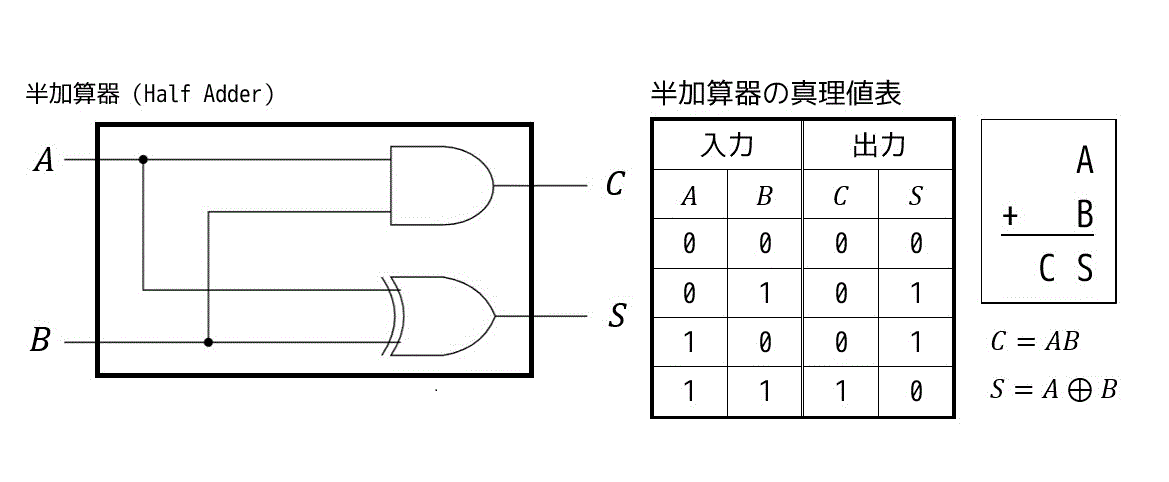
出力は加算結果 \( S \) (Sumの略)と繰り上がり \( C \) の2つで表現されます。
加算結果 \( S \) だけだと、1+1をした際にオーバーフローしてしまい正しい加算結果が得られないため、繰り上がりを出力する \( C \) を使います。
出力を \( CS \) の順に2進数でみると、\( A + B \) の結果になっているのがわかりますね。
(2) 全加算器 (Full Adder)
しかし、実際の加減算では、複数桁の計算をすることがほとんどです。
複数桁の計算をする場合には、下位の桁からの桁上がり*1を考える必要がありますね。
下位からの桁上がりにも対応したものがこの全加算器となります。
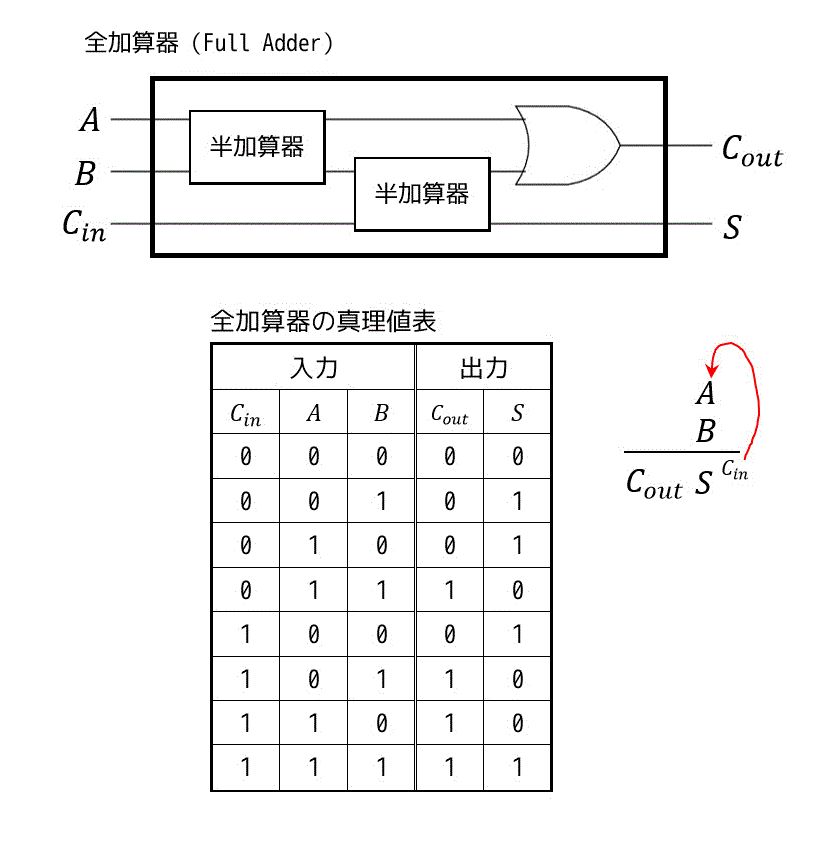
半加算器でもあった入力 \( A,B \) に加え、下位からの桁上がりを考慮する \( C_{in} \) もありますね。
\( C_{in} \) が0のときは桁上がりがない状態、1のときは桁上がりがある状態を表します。
桁上がりがあるときは、10進数のときと同様に計算結果に1を足してあげなければなりません*2。
なので、出力を \( C_{out} S \) の順に2進数でみると、\( A + B + C_{in} \) の結果になっているのがわかりますね。
(3) エンコーダ
我々が日常的に使用しているデータ(例:10進数)などを計算機はそのまま理解をしてくれるとは限りません。
そのままだと理解できないようなデータの場合、計算機上で理解できるようなもの(例:2進数)に変換する必要があります。これをエンコード(符号化)といいます。
また、エンコードを行う装置をエンコーダと呼びます。
下の図は、4つの入力を2つの出力の組(2進数)として表したものとなります。
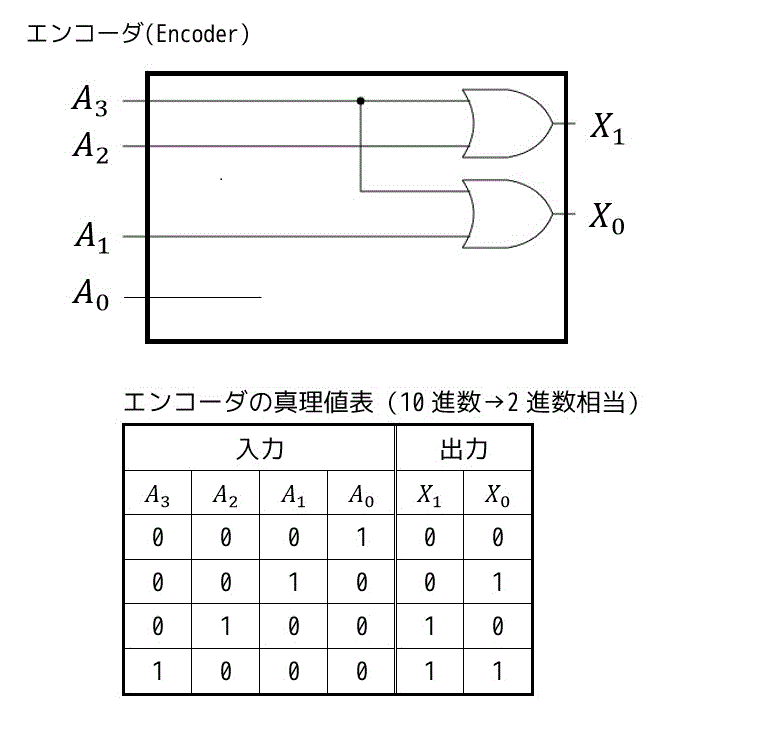
このように、エンコーダは各入力信号を一定の規則に従って複数の信号の組として出力することで機械で理解できるような信号の形(2進数など)に変換してあげることができます。
(4) デコーダ
エンコーダを使って符号化して処理したデータはそのままの状態では人間が理解することができません。なので、人間ができる形に戻してあげる必要があります。
符号化されたデータを人間が理解できるような形に戻すことをデコード(復号)と言います。
また、デコードを行う装置をデコーダと呼びます。
下の図は、2つの入力の組み合わせを独立した4つの出力にした回路となります。
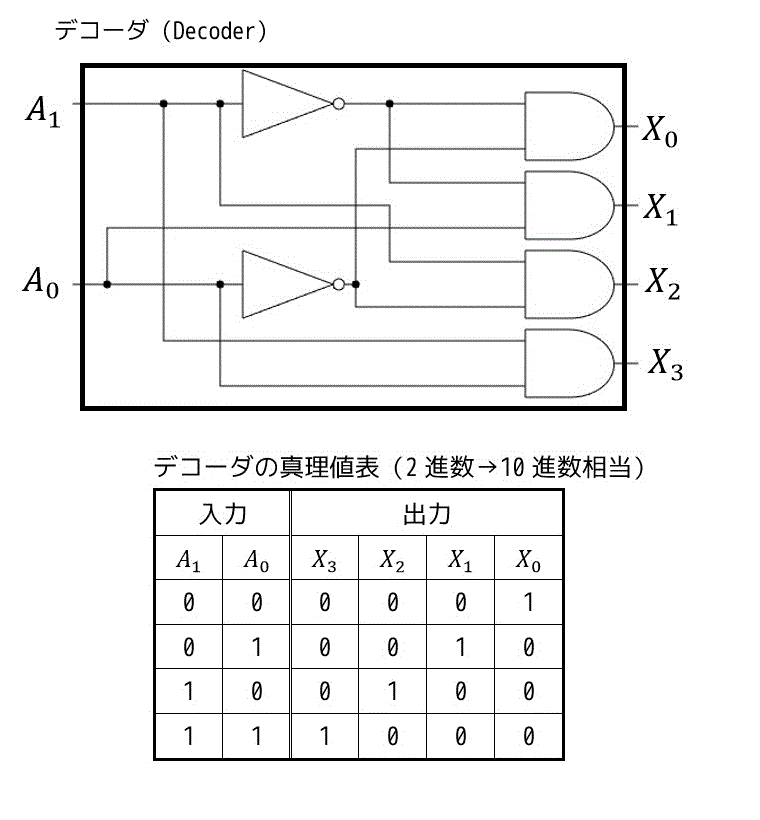
このようにデコーダは、複数の入力の組み合わせをそれぞれの出力にすることで人間ができるような出力の形に変換することができます。
(5) マルチプレクサ
マルチプレクサは、2つ(もしくはそれ以上)の入力を選択信号を使って1つだけ選び、選ばれた入力を出力する回路となります。
下の回路の場合、入力 \( A_1 \),\( A_0 \) の2つから選択信号 \( S \) で選ばれた方を出力する回路となります。
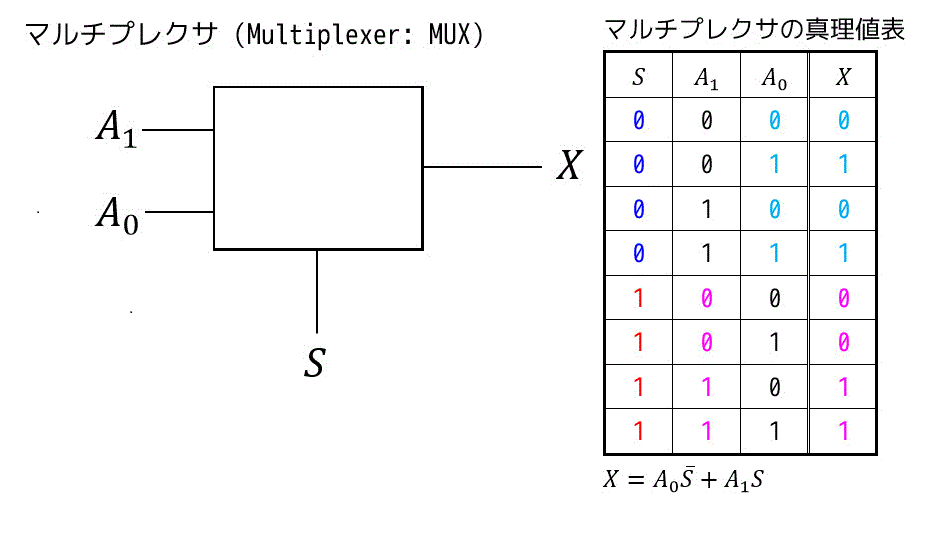
\( S \) が0のときは、\( A_0 \) の入力がそのまま、\( S \) が1のときは \( A_1 \) の入力がそのまま出力されていることがわかりますね。
マルチプレクサの中の回路をAND, OR, NOTの3つで表現すると、下の図で表現することができます。
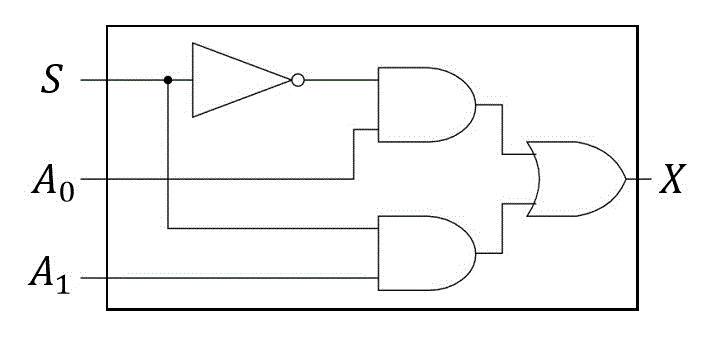
(6) デマルチプレクサ
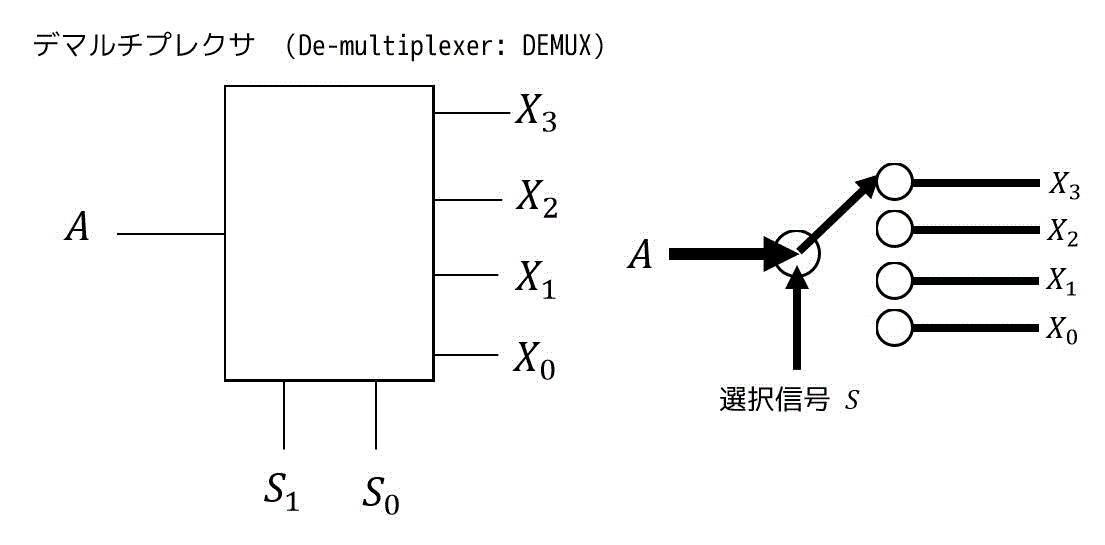
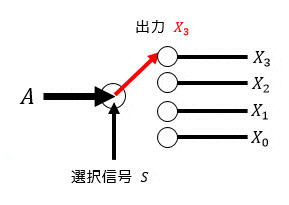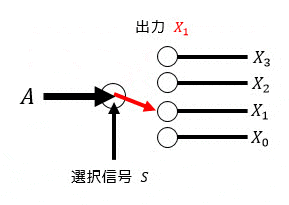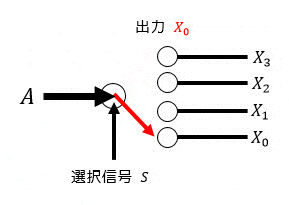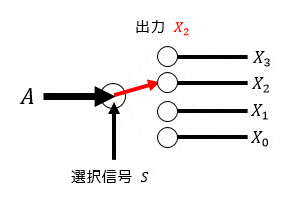
デマルチプレクサは、1つの入力を選択信号を使うことで選択信号で示された出力へ出力する回路です。
下の回路の場合、1つの入力 \( A \) を2つの選択信号 \( S_0 \), \( S_1 \) で選ばれた出力 \( X_0 \), \( X_1 \), \( X_2 \), \( X_3 \) へ出力する回路となります。
右下の図は、デマルチプレクサのイメージとなります。
矢印を切り替えることによって出力箇所を変えると思ってください。
デマルチプレクサの出力の切り替えのイメージをアニメーションでも表現してみました。
真理値表で示すと以下の通りとなります。
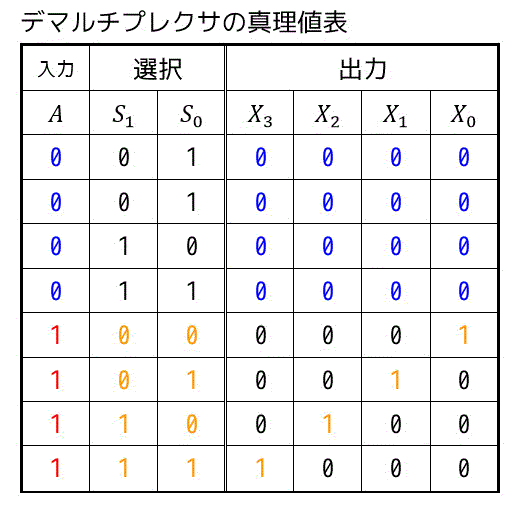
入力 \( A \) が0のときはどこが選択されようが出力されないので全部の出力が0になっていますね。
入力 \( A \) が1のときは選択信号 \( S_1 \), \( S_0 \) によって出力される変数が変わっていることがわかりますね。
スポンサードリンク
2.順序回路
今まで考えてきた組み合わせ回路は、現在の入力だけで出力が決まる論理回路でしたね。
順序回路は、現在の入力だけではなく、過去の入力を出力に反映させることができる回路です。
言い換えると、過去の入力を記憶させることができる回路です。
では、順序回路の例を簡単にですが紹介していきましょう。
(1) フリップフロップ
フリップフロップは1bitの情報を記憶することができる回路です。
主にD, T, RS, JKの4つのフリップフロップがあります。
フリップフロップについては、こちらの記事に詳しく書いたのでこちらの記事をご覧ください。
(2) レジスタ
レジスタは、複数のフリップフロップを使い、データを一時的に記憶させ、演算など必要なときに高速で読み出せる装置です。
(3) メモリ(SRAM)
メモリ(SRAM)はフリップフロップの順序回路を用いて情報を記録しています。
似たようなメモリにDRAMがありますが、DRAMはフリップフロップではなく、コンデンサの電荷で情報を記録しています。
SRAMはDRAMに比べて、リフレッシュ動作*3が不要なので、低消費電力かつ高速に動作させることができるが、コストが高いのが欠点です。
☆余談☆
皆さんが昔遊んでいたファミコン、GBAのセーブデータの多くはSRAMに格納されています(カセットにバッテリーが入っています)。
低消費電力なのですが、それでも5~10年経ってしまうとセーブデータが消滅してしまいます。このように、電力供給を続けないとデータが吹っ飛んでしまう性質のことを揮発性といいます。
もちろん最近のゲーム機*4は不揮発性(電力供給がなくてもデータが吹っ飛ばない)のフラッシュメモリやサーバー管理などがされているため、セーブデータの寿命をする心配はありません。
(4) カウンタ
カウンタは、複数のフリップフロップを使って値を数える回路です。
値を数えるためには、前の状態を覚えてないと数えることはできませんね*5。なので、組み合わせ回路では表現できません。
スポンサードリンク
3.練習問題
では、少しだけですが、練習してみましょう!
練習1
組み合わせ回路ではないパーツを1つ選びなさい。
- 全加算器
- デマルチプロセッサ
- フリップフロップ
- デコーダ
練習2
マルチプロセッサの説明として正しいものを1つ選びなさい。
- 2つ以上の入力の1つを選択し、出力するパーツ
- 1ビットの情報を記録するパーツ
- 1つの信号を複数の信号の組として出力するパーツ
- 2つの入力 \( A,B \) の加算をするパーツ
練習3
図は全加算器を表す論理回路である。

図中の \( x \) に 1、\( y \) に 0、\( z \) に 1 を入力したとき、出力となる \( c \)(けた上げ数)、\( s \)(和)の値はどれか。
| \( c \) | \( s \) | |
| ア | 0 | 0 |
| イ | 0 | 1 |
| ウ | 1 | 0 |
| エ | 1 | 1 |
4.練習問題の答え
練習1
解答:3
フリップフロップは情報を記録するパーツなので組み合わせ回路ではなく、順序回路である。
練習2
解答:1
その他の選択肢
- 正解(マルチプレクサ)
- フリップフロップのこと
- エンコーダのこと
- 半加算器のこと
練習3
解答:ウ
全加算器は、3つの入力(\( x \), \( y \) 桁上り \( z \))の和を2進数(キャリー \( c \) と1ビットの計算結果 \( s \) )で出力するパーツである。
回路には、どれが桁上がりを検知するビットかは書かれていないが、どのビットが桁上りを検知するビットであろうが和は変わらないので、問題なく計算を行うことができる。
今回は1+0+1なので、桁上りが発生し、キャリー \( c \) は1、1ビットの計算結果は0(オーバーフローする)となるので答えはウとなる。
5.さいごに
今回は論理回路分野の基礎として、組み合わせ回路、順序回路について代表的なパーツを紹介しながらまとめていきました。
まずは大雑把でいいので組み合わせ回路、順序回路にはどんなものがあるのか(そしてどんな特徴があるのか)を理解すればOKです。
具体的なことは詳しく中身を勉強するとき(論理回路などを学ぶとき)に理解しなおせば大丈夫です。
*1:わかりやすく10進数で説明します。10の位の部分だけを加算する回路があるとします。この回路で45+99を計算するためには、4+9を計算するだけでなく、1つ下の位(今回は1の位)が桁上がりしているかを考慮する必要がありますね。半加算器では1の位が桁上がりしているかの確認をすることができません。
*2:先ほど例に出した10進数で例えると、45+99の10の位の計算結果では、4+9だけでなく、桁上がりを考慮した4+9+1をしてあげる必要がある。
*3:DRAMに蓄えられたコンデンサは一定時間が経過すると自然放電してしまい、データが消滅するので消滅しないように情報の読み出しと書き出しを繰り返している
*4:プレステ(メモリーカード)、DSのセーブデータ、PSP(メモリーカード)、Switchなど
*5:我々は普段1,2,3,4… と何気なく普段数えていますが、数えるためには一つ前の数字を覚えてないと数えられませんよね。例えば、28を数えるためには「前の数字は27だから次は28」というのが頭の中でわかっていないと数えられませんね。回路の場合でも同様です。
関連広告・スポンサードリンク






![うさぎでもわかる画像処理 Part02 トーンカーブと画像処理 [Python・MATLABコード付き]](https://www.momoyama-usagi.com/wp-content/uploads/ip1-18-150x150.jpg)