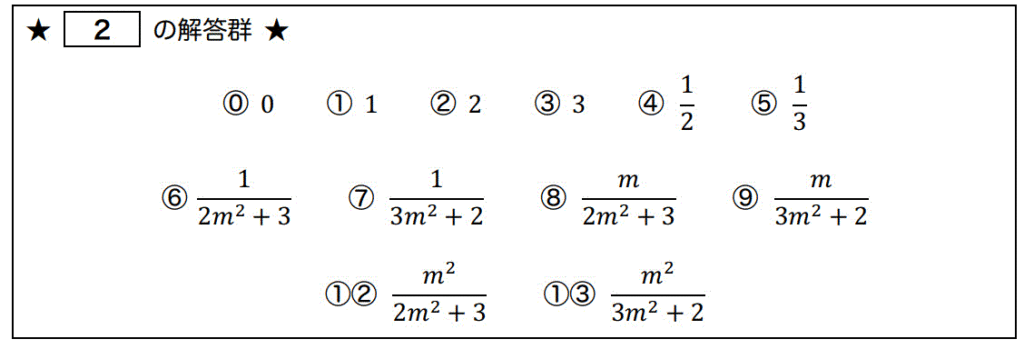
スポンサードリンク
こんにちは、ももやまです。
コンパイラ(言語処理系)の勉強をしていると、
- LL(1)文法
- First集合
- Follow集合
- Director集合
などの不思議な用語が出てきますよね。しかも、これらの定義(特にFirst集合やFollow集合)の定義は少し難解です。
文法
コンパイラ補助資料 佐々木晃 よりに関して、記号列 、非終端記号 について、 , および は次のように定義される。 ただし なら とする。
そこで今回は、
- LL(1)文法とはそもそも何か?
- First, Follow, Director集合を求めて何がうれしいのか
- First, Follow, Director集合の求め方
の3点を中心に、LL(1)文法とFirst・Follow・Director集合のお勉強をしていきましょう。
本記事では特に指示がない限り、文章中に出てくる小文字・大文字・ギリシャ文字は
- 小文字
- 大文字
を表します。
スポンサードリンク
1. LL(1)文法とは
ある文字列
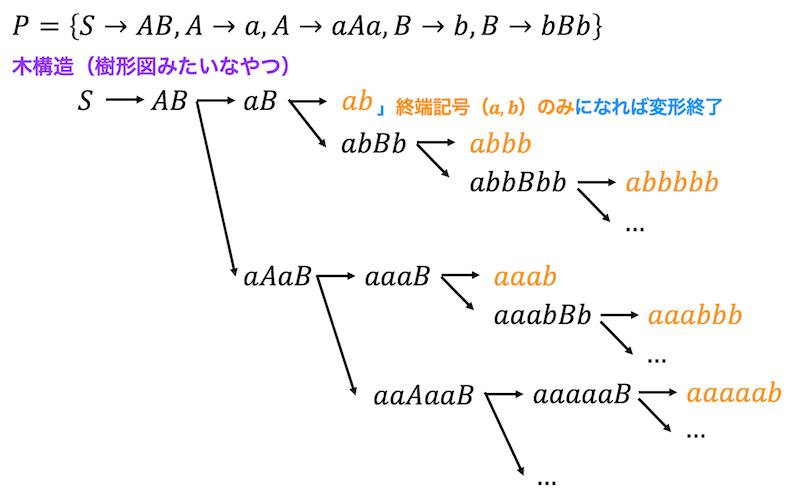
しかし、やみくもに総当たりで試す方法は、処理的にかなり無駄が発生してしまいます[1] … Continue reading。
そこで、構文解析をする際に1文字だけ先読みし、どの生成規則を使えばよいかを決めてから実際に変換していく方法が考えられました。
このように、1文字だけ先読みすれば、文字列を後戻りすることなく構文解析ができる(文法を満たすか確認できる)文法からなる文法のことをLL(1)文法と呼びます[2] … Continue reading。
LL(1)文法とは言えない文法(=1文字だけ先読みするだけでは文字列を後戻りせずに構文解析ができない)文法の例も見てみましょう。
例えば、非終端記号(かつ出発記号)
この文法規則に
しかし、1文字目
の2つがあるため、1文字先読みしただけでは
この例から分かる通り、LL(1)文法かどうかは文法の生成規則のみで決まります。
ここで、LL(1)文法を満たす生成規則であるかを機械的に確認する手法として導入されたのがFirst・Follow・Director集合という概念なのです!
つぎの第2章からは、
- 実際にFirst, Follow, Director集合の求め方の解説
- なぜ機械的にLL(1)文法を満たすのかがわかるのか
の2点について解説していきます。
スポンサードリンク
2. First集合
(1) First 集合とはなにか
First集合
数式で書くと、
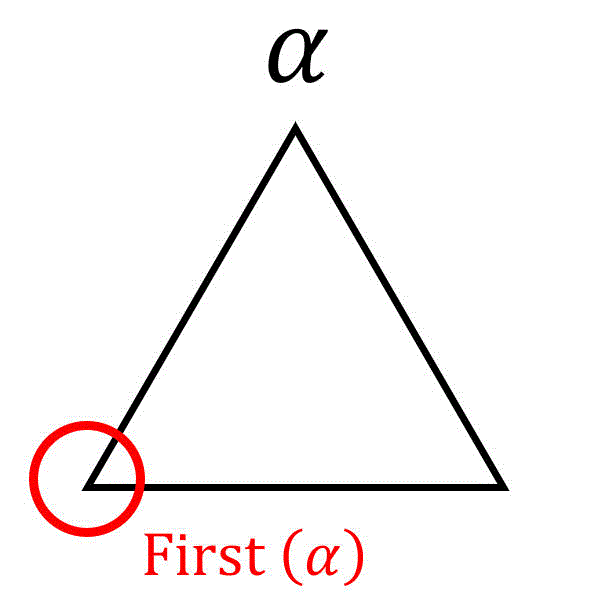
例えば、
(2) First 集合で頭にいれておくべき公式
※ 公式を丸暗記するのではなく、理屈を理解してから頭に入れましょう。
規則1[R1] First(a) … 終端記号1文字
終端記号
よって、終端記号1文字
※ 以後、この規則を用いた変換をする場合は
規則2[R2] First(A) … 非終端記号1文字の場合
非終端記号
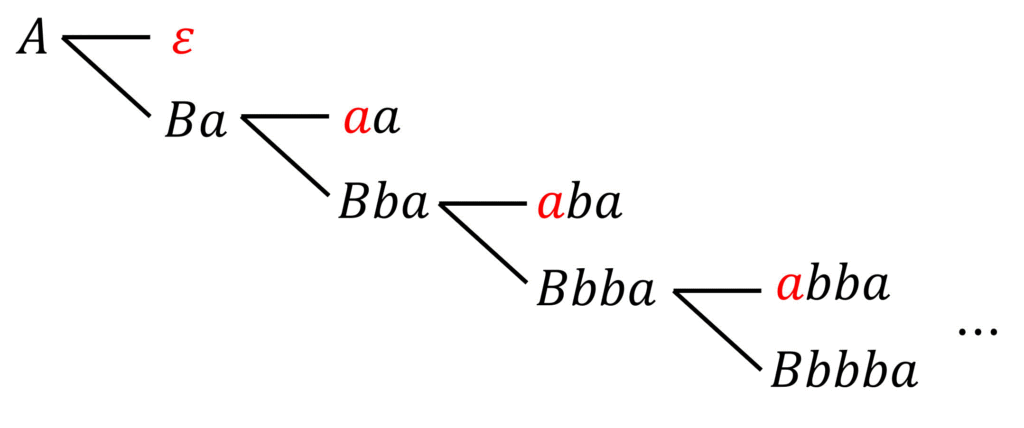
なのでもう少し機械的に
例えば、
言い換えると、「
つまり、
1つ例を見てみましょう。
この場合、
ここで1点注意が必要です非終端記号
※ 以後、この規則を用いた変換をする場合は
規則3[R3] First(αβ…) … 2文字以上の場合
First集合は、「文字列に生成規則を加えて全て終端記号にした際に、先頭に来る可能性がある終端記号」を表しているのでしたね。
そのため、(First集合を求めるだけであれば)最初の1文字さえわかってしまえば、(最初の1文字が空文字とはならない限り)残りの後ろは何が来ようが関係ありません。
よって、文字列
一方、
※
まとめると、2文字以上の文字列
※ 以後、この規則を用いた変換をする場合は
注意: 左再帰 A → Aα が含まれる場合のFirst集合
この形になった場合は、計算途中に出てくる
また、
しかし、左再帰になる規則の部分だけに着目してみると、
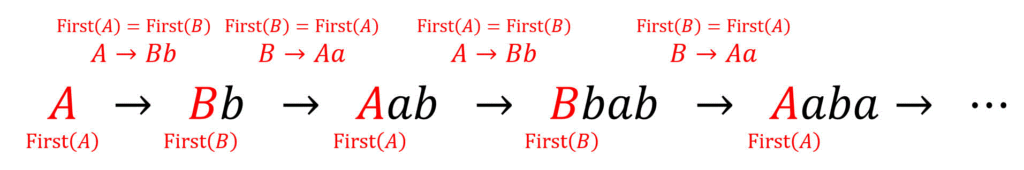
そのため、間接的な左再帰が出てきた際(=一意に答えが決定できないような形が出てきた場合)には、間接的な左再帰が出てくる式(例えば
今回の場合は、
公式1[R1] 終端記号1文字
※1: 例題・練習問題で公式1を適用する場合は
※2:
※3:
公式2[R2] 非終端記号1文字
※1. 例題・練習問題で公式2を適用する場合は
※2.
公式3[R3] 2文字以上の文字列
※1: 例題・練習問題で公式3を適用する場合は
※2: 1文字目も2文字目も空文字の可能性があれば、1文字目~3文字目のFirst集合の和を取ればOK[5]一般化すると、1文字目からn文字目までの文字すべてに空文字があれば、1文字目~n+1文字目の和を取ればOK。。
(3) 例題で確認!
ここからは、1題例題を実際に解いてみましょう。
次の文法
(1)
(2)
(3)
をそれぞれ求めなさい。
解説の前に、First集合を求める手順について確認しておきましょう。
ある非終端記号
Step1.
Step2. Step1で探したすべての生成規則の生成先(右辺)
Step3. Step2で求めたFirst集合の和を取る。
First(S) の求め方
そのため、
First(A) の求め方
そのため、
ここで、それぞれのFirst集合は、
First(B) の求め方
そのため、
ここで、それぞれのFirst集合は、
※
スポンサードリンク
3. Follow集合
(1) Follow 集合とはなにか
Follow集合
数式で書くと、
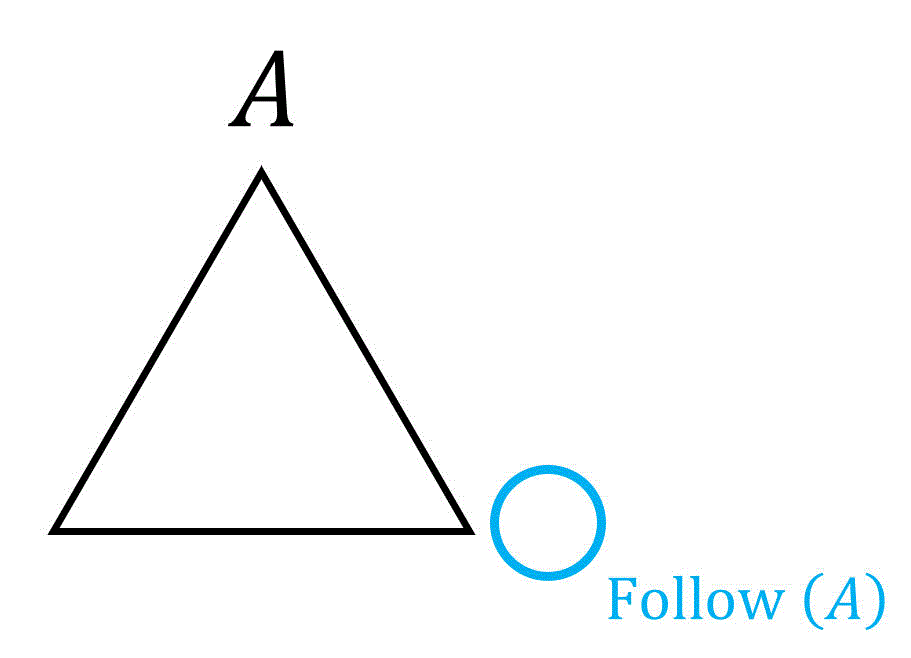
(水色の丸部分に来る終端記号の文字の候補を表す)
例えば、
1点注意が必要なのは、Follow集合の要素に「空文字
その代わりに、「
(2) Follow 集合で頭にいれておくべき3つの公式
各非終端記号に対してFollow集合を求めていくときには、公式1~公式3で出てきた要素すべての和を取ることで求めます。
そこで、この「(2) Follow集合で頭にいれておくべき3つの公式」では、公式1~公式3の式の紹介だけでなく、何故この式でFollow集合が求められるのかまで説明していきます。
公式1. 出発記号 S の直後は必ず文字列の終端 $
文脈自由文法では、下のようにどの文字列も出発記号
そのため、出発記号の後ろは必ず文字列の終端となりますね。

そのため、最初に出発記号に対するFollow集合
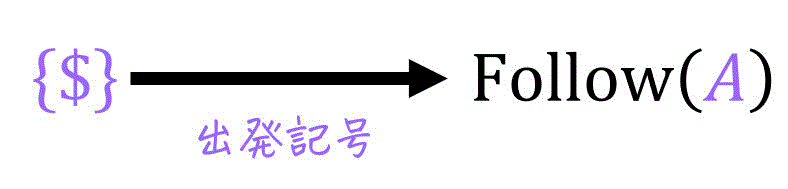
※1: 出発記号ではない非終端記号に対しては何もしなくてOKです。
※2:
公式2. 直後の文字が空文字にならない場合
Follow集合は、「ある非終端記号の直後に来る(終端記号の)文字の候補」を表すため、Follow集合を求める際には、まずは生成規則の生成元ではなく、生成先側の文字列に着目します。
例えば、
このように、
もう少し一般化して、
まず、求めたい非終端記号
例えば、
※1
※2
ここで、
また、先ほど生成規則を
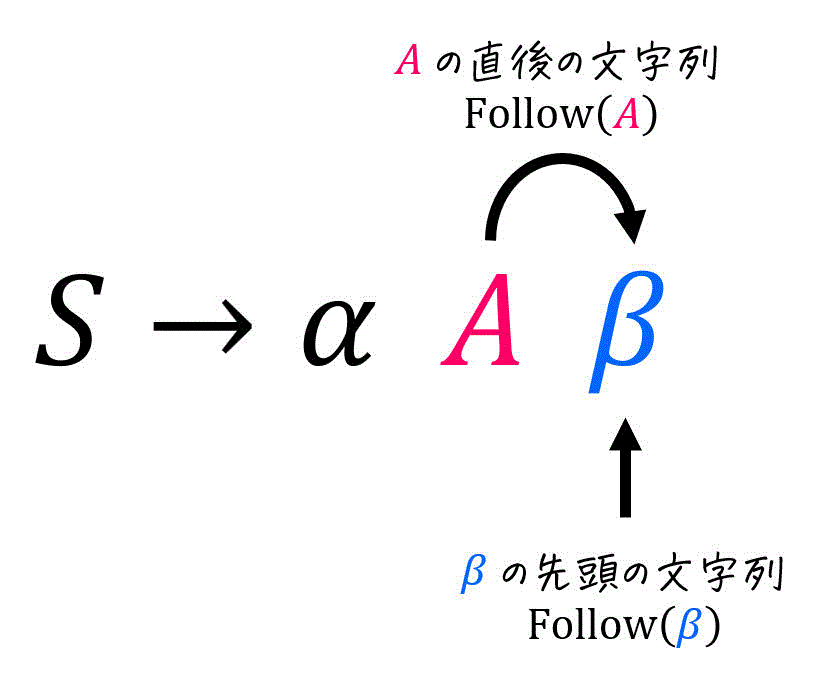
そのため、生成規則
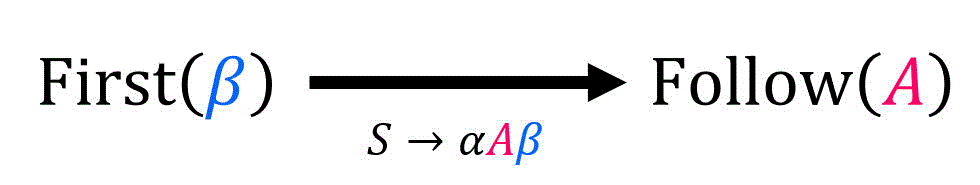
ただし、First集合の要素に
さらに、
公式3. 直後の文字が空文字になる可能性がある場合
生成規則
-
(つまり -
(つまり
は、生成先
ここで、
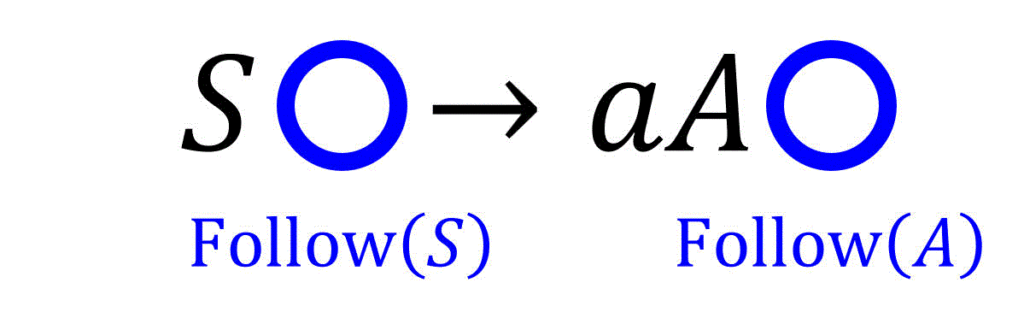
つまり、
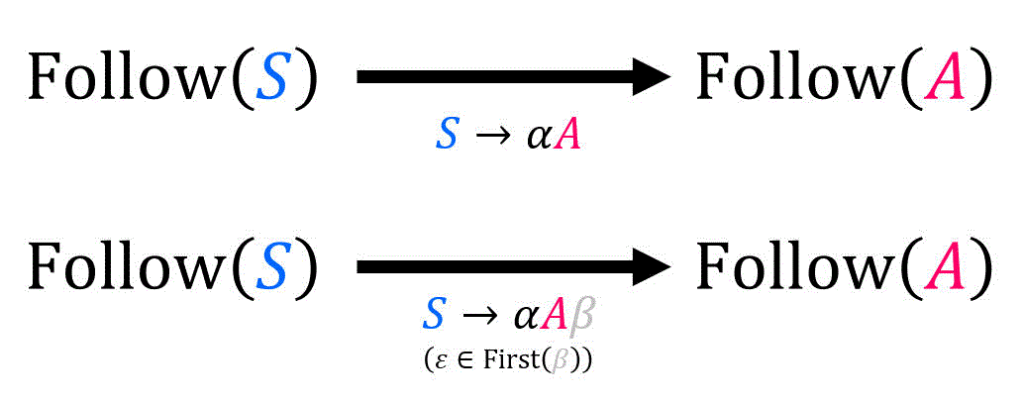
(本記事では分かりやすさ重視のため、2つに分けています)
注意: 右再帰 A → αAが含まれる場合
そのため、右再帰
特に注意が必要なのが、
この場合、生成規則
さらに、
すると、
という「無限ループ」が発生し、訳が分からないことが起こってしまいます。
ここで、式ではなく意味的に考えてみましょう。ある非終端記号
そこで、ある非終端記号
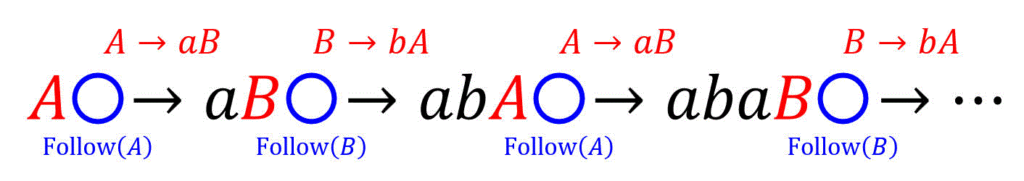
すると、
よって、
そのため、Follow集合を求める際には、直接的な右再帰規則
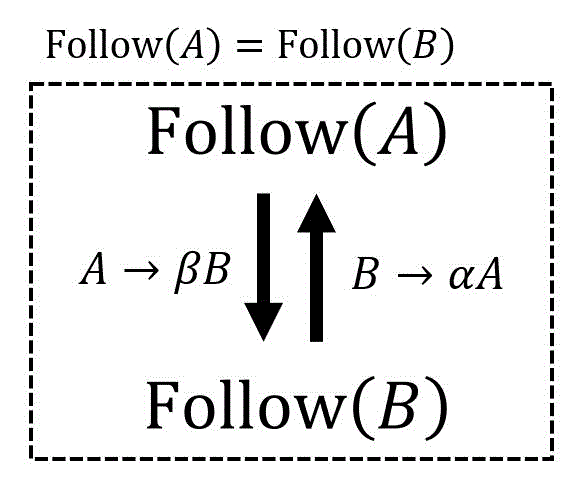
Follow集合は等しくなる(=一心同体)
Follow集合は[公式1]~[公式3]で出てきた要素の和で求められる。
※ ただし、
[公式1] 出発記号

に分けて
※
例1:
例2:
例3:
[公式2]
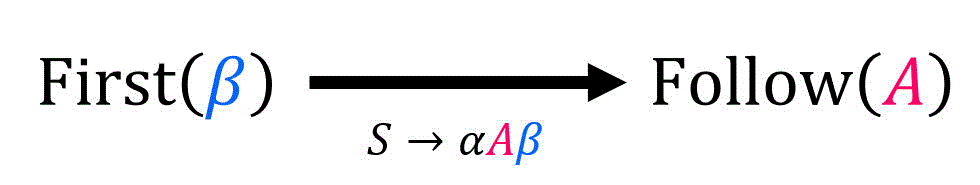
[公式3]

※
(3) 例題で確認!
ここからは、例題1でも出てきた文法を使って、実際にFollow集合を求め方を見ていきましょう。
次の文法
(1)
(2)
(3)
をそれぞれ求めなさい。
※ 必要であれば例題1で求めた
解説の前に、もう1度Follow集合を求める手順について確認しておきましょう。
ある非終端記号
[公式1] 出発記号かどうかの確認

[公式2], [公式3] では
※
[公式2]
生成規則
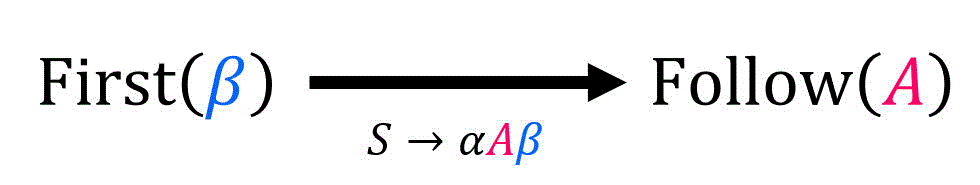
[公式3]

(1) Follow(S) の求め方
まず、
つぎに、
着目した生成規則の生成先
[公式2]
生成規則
[公式3]
よって、
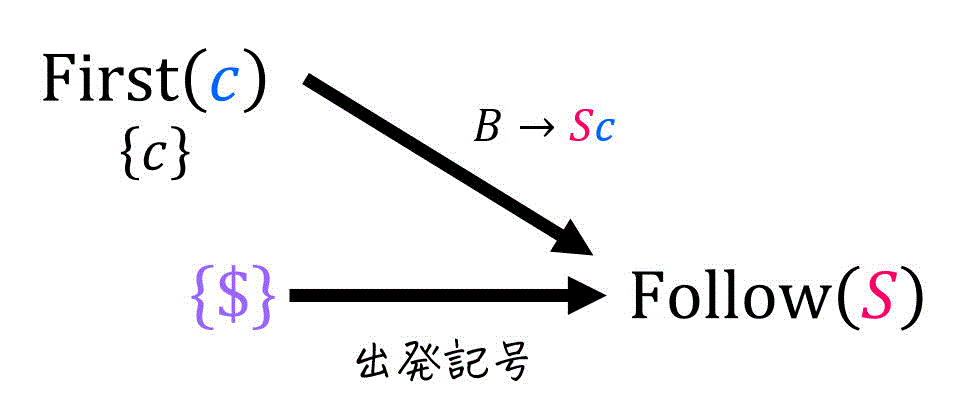
(2) Follow(A) の求め方
[公式1]
つぎに、
着目した規則の生成先
[公式2]
[公式3]
生成規則
したがって、
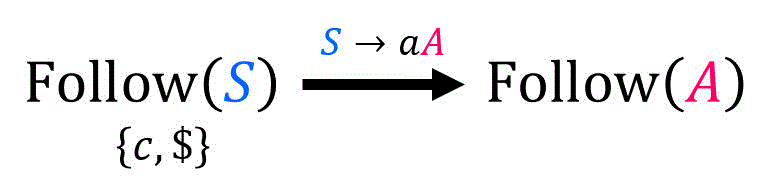
(3) Follow(B) の求め方
[公式1]
ここで、
着目した生成規則の生成先
[公式2]
生成規則
[公式3]
生成規則
したがって、
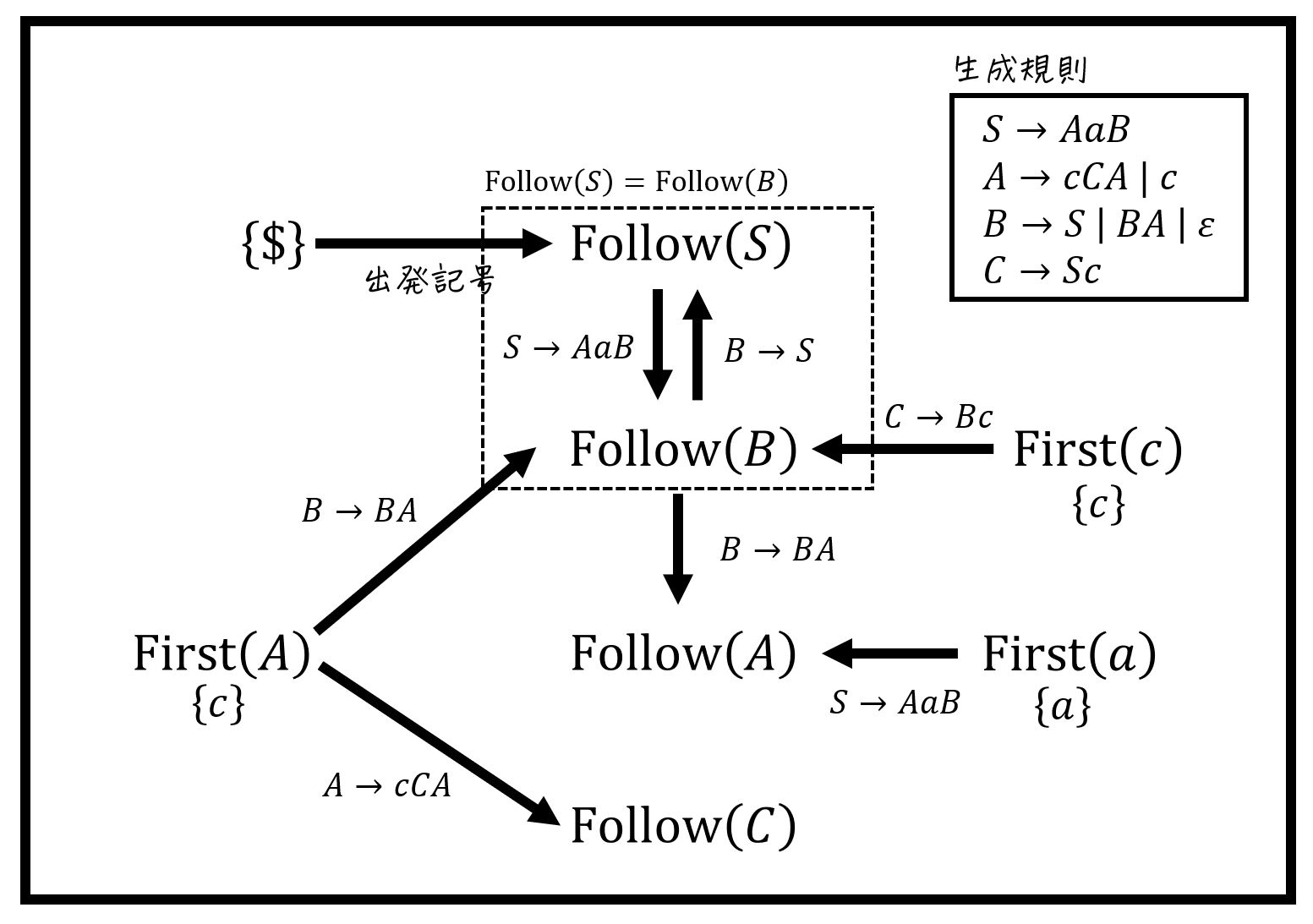
(4) Follow集合の計算ミスを防ぐコツ:図を書く
※ このアイデアは、国島 丈生様のこちらのサイトを参考にさせていただきました。
(FOLLOW()の計算を間違えにくくする工夫)
Follow集合は、First集合に比べて計算が複雑になるため、計算ミスがかなり出てきます[8]実際に私もよく計算ミスします。。
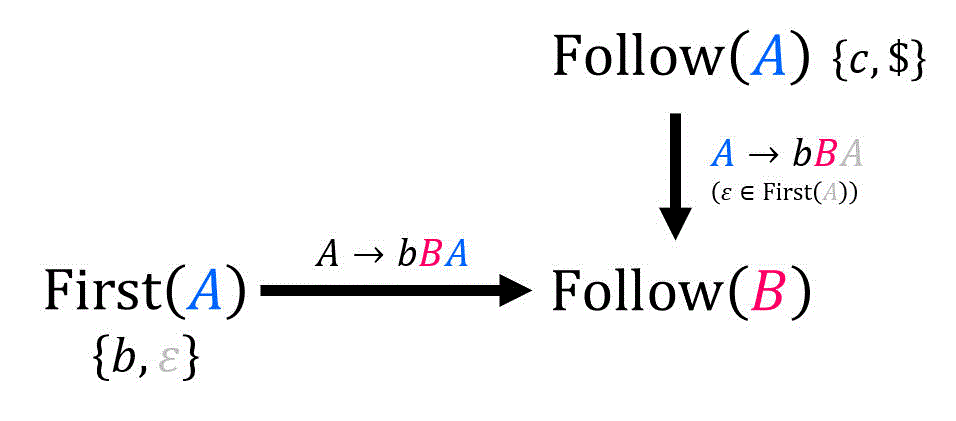
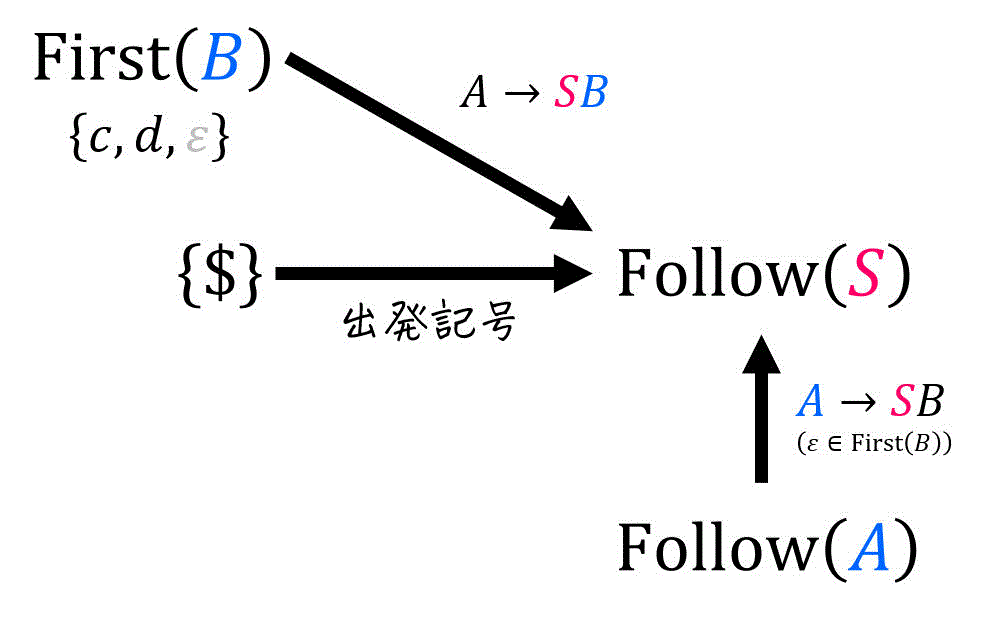
そこで、今回の記事では下の図ように「Follow集合にどの集合の要素が追加されているか」を図で表現しています[9]下の図の場合「
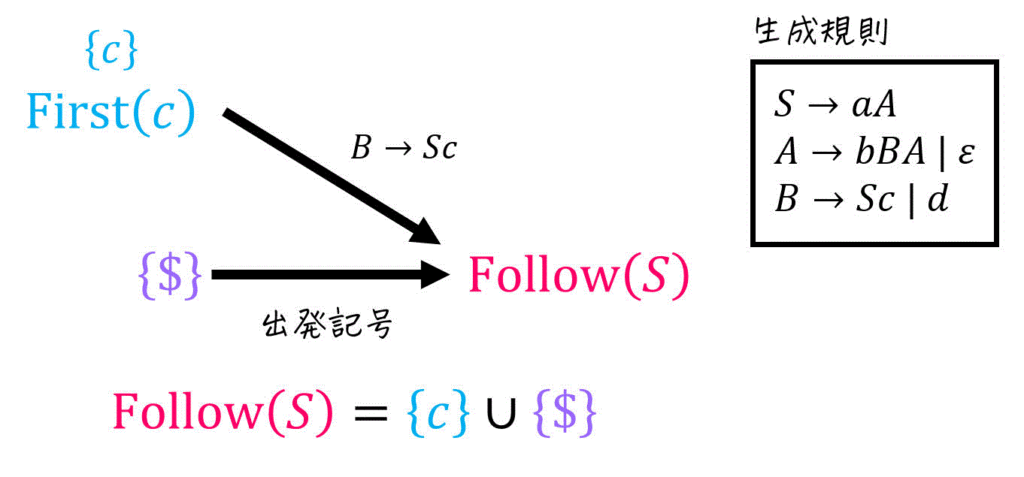
(例題2の(1)に相当)
さらに、各非終端記号ごとに書いたFollow集合の計算図示を下のように1つにまとめることで、Follow集合同士の関係(どのFollow集合の要素がどのFollow集合に加えられているのか)も明確にすることができます。
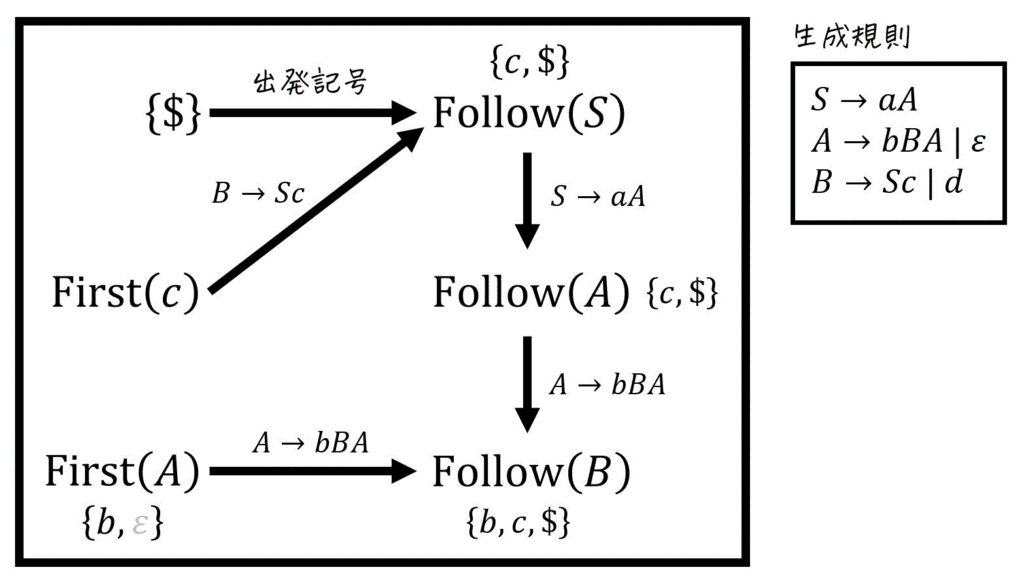
図を書くことで、「矢印に従って集合を追加していく」するだけで簡単にFollow集合を求めることができます!
※ 追加時に
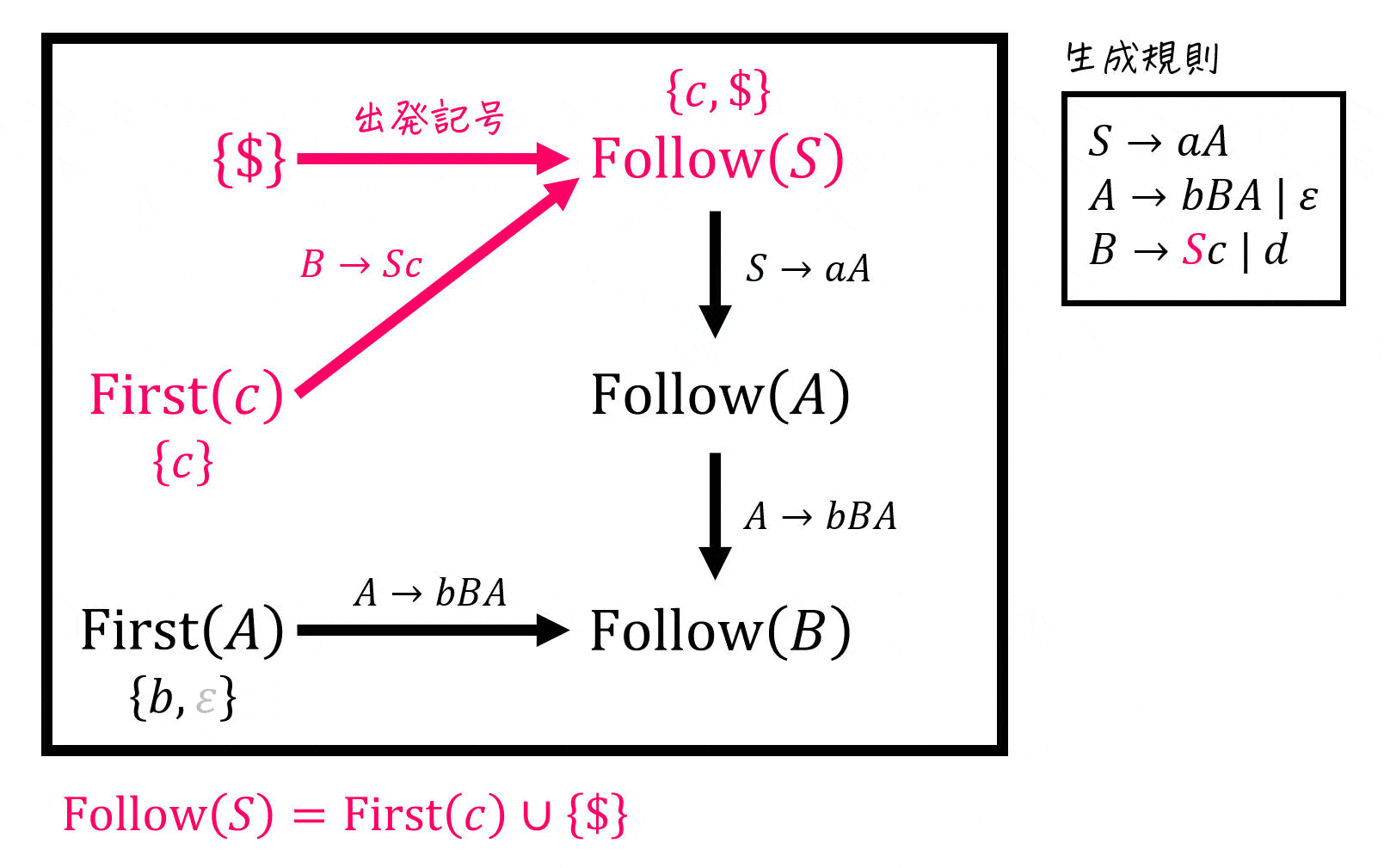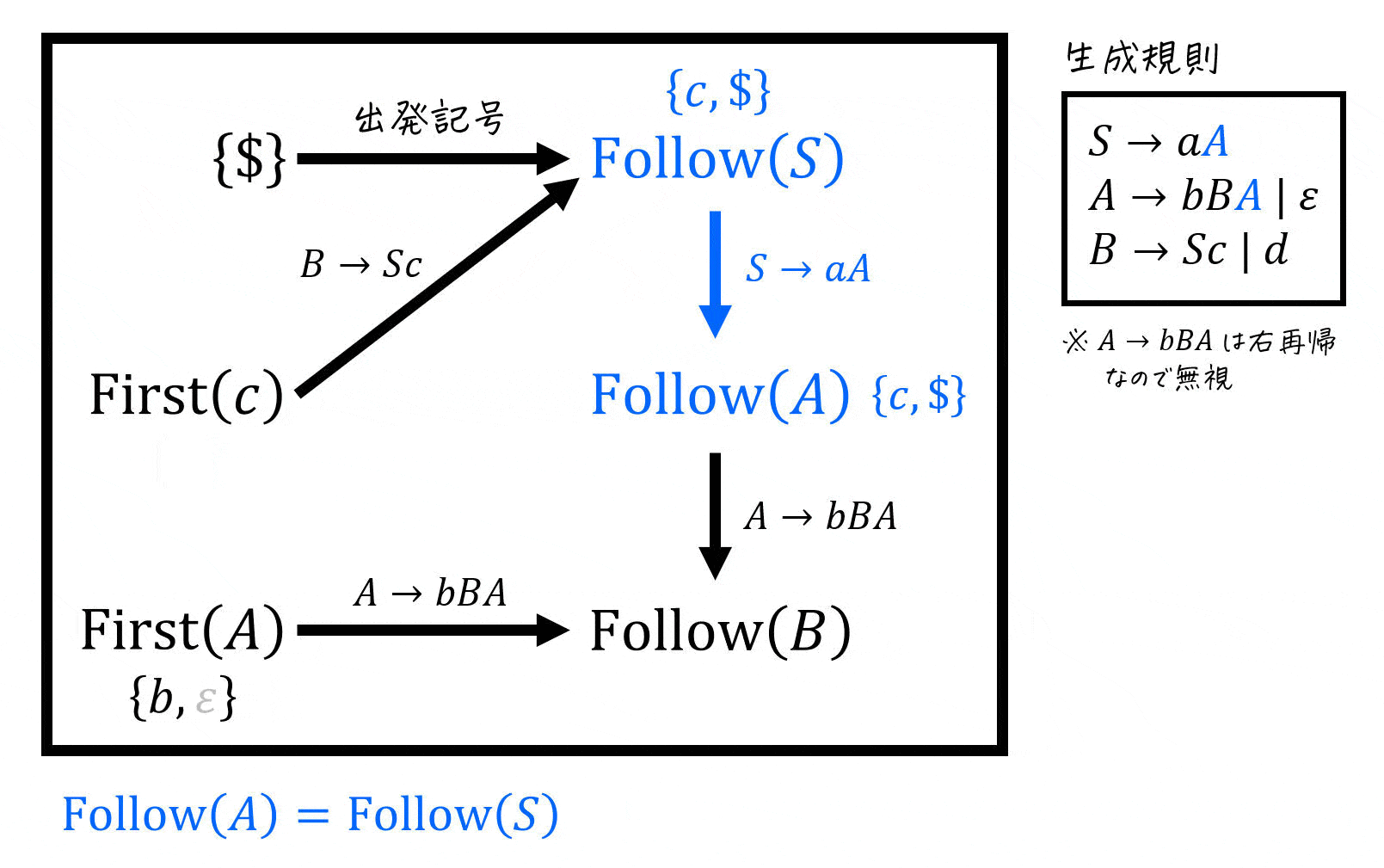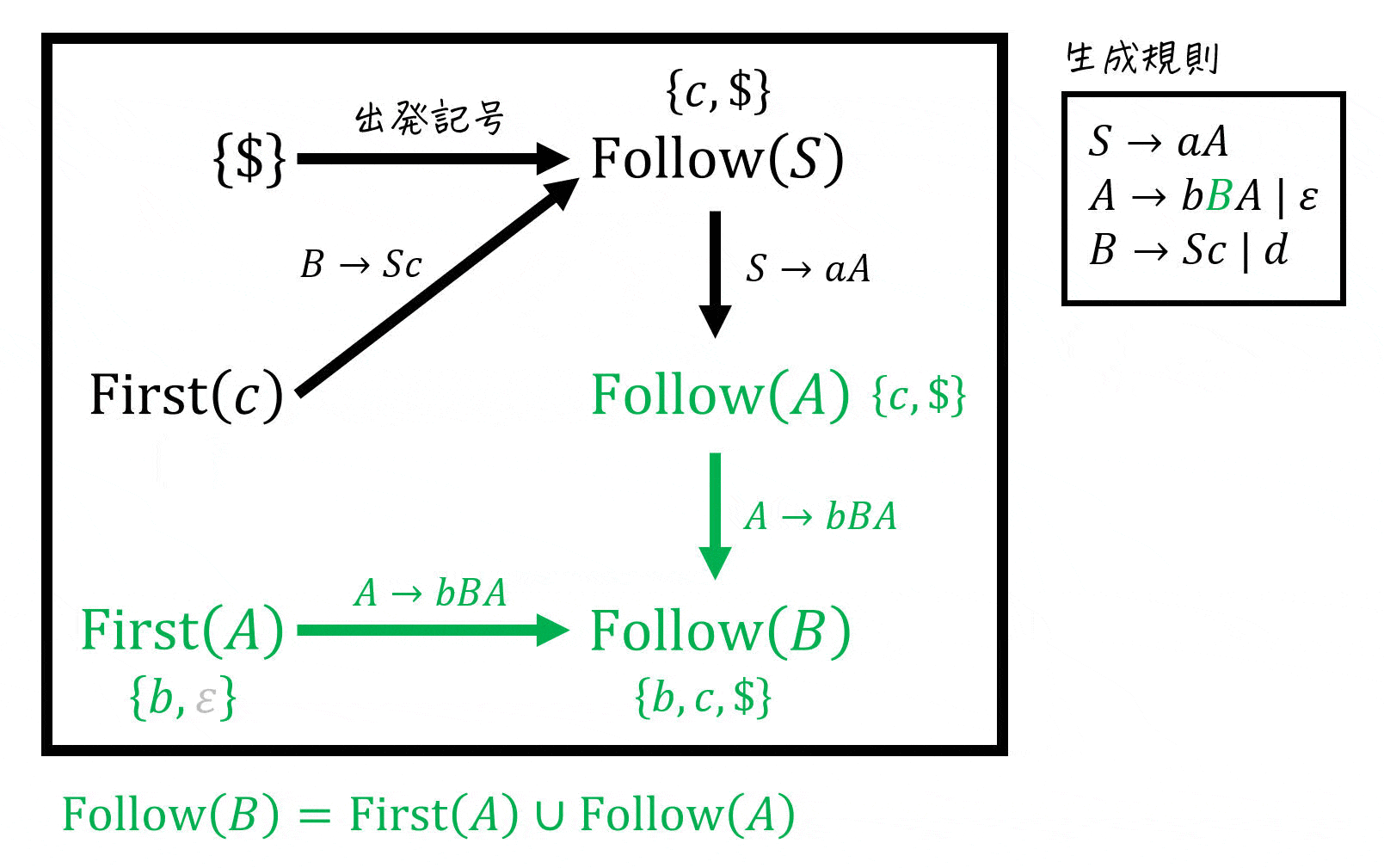
さらに図を書くもう1つメリットは検算が容易にできることです。
理由は、「ある集合
例えば、下の図は
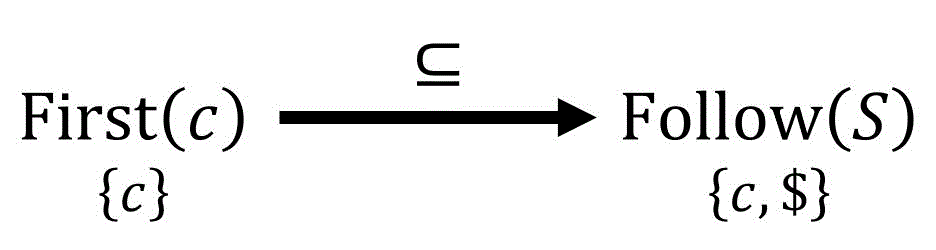
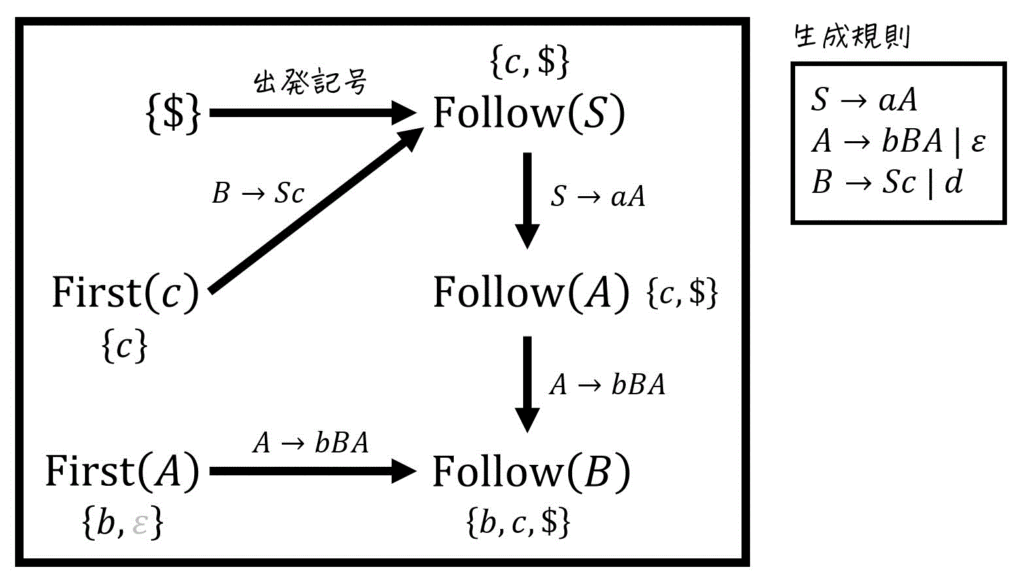
この包含関係を、書いた図の中に出てくる矢印それぞれ(下の図の場合は5か所)でチェックします[11]具体的には、
※ 1つでも成り立っていないものがあれば、計算ミスをしています。
4. Director集合とLL(1)文法の判定
(1) Director集合とは
ある文法がLL(1)文法、つまり「1文字の先読みをするだけで、与えられた文字列を構文解析できる文法」とはどのような文法なのかをもう少し詳しく見ていきましょう。
例えば、文字列
まず、1文字目を先読みすると
このように、同じ非終端記号から生成される文字列を終端記号にした文字列の先頭が
言い換えると、LL(1)文法であるかを判定するためには、同一非終端記号から生成されるすべての生成規則に対し、生成される可能性がある「終端記号の文字列の先頭文字」がすべて異なっていればOKですね。
(2) Director集合の定義と計算公式
LL(1)文法であるかを機械的に判定するために登場したのがDirector集合です。
Director集合は、生成規則
[Director集合の計算公式1] αに空文字が来ない場合
ここで、生成規則
よって、
[Director集合の計算公式2] αに空文字が来る可能性がある場合
しかし、
よって、
ある生成規則
ここで、Director集合はつぎのように計算ができる。
[公式1]※ 特に
(3) Director集合を用いたLL(1)文法の判定
LL(1)文法であるかどうかは、同一非終端記号から生成されるすべての生成規則に対し、生成される可能性がある「非終端記号の文字列の先頭文字」がすべて異なっていればOKでしたね。
このLL(1)文法であるかの判定をDirector集合を用いて書くと下のようになります。
ある文法がLL(1)文法であることを確認するためには、2つ以上の生成元を持つすべての非終端記号に対し、同じ生成元
生成規則
(i)
(ii)
この(i), (ii)で出てきた式(合計4つ)がすべて成立すればLL(1)文法であることが言えます。一方、どれか1つでも成立しなかった時点でLL(1)文法ではありません。
(4) 例題で確認してみよう
Director集合の算出、およびLL(1)文法の確認を例題で確認していきましょう。
次の文法
※ 必要であれば例題1, 例題2で求めた
[解説]
LL(1)文法であるか判定するためには、2つ以上の生成規則を持つ各非終端記号に対して、Director集合を取り、その積を確認します。
(i)
(ii)
(i), (ii)よりLL(1)文法であることが確認できた。
※
5. 練習問題
それでは、ここまでの学習内容を練習問題を通じておさらいしていきましょう。
今回は、2問の練習問題を用意しています。
練習1.
次の文法
(1)
(2)
(3) この文法
練習2.
次の文法
(1)
(2)
(3) この文法
6. 練習問題の答え
解答1.
規則
(1) First集合の算出
[略解](i)
(ii)
そのため、
ここでそれぞれの項のFirst集合は以下のように計算できる。
よって、
(iii)
そのため、
ここでそれぞれの項のFirst集合は以下のように計算できる。
よって、
(2) Follow集合の算出
[略解](i)
ここで、
なので、
なので、
よって、
(ii)
[a]
なので、
[b]
なので、
よって、
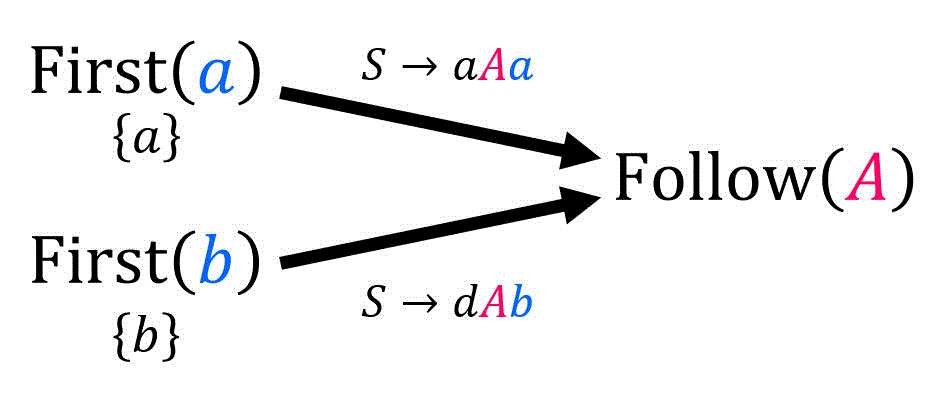
(iii)
[a]
なので、
[b]
なので、
※ 式から察している人もいるかもしれませんが、[a] の生成式と全く同じ結果が出てきます。
よって、
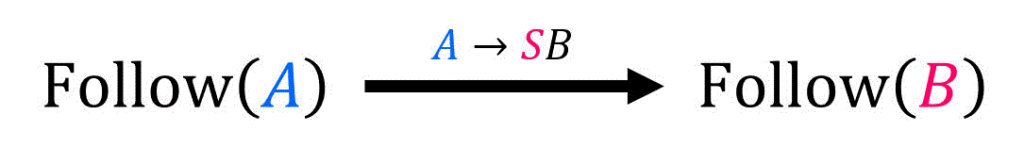
(代表として
それぞれの計算結果をまとめてFollow集合を算出
先ほど出した
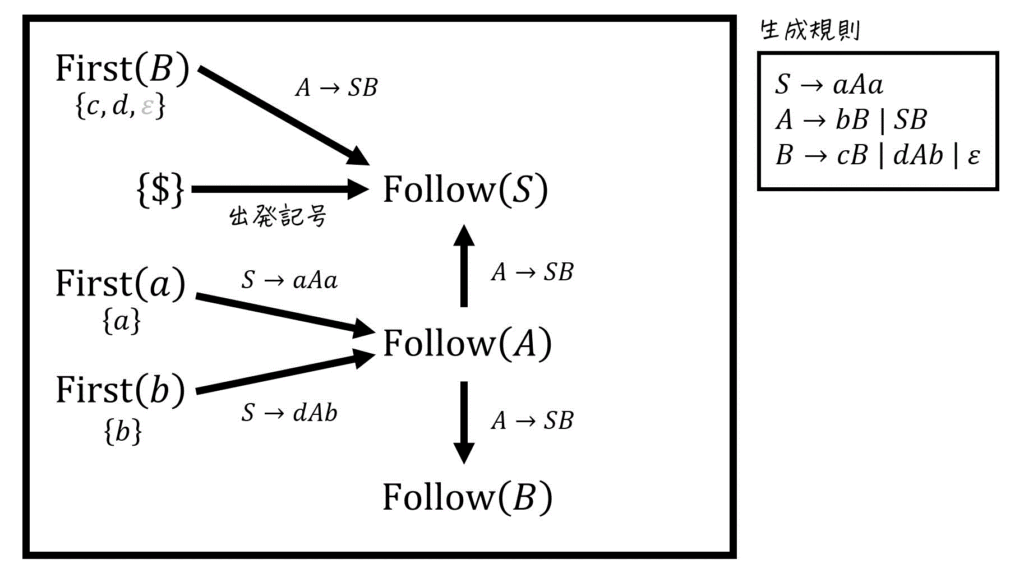
あとは、求められるFollow集合から順にFollow集合を求めていけばOK。
※ 今回の場合は、
(ii)
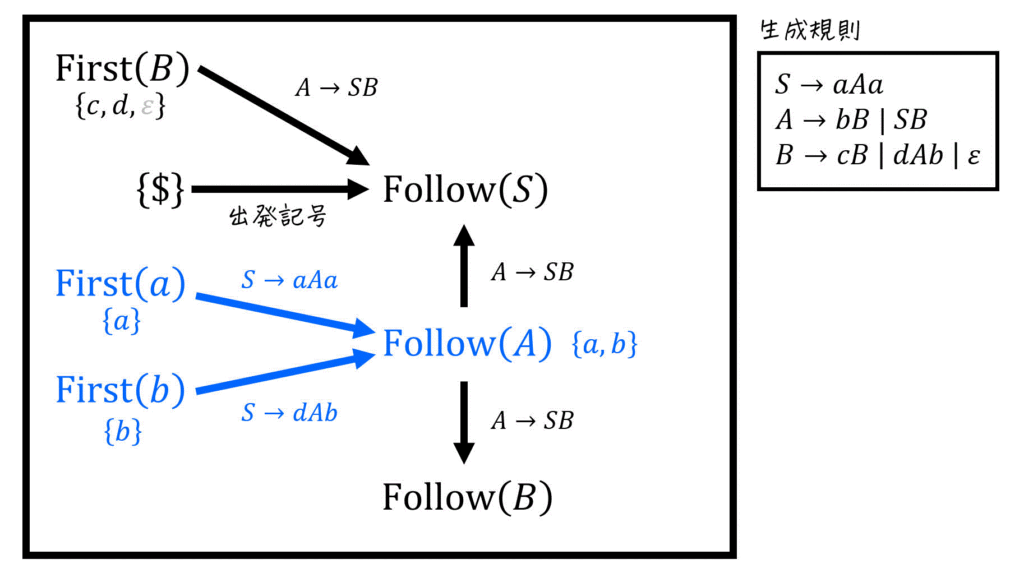
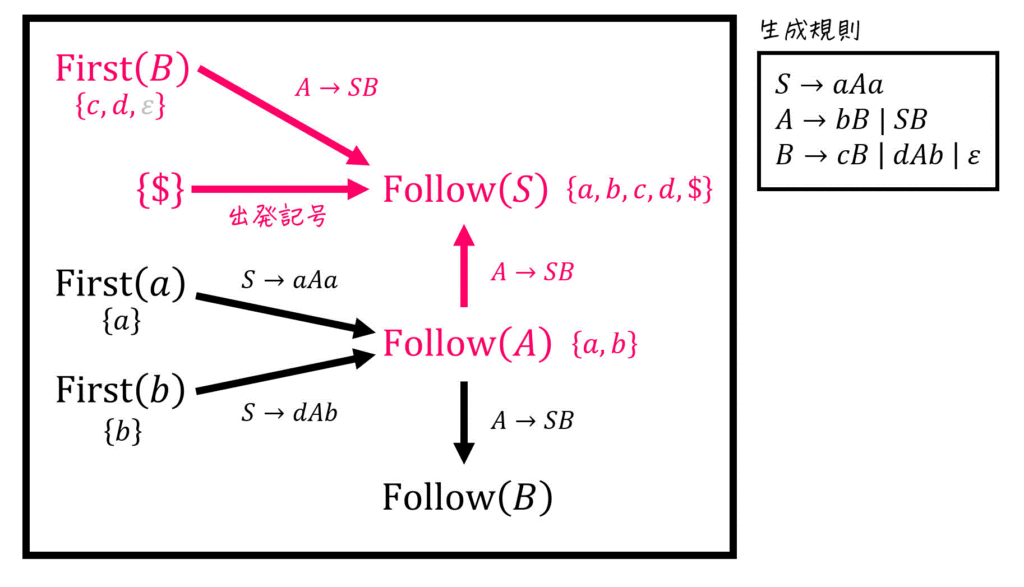
(i)
(iii)
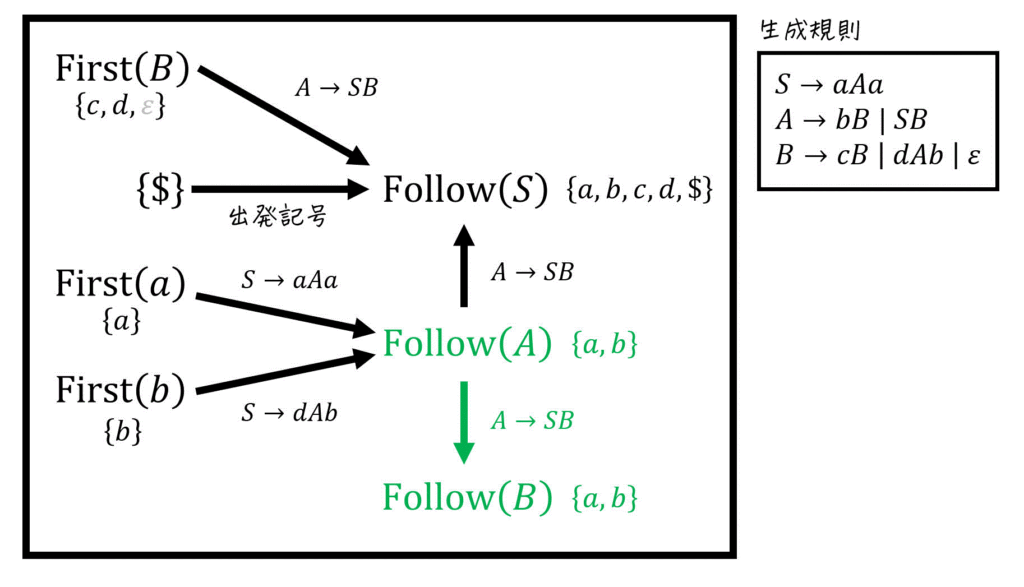
(3) Director集合の算出とLL(1)文法の判定
各非終端記号に対して、生成元から2つ以上の生成規則を持つものは、
である。あとは、非終端記号ごとに「どの生成規則同士の積をとっても、Director集合が空集合になること」を確認すればOK。
1)
2)
1), 2) より、題意の文法はLL(1)文法である。
解答2.
規則
(1) First集合の算出
[略解](i)
(ii)
そのため、
ここでそれぞれの項のFirst集合は以下のように計算できる。
よって、
(iii)
ただし、
ここで、
(iv)
よって、
(2) Follow集合の算出
[略解](i)
ここで、
なので、
よって、
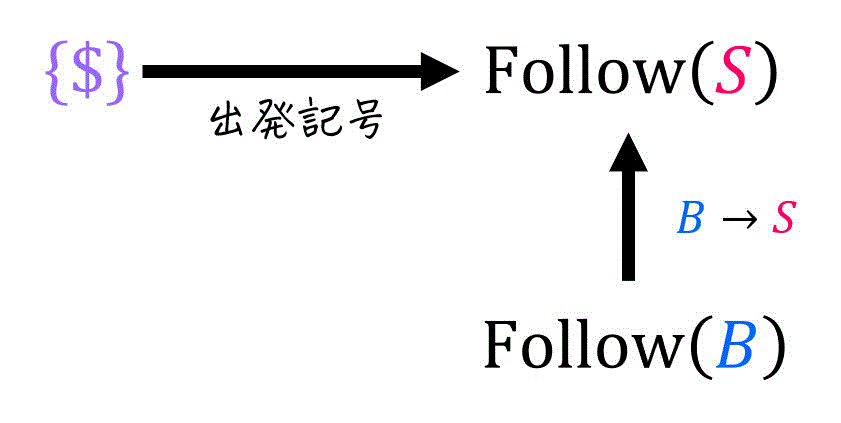
(ii)
ここで、
[ii-a]
なので、
[ii-b]
この規則では、
なので、
よって、
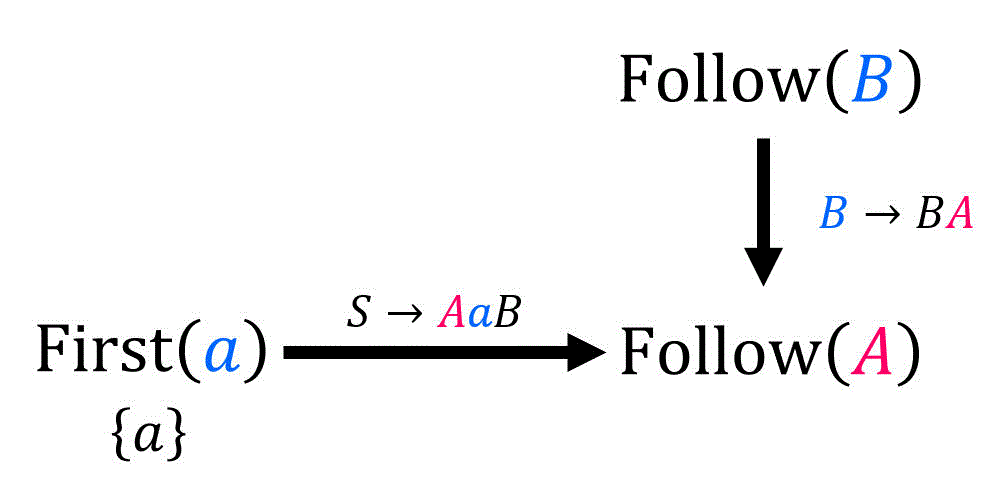
(iii)
ここで、
[iii-a]
この規則では、
なので、
[iii-b]
なので、
[iii-c]
なので、
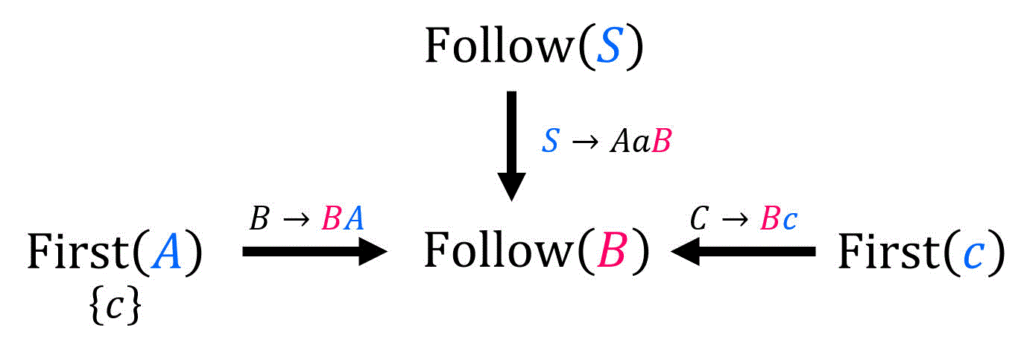
(iv)
ここで、
この規則について、
なので、
よって、
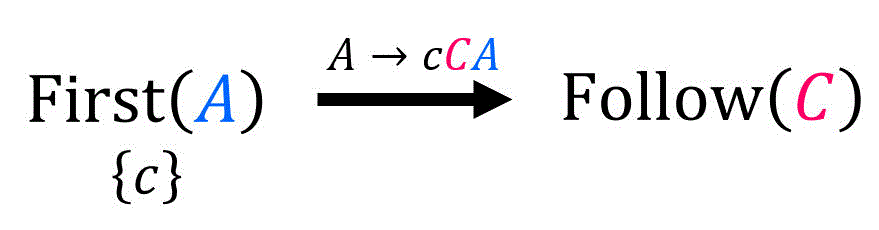
それぞれの計算結果をまとめてFollow集合を算出
先ほど出した
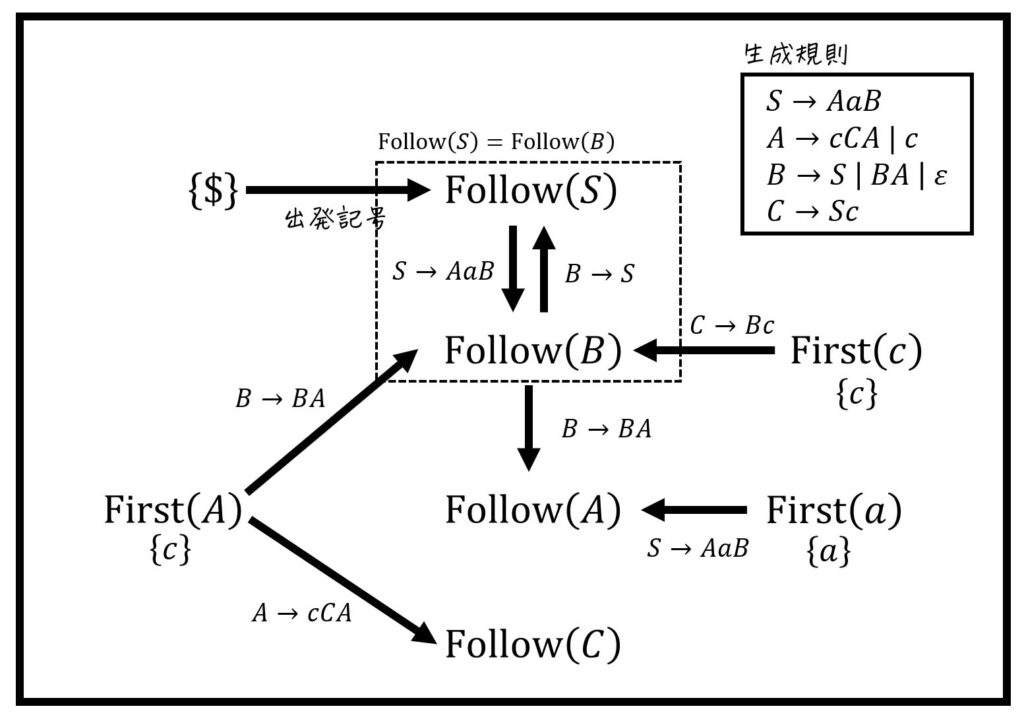
※ 点線部分は、間接的な右再帰により、2つのFollow集合が等しい(=一心同体)になっていることを表す。つまり
あとは、求められるFollow集合から順にFollow集合を求めていけばOK。
※ 今回の場合は、
(iv)
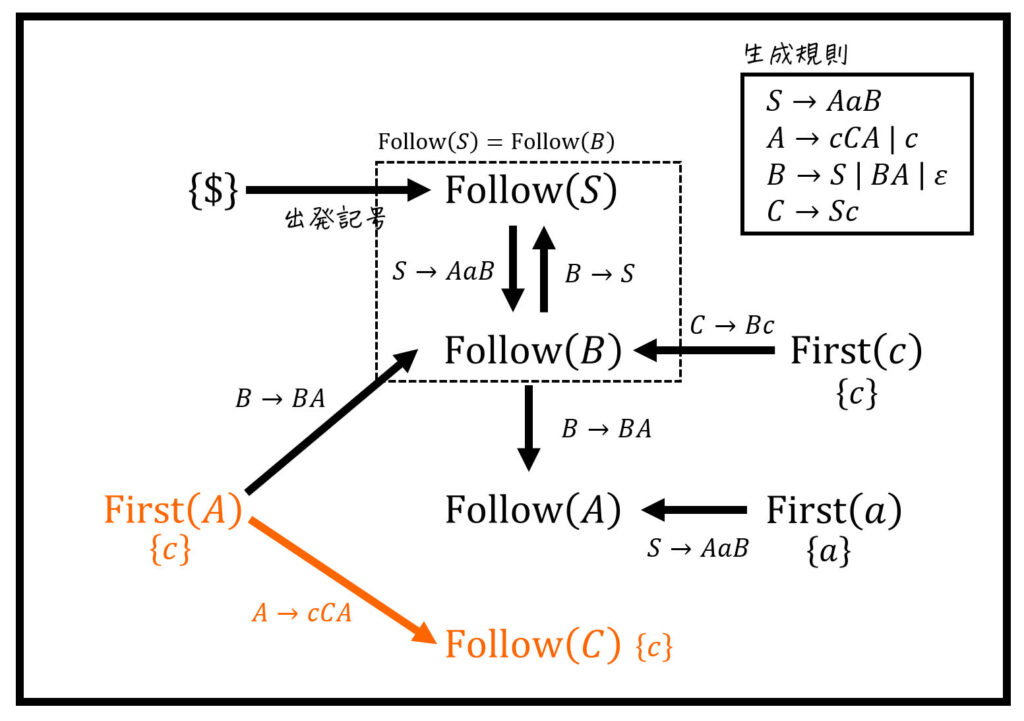
(i), (iii)
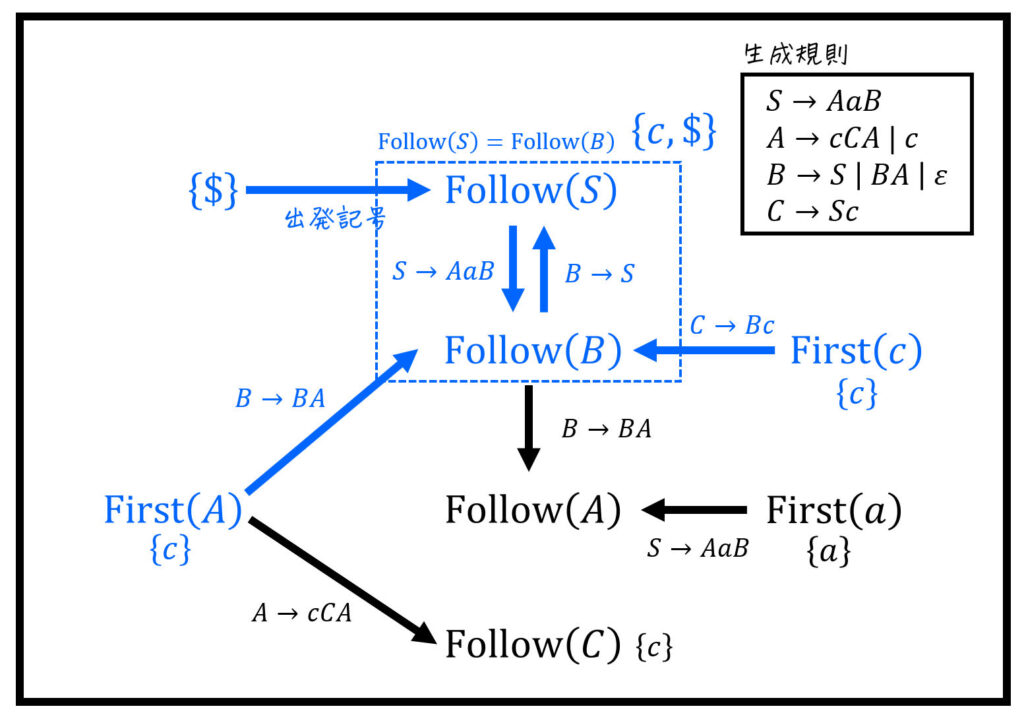
(ii)
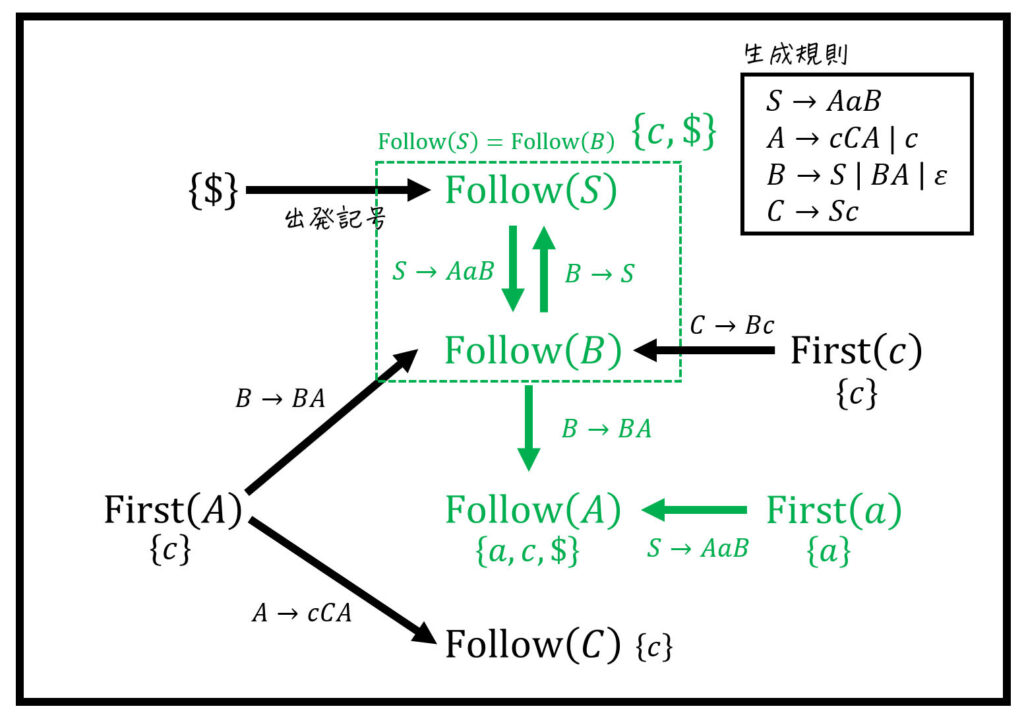
(3) Director集合の計算・LL(1)文法の判定
各非終端記号に対して、生成元から2つ以上の生成規則を持つものは、
である。あとは、非終端記号ごとに「どの生成規則同士の積をとっても、Director集合が空集合になること」を確認すればOK。
1)
よって、題意の文法はLL(1)文法ではない。
※ 1つでも
7. さいごに
かなり長い記事となっていましたが、以上が
- LL(1)文法
- First集合
- Follow集合
- Director集合
に関する説明でした。
この記事を見て、少しでもLL(1)文法やFirst, Follow, Director集合の計算の方法について理解いただけたのであれば非常にうれしいです。
次回は、左再帰な文法についての「問題点」と「左再帰を解消する方法」について説明する予定です。
[練習問題の中に入れられなかったおまけ問題] 生成規則注釈
| ↑1 | 10文字弱、かつ生成規則が4つであればやみくもにやってもそこまで時間はかかりませんが、実際のプログラムに対して構文解析をする場合、膨大な文字数かつ膨大な生成規則があるため、やみくもにやっていると日が暮れてしまいます。 |
|---|---|
| ↑2 | もう少し詳しく言うと、LL(1)文法はトップダウン構文解析(出発記号を起点として、どんどん生成規則を用いて分解していきながら解析する方法)において、1文字だけ先読みすることで文字列を後戻りすることなく構文解析ができる文法です。 |
| ↑3 | |
| ↑4 | いったん |
| ↑5 | 一般化すると、1文字目からn文字目までの文字すべてに空文字があれば、1文字目~n+1文字目の和を取ればOK。 |
| ↑6 | |
| ↑7 | |
| ↑8 | 実際に私もよく計算ミスします。 |
| ↑9 | 下の図の場合「 |
| ↑10 | 集合 |
| ↑11 | 具体的には、 |
| ↑12 |
関連広告・スポンサードリンク