スポンサードリンク
こんにちは、ももやまです!
今回は情報理論で習う「情報量」について簡単にまとめてみたいと思います!
情報量、エントロピーの理解には「確率」に関する知識が必須です。
確率についてあまりよく分かってない、苦手だなと思う人のために確率の要点をまとめた記事を下に用意したので、ぜひご覧ください。
目次
スポンサードリンク
1.「情報量」とは…?
皆さんは、情報といえばどんな情報を浮かびますか?
- 昨日の天気は晴れのち雪
- 今年のK大学の入試問題
- NくんとCさんが付き合っている
- 今ならLINE Payを使うとポイント5%アップ
などなど様々な情報を浮かべると思います。
しかし、その情報がどれほどの大きさを持っているかは文章だけでは比べることができません。そんなときに使われるのが情報量です。
情報量の大きさは、以下のようにして定義することができます。
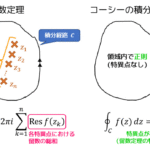
情報量は起こる確率 \( n \) として \[\log_2 \frac{1}{n} = - \log_2 n \]
と定義できる。*1
また、底が2のときの情報量の単位はビット[bit]で表される。
(今回の記事では大体省略しています)
たとえば、2択の問題があるとします。このとき、(何もしらない前提だと)正解する確率は1/2ですね。
なので、「正解がどっちなのか」という情報は \( - \log_2 \frac{1}{2} = 1 \) となり、1[bit]となります。
では、2択ではなく4択問題になるとどうなるでしょう。
この場合は、正解する確率は1/4になりますね。
なので、「正解はどれなのか」という情報は \( - \log_2 \frac{1}{4} = 2 \) となり、2[bit]となります。
このように、より確率が少ない(珍しい)情報を知ることほど情報量は大きくなることがわかりますね。
スポンサードリンク
2.エントロピー(平均情報量)
例えば、このような抽選を考えましょう。
| 確率 | 総数 | 情報量 | |
| 1等 | 0.2% | 2 | 8.966 |
| 2等 | 1.8% | 18 | 5.796 |
| 3等 | 5.0% | 50 | 4.322 |
| 4等 | 10.0% | 100 | 3.322 |
| はずれ | 83.0% | 830 | 0.269 |
| 合計 | 1000 |
このような抽選の場合、確率の小さい1等や2等が当選するという情報を得られたらそれはすごい情報ですよね。しかし、「はずれ」が出ることを知ってもそもそもの確率が高く当たり前なので全くうれしくありません。
そこで使うのがエントロピー(平均情報量)です。
エントロピーを求めることで、情報源(今回の場合は抽選)の不確かさを数値化することができます。
エントロピーは、以下のように定義されます。
記憶のない(独立な)情報源 \( A \) のそれぞれの事象が起こる確率をそれぞれ \( p(1),p(2),p(3), \cdots, p(n) \) とすると、平均情報量(エントロピー)は\[ - \sum_{i=1}^{n} p(i) \log_2 p(i) \]となる。
言い換えると、エントロピーは情報量の期待値を表します。
(1) 情報源が2つの場合
まずは情報源が2つの場合を考えましょう。
例えば、コインがあるとします。
理想的なコインを投げたとき、表が出る確率は1/2、裏が出る確率は1/2ですね。
よって、コインを投げるという情報源のエントロピーは、\[ - \frac{1}{2} \log_2 \frac{1}{2} - \frac{1}{2} \log_2 \frac{1}{2} = 1 \]となり、エントロピーは1となります。
では、理想的なコインをいじくって表が出る確率を1/4、裏が出る確率を3/4としてみましょう。
すると、情報源の平均情報量は\[ - \frac{1}{4} \log_2 \frac{1}{4} - \frac{3}{4} \log_2 \frac{3}{4} \fallingdotseq 0.811 \]となり、エントロピーが0.811となります。ともに1/2のコインを投げる場合に比べて情報量が減っていますね。
さらに極端なコインを投げてみます。表が100%出て、裏が一切出ないコインを投げた場合、そのエントロピーは\[ -1 \log_2 1 - \lim_{x \to 0} x \log_2 x = 0 \]となり、0[bit]、となります。言い換えると、一切情報をもたないと言えます。
確かに表が絶対出るコインで、どちらか出るか知ったところで新しい情報なんてありませんよね。
いびつなコインを投げたときに表が出る確率を \( p \) 、裏が出る確率を \( 1-p \) としたときのエントロピー \( H(X) \) をグラフにするとこのようなグラフになります。
縦軸がエントロピー \( H(X) \)、横軸が表が出る確率 \( p \) となります。
グラフを見ると、\( p = 1/2 \) のときが一番エントロピーが一番大きくなっていますね。確かに、「表が裏が均一な確率」で出るときは「表が1/4、裏が3/4の確率」で出る場合に比べたらどちらの面が出るかは予想しにくいですよね(なのでどちらが出ると知ったときの情報量が多い)。
さらに、極端な例(表か裏が出るかが確実にわかる場合)のときはどちらが出るか知ったところで「もともとどちらが出るかはわかっているので」情報があるとは言えませんよね。
(2) 情報源を少し増やした場合
少し情報源の数を増やしてみましょう。
理想的なサイコロを想像してください。
理想的なサイコロの場合、それぞれの出目が出る確率は 1/6 ですよね。なのでサイコロの出目の情報のエントロピーは、\[ - 6 \cdot \frac{1}{6} \log_2 \frac{1}{6} \fallingdotseq 2.585 \]となります。
ではちょっとサイコロを改造して、それぞれの出目が出る確率を変えてみましょう。
- 4,5,6の出目はそれぞれ確率1/4
- 1,2,3の出目はそれぞれ確率1/12
で出るインチキサイコロの出目の情報のエントロピーを求めてみましょう。エントロピーは、\[ -3 \cdot \frac{1}{4} \log_2 \frac{1}{4} - 3 \cdot \frac{1}{12} \log_2 \frac{1}{12} \fallingdotseq 2.396 \]となり、出目が平等に出るサイコロに比べてエントロピーが減りましたね。*2
さらにインチキなサイコロにしてみます。1しか出ないサイコロなんてどうでしょうか。1しか出ないサイコロのエントロピーは、\[ -\frac{1}{6} \log_2 1 - \frac{5}{6} \cdot \lim_{x \to 0} x \log_2 x = 0 \]となり、2択の場合と同じく、全く情報がないことがわかります。
記憶のない(独立な)情報源のエントロピーが最大のときは、
すべての事象が同じ確率
とき*3である。また、エントロピーが最小(0)のときは、
いずれか1つの事象の確率が1、それ以外の事象の確率が0
のときである。
(3) さらに情報源を増やした場合
さらに、情報源の数を増やしてみましょう。
皆さんは100面ダイスをご存知ですか? TRPGなどで使うことが多いですよね。
100面ダイスは、1~100が均一な(それぞれ1%の)確率で出ますよね。
このときの平均情報量は、\[ -100 \cdot \frac{1}{100} \log_2 \frac{1}{100} \fallingdotseq 6.644 \]となります。
ここで、天の声Aから、「つぎにダイスを振ったときに100が出るか出ないかを教えてあげよう。」と言われました。このとき、あなたは天の声Aさんの情報は価値のあるものといえるでしょうか。
このとき、この天の声Aさんの情報のエントロピーはいくらになるかを計算してみましょう。100が出る確率は1%、それ以外が出る確率は99%なので、エントロピーは、\[ -\frac{1}{100} \log_2 \frac{1}{100} - \frac{99}{100} \log_2 \frac{99}{100} \fallingdotseq 0.081 \]となり、「100が出ないという情報」はたったの0.08[bit]しかないのです。つまり天の声Aさんの情報は大した情報ではないってことがわかります。(天の声Aさんに失礼)
実際100面ダイスを振って100が出るか出ないかは振る前にだいたい予測がつきますよね…。
つぎに、天の声Bさんから「つぎにダイスを振ったときに96以上が出るか出ないかを教えてあげよう。」と言われました。天の声Aさんの情報よりは少し詳しい情報ですね。
またエントロピーを計算してみましょう。96以上が出る確率は5%、それ以外が出る確率は95%なので、エントロピーは、\[ -\frac{1}{20} \log_2 \frac{1}{20} - \frac{19}{20} \log_2 \frac{19}{20} \fallingdotseq 0.286 \]となります。確かに天の声Aさんの情報よりも大事な情報だということができますね。
また天の声が聞こえてきました。「このダイスは51以上が出るかでないかを教えてあげよう。」前の2つの声に比べて非常に範囲が狭まりましたね。
51以上か50以下が出るかは普通の人であればどちらが出るかは予測しにくいですよね。
実際エントロピーを計算すると、\[ -\frac{1}{2} \log_2 \frac{1}{2} - \frac{1}{2} \log_2 \frac{1}{2} = 1 \]と、かなり大きい数値になってます。つまり、前の2つの天の声の情報に比べたら重みがある情報と言うことができます。
スポンサードリンク
スポンサードリンク
3.相互情報量
最後に相互情報量についてです。
相互情報量は、2つの情報が互いに影響を及ぼす量のことを表します。
数字が大きければ大きいほど、2つの情報が影響を及ぼしているということなので、1つの情報を見ただけでもう1つの情報を判別しやすいと言うことが出来ます。
例えば、カープの勝敗を伝える情報源 \( A \) があったとします。
100日間のカープの勝敗を記録した結果、60日は勝利、40日は負けていました。言い換えると、\( 3/5 \) の確率でカープは勝利し、\( 2/5 \) の確率でカープは負けると言えます。よって、カープの勝敗を伝える情報源のエントロピー \( H(A) \) は、\[ H(A) = - \frac{3}{5} \log_2 \frac{3}{5} - \frac{2}{5} \log_2 \frac{2}{5} \fallingdotseq 0.971\]となります。
さらにもう1つ情報源 \( B \) を追加します。カープファンであるMくんのカープの試合があった翌日の機嫌を100日間集計した結果、機嫌がよい日が55日、機嫌が悪い日が45日ありました。すると、この情報源のエントロピー \( H(B) \) は、\[ H(B) = - \frac{11}{20} \log_2 \frac{11}{20} - \frac{9}{20} \log_2 \frac{9}{20} \fallingdotseq 0.993\]となります。
この2つの情報 \( A,B \) を100日間記録していったところ、つぎの表の結果が得られました。
| 勝利 | 敗北 | 合計 | |
| 機嫌良 | 40 | 15 | 55 |
| 機嫌悪 | 20 | 25 | 45 |
| 合計 | 60 | 40 | 100 |
さて、この情報源 \( A \) と情報源 \( B \) はどれほど影響を及ぼしているかを相互情報量を計算することで計算してみましょう。
計算方法は3つあるので、1つずつ計算をしていきます。
(1) Mくんの機嫌を中心に考える
まずは、Mくんの機嫌を中心に考える方法です。Mくんの機嫌と、カープの勝敗がわかった際のMくんの機嫌の良し悪しの情報量の2つを比較します。
カープが勝利したとき、敗北した際のMくんの機嫌が良いときと悪いときの条件付き確率を求めていきます。
条件付き確率を求める時は、このように表に色をつけると計算がしやすいのでおすすめです。
| 勝利 | 敗北 | 合計 | |
| 機嫌良 | 40 | 15 | 55 |
| 機嫌悪 | 20 | 25 | 45 |
| 合計 | 60 | 40 | 100 |
(a) カープ勝利時のMくんの機嫌が良い条件付き確率 \( P(B_{good}|A_{win}) \)
カープが勝った60日のうち、Mくんの機嫌が良いときは40日ありました。なので条件つき確率は、\[ P(B_{good}|A_{win}) = \frac{40}{60} = \frac{2}{3}\]となります。
(b) カープ勝利時のMくんの機嫌が悪い条件付き確率 \( P(B_{bad}|A_{win}) \)
カープが勝った60日のうち、Mくんの機嫌が悪いときは20日ありました。なので条件つき確率は、\[ P(B_{good}|A_{bad}) = \frac{20}{60} = \frac{1}{3}\]となります。
(c) カープ敗北時のMくんの機嫌が良い条件付き確率 \( P(B_{good}|A_{lose}) \)
カープが負けた40日のうち、Mくんの機嫌が良いときは15日ありました。なので条件つき確率は、\[ P(B_{good}|A_{lose}) = \frac{15}{40} = \frac{3}{8}\]となります。
(d) カープ敗北時のMくんの機嫌が悪い条件付き確率 \( P(B_{bad}|A_{lose}) \)
カープが負けた40日のうち、Mくんの機嫌が悪いときは25日ありました。なので条件つき確率は、\[ P(B_{bad}|A_{lose}) = \frac{25}{40} = \frac{5}{8}\]となります。
つぎにカープの勝敗が分かったときのMくんの機嫌の良し悪しの情報量を表す条件つきエントロピーをもとめます。カープが勝利する確率は \( 3/5 \)、敗北する確率は \( 2/5 \) なので条件つき情報量 \( H(B|A) \) は、\[ H(B|A) = - \frac{3}{5} \left( \frac{2}{3} \log_2 \frac{2}{3} + \frac{1}{3} \log_2 \frac{1}{3} \right) - \frac{2}{5} \left( \frac{3}{8} \log_2 \frac{3}{8} + \frac{5}{8} \log_2 \frac{5}{8} \right) \fallingdotseq 0.933 \]
となります。相互情報量は、Mくんの機嫌を伝える情報のエントロピー \( H(B) \) から、カープの勝敗が判明したときのMくんの機嫌の良し悪しを伝える条件つきエントロピー \( H(B|A) \) を引いた値で求めることができます。よって相互情報量 \( I(A;B) \) は、\[ I(A;B) = H(B) - H(B|A) \fallingdotseq 0.993 - 0.933 = 0.060 \]と計算することができます。
(2) カープの試合を基準に考える
Mくんではなく、カープの試合を基準に考えてから相互情報量を出す方法もあります。
この場合は、カープの試合を伝える情報源と、Mくんの機嫌がわかった際のカープの勝敗を表す情報源を比較します。
(1)と同じように条件つき確率を求めていきます。
| 勝利 | 敗北 | 合計 | |
| 機嫌良 | 40 | 15 | 55 |
| 機嫌悪 | 20 | 25 | 45 |
| 合計 | 60 | 40 | 100 |
(a) Mくんの機嫌が良いときのカープが勝利した条件つき確率 \( P(A_{win}|B_{good}) \)
Mくんの機嫌がよかった55日のうち、カープが勝利していたのは40試合なので、条件つき確率は、\[ P(A_{win}|B_{good}) = \frac{40}{55} = \frac{8}{11}\]となります。
(b) Mくんの機嫌が良いときのカープが負けた条件つき確率 \( P(A_{lose}|B_{good}) \)
Mくんの機嫌がよかった55日のうち、カープが負けていたのは15試合なので、なので条件つき確率は、\[ P(A_{win}|B_{good}) = \frac{15}{55} = \frac{3}{11}\]となります。
(c) Mくんの機嫌が悪いときのカープが勝利した条件つき確率 \( P(A_{win}|B_{bad}) \)
Mくんの機嫌が悪かった45日のうち、カープが勝利していたのは20試合なので、条件つき確率は、\[ P(A_{win}|B_{bad}) = \frac{20}{45} = \frac{4}{9}\]となります。
(d) Mくんの機嫌が悪いときのカープが敗北した条件つき確率 \( P(A_{lose}|B_{bad}) \)
Mくんの機嫌が悪かった45日のうち、カープが負けたのは25試合なので、条件つき確率は、\[ P(A_{lose}|B_{bad}) = \frac{25}{45} = \frac{5}{9}\]となります。
条件つき確率を求め終えたら、今度は「Mくんの機嫌の良し悪しが分かった場合のカープの勝敗を表す条件つきエントロピー \( H(A|B) \) 」をもとめます。Mくんの機嫌が良い確率は \( 11/20 \)、悪い確率は \( 9/20 \) なので条件つき情報量 \( H(A|B) \) は、\[ H(A|B) = - \frac{11}{20} \left( \frac{8}{11} \log_2 \frac{8}{11} + \frac{3}{11} \log_2 \frac{3}{11} \right) - \frac{9}{20} \left( \frac{4}{9} \log_2 \frac{4}{9} + \frac{5}{9} \log_2 \frac{5}{9} \right) \fallingdotseq 0.911 \]と求められます。
相互情報量は、カープの勝敗を伝える情報のエントロピー \( H(A) \) から、Mくんの機嫌が判明したときのカープの勝敗を伝える条件つきエントロピー \( H(A|B) \) を引いた値で求めることができます。よって相互情報量 \( I(A;B) \) は、\[ I(A;B) = H(A) - H(A|B) \fallingdotseq 0.971 - 0.911 = 0.060 \]と計算することができます。
(3) 2つのエントロピーと結合エントロピーの差分で求める
最後に条件付き確率を使わない方法を説明したいと思います。
| 勝利 | 敗北 | 合計 | |
| 機嫌良 | 40 | 15 | 55 |
| 機嫌悪 | 20 | 25 | 45 |
| 合計 | 60 | 40 | 100 |
まずは、次の4つの確率をもとめます。表からすべて読み取れるのでややこしい計算は必要ありません。
(a) 「カープが勝利」かつ「Aくんの機嫌が良い」確率
全100日間の中で、(a)に該当する日は40日ありました。なので確率は \( 2/5 \)
(b) 「カープが勝利」かつ「Aくんの機嫌が悪い」確率
全100日間の中で、(a)に該当する日は20日ありました。なので確率は \( 1/5 \)
(c) 「カープが敗北」かつ「Aくんの機嫌が良い」確率
全100日間の中で、(a)に該当する日は15日ありました。なので確率は \( 3/20 \)
(d) 「カープが敗北」かつ「Aくんの機嫌が悪い」確率
全100日間の中で、(a)に該当する日は25日ありました。なので確率は \( 1/4 \)
と求められます。
つぎに、(a),(b),(c),(d)の情報からなる情報源のエントロピー\( H(A;B) \) をもとめます(結合エントロピーと呼びます)。
\[ H(A;B) = - \frac{2}{5} \log_2 \frac{2}{5} - \frac{1}{5} \log_2 \frac{1}{5} - \frac{3}{20} \log_2 \frac{3}{20} - \frac{1}{4} \log_2 \frac{1}{4} \fallingdotseq 1.904 \]
相互情報量 \( I(A;B) \) は、もともとのエントロピー \( H(A) \) と \( H(B) \) から、結合エントロピー \( H(A;B) \) の差分で求められます。よって相互情報量 \( I(A;B) \) は、\[ I(A;B) = H(A) + H(B) - H(A;B) \fallingdotseq 0.971 + 0.993 - 1.904 = 0.060 \]と計算することができます。
以上3つの方法で情報量を求めることができます。
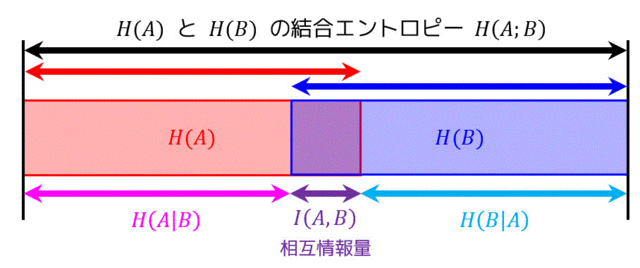
これら3つを表と式で表すとこのようになります。
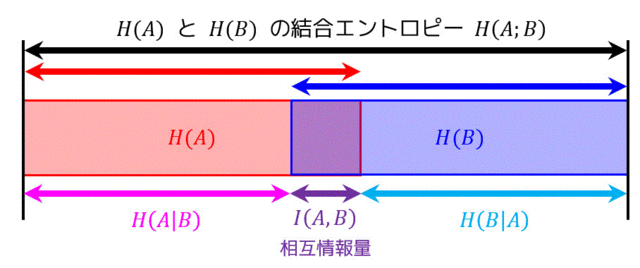
相互情報量 \( I(A;B) \) は3つの方法で求めることができる。\[\begin{align*} I(A;B) & = H(A) - H(A|B) \\ I(A;B) & = H(B) - H(B|A) \\ I(A;B) & = H(A) + H(B) - H(A;B)
\end{align*} \]
4.極端な場合の相互情報量
最後に、極端な例の場合の相互情報量を紹介したいと思います。
(1) 相互情報量が全くない状態
まずは、相互情報量がまったくない状態、言い換えると2つの情報が全く関連性のない状態を考えます。例えば、つぎのような状態を考えましょう。
情報源 \( A \) :ホークスの勝敗を伝える情報源
情報源 \( B \) :カープファンであるMくんの機嫌を伝える情報源
この2つの情報 \( A,B \) を100日間記録していったところ、つぎの表の結果が得られました。
| 勝利 | 敗北 | 合計 | |
| 機嫌良 | 45 | 30 | 75 |
| 機嫌悪 | 15 | 10 | 25 |
| 合計 | 60 | 40 | 100 |
さて、この情報源 \( A \) と情報源 \( B \) はどれほど影響を及ぼしているかを相互情報量を計算することで計算してみましょう。
今回は、ホークスの試合を基準に考えてみましょう。
相互情報量がないということは、Mくんの機嫌が良かろうが悪かろうがホークスの勝敗には関係ない、つまりMくんの機嫌によってホークスが勝利(or敗北)する条件つき確率は変わらないということになります。
ホークスが勝利する確率は \( 3/5 \)、ホークスが敗北する確率は \( 2/5 \) なので、ホークスの勝敗を伝える情報源 \( A \) のエントロピー \( H(A) \) は、\[ H(A) = - \frac{3}{5} \log_2 \frac{3}{5} - \frac{2}{5} \log_2 \frac{2}{5} \fallingdotseq 0.971\]となります。
つぎに条件つき確率を求めていきます。
| 勝利 | 敗北 | 合計 | |
| 機嫌良 | 45 | 30 | 75 |
| 機嫌悪 | 15 | 10 | 25 |
| 合計 | 60 | 40 | 100 |
(a) Mくんの機嫌が良いときのホークスが勝利した条件つき確率 \( P(A_{win}|B_{good}) \)
Mくんの機嫌がよかった75日のうち、ホークスが勝利していたのは45試合なので、条件つき確率は、\[ P(A_{win}|B_{good}) = \frac{45}{75} = \frac{3}{5}\]となります。
(b) Mくんの機嫌が良いときのホークスが負けた条件つき確率 \( P(A_{lose}|B_{good}) \)
Mくんの機嫌がよかった75日のうち、カープが負けていたのは30試合なので、なので条件つき確率は、\[ P(A_{win}|B_{good}) = \frac{30}{75} = \frac{2}{5}\]となります。
(c) Mくんの機嫌が悪いときのホークスが勝利した条件つき確率 \( P(A_{win}|B_{bad}) \)
Mくんの機嫌が悪かった25日のうち、カープが勝利していたのは15試合なので、条件つき確率は、\[ P(A_{win}|B_{bad}) = \frac{15}{25} = \frac{3}{5}\]となります。
(d)Mくんの機嫌が悪いときのホークスが敗北した条件つき確率 \( P(A_{lose}|B_{bad}) \)
Mくんの機嫌が良い確率は \( 3/4 \)、悪い確率は \( 1/4 \) なので条件つき情報量 \( H(A|B) \) は、\[ H(A|B) = - \frac{3}{4} \left( \frac{3}{5} \log_2 \frac{3}{5} + \frac{2}{5} \log_2 \frac{2}{5} \right) - \frac{1}{4} \left( \frac{3}{5} \log_2 \frac{3}{5} + \frac{2}{5} \log_2 \frac{2}{5} \right) \fallingdotseq 0.971 \]と求められます。
条件つき確率を求めると、Mくんの機嫌が良かろうが悪かろうがホークスが敗北した確率は変わらないことがわかりますね。
よって相互情報量 \( I(A;B) \) は、\[ I(A;B) = H(A) - H(A|B) = 0 \]となり、全く相互情報量がないことがわかります。
(2) 相互情報量が非常に大きい場合
相互情報量が非常に大きい場合、つまり2つの情報が非常に影響している状態を考えます。また次のような情報源を考えます。
情報源 \( A \) :ホークスの勝敗を伝える情報源
情報源 \( B \) :熱狂的なホークスファンの先生の機嫌を
この2つの情報 \( A,B \) を100日間記録していったところ、つぎの表の結果が得られました。
| 勝利 | 敗北 | 合計 | |
| 機嫌良 | 57 | 0 | 57 |
| 機嫌悪 | 0 | 43 | 43 |
| 合計 | 57 | 43 | 100 |
さて、この情報源 \( A \) と情報源 \( B \) はどれほど影響を及ぼしているかを相互情報量を計算することで計算してみましょう。
今回は、熱狂的なファンを基準に考えます。
情報源 \( B \) のエントロピー \( H(B) \) は、\[ H(B) = - \frac{57}{100} \log_2 \frac{57}{100} - \frac{43}{100} \log_2 \frac{43}{100} \fallingdotseq 0.986\]となります。
| 勝利 | 敗北 | 合計 | |
| 機嫌良 | 57 | 0 | 57 |
| 機嫌悪 | 0 | 43 | 43 |
| 合計 | 57 | 43 | 100 |
(a) ホークス勝利時の先生の機嫌が良い条件付き確率 \( P(B_{good}|A_{win}) \)
ホークスが勝った57日のうち、先生の機嫌が良いときは57日ありました。なので条件つき確率は、\[ P(B_{good}|A_{win}) = \frac{57}{57} = 1\]となります。
(b) ホークス勝利時の先生の機嫌が悪い条件付き確率 \( P(B_{good}|A_{bad}) \)
ホークスが勝った57日のうち、先生の機嫌が悪いときは0日ありました。なので条件つき確率は、\[ P(B_{good}|A_{bad}) = \frac{0}{57} = 0\]となります。
(c) ホークス敗北時の先生の機嫌が良い条件付き確率 \( P(B_{good}|A_{lose}) \)
ホークスが負けた43日のうち、先生の機嫌が良いときは0日ありました。なので条件つき確率は、\[ P(B_{good}|A_{lose}) = \frac{0}{43} = 0\]となります。
(d) ホークス敗北時の先生の機嫌が悪い条件付き確率 \( P(B_{bad}|A_{lose}) \)
ホークスが負けた43日のうち、先生の機嫌が悪いときは43日ありました。なので条件つき確率は、\[ P(B_{bad}|A_{lose}) = \frac{43}{43} = 1\]となります。
ホークスが勝つ確率は \( 57/100 \)、負ける確率は \( 43/100 \) なので条件つき情報量 \( H(A|B) \) は、\[ H(A|B) = - \frac{57}{100} \left( 1 \log_2 1 + \lim_{x \to 0} x \log_2 x \right) - \frac{43}{100} \left(\lim_{x \to 0} x \log_2 x + 1 \log_2 1 \right) = 0 \]と求められます。*4
よって相互情報量 \( I(A;B) \) は、\[ I(A;B) = H(A) - H(A|B) = H(A) \fallingdotseq 0.986 \]となります。言い換えると、\( H(A) \) か \( H(B) \) のどちらかの情報を知ることができれば、もう一方の情報はすぐわかる、ということを表します。
5.さいごに
今回は、情報の量を数値化する際に使われる情報量と情報量の期待値を表すエントロピー(平均情報量)、2つの情報にどれくらい関連性があるかを調べる相互情報量についてまとめました。
この記事が情報量についての理解の助けとなれば幸いです。
関連広告・スポンサードリンク