スポンサードリンク
こんにちは、ももやまです。
前回の「うさぎでもわかる画像処理 Part02」では、画像処理の中でも最も基本的な画像内の各画素値を自身の画素値のみを使って、一定のルールを用いて変換していく方法(トーンカーブ)について説明していきました。
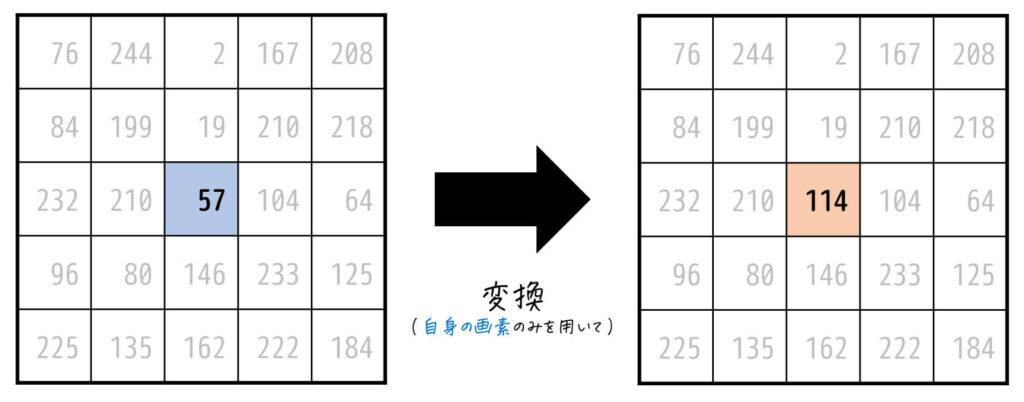
(トーンカーブ)
トーンカーブを用いた画像処理でも、様々な画像処理ができるのですが、自身の画素値のみを書き換えていく画像処理では出来ることに限りがあります。
そこで今回と次回の2回にわたって、画像内の各画素値を変換していく際に自身の画素値だけでなく、周りの画素の画素値を利用しながら画像処理をしていく方法(フィルタ、空間フィルタリングなどと呼ばれます)について学習していきましょう。
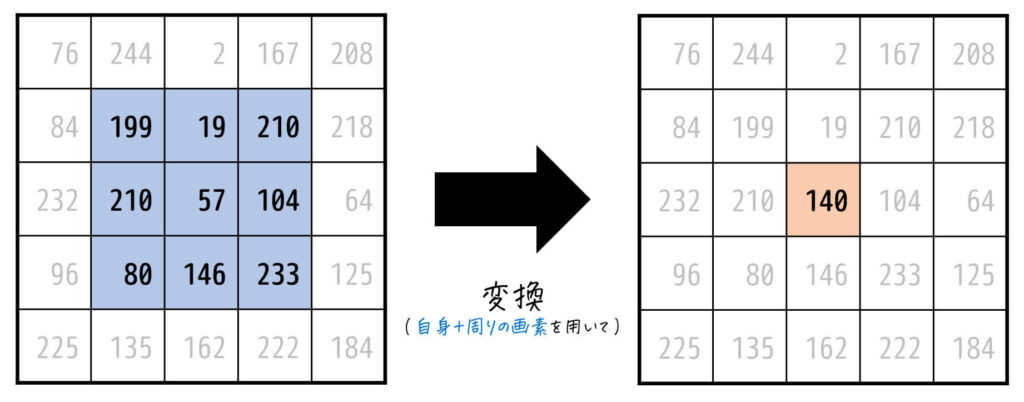
(フィルタ・空間フィルタリング)
今回の記事では、フィルタの中でも線形フィルタに着目してみていきます。
スポンサードリンク
1. 線形フィルタのいろは
(1) 線形フィルタとは
画像処理の世界で出てくるフィルタは、
- 線形フィルタ
- 非線形フィルタ
の2つに分けることができます。
さらに、入力画像 \( A \) の \( i \) 行 \( j \) 列の画素値を \( A_{i,j} \)、出力画像 \( B \) の \( i \) 行 \( j \) 列の画素値を \( B_{i,j} \) としたときに\[
B_{m,n} = \sum^{N}_{n = -N} \sum^{M}_{m = -M} A_{i+m,j+n} H_{m,n}
\]の式(たたみこみ演算)で表されるようなフィルタのことを線形フィルタとよび、このときの \( H_{m,n} \) がフィルタを表す \( 2M+1 \) × \( 2N+1 \) 行列 \( H \) の \( m \) 行 \( n \) 列の係数を表します。
例えば、下のフィルタは3×3行列で表されていますね。
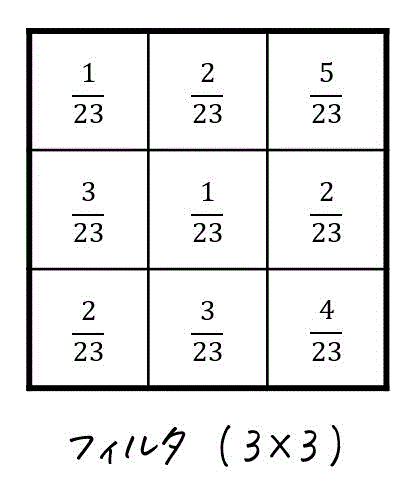
(2) 線形フィルタの計算の様子を見てみよう
では、(1)の例で出したフィルタ\[
\left( \begin{array}{ccc} \frac{1}{23} & \frac{2}{23} & \frac{5}{23} \\ \frac{3}{23} & \frac{1}{23} & \frac{2}{23} \\ \frac{2}{23} & \frac{3}{23} & \frac{4}{23} \end{array} \right)
\]を使って、たたみこみ式\[
B_{m,n} = \sum^{N}_{n = -N} \sum^{M}_{m = -M} A_{i+m,j+n} H_{m,n}
\]でどんな計算をしているかを下のアニメーションで確認してみましょう。
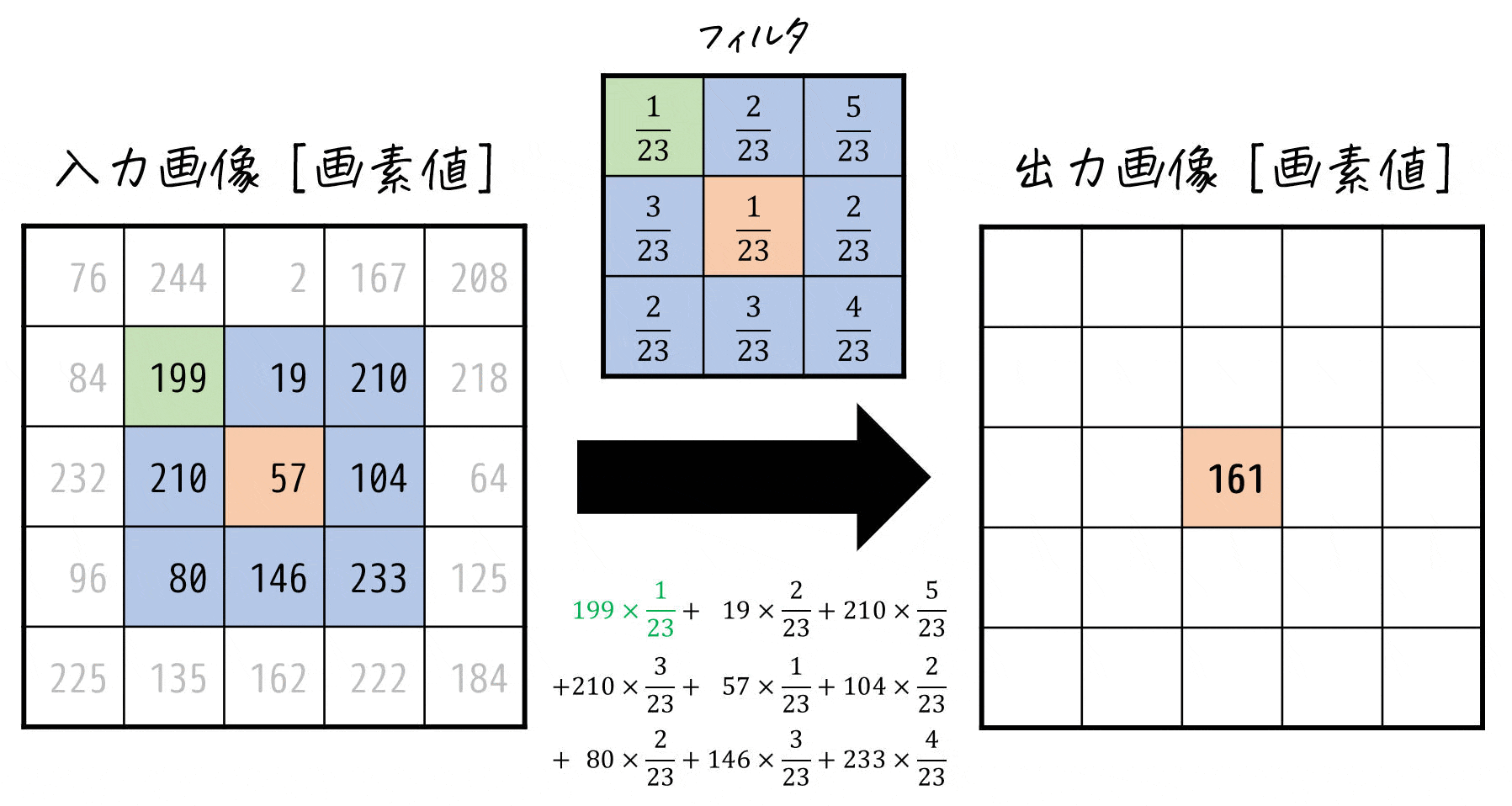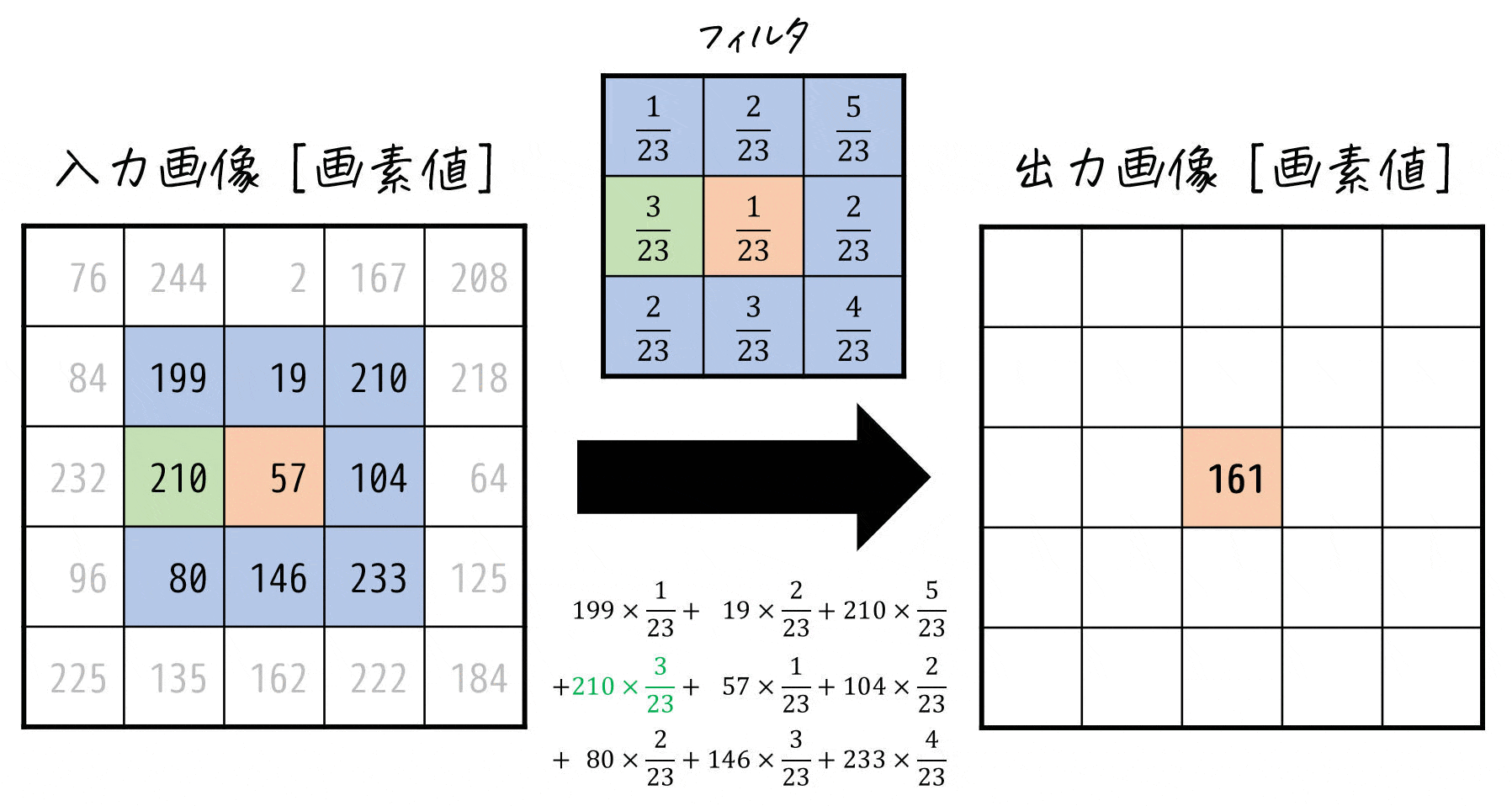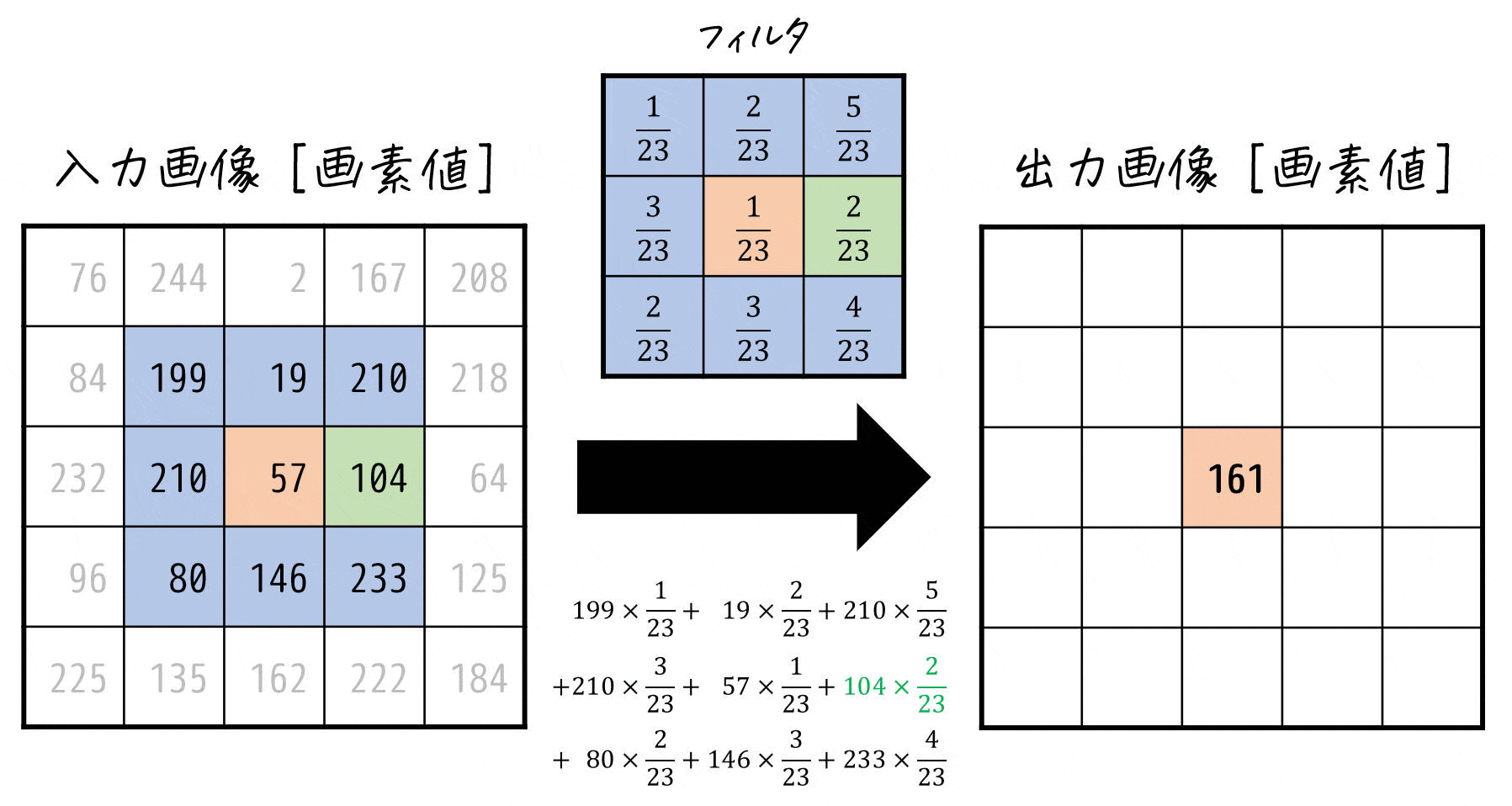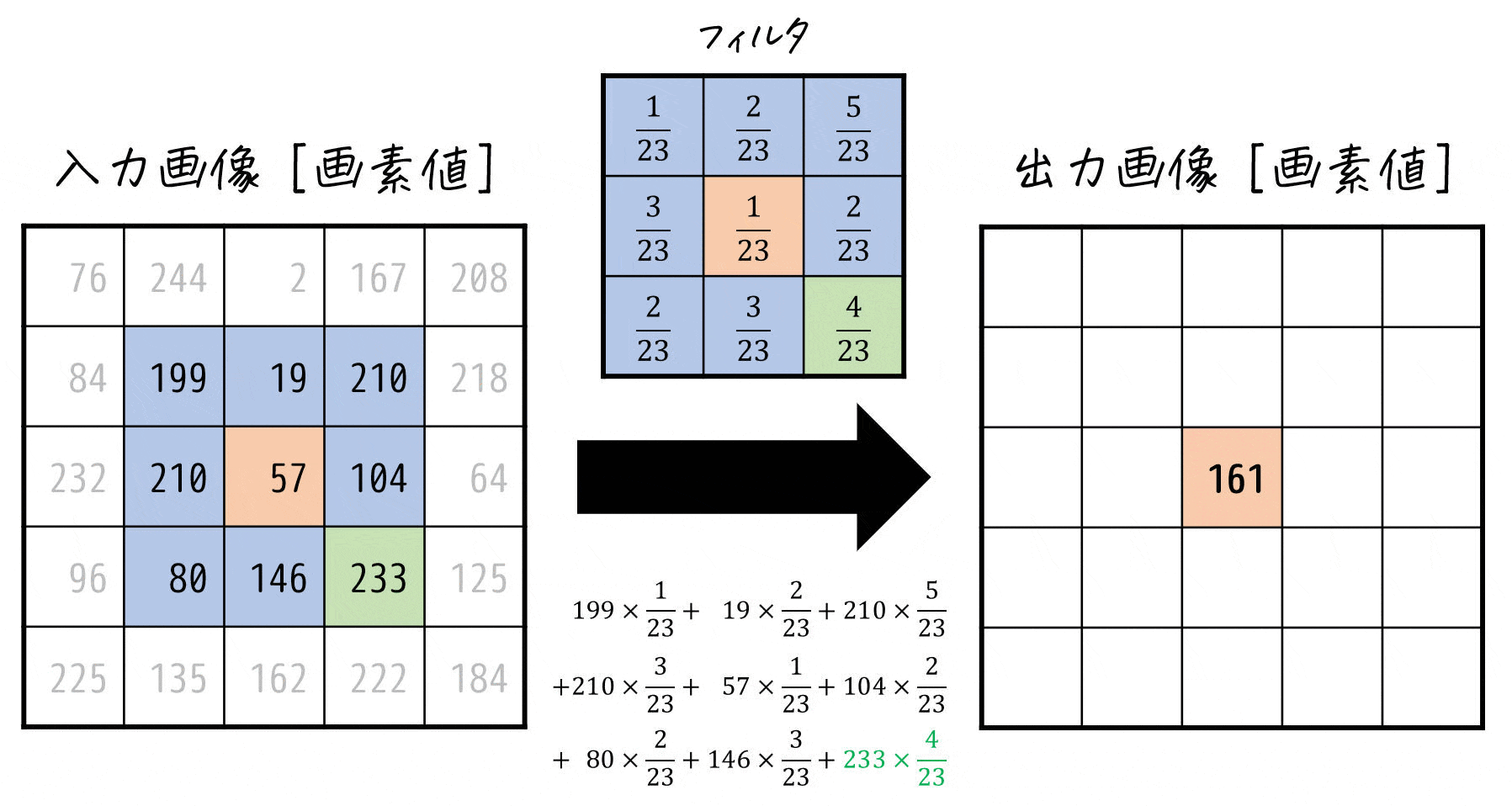
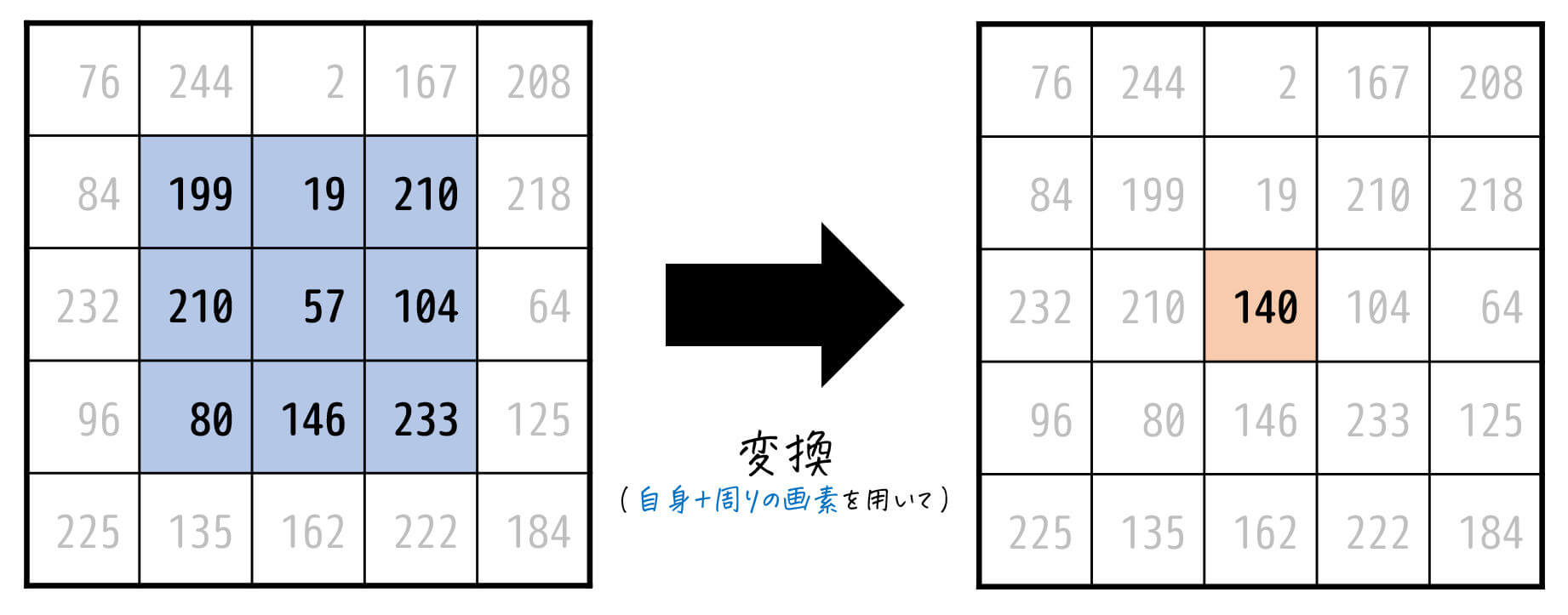
このように線形フィルタでは、着目した画素とその周囲の各画素値ごとに対応するフィルタの係数を掛け、それらをすべて足したものを着目した画素の新たな画素値とする計算を各画素ごとに行っているのです!
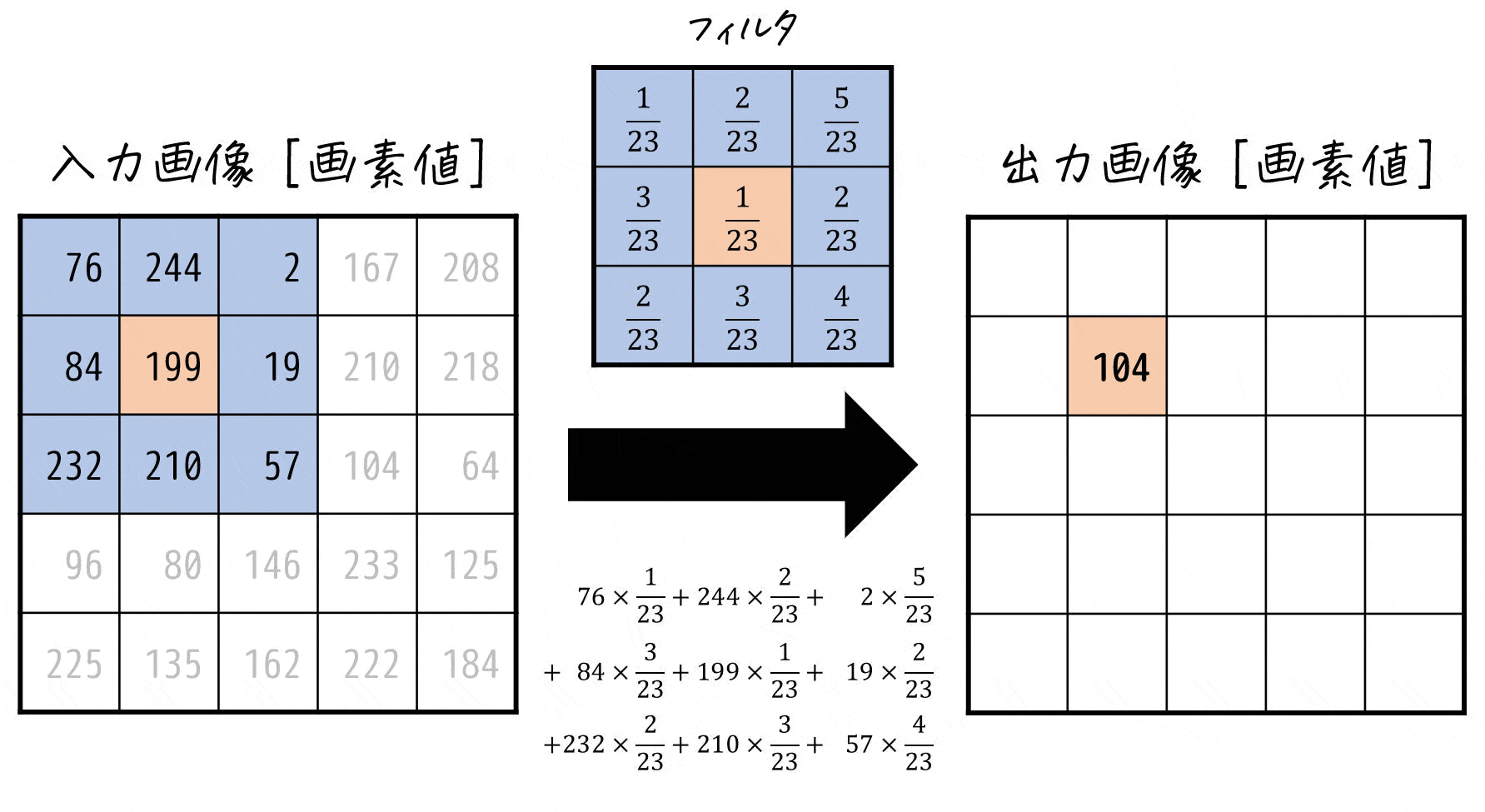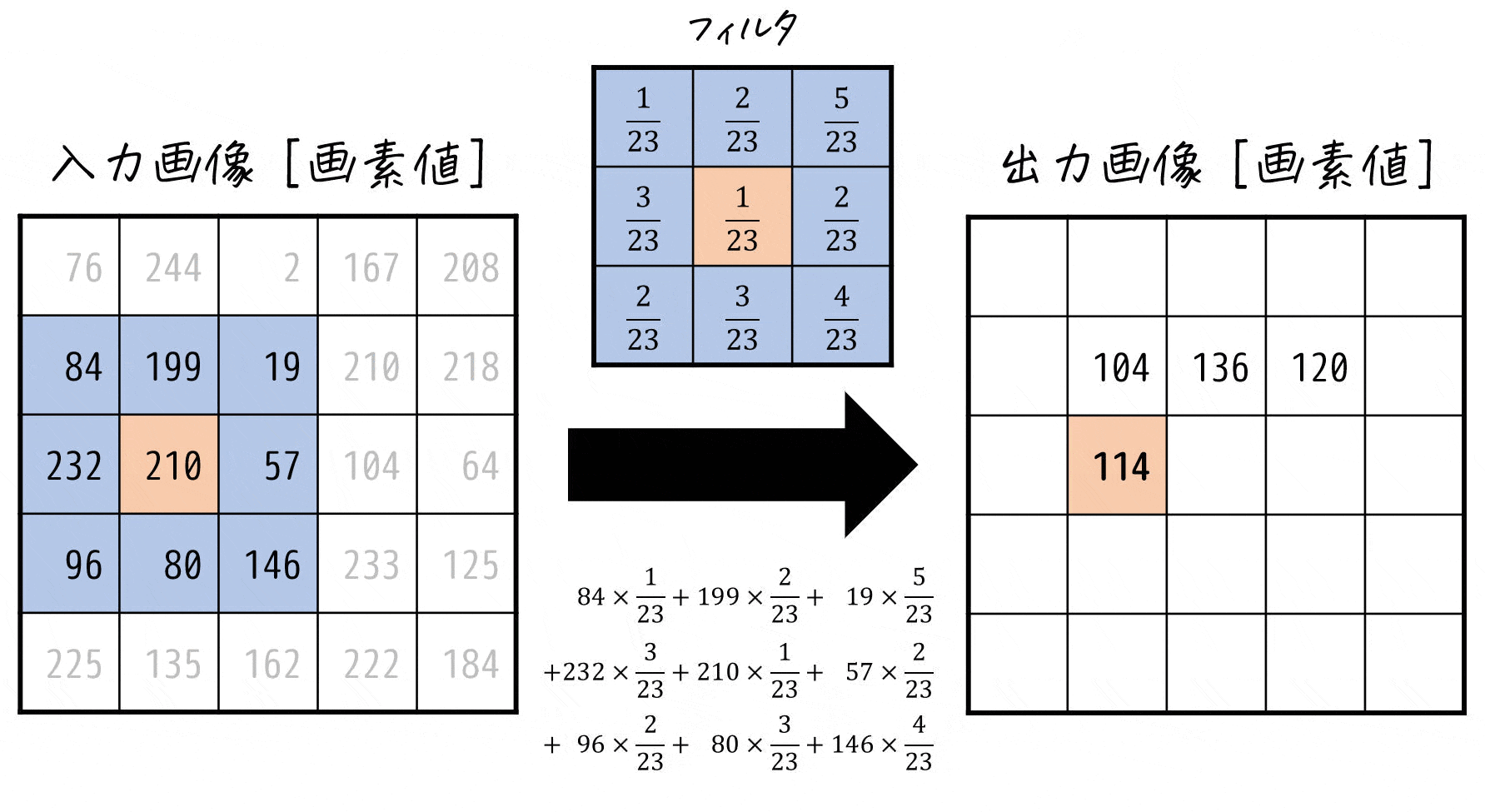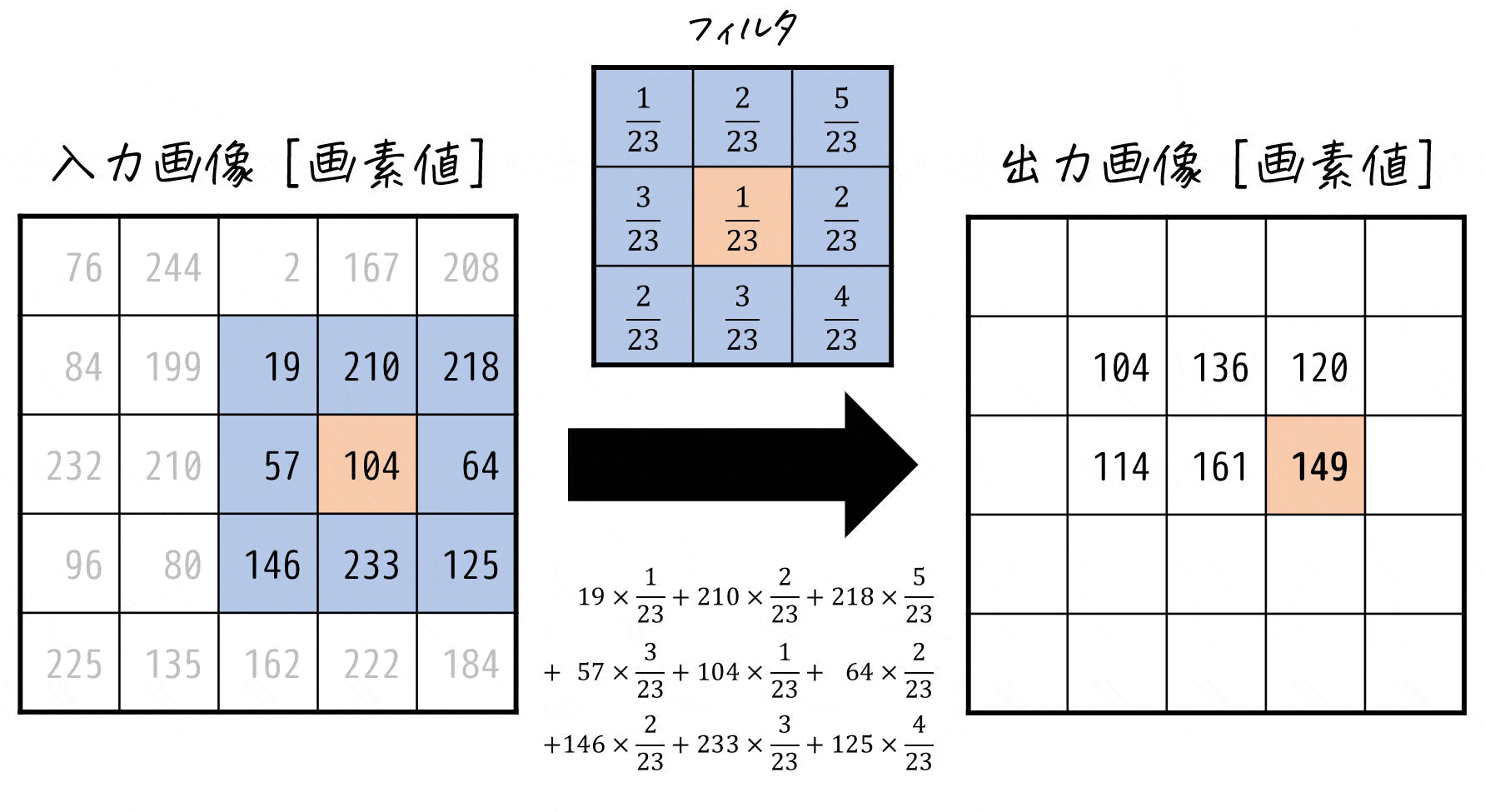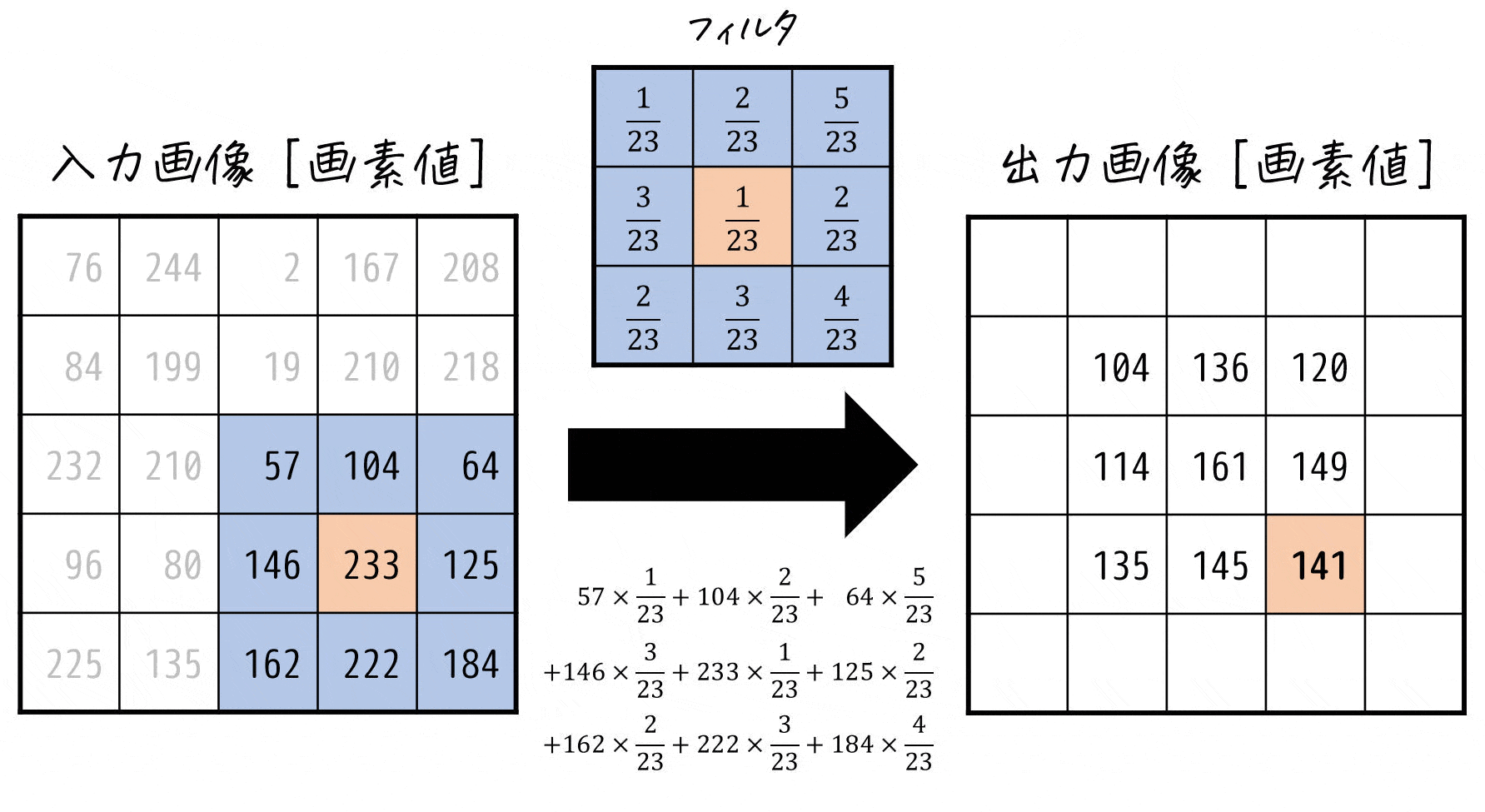
※ 端の画素をどうするかについては、様々な考え方がありますが、本記事では端の画素は画像処理をしない(=画素値0)としたいと思います。
(3) 例題で確認!
図1で表される元画像、および図2で示されるフィルタ(a), (b)がある。
(1), (2)の問いに答えなさい。
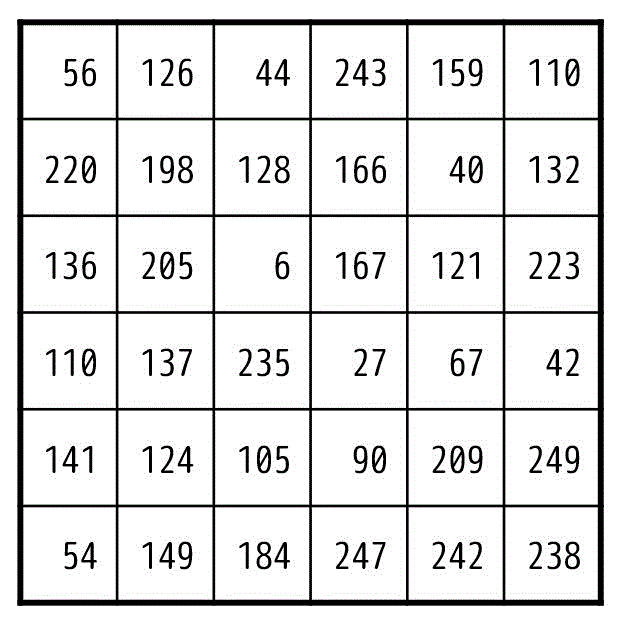
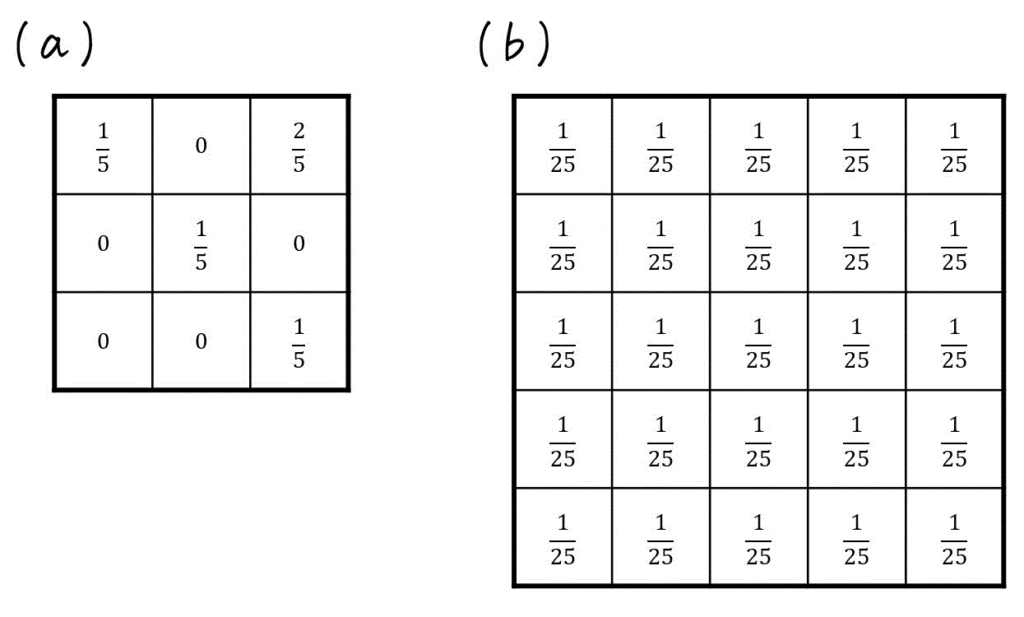
(1) フィルタ (a) を適用したときの、図3のアに当てはまる画素値を答えなさい。ただし、小数点以下を四捨五入し、整数値で答えること。
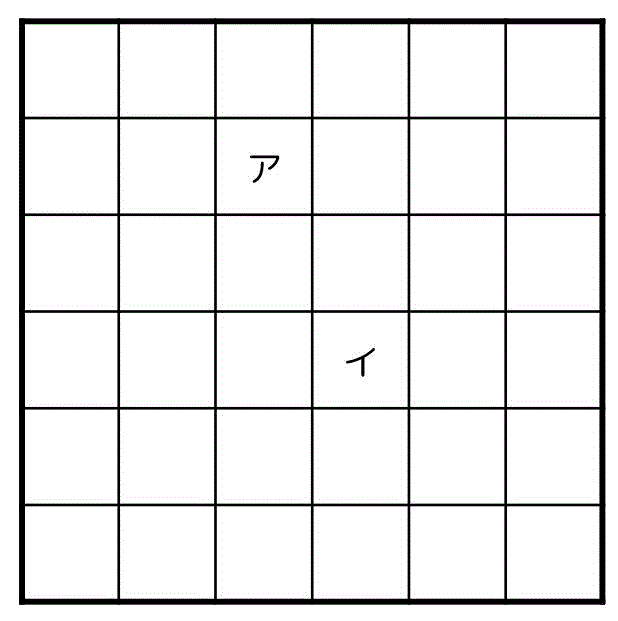
(2) フィルタ (b) を適用したときの、図3のイに当てはまる画素値を答えなさい。ただし、小数点以下を四捨五入し、整数値で答えること。
(1)
フィルタ (a) \[
\left( \begin{array}{ccc} \frac{1}{5} & 0 & \frac{2}{5} \\ 0 & \frac{1}{5} & 0 \\ 0 & 0 & \frac{1}{5} \end{array} \right)
\]を適用した場合の [ア] の画素値を求めればOK。
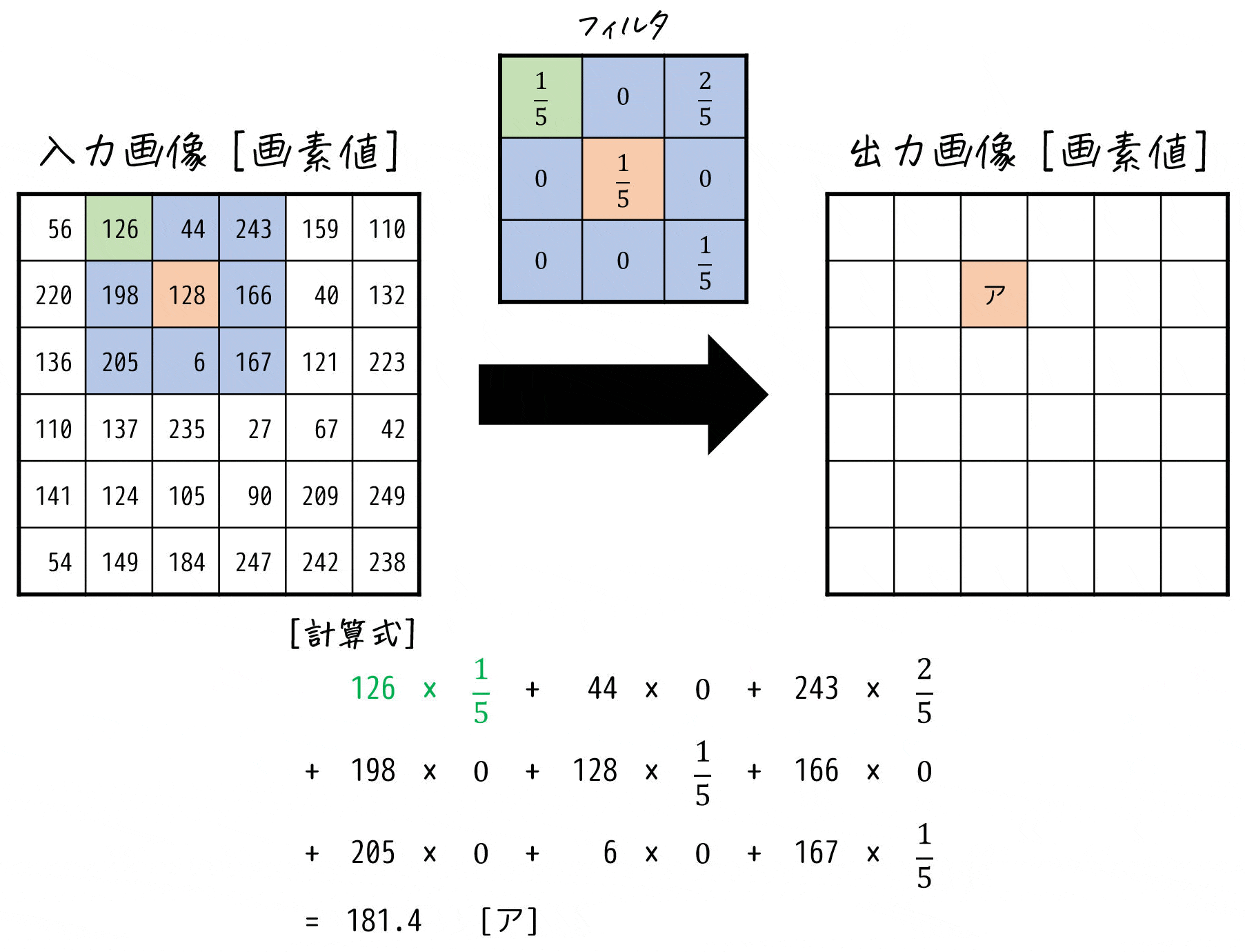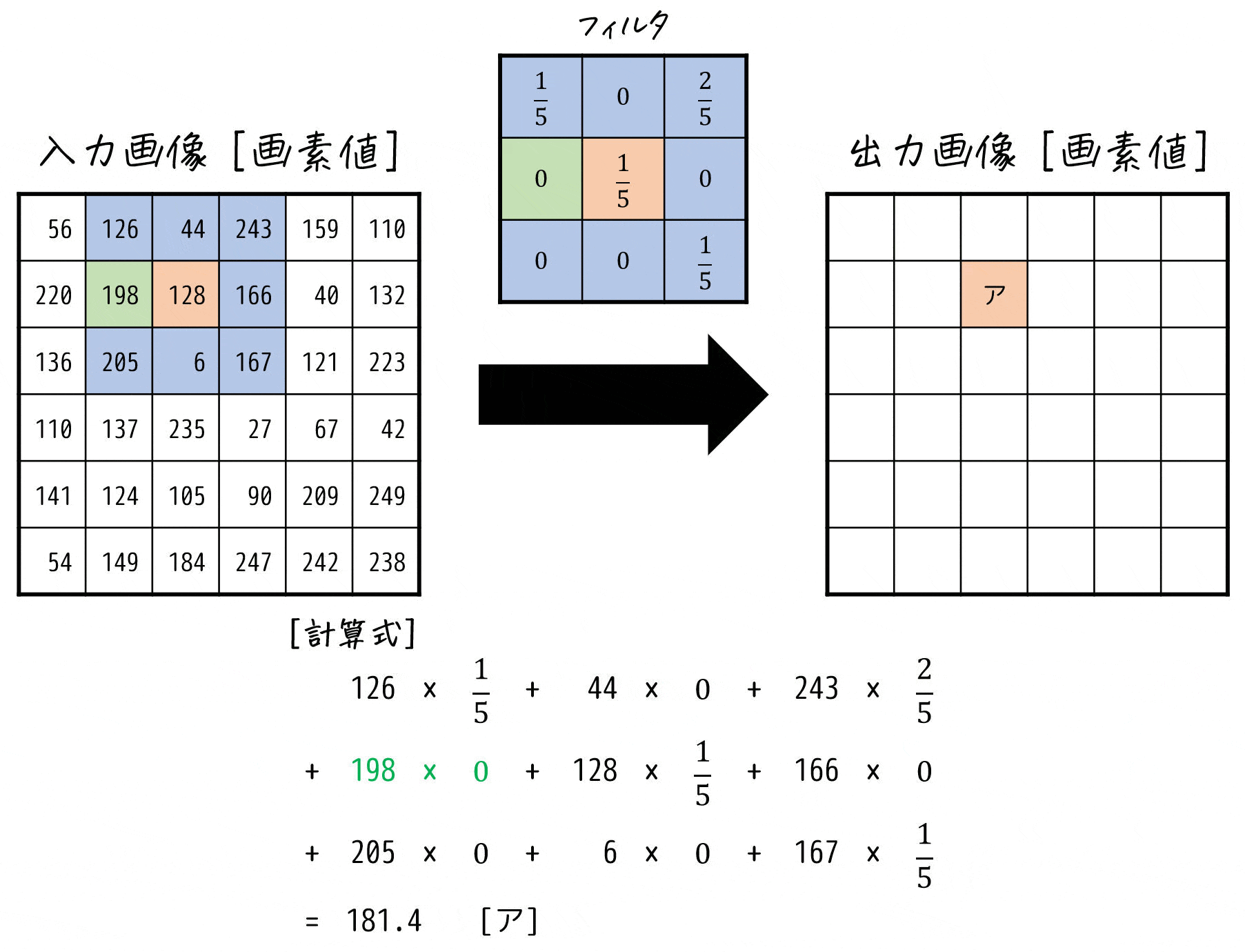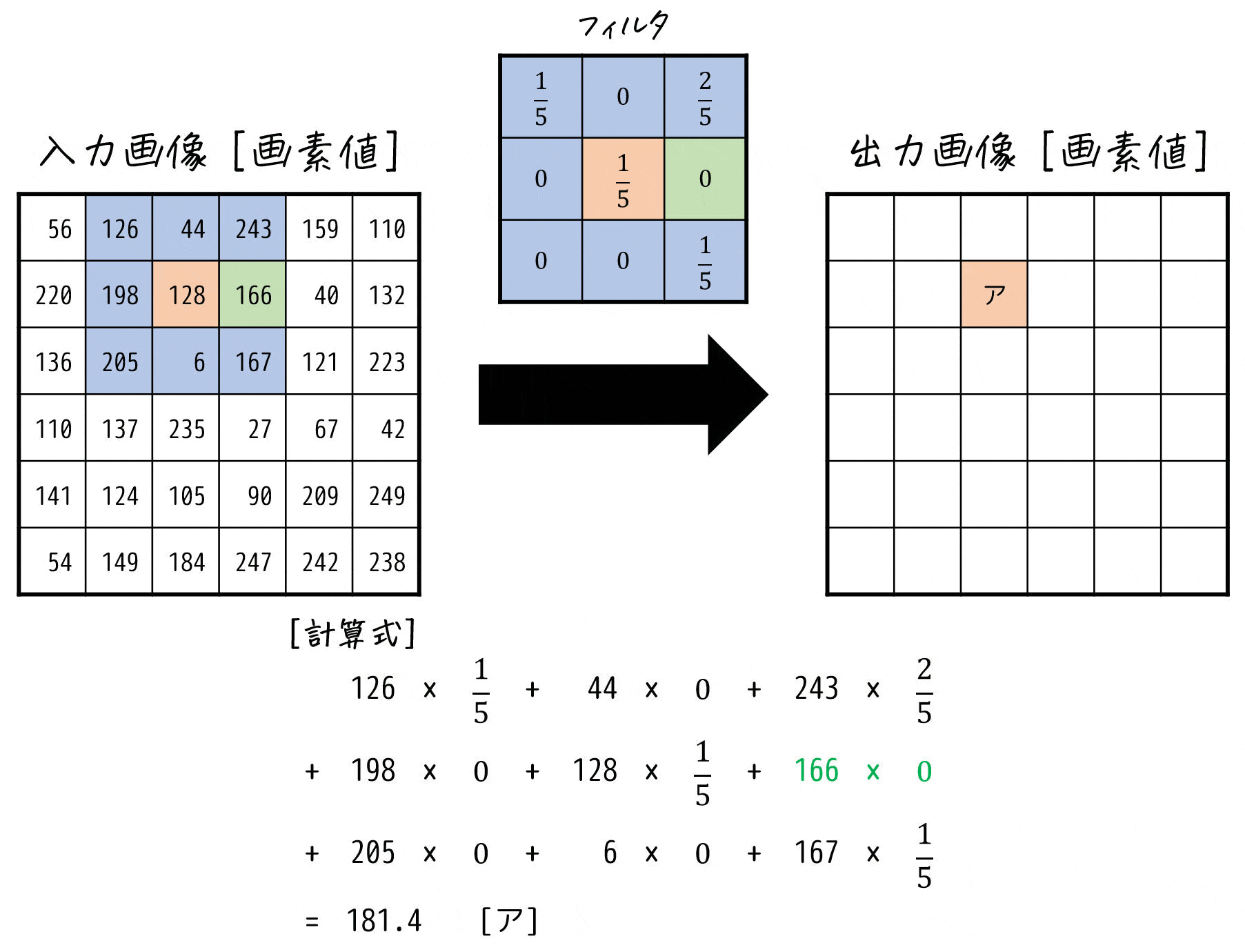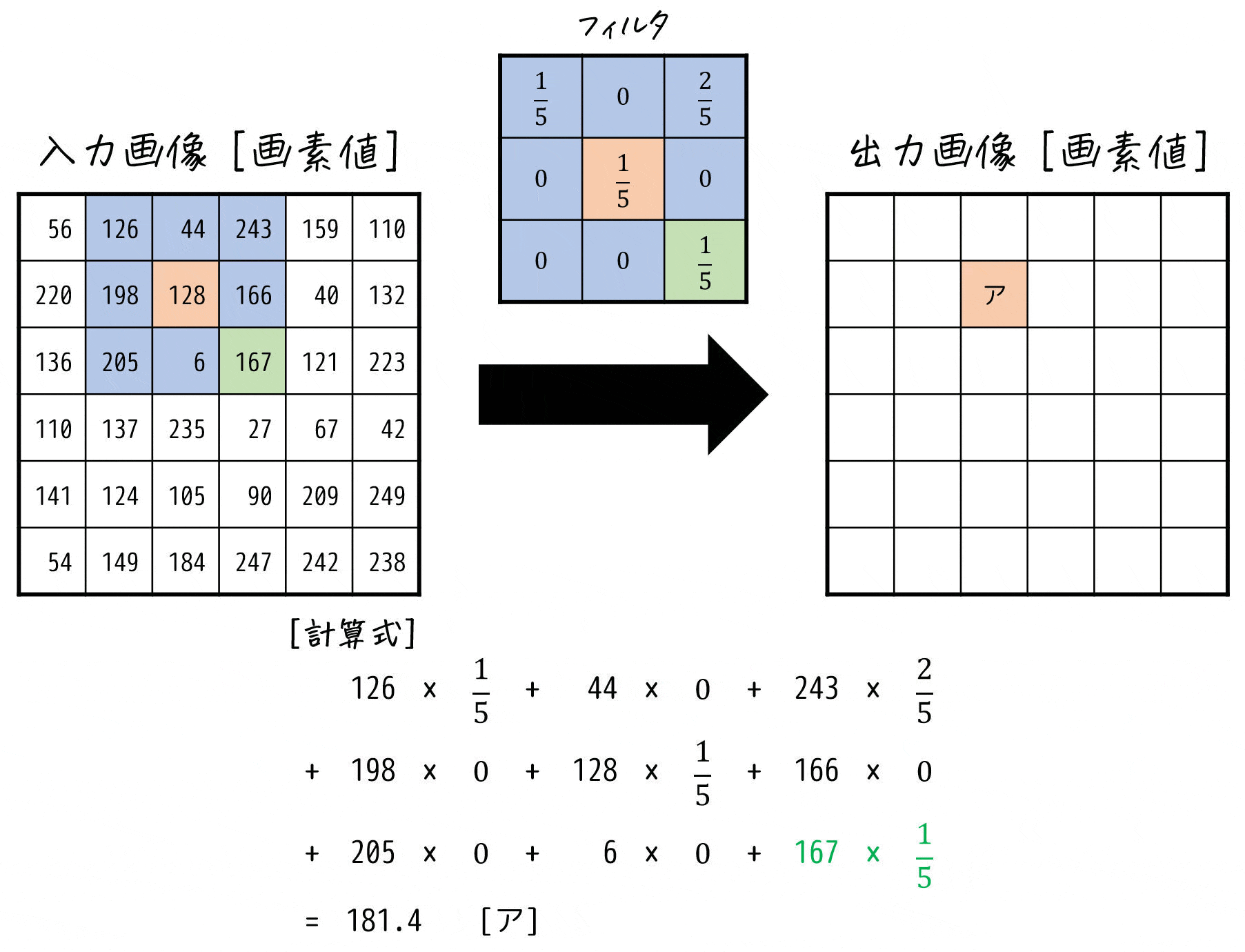
よって [ ア ] の画素値は181となる。
(2)
フィルタ (b) \[
\left( \begin{array}{ccc} \frac{1}{25} & \frac{1}{25} & \frac{1}{25} & \frac{1}{25} & \frac{1}{25} \\ \frac{1}{25} & \frac{1}{25} & \frac{1}{25} & \frac{1}{25} & \frac{1}{25} \\ \frac{1}{25} & \frac{1}{25} & \frac{1}{25} & \frac{1}{25} & \frac{1}{25} \\ \frac{1}{25} & \frac{1}{25} & \frac{1}{25} & \frac{1}{25} & \frac{1}{25} \\ \frac{1}{25} & \frac{1}{25} & \frac{1}{25} & \frac{1}{25} & \frac{1}{25} \end{array} \right)
\]を適用した場合の [イ] の画素値を求めればOK。
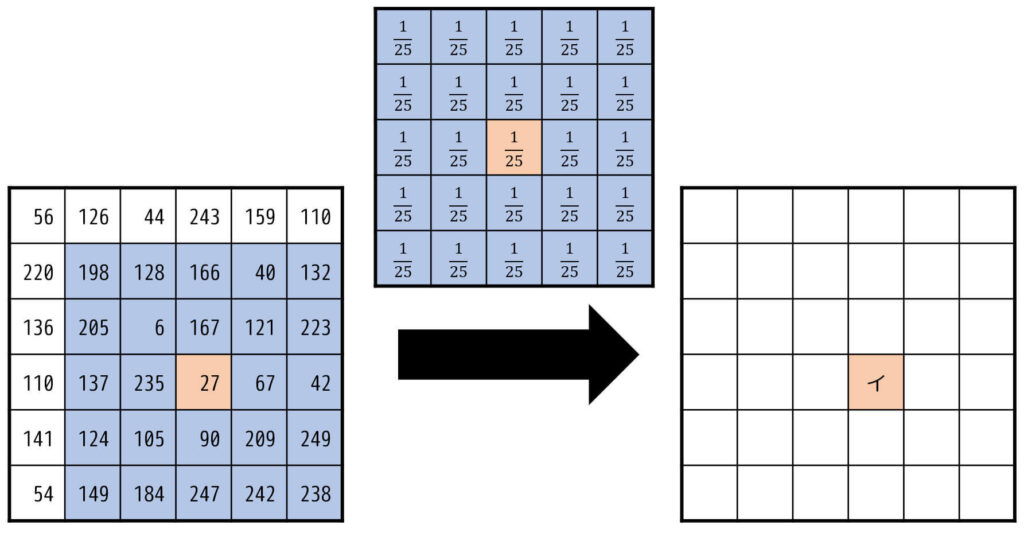
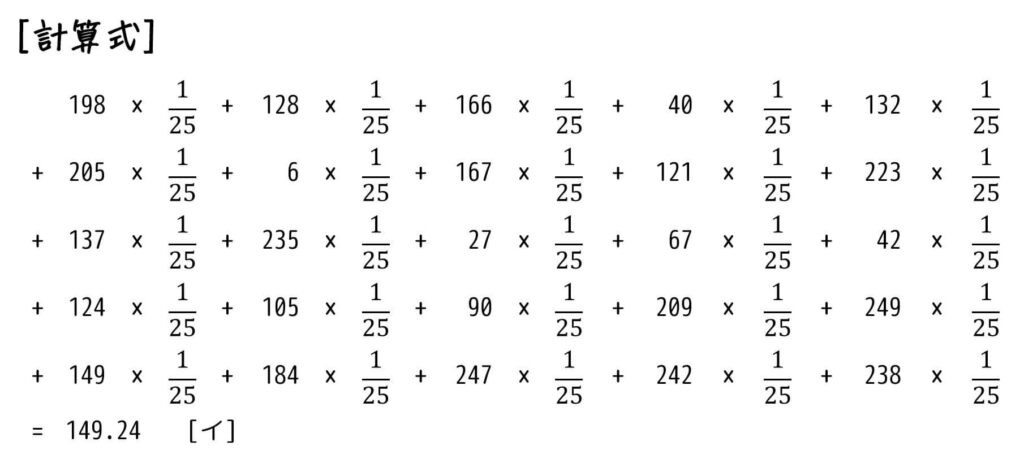
よって [ イ ] の画素値は149となる。
(4) 線形フィルタの演算をする関数(ソースコード)
実際に入力画像と線形フィルタを設定すると、画像処理を行う関数をPythonとMATLABで作成しました。
Python
def applyFilter(img,filt):
# 入力画像のサイズ取得
img_row = img.shape[0]
img_col = img.shape[1]
# フィルタのサイズ取得 (適さないフィルタサイズの場合はエラーを返す)
filt_row = filt.shape[0]
filt_col = filt.shape[1]
if (filt_row % 2 == 0) or (filt_col % 2 == 0):
print("フィルタサイズ設定に誤りがあります。")
return img
# 結果画像初期化
result_img = np.zeros( (img_row,img_col) )
# フィルタの中心部分算出
filt_mid = int(filt_row / 2)
# フィルタ適用
for row in range(img_row):
for col in range(img_col):
if (row - filt_mid < 0) or (col - filt_mid < 0) or ( (row + filt_mid >= img_row) ) or ( (col+ filt_mid >= img_col) ):
continue # 端の画素は無視 (画素値0)
tmp_result = img[row - filt_mid:row + filt_mid + 1,col - filt_mid:col + filt_mid + 1] # 計算に使う周りの画素取得
tmp_result = tmp_result * filt
result_img[row,col] = round(np.sum(tmp_result))
return result_img
MATLAB
function [result_img] = applyFilter(img,filt)
img_row = size(img,1);
img_col = size(img,2);
filt_row = size(filt,1);
filt_col = size(filt,2);
if mod(filt_row,2) == 0 || mod(filt_col,2) == 0
disp("フィルタサイズ設定に誤りがあります。");
result_img = img;
return
end
result_img = zeros(img_row,img_col,'uint8');
filt_mid = uint32(filt_row / 2) - 1; % MATLABは要素が1スタートなのでPythonに慣れている人は注意!
for row = 1:img_row
for col = 1:img_col
if (row - filt_mid < 1) || (col - filt_mid < 1) || (row + filt_mid > img_row) || (col + filt_mid > img_col)
continue % 端は無視 (画素値0とする)
end
tmp_result = img(row - filt_mid:row + filt_mid,col - filt_mid:col + filt_mid); % 計算に使う周りの画素取得
tmp_result = double(tmp_result) .* filt;
result_img(row,col) = uint8(sum(tmp_result,'all'));
end
end
end
フィルタについての確認ができたところで、ここからは画像処理の世界によく出てくる代表的なフィルタを見ていきましょう。
スポンサードリンク
2. 平滑化
ここでは、元の画像の画素値変化(濃淡変化)を小さくするフィルタを紹介します。
平滑化フィルタを適用することで、画像の濃淡変化を小さくした画像(=元画像をぼかした画像)を生成することができます。
(1) 平均化フィルタ (移動平均フィルタ)
各画素を「自分自身とその周りの画素値の平均値」を新たな画素値とするフィルタです。\[\left( \begin{array}{ccc} \frac{1}{9} & \frac{1}{9} & \frac{1}{9} \\ \frac{1}{9} & \frac{1}{9} & \frac{1}{9} \\\frac{1}{9} & \frac{1}{9} & \frac{1}{9} \end{array} \right), \ \ \
\left( \begin{array}{ccc} \frac{1}{25} & \frac{1}{25} & \frac{1}{25} & \frac{1}{25} & \frac{1}{25} \\ \frac{1}{25} & \frac{1}{25} & \frac{1}{25} & \frac{1}{25} & \frac{1}{25} \\ \frac{1}{25} & \frac{1}{25} & \frac{1}{25} & \frac{1}{25} & \frac{1}{25} \\ \frac{1}{25} & \frac{1}{25} & \frac{1}{25} & \frac{1}{25} & \frac{1}{25} \\ \frac{1}{25} & \frac{1}{25} & \frac{1}{25} & \frac{1}{25} & \frac{1}{25} \end{array} \right)
\]
「自分自身とその周りの画素値の平均」をとるため、隣り合う画素同士の画素値の差が減り、濃淡変化が緩やかになるため、元画像をぼかした画像が生成されます。
例えば下の変換は、自分+周り1画素の平均値をとった3×3の平均化フィルタを表します。
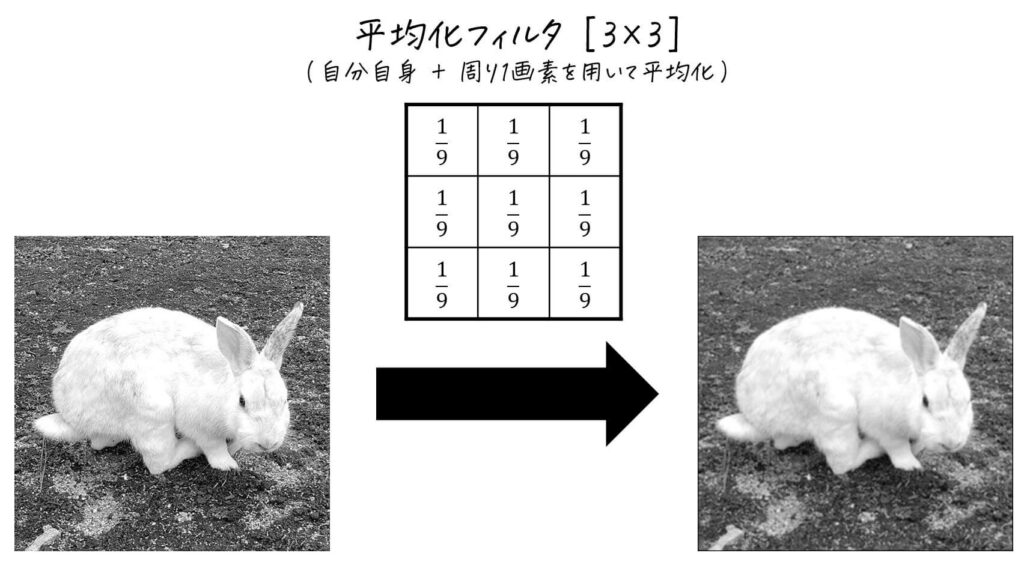
「自分+周り2画素」をとった5×5のフィルタを使った平均化も見てみましょう。

2つの変換を比べてみると、より広い周囲の画素値の平均をとった5×5フィルタの方が、よりぼかされた画像が生成されているのが特徴です。

(2) 加重平均化フィルタ [重み付き平均化]
平均化をする際に単純に平均化するのではなく、下のように「自分自身の画素(フィルタの中心)に近いほど重み大、遠いほど重み小」なフィルタを使って平均化をすることがあります。
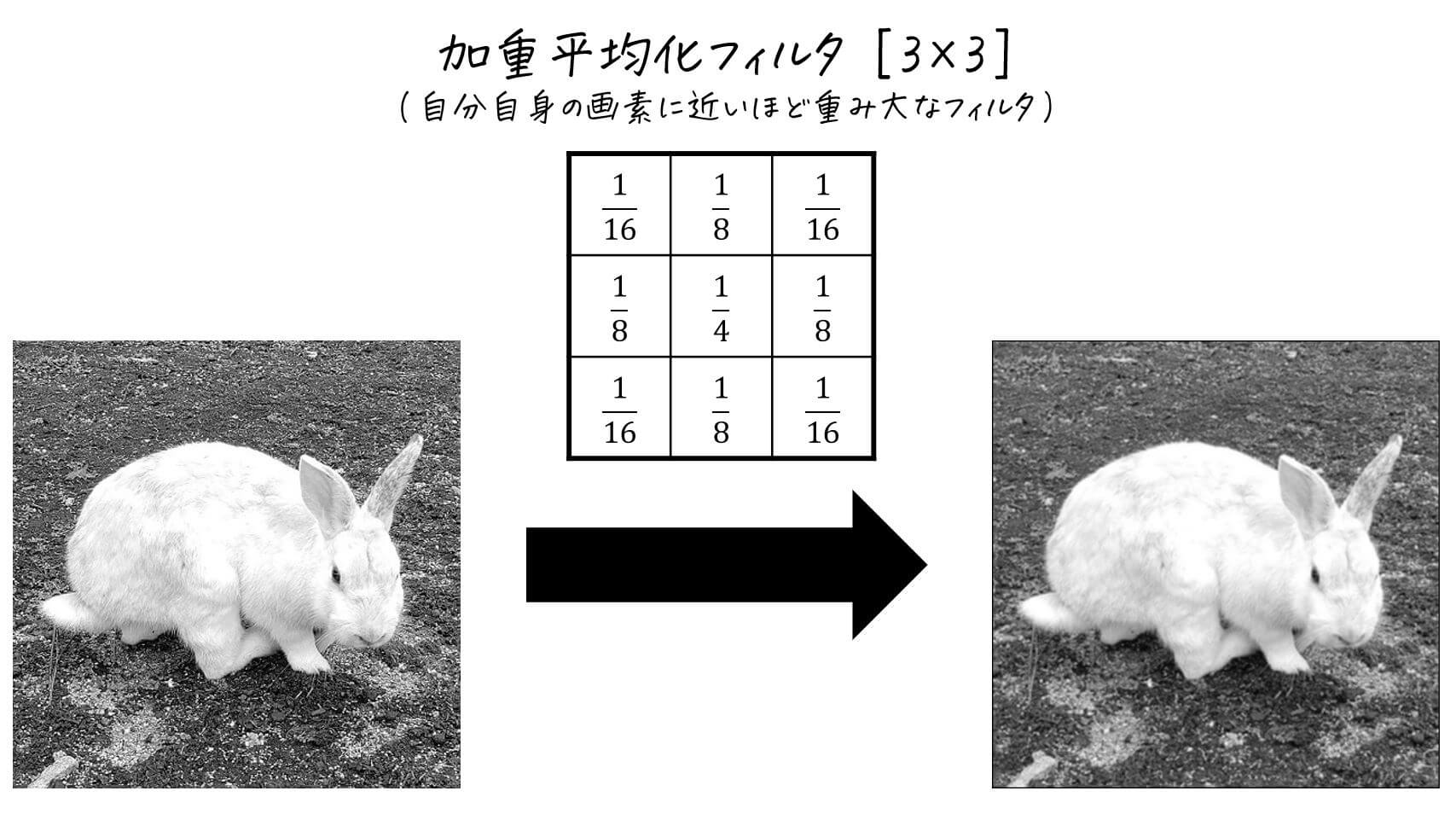
このようなフィルタのことを加重平均化フィルタと呼び、加重平均化フィルタを使って平均化をすることを重み付き平均化と呼びます。
また、フィルタの重みをガウス分布(正規分布)\[
h_{x,y} = \frac{1}{2 \pi \alpha^2} e^{ - \frac{x^2 + y^2}{2 \alpha^2} }
\]に近づけたフィルタのことをガウシアンフィルタと呼びます。
(3) 特定方向への平滑化
特定方向へ画像をぼかすことができるフィルタもあります。
(i) 横方向へ平滑化
横方向のみに対して画素値の平均を取っていきます。
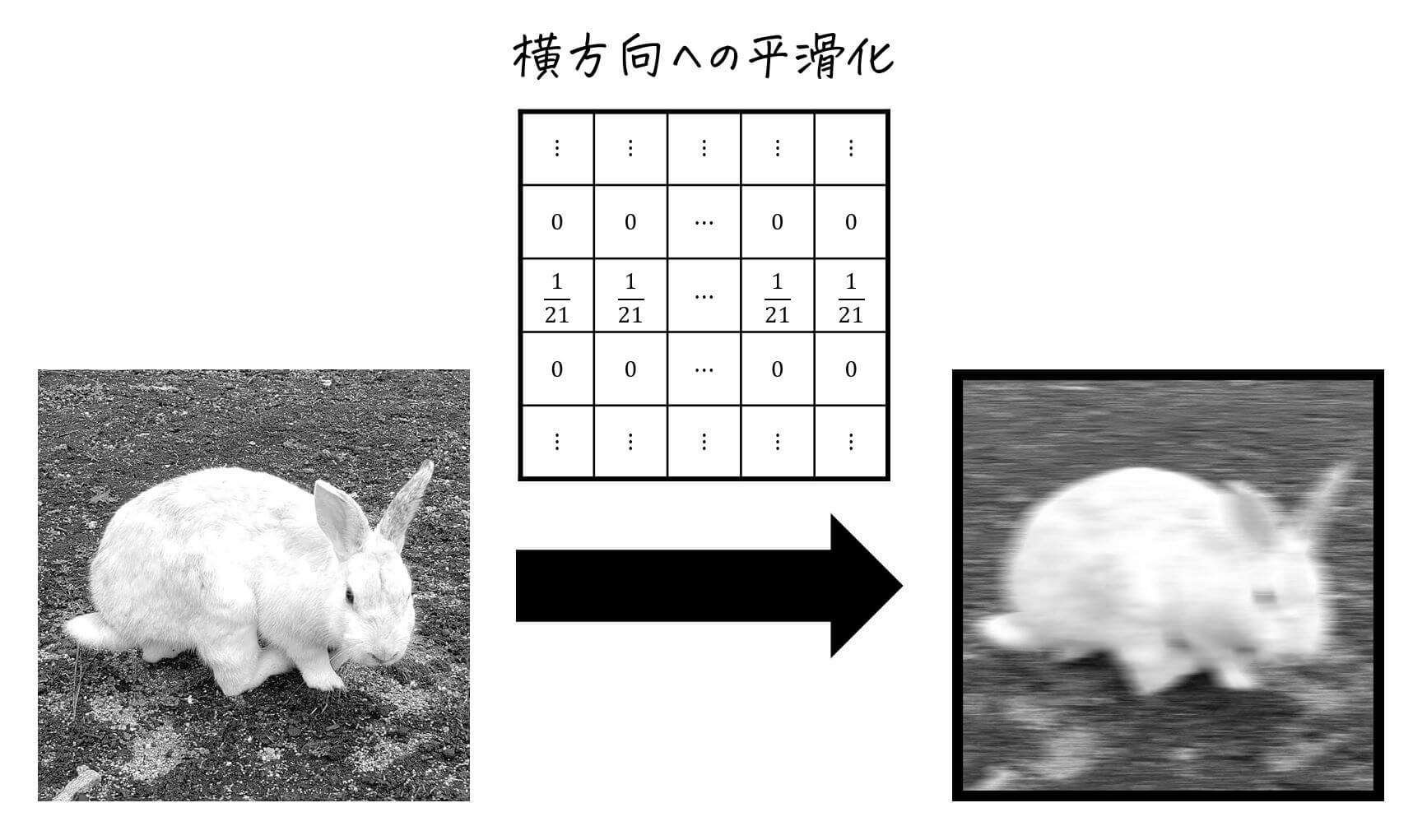
例えば上の例の場合、自分自身の画素と横±10画素の画素値の平均\[
B_{x,y} = \frac{1}{21} \left( A_{x-10,y} + A_{x-9,y} + \cdots + A_{x,y} + \cdots + A_{x+9,y} + A_{x+10,y} \right)
\]を取っています。
※注意(以後同様)
- \( A_{x,y} \) が元画像、\( B_{x,y} \) が変換後の \( x \) 行 \( y \) 列の画素値を表しています。
- 横方向を \( x \)、縦方向を \( y \) としています。
(ii) 縦方向へ平滑化
縦方向のみに対して画素値の平均を取っていきます。
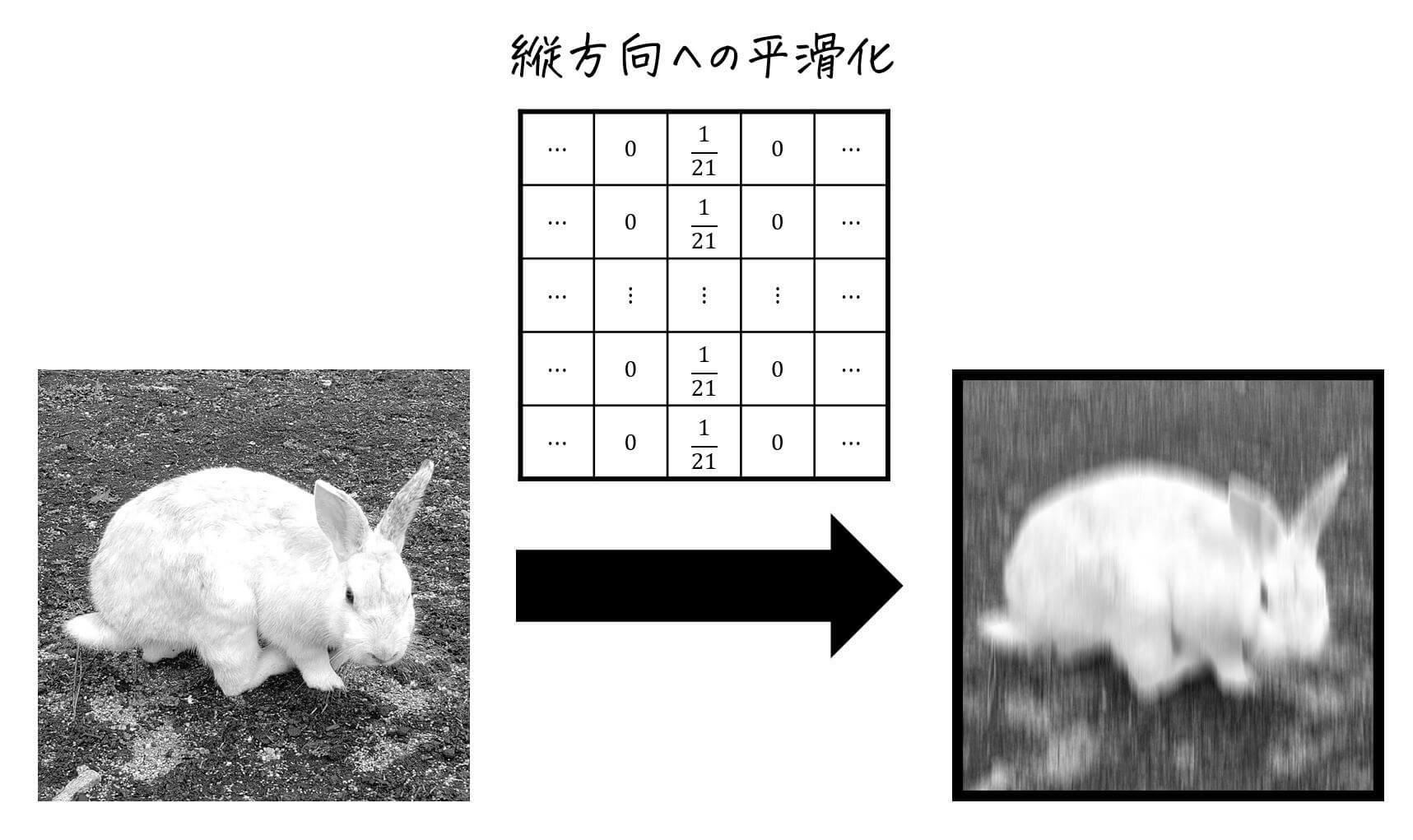
例えば上の例の場合、自分自身の画素と縦±10画素の画素値の平均\[
B_{x,y} = \frac{1}{21} \left( A_{x,y-10} + A_{x,y-9} + \cdots + A_{x,y} + \cdots + A_{x,y+9} + A_{x,y+10} \right)
\]を取っています。
(iii) 斜め方向へ平滑化
左上方向から右下方向に対して画素値の平均を取っていきます。
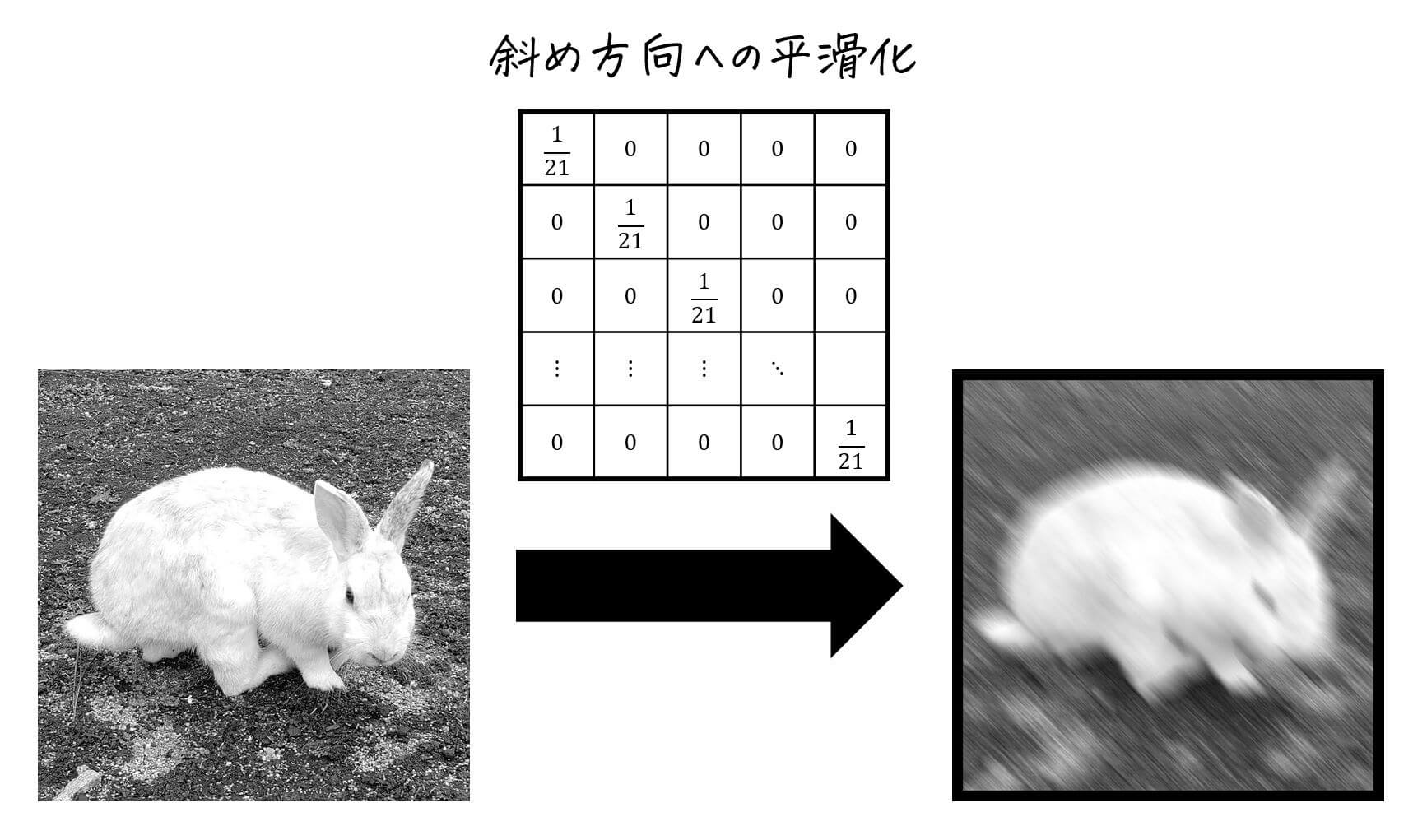
例えば上の例の場合、基準に左上方向から右下方向に向かって±自分自身の画素10画素の画素値の平均\[
B_{x,y} = \frac{1}{21} \left( A_{x-10,y-10} + A_{x-9,y-9} + \cdots + A_{x,y} + \cdots + A_{x+9,y+9} + A_{x+10,y+10} \right)
\]を取っています。
スポンサードリンク
3. 鮮鋭化
「3. 平滑化」で出てきたフィルタ、 元の画像の画素値変化(濃淡変化)を小さくすることで、元画像をぼかした画像を生成するフィルタでしたね。
鮮鋭化は、「3. 平滑化」とは反対に元の画像の画素値変化(濃淡変化)を大きくする変換をするフィルタです。
鮮鋭化フィルタを適用することで、画像の濃淡変化を大きくした画像(=元画像のエッジを強調した画像)を生成することができます。
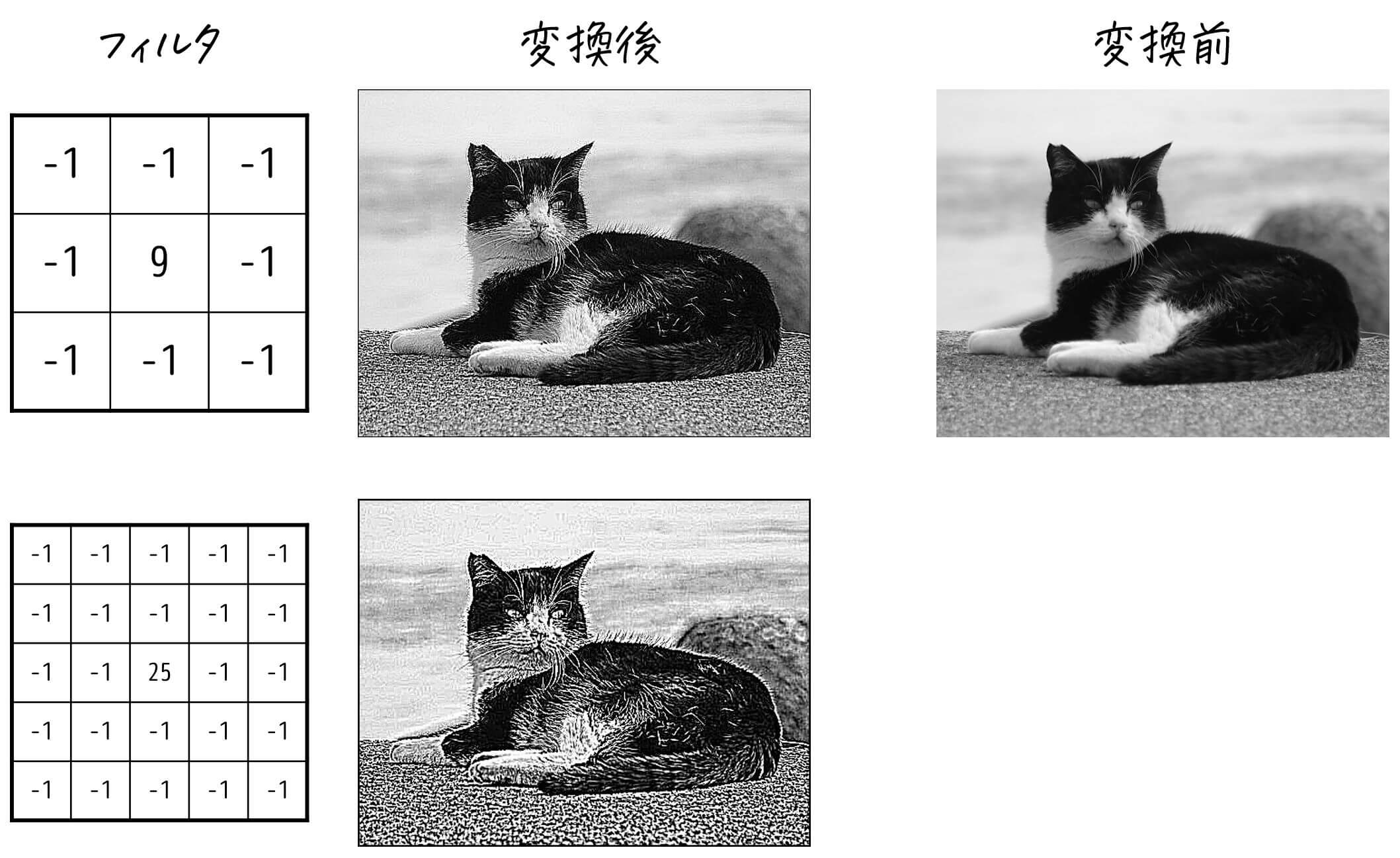
具体的には、各画素ごとに、「自分自身の画素を定数倍(=強調)し、周りの画素値を一定量引いたもの」を新たな画素値にしていきます。\[\left( \begin{array}{ccc} \textcolor{blue}{-1} & \textcolor{blue}{-1} & \textcolor{blue}{-1} \\ \textcolor{blue}{-1} & \textcolor{red}{9} & \textcolor{blue}{-1} \\ \textcolor{blue}{-1} & \textcolor{blue}{-1} & \textcolor{blue}{-1} \end{array} \right), \ \ \
\left( \begin{array}{ccc} \textcolor{blue}{-1} & \textcolor{blue}{-1} & \textcolor{blue}{-1} & \textcolor{blue}{-1} & \textcolor{blue}{-1} \\ \textcolor{blue}{-1} & \textcolor{blue}{-1} & \textcolor{blue}{-1} & \textcolor{blue}{-1} & \textcolor{blue}{-1} \\ \textcolor{blue}{-1} & \textcolor{blue}{-1} & \textcolor{red}{25} & \textcolor{blue}{-1} & \textcolor{blue}{-1} \\ \textcolor{blue}{-1} & \textcolor{blue}{-1} & \textcolor{blue}{-1} & \textcolor{blue}{-1} & \textcolor{blue}{-1} \\ \textcolor{blue}{-1} & \textcolor{blue}{-1} & \textcolor{blue}{-1} & \textcolor{blue}{-1} & \textcolor{blue}{-1} \end{array} \right)
\]
「自分自身の画素値を定数倍+周りの画素値を一定値引く」ため隣り合う画素同士の画素値の差が増え、濃淡変化が大きくなるため、元画像のエッジを強調した画像が生成されます。

なお、「3. 平滑化」のときと同じように、範囲が広いフィルタの方が、よりフィルタが強く作用します。
4. 1次微分によるエッジ抽出
皆さんは高校時代に「微分」について学びましたね。
ここで、「画像処理の世界でも微分って出てくるの?」と思った人も多いと思います。実は、微分
(1) 画素の微分とは
ある関数 \( f(x) \) を微分したもの(導関数) \( f'(x) \) は\[
f'(x) = \lim_{h \to 0} \frac{f(x+h) - f(x)}{h}
\]で計算できるのでしたね。
日本語でいうと、「\( x \) をほんの少し増やしたときの、\( f(x) \) の変化の度合い」を表したのが導関数ですね。
なので、画像を微分すると「画素値の変化の度合い」が得られそうな感じがしますね。さらに、「画素値の変化の度合い」を得ることで、特に画素値が変化している部分(=エッジ)を得ることができます。
しかし、微分をフィルタとして取り入れるためには、以下の2つの問題を解決する必要があります。
- 画像 \( A_{x,y} \) を関数として見る場合、1変数 \( f(x) \) ではなく、横方向 \( x \)、縦方向 \( y \) の2変数関数 \( f(x,y) \) で表現する必要があること
- \( h \to 0 \) という極限操作が画像処理の世界ではできないこと
というわけで、1つずつ順番に解決していきましょう。
(i) 2変数関数の微分とは
2変数関数 \( f(x,y) \) の微分ですが、下のように「\( x \) での微分」と「\( y \) での微分」のように、微分する変数を1つ指定し、それ以外の変数を定数として考えることで、高校時代で習った1変数の微分と同じような感覚で微分ができます。\[
\textcolor{blue}{ f_x(x,y) = \lim_{h \to 0} \frac{f(x+h,y) - f(x,y)}{h} }
\]\[
\textcolor{red}{ f_y(x,y) = \lim_{h \to 0} \frac{f(x,y+h) - f(x,y)}{h} }
\]この方法のことを、偏微分と呼びます。
※ 偏微分についてもっと知りたい人は、偏微分についての記事のリンクを貼っているので是非こちらのリンクをご覧ください。
[注意]
単に \( f'(x,y) \) と表すと \( x \), \( y \) どちらの変数で微分したかわからなくなるので、
- \( f(x,y) \) を \( x \) で微分した場合 → \( f_x (x,y) \)
- \( f(x,y) \) を \( y \) で微分した場合 → \( f_y (x,y) \)
と表記することにします[1]なお、偏微分を正式に表す場合は、\[
f_x (x,y) = \frac{ \partial }{ \partial x } f(x,y) , \ \ \ f_y (x,y) = \frac{ \partial }{ \partial y } f(x,y)
\]と表記します。。
(ii) 画像処理での微分の表現
画像処理は、1画素単位での処理となるため、\( h \to 0 \) のように「0に近づける」のような操作ができません。
そこで、画像処理で微分を表現する場合は\[
f_x = \frac{f(x+h,y) - f(x,y)}{h}
\]\[
f_y = \frac{f(x,y+h) - f(x,y)}{h}
\]に対し、\( h = 1 \) を代入し、「隣り合う画素の差分を取る」ことで微分を表現します。
実際に \( h = 1 \) を代入すると、\( x \) 方向(横方向)・\( y \) 方向(縦方向)の微分は下の式で表されます。
[\( x \) 方向(横方向)の微分]\[
f_x(x,y) = f(x+1,y) - f(x,y)
\]
[\( y \) 方向(横方向)の微分]\[
f_y(x,y) = f(x,y+1) - f(x,y)
\]
(2) 1次微分フィルタ
(1)で導出した式\[
f_x(x,y) = f(x+1,y) - f(x,y)
\]\[
f_y(x,y) = f(x,y+1) - f(x,y)
\]をフィルタの形に書き換えることで、1次微分フィルタを導出できます。
| 方向 | 式 | フィルタ |
|---|---|---|
| 横方向(\( x \) 方向) | \( f_x(x,y) = \textcolor{deepskyblue}{f(x+1,y)} - \textcolor{magenta}{f(x,y)} \) | \( \left( \begin{array}{ccc} 0 & 0 & 0 \\ 0 & \textcolor{magenta}{-1} & \textcolor{deepskyblue}{1} \\ 0 & 0 & 0 \end{array} \right) \) |
| 縦方向(\( y \) 方向) | \( f_y (x,y) = \textcolor{deepskyblue}{f(x,y+1)} - \textcolor{magenta}{f(x,y)} \) | \( \left( \begin{array}{ccc} 0 & 0 & 0 \\ 0 & \textcolor{magenta}{-1} & 0 \\ 0 & \textcolor{deepskyblue}{1} & 0 \end{array} \right) \) |
[横方向 (\( x \) 方向) のフィルタ適用例]
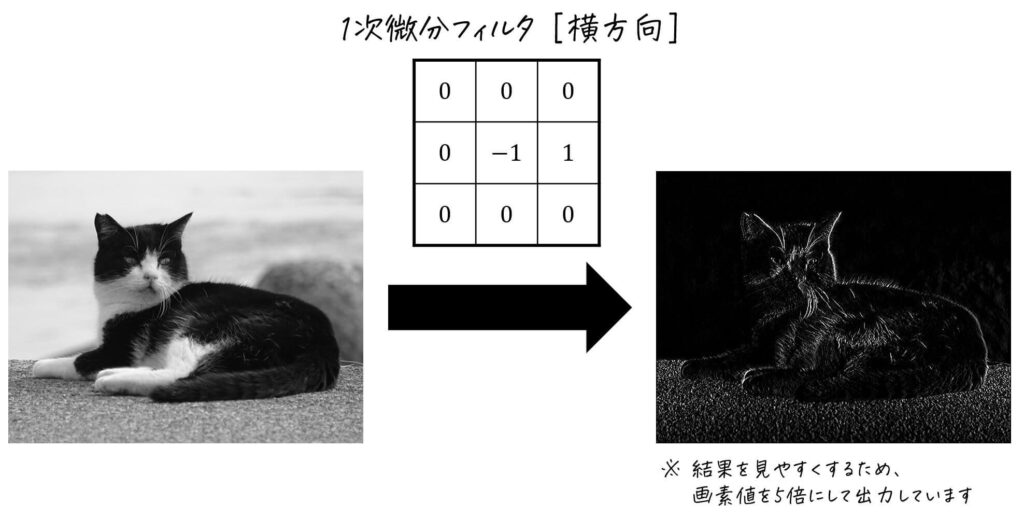
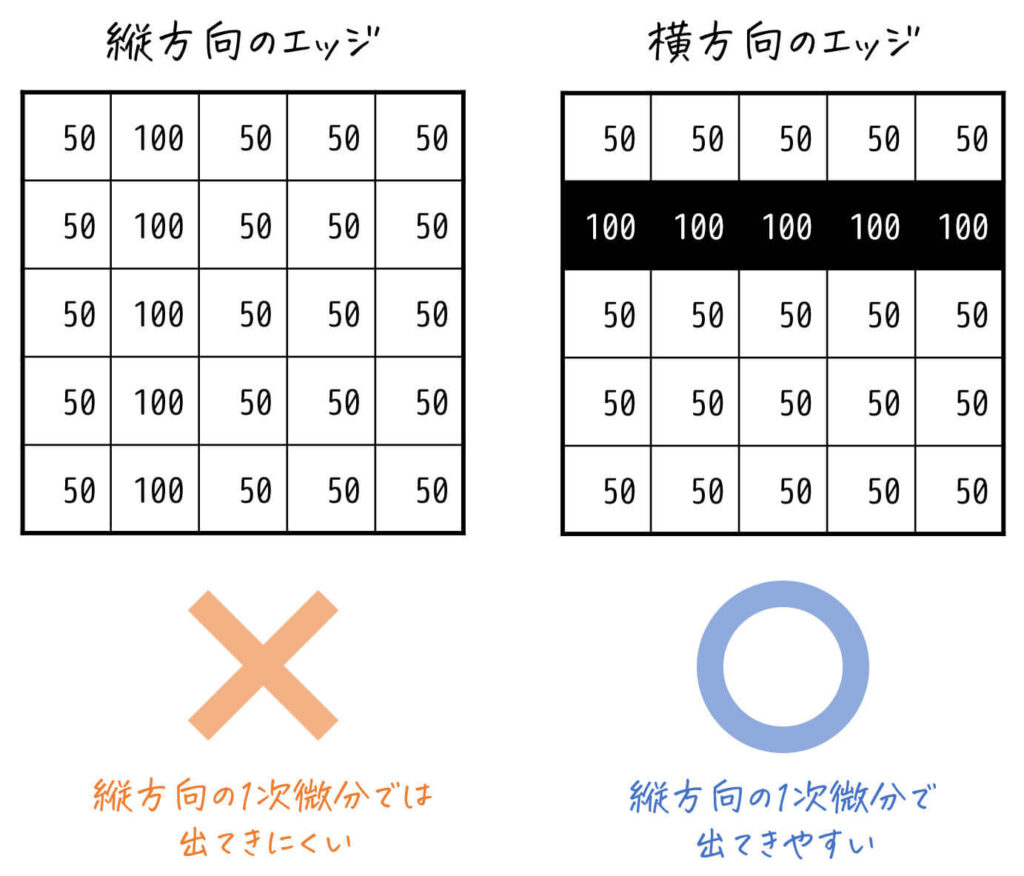
横方向の1次微分フィルタを適用すると、横方向の画素値変化が可視化されるため、出力画像には縦方向のエッジが強く出てきます。
一方、縦方向の画素値変化は可視化されないため、横方向のエッジは出力画像にあまり出てきません。
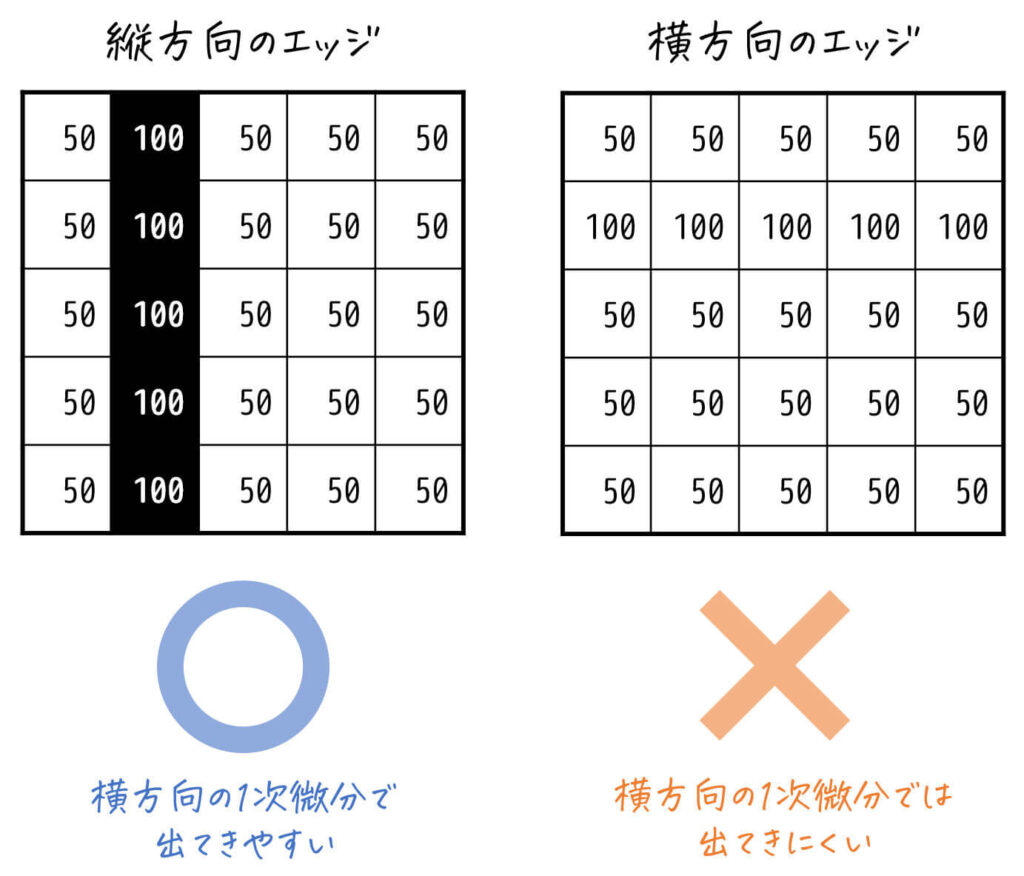
[縦方向 (\( y \) 方向) のフィルタ適用例]
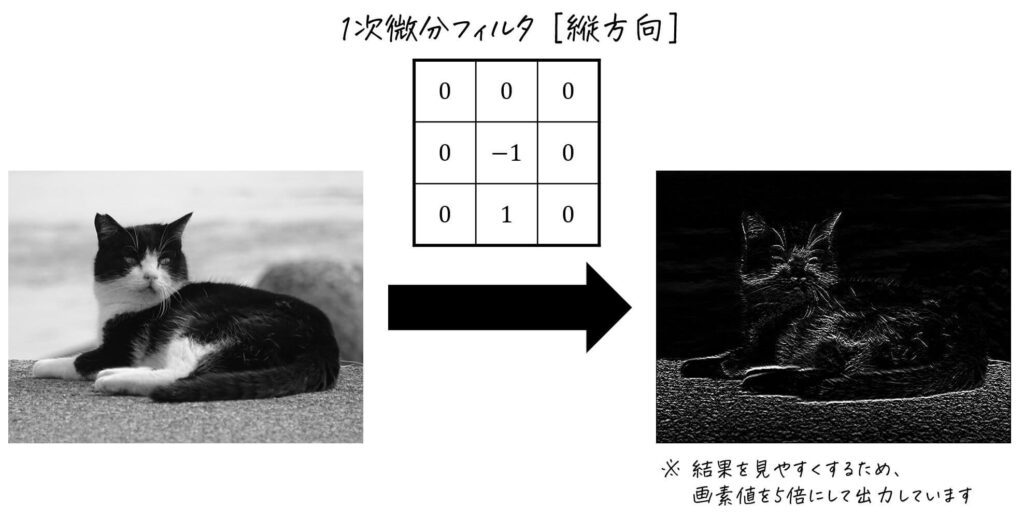
縦方向の1次微分フィルタを適用することで、縦方向の画素値変化が可視化されるため、出力される画像には横方向のエッジが強く出てきます。
一方、横方向の画素値変化は可視化されないため、縦方向のエッジは出力画像にあまり出てきません。
(3) 様々な1次微分フィルタ
画像の微分は、各画素ごとに「隣り合う画素の差分を取る」ことで求めることができるのですが、差分を取り方として、\[
f_x(x,y) = f(x+1,y) - f(x,y)
\]\[
f_y(x,y) = f(x,y+1) - f(x,y)
\]というとり方以外にも以外にも¥[
f_x(x,y) = f(x,y) - f(x-1,y)
\]\[
f_y(x,y) = f(x,y) - f(x,y-1)
\]で差分を取ることもできますね。
そのため、1次微分フィルタを下のように書くこともできます。
| 方向 | 式 | フィルタ |
|---|---|---|
| 横方向(\( x \) 方向) | \( f_x(x,y) = \textcolor{deepskyblue}{f(x,y)} - \textcolor{magenta}{f(x-1,y)} \) | \( \left( \begin{array}{ccc} 0 & 0 & 0 \\ \textcolor{magenta}{-1} & \textcolor{deepskyblue}{1} & 0 \\ 0 & 0 & 0 \end{array} \right) \) |
| 縦方向(\( y \) 方向) | \( f_y (x,y) = \textcolor{deepskyblue}{f(x,y)} - \textcolor{magenta}{f(x,y-1)} \) | \( \left( \begin{array}{ccc} 0 & \textcolor{magenta}{-1} & 0 \\ 0 & \textcolor{deepskyblue}{1} & 0 \\ 0 & 0 & 0 \end{array} \right) \) |
また、2つの差分のとり方\[
f_x(x,y) = f(x+1,y) - f(x,y) , \ \ \ f_x(x,y) = f(x,y) - f(x-1,y)
\]\[
f_y(x,y) = f(x,y+1) - f(x,y) , \ \ \ f_y(x,y) = f(x,y) - f(x,y-1)
\]の平均をとって、\[\begin{align*}
f_x(x,y) & = \frac{1}{2} \left[ \left\{ f(x+1,y) - f(x,y) \right\} + \left\{ f(x,y) - f(x-1,y) \right\} \right]
\\ & = \frac{1}{2} \left\{ f(x+1,y) - f(x-1,y) \right\}
\end{align*}\]
\[\begin{align*}
f_y(x,y) & = \frac{1}{2} \left[ \left\{ f(x,y+1) - f(x,y) \right\} + \left\{ f(x,y) - f(x,y-1) \right\} \right]
\\ & = \frac{1}{2} \left\{ f(x,y+1) - f(x,y-1) \right\}
\end{align*}\]とする方法もあります。
この方法の場合の1次フィルタは、下のようになります。
| 方向 | 式 | フィルタ |
|---|---|---|
| 横方向(\( x \) 方向) | \( f_x(x,y) = \textcolor{deepskyblue}{\frac{1}{2} f(x+1,y)} \textcolor{magenta}{\frac{-1}{2} f(x-1,y)} \) | \( \left( \begin{array}{ccc} 0 & 0 & 0 \\ \textcolor{magenta}{-\frac{1}{2} } & 0 & \textcolor{deepskyblue}{ \frac{1}{2} } \\ 0 & 0 & 0 \end{array} \right) \) |
| 縦方向(\( y \) 方向) | \( f_y(x,y) = \textcolor{deepskyblue}{\frac{1}{2} f(x,y+1)} \textcolor{magenta}{\frac{-1}{2} f(x,y-1)} \) | \( \left( \begin{array}{ccc} 0 & \textcolor{magenta}{- \frac{1}{2} } & 0 \\ 0 & 0 & 0 \\ 0 & \textcolor{deepskyblue}{ \frac{1}{2} } & 0 \end{array} \right) \) |
このように、同じ「横(縦)方向の1次微分」でも、フィルタの書き方が3通りもあるのです。
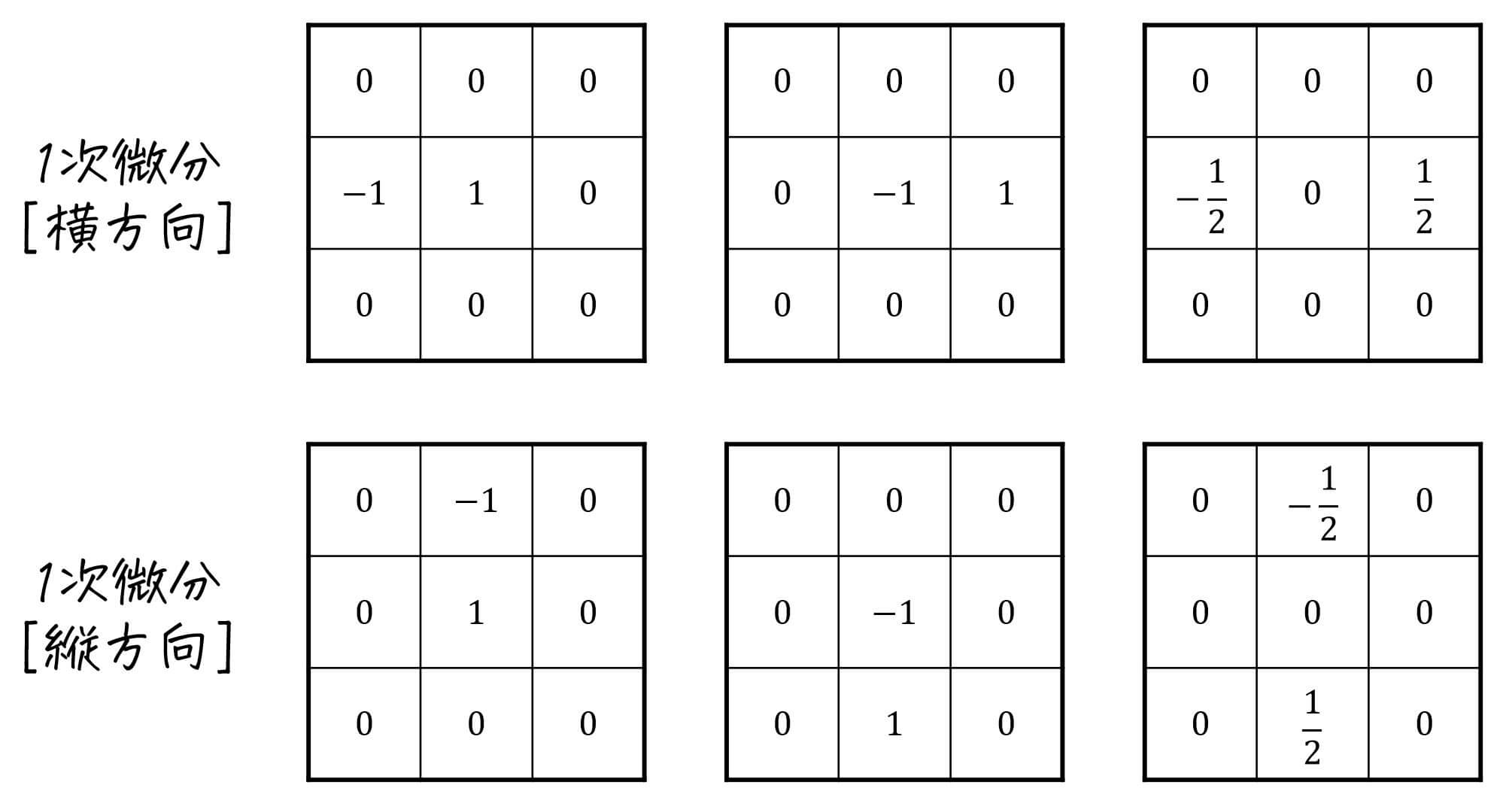
※ 3番目のフィルタの係数 \( \frac{1}{2} \) は省略して、\[
\left( \begin{array}{ccc} 0 & 0 & 0 \\ \textcolor{magenta}{- 1 } & 0 & \textcolor{deepskyblue}{ 1 } \\ 0 & 0 & 0 \end{array} \right) , \ \ \ \left( \begin{array}{ccc} 0 & 0 & 0 \\ \textcolor{magenta}{- 1 } & 0 & \textcolor{deepskyblue}{ 1 } \\ 0 & 0 & 0 \end{array} \right)
\]と表現することも多いです。(ただし出力される画像の画素値は2倍になる)
5. プレヴィットフィルタ
(1) 1次微分フィルタの欠点
「5. 1次微分フィルタ」では、エッジ(=画素値が特に変化している部分)を得ることができるのでしたね。
しかし、同時に画像に含まれるノイズも1次微分フィルタにより強調されてしまいます。
そこで、
(2) プレヴィットフィルタの仕組み [横方向]
1次微分フィルタと同じようにプレヴィットフィルタにも横方向(\( x \) 方向)、縦方向(\( y \) 方向)それぞれのフィルタがありますが、まず横方向のプレヴィットフィルタから見ていきましょう。
横方向の1次微分フィルタでは、次の2つの式の\[
f(x+1,y) - f(x,y) , \ \ \ f(x,y) - f(x-1,y)
\]の平均値を出力画素値(=偏導関数)とするのでしたね。
プレヴィットフィルタでは、この2つの式に加え、縦方向の前後の画素 \( y \pm 1 \) に対しても\[
f(x+1,y-1) - f(x,y-1) , \ \ \ f(x,y-1) - f(x-1,y-1)
\]\[
f(x+1,y+1) - f(x,y+1) , \ \ \ f(x,y+1) - f(x-1,y+1)
\]のように「隣り合う画素の差分を取る」ということをします。
これら6つの式の平均
\[\begin{align*}
g(x,y) & = \frac{1}{6} \left\{ f(x+1,y) - f(x,y) \right\} + \frac{1}{6} \left\{ f(x,y) - f(x-1,y) \right\}
\\ & + \frac{1}{6} \left\{ f(x+1,y-1) - f(x,y-1) \right\} + \frac{1}{6} \left\{ f(x,y-1) - f(x-1,y-1) \right\}
\\ & + \frac{1}{6} \left\{ f(x+1,y) - f(x,y) \right\} + \frac{1}{6} \left\{ f(x,y) - f(x-1,y) \right\}
\\ & = \frac{1}{6} \left\{ \textcolor{red}{f(x-1,y-1)} + \textcolor{blue}{f(x+1,y-1)} + \textcolor{deepskyblue}{f(x-1,y)} + \textcolor{magenta}{f(x+1,y)} + \textcolor{orange}{f(x-1,y+1)} + \textcolor{green}{f(x+1,y+1)} \right\}
\end{align*}\]
をとったフィルタが、プレヴィットフィルタ\[ \frac{1}{6}
\left( \begin{array}{ccc} \textcolor{red}{- 1 } & 0 & \textcolor{blue}{ 1 }\\ \textcolor{magenta}{- 1 } & 0 & \textcolor{deepskyblue}{ 1 } \\ \textcolor{orange}{- 1 } & 0 & \textcolor{green}{ 1 } \end{array} \right)
\]となります。

(3) プレヴィットフィルタの仕組み [縦方向]
縦方向のプレヴィットフィルタも、横方向のときと同じように1次微分で使った2つの式\[
f(x,y+1) - f(x,y) , \ \ \ f(x,y) - f(x,y-1)
\]に加え、横方向の前後の画素 \( x \pm 1 \) に対しても\[
f(x-1,y+1) - f(x,y) , \ \ \ f(x-1,y) - f(x,y-1)
\]\[
f(x+1,y+1) - f(x,y) , \ \ \ f(x+1,y) - f(x,y-1)
\]のように「隣り合う画素の差分を取った」式を作ります。
合計6つの式の平均
\[\begin{align*}
g(x,y) & = \frac{1}{6} \left\{ f(x,y+1) - f(x,y) \right\} + \frac{1}{6} \left\{ f(x,y) - f(x,y-1) \right\}
\\ & + \frac{1}{6} \left\{ f(x-1,y+1) - f(x-1,y) \right\} + \frac{1}{6} \left\{ f(x-1,y) - f(x-1,y-1) \right\}
\\ & + \frac{1}{6} \left\{ f(x+1,y+1) - f(x+1,y) \right\} + \frac{1}{6} \left\{ f(x+1,y) - f(x+1,y-1) \right\}
\\ & = \frac{1}{6} \left\{ \textcolor{red}{f(x-1,y-1)} + \textcolor{magenta}{f(x,y-1)} + \textcolor{orange}{f(x+1,y-1)} + \textcolor{blue}{f(x-1,y+1)} + \textcolor{deepskyblue}{f(x,y+1)} + \textcolor{green}{f(x+1,y+1)} \right\}
\end{align*}\]
をとったものが縦方向のプレヴィットフィルタとなります。
\[ \frac{1}{6}
\left( \begin{array}{ccc} \textcolor{red}{- 1 } & \textcolor{magenta}{ -1 } & \textcolor{orange}{- 1 } \\ 0 & 0 & 0 \\ \textcolor{blue}{ 1 } & \textcolor{deepskyblue}{ 1 } & \textcolor{green}{ 1 } \end{array} \right)
\]

6. ソーベルフィルタ
横/縦方向のブレットフィルタでは、下の6種類の方法で「隣り合う画素の差分を取る」ことをし、それらの平均をとっていましたね。
横方向ブレットフィルタ:平均化する数式一覧
| 着目する \( y \) | 数式 |
|---|---|
| \( y - 1 \) に対して | \( f(x+1,y-1) - f(x,y-1) \) と \( f(x,y-1) - f(x-1,y-1) \) |
| \( y \) に対して | \( f(x+1,y) - f(x,y-1) \) と \( f(x,y) - f(x-1,y-1) \) |
| \( y + 1 \) に対して | \( f(x+1,y+1) - f(x,y-1) \) と \( f(x,y+1) - f(x-1,y-1) \) |
縦方向ブレットフィルタ:平均化する数式一覧
| 着目する \( x \) | 数式 |
|---|---|
| \( x - 1 \) に対して | \( f(x-1,y+1) - f(x-1,y) \) と \( f(x-1,y) - f(x,y-1) \) |
| \( x \) に対して | \( f(x,y+1) - f(x,y) \) と \( f(x,y) - f(x,y-1) \) |
| \( x + 1 \) に対して | \( f(x+1,y+1) - f(x+1,y) \) と \( f(x+1,y) - f(x+1,y-1) \) |
ソーベルフィルタでも、同じように6種類の方法で「隣り合う画素の差分を取る」のですが、ソーベルフィルタの場合は、着目している画素と同じ方向に対して2倍の重みをつけてから平均化をします。
横方向ソーベルフィルタ:平均化する数式一覧
| 着目する \( y \) | 数式 |
|---|---|
| \( y - 1 \) に対して | \( f(x+1,y-1) - f(x,y-1)\) と \( f(x,y-1) - f(x-1,y-1) \) |
| \( y \) に対して | \( 2 f(x+1,y) - 2 f(x,y-1) \) と \( 2f(x,y) - 2 f(x-1,y-1) \) |
| \( y + 1 \) に対して | \( f(x+1,y+1) - f(x,y-1) \) と \( f(x,y+1) - f(x-1,y-1) \) |
縦方向ブレットフィルタ:平均化する数式一覧
| 着目する \( x \) | 数式 |
|---|---|
| \( x - 1 \) に対して | \( f(x-1,y+1) - f(x-1,y) \) と \( f(x-1,y) - f(x,y-1) \) |
| \( x \) に対して | \( 2 f(x,y+1) - 2 f(x,y) \) と \( 2 f(x,y) - 2 f(x,y-1) \) |
| \( x + 1 \) に対して | \( f(x+1,y+1) - f(x+1,y) \) と \( f(x+1,y) - f(x+1,y-1) \) |
2倍の重みをつけたあとは、平均を取ればOKです。
[横方向ソーベルフィルタ]
導出)
\[\begin{align*}
g(x,y) & = \frac{2}{8} \left\{ f(x+1,y) - f(x,y) \right\} + \frac{2}{8} \left\{ f(x,y) - f(x-1,y) \right\}
\\ & + \frac{1}{8} \left\{ f(x+1,y-1) - f(x,y-1) \right\} + \frac{1}{8} \left\{ f(x,y-1) - f(x-1,y-1) \right\}
\\ & + \frac{1}{8} \left\{ f(x+1,y) - f(x,y) \right\} + \frac{1}{8} \left\{ f(x,y) - f(x-1,y) \right\}
\\ & = \frac{1}{8} \left\{ \textcolor{red}{f(x-1,y-1)} + \textcolor{blue}{f(x+1,y-1)} + \textcolor{magenta}{2 f(x-1,y)} + \textcolor{deepskyblue}{2 f(x+1,y)} + \textcolor{orange}{f(x-1,y+1)} + \textcolor{green}{f(x+1,y+1)} \right\}
\end{align*}\]
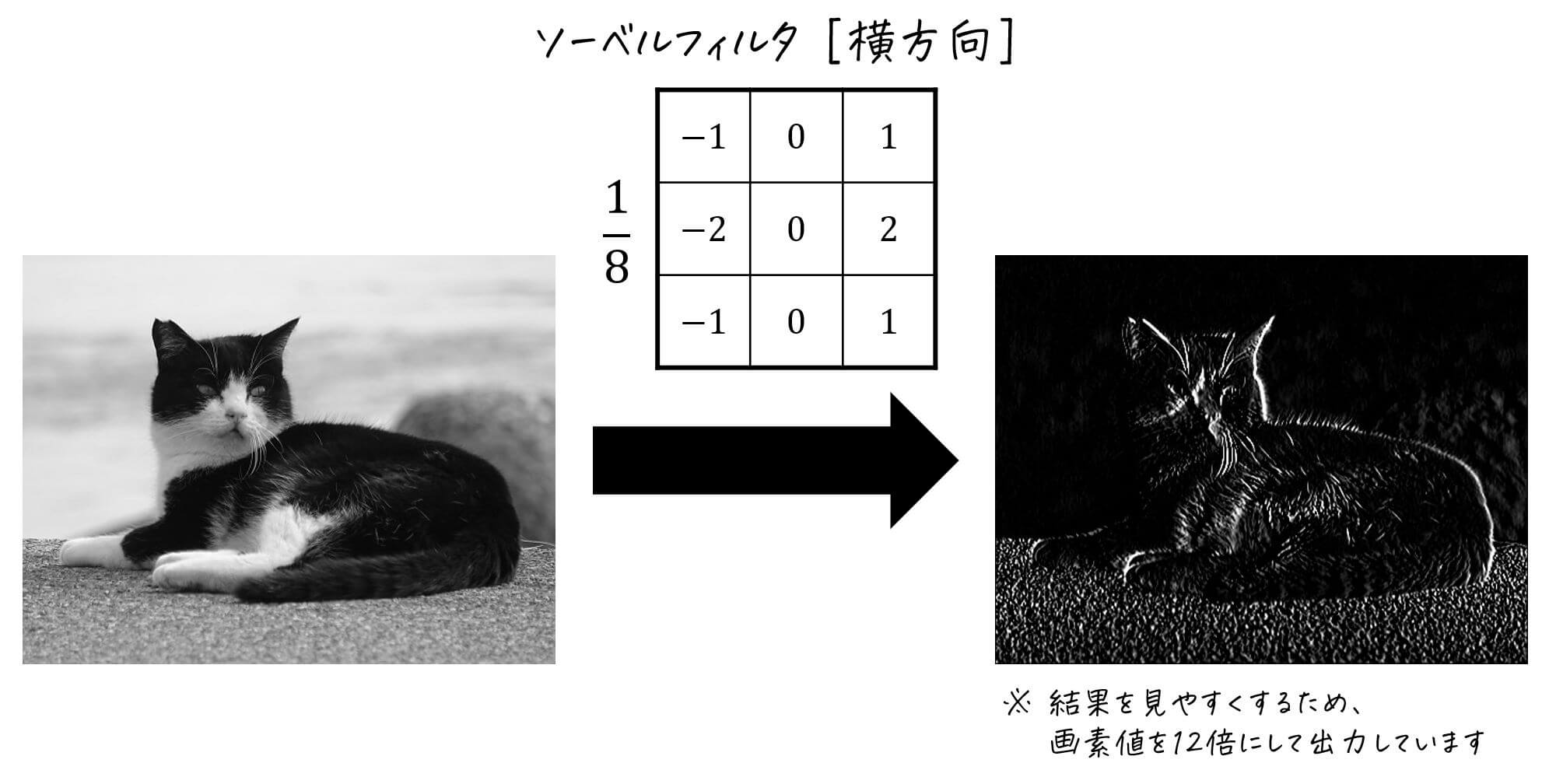
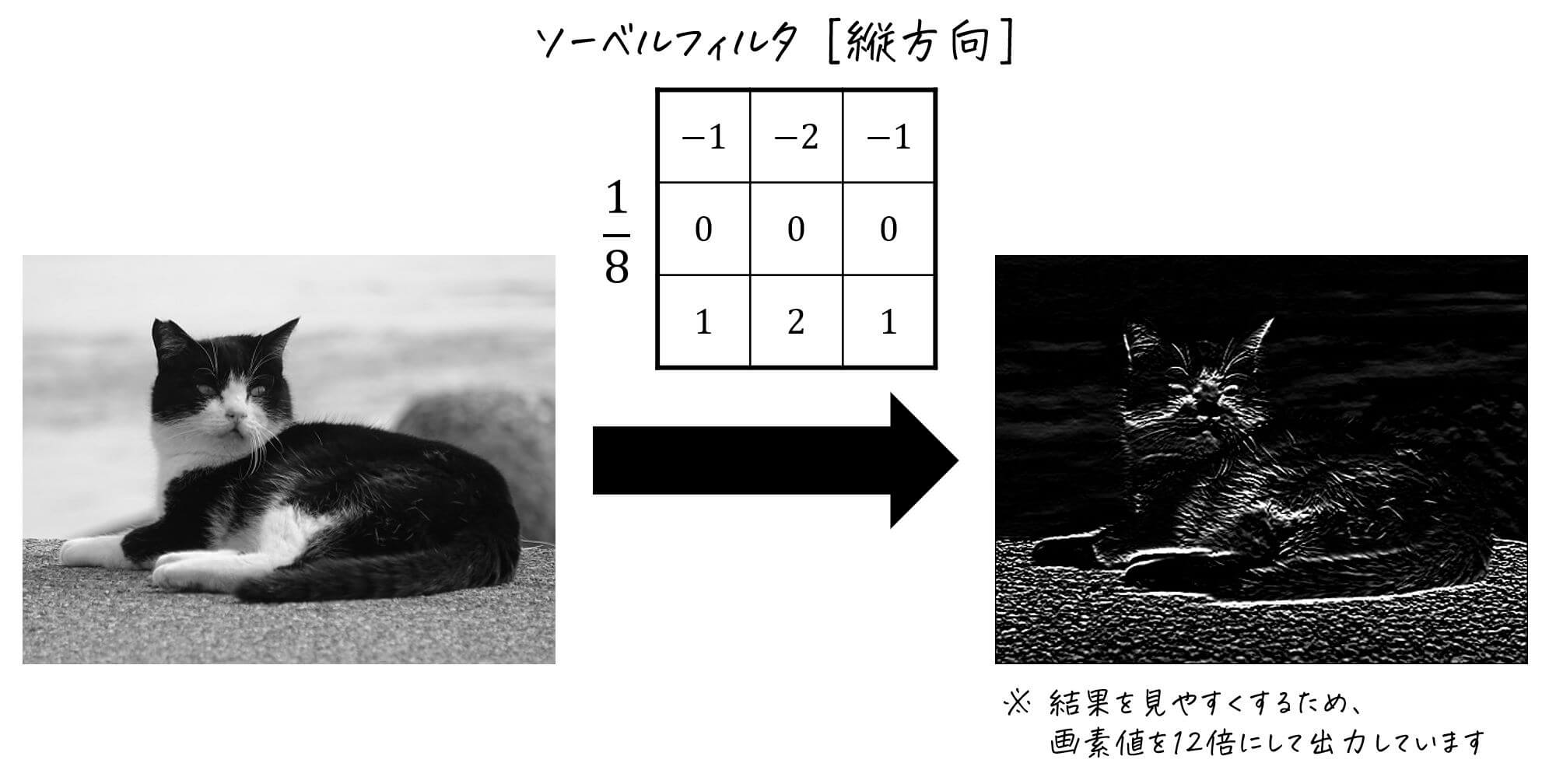
結果)\[ \frac{1}{8}
\left( \begin{array}{ccc} \textcolor{red}{- 1 } & 0 & \textcolor{blue}{ 1 }\\ \textcolor{magenta}{- 2 } & 0 & \textcolor{deepskyblue}{ 2 } \\ \textcolor{orange}{- 1 } & 0 & \textcolor{green}{ 1 } \end{array} \right)
\]
変換例)
[縦方向ソーベルフィルタ導出]
\[\begin{align*}
g(x,y) & = \frac{2}{8} \left\{ f(x,y+1) - f(x,y) \right\} + \frac{2}{8} \left\{ f(x,y) - f(x,y-1) \right\}
\\ & + \frac{1}{8} \left\{ f(x-1,y+1) - f(x-1,y) \right\} + \frac{1}{8} \left\{ f(x-1,y) - f(x-1,y-1) \right\}
\\ & + \frac{1}{8} \left\{ f(x+1,y+1) - f(x+1,y) \right\} + \frac{1}{8} \left\{ f(x+1,y) - f(x+1,y-1) \right\}
\\ & = \frac{1}{8} \left\{ \textcolor{red}{f(x-1,y-1)} + \textcolor{magenta}{2 f(x,y-1)} + \textcolor{orange}{f(x+1,y-1)} + \textcolor{blue}{f(x-1,y+1)} + \textcolor{deepskyblue}{2 f(x,y+1)} + \textcolor{green}{f(x+1,y+1)} \right\}
\end{align*}\]
結果)\[
\frac{1}{8}
\left( \begin{array}{ccc} \textcolor{red}{- 1 } & \textcolor{magenta}{ -2 } & \textcolor{orange}{- 1 } \\ 0 & 0 & 0 \\ \textcolor{blue}{ 1 } & \textcolor{deepskyblue}{ 2 } & \textcolor{green}{ 1 } \end{array} \right)
\]
変換例)
7. 2次微分フィルタ
(1) 2次微分が表すものとは
2次微分は、微分したもの \( f'(x) \) に対してさらに微分をすることをいいます。数式で書くと、\[
f''(x) = \lim_{h \to 0} \frac{f'(x+h) - f'(x)}{h}
\]となります。
日本語で説明すると
- \( x \) の変化量を表したものが \( f'(x) \) → 1次微分
- \( f'(x) \) の変化量を表したものが \( f''(x) \) → 2次微分
といえますね。
そのため、画像を2次微分すると「画素値の変化度合いの大小」が得られそうな感じがしますね。「画素値の変化度合いの大小」を得ることで、特に画素値が変化している部分(=エッジ)を1次微分に比べて正確に得ることができます。
(2) 2次微分フィルタの導出
ここからは、(3×3の)2次微分フィルタを導出してみましょう。
\( x \) 方向 (縦方向) の2次微分
2変数関数の \( x \) に関する1次微分は、\[
f_x(x,y) = \lim_{h \to 0} \frac{f(x+h,y) - f(x,y)}{h}
\]で計算できるのでしたね。
\( x \) に関する2次微分は、\( x \) で1次微分した関数 \( f_x (x,y) \) に対して、さらにもう1度微分することで求めることができます。\[
f_{xx} (x,y) = \lim_{h \to 0} \frac{f_x(x+h,y) - f_x(x,y)}{h}
\]※ \( x \) に関する2次微分を適用した関数を \( f_{xx} \) で表記します[2]\( \frac{ \partial^2}{ \partial x^2} \) と表記されることもあります。。
ただし、画像処理の世界では極限計算 \( h \to 0 \) ができないので、代わりに \( h = 1 \) とし、\[
f_{xx} (x,y) = f_x(x+1,y) - f_x(x,y)
\]を求めることで \( x \) に関する2次微分を求めます。
ここで、1次微分 \( f_x(x+1,y) \), \( f_x(x,y) \) は\[
f_x (x+1,y) = f(x+1,y) - f(x,y)
\]\[
f_x(x,y) = f(x,y) - f(x-1,y)
\]と書き換えることができますね[3]1階微分の法則 \( f_x (x,y) = f_x (x+1,y) - f_x (x,y) \), \( f_x (x,y) = f_x (x,y) - f_x (x-1,y) \) より。
よって、2次微分を\[\begin{align*}
f_{xx} (x,y) & = f_x(x+1,y) - f_x(x,y)
\\ & = \left\{ f(x+1,y) - f(x,y) \right\} + \left\{ f(x,y) - f(x-1,y) \right\}
\\ & = \textcolor{magenta}{f(x+1,y)} \textcolor{green}{-2 f(x,y)} + \textcolor{deepskyblue}{f(x-1,y)}
\end{align*}\]と変形できるため、2次微分フィルタは\[
\left( \begin{array}{ccc} 0 & 0 & 0 \\ \textcolor{deepskyblue}{1} & \textcolor{green}{-2} & \textcolor{magenta}{1} \\ 0 & 0 & 0 \end{array} \right)
\]と導出できます。
[実際に横方向の2次微分フィルタを適用すると…?]
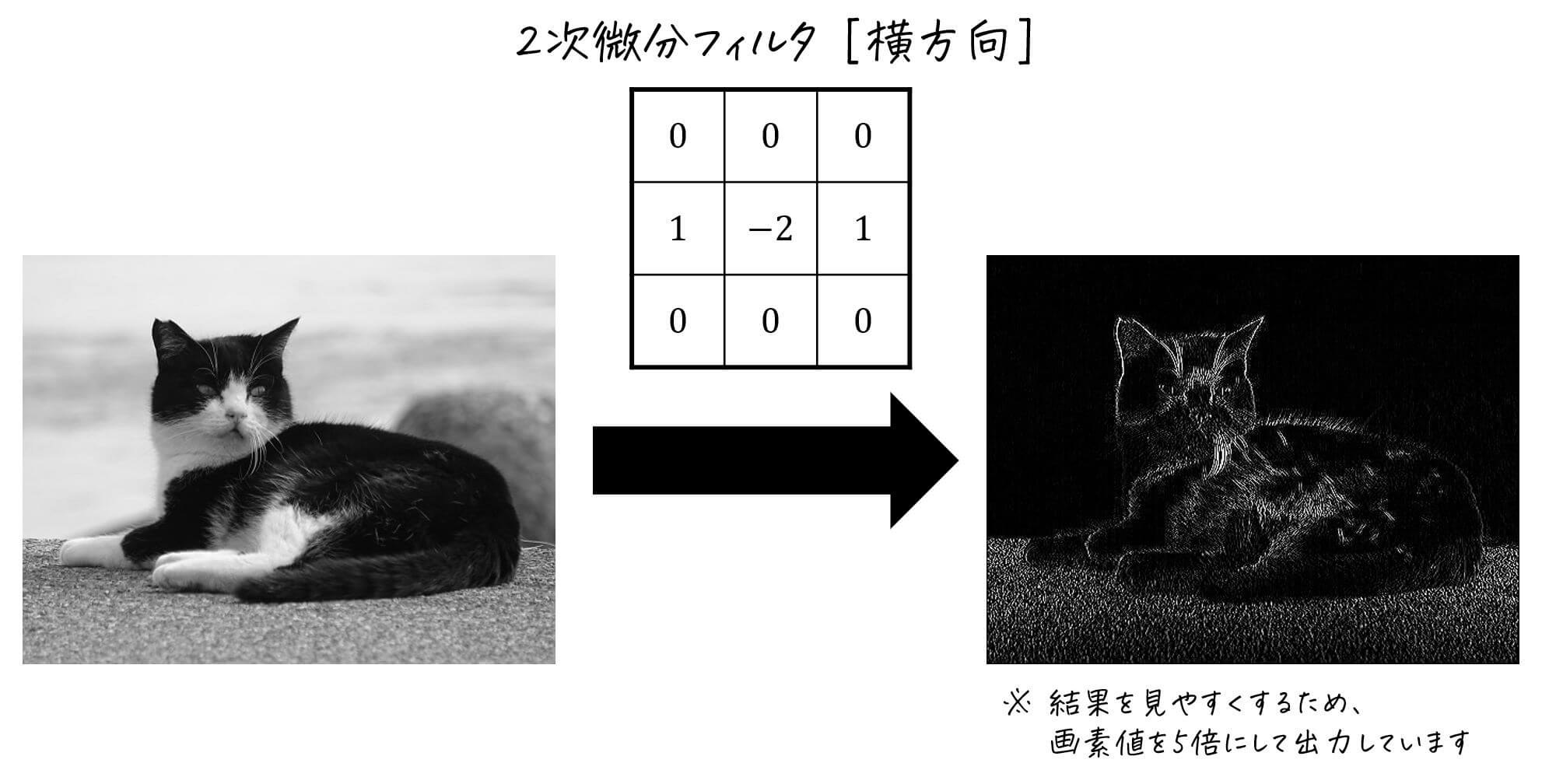
横方向の2次微分フィルタを適用することで、横方向の画素値変化が可視化されます。可視化された画像には縦方向のエッジが入っているのが特徴です。
\( y \) 方向 (横方向) の2次微分
\( x \) 方向のときと同じように、\( y \) に関する2次微分は、\( y \) で1次微分した関数 \( f_y (x,y) \) に対して、さらにもう1度微分することで求めることができます。\[
f_{yy} (x,y) = \lim_{h \to 0} \frac{f_y(x,y+h) - f_y(x,y)}{h}
\]※ \( y \) に関する2次微分を適用した関数を \( f_{yy} \) で表記します[4]\( \frac{ \partial^2}{ \partial y^2} \) と表記されることもあります。。
ただし、先程も言った通り画像処理の世界では極限計算 \( h \to 0 \) ができないので、代わりに \( h = 1 \) とし、\[
f_{yy} (x,y) = f_y(x,y+1) - f_y(x,y)
\]を求めることで \( y \) に関する2次微分を求めます。
ここで、1次微分 \( f_y(x,y+1) \), \( f_y(x,y) \) は\[
f_y (x,y+1) = f(x,y+1) - f(x,y)
\]\[
f_y(x,y) = f(x,y) - f(x,y-1)
\]と書き換えられますね[5]1階微分の法則 \( f_y (x,y) = f_y (x,y+1) - f_y(x,y) \), \( f_y (x,y) = f_y (x,y) - f_y(x,y-1) \) より。
よって、2次微分を\[\begin{align*}
f_{yy} (x,y) = f_y(x,y+1) - f_y(x,y)
\\ & = \left\{ f(x,y+1) - f(x,y) \right\} + \left\{ f(x,y) - f(x,y-1) \right\}
\\ & = \textcolor{magenta}{f(x,y+1)} \textcolor{green}{-2 f(x,y)} + \textcolor{deepskyblue}{f(x,y-1)}
\end{align*}\]と変形できるため、2次微分フィルタは\[
\left( \begin{array}{ccc} 0 & \textcolor{deepskyblue}{1} & 0 \\ 0 & \textcolor{green}{-2} & 0 \\ 0 & \textcolor{magenta}{1} & 0 \end{array} \right)
\]と導出できます。

縦方向の2次微分フィルタを適用することで、縦方向の画素値変化が可視化されます。可視化された画像には横方向のエッジが入っているのが特徴です。
8. ラプラシアンフィルタ
「7. 2次微分フィルタ」では、横方向・縦方向それぞれの画素値変化の度合いを可視化することができますが、一度に「横方向と縦方向両方」の画素値の度合いを可視化することができます。
そこで、\( x \) に関する2次微分 \( f_{xx} (x,y) \) と、\( y \) に関する2次微分 \( f_{yy} (x,y) \) を足したフィルタを考えましょう。(ラプラシアンフィルタと呼ばれます[6]2変数関数 \( f(x,y) \) のラプラシアンが\[ f_{xx} (x,y) + f_{yy} (x,y) \]で定義されることから名前が付けられています。。)
ここで、\[
f_{xx} = f(x+1,y) - 2 f(x,y) + f(x-1,y)
\]\[
f_{yy} = f(x,y+1) - 2 f(x,y) + f(x,y-1)
\]なので、\( f_{xx} (x,y) \) と \( f_{yy} (x,y) \) を足した和 \( g(x,y) \) は\[\begin{align*}
g(x,y) & = f_{xx} (x,y) + f_{yy} (x,y)
\\ & = \left\{ f(x+1,y) - 2 f(x,y) + f(x-1,y) \right\} + \left\{ f(x,y+1) - 2 f(x,y) + f(x,y-1) \right\}
\\ & = \textcolor{red}{f(x-1,y)} + \textcolor{orange}{f(x,y-1)} \textcolor{green}{-4 f(x,y)} + \textcolor{deepskyblue}{ f(x, y+1) } + \textcolor{blue}{ f(x+1,y) }
\end{align*}\]となるため、ラプラシアンフィルタは\[
\left( \begin{array}{ccc} 0 &\textcolor{red}{1} & 0 \\ \textcolor{orange}{1} & \textcolor{green}{-4} & \textcolor{deepskyblue}{1} \\ 0 & \textcolor{blue}{1} & 0 \end{array} \right)
\]と求められます。

9. 練習問題
最後に、練習問題で軽くフィルタについておさらいしておきましょう。
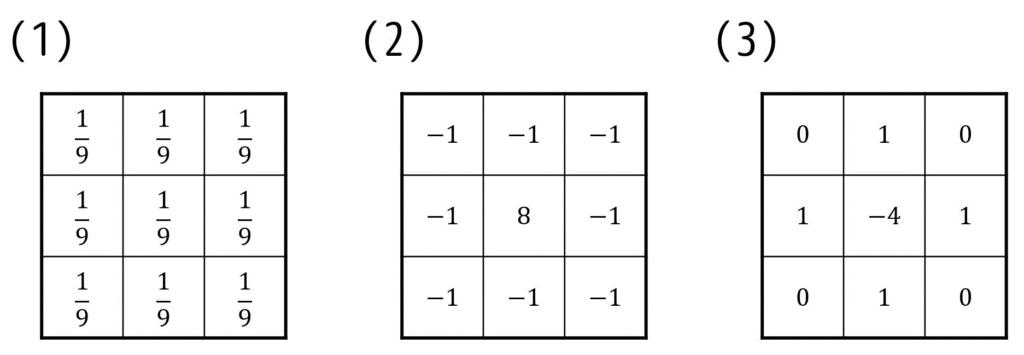
ある画像に対して、次の(1)~(3)で示されるフィルタを加えたときの出力画像を表した説明として、正しいものを1つずつ選び番号で答えなさい。
[選択肢]
- 元画像のエッジが強調された画像が出力された。
- 元画像がぼやけた画像が出力された。
- 元画像のエッジ部分だけが出力された。
[解説]
(1) 2 → 平滑化
(2) 1 → 鮮鋭化
(3) 3 → ラプラシアンフィルタ
注釈
| ↑1 | なお、偏微分を正式に表す場合は、\[ f_x (x,y) = \frac{ \partial }{ \partial x } f(x,y) , \ \ \ f_y (x,y) = \frac{ \partial }{ \partial y } f(x,y) \]と表記します。 |
|---|---|
| ↑2 | \( \frac{ \partial^2}{ \partial x^2} \) と表記されることもあります。 |
| ↑3 | 1階微分の法則 \( f_x (x,y) = f_x (x+1,y) - f_x (x,y) \), \( f_x (x,y) = f_x (x,y) - f_x (x-1,y) \) より |
| ↑4 | \( \frac{ \partial^2}{ \partial y^2} \) と表記されることもあります。 |
| ↑5 | 1階微分の法則 \( f_y (x,y) = f_y (x,y+1) - f_y(x,y) \), \( f_y (x,y) = f_y (x,y) - f_y(x,y-1) \) より |
| ↑6 | 2変数関数 \( f(x,y) \) のラプラシアンが\[ f_{xx} (x,y) + f_{yy} (x,y) \]で定義されることから名前が付けられています。 |
関連広告・スポンサードリンク