![[基本情報・応用情報] うさぎでもわかる情報理論 第3羽 ハフマン符号化](https://www.momoyama-usagi.com/wp-content/uploads/joho3-2-3.jpg)
スポンサードリンク
こんにちは、ももうさです。
前回では、「一意復号可能な符号」と「瞬時復号可能な符号」がどのような符号なのかについてみていきました。
今回は、文字列を瞬時復号可能な符号かつ瞬時復号可能な符号の中で平均符号長が最も短くなるように符号化をするハフマン符号化方式について、例題や練習問題を解きながら見ていきましょう。
さらに、実際に基本情報や応用情報でハフマン符号化がどのように出題され、どのように解いていけばよいのかについても、確認しましょう。
スポンサードリンク
1. まずは例題で確認
まずは、例題でハフマン符号化の方法を見ていきましょう。
つぎの表は、とある文字列中(情報源)に出てくる文字の出現確率を表にしたものである。
| 文字(記号) | 符号 (ビット表記) | 出現確率 |
|---|---|---|
| A | (ア) | 12% |
| B | (イ) | 56% |
| C | (ウ) | 4% |
| D | (エ) | 20% |
| E | (オ) | 8% |
(1) この文字列をハフマン符号化法によって符号化し、ビット表記の (ア) ~ (オ) に当てはまるビット表記を答えなさい。
(2) (1)で符号化した符号の平均符号長 \( L \) を小数第2位まで答えなさい。(必要であれば小数第3位を四捨五入すること)
Step1. 各文字を出現確率 (回数) の多い順に並べ、各文字ごとを独立したグループとする
ハフマン符号化をする際にはまず、与えられた文字(記号・情報)をそれぞれ独立したグループとしてから、出現確率が大きい順に並び替えます。
| グループ (文字) | 出現確率 |
|---|---|
| B | 56% |
| D | 20% |
| A | 12% |
| E | 8% |
| C | 4% |
今回の場合は5種類あるため、5つの独立したグループが出てきます。
※ 並び変える際に、文字と出現確率の対応を書き間違えないようにしましょう。
Step2. 出現確率が低い2つのグループを1つにしていきながら、二分木を作る
つぎに、グループ数が1になるまで、各グループの中から出現確率が低い2つのグループを探し出し、その2つのグループをひとまとめにしていきます。
Step2-1. 5グループ → 4グループ
| グループ (文字) | 出現確率 |
|---|---|
| B | 56% |
| D | 20% |
| A | 12% |
| E | 8% |
| C | 4% |
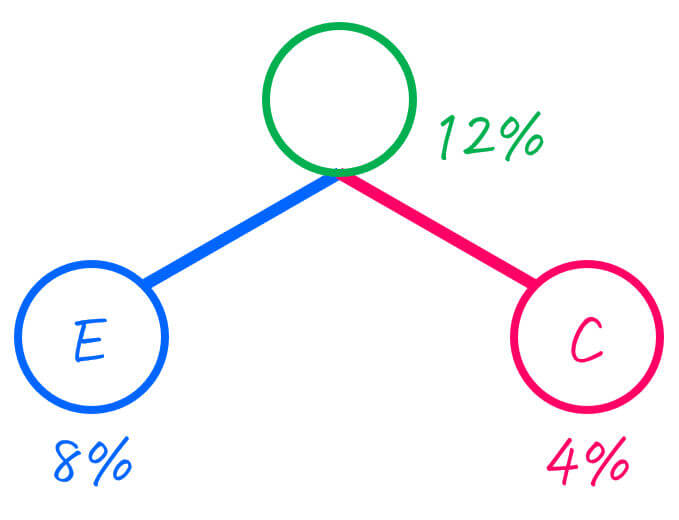
出現確率が低い2つのグループは、EとCなので、この2つをひとまとめにします。
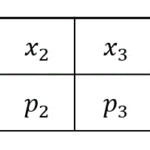
(ひとまとめにしたグループの出現確率は、2つのグループの出現確率の合計です[1]今回の場合は、Eの出現確率が6%、Cの出現確率が6%なので、ひとまとめにしたグループの出現確率は、6% + 6% = 12% となります。。)
| グループ (文字) | 出現確率 |
|---|---|
| B | 56% |
| D | 20% |
| A | 12% |
| EC | 12% |
さらに、ひとまとめにした2つのグループを子とし、二分木をつくります[2] … Continue reading。
Step2-2. 4グループ → 3グループ
| グループ (文字) | 出現確率 |
|---|---|
| B | 56% |
| D | 20% |
| A | 12% |
| EC | 12% |
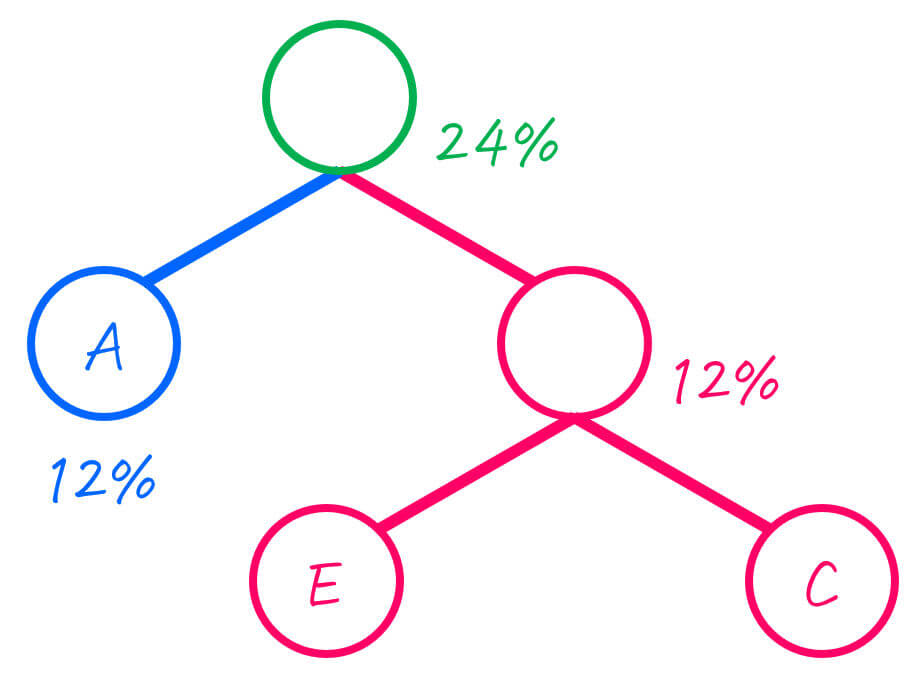
出現確率が低い2つのグループは、AとECなので、この2つをひとまとめにします。
| グループ (文字) | 出現確率 |
|---|---|
| B | 56% |
| AEC | 24% |
| D | 20% |
さらに、ひとまとめにした2つのグループを子とし、二分木をつくります。
Step2-3. 3グループ → 2グループ
| グループ (文字) | 出現確率 |
|---|---|
| B | 56% |
| AEC | 24% |
| D | 20% |
出現確率が低い2つのグループは、AECとDなので、この2つをひとまとめにします。
| グループ (文字) | 出現確率 |
|---|---|
| B | 56% |
| AECD | 44% |
さらに、ひとまとめにした2つのグループを子とし、二分木をつくります。
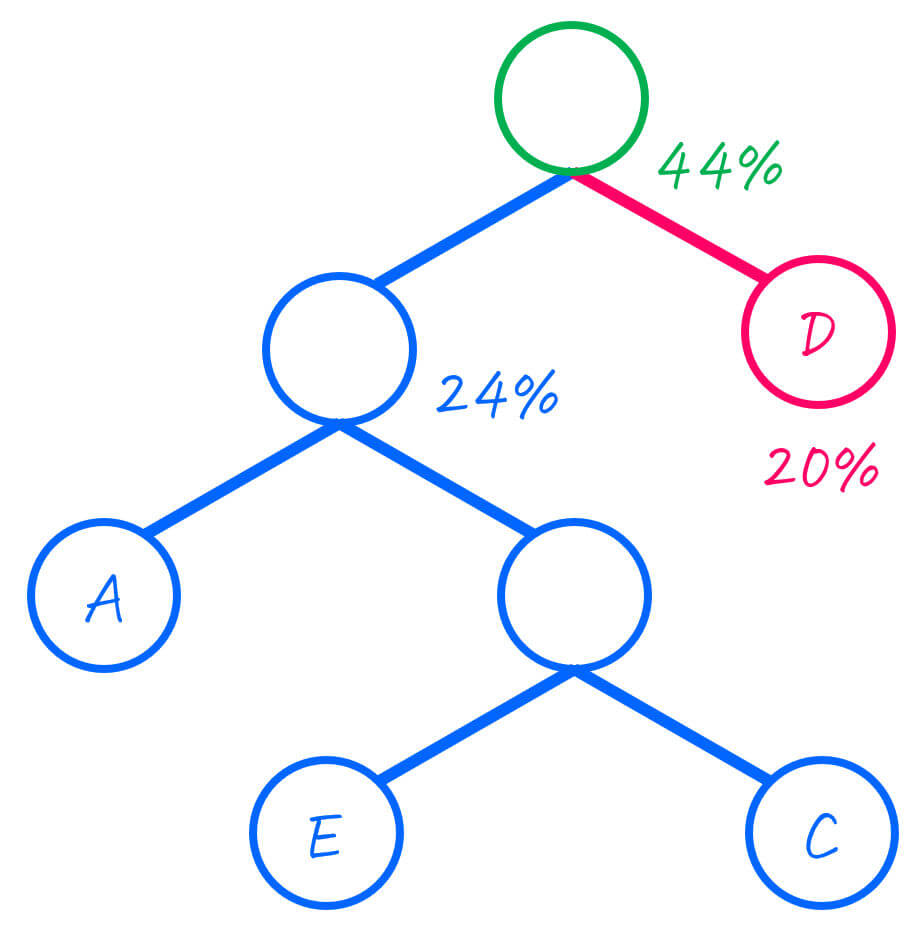
Step2-1. 2グループ → 1グループ
| グループ (文字) | 出現確率 |
|---|---|
| B | 56% |
| AECD | 44% |
出現確率が低い2つのグループ(BとAECD)をひとまとめにします。
(残り2グループなので、その2グループが出現確率が低い2グループとなります。)
| グループ (文字) | 出現確率 |
|---|---|
| BAECD | 100% |
いつものように、ひとまとめにした2つのグループを子とし、二分木をつくりましょう。
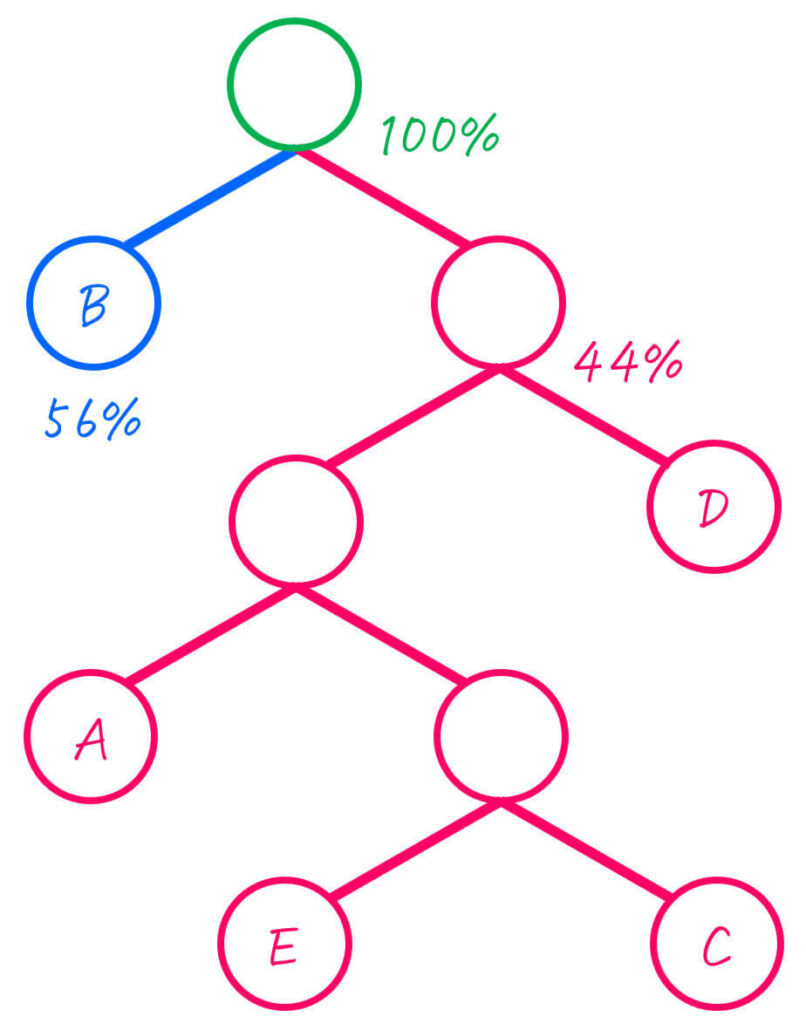
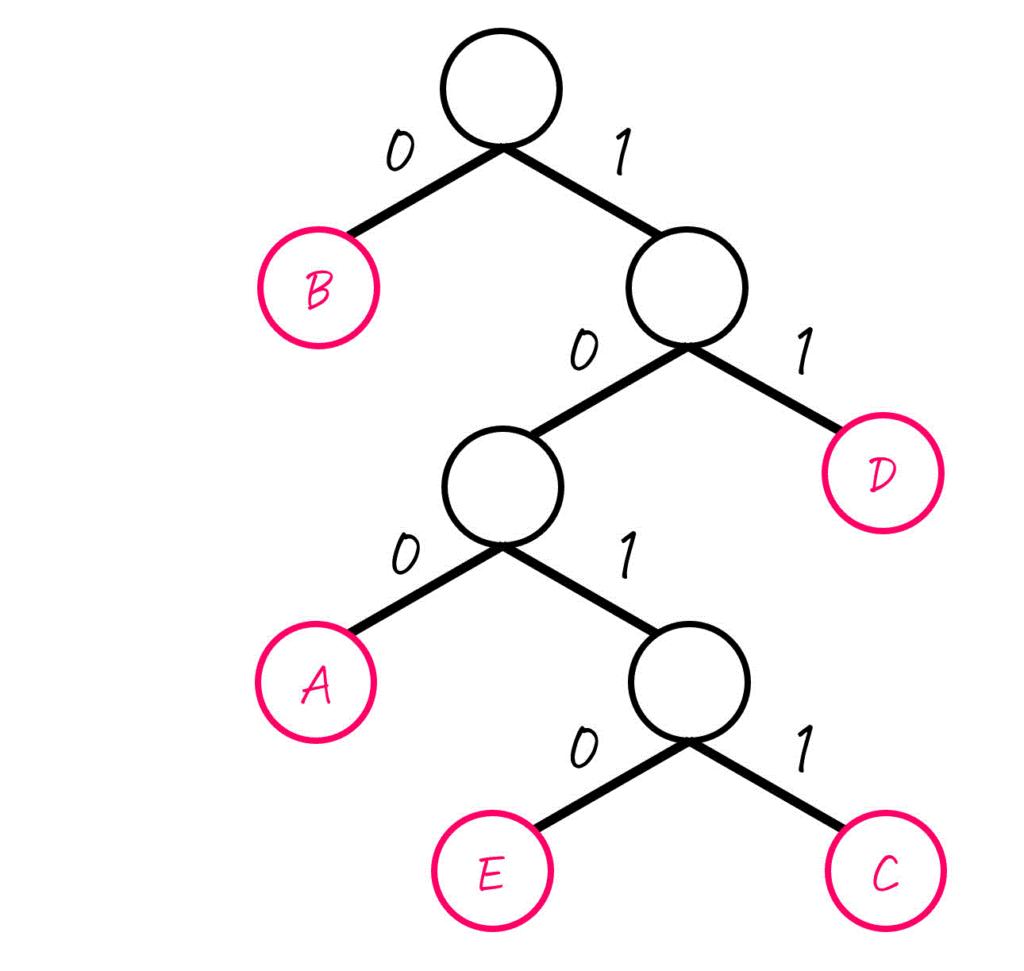
Step3. 作成した二分木から各文字(情報)ごとの符号を求める
ここからは、作成した二分木を見ていくことで、各文字ごとの符号を求めていきましょう。
まず、下のように各節(ノード)の左側を0、右側を1として考えます。
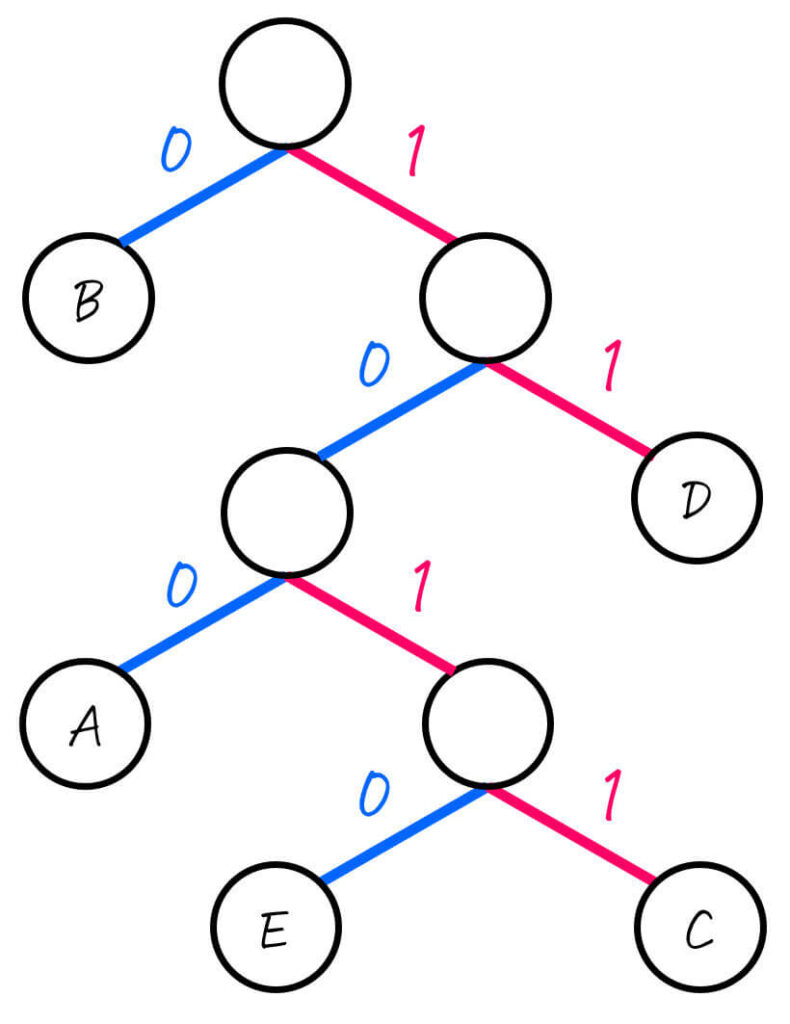
あとは、各文字(A~E)に対応するノードごとに「木構造の一番上の部分から対応するノードまでたどっていく」という操作をし、たどっていく際に通った0, 1を左から順番に並べていったものが符号となります。
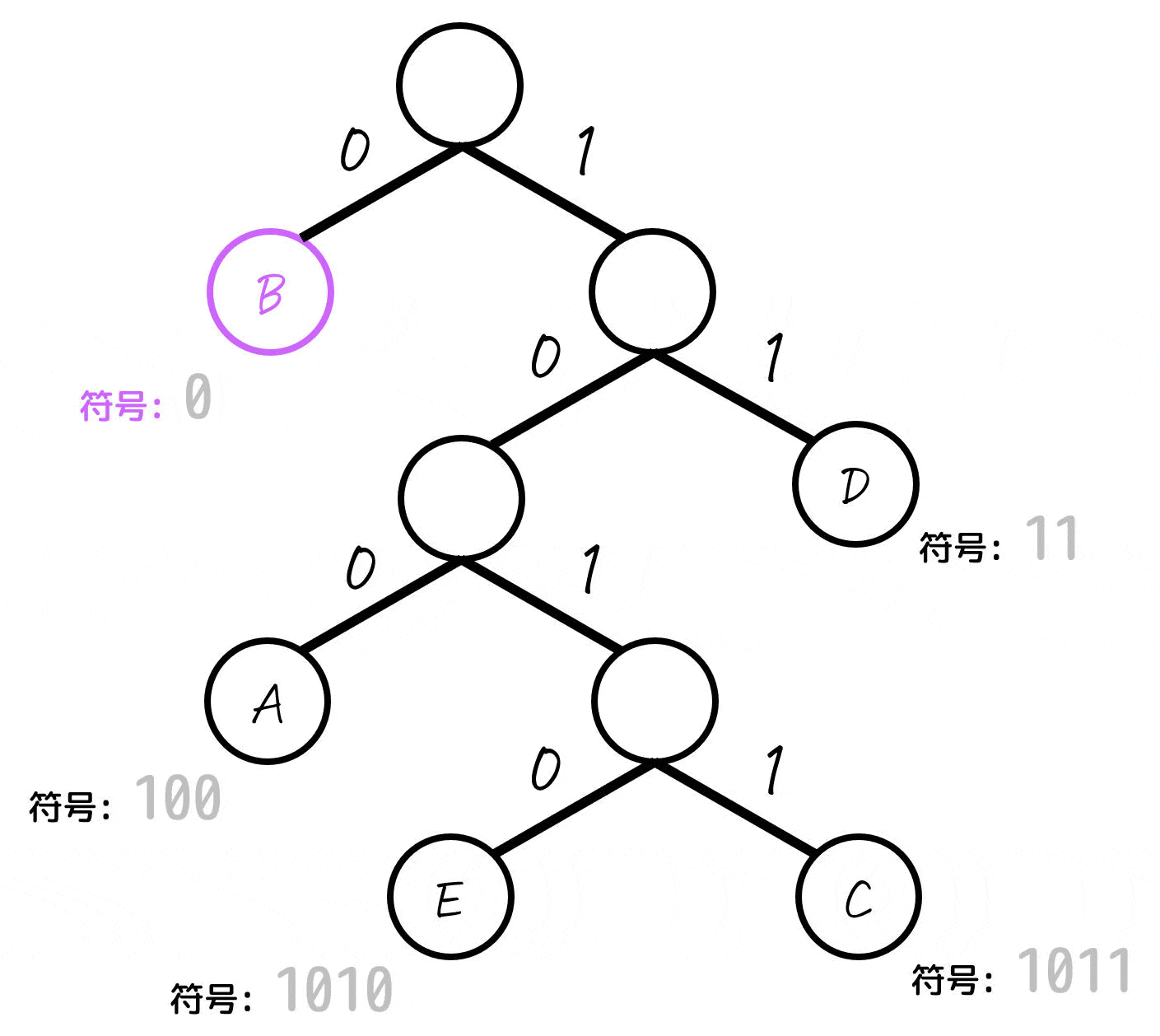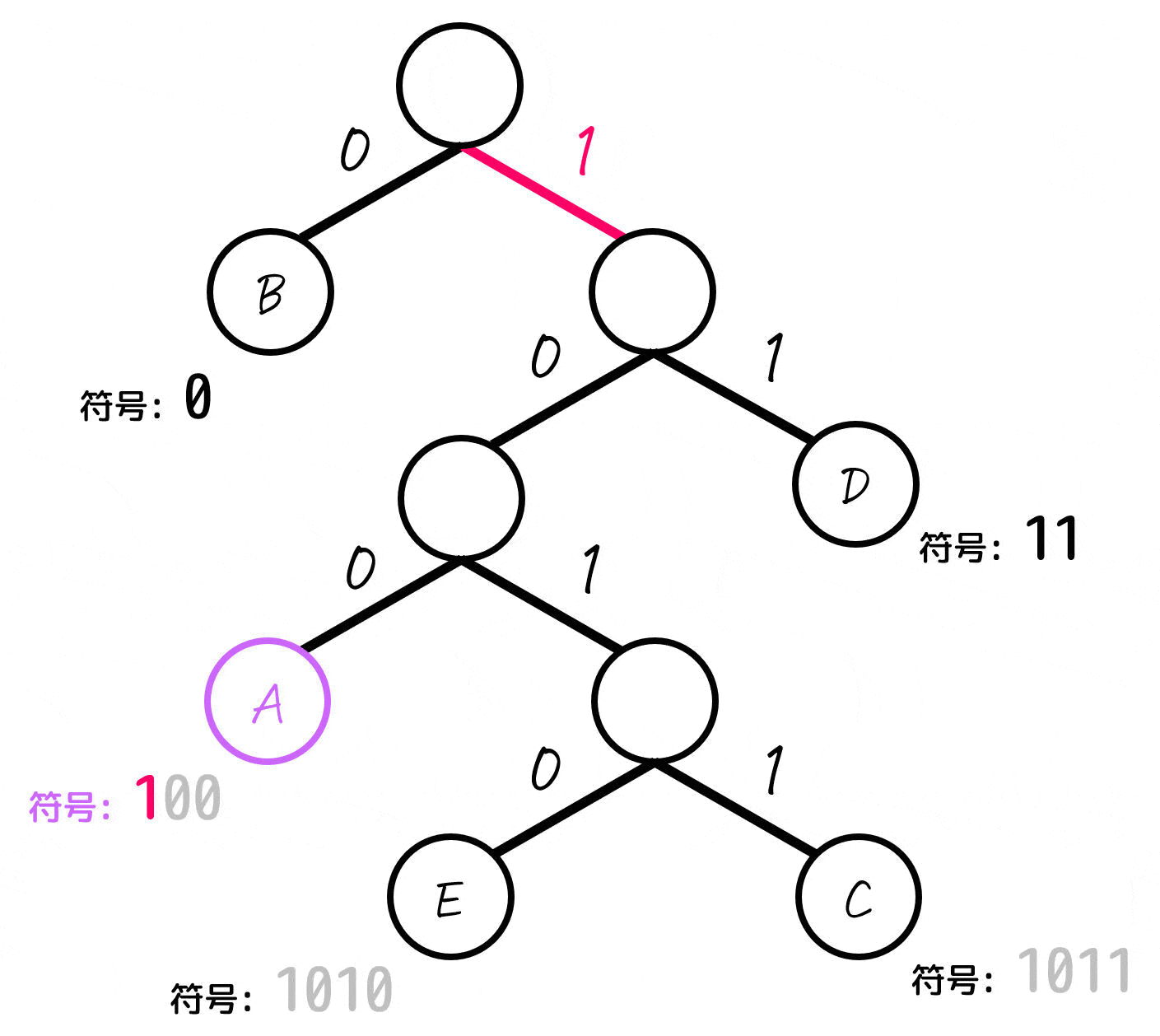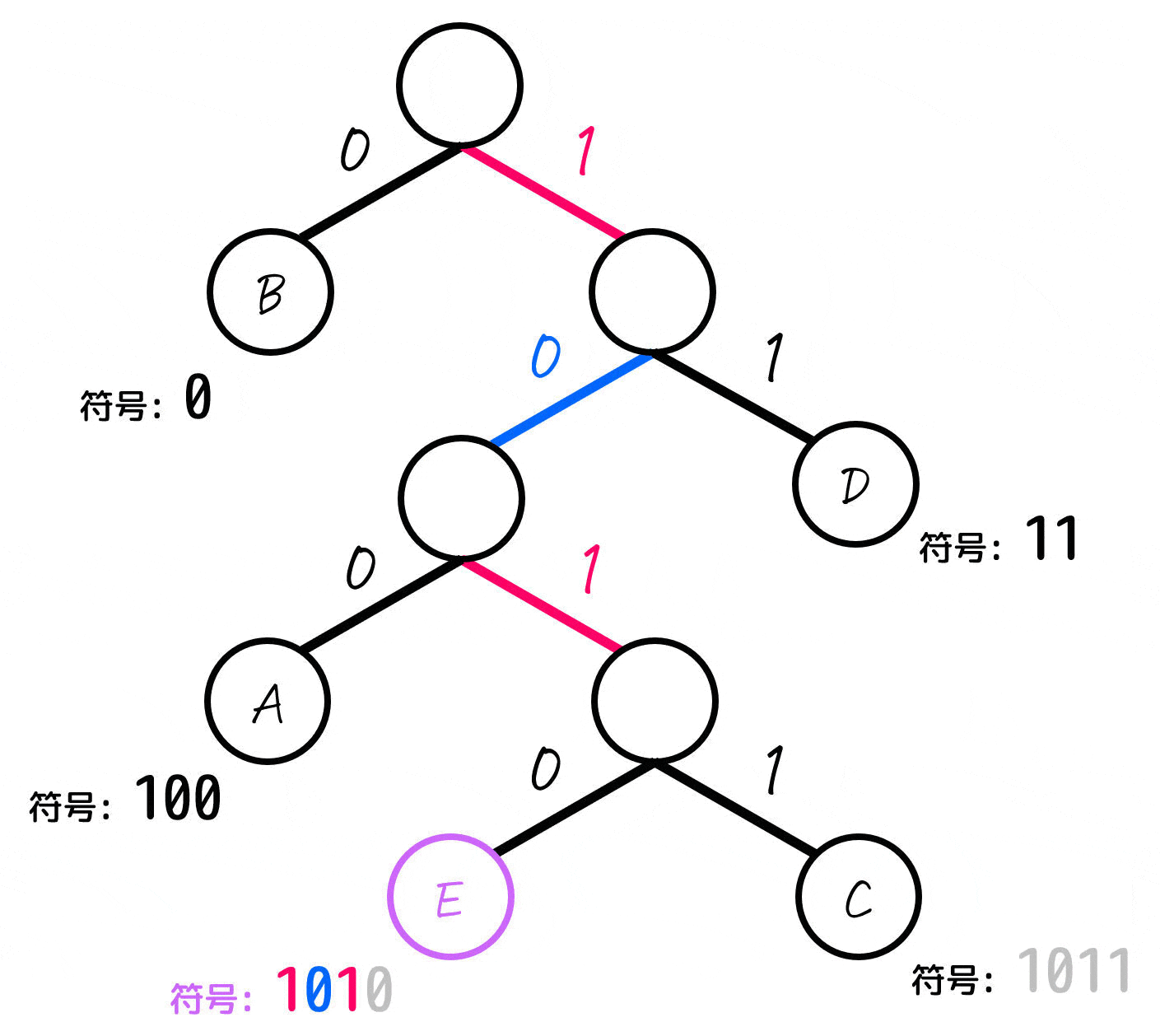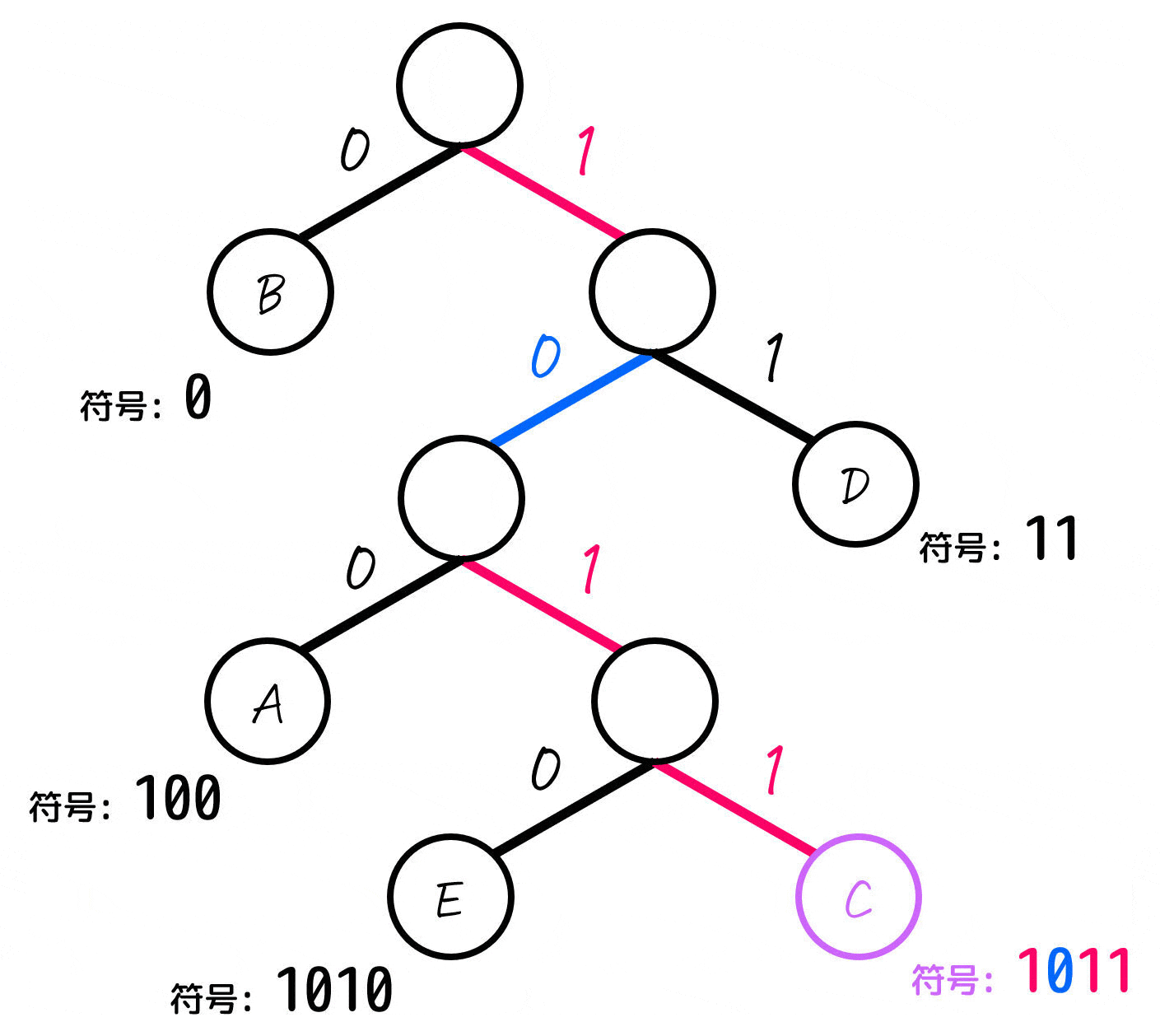
よって、各文字A~Eごとの符号は下のように求まります。
| 文字(記号) | 符号 (ビット表記) | 出現確率 |
|---|---|---|
| A | 100 | 12% |
| B | 0 | 56% |
| C | 1011 | 4% |
| D | 11 | 20% |
| E | 1010 | 8% |
結果を見てみると、出現確率が高い符号には短い符号を、出現確率が低い符号には長い符号が付いていることがわかりますね。
このようにハフマン符号では、文字列の平均符号長がなるべく短くなるような符号の決め方を機械的に決めることができるのです!
(2)
平均符号長は、各文字ごとに「符号長(符号の文字数) × 出現確率」を求め、それらを足すことで求めることができます。
今回の場合は、各文字ごとの「符号長」、および「符号長 × 出現確率」を下のように求めることができます。
| 文字(記号) | 符号 (ビット表記) | 符号長 | 出現確率 | 符号長 × 出現確率 |
|---|---|---|---|---|
| A | 100 | 3 | 12% | 0.36 |
| B | 0 | 1 | 56% | 0.56 |
| C | 1011 | 4 | 4% | 0.16 |
| D | 11 | 2 | 20% | 0.40 |
| E | 1010 | 4 | 8% | 0.32 |
よって、平均符号長 \( L \) は\[\begin{align*}
L & = 0.36 + 0.56 + 0.16 + 0.40 + 0.32
\\ & = 1.80
\end{align*}\]と求まります。
ある文字列 (情報) をハフマン符号化する場合、次の1-3を順にすればOK。
- 各文字(情報)を出現確率(出現頻度)の高い順に並べ、それぞれを独立したグループと考える
- 各グループの中で、出現確率が低い2つのグループを1つにしていきながら、グループが1つになるまで二分木を作っていく。
- 作成した二分木から、各文字ごとの符号を求める
スポンサードリンク
2. ハフマン符号化と瞬時復号可能性
(1) 瞬時復号可能な符号とは
下のように、後戻りせずに符号化した文字列を復号することができる符号のことを、瞬時復号可能な符号と呼びます。

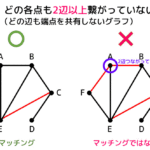
瞬時復号可能であるためには、どの符号語に対しても、頭部分に自身以外の符号語が出てこないかどうかで判定をすることができます。
(2) ハフマン符号化法で符号化した符号は必ず瞬時復号可能(かつ平均符号長が最小)!
ハフマン符号法で符号化を行うと符号は、必ず (平均符号長が最小の) 瞬時復号可能な符号になる点が大きな特徴です。
ここで、ハフマン符号化により符号化すると、必ず瞬時復号可能となることを二分木を使って確認しましょう。
まず、瞬時復号可能ではない符号を二分木で表すと、下のように各文字列が葉ではないノードが出てきますね。
つまり、葉ではないノードに対応する情報 (文字) があった時点で、何かしらの接頭語となっている符号が存在していることになります。
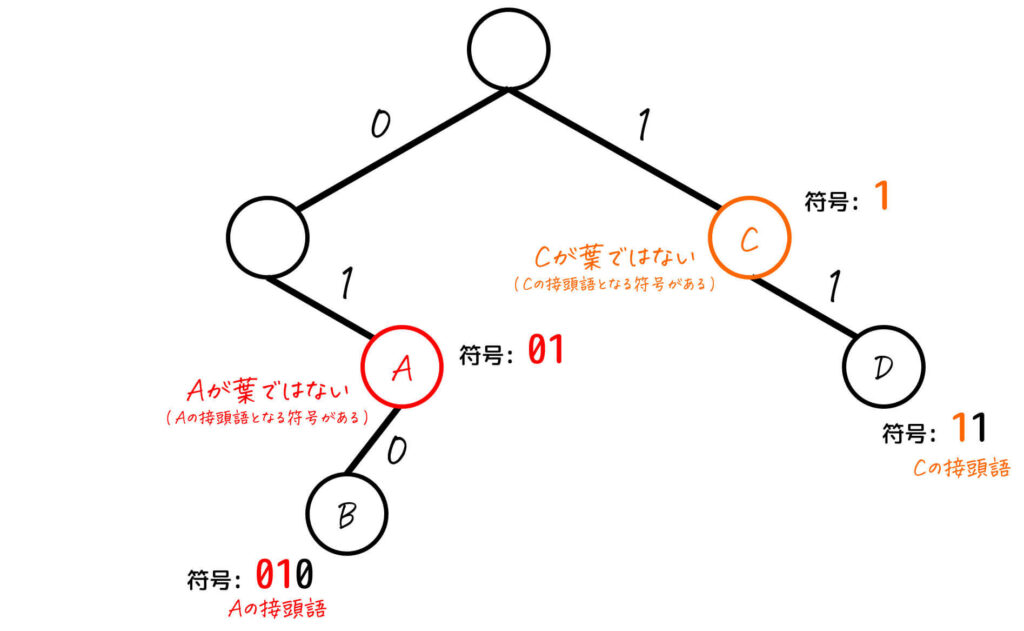
これを言い換えると、「全ての文字に対する各ノードがすべて葉ノードになっている」ことを確認できれば、接頭語となっている符号が存在しないこと、つまり符号が瞬時復号可能であることも確認ができます。
(全ての文字列に対するノードが葉ノード)
ハフマン符号化法によって符号化した符号が必ず平均符号長最小の瞬時復号可能な符号となる性質は、基本情報や応用情報の午前問題を解く際にかなり使えるので、必ず覚えておきましょう!!
※ 二分木を使って符号化をする方法には、ハフマン符号化のほかにシャノン・ファノ符号化もあります。シャノン・ファノ符号化はハフマン符号化とは異なるアルゴリズムで二分木を作成していきますが、瞬時復号可能となる理由はハフマン符号化と同じです[3]。
スポンサードリンク
3. 練習問題
つぎの表は、とある文字列中(情報源)に出てくる文字の出現回数を表にしたものである。
| 文字(記号) | 符号 (ビット表記) | 出現回数 |
|---|---|---|
| A | (ア) | 5 |
| B | (イ) | 1 |
| C | (ウ) | 6 |
| D | (エ) | 4 |
| E | (オ) | 3 |
| F | (カ) | 1 |
(1) この文字列をハフマン符号化法によって符号化し、ビット表記の (ア) ~ (カ) に当てはまるビット表記を答えなさい。
(2) (1)で符号化した符号の平均符号長 \( L \) を小数第2位まで答えなさい。(必要であれば小数第3位を四捨五入すること)
4. 練習問題の答え
(1)を解く前に各文字の出現回数から出現確率を求めましょう。((2)で使うため)
各文字の出現確率は、( 各文字の出現回数 ) ÷ ( 文字全体の出現回数[今回の場合は20] ) で求めることができます。
| 文字(記号) | 符号 (ビット表記) | 出現回数 | 出現確率 |
|---|---|---|---|
| A | (ア) | 5 | 25% |
| B | (イ) | 1 | 5% |
| C | (ウ) | 6 | 30% |
| D | (エ) | 4 | 20% |
| E | (オ) | 3 | 15% |
| F | (カ) | 1 | 5% |
(1) ハフマン符号による符号化
Step1. 各文字を出現確率 (回数) の多い順に並べ、各文字ごとを独立したグループとする
まず、与えられた文字(記号・情報)をそれぞれ独立したグループとしてから、出現確率が大きい順に並び替えます。
| グループ (文字) | 出現確率 |
|---|---|
| C | 30% |
| A | 25% |
| D | 20% |
| E | 15% |
| B | 5% |
| F | 5% |
今回の場合は6種類あるため、6つの独立したグループが出てきます。
Step2. 出現確率が低い2つのグループを1つにしていきながら、二分木を作る
つぎに、1グループになるまで、「出現確率が低い2つのグループを1つにまとめる」という操作を繰り返します。
Step2-1. 6グループ → 5グループ
| グループ (文字) | 出現確率 |
|---|---|
| C | 30% |
| A | 25% |
| D | 20% |
| E | 15% |
| B | 5% |
| F | 5% |
まずは、出現確率が低い2つのグループは、BとFなので、この2つをひとまとめにします。
| グループ (文字) | 出現確率 |
|---|---|
| C | 30% |
| A | 25% |
| D | 20% |
| E | 15% |
| BF | 10% |
さらに、ひとまとめにした2つのグループを子とし、二分木をつくります。
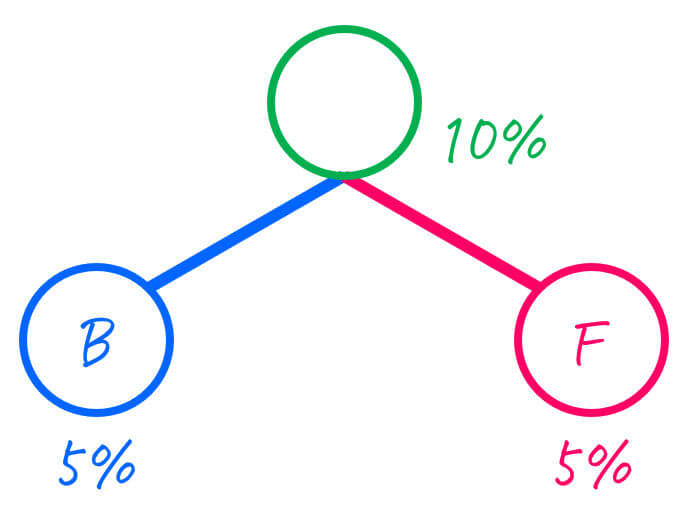
Step2-2. 5グループ → 4グループ
| グループ (文字) | 出現確率 |
|---|---|
| C | 30% |
| A | 25% |
| D | 20% |
| E | 15% |
| BF | 10% |
出現確率が低い2つのグループは、BとFなので、この2つをひとまとめにします。
| グループ (文字) | 出現確率 |
|---|---|
| C | 30% |
| A | 25% |
| EBF | 25% |
| D | 20% |
さらに、ひとまとめにした2つのグループを子とし、二分木をつくります。
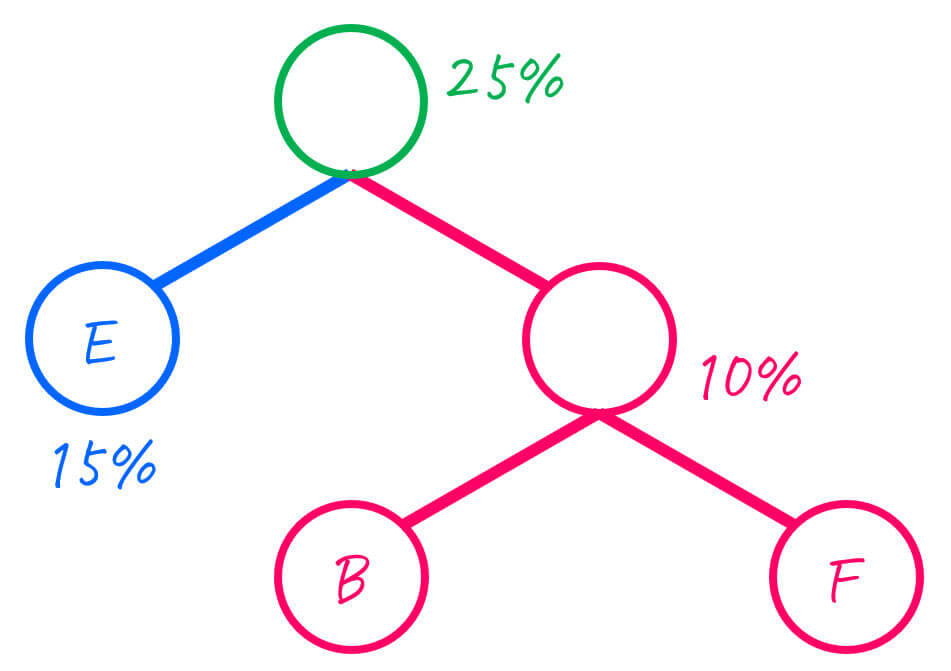
Step2-3. 4グループ → 3グループ
| グループ (文字) | 出現確率 |
|---|---|
| C | 30% |
| A | 25% |
| EBF | 25% |
| D | 20% |
まずは、出現確率が低い2つのグループは、EBFとDなので、この2つをひとまとめにします。
| グループ (文字) | 出現確率 |
|---|---|
| EBFD | 45% |
| C | 30% |
| A | 25% |
さらに、ひとまとめにした2つのグループを子とし、二分木をつくります。
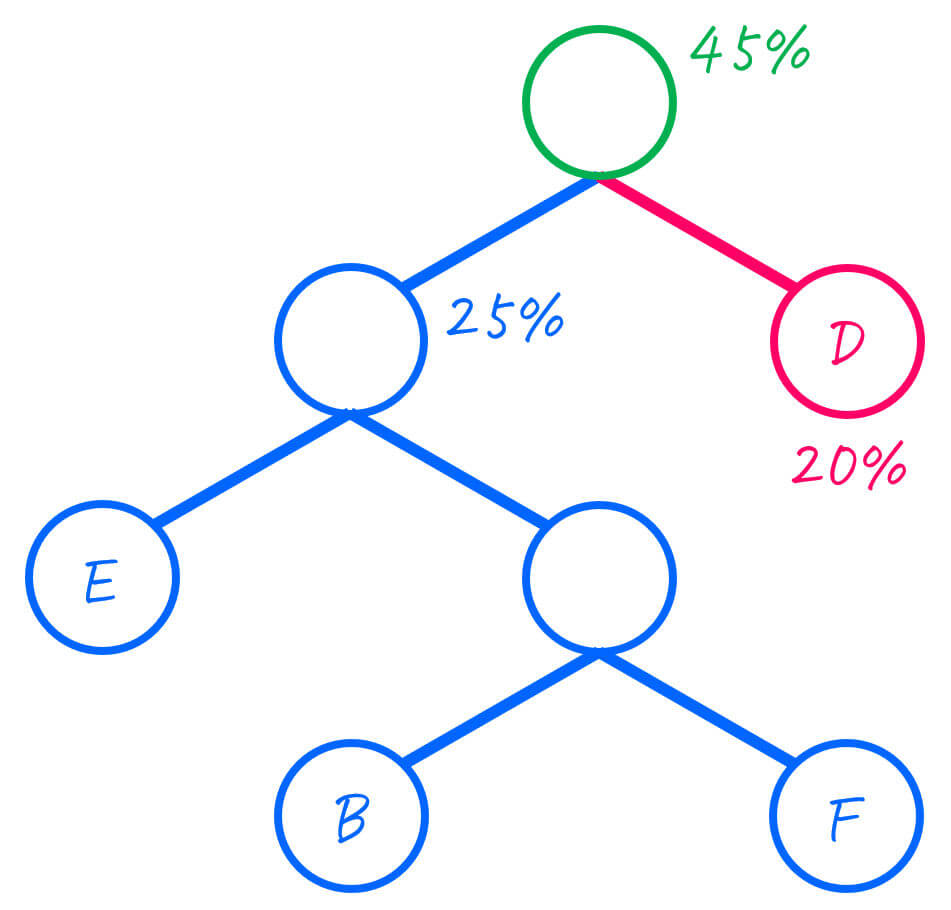
Step2-4. 3グループ → 2グループ
| グループ (文字) | 出現確率 |
|---|---|
| EBFD | 45% |
| C | 30% |
| A | 25% |
出現確率が低い2つのグループは、CとAなので、この2つをひとまとめにします。
| グループ (文字) | 出現確率 |
|---|---|
| CA | 55% |
| EBFD | 45% |
さらに、ひとまとめにした2つのグループを子とし、二分木をつくります。
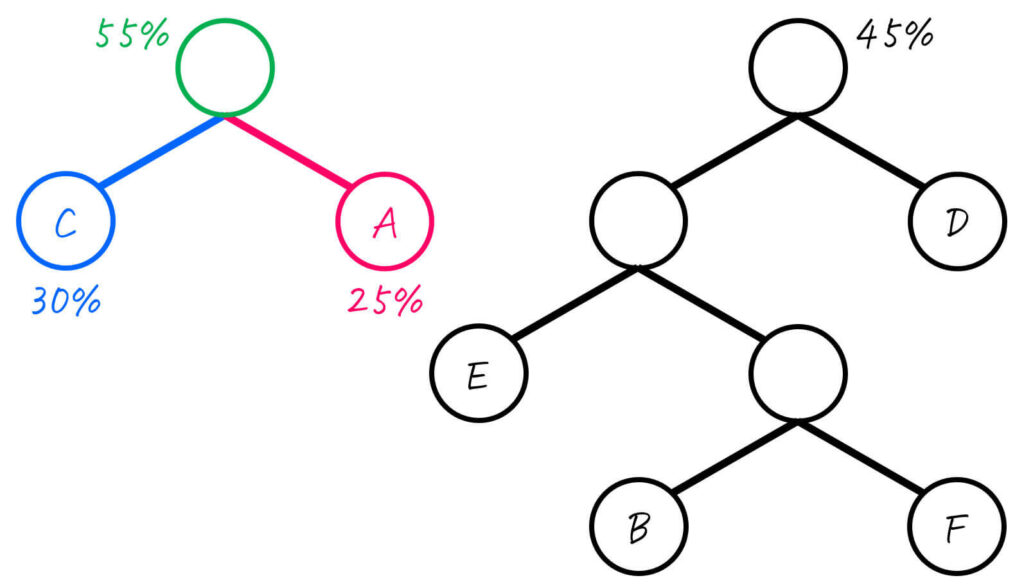
Step2-5. 2グループ → 1グループ
残りの2つのグループ(CAとEBFD)をひとまとめにします。
| グループ (文字) | 出現確率 |
|---|---|
| CA | 55% |
| EBFD | 45% |
このグループを子とし、二分木をつくれば、二分木の完成です。
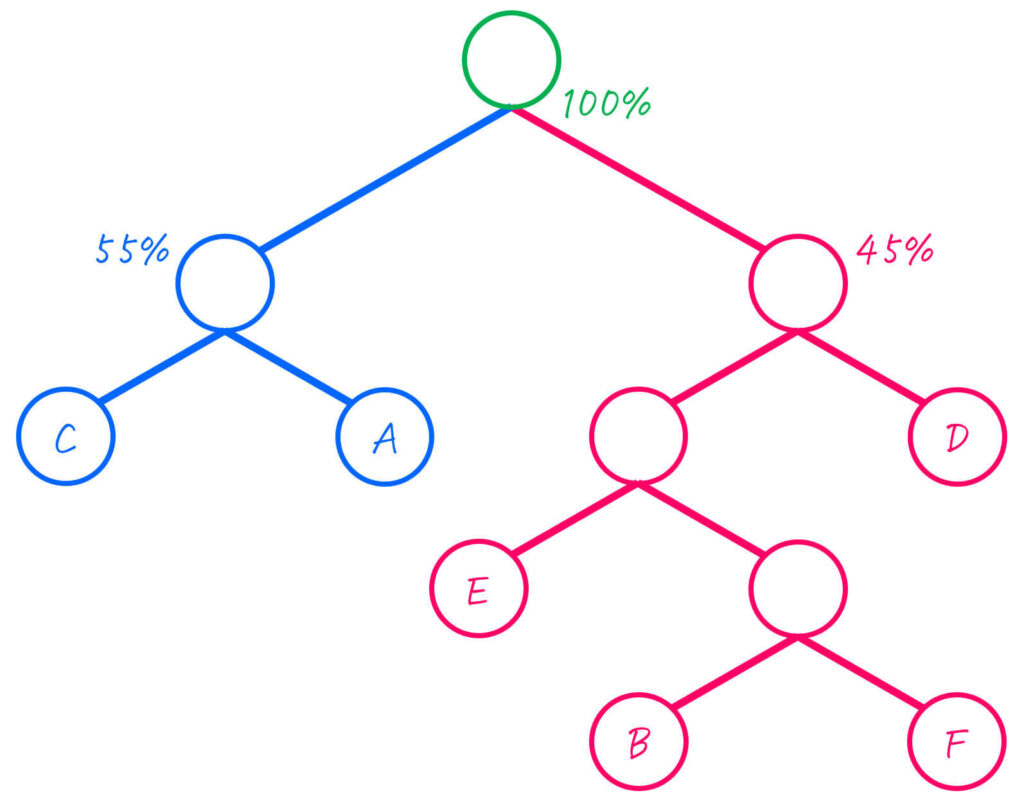
Step3. 作成した二分木から各文字(情報)ごとの符号を求める
二分木が完成したら、つぎの方法で符号を求めていきます。
- 二分木の各節(ノード)の左側を0、右側を1とする
- 各文字(A~F)ごとに、以下の操作を実施
- 木構造の一番上の部分から対応するノードまでたどっていく
- たどった際に通った0, 1を左から順番に並べたものを符号にする
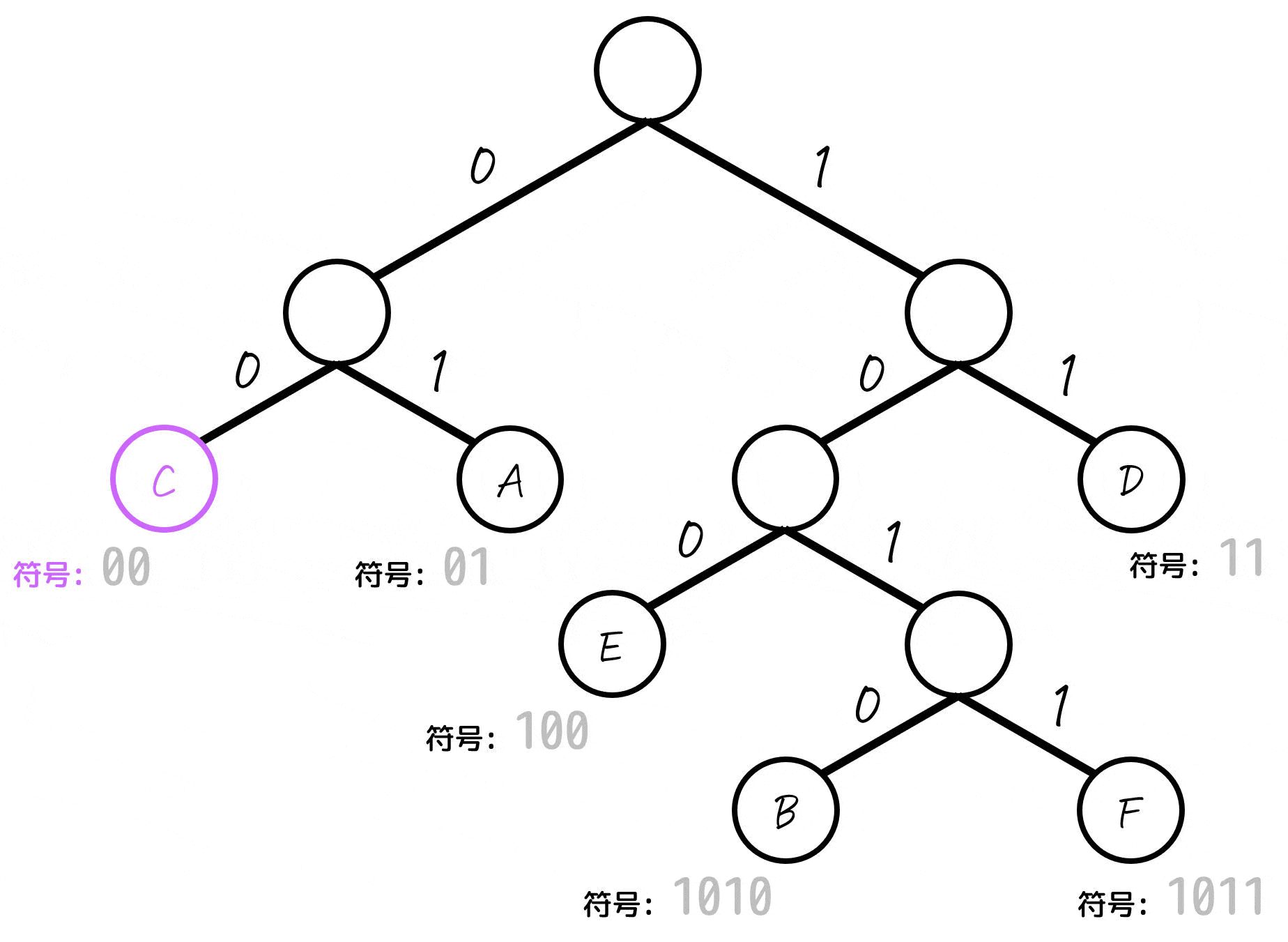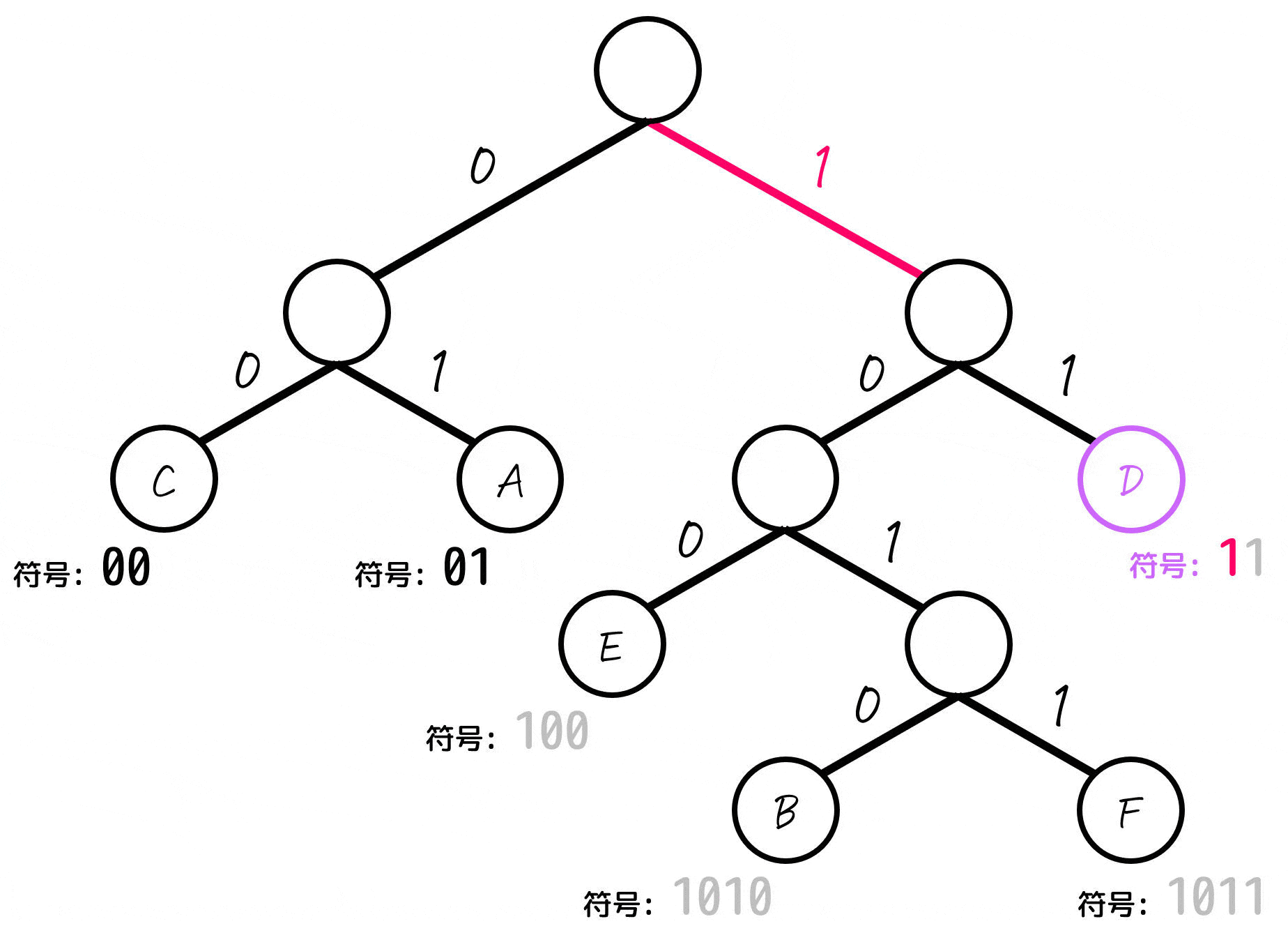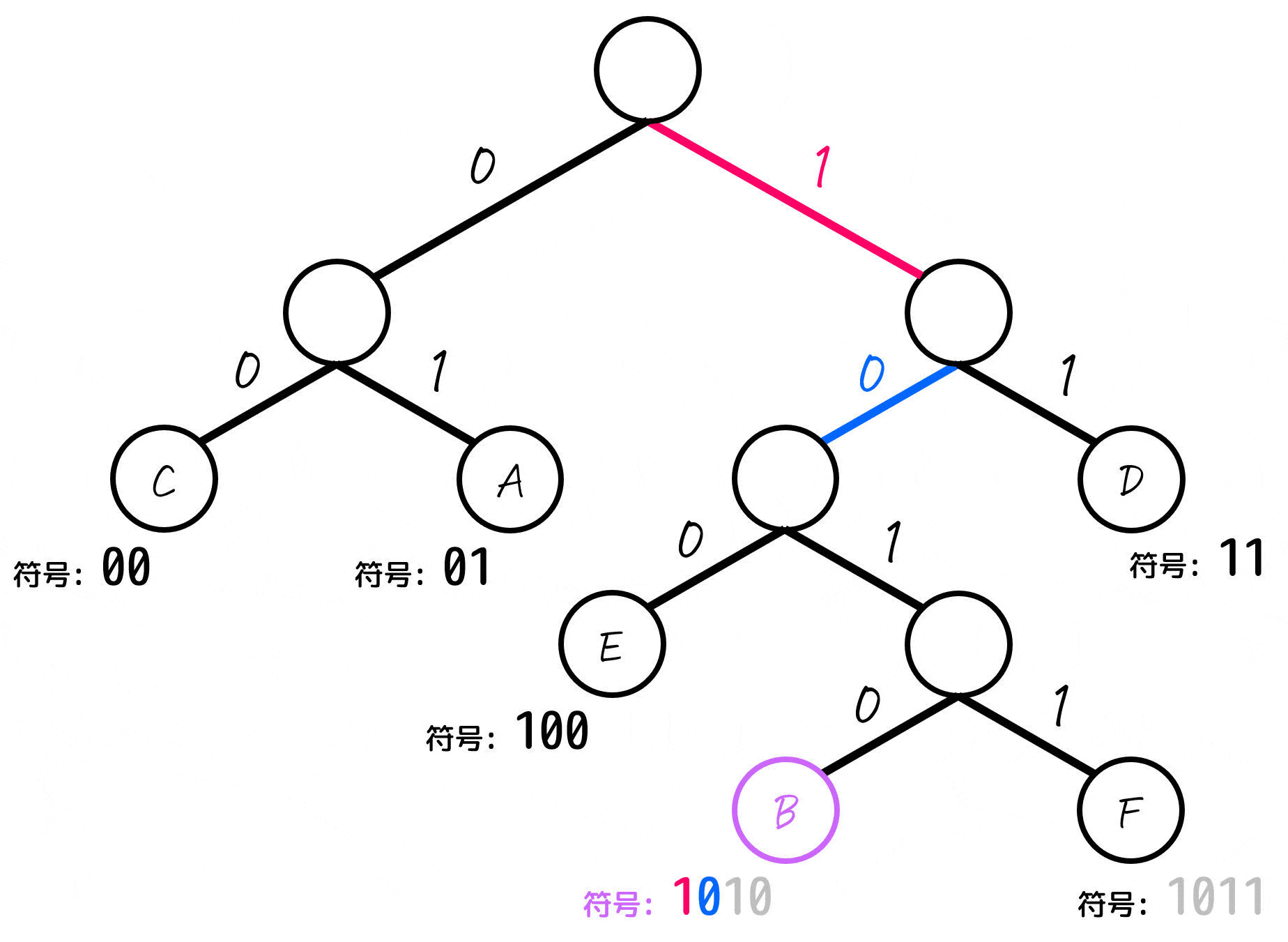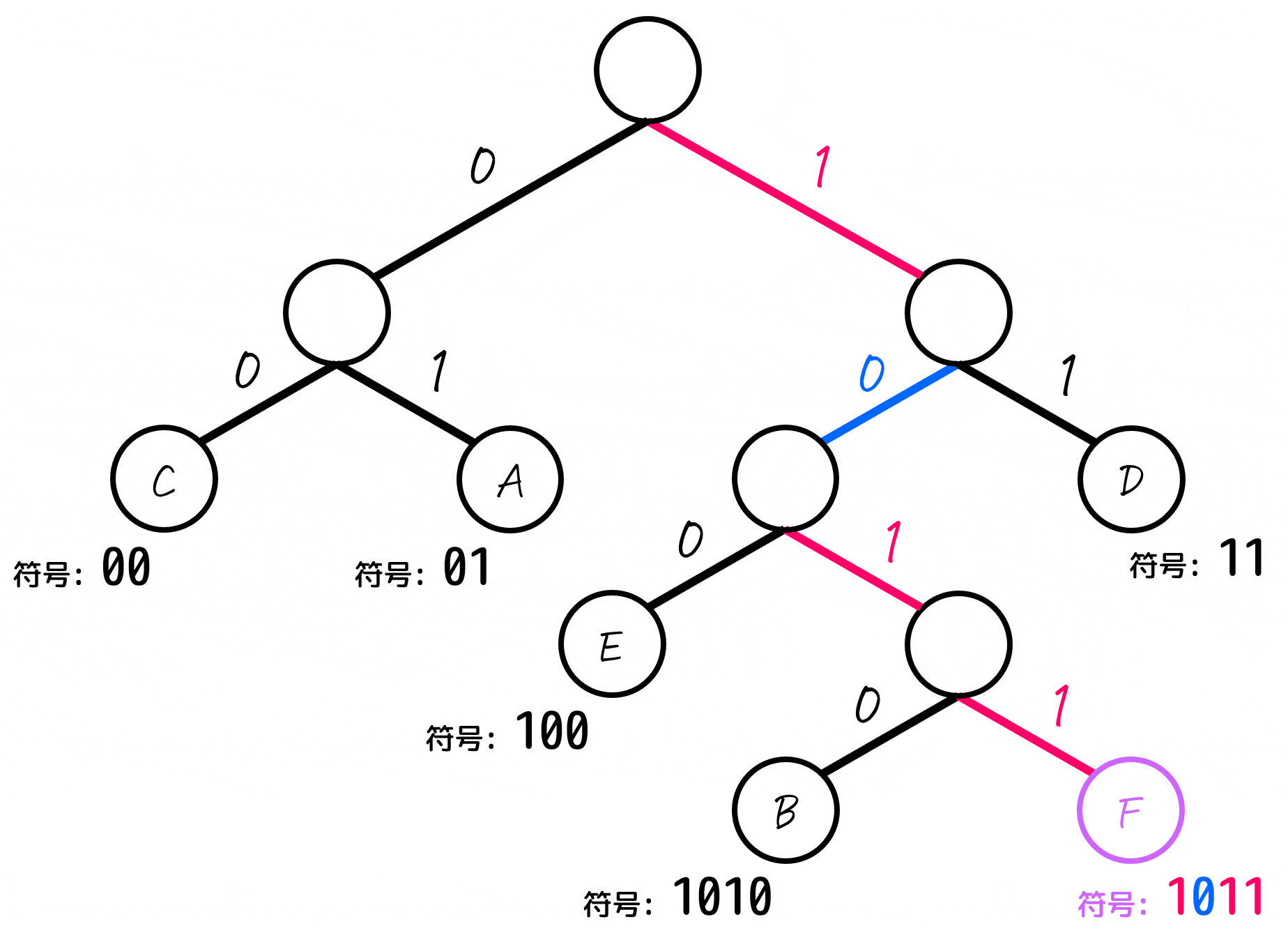
よって、各文字A~Fごとの符号は下のように求まります。
| 文字(記号) | 符号 (ビット表記) | 出現確率 |
|---|---|---|
| A | 01 | 25% |
| B | 1010 | 5% |
| C | 00 | 30% |
| D | 11 | 20% |
| E | 100 | 15% |
| F | 1011 | 5% |
(2) 平均符号長の計算
まず、各文字ごとの「符号長」および「符号長 × 出現確率」を求めましょう。
| 文字(記号) | 符号 (ビット表記) | 符号長 | 出現確率 | 符号長 × 出現確率 |
|---|---|---|---|---|
| A | 01 | 2 | 25% | 0.50 |
| B | 1010 | 4 | 5% | 0.20 |
| C | 00 | 2 | 30% | 0.60 |
| D | 11 | 2 | 20% | 0.40 |
| E | 100 | 3 | 15% | 0.45 |
| F | 1011 | 4 | 5% | 0.20 |
あとは、A~Fごとに求めた「符号長 × 出現確率」をすべて足すことで平均符号長 \( L \) を求めることができます。\[\begin{align*}
L & = 0.50 + 0.20 + 0.60 + 0.40 + 0.45 + 0.20
\\ & = 2.35
\end{align*}\]
5. [問題] 基本情報・応用情報での問われ方
最後に、実際に基本情報・応用情報でハフマン符号化はどのように問われるかを見ていきましょう。
(1) 基本情報の午前問題の例
出現頻度の異なるA、B、C、D、Eの5文字で構成される通信データを、ハフマン符号化を使って圧縮するために、符号表を作成した。aに入る符号として、適切なものはどれか。
| 文字 | 出現頻度 (%) | 符号 |
|---|---|---|
| A | 26 | 00 |
| B | 25 | 01 |
| C | 24 | 10 |
| D | 13 | [ a ] |
| E | 12 | 111 |
ア: 001
イ: 010
ウ: 101
エ: 110
[基本情報技術者 平成30年秋期 午前問4]
(2) 応用情報の午前問題の例
符号化方式に関する記述のうち、ハフマン方式はどれか。
ア: 0と1の数字で構成する符号の中で,0又は1の連なりを一つのブロックとし,このブロックに長さを表す符号を割り当てる。
イ: 10進数字の0~9を4ビット2進数の最初の10個に割り当てる。
ウ: 発生確率が分かっている記号群を符号化したとき,1記号当たりの平均符号長が最小になるように割り当てる。
エ: 連続した波を標本化と量子化によって0と1の数字で構成する符号に割り当てる。
[応用情報技術者 平成30年秋期 午前問5]
6. [解答] 基本情報・応用情報での問われ方
(1) 基本情報の午前問題の例
解答: エ
基本情報では問題には必ず選択肢が与えられています。
(応用情報でも午前問題と一部の午後問題には与えられています。)
そのため、ハフマン符号化を行った符号の特徴である
- 必ず瞬時復号可能となる
- 瞬時復号可能な符号の中でも平均符号長が最短となる
を満たしていない選択肢を消去していくことで、ハフマン符号化をしなくても正解に導けることがあります。
今回の場合、
ア → Aの符号00の接頭語となるためNG
イ → Bの符号01の接頭語となるためNG
ウ → Cの符号10の接頭語となるためNG
となるため、ハフマン符号化をしなくても残った エ が正解とわかります。
また、「瞬時復号可能」かを調べるのであれば下のように図を書くのも有効です。
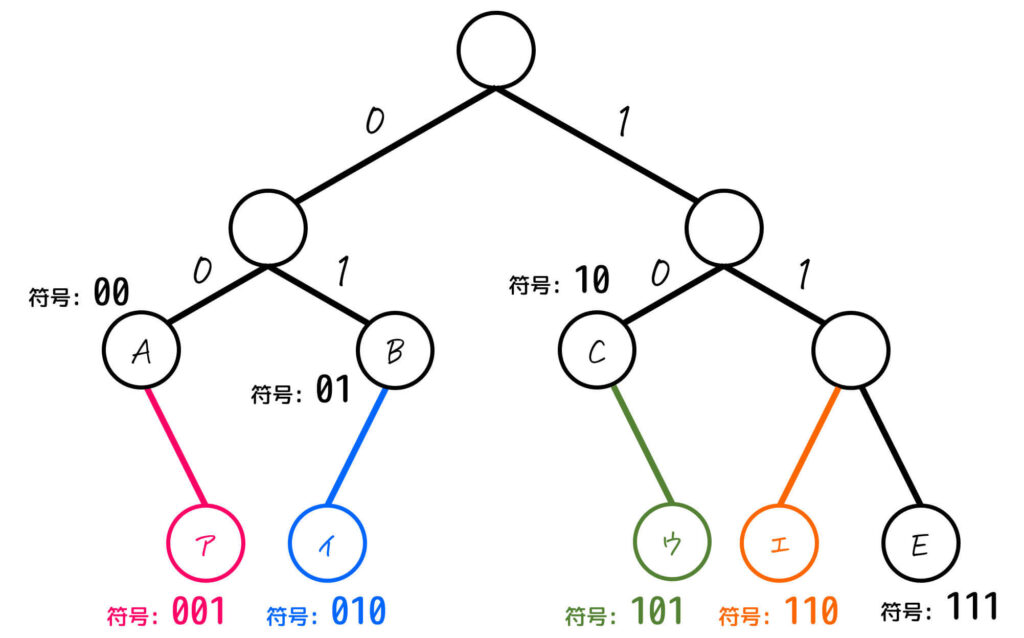
図を見ると、ア~ウのノードを追加すると、どこかしらのノードが葉ではなくなりますね。なので、ア~ウの選択肢は誤りであることがわかります。
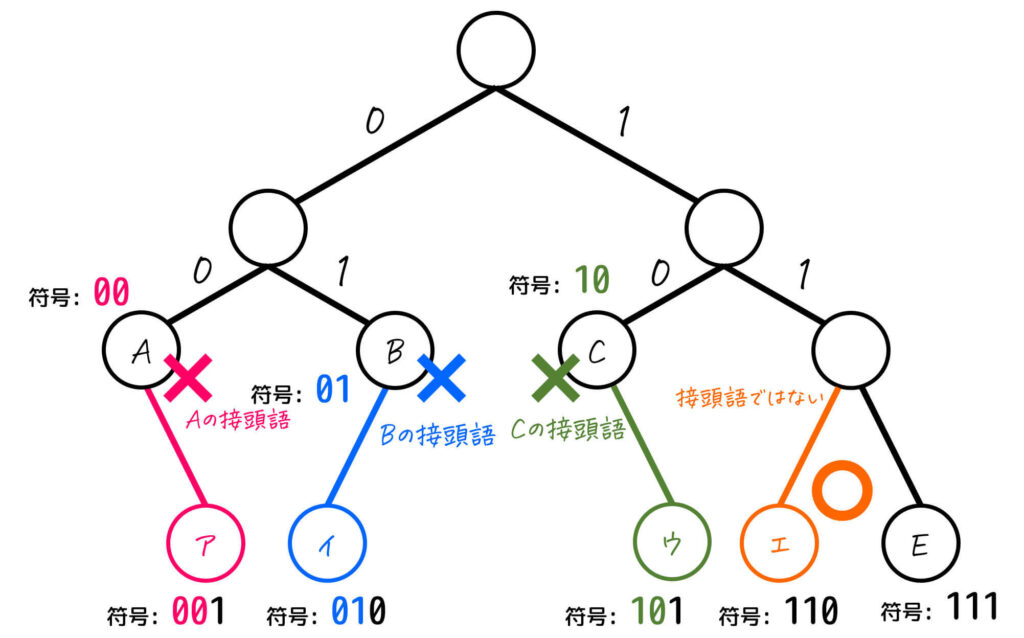
(2) 応用情報の午前問題の例
解答: ウ
ハフマン符号に関する知識の問題です。ハフマン符号について知っているだけで、1問分の得点が得られるおいしい問題なので、必ず得点をしておきたいですね。
[他の選択肢]ア: 不正解。ラングレス法に関する説明。
イ: 不正解。二進化十進数 (BCD、Binary-coded decimal) に関する説明。
ウ: 正解。ハフマン符号化に関する説明。
エ: 不正解。ディジタル化の説明。
関連広告・スポンサードリンク
![[基本情報・応用情報] うさぎでもわかる情報理論 第3羽 ハフマン符号化](https://www.momoyama-usagi.com/wp-content/uploads/joho1-11.gif)