スポンサードリンク
こんにちは、ももやまです。
目次
スポンサードリンク
1. 順序回路とは?
(1) 今までの論理回路 (組み合わせ回路) のおさらい
順序回路を勉強する前に、まずは今まで勉強してきた論理回路のおさらいをしましょう。
今まで勉強してきた論理回路は、下のようにANDゲート、ORゲート、NOTゲートなどの基本的な論理演算を行う部品を組み合わせることで出来た回路ですね。
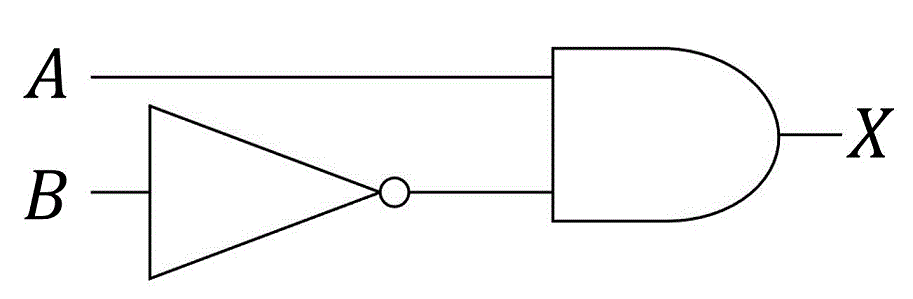
例えば、この回路に \( A = 1 \), \( B = 0 \) を入力すると、絶対に \( X = 1 \) を返しますね。5分後に \( (A,B) = (1,0) \) を代入しても \( X = 1 \) を返すし、100年後に \( (A,B) = (1,0) \) を代入しても絶対にこの回路は \( X = 1 \) を返します。
つまり、今まで習ってきた論理回路は、出力結果が現時点での入力だけで決まるものだと言えますね。
このように、現時点の入力だけで出力が決まるような回路のことを組み合わせ回路と呼びます。
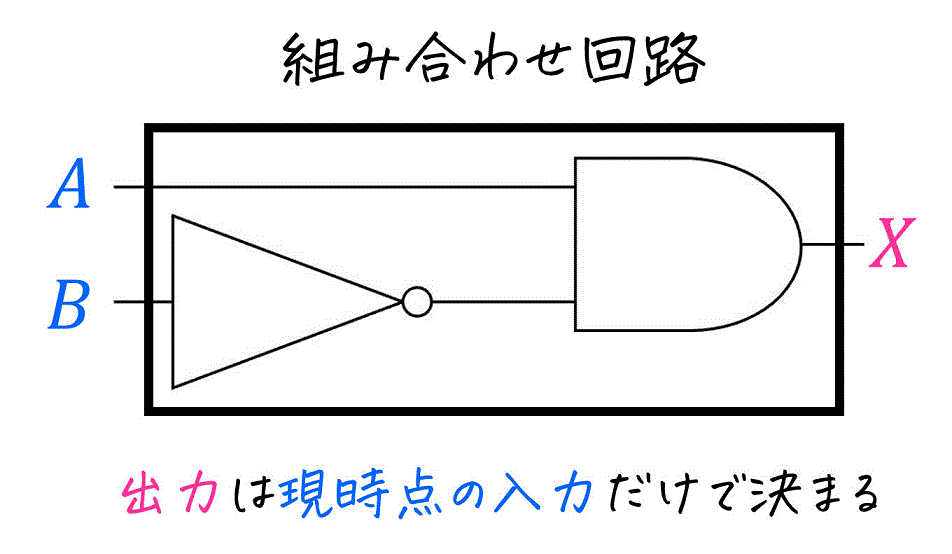
(2) 順序回路
それでは、本題の順序回路に入って行きましょう。
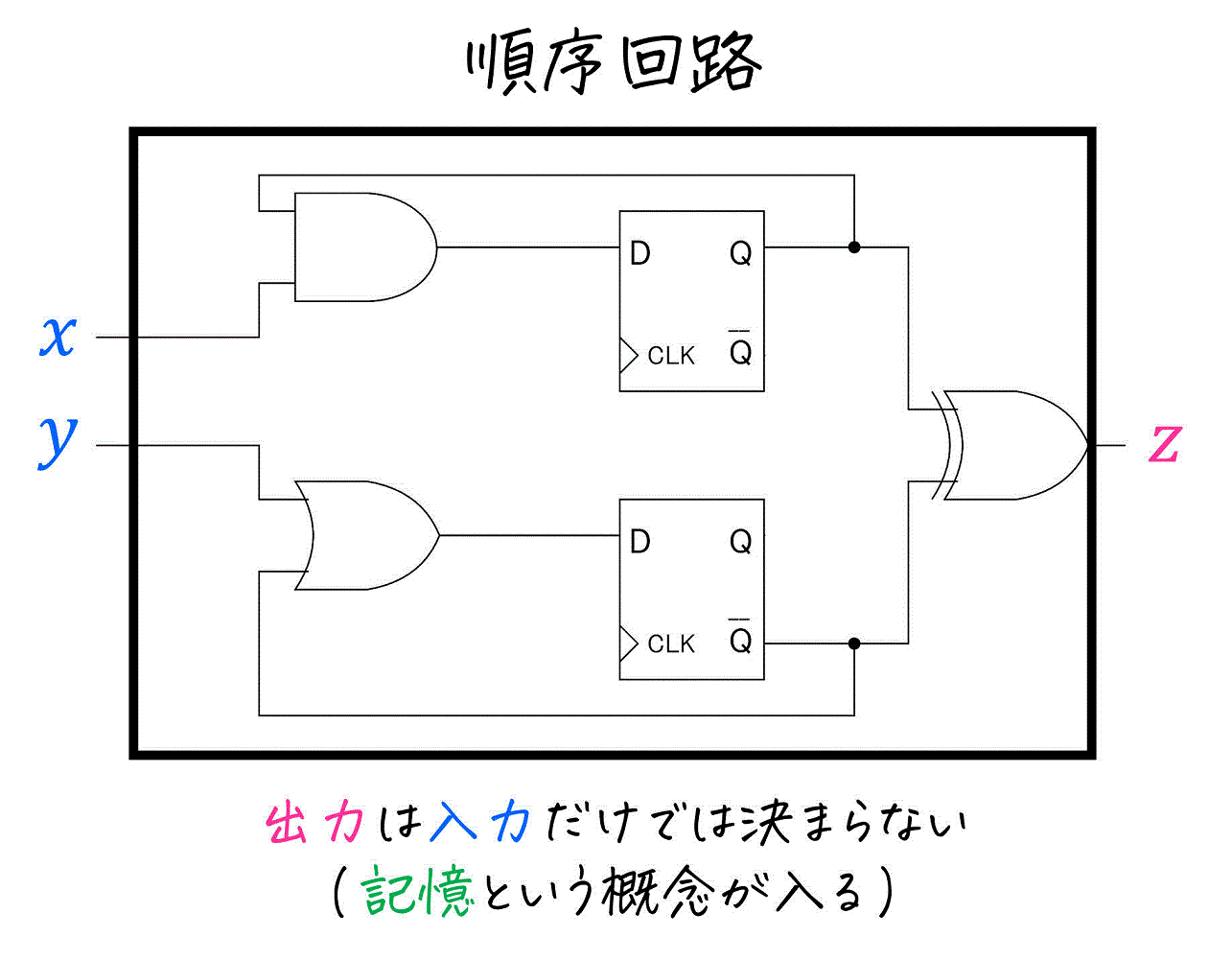
順序回路は、出力が現時点の入力だけでなく、過去に入力した値によっても変わる論理回路のことを言います。
組み合わせ回路に記憶(過去の入力)という概念が追加された回路だと思っていただけたらOKです。
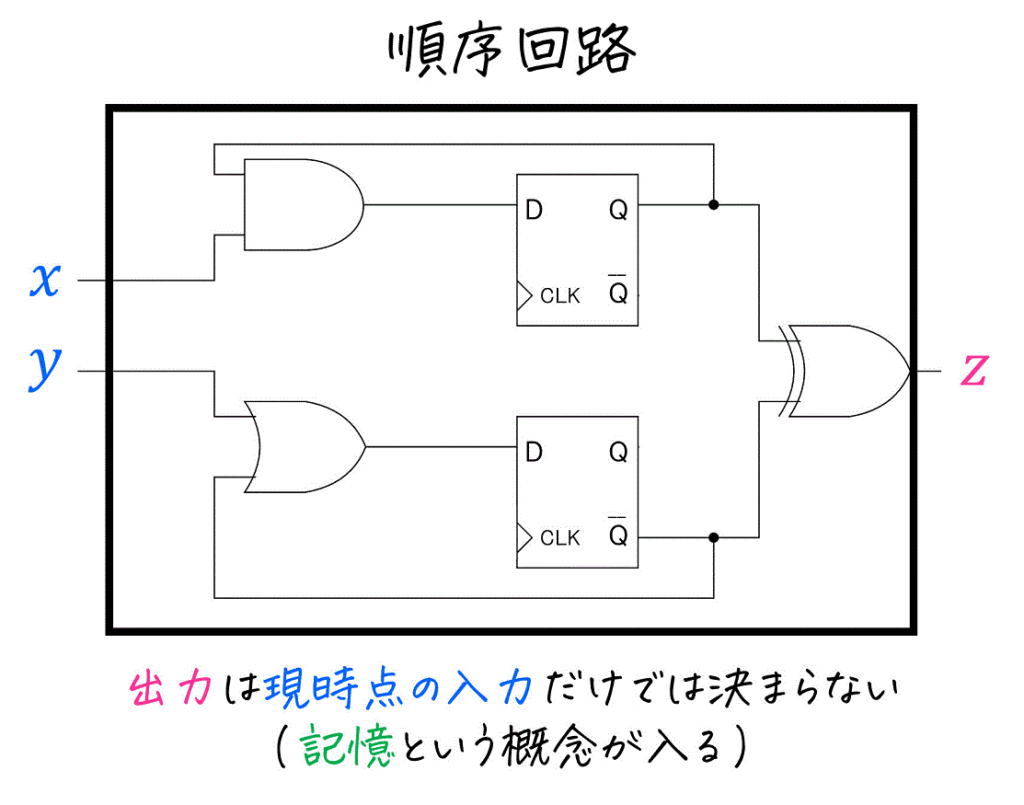
※ 回路の中に \( D \) やら \( Q \) が書かれた謎の部品がありますが、この記事の2章で詳しく説明するので、気になる方は2章をご覧ください
順序回路は、現時点の入力だけでなく、過去に入力された値によっても出力を変えることができるため、組み合わせ回路に比べてより多機能な装置を設計をすることができます。
具体的に
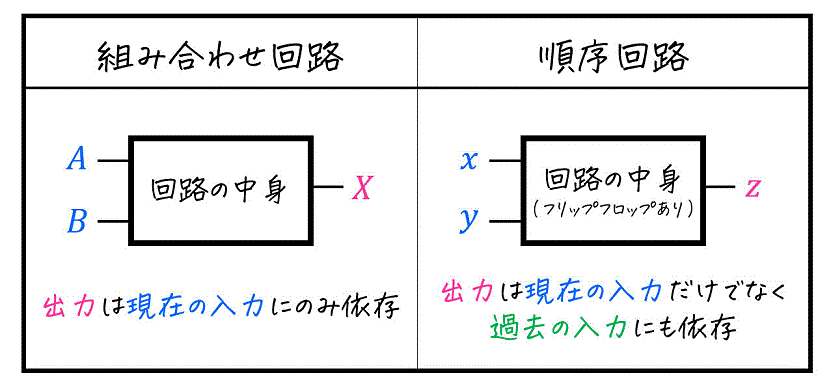
まとめ:組み合わせ回路と順序回路
スポンサードリンク
2. フリップフロップ
現在の入力だけでなく、過去の入力にも出力が影響する回路(順序回路)を作るためには、過去に入力された値を記憶するような部品が必要ですね。
このように、過去に入力された値(0か1)を記憶する部品のことをフリップフロップと呼びます。
0か1を記憶するということは、フリップフロップは1ビットの値を記憶できる装置と言い換えることもできますね。
この章では、
- フリップフロップの基本的な動き
- 様々なフリップフロップの紹介(4種類)
の2つに着目してフリップフロップの知識をつけていきましょう。
(1) フリップフロップの基本的な動き
まずは、どのフリップフロップにも共通する基本的な特徴について説明していきます。
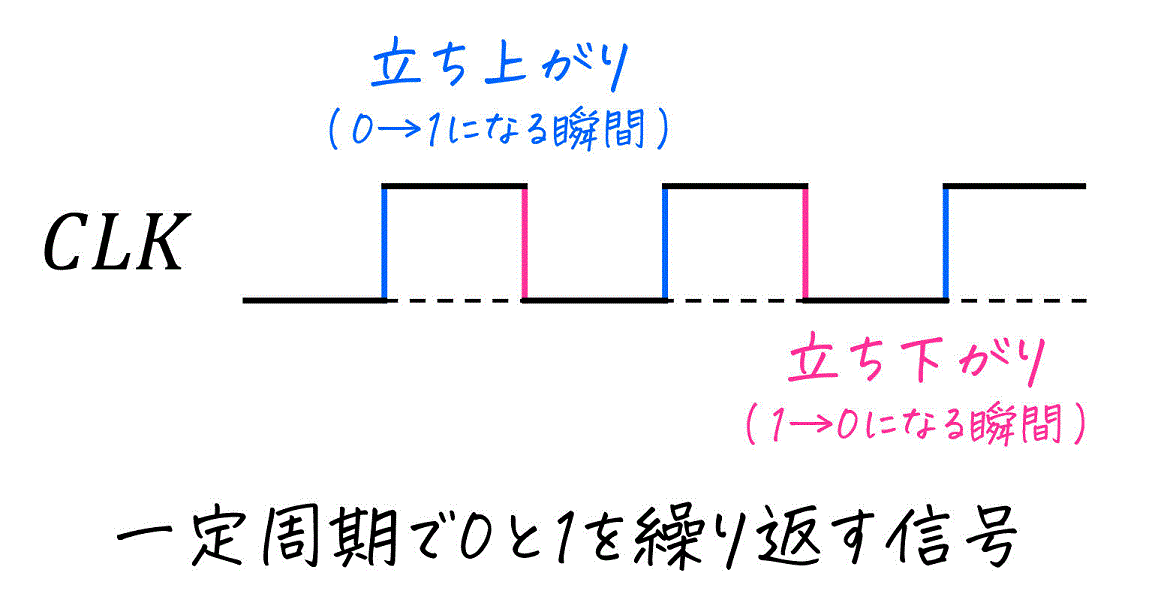
まず、フリップフロップの特徴として、入力が変化した直後(図の赤丸部分)には入力された値が同期されず、出力が変化しないという特徴があります。
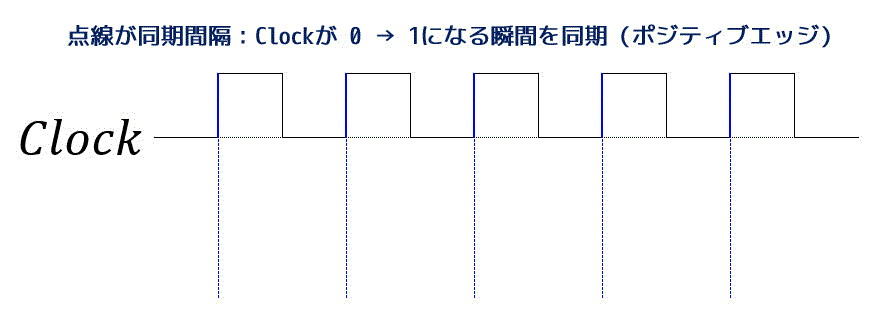
では、いつ同期され、出力が変化するのかというと、クロック (CLK・Clock) と呼ばれる周期的に0と1が変化する信号が切り替わったタイミングで変化します。(図の青丸部分)
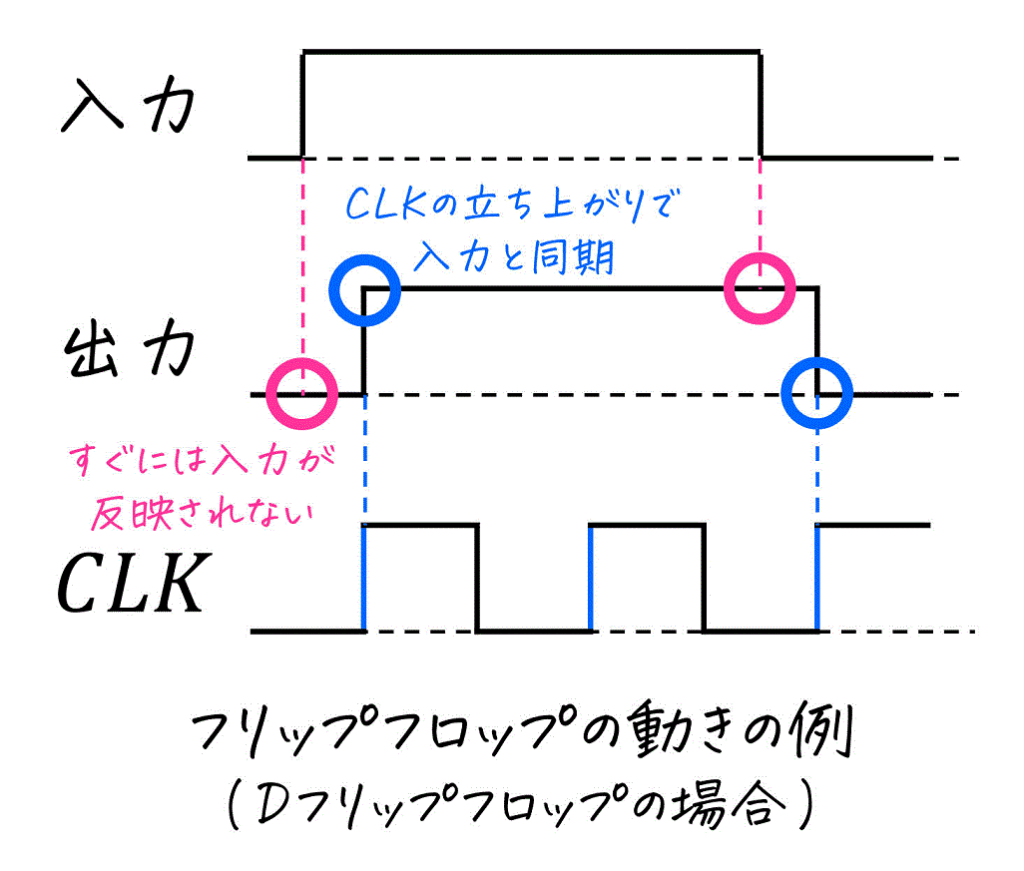
※1 上の出力は、CLKが立ち上がった際に入力されている値がそのまま出力値となるフリップフロップです。
(Dフリップフロップと呼ばれます)
※2 今回はCLKが 0 → 1 となったタイミング(立ち上がり)で出力が変化することにしましょう。余談ですが、このようなタイプのことをポジティブエッジと呼ぶこともあります[1]逆に 1 → 0 … Continue reading。
先ほど説明した2つの特徴
- 入力が変化してもすぐには出力は変化しない
- CLKが0→1となった瞬間(立ち上がり)で入力値が同期され、出力が変化する
を言い換えると、CLKが立ち上がるまで前に入力された値を記憶(キープ)していると言えますよね。
キープしている
(2) 様々なフリップフロップ
つぎに、全4種類のフリップフロップがどのような特徴を持っているかを、見ていきましょう。
(試験に出る順に紹介をしています。)
(i) Dフリップフロップ (D-FF) [超重要!]
Dフリップフロップは、CLKが立ち上がる瞬間の \( D \) の値をそのまま次状態 \( Q_{n+1} \) とする最も基本的なフリップフロップです。
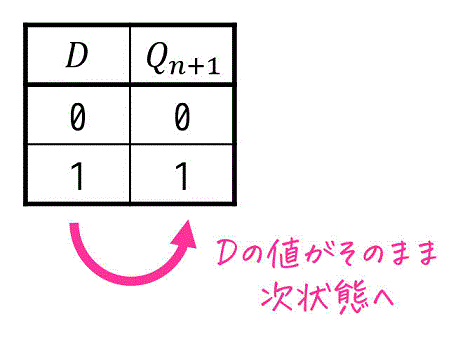
実際にDフリップフロップの動きをアニメーションにしてみました。
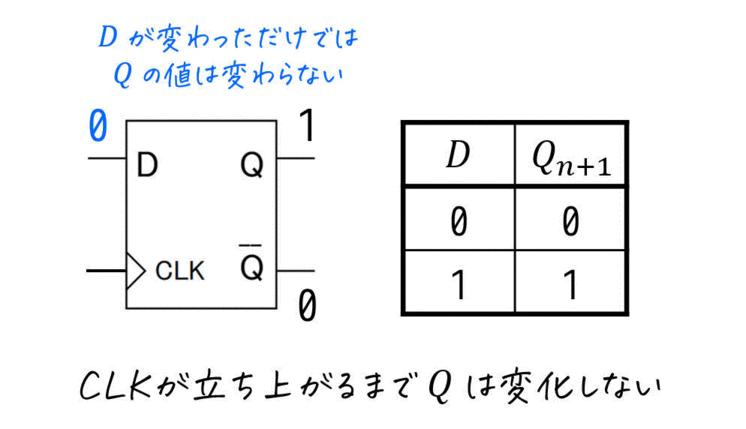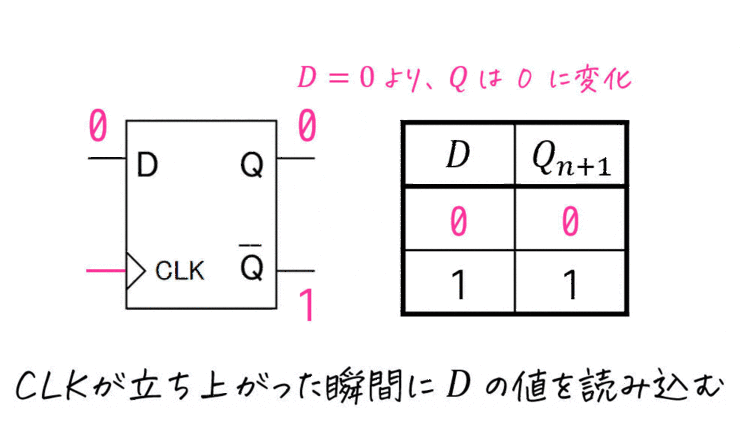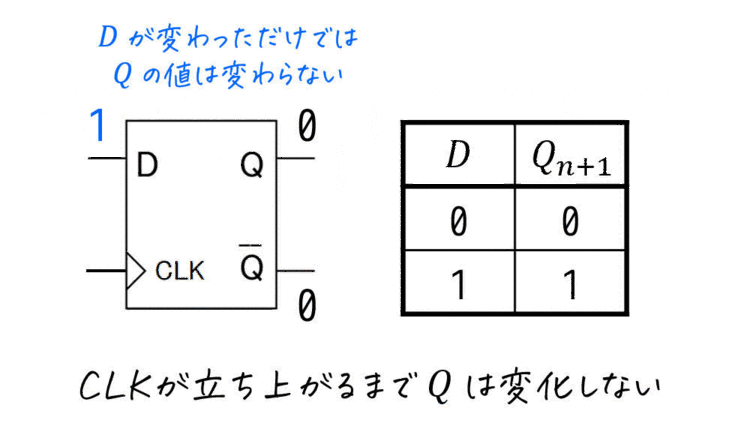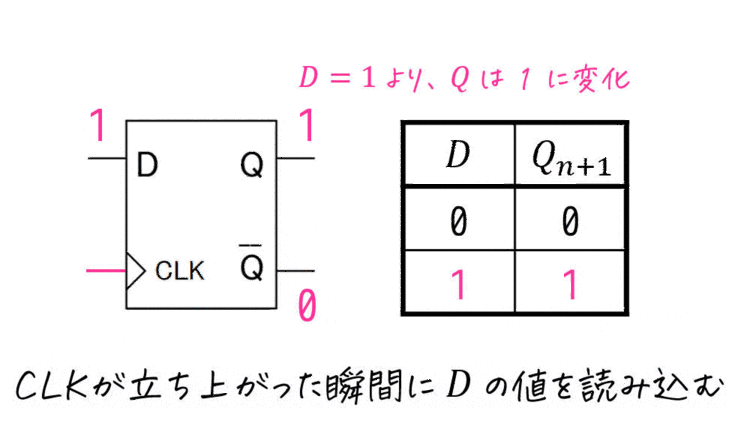
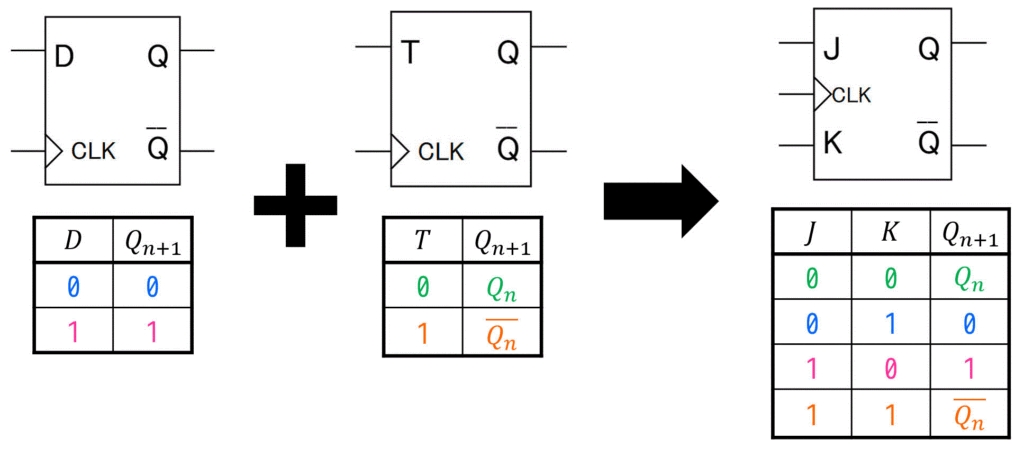
(ii) JKフリップフロップ [重要!]
JKフリップフロップは、2つの入力 \( J \), \( K \) を用いることで、「次状態 \( Q_{n+1} \) の値を0 もしくは 1にする」2種類の操作に加えて、「現状態 \( Q_n \) の値を保持する」と「現状態 \( Q_n \) の値を反転する」操作も可能な(全部で4種類の操作ができる)フリップフロップです。
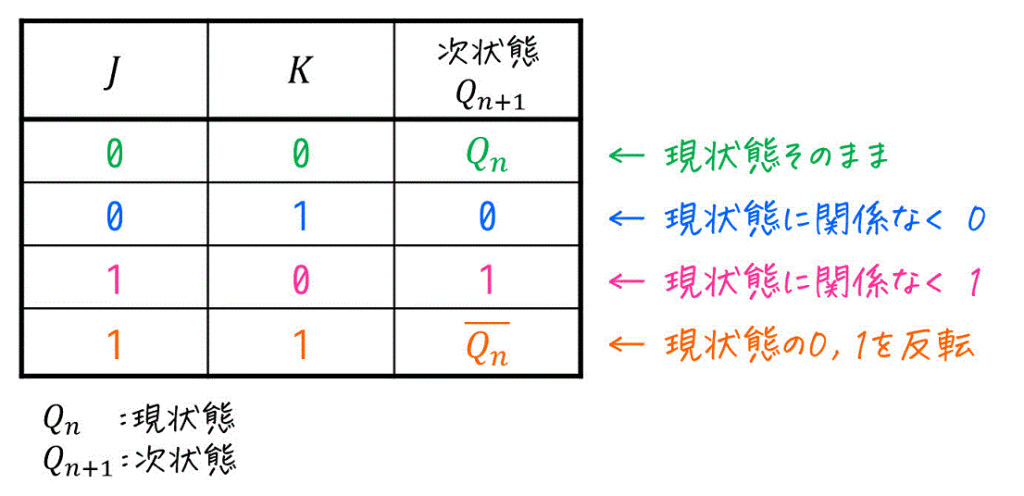
実際に、JKフリップフロップの動きを見てみましょう。
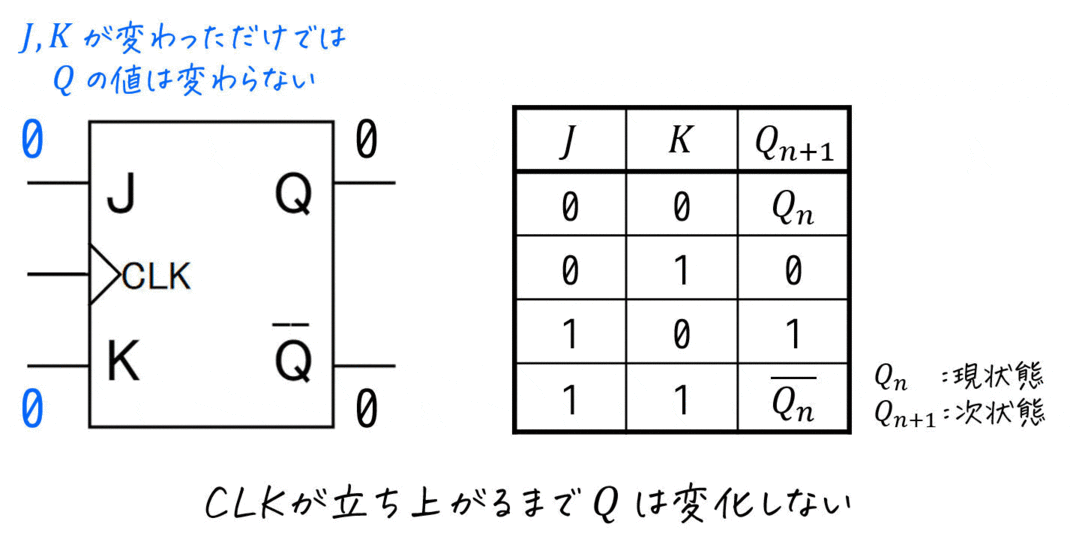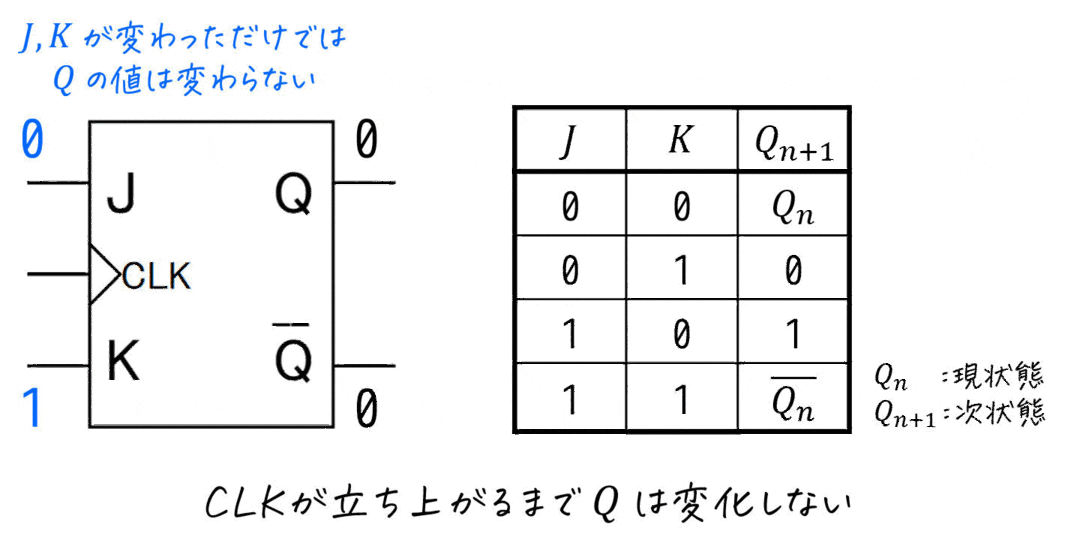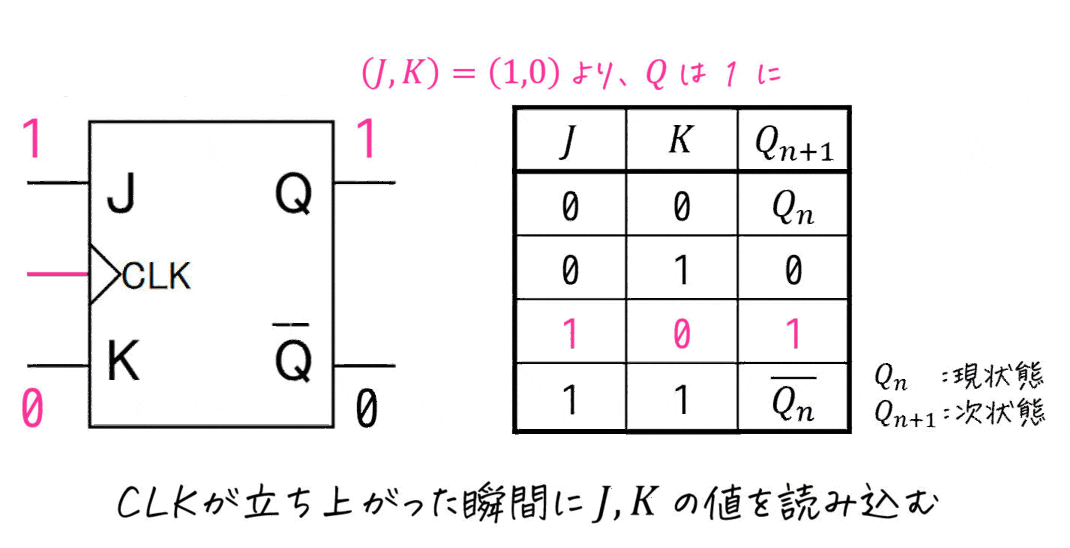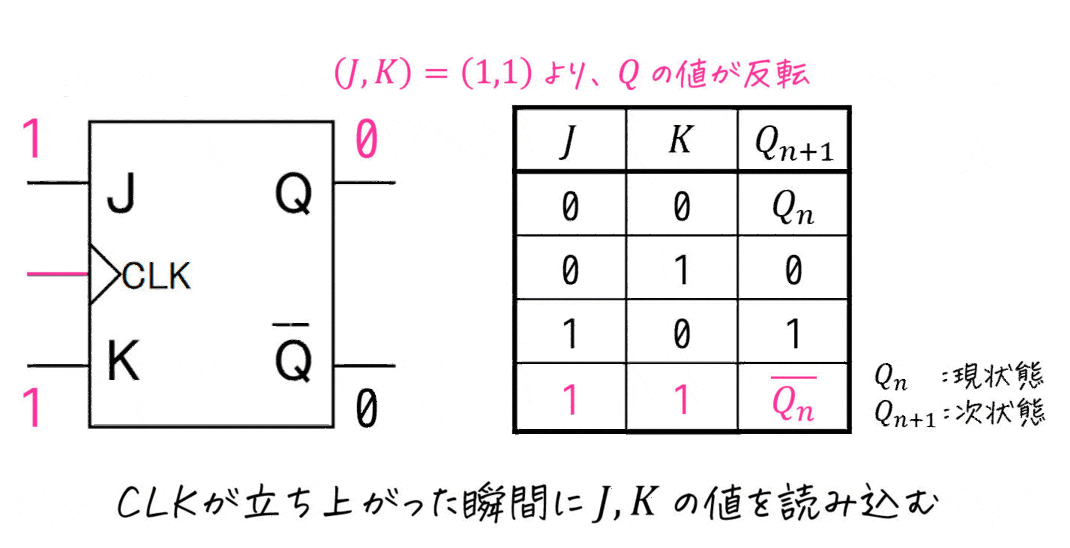
(決して女子高生のJKではありません。)
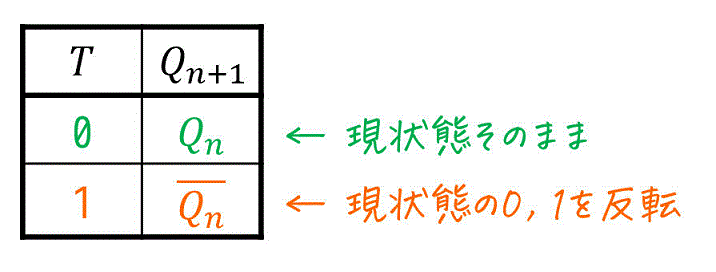
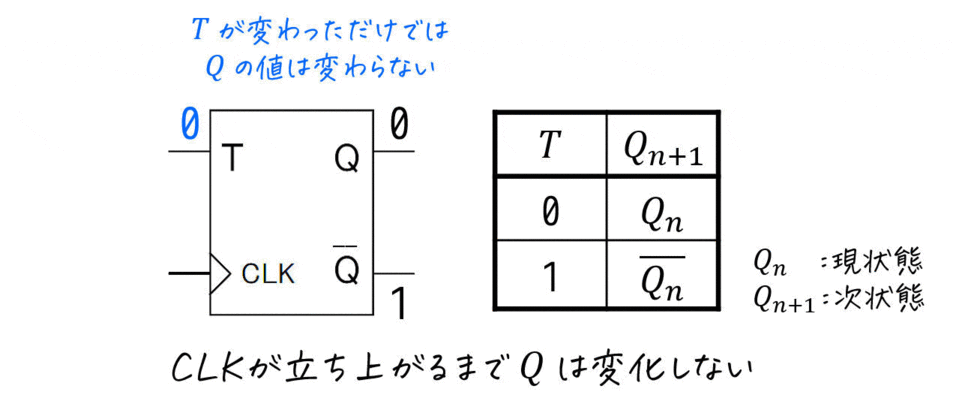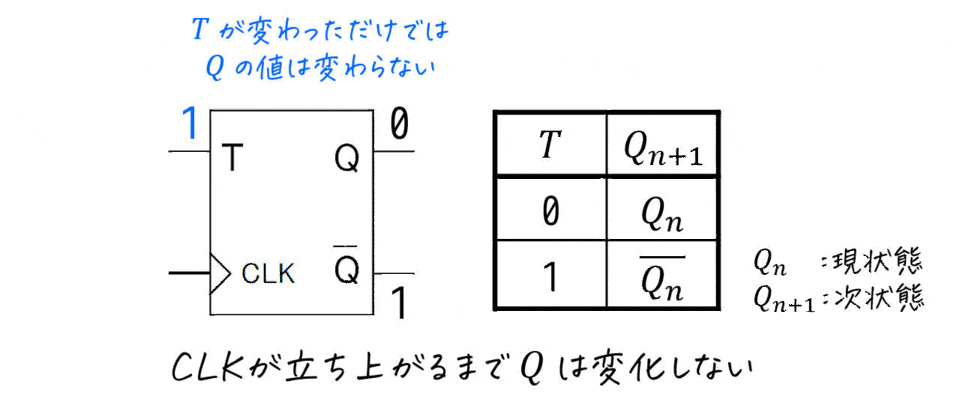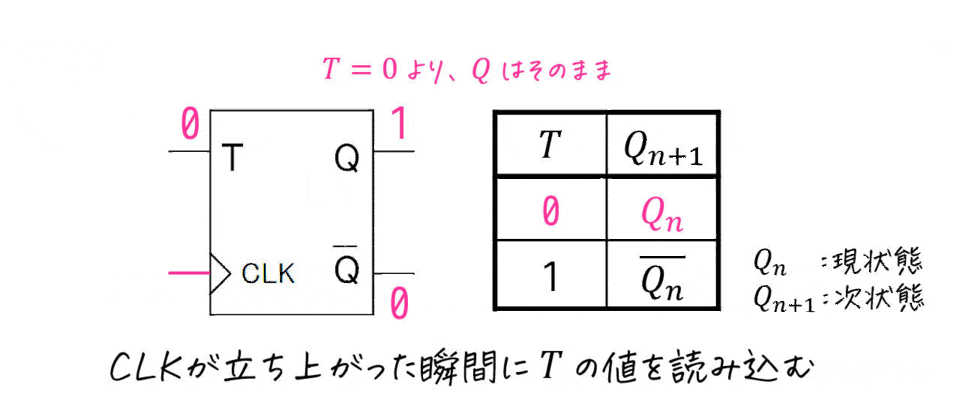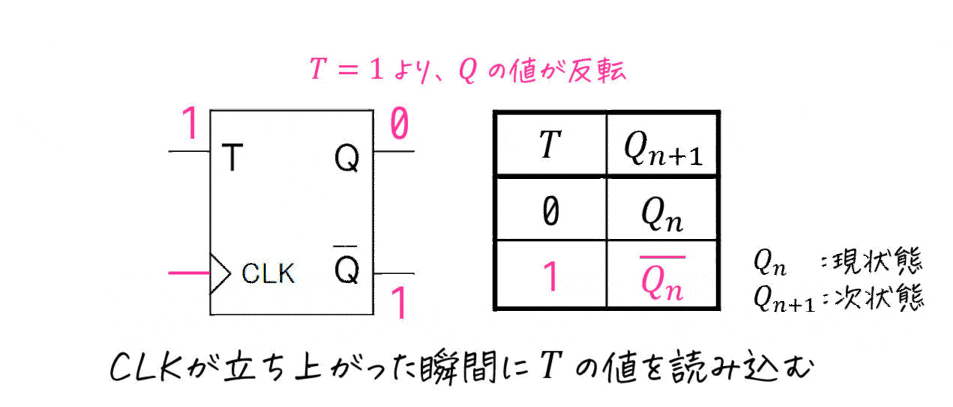
(iii) Tフリップフロップ
JKフリップフロップの入力 \( J \), \( K \) を1つにくっつけたフリップフロップをTフリップフロップと呼びます。
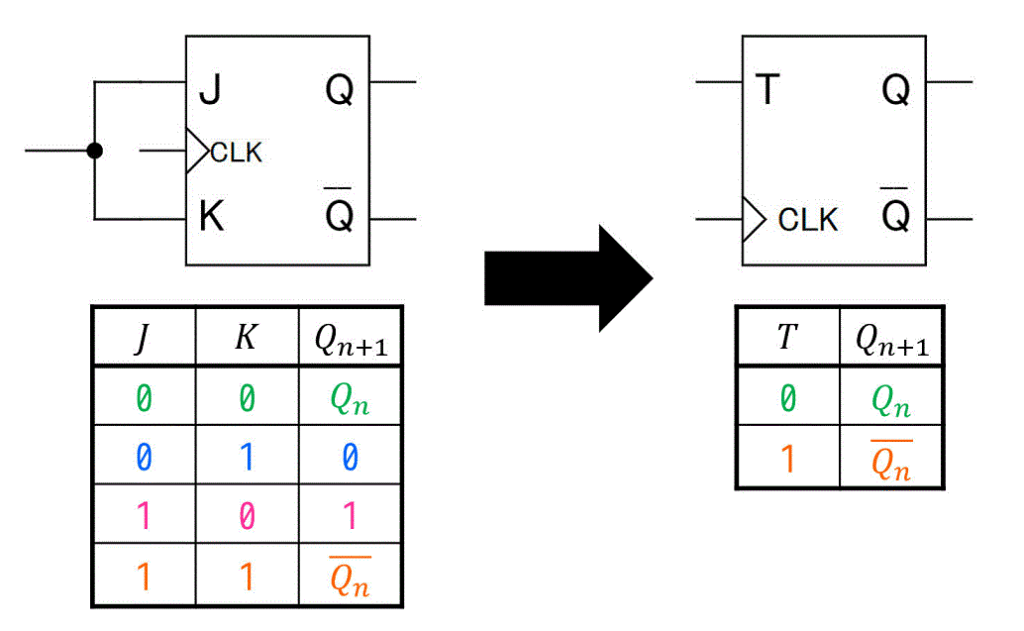
Tフリップの次状態(出力)\( Q_{n+1} \) は、JKフリップフロップの
- \( (J,K) = (0,0) \) のときの出力 → Tフリップフロップの \( T = 0 \) のとき
- \( (J,K) = (1,1) \) のときの出力 → Tフリップフロップの \( T = 1 \) のとき
となっているのが特徴です。
アニメーションでもTフリップフロップの動きを見てみましょう。
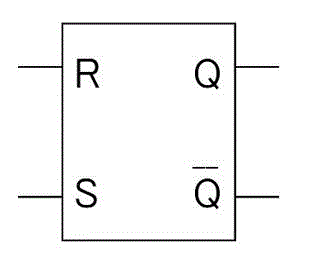
(iv) RSフリップフロップ
JKフリップフロップの \( (J,K) = (1,1) \) のときを禁止入力(そもそも入力として考えることができない)としたものをRSフリップフロップと呼びます[2] … Continue reading。
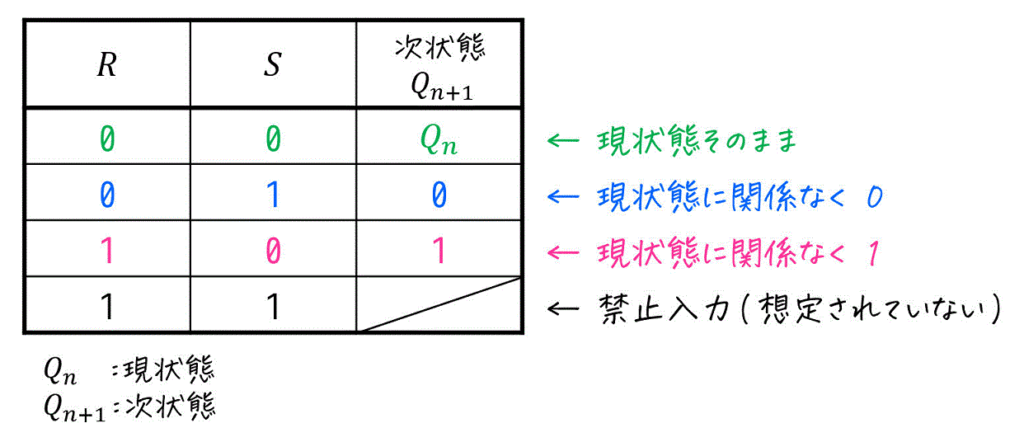
RSフリップフロップの動作は、\( (R,S) = (1,1) \) が禁止入力となっている点以外はJKフリップフロップの動作と全く同じです。
JKフリップフロップの動きを理解することができれば、RSフリップフロップの動きもすぐに理解することができます。
※ そのため、本記事ではRSフリップフロップの練習問題を割愛しました。
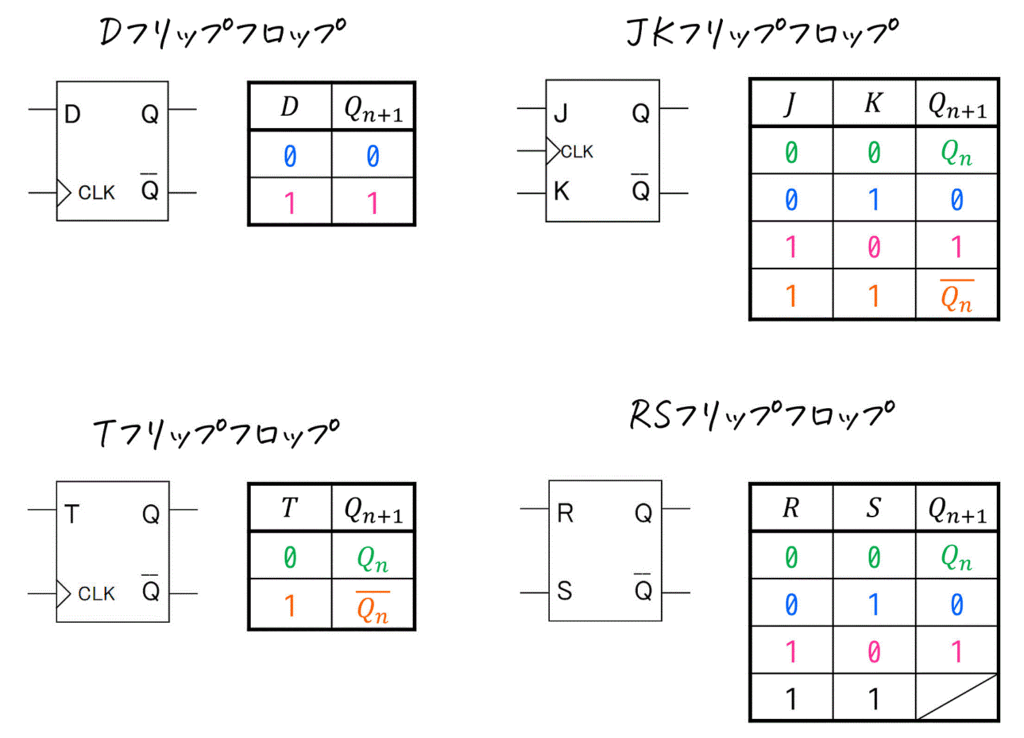
[まとめ] フリップフロップ
今回紹介した4つのフリップフロップの動きをまとめて確認しましょう。
(3) フリップフロップで記憶できる値の範囲
フリップフロップは、単品では0と1の2つの値しか記憶させることができません。
そんなフリップフロップですが、2つあればどうでしょうか。1つ目のフリップフロップで2つの値、2つ目の値でも2つの値を記憶させることができるので、\( 2 \times 2 = 4 \) 通りの値(状態)を記憶させることができますね。
もっともっと増やして10個あればどうでしょうか。
2つの値を記憶できるフリップフロップが10個あるので、合計で \( 2^{10} = 1024 \) 個の値(状態)を記憶させることができます。
最後に「\( n \) 個のフリップフロップで表すことができる値・状態は何個あるか」を考えてみましょう。
2つの値が記憶できるフリップフロップが \( n \) 個あるので、\( 2^n \) 通りの値(状態)を記憶することができますね。
このように、単品では2通りの値しか記憶ができない弱弱しい(?)フリップフロップですが、複数個組み合わせることで大量の値を記憶させることが可能になるのです。
例題で確認!
フリップフロップを用いて0から1, 2, 3, … と1ずつ増えていくアップカウンタを作る。次の(1)~(3)の問いに答えなさい。
(1) 3個のフリップフロップを使う場合、最大いくつまでこのアップカウンタで数えることができるか答えなさい。
(2) 25まで数えることができるアップカウンタを作りたい。フリップフロップは最低何個必要か。
[解説]
(1)
答え: 7まで
2つの値を記憶できるフリップフロップが3個あるため、\( 2^3 = 8 \) 個の値を記憶させることができます。
しかし、答えを「8まで!」としてしまうのはちょっと早とちり。理由は、0(カウントされていない状態)もフリップフロップで記憶する必要があるからです。
そのため、0の状態を抜いた残りの7個を1, 2, 3, …, 7 の記憶に充てることができますね。
よって答えは7。
(2)
答え: 5個
まず、フリップフロップが4個の場合、\( 2^4 = 16 \) 通りの値(つまり0から15まで)の値を記憶させることができます。しかし、これでは少し足りません。
そこで、1つ増やして5個にすると、\( 2^5 = 32 \) 通りの値(つまり0から31まで)の値を記憶させることができるため、25を数えるための状態も用意できますね。
よって、フリップフロップは最低5個必要なことがわかる。
最後に、フリップフロップで記憶できる状態数を一般化(\( n \) を用いた形)で表すこととしましょう。
1つのフリップフロップでは、0と1の2つの状態(1ビット分)を記憶することができる。
(1) このフリップフロップを \( n \) 個組み合わせると、\( 2^n \) 個の状態(\( n \) ビット分)を記憶することができる。
(2) フリップフロップで0から1, 2, 3とカウントアップするアップカウンタを作る場合、\( n \) 個のフリップフロップを使うと0から \( 2^n - 1 \) まで数えることができる[3]\( n \) 個のフリップフロップで記憶できる状態数は \( 2^n \) ですが、そのうちの1つを0を記憶するために使う必要があるので \( 2^n - 1 \) です。。
※ (1), (2) とも丸暗記せずになぜそうなるのかを説明できるようにしましょう。
スポンサードリンク
3. 順序回路を読んでみよう! Dフリップフロップ編
順序回路を読む際には、「CLKの立ち上がり(同期される瞬間)に、フリップフロップの状態(次状態)や出力値がどのように変わるのか」を「同期される直前のフリップフロップの状態(現状態)や入力」ごとに列挙することで解読をします。
この解読でよく使われるのが、状態遷移表、状態遷移図です。
ここからは実際の順序回路を使って、状態遷移表や状態遷移図の書き方を練習しながら状態遷移図順序回路を読む練習をしていきましょう!
まずは、最も基本的なDフリップフロップの読み方です!
つぎの順序回路がある。(1)~(4)の問いに答えなさい。
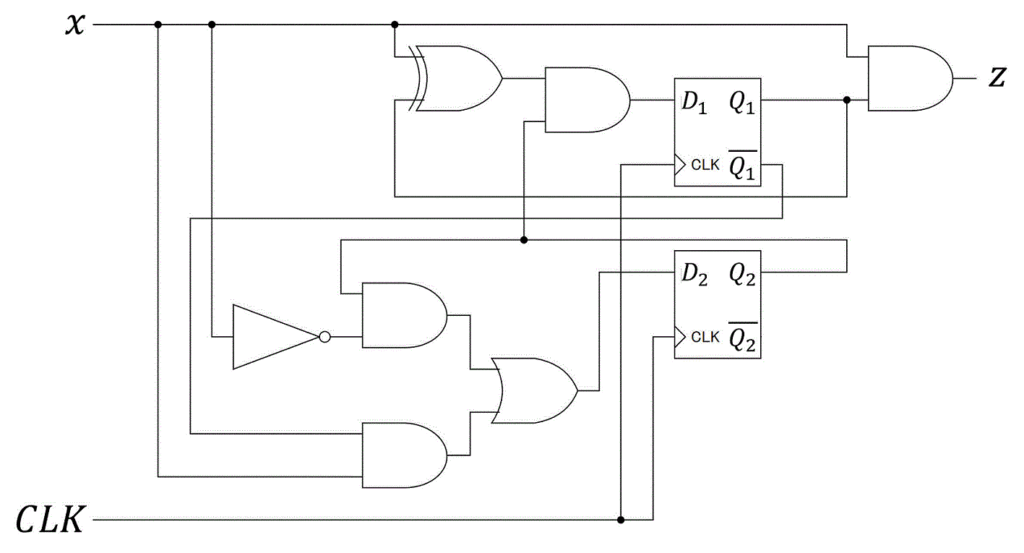
(1) 各フリップフロップ \( D_1 \), \( D_2 \)、および出力 \( z \) の入力方程式を \( x \), \( Q_1 \), \( Q_2 \) を用いた形で表しなさい。
(2) この順序回路の状態遷移表を書きなさい。
(1) 入力方程式の求め方
下のように、各部品にどの値が来ているかをメモしながらたどっていきましょう。
CLKの線は無視してOKです。
(状態遷移表や状態遷移図を書くときにも使いません。)
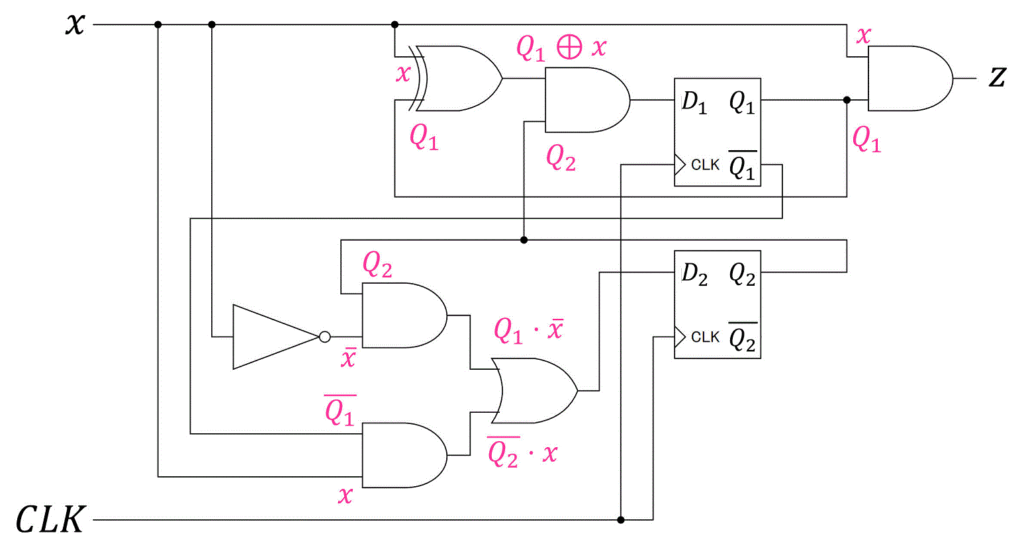
すると、\[\begin{align*}
D_1 & = (Q_1 \oplus x) \cdot Q_2 \\
D_2 & = (Q_1 \cdot \bar{x} ) + (\bar{Q_2} \cdot x) \\
z & = Q_1 \cdot x
\end{align*}\]となりますね。
(2) 状態遷移表の書き方
状態遷移表は、「現状態と入力の全部のパターンに対して、次状態や出力を列挙する」ことで、順序回路の動きを把握するという役割があります。
そのため、状態遷移表には、
- フリップフロップの現状態
- 入力
- フリップフロップの次状態
- 出力
の4つの情報を書きます。
ここで、順序回路の状態遷移表を書く際には、
- フリップフロップの現状態と入力を順番に羅列する
(組み合わせ回路の場合、真理値表の入力部分を書くのに相当) - フリップフロップの入力を求める
(組み合わせ回路の場合、真理値表の出力部分を書くのに相当) - フリップフロップの入力から、次状態を求める
(各フリップフロップで一番変わるのがこの部分)
の3ステップに分けて書いていくのがおすすめです。
Step1. フリップフロップの現状態と入力を羅列
まずは、フリップフロップの現状態と入力を順番に全パターン列挙していきましょう。
※ 余談ですが、111, 110, 101, … と降順に列挙してもいいですし、数字ではなくT, Fなどを用いて書いてもOKです。
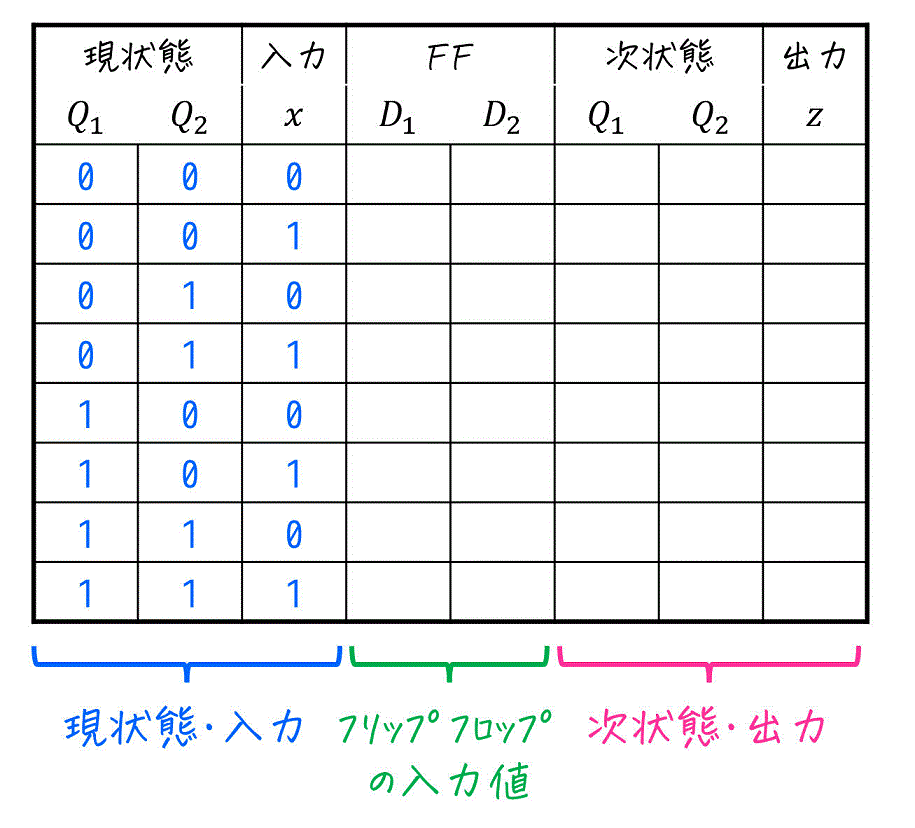
Step2. フリップフロップの入力値・順序回路の出力を羅列
次に、(1)で求めた入力方程式\[\begin{align*}
D_1 & = (Q_1 \oplus x) \cdot Q_2 \\
D_2 & = (Q_1 \cdot \bar{x} ) + (\bar{Q_1} \cdot x) \\
z & = Q_1 \cdot x
\end{align*}\]から、各フリップフロップの入力値 \( D_1 \), \( D_2 \) 、および出力 \( z \) を求めます。
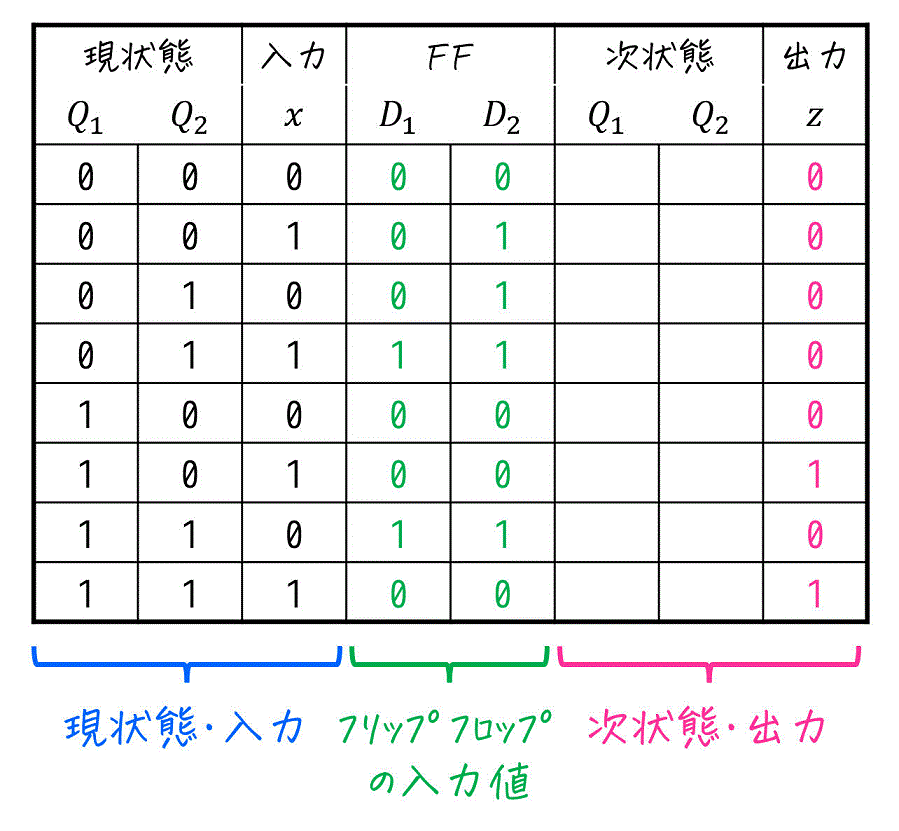
Step3. フリップフロップの入力値から次状態を求める
最後に、フリップフロップの入力値から次状態を求めればOKです。
Dフリップフロップの場合は、次状態は \( D \) の値をそのまま持ってくるだけで求められます。
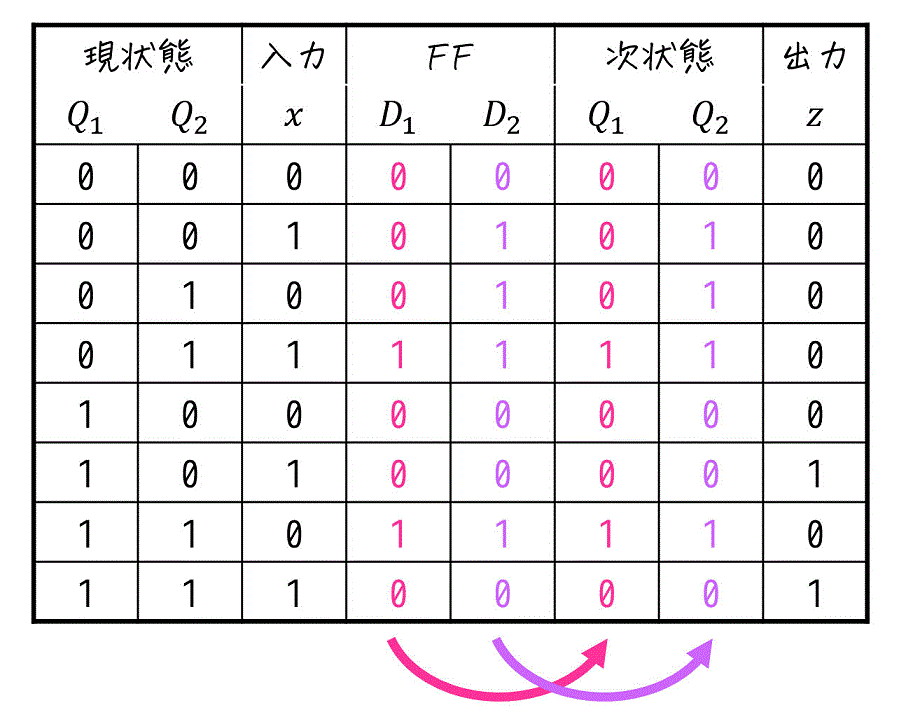
これで、状態遷移表の完成です!
(3) 状態遷移図の書き方
フリップフロップがどのような働きをするかは、「すべての現状態・入力」のパターンに対して(つまり行ごとに)、下の[1], [2]のルールによってつくられる状態遷移図を書くことで直観的に理解することができます。
[1] 状態は〇で囲み、その中に状態の名前を書く。(指示がなければ状態の名前は好きにつけてOK)

※ このとき、変化前の状態を「遷移元」、変化後の状態を「遷移先」と呼びます。
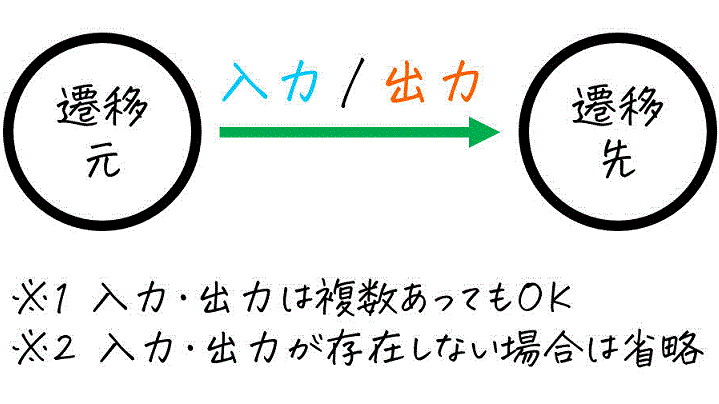
一見書くのが難しそうに見えますが、状態遷移表さえ書いてしまえば「現状態」と「次状態」、および「入力」と「出力」を順番に見ていくことで、機械的に状態遷移図を書くことができます。
まずは、一番上の行のパターンを状態遷移図にしましょう。
※ 今回は、状態遷移図の名前を \( Q_1 Q_2 \) とします。
(\( Q_1 \), \( Q_2 \) には実際の値が入る)
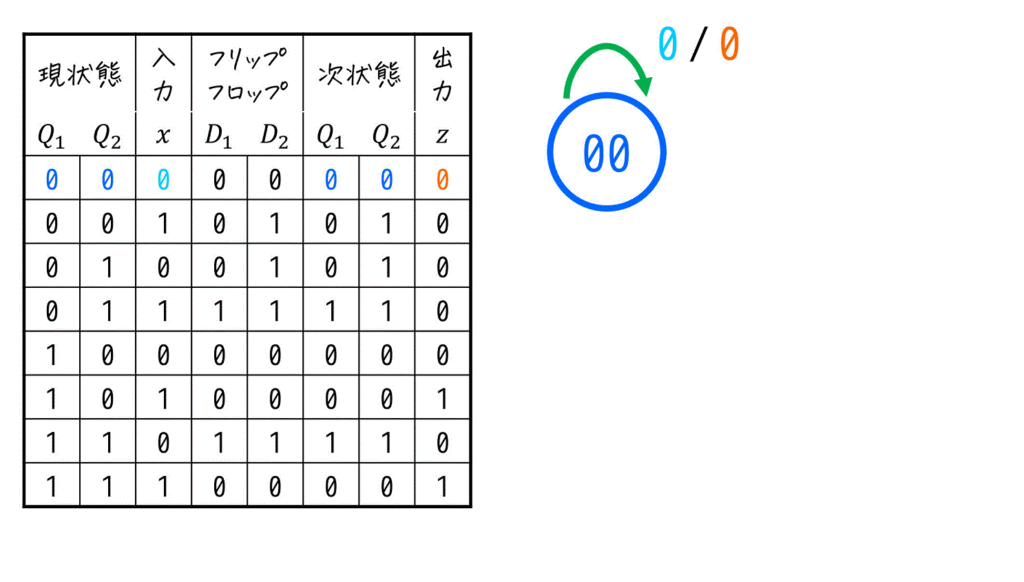
続いて、2行目の行のパターンを状態遷移図にしましょう。
(前の行で書いた状態遷移図に追記していく形で書いてください。)
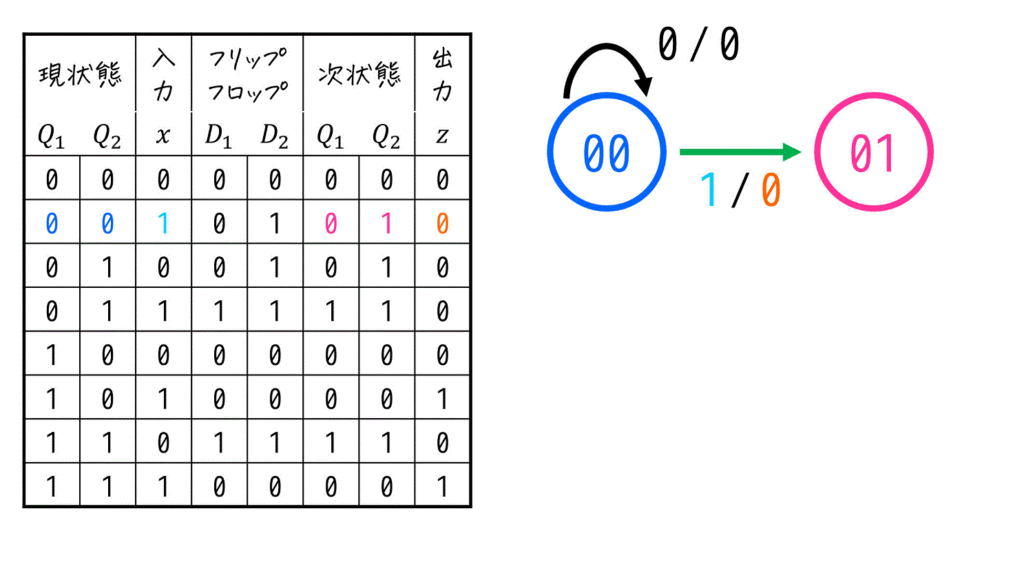
この流れを、一番下の行のパターンまで行っていけばOKです。
すると、右下のような状態遷移図を書くことができます。
(この状態遷移図が(3)の答えです)
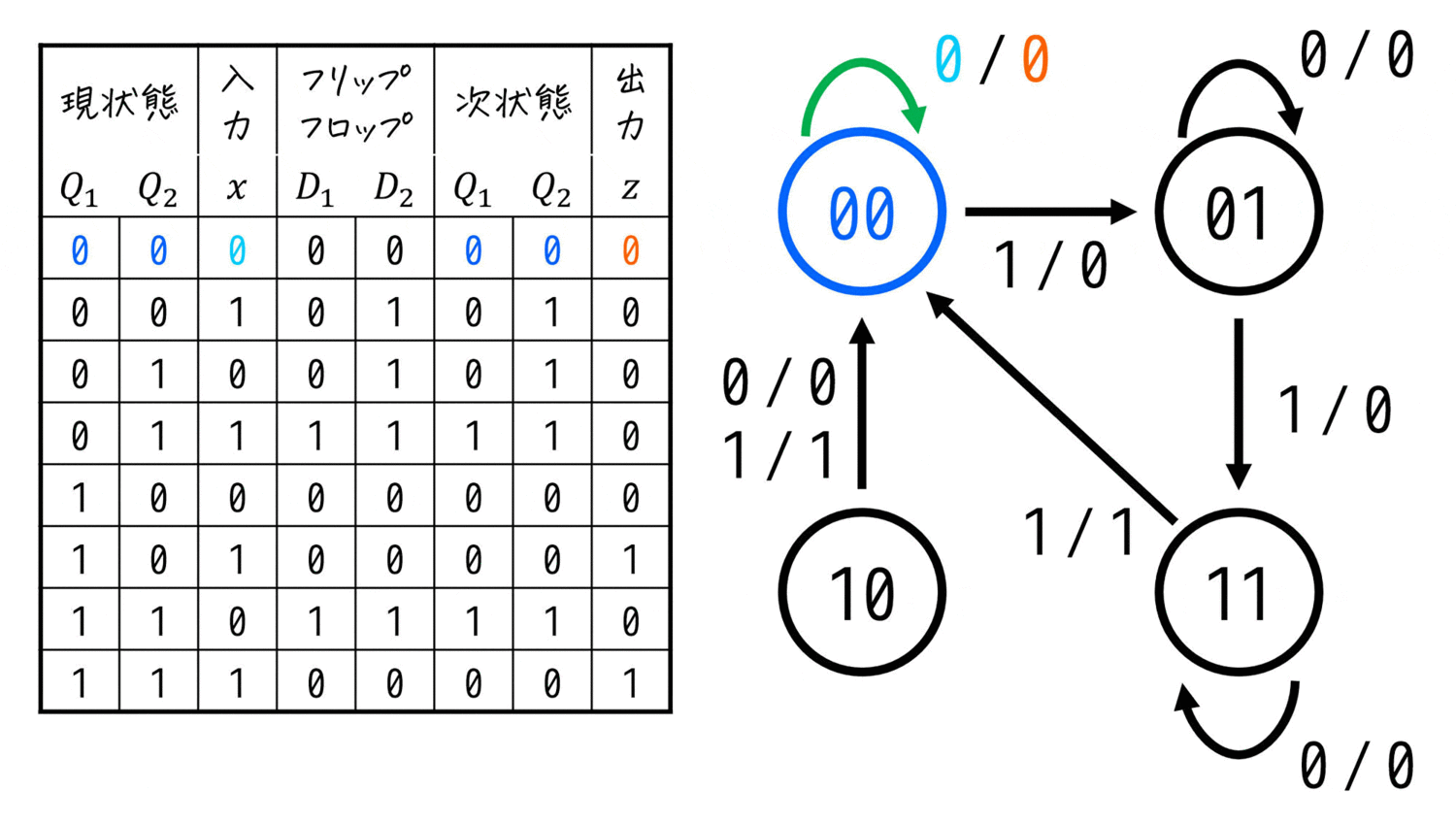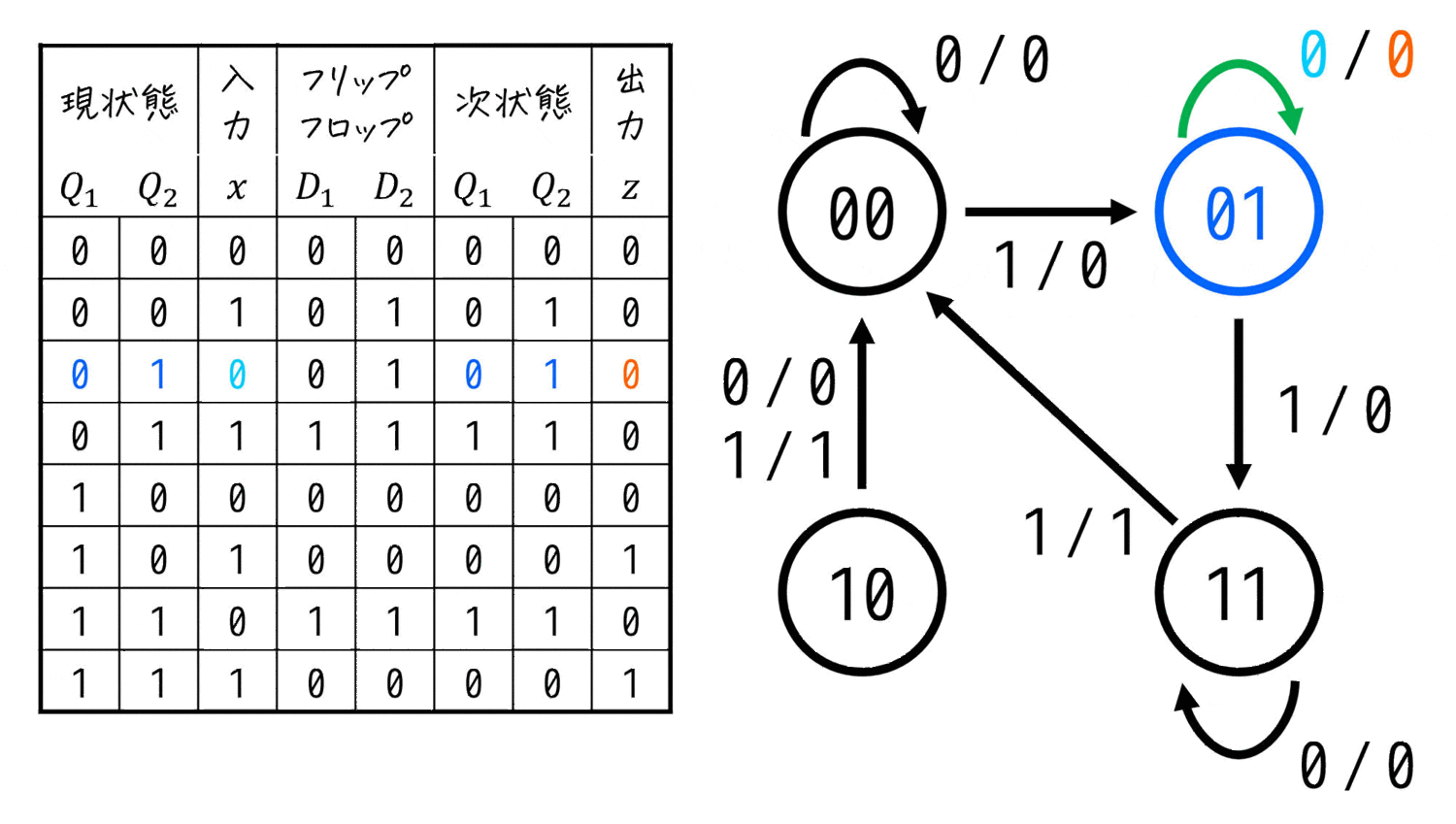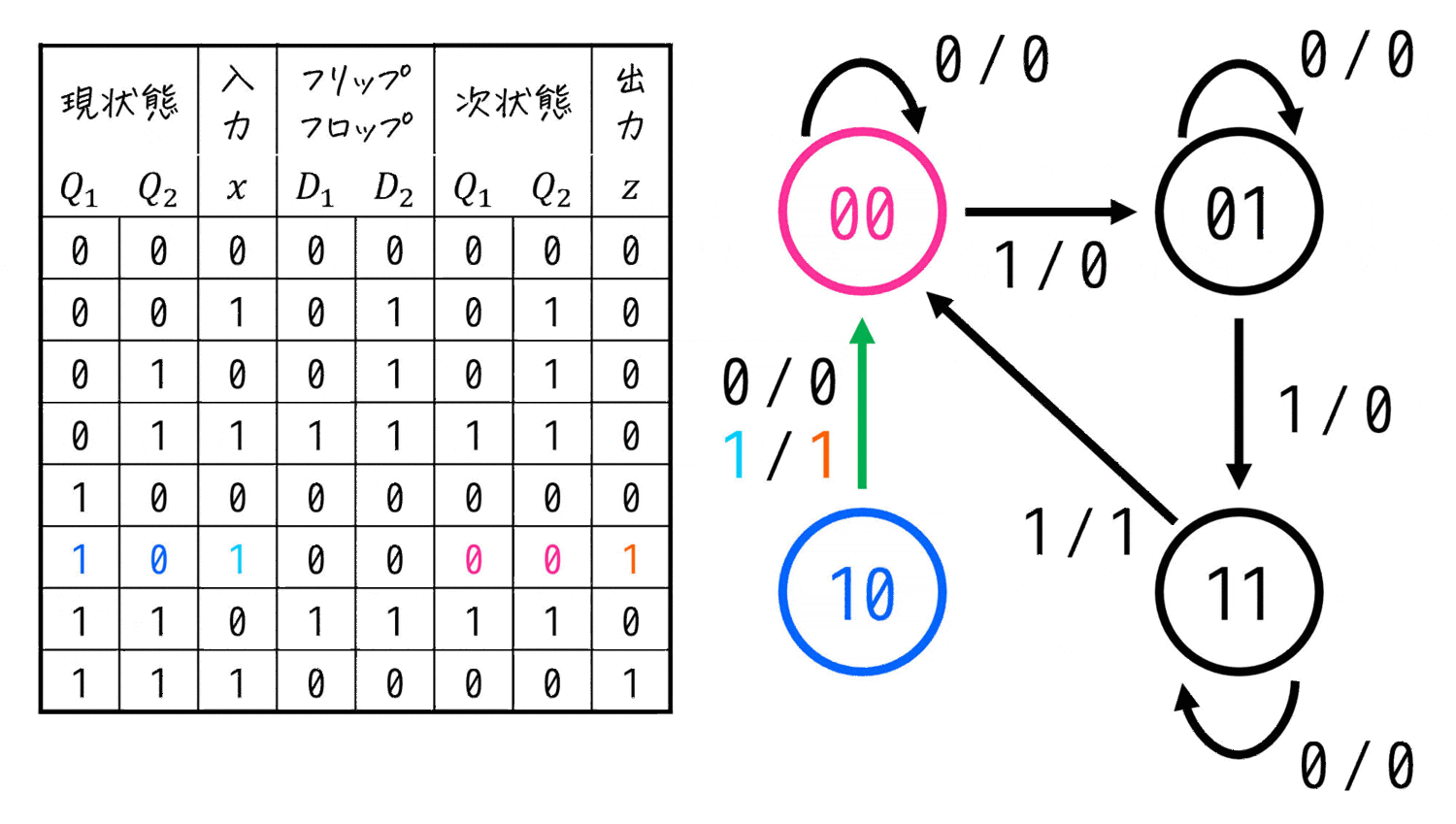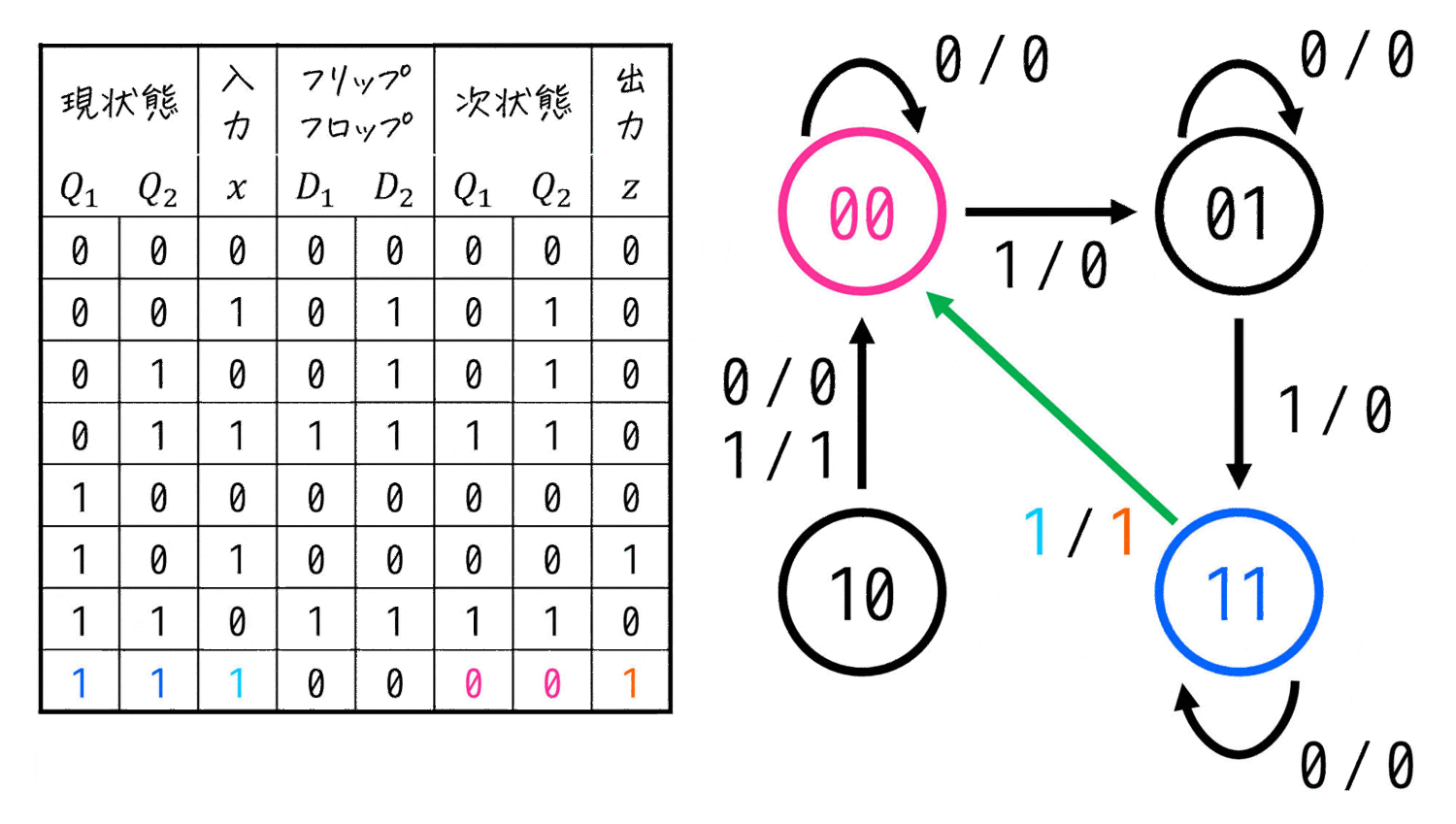
(4) 状態遷移図から順序回路が何をするかを考える
最後に、必要であれば求めた状態遷移図から順序回路が何をしているのかを考えましょう。
今回の場合、状態00, 01, 11の3つに注目するのがポイントです。
すると、下のような点に気づくと思います。
- 入力 \( x \) が0のときには遷移元と遷移先が同じ(遷移しない)
- 入力 \( x \) が1のときは、遷移元と遷移先が異なる(状態が遷移する)
- 00 → 01
- 01 → 11
- 11 → 00
- 11 → 00 に遷移するときだけ出力 \( z \) が1になる
これを少しまとめると
- 00から3回 \( x = 1 \) が入力されると00に戻ってくる
- 11 → 00 に遷移(00の状態から3回目の \( x = 1 \) が入力されたタイミング)で出力が \( z = 1 \) となる
となりますね。
よって、この回路は「1が3回入力されるごとに出力が1となる回路」ということができますね。
(1の入力回数が3の倍数であるかをチェックする回路などと答えてもOKです)
4. 順序回路を読んでみよう! JKフリップフロップ編
今度は、JKフリップフロップが用いられている順序回路を読んでみましょう。
つぎの順序回路がある。(1)~(3)の問いに答えなさい。
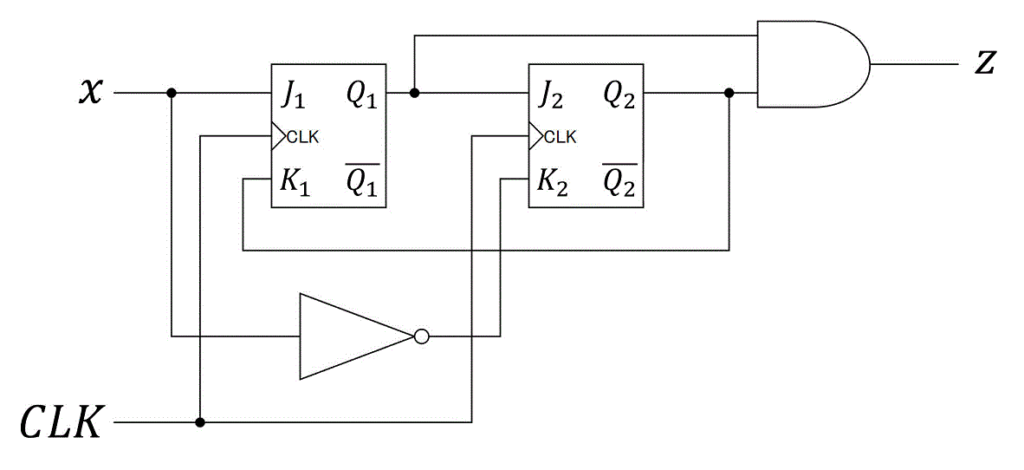
(1) 各フリップフロップ \( J_1 \), \( K_1 \), \( J_2 \), \( K_2 \)、および出力 \( z \) の入力方程式を \( x \), \( Q_1 \), \( Q_2 \) を用いた形で表しなさい。
(2) この順序回路の状態遷移表を書きなさい。
(3) (2)から、この順序回路の状態遷移図を書きなさい。
(1) 入力方程式の導出
Dフリップフロップのときと同じく、各部品にどの値が来ているかをメモしながらたどっていきましょう。
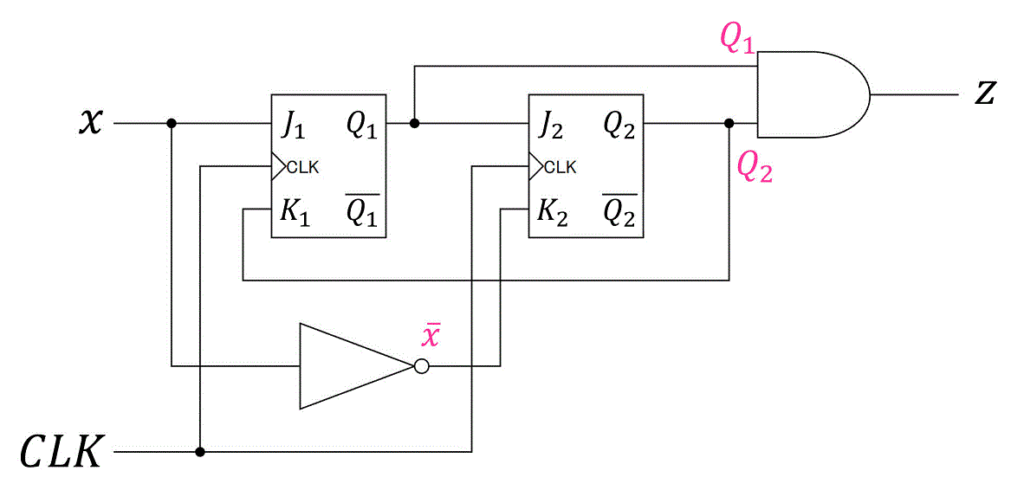
よって、\[\begin{align*}
J_1 & = x \\
K_1 & = Q_2 \\
J_2 & = Q_1 \\
K_2 & = \bar{x} \\
z & = Q_1 \cdot Q_2
\end{align*}\]と入力方程式を求められます。
(2) 状態遷移表の書き方 [JKフリップフロップ]
状態遷移表を書くときは、
- フリップフロップの現状態と入力を順番に羅列する
- フリップフロップの入力を求める
(JKフリップフロップでは、入力が \( J \) と \( K \) の2つある点に注意) - フリップフロップの入力から、次状態を求める
の3ステップに分けて書くのでしたね。
この状態遷移表の3ステップは、細かい部分は変わるものの、流れはどのフリップフロップでも変わりません。
Step1. フリップフロップの現状態と入力を羅列
まずは、フリップフロップの現状態 \( Q_1 \), \( Q_2 \) と入力 \( x \) を順番に全パターン列挙していきます。
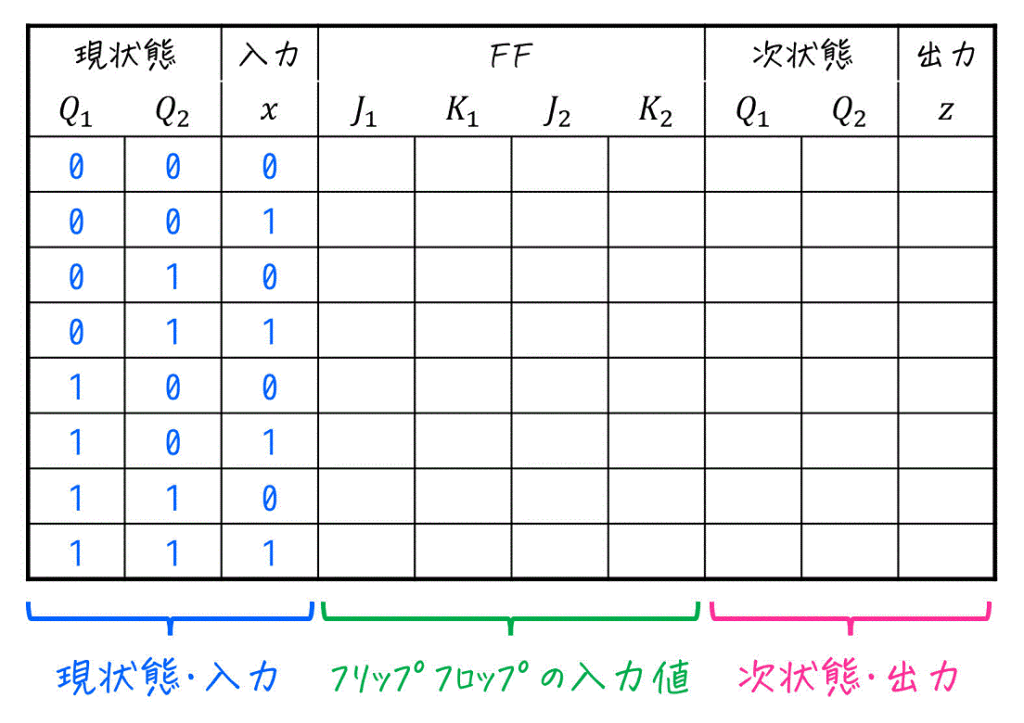
Step2. フリップフロップの入力・順序回路の出力を求める
(1)で求めた入力方程式\[\begin{align*}
J_1 & = x \\
K_1 & = Q_2 \\
J_2 & = Q_1 \\
K_2 & = \bar{x} \\
z & = Q_1 \cdot Q_2
\end{align*}\]から、フリップフロップの入力値 \( J_1 \), \( K_1 \), \( J_2 \), \( K_2 \)、および出力 \( z \) を求めましょう。
(ここまではDフリップフロップのときと同じです)
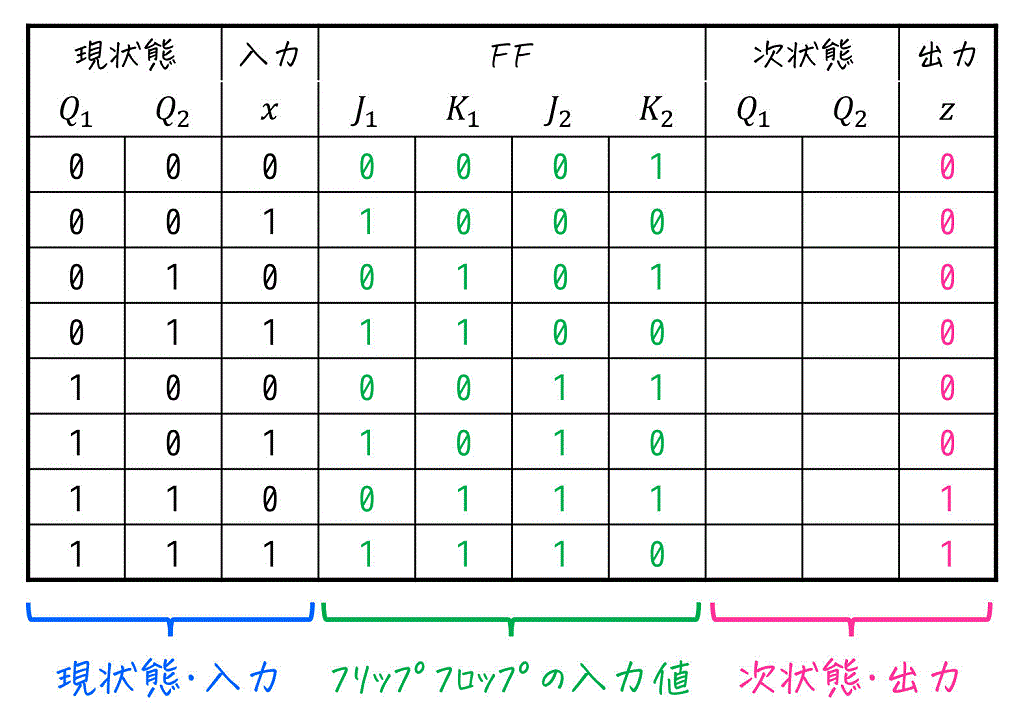
Step3. フリップフロップの入力値から次状態を求める
Step2で求めたフリップフロップの入力値から次状態を求めればOKです。ここが、Dフリップフロップのときと一番変わるポイントです。
Dフリップは、FFの入力値がそのまま次状態となりますが、JKフリップフロップは \( J \), \( K \) の組み合わせで下の表のように次状態 \( Q_{n+1} \) が決まるので、少し注意が必要です。

実際に現状態とフリップフロップの入力値に注意しながら、次状態の表を埋めていくと下の表のようになります。
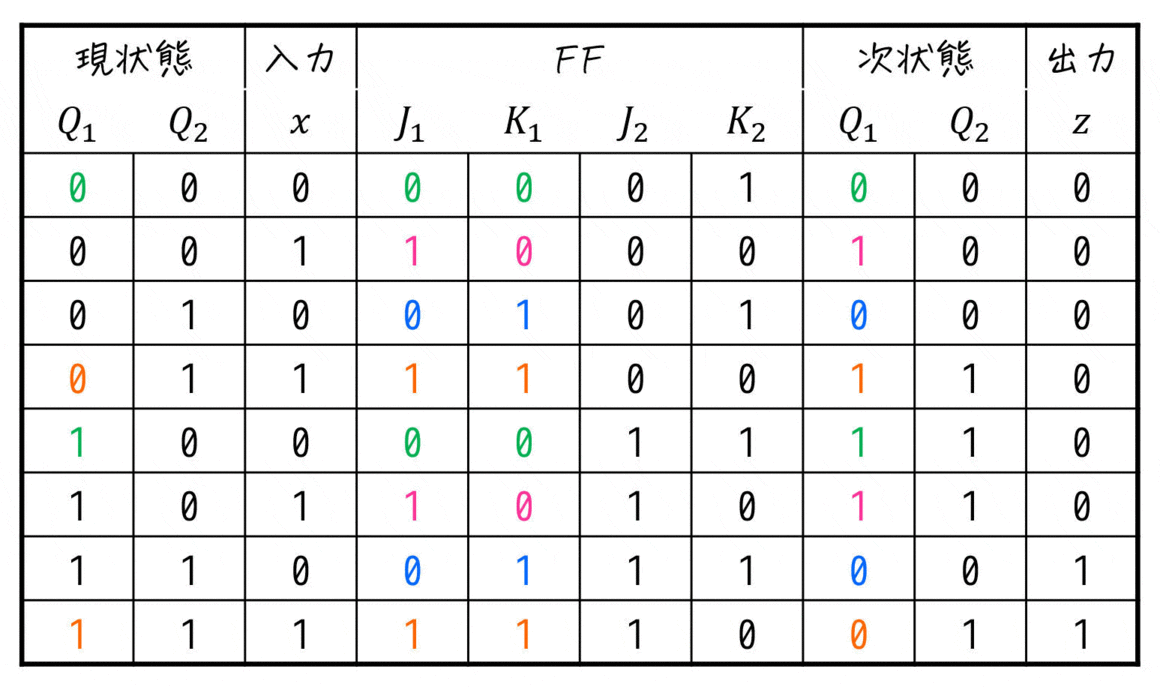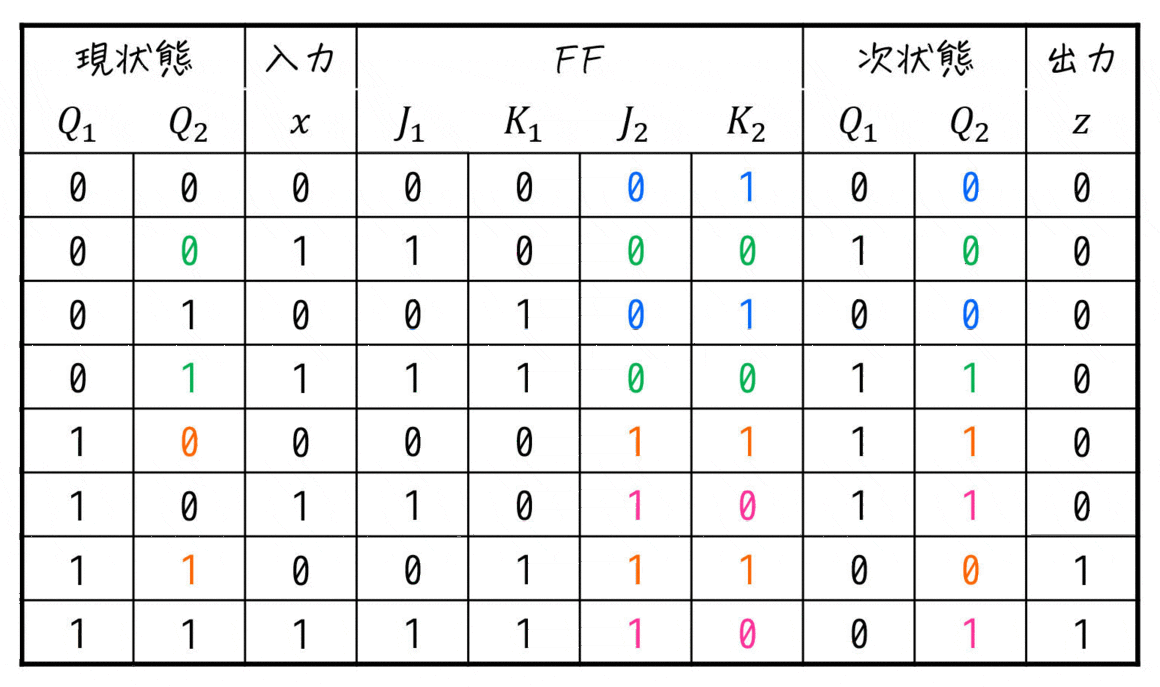
これで状態遷移表の完成です。
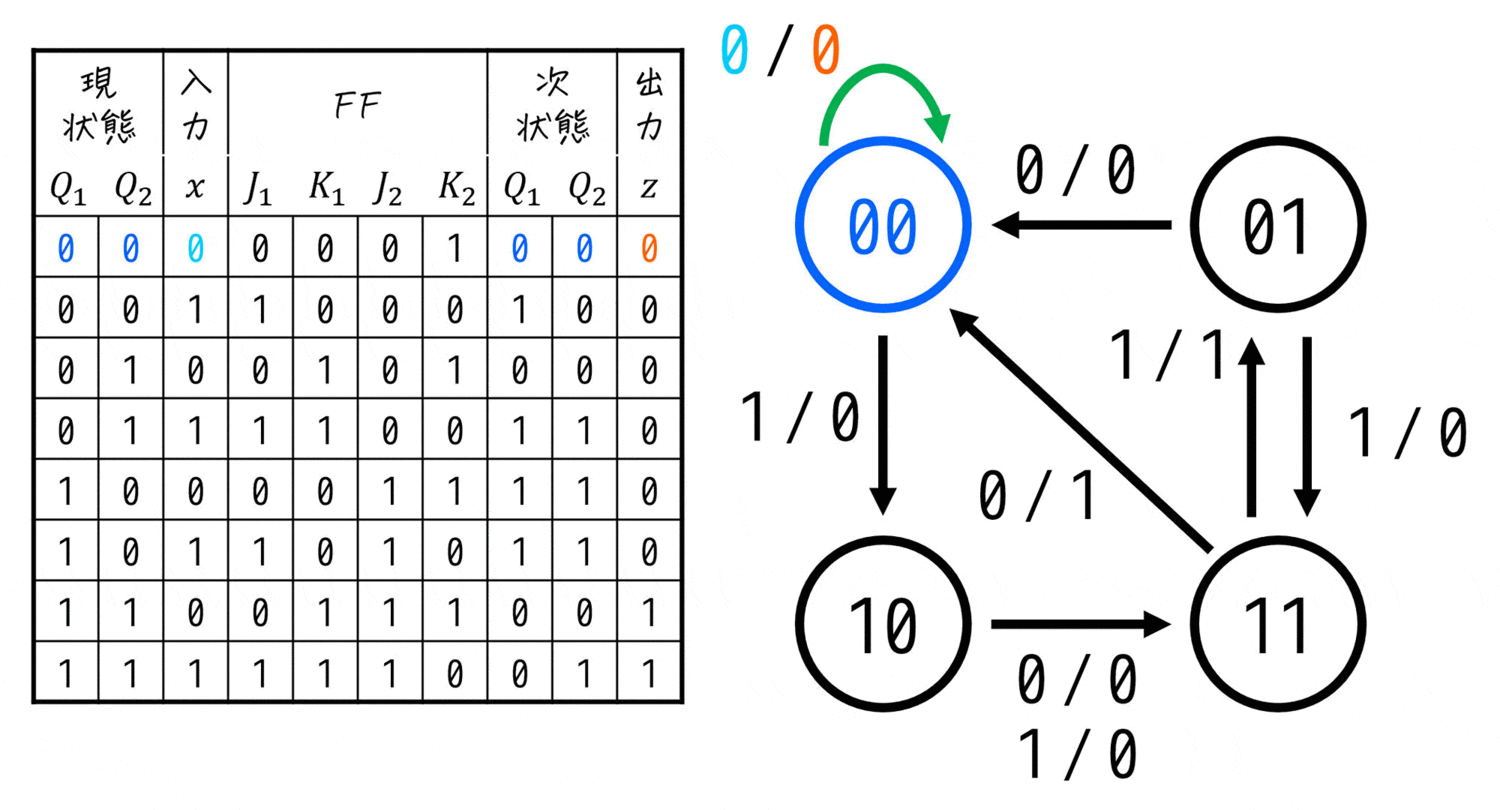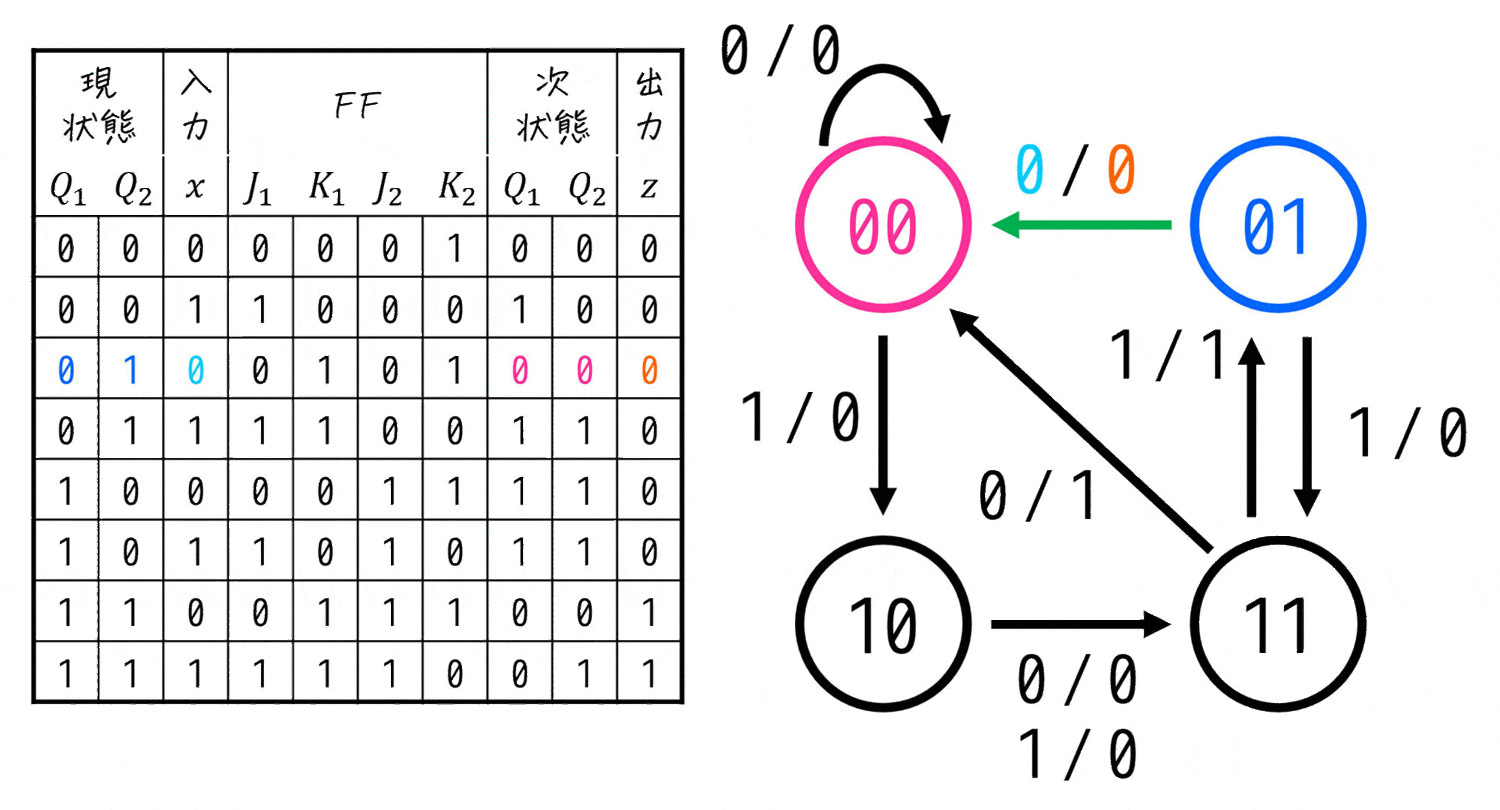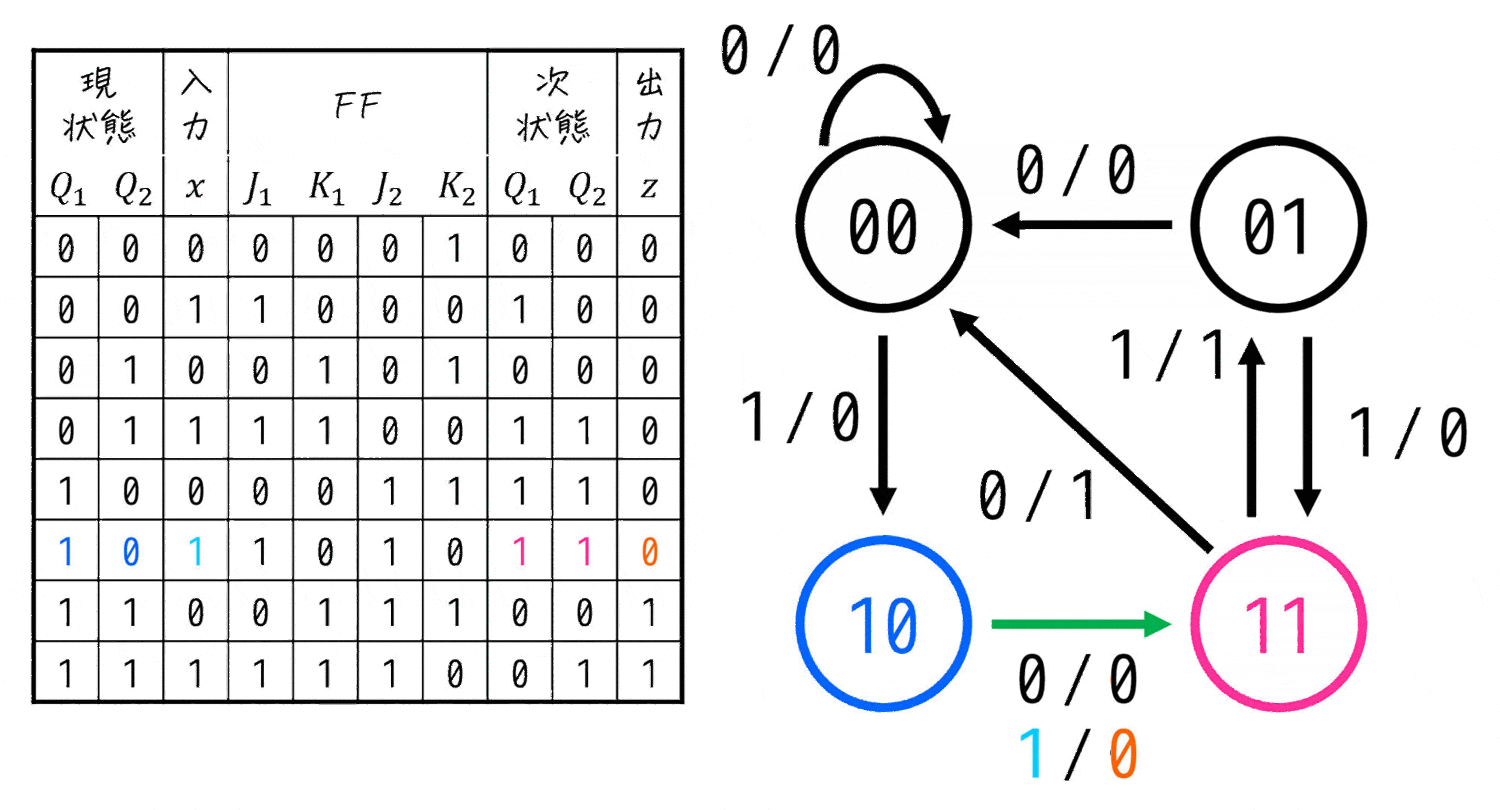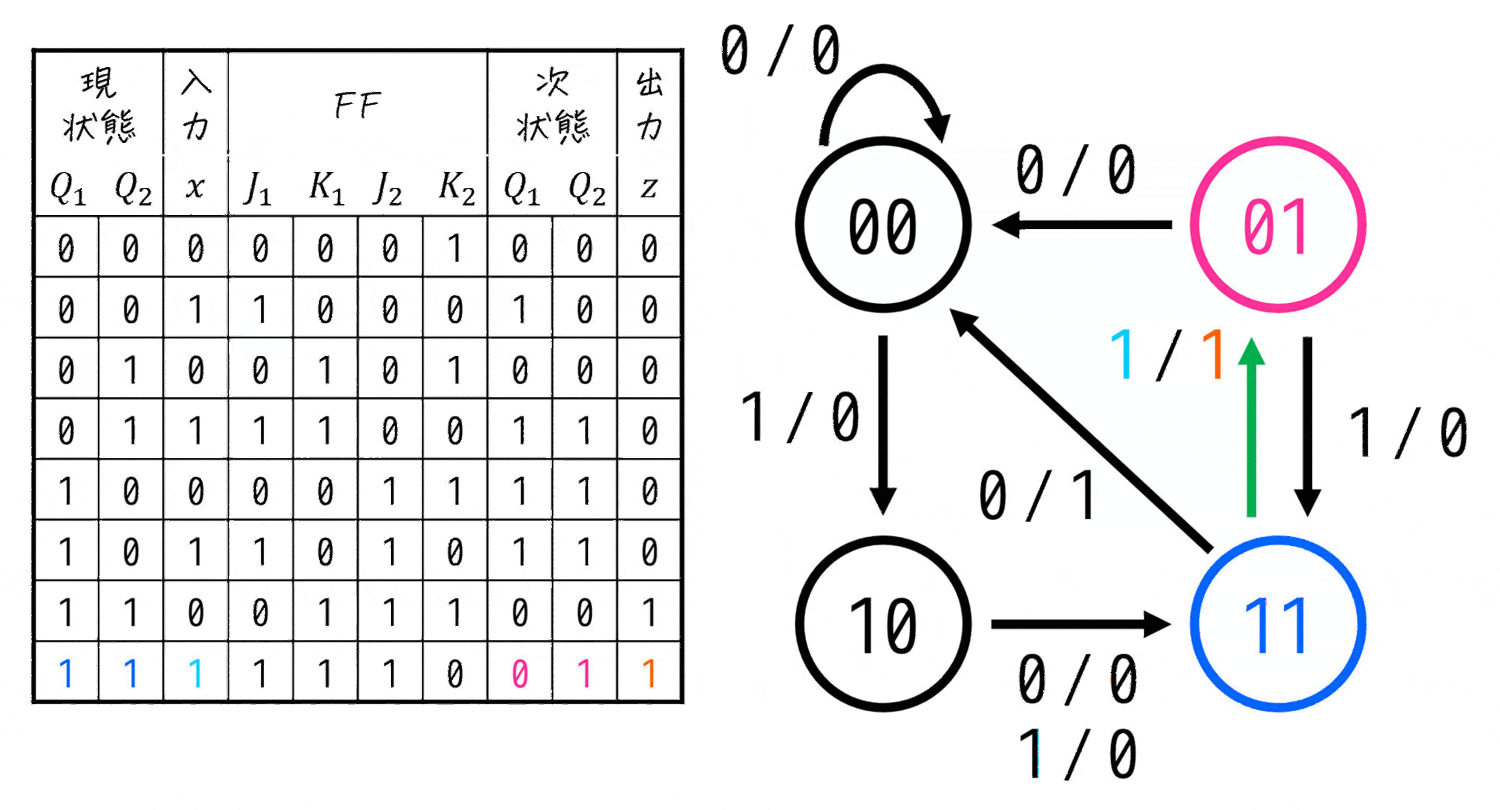
(3) 状態遷移図の書き方
状態遷移表さえかけてしまえば、あとはDフリップフロップのときと同じように状態遷移図を書きだすことができます。
具体的には、状態遷移表の上の行から順番に、「現状態から次状態の変化と、そのときの入力と出力」を図にしながら追っていけばOKです。
5. 順序回路を読んでみよう! Tフリップフロップ編
ちょっと順序回路を読んだり、状態遷移表や状態遷移図を書くのにも慣れてきましたか?
今度は、Tフリップフロップが含まれる順序回路を読む練習もしてみましょう。
つぎの順序回路がある。(1)~(3)の問いに答えなさい。
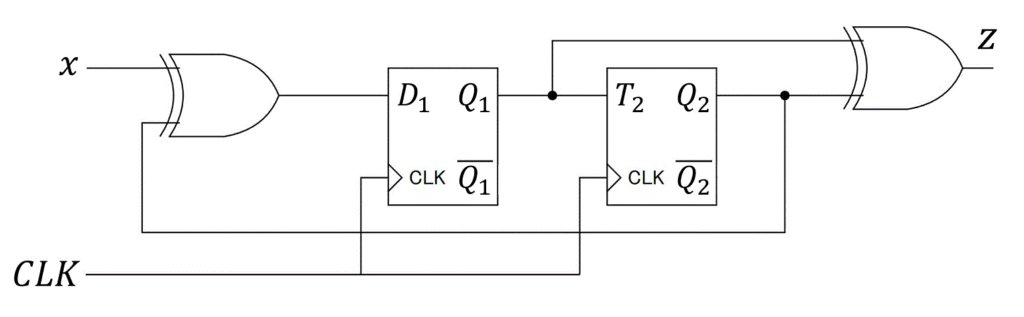
(1) 各フリップフロップ \( D_1 \), \( T_2 \)、および出力 \( z \) の入力方程式を入力 \( x \), および現状態 \( Q_1 \), \( Q_2 \) を用いた形で表しなさい。
(2) この順序回路の状態遷移表を書きなさい。
(3) (2)から、この順序回路の状態遷移図を書きなさい。
(1) 入力方程式の導出
各部品にどの値が来ているかをメモしながら \( D_1 \), \( T_2 \), \( z \) を入力 \( x \) と現状態 \( Q_1 \), \( Q_2 \) で書き直しましょう。
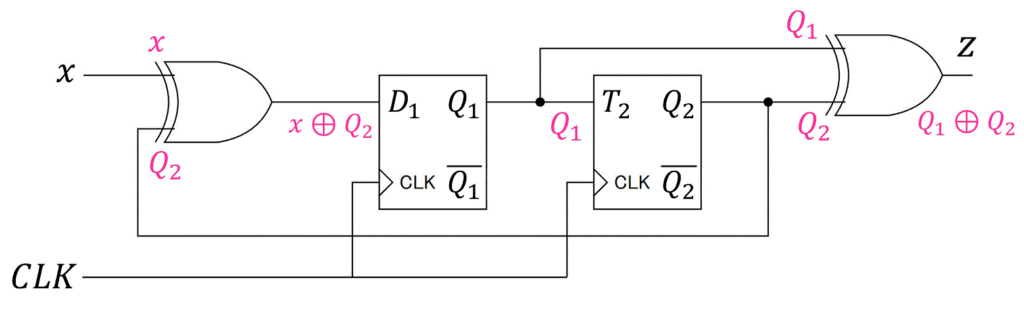
よって、入力方程式は\[\begin{align*}
D_1 & = Q_2 \oplus x \\
T_2 & = Q_1 \\
z & = Q_1 \oplus Q_2
\end{align*}\]と求められます[4]\( D_1 \) を \( x \oplus Q_2 \) でなく、\( Q_2 \oplus x \) と書いたのは、状態遷移表の項目が左側から順に \( Q_1 \), \( Q_2 \), \( x \) … Continue reading。
(2) 状態遷移表を求める
状態遷移表を求める際には、この3ステップを思い出しましょう。
- フリップフロップの現状態と入力を順番に羅列する
- フリップフロップの入力を求める
- フリップフロップの入力から、次状態を求める
Step1. 現状態と入力の羅列
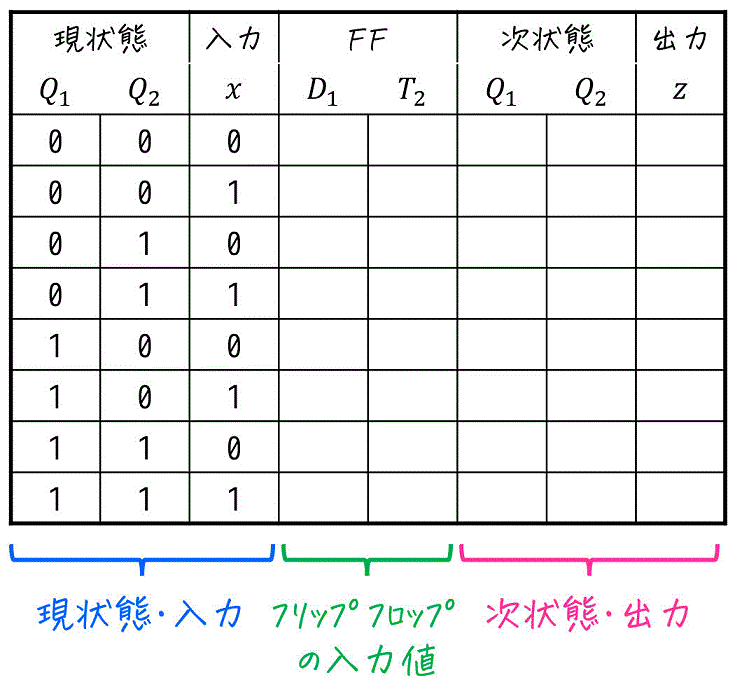
Step2. フリップフロップの入力・順序回路の出力を求める
入力方程式\[\begin{align*}
D_1 & = Q_2 \oplus x \\
T_2 & = Q_1 \\
z & = Q_1 \oplus Q_2
\end{align*}\]を利用してフリップフロップの入力と順序回路の出力を求めましょう。
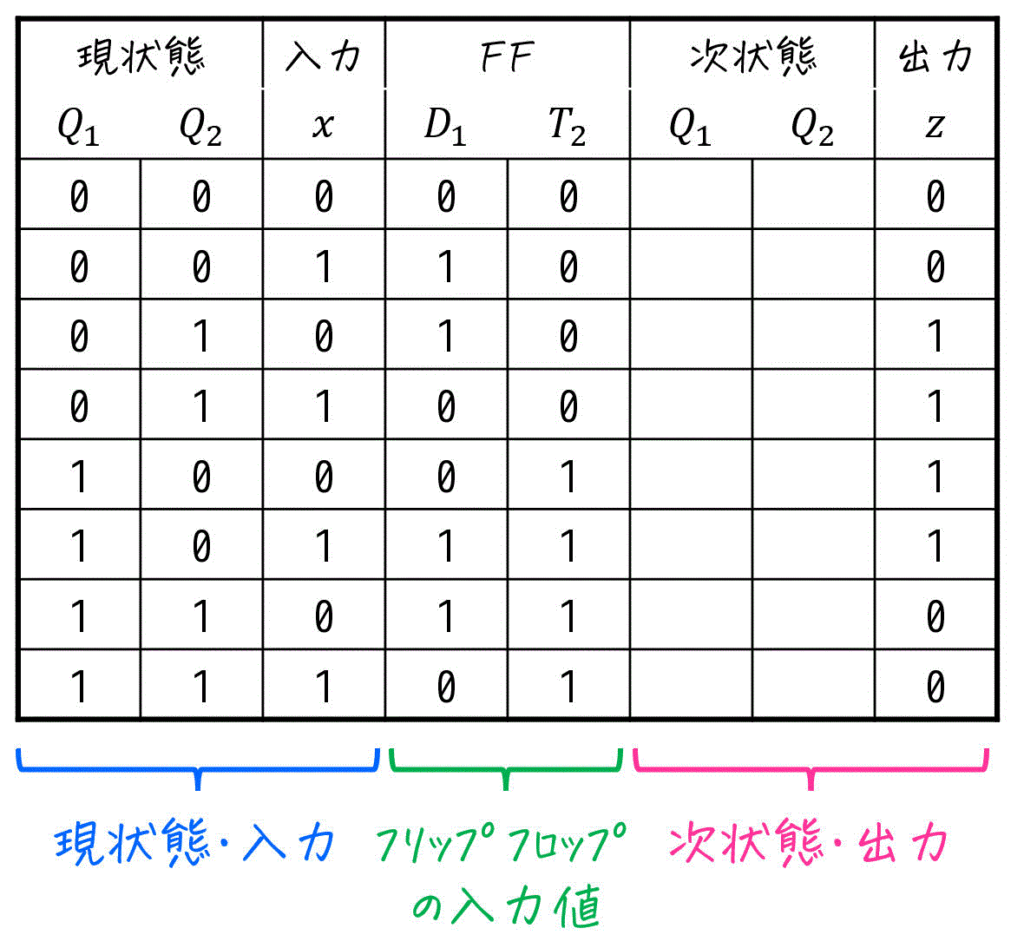
Step3. フリップフロップの入力値から次状態を求める
Dフリップフロップの場合は、入力値 \( D \) がそのまま次状態となります。
一方、Tフリップの場合は、\( T \) の値が0であれば次状態は現状態と同じに、\( T \) の値が1であれば次状態は現状態の0, 1を反転させたものとなります。

よって次状態は下のように求めることができます。
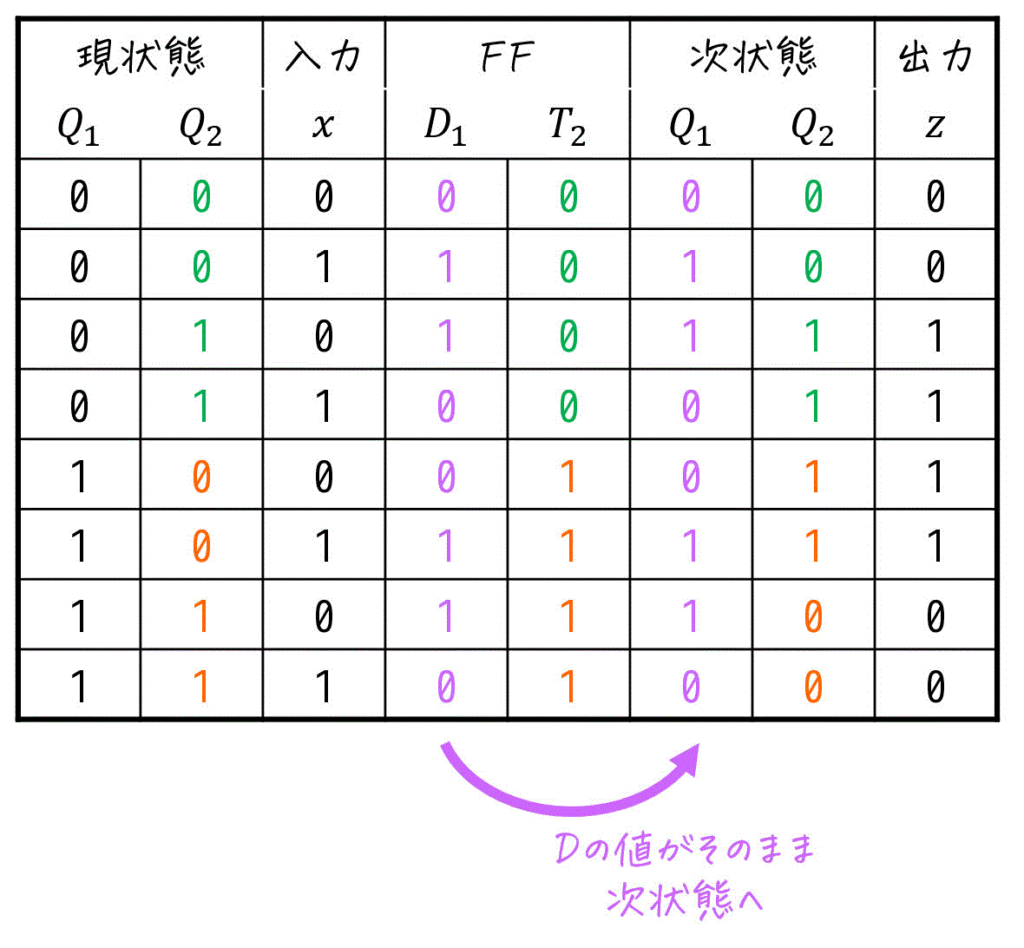
次状態が求まれば状態遷移表の完成です。
(3) 状態遷移図を求める
状態遷移図は、上の行から順番に「現状態からの遷移先(次状態)」と、そのときの入出力を追っていけば書くことができます。
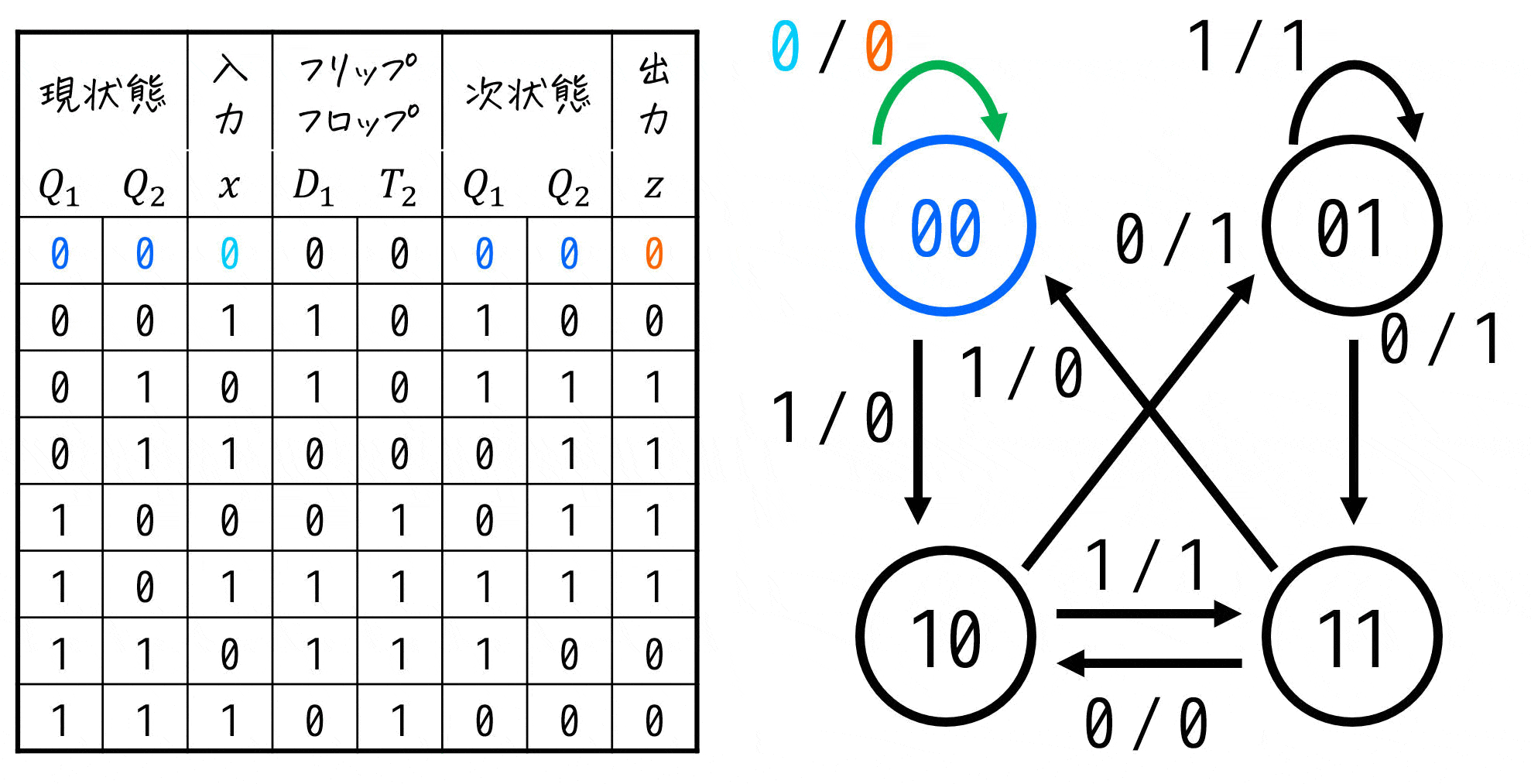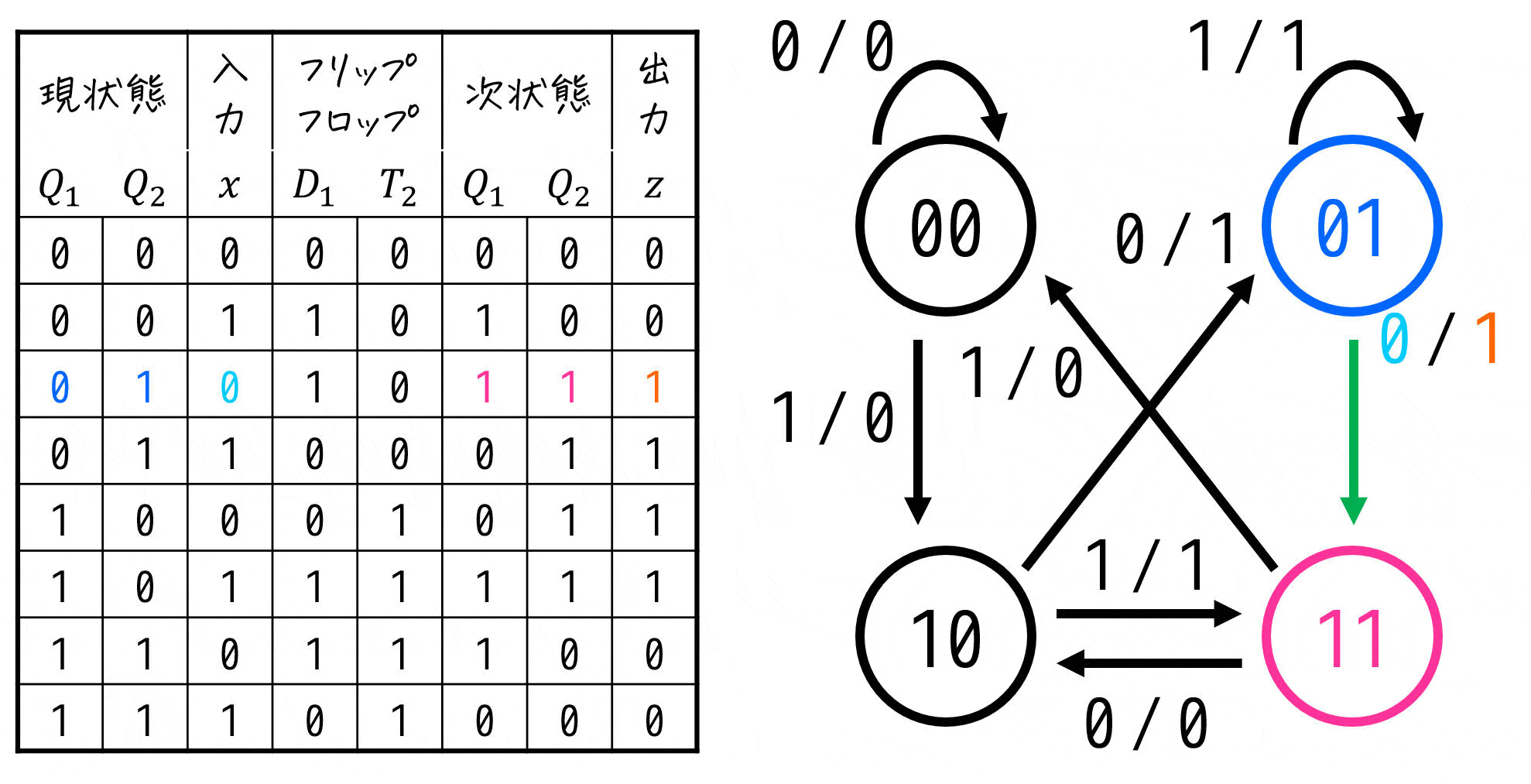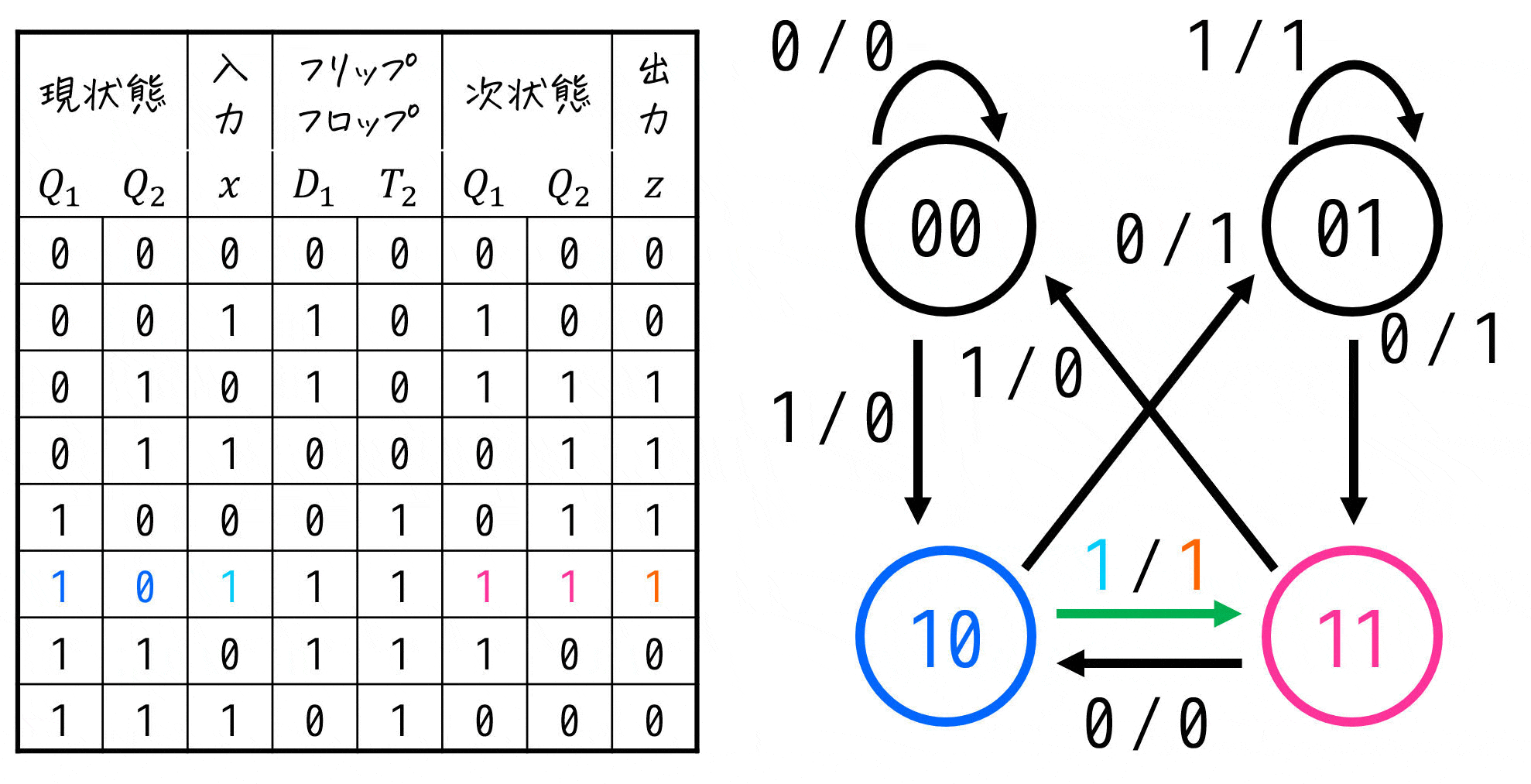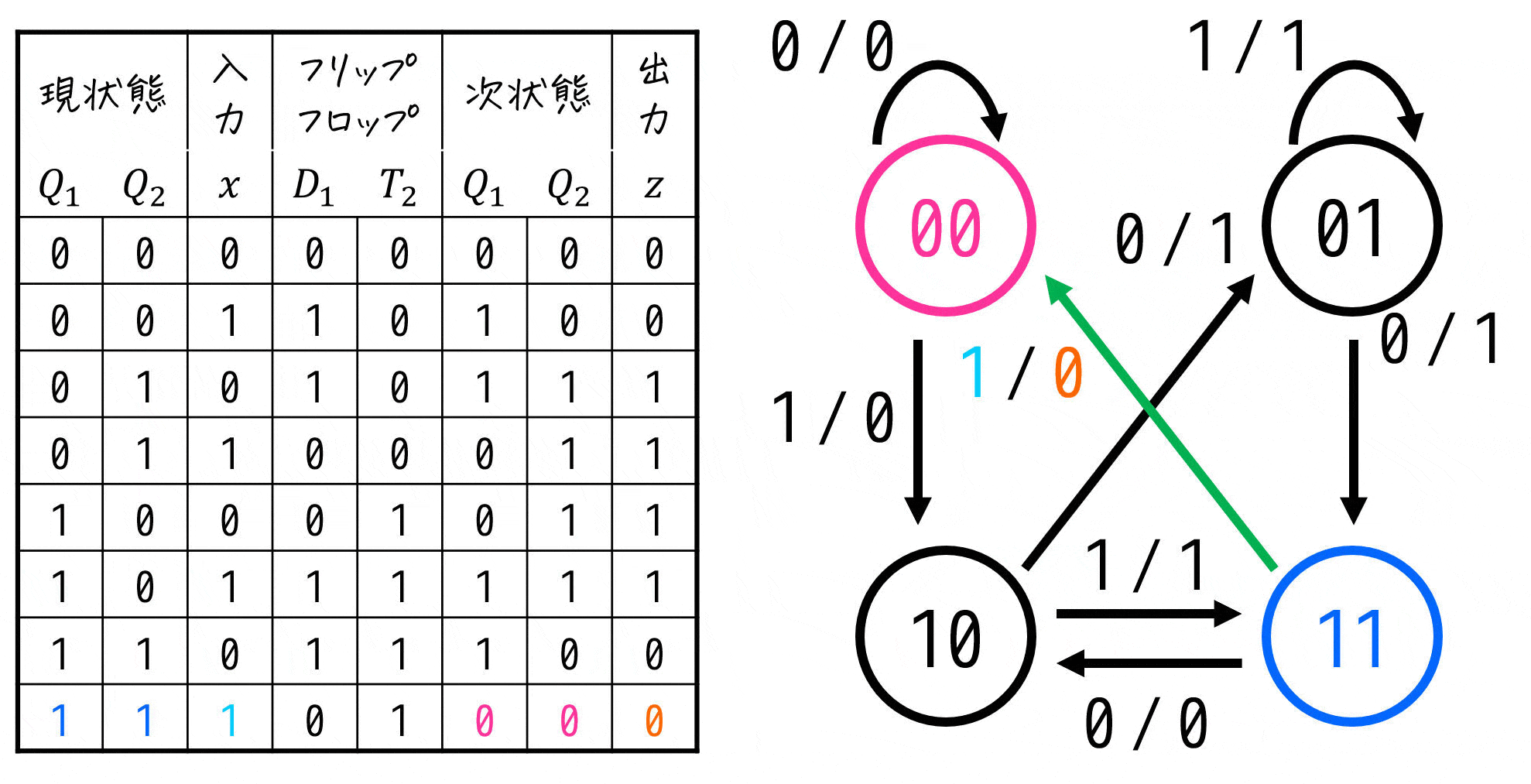
5. [応用編1] 入力が複数の順序回路を読んでみよう!
順序回路を読んだり、状態遷移表や状態遷移図を書くのにはだいぶ慣れてきましたか?
ここからは、少し複雑な順序回路を読んでいきましょう。まずは、入力が複数ある順序回路です。
つぎの順序回路がある。(1)~(3)の問いに答えなさい。
ただし、CLKの配線は省略している。
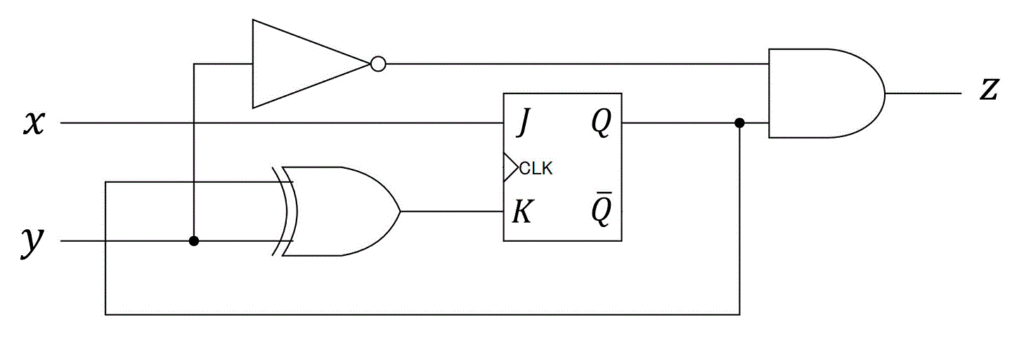
(1) フリップフロップ \( J \), \( K \)、および出力 \( z \) の入力方程式を入力 \( x \), \( y \) および現状態 \( Q \) を用いた形で表しなさい。
(2) この順序回路の状態遷移表を書きなさい。
(3) (2)から、この順序回路の状態遷移図を書きなさい。
(1) 入力方程式の導出
いつものように、部品ごとに入出力を書きながら順序回路をたどっていきましょう。
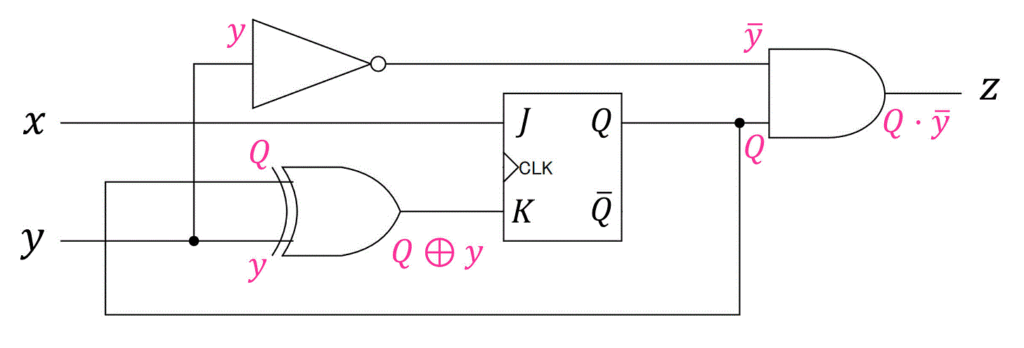
よって、入力方程式は\[\begin{align*}
J & = x \\
K & = Q \oplus y \\
z & = Q \cdot \bar{y}
\end{align*}\]と書くことができます。
(2) 状態遷移表を求める
入力や出力が変化しても、状態遷移表を求める下の3ステップは変わりません。
- フリップフロップの現状態と入力を順番に羅列する
- フリップフロップの入力を求める
- フリップフロップの入力から、次状態を求める
これまでの3問と同じように状態遷移表を求めていけばOKです。
Step1. 現状態と入力の羅列
まずは現状態 \( Q \) と入力 \( x \), \( y \) を羅列しましょう。
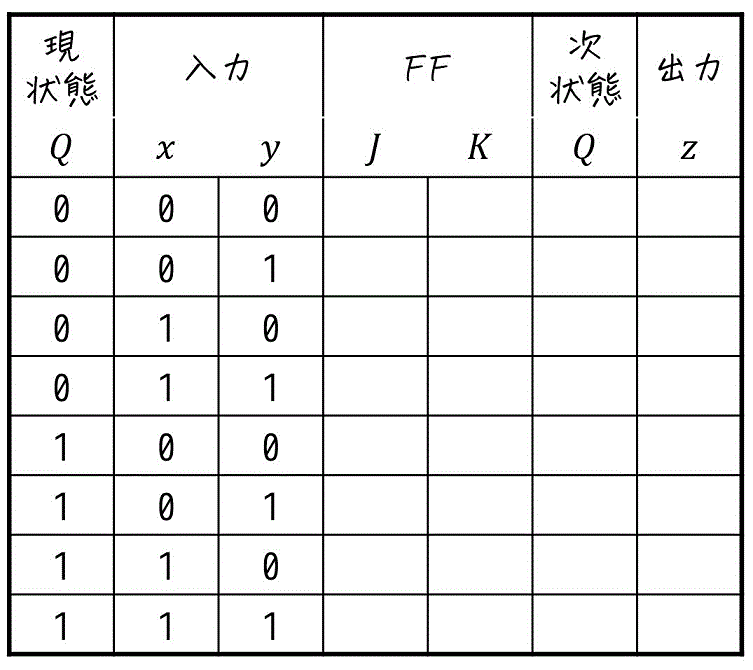
Step2. フリップフロップの入力・順序回路の出力を求める
入力方程式\[\begin{align*}
J & = x \\
K & = Q \oplus y \\
z & = Q \cdot \bar{y}
\end{align*}\]を使って求めてフリップフロップの入力 \( J \), \( K \)、および出力 \( z \) を求めていきましょう。
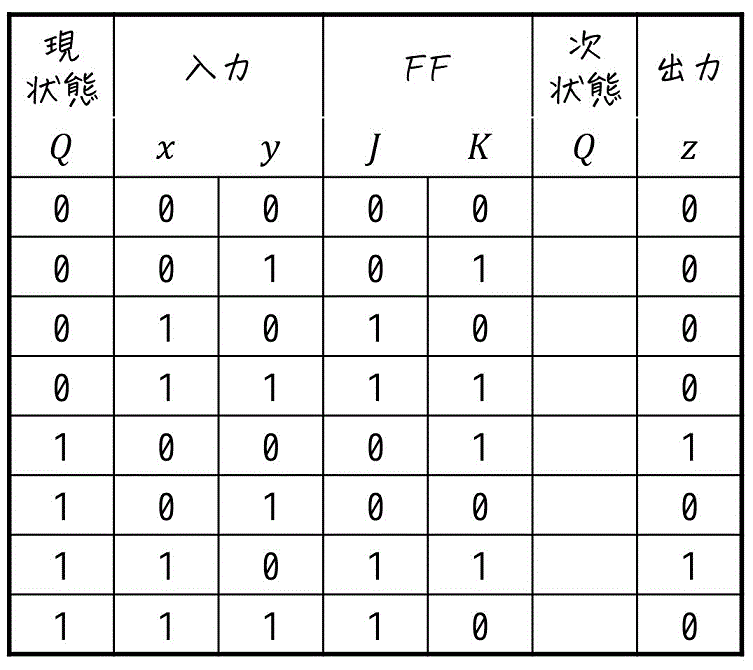
Step3. 次状態を求める
あとは、次状態が求まれば状態遷移表の完成です!
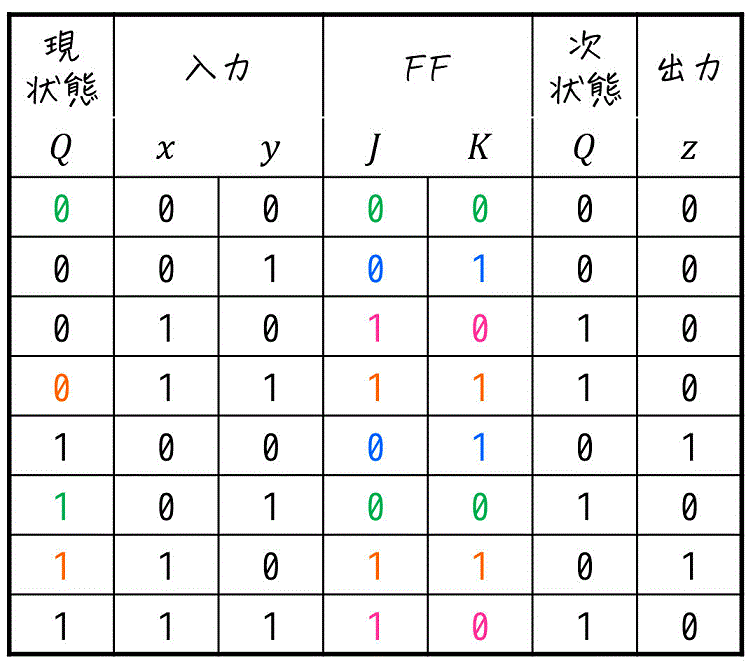
(3) 状態遷移図を求める
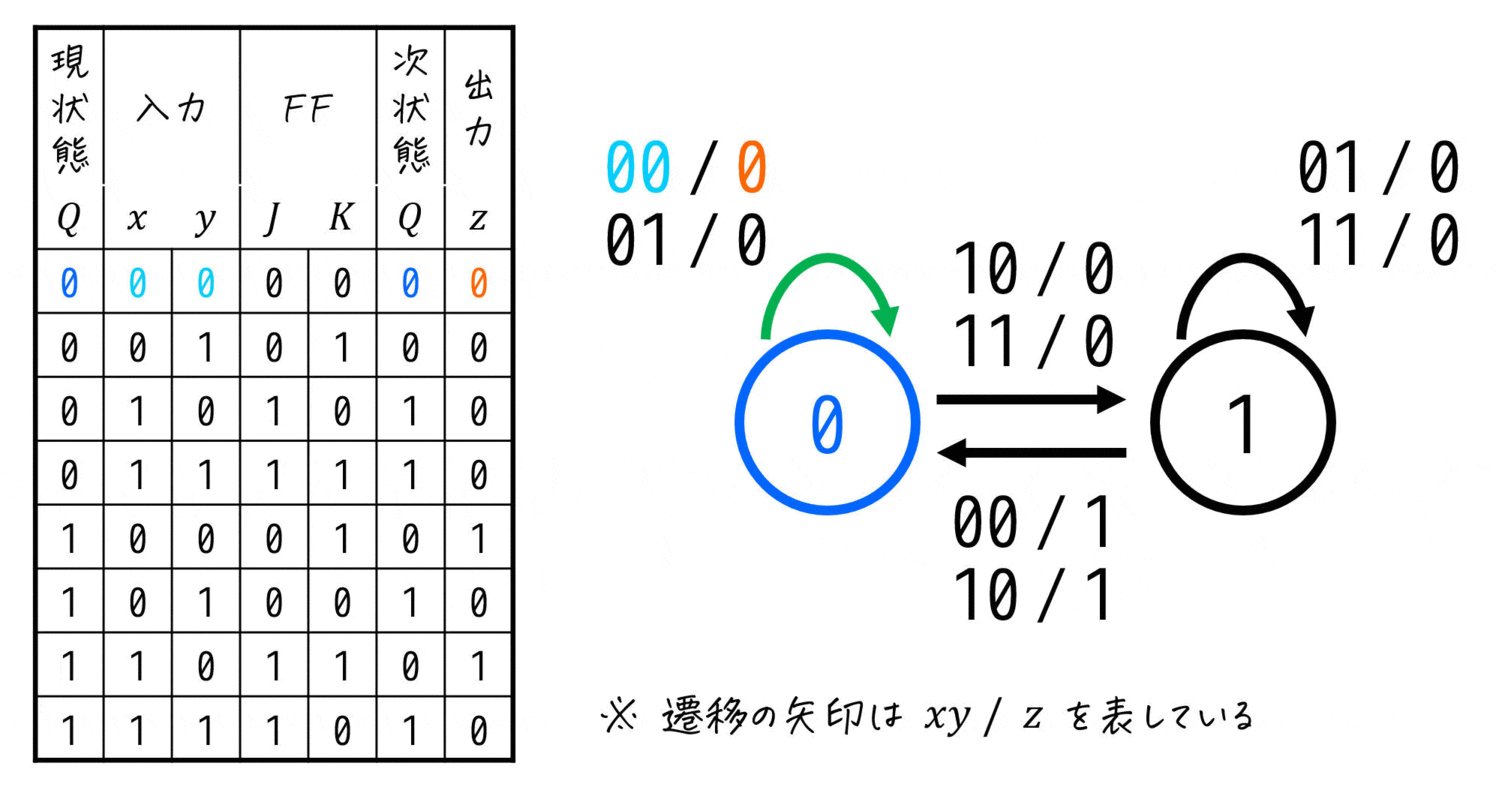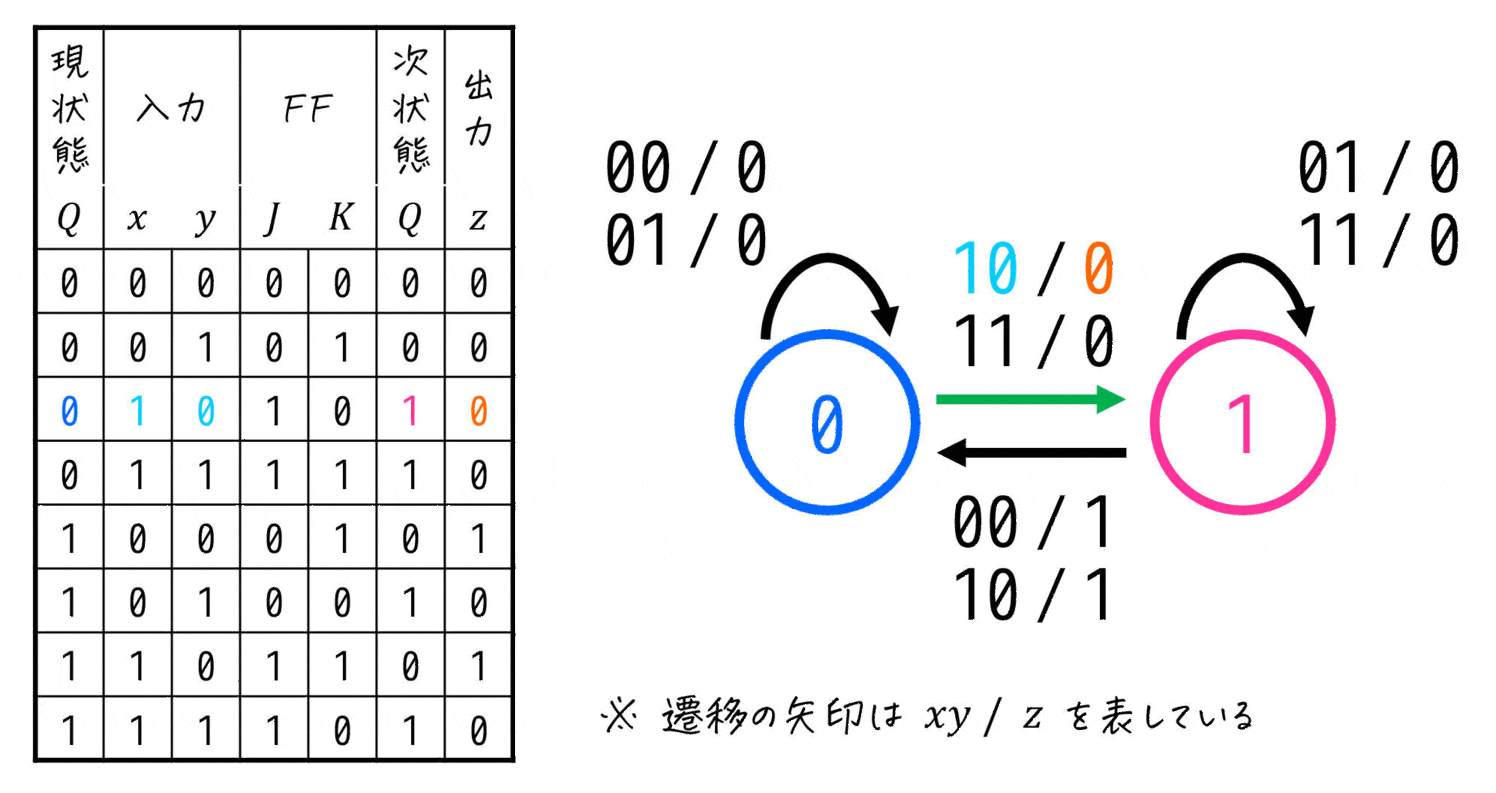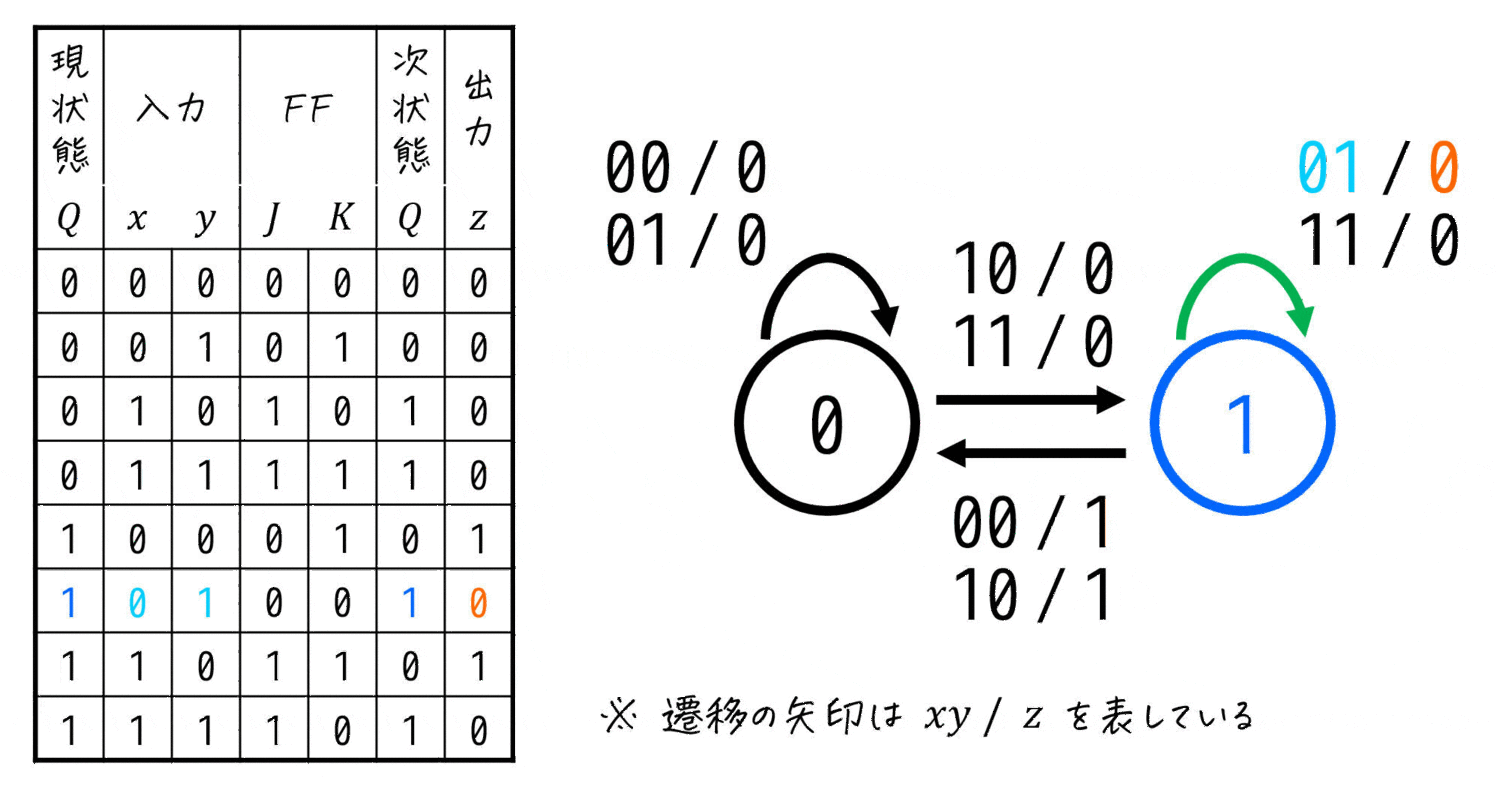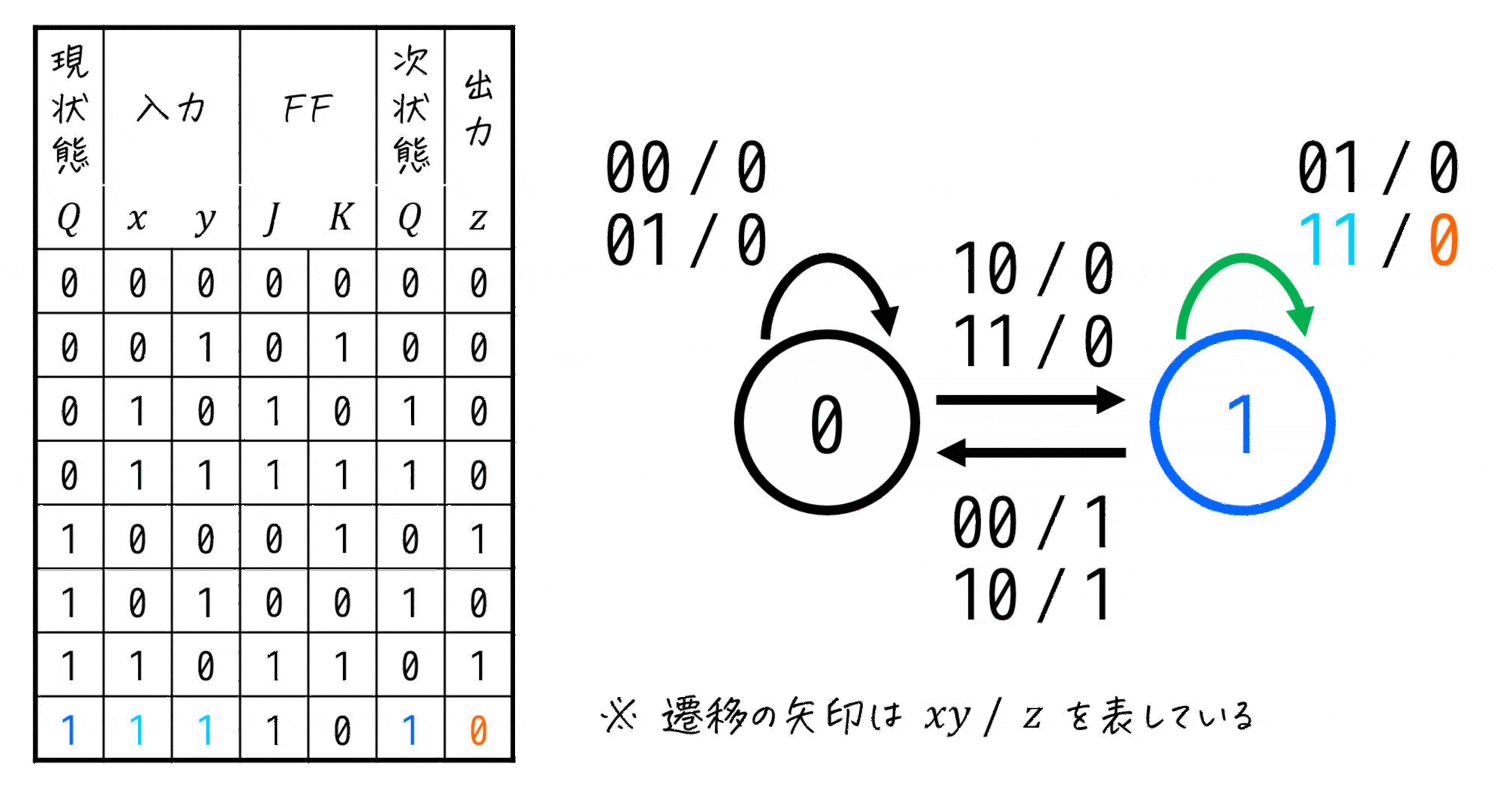
いつものように上の行から「現状態から次状態はどの状態になるか」と、そのときの入力、出力を書いていけばOKです。
ただし、今回は入力が2変数なので、どこかに「入力 / 出力 を \( xy \) / \( z \) とする」などと表記しておきましょう[5]書いておかなないと、入力が \( xy \) で書かれているのか \( yx \) で書かれているのかわからないため。。
6. [応用編2] 3つのFFからなる順序回路を読んでみよう
最後は、3つのフリップフロップからなる順序回路を読んでみましょう。
※ この問題は状態遷移図が複雑なことになるため、状態遷移図は求めなくてOKです。
つぎの順序回路がある。(1)~(3)の問いに答えなさい。ただし、CLKの配線は省略している。
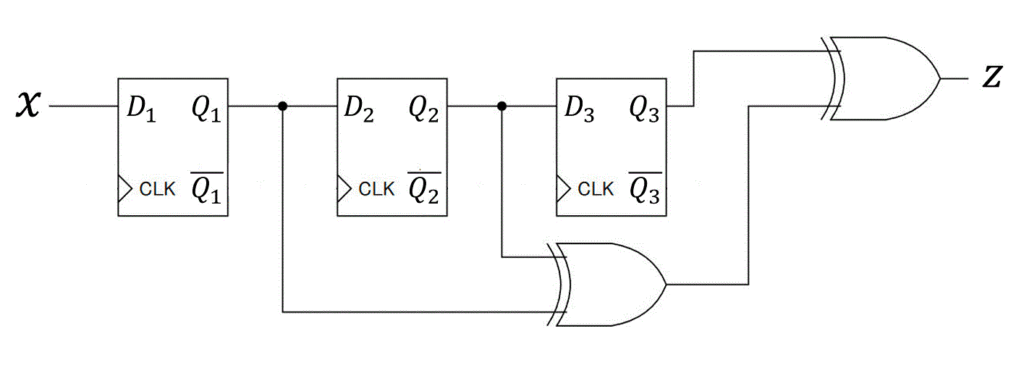
(1) フリップフロップ \( D_1 \), \( D_2 \), \( D_3 \)、および出力 \( z \) の入力方程式を入力 \( x \) および現状態 \( Q_1 \), \( Q_2 \), \( Q_3 \) を用いた形で表しなさい。
(2) この順序回路の状態遷移表を書きなさい。
(1) 入力方程式の導出
今までと同じように、まずは各部品の入力、出力を書いてから入力方程式を求めていきましょう。
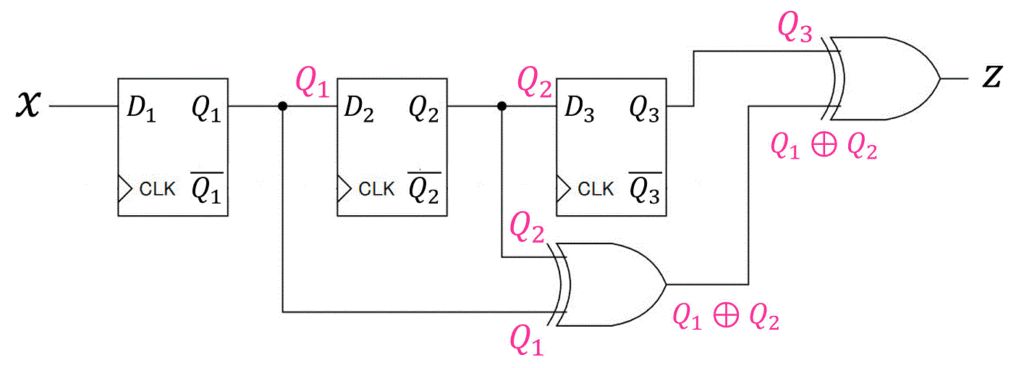
よって、\[\begin{align*}
D_1 & = x \\
D_2 & = Q_1 \\
D_3 & = Q_2 \\
z & = ( Q_1 \oplus Q_2 ) \oplus Q_3
\end{align*}\]と求めることができます。
※ \( z \) の状態方程式は、括弧を外して\[
z = Q_1 \oplus Q_2 \oplus Q_3
\]としてもOKです。
(2) 状態遷移表を求める
どれだけフリップフロップの数が増えようが、状態遷移表を求める下の3ステップは変わりません。
- フリップフロップの現状態と入力を順番に羅列する
- フリップフロップの入力を求める
- フリップフロップの入力から、次状態を求める
ただし、今回は現状態 \( Q_1 \), \( Q_2 \), \( Q_3 \) と入力 \( x \) の4つの0/1をもれなく網羅する必要があるため、\( 2^4 = 16 \) パターンを網羅する必要があるため、ケアレスミスに要注意です。
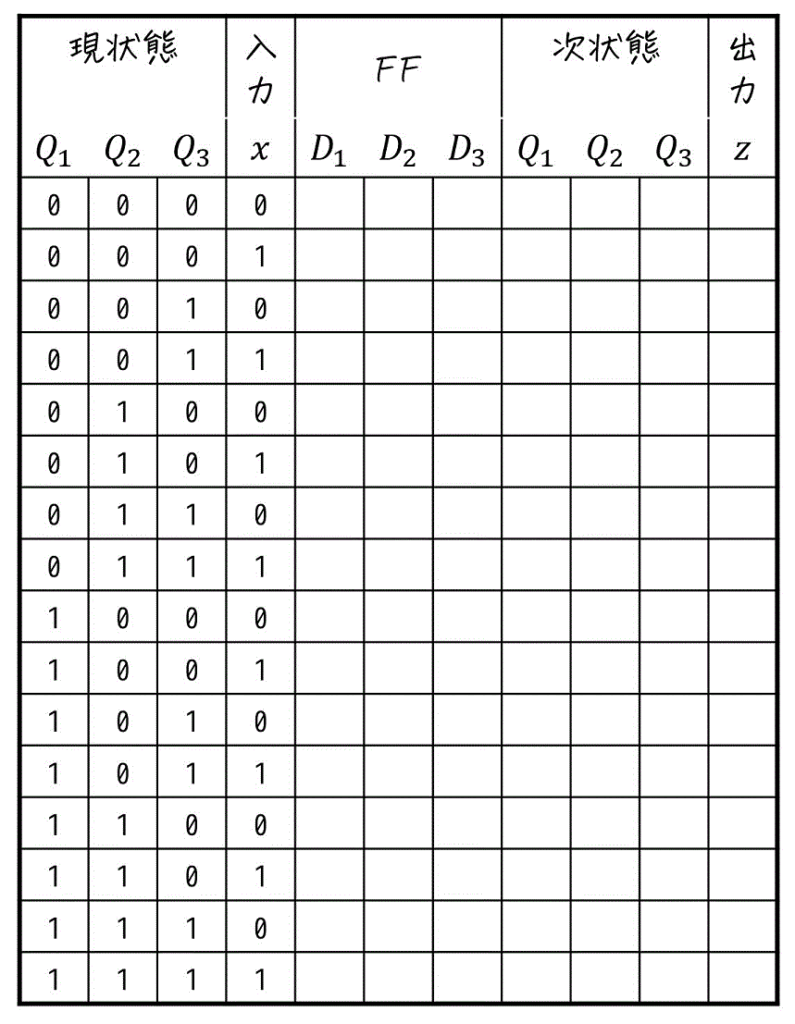
この表を埋めていくと、下のように状態遷移表を求めることができます。
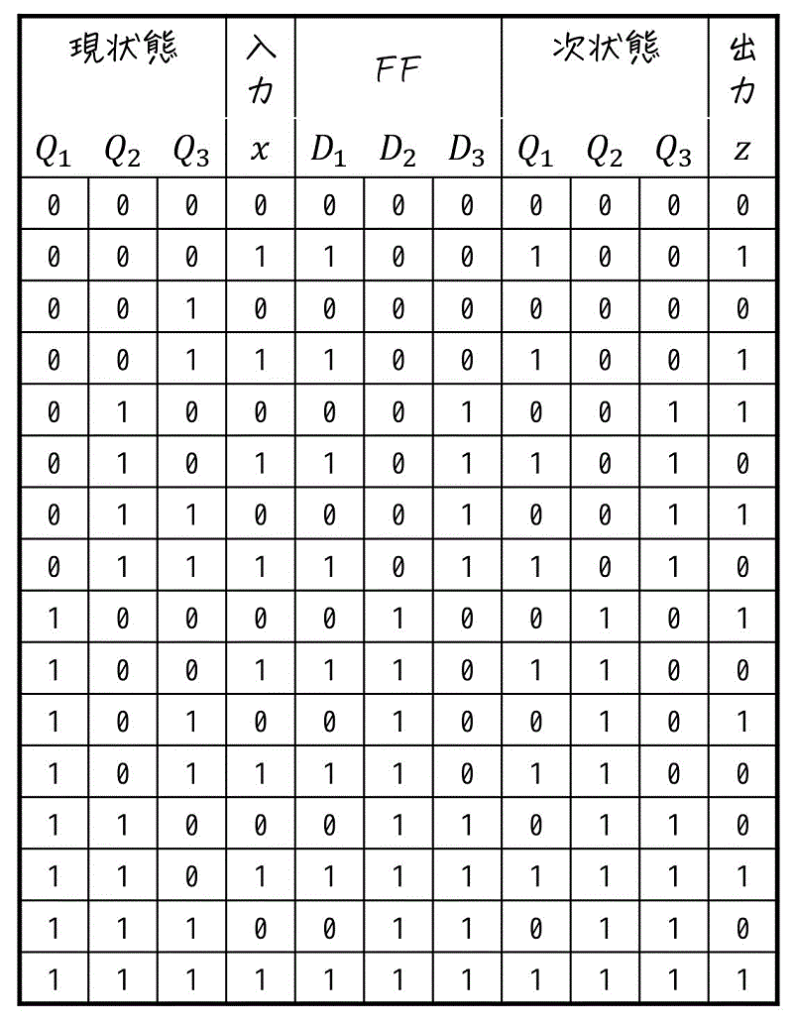
※ 今回は3種類ともDフリップフロップなので、フリップフロップの入力がそのまま次状態となります。
なので、フリップフロップの入力 \( D_1 \), \( D_2 \), \( D_3 \) さえ書いてしまえば、次状態はあっという間に求められますね。
7. さいごに
今回は、フリップフロップの読み方について学習していきました。
ここで、順序回路の読み方(状態遷移図を求める方法)について復習しましょう。
Step1. フリップフロップの次状態および出力を、フリップフロップの現状態 \( Q_1 \), \( Q_2 \), … および入力で表される入力方程式で書く。
Step2. つぎの3ステップで状態遷移表を書く
- 現状態と入力を羅列する(昇順もしくは降順に)
- 入力方程式を利用して、「各フリップフロップの入力」と「順序回路の出力」を求める
- フリップフロップの入力値から次状態を求める
Step3. Step2で求めた状態遷移表を各行ごとに
- 現状態から次状態への遷移
- 遷移時の入力、および出力
に着目して読んでいき、状態遷移図を書く。
次回からは、「順序回路を設計する方法」について説明をしたいと思います。
それでは、また次回。
注釈
| ↑1 | 逆に 1 → 0 になったタイミング(立ち下がり)で出力が変化するタイプのことをネガティブエッジと呼びます。ネガティブエッジの場合は、下の図の赤色部分で入力が同期され、出力が変化します。
|
|---|---|
| ↑2 | 一般的には、RSフリップの禁止入力を使えるように拡張したものがJKフリップフロップと説明されることが多いです。しかし、今回は試験に出る順に解説しているため、JKフリップフロップの \( (J,K)=(1,1) \) のときを禁止入力としたものがSRフリップフロップと説明しています。 |
| ↑3 | \( n \) 個のフリップフロップで記憶できる状態数は \( 2^n \) ですが、そのうちの1つを0を記憶するために使う必要があるので \( 2^n - 1 \) です。 |
| ↑4 | \( D_1 \) を \( x \oplus Q_2 \) でなく、\( Q_2 \oplus x \) と書いたのは、状態遷移表の項目が左側から順に \( Q_1 \), \( Q_2 \), \( x \) となっているため、普通に書くよりも処理しやすくなるため。 |
| ↑5 | 書いておかなないと、入力が \( xy \) で書かれているのか \( yx \) で書かれているのかわからないため。 |
関連広告・スポンサードリンク