うさぎでもわかる論理回路　カルノー図編

こんにちは、ももやまです。
今回は論理式を単純化するカルノー図について説明します。

 

カルノー図は、2変数～4変数（無茶すれば6変数くらいまでならいける）の論理式を簡略化するために使います。

主に4変数の論理式を簡略化する際に使います。

 

www.momoyama-usagi.com

 

 

スポンサードリンク

１．カルノー図の書き方

まずは、カルノー図の書き方を説明します。

4変数の場合、3変数の場合、2変数の場合に順番に説明していきたいと思います。

(1) 4変数の場合

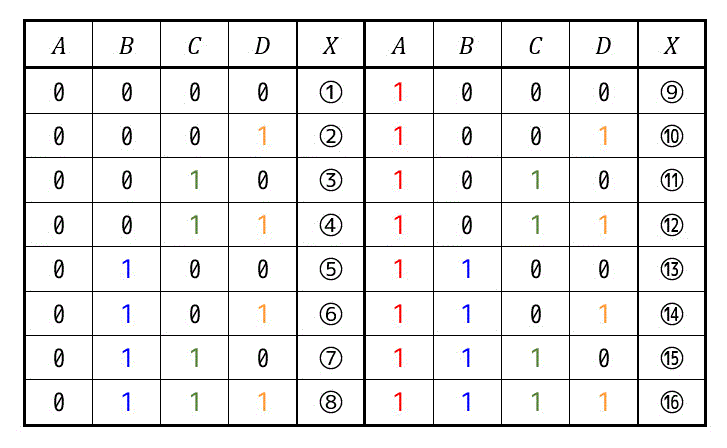
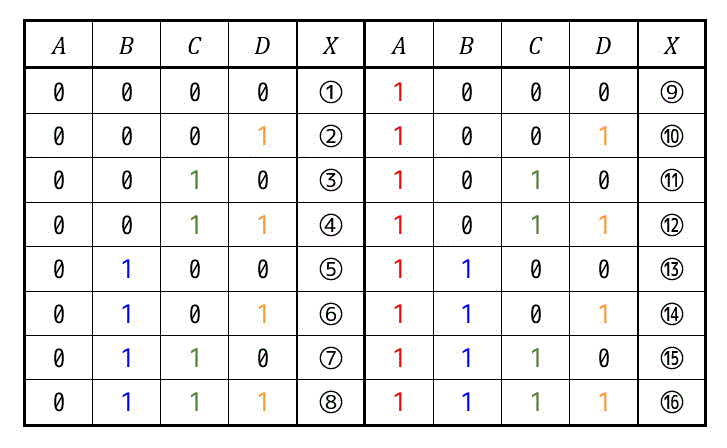
4変数の真理値表の値をそれぞれ①～⑯とします。

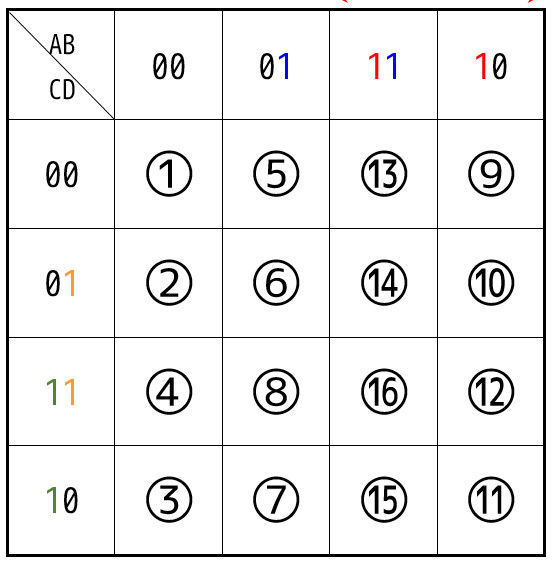
4変数のカルノー図の場合、このような図を書くことになります。

 

カルノー図の真理値の表し方は、先生によって、

(1) ABとCDの真理値を書く人

(2)それぞれの変数が真の部分を矢印で表す人

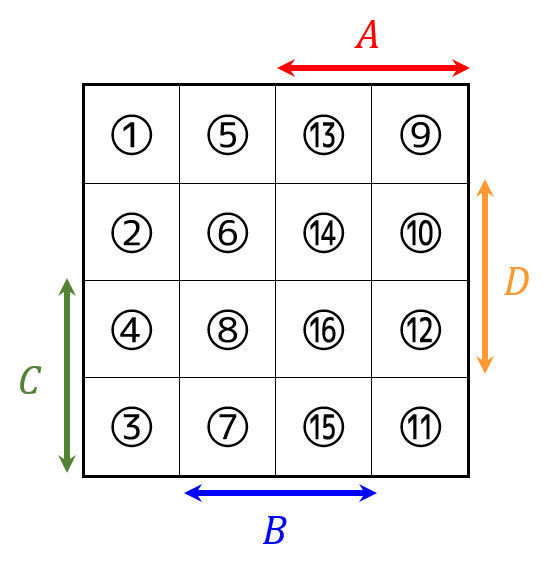
の2パターンいます。

今回は2パターンどちらの書き方を習った人でもわかるように両方示します。

 

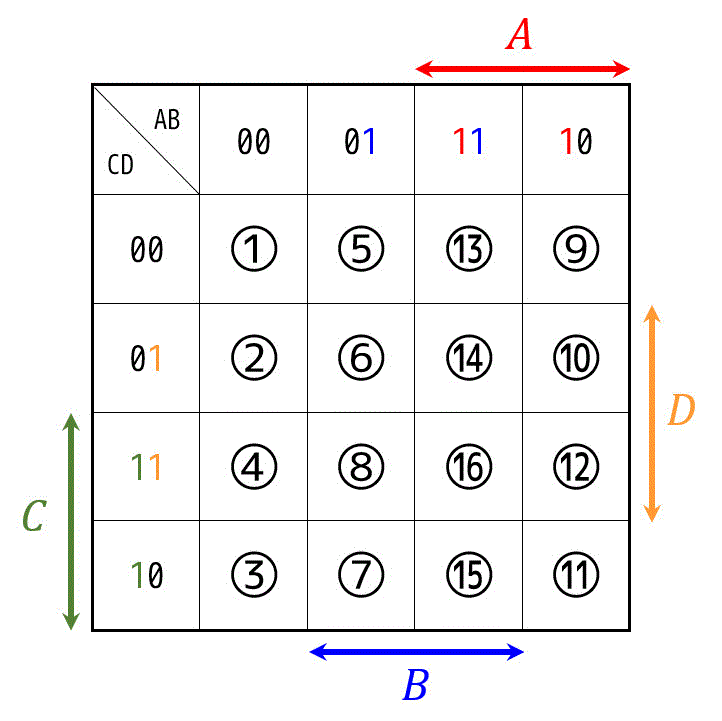
4変数なので、\( 2^4 \) で全部で16の状態があります。
上で書いた真理値表の①～⑯が下のカルノー図の①～⑯の要素に相当します。

 

では、カルノー図の真理値を読み取って見ましょう。例えば、⑤のA,B,C,Dそれぞれの真理値はどうなっているでしょうか。

⑤の要素はABが01、CDが00なので、ABCD = 0100 ですね。
確かに上の真理値表の場所と一致していますね。

矢印で読み取るのであれば、Bの部分だけ⑤の要素に該当していますね。
なので、Bは1、それ以外は0となり、ABCD = 0100 と読めます。

 

ここで少し「あれ？」と思った人が多いと思います。

真理値表だと00, 01, 10, 11の順番で並んでいるはずですが、00, 01, 11, 10となっていますね。

なんで 00→01→10→11 の順番じゃないの！！　と思う人が多いと思います。

しかし、00→01→11→10となっているのにはちゃんとした理由があります。

 

カルノー図では、論理式を単純化するためにわざと2ビットのうちの片方を固定して隣合っている場所が1ビットしか違わないようにするためです。

01→10は2ビット違いますね。なので、わざと01→11→10の順番にすることでどの要素も1ビットずつしか変わらないようにするのです。

カルノー図は、隣り合った要素は1ビットしか違わないのを利用して単純化を行います。

(2) 3変数の場合

3変数のカルノー図も紹介しましょう。
それぞれの真理値表の値が下のように①～⑧で表されるとします。

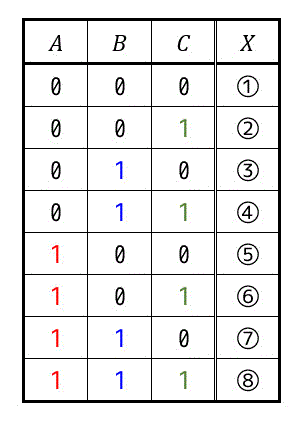
すると、カルノー図はこのようになります。

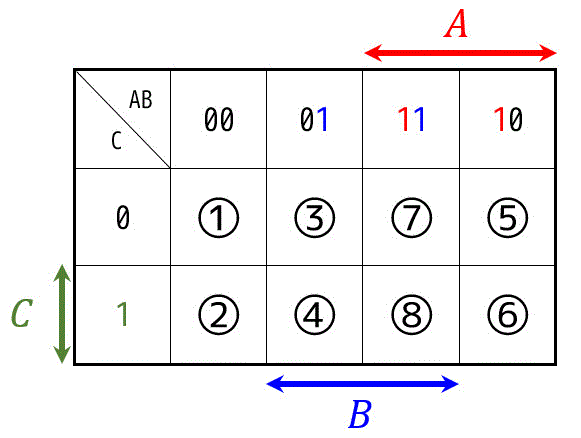
4変数のCDのところが1変数減ってCだけになりました。

(3) 2変数の場合

2変数のカルノー図も紹介します。

それぞれの真理値表の値が下のように①～④で表されるとします。

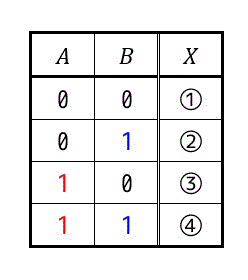
すると、カルノー図は下のようになります。

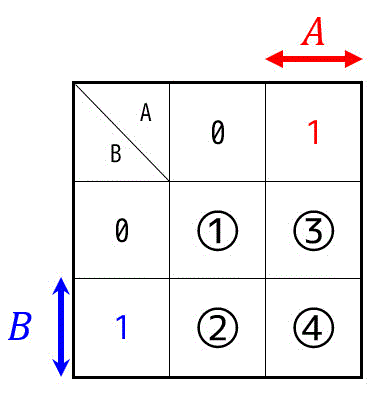
ただし、2変数の論理変数を簡略化する際には、ブール代数の変形規則を使ったほうが早いです。

スポンサードリンク

２．カルノー図を使った簡略化の方法

それでは、簡略化の仕方を順番に説明していきましょう。

カルノー図を使って簡略化するのは4変数の場合が多いため、今回は4変数で説明します。

3変数、2変数の場合でも4変数と同様の方法で簡略化することができます。

 

Step1. 囲める組み合わせをすべて調べる（主項を求める）

カルノー図では真理値が1となっている部分にだけ注目します。

まず、1を囲える組み合わせをすべて調べます。

ただし、つぎの条件に従って囲うことに注意してください。

ルール1：囲める大きさは 2のべき乗×2のべき乗

1つめのルールとしては、囲えるサイズに制限があるということです。

必ず2のべき乗×2のべき乗*1で囲う必要があります。

 

4変数のカルノー図の場合は4×4のサイズなので、囲める大きさの組み合わせとしては

• 1×1
• 1×2（2×1）
• 1×4（4×1）
• 2×2
• 2×4（4×2）
• 4×4

この6パターンしかありません。

例えば、つぎの緑色の囲い方は2×2なので囲うことができますが、赤色の囲い方は1×3なのでルールに違反し、囲うことができません。

 

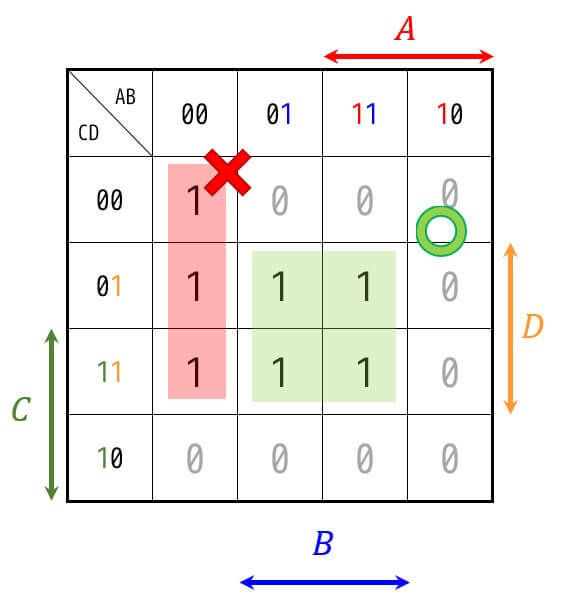
ルール2：重複して囲ってもOK

囲う際には、重複して囲っても問題ありません。
例えば、このように囲うことができます。

（青色部分は \( B \)、緑色部分は \( C \) を表しています。）

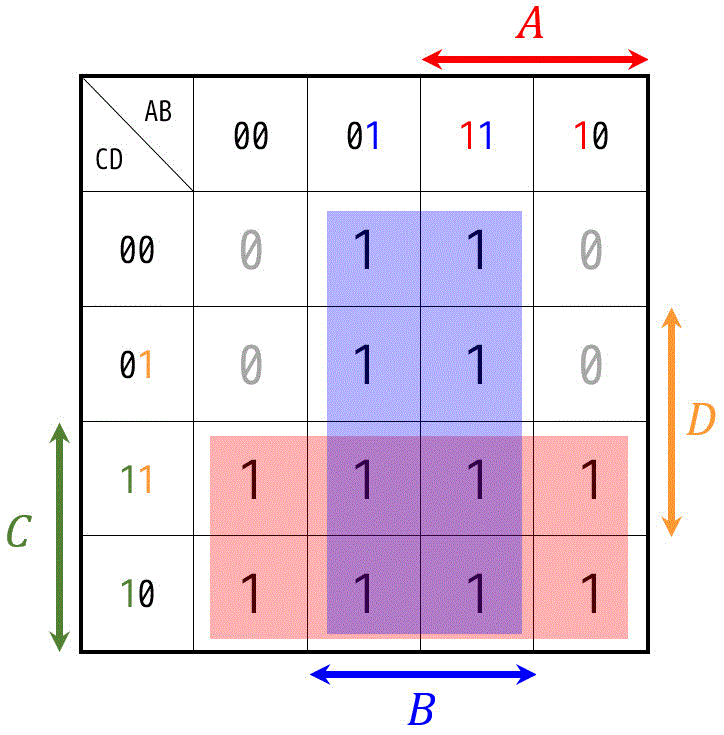
ルール3：四隅はつながっている

カルノー図の四隅はつながっています。

FFやドラクエの世界地図みたいにつながっていると考えてください。

 

例えば、このような囲い方ができます。

 

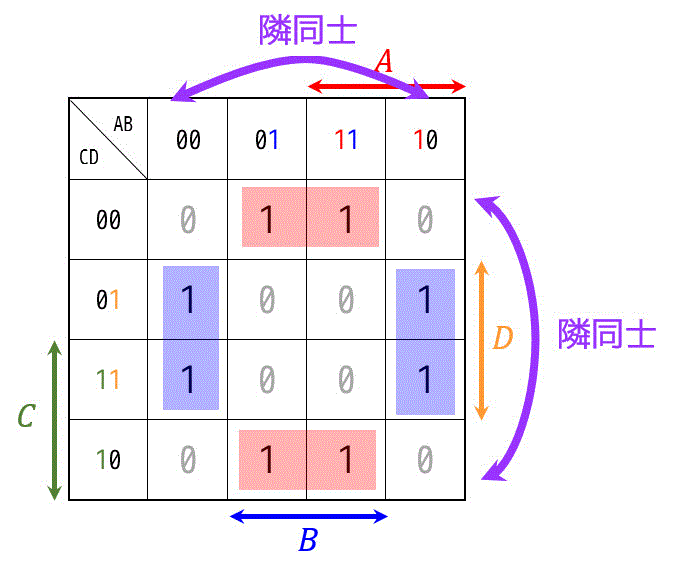
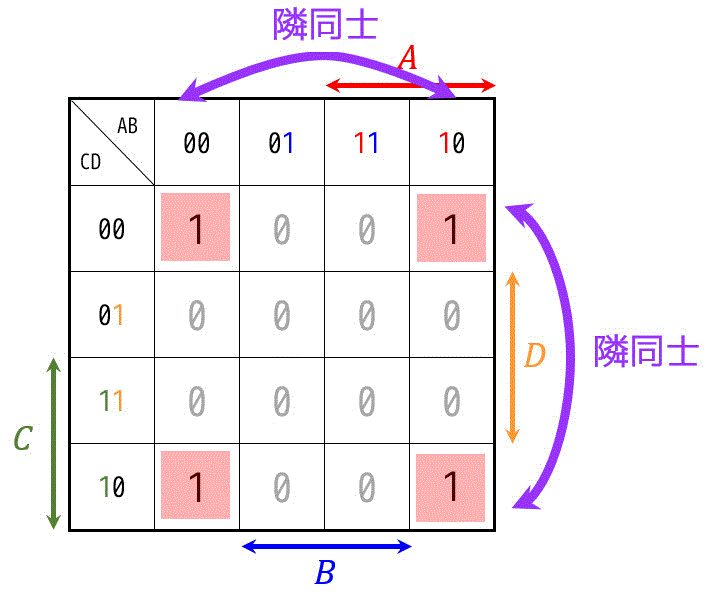
特に忘れがちなのが、下のような4隅のパターンです。

（この場合は \( \bar{B} \bar{D} \) を表しています。）

では実際に1つこちらのカルノー図を例として囲ってみましょう。

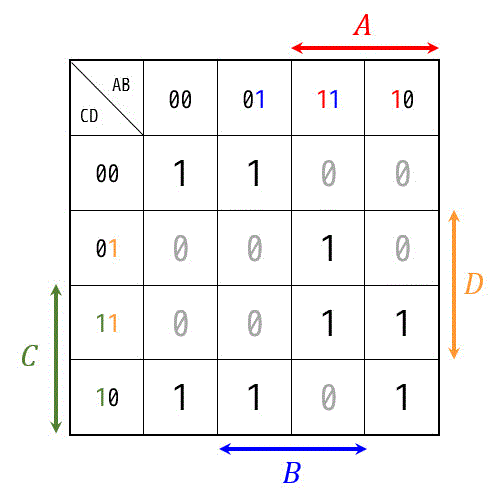
この図形の囲える組み合わせは、下のようになります。

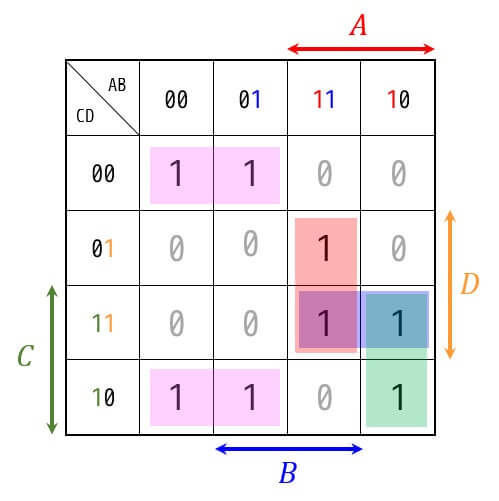
ピンク色の部分は2×2で囲うことが必要です。

つぎに、囲った部分を論理式に変形します。
論理式に変換する際には、囲った部分のABCDの値に注目します。

例えばピンク色（2×2）に注目すると

• A → 囲った4箇所とも 0 → \( \bar{A} \)
• B → 囲った4箇所に0と1が両方ある → 無視
• C → 囲った4箇所に0と1が両方ある → 無視
• D → 囲った4箇所ともに0　→ \( \bar{D} \)

となるので、ピンク色の部分の論理式は \( \bar{A} \bar{D} \) となります。

赤色で囲われている部分を見ていくと、Cは0,1ともに存在するので無視、Aは1、Bは1、Dは1なので赤色で囲われている部分の論理式は \( ABD \) となります。

緑色で囲われている部分を見ていくと、Dは0,1ともに存在するので無視、Aは1、Bは0、Cは1なので緑色で囲われている部分の論理式は \( A\bar{B}C \) となります。

青色で囲われている部分を見ていくと、Bは0,1ともに存在するので無視、A,C,Dはすべて1なので青色で囲われている部分の論理式は \( ACD \) となります。

 

よって囲えるすべての組み合わせを論理式で表すと、\( \bar{A} \bar{D} \), \( ABD \), \( A \bar{B} C \), \( ACD \) となり、これら4つが主項となります。

Step2. 独立して囲まれている場所を探す（特異最小項を調べる）

次にStep1で囲ったカルノー図から、1箇所からしか囲まれていない場所をすべて探します。

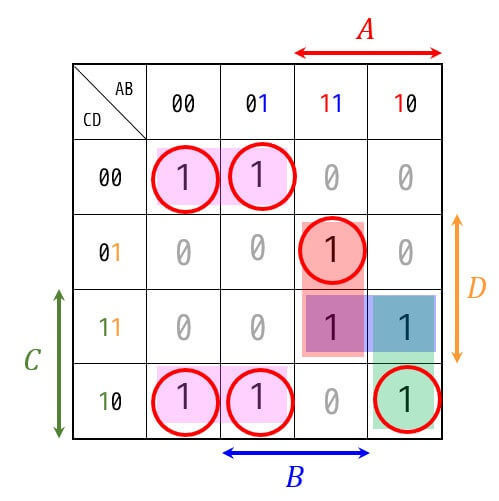
今回の場合だとこの6つ*2が1箇所しか囲まれていません（特異最小項となります）。

Step3. 特異最小項を囲っている要素を探す（必須主項を探す）

つぎに、特異最小項を囲っている要素*3をすべて探します。

今回の場合だと、この5つの要素（主項）が該当します。

 

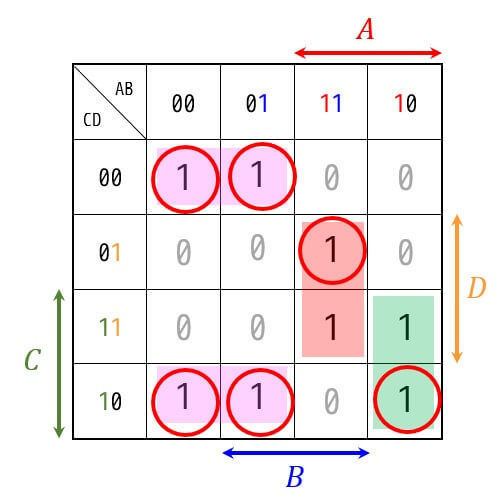
4つの中で、必須主項に該当するものは、、\( \bar{A} \bar{D} \), \( ABD \), \( A \bar{B} C \) の3つとなります。

Step4. まだ囲われていない1があるか確認

まだ囲われていない1があるかを確認します。
もしあれば囲ってあげます。

今回はないのでこのステップはなくてOKです。

Step5. 必須主項＋Step4で囲った主項の論理和が完成品

最後に、今まで求めた必須主項とStep4で囲った主項の論理和をとります。それが簡略化された最小論理和系となります。今回の場合だと、\[X = \bar{A} \bar{D} + ABD + A \bar{B} C \] となります。

スポンサードリンク

３．Don't care

今までのパターンであれば、すべての論理変数の組み合わせに対して0,1の値が決まっていました。しかし、実際には0,1両方に決めなくていい場合があります。

わかりやすい例を1つあげてみましょう。例えば月を4ビットの論理変数で表すとしましょう。このとき、0001b (1d)～ 1100 (12d) までは存在しますが、0月、13月、14月、15月などは存在しませんね。

このように、0,1を決める必要がない論理変数は Don't care（ドントケア）、禁止入力、「どーでもいい」と言われます。

 

0,1 を決める必要がなければ 0,1 どっちが出力されても問題ありませんね。
そもそも存在しないんですから。

なので、Don't careを考える際には、なるべく論理回路が単純化されるように0,1を振ってあげます。

Don't careの項を使ってさらに単純化されそうであれば1を振り、単純化できそうにない（複雑な回路になりそうな）ときには0を振ってあげればいいのです。

 

例えば、つぎのカルノー図を考えてみましょう。

XはDon't careを表します。
X以外にも \( \phi \) などの記号が使われます。

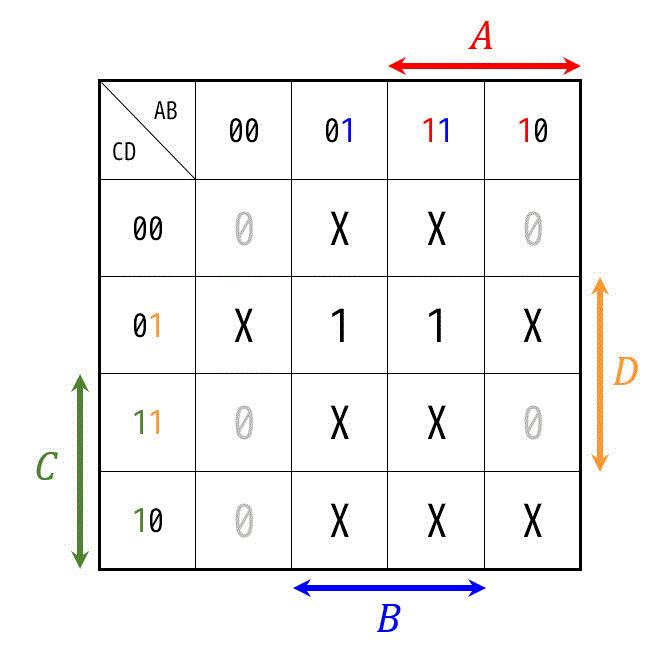
もし、Xがすべて0としたら、このような囲い方になります。
（論理式：\( B \bar{C} D \)）

 

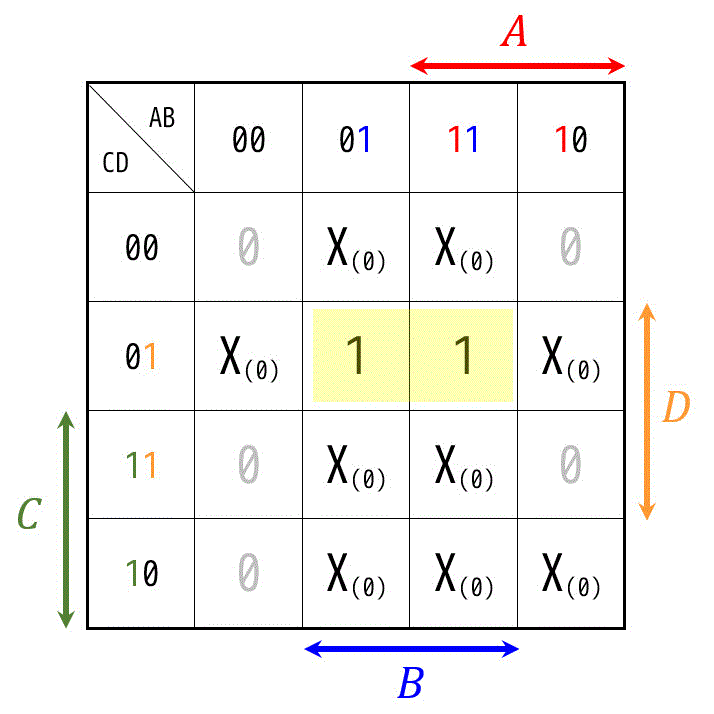
では、Don't careをなるべくうまく使って大きく囲う方法を考えましょう。

囲い方としては、つぎの緑色のパターンと黄色のパターンの2つが考えられます。

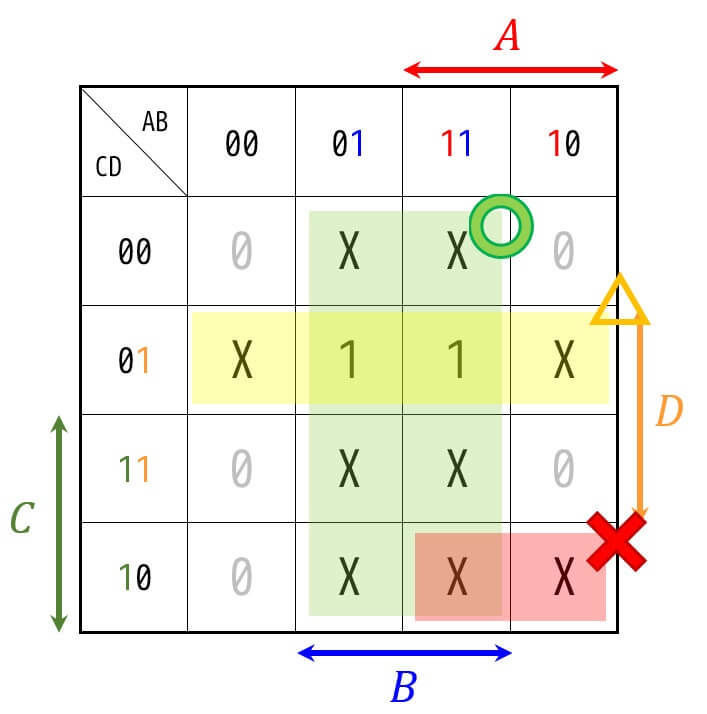
黄色の囲い方は1×4、緑色の囲い方だと2×4なので、緑色の囲い方のほうがより大きく囲えていることがわかりますね。

 

なるべく論理式を簡略化したいので、赤色の囲い方のような必要ないDon't careは囲わないことに注意が必要です*4。

 

確かに、黄色の囲い方だと、\( \bar{C} D \)、緑色の囲い方だと\( B \) となるため、緑色の囲い方をしたほうがより論理式（および論理回路）を単純化することができますね。

 

なので、今回の場合は、下のような緑色の囲い方が、論理式を最も単純化する囲い方となります。

 

 

 

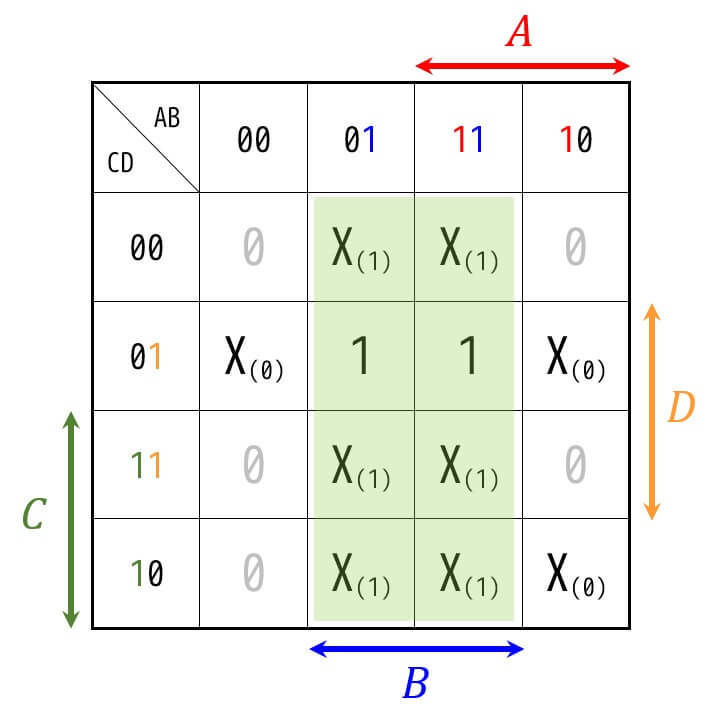
４．練習問題

では、実際にカルノー図の練習をしてみましょう。
1問だけ応用情報の過去問を載せています。

練習1

下に表される真理値表で表される論理式 \( X \) があるとする。

 

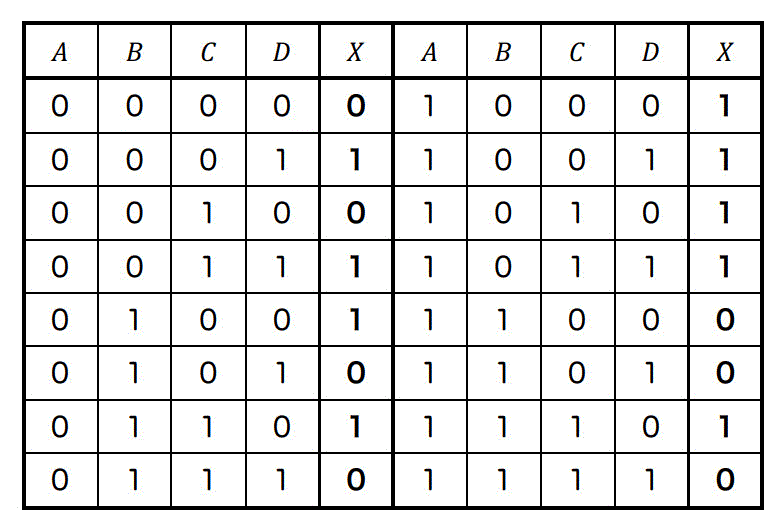
つぎの問いに答えなさい。

(1) 上の真理値表からカルノー図を書きなさい。
(2) すべての主項を求めなさい。
(3) 特異最小項を求めなさい。
(4) 必須主項を求めなさい。
(5) 入出力の関係を簡単化された論理関数で表しなさい。

練習2

A,B, C, Dを論理変数とするとき、次のカルノー図と等価な論理式はどれか。

[応用情報技術者平成26年秋期 午前問1]

 

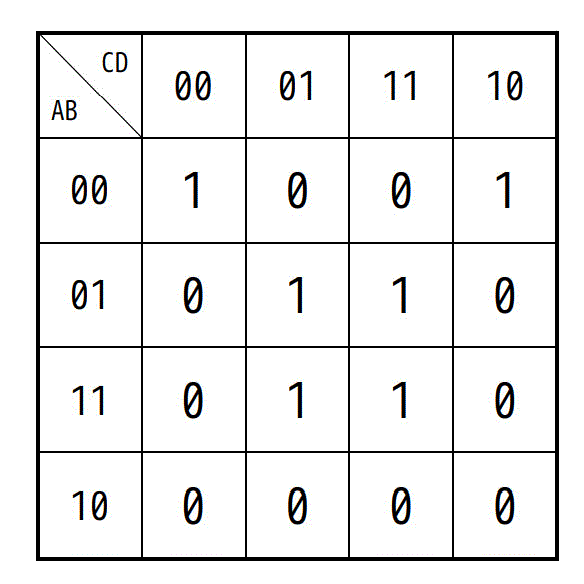
ア：\( A \cdot B \cdot \bar{C}  \cdot D + \bar{B} \cdot \bar{D} \)
イ：\( \bar{A} \cdot \bar{B} \cdot \bar{C} \cdot \bar{D} + B \cdot D \)
ウ：\( A \cdot B \cdot D + \bar{B} \cdot \bar{D} \)
エ：\( \bar{A} \cdot \bar{B} \cdot \bar{D} + B \cdot D \)

 

練習3

1月〜12月の中から、冬の季節と春の季節（12月、1月、2月、3月、4月、5月が該当）を判定するだけの謎回路を作成する。

入力は4変数 \( A,B,C,D \) であり、出力は \( X \) である。

 

入力変数は上位から順番に A, B, C, D の順番で表され、月として入力しない月（0、13、14、15）はDon't careとする。

例えば、7月は2進数で0111と表される。このとき、Aは0、B,C,Dは1となる。

 

(1) 入力A,B,C,Dにおける出力Xの真理値表を書きなさい。Don't care はXとすること。
(2) (1)の真理値表からカルノー図を書きなさい。
(3) すべての主項を求めなさい。
(4) 特異最小項を求めなさい。
(5) 必須主項を求めなさい。
(6) 入出力の関係を簡単化された論理関数で表しなさい。
(7) (6)の論理式をAND, OR, NOT回路で表しなさい。

 

５．練習問題の解答

解答1

(1)

カルノー図は以下のようになる。
ABとCDの順番はどちらでもよい。

 

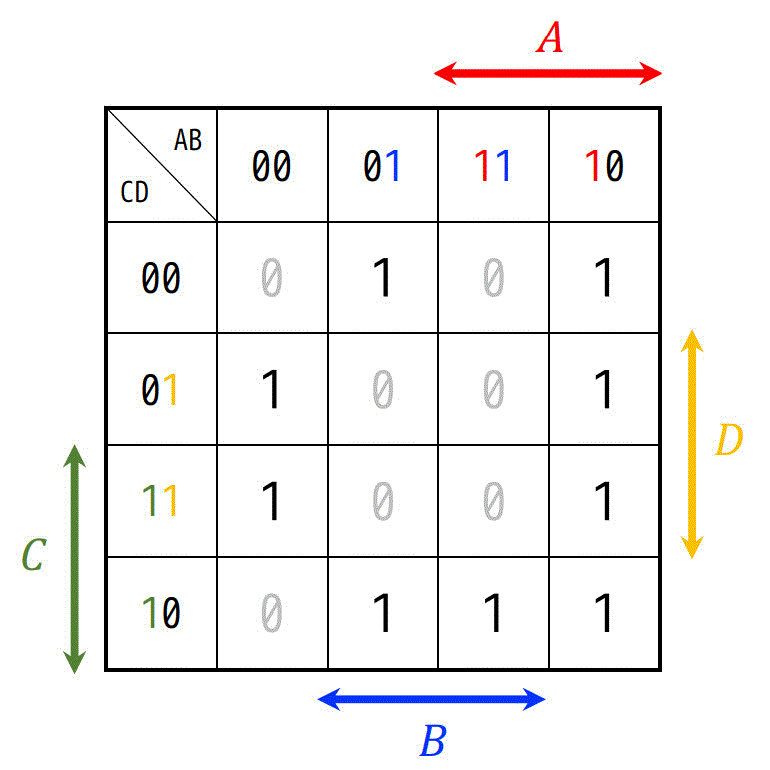
(2)

すべての主項を求めるためには、囲い方の組み合わせすべてを求めればよい。

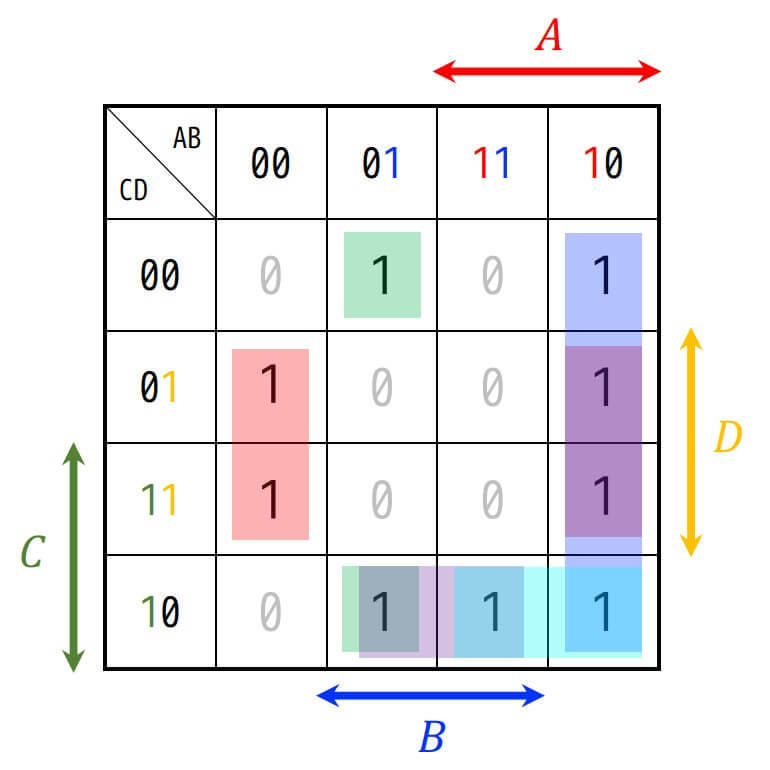
このように囲うことができる。

その結果、\( \bar{B} D \), \( A \bar{B} \), \( \bar{A} B \bar{D} \), \( AC \bar{D} \), \( BC \bar{D} \) の5つの主項が求まる。

 

(3)

特異最小項は、1箇所からしか囲われていない場所（論理変数）である。

今回の場合、○で囲んだ4箇所が特異最小項に該当する。

 

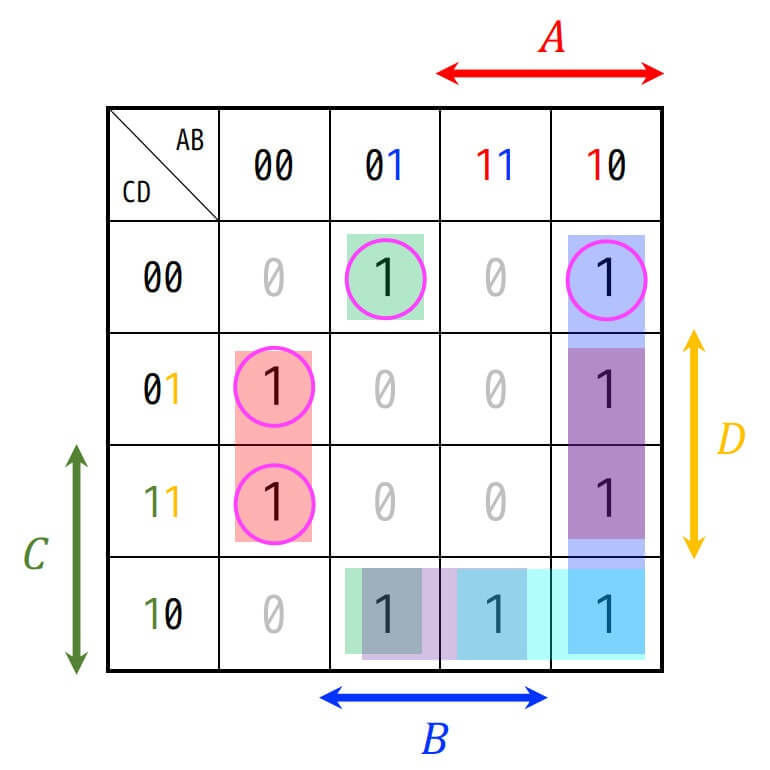
特異最小項を論理変数で表すと、\( \bar{A} \bar{B} \bar{C} D \), \( \bar{A} \bar{B} C D \), \( \bar{A} B \bar{C} \bar{D} \), \( A \bar{B} \bar{C} \bar{D} \) の4つとなる。

 

(4)

必須主項は、特異最小項が含まれている主項を表す。

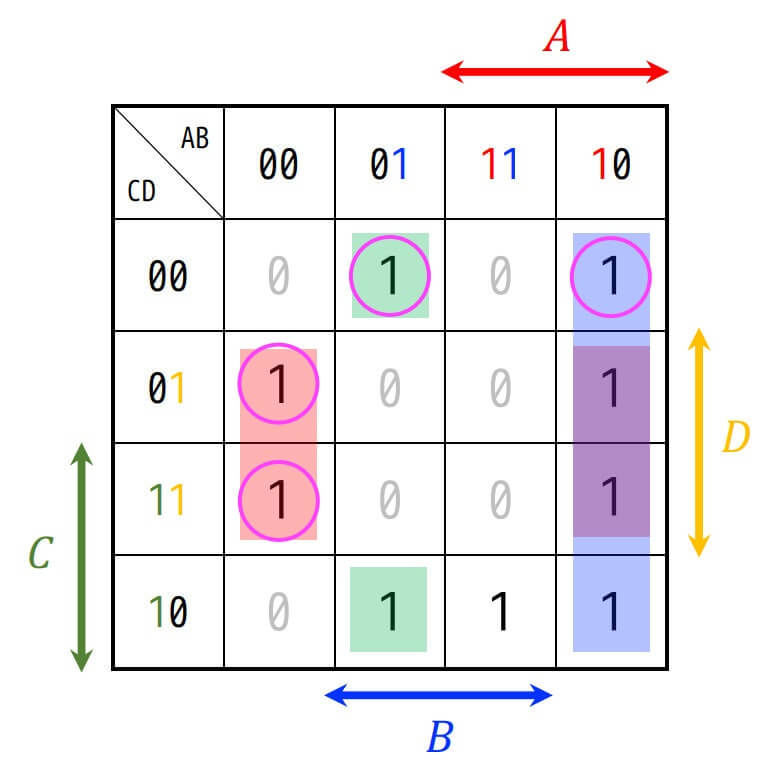
今回の場合、\( \bar{B} D \), \( A \bar{B} \), \( \bar{A} B \bar{D} \) の3つが必須主項となる。

 

(5)

簡略化された論理関数を求める前に、まだ囲われていない1がないかどうかを確認します。

今回は1つだけ残っているので残りの主項 \( AC \bar{D} \), \( BC \bar{D} \) の中から、なるべく少ないかつ単純な（リテラル数が少ない）主項を選んですべての1が囲まれるようにします。

今回は、どちらを選んでも大丈夫です。試しに、 \( AC \bar{D} \) でやってみます。
すると、カルノー図は下のようになり、確かにすべての1が囲まれますね。

 

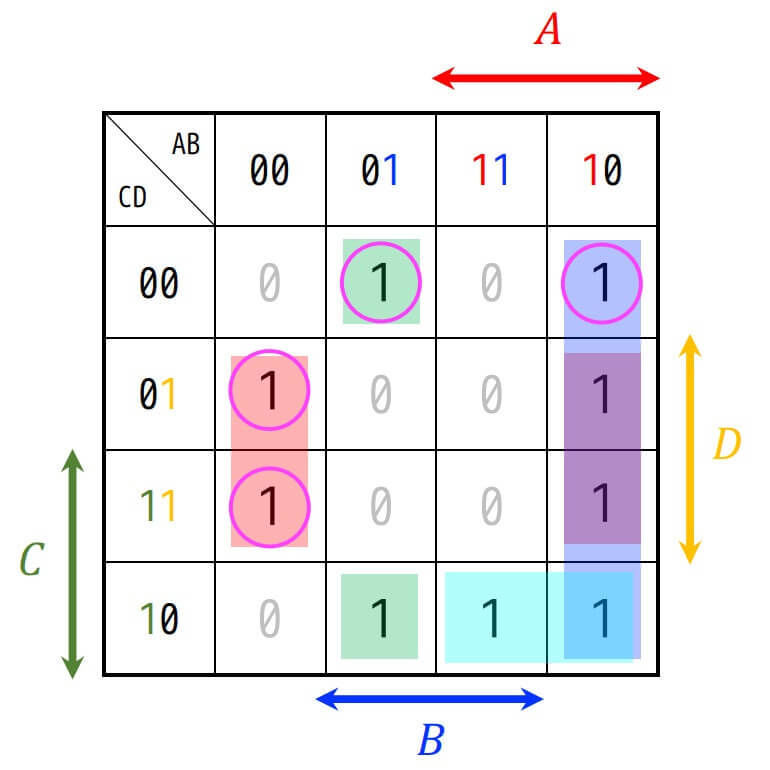
よって簡単科された論理関数は必須主項である \( \bar{B} D \), \( A \bar{B} \), \( \bar{A} B \bar{D} \) の3つと、最後に選んだ主項 ( \( AC \bar{D} \), \( BC \bar{D} \) ）のどちらかの合計4つの論理和で表されます。よって答えは\[ X = \bar{B} D + A \bar{B} + \bar{A} B \bar{D} + AC \bar{D} \] もしくは\[X =  \bar{B} D + A \bar{B} + \bar{A} B \bar{D} + BC \bar{D} \]となります（どっちでも正解）。

 

解答2

解答：エ

カルノー図を囲ってあげると、下のような形になります。

 

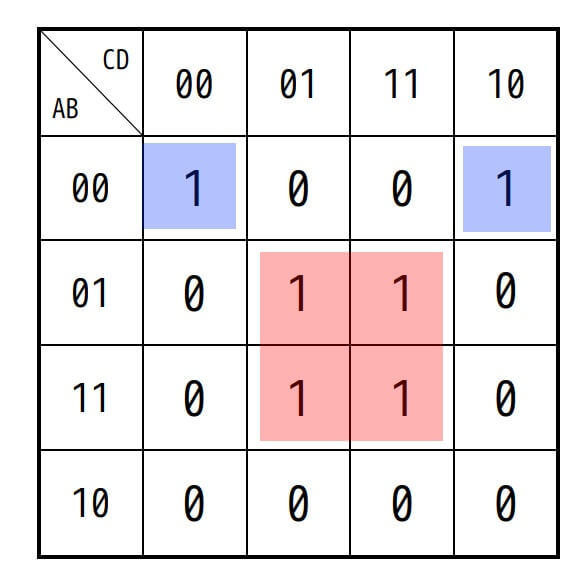
主項：\( BD \), \( \bar{A} \bar{B} \bar{D} \)
特異最小項：真理値が1の中のすべての論理変数
必須主項：\( BD \), \( \bar{A} \bar{B} \bar{D} \)

なので、等価な論理式は \[ BD + \bar{A} \bar{B} \bar{D} \] となり、答えはエとなります。

 

解答3

(1)

真理値表は以下の通りとなる。
ただし、XはDon't careを表す。

 

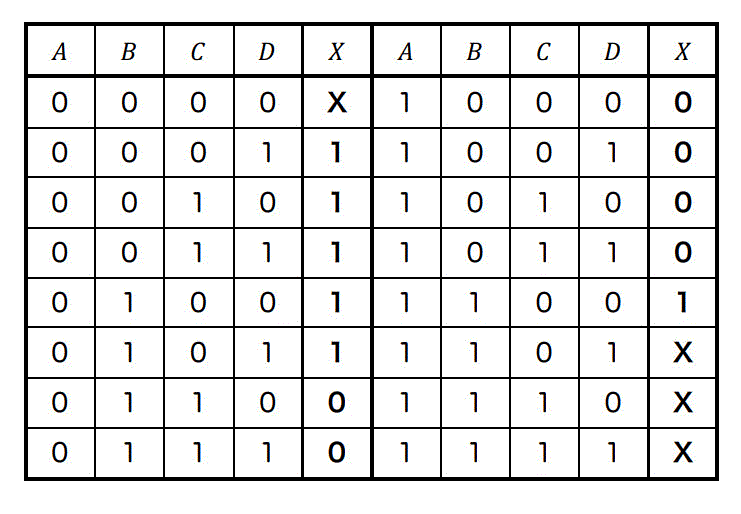
(2)

カルノー図は以下の通りとなる。
AB,CDの順番は逆でもOK。

 

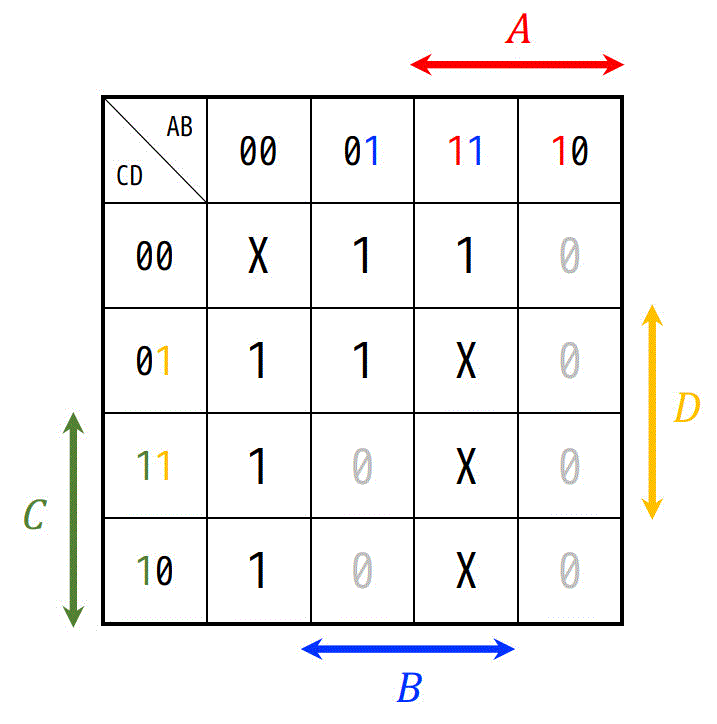
(3)

主項は、1が1つでも含まれている囲い方のすべての組み合わせとなる。

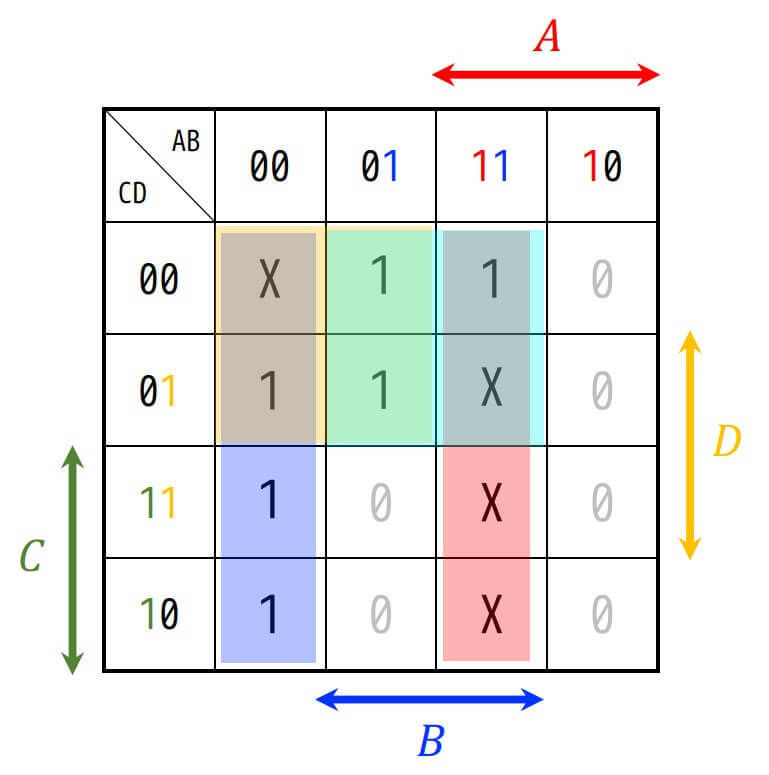
今回の場合は、4つの主項 \( \bar{A} \bar{B} \), \( AB \), \( \bar{A} \bar{C} \), \( B \bar{C} \) となる。

(4)

特異最小項は、1箇所からしか囲われていない場所（論理変数）である。

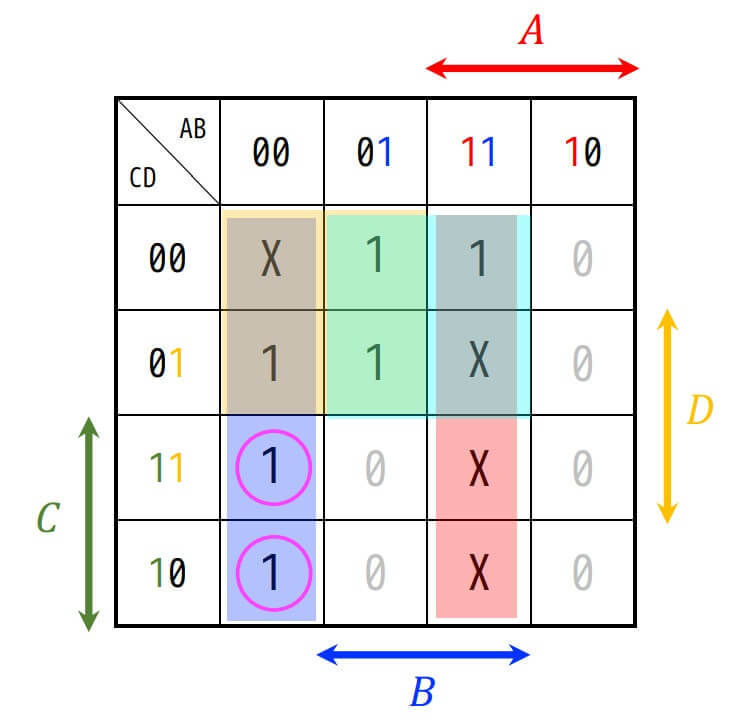
今回の場合、○で囲んだ2箇所が特異最小項に該当する。

 

特異最小項を論理変数で表すと \( \bar{A} \bar{B} CD \), \( \bar{A} \bar{B} C \bar{D} \) となる。

(5)

必須主項は、特異最小項が含まれている主項を表す。

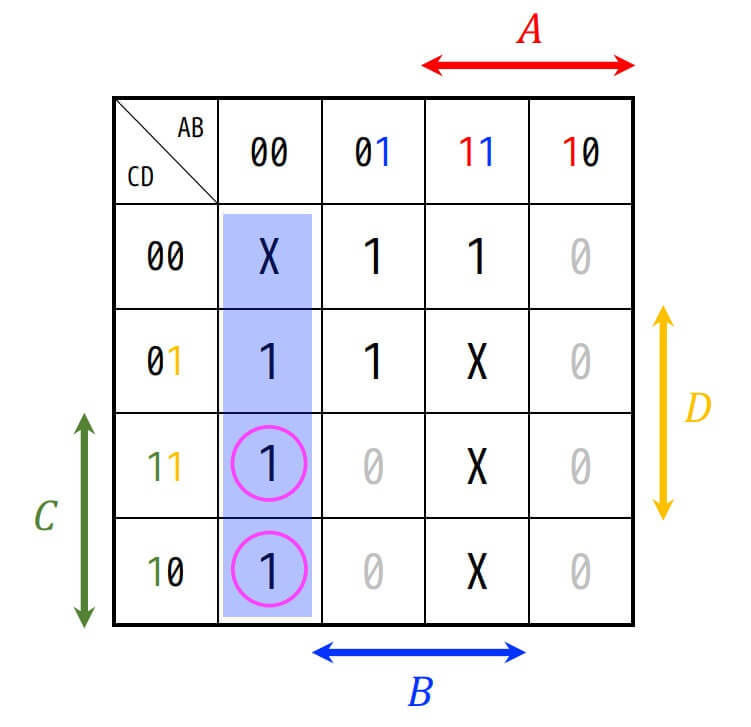
今回の場合は、\( \bar{A} \bar{B} \) だけとなる。

(6)

まだ囲われていない1がないかどうかを確認します。

今回はまだ3つも残っているため、残りの主項 \( AB \), \( \bar{A} \bar{C} \), \( B \bar{C} \) の中からなるべく主項の数が少なく、かつ単純な（大きく囲える）主項を選びます。

今回は、\( B \bar{C} \) を選べば、主項の数が少なく、かつ単純な論理式にすることができます。

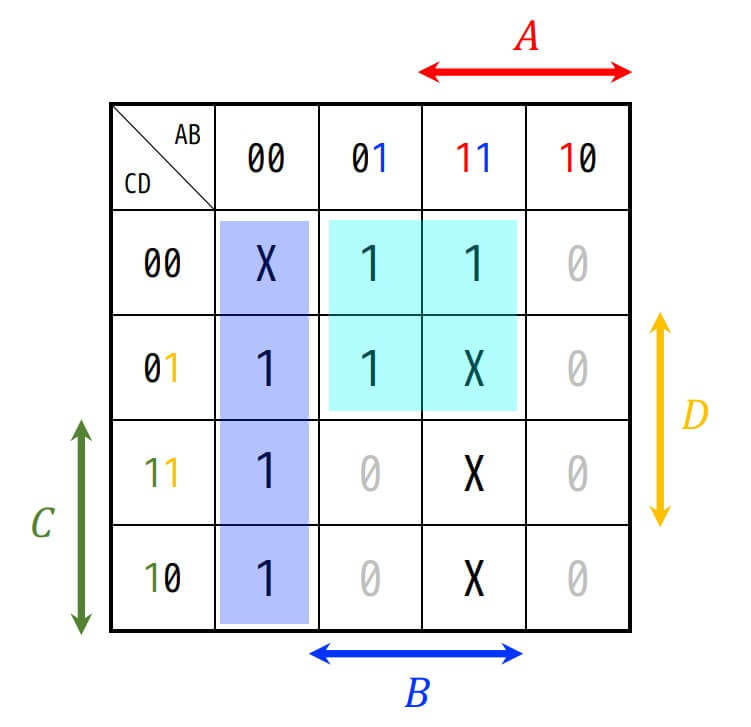
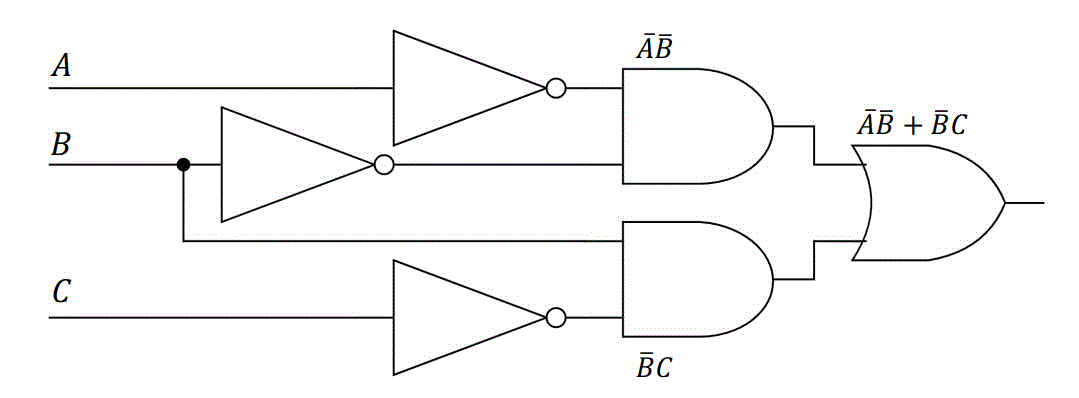
よって簡単科された論理関数は必須主項である \( \bar{A} \bar{B} \) と、最後に選んだ主項 \( B \bar{C} \) の合計2つの論理和で表されます。よって答えは\[ X = \bar{A} \bar{B} + B \bar{C} \] となる。

(7)

おまけ問題。前回の論理関数の基本を使う。

\( \bar{A} \bar{B} + B \bar{C} \) の論理回路は、下のようになる。

論理回路の書き方などについては、こちらにまとめているので、もしわからなければこちらのサイトをご覧ください。

www.momoyama-usagi.com

 

 

６．さいごに

今回は、2変数〜4変数（特に4変数）を人間がわかりやすく単純化するカルノー図についてまとめました。

 

5変数以上の簡略化の場合は、カルノー図ではなく、クワインーマクラスキー法などを使うことが多いです。